Содержание:
- § 1 Усеченная пирамида в повседневности
- § 2 Площадь боковой поверхности правильной усеченной пирамиды
§ 1 Усеченная пирамида в повседневности
На уроке мы рассмотрим усеченную пирамиду, а именно правильную усеченную пирамиду. Разберем свойства усеченной пирамиды и докажем теорему о площади боковой поверхности правильной усеченной пирамиды.
Если посмотреть на купюру 1 доллар, то можно увидеть на ней пирамиду, разделенную на две части, таким же образом как мы поступили сейчас с вами, проводя сечение параллельное основанию пирамиды. Загадка, не иначе. Для чего и зачем это сделано. Догадок много. И в данном случае прослеживается желание наделить бумагу магической силой пирамид, еще и усилив ее масонским символом в вершине. Как повествует одна мудрая пословица «если бы не строители пирамид, кто бы знал имена фараонов». Попробуйте найти еще примеры усеченной пирамиды, и вы будете удивлены своим находкам.
§ 2 Площадь боковой поверхности правильной усеченной пирамиды
Прежде чем говорить о свойствах правильной усеченной пирамиды напомним ее определение. Усеченная пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью, параллельной основанию. Основания правильной усеченной пирамиды – правильные многоугольники, а боковые грани – равнобедренные трапеции. Высоты этих трапеций называются апофемами. Площадью боковой поверхности усеченной пирамиды называется сумма площадей ее боковых граней.
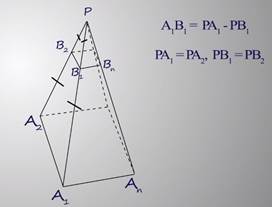
Думаю, Вы заметили, одно из утверждений требует доказательства. Боковые грани правильной усеченной пирамиды равнобедренные трапеции. Докажем этот факт. Рассмотрим боковую грань пирамиды – равнобедренный треугольник РА1А2 с боковыми сторонами РА1 и РА2. Отрезок В1В2 в этом треугольнике параллелен основанию, а значит, мы можем рассматривать два подобных треугольника А1А2 и РВ1В2, оба они равнобедренные. Выразим сторону А1В1, она равна разности РА1 и РВ1, а так как РА1=РА2, и РВ1=РВ2, то разность примет вид: РА2 – РВ2, а это есть отрезок А2В2. Приравняем начало и конец данного рассуждения и получим А1В1=А2В2, что и требовалось доказать! Боковые грани правильной усеченной пирамиды являются равнобедренными трапециями.
Раз мы доказали, что боковые грани правильной усеченной пирамиды равнобедренные трапеции, то мы сможем с легкостью вывести формулу для вычисления площади боковой поверхности такого многогранника. Площадь одной грани находится как полусумма ребер оснований умноженная на апофему. Просуммируем все грани и вынесем за скобки общий множитель ½ апофемы. В скобках получится сумма ребер верхнего основания и сумма ребер нижнего основания, что является их периметрами. Множитель ½ из суммы периметров сделает полусумму периметров и формула примет готовый вид. Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему.
Мы с вами справились с доказательствами утверждений и выводом очень важной формулы применяемой при решении задач.
Список использованной литературы:
- Геометрия. 10 – 11 классы : учебник для общеобразоват. учреждений : базовый и профил. уровни / [ Л. С. Атанасян, В. Ф. Бутузов, С.Б. Кадомцев и др.]. – 22-е изд. – М. : Просвещение, 2013. – 255 с. : ил. – (МГУ – в школе)
- Учебно – методическое пособие в помощь школьному учителю. Составитель Яровенко В.А. Поурочные разработки по геометрии к учебному комплекту Л. С. Атанасяна и др. ( М. : Просвещение) 10 класс
- Рабинович Е. М. Задачи и упражнения на готовых чертежах. 10 – 11 классы. Геометрия. – М. : Илекса , 2006 . – 80 с.
- М. Я Выгодский Справочник по элементарной математике М.: АСТ Астрель , 2006. – 509с.
- Аванта+. Энциклопедия для детей. Том 11. Математика 2-е изд., перераб.— М.: Мир энциклопедий Аванта+: Астрель 2007. — 621 с. Ред. коллегия: М. Аксёнова, В. Володин, М.Самсонов.
Использованные изображения:
Боковая поверхность правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему:
Sбок=1/2(p1+ p2) a
где р1 и р2 – периметры оснований, а– апофема ( высота боковой грани)
Полусумму периметров оснований найти очень просто. Каждое из них имеет 3 стороны, поэтому
3·(3+11):2= 42:2=21 см
Боковая грань правильной усеченной пирамиды – равнобедренная трапеция.
Апофему найдем по теореме Пифагора из треугольника, в котором боковаое ребро – гипотенуза, апофема и полуразность оснований трапеции – катеты.
h²=5² -( (11-3):2)²=5²-4²=9
h=√ 9=3 см
Sбок=21·3=63 см²
Материал урока.
На прошлых уроках
мы работали с пирамидами. Давайте вспомним, какой многогранник называется
пирамидой, что такое правильная пирамида, вспомним свойства правильной пирамиды.
Многогранник, составленный из -угольника и
треугольников, называется пирамидой.
Пирамида называется правильной,
если ее основание – правильный многоугольник.
Площадь боковой поверхности правильной
пирамиды равна половине произведения периметра основания на апофему.
Все боковые ребра правильной пирамиды
равны, а боковые грани являются равными равнобедренными треугольниками.
Пусть нам дана
пирамида PA1A2…An. Проведем секущую плоскость β,
параллельную плоскости основания пирамиды и пусть эта плоскость пересекает
боковые ребра в точках B1,B2,…,
Bn.
Плоскость β
разбивает пирамиду на две фигуры: пирамиду PB1B2…Bn и многогранник. Многогранник, гранями которого являются n-угольники A1A2…An и B1B2…Bn, расположенные в параллельных плоскостях и n четырехугольников A1A2B2B1, A2A3B3B2,…, AnA1B1Bn называется
усеченной пирамидой.
Вокруг нас много
примеров усеченных пирамид. Вытяжка над кухонной плитой имеет форму усеченной
пирамиды.клавиши клавиатуры и другие предметы.
N-угольники
A1A2…An и B1B2…Bn называются соответственно верхним и нижним основанием.
Четырехугольники A1A2B2B1, A2A3B3B2,…, AnA1B1Bn называются боковыми
гранями.
Отрезки A1B1,…, AnBn называются боковыми рёбрами
усеченной пирамиды.
Усеченную пирамиду
обозначают так A1A2…AnB1B2…Bn. Возьмем на верхнем основании произвольную
точку C и из этой точки опустим перпендикуляр на нижнее
основание. Этот перпендикуляр называется высотой усеченной пирамиды.
Теперь давайте
докажем, что боковые грани усеченной пирамиды – это трапеции.
Для доказательства
рассмотрим грань A1A2B2B1. Понятно,
что для других боковых граней доказательство будет проводится аналогично.
Поскольку секущая
плоскость проводилась параллельно плоскости основания, то можно записать, что A1A2
параллельно B1B2.
Очевидно, что две другие стороны четырехугольника A1A2B2B1 не параллельны (они пересекаются в точке P). Получаем, что этот четырехугольник – трапеция. Очевидно,
что все остальные боковые грани тоже будут трапециями.
Как и в случае с
пирамидой, усеченная пирамида тоже может быть правильной.
Усеченная пирамида
называется правильной, если она получена сечением правильной пирамиды
плоскостью, параллельной основанию.
Основаниями
усеченной пирамиды являются правильные многоугольники, а боковые грани –
равнобедренные трапеции.
Высоты этих трапеций
называются апофемами.
Объединение боковых граней называется боковой
поверхностью усеченной пирамиды, а объединение всех граней называется полной
поверхностью усеченной пирамиды. Тогда площадью боковой поверхности
пирамиды называется сумма площадей ее боковых граней.
А площадью полной поверхности пирамиды называется
сумма площадей всех ее граней.
Теперь давайте
сформулируем и докажем теорему о площади боковой поверхности правильной
усеченной пирамиды.
Площадь боковой
поверхности правильной усеченной пирамиды равна произведению полусуммы
периметров основания на апофему.
Доказательство.
Запишем формулу для
нахождения площади боковой поверхности усеченной пирамиды.
Поскольку усеченная
пирамида правильная, значит, ее гранями будут равнобедренные трапеции.
Площадь равнобедренной
трапеции равна произведению полусуммы оснований на высоту. Высота боковой грани
есть ничто иное как апофема усеченной пирамиды.
Подставим все в
исходную формулу, вынесем половину апофемы за скобки, а в скобках сгруппируем
стороны по основаниям. Тогда получим, что площадь боковой поверхности будет
равна произведению полусуммы периметров оснований усеченной пирамиды на
апофему.
Что и
требовалось доказать.
Решим несколько
задач.
Задача. Стороны
оснований правильной усеченной четырехугольной пирамиды равны
и
. Высота пирамиды
равна . Найти площадь
боковой поверхности.
Решение.
Ответ. 120
см2
Решим еще одну
задачу.
Задача. Пирамида
пересечена плоскостью, параллельной основанию. Доказать что боковые ребра и
высота пирамиды делятся этой плоскостью на пропорциональные части.
Решение.
Что и
требовалось доказать.
Решим еще одну
задачу.
Задача. Правильная
треугольная пирамида с высотой
и стороной основания
равной рассечена плоскостью
, проходящей через
середину высоты
параллельно
основанию . Найти площадь
боковой поверхности полученной усеченной пирамиды.
Решение.
Ответ.
135 см2.
Подведем итоги
урока. Сегодня на уроке мы познакомились с такими понятиями как усеченная
пирамида, правильная усеченная пирамида. Рассмотрели свойства правильной
усеченной пирамиды. Решили несколько задач.
Слайд 2УСЕЧЕННАЯ ПИРАМИДА
Плоскость параллельная основанию пирамиды, разбивает её на два многогранника. Один
из них является пирамидой, а другой называется усечённой пирамидой.
Усеченная пирамида – это часть полной пирамиды, заключенная между её основанием и секущей плоскостью, параллельной основанию данной пирамиды
Слайд 3ПОНЯТИЕ УСЕЧЕННОЙ ПИРАМИДЫ
ОСНОВАНИЯ
С
Н
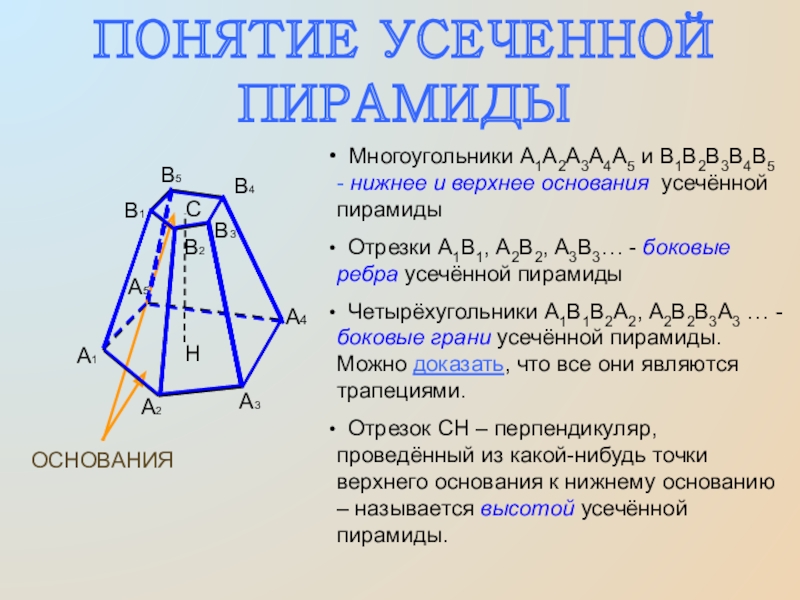
Многоугольники А1А2А3А4А5 и В1В2В3В4В5 – нижнее и верхнее
основания усечённой пирамиды
Отрезки А1В1, А2В2, А3В3… – боковые ребра усечённой пирамиды
Четырёхугольники А1В1В2А2, А2В2В3А3 … – боковые грани усечённой пирамиды. Можно доказать, что все они являются трапециями.
Отрезок СН – перпендикуляр, проведённый из какой-нибудь точки верхнего основания к нижнему основанию – называется высотой усечённой пирамиды.
Слайд 4ПРАВИЛЬНАЯ УСЕЧЕННАЯ ПИРАМИДА
Усеченная пирамида называется правильной, если она получена сечением
правильной пирамиды плоскостью, параллельной основанию.
Основания – правильные многоугольники .
Боковые грани – равные равнобедренные трапеции.
Высоты этих трапеций называются апофемами.
Слайд 5ПРАВИЛЬНАЯ ПИРАМИДА
Пирамида называется правильной, если её основание – правильный многоугольник,
а отрезок , соединяющий вершину с центром основания, является её высотой.
Все боковые рёбра правильной пирамиды равны, а грани являются равными равнобедренными треугольниками.
Высота боковой грани правильной пирамиды называется апофемой. Все апофемы правильной пирамиды равны друг другу.
Слайд 6ПИРАМИДА
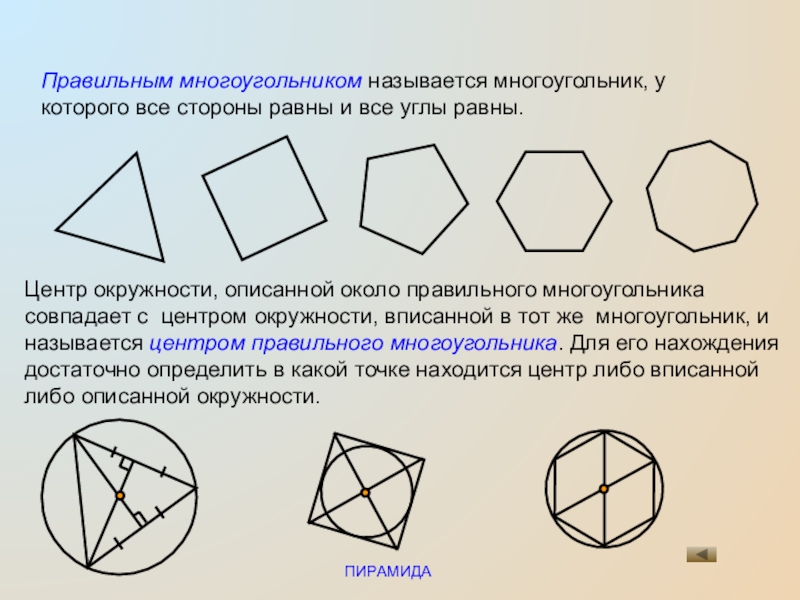
Правильным многоугольником называется многоугольник, у которого все стороны равны и все
углы равны.
Центр окружности, описанной около правильного многоугольника совпадает с центром окружности, вписанной в тот же многоугольник, и называется центром правильного многоугольника. Для его нахождения достаточно определить в какой точке находится центр либо вписанной либо описанной окружности.
Слайд 7ПИРАМИДА
СОДЕРЖАНИЕ
УСЕЧЕННЫЕ ПИРАМИДЫ
Слайд 8 Площадью полной поверхности пирамиды (Sполн) пирамиды называется сумма площадей всех
её граней: основания и всех боковых граней.
Sполн =Sбок+Sосн
Площадью боковой поверхности (Sбок) пирамиды называется сумма площадей её боковых граней.
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему. (Доказательство на следующем слайде)
Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров оснований на апофему.
ПЛОЩАДЬ ПОВЕРХНОСТИ УСЕЧЁННОЙ ПИРАМИДЫ
Sполн.усеч .= Sбок + Sверхн.осн. + Sнижн.осн.
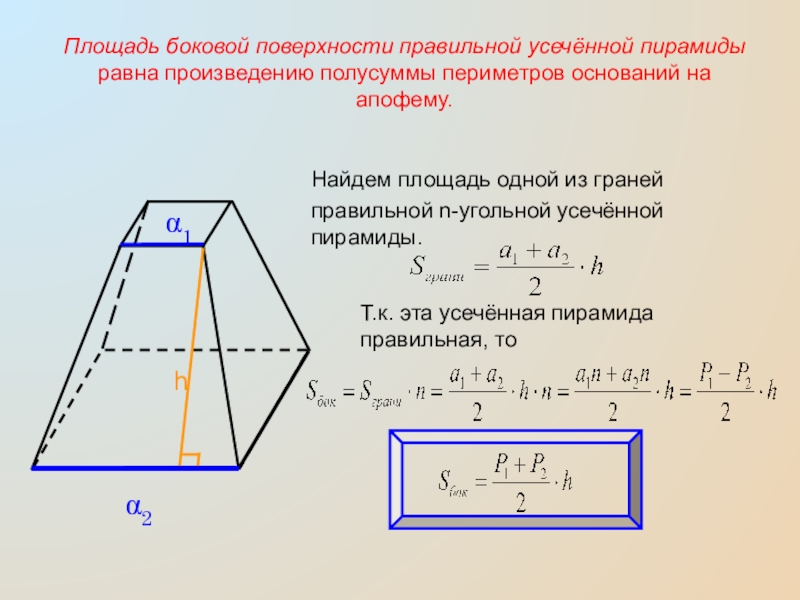
Слайд 9Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров оснований
на апофему.
Найдем площадь одной из граней правильной n-угольной усечённой пирамиды.
α2
α1
h
Т.к. эта усечённая пирамида правильная, то
Теорема
Площадь
боковой поверхности правильной усеченной
пирамиды равна произведению полусуммы
периметров основания на апофему.
Доказательство
Если
сторона основания а, число сторон n,
то боковая поверхность пирамиды равна:
Где
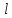-апофема,
а
-периметр
основания пирамиды. Теорема доказана.
Призма
Рассмотрим
два разных многоугольника А1А2…An
и B1B2…Bn
расположенны в параллельных плоскостях
α
и β так, что отрезки А1B1,
А2B2,
…, AnBn,
соединяющие соответственные вершины
многоугольников, параллельны. Каждый
из n-четырехугольников
А1А2B2B1,
A2A3B3B2,
AnA1B1Bn
Является
параллелограм, так как имеет попарно
параллельные противоположные стороны.
Например, в четырехугольнике А1А2B2B1
стороны А1B1
и А2B2
параллельны
по условию, а стороны А1А2
и B2B1
по
свойству параллельных плоскостей,
пересечены третьей плоскостью.
Многогранник,
составленный из двух равных многоугольников
А1А2…Аn
и В1В2…Вn,
расположенных а параллельных плоскостях,
и n-параллелограмов,
называется призмой.
Многоугольники
А1А2…Аn
и В1В2…Вn
называются
основаниями, а параллелограмы –
боковыми гранями призмы. Отрезки А1В1,
А2В2,
AnBn
называются боковыми ребрами призмы.
Эти ребра как противоположные стороны
параллелограмов, последовательно
приложенных друг к другу, равны и
параллельны.Призму с основаниями А1А2…Аn
и В1В2…Вn
обозначают
А1А2…АnВ1В2…Вn
и называют n-угольной
призмой.
Перпендикуляр,
проведенный из какой-нибуть точки одного
основания к плоскости другого основания,
называется высотой призмы.
Если
боковые ребра призмы перпендикулярны
к основаниям ,то призма называется
прямой, в противном случае – наклонной.
Высота прямой призмы равна её боковому
ребру.
Прямая
призма называется правильной, если её
основания – правильные многоугольники.
У такой призмы все боковые грани –
равные прямоугольники.
Площадью
полной поверхности призмы называется
сумма всех её граней, а площадью боковой
поверхности призмы – сумма площадей
её боковых граней. Площадь Sполн
полной
поверхности выражается через площадь
Sбок
боковой поверхноси и площадь Sосн
основания призмы форулой
Sбок+2Sосн
Докажем
теорему о площади поверхности прямой
призмы.
Теорема
Площадь
боковой поверхности призмы равна
произведению периметра основания на
высоту призмы.
Доказательство
Боковые
грани прямой призмы – прямоугольники,
основания которых – стороны основания
призмы, а высоты равны высоте h
призмы, Площадь боковой поверхности
призмы равна сумме площадей указанных
прямойгольников, т.е. равна сумме
произведений сторон основания на высоту
h.
Вынося множитель h
за скобку, получим в скобках сумму сторон
основания призмы, т.е. его периметр Р.
Итак, Sбок=Ph.
Теорема доказана.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
