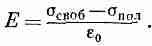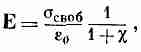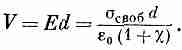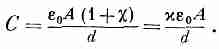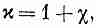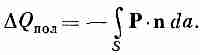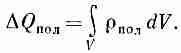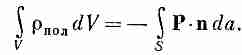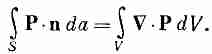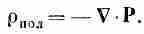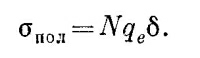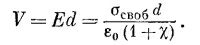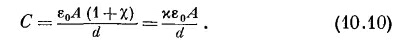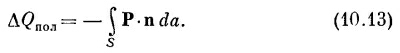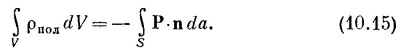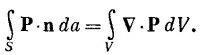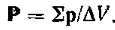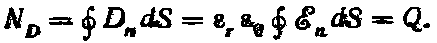Как найти поляризационный заряд

Посмотрим теперь,
что дает эта модель для конденсатора с
диэлектриком. Рассмотрим сначала лист
материала, в котором на единицу объема
приходится дипольный момент Р. Полу­чится
ли в результате в среднем какая-нибудь
плотность заря­дов? Нет, если Р
постоянен.

Если
положительные и отрицательные заряды,
смещенные относительно друг друга,
имеют одну и ту же среднюю плот­ность,
то сам факт их смещения не приводит к
появлению сум­марного заряда внутри
объема. С другой стороны, если бы Р в
одном месте был больше, а в другом меньше,
то это означало бы, что в некоторые
области попало больше зарядов, чем
отту­да вышло; тогда мы бы могли
получить объемную плотность за­ряда.
В случае плоского конденсатора
предположим, что Р — величина постоянная,
поэтому достаточно будет только
посмот­реть, что происходит на
поверхностях. На одной поверхности
отрицательные заряды (электроны)
эффективно выдвинулись на расстояние
,
а на другой поверхности они сдвинулись
внутрь, оставив положительные заряды
снаружи на эффективном расстоянии .
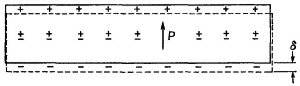
Возникает, как показано на фиг. 10.5,
поверх­ностная плотность зарядов,
которую мы будем называть поляризационным
зарядом.

Э

тот
заряд можно подсчитать следующим
образом. Если пло­щадь пластинки равна
А, то
число электронов, которое ока­жется
на поверхности, есть произведение А
и N
(числа
электро­нов на единицу объема), а также
смещения S,
которое,
как мы предполагаем, направлено
перпендикулярно к поверхности. Полный
заряд получится умножением на заряд
электрона q_e
.
Чтобы
найти поверхностную плотность
поляризационных за­рядов, индуцируемую
на поверхности, разделим на А.
Вели­чина
поверхностной плотности зарядов равна

Но
она равна как раз длине Р
вектора
поляризации Р [формула (10.4)]:

Фиг.
10.5. Диэлектрик в однородном поле.
Положительные заряды сместились на
расстояние 
относи­тельно отрицательных.

(10.5)

Поверхностная
плотность зарядов равна поляризации
внутри материала. Поверхностный заряд,
конечно, на одной поверх­ности
положителен, а на другой отрицателен.

Предположим
теперь, что наша пластинка служит
диэлектри­ком в плоском конденсаторе.
Пластины
конденсатора
также име­ют поверхностный заряд
(который мы обозначим _своб,
потому что заряды в проводнике могут
двигаться «свободно» куда угодно).
Конечно, это тот самый заряд, который
мы сообщили конденсатору при его зарядке.
Следует подчеркнуть, что _пол
существует
только благодаря _своб.
Если, разрядив конденсатор, удалить
_своб,
то _пол
также исчезнет, но он не стечет по
проволо­ке, которой разряжают
конденсатор, а уйдет назад внутрь
ма­териала, за счет релаксации
поляризации в диэлектрике.

Т

еперь
мы можем применить теорему Гаусса к
поверхности S,
изображенной
на фиг. 10.1. Электрическое поле Е
в
диэлект­рике равно полной
поверхностной
плотности зарядов, деленной на ₀.
Очевидно, что _пол
и _своб
имеют разные знаки, так что

(10.6)

З

аметьте,
что поле Е₀
между
металлической пластиной и по­верхностью
диэлектрика больше поля Е;
оно
соответствует только _своб.
Но нас здесь интересует поле внутри
диэлектрика, которое занимает почти
весь объем, если диэлектрик заполняет
почти весь промежуток между пластинами.
Используя формулу (10.5), можно написать

(10.7)

Из этого уравнения
мы не можем определить электрическое
поле, пока не узнаем, чему равно Р. Здесь
мы, однако, предпо­лагаем, что Р зависит
от Е и, более того, пропорционально Е.
Эта пропорциональность обычно записывается
в виде

(10.8)

Постоянная

(греческое «хи») называется диэлектрической
вос­приимчивостью диэлектрика.

Т

огда
выражение (10.7) приобретает вид

(10.9)

откуда
мы получаем множитель 1/(1+),
показывающий, во сколько раз уменьшилось
поле.

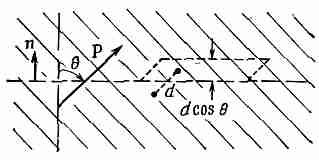
Фиг. 10.6. Количество ааряда,
прошедшее через элемент вообра­жаемой
поверхности в диэлект­рике,
пропорционально компонен­те Р,
нормальной к поверхности.

Н

апряжение
между пластинами есть интеграл от
электри­ческого поля. Раз поле
однородно, интеграл сводится просто к
произведению Е
и
расстояния между пластинами d.
Мы
по­лучаем

П

олный
заряд конденсатора есть _своб
А, так
что емкость, определяемая формулой
(10.2), оказывается равной

(10.10)

Мы объяснили
явление, наблюдавшееся на опыте. Если
заполнить плоский конденсатор
диэлектриком, емкость возрастает на
множитель

(10.11)

который характеризует
свойства данного материала. Наше
объяснение останется, конечно, неполным,
пока мы не объясним (а это мы сделаем
позже), как возникает атомная поляризация.

Обратимся теперь
к чуть более сложному случаю — когда
поляризация Р не всюду одинакова. Мы
уже говорили, что если поляризация
непостоянна, то вообще может возникнуть
объемная плотность заряда, потому что
с одной стороны в ма­ленький элемент
объема может войти больше зарядов, чем
вый­дет с другой. Как определить,
сколько зарядов теряется или приобретается
в маленьком объеме?

Подсчитаем
сначала, сколько зарядов проходит через
вооб­ражаемую плоскость, когда материал
поляризуется. Коли­чество заряда,
проходящее через поверхность, есть
просто Р,
умноженное
на площадь поверхности, если поляризация
направлена по нормали
к
поверхности. Разумеется, если поля­ризация
касательна,
к
поверхности, то через нее не пройдет ни
одного заряда.

Продолжая
прежние рассуждения, легко понять, что
коли­чество заряда, прошедшее через
любой элемент поверхности, пропорционально
компоненте
Р,
перпендикулярной
к
поверх­ности. Сравним фиг. 10.6 и 10.5. Мы
видим, что уравнение (10.5) в общем случае
должно быть записано так:

(10.12)

Фиг. 10.7. Неоднородная поляризация Р
может приво­дить к появлению
результиру­ющего заряда внутри
диэлек­трика.

Если
мы имеем в виду воображаемый элемент
поверхности внутри
диэлектрика,
то формула (10.12) дает заряд, который
прошел через поверхность, но не приводит
к результирующему поверхностному
заряду, потому что возникают равные и
про­тивоположно направленные вклады
от диэлектрика по обе стороны поверхности.

О

днако
смещение зарядов может привести к
появлению объемной
плотности
зарядов. Полный заряд, выдвинутый из
объема V
за счет
поляризации, есть интеграл от внешней
нор­мальной составляющей Р по
поверхности S,
охватывающей
объем (фиг. 10.7). Такой же излишек зарядов
противоположного знака остается внутри.
Обозначая суммарный заряд внутри F
через
Q_пол,
запишем

(10.13)

М

ы
можем отнести Q_пол
за счет объемного распределения
заряда с плотностью _пол,
так что

(10.14)

Комбинируя оба
уравнения, получаем

(10.15)

Мы получили разновидность теоремы
Гаусса, связывающую плотность заряда
поляризованного материала с вектором
поля­ризации Р. Мы видим, что она
согласуется с результатом, полученным
для поверхностного поляризационного
заряда или же для диэлектрика в плоском
конденсаторе. Уравнение (10.15) с гауссовой
поверхностью S, изображенной
на фиг. 10.1, дает в правой части интеграл
по поверхности, равный РA,
а в левой части заряд внутри объема
оказывается _пол
A, так
что мы снова получаем =Р.

Т

очно
так же, как мы делали в случае закона
Гаусса для электростатики, мы можем
перейти в уравнении (10.15) к диф­ференциальной
форме, пользуясь математической теоремой
Гаусса:

Мы получаем

(10.16)

Если поляризация неоднородна, ее
дивергенция определяет появляющуюся
в материале результирующую плотность
заря­дов. Подчеркнем, что это совсем
настоящая плотность зарядов; мы
называем ее «поляризационным зарядом»,
только чтобы помнить, откуда она взялась.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Главная >> Фейнмановские лекции по физике >> Том 5 >> Глава 10. Диэлектрики

Поляризационные заряды

Посмотрим теперь, что дает эта модель для конденсатора с диэлектриком. Рассмотрим сначала лист материала, в котором на единицу объема приходится дипольный момент Р. Получится ли в результате в среднем какая-нибудь плотность зарядов? Нет, если Р постоянен.

 

Но она равна как раз длине Р вектора поляризации Р [формула  (10.4)]:

 

 

Заметьте, что поле Е₀ между металлической пластиной и поверхностью диэлектрика больше поля Е; оно соответствует только σ_своб. Но нас здесь интересует поле внутри диэлектрика, которое занимает почти весь объем, если диэлектрик заполняет почти весь промежуток между пластинами. Используя формулу (10.5), можно написать

 

Из этого уравнения мы не можем определить электрическое поле, пока не узнаем, чему равно Р. Здесь мы, однако, предполагаем, что Р зависит от Е и, более того, пропорционально Е. Эта пропорциональность обычно записывается в виде

 

 

 

Полный заряд конденсатора есть σ_своб  А, так что емкость, определяемая  формулой  (10.2),   оказывается  равной

 

Мы объяснили явление, наблюдавшееся на опыте. Если заполнить плоский конденсатор диэлектриком, емкость возрастает на множитель             .                                                  

 

Продолжая прежние рассуждения, легко понять, что количество заряда, прошедшее через любой элемент поверхности, пропорционально компоненте Р, перпендикулярной к поверхности. Сравним фиг. 10.6 и 10.5. Мы видим, что уравнение (10.5) в общем случае должно быть записано так:

 

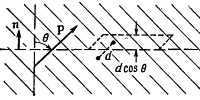
Если мы имеем в виду воображаемый элемент поверхности внутри диэлектрика, то формула (10.12) дает заряд, который прошел через поверхность, но не приводит к результирующему поверхностному заряду, потому что возникают равные и противоположно направленные вклады от диэлектрика по обе стороны поверхности.

Однако смещение зарядов может привести к появлению объемной плотности зарядов. Полный заряд, выдвинутый из объема V за счет поляризации, есть интеграл от внешней нормальной составляющей Р по поверхности S, охватывающей объем (фиг. 10.7). Такой же излишек зарядов противоположного знака остается внутри. Обозначая суммарный заряд внутри V через ΔQ_пол,  запишем

 

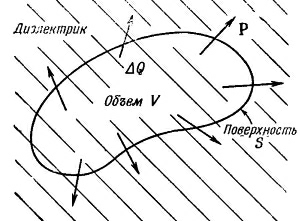
Мы  можем  отнести  ΔQ_пол  за счет объемного распределения заряда с плотностью ρ_пол, так что

 

Комбинируя оба уравнения, получаем

 

 

Мы получаем

 

Если поляризация неоднородна, ее дивергенция определяет появляющуюся в материале результирующую плотность зарядов. Подчеркнем, что это совсем настоящая плотность зарядов; мы называем ее «поляризационным зарядом», только чтобы помнить, откуда она взялась.

СМОТРИТЕ ТАКЖЕ:

Социальные комментарии Cackle

Векторы поляризованности и смещения

В предыдущей статье было показано, что вследствие поляризации диэлектрика, т. е. смещения его связанных зарядов, изменяется напряженность электрического поля. Результирующее влияние диэлектрика на электрическое поле оценивают векторной величиной, называемой поляризованностью Р (вектором поляризации).

Средняя интенсивность поляризации P_ср определяется как сумма дипольных моментов в единице объема диэлектрика, а чтобы найти поляризованность в данном месте поля, надо выбрать достаточно малый объем ΔV:

Единица измерения поляризованности

[P] = [ql/V] = Кл*м/м 3 = Кл/м 2.

Вектор поляризации направлен навстречу вектору напряженности электрического поля связанных зарядов E_п.(рис. 4.12).
Вектор поляризации для большинства диэлектриков (за исключением группы сегнетоэлектриков) пропорционален напряженности электрического поля:

и его направление совпадает с направлением внешнего E_вн и результирующего Е полей (риc. 4.12).

Коэффициент k называется электрической восприимчивостью диэлектрика и характеризует его способность поляризоваться.

При расчетах электрических полей в диэлектриках с различными диэлектрическими проницаемостями пользуются еще вектором электрического смещения.

Электрическое смещение D связано с напряженностью электрического ноля простым соотношением

откуда можно определить единицу намерения электрического смещения:

которая такая же, как у вектора, поляризации и у поверхностной плотности зарядов на электродах.

Электрическое смещение и поверхностная плотность свободных зарядов численно одинаковы на поверхности всех проводящих тел, находящихся в электростатическом поле. Например, у внутренней поверхности пластины плоского конденсатора (рис. 4.8) напряженность однородного электрического поля, как и в любой точке однородного поля (4.10),

а электрическое смещение в любой точке поля, в том числе и у металлической поверхности,

т. е. совпадает с поверхностной плотностью заряда на пластине.

Из (2а) следует, что при заданной плотности поверхностных свободных зарядов на электродах электрическое смещение в однородном диэлектрике с диэлектрической проницаемостью ε_a не зависит от ε_a, а напряженность электрического поля зависит. Поэтому можно сказать, что на напряженность электрического поля определяется и свободными (на электродах) и связанными (в диэлектриках) зарядами, т. е. поляризацией диэлектрика, а электрическое смещение в однородном диэлектрике не зависит от связанных зарядов.

Связь между тремя векторными величинами, характеризующими электрическое поле в диэлектрике, выражается равенством

Приняв во внимание (1) и (2), получим

откуда диэлектрическая проницаемость

а электрическая восприимчивость

Рис.1 Поле заряженного шара

Рассмотрим еще неоднородное электрическое поле заряженного металлическою шара (рис. 1), радиус которого R_ш. Известно, что электрический заряд Q находится на поверхности такого шара. Поверхностная плотность заряда

Поле металлического шара с зарядом Q совпадает вне шара с полем равного ему по значению точечного заряда Q, расположенного в центре шара (4.8); поэтому напряженность поля на расстоянии R от центра шара и в частности, у его наружной поверхности, т.е. при R = R_ш,

а электрическое смещение

т. е. равно поверхностной плотности заряда.

Внутри металлического шара поля нет, как и во всяком проводнике в условиях электростатики , Поэтому потенциалы всех точек шара одинаковые, т. е. шар — эквипотенциальное тело, как и всякое металлическое тело в электростатическом поле.

Аналогично потоку вектора напряженности поля (4.7) применяется понятие потока вектора электрического смешения.

Поток вектора смещения N_D в однородном поле равен произведению численного значения вектора смещения D и площадки S, во всех точках которой вектор смещения имеет одинаковое значение и направлен перпендикулярно к ней, т. е.

При неоднородном поле произвольную поверхность площадью S разбивают на элементарные, в пределах каждой на которых смещение одинаково; так что поток вектора
смещения через такую элементарную площадку

где D_n— нормальная составляющая вектора смещения (перпендикулярная к элементарной площадке).

Поток вектора смещения через произвольную замкнутую поверхность находится суммированием элементарных потоков:
Так как D = ε_aE и соответственно D_n = ε_aE_n, то поток вектора смещения

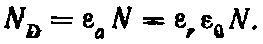
В частности, в случае шаровой поверхности

Таким образом, поток вектора электрического смещения через шаровую поверхность равен заряду, расположенному внутри поверхности.

Полученное выражение N_D = Q справедливо для замкнутой поверхности любой формы, охватывающей заряд как в однородной среде с ε_r = const, так и в среде, диэлектрическая проницаемость которой неодинакова в различных участках среды, например в двухслойном конденсаторе.

На поверхности шара,

откуда определяется электрическое смещение у поверхности шара: что согласуется с (5).

Вектор поляризации

Вы будете перенаправлены на Автор24

Что такое вектор поляризации

Для того, чтобы с количественной точки зрения описать поляризацию диэлектрика, пользуются вектором поляризации (поляризованностью ($overrightarrow

$)), который является электрическим моментом единицы объема диэлектрика:

где $overrightarrow<triangle p>$ — дипольный момент элемента диэлектрика.

В том случае, если диэлектрик состоит из неполярных молекул, то дипольный момент диэлектрика можно разделить на две части: момент каждой молекулы и дипольные моменты всех молекул в единице объема.

Получается, что для неполярных молекул вектор поляризованности можно определить, как:

где суммирование идет относительно всех молекул в объеме $triangle V$. $N$ — концентрация молекул, $overrightarrow$ — индуцированный дипольный момент (Он одинаковый у всех молекул). $overrightarrowuparrow uparrow overrightarrow$.

Формула поляризованности для полярных молекул

Формула поляризованности для полярных молекул имеет вид:

где $leftlangle overrightarrow

rightrangle $ — среднее значение дипольных моментов, которые равны по модулю, но разнонаправлены.

В изотропных диэлектриках средние дипольные моменты совпадают по направлению с напряженностью внешнего электрического поля. У диэлектриков с полярного типа молекулами, вклад в поляризованность от наведенных зарядов много меньше, чем вклад от переориентации поля.

Ионная решеточная поляризации описывается формулой (3). В большинстве случаев такая поляризация является анизотропной.

У электретов (диэлектрические вещества, которые в отсутствии электрического поля долгое время сохраняют поляризованность) и сегнетоэлектриков (диэлектрические вещества, которые при определенных температурах могут спонтанно поляризоваться при отсутствии внешнего электрического поля) поляризованность может быть отлична от нуля даже если $overrightarrow=0.$ У остальных диэлектриков при $overrightarrow=0$, $overrightarrow

=0$. У изотропных диэлектриков поляризованность связана с напряженностью поля в той же точке уравнением (система СИ):

[overrightarrow

=varkappa <varepsilon >_0overrightarrow left(4right),]

где $varkappa $ — диэлектрическая восприимчивость (безразмерная величина).

В анизотропных диэлектриках направление вектора напряженности и вектора поляризации не совпадают. И их связь устанавливается в виде:

где индексы i,j — нумеруют компоненты по осям декартовой системы координат ($i=x, y,z;j=x, y,z. )$), $<varkappa >_$ — тензор диэлектрической восприимчивости.

Зависимость $overrightarrow

(overrightarrow)$ в общем случае представлена в виде:

Формула (6) показывает, что поляризованность зависит не только от первой степени напряженности электрического поля, но и от ее высших степеней. Если зависимость в (6) от высших степеней играет существенную роль, то диэлектрик нелинейный. Подобная нелинейность проявляется в сильных полях, так же существуют некоторые специальные вещества. Если нелинейность не существенна, то используют формулы вида (5).

При неоднородной поляризации, поляризационные заряды могут появляться не только на поверхности диэлектрика, но и в его объеме. Плотность объемных связанных зарядов ($<rho >_$) равна:

Формула (7) показывает, что объемные заряды возникают только в случае неоднородной поляризации. При переходе из одного диэлектрика в другой, поверхностная плотность связанных зарядов ($<sigma >_$) равна:

где $overrightarrow$- единичный вектор нормали, который направлен из первой во вторую среду, $overrightarrow;;overrightarrow$ — векторы поляризации второй и первой среды. Заметим, что вакуум можно рассматривать как диэлектрик, поляризованность которого равна нулю.

Единица измерения $left[Pright]=frac<Кл><м^2>$.

Готовые работы на аналогичную тему

Задание: Чему равна объемная плотность зарядов в диэлектрике, если вектор поляризованности задан функцией: $overrightarrow

=frac<overrightarrow>,$ где $overrightarrow$ — единичный орт, r — модуль радиус-вектора.

Основой для решения задачи служит формула связи плотности объёмных зарядов с вектором поляризации диэлектрика:

В нашем случае, формула (1.1) преобразуется к виду:

Ответ: Объемная плотность зарядов при заданном векторе поляризованности равна нулю.

Задание: Вектор поляризации бесконечной пластины поляризованного диэлектрика задан выражением: $overrightarrow

=overrightarrow(1-frac)$, где $overrightarrow$ — единичный вектор, перпендикулярный пластине, y — расстояние от середины пластины, a — половина толщины пластины. Найдите напряженность электрического поля внутри пластины, разность потенциалов между ее поверхностями.

Вектор напряженности и вектор поляризации направлены в разные стороны.

Основанием для решения задачи выберем уравнение:

Следовательно, если мы знаем закон изменения вектора поляризации из условия задачи, следовательно:

Разность потенциалов может быть найдена, если известен закон изменения напряженности, как:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 04 12 2022

Связь вектора поляризации со связанными зарядами — справочник студента

Рассмотрим плоскопараллельный слой однородного изотропного диэлектрика находящийся в однородном электрическом поле, созданном в вакууме. Пусть вектор напряженности поля составляет угол Q с нормалью. В однородном изотропном диэлектрике вектор поляризации будет направлен по вектору напряженности (рис.39).

В результате поляризации на гранях диэлектрика появятся поляризационные заряды с поверхностной плотностью :

Поверхностная плотность связанных зарядов равна проекции вектора поляризации на направление нормали к поверхности диэлектрика. Физический смысл этой величины в том, что она равна величине заряда, который смещается через единичную площадку в направлении нормали к ней.

Рассмотрим случай диэлектрика с неполярными молекулами, хотя полученные результаты будут справедливы для всех изотропных диэлектриков. Выделим некоторый объем в диэлектрике, ограниченный поверхностью S (рис.40).

Из рис.40 видно, что через те участки поверхности, где напряженность направлена вовнутрь, часть отрицательных зарядов покинет рассматриваемый объем, а через участки, где напряженность направлена наружу, в область войдет дополнительно отрицательный заряд.

Если вошедший и вышедший заряды не равны друг другу, то внутри области

появится объемный поляризационный заряд , а на ее поверхности – поверхностный поляризационный заряд .

• Теорема Остроградского-Гаусса для вектора поляризации: поток вектора поляризации через любую замкнутую поверхность равен полному поляризационному заряду внутри этой поверхности, взятому с противоположным знаком.
• В дифференциальной форме: или
• Физический смысл этого выражения в том, что источниками линий вектора поляризации являются только связанные заряды.
• При поляризации диэлектрика поверхностные поляризационные заряды возникают всегда, а объемные поляризационные заряды могут возникать только в неоднородных диэлектриках или в неоднородных полях.

Типы поляризации диэлектрика

• В отсутствие электрического поля
• При наличии электрического поля

Вектор поляризации (Поляризованность) P– векторная характеристика поляризации вещества, равная сумме дипольных моментов молекул вещества, занимающего единичный объём.

Дипольный момент молекулы параллелен и пропорционален напряжённости электрического поля:

где β – поляризуемостьмолекулы. здесь N – число молекул, n – концентрация. Обозначим – диэлектрическая восприимчивость вещества;

В поляризованном диэлектрике на его краях образуются связанные заряды. Каждый из связанных зарядов входит в состав диполя. σсв— поверхностная плотность связанных зарядов. Установим связь между поверхностной плотностью связанных зарядов (σсв) и вектором поляризации( ⃗P ). Вид сбоку на пластину диэлектрика. ⃗E⊥пластине

1. В общем случае σсв =Pn
2. Поверхностная плотность связанных зарядов равна проекции вектора поляризации на
3. внешнюю нормаль (Pn) к поверхности диэлектрика.
4. Теорема Остроградского-Гаусса для вектора Р: поток поляризованности сквозь произвольную замкнутую поверхность равен сумме связанных зарядов, охваченной этой поверхностью, взятой с обратным знаком.

Сторонние и связанные заряды диэлектрика. Вывод теоремы Остроградского-Гаусса для поля в диэлектрике. Вектор электрического смещения н его связь с напряженностью поля. Диэлектрическая проницаемость вещества. Третье уравнение Максвелла.

Сторонние заряды – это заряды, расположенные за пределами диэлектрика, а также заряды, которые хотя и находятся в пределах диэлектрика, но не входят в состав его молекул.

Связанные заряды – это заряды, входящие в состав атомов и молекул диэлектрика. Под действием поля они могут лишь немного смещаться из своих положений равновесия. Плотность связанных зарядов равна по абсолютной величине проекции поляризованности на направление внешней нормали рассматриваемой поверхности

• ТеоремаОстроградского-Гаусса утверждает: поток вектора напряженности электростатического полячерез произвольную замкнутую поверхностьпрямо пропорционален алгебраической сумме свободных зарядов, расположенных внутри этой поверхности.
• – электрическое смещение (электрическая индукция);
• — теорема Остроградского-Гаусса для электрического смещения: поток вектора электрического смещения сквозь произвольную замкнутую поверхность равен сумме свободных зарядов, охваченных этой поверхностью.
• D – это вспомогательная векторная характеристика электрического поля, помогающая расчёту E.Связь напряженности (Е) и вектора электрического смещения (D)
• Где ε- Относительнаядиэлектри́ческаяпроница́емость среды.

Относительнаядиэлектри́ческаяпроница́емость среды — физическая величина, характеризующая свойства изолирующей (диэлектрической) среды и показывающая, во сколько раз сила взаимодействия двух электрических зарядов в этой среде меньше, чем в вакууме. Значение ε вакуума равно единице, для реальных сред ε > 1. Для воздуха и большинства других газов в нормальных условиях значение ε близко к единице в силу их низкой плотности. Электрическая постояннаяε0 ≈ 8.85·10−12 Ф/м

Третье уравнение Максвелла определяет источники электрического поля. Физический смысл этого уравнения состоит в том, что электрическое поле в некоторой области пространства связано с электрическим зарядом внутри этой поверхности.

Дата добавления: 2016-07-05; просмотров: 2788;

Вектор поляризации. Его связь с поверхностной плотностью связанных зарядов

⇐ ПредыдущаяСтр 26 из 42Следующая ⇒

Вектор поляризации.
Количественное	описание	производится	с	помощью	вектора
поляризации.	Когда внешнего поля нет, суммарный дипольный момент

равен нулю (исключение составляют сегнетоэлектрики, электреты). Под влиянием внешнего электрического поля возникает поляризация, которую характеризуем дипольным моментом единицы объема — вектором

поляризации P :	
p
V
P 	(2.2.1)
V
	
Здесь	p дипольный	момент	молекулы.	Размерность	вектора	поляризации	равна	P	q	,	которая
	L2	

совпадает с размерностью напряженности электрического поля.

Естественно, что вектор поляризации зависит от внешнего поля, как и наведенный поляризационный заряд (связанный). Поляризация приводит к появлению индукционного связанного заряда на поверхности, а иногда и в объеме. Вектор поляризации зависит от связанного заряда.

Связь между вектором поляризации и поверхностной плотностью заряда.

Рассмотрим диэлектрик, имеющий форму косого параллелепипеда, и поместим его в однородное электрическое поле E (рис. 2.4). На боковых гранях появятся поляризационные заряды с плотностью ’.

Если S — площадь боковой грани, то диэлектрик приобретает дипольный момент, равный ’ Sl , где l -вектор длины параллелепипеда, направленный вдоль электрического поля или, что то же, от отрицательных зарядов к положительным.

Тогда вектор поляризации равен:

P  S l	(2.2.2)
V
Здесь объем параллелепипеда определяется как
S –	+
E	V  SlCos, который можно выразить через
n	–	S +	скалярное произведение	вектора	нормали к
–	E	+		боковой грани и вектора l	:
V  S l ,n	(2.2.3)
–	+	n		
Умножим (2.2.2) скалярно на вектор нормали и,
l	воспользовавшись (2.2.3), получим:
S
Рис. 2.4.	Pn 	l ,n		(2.2.4)
V

Итак, получаем связь между поверхностной плотностью поляризационного заряда и нормальной

составляющей вектора поляризации Pn:
 Pn  Pn	(2.2.5)

Это соотношение справедливо как для положительного, так и отрицательного зарядов. Отметим, что можно интерпретировать уравнение (2.2.5) следующим образом: связанный заряд на поверхности появляется при включении внешнего поля как заряд проходящий (смещаемый) изнутри объема через его поверхность.

Диэлектрики в электрическом поле. Классификация, связанные заряды, вектор поляризованности. Связь между диэлектрической проницаемостью и восприимчивостью, связанными зарядами и поляризованностью

Связанные заряды. В результате процесса поляризации в объеме (или на поверхности) диэлектрика возникают нескомпенсированные заряды, которые называются поляризационными, или связанными.

Частицы, обладающие этими зарядами, входят в состав молекул и под действием внешнего электрического поля смещаются из своих положений равновесия, не покидая молекулы, в состав которой они входят. Связанные заряды характеризуют поверхностной плотностью . Выделим в поляризованном диэлектрике наклонную призму с основанием S и ребром L, параллельным вектору поляризации P (рис. 2.4). В результате поляризации на одном из оснований призмы появятся отрицательные заряды с поверхностной плотностью , а на другой положительные заряды с плотностью . С макроскопической точки зрения, рассматриваемый объем эквивалентен диполю, образованному зарядами и , которые отстоят друг от друга на расстояние L, тогда электрический момент призмы равен .

С другой стороны, электрический момент единицы объема равен , где — угол, между направлением нормали к основанию призмы и вектором P. Произведение есть объем призмы.

Приравняв друг к другу оба выражения для электрического момента, получаем, что поверхностная плотность связанных зарядов равна нормальной составляющей вектора поляризации:

• где n — единичный вектор нормали к поверхности диэлектрика.
• Если вектор поляризации P различен в разных точках объема диэлектрика, то в диэлектрике возникают объемные поляризационные заряды, объемная плотность которых .

Электрическое поле в диэлектрике. Рассмотрим плоский однородный диэлектрический слой, расположенный между двумя разноименно заряженными плоскостями (рис. 2.5). Пусть напряженность электрического поля, которое создается этими плоскостями в вакууме, равна ,

где — поверхностная плотность зарядов на пластинах (эти заряды называют свободными). Под действием поля диэлектрик поляризуется, и на его гранях появляются поляризационные или связанные заряды. Эти заряды создают в диэлектрике электрическое поле , которое направлено против внешнего поля .

1. ,
2. где — поверхностная плотность связанных зарядов. Результирующее поле внутри диэлектрика
3. .

Поверхностная плотность связанных зарядов меньше плотности свободных зарядов, и не все поле E0 компенсируется полем диэлектрика: часть линий напряженности проходит сквозь диэлектрик, другая часть обрывается на связанных зарядах (рис. 2.5). Вне диэлектрика . Следовательно, в результате поляризации поле внутри диэлектрика оказывается слабее, чем внешнее .

где — диэлектрическая проницаемость среды. Из формулы видно, что диэлектрическая проницаемость показывает, во сколько раз напряженность поля в вакууме больше напряженности поля в диэлектрике. Для вакуума , для диэлектриков .

• Электрическая поляризуемость среды характеризуется величиной диэлектрической восприимчивости, являющейся коэффициентом линейной связи между поляризацией диэлектрика P и внешним электрическим полем E в достаточно малых полях:
• Восприимчивость связана с диэлектрической проницаемостью ε соотношением

Электроемкость (определение, единицы измерения). Емкость конденсатора. Плоский конденсатор.

1. Единицы емкости.
2. Емкостью 1Ф (фарад) обладает такой проводник, у которого потенциал возрастает на 1 В при сообщении ему заряда в 1 Кл.
3. Емкостью 1Ф обладал бы уединенный шар, радиус которого был бы равен 13 радиусам Солнца.
4. Емкость Земли 700 мкФ
5. Если проводник не уединенный, то потенциалы складываются по правилу суперпозиции и емкость проводника меняется.
6. Конденсаторы (condensare — сгущение).

Можно создать систему проводников, емкость которой не зависит от окружающих тел. Первые конденсаторы — лейденская банка (Мушенбрук, сер. XVII в.).

Конденсатор представляет собой систему из двух проводников, разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников. Проводники наз.

обкладками конденсатора.

Если заряды пластин конденсатора одинаковы по модулю и противоположны по знаку, то под зарядом конденсатора понимают абсолютное значение заряда одной из его обкладок.

Электроемкостью конденсатора называют отношение заряда конденсатора к разности потенциалов между обкладками: .

При подключении конденсатора к батарее аккумуляторов происходит поляризация диэлектрика внутри конденсатора и на обкладках появляютсязаряды — конденсатор заряжается. Электрические поля окружающих тел почти не проникают через металлические обкладки и не влияют на разность потенциалов между ними.

Связь вектора поляризации со связаными зарядами — Математика

ρb = — ∆(перевернуть) P(СИ и СГС )

оляризация диэлектриков — явление, связанное с ограниченным смещением связанных зарядов в диэлектрике или поворотом электрических диполей, обычно под воздействием внешнего электрического поля, иногда под действием других внешних сил или спонтанно.

Поляризацию диэлектриков характеризует вектор электрической поляризации. Физический смысл вектора электрической поляризации — это дипольный момент, отнесенный к единице объема диэлектрика. Иногда вектор поляризации коротко называют просто поляризацией.

§ Вектор поляризации применим для описания макроскопического состояния поляризации не только обычных диэлектриков, но и сегнетоэлектриков, и, в принципе, любых сред, обладающих сходными свойствами. Он применим не только для описания индуцированной поляризации, но и спонтанной поляризации (у сегнетоэлектриков).

Поляризация — состояние диэлектрика, которое характеризуется наличием электрического дипольного момента у любого (или почти любого) элемента его объема.

Различают поляризацию, наведенную в диэлектрике под действием внешнего электрического поля, и спонтанную (самопроизвольную) поляризацию, которая возникает всегнетоэлектриках в отсутствие внешнего поля. В некоторых случаях поляризация диэлектрика (сегнетоэлектрика) происходит под действием механических напряжений, сил трения или вследствие изменения температуры.

Поляризация не изменяет суммарного заряда в любом макроскопическом объеме внутри однородного диэлектрика.

Однако она сопровождается появлением на его поверхности связанных электрических зарядов с некоторой поверхностной плотностью σ.

Эти связанные заряды создают в диэлектрике дополнительное макроскопическое поле с напряженностью Е1, направленное против внешнего поля с напряженностью Е0. Результирующая напряженность поля Е внутри диэлектрика Е=Е0-Е1.

В зависимости от механизма поляризации, поляризацию диэлектриков можно подразделить на следующие типы:

§ Электронная — смещение электронных оболочек атомов под действием внешнего электрического поля. Самая быстрая поляризация (до 10−15 с). Не связана с потерями. сен мал

§ Ионная — смещение узлов кристаллической структуры под действием внешнего электрического поля, причем смещение на величину, меньшую, чем величина постоянной решетки. Время протекания 10−13 с, без потерь.

§ Дипольная (Ориентационная) — протекает с потерями на преодоление сил связи и внутреннего трения. Связана с ориентацией диполей во внешнем электрическом поле.

§ Электронно-релаксационная — ориентация дефектных электронов во внешнем электрическом поле.

§ Ионно-релаксационная — смещение ионов, слабо закрепленных в узлах кристаллической структуры, либо находящихся в междуузлие.

§ Структурная — ориентация примесей и неоднородных макроскопических включений в диэлектрике. Самый медленный тип.

§ Самопроизвольная (спонтанная) — благодаря этому типу поляризации у диэлектриков, у которых он наблюдается, поляризация проявляет существенно нелинейные свойства даже при малых значениях внешнего поля, наблюдается явление гистерезиса.

Такие диэлектрики (сегнетоэлектрики) отличаются очень высокими значениями диэлектрической проницаемости (от 900 до 7500 у некоторых видов конденсаторной керамики).

Введение спонтанной поляризации, как правило, увеличивает тангенс угла потерь материала (до 10−2)

§ Резонансная — ориентация частиц, собственные частоты которых совпадают с частотами внешнего электрического поля.

§ Миграционная поляризация обусловлена наличием в материале слоев с различной проводимостью, образованию объемных зарядов, особенно при высоких градиентах напряжения, имеет большие потери и является поляризацией замедленного действия.

Поляризация диэлектриков (за исключением резонансной) максимальна в статических электрических полях. В переменных полях, в связи с наличием инерции электронов, ионов и электрических диполей, вектор электрической поляризации зависит от частоты. В связи с этим вводится понятие дисперсии диэлектрической проницаемости.

Диэлектрики Виды диэлектриков и их поляризация Теорема Гаусса для вектора поляризации Вектор электрического смещения Теорема Гаусса для вектора электрического. — презентация

• 1 Диэлектрики Виды диэлектриков и их поляризация Теорема Гаусса для вектора поляризации Вектор электрического смещения Теорема Гаусса для вектора электрического смещения Условия на границе раздела двух диэлектриков
• 2 Классы веществ Все известные в природе вещества, в соответствии с их способностью проводить электрический ток, делятся на три основных класса: диэлектрики полупроводники проводники
• 3 В качестве примеров использования различных диэлектриков можно привести: сегнетоэлектрики – электрические конденсаторы, ограничители предельно допустимого тока, позисторы, запоминающие устройства; пьезоэлектрики – генераторы ВЧ и пошаговые моторы, микрофоны, наушники, датчики давления, частотные фильтры, пьезоэлектрические адаптеры; пироэлектрики – позисторы, детекторы ИК- излучения, болометры (датчики инфракрасного излучения), электрооптические модуляторы.

4 Диэлектрики – вещества, практически не проводящие электрического тока, так как в них отсутствуют свободные заряды, способные перемещаться на значительные расстояния. Тем не менее при внесении диэлектрика в электрическое поле на его поверхности появляются электрические заряды, называемые поляризационными.

5 Смещение электрических зарядов вещества под действием электрического поля, в результате чего на поверхности, а также, вообще говоря, и в его объеме появляются нескомпенсированные заряды, называется поляризацией.

6 ЭЛЕКТРОННАЯ ПОЛЯРИЗАЦИЯ Молекулы некоторых диэлектриков не имеют собственного дипольного момента. Такие молекулы называются неполярными. Центры тяжести положительного и отрицательного зарядов у таких молекул совпадают.

7 При внесении диэлектрика в электрическое поле происходит смещение зарядов в пределах молекулы: положительных – по полю, отрицательных — против поля. Молекула приобретает дипольный момент.

8 ОРИЕНТАЦИОННАЯ ПОЛЯРИЗАЦИЯ Молекулы других диэлектриков могут иметь собственный дипольный момент. Центры тяжести положительного и отрицательного зарядов у таких молекул не совпадают. Молекулы называются полярными.

9 ИОННАЯ ПОЛЯРИЗАЦИЯ

10 Этот тип поляризации характерен для твердых диэлектриков, у которых решетка построена из положительных и отрицательных ионов. Подрешетки располагаются таким образом, что электрический момент кристаллов равен нулю. При включении поля подрешетки сдвигаются друг относительно друга, кристалл приобретает электрический момент.

11 Под действием электрического поля в пределах каждой молекулы происходит смещение зарядов, положительных по полю, отрицательных против поля. В результате чего неполярная молекула приобретает дипольный момент.

Полярная молекула обладает собственным дипольным моментом.

В отсутствии поля дипольные моменты полярных молекул ориентированы хаотично, под действием внешнего электрического поля дипольные моменты ориентируются преимущественно по полю.

12 Во всех случаях на поверхности диэлектрика появляются поверхностные связанные заряды.

13 Внутри диэлектрика электрические заряды диполей компенсируют друг друга. Но на внешних поверхностях диэлектрика, появляются заряды противоположного знака (поверхностно связанные заряды).

14 Обозначим напряженность электростатического поля связанных зарядов а напряженность внешнего поля. Результирующее электростатическое поле внутри диэлектрика В проекциях

15 Вектор поляризации Для количественного описания поляризации диэлектрика берут дипольный момент единицы объема где — физически бесконечно малый объем. Вектор поляризации (поляризованность) представим в виде:

16 Другое выражение связано с представлением диэлектрика как смеси двух «жидкостей»: положительной и отрицательной. Если выделить объем то он будет содержать — положительный заряд и — отрицательный заряд.

1. 17 Для большинства изотропных диэлектриков где — диэлектрическая восприимчивость, а — поляризуемость одной молекулы, которая показывает насколько легко индуцировать электрическим полем дипольный момент у атома.
2. 18 Теорема Гаусса для вектора поляризации Поток вектора сквозь произвольную замкнутую поверхность равен взятому с противоположным знаком избыточному связанному заряду диэлектрика в объеме, охватываемом поверхностью
3. 19 Выберем гауссову поверхность, частично охватывающую диэлектрик,
4. 20 В результате поляризации диэлектрика через сечение проходит: — положительный связанный заряд, — отрицательный связанный заряд.
5. 21 Суммарный связанный заряд, прошедший через сечение равен Таким образом Просуммировав по всей поверхности, получаем
6. 22 Вышедший через поверхность заряд равен по модулю, но противоположен по знаку связанному избыточному заряду, оставшемуся внутри поверхности Доказано В дифференциальной форме
7. 23 Поведение вектора P на границе двух сред Воспользуемся теоремой Гаусса для вектора поляризации Пренебрегая потоком через боковую поверхность, запишем
8. 24 Учитывая, что получим или Если вторая среда вакуум, то

25 Рассмотрим поведение вектора на границе раздела двух диэлектриков. В качестве гауссовой поверхности возьмем небольшой цилиндр. Высоту цилиндра будем считать пренебрежимо малой, а настолько малой, чтобы вектор для каждой точки можно было бы считать одинаковым. Нормаль к поверхности всегда будем проводить от первого диэлектрика ко второму.

26 Знак проекции определяет и знак Если то на поверхности диэлектрика находится положительный заряд, если же то отрицательный.

27 Вектор электрического смещения Рассмотрим теорему Гаусса для электростатического поля, которое в общем случае создается как сторонними, так и связанными зарядами Преобразуем формулу

28 Продолжим преобразования Вектор называют вектором электрического смещения. Вектор электрического смещения вводится для удобства расчета полей в средах.

29 Теорема Гаусса для вектора Приходим к теореме Гаусса для вектора Поток вектора электрического смещения сквозь произвольную замкнутую поверхность равен алгебраической сумме сторонних зарядов, охватываемых этой поверхностью. В дифференциальной форме

30 В случае изотропных диэлектриков, для которых справедливо получаем Величина называется диэлектрической проницаемостью вещества.

31 Поле вектора также может быть представлено с помощью линий, направление и густота которых определяются точно так же как и для линий вектора Источниками и стоками поля являются только сторонние заряды. Только на них могут начинаться и заканчиваться линии вектора Через область поля, где находятся связанные заряды, линии вектора проходят не прерываясь.

32 Условия на границе раздела двух диэлектрических сред. Найдем циркуляцию вектора вдоль контура, имеющего форму вытянутого прямоугольника. Тангенциальная составляющая вектора не испытывает скачок на границе раздела.

33 Воспользуемся теоремой Гаусса для вектора Возьмем очень малой высоты цилиндр, расположив его на границе раздела. В общем случае на границе раздела могут находиться сторонние заряды.

34 Тогда Если сторонние заряды на границе раздела отсутствуют, то Нормальная составляющая вектора электрического смещения не испытывает скачок на границе раздела двух сред, если нет сторонних зарядов на границе.

35 Рассмотрим полученные условия Разделим одно на другое, получим

36 Рассмотрим рисунок. Из рис. ясно, что Следовательно,

• 37 Полученный закон преломления справедлив и для линий вектора электрического смещения
• 38 Смысл диэлектрической постоянной Поместим диэлектрик в однородное электрическое поле Учтем, что тогда
• 39 Таким образом, диэлектрическая постоянная показывает во сколько раз ослабляется поле внутри диэлектрика. Умножим обе части на, получим
• 40

41 СЕГНЕТОЭЛЕКТРИКИ В 1920 г. была открыта спонтанная (самопроизвольная) поляризация. Всю группу веществ, назвали сегнетоэлектрики (или ферроэлектрики).

Все сегнетоэлектрики обнаруживают резкую анизотропию свойств (сегнетоэлектрические свойства могут наблюдаться только вдоль одной из осей кристалла).

У изотропных диэлектриков поляризация всех молекул одинакова, у анизотропных – поляризация, и следовательно, вектор поляризации в разных направлениях разные.

42 Основные свойства сегнетоэлектриков: 1. Диэлектрическая проницаемость ε в некотором температурном интервале велика( ). 2. Значение ε зависит не только от внешнего поля E 0, но и от предыстории образца (явление гистерезиса). 3.

Диэлектрическая проницаемость ε (а следовательно, и Р ) – нелинейно зависит от напряженности внешнего электростатического поля (нелинейные диэлектрики). 4. Наличие точки Кюри — температуры, при которой сегнетоэлектрические свойства исчезают.

1. 43 Например: Титанат бария — ; Сегнетова соль — Ниобат лития —
2. 44 ПЕТЛЯ ГИСТЕРЕЗИСА
3. 45 Стремление к минимальной потенциальной энергии и наличие дефектов структуры приводит к тому, что сегнетоэлектрик разбит на домены
4. 46 ЭЛЕКТРЕТЫ Среди диэлектриков есть вещества, называемые электреты – диэлектрики, длительно сохраняющие поляризованное состояние после снятия внешнего электростатического поля (аналоги постоянных магнитов).

47 ПЬЕЗОЭЛЕКТРИКИ Некоторые диэлектрики поляризуются не только под действием электрического поля, но и под действием механической деформации. Это явление называется пьезоэлектрическим эффектом.

Явление открыто братьями Пьером и Жаком Кюри в 1880 году. Если на грани кристалла наложить металлические электроды (обкладки) то при деформации кристалла на обкладках возникнет разность потенциалов.

Если замкнуть обкладки, то потечет ток.

49 Возможен и обратный пьезоэлектрический эффект: Возможен и обратный пьезоэлектрический эффект: Возникновение поляризации сопровождается механическими деформациями. Возникновение поляризации сопровождается механическими деформациями.

Если на пьезоэлектрический кристалл подать напряжение, то возникнут механические деформации кристалла, причем, деформации будут пропорциональны приложенному электрическому полю Е 0.

Если на пьезоэлектрический кристалл подать напряжение, то возникнут механические деформации кристалла, причем, деформации будут пропорциональны приложенному электрическому полю Е 0.

Сейчас известно более 1800 пьезокристаллов.Сейчас известно более 1800 пьезокристаллов. Все сегнетоэлектрики обладают пьезоэлектрическими свойствами Все сегнетоэлектрики обладают пьезоэлектрическими свойствами Используются в пьезоэлектрических адаптерах и других устройствах). Используются в пьезоэлектрических адаптерах и других устройствах).

50 ПИРОЭЛЕКТРИКИ Пироэлектричество – появление электрических зарядов на поверхности некоторых кристаллов при их нагревании или охлаждении.

При нагревании один конец диэлектрика заряжается положительно, а при охлаждении он же – отрицательно. Появление зарядов связано с изменением существующей поляризации при изменении температуры кристаллов.

Все пироэлектрики являются пьезоэлектриками, но не наоборот. Некоторые пироэлектрики обладают сегнетоэлектрическими свойствами.

51 ПРИМЕНЕНИЕ ДИЭЛЕКТРИКОВ В качестве примеров использования различных диэлектриков можно привести: сегнетоэлектрики – электрические конденсаторы, ограничители предельно допустимого тока, позисторы, запоминающие устройства; пьезоэлектрики – генераторы ВЧ и пошаговые моторы, микрофоны, наушники, датчики давления, частотные фильтры, пьезоэлектрические адаптеры; пироэлектрики – позисторы, детекторы ИК- излучения, болометры (датчики инфракрасного излучения), электрооптические модуляторы.

[spoiler title=”источники:”]

http://spravochnick.ru/fizika/elektrostatika/vektor_polyarizacii/

http://school16rostov.ru/tehnicheskie/svyaz-vektora-polyarizatsii-so-svyazannymi-zaryadami-spravochnik-studenta.html

[/spoiler]

Для школьников.

Задача 1. Металлический заряженный шар окружён толстым слоем диэлектрика. Нарисуйте картину силовых линий электрического поля внутри и вне диэлектрика.

Решение. Из рисунка видно, что металлический шар заряжен положительно (избыточные положительные заряды распределены по поверхности шара). Понимаем это так, что с поверхности шара удалена часть свободных электронов.

К шару примыкает толстый слой диэлектрика, то есть диэлектрик находится в электрическом поле, созданным заряженным проводником. Под действием этого поля диэлектрик поляризуется, то есть его молекулы (диполи) стремятся расположиться так, чтобы отрицательный заряд диполя сместился против направления силовых линий поля (отрицательные поляризационные заряды расположатся на границе диэлектрика вблизи положительных зарядов проводника).

Положительные поляризационные заряды расположатся на внешней поверхности диэлектрика.

Таким образом, внутри диэлектрика существует и поле, созданное проводником, и поле, создаваемое поляризационными зарядами, направленное против электрического поля проводника и ослабляющее его. Поэтому на границе с диэлектриком густота силовых линий скачком уменьшается, а при выходе из диэлектрика увеличивается.

Степень ослабления электрического поля в диэлектрике (отношение напряжённости электрического поля в воздухе к напряжённости результирующего поля в диэлектрике) называется диэлектрической проницаемостью диэлектрика.

Задача 2. В жидкий диэлектрик, с известной диэлектрической проницаемостью, погружен положительно заряженный шар известного радиуса и заряда. Определить величину и знак поляризационного заряда и плотность его распределения.

Решение. На рисунке показано, что избыточный положительный заряд проводника распределён по его поверхности равномерно, так как кривизна поверхности во всех точках одинакова. Заряженный шар окружён жидким диэлектриком.

Диэлектрик в электрическом поле заряженного шара поляризуется, то есть на границе с положительно заряженным шаром с зарядом

существует отрицательный поляризационный заряд, обозначенный через

Нам нужно найти величину поляризационного заряда и его плотность (заряд, приходящийся на единицу поверхности).

Если бы вокруг заряженного шара не было диэлектрика, то напряжённость электрического поля была бы равна

При наличии диэлектрика напряжённость поля равна

Их разность равна напряжённости поля, создаваемого поляризационными зарядами, размещёнными около заряженного шара:

Учитывая их равномерное расположение около поверхности заряженного шара, можно найти напряжённость поля, создаваемого поляризационными зарядами ещё по формуле

Приравняв два последних выражения, найдём величину поляризационного заряда:

Разделив этот заряд на поверхность сферы, найдём плотность связанного поляризационного заряда:

Здесь

есть плотность распределения свободных зарядов на поверхности шара.

Таким образом, на конкретных примерах нами рассмотрена суть явления поляризации диэлектрика.

К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.

Предыдущая запись: Занятие 51. Явление поляризации диэлектрика.

Следующая запись: Занятие 52. Почему внутри заряженного проводника электрического поля нет? Явление электростатической индукции.

Ссылки на занятия до электростатики даны в Занятии 1.

Ссылки на занятия (начиная с электростатики) даны в Занятии 45.

Поляризационный заряд

Cтраница 1

Поляризационный заряд ( его часто называют также связанным зарядом) можно выразить через дипольный момент единицы объема. Если речь идет об изотропных телах, то смещение связанных зарядов при наложении поля происходит вдоль электрических силовых линий. Поэтому вектор поляризации параллелен вектору напряженности. Благодаря поляризации на основаниях цилиндра соберутся равные по величине и противоположные по знаку связанные заряды. SL Дипольный момент, отнесенный к единице объема, будет равен P crnoi. Мы приняли в этом расчете, что основания цилиндра перпендикулярны к направлению поляризации. Если площадки будут наклонены к силовым линиям под углом ер, то плотность заряда на них будет меньшей пропорционально косинусу угла наклона.
 [1]

Поляризационные заряды увеличивают заряд на электродах по сравнению с зарядом в отсутствие диэлектрика, когда между ними находится вакуум. Соотношение зарядов конденсатора, между которыми помещен диэлектрик, и зарядов электродов, находящихся в вакууме, при одинаковой разности потенциалов характеризует относительную диэлектрическую проницаемость е, которая представляет собой безразмерную величину больше единицы.
 [2]

Поляризационные заряды в некоторых диэлектриках ( стекло, эбонит) могут сохраняться в течение некоторого времени после прекращения действия на них внешнего электрического поля, но вследствие теплового движения дипольные молекулы в конце концов теряют ориентацию, а поэтому поляризационные заряды исчезают. Однако имеются диэлектрики ( смесь различных сортов воска и смол, некоторые полимеры и др.), так называемые электреты, которые сохраняют в течение длительного времени состояние поляризации и создают электрическое поле в окружающем их пространстве.
 [3]

Поляризационные заряды, по знаку противоположные заряду проводника, притягиваются к проводнику. В результате электрический потенциал проводника уменьшается, хотя накопленный на нем электрический заряд остался без изменений.
 [4]

Поляризационный заряд и связанная с ним диэлектрическая проницаемость зависят от дипольного момента молекул и числа диполей в единице объема вещества. Например, дипольный момент спиртов, обусловленный полярной гидроксильной группой, практически одинаков ( 1 67 Д у метилового спирта, 1 64 Д у н-амилового спирта), однако диэлектрическая проницаемость в гомологическом ряду постепенно снижается: у метилового спирта она равна 33 6, у н-пропилового спирта 21 2 и у н-амилового 10 8, что объясняется уменьшением числа диполей в единице объема при увеличении молекулярной массы.
 [6]

Поляризационные заряды, находящиеся на противоположных гранях кристалла турмалина, притягивают находящиеся в воздухе в небольших количествах заряженные пылинки и ионы. Прилипая к граням кристалла ( рис. 1.47), эти пылинки и ионы постепенно нейтрализуют поляризационные заряды и уничтожают поле поляризованного кристалла.
 [7]

Поляризационный заряд ( его часто называют также связанным зарядом) можно выразить через дипольный момент единицы объема. Если речь идет об изотропных телах, то смещение связанных зарядов при наложении поля происходит вдоль электрических силовых линий. Поэтому вектор поляризации параллелен вектору напряженности. Благодаря поляризации на основаниях цилиндра соберутся равные по величине и противоположные по знаку связанные заряды. Дипольный момент, отнесенный к единице объема, будет равен Р впол. Мы приняли в этом расчете, что основания цилиндра перпендикулярны к направлению поляризации. Если площадки будут наклонены к силовым линиям под углом ф, то плотность заряда на них будет меньшей пропорционально л косинусу угла наклона.
 [8]

Поляризационные заряды желобковых возмущений создают вблизи поверхности плазмы местные азимутальные электрические поля, которые вызывают нарастание начальных возмущений и дрейф плазмы к стенке. Если окружить плазму системой изолированных электродов и изменять потенциалы этих электродов так, чтобы в каждый момент времени всюду по азимуту создавались электрические поля, противоположные по направлению поляризационным полям в плазме, то таким способом можно ослабить и, в пределе, полностью подавить нарастание желобковых возмущений. Управление потенциалами отдельных электродов должно производиться, разумеется, автоматически. Это осуществляется системой небольших емкостных датчиков, размещенных вблизи электродов и следящих за изменениями потенциала на поверхности плазмы. Сигналы с датчиков усиливаются и в нужной фазе подаются обратно на соответствующие электроды.
 [9]

Поэтому поляризационные заряды часто кз зываются еще связанными зарядами.
 [11]

Образование поляризационных зарядов на гранях, перпендикулярных оси X, при действии силы по оси X называется продольным пьезоэффектом.
 [12]

Где располагаются поляризационные заряды в поляризованном однородном и изотропном диэлектрике.
 [13]

При этом поляризационные заряды оказываются сосредоточенными преимущественно в тонких приэлектродных слоях.
 [15]

Страницы:  

   1

   2

   3

   4