Как найти поляризацию поля - Сайт, где вы сможете решить свои вопросы

Поляризованные поля

Введение в поляризацию

Можно использовать программное обеспечение Phased Array System Toolbox™, чтобы симулировать радиолокационные системы, которые передают, распространяют, отражают и получают поляризованные электромагнитные поля. Включением этой возможности тулбокс может реалистично смоделировать взаимодействие радарных волн с целями и средой.

Это – основное свойство плоских волн в свободном пространстве, что направления векторов электрического и магнитного поля являются ортогональными к их направлению распространения. Направление распространения электромагнитной волны определяется вектором Poynting

В этом уравнении E представляет электрическое поле, и H представляет магнитное поле. Количество, S, представляет величину и направление потока энергии волны. Уравнения Максвелла, когда применился к плоским волнам, приводят к результату, которым связаны электрические и магнитные поля

Векторный s, единичный вектор в направлении S, представляет направление распространения волны. Количество, Z, является wave impedance и является функцией электрической проницаемости и магнитной проницаемостью носителя, в котором перемещается волна.

После управления этими двумя уравнениями вы видите, что электрические и магнитные поля являются ортогональными к направлению распространения

Этот последний результат доказывает, что существует действительно только два независимых компонента электрического поля, пометил _Ex и _Ey. Точно так же магнитное поле может быть описано в терминах двух независимых компонентов. Из-за ортогональности полей электрическое поле может быть представлено в терминах двух единичных векторов, ортогональных к направлению распространения.

Единичные векторы вместе с единичным вектором в направлении распространения

сформируйте предназначенную для правой руки ортонормированную триаду. Позже, эти векторы и координаты, которые они задают, будут связаны с координатами определенной радиолокационной системы. В радиолокационных системах распространено использовать индексы, H и V, обозначая горизонтальные и вертикальные компоненты, вместо x и y. Поскольку электрические и магнитные поля определяются друг другом, только свойства электрического поля должны быть, рассматривают.

Для радиолокационной системы электрическое и магнитное поле является на самом деле сферическими волнами, а не плоскими волнами. Однако на практике эти поля обычно измеряются в далекой полевой области или зоне излучения радарного источника и являются приблизительно плоскими волнами. В далеком поле волны называются волнами quasi-plane. Точка находится в far field, если его расстояние, R, из источника удовлетворяют R ≫D²/λ, где D является типичной размерностью источника, является ли это одной антенной или массивом антенн.

Поляризация применяется к чисто синусоидальным сигналам. Самое общее выражение для синусоидальной плоской волны имеет форму

Количества _Ex0 и _Ey0 являются с действительным знаком, неотрицательным, амплитудами компонентов электрического поля и _ϕx и _ϕy, являются фазами поля. Это выражение является самым общим, используемым для поляризованной волны. Электромагнитной волной является polarized, если отношение амплитуд его компонентов и разности фаз между ним компоненты не изменяется со временем. Определение поляризации может быть расширено, чтобы включать сигналы narrowband, для которых полоса пропускания мала по сравнению с центром или несущей частотой сигнала. Амплитудное отношение и различие в фазах варьируются медленно со временем, когда по сравнению с периодом волны и может считаться постоянным по многим колебаниям.

Можно обычно подавлять пространственную зависимость поля и писать вектор электрического поля как

Линейная и круговая поляризация

Предыдущее уравнение для поляризованной плоской волны показывает, что совет двумерного вектора электрического поля проходит путь, который находится в плоскости, ортогональной к направлению поля распространения. Форма пути зависит от величин и фаз компонентов. Например, если _ϕx = _ϕy, можно удалить временную зависимость и запись

Это уравнение представляет прямую линию через начало координат с положительным наклоном. С другой стороны предположите _{ϕx = ϕy + π}. Затем совет вектора электрического поля следует за прямой линией через начало координат с отрицательным наклоном

Эти два случая поляризации называют linear polarized, потому что поле всегда колеблется вдоль прямой линии в ортогональной плоскости. Если _{Ex0= 0}, полем является vertically polarized, и если _{Ey0 = 0} поле является horizontally polarized.

Различный случай происходит, когда амплитуды являются тем же самым, _Ex = _Ey, но фазы отличаются ±π/2

Путем обработки на квадрат обеим сторонам можно показать, что совет вектора электрического поля выполняет уравнение круга

В то время как это уравнение дает путь, вектор берет, это не говорит вам в том, какое направление вектор электрического поля перемещается вокруг круга. Это вращается по часовой стрелке или против часовой стрелки? Направление вращения зависит от знака π/2 в фазе. Вы видите эту зависимость путем исследования движения совета векторного поля. Примите общий угол фазы, ϕ = 0. Это предположение допустимо, потому что общая фаза только определяет стартовую позицию вектора и не изменяет форму его пути. Во-первых, посмотрите на случай +π/2 для волны, перемещающейся вдоль s – направление (из страницы). В t=0 вектор указывает вдоль x – ось. Один период четверти позже, вектор указывает вдоль отрицательной оси y-. После другого периода четверти это указывает вдоль отрицательной оси x-.

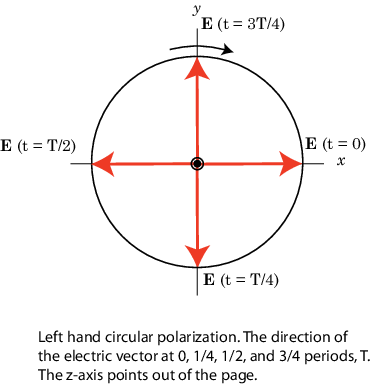
MATLAB^® использует соглашение IEEE присвоить имена поляризация, выполненная левой рукой, или выполненная правой рукой, направлению вращения электрического вектора, а не по часовой стрелке или против часовой стрелки. При использовании этого соглашения левая или правая хиральность определяется путем обращения левого или правого ползунка вдоль направления распространения волны. Затем выровняйте кривую пальцев к направлению вращения поля в данной точке в пространстве. Если вращение следует за кривой вашей левой руки, то волна предназначена для левой руки поляризованный. Если вращение следует за кривой вашей правой руки, то волна предназначена для правой руки поляризованный. В предыдущем сценарии поле является предназначенным для левой руки циркулярным поляризованным (LHCP). Разность фаз –π/2 соответствует предназначенной для правой руки циркулярной поляризованной волне (RHCP). Следующая фигура обеспечивает 3D представление того, на что похожа электромагнитная волна LHCP, когда она перемещается в s – направление.

Когда термины по часовой стрелке или против часовой стрелки используются, они зависят от того, как вы смотрите на волну. Если вы смотрите вдоль направления распространения, то направление по часовой стрелке соответствует поляризации, выполненной правой рукой, и против часовой стрелки соответствует поляризации, выполненной левой рукой. Если вы смотрите на то, куда волна прибывает из, то по часовой стрелке соответствует поляризации, выполненной левой рукой, и против часовой стрелки соответствует поляризации, выполненной правой рукой.

Круговая поляризация, выполненная левой рукой,

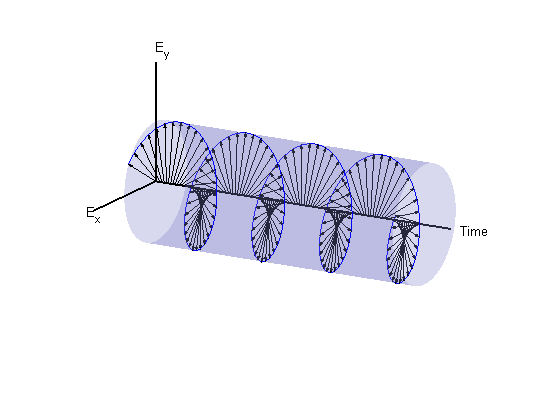
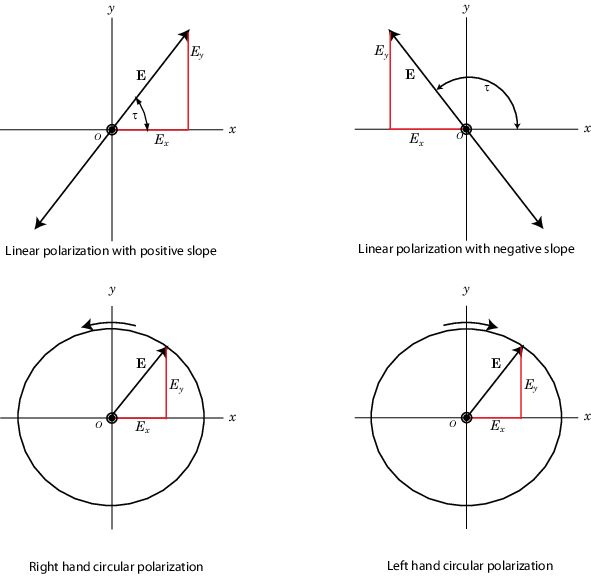
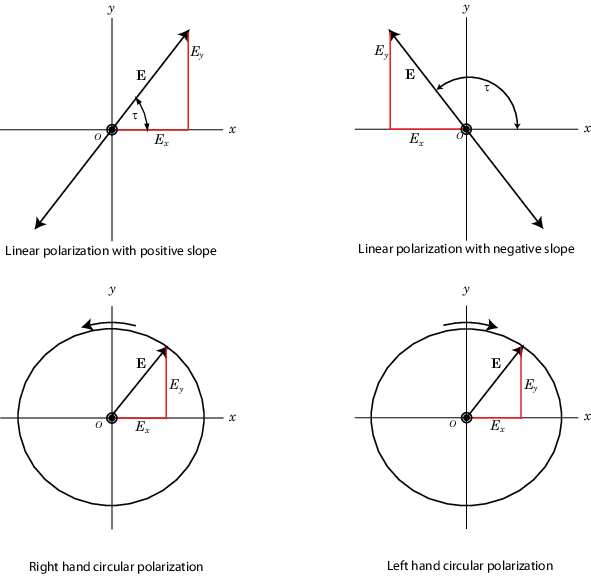
Рисунок ниже показывает внешний вид линейных и циркулярных поляризованных полей, когда они двигают вас вдоль s – направление.

Линейная и круговая поляризация

Эллиптическая поляризация

Помимо линейных и круговых состояний поляризации, третий тип поляризации является эллиптической поляризацией. Эллиптическая поляризация включает линейную и круговую поляризацию как особые случаи.

Как с линейной или круговой поляризацией, можно удалить временную зависимость, чтобы получить местоположение точек, что совет вектора электрического поля перемещается

В этом случае, _{φ = φy – φx}. Это уравнение представляет наклоненный двумерный эллипс. Его размер и форма определяются амплитудами компонента и разностью фаз. Присутствие перекрестного термина указывает, что эллипс наклоняется. Уравнение не делает, так же, как в циркулярном поляризованном случае, предоставляет любую информацию о направлении вращения. Например, следующий рисунок показывает мгновенное состояние электрического поля, но не указывает на направление, в котором вращается поле.

Размер и форма двумерного эллипса могут быть заданы тремя параметрами. Эти параметры являются длинами ее двух осей, полуглавной оси, a, и полунезначительной оси, b, и угла наклона, τ. Следующая фигура иллюстрирует три параметра наклоненного эллипса. Можно вывести их из двух амплитуд электрического поля и разности фаз.

Эллипс поляризации

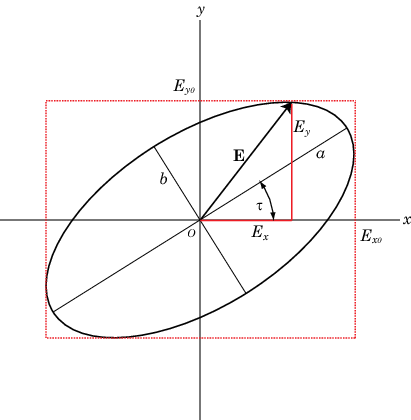
Поляризация может лучше всего быть изучена в терминах комплексных сигналов. Комплексное представление поляризованной волны имеет форму

Задайте комплексный polarization ratio как отношение комплексных амплитуд

где _{ϕ = ϕy} – _ϕx.

Полезно ввести polarization vector. Поскольку комплекс поляризовал электрическое поле выше, вектор поляризации, P, получен путем нормализации электрического поля

где _Эм² = _Ex0² + _Ey0² величина волны.

Полный размер эллипса поляризации не важен, потому что это может варьироваться, когда волна перемещается через пробел, особенно посредством геометрического затухания. То, что важно, является формой эллипса. Таким образом значительные параметры эллипса являются отношением его размерностей оси, a/b, вызвал axial ratio, и tilt angle, τ. Оба из этих количеств могут быть определены из отношения амплитуд компонента и разности фаз, или, эквивалентно, от отношения поляризации. Другим количеством, эквивалентным коэффициенту эллиптичности, является ellipticity angle, ε.

В программном обеспечении Phased Array System Toolbox можно использовать polratio функционируйте, чтобы преобразовать комплексные амплитуды fv=[Ey;Ex] к отношению поляризации.

Угол наклона

Угол наклона задан как положительное (против часовой стрелки) угол поворота от x – ось к полуглавной оси эллипса. Из-за свойств симметрии эллипса угол наклона, τ, должен только быть заданным в области значений –π/2 ≤ τ ≤ π/2. Можно найти угол наклона путем определения вращаемой системы координат, в которой полуглавные и полунезначительные оси выравниваются с вращаемыми осями координат. Затем уравнение эллипса не имеет никаких перекрестных терминов. Решение принимает форму

где _{φ = φy – φx}. Заметьте, что можно переписать это уравнение строго в терминах амплитудного отношения и разности фаз.

Коэффициент эллиптичности и угол эллиптичности

После решения для угла наклона можно определить полуглавные и полунезначительные длины оси. Концептуально, вы вращаете эллипс по часовой стрелке углом наклона и измеряете длины пересечений эллипса с x – и y – оси. Точка пересечения с большим значением является полуглавной осью, a, и тот с меньшим значением является полунезначительной осью, b.

Коэффициент эллиптичности задан как AR = a/b и, конструкцией, всегда больше или равен одной. Угол эллиптичности задан

и всегда находится в range–π/4 ≤ τ ≤ π/4.

Если вы задаете вспомогательный угол, α,

затем, углом эллиптичности дают

И коэффициент эллиптичности и угол эллиптичности заданы от амплитудного отношения и разности фаз и независимы от общей величины поля.

Направление вращения

Для эллиптической поляризации, так же, как с круговой поляризацией, вам нужен другой параметр, чтобы полностью описать эллипс. Этот параметр должен обеспечить направление вращения или направление, которое совет электрического (или магнитный вектор) перемещает вовремя. Скорость изменения угла, который вектор поля делает с x – ось, является пропорцией к –sin φ, где φ является разностью фаз. Если sin φ положителен, скорость изменения отрицательна, указывая, что поле имеет поляризацию, выполненную левой рукой. Если sin φ отрицателен, скорость изменения является положительной или поляризацией, выполненной правой рукой.

Функция polellip позволяет вам найти значения параметров эллипса поляризации от любого полевым компонентом векторный fv=[Ey;Ex] или отношение поляризации, p.

fv=[Ey;Ex];
[tau,epsilon,ar,rs] = polellip(fv);
p = polratio(fv);
[tau,epsilon,ar,rs] = polellip(p);

Переменные tauepsilon, ar и rs представляйте угол наклона, угол эллиптичности, коэффициент эллиптичности и направление вращения, соответственно. Оба синтаксиса дают тот же результат.

Сводные данные значения поляризации

Это сводные таблицы несколько различных общих видов поляризации и значения амплитуд, фаз и отношения поляризации, которые производят их:

Поляризация	Амплитуды	Фазы	Отношение поляризации
Линейный положительный наклон	Любые неотрицательные вещественные значения для _{Ex, Ey}.	_{φy = φx}	Любое неотрицательное вещественное число
Линейный отрицательный наклон	Любые неотрицательные вещественные значения для _{Ex, Ey}	_{φy = φx+ π}	Любое отрицательное вещественное число
Предназначенный для правой руки проспект	_Ex=Ey	_{φy= φx– π/2}	–i
Предназначенный для левой руки проспект	_Ex=Ey	_{φy= φx + π/2}	i
Предназначенный для правой руки эллиптический	Любые неотрицательные вещественные значения для _{Ex, Ey}	_{sin (φy– φx) < 0}	sin(arg ρ) < 0
Предназначенный для левой руки эллиптический	Любые неотрицательные вещественные значения для _{Ex, Ey}	_{sin (φy– φx) >0}	sin(arg ρ) > 0

Основы линейной и круговой поляризации

Как показано ранее можно описать поляризованное электрическое поле как линейную комбинацию базисных векторов вдоль направлений y и x. Например, комплексные векторы электрического поля для волны предназначенного для правой руки циркулярного поляризованного (RHCP) и волны предназначенного для левой руки циркулярного поляризованного (LHCP), примите форму:

В этом уравнении положительный знак для поля LHCP, и знак минус для поля RHCP. Этим двум специальным комбинациям можно дать новое имя. Задайте новый набор базисного вектора, названный круговым базисным комплектом

Можно описать любое поляризованное поле в терминах кругового базисного комплекта вместо линейного базисного комплекта. С другой стороны можно также записать линейный базис поляризации в терминах базиса круговой поляризации

Любое общее эллиптическое поле может быть записано как комбинация круговых базисных векторов

Вектор Джонса

Поляризованное поле является ортогональным к направлению волны распространения. Таким образом поле может быть полностью задано двумя комплексными компонентами вектора электрического поля в плоскости поляризации. Формулировка поляризованной волны в терминах двухкомпонентных векторов называется формулировкой Jones vector. Формулировка вектора Джонса может быть описана или в линейном базисе или в круговом базисе или любом базисе. Эта таблица показывает представление общей поляризации в линейном базисе и круговом базисе.

Общая поляризация	Вектор Джонса в линейном базисе	Вектор Джонса в круговом базисе
Вертикальный	[0;1]	`1/sqrt(2)*[-1;1]`
Горизонталь	[1;0]	`1/sqrt(2)*[1;1]`
Линейные 45 °	`1/sqrt(2)*[1;1]`	`1/sqrt(2)*[1-1i;1+1i]`
Линейные 135 °	`1/sqrt(2)*[1;-1]`	`1/sqrt(2)*[1+1i;1-1i]`
Правильный проспект	`1/sqrt(2)*[1;-1i]`	[0;1]
Оставленный проспект	`1/sqrt(2)*[1;1i]`	[1;0]

Параметры Стокса и сфера Пуанкаре

Эллипс поляризации является мгновенным представлением поляризованной волны. Однако его параметры, угол наклона и угол эллиптичности, часто не непосредственно измеримы, особенно на очень высоких частотах, таких как легкие частоты. Однако можно определить поляризацию из измеримой интенсивности поляризованного поля.

Измеримая интенсивность является параметрами Стокса, _S0, _S1, _S2 и _S3. Первый параметр Стокса, _S0, описывает общую интенсивность поля. Второй параметр, _S1, описывает превосходство линейной горизонтально поляризованной интенсивности по линейной вертикально поляризованной интенсивности. Третий параметр, _S2, описывает превосходство линейно поляризованной интенсивности на +45 ° линейно, 135 ° поляризовали интенсивность. Наконец, _S3 описывает превосходство правильной циркулярной поляризованной интенсивности по левой циркулярной поляризованной интенсивности. Параметры Стокса заданы как

Для полностью поляризованных полей можно показать усреднением во времени уравнение эллипса поляризации это

Таким образом существуют параметры только трех независимого Стокса.

Для частично поляризованных полей, напротив, параметры Стокса удовлетворяют неравенству

Топит параметры, связаны с наклоном и углами эллиптичности, τ и ε

и обратно пропорционально

После того, как вы измерите параметры Стокса, форма эллипса полностью определяется предыдущими уравнениями.

Двумерная сфера Poincaré может помочь вам визуализировать состояние поляризованной волны. Любая точка на или в сфере представляет состояние поляризации, определенной четырьмя параметрами Стокса, _{S0, S1, S2} и _S3. На сфере Poincaré угол от плоскости _S1-S2 до точки на сфере является дважды углом эллиптичности, ε. Угол от оси _S1- до проекции точки в плоскость _S1-S2 является дважды углом наклона, τ.

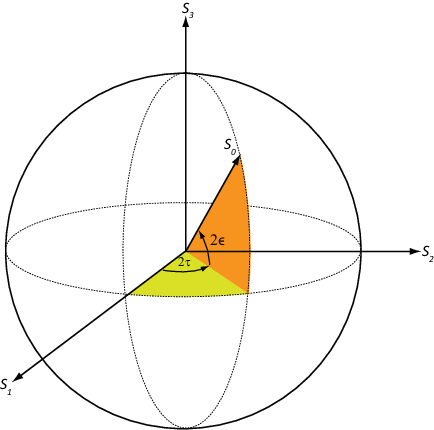
Как пример, решите для параметров Стокса поля RHCP, fv=[1,-i], использование stokes функция.

Источники поляризованных полей

Пара антенн, распространяющая электромагнитное излучение к электрическим токам в проводах, электромагнитным полям в волноводах или апертурных полях. Эта связь является явлением, характерным и для передающих и для приемных антенн. Для некоторых передающих антенн, исходных токов в проводном продукте электромагнитные волны, что перенос степени во всех направлениях. Иногда антенна обеспечивает средние значения для ведомой электромагнитной волны на линии электропередачи к переходу к волнам свободного пространства, таким как волновод, питающийся спутниковые антенны. Для приемных антенн электромагнитные поля могут побудить токи в проводах генерировать сигналы, которые будут затем усилены и переданы детектору.

Для передающих антенн форма антенны выбрана, чтобы улучшить степень, спроектированную в данное направление. Для приемных антенн вы выбираете форму антенны, чтобы улучшить степень, полученную от конкретного направления. Часто, много передающих антенн или приемных антенн формируются в array. Массивы увеличивают переданную степень для системы передачи или чувствительность для системы получения. Они улучшают направленность по одной антенне.

Антенна может быть присвоена поляризация. Поляризация передающей антенны является поляризацией своей излученной волны в далеком поле. Поляризация приемной антенны является на самом деле поляризацией плоской волны, от данного направления, приводящего к максимальной мощности на терминалах антенны. Теоремой взаимности все передающие антенны могут служить приемными антеннами и наоборот.

Каждая антенна или массив имеют связанную локальную Декартову систему координат (x,y,z) как показано в следующем рисунке. Смотрите Системы Глобальной и Локальной координаты для получения дополнительной информации. Система локальной координаты может также быть представлена сферической системой координат с помощью азимута, вертикального изменения и координат области значений, az, el, r, или альтернативно писаться, (φ,θ,r), как показано. В каждой точке в далеком поле можно создать набор модульных сферических базисных векторов, {e^H,e^V,r^}. Базисные векторы выравниваются с направлениями (φ,θ,r), соответственно. В далеком поле электрическое поле является ортогональным к единичному вектору r^. Компоненты поляризованного поля относительно этого базиса, _(EH,EV), называются горизонтальными и вертикальными компонентами поляризованного поля. В радаре распространено использовать (H,V) вместо (x,y), чтобы обозначить компоненты поляризованного поля. В далеком поле поляризованное электрическое поле принимает форму

В этом уравнении количество F (φ,θ) называется vector radiation pattern источника и содержит угловую зависимость поля в области далекого поля.

Короткий дипольный антенный элемент

Самая простая поляризованная антенна является дипольной антенной, которые состоят из длины разделения провода, связанного в середину с коаксиальным кабелем. Самый простой диполь, с математической точки зрения, является диполем Hertzian, в котором длина провода намного короче, чем длина волны. Схема короткой дипольной антенны длины L появляется на следующем рисунке. Эта антенна питается коаксиальным каналом, который разделяет в два провода равной длины длины L/2. Ток, I, проходит z – ось и принят, чтобы быть тем же самым во всех точках в проводе.

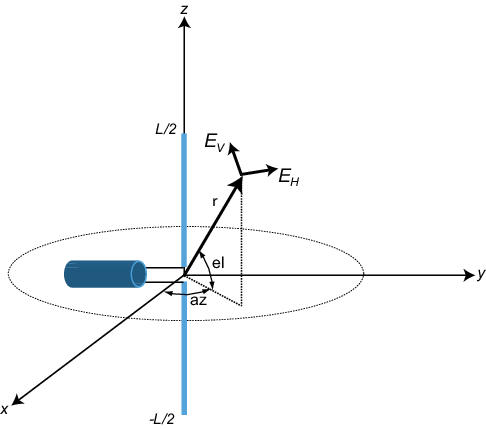
Электрическое поле в далеком поле имеет форму

Следующий пример вычисляет вертикальные и горизонтальные компоненты поляризации поля. Вертикальная компонента является функцией угла возвышения и по оси симметрична. Горизонтальная компонента исчезает везде.

Тулбокс позволяет вам смоделировать короткую дипольную антенну с помощью phased.ShortDipoleAntennaElement Система object™.

Компоненты поляризации короткого диполя

Вычислите вертикальные и горизонтальные компоненты поляризации поля, созданного антенной короткого диполя, указанной вдоль z-направления. Постройте компоненты в зависимости от угла возвышения от 0 ° до 360 °.

Примечание: Этот пример запускается только в R2016b или позже. Если вы используете более ранний релиз, заменяете каждый вызов функции с эквивалентным step синтаксис. Например, замените myObject(x) с step(myObject,x).

Создайте phased.ShortDipoleAntennaElement Система object™.

antenna = phased.ShortDipoleAntennaElement(...
    'FrequencyRange',[1,2]*1e9,'AxisDirection','Z');

Вычислите ответ антенны. Поскольку аргумент угла возвышения к antenna ограничивается ±90 °, вычислите ответы для азимута на 0 ° и затем для азимута на 180 °. Объедините эти два ответа в графике. Рабочая частота антенны составляет 1,5 ГГц.

el = [-90:90];
az = zeros(size(el));
fc = 1.5e9;
resp = antenna(fc,[az;el]);
az = 180.0*ones(size(el));
resp1 = antenna(fc,[az;el]);

Наложите ответы на том же рисунке.

figure(1)
subplot(121)
polar(el*pi/180.0,abs(resp.V.'),'b')
hold on
polar((el+180)*pi/180.0,abs(resp1.V.'),'b')
str = sprintf('%sn%s','Vertical Polarization','vs Elevation Angle');
title(str)
hold off
subplot(122)
polar(el*pi/180.0,abs(resp.H.'),'b')
hold on
polar((el+180)*pi/180.0,abs(resp1.H.'),'b')
str = sprintf('%sn%s','Horizontal Polarization','vs Elevation Angle');
title(str)
hold off

График показывает, что горизонтальная компонента исчезает, как ожидалось.

Пересеченный дипольный антенный элемент

Можно использовать перекрестную дипольную антенну, чтобы сгенерировать циркулярно поляризованное излучение. Антенна пересеченного диполя состоит из двух идентичных, но ортогональных антенн короткого диполя, которые поэтапно осуществлены на расстоянии в 90 °. Схема пересеченной дипольной антенны появляется в следующем рисунке. Электрическое поле, созданное антенной пересеченного диполя, созданной из y – направило короткий диполь, и z – предписал, чтобы короткий диполь имел форму

_EV/EH отношения поляризации, когда оценено вдоль x – ось, является только –i, что означает, что поляризацией является точно RHCP вдоль x – ось. Это – преимущественно RHCP, когда наблюдательный пост близко к x – ось. Переезжая от x – ось, поле становится смесью LHCP и поляризации RHCP. Вдоль –x – ось, поле является поляризованным LHCP. Фигура иллюстрирует для точки около x, что полем является, в основном, RHCP.

Тулбокс позволяет вам смоделировать антенну пересеченного диполя с помощью phased.CrossedDipoleAntennaElement Системный объект.

LHCP и компоненты поляризации RHCP

Этот пример строит правые и левые компоненты круговой поляризации полей, сгенерированных антенной пересеченного диполя на уровне 1,5 ГГц. Вы видите, как круговая поляризация изменяется от чистого RHCP под 0 углами азимута степеней к чистому LHCP под 180 углами азимута степеней, обоим в 0 углах возвышения степеней.

Создайте phased.CrossedDipoleAntennaElement объект.

fc = 1.5e9;
antenna = phased.CrossedDipoleAntennaElement('FrequencyRange',[1,2]*1e9);

Вычислите предназначенные для левой руки и предназначенные для правой руки компоненты круговой поляризации из ответа антенны.

az = [-180:180];
el = zeros(size(az));
resp = antenna(fc,[az;el]);
cfv = pol2circpol([resp.H.';resp.V.']);
clhp = cfv(1,:);
crhp = cfv(2,:);

Постройте оба компонента круговой поляризации при 0 вертикальных изменениях степеней.

polar(az*pi/180.0,abs(clhp))
hold on
polar(az*pi/180.0,abs(crhp))
title('LHCP and RHCP vs Azimuth Angle')
legend('LHCP','RHCP')
hold off

Массивы, поддерживающие поляризацию

Можно создать поляризованные поля из массивов при помощи поляризованных антенных элементов как значение Elements свойство Системного объекта массивов. Все массивы Phased Array System Toolbox поддерживают поляризацию.

Матрица поперечного сечения рассеяния

После того, как поляризованное поле создается системой антенны, поле исходит в область далекого поля. Когда поле распространяет в свободное пространство, свойства поляризации остаются неизменными, пока поле не взаимодействует с материальным веществом, которое рассеивает поле во многие направления. В таких ситуациях амплитуда и поляризация рассеянной волны могут отличаться от инцидентной поляризации волны. Рассеянная поляризация волны может зависеть от направления, в котором наблюдается рассеянная волна. Точный способ, которым изменения поляризации зависят от свойств рассеивающегося объекта. Количество, описывающее ответ объекта к падающему полю, называется радарной матрицей поперечного сечения рассеяния (RSCM), S. Можно измерить матрицу рассеяния можно следующим образом. Когда модульная амплитуда, горизонтально поляризованная волна рассеивается, и горизонталь и вертикальный рассеянный компонент, производится. Вызовите эти два компонента _SHH и _SVH. Эти компоненты являются комплексными числами, содержащими амплитуду и фазовые переходы от инцидентной волны. Точно так же, когда модульной амплитудой, вертикально поляризованная волна рассеивается, горизонталь и вертикальный рассеянный произведенный компонент, является _SHV и _SVV. Поскольку, любое падающее поле может быть разложено на горизонтальные и вертикальные компоненты, можно расположить эти количества в матрицу и записать рассеянное поле в терминах падающего поля

В общем случае матрица поперечного сечения рассеяния зависит от углов, которые падающие и рассеянные поля делают с объектом. Когда падающее поле рассеивается назад к передающей антенне или, backscattered, матрица рассеяния симметрична.

Сигнатура поляризации

Чтобы понять, как рассеянная волна зависит от поляризации падающей волны, необходимо изучить все возможные поляризации рассеянного поля для каждой падающей поляризации. Поскольку этот объем данных затрудняет, чтобы визуализировать, рассмотрите два случая:

Для случая copolarization рассеянная поляризация имеет ту же поляризацию как падающее поле.
Для случая cross-polarization рассеянная поляризация имеет ортогональную поляризацию к падающему полю.

Можно представлять падающие поляризации в терминах пары угла наклона-угла эллиптичности (τ,ε). Каждый единичный падающий вектор поляризации может быть описан как

в то время как ортогональный вектор поляризации

Когда вы имеете матрицу RSCM, S, формируете сигнатуру сополяризации путем вычисления

где []* обозначает комплексное спряжение. Чтобы получить подпись перекрестной поляризации, вычислить

Можно вычислить как сигнатуры сополяризации, так и сигнатуры перекрестной поляризации, с помощью polsignature функция. Эта функция возвращает абсолютное значение рассеянной мощности (нормированный на ее максимальное значение). Следующий пример показывает, как построить сигнатуры поляризации для матрицы RSCM

для всех возможных падающих поляризаций. Диапазон значений угла эллиптичности и наклона охватывает весь возможный диапазон поляризаций.

Построение Поляризационных Сигнатур

Построение сигнатур сополяризации и кросс-поляризации матрицы рассеяния

[2i0.50.5-i].

Задайте матрицу рассеяния. и укажите диапазон углов эллиптичности и ориентации (наклон) углы, которые задают виды поляризации. Эти углы покрывают все возможные состояния падающей поляризации.

rscmat = [1i*2,0.5;0.5,-1i];
el = [-45:45];
tilt = [-90:90];

Постройте сигнатуры сополяризации для всех падающих поляризаций.

polsignature(rscmat,'c',el,tilt)

Постройте подписи перекрестной поляризации для всех падающих поляризаций.

polsignature(rscmat,'x',el,tilt)

Потеря поляризации из-за несоответствия поля и приемника

Антенна, которая используется для приема поляризованных электромагнитных волн, достигает своей максимальной выходной мощности, когда поляризация антенны согласована с поляризацией падающего электромагнитного поля. В противном случае происходит потеря поляризации:

Потеря поляризации вычисляется из проекции (или скалярное произведение) вектора электрического поля переданного поля на вектор поляризации приемника.
Потеря происходит, когда существует несоответствие в направлении этих двух векторов, не в их величинах.
Коэффициент потерь поляризации описывает долю падающей мощности, которая имеет правильную поляризацию для приема.

Используя сферический базис передатчика в положении приемника, можно представлять падающее электрическое поле, _{(EiH, EiV)},

Можно представлять вектор поляризации приемника, _{(PH, PV)}, в локальном сферическом базисе приемника:

Следующий рисунок показывает конструкцию сферических базисных векторов передатчика и приемника.

Поляризационные потери определяются:

и находится в интервале между 0 и 1. Поскольку векторы заданы относительно различных систем координат, они должны быть преобразованы в глобальную систему координат, чтобы сформировать проекцию. Функция тулбокса polloss вычисляет несоответствие поляризации между падающим полем и поляризованной антенной.

Чтобы достигнуть максимальной выходной мощности от приемной антенны, совпадающий вектор поляризации антенны должен быть сопряженным комплексным числом вектора поляризации входящего поля. Как пример, если входящее поле является RHCP с вектором поляризации, данным er=12(ex−iey), оптимальная поляризация антенны приемника является LHCP. В представлении сопряженного комплексного числа нуждаются, потому что полевая поляризация описана относительно его направления распространения, тогда как поляризация получить антенны обычно задается в терминах направления распространения к антенне. Сопряженное комплексное число корректирует для противоположного смысла поляризации при получении.

Как пример, если передающая антенна передает поле RHCP, коэффициенты потерь поляризации для различной полученной поляризации антенны

Получите поляризацию антенны	Получите вектор поляризации антенны	Коэффициент потерь поляризации	Коэффициент потерь поляризации (дБ)
Линейная горизонталь	e _H	1/2	3 дБ
Вертикальный линейный	e _V	1/2	3
RHCP	er=12(ex−iey)	0	∞
LHCP	el=12(ex+iey)	1	0

Радар модели, передающий поляризованное излучение

Этот пример демонстрирует радар отслеживания на основе 31 31 универсального прямоугольного массива (URA) (с 961 элементом). Радар спроектирован, чтобы следовать за движущейся целью. В каждый раз момент радар указывает в известном направлении цели. Основные радарные требования являются вероятностью обнаружения, pd, вероятность ложного предупреждения, pfa, максимальная однозначная область значений, max_range, и разрешение области значений, range_res, (все единицы расстояния исчисляются в метрах). range_gate параметр ограничивает необходимую область областью значений, меньшей, чем максимальная область значений. Рабочая частота установлена в fc. Симуляция длится numpulses импульсы.

Радарное определение

Настройте радарные рабочие параметры. Существующий радарный проект выполняет следующим техническим требованиям.

pd = 0.9;            % Probability of detection
pfa = 1e-6;          % Probability of false alarm
max_range = 1500*1000; % Maximum unambiguous range
range_res = 50.0;    % Range resolution
rangegate = 5*1000;  % Assume all objects are in this range
numpulses = 200;     % Number of pulses to integrate
fc = 8e9;            % Center frequency of pulse
c = physconst('LightSpeed');
tmax = 2*rangegate/c; % Time of  echo from object at rangegate

Импульсный интервал повторения

Установите импульсный интервал повторения, PRI, и импульсная частота повторения, PRF, на основе максимальной однозначной области значений.

PRI = 2*max_range/c;
PRF = 1/PRI;

Переданный сигнал

Настройте передаваемую прямоугольную форму сигнала с помощью phased.RectangularWaveform System object(TM). Ширина импульса формы волны, pulse_width, и ширина полосы пропускания импульса, pulse_bw, определяются разрешением области значений, range_res, который вы выбираете. Задайте частоту дискретизации, fs, быть дважды шириной полосы пропускания импульса. Частота дискретизации должна быть целочисленным кратным PRF. Поэтому измените частоту дискретизации, чтобы удовлетворить требованию.

pulse_bw = c/(2*range_res);    % Pulse bandwidth
pulse_width = 1/pulse_bw;               % Pulse width
fs = 2*pulse_bw;                        % Sampling rate
n = ceil(fs/PRF);
fs = n*PRF;
waveform = phased.RectangularWaveform('PulseWidth',pulse_width,'PRF',PRF,...
    'SampleRate',fs);

Антенны и массив URA

Массив состоит из антенных элементов короткого диполя. Используйте phased.ShortDipoleAntennaElement Системный объект, чтобы создать антенну короткого диполя, ориентированную вдоль оси z.

antenna = phased.ShortDipoleAntennaElement(...
    'FrequencyRange',[5e9,10e9],'AxisDirection','Z');

Задайте 31 31, Тейлор заострился универсальный прямоугольный массив с помощью phased.URA Системный объект. Установите размер массива с помощью количества строк, numRows, и количество столбцов, numCols. Расстояние между элементами, d, немного меньше, чем половина длины волны, lambda. Вычислите заострение массивов, tw, использование отдельных окон Тейлора для направлений строки и столбца. Получите веса Тейлора с помощью taylorwin функция. Постройте ответ трехмерного массива с помощью массива pattern метод.

numCols = 31;
numRows = 31;
lambda = c/fc;
d = 0.9*lambda/2; % Nominal spacing
wc = taylorwin(numCols);
wr = taylorwin(numRows);
tw = wr*wc';
array = phased.URA('Element',antenna,'Size',[numCols,numRows],...
    'ElementSpacing',[d,d],'Taper',tw);
pattern(array,fc,-180:180,-90:90,'CoordinateSystem','polar','Type','powerdb',...
    'Polarization','V');

Радарное движение платформы

Затем установите положение и движение радарной платформы в phased.Platform Системный объект. Радар принят, чтобы быть стационарным и расположен в источник. Установите Velocity свойство к [0,0,0] и InitialPosition свойство к [0,0,0]. Установите InitialOrientationAxes свойство к единичной матрице, чтобы выровнять радарные оси координат платформы с глобальной системой координат.

radarPlatformAxes = [1 0 0;0 1 0;0 0 1];
radarplatform = phased.Platform('InitialPosition',[0;0;0],...
    'Velocity',[0;0;0],'OrientationAxes',radarPlatformAxes);

Передатчики и приемники

В радаре сигнал распространяет в форме электромагнитной волны. Сигнал излучен и собран антеннами, используемыми в радиолокационной системе. Сопоставьте массив с Системным объектом излучателя, phased.Radiator, и два коллектора System objects, phased.Collector. Установите WeightsInputPort свойство излучателя к true включить динамическое регулирование переданного сигнала при каждом выполнении излучателя. Создание этих двух коллекторов допускает набор и горизонтальных и вертикальных компонентов поляризации.

radiator = phased.Radiator('Sensor',array,'OperatingFrequency',fc,...
    'PropagationSpeed',c,'CombineRadiatedSignals',true,...
    'Polarization','Combined','WeightsInputPort',true);
collector1 = phased.Collector('Sensor',array,'OperatingFrequency',fc,...
    'PropagationSpeed',c,'Wavefront','Plane','Polarization','Combined',...
    'WeightsInputPort',false);
collector2 = phased.Collector('Sensor',array,'OperatingFrequency',fc,...
    'PropagationSpeed',c,'Wavefront','Plane','Polarization','Combined',...
    'WeightsInputPort',false);

Оцените пиковую мощность, необходимую в phased.Transmitter Системный объект, чтобы вычислить желаемые излученные уровни мощности. Переданная пиковая мощность является степенью, требуемой достигнуть ОСШ минимального обнаружения, snr_min. Можно определить минимальный ОСШ из вероятности обнаружения, |pd |, и вероятности ложного предупреждения, pfa, использование albersheim функция. Затем вычислите пиковую мощность, peak_power, от основного уравнения радиолокации. Пиковая мощность зависит от полного усиления сигнала, которое является суммой усиления элемента передачи, TransmitterGain и усиление массивов, AG. Пиковая мощность также dependson максимальная область значений обнаружения, rangegate. Наконец, необходимо предоставить эффективную площадь рассеяния цели, tgt_rcs. Скалярное поперечное сечение радара используется в этой секции кода в качестве приближения даже при том, что полное вычисление поляризации более позднее использование матрица рассеяния поперечного сечения радара 2 на 2.

Используя формулу основного уравнения радиолокации, оцените общую переданную степень достигнуть необходимого ОСШ обнаружения с помощью всех импульсов.

ОСШ имеет вклады от усиления элемента передачи, а также усиления массивов. Вычислите сначала оценку усиления массивов, затем добавьте усиление массивов в усиление передатчика, чтобы получить пиковую мощность, которая достигает желаемого ОСШ.

Используйте аппроксимированное целевое сечение 1,0 для основного уравнения радиолокации даже при том, что анализ призывает к полной матрице рассеяния.
Установите максимальную область значений быть равной значению ‘rangegate’, поскольку цели вне той области значений неинтересны.
Вычислите усиление массивов как 10*log10 (число элементов)
Примите, что каждый элемент имеет усиление 20 дБ.

snr_min = albersheim(pd, pfa, numpulses);
AG = 10*log10(numCols*numRows);
tgt_rcs = 1;
TransmitterGain = 20;
tau = waveform.PulseWidth;
Ts = 290;
dbterm = db2pow(snr_min - 2*TransmitterGain + AG);
peak_power = (4*pi)^3*physconst('Boltzmann')*Ts/tau/tgt_rcs/lambda^2*rangegate^4*dbterm

transmitter = phased.Transmitter('PeakPower',peak_power,'Gain',TransmitterGain,...
    'LossFactor',0,'InUseOutputPort',true,'CoherentOnTransmit',true);

Задайте цель

Мы хотим симулировать импульс, возвращается из цели, которая вращается так, чтобы матрица поперечного сечения рассеяния изменилась от импульса до импульса. Создайте вращающийся целевой объект и движущуюся целевую платформу. Вращающаяся цель представлена позже как зависимая углом матрица рассеяния. Вращение в градусах в секунду.

targetSpeed = 1000;
targetVec = [-1;1;0]/sqrt(2);
target = phased.RadarTarget('EnablePolarization',true,...
    'Mode','Monostatic','ScatteringMatrixSource','Input port',...
    'OperatingFrequency',fc);
targetPlatformAxes = [1 0 0;0 1 0;0 0 1];
targetRotRate = 45;
targetplatform = phased.Platform('InitialPosition',[3500.0; 0; 0],...
    'Velocity', targetSpeed*targetVec);

Другие Системные объекты

Регулирование вектора задано phased.SteeringVector Системный объект.
Формирователь луча задан phased.PhaseShiftBeamformer Системный объект. DirectionSource свойство установлено в 'Input Port' включить формирователь луча к всегда точкам к известному целевому направлению при каждом выполнении.
Распространитель свободного пространства, использующий phased.FreeSpace Системный объект.
Модель предусилителя приемника использование phased.ReceiverPreamp системный объект.

Распространение сигнала

Поскольку отраженные сигналы получены массивом, используйте формирователь луча, указывающий на держащееся направление, чтобы получить объединенный сигнал.

steeringvector = phased.SteeringVector('SensorArray',array,'PropagationSpeed',c,...
    'IncludeElementResponse',false);
beamformer = phased.PhaseShiftBeamformer('SensorArray',array,...
    'OperatingFrequency',fc,'PropagationSpeed',c,...
    'DirectionSource','Input port');
channel = phased.FreeSpace('SampleRate',fs,...
    'TwoWayPropagation',true,'OperatingFrequency',fc);
% Define a receiver with receiver noise
amplifier = phased.ReceiverPreamp('Gain',20,'LossFactor',0,'NoiseFigure',1,...
    'ReferenceTemperature',290,'SampleRate',fs,'EnableInputPort',true,...
    'PhaseNoiseInputPort',false,'SeedSource','Auto');

Для такого большого PRI и частоты дискретизации, будет слишком много выборок на элемент. Это вызовет проблемы с коллектором, который имеет 961 канал. Чтобы сохранить количество отсчетов управляемым, установите максимальную область значений 5 км. Мы знаем, что цель в этой области значений.

Этот набор осей задает направление осей локальной координаты относительно глобальной системы координат. Это – ориентация цели.

Обработка цикла

Предварительно выделите массивы для сбора данных, которые будут построены.

sig_max_V  = zeros(1,numpulses);
sig_max_H  = zeros(1,numpulses);
tm_V = zeros(1,numpulses);
tm_H = zeros(1,numpulses);

После того, как все Системные объекты создаются, цикл по количеству импульсов, чтобы создать отраженные сигналы.

maxsamp = ceil(tmax*fs);
fast_time_grid = (0:(maxsamp-1))/fs;
rotangle = 0.0;
for m = 1:numpulses
    x = waveform(); % Generate pulse
    % Capture only samples within range gated
    x = x(1:maxsamp);
    [s, tx_status] = transmitter(x);   % Create transmitted pulse
    % Move the radar platform and target platform.
    [radarPos,radarVel] = radarplatform(1/PRF);
    [targetPos,targetVel] = targetplatform(1/PRF);    
    % Compute the known target angle
    [targetRng,targetAng] = rangeangle(targetPos,...
        radarPos,...
        radarPlatformAxes);
    % Compute the radar angle with respect to the target axes.
    [radarRng,radarAng] = rangeangle(radarPos,...
        targetPos,...
        targetPlatformAxes);    
    % Calculate the steering vector designed to track the target
    sv = steeringvector(fc,targetAng);
    % Radiate the polarized signal toward the targat
    tsig1 = radiator(s,targetAng,radarPlatformAxes,conj(sv));
    % Compute the two-way propagation loss (4*pi*R/lambda)^2
    tsig2 = channel(tsig1,radarPos,targetPos,radarVel,targetVel);
    % Create a very simple model of a changing scattering matrix
    scatteringMatrix = [cosd(rotangle),0.5*sind(rotangle);...
        0.5*sind(rotangle),cosd(rotangle)];
    rsig1 = target(tsig2,radarAng,targetPlatformAxes,scatteringMatrix);  % Reflect off target
    % Collect the vertical component of the radiation.
    rsig3V = collector1(rsig1,targetAng,radarPlatformAxes);   
    % Collect the horizontal component of the radiation. This
    % second collector is rotated around the x-axis to be more
    % sensitive to horizontal polarization
    rsig3H = collector2(rsig1,targetAng,rotx(90)*radarPlatformAxes);  
    % Add receiver noise to both sets of signals
    rsig4V = amplifier(rsig3V,~(tx_status>0)); % Receive signal
    rsig4H = amplifier(rsig3H,~(tx_status>0)); % Receive signal
    % Beamform the signal
    rsigV = beamformer(rsig4V,targetAng); % Beamforming
    rsigH = beamformer(rsig4H,targetAng); % Beamforming   
    % Find the maximum returns for each pulse and store them in
    % a vector. Store the pulse received time as well.
    [sigmaxV,imaxV] = max(abs(rsigV));
    [sigmaxH,imaxH] = max(abs(rsigH));
    sig_max_V(m) = sigmaxV;
    sig_max_H(m) = sigmaxH;
    tm_V(m) = fast_time_grid(imaxV) + (m-1)*PRI;
    tm_H(m) = fast_time_grid(imaxH) + (m-1)*PRI;
    
    % Update the orientation of the target platform axes
    targetPlatformAxes = ...
        rotx(PRI*targetRotRate)*targetPlatformAxes;
    rotangle = rotangle + PRI*targetRotRate;
end
% Plot the vertical and horizontal polarization for each pulse as a
% function of time.
plot(tm_V,sig_max_V,'.')
hold on
plot(tm_H,sig_max_H,'r.')
hold off
xlabel('Time (sec)')
ylabel('Amplitude')
title('Vertical and Horizontal Polarization Components')
legend('Vertical','Horizontal')
grid on

Источник

Для
количественного описания поляризации
диэлектрика вводят
вектор поляризации
(поляризованность).

Если
внешнее электрическое поле или диэлектрик
неоднородны, то степень поляризации
оказывается разной в различных точках
диэлектрика. Чтобы характеризовать
поляризацию в данной точке, необходимо
выделить бесконечно малый объем V,
содержащий эту точку, затем найти
векторную сумму дипольных моментов
молекул в этом объеме, тогда вектор
поляризации

,
(2)

где
р_i

дипольный момент i-й
молекулы.

Поляризованностью
называют
геометрическую сумму дипольных моментов
молекул единицы объема диэлектрика.

В
Си единицей измерения поляризованости
является Кл/м².

На
основании экспериментов установлено,
что поляризованность неполярных
диэлектриков линейно зависит от
напряженности внешнего электрического
поля, т. е.

=
n₀
₀=æ,
(3)

где
æ

диэлектрическая восприимчивость
диэлектрика (безразмерна), зависит от
рода диэлектрика и не зависит от
напряженности внешнего электрического
поля. Поляризованность можно найти по
формуле

=
n_o,
(4)

где
р_i= ₀_iЕ

электрический дипольный момент i-й
молекулы;

концентрация
молекул; n

число всех молекул в объеме V;

æ
= n₀

0; 
= 4r³

коэффициент, характеризующий поляризуемость
атома, зависит от свойств атома.

Поляризованность
полярного диэлектрика

.
(5)

где

средний дипольный момент одной молекулы.

В
слабых электрических полях поляризованность
полярных диэлектриков рассчитывают по
формуле

.
(6)

Диэлектрическую
восприимчивость находят по формуле
Дебая-Ланжевена

æ
=
.
(7)

2.6. Основные уравнения электростатики диэлектриков

2.6.1. Теорема Гаусса для поля вектора поляризации ()

Рис. 4

Пусть произвольная
замкнутая поверхность S
охватывает некоторую часть изотропного
диэлектрика.

При
внесении диэлектрика во внешне
электростатическое поле он поляризуется.
Найдем заряд, который проходит через
малый элемент dS
замкнутой поверхности S
(рис. 4).

Если
₊
и
_

векторы, характеризующие смещение
положительного и отрицательного
связанных зарядов, то через элемент
поверхности dS
наружу поверхности S
выйдет положительный заряд dq₊^*=₊dSсos.

Согласно
закону сохранения заряда одновременно
через элемент dS
внутрь поверхности S
войдет отрицательный заряд dq_^*=_dSсos.
Тогда суммарный связанный заряд,
выходящий наружу поверхности S
через элемент dS,

dq^*=₊dSсos+_dScos.

С
учетом того, что
=,для
суммарного заряда получим

dq^*=dScos,
(8)

где
=₊+
_

расстояние, на которое сместились
положительные и отрицательные связанные
заряды изотропного диэлектрика друг
относительно друга при поляризации.
Поскольку
=
дипольный момент единицы объема
диэлектрика, или Р =иdq^*
= PdSсos,
то суммарный связанный заряд

.
(9)

Скалярное
произведение в формуле (6.9) является
элементарным потоком вектора
сквозь произвольную замкнутую поверхность.

Интегрируя
выражение (4.9) по всей замкнутой поверхности
S,
найдем полный заряд, который вышел при
поляризации из объема, охватываемого
этой поверхностью, т. е.

q^*
==
q^*.
(10)

Внутри
замкнутой поверхности S
останется избыточный связанный заряд
q^*.
Таким образом, вышедший заряд равен
оставшемуся внутри поверхности S
избыточному связанному заряду с обратным
знаком.

Вывод:
Поток вектора

сквозь
произвольную замкнутую поверхность
равен взятому с обратным знаком
избыточному связанному заряду диэлектрика
в объеме, охватываемом этой поверхностью,
т. е.

=
q^*.
(11)

Следовательно,
формула (11) выражает теорему Гаусса для
вектора поляризации
.

В
дифференциальной форме теорема Гаусса
для вектора поляризации
записывается
в виде

,
(12)

т.
е. дивергенция поля вектора
равна с обратным знаком объемной
плотности избыточного связанного
заряда.

Замечание:
объемная
плотность избыточных связанных зарядов
внутри диэлектрика равна нулю при
одновременном выполнении следующих
условий:

внутри
диэлектрика не должно быть сторонних
зарядов (
= 0);

2)
диэлектрик должен быть изотропным и
однородным.

Источник

Introduction to Polarization

You can use the Phased Array System Toolbox™ software to simulate radar systems that transmit, propagate, reflect,
and receive polarized electromagnetic fields. By including this capability, the
toolbox can realistically model the interaction of radar waves with targets and the
environment.

It is a basic property of plane waves in free-space that the directions of the
electric and magnetic field vectors are orthogonal to their direction of
propagation. The direction of propagation of an electromagnetic wave is determined
by the Poynting vector

In this equation, E represents
the electric field and H represents the magnetic
field. The quantity, S, represents the magnitude
and direction of the wave’s energy flux. Maxwell’s equations, when applied to plane
waves, produce the result that the electric and magnetic fields are related by

The vector s, the unit vector in
the S direction, represents the direction of
propagation of the wave. The quantity, Z, is the wave
impedance and is a function of the electric permittivity and the
magnetic permeability of medium in which the wave travels.

After manipulating the two equations, you can see that the electric and magnetic
fields are orthogonal to the direction of propagation

This last result proves that there are really only two
independent components of the electric field, labeled
E_x and
E_y. Similarly, the magnetic field
can be expressed in terms of two independent components. Because of the
orthogonality of the fields, the electric field can be represented in terms of two
unit vectors orthogonal to the direction of propagation.

The unit vectors together with the unit vector in direction of propagation

form a right-handed orthonormal triad. Later, these vectors and
the coordinates they define will be related to the coordinates of a specific radar
system. Because the electric and magnetic fields are determined by each other, only
the properties of the electric field need be consider.

For a radar system, the electric and magnetic field are actually spherical waves,
rather than plane waves. However, in practice, these fields are usually measured in
the far field region or radiation zone of the radar source and are approximately
plane waves. In the far field, the waves are called
quasi-plane waves. A point lies in the far
field if its distance, R, from the source
satisfies R ≫D²/λ where
D is a typical dimension of the source, whether it is a
single antenna or an array of antennas.

Polarization applies to purely sinusoidal signals. The most general expression for
a sinusoidal plane-wave has the form

The quantities E_x0 and
E_y0 are the real-valued,
non-negative, amplitudes of the components of the electric field and
ϕ_x and
ϕ_y are field’s phases. This
expression is the most general one used for a polarized wave.
An electromagnetic wave is polarized if the ratio of the
amplitudes of its components and phase difference between it components do not
change with time. The definition of polarization can be broadened to include
narrowband signals, for which the bandwidth is small
compared to the center or carrier frequency of the signal. The amplitude ratio and
phases difference vary slowly with time when compared to the period of the wave and
may be thought of as constant over many oscillations.

You can usually suppress the spatial dependence of the field and write the
electric field vector as

Linear and Circular Polarization

The preceding equation for a polarized plane wave shows that the tip of the
two-dimensional electric field vector moves along a path which lies in a plane
orthogonal to field’s direction of propagation. The shape of the path depends upon
the magnitudes and phases of the components. For example, if
ϕ_x =
ϕ_y, you can remove the time
dependence and write

This equation represents a straight line through the origin with positive slope.
Conversely, suppose ϕ_x = ϕ_y +
π. Then, the tip of the electric field vector follows a straight line
through the origin with negative slope

These two polarization cases are named linear
polarized because the field always oscillates along a straight line
in the orthogonal plane. If E_x0= 0, the
field is vertically polarized, and if
E_y0 = 0 the field is
horizontally polarized.

A different case occurs when the amplitudes are the same,
E_x =
E_y, but the phases differ by
±π/2

By squaring both sides, you can show that the tip of the electric
field vector obeys the equation of a circle

While this equation gives the path the vector takes, it does not tell you in what
direction the electric field vector travels around the circle. Does it rotate
clockwise or counterclockwise? The rotation direction depends upon the sign of
π/2 in the phase. You can see this dependency by examining
the motion of the tip of the vector field. Assume the common phase angle, ϕ
= 0. This assumption is permissible because the common phase only
determines starting position of the vector and does not change the shape of its
path. First, look at the +π/2 case for a wave travelling along
the s-direction (out of the page). At t=0, the
vector points along the x-axis. One quarter period later, the
vector points along the negative y-axis. After another quarter
period, it points along the negative x-axis.

MATLAB^® uses the IEEE convention to assign the names
right-handed or left-handed
polarization to the direction of rotation of the electric vector, rather than
clockwise or counterclockwise. When
using this convention, left or right handedness is determined by pointing your left
or right thumb along the direction of propagation of the wave. Then, align the curve
of your fingers to the direction of rotation of the field at a given point in space.
If the rotation follows the curve of your left hand, then the wave is left-handed
polarized. If the rotation follows the curve of your right hand, then the wave is
right-handed polarized. In the preceding scenario, the field is left-handed
circularly polarized (LHCP). The phase difference –π/2
corresponds to right-handed circularly polarized wave (RHCP). The following figure
provides a three-dimensional view of what a LHCP electromagnetic wave looks like as
it moves in the s-direction.

When the terms clockwise or
counterclockwise are used they depend upon how you look at
the wave. If you look along the direction of propagation, then the clockwise
direction corresponds to right-handed polarization and counterclockwise corresponds
to left-handed polarization. If you look toward where the wave is coming from, then
clockwise corresponds to left-handed polarization and counterclockwise corresponds
to right-handed polarization.

Left-Handed Circular Polarization

The figure below shows the appearance of linear and circularly polarized fields as
they move towards you along the s-direction.

Linear and Circular Polarization

Elliptic Polarization

Besides the linear and circular states of polarization, a third type of
polarization is elliptic polarization. Elliptic polarization
includes linear and circular polarization as special cases.

As with linear or circular polarization, you can remove the time dependence to
obtain the locus of points that the tip of the electric field vector travels

In this case, φ = φ_y –
φ_x. This equation represents a tilted
two-dimensional ellipse. Its size and shape are determined by the component
amplitudes and phase difference. The presence of the cross term indicates that the
ellipse is tilted. The equation does not, just as in the circularly polarized case,
provide any information about the rotation direction. For example, the following
figure shows the instantaneous state of the electric field but does not indicate the
direction in which the field is rotating.

The size and shape of a two-dimensional ellipse can be defined by three
parameters. These parameters are the lengths of its two axes, the semi-major axis,
a, and semi-minor axis, b, and a tilt
angle, τ. The following figure illustrates the three parameters
of a tilted ellipse. You can derive them from the two electric field amplitudes and
phase difference.

Polarization Ellipse

Polarization can best be understood in terms of complex signals. The complex
representation of a polarized wave has the form

Define the complex polarization ratio as
the ratio of the complex amplitudes

where ϕ = ϕ_y –
ϕ_x.

It is useful to introduce the polarization vector. For the
complex polarized electric field above, the polarization vector, P, is obtained by normalizing the electric field

where
E_m² =
E_x0² +
E_y0² is the
magnitude of the wave.

The overall size of the polarization ellipse is not important because that can
vary as the wave travels through space, especially through geometric attenuation.
What is important is the shape of the ellipse. Thus, the significant ellipse
parameters are the ratio of its axis dimensions, a/b, called the
axial ratio, and the tilt angle,
τ. Both of these quantities can be determined from the ratio
of the component amplitudes and the phase difference, or, equivalently, from the
polarization ratio. Another quantity, equivalent to the axial ratio, is the
ellipticity angle, ε.

In Phased Array System Toolbox, use the polratio function to convert the
complex amplitudes fv=[Eh;Ev] to the polarization ratio.

In radar
systems, it is common to use the subscripts, H and
V, denoting the horizontal and vertical components, instead
of x and y. Phased Array System Toolbox functions follow this convention for writing polarized fields where
E_H corresponds to
E_X and
E_V corresponds to
E_V.

Tilt Angle

The tilt angle is defined as the positive (counterclockwise) rotation angle
from the x-axis to the semi-major axis of the ellipse.
Because of the symmetry properties of the ellipse, the tilt angle,
τ, need only be defined in the range –π/2 ≤ τ ≤
π/2. You can find the tilt angle by determining the rotated
coordinate system in which the semi-major and semi-minor axes align with the
rotated coordinate axes. Then, the ellipse equation has no cross-terms. The
solution takes the form

where φ = φ_V –
φ_H. Notice that you can rewrite this
equation strictly in terms of the amplitude ratio and the phase
difference.

Axial Ratio and Ellipticity Angle

After solving for the tilt angle, you can determine the semi-major and
semi-minor axis lengths. Conceptually, you rotate the ellipse clockwise by the
tilt angle and measure the lengths of the intersections of the ellipse with the
H– and V-axes. The point of
intersection with the larger value is the semi-major axis, a,
and the one with the smaller value is the semi-minor axis,
b.

The axial ratio is defined as AR = a/b
and, by construction, is always greater than or equal to one. The
ellipticity angle is defined by

and always lies in the range –π/4 ≤ ε ≤
π/4.

If you define the auxiliary angle, α, by

then, the ellipticity angle is given by

Both the axial ratio and ellipticity angle are defined from
the amplitude ratio and phase difference and are independent of the overall
magnitude of the field.

Rotation Sense

For elliptic polarization, just as with circular polarization, you need
another parameter to completely describe the ellipse. This parameter must
provide the rotation sense or the direction that the tip of the electric (or
magnetic vector) moves in time. The rate of change of the angle that the field
vector makes with the x-axis is proportion to –sin
φ where φ is the phase difference. If
sin φ is positive, the rate of change is negative,
indicating that the field has left-handed polarization. If sin
φ is negative, the rate of change is positive or right-handed
polarization.

The function polellip lets you find the values
of the parameters of the polarization ellipse from either the field component
vector fv=[Eh;Ev] or the polarization ratio,
p.

fv=[Ey;Ex];
[tau,epsilon,ar,rs] = polellip(fv);
p = polratio(fv);
[tau,epsilon,ar,rs] = polellip(p);

The
variables tau, epsilon,
ar and rs represent the tilt angle,
ellipticity angle, axial ratio and rotation sense, respectively. Both syntaxes
give the same result.

Polarization Value Summary

This table summaries several different common polarization states and the
values of the amplitudes, phases, and polarization ratio that produce
them:

Polarization	Amplitudes	Phases	Polarization Ratio
Linear positive slope	Any non-negative real values for E_H, E_V.	φ_V = φ_H	Any non-negative real number
Linear negative slope	Any non-negative real values for E_H, E_V	φ_V = φ_H+ π	Any negative real number
Right-Handed Circular	E_H=E_V	φ_V= φ_H– π/2	–i
Left-Handed Circular	E_H=E_V	φ_V= φ_H + π/2	i
Right-Handed Elliptical	Any non-negative real values for E_H, E_V	sin (φ_V– φ_H) < 0	sin(arg ρ) < 0
Left-Handed Elliptical	Any non-negative real values for E_H, E_V	sin (φ_V– φ_H) >0	sin(arg ρ) > 0

Linear and Circular Polarization Bases

As shown earlier, you can express a polarized electric field as a linear
combination of basis vectors along the H and V
directions. For example, the complex electric field vectors for the right-handed
circularly polarized (RHCP) wave and the left-handed circularly polarized (LHCP)
wave, take the form:

In this equation, the positive sign is for the LHCP field and the
negative sign is for the RHCP field. These two special combinations can be given a
new name. Define a new basis vector set, called the circular basis set

You can express any polarized field in terms of the circular
basis set instead of the linear basis set. Conversely, you can also write the linear
polarization basis in terms of the circular polarization basis

Any general elliptic field can be written as a combination of
circular basis vectors

Jones Vector

The polarized field is orthogonal to the wave’s direction of propagation.
Thus, the field can be completely specified by the two complex components of the
electric field vector in the plane of polarization. The formulation of a
polarized wave in terms of two-component vectors is called the Jones
vector formulation. The Jones vector formulation can be
expressed in either a linear basis or a circular basis or any basis. This table
shows the representation of common polarizations in a linear basis and circular
basis.

Common Polarizations	Jones Vector in Linear Basis	Jones Vector in Circular Basis
Vertical	`[0;1]`	`1/sqrt(2)*[-1;1]`
Horizontal	`[1;0]`	`1/sqrt(2)*[1;1]`
45° Linear	`1/sqrt(2)*[1;1]`	`1/sqrt(2)*[1-1i;1+1i]`
135° Linear	`1/sqrt(2)*[1;-1]`	`1/sqrt(2)*[1+1i;1-1i]`
Right Circular	`1/sqrt(2)*[1;-1i]`	`[0;1]`
Left Circular	`1/sqrt(2)*[1;1i]`	`[1;0]`

Stokes Parameters and the Poincaré Sphere

The polarization ellipse is an instantaneous representation of a polarized
wave. However, its parameters, the tilt angle and the ellipticity angle, are
often not directly measurable, particularly at very high frequencies such as
light frequencies. However, you can determine the polarization from measurable
intensities of the polarized field.

The measurable intensities are the Stokes parameters,
S₀,
S₁,
S₂, and
S₃. The first Stokes
parameter, S₀, describes the total
intensity of the field. The second parameter,
S₁, describes the preponderance of
linear horizontally polarized intensity over linear vertically polarized
intensity. The third parameter, S₂,
describes the preponderance of linearly +45° polarized intensity over
linearly 135° polarized intensity. Finally,
S₃ describes the preponderance
of right circularly polarized intensity over left circularly polarized
intensity. The Stokes parameters are defined as

For completely polarized fields, you can show by time averaging the
polarization ellipse equation that

Thus, there are only three independent Stokes’
parameters.

For partially polarized fields, in contrast, the Stokes parameters satisfy
the inequality

The Stokes parameters are related to the tilt and ellipticity angles,
τ and ε

and inversely by

After you measure the Stokes’ parameters, the shape of the
ellipse is completely determined by the preceding equations.

The two-dimensional Poincaré sphere can help you visualize the state of a
polarized wave. Any point on or in the sphere represents a state of polarization
determined by the four Stokes parameters, S₀,
S₁, S₂, and
S₃. On the Poincaré sphere,
the angle from the
S₁-S₂ plane
to a point on the sphere is twice the ellipticity angle, ε.
The angle from the S₁– axis to the
projection of the point into the
S₁-S₂
plane is twice the tilt angle, τ.

As an example, solve for the Stokes parameters of a RHCP field,
fv=[1,-i], using the stokes function.

Sources of Polarized Fields

Antennas couple propagating electromagnetic radiation to electrical currents in
wires, electromagnetic fields in waveguides or aperture fields. This coupling is a
phenomenon common to both transmitting and receiving antennas. For some transmitting
antennas, source currents in a wire produce electromagnetic waves that carrying
power in all directions. Sometimes an antenna provides a means for a guided
electromagnetic wave on a transmission line to transition to free-space waves such
as a waveguide feeding a dish antennas. For receiving antennas, electromagnetic
fields can induce currents in wires to generate signals to be then amplified and
passed on to a detector.

For transmitting antennas, the shape of the antenna is chosen to enhance the power
projected into a given direction. For receiving antennas, you choose the shape of
the antenna to enhance the power received from a particular direction. Often, many
transmitting antennas or receiving antennas are formed into an
array. Arrays increase the transmitted power for a
transmitting system or the sensitivity for a receiving system. They improve
directivity over a single antenna.

An antenna can be assigned a polarization. The polarization of a transmitting
antenna is the polarization of its radiated wave in the far field. The polarization
of a receiving antenna is actually the polarization of a plane wave, from a given
direction, resulting in maximum power at the antenna terminals. By the reciprocity
theorem, all transmitting antennas can serve as receiving antennas and vice
versa.

Each antenna or array has an associated local Cartesian coordinate system
(x,y,z) as shown in the following figure. See Global and Local Coordinate Systems for more information. The local
coordinate system can also be represented by a spherical coordinate system using
azimuth, elevation and range coordinates, az, el, r, or
alternately written, (φ,θ,r), as shown. At each point in the far
field, you can create a set of unit spherical basis vectors, {e^H,e^V,r^}. The basis vectors are aligned with the (φ,θ,r)
directions, respectively. In the far field, the electric field is orthogonal to the
unit vector r^. The components of a polarized field with respect to this basis,
(E_H,E_V),
are called the horizontal and vertical components of the polarized field. In radar,
it is common to use (H,V) instead of (x,y) to
denote the components of a polarized field. In the far field, the polarized electric
field takes the form

In this equation, the quantity F(φ,θ) is called the vector radiation
pattern of the source and contains the angular dependence of the
field in the far-field region.

Short Dipole Antenna Element

The simplest polarized antenna is the dipole antenna which consist
of a split length of wire coupled at the middle to a coaxial cable.
The simplest dipole, from a mathematical perspective, is the Hertzian dipole,
in which the length of wire is much shorter than a wavelength. A diagram
of the short dipole antenna of length L appears
in the next figure. This antenna is fed by a coaxial feed which splits
into two equal length wires of length L/2. The
current, I, moves along the z-axis
and is assumed to be the same at all points in the wire.

The electric field in the far field has the form

The next example computes the vertical and horizontal polarization
components of the field. The vertical component is a function of elevation
angle and is axially symmetric. The horizontal component vanishes
everywhere.

The toolbox lets you model a short dipole antenna using the phased.ShortDipoleAntennaElement
System object™.

Short-Dipole Polarization Components

Compute the vertical and horizontal polarization components of the field created by a short-dipole antenna pointed along the z-direction. Plot the components as a function of elevation angle from 0° to 360°.

Create the phased.ShortDipoleAntennaElement System object™.

antenna = phased.ShortDipoleAntennaElement(...
    'FrequencyRange',[1,2]*1e9,'AxisDirection','Z');

Compute the antenna response. Because the elevation angle argument to antenna is restricted to ±90°, compute the responses for 0° azimuth and then for 180° azimuth. Combine the two responses in the plot. The operating frequency of the antenna is 1.5 GHz.

el = -90:90;
az = zeros(size(el));
fc = 1.5e9;
resp = antenna(fc,[az;el]);
az = 180.0*ones(size(el));
resp1 = antenna(fc,[az;el]);

Overlay the responses in the same figure.

figure(1)
subplot(121)
polarplot(el*pi/180.0,abs(resp.V.'),'b')
hold on
polarplot((el+180)*pi/180.0,abs(resp1.V.'),'b')
str = sprintf('%sn%s','Vertical Polarization','vs Elevation Angle');
title(str)
hold off
subplot(122)
polarplot(el*pi/180.0,abs(resp.H.'),'b')
hold on
polarplot((el+180)*pi/180.0,abs(resp1.H.'),'b')
str = sprintf('%sn%s','Horizontal Polarization','vs Elevation Angle');
title(str)
hold off

The plot shows that the horizontal component vanishes, as expected.

Crossed Dipole Antenna Element

You can use a cross-dipole antenna to generate circularly-polarized
radiation. The crossed-dipole antenna consists of two identical but
orthogonal short-dipole antennas that are phased 90° apart. A
diagram of the crossed dipole antenna appears in the following figure.
The electric field created by a crossed-dipole antenna constructed
from a y-directed short dipole and a z-directed
short dipole has the form

The polarization ratio E_V/E_H,
when evaluated along the x-axis, is just –i which
means that the polarization is exactly RHCP along the x-axis.
It is predominantly RHCP when the observation point is close to the x-axis.
Moving away from the x-axis, the field becomes
a mixture of LHCP and RHCP polarizations. Along the –x-axis,
the field is LHCP polarized. The figure illustrates, for a point near
the x, that the field is primarily RHCP.

The toolbox lets you model a crossed-dipole antenna using the phased.CrossedDipoleAntennaElement
System object.

LHCP and RHCP Polarization Components

This example plots the right-hand and left-hand circular polarization components of fields generated by a crossed-dipole antenna at 1.5 GHz. You can see how the circular polarization changes from pure RHCP at 0 degrees azimuth angle to pure LHCP at 180 degrees azimuth angle, both at 0 degrees elevation angle.

Create the phased.CrossedDipoleAntennaElement object.

fc = 1.5e9;
antenna = phased.CrossedDipoleAntennaElement('FrequencyRange',[1,2]*1e9);

Compute the left-handed and right-handed circular polarization components from the antenna response.

az = [-180:180];
el = zeros(size(az));
resp = antenna(fc,[az;el]);
cfv = pol2circpol([resp.H.';resp.V.']);
clhp = cfv(1,:);
crhp = cfv(2,:);

Plot both circular polarization components at 0 degrees elevation.

polar(az*pi/180.0,abs(clhp))
hold on
polar(az*pi/180.0,abs(crhp))
title('LHCP and RHCP vs Azimuth Angle')
legend('LHCP','RHCP')
hold off

Arrays Supporting Polarization

You can create polarized fields from arrays by using polarized antenna
elements as a value of the Elements property of an array
System object. All Phased Array System Toolbox arrays support polarization.

Scattering Cross-Section Matrix

After a polarized field is created by an antenna system, the field radiates to the
far-field region. When the field propagates into free space, the polarization
properties remain unchanged until the field interacts with a material substance
which scatters the field into many directions. In such situations, the amplitude and
polarization of the scattered wave can differ from the incident wave polarization.
The scattered wave polarization may depend upon the direction in which the scattered
wave is observed. The exact way that the polarization changes depends upon the
properties of the scattering object. The quantity describing the response of an
object to the incident field is called the radar scattering cross-section matrix
(RSCM), S. You can measure the scattering matrix as follows. When
a unit amplitude horizontally polarized wave is scattered, both a horizontal and a
vertical scattered component are produced. Call these two components
S_HH and
S_VH. These components are complex
numbers containing the amplitude and phase changes from the incident wave.
Similarly, when a unit amplitude vertically polarized wave is scattered, the
horizontal and vertical scattered component produced are
S_HV and
S_VV. Because, any incident field
can be decomposed into horizontal and vertical components, you can arrange these
quantities into a matrix and write the scattered field in terms of the incident field

In general, the scattering cross-section matrix depends upon the
angles that the incident and scattered fields make with the object. When the
incident field is scattered back to the transmitting antenna or,
backscattered, the scattering matrix is symmetric.

Polarization Signature

To understand how the scattered wave depends upon the polarization of the
incident wave, you need to examine all possible scattered field polarizations
for each incident polarization. Because this amount of data is difficult to
visualize, consider two cases:

For the copolarization case, the scattered
polarization has the same polarization as the incident field.
For the cross-polarization case, the
scattered polarization has an orthogonal polarization to the
incident field.

You can represent the incident polarizations in terms of the tilt
angle-ellipticity angle pair (τ,ε). Every unit incident polarization vector can be expressed as

while the orthogonal polarization vector is

When you have an RSCM matrix, S, form the
copolarization signature by computing

where []* denotes complex conjugation. To
obtain the cross-polarization signature, compute

You can compute both the copolarization and cross
polarization signatures using the polsignature function. This
function returns the absolute value of the scattered power (normalized by its
maximum value). The next example shows how to plot the polarization signatures
for the RSCM matrix

for all possible incident polarizations. The range of values
of the ellipticity angle and tilt span the entire possible range of
polarizations.

Plot Polarization Signatures

Plot the copolarization and cross-polarization signatures of the scattering matrix

[2i0.50.5-i].

Specify the scattering matrix. and specify the range of ellipticity angles and orientation (tilt) angles that define the polarization states. These angles cover all possible incident polarization states.

rscmat = [1i*2,0.5;0.5,-1i];
el = [-45:45];
tilt = [-90:90];

Plot the copolarization signatures for all incident polarizations.

polsignature(rscmat,'c',el,tilt)

Plot the cross-polarizations signatures for all incident polarizations.

polsignature(rscmat,'x',el,tilt)

Polarization Loss Due to Field and Receiver Mismatch

An antenna that is used to receive polarized electromagnetic waves achieves its
maximum output power when the antenna polarization is matched to the polarization of
the incident electromagnetic field. Otherwise, there is polarization loss:

The polarization loss is computed from the projection (or dot product)
of the transmitted field’s electric field vector onto the receiver
polarization vector.
Loss occurs when there is a mismatch in direction of the two vectors,
not in their magnitudes.
The polarization loss factor describes the fraction of incident power
that has the correct polarization for reception.

Using the transmitter’s spherical basis at the receiver’s position, you can
represent the incident electric field, (E_iH,
E_iV), by

You can represent the receiver’s polarization vector,
(P_H, P_V),
in the receiver’s local spherical basis by:

The next figure shows the construction of the transmitter and receiver spherical
basis vectors.

The polarization loss is defined by:

and varies between 0 and 1. Because the vectors are defined with
respect to different coordinate systems, they must be converted to the global
coordinate system to form the projection. The toolbox function polloss computes the polarization mismatch between an incident field
and a polarized antenna.

To achieve maximum output power from a receiving antenna, the matched antenna
polarization vector must be the complex conjugate of the incoming field’s
polarization vector. As an example, if the incoming field is RHCP, with polarization
vector given by er=12(ex−iey), the optimum receiver antenna polarization is LHCP. The
introduction of the complex conjugate is needed because field polarizations are
described with respect to its direction of propagation, whereas the polarization of
a receive antenna is usually specified in terms of the direction of propagation
towards the antenna. The complex conjugate corrects for the opposite sense of
polarization when receiving.

As an example, if the transmitting antenna transmits an RHCP field, the
polarization loss factors for various received antenna polarizations are

Receive Antenna Polarization	Receive Antenna Polarization Vector	Polarization Loss Factor	Polarization Loss Factor (dB)
Horizontal linear	e_H	1/2	3 dB
Vertical linear	e_V	1/2	3
RHCP	er=12(ex−iey)	0	∞
LHCP	el=12(ex+iey)	1	0

Model Radar Transmitting Polarized Radiation

This example models a tracking radar based on a 31-by-31 (961-element) uniform rectangular array (URA). The radar is designed to follow a moving target. At each time instant, the radar points in the known direction of the target. The basic radar requirements are the probability of detection, pd, the probability of false alarm, pfa, the maximum unambiguous range, max_range, and the range resolution, range_res, (all distance units are in meters). The range_gate parameter limits the region of interest to a range smaller than the maximum range. The operating frequency is set in fc. The simulation lasts for numpulses pulses.

Radar Definition

Set up the radar operating parameters. The existing radar design meets the following specifications.

pd = 0.9;            % Probability of detection
pfa = 1e-6;          % Probability of false alarm
max_range = 1500*1000; % Maximum unambiguous range
range_res = 50.0;    % Range resolution
rangegate = 5*1000;  % Assume all objects are in this range
numpulses = 200;     % Number of pulses to integrate
fc = 8e9;            % Center frequency of pulse
c = physconst('LightSpeed');
tmax = 2*rangegate/c; % Time of  echo from object at rangegate

Pulse Repetition Interval

Set the pulse repetition interval, PRI, and pulse repetition frequency, PRF, based on the maximum unambiguous range.

PRI = 2*max_range/c;
PRF = 1/PRI;

Transmitted Signal

Set up the transmitted rectangular waveform using the phased.RectangularWaveform System object™. The waveform pulse width, pulse_width, and pulse bandwidth, pulse_bw, are determined by the range resolution, range_res, that you select. Specify the sampling rate, fs, to be twice the pulse bandwidth. The sampling rate must be an integer multiple of the PRF. Therefore, modify the sampling rate to satisfy the requirement.

pulse_bw = c/(2*range_res);    % Pulse bandwidth
pulse_width = 1/pulse_bw;               % Pulse width
fs = 2*pulse_bw;                        % Sampling rate
n = ceil(fs/PRF);
fs = n*PRF;
waveform = phased.RectangularWaveform('PulseWidth',pulse_width,'PRF',PRF,...
    'SampleRate',fs);

Antennas and URA Array

The array consists of short-dipole antenna elements. Use the phased.ShortDipoleAntennaElement System object to create a short-dipole antenna oriented along the z-axis.

antenna = phased.ShortDipoleAntennaElement(...
    'FrequencyRange',[5e9,10e9],'AxisDirection','Z');

Define a 31-by-31 Taylor tapered uniform rectangular array using the phased.URA System object. Set the size of the array using the number of rows, numRows, and the number of columns, numCols. The distance between elements, d, is slightly smaller than one-half the wavelength, lambda. Compute the array taper, tw, using separate Taylor windows for the row and column directions. Obtain the Taylor weights using the taylorwin function. Plot the 3-D array response using the array pattern method.

numCols = 31;
numRows = 31;
lambda = c/fc;
d = 0.9*lambda/2; % Nominal spacing
wc = taylorwin(numCols);
wr = taylorwin(numRows);
tw = wr*wc';
array = phased.URA('Element',antenna,'Size',[numCols,numRows],...
    'ElementSpacing',[d,d],'Taper',tw);
pattern(array,fc,-180:180,-90:90,'CoordinateSystem','polar','Type','powerdb',...
    'Polarization','V');

Radar Platform Motion

Next, set the position and motion of the radar platform in the phased.Platform System object. The radar is assumed to be stationary and positioned at the origin. Set the Velocity property to [0,0,0] and the InitialPosition property to [0,0,0]. Set the InitialOrientationAxes property to the identity matrix to align the radar platform coordinate axes with the global coordinate system.

radarPlatformAxes = [1 0 0;0 1 0;0 0 1];
radarplatform = phased.Platform('InitialPosition',[0;0;0],...
    'Velocity',[0;0;0],'OrientationAxes',radarPlatformAxes);

Transmitters and Receivers

In radar, the signal propagates in the form of an electromagnetic wave. The signal is radiated and collected by the antennas used in the radar system. Associate the array with a radiator System object, phased.Radiator, and two collector System objects, phased.Collector. Set the WeightsInputPort property of the radiator to true to enable dynamic steering of the transmitted signal at each execution of the radiator. Creating the two collectors allows for collection of both horizontal and vertical polarization components.

radiator = phased.Radiator('Sensor',array,'OperatingFrequency',fc,...
    'PropagationSpeed',c,'CombineRadiatedSignals',true,...
    'Polarization','Combined','WeightsInputPort',true);
collector1 = phased.Collector('Sensor',array,'OperatingFrequency',fc,...
    'PropagationSpeed',c,'Wavefront','Plane','Polarization','Combined',...
    'WeightsInputPort',false);
collector2 = phased.Collector('Sensor',array,'OperatingFrequency',fc,...
    'PropagationSpeed',c,'Wavefront','Plane','Polarization','Combined',...
    'WeightsInputPort',false);

Estimate the peak power needed in the phased.Transmitter System object to calculate the desired radiated power levels. The transmitted peak power is the power required to achieve a minimum-detection SNR, snr_min. You can determine the minimum SNR from the probability of detection, pd, and the probability of false alarm, pfa, using the albersheim function. Then, compute the peak power, peak_power, from the radar equation. The peak power depends on the overall signal gain, which is the sum of the transmitting element gain, TransmitterGain and the array gain, AG. The peak power also depends on the maximum detection range, rangegate. Finally, you need to supply a target cross-section value, tgt_rcs. A scalar radar cross section is used in this code section as an approximation even though the full polarization computation later uses a 2-by-2 radar cross section scattering matrix.

Using the radar equation formula, estimate the total transmitted power to achieve a required detection SNR using all the pulses.

The SNR has contributions from the transmitting element gain as well as the array gain. Compute first an estimate of the array gain, then add the array gain to the transmitter gain to get the peak power which achieves the desired SNR.

Use an approximate target cross section of 1.0 for the radar equation even though the analysis calls for the full scattering matrix.
Set the maximum range to be equal to the value of ‘rangegate’ since targets outside that range are of no interest.
Compute the array gain as 10*log10(number of elements)
Assume each element has a gain of 20 dB.

snr_min = albersheim(pd, pfa, numpulses);
AG = 10*log10(numCols*numRows);
tgt_rcs = 1;
TransmitterGain = 20;
tau = waveform.PulseWidth;
Ts = 290;
dbterm = db2pow(snr_min - 2*TransmitterGain + AG);
peak_power = (4*pi)^3*physconst('Boltzmann')*Ts/tau/tgt_rcs/lambda^2*rangegate^4*dbterm

transmitter = phased.Transmitter('PeakPower',peak_power,'Gain',TransmitterGain,...
    'LossFactor',0,'InUseOutputPort',true,'CoherentOnTransmit',true);

Define Target

We want to simulate the pulse returns from a target that is rotating so that the scattering cross-section matrix changes from pulse to pulse. Create a rotating target object and a moving target platform. The rotating target is represented later as an angle-dependent scattering matrix. Rotation is in degrees per second.

targetSpeed = 1000;
targetVec = [-1;1;0]/sqrt(2);
target = phased.RadarTarget('EnablePolarization',true,...
    'Mode','Monostatic','ScatteringMatrixSource','Input port',...
    'OperatingFrequency',fc);
targetPlatformAxes = [1 0 0;0 1 0;0 0 1];
targetRotRate = 45;
targetplatform = phased.Platform('InitialPosition',[3500.0; 0; 0],...
    'Velocity', targetSpeed*targetVec);

Other System Objects

Steering vector defined by phased.SteeringVector System object.
Beamformer defined by phased.PhaseShiftBeamformer System object. The DirectionSource property is set to 'Input Port' to enable the beamformer to always points towards the known target direction at each execution.
Free-space propagator using the phased.FreeSpace System object.
Receiver preamp model using the phased.ReceiverPreamp system object.

Signal Propagation

Because the reflected signals are received by an array, use a beamformer pointing to the steering direction to obtain the combined signal.

steeringvector = phased.SteeringVector('SensorArray',array,'PropagationSpeed',c,...
    'IncludeElementResponse',false);
beamformer = phased.PhaseShiftBeamformer('SensorArray',array,...
    'OperatingFrequency',fc,'PropagationSpeed',c,...
    'DirectionSource','Input port');
channel = phased.FreeSpace('SampleRate',fs,...
    'TwoWayPropagation',true,'OperatingFrequency',fc);
% Define a receiver with receiver noise
amplifier = phased.ReceiverPreamp('Gain',20,'LossFactor',0,'NoiseFigure',1,...
    'ReferenceTemperature',290,'SampleRate',fs,'EnableInputPort',true,...
    'PhaseNoiseInputPort',false,'SeedSource','Auto');

For such a large PRI and sampling rate, there will be too many samples per element. This will cause problems with the collector which has 961 channels. To keep the number of samples manageable, set a maximum range of 5 km. We know that the target is within this range.

This set of axes specifies the direction of the local coordinate axes with respect to the global coordinate system. This is the orientation of the target.

Processing Loop

Pre-allocate arrays for collecting data to be plotted.

sig_max_V  = zeros(1,numpulses);
sig_max_H  = zeros(1,numpulses);
tm_V = zeros(1,numpulses);
tm_H = zeros(1,numpulses);

After all the System objects are created, loop over the number of pulses to create the reflected signals.

maxsamp = ceil(tmax*fs);
fast_time_grid = (0:(maxsamp-1))/fs;
rotangle = 0.0;
for m = 1:numpulses
    x = waveform(); % Generate pulse
    % Capture only samples within range gated
    x = x(1:maxsamp);
    [s, tx_status] = transmitter(x);   % Create transmitted pulse
    % Move the radar platform and target platform.
    [radarPos,radarVel] = radarplatform(1/PRF);
    [targetPos,targetVel] = targetplatform(1/PRF);    
    % Compute the known target angle
    [targetRng,targetAng] = rangeangle(targetPos,...
        radarPos,...
        radarPlatformAxes);
    % Compute the radar angle with respect to the target axes.
    [radarRng,radarAng] = rangeangle(radarPos,...
        targetPos,...
        targetPlatformAxes);    
    % Calculate the steering vector designed to track the target
    sv = steeringvector(fc,targetAng);
    % Radiate the polarized signal toward the targat
    tsig1 = radiator(s,targetAng,radarPlatformAxes,conj(sv));
    % Compute the two-way propagation loss (4*pi*R/lambda)^2
    tsig2 = channel(tsig1,radarPos,targetPos,radarVel,targetVel);
    % Create a very simple model of a changing scattering matrix
    scatteringMatrix = [cosd(rotangle),0.5*sind(rotangle);...
        0.5*sind(rotangle),cosd(rotangle)];
    rsig1 = target(tsig2,radarAng,targetPlatformAxes,scatteringMatrix);  % Reflect off target
    % Collect the vertical component of the radiation.
    rsig3V = collector1(rsig1,targetAng,radarPlatformAxes);   
    % Collect the horizontal component of the radiation. This
    % second collector is rotated around the x-axis to be more
    % sensitive to horizontal polarization
    rsig3H = collector2(rsig1,targetAng,rotx(90)*radarPlatformAxes);  
    % Add receiver noise to both sets of signals
    rsig4V = amplifier(rsig3V,~(tx_status>0)); % Receive signal
    rsig4H = amplifier(rsig3H,~(tx_status>0)); % Receive signal
    % Beamform the signal
    rsigV = beamformer(rsig4V,targetAng); % Beamforming
    rsigH = beamformer(rsig4H,targetAng); % Beamforming   
    % Find the maximum returns for each pulse and store them in
    % a vector. Store the pulse received time as well.
    [sigmaxV,imaxV] = max(abs(rsigV));
    [sigmaxH,imaxH] = max(abs(rsigH));
    sig_max_V(m) = sigmaxV;
    sig_max_H(m) = sigmaxH;
    tm_V(m) = fast_time_grid(imaxV) + (m-1)*PRI;
    tm_H(m) = fast_time_grid(imaxH) + (m-1)*PRI;
    
    % Update the orientation of the target platform axes
    targetPlatformAxes = ...
        rotx(PRI*targetRotRate)*targetPlatformAxes;
    rotangle = rotangle + PRI*targetRotRate;
end
% Plot the vertical and horizontal polarization for each pulse as a
% function of time.
plot(tm_V,sig_max_V,'.')
hold on
plot(tm_H,sig_max_H,'r.')
hold off
xlabel('Time (sec)')
ylabel('Amplitude')
title('Vertical and Horizontal Polarization Components')
legend('Vertical','Horizontal')
grid on

Источник

У этого термина существуют и другие значения, см. Поляризация.

Схематическое изображение ориентации диполей в диэлектрической среде под воздействием электрического поля

Поляриза́ция диэле́ктриков — явление, связанное с ограниченным смещением связанных зарядов в диэлектрике или поворотом электрических диполей, обычно под воздействием внешнего электрического поля.

Поляризацию диэлектриков характеризует вектор электрической поляризации. Физический смысл данного вектора — это дипольный момент, отнесённый к единице объёма диэлектрика. Иногда вектор поляризации коротко называют просто поляризацией (и получается, что один термин обозначает и явление, и его количественный показатель).

Различают поляризацию, наведённую в диэлектрике под действием внешнего поля, и спонтанную (самопроизвольную) поляризацию, которая возникает в сегнетоэлектриках при отсутствии внешнего поля. В некоторых случаях поляризация диэлектрика (сегнетоэлектрика) происходит под действием механических напряжений, сил трения или вследствие изменения температуры.

Поляризация не изменяет суммарного заряда в любом макроскопическом объёме внутри однородного диэлектрика. Однако она сопровождается появлением на его поверхности связанных электрических зарядов с некоторой поверхностной плотностью σ. Эти связанные заряды создают в диэлектрике дополнительное макроскопическое поле c напряжённостью ${mathbf E}_{1}$ , направленное против внешнего поля с напряжённостью ${mathbf E}_{0}$ . В результате напряжённость поля внутри диэлектрика будет выражаться равенством ${displaystyle mathbf {E} =mathbf {E} _{0}-mathbf {E} _{1}}$ ,

Аналогом электрической поляризации в сфере магнетизма является эффект намагничивания, характеризуемый вектором намагниченности.

Типы поляризации[править | править код]

В зависимости от механизма поляризации, поляризацию диэлектриков можно подразделить на следующие типы:

Электронная — смещение электронных оболочек атомов под действием внешнего электрического поля. Самая быстрая поляризация (до 10⁻¹⁵ с). Не связана с потерями энергии.
Ионная — смещение узлов кристаллической решетки под действием внешнего электрического поля, причем смещение на величину, меньшую, чем величина постоянной решетки. Время протекания 10⁻¹³ с, без потерь.
Дипольная (Ориентационная) — протекает с потерями на преодоление сил связи и внутреннего трения. Связана с ориентацией диполей во внешнем электрическом поле.
Электронно-релаксационная — ориентация дефектных электронов во внешнем электрическом поле.
Ионно-релаксационная — смещение ионов, слабо закрепленных в узлах кристаллической структуры, либо находящихся в междуузлие.
Структурная — ориентация примесей и неоднородных макроскопических включений в диэлектрике. Самый медленный тип.
Самопроизвольная (спонтанная) — возникает в отсутствие внешнего электрического поля. Наблюдается в материалах, состоящих из отдельных доменов (областей). В каждом из доменов имеет своё, отличное от других доменов, направление, в результате чего суммарный дипольный момент материала равен нулю. При наложении внешнего электрического поля дипольные моменты доменов ориентируются вдоль поля. Возникающая при этом поляризация проявляет существенно нелинейные свойства даже при малых значениях внешнего поля; наблюдается явление гистерезиса. Такие диэлектрики (сегнетоэлектрики) отличаются очень высокими значениями диэлектрической проницаемости (от 900 до 7500 у некоторых видов конденсаторной керамики).
Резонансная — ориентация частиц, собственные частоты колебания которых совпадают с частотами внешнего электрического поля.
Миграционная поляризация обусловлена наличием в материале слоев с различной проводимостью, образованию объёмных зарядов, особенно при высоких градиентах напряжения; имеет большие потери и является поляризацией замедленного действия.

Поляризация диэлектриков (за исключением резонансной) максимальна в статических электрических полях. В переменных полях, в связи с наличием инерции электронов, ионов и электрических диполей, вектор электрической поляризации зависит от частоты.

Механизмы поляризации[править | править код]

Основной источник: ^[1]

Индуцированная электрическим полем
- Упругая (деформационная)
- Тепловая (прыжковая)
- Объемно-зарядная (миграционная)

Сравнительные параметры различных типов поляризации

Поляризация	Смещение частиц, нм, в поле $10^{6}$ В/м	Время релаксации, с	Концентрация частиц, ${displaystyle m^{-3}}$
Упругая (смещения)	$10^{-6}$	${displaystyle 10^{-12}-10^{-16}}$	$10^{{28}}$
Тепловая (прыжковая)		${displaystyle 10^{-6}-10^{-10}}$	$10^{{25}}$
Объемно-зарядная (миграционная)	$10^{{6}}$	${displaystyle 10^{4}-10^{-4}}$	$10^{{23}}$

Вызванная неэлектрическим воздействием
- Пьезополяризация
- Пирополяризация
- Фотополяризация
Существующая без внешних воздействий
- Спонтанная
- Остаточная

Зависимость вектора поляризации от внешнего поля[править | править код]

В постоянном поле[править | править код]

В слабых полях[править | править код]

В постоянном или достаточно медленно меняющемся от времени внешнем электрическом поле при достаточно малой величине напряженности этого поля, вектор поляризации (поляризованность) P, как правило (исключение составляют сегнетоэлектрики), линейно зависит от вектора напряженности поля E:

(в системе СГС),

${mathbf P}=varepsilon _{0}chi {mathbf E}$

(в Международной системе единиц (СИ); дальше формулы в этом параграфе приводятся только в СГС, формулы СИ и дальше отличаются лишь электрической постоянной $varepsilon _{0}$

)

где chi — коэффициент, зависящий от химического состава, концентрации, структуры (в том числе от агрегатного состояния) среды, температуры, механических напряжений и т. д. (от одних факторов более сильно, от других слабее, конечно же и в зависимости от диапазона изменений каждого), и называемый (электрической) поляризуемостью (а чаще, по крайней мере для того случая, когда он выражается скаляром — диэлектрической восприимчивостью) данной среды. Для однородной среды фиксированного состава и структуры в фиксированных условиях её можно считать константой. Однако в связи со всем сказанным выше вообще говоря chi зависит от точки пространства, времени (явно или через другие параметры) и т. д.

Для изотропных^[2] жидкостей, изотропных твердых тел или кристаллов достаточно высокой симметрии chi — просто число (скаляр). В более общем случае (для кристаллов низкой симметрии, под действием механических напряжений и т. д.) chi — тензор (симметричный тензор второго ранга, вообще говоря невырожденный), называемый тензором поляризуемости. В этом случае можно переписать формулу так (в компонентах):

$P_{i}=sum _{j} chi _{{ij}}E_{j},$

где величины со значками соответствуют компонентам векторов и тензора, соответствующим трем пространственным координатам.

Можно заметить, что поляризуемость — одна из наиболее удобных физических величин для простой иллюстрации физического смысла тензоров и применения их в физике.

Как и для всякого симметричного невырожденного тензора второго ранга, для тензора поляризуемости можно выбрать (если среда неоднородная — то есть тензор зависит от точки пространства — то по крайней мере локально, если же среда однородная, то и глобально) т. н. собственный базис — прямоугольные декартовы координаты, в которых матрица $chi _{{ij}}$ становится диагональной, то есть приобретает вид, при котором из девяти компонент $chi _{{ij}}$ отличными от нуля являются лишь три: $chi _{{11}}$ , $chi _{{22}}$ и $chi _{{33}}$ . В этом случае, обозначив для простоты $chi _{{ii}}$ как $chi _{i}$ , вместо предыдущей формулы получаем более простую

$P_{i}=chi _{i}E_{i}.$

Величины $chi _{i}$ называют главными поляризуемостями (или главными диэлектрическими восприимчивостями). Если среда в отношении поляризуемости изотропна, то все три главные поляризуемости равны друг другу, а действие тензора сводится к простому умножению на число.

В сильных полях[править | править код]

В достаточно сильных полях^[3] всё описанное выше осложняется тем, что по мере роста напряженности электрического поля рано или поздно теряется линейность зависимости P от E.

Характер появляющейся нелинейности и характерная величина поля, с которой нелинейность становится заметной, зависит от индивидуальных свойств среды, условий и т.п.

Можно выделить их связь с типами поляризации, описанными выше.

Так для электронной и ионной поляризации при полях, приближающихся к величинам порядка отношения потенциала ионизации к характерному размеру молекулы U₀/D, характерно сначала ускорение роста вектора поляризации с ростом поля (увеличение наклона графика P(E)), затем плавно переходящее в пробой диэлектрика.

Дипольная (Ориентационная) поляризация при обычно несколько более низких значениях напряженности внешнего поля — порядка kT/p (где p — дипольный момент молекулы, T — температура, k — константа Больцмана) — то есть когда энергия взаимодействия диполя (молекулы) с полем становится сравнимой со средней энергией теплового движения (вращения) диполя — наоборот начинает достигать насыщения (при дальнейшем росте напряженности поля должен рано или поздно включиться сценарий электронной или ионной поляризации, описанный выше, и кончающийся пробоем).

В зависящем от времени поле[править | править код]

Зависимость вектора поляризации от быстро меняющегося во времени внешнего поля достаточно сложна. Она зависит от конкретного вида изменения внешнего поля со временем, быстроты этого изменения (или, скажем, частоты колебаний) внешнего поля, превалирующего механизма поляризации в данном веществе или среде (который тоже оказывается разным для разных зависимостей внешнего поля от времени, частот и т. д.).

При достаточно медленном изменении внешнего поля поляризация в целом происходит как в постоянном поле или очень близко к этому (впрочем то, насколько медленным должно быть для этого изменение поля, зависит, и зачастую крайне сильно, от превалирующего типа поляризации и других условий, например температуры).

Одним из наиболее распространенных подходов к изучению зависимости поляризации от характера меняющегося во времени поля является исследование (теоретическое и экспериментальное) случая синусоидальной зависимости от времени внешнего поля и зависимости вектора поляризации (также меняющегося в этом случае по синусоидальному закону с той же частотой), его амплитуды и сдвига фазы от частоты.

Каждому механизму поляризации в целом соответствует тот или иной диапазон частот и общий характер зависимости от частоты.

Диапазон частот, в котором имеет смысл говорить о поляризации диэлектриков как таковой, простирается от нуля где-то до ультрафиолетовой области, в которой становится интенсивной ионизация под действием поля.

См. также[править | править код]

Диэлектрики
Вектор электрической поляризации
Электрическая индукция
Электростатическая индукция
Дипольный момент
Сегнетоэлектрики

Примечания[править | править код]

↑ Рез, 1989, с. 65.
↑ Обычно жидкости можно считать изотропными, однако это может оказаться верно не для всех классов жидкостей и может быть нарушено различными возмущениями (иногда — очень сильно, например, для растворов полимеров итп), поэтому лучше уточнить это явно.
↑ В этом параграфе подразумевается, что поле постоянно или медленно меняется во времени — то есть затронуты только вопросы, связанные с большой величиной напряженности поля; усложнения, связанные с достаточно быстрым изменением поля со временем, описаны далее в отдельном параграфе.

Литература[править | править код]

Рез И. С., Поплавко Ю. М. Диэлектрики. Основные свойства и применение в электронике. — М.: Радио и связь, 1989. — 288 с. — ISBN 5-256-00235-X.

Ссылки[править | править код]

dic.academic.ru/dic.nsf/natural_science/10203
dic.academic.ru/dic.nsf/polytechnic/7019

Некоторые внешние ссылки в этой статье ведут на сайты, занесённые в спам-лист.

Эти сайты могут нарушать авторские права, быть признаны неавторитетными источниками или по другим причинам быть запрещены в Википедии. Редакторам следует заменить такие ссылки ссылками на соответствующие правилам сайты или библиографическими ссылками на печатные источники либо удалить их (возможно, вместе с подтверждаемым ими содержимым).

Список проблемных доменов

dic.academic.ru

Источник

Векторы поляризованности и смещения

В предыдущей статье было показано, что вследствие поляризации диэлектрика, т. е. смещения его связанных зарядов, изменяется напряженность электрического поля. Результирующее влияние диэлектрика на электрическое поле оценивают векторной величиной, называемой поляризованностью Р (вектором поляризации).

Средняя интенсивность поляризации P_ср определяется как сумма дипольных моментов в единице объема диэлектрика, а чтобы найти поляризованность в данном месте поля, надо выбрать достаточно малый объем ΔV: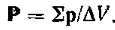

Единица измерения поляризованности

[P] = [ql/V] = Кл*м/м 3 = Кл/м 2.

Вектор поляризации направлен навстречу вектору напряженности электрического поля связанных зарядов E_п.(рис. 4.12).
Вектор поляризации для большинства диэлектриков (за исключением группы сегнетоэлектриков) пропорционален напряженности электрического поля:

и его направление совпадает с направлением внешнего E_вн и результирующего Е полей (риc. 4.12).

Коэффициент k называется электрической восприимчивостью диэлектрика и характеризует его способность поляризоваться.

При расчетах электрических полей в диэлектриках с различными диэлектрическими проницаемостями пользуются еще вектором электрического смещения.

Электрическое смещение D связано с напряженностью электрического ноля простым соотношением

откуда можно определить единицу намерения электрического смещения:

которая такая же, как у вектора, поляризации и у поверхностной плотности зарядов на электродах.

Электрическое смещение и поверхностная плотность свободных зарядов численно одинаковы на поверхности всех проводящих тел, находящихся в электростатическом поле. Например, у внутренней поверхности пластины плоского конденсатора (рис. 4.8) напряженность однородного электрического поля, как и в любой точке однородного поля (4.10),

а электрическое смещение в любой точке поля, в том числе и у металлической поверхности,

т. е. совпадает с поверхностной плотностью заряда на пластине.

Из (2а) следует, что при заданной плотности поверхностных свободных зарядов на электродах электрическое смещение в однородном диэлектрике с диэлектрической проницаемостью ε_a не зависит от ε_a, а напряженность электрического поля зависит. Поэтому можно сказать, что на напряженность электрического поля определяется и свободными (на электродах) и связанными (в диэлектриках) зарядами, т. е. поляризацией диэлектрика, а электрическое смещение в однородном диэлектрике не зависит от связанных зарядов.

Связь между тремя векторными величинами, характеризующими электрическое поле в диэлектрике, выражается равенством

Приняв во внимание (1) и (2), получим

откуда диэлектрическая проницаемость

а электрическая восприимчивость

Рис.1 Поле заряженного шара

Рассмотрим еще неоднородное электрическое поле заряженного металлическою шара (рис. 1), радиус которого R_ш. Известно, что электрический заряд Q находится на поверхности такого шара. Поверхностная плотность заряда

Поле металлического шара с зарядом Q совпадает вне шара с полем равного ему по значению точечного заряда Q, расположенного в центре шара (4.8); поэтому напряженность поля на расстоянии R от центра шара и в частности, у его наружной поверхности, т.е. при R = R_ш,

а электрическое смещение

т. е. равно поверхностной плотности заряда.

Внутри металлического шара поля нет, как и во всяком проводнике в условиях электростатики , Поэтому потенциалы всех точек шара одинаковые, т. е. шар — эквипотенциальное тело, как и всякое металлическое тело в электростатическом поле.

Аналогично потоку вектора напряженности поля (4.7) применяется понятие потока вектора электрического смешения.

Поток вектора смещения N_D в однородном поле равен произведению численного значения вектора смещения D и площадки S, во всех точках которой вектор смещения имеет одинаковое значение и направлен перпендикулярно к ней, т. е.

При неоднородном поле произвольную поверхность площадью S разбивают на элементарные, в пределах каждой на которых смещение одинаково; так что поток вектора
смещения через такую элементарную площадку

где D_n— нормальная составляющая вектора смещения (перпендикулярная к элементарной площадке).

Поток вектора смещения через произвольную замкнутую поверхность находится суммированием элементарных потоков:
Так как D = ε_aE и соответственно D_n = ε_aE_n, то поток вектора смещения

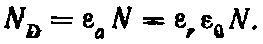
В частности, в случае шаровой поверхности

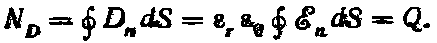
Таким образом, поток вектора электрического смещения через шаровую поверхность равен заряду, расположенному внутри поверхности.

Полученное выражение N_D = Q справедливо для замкнутой поверхности любой формы, охватывающей заряд как в однородной среде с ε_r = const, так и в среде, диэлектрическая проницаемость которой неодинакова в различных участках среды, например в двухслойном конденсаторе.

На поверхности шара,

откуда определяется электрическое смещение у поверхности шара: что согласуется с (5).

Виды поляризации электромагнитных волн

В любой электромагнитной волне векторы напряженности электрического поля Е, индукции магнитного поля В и вектор скорости волны и образуют взаимно перпендикулярную правую тройку векторов: Ё±В1и (рис. 19.1).

Рис. 19.1. Структура электромагнитной волны

При распространении волны векторы В и Е всегда изменяются в пространстве одинаковым образом, описывая одинаковые по форме кривые, но во взаимно перпендикулярных плоскостях. Поэтому достаточно знать, как изменяется в пространстве один из этих векторов, поведение другого будет аналогичным.

Специальными опытами установлено, что действие электромагнитной волны на глаз, фотоприемники и многие другие объекты оказывает электрический вектор Е волны, поэтому его называют также световым вектором волны.

Поляризация электромагнитной волны зависит от поведения ее электрического и магнитного полей в пространстве при распространении волны и определяется видом той кривой, которую описывает проекция электрического вектора Е волны за один период колебания в плоскости наблюдения. Плоскость наблюдения — это плоскость, перпендикулярная направлению распространения волны (см. рис. 19.1), при этом свет должен распространяться к наблюдателю. Ясно, что проекция магнитного вектора В волны описывает в плоскости наблюдения такую же по форме кривую, что и вектор Е , но в перпендикулярном ему направлении. Рассмотрим основные виды поляризации.

Линейная (плоская) поляризация: в процессе распространения волны вектор Е колеблется все время в одной и той же пространственной плоскости (см. рис. 19.1), которую называют плоскостью колебаний вектора Е (иногда также

Рис. 19.2. Виды поляризации электромагнитных волн: а — линейная (плоская); б — круговая; в — эллиптическая; г — неполяризованная; д — частично поляризованная

плоскостью поляризации волны). Проекция вектора Е на плоскость наблюдения в этом случае будет иметь вид отрезка прямой линии, в связи с чем эту поляризацию и называют линейной или плоской (рис. 19.2, а).

Отметим, что плоскость колебания магнитного вектора волны будет перпендикулярна плоскости колебаний вектора Е .

Круговая (циркулярная) поляризация: вектор Е за один период волны делает полный оборот вокруг направления распространения волны, при этом его длина остается постоянной. В плоскости наблюдения проекция вектора Е описывает круг, что и определяет название такой поляризации. Если вектор вращается по часовой стрелке (волна должна распространяться к наблюдателю), то поляризация называется правой круговой (пр), а если против часовой стрелки, то левой круговой (л) поляризацией (рис. 19.2, б).

Эллиптическая поляризация: вектор Е за один период волны делает полный оборот вокруг направления распространения волны, но при этом его величина изменяется таким образом, что конец его описывает в плоскости наблюдения эллипс. Если для наблюдателя вектор Е вращается по часовой стрелке, то поляризация называется правой (пр), а если против — левой (л) эллиптической (рис. 19.2, в).

Это виды полной поляризации света. Полностью поляризованный свет можно с помощью специальных поляризационных приборов (компенсаторов и фазовых пластинок) преобразовать без уменьшения интенсивности из одной формы в другую (например линейно поляризованный свет в цирку- лярно поляризованный, и наоборот).

Естественный свет — свет, испускаемый обычными источниками, т.е. солнцем, пламенем, электрической лампочкой; он является неполяризованным (рис. 19.2, г). Такой свет можно рассматривать как совокупность множества линейно поляризованных волн с одинаковыми амплитудами и всеми возможными ориентациями вектора Е в плоскости наблюдения. По своим поляризационным свойствам такой свет существенно отличается и от линейно поляризованного, и от циркулярно поляризованного света.

Частично поляризованный свет можно рассматривать как совокупность линейно поляризованного и естественного света (рис. 19.2, д) либо как совокупность множества линейно поляризованных волн с различными направлениями колебаний вектора Е, амплитуда которого неодинакова в различных направлениях. Поэтому концы этих векторов лежат не на окружности, как у естественного света, а на эллипсе. Форма такого эллипса может быть разной: от почти круговой (такой свет по своим свойствам близок к естественному) до сильно вытянутой (близок к линейно поляризованному). Поэтому для количественного описания частично поляризованного света вводится специальный параметр — степень поляризации р, который может принимать значения от нуля до единицы:

где 7_тах и 7_min — интенсивность линейно поляризованных волн вдоль большой и малой осей эллипса.

Основы радиолокации

Поляризация электромагнитных волн

Рисунок 1. Радиолокатор станции наведения ракет зенитного ракетного комплекса С-75 («Fan Song E») .
Фото взято с сайта www.pvo.guns.ru

Поле, излучаемое антенной, состоит из электрических и магнитных силовых линий. В этом поле силовые линии электрического поля перпендикулярны силовым линиям магнитного поля. Направления обеих этих составляющих зависят от положения антенны относительно земной поверхности. Направление вектора электрической напряженности определяет направление поляризации электромагнитной волны. Различают линейную и круговую поляризацию.

Рисунок 2. Электрическое поле с вертикальной линейной поляризацией

Рисунок 3. Электрическое поле с горизонтальной линейной поляризацией

Линейная поляризация

Установленные горизонтально или вертикально антенны предназначены для излучения и приема, соответственно, горизонтально или вертикально поляризованных волн. В случае несовпадения поляризации волны и антенны будет меняться величина принимаемого сигнала, поскольку будет меняться величина проекции вектора поляризации волны на направление поляризации антенны.

Линейная поляризация имеет две основные формы:

в вертикально поляризованной волне электрические силовые линии лежат в вертикальной плоскости;
в горизонтально поляризованной волне электрические силовые линии лежат в горизонтальной плоскости.

Максимальный принятый сигнал соответствует ситуации, когда приемная антенна ориентирована в том же направлении, что и передающая.

Рисунок 4. Радиолокатор станции наведения ракет зенитного ракетного комплекса С-125 («Нева»).
Фото взято с сайта www.pvo.guns.ru

Конечно, в дополнении к горизонтальной и вертикальной поляризации, линейная поляризация может принимать и другие, промежуточные между этими двумя основными, направления. В частности, специально выделяются средние положения (под углом 45º):

с наклоном +45º и
с наклоном -45º.

При использовании проволочной одиночной антенны (штыревой антенны) максимальный принятый сигнал будет соответствовать ситуации, когда антенна ориентирована в пространстве так же, как и плоскость, в которой колеблется вектор электрической напряженности волны. Таким образом, вертикальная антенна используется для эффективного приема вертикально поляризованных волн, а горизонтальная – для приема горизонтально поляризованных.

Круговая поляризация

Рисунок 5. Формирование круговой поляризации.

Рисунок 5. Формирование круговой поляризации. Здесь имеется поясняющая анимация (50 кБайт). Для презентации в классе рекомендуется представление demonstrations.wolfram.com

При круговой поляризации силовые линии электрического поля вращаются на 360° с каждым циклом колебания высокочастотной энергии. Круговая поляризация возникает когда на две линейно поляризованные антенны, развернутые друг относительно друга на 90°, подаются два входных сигнала, сдвинутых по фазе на 90° друг относительно друга (Рисунок 5). Рассмотрение поляризации ведется по электрическому полю, поскольку интенсивность электромагнитной волны обычно измеряют в единицах напряженности электрического поля (вольт, милливольт или микровольт на метр). В некоторых случаях ориентация вектора электрической напряженности не остается постоянной, а вращается вместе с распространением волны в пространстве. В таких условиях существуют как горизонтальные, так и вертикальные компоненты поля, волна имеет эллиптическую поляризацию.

В зависимости от направления вращения вектора напряженности круговая поляризация может быть левой или правой. Волна с круговой поляризацией, отраженная дождевой каплей сферической формы, меняет направление поляризации на противоположное. Приемная антенна не пропускает волну с направлением поляризации, противоположным излученной, тем самым сводя к минимуму сигнал от дождевых капель. Отражение от самолета или другой реальной цели будет иметь существенно большую интенсивность, поскольку форма цели не является сферической.

Для наилучшего приема отраженных сигналов поляризации приемной и передающей антенн должны совпадать. В противном случае возникают значительные потери, на практике достигающие 20 … 30 дБ.

При возникновении сильных помех, вызванных отражениями от гидрометеоров, часто применяют круговую поляризацию (если такая возможность имеется). Это дает возможность снизить влияние маскирования полезного сигнала помехами.

Деполяризация

При рассеянии на цели электромагнитной волны ее поляризация может изменяться. В оптическом диапазоне деполяризацией называют изменения в степени поляризованности частично поляризованной волны при ее рассеянии. Например, рассеянная целью волна может иметь большую степень поляризации чем падающая на нее волна, в этом случае деполяризация имеет отрицательную величину.

Деполяризация также показывает пространственное или временное изменение степени поляризации для полностью поляризованной волны, что означает, что может меняться ориентация плоскости поляризации. В этом значении термин «деполяризация» используется, когда речь идет о когерентных высокочастотных волнах. Двухполяризационные метеорологические радиолокаторы имеют возможность излучать волны на двух ортогональных поляризациях (H или V) и принимать как на той же поляризации так и на кросс-поляризации (ортогональной). В таких случаях используют следующие обозначения приемных каналов:

HH — излучается и принимается горизонтальная поляризация;
VV — излучается и принимается вертикальная поляризация;
HV — излучается горизонтальная, а принимается вертикальная поляризация;
VH — излучается вертикальная, принимается горизонтальная поляризация.

Издатель: Кристиан Вольф, Автор: Андрій Музиченко
Текст доступен на условиях лицензий: GNU Free Documentation License
а также Creative Commons Attribution-Share Alike 3.0 Unported License,
могут применяться дополнительные условия.
(Онлайн с ноября 1998 года)

[spoiler title=”источники:”]

http://studref.com/467506/meditsina/vidy_polyarizatsii_elektromagnitnyh_voln

http://www.radartutorial.eu/06.antennas/an06.ru.html

[/spoiler]

Источник

Поляризованные поля

Введение в поляризацию

Линейная и круговая поляризация

Эллиптическая поляризация

Угол наклона

Коэффициент эллиптичности и угол эллиптичности

Направление вращения

Сводные данные значения поляризации

Основы линейной и круговой поляризации

Вектор Джонса

Параметры Стокса и сфера Пуанкаре

Источники поляризованных полей

Короткий дипольный антенный элемент

Пересеченный дипольный антенный элемент

LHCP и компоненты поляризации RHCP

Массивы, поддерживающие поляризацию

Матрица поперечного сечения рассеяния

Сигнатура поляризации

Построение Поляризационных Сигнатур

Потеря поляризации из-за несоответствия поля и приемника

Радар модели, передающий поляризованное излучение

2.6. Основные уравнения электростатики диэлектриков

2.6.1. Теорема Гаусса для поля вектора поляризации ()

Introduction to Polarization

Linear and Circular Polarization

Elliptic Polarization

Tilt Angle

Axial Ratio and Ellipticity Angle

Rotation Sense

Polarization Value Summary

Linear and Circular Polarization Bases

Jones Vector

Stokes Parameters and the Poincaré Sphere

Sources of Polarized Fields

Short Dipole Antenna Element

Crossed Dipole Antenna Element

LHCP and RHCP Polarization Components

Arrays Supporting Polarization

Scattering Cross-Section Matrix

Polarization Signature

Plot Polarization Signatures

Polarization Loss Due to Field and Receiver Mismatch

Model Radar Transmitting Polarized Radiation

Типы поляризации[править | править код]

Механизмы поляризации[править | править код]

Зависимость вектора поляризации от внешнего поля[править | править код]

В постоянном поле[править | править код]

В слабых полях[править | править код]

В сильных полях[править | править код]

В зависящем от времени поле[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Векторы поляризованности и смещения

Виды поляризации электромагнитных волн

Основы радиолокации

Поляризация электромагнитных волн

Линейная поляризация

Круговая поляризация

Деполяризация

Вам также может понравиться

Как в зуме исправить имя с фамилией

Как найти изменение длины стержня

Как найти калмыка на болотах

Добавить комментарий Отменить ответ