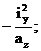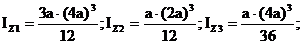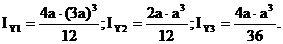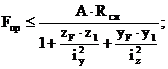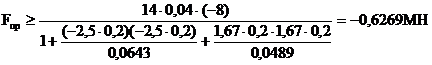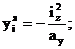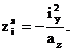При сложном профиле
сечения стержня для определения опасной
точки предварительно находится положение
нейтральной линии. Учитывая, что на
нейтральной линии напряжения равны
нулю, получаем:
Здесь х0
и у0– координаты любой
точки нейтральной линии. Уравнение
нейтральной линии будет иметь вид
.
(10.3)
Это – уравнение
прямой, не проходящей через начало
координат (рис. 10.2).
По уравнению можно
определить отрезки, отсекаемые нейтральной
линией на координатных осях. Обозначим
эти отрезки (см. рис. 10.2) через ахи ау.
Е
Рис. 10.2
сли принять, чтоу0
= 0, х0
= ах,
то из уравнения (10.3)
получим
Принимая х0
= 0, у0
= ау,
будем иметь
Решая эти уравнения,
получим отрезки, отсекаемые нейтральной
линией на координатных осях:
,
.
(10.4)
Исследование этих
формул показывает, что точка приложения
силы и нейтральная ось лежат по разные
стороны относительно центра тяжести
сечения.
Отметим, что
нейтральная линия делит поперечное
сечение стержня на две зоны – сжатую и
растянутую. Проводя параллельно
нейтральной линии касательные к контуру
сечения, найдем опасные точки С
и D,
лежащие в растянутой и сжатой зонах
(см. рис. 10.2).
Условие прочности
для стержня из пластичного материала
запишется в виде

где хоп
и yоп
– координаты точки, наиболее удаленной
от нейтральной линии (точка D
на рис. 10.2).
Для стержней,
выполненных из неравнопрочного материала,
расчет на прочность ведется для двух
опасных точек (в растянутой и сжатой
зонах).
Условия прочности
имеют вид:


(10.6)
Здесь
и
– координаты опасных точек соответственно
в растянутой и сжатой зонах.
10.3. Ядро сечения
Из анализа формул
(10.4) можно отметить характерные
особенности, связанные с поведением
нейтральной линии при различных
положениях силы F.
Если сила F
приложена
в центре тяжести сечения (хF
= 0, уF
= 0), то нейтральная линия отсекает на
координатных осях отрезки равные
бесконечности (ах
=
ау
=
Напряжение при этом определяется
выражением
,
т.е. имеется центральное растяжение или
сжатие с равномерным распределением
напряжений по всему сечению.
С
увеличением координат точки приложения
силыхF
и уF
нейтральная линия будет приближаться
к сечению и при некотором положении
точки приложения силы (1
на рис. 10.3) она коснется контура сечения
(линия n1 n1).
При дальнейшем увеличении эксцентриситета
нейтральная линия пересечет контур
сечения (см. рис. 10.2), разделив все сечение
на две области – растянутую и сжатую.
Понятно, что в случае, когда нейтральная
линия касается контура сечения, все
сечение испытывает напряжение одного
знака. Отсюда следует определение ядра
сечения как
области, очерченной вокруг центра
тяжести и специфичной тем, что продольная
сила, приложенная в любой точке этой
области, вызывает во всех точках
поперечного сечения напряжения одного
знака. Из определения ядра сечения
вытекает порядок его построения:
задаваясь всевозможными положениями
нейтральной линии как касательной к
контуру сечения, вычисляют соответствующие
координаты полюса силы:
,
.
(10.7)
Совокупность
полученных точек дает контур ядра
сечения.
На рис. 10.3 приведены
сечение и построенное для него ядро.
Показаны положения, которые нейтральная
линия последовательно занимает при ее
«обкатке» вокруг контура сечения,
и
соответствующие этим положениям точки
приложения силы. При этом перемещение
полюса силы между точками 1
и 2,
2
и 3,
5
и 1
происходит по прямым линиям.
Обоснованием
перехода между точками приложения силы
по прямым линиям является легко
доказываемая теорема: если нейтральная
линия вращается вокруг некоторой точки
А,
то сила F
перемещается
по прямой, не проходящей через центр
тяжести сечения.
|
|
|
|
Рис. |
Рис. |
Для доказательства
покажем, что при любом положении силы
FС
на прямой 12
линия nC
nCпроходит через
точку А,
т.е. А
= 0 (рис. 10.4).
Разложим силу Fс
на две
параллельные составляющие FС1
и FС2.
От каждой из этих двух составляющих
напряжение А
= 0, т.к. точка А
одновременно принадлежит обеим
нейтральным линиям: n1n1
и n2n2.
Точка С
взята произвольно, значит, при любом
положении силы F
на прямой 12
напряжение в точке A
равно нулю.
Сделаем следующее
замечание, касающееся построения ядра
сечения. При рассмотрении любого контура,
имеющего «впадины», нейтральная линия
должна «катиться» по огибающей контура,
иначе она будет пересекать сечение.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ НЕЙТРАЛЬНОЙ ЛИНИИ
СОДЕРЖАНИЕ
1. Внутренние усилия и напряжения в сечении …….5
2. Определение положения нейтральной линии…….6
3. Расчеты на прочность …………………………….. 7
4. Построения ядра сечения………………………….. 9
5. Пример расчета ……………………………………10
7. Вопросы для самоконтроля ………………… ……18
8. Расчетно-графическая работа « Расчет жесткого бруса на внецентренное сжатие» ……………….18
ВВЕДЕНИЕ
Сложное сопротивление, при котором прямолиней-ный жесткий брус (рис.1) сжат или растянут силой, направленной параллельно его оси и не проходящей через центр тяжести сечения, называется внецентренном сжатием или внецентренном растяжением.
Рис.1. Схема приложения нагрузки
В том случае, когда на брус действуют несколько параллельных сил, то при расчетах будет рассматриваться их равнодействующая.
При внецентренном приложении нагрузки в попереч-ных сечениях элементов возникают продольная сила N и изгибающие моменты относительно осейy и z MY и MZ .
Так как такие элементы конструкций как колонны, мостовые опоры или фундаменты сооружений обычно подвержены действию сжимающих сил, то ограничимся рассмотрением случая внецентренного сжатия.
Проанализируем, какие внутренние усилия и напряжения могут возникать в рассматриваемом нормальном поперечном сечении бруса при внецентренном сжатии.
Внутренние усилия и напряжения в сечении
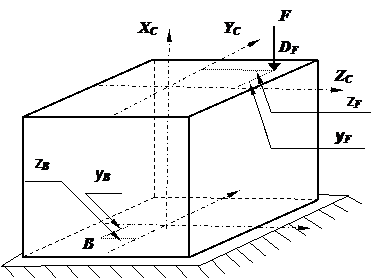
Рис. 2. Схема приложения нагрузки к брусу
Оси ус и zc – главные центральные оси сечения (главные оси инерции). Для определения напряжение в точке В поперечного сечения, площадь которого обозна-чена символом А, необходимо знать величину и знак внутренних усилий, действующих в этом сечении. Внутренние усилия определяются по следующим формулам:
В приведенных формулах знак изгибающего момента определяется по следующему принципу: положительный изгибающий момент должен вызывать растяжение волокон с положительными координатами в выбранной системе отсчета, а отрицательный момент должен вызывать сжатие этих волокон.
Нормальные напряжения в точке В:

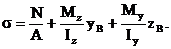
В этой формуле знак внутренних усилий принимается в соответствии с (1), а координаты точки В zВ и yВ вводятся со своими знаками.
ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ НЕЙТРАЛЬНОЙ ЛИНИИ
Так как нейтральная (нулевая) линия отделяет сжатую зону сечения от растянутой, то нормальные напряжения в точках, лежащих на нейтральной линии равны 0:
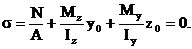
Подставляя в уравнение (3) значения внутренних усилий и квадраты радиусов инерции сечения относительно главных осей вместо осевых моментов инерции, получаем следующее выражение:
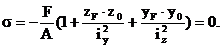
В выражении (4) 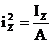
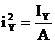
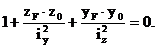
Уравнение (5) – уравнение нейтральной линии, которым удобнее пользоваться, приведя его к уравнению в отрезках:
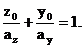
Здесь aZ и aY – отрезки, отсекаемые нейтральной линией на координатных осях, определяемые по формулам:
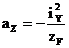
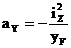
Для построения нейтральной линии рассчитываются отрезки az и ay, в масштабе откладываются от начала координат и нейтральная линия проводится через концы этих отрезков. Координаты полюса zF и yF должны вводится в расчет с учетом правила знаков.
РАСЧЕТЫ НА ПРОЧНОСТЬ
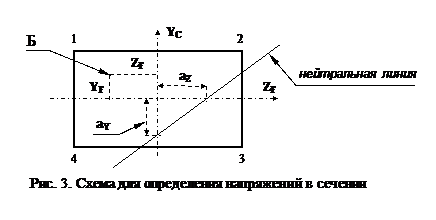
При внецентренном сжатии нормальные напряжения в сечении изменяются по линейному закону пропорцио-нально расстоянию от нейтральной линии. На рис. 3 пока-зан полюс (точка Б, в которой приложена сжимающая сила F) и положение нейтральной линии сечения.
Наиболее удалены от нейтральной линии точка 1 c координатами z1 и y1 и точка 3, координаты которой z3 и y3. В этих точках возникают экстремальные напряжения: наибольшие сжимающие в т. 1, а наибольшие растягиваю-щие в т. 3. Величина напряжений в этих точках определя-ется в соответствии с (2):
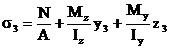
Условия прочности для рассматриваемой схемы: s1 ≤ Rсж и s3 ≤ Rраст. Используя уравнение (4), можно записать условия прочности в следующем виде:
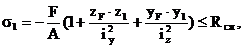
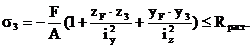
В эти уравнения координаты полюса и точек, в которых определяются напряжения, подставляются с учетом их знаков.
Условия (8) и (9) позволяют решать следующие три типа задач при внецентренном приложении нагрузки:
А. Проектная задача
Задано значение силы F, расчетные сопротивления материала бруса Rсж и Rраст, координаты полюса и точек сечения, в которых действуют экстремальные напряжения. Требуется рассчитать размеры поперечного сечения. Для выполнения поставленной задачи все геометрические характеристики (А, IZ, IY) выражаются через один параметр – или высоту, или ширину сечения. Из двух значений площади, вычисленной по формулам (8) и (9), за искомую следует принять большую.
Б. Определение несущей способности
Задано: расчетные сопротивления материала бруса Rсж и Rраст, геометрические характеристики сечения А, IZ, IY, координаты полюса и тех точек, в которых действуют экстремальные напряжения. Требуется определить предельное значение сжимающей силы F. Из двух полученных значений силы F, за искомое принимается наименьшее.
В. Проверочная задача
Задано: геометрические характеристики сечения А, IZ, IY, координаты полюса и точек, в которых действуют экстремальные напряжения, расчетные сопротивления материала бруса Rсж и Rраст, значение силы F. Требуется проверить выполнение условий (8) и (9).
ПОСТРОЕНИЕ ЯДРА СЕЧЕНИЯ
В зависимости от точки приложения внешней сжимающей нагрузки к брусу, нейтральная линия может пересекать сечение, касаться его или проходить вне сечения. Эти варианты показаны на рис. 4.
При внецентренном приложении нагрузки к брусу, выполненному из таких хрупких материалов, как бетон, кирпичная или бутовая кладка, возникает задача о том, как приложить сжимающую силу F, чтобы в поперечном сечении возникали только сжимающие напряжения. Решение этой задачи производится путем построения ядра сечения.
Ядром сечения называется очерченная вокруг центра тяжести сечения область, обладающая следующим свойством: сила F, приложенная в этой области, вызовет по всему поперечному сечению напряжения одного знака.
Контур ядра сечения строится в следующей последовательности:
– проводятся несколько касательных вокруг контура сечения, которые принимаются за нейтральные линии;
– определяются аz и ay – отрезки, которые нейтраль-ные линии отсекают на осях zc и yc;
– используя зависимости (7), определяются координа-ты характерных точек ядра сечения:
yя = 
– по найденным точкам yя и zя строится контур ядра сечения.
ПРИМЕР РАСЧЕТА
На рис. 5 показана схема жесткого бруса и прило-женная к нему нагрузка.
Для поперечного сечения, расположенного в основании бруса, требуется: определить величину предельной силы F, приложенной в указанной точке, определить положение нейтральной линии, рассчитать напряжения в характерных точках контура, построить эпюру этих напряжений и построить ядро сечения.
Расчетные сопротивления материала бруса:
Rсж = 8 МПа, а Rраст = 2 МПа. Параметр «a» показанного на рис. 6 сечения равен 0,2м.
Последовательность расчета следующая.
1. Определение координат центра тяжести сечения
Для этого поперечное сечение сложной формы разбивается на простые фигуры, площади и положения центров тяжести которых известно. В рассматриваемом примере сечение разбито два прямоугольника и два одинаковых треугольника. Один прямоугольник площадью А1 = 12а 2 , второй площадью А2 = 2а 2 ; площадь каждого треугольника А3 =2а 2 .
Статический момент площади сечения относительно произвольной начальной оси Z0:

Расстояние уС от оси Z0 до оси ZС
2. Вычисление квадратов радиусов инерции
Квадраты радиусов инерции сечения рассчитываются по формулам: iz 2 = IZC /A, iy 2 = IYC /A, где

Подстановка этих значений в выражения
главных моментов инерции дает следующие
IZC = 17,111а 4 ; IYC = 22,500а 4 .
Квадраты радиусов инерции сечения:
iz 2 = 17,111a 4 /14a 2 = 1,222a 2 = 0,0489м 2 ;
iy 2 = 22,5a 4 /14a 2 = 1,607a 2 = 0,0643м 2 .
3. Определение положения нейтральной линии
Координаты точки приложения сжимающей силы F (координаты полюса): zF = – 2,5a; yF = 1,67a
Отрезки, отсекаемые нейтральной линией на коорди-натных осях: аz = – iy 2 /zF, аy = – iz 2 /yF.
аy = – iz 2 /yF = -1,222a 2 /1,67a = – 0,732a = – 0,146м.
4. Определение предельного значения
Наиболее удалены от нейтральной линии следующие точки:
– в сжатой зоне точка 1, координаты которой z1 = – 2,5a, y1 = 1,67a;
– в растянутой зоне – точка 3 с координатами z3 =1,5a, y3 = – 2,33a.



Для этих точек должны соблюдаться условия прочности – напряжения в них не должны превышать расчетных сопротивлений материала:
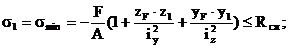
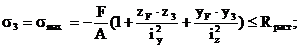
Из выражения (*) предельная величина сжимающей силы Fпр, приложенной в т.1:
Подставляя числовые значения величин, входящих в это неравенство (с учетом знака Rсж), получим:
Из выражения (**) вычисляется значение Fпр:

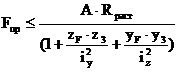


Нормальные напряжения в произвольной точке сечения определяются по формуле:



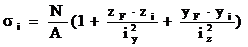
Подставляя в эту формулу значения N = (–)Fпр и координаты характерных контурных точек, вычисляют действующие в них напряжения.
В табл.1 показаны координаты характерных точек сечения и даны результаты выполненных расчетов по определению напряжений в этих точках.
Для построения эпюры, показывающей распределение нормальных напряжений по поперечному сечению бруса, сечение удобно показывать в изометрической проекции. Эпюра s приведена на рис. 9.
| № точек контура | Координаты точек | Напряжения s, МПа |
| zi | yi | |
| -2,5а (-0,5м) | 1,67а (0,334м) | – 3,18 |
| 2,5а (0,5м) | 1,67а (0,334м) | + 0,27 |
| 1,5а (0,3м) | -2,33а (-0,466м) | + 2,00 |
| 0,5а (0,1м) | -2,33а (-0,466м) | + 1,31 |
| 0,5а (0,1м) | -0,33а (-0,066м) | + 0,10 |
| -0,5а (-0,1м) | -0,33а (-0,066м) | – 0,59 |
| -0,5а (-0,1м) | -2,33а (-0,466м) | + 0,62 |
| -1,5а (-0,3м) | -2,33а (-0,466м) | – 0,07 |
6. Построение ядра сечения
Для построения ядра сечения проводятся четыре касательные к контуру сечения, которые рассматриваются как нулевые линии и определяются отрезки, отсекаемые касательными (нулевыми линиями) на главных центральных осях инерции.
Касательная II-II: az = ¥, ay = -2,33a
Касательная III-III: az =1,58а, ay = -8,33a
Касательная IV-IV: az = -1,58а, ay = -8,33a
Зная величину отрезков, отсекаемых нулевыми линиями на координатных осях, определяются координаты ядра сечения:
На рис.8 показаны нулевые линии и построено ядро сечения.
Результаты определения характерных точек ядра сечения обычно выполняются в табличном виде. Итоги выполненных расчетов приводятся в табл. 2, в которой даны координаты характерных точек ядра сечения.
Соединяя точки ядра 1-3-2-4 прямыми линиями, получаем контур ядра сечения.
| Нулевая линия | Отрезки, отсекаемые на координатных осях | № точек ядра | Координаты точек ядра | |
| аz | аy | yя | zя | |
| I-I | ¥ | 1,67a (0,334см) | – 0,73а (- 0,146м) | |
| II-II | ¥ | -2,33а (-0,466м) | 0,52а (0,105м) | |
| III-III | 2,08а (0,416м) | -8,33а (-1,666м) | 0,15а (0,029м) | -0,77а (-0,155м) |
| IV-IV | -2,08а (-0,416м) | -8,33а (-1,666м) | 0,15а (0,029м) | 0,77а (0,155м) |
ЛИТЕРАТУРА
1.Александров А.В., Потапов В.Д., Державин Б.П. Сопротивление материалов: Учеб. для вузов.– 2-е изд. – М.: Высш. шк., 2001. -560с.
2. Сопротивление материалов с основами теории упру-гости и пластичности: Учеб. для вузов под ред. Г.С. Варда-няна. – М.: Изд-во АСВ, 1995. -568с.
3. Павлов П.А., Паршин Л.К., Мельников Б.Е., Шерсте-нев И.А. Сопротивление материалов: Учеб. пособ./под ред. Б.Е. Мельникова – СПб.: Изд-во «Лань», 2003. -528с.
4. Сопротивление материалов: Руководство для реше-ния задач и выполнения лабораторных и расчетно-графических работ / В.А. Копнов, С.Н. Кривошапко. – М.: Высш. шк., 2003. – 351с.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Как определяются внутренние усилия в сечениях жесткого бруса при внецентренном действии нагрузки?
2. Как определяется положение нейтральной (нулевой) линии при внецентренном сжатии или растяжении?
3. Указать, какой из перечисленных факторов повлияет на положение нейтральной линии:
– изменение величины приложенной внешней силы;
– изменение точки приложения этой силы;
– изменениие знака приложенной внешней силы.
4. Как определяется напряжение в заданной точке сечения при внецентренном действии нагрузки?
5. Что называется ядром сечения? Как строится ядро?
6. Какие типы задач позволяет решить условие прочнос-ти при внецентренном приложении нагрузки?
Уравнение нейтральной линии в сопромате
§1 Понятие изгиба. Нейтральная линия.
Определение: Изгибом называется вид деформации, при котором происходит искривление оси бруса. В дальнейшем будем рассматривать деформацию плоского прямого изгиба, при котором силовая плоскость проходит через одну из главных центральных осей сечения.
Кроме прямого, может возникать косой изгиб, при котором силовая плоскость совпадает только с одной центральной осью, т.е. происходит под некоторым углом к главным центральным осям.
В зависимости от возникающих в балке внутренних силовых факторов (ВСФ) различают чистый и поперечный изгиб (рис. 6.3).
Чистым изгибом называется изгиб, при котором в сечении балки возникает только изгибающий момент, а поперечным называется изгиб, при котором действуют как изгибающий момент, так и поперечная сила.
К
ак показывают расчеты нейтральная линия проходит через главную центральную ось сечения, расположенную перпендикулярно к силовой линии.
Нейтральную линию иногда называют нулевой линией, т.к. в ее точках нормальные напряжения и продольные деформации отсутствуют (σ = 0; ε = 0).
§2 Напряжения при чистом и поперечном изгибе.
Основное условие прочности.
В теории изгиба принимаются такие допущения:
1) Справедлива гипотеза плоских сечений.
2) По высоте сечения бруса волокна не имеют веса, т.е. не давят друг на друга. Принимается упрощенная схема напряженного состояния.
3
) по ширине сечения бруса напряжения являются постоянными.
С учетом принятых допущений и рассматривая четыре стороны задачи для чистого изгиба, при котором возникают только нормальные напряжения можно использовать следующую расчетную зависимость.
где σ(y) – нормальные напряжения в точке
сечения бруса, находящейся на
расстоянии y под нейтральной
Mизг – изгибающий момент в данном
Ix – осевой момент инерции сечения
y – ордината последней точки.
Анализируя зависимость (15.1) можно заключить, что нормальное напряжение изменяется по линейному закону, увеличиваясь от центра сечения к его краям. Причем максимальные напряжения, возникающие в крайних волокнах можно определить по известной формуле:
где – осевой момент сопротивления [м 3 ].
Зависимость (15.1) и (15.2) графически можно представить в виде следующей эпюры напряжений (рис. 6.8).
При проектировании балочных конструкций целесообразно применять профили, имеющие рациональную форму с точки зрения полученной эпюры напряжений. Считается, что профиль (или сечение), у которого большая часть материала располагается в крайних волокнах является рациональным. Например, двутавр, швеллер, пустотелый прямоугольник, сдвоенный уголок.
Расчет на прочность при чистом изгибе производится по следующему условию прочности
Условие (15.3) является основным условием прочности при изгибе. При помощи этого условия можно выполнить известные виды расчетов: проверочный, проектировочный и максимальной нагрузки.
– проверочный по (15.3)
При расчете на прочность балок из разных материалов необходимо учитывать их способность сопротивляться растягивающим и сжимающим напряжениям. При этом следует придерживаться следующих рекомендаций:
1. Если балка изготовлена из пластичного материала, одинаково работающего на растяжение-сжатие, т.е. ([σр] = [σc]), то целесообразно использовать сечения, симметричные относительно нейтральной линии. В этом случае на прочность проверяются крайние точки сечения балки σmax = |σmin| (рис.6.9).
2. Если материал балки хрупкий, лучше работающий на сжатие, чем на растяжение ([σр] >l, в противном случае этими напряжениями можно пренебрегать.
§3 Главные напряжения при изгибе.
Полная проверка прочности балок при изгибе
В общем случае при изгибе в сечениях балки действуют как нормальные, так и касательные напряжения. Любая точка балки находится в упрощенном плоском напряженном состоянии.
Решая обратную задачу можно найти положение главной площадки и величины главных напряжений (σ1, σ3).
Анализируя напряженное состояние при изгибе для опасных точек балки и используя (16.3)-(16.6) можно выполнить полную проверку прочности балки при изгибе, для этого необходимо рассмотреть три типа опасных точек в разных сечениях исследуемой балки. Проведем т0акую проверку, выбрав следующую расчетную схему (рис. 6.15)
Полная проверка прочности балки при изгибе выполняется по трем типам опасных точек. Опасная точка I типа: по длине балки находится сечения, где действует максимальный по модулю изгибающий момент (сечение I-I), а по высоте балки – в крайних волокнах от нейтральной линии, где имеют место максимальные нормальные напряжения (точки 1 и 5). В этих точках имеет место линейное напряженное состояние. Условие прочности для точек I типа имеет такой вид (основное условие прочности)
О
пасные точки II типа располагаются по длине балки в сечениях с максимальной поперечной силой (сечение II-II левое и правое), а по высоте балки – на уровне нейтральной линии (точка 3 левая и правая), где действует максимальное касательное напряжение. В этих точках возникает частный случай плоского напряженного состояния – чистый сдвиг. Условие прочности имеет такой вид
Опасные точки III типа располагаются в сечениях балки, где возникает неблагоприятное сочетание больших изгибающего момента и поперечной силы (сечение III-III левое и правое), а по высоте балки – между крайними волокнами и нейтральной линией, где одновременно большие нормальные и касательные напряжения (точки 2 и 4 левая, правая). в этих точках возникает упрощенное плоско-напряженное состояние. Условие прочности для точек III типа записывается согласно теории прочности (например, для пластичного материала: по III или IV теории).
Если по мере выполнения расчетов прочность по одному из условий не выполняется, то необходимо увеличить размеры сечения балки или увеличить номер профиля согласно таблиц сортамента.
Приведенный выше анализ напряженного состояния балок при изгибе позволяет грамотно конструировать элементы сооружений и рационально выбирать их поперечные сечения, например, для железобетонных конструкций целесообразно использовать стальную арматуру и располагать её по линиям, совпадающим с траекторией главных растягивающих напряжений.
§4 Деформации при изгибе. Общие понятия.
В теории изгиба расчет на прочность в большинстве случаев выполняется расчетом на жесткость. В этом случае оценивается упругая податливость балки и определяются такие её размеры, чтобы возникающие деформации не превышали допустимых пределов, т.е. условие жесткости можно представить в таком виде
где fmax – максимальная расчетная деформация;
[f] – допускаемая деформация.
Рассмотрим основные элементы деформированного состояния балки (рис.6.16).
упругая линия (у.л.) – искривленная ось балки под действием нагрузки;
y – прогиб – вертикальное перемещение, отсчитываемое перпендикулярно к исходной оси балки;
u – горизонтальное перемещение или смещение балки (обычно бесконечно малая величина, ≈ 0);
θ – угол поворота сечения к заданной точке.
При изгибе балки линейная и угловая деформации (y и θ) имеют свои правила знаков согласно следующей схеме (рис.6.17).
Правило знаков для y:
Правило знаков для θ:
против часовой стрелки «+»,
по часовой стрелке «–».
Для левой системы координат наоборот.
Между прогибом и углом поворота существует дифференциальная зависимость, которую можно получить рассматривая координаты некоторой плоской кривой (рис.6.18).
При нахождении линейных или угловых деформаций для реальных балок необходимо знать её уравнение упругой линии УУЛБ (уравнение упругой линии балки), имеющее такой общий вид:
Рассмотрим некоторые методы нахождения деформаций при изгибе, основанные на составлении и решении уравнения упругой линии балки.
§5 Дифференциальное уравнение упругой линии балки и его интегрирование.
Из теории изгиба известна зависимость кривизны балки следующего вида
С другой стороны из курса высшей математики кривизна плоской кривой может быть представлена через её координаты следующим образом:
Приравнивая (18.3) и (18.4) получим точное ДУУЛБ
Полученное дифференциальное уравнение имеет большие трудности при решении, поэтому его упрощают, учитывая известную гипотезу малости деформаций
Учитывая небольшие углы поворота сечений для реальных балок получаем следующее приближенное ДУУЛБ, которое будет называться в дальнейшем основным дифференциальным уравнением упругой линии балки.
Данное уравнение справедливо для правой системы координат.
Полученное уравнение решается путем двойного интегрирования
В этом решении произвольные постоянные интегрирования представляют собой по геометрическому смыслу соответственно угол поворота и прогиб в начале координат
Произвольные постоянные интегрирования определяются из граничных или начальных условий построения расчетной схемы балки. Рассмотрим основные разновидности граничных условий.
Виды граничных условий
Рассмотренный выше метод расчета перемещений при изгибе называется методом непосредственного интегрирования дифференциального уравнения упругой линии балки МНИ ДУУЛБ.
Для его применения необходимо:
- Выбрать систему координат (в крайнем сечении балки)
- Для каждого силового участка балки составляется общее уравнение моментов, которое подставляется в основное ДУУЛБ.
- Решается ДУУЛБ путем двойного интегрирования и определяется произвольная постоянная интегрирования из граничных условий.
- В полученное уравнение упругой линии балки подставляются поочередно абсциссы искомых точек и определяются прогибы. Аналогично находятся углы поворотов с использованием дифференциальной зависимости (18.1).
МНИ обладает существенным недостатком, который заключается в том, что для решения балок с большим количеством силовых участков необходимо определить большое количество произвольных постоянных интегрирования (например, для n участков будет 2n таковых), поэтому данный метод целесообразно использовать только для балок, имеющих один или два участка. Для устранения названного недостатка предлагается более совершенный метод, основанный на ДУУЛБ и более рациональном его решении.
§6 Метод начальных параметров.
Универсальное уравнение упругой линии балки (УУУЛБ).
В отличие от предыдущего метода в предлагаемом методе ДУУЛБ составляется таким образом, что независимо от количества силовых участков балки приходится находить только две произвольных постоянных интегрирования – прогиб и угол поворота в начале координат (y0, θ0). Это достигается путем применения специальных правил при составлении уравнения моментов или уравнений прогибов. В этом случае все решение сводится к составлению УУУЛБ применительно к заданной расчетной схеме балки.
Общий вид УУУЛБ будет следующим:
После дифференцирования (18.13) получим универсальное уравнение углов поворота балки УУУЛБ.
где y0, θ0 – геометрические начальные параметры, т.е. прогиб и угол поворота в начале координат, определяются по граничным условиям;
М0, Q0 – статические начальные параметры, т.е. изгибающий момент и поперечная сила в начале координат; они определяются по условиям нагружения или по уравнениям равновесия.
Mi, Fi, qi – момент, сосредоточенная сила и распределенная нагрузка в i том сечении балки соответственно. Они включаются в уравнение со своими знаками в соответствии с «правилом зонтика» для изгибающего момента.
ki – величина, характеризующая неравномерно распределенную нагрузку, например, треугольную или трапециевидную.
Д
ля решения задач по нахождению перемещений в балках методом начальных параметров необходимо (пример: рис.6.23):
2) Для последнего силового участка балки составляется универсальное уравнение упругой линии балки УУУЛБ.
Для составления выражения для распределенной нагрузки её предварительно продолжают до конца (последнего) сечения и вводят дополнительную компенсирующую нагрузку обратного направления.
3) Определяются начальные параметры УУУЛБ.
Геометрические начальные параметры.
Статические начальные параметры.
4) Подставляются все найденные начальные параметры в исходное УУУЛБ и путем дифференцирования получается универсальное уравнение углов поворота балки УУУЛБ.
В этом же пункте определяются искомые перемещения, для чего в соответствующее уравнение подставляется абсцисса искомой точки и отбрасываются слагаемые, характеризующие внешние нагрузки, которые находятся за пределами рассматриваемого участка.
Рассмотренный метод начальных параметров является достаточно простым и универсальным, но имеет следующие недостатки.
1) Он не применим для балок с ломаной осью, рамным систем и кривых брусьев.
2) Не позволяет определить перемещение в произвольных направлениях, кроме вертикального.
Для устранения этих недостатков в курсе сопротивления материалов широко применяются так называемые энергетические способы, основанные на известном законе сохранения энергии.
§7 Потенциальная энергия упругой деформации (ПЭУД)
в общем случае нагружения бруса. Теорема Кастильяно.
На основании закона сохранения энергии работа внешних сил на перемещениях точек системы равна потенциальной энергии упругой деформации
Основываясь на положениях этого закона можно зная величину энергии, накопленной брусом, найти перемещение ее точек при известных внешних нагрузках. Получим общую зависимость для ПЭУД произвольного бруса, находящегося под воздействием разнообразных внешних нагрузок, для этого составим сумму работ, совершаемых шестью внутренними силовыми факторами.
Учитывая известное выражение работ для простых деформаций получим следующее выражение
kx, ky – безразмерные коэффициенты, характеризующие форму сечения бруса при сдвиге.
Для нахождения перемещений с помощью ПЭУД применяется так называемая теорема Кастильяно:
Обобщенные перемещения в точке приложения некоторой обобщенной нагрузки представляют собой частную производную потенциальной энергии по заданной обобщенной нагрузке.
где δk – обобщенное перемещение в точке К, где приложена внешняя обобщенная нагрузка, по ее направлению.
FK – обобщенная нагрузка, действующая в точке К.
Под обобщенным перемещением понимается перемещение, вызываемое соответствующей обобщенной нагрузкой. В частности,
Д
анная теорема обладает тем недостатком, что позволяет находить только перемещения, соответствующие данной обобщенной нагрузке, только в точке её приложения и только по ее направлению.
§8 Метод для нахождения перемещений в упругих системах.
Недостатки теоремы Кастильяно можно устранить, если использовать прием, предложенный Мором-Максвеллом. Этот метод основан на применении так называемой фиктивной обобщенной нагрузки Φ.
1) В заданной точке системы прикладывается соответствующая обобщенная параметром фиктивная нагрузка, которая условно принимается равной единице.
Направление приложения фиктивной нагрузки соответствует искомому направлению. Для прогиба удобно единичную силу направлять снизу вверх согласно положительному направлению прогиба (см. правило знаков для прогиба). Единичный момент направляется против часовой стрелки в соответствии с положительным направлением угла поворота.
2) Определяется потенциальная энергия упругой деформации всей системы, которая подставляется в зависимость , выражающую теорему Кастильяно и производится расчет частной производной по данной фиктивной нагрузке.
В полученном выражении исключается фиктивная нагрузка, т.к. ее на самом деле нет.
Для удобства практического расчета все преобразования рассмотренные выше исключаются и расчет перемещений выполняется по формуле, называемой интегралом Мора (запишем применительно к деформации изгиба).
где – изгибающий момент от действия единичной фиктивной нагрузки в i том сечении системы.
– изгибающий момент от действия внешней нагрузки для i того сечения.
Рассмотрим следующий пример (рис.6.25).
Выбирается вспомогательная схема, которая загружается соответствующей единичной нагрузкой. Чтобы взять вспомогательную схему, надо на исходной схеме отбросить все внешние нагрузки.
Для исходной и вспомогательной схем составляются общие выражения изгибающих моментов по всем участкам, которые подставляются в интеграл Мора.
Метод Мора является самым сильным по возможности расчета перемещений (его можно применить для любой схемы), однако его недостатком является высокая трудоемкость при расчете систем с большим количеством силовых участков.
Для сокращения сложности таких расчетов интеграл Мора обычно заменяют операцией умножения согласно способа Верещагина (1924 г.).
§9 Способ Верещагина и его применение
Предлагаемый способ является графо-аналитическим способом решения интеграла Мора, который заключается в «перемножении» эпюр изгибающих моментов по силовым участкам заданной системы. Такое решение возможно благодаря тому, что для систем, имеющих прямолинейные участки эпюра изгибающих моментов от единичной нагрузки имеет линейные очертания (прямоугольник, треугольник, трапеция).
Согласно способа Верещагина искомое перемещение представляет собой произведение площади грузовой эпюры на ординату единичной эпюры, которая располагается под центром тяжести грузовой эпюры на данном участке.
где ωi – площадь грузовой эпюры на i том участке.
– ордината единичной эпюры под центром тяжести грузовой на i том участке.
Рассмотрим пример (рис.6.28)
При использовании способа Верещагина для упрощения расчетов можно учитывать следующие рекомендации.
1) При перемножении эпюр, имеющих линейные очертания можно использовать площадь одной из них, а ординату другой в прямом и обратном порядке.
2) Если перемножаемые эпюры имеют сложную форму, то можно их разбивать на простые части и перемножать по отдельности.
3) В некоторых случаях сложные эпюры удобно перемножать, используя прием расслоения эпюр. В этом случае в пределах данного участка строятся эпюры от каждой нагрузки в отдельности, которые перемножаются поочередно с единичной эпюрой.
4) При перемножении эпюры, имеющей форму скрученной трапеции, ее целесообразно дополнить до двух треугольников, которые затем перемножаются по отдельности с другой эпюрой.
5) Когда обе перемножаемые эпюры имеют сложную форму можно использовать так называемую формулу Симпсона.
Способ Верещагина является достаточно удобным и простым для расчета перемещений в упругих системах при любых видах деформаций. Однако его нельзя применить для систем, имеющих криволинейные участки.
§10 Статически неопределимые системы при изгибе.
Каноническое уравнение метода сил (КУМС).
Статически неопределимая система (СНС) при изгибе обладает теми же свойствами, что СНС при растяжении-сжатии и кручении, однако имеют следующую особенность.
Степень неопределимости в таких системах может быть образована как внешними, так и внутренними признаками построения СНС.
Система неопределима внешним образом, если её элементы имеют ограничения по перемещению в пространстве. Такие ограничения накладываются опорными связями и в этом случае степень СНС по внешним признакам находится по известной формуле
где R – число неизвестных реакций опор СНС,
У – число уравнений статики.
Степень СНС образована внутренними признаками, если они накладывают ограничения на относительные перемещения точек системы по отношению друг к другу. К ним относятся дополнительные элементы, шарниры, узлы и прочие геометрические факторы.
В этом случае степень СНС по внутренним признакам находится по следующей формуле
где K – число замкнутых контуров СНС (например, рамок),
У – число шарниров, врезанных в элемент СНС в пересчете на простые шарниры.
П
ростым называется шарнир, в котором сходятся только два стержня.
Сложный шарнир, в котором сходятся более 3 х стержней можно заменить n–1 простыми шарнирами (n – число стержней, сходящихся в сложном шарнире).
Таким образом, степень СНС можно определить сложив зависимости (21.1) и (21.2).
Для решения СНС при изгибе в курсе сопротивления материалов применяются метод сил, метод перемещений и комбинированный метод. Наиболее часто применяется метод сил, в частности прием сравнения перемещений, канонические уравнения метода сил (КУМС) и уравнения трех моментов.
Удобно и математически относительно несложно провести решение СНС с применением КУМС.
Д
ля составления канонических уравнений устанавливается число лишних связей системы. Эти лишние связи (например, реакции опор) обозначаются буквами Xi независимо от того сила это или момент (рис.6.34)
Для каждой лишней опоры составляется уравнение деформаций в виде суммы перемещений, вызванных действиями всех лишних связей и внешних нагрузок, причем эти деформации на опорах должны равняться нулю. Для удобства записи и решения эти уравнения составляются по определенному правилу (или канону).
В общем случае КУМС записывается так:
где δij – перемещение в i той точке под действием единичной силы, приложенной к j той точке.
δ11, δ22, δ33, . δnn – главные коэффициенты КУМС, представляющие собой единичные перемещения в i той точке под действием единичной силы, приложенной в той же точке. Они определяются по способу Верещагина путем перемножения эпюр от единичных сил «самих на себя».
δ12, δ13, . δij – побочные коэффициенты, представляющие собой единичные перемещения, определяемые по способу Верещагина путем перемножения единичных эпюр между собой.
Δ1F, Δ2F, . ΔnF – грузовое перемещение, определяемое как перемещение в i той точке под действием системы внешних нагрузок.
По способу Верещагина оно находится путем перемножения грузовой эпюры момента на единичную эпюру под действием i той единичной силы.
Определив все единичные и грузовые перемещения КУМС, решается данная система и определяются неизвестные усилия X1; X2; X3 . Xi . Xn.
По завершении раскрытия неопределимости СНС строятся необходимые эпюры (для рамы – N, Q и M). и выполняются две проверки – статическая и деформационная.
Статическая проверка заключается в проверке равновесия элементов или узлов системы (см. задачу № 12 РПР-2).
Деформационная проверка сводится к расчету перемещений тех точек системы, где действуют лишние связи (Xi). Обычно проверяется равенство нулю перемещений в опорах системы. Для этого необходимо по способу Верещагина перемножить конечную эпюру изгибающих моментов с единичной эпюрой, построенной для i той лишней связи.
В некоторых случаях при решении СНС можно уменьшить количество перемножений эпюр, если использовать эффект симметрии геометрического построения или силового нагружения системы (рис.6.35).
В следующем случае система рассекается по оси симметрии и в качестве лишних связей выбираются внутренние силовые факторы в проведенном сечении.
Тогда единичные эпюры от соответствующих внутренних силовых факторов будут иметь либо симметричную, либо кососимметричную формы
Следовательно, при перемножении симметричной эпюры на кососимметричную получаем перемещение равное нулю.
Вы бы купили подержанный автомобиль у этого человека? Морт Сал о Ричарде Никсоне
ещё >>
Сложное сопротивление
По этой ссылке вы найдёте полный курс лекций по математике:
Сложное сопротивление 1.1. Общие понятия 1.2. Косой изгиб 1.3. Нормальные напряжения при косом изгибе 1.4. Перемещение при косом изгибе 1.5. Примеры расчетов на косой изгиб 1.6. Изгиб с растяжением или сжатием 1.7. Внецентренное растяжение или сжатие стержней большой жесткости 1.8. Ядро сечения 1.9. Пример построения ядра сечения 1.10. Изгиб с кручением стержней круглого сечения Библиографический список 4 1. Сложное сопротивление 1.1
Общие понятия Под сложным сопротивлением понимают совокупность простых видов деформаций бруса, при которых в его поперечных сечениях одновременно возникает более одного внутреннего силового фактора. Исключением является прямой поперечный изгиб, который не принято рассматривать, как случай сложного сопротивления, хотя при этом в сечениях и возникают два внутренних силовых фактора: изгибающий момент и поперечная сила.
Этот вид деформации рассматривается как простой потому, что в подавляющем большинстве случаев расчеты на прочность и жесткость ведутся без учета влияния поперечных сил, т. е. по одному силовому фактору – изгибающему моменту. Напряжения и деформации при сложном сопротивлении могут быть в большинстве случаев вычислены на основании принципа независимости действия сил. Для этого сложная деформация раскладывается на простые.
Для каждой простой деформации находят напряжения и перемещения. Суммарное напряжение или перемещение определяют алгебраическим или геометрическим их сложением. Среди случаев сложного сопротивления стержней наиболее часто встречаются следующие сочетания простых видов нагружения: косой изгиб (рис. 1.1, а), внецентренное растяжение или сжатие (рис. 1.1, б) и одновременное действие кручения с изгибом (рис. 1.1, в), изгиб с растяжением или сжатием и т. д. Рис. 1.1 1.2.
Косой изгиб Косым изгибом называется такой вид изгиба, при котором плоскость действия изгибающего момента в поперечном сечении бруса не проходит ни через 5 одну из главных центральных осей этого сечения, или не совпадает ни с одной из главных плоскостей (рис. 1.2). Под главной плоскостью понимают плоскость, проходящую через продольную ось балки и одну из главных центральных осей поперечного сечения. Например, для прямоугольного сечения (рис. 1.2, г) – это плоскости, проходящие через оси ZX, YX.
Косой изгиб можно подразделить на плоский и пространственный. Плоский косой изгиб – это вид сложного сопротивления, когда все внешние силы расположены в одной плоскости (рис. 1.1, а,1.2, а), называемой силовой, и эта плоскость не совпадает ни с одной из главных плоскостей. Пространственный косой изгиб отличается от плоского лишь тем, что внешние силы не находятся в одной плоскости и изогнутая ось балки будет уже не плоской, а пространственной кривой.
Плоский косой изгиб представляет собой частный случай пространственного изгиба. Рис. 1.2 1.3. Нормальные напряжения при косом изгибе 6 Рассмотрим определение напряжений при косом изгибе (рис. 1.2, а). Прежде всего, все нагрузки, действующие в произвольной плоскости, разложим на составляющие, расположенные в главных плоскостях (рис. 1.2, б), и построим эпюры изгибающих моментов Мz и Му (рис. 1.2, в), т. е. приведем сложный изгиб к двум плоским изгибам М Мz2 М у2 .
В произвольном сечении с координатой х установим величину и направление изгибающих моментов Мz и Му (1.2, в). Напряжение в какой-либо точке сечения найдём в соответствии с принципом независимости действия сил (рис. 1.3.): Знак нормальных напряжений зависит от направления изгибающих моментов. Например, для точки В (рис. 1.3, а) оба слагаемых положительны, так как оба момента Мz и Му вызывают в точке В растяжение, растягивающее напряжение. В точке D напряжение определяется как где уD и zD – координаты точки.
Для произвольной точки сечения напряжения определяются по формуле (1.2) Все параметры, входящие в эту формулу, подставляются по модулю, а знаки перед составляющими слагаемыми определяем из физических соображений: если изгибающий момент Мz или Му вызывает в точке растягивающее напряжение, то перед составляющей должен быть знак плюс, сжимающее напряжение – знак минус. Опасные точки в сечении при косом изгибе определяются по положению нейтральной линии.
Возможно вам будут полезны данные страницы:
Нейтральная линия – это геометрическое место точек, в которых нормальные напряжения равны нулю. Уравнение нейтральной линии при косом изгибе имеет вид (1.4) где β – угол наклона нейтральной линии. По положению нейтральной линии определяется положение точки в сечении, как наиболее удалённой от нейтральной оси, например точка В и точка D (рис. 1.3). В опасных точках напряжения достигают наибольшей величины.
Для пластичных материалов условие прочности запишется для одной, наиболее удалённой точки от нейтральной оси (рис.1.3): где ув и zв – координаты опасной точки. Для сечений типа прямоугольного, двутавра, швеллера и т.д. имеющих ярко выраженные угловые точки, условие прочности можно записать в виде: – осевые моменты сопротивления. Для хрупких материалов условие прочности записывают для двух опасных точек, наиболее удалённых от нейтральной линии (точки В и т. D): координаты опасных точек. 8 1.4.
Перемещение при косом изгибе Определим прогиб консольно-защемленной балки, нагруженной на конце силой Р, действующей под углом α к вертикали. Разложим силу Р на составляющие РуР soc. (рис. 1.4). Прогиб на свободном конце балки по оси у от силы Ру составит аналогично Суммарный прогиб балки Рис. 1.4 1.5. Примеры расчетов на косой изгиб Пример 1.1 Рассмотрим балку длиной l = 3 м, составленную из двух швеллеров № 16 и нагруженную силами Р1 = 6 кН и Р2 = 4 кН, как показано на рис. 1.5.
Угол наклона сечения к горизонту α = 15є (рис. 1.5, б). 9 Найти величину наибольшего напряжения в опасном сечении и величину и направление полного перемещения сечения С. Рис. 1.5 Решение 1. Геометрические характеристики сечения. Находим по сортаменту геометрические характеристики для швеллера №16 и с учетом этого вычисляем их для рассматриваемого сечения (рис. 1.5): где 18,1 – координата центра тяжести швеллера (рис. 1.5, в).
10 Тогда осевые моменты сопротивления Wz и Wу определяется по зависимости – ширина полки швеллера. 2. Найдем проекции внешних сил на главные оси сечения. 3.Определяем реакции опор в главных плоскостях и строим эпюры изгибающих моментов (рис. 1.6) в этих плоскостях. Плоскость Плоскость Выполняем проверку правильности определение реакции Аналогично Реакции определены, верно. Вычисляем изгибающие моменты в характерных сечениях: Строим эпюры Мz и Му (рис. 1.6, а,б) Рис. 1.6 4.
Находим максимальные напряжения в сечении С: Максимальное напряжение в сечении D Видим, что опасным является сечение D 5. Устанавливаем положение нейтральной линии в сечении С. Используем формулу (1.4): Отсюда находим угол наклона β нейтральной линии: β=25є30’ (отсчитывается от оси Z). 6. Направление полного перемещения перпендикулярно к нейтральной линии (отсчитывается таким же углом β=25є30’ от оси У (рис. 1.5)). 7. Найдём вертикальную составляющую ∆у полного перемещения (рис. 1.5).
Для этого используем интеграл Мора и формулу Верещагина. 12 Приложим к сечению С единичную силу и построим эпюру единичных моментов (рис 1.6, в). Тогда прогиб в вертикальной плоскости: Аналогично определяются перемещения в горизонтальной плоскости где М 2 – эпюра изгибающих моментов от единичной силы, приложенной в точке С параллельно оси Z (в горизонтальной плоскости): Полный прогиб определяем как геометрическую сумму прогибов в вертикальной и горизонтальной плоскостях: 1.6.
Изгиб с растяжением или сжатием Изгибом с растяжением (сжатием) называется такой вид сложного сопротивления, при котором в поперечном сечении стержня возникают продольная сила и изгибающий момент (моменты). Если на балку действуют силы, пересекающие ее ось, но не лежащие ни в одной из главных плоскостей, то имеет место сложный изгиб с растяжением или сжатием (рис. 1.8, а). При расчете прежде всего показываем расчётную схему (рис. 1.8, б) стержня.
Для этого разложим все нагрузки на составляющие по главным осям сечения (Z, У), продольной оси Х балки и построим эпюры внутренних усилий (рис. 1.8, в). Для других точек (например, точки D) нормальные напряжения будут определятся по формуле (1.6) т. е. знаки минус связаны с тем, что силовые факторы Мz и Му вызывают в точке D деформацию сжатие. Таким образом, если силовые факторы – продольная сила N, моменты Мz, Му вызывают в рассматриваемой точке сжатие, то вводится знак минус перед соответствующим членом уравнения, если растяжение, то плюс. С учетом этого формула (1.6) для нормальных напряжений имеет вид (1.7)
Для проверки прочности балки необходимо найти опасную точку в сечении, в которой нормальные напряжения достигнут максимальной величины.
Опасные точки в сечении определяются по положению нейтральной линии. Это точки наиболее удалённые от нее. Рис. 1.8 При выводе уравнения нейтральной линии введём условность: главные центральные оси (У, Z) направлять таким образом, чтобы в первом квадранте складывались напряжения одного и того же знака (рис. 1.8, г). Эта условность позволяет при записи уравнения нейтральной линии опустить знаки перед составляющими в формуле (1.7).
С учётом этого уравнение нейтральной линии имеет вид (1.8) где у0 и z0 – координаты точек, лежащих на нейтральной линии. Из формулы (1.8) видим, что нейтральная линия не проходит через центр тяжести сечения и представляет собой прямую, отсекающую отрезки на осях координат. Отрезки, отсекаемые ею на осях координат: при 0 , (1.9) Знак минус в формуле (1.9) означает, что отрезки должны быть отложены в сторону, противоположную направлению главных центральных осей Z, Y.
Для сечения (рис. 1.9) наиболее опасными точками являются точка В и точка D. Рис. 1.9 Для хрупких материалов опасных точек в сечении две – это точки В и D как наиболее удалённые от нейтральной оси. В этом случае условие прочности для двух опасных точек где индекс ” р ” – означает растяжение, “c” – сжатие. 1.7. Внецентренное растяжение или сжатие стержней большой жесткости. 16 Внецентренным растяжением или сжатием называется такой вид деформации, при котором равнодействующая внешних сил параллельна оси стержня, но смещена относительно этой оси. Точка приложения силы называется полюсом п (рис. 1.10,а).
Расстояние l от полюса до центра тяжести сечения называется эксцентриситетом силы. Эксцентриситеты силы (zр и ур) относительно главных осей У и Z являются координатами полюса. Рис. 1.10 Таким образом, при внецентренном растяжении (сжатии) силой Р в поперечных сечениях возникают три внутренних силовых фактора, постоянных по длине стержня (рис. 1.10, б): Следовательно, внецентренное растяжение (сжатие) представляет собой совокупность изгиба и осевого растяжения (сжатия).
Нормальные напряжения в произвольной точке какого-либо сечения с координатами z, у определяются по формуле, аналогично формуле (1.7) где знаки слагаемых можно определить, исходя из характера деформации, также как при изгибе с растяжением (сжатием). Подставив сюда выражение (1.10), получим Из раздела “Геометрические характеристики плоских сечений” известно, что где iz и iу – радиусы инерции сечения. Подставив (1.12) в (1.10), получим формулу для определения нормальных напряжений в этом виде: Уравнение нейтральной линии находим из условия, что σ = 0, тогда где у и z – координаты текущей точки нейтральной линии.
Из выражения (1.14) видно, что нейтральная линия не проходит через начало координат, и ее положение удобнее находить по отрезкам, отсекаемым ею на координатных осях (рис. 1.11), либо по формуле (1.9). (1.15) Формулы (1.15) показывают, что отрезки ay иaz имеют знаки, противоположные координатам точки приложения ур и zр. Так, если внешняя сила Р приложена в точке первого квадранта, то нейтральная линия отсекает отрезки ay и z a в третьем квадранте (рис. 1.12).
Чем ближе полюс к центру тяжести сечения, тем дальше от него нейтральная линия и наоборот. Рис. 1.12 Зная положение нейтральной линии и определив координаты опасных точек уоп и zоп, как наиболее удаленных от неё, можно записать формулы для нормальных напряжений в этих точках и условие прочности (1.16) В случае, представленном на рис. 1.11, опасными являются точки В и D. 1.8. Ядро сечения 19 Существуют некоторые материалы, которые плохо сопротивляются растяжению (кирпич, камень, бетон и т.п.).
Для рационального проектирования конструкций из таких материалов необходимо, чтобы в сечениях элементов не появлялись растягивающие напряжения. Этого можно добиться, если точка приложения силы будет размещена в некоторой области вокруг центра тяжести сечения, называемой ядром сечения. Ядро сечения характеризуется тем, что всякая продольная сила, приложенная внутри этой области, вызывает во всех точках поперечного сечения нормальные напряжения одного знака.
Для построения ядра сечения рекомендуется задавать возможные положения нейтральной линии так, чтобы она касалась контура сечения, не пересекая его, и находить соответствующую точку приложения силы, соответствующую одной из вершин ядра сечения. При повороте нейтральной линии вокруг угла контура сечения точки полюса будут находиться на линии, соединяющей вершины ядра. 1.9. Пример построения ядра сечения Рассмотрим методику построения ядра сечения на примере прямоугольной фигуры (рис. 1.13). Рис. 1.13
Сечение имеет размеры В Ч Н; его геометрические характеристики Пусть нейтральная линия занимает положение 1-1, тогда отрезки, отсекаемые ею на координатных осях, По формуле (1.15) найдём координаты первой точки (приложения силы (вершины ядра сечения)): Если повторить подобные рассуждения для положенной нейтральной линии 2- 2, 3-3 и 4-4, то получим координаты точек 2, 3 и 4. Соединив эти точки прямыми линиями, получим ядро сечения для прямоугольника.
Таким образом, ядро сечения имеет форму прямоугольника, содержащего столько строк, сколько касательных можно провести к данному сечению. Пример 1.2 Колонна, поперечное сечение которой показано на рис.1.14, нагружена сжимающей силой Р=240кН, приложенной в точке К. Размеры сечения В1=16 см, Н1=4 см, В2=2 см, Н2=20 см. Требуется: 1. Определить положение нейтральной линии. 2. Определить наибольше растягивающее и сжимающее напряжения. 3. Построить плоскую эпюру напряжений. 21 Рис. 1.14 Решение 1.
Вычисляем геометрические характеристики сечения: – Площади элементов сечения А1=16 ּ4=64 см2; А2=20 ּ2=40 см2; А=А1+ А2=64+40=104 см2; – Положение центра тяжести – Проводим центральную ось Z. – Расстояние между осями Z1, Z2 простых фигур и центральной осью Z: – Моменты инерции относительно центральных осей: – Квадраты радиусов инерции сечения: 2. Координаты полюса: 2. Отрезки, отсекаемые нейтральной линией на осях координат: 3. Проводим нейтральную линию в сечении (рис.1.15).
Опасные точки сечения: точка D – наибольшие сжимающие напряжения; координаты точки zD=-8,0 см; уD=-6,6 см; точка В – наибольшие растягивающие напряжения; 23 координаты точки zВ=8,0 см; уВ=-2,6 см. Рис. 1.15 5. Находим напряжения в опасных точках по формуле (1.16) Напряжения сжатия: Напряжения растяжения: 6. Строим эпюру напряжений (рис. 1.15). 24 1.10.
Изгиб с кручением стержней круглого сечения Это такой вид сложного сопротивления, когда в поперечных сечениях стержня (вала) возникают изгибающий и крутящий моменты. Сочетания изгиба с кручением стержней круглого поперечного сечения чаще всего встречается при расчёте валов. Силы, действующие на вал (давление зубчатых колёс или натяжение ремней, собственный вес шкивов и вала), вызывают в поперечных сечениях в общем случае крутящий момент (Мк), изгибающие моменты (Мz , Му) и поперечные силы (Qу , Qz) в двух плоскостях (рис. 1.16).
В поперечном сечении круглого стержня возникают нормальные напряжения от изгиба, а также касательные напряжения от кручения и изгиба. Вследствие малой величины касательными напряжениями от поперечных сил можно пренебречь. Для расчёта стержней круглого поперечного сечения прежде всего необходимо построить эпюры изгибающих и крутящих моментов от заданных внешних сил. Нагрузки раскладывают на составляющих вдоль координатных осей и строят эпюры изгибающих моментов Мz и Му (рис. 1.16).
Поскольку вал имеет круглое поперечное сечение, то любая ось, проходящая через центр тяжести его, является главной осью. Следовательно, при действии изгибающих моментов в разных плоскостях не будет косого изгиба, а будет происходить лишь плоский изгиб в плоскости действующего результирующего изгибающего момента ММM и zу 22 . (1.17) По эпюрам результирующего изгибающего и крутящего моментов (рис. 1.16, г, д) находят опасное сечение, где эти моменты достигают наибольшего значения. 25 Рис. 1.16
На участках вала, где линии, очерчивающие эпюры моментов, пересекают базовую ось в одной точке, эпюра результирующих моментов очерчивается прямой линией (крайний правый участок ВС). На участках CD и DE эпюра результирующих моментов очерчивается параболой, так как вышесказанное условие не соблюдается. Здесь силовые линии в каждом смежном сечении меняют своё положение. Рассмотрим произвольное сечение вала на расстоянии х от правого конца. В этом сечении (рис. 1.17), как следует из построенных эпюр, действуют изгибающие моменты Mz, M y, крутящий момент Mк и поперечные силы. Рис. 1.17
Наибольшие касательные напряжения при кручении в данном поперечном сечении действуют на поверхность вала и определяются по зависимости xam, где Mк крутящий момент в рассматриваемом сечении; полярный момент сопротивления; радиус сечения. Для сплошного круглого сечения . Наибольшее нормальное напряжение от результирующего изгибающего момента Ми определяется по зависимости Wи WzWy момент сопротивления при изгибе. Для круглого сечения Сопоставляя Wи с W , можно заметить, что WWи.
Точки, в которых действуют максимальные нормальные напряжения, находятся на пересечении границы контура (окружности) плоскостью результирующего изгибающего момента (рис. 1.18) Рис.1.18 27 Таким образом, наибольшие нормальные напряжения будут в точках В и D, а так же наибольшие касательные напряжения от кручения, а следовательно, и главные напряжения. Причем касательные напряжения действуют в плоскости поперечного сечения, а нормальные перпендикулярно сечению (рис. 1.19). Рис. 1.19
Ввиду того что нормальное и касательное напряжения взаимно перпендикулярны, материал испытывает плоское напряженное состояние, и расчет на прочность ведется с использованием теорий прочности. Третья теория прочности (теория наибольших касательных напряжений) и четвертая (энергетическая теория) используются для пластичных материалов, а теория Мора – для хрупких.
В соответствии с третьей теорией прочности условие прочности записывается через эквивалентные напряжения экв и имеет вид (1.20) а по четвертой теории прочности (1.21) Подставляя в эту формулу выражения для напряжений (1.19) и (1.18), получим где называют приведенным моментом по четвертой теории прочности. При расчете по третьей теории 28 Если вал выполнен из хрупкого материала, то следует пользоваться теорией прочности Мора:
Обратим внимание, что если материал пластичный, то тогда из (1.24) вытекает третья теория прочности. Пример 1.3 Стальной вал круглого поперечного сечения (рис. 1.20) вращается с постоянной скоростью и передает мощность N=81,2 кВт посредством зубчатого колеса с окружным усилием Р и шкива, усилия в ведущей и ведомой ветвях которого соответственно равны 2t и t. Ветви ремня параллельны друг другу и наклонены к горизонту под углом , а окружное усилие действует под углом β 0.
Частота вращения вала n 970 об/мин. Диаметр шкива D1=650 мм, диаметр зубчатого колеса D2=400 мм. Длины участков: l150 мм. Допускаемое напряжение []=100 МПа. Требуется: 29 1. Изобразить расчетную схему вала и перенести на нее все внешние силы и моменты (включая реакции опор). 2. Разложить окружное усилие и усилия ветвей ремня на составляющие в вертикальной и горизонтальной плоскостях.
Построить эпюры изгибающих и крутящих
Построить эпюры изгибающих и крутящих моментов. 3. Установить опасное сечение вала и определить его диаметр, используя четвертую теорию прочности. 30 Рис. 1.20 Решение 1. Угловая скорость вращения вала 2. Крутящий момент, подаваемый на вал 3. Усилия, действующие на вал: 4 Нк. 4. Проекция внешних сил на координатные оси и реакции опор: плоскость XOУ: плоскость XOZ: 5.
Расчетная схема вала с нагрузками показана на рис. 1.20, б. 6. Находим значения изгибающих моментов в характерных сечениях и строим эпюры моментов: Эпюры изгибающих моментов МZ и M у показаны на рис. 1.20, в, г. 7. Строим суммарную эпюру изгибающих моментов Эпюра суммарных изгибающих моментов показана на рис. 1.20, д. Эпюра крутящих моментов – на рис. 1.3, е. 8. Опасным является левое опорное сечение, где Ми 1,618 м и 9.
Приведенный момент по четвертой теории прочности 10. Из условия прочности требуемая геометрическая характеристика Учитывая, что 0,1 3, найдем требуемый диаметр вала 11. Окончательно принимаем значение диаметра d в соответствии со стандартными значениями, которые в интервале от 50 до 100 мм кратные пяти, а в интервале от 100 и выше кратные десяти. Для нашего случая принимаем d5 5 мм.
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
[spoiler title=”источники:”]
http://davaiknam.ru/text/izgib-1-ponyatie-izgiba-nejtralenaya-liniya
http://natalibrilenova.ru/slozhnoe-soprotivlenie/
[/spoiler]
Геометрические характеристики плоских сечений
Иметь представление о физическом смысле и порядке определения
осевых, центробежных и полярных моментов инерции, о главных центральных осях и
главных центральных моментах инерции.
Знать формулы моментов инерции
простейших сечений, способы вычисления моментов инерции при параллельном переносе осей.
При растяжении, сжатии, смятии и сдвиге деталь сопротивляется деформации всем сечением одинаково. Здесь
геометрической характеристикой
сечения является площадь.
При кручении и изгибе сечение сопротивляется
деформации не одинаково, при расчетах напряжений появляются другие геометрические
характеристики сечения, влияющие на сопротивления сечения деформированию.
Статический момент площади сечения
Рассмотрим
произвольное сечение (рис. 1).
Если разбить сечение на бесконечно малые площадки аА и
умножить каждую площадку на расстояние до
оси координат и проинтегрировать
полученное выражение, получим
статический момент площади сечения:
Для симметричного сечения статические
моменты каждой половины площади равны по величине и имеют разный знак.
Следовательно, статический момент относительно оси симметрии равен нулю.
Статический момент используется при
определении положения центра тяжести сечения:
Формулы
для определения положения центра тяжести можно записать в виде
Центробежным моментом инерции сечения
называется взятая по
всей площади сумма произведений элементарных площадок на обе координаты:
Центробежный момент инерции может быть положительным, отрицательным и равным нулю. Центробежный момент
инерции относительно осей, проходящих через центр тяжести сечения,
равен нулю.
Оси, относительно
которых центробежный момент равен нулю, называются главными. Главные оси,
проходящие через центр тяжести, называют главными центральными осями сечения.
Осевые
моменты инерции
Осевым моментом инерции сечения относительно некоторой
оси, лежащей в этой же плоскости, называется взятая по всей площади сумма
произведений элементарных площадок на квадрат их расстояния до этой оси:
1) осевой
момент инерции сечения относительно оси Ох
21 осевой момент инерции сечения
относительно оси Оу
Полярный
момент инерции сечения
Полярным моментом инерции сечения
относительно некоторой точки
(полюса) называется взятая по вс^й площади сумма произведений элементарных
площадок на квадрат их расстояния до этой точки:
где р — расстояние до полюса
(центра поворота) (рис. 25.1).
Поскольку , получим: полярный момент инерции
сечения равен сумме осевых:
Осевые моменты инерции характеризуют сопротивление сечения
повороту относительно соответствующей оси.
Полярный момент инерция характеризует сопротивление сечения
повороту вокруг полюса (начала координат). Единицы измерения моментов инерции: м4; см4;
мм4.
Моменты
инерции простейших сечений
Осевые моменты инерции прямоугольника (рис. 25.2)
Представим
прямоугольник высотой Н и шириной Ъ
в виде сечения, составленного из бесконечно тонких полос. Запишем площадь такой полосы: Ъбу — аА. Подставим
в формулу осевого момента 
Ох:
По
аналогии, если разбить прямоугольник на вертикальные по лосы, рассчитать
площади полос и подставить в формулу для осевого момента инерции относительно
оси Оу, получим:
Очевидно, что при /г > Ъ сопротивление
повороту относительно
оси Ох больше, чем относительно Оу.
Для квадрата:

Для круга вначале вычисляют полярный момент
инерции, затем — осевые.
Представим круг в виде совокупности бесконечно
тонких колец (рис. 25.3).
Площадь каждого кольца можно рассчитать как площадь прямоугольника
с длинной стороной, равной длине соответствующей окружности, и высотой, равной толщине кольца:
Подставим это выражение для площади в формулу
для полярного момента инерции:
Получим формулу для
расчета полярного момента инерции круга:
Подобным
же образом можно получить формулу для расчета полярного
момента инерции кольца:
где а — наружный
диаметр кольца; аън — внутренний диаметр кольца
Если обозначить йвн/^
= с, то
Осевые
моменты инерции круга и кольца
Используя известную связь между осевыми и полярным моментами инерции, получим:
Моменты
инерции относительно параллельных осей
Оси Охо и Ох параллельны
(рис. 25.4).
При параллельном переносе прямоугольной системы осей уоОхо в новое положение уоОх
значения моментов инерции ^х, 3″у, ^Xу
заданного сечения меняются. Задается формула перехода без вывода.
здесь ^x — момент инерции
относительно оси Ох; ^Xй — момент инерции относительно оси
Ох0;
А — площадь сечения; а — расстояние между осями Ох и
Охо-
Главные
оси и главные моменты инерции
Главные оси — это оси, относительно которых осевые моменты инерции принимают
экстремальные значения: минимальный и максимальный.
Главные центральные моменты инерции рассчитываются относительно
главных осей, проходящих через центр тяжести.
Примеры
решения задач
Пример 1. Определить величину осевых моментов инерции плоской фигуры
относительно осей Ох и Оу (рис. 25.5).
Решение
1. Определим осевой момент инерции
относительно оси Ох. Используем формулы для главных центральных
моментов. Представим
момент инерции сечения как разность
моментов инерции круга и прямоугольника.
Для круга
Для прямоугольника
Для
прямоугольника ось Ох не проходит через ЦТ. Момент инерции
прямоугольника относительно оси Ох:
где А — площадь сечения; а — расстояние между осями Ох
и Охо.
Момент инерции сечения
2. Осевой момент инерции относительно оси Оу:
Момент инерции сечения