- Учебники
- 5 класс
- Математика 👍
- Мерзляк
- №300

авторы: Мерзляк, Полонский, Якир.
издательство: Вентана-Граф, 2018 г.
Посмотреть глоссарий
Математика 5 класс Мерзляк. Номер №300
- Предыдущее
- Следующее
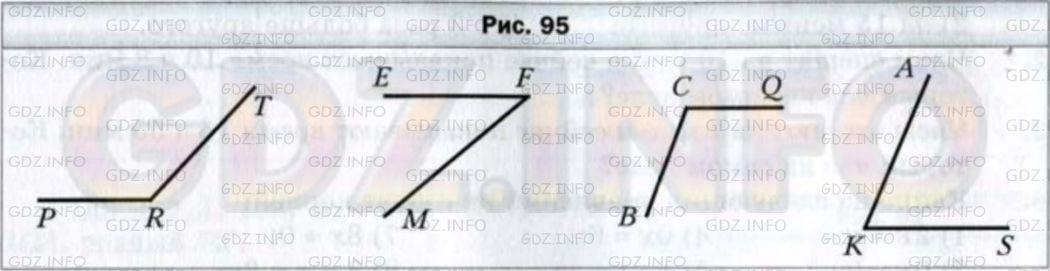
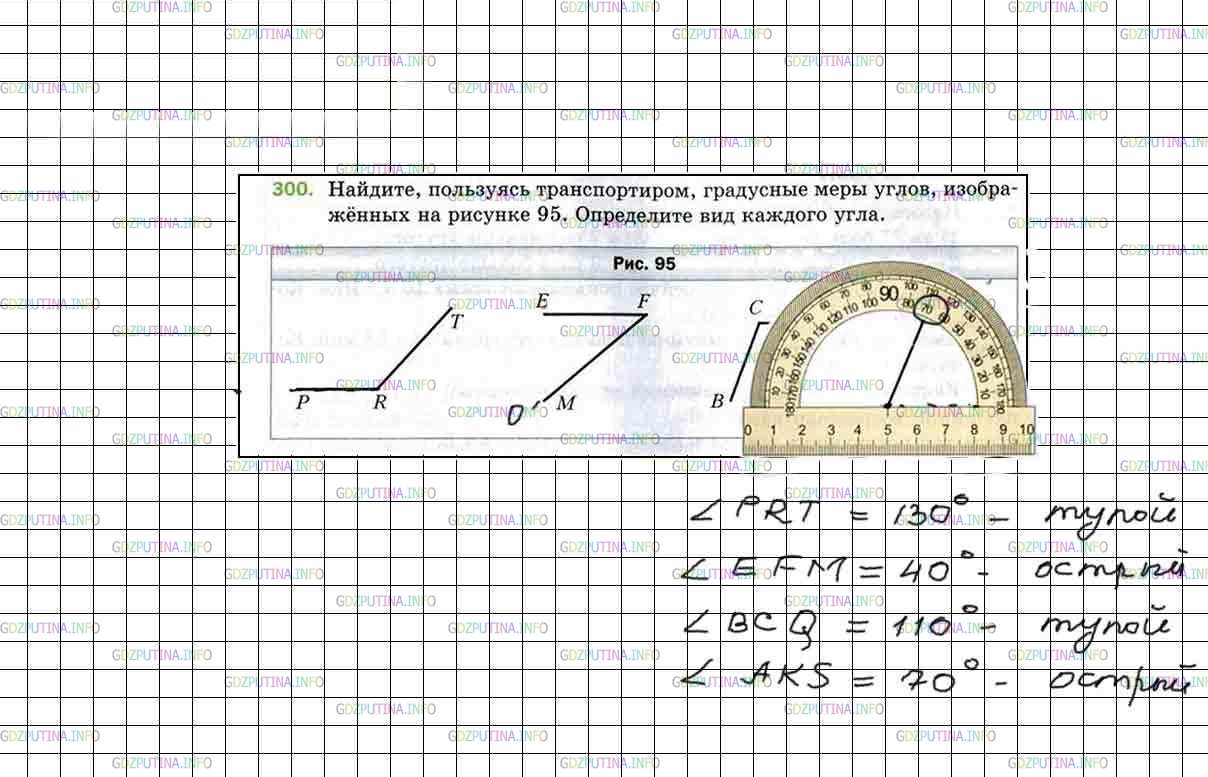
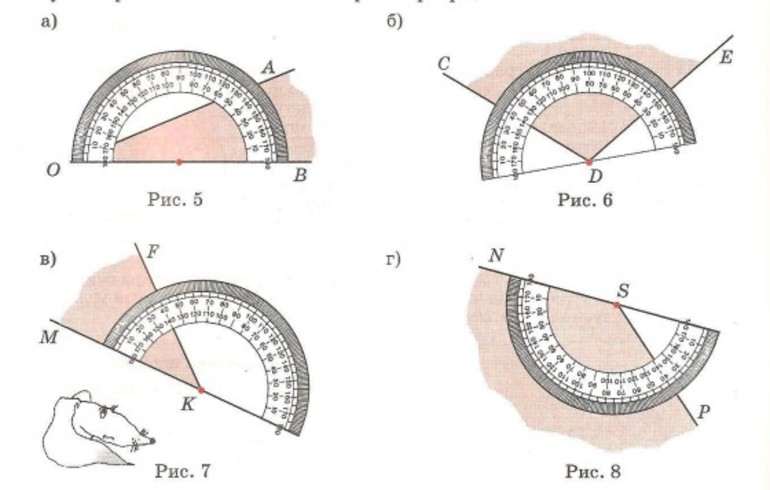
Найдите, пользуясь транспортиром, градусные меры углов, изображенных на рисунке 95. Определите вид каждого угла.


reshalka.com
Математика 5 класс Мерзляк. Номер №300
Решение
![]() Получай решения и ответы с помощью нашего бота
Получай решения и ответы с помощью нашего бота
![]() Посмотреть калькулятор Натуральные числа
Посмотреть калькулятор Натуральные числа
∠PRT = 133° − острый;
∠EFM = 40° − острый;
∠BCQ = 110° − тупой;
∠AKS = 67° − острый.
- Предыдущее
- Следующее
Нашли ошибку?
Посмотреть глоссарий
![]()
Нашли ошибку?
Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом


ГДЗ (готовое домашние задание из решебника) на Номер №300 по учебнику Математика. 5 класс. Учебник для учащихся общеобразовательных организаций / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. – М. : Вентана-Граф, 2014-2018г.
Условие
Найдите, пользуясь транспортиром, градусные меры углов, изображенных на рисунке 95. Определите вид каждого угла.
Решение 1
Подробное решение

Белый фонпереписывать в тетрадь
Цветной фонтеория и пояснения
Решение 2
Решение 3

Решение 4
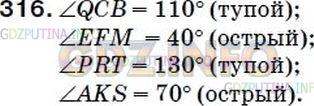
Решение 5

Решение 6
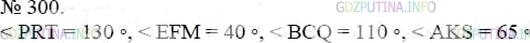
Популярные решебники
Ваше сообщение отправлено
и скоро будет рассмотрено
На прошлом уроке выяснилось, что единицей измерения углов и дуг является градус, равный $frac{1}{360}$ окружности. Измерение углов, следовательно, представляет из себя «процесс нахождения», сколько частей окружности ($frac{x}{360}$) заключено между сторонами угла.
Это отвечает на большую часть вопросов, что мы задавали ранее, однако не на все. Теперь, когда у нас есть единица измерения, нужно разобраться с правилами, определяющими, что в себя включает геометрия измерения углов.
Измерение углов — основное свойство
Начертим на плоскости угол $angle{BAC}$ и проведем между его сторонами $AB$ и $AC$ луч $AD$. Допустим, нам известна градусная мера $angle{DAC}$ и $angle{BAD}$.
Чему будет равен $angle{BAC}$?
Мы помним аксиому, задающую, что длина отрезка равняется сумме длин частей, на которые он разбивается любой его точкой. Измерение углов также подчиняется аксиоме «длины», только, конечно, вместо «длины» мы будем говорить «градусной меры»:
$A_8$. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.
Геометрия измерения углов: $0^circ$
Включает ли в себя геометрия измерения углов нулевые величины? Оказалось, что аксиома суммы частей применима как к отрезкам, так и к углам. А применима ли к углам аксиома «нулевой фигуры»? В отличие от отрезка, длина которого всегда задается строго больше нуля, о нулевых углах говорить можно.
Учтите, что в некоторых учебниках тем не менее встречается следующая аксиома: «Каждый угол имеет определенную градусную меру, бóльшую нуля». Это не совсем верно, поскольку тригонометрические функции могут принимать аргумент в виде нуля. Даже отрицательные аргументы.
Что это означает — не суть. Главное, что далее в курсе математики измерение углов может иметь дело с условным $angle{A}=0^circ$. Чтобы путаницу предупредить, аксиому углов $>0$ мы вводить не будем. А угол, равный нулю, будем представлять как угол, у которого стороны являются совпадающими лучами.
Измерение углов — основное свойство: задача
Условие. Проведено измерение углов, в результате которого получены следующие градусные меры: $angle{FDK}=38^circ$, $angle{KDM}=26^circ$, $angle{MDA}=32^circ$.
Чему равен $angle{FDA}$?
Дано:
$angle{FDK}=38^circ$
$angle{KDM}=26^circ$
$angle{MDA}=32^circ$
Решение. Воспользуемся аксиомой суммы градусных мер углов. Так, величина $angle{FDA}$ будет определяться суммой величин углов, его составляющих. Именно:
$$angle{FDA}=angle{FDK}+angle{KDM}+angle{MDA}$$
Градусные меры всех трех углов заданы по условию. Остается только их сложить. Имеем следующее:
$$angle{FDA}=38^circ+26^circ+32^circ=96^circ$$
Ответ: $96^circ$.
Измерение углов транспортиром
Измерительным инструментом углов является транспортир. Он представляет из себя пластину, выполненную в форме круга или полукруга, основанием которого иногда бывает линейка. Разметка полукругового транспортира состоит из 180 градусов, кругового — из 360. По своей сути транспортир — это конечный результат идеи о делении окружности на 360 ровных частей и нанесении на окружность соответствующей разметки.
Полукруговой транспортир
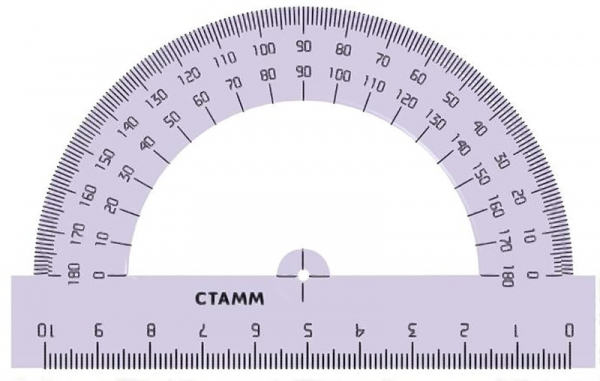
Круговой транспортир

Как пользоваться транспортиром для измерений
Измерение углов в школьном курсе геометрии вполне обходится упрощенной версией транспортира — полукруговой. На самом деле, транспортир используется не только для измерения, но и для построения углов. Вначале мы разберем, как проводить измерение углов транспортиром.
Шаг первый
Совместите точку отсчета инструмента с вершиной измеряемого угла. Одну из сторон угла расположите параллельно основанию транспорта: эта сторона должна указывать на нулевую отметку.
Шаг второй
Совместив основание со стороной угла, можно переходить к измерению угла. Вторая сторона угла будет указывать на некоторую отметку градусной шкалы. Если вдруг «поворотная» сторона не доходит до разметки, дорисуйте ее линейкой до необходимой длины.
Шаг третий
Зафиксируйте величину угла. Измерение углов транспортиром не допускает округление градусной меры без необходимости. Если транспортир показывает «$61^circ$», не стоит округлять значение до «$60^circ$».
В нашем же случае угол составляет ровно $60^circ$.
Как начертить угол транспортиром
Выше было продемонстрировано измерение углов с помощью транспортира без вспомогательной линейки. Транспортиры с основанием в виде сантиметровой линейки — тоже полезный инструмент, в особенности для откладывания углов. Давайте посмотрим, как начертить угол транспортиром, откладывая при этом на сторонах угла отрезки определенной длины.
Задача. Отложить $angle{BAC}=80^circ$ так, чтобы при этом отрезки $AC$ и $AB$ равнялись $4~см$ и $3~см$ соответственно.
☝️ Откладываем сторону на основании
В первую очередь на риске отсчета отметим точку $A$ — это будет вершина откладываемого угла. Проведем от точки $A$ луч, параллельный основанию транспортира. Первая часть откладывания угла выполнена.
✌️Откладываем вторую сторону угла
Чтобы начертить угол транспортиром, необходимо отметить еще одну точку на отметке $80^circ$. Отметим риску $80^circ$ небольшой вспомогательной точкой. Теперь проведем через эту вспомогательную точку и точку $A$ луч.
Нюанс!
Обратите внимание, что углы принято откладывать против часовой стрелки. Альтернативная разметка ниже основной — по часовой стрелке — предлагается на транспортире, чтобы было удобно проводить измерение углов. Ориентация углов на плоскости разная, и не всегда бывает хорошо иметь под рукой разметку, нанесенную только против часовой стрелки.
Построения линейкой
Руководствуясь условием поставленной задачи, отметим точку $C$ на основании таким образом, чтобы расстояние между точками $A$ и $C$ составляло $4~см$. Применим для этого линейку. Проделаем ту же самую последовательность действий с точкой $B$ с поправкой на $AB=3~см$.
Немного самостоятельной практики!
Возьмите карандаш, транспортир и лист бумаги. Отложите от стороны на основании транспортира два произвольных угла в границе $0^circ<x<180^circ$. Поделитесь в комментариях к уроку, какие градусные меры вы выбрали для углов.
Типы углов по градусам
Вероятно, ранее вам приходилось слышать определения для углов наподобие «острый», «тупой» и так далее. Эти определения задают типы углов по градусам. Зачем и кому это нужно? Цель очень даже приземленная: типы углов по градусам позволяют быстро сориентироваться, в каких границах значений располагается градусная мера угла. «Острый», «тупой» и прочее — это слова-маркеры.
Предлагаем с этими маркерами познакомимся поближе, дабы научиться проводить измерение углов на глаз.
Острый угол. Угол, градусная мера которого располагается в границах $0^circleq{x}<90^circ$. Заметьте, что угол, составляющий $0^circ$, считается острым. Пример острого угла: $angle{alpha}=50^circ$.
Тупой угол. Угол, градусная мера которого располагается в границах $90^circ<x<180^circ$. Пример тупого угла: $angle{beta}=130^circ$.
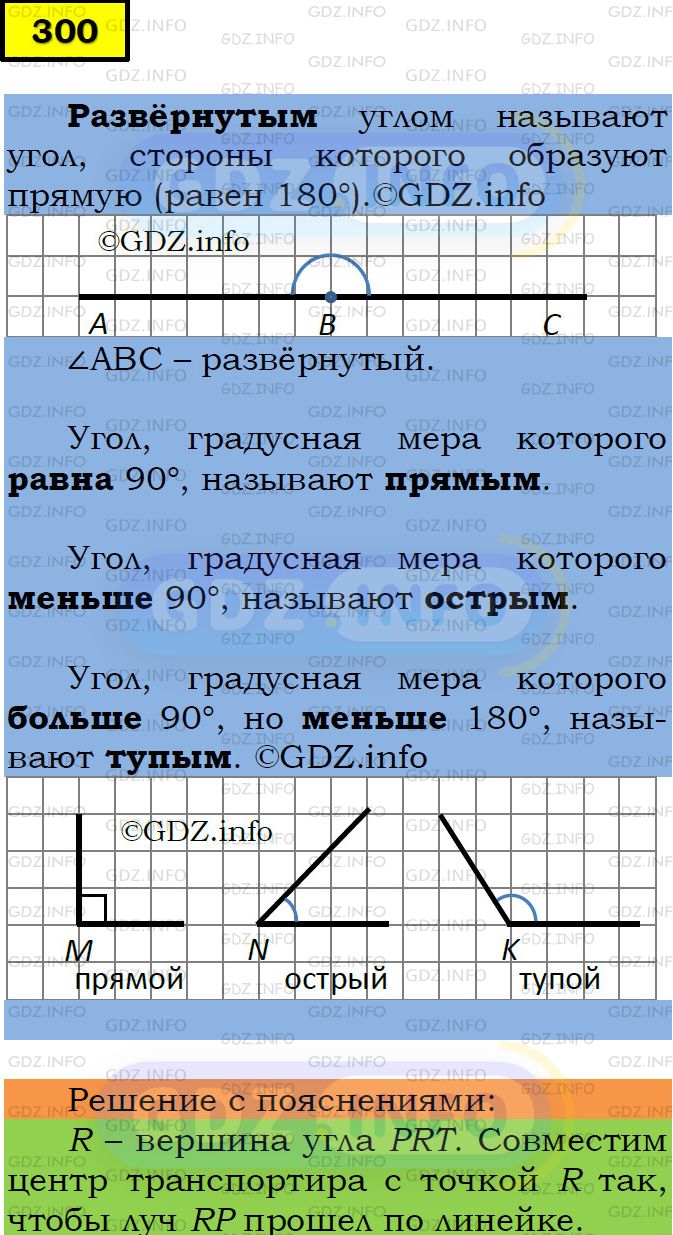
Развернутый и прямой углы. Заметьте, что выше границы для $90^circ$ и $180^circ$ устанавливаются строгими неравенствами. Это важные доли окружности, поэтому для них имеются отдельные названия. Так, угол, равный $90^circ$ ($frac{1}{4}$ окружности), называется прямым. Угол в $180^circ$ ($frac{1}{2}$ окружности) называется развернутым.
Прямой угол ($90^circ$)
Развернутый угол ($180^circ$)
Выпуклый угол. Когда градусная мера угла располагается в границах $180^circ<x<360^circ$, такой угол называется выпуклым.
Например, выпуклым углом является $angle{gamma}=260^circ$.
Выпуклые углы удобнее измерять круговым транспортиром. Однако если в наличии только полукруговой, можно вначале «отбить» развернутый угол ($180^circ$), а остальную часть измерить как острый угол. Полученное значение складывается с градусной мерой развернутого угла. На примере угла выше:
$$180^circ+80^circ=260^circ$$
Полный угол. Под полным углом понимается угол, равный полному обороту окружности, то есть составляющий $360^circ$.
Заметьте, что стороны полных и нулевых углов располагаются на одной прямой.
Измерение углов. Транспортир. Виды углов
Нам известно, что при измерении отрезков, мы сравниваем измеряемый отрезок с отрезком, который принят за единицу измерения (1 мм, 1 см, 1 м и т.д.). Аналогично происходит измерение углов: чтобы измерить угол его сравнивают с углом, который принят за единицу измерения – с градусом, записывают так 1 ° .
Градусная мера угла – это число, которое показывает, сколько раз градус и его части укладываются в данном угле.
Пример:
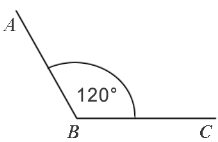
Градусная мера угла ABC равна 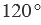 . Говорят: “Угол ABC равен 120 градусам”. Пишут:
. Говорят: “Угол ABC равен 120 градусам”. Пишут:  .
.
Транспортир – это измерительный инструмент, который используется для измерения и построения углов. Состоит из линейки (прямолинейной шкалы) и полукруга (угломерной шкалы: внутренней и внешней), который разделен на градусы от 0 до 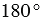 .
.
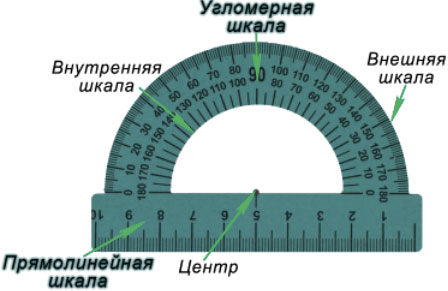
Для того чтобы измерить угол, необходимо совместить вершину угла с центром транспортира, при этом одна из сторон угла должна пройти через нулевое деление шкалы, тогда вторая сторона угла укажет градусную меру угла.
Пример: Измерим угол ABC, для этого совместим точку B с центром транспортира, и расположим транспортир так, чтобы сторона BC прошла через нулевое деление шкалы (обратите внимание отсчёт угла ведётся по той шкале, через нулевое деление которой пройдет одна из сторон угла: в нашем случае по внутренней шкале).
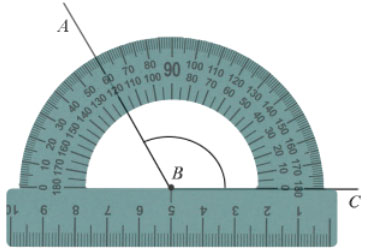
Вторая сторона при этом, как мы видим, проходит через деление шкалы 120, значит: 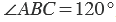 .
.
Свойства:
 АОС =
АОС =  АОВ +
АОВ +  ВОС.
ВОС.
Виды углов:
- Острый угол – угол, градусная мера которого меньше 90 ° .
- Прямой угол – угол, градусная мера которого равна 90 ° .

- Тупой угол – угол, градусная мера которого больше 90 °, но меньше 180 ° .
Биссектриса развернутого угла делит его на два угла, градусная мера каждого из которых равна 90 0 .
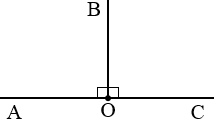
 АОС – развернутый, ОВ – биссектриса,
АОС – развернутый, ОВ – биссектриса,  АОВ =
АОВ =  ВОС = 90 0 .
ВОС = 90 0 .
Поделись с друзьями в социальных сетях:
Транспортир – как правильно пользоваться инструментом для построения и измерения углов?

Люди обычно сталкиваются с транспортирами в математике, когда учатся в школе создавать точные геометрические фигуры. Возможно, у многих из них никогда больше не будет причин снова использовать эти приборы, тем не менее транспортиры имеют долгую историю применения в различных областях.
История изобретения
Происхождение этого математического инструмента восходит к жрецам в Египте и Вавилоне, которые установили меру углов в градусах, минутах и секундах. Однако до времён классической Греции тригонометрия не использовалась в математике.
Во втором веке до нашей эры астроном Гиппарх из Никии изобрёл тригонометрический стол, для измерения треугольников. Затем Птолемей включил в свою великую астрономическую книгу «Альмагест» таблицу, с угловыми приращениями от 0 до 180°, с погрешностью менее 1/3600 единиц. Он также объяснил метод составления этой таблицы, и на протяжении всей книги приводил много примеров того, как вычислять с помощью неё неизвестные элементы фигур.
Птолемей также был автором, так называемой теоремы Менелая для решения сферических треугольников, и на протяжении многих веков его тригонометрия была основным пособием для астрономов.
Возможно, в то же время, учёные Индии также разработали тригонометрическую систему, основанную на функции синуса, которая, в отличие от используемого в настоящее время синуса, была не пропорцией, а длиной стороны, противоположной углу в прямом треугольнике этой гипотенузы. Индийские математики использовали разные значения для этого в своих таблицах.
Томас Бландевиль рассказал о приборе специально созданном, для рисования и измерения фигур в своём «Кратком описании универсальных карт» 1589 года. Как видно из названия, он применял его, чтобы править навигационные карты для использования в высоких широтах.
Другие европейские математики также описывали подобные приборы примерно в то же время. Независимо от того, кто первым придумал этот инструмент, к началу XVII века он вошёл в стандартную практику мореплавателей и геодезистов. К XVIII веку транспортиры начали появляться в учебниках по геодезии и геометрии.
Транспортиры в современном понимании возникли во второй половине XVIII века, когда такие учёные, как Джесси Рамсден и Георг Фридрих Брандер, усовершенствовали ранее созданные устройства.
В то время предпочтительными материалами для их изготовления были:

В первой половине XX века начали применять олово и целлулоид.
Называться транспортиром (рус.) прибор стал в 1610 году. Термин произошёл от средневекового слова protractor, что означает «переносить», который, в свою очередь, произошел от латинского слова protrahere «тянуть вперёд».
Разновидности и использование
Транспортир — это простой гониометр для измерения или создания угла. Он выглядит как круглый или полукруглый диск с делением. Диск может быть изготовлен из пластика, прочной бумаги или листового металла. Типичными являются диаметры от 8 до 15 см и деления на 1° и 0,5°, при измерении также 0,5 Гон (новый градус). Точность составляет от 0,1 до 0,5° в зависимости от диаметра шкалы. Более точные приборы имеют поворотную рейку со шкалой (длина до миллиметра).
Частично из-за различного использования их изготавливают во многих формах: знакомый полукруг, а также круги, прямоугольники, квадраты или четверть круга (квадранты). Они также могут иметь различные диаметры. Их изготавливают из латуни, стали, дерева, слоновой кости или пластика. Самой распространённой формой является полукруг с ограничительной шкалой в 180 градусов.
Угловой транспортир — градуированный круглый инструмент с одной поворотной рукой; используется для измерения или разметки. В строительстве часто требуется отмерить угол в 90 градусов. Иногда прилагается шкала Вернье, чтобы дать более точные показания. Прибор широко применяется для изготовления архитектурных и механических чертежей, хотя его использование уменьшилось с появлением современного программного обеспечения для рисования.
Универсальные транспортиры скоса используются изготовителями инструментов; поскольку они делают измерения посредством механического контакта с предметом, то классифицируются как механические транспортиры.
Угловой транспортир применяется для того, чтобы измерить и проверить углы с очень жёсткими допусками. Он считывает до 5 угловых минут (5 или 1/12°) и может измерять от 0 до 360°.
Сегодня также применяются электронные приборы, которые обычно работают с поворотным датчиком. Кроме того, связанными с транспортиром приборами являются:
- теодолит;
- оптический транспортир в строительной промышленности и геодезии;
- инклинометр для определения уклонов и косвенной альтиметрии;
- секстант для навигации.
Измерение градусов угла
Для того чтобы научиться пользоваться транспортиром инструкция нужна на начальном этапе. Для его освоения достаточно нескольких минут и примеров (смотреть онлайн) того, как можно измерить и построить угол с помощью этого прибора.
Измерить угол, значит найти его величину. Углы разделяют на три типа: острый, тупой и прямой. Прямоугольный имеет 90 градусов. Все углы что имеют больше этого значения называются тупыми, и соответственно меньше 90 градусов называются острыми. Развёрнутый угол имеет 180 градусов.

Понимание того, что углы являются частями окружностей, полезно, потому что тогда конструкция транспортира обретает смысл. Поскольку полный круг имеет 360º, отдельный угол должен быть меньше этого числа, потому что он часть круга.
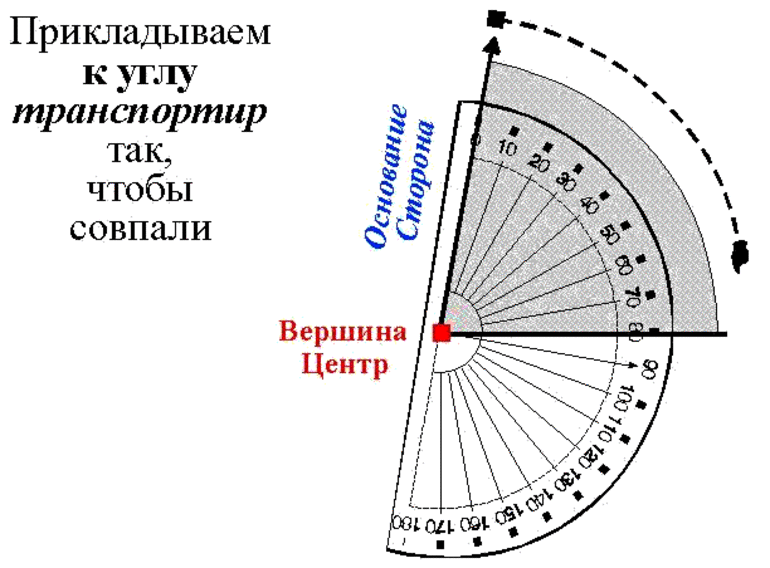
Алгоритм измерения следующий: для того чтобы измерить угол транспортиром необходимо приложить его центр верхней кромки линейки к вершине измеряемого угла. Вершина — это точка, в которой две из трёх сторон треугольника пересекаются.
Нижнюю планку (основание) транспортира нужно выставить горизонтально. Каждый транспортир имеет точку, спроектированную в центре основания, Эта средняя точка располагается на вершине угла, который должен быть измерен или нанесён на график. Другая сторона должна пересекать транспортир в одной из точек его дуги.
Если вторая сторона (линия) до дуги не доходит нужно продолжить её с помощью простой или масштабной линейки. То число, на шкале дуги, которое будет пересечено линией и есть величина угла в градусах.
Для удобства на большинстве транспортиров сделано две шкалы, внутренняя и внешняя, которые отображают числа в каждой строке.
Построение угла
Берётся чистый лист бумаги в клетку. На нём карандашом отмечается точка, от которой проводиться прямая линия, как одна из сторон будущего угла. Эта черта служит для того, чтобы задать направление второй стороне. В простых упражнениях, для приобретения навыка построения угла, линия проводится горизонтально.
Центр основы транспортира располагается на любом из концов черты, который будет вершиной угла. Эта точка отмечается на бумаге карандашом. И именно к этому месту, внутри отверстия и присоединяется вершина угла, одна из сторон которого должна совпадать в горизонтальной плоскости с внутренней стороной линейки транспортира.
Затем на шкале отмечается необходимый градус. С внутренней стороны отверстия также обозначается точка возле этого градуса. И от вершины проводится прямая линия к этой точке. Таким образом, получается необходимый угол.
Для того чтобы правильно пользоваться транспортиром очень важно его выровнять, и точно прикладывать, для получения верных измерений.
Пересечённые линии в верхней части прямой кромки линейки должны совпадать с вершиной (конечной точкой), где соединяются два луча.
Измерение углов. Транспортир
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти

На уроке мы вспомним, что такое единицы измерения, узнаем какими единицами можно измерять углы, познакомимся с такой единицей измерения, как градус, научимся измерять углы в градусах и чертить их с помощью транспортира. Также мы узнаем о других единицах измерения углов, которые применяются в различных ситуациях.
Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Измерение» и «Связь числа и геометрии. Часть 1. Измерения в геометрии. Свойства фигур»
[spoiler title=”источники:”]
http://nauka.club/matematika/transportir.html
http://interneturok.ru/lesson/matematika/5-klass/instrumenty-dlja-vychislenij-i-izmerenij/izmerenie-uglov-transportir
[/spoiler]
Математика
5 класс
Урок № 27
Углы. Измерение углов
Перечень рассматриваемых вопросов:
– понятие «угол», «величина угла»;
– виды углов;
– построение углов;
– измерение величины угла.
Тезаурус
Угол – геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки, которая называется вершиной угла.
Градус – единица измерения углов, составляющая часть развёрнутого угла.
Градусная мера угла – число, которое показывает, сколько единиц измерения (градусов) содержится между сторонами этого угла.
Обязательная литература
Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
Дополнительная литература
1. Чулков П. В. Математика: тематические тесты. 5 класс. // П. В. Чулков, Е. Ф. Шершнёв, О.Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.
Теоретический материал для самостоятельного изучения
«Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Всё вокруг – геометрия», – сказал в своё время французский архитектор Ле Корбюзье, и трудно с ним не согласиться. Геометрические фигуры постоянно встречаются в творениях природы и человека.
Сегодня мы рассмотрим ещё одну геометрическую фигуру – угол, разберём его виды и опишем процесс построения и измерения углов.
Для начала определим, что называют углом.
Углом называют геометрическую фигуру, образованную двумя лучами, выходящими из одной точки.
Построим угол. Для этого отметим на плоскости точку О и проведём два луча – ОК и ОМ. Получим геометрическую фигуру, образованную точкой О и двумя лучами, исходящими из этой точки. Такую геометрическую фигуру и называют углом.

Лучи ОК и ОМ называют сторонами угла, точку О – общее начало этих лучей – называют вершиной угла.
Обозначается угол чаще всего тремя буквами. Например, ∠КОМ или ∠МОК. В середине пишется буква, которой обозначена вершина угла. Также угол можно обозначать и одной буквой, поставленной у вершины угла. Например, ∠О.
Начертим два луча, исходящих из точки О и принадлежащих одной прямой.
Лучи ОС и OК вместе с точкой О дополняют друг друга до прямой – это дополнительные лучи. Угол называют развёрнутым, если его стороны являются дополнительными лучами.
Угол СОК – развёрнутый.

Построим развёрнутый угол АОВ и полуокружность с центром в точке О. Полуокружность разделим на 180 равных частей. Если построим углы с вершиной в точке О, стороны которых проходят через точки деления полуокружности, то таких углов будет 180. Один такой угол будет составлять часть развёрнутого угла.
рисунок
Меру угла, составляющего часть развёрнутого угла, принимают за единицу измерения углов и называют градусом. Обозначают: 1º.
Градусной мерой угла называют число, которое показывает, сколько единиц измерения (градусов) содержится между сторонами этого угла.
Например, градусная мера угла КOВ равна 25 градусам, так как в нём единица измерения градус содержится двадцать пять раз. Записывают: ∠КОВ = 25º.
рисунок
Стоит отметить, что для более точного измерения угла используют доли градуса:
– минуты, которые обозначают одной чёрточкой сверху над цифрой справа,
– секунды, которые обозначаются двумя чёрточками над цифрой справа.
В одном градусе содержится 60 минут, а в одной минуте – 60 секунд.
Например, если угол А равен 10 градусам 5 минутам, записывают: ∠А = 10º5′.
Градусная мера развёрнутого угла равна 180º.
Для измерения углов в градусах пользуются прибором, который называется транспортиром. На транспортире имеется шкала – полуокружность, разделённая на 180 равных частей. На линейке транспортира чёрточкой отмечен центр полуокружности транспортира.
Чтобы найти градусную меру угла, например, угла АВС, нужно совместить центр транспортира с вершиной угла, в данном случае точкой В; расположить линейку транспортира так, чтобы одна из сторон угла прошла через начало отсчёта шкалы транспортира – ноль градусов (в данном случае сторона АВ), и найти на шкале транспортира деление, через которое проходит другая сторона угла – в данном случае сторона ВС.
Это деление шкалы покажет градусную меру угла. В нашем случае – это 120º.
Транспортир применяется также для построения угла, мера которого известна. Построим, например, угол KNM, равный 60º. Для этого:
– проведём луч NM;
– совместим центр транспортира с точкой N;
– расположим линейку транспортира так, чтобы луч NM прошёл через начало отсчёта шкалы транспортира;
– найдём на шкале транспортира деление, соответствующее шестидесяти градусам, и отметим напротив него точку К;
– проведём луч NK. Мы построили угол KNM, равный 60º.
Ответить на вопрос, равны ли углы, и, если не равны, то какой из них больше или меньше, можно, сравнивая их градусные меры. Углы с равными градусными мерами равны. Из двух углов больше тот, который имеет большую градусную меру; а меньше тот, который имеет меньшую градусную меру.
Углы можно сравнить также наложением. Если при этом они совпадают, то равны.
Помимо развёрнутого, углы можно разделить на следующие виды: прямой, острый и тупой.
Угол называют прямым, если его градусная мера равна 90º.

Острым – если его градусная мера меньше 90º.

Тупым – если его градусная мера больше 90º и меньше 180º.

Рассмотрим ещё два вида углов, которые встречаются в геометрических задачах: это вертикальные углы, то есть пара углов с общей вершиной, которые образованы при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого. Например, угол один и два.

И смежные углы – это два угла, у которых одна сторона общая, а две другие являются дополнительными полупрямыми.
Например, угол САВ и угол САD.

Вместе смежные углы составляют развёрнутый угол. Следовательно, сумма величин смежных углов составляет 180º.
Итак, сегодня мы познакомились с разными видами углов и научились строить их с помощью транспортира.
Для определения величины углов используется прибор, который называют транспортир. Но существуют и более высокоточные приборы.
Так, гониометр использовался для определения положения судна в море или океане.

Теодолит – прибор для измерения горизонтальных и вертикальных углов при геодезических работах, в строительстве и т. п.

Секстант применялся для измерения высоты Солнца над горизонтом с целью определения географических координат той местности, в которой производится измерение, и на судах.

Посох Якова, служащий для измерения углов, – один из первых инструментов для астрономических наблюдений.



