Самой распространённой процедурой в инженерной геодезии считается построение теодолитного хода – системы ломаных линий и измеренных между ними углов. Замкнутым его называют, если он опирается только на один исходный пункт, а его стороны образуют многоугольную фигуру. Рассмотрим подробнее, как создается теодолитный ход замкнутого типа и какие у него особенности.
Содержание
- 1 Разновидности теодолитных ходов
- 2 Порядок выполнения работ
- 3 Обработка данных
- 4 Уравнивание
- 5 Определение дирекционных углов
- 5.1 Создавайте будущее вместе с нами
- 6 Вычисление румбов
- 7 Приращения координат
- 8 Линейная невязка и невязка приращения значений координат
- 9 Вычисление координат
Разновидности теодолитных ходов
Ходы могут образовывать целые сети, пересекаясь между собой и охватывая значительные территории, а их форма определяется особенностями местности. Их принято разделять на:
– замкнутый (полигон);
– разомкнутый;
– висячий;
– диагональный (прокладывают внутри других ходов).Если необходимо заснять ровный участок, вроде строительной площадки, лучшим выбором будет полигон. На объектах вытянутого типа, вроде автодорог, принято использовать разомкнутый ход, а висячий – для съемки закрытой местности, вроде глухих улиц.

Замкнутый ход по своей сути является многоугольной фигурой и опирается только на один базовый пункт с установленными координатами и дирекционным углом. Вершинами стороны выступают точки, закрепленными на местности, а отрезками – расстояние между ними. Его чаще всего создают для съемки стройплощадок, жилых зданий, промышленных сооружений или земельных участков.
Порядок выполнения работ
Как и другие геодезические мероприятия, эта процедура проводится с предварительной подготовкой для получения точных метрических данных. Немаловажную роль играет также их математическая обработка. Сами работы выполняются по принципу от общего к частному и состоят из следующих этапов:
- Рекогносцировка местности. Оценка снимаемой территории, изучение ее особенностей. На этом этапе определяется местоположение снимаемых точек.
- Полевая съемка. Работы непосредственно уже на местности. Выполнение линейных и угловых измерений, составление абрисов, предварительные расчеты и внесение изменений при необходимости.
- Камеральная обработка. Завершающий этап работ, который заключается в вычислении координат замкнутого теодолитного хода и последующего составления плана и технического отсчета.
Рекогносцировка и полевые измерения выполняются непосредственно на объекте и являются наиболее трудоемкими и затратными мероприятиями. Тем не менее, от качества их проведения зависит дальнейший результат.
Обработка данных проводится уже в помещении. Сегодня она осуществляется при помощи специального программного обеспечения, хотя и ручные расчеты все также остаются актуальными и могут быть использованы геодезистом в целях проверки.
Обработка данных
Обработка результатов измерений замкнутого теодолитного хода позволит оценить качество проделанной работы и внести исправления в полученные геометрические величины. Чтобы убедится в том, что угловые и линейные измерения находятся в допуске, еще во время полевых работ выполняют первичные расчеты.
Для вычисления значений координат точек замкнутого хода используют такие данные:
– координаты исходного пункта;
– исходный дирекционный угол;
– горизонтальные углы;
– длины сторон.

Полевые измерения, выполненные даже при соблюдении всех правил и требований, будут иметь неточности. Они обусловлены систематическими и техническими ошибками, а также человеческим фактором.
Расчеты проводятся в определенной последовательности, которую рассмотрим далее.
Уравнивание
При начале расчетов определяют теоретическую сумму углов , а потом увязывают их, распределяя между ними угловую невязку.
(sum beta _{теор}=180^{circ}cdot (n-2))
n- количество точек полигона;
(f_{beta }=sum beta _{изм}-180^{circ}cdot (n-2))
(sum beta _{изм})– значение измеренных угловых величин;
Для получения (f_{beta }), необходимо рассчитать разность между (beta _{изм}), в которой присутствуют погрешности, и (sum beta _{теор}).
В уравнивании (f_{beta }) выступает как показатель точности проведенных измерительных работ, а ее значение не должно быть выше предельной величины, определяемой из следующей формулы:
(f_{beta 1}=1,5tsqrt{n})
t-точность измерительного устройства,
n – количество углов.
Уравнивание заканчивается равномерным распределением полученной невязки между угловыми величинами.
Определение дирекционных углов
При известном значении дирекционного угла ((alpha )) одной стороны и горизонтального ((beta )) можно определить значение следующей стороны:
(alpha _{n+1}=alpha _{n}+eta )
(eta =180^{circ}-beta _{пр})
(beta _{пр})– значение правого по ходу угла, из чего следует:
(alpha _{n+1}=alpha _{n}+180^{circ}-beta _{пр})
Для левого ((beta _{лев})) эти знаки будут противоположными:
(alpha _{n+1}=alpha _{n}-180^{circ}+beta _{лев})
Создавайте будущее вместе с нами
Присоединяйтесь к нашей команде: мы создаем финтех-сервисы для 28 млн клиентов и опережаем рынок на 5 лет. Работаем на результат и делаем больше, чем от нас ждут.
Поскольку значение дирекционного угла не может быть больше, чем (360^{circ}), то из него, соответственно, отнимают (360^{circ}). В случае с отрицательным углом, необходимо к предыдущему (alpha ) добавить (180^{circ}) и отнять значение (beta _{испр}).
Вычисление румбов
У румбов и дирекционных углов существует взаимосвязь, а определяют их по четвертям, которые носят название четырех сторон света. Как видно из табл.1. расчёты проводят согласно установленной схеме.
Таблица 1. Расчеты румба в зависимости от пределов дирекционного угла.
| Четверть | Название относительно стороны света | Пределы α | Формула | Знаки приращений | |
| ΔХ | ΔУ | ||||
| I | СВ (северо-восточный) | 0° – 90° | r = α | + | + |
| II | ЮВ (юго-восточный) | 90°-180° | r = 180° – α | – | + |
| III | ЮЗ (юго-западный) | 180°-270° | r = α – 180° | – | – |
| IV | СЗ (северо-западный) | 270°-360° | r = 360° – °α | + | – |
Приращения координат
Для приращений координат в замкнутом ходе применяют формулы, использующиеся при решении прямой геодезической задачи. Ее суть состоит в том, что по известным значениям координат исходного пункта, дирекционного угла и горизонтального приложения можно определить координаты следующего. Исходя из этого, формула приращения значений будет иметь следующий вид:
(Delta X = dcdot cos alpha )
(Delta Y = dcdot sin alpha )
d-горизонтальное проложение;
α-горизонтальный угол.

Для полигона, который имеет вид замкнутой геометрической фигуры, теоретическая сумма приращений будет равняться нулю для обеих координатных осей:
(sum Delta X_{теор}= 0)
(sum Delta Y_{теор}= 0)
Линейная невязка и невязка приращения значений координат
Несмотря на вышесказанное, случайные погрешности не позволяют алгебраическим суммам выйти в ноль, поэтому они будут равняться другим невязкам приращений координат:
(f_{x}sum_{i=1}^{n}Delta X_{1})
(f_{y}sum_{i=1}^{n}Delta Y_{1})
Переменные (f_{x}) и (f_{y}) – проекции линейной невязки (f_{p}) на координатной оси, которую можно рассчитать по формуле:
(f_{p}=sqrt{f_{x}^{2}+f_{y}^{2}})
При этом (f_{p}), не должно быть боле, чем 1/2000 от доли периметра полигона, а распределения (f_{x}) и (f_{y}) проводится следующим образом:
(delta X_{i}=-frac{f_{x}}{P}d_{i} )
(delta Y_{i}=-frac{f_{y}}{P}d_{i} )
В этих формулах (delta X_{i}) и (delta Y_{i}) – поправки приращения координат.
і- номера точек;
В расчетах важно не забывать о значениях алгебраической суммы, иначе говоря – знаках. При внесении поправок они должны быть противоположны знакам невязок.
После приращений и внесения поправок в данные измерений, проводят расчет их исправленных значений.
Вычисление координат
Когда будут произведены увязки приращений точек полигона, следует определение координат, которое осуществляют с использованием следующих формул:
(X_{пос}=X_{пр}+Delta X_{исп})
(Y_{пос}=Y_{пр}+Delta Y_{исп})
Значения (X_{пос}) (Y_{пос}) – координаты последующих пунктов, (X_{пр}) и (Y_{пр}) – предыдущих.
(Delta X_{исп}) и (Delta Y_{исп}) – исправленные приращения между этими двумя значениями.
Если координаты первой и последней точки совпадают, то обработку можно считать завершённой.
На основе полученных координат и составленных во время полевых измерений абрисов в дальнейшем составляется план теодолитного хода.
После этого, по формулам (7.92), с учетом исправленных значений превышений, вычисляют высоты точек теодолитного хода с определением контрольного значения высоты конечной точки хода
Пример обработки ведомости высот приведен в табл. 7.8 для схемы рис. 7.23.
Пример 7.16. Обработка ведомости высот разомкнутого теодолитного хода.
В схеме теодолитного хода наведение на веху, установленную в последующей точке, выполнено на высоту прибора, в связи с чем вычисление превышений производилось по формуле (7.91).
Поправки в превышения записаны в ведомости над значениями вычисленных превышений.
Жирным шрифтом выделены исходные данные.
|
Таблица 7.8 |
|||||||
|
Ведомость высот разомкнутого теодолитного хода |
|||||||
|
№№ |
Горизонтальные |
Углы |
Превышения |
Высоты |
№№ |
||
|
точек |
проложения, м |
наклона |
вычисленные |
исправленные |
точек, м |
точек |
|
|
А |
189,04 |
+4о36,5′ |
(-0,02) |
+15,22 |
142,75 |
A |
|
|
1 |
113,86 |
+2о27,0′ |
+15,24 |
157,97 |
1 |
||
|
(-0,02) |
+4,85 |
||||||
|
2 |
121,57 |
-0о43,7′ |
+4,87 |
162,82 |
2 |
||
|
(-0,02) |
-2,60 |
||||||
|
3 |
93,39 |
-2о11,3′ |
-2,58 |
160,22 |
3 |
||
|
(-0,01) |
-3,58 |
||||||
|
4 |
163,61 |
+4о08,0′ |
-3,57 |
156,64 |
4 |
||
|
(-0,02) |
+11,80 |
168,44 |
|||||
|
D |
+11,82 |
D |
|||||
|
å d = 681 ,47 |
å hВЫЧ |
= + 25,78 |
|||||
|
м |
å hТЕОР |
м |
|||||
|
= + 25,69 |
|||||||
|
м |
|||||||
|
fh =+0,09 м |
fhДОП=±0,12 м |
Замкнутый теодолитный ход во многом является частным случаем разомкнутого теодолитного хода, полагая в последнем ХН = ХК, YH = YK, HH =HK. Одной из особенностей замкнутого хода является возможность контроля результатов полевых измерений, а также оценки точности без привлечения процедуры привязки к исходным геодезическим пунктам геодезической основы (геодезической опорной сети). В соответствии с этим несколько изменим порядок обработки указанного вида теодолитных ходов.
213
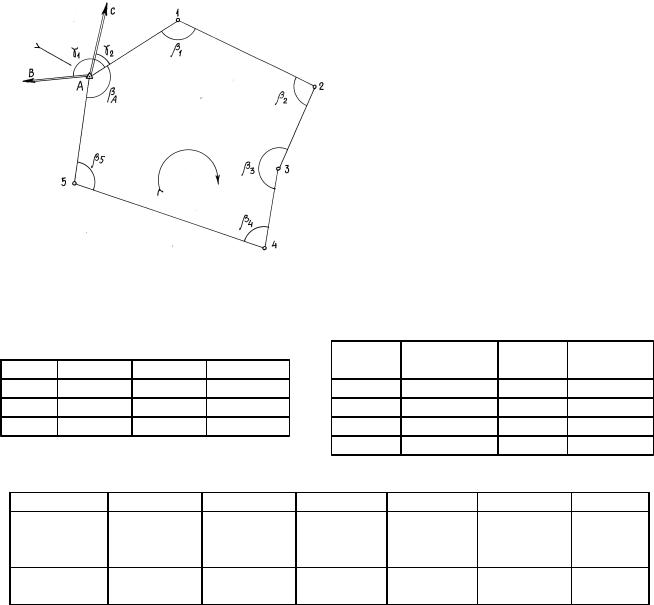
Пояснения по обработке замкнутого теодолитного хода рассмотрим совместно с примером, соответствующим схеме замкнутого хода, приведенной на рис. 7.26.
Рис. 7.26. Замкнутый теодолитный ход
представлены в табл. 7.10 и 7.11.
|
Таблица 7.9 |
|||
|
Точки |
А |
В |
С |
|
Х, м |
4216,563 |
6692,552 |
5594,790 |
|
Y, м |
7018,427 |
5172,041 |
11036,256 |
|
Н, м |
111,65 |
– |
– |
Исходные данные. Запроектирован замкнутый теодолитный ход повышенной точности (допустимая относительная погрешность 1:7500). Горизонтальные углы измерены теодолитом Т5. Длины линий измерены светодальномером с относительной погрешностью 1:10000. Углы наклона измерены теодолитом Т5 с округлением результатов до 0,1′. Допустимая угловая невязка в полигоне не более ± 10′′
 n . Координаты исходных пунктов Государственной геодезической сети представлены в таблице 7.9. Результаты измерений
n . Координаты исходных пунктов Государственной геодезической сети представлены в таблице 7.9. Результаты измерений
|
Таблица 7.10 |
|||
|
Обозна- |
Значение |
Обозна- |
Значение |
|
чение |
угла |
чение |
угла |
|
γ 1 |
154о25’00,0″ |
β 2 |
90о40’30” |
|
γ 2 |
46о38’15,6″ |
β 3 |
191о46’25” |
|
β А |
127о14’05” |
β 4 |
85о10’00” |
|
β 1 |
124о13’05” |
β 5 |
100о54’10” |
|
Таблица 7.11 |
||||||
|
Параметр |
А-1 |
1-2 |
2-3 |
3-4 |
4-5 |
5-А |
|
Наклонные |
||||||
|
расстояния |
77,396 |
109,891 |
64,282 |
56,143 |
142,789 |
77,906 |
|
S, м |
||||||
|
Углы |
-2о00,5′ |
+1о16,3′ |
+4о25,6′ |
-3о38,8′ |
+0о46,5′ |
-2о12,4′ |
|
наклона, ν |
Из решения обратных геодезических задач по дирекционным углам исходных направлений и значениям примычных углов вычислен дирекционный угол линии теодолитного хода А-1: αА1 = 117о42’15,2″. Аналогичные вычисления дирекционных углов линий теодолитного хода при его азимутальной привязке были выполнены при обработке разомкнутого теодолитного хода (§ 75). В данном случае необходимо определить только значение дирекционного угла одной линии теодолитного хода.
Пример обработки ведомости координат замкнутого теодолитного хода приведен в табл. 7.12.
214

76.1. Оценка точности угловых измерений и вычисление дирекционных углов
В замкнутом теодолитном ходе (полигоне) могут быть измерены внутренние, либо внешние горизонтальные углы β (рис. 7.26). Если принять направление обхода по часовой стрелке, то все внутренние горизонтальные углы, показанные на схеме, будут правыми по ходу.
Теоретическая сумма горизонтальных углов замкнутого многоугольника равна:
– для внутренних углов:
|
å β ТЕОР |
= 180 0 (n − 2) ; |
(7.100) |
|
– для внешних углов: |
||
|
å β ТЕОР |
= 180 0 (n + 2) , |
(7.101) |
где n – число измеренных внутренних или внешних углов.
Угловая невязка в этом случае может быть определена по формуле
|
fβ = å β ИЗМ − å β ТЕОР . |
(7.102) |
В дальнейшем обработка результатов угловых измерений подобна обработке результатов угловых измерений разомкнутого теодолитного хода: вычисление допустимой угловой невязки по формуле (7.69); проверка условия (7.70); вычисление поправок в углы и контроль их вычисления по формулам (7.71) и (7.72); исправление углов по формуле (7.73) и контроль их исправления по соблюдению равенства
|
å β ИСПР = å β ТЕОР . |
(7.103) |
Дирекционные углы линий замкнутого теодолитного хода вычисляют последовательно по ходу с контрольным вычислением дирекционного угла его линии, вычисленного при азимутальной привязке. Так, следуя обозначениям на схеме рис. 7.26 и принятому направлению хода,
|
α 23 |
= α 12 |
± 180 0 |
− |
β 2ИСПР |
|
|
α 12 |
= α А1ИСХ ± 180 0 − β 1ИСПР |
||||
|
α 34 |
= α 23 |
± 180 0 |
− |
β 3ИСПР |
|
|
α 45 = α 34 ± 180 0 − |
β 4ИСПР |
(7.104) |
|||
|
α 5 А = α 45 |
± 180 0 |
− |
β 5ИСПР |
α А1ВЫЧ = α 5 А ± 180 0 − β АИСПР
Контрольное значение дирекционного угла, полученное по последнему выражению формул (7.104) для линии А1 должно точно соответствовать его исходному значению.
Таблица 7.12
Пример. 7.17.
Ведомость координат замкнутого теодолитного хода
|
№ |
Горизонтал |
Дирекцион- |
Горизон- |
Приращения |
Координаты, м |
|||
|
№ |
ьные углы |
ные углы |
тальные |
координат, м |
||||
|
то- |
β |
α |
проложе- |
(поправки) |
||||
|
чек |
(поправки) |
ния, м |
Х |
Y |
X |
Y |
||
|
d |
||||||||
|
А |
4216,563 |
7018,427 |
215
|
1 |
117о42’15,2″ |
77,348 |
(-0,005) |
(-0,006) |
|||
|
(+3,1″) |
-35,960 |
+68,481 |
4180,598 |
7086,902 |
|||
|
2 |
124о15’12“ |
173о27’00,1″ |
109,854 |
(-0,007) |
(-0,009) |
||
|
(+3,2″) |
-109,137 |
+12,531 |
4071,454 |
7099,424 |
|||
|
3 |
90о40’14“ |
262о46’42,9″ |
64,090 |
(-0,004) |
(-0,005) |
||
|
(+3,3″) |
-8,056 |
-63,582 |
4063,394 |
7035,837 |
|||
|
4 |
191о46’32“ |
251о00’07,6″ |
56,029 |
(-0,004) |
(-0,005) |
||
|
(+3,2″) |
-18,239 |
-52,977 |
4045,151 |
6982,855 |
|||
|
5 |
85о09’36“ |
345о50’28,4″ |
142,786 |
(-0,009) |
(-0,013) |
||
|
(+3,1″) |
+138,448 |
-34,927 |
4183,590 |
6947,915 |
|||
|
А |
100о54’12“ |
64о56’13,3″ |
77,848 |
(-0,005) |
(-0,006) |
4216,563 |
7018,427 |
|
(+3,1″) |
å d |
+32,978 |
+70,518 |
||||
|
127о13’55“ |
117о42’15,2“ |
fX |
fY |
||||
|
1 |
å β ИЗМ |
527,955 |
+0,034 |
+0,044 |
|||
|
719о59’41” |
fАБС |
fОТН = |
|||||
|
å β ТЕОР |
0,0556 |
1 |
|||||
|
720о00’00” |
fОТН ДОП |
9500 |
|||||
|
fβ |
-19″ |
1 |
|||||
|
7500 |
|||||||
|
fβ доп |
± 24″ |
76.2. Вычисление приращений координат и оценка точности хода
Поскольку начальная и конечная точки замкнутого теодолитного хода совмещены, то, как следует из формул (7.77), теоретические суммы приращений координат, вычисленных из решения прямой геодезической задачи, должны быть равны нулю, т.е.
|
å Х ТЕОР = 0 ; å YТЕОР = 0 , |
(7.105) |
а невязки в приращениях координат определятся только суммами полученных соответствующих приращений
|
f X = å X ВЫЧ ; fY = å YВЫЧ . |
(7.106) |
Далее оценка точности хода заключается в вычислении абсолютной невязки хода (7.80), относительной невязки хода (7.81) и в сравнении последней с допустимой относительной невязкой, установленной для данного вида работ соответствующей инструкцией или техническим заданием.
По аналогии с разомкнутым теодолитным ходом физический смысл невязок в приращениях координат тот же (рис. 7.24 б).
76.3. Уравнивание приращений координат и вычисление координат точек хода
Поправки в приращения координат (весовые) вычисляются по формулам (7.84) с контролем их вычислений по формулам (7.85). Контрольные суммы исправленных (7.86) приращений координат для замкнутого теодолитного хода должны быть равны нулю, т.е.
|
å Х ИСПР = 0 ; å YИСПР = 0 . |
(7.107) |
216
Теодолитный ход – это геодезическое построение в виде ломаной линии, вершины которой закрепляются на местности, и на них измеряются горизонтальные углы βi между сторонами хода и длины сторон Si. Закрепленные на местности точки называют точками теодолитного хода.
Построение теодолитного хода состоит из двух этапов. Это:
1. Построение ломаной линии на местности и осуществление полевых работ;
2. Математическое уравнивание хода и выполнение камеральной обработки полученных результатов.
Оба этапа выполняются строго по установленному регламенту с соблюдением норм и правил. Точность построения и обработки результатов обеспечивает правильность работы и последующую безопасность строительства или осуществления любой другой деятельности на местности. Теодолитный ход относиться к геодезическим работам цены на которые на сегодняшний день очень вариативные.
Основные виды теодолитного хода.
Теодолитный ход – это разомкнутая или замкнутая ломаная линия. В зависимости от формы построения, различают несколько видов ходов:
Разомкнутый теодолитный ход, опирающийся на два пункта с известными координатами и два дирекционных угла. Разомкнутый ход можно охарактеризовать как простую линию. Проект трассы или любого другого продолжительного участка невозможен без разомкнутой линии. Опора у нее на известные точки. В отличие от замкнутого, начало и конец располагаются в разных точках.
Разомкнутый теодолитный ход, опирающийся на один исходный пункт и один дирекционный угол – такой ход еще называют висячим. Висячий ход используют редко, потому что для его вычисления потребуется специальная формула. Суть его такова, что он имеет только начало в определенной точке координат. Конец нужно вычислять.
Замкнутый ход по своей сути является многоугольной фигурой и опирается только на один базовый пункт с установленными координатами и дирекционным углом. Вершинами стороны выступают точки, закрепленными на местности, а отрезками – расстояние между ними. Его чаще всего создают для съемки стройплощадок, жилых зданий, промышленных сооружений или земельных участков.
Диагональный (прокладывают внутри других ходов). Если необходимо заснять ровный участок, вроде строительной площадки, лучшим выбором будет полигон. На объектах вытянутого типа, вроде автодорог, принято использовать разомкнутый ход, а висячий – для съемки закрытой местности, вроде глухих улиц
Порядок выполнения работ
Как и другие геодезические мероприятия, эта процедура проводится с предварительной подготовкой для получения точных метрических данных. Немаловажную роль играет также их математическая обработка. Сами работы выполняются по принципу от общего к частному и состоят из следующих этапов:
1. Рекогносцировка местности. Оценка снимаемой территории, изучение ее особенностей. На этом этапе определяется местоположение снимаемых точек.
2. Полевая съемка. Работы непосредственно уже на местности. Выполнение линейных и угловых измерений, составление абрисов, предварительные расчеты и внесение изменений при необходимости.
3. Камеральная обработка. Завершающий этап работ, который заключается в вычислении координат замкнутого теодолитного хода и последующего составления плана и технического отсчета.
Рекогносцировка и полевые измерения выполняются непосредственно на объекте и являются наиболее трудоемкими и затратными мероприятиями. Тем не менее, от качества их проведения зависит дальнейший результат.
Обработка данных проводится уже в помещении. Сегодня она осуществляется при помощи специального программного обеспечения, хотя и ручные расчеты все также остаются актуальными и могут быть использованы геодезистом в целях проверки.
Обработка данных
Обработка результатов измерений замкнутого теодолитного хода позволит оценить качество проделанной работы и внести исправления в полученные геометрические величины. Чтобы убедится в том, что угловые и линейные измерения находятся в допуске, еще во время полевых работ выполняют первичные расчеты.
Для вычисления значений координат точек замкнутого хода используют такие данные: – координаты исходного пункта;
– исходный дирекционный угол;
– горизонтальные углы;
– длины сторон.
Уравнивание
При начале расчетов определяют теоретическую сумму углов , а потом увязывают их, распределяя между ними угловую невязку.
∑βтеор=180∘⋅(n−2)
n- количество точек полигона
fβ=∑βизм−180∘⋅(n−2)
∑βизм – значение измеренных угловых величин;
Для получения fβ, необходимо рассчитать разность между βизм, в которой присутствуют погрешности, и ∑βтеор.
В уравнивании fβ выступает как показатель точности проведенных измерительных работ, а ее значение не должно быть выше предельной величины, определяемой из следующей формулы:
fβ1=1,5tn−−√
t-точность измерительного устройства,
n – количество углов.
Уравнивание заканчивается равномерным распределением полученной невязки между угловыми величинами.
Определение дирекционных углов
При известном значении дирекционного угла (α) одной стороны и горизонтального (β) можно определить значение следующей стороны:
αn+1=αn+η
η=180∘−βпр
βпр – значение правого по ходу угла, из чего следует:
αn+1=αn+180∘−βпр
Для левого (βлев) эти знаки будут противоположными:
αn+1=αn−180∘+βлев
Поскольку значение дирекционного угла не может быть больше, чем 360∘, то из него, соответственно, отнимают 360∘. В случае с отрицательным углом, необходимо к предыдущему α добавить 180∘ и отнять значение βиспр.
Вычисление румбов
У румбов и дирекционных углов существует взаимосвязь, а определяют их по четвертям, которые носят название четырех сторон света. Как видно из табл.1. расчёты проводят согласно установленной схеме.
Таблица 1. Расчеты румба в зависимости от пределов дирекционного угла.
Приращения координат
Для приращений координат в замкнутом ходе применяют формулы, использующиеся при решении прямой геодезической задачи. Ее суть состоит в том, что по известным значениям координат исходного пункта, дирекционного угла и горизонтального приложения можно определить координаты следующего. Исходя из этого, формула приращения значений будет иметь следующий вид:
ΔX=d⋅cosα
ΔY=d⋅sinα
d-горизонтальное проложение;
α-горизонтальный угол.
Для полигона, который имеет вид замкнутой геометрической фигуры, теоретическая сумма приращений будет равняться нулю для обеих координатных осей:
∑ΔXтеор=0
∑ΔYтеор=0
Линейная невязка и невязка приращения значений координат
Несмотря на вышесказанное, случайные погрешности не позволяют алгебраическим суммам выйти в ноль, поэтому они будут равняться другим невязкам приращений координат:
fx∑ni=1ΔX1
fy∑ni=1ΔY1
Переменные fx и fy – проекции линейной невязки fp на координатной оси, которую можно рассчитать по формуле:
fp=f2x+f2y−−−−−−√
При этом fp, не должно быть боле, чем 1/2000 от доли периметра полигона, а распределения fx и fy проводится следующим образом:
δXi=−fxPdi
δYi=−fyPdi
В этих формулах δXi и δYi – поправки приращения координат.
і- номера точек;
После приращений и внесения поправок в данные измерений, проводят расчет их исправленных значений.
Вычисление координат
Когда будут произведены увязки приращений точек полигона, следует определение координат, которое осуществляют с использованием следующих формул:
Xпос=Xпр+ΔXисп
Yпос=Yпр+ΔYисп
Значения Xпос Yпос – координаты последующих пунктов, Xпр и Yпр – предыдущих.
ΔXисп и ΔYисп – исправленные приращения между этими двумя значениями.
Если координаты первой и последней точки совпадают, то обработку можно считать завершённой.
На основе полученных координат и составленных во время полевых измерений абрисов в дальнейшем составляется план теодолитного хода.
