Как найти пороговую энергию – Сайт, где вы сможете решить свои вопросы

From Wikipedia, the free encyclopedia

In particle physics, the threshold energy for production of a particle is the minimum kinetic energy that must be imparted to one of a pair of particles in order for their collision to produce a given result.^[1] If the desired result is to produce a third particle then the threshold energy is greater than or equal to the rest energy of the desired particle. In most cases, since momentum is also conserved, the threshold energy is significantly greater than the rest energy of the desired particle.

The threshold energy should not be confused with the threshold displacement energy, which is the minimum energy needed to permanently displace an atom in a crystal to produce a crystal defect in radiation material science.

Example of pion creation[edit]

Consider the collision of a mobile proton with a stationary proton so that a ${displaystyle {pi }^{0}}$ meson is produced:^[1] ${displaystyle p^{+}+p^{+}to p^{+}+p^{+}+pi ^{0}}$

We can calculate the minimum energy that the moving proton must have in order to create a pion.
Transforming into the ZMF (Zero Momentum Frame or Center of Mass Frame) and assuming the outgoing particles have no KE (kinetic energy) when viewed in the ZMF, the conservation of energy equation is:

$E=2gamma m_{p}c^{2}=2m_{p}c^{2}+m_{pi }c^{2}$

Rearranged to

$gamma ={frac {1}{{sqrt {1-beta ^{2}}}}}={frac {2m_{p}c^{2}+m_{pi }c^{2}}{2m_{p}c^{2}}}$

By assuming that the outgoing particles have no KE in the ZMF, we have effectively considered an inelastic collision in which the product particles move with a combined momentum equal to that of the incoming proton in the Lab Frame.

Our $c^{2}$ terms in our expression will cancel, leaving us with:

${displaystyle beta ^{2}=1-left({frac {2m_{p}}{2m_{p}+m_{pi }}}right)^{2}approx 0.130}$

${displaystyle beta approx 0.360}$

Using relativistic velocity additions:

${displaystyle v_{text{lab}}={frac {u_{text{cm}}+V_{text{cm}}}{1+u_{text{cm}}V_{text{cm}}/c^{2}}}}$

We know that ${displaystyle V_{cm}}$ is equal to the speed of one proton as viewed in the ZMF, so we can re-write with ${displaystyle u_{cm}=V_{cm}}$ :

${displaystyle v_{text{lab}}={frac {2u_{text{cm}}}{1+u_{text{cm}}^{2}/c^{2}}}approx 0.64c}$

So the energy of the proton must be $E=gamma m_{p}c^{2}={frac {m_{p}c^{2}}{{sqrt {1-(v_{{text{lab}}}/c)^{2}}}}}=1221,$ MeV.

Therefore, the minimum kinetic energy for the proton must be ${displaystyle T=E-{m_{p}c^{2}}approx 280}$ MeV.

Example of antiproton creation[edit]

At higher energy, the same collision can produce an antiproton:

${displaystyle p^{+}+p^{+}to p^{+}+p^{+}+p^{+}+p^{-}}$

If one of the two initial protons is stationary, we find that the impinging proton must be given at least ${displaystyle 6m_{p}c^{2}}$ of energy, that is, 5.63 GeV. On the other hand, if both protons are accelerated one towards the other (in a collider) with equal energies, then each needs to be given only ${displaystyle m_{p}c^{2}}$ of energy.^[1]

A more general example[edit]

Consider the case where a particle 1 with lab energy $E_{1}$ (momentum $p_{1}$ )
and mass $m_{1}$ impinges on a
target particle 2 at rest in the lab, i.e. with lab energy $E_{2}$ and mass $m_{2}$ .
The threshold energy $E_{{1,{text{thr}}}}$ to produce three particles of masses $m_{a}$ , $m_b$ ,
$m_{c}$ , i.e.

$1+2to a+b+c,$

is then found by assuming that these three particles are at rest in the center of mass frame (symbols with
hat indicate quantities in the center of mass frame):

$E_{{text{cm}}}=m_{a}c^{2}+m_{b}c^{2}+m_{c}c^{2}={hat {E}}_{1}+{hat {E}}_{2}=gamma (E_{1}-beta p_{1}c)+gamma m_{2}c^{2}$

Here $E_{{text{cm}}}$ is the total energy available in the center of mass frame.

Using $gamma ={frac {E_{1}+m_{2}c^{2}}{E_{{text{cm}}}}}$ , $beta ={frac {p_{1}c}{E_{1}+m_{2}c^{2}}}$ and
$p_{1}^{2}c^{2}=E_{1}^{2}-m_{1}^{2}c^{4}$ one derives that

${displaystyle E_{1,{text{thr}}}={frac {(m_{a}+m_{b}+m_{c})^{2}-(m_{1}^{2}+m_{2}^{2})}{2m_{2}}}c^{2}}$ ^[2]

References[edit]

^ ^a ^b ^c Michael Fowler. “Transforming Energy into Mass: Particle Creation”. Particle Creation. Archived from the original on Aug 15, 2022.
^ Jackson, John. Classical Electrodynamics. Wiley. pp. 533–539. ISBN 978-0-471-30932-1.

http://galileo.phys.virginia.edu/classes/252/particle_creation.html

Источник

Макеты страниц

Одной из общих задач ядерной физики и физики частиц высоких энергий является задача о соударении двух частиц. Налетающая частица 1 с массой импульсом и энергией сталкивается с частицей 2 («мишень») с массой которая неподвижна в лабораторной системе координат. Соударение может быть простым упругим рассеянием

(12.27)

Штрихи показывают, что направление полета частиц после соударения будет, вообще говоря, отличным от исходного. В других случаях соударение может привести к реакции

(12.28)

в которой образуются две или несколько частиц и по крайней мере одна из них отлична от налетающих частиц. Упругое рассеяние возможно всегда; что касается ядерных реакций, то возможность

их осуществления определяется различием масс частиц и начальной энергией налетающей частицы. Чтобы произвести соответствующий энергетический расчет в наиболее простой кинематической форме, удобно перейти к координатной системе которой налетающая частица и мишень имеют равные и противоположно направленные импульсы. Эта система называется (не совсем удачно) системой центра масс (или системой центра инерции) и обозначается как система ЦМ.

Фиг. 12.2. Векторы импульсов при упругом рассеянии или при двухчастичной реакции в системе ЦМ.

Рассеянные частицы (или продукты реакции в двухчастичных реакциях) имеют в системе ЦМ равные и противоположные импульсы, составляющие угол с направлением первоначальных импульсов. На фиг. 12.2 показаны векторы импульсов при упругом рассеянии или двухчастичной ядерной реакции. В случае упругого рассеяния а при ядерной реакции величина q определяется из условия сохранения полной энергии (включая энергии покоя) в системе ЦМ.

Соотношение, позволяющее перейти от энергий и импульсов в лабораторной системе к соответствующим величинам в системе ЦМ, можно найти либо непосредственно с помощью преобразования Лоренца от системы К к системе причем относительная скорость определяется из требовайия либо используя инвариантность скалярного произведения. Выбирая последний способ, рассмотрим скалярное произведение

(12.29)

Здесь левая часть ракенства вычисляется в лабораторной системе, где , а правая часть — в системе ЦМ, где Поэтому мы получаем

(12.30)

Используя равенство находим, что полная энергия в системе ЦМ равна

(12.31)

В отдельности энергии можно определить, рассматривая скалярные произведения типа

отсюда получаем

Отметим сходство этих выражений с соотношениями (12.21) и (12.22). Величина импульса получается из (12.33):

(12.34)

Параметры лорендовского преобразования можно, определить, учтя, что . Отсюда

(12.35)

Для нерелятивистского движения кинетическая энергия в системе ЦМ описывается выражением

(12.36)

Аналогично скорость и импульс в системе ЦМ будут

(12.37)

Таким образом, обычные нерелятивистские результаты получаются из строгих релятивистских формул. В случае ультрарелятивистского движения рассматриваемые величины принимают следующие приближенные предельные значения:

(12.38)

Мы видим, что энергия в системе ЦМ растет только как корень квадратный из энергии налетающей частицы. Отсюда следует, что в системе ЦМ очень трудно получать ультравысокие энергии при бомбардировке неподвижных мишеней. Наиболее высокоэнергетические существующие ускорители частиц [в ЦЕРН вблизи Женевы (Швейцария) и в Брукхейвене (США)] дают протоны с энергией Если мишенями служат неподвижные нуклоны, то полная энергия в системе ЦМ будет Для получения энергии в системе ЦМ необходимо бомбардировать неподвижные нуклоны протонами с энергией свыше В связи с этим были предприняты значительные усилия для получения в ускорит елях так называемых встречных, или сталкивающихся, пучков, для которых лабораторная система является системой ЦМ.

При реакции двух исходных частиц с массами образуются две или несколько частиц с массами Пусть — разность между суммой масс конечных и начальных частиц

(12.39)

Если величина положительна, то существует такая энергия Тпор налетающей частицы, называемая порогом данной реакции, ниже которой реакция не происходит. Реакция энергетически возможна, если энергия достаточна для создания в системе ЦМ требуемых частиц с нулевой кинетической энергией. Отсюда следует, что

(12.40)

С помощью (12.31) легко найти пороговую кинетическую энергию налетающей частицы

(12.41)

Первые два члена в скобках имеют нерелятивистское происхождение, а последний дает релятивистскую поправку. Рассмотрим для примера пороговую энергию фоторождения нейтральных -мезонов на протонах

Так как фотон не имеет массы покоя, то разность масс а масса мишени Поэтому для пороговой энергии получаем

В качестве другого примера рассмотрим рождение пары протон — антипротон при протон-протонных соударениях

Разность масс Из (12.41) находим

В этом примере пороговая энергия в 3 раза больше реальной разности масс, тогда как в примере с фоторождением она больше лишь на 7,2%. Расчеты порогов для других ядерных реакций отнесены к задаче 12.1 в конце главы.

Источник

6.6.Закон сохранения энергии – импульса

Внерелятивистской физике (механике Ньютона) существуют два раздельных закона сохранения – закон сохранения энергии и закон сохранения импульса. В релятивистской физике вектор импульса и энергия являются компонентами единого четырехвектора

энергии – импульса. Квадрат этого четырехвектора (Р, i(E / c)) является релятивистским

инвариантом. Поэтому, в физике элементарных частиц большую роль играет инвариантность квадрата этого четырехвектора:

	Е2 − Р2с2	= Inv		(6.6.1)
Закон сохранения четырехвектора предполагает сохранение полного импульса и
суммарной энергии системы:
∑Pi = ∑Pj	∑Ei = ∑E j	,	(6.6.2)
i	j	, i	j

где ∑Pi и ∑Pj – векторные суммы импульсов частиц до и после реакции, а ∑Ei и

i	j	i
∑E j	– суммы энергий системы частиц до и после реакции соответственно. В принципе,

закон сохранения энергии – импульса в виде (6.6.2) может быть использован для анализа реакций, происходящих с элементарными частицами. Однако, такой анализ возможен далеко не всегда. Значительно чаще используется закон сохранения инварианта (6.6.1).

Рассмотрим теперь, как из трансляционной инвариантности квантовой системы следует закон сохранения импульса. Если квантовая система инвариантна относительно переноса начала системы координат на произвольный вектор аr, то ψ′(r + a) =ψ(r ) .

Разлагая ψ′(r + a) в ряд по вектору a , имеем:

′ r r

′ r

′

′ r

(r + a) =

ψ (r ) +

(a )ψ (r ) + (1/ 2!)(a )

ψ (r )

+ (1/ 3!)(a )

(r ) +….

+…..)ψ

′′ r

′ r

= (1+ (a ) + (1/ 2!)(a )

+ (1/ 3!)(a )

(r ) = exp{(a )}ψ (r ) .

Чтобы

получить

закон

′

к полученному

преобразования функции ψ (r ) , нужно

соотношению применить оператор

} . Напомним, что

= exp{(−a )} = exp{(−i / h)a

оператор градиента связан с

оператором

импульса

соотношением:

rˆ

= (h/ i) .

Таким

образом, мы имеем для преобразования волновой функции соотношение:

′	r	r	rˆ	r
		p)} ψ (r )
ψ (r ) = exp{(−i / h)(a	(6.6.3)

Следовательно, оператор импульса рv есть генератор унитарного преобразования волновой функции

r	rˆ
U = exp{(−i / h)(a	p)},

а оператор импульса есть оператор сохраняющейся величины – наблюдаемой величины импульса.

Аналогично тому, как мы поступали в случае трансляционной инвариантности, получая закон сохранения импульса, можно, воспользовавшись инвариантностью системы относительно изменения начала отсчета времени, вывести закон сохранения энергии. Это представляется читателю сделать самостоятельно.

Покажем теперь, как закон сохранения в виде (6.6.1) дает возможность найти величину пороговой энергии для реакции с образованием большого числа частиц. Рассмотрим реакцию типа

а + А = ∑bi

Обозначим массы покоя частиц, вступающих в реакцию через ma и M A , а массы покоя получающихся в реакции частиц через mi . В лабораторной системе отсчета ядро А

покоится и полная энергия системы до реакции равна: E = M Ac2 + (ma c2 )2 + p2c2 . Определим пороговую энергию Eпорог как кинетическую энергию налетающей частицы а, необходимую для производства требуемой реакции:

Епорог = Ta = ma2c4 + p2c2 − ma c2 .

Импульс системы до реакции в лабораторной системе отсчета равен импульсу частицы а: рr = рrа . Тогда величина инварианта до реакции будет равна:

Е2 − р2 с2 =

(МАс2 + ma2c4 + p2c2 )2 − p2 c2 = M A2 c4 + ma2c4 + 2M Ac2 ma2 c4 + p2c2 =

= M A2 c4 + ma2c4 + 2M Ac2 (Eпорог + ma c2 ) = (M A + ma )2 c4 + 2M Ac2 Eпорог .

Значение инварианта системы после реакции найдем в системе центра инерции разлетающихся частиц, в которой суммарный импульс частиц равен нулю. В таком случае инвариант системы частиц после реакции будет равен просто квадрату сумм масс покоя

разлетающихся частиц, помноженному на с4 : Е2 − р2с2	= (∑mi )2 c4 . Используя условие
		ш
(6.6.1), для Епорог получаем:
Епорог =	(∑mi )2 − (M A + ma )2	c2
i
2M A
	(6.6.4)

Воспользовавшись соотношением (6.6.4), найдем пороговую энергию для реакции рождения электрон – позитронной пары фотоном: γ → е− + е+ .Так как масса покоя

фотона равна нулю, то по формуле (6.6.4) мы получим, что пороговая энергия такой реакции будет бесконечно большой. Однако, в присутствии какой – нибудь частицы, пороговая энергия будет конечной. Чтобы эту энергию найти, запишем реакцию в виде:

γ + А → А+ е+ + е−

Масса частицы А равна М , масса налетающей частицы (фотона) m = 0 . Массы частиц, получившихся после реакции равны M , m0 , m0 . Используя формулу (6.4.4), получаем

Eпорог =	(M + 2m	)2	− M 2	c2 = 2m0c2 (1+	m	0
0				) .
2M		M

Если рождение пары происходит вблизи ядра, то пороговая энергия лишь немного превышает значение, равное сумме масс покоя электрона и позитрона. Если же рождение пары происходит в присутствии электрона, тогда M = m0 и пороговая энергия

Епорог = 4m0c2 (то есть почти в два раза больше). Найдем пороговую энергию реакции, в которой получается антипротон. Как известно, антипротон получается в результате столкновения протонов: р + р → р + р + р + р. Тогда M A = M p , ma = M p а все mi = M p . Подставляя в формулу (6.4.4), получаем:

Eпорог = 6М рс2 .

Рассмотренные законы являются абсолютными, то есть, выполняющимися при любых процессах, в любых реакциях. Законы сохранения электрического заряда, лептонных зарядов, барионного заряда, момента импульса и закон сохранения энергии – импульса не имеют исключений и выполняются всегда (впрочем, в отношении закона сохранения барионного заряда – см. оговорку в начале этой главы). Наряду с этими законами, в физике элементарных частиц существуют и так называемые неабсолютные законы, которые выполняются лишь в случае, когда отсутствуют некоторые из четырех рассмотренных взаимодействий (чаще всего, когда процесс или реакция происходит без участия ядерного слабого взаимодействия). Эти неабсолютные законы сохранения оказываются очень полезными при рассмотрении некоторых явлений.

7. Изотопический спин. Зарядовые мультиплеты. Закон сохранения изотопического спина

Понятие изотопического спина ввел Вернер Гейзенберг. Изучая свойства нейтрона и протона, он пришел к выводу, что эти две частицы очень близки по своим свойствам. Различие заключается лишь в том, что протон заряжен, в то время как нейтрон нейтрален. Гейзенберг предложил считать нейтрон и протон разными зарядовыми состояниями одной и той же частицы – нуклона. Для характеристики зарядового состояния Гейзенберг ввел особую величину – изотопический (изобарический) спин – векторную величину, которая

определяет зарядовое состояние нуклона. Свойства вектора изоспина Т аналогичны свойствам обычного спина. Так, для системы нейтрон – протон (нуклон), волновая функция протона и нейтрона в дираковских обозначениях будет иметь вид:

p = 1/ 2,+1/ 2 ,

n = 1/ 2,−1/ 2 .

(7.1)

Здесь указано, что длина вектора Т и для нейтрона и для протона , определяемая квантовым числом равнным ½, равна Т(Т +1) = 3/ 4 а третья проекция для протона и нейтрона (точнее, максимальное значение его проекции на любую ось) отличается знаком,

Положительно заряженный протон имеет проекцию вектора Т на третью ось, равную +1/2, а нейтрон – -1/2. Таким образом, третья проекция вектора изоспина определяет

зарядовое состояние частицы. Собственное значение оператора Т2 и для протона и для нейтрона равно:

Т2 p = T (T +1) p = 3/ 4 p

T 2 n = T (T +1) n = 3/ 4 n ,

а собственные значения оператора T3 будут для протона и нейтрона различными:

T3 p = +1/ 2 p , T3	n = −1/ 2 n .
Заряд нуклона определяется выражением:
QN = e(1/ 2 +T3 )N	(7.2)

Для ядра с массовым числом А, состоящим из Z протонов и N = A − Z нейтронов, имеем:

Q / e = A / 2 +T3 ,

где T3 =1/ 2Z + (−1/ 2)N = (Z − N) / 2 .

Оказалось, что понятие изотопического спина можно ввести для всех адронов. Термин адроны был введен советским физиком Окунем. Адронами являются все частицы, являющиеся либо источниками сильного ядерного взаимодействия, либо переносчиками такового. Таким образом, адронами являются все барионы, все мезоны и все резонансы.

Для тройки пионов (π ± ,π 0 ) вводится изоспин Т =1. Заряд пиона очень просто связан с третьей компонентой изоспина

Ядерное сильное взаимодействие инвариантно относительно поворотов вектора изоспина на любой угол относительно любой оси. (зарядовая независимость сильного взаимодействия). Это обстоятельство делает возможным использовать изоспин системы в качестве сохраняющейся величины (интеграла движения) в процессах, которые происходят в результате сильного ядерного взаимодействия.

Все объекты физики элементарных частиц, которые приведены в таблицах элементарных частиц, могут быть объединены в четыре группы зарядовых

мультиплетов: синглеты (η,η′ – мезоны, Λ0	и	Ω− гипероны Т = 0,Т3 = 0 ),	дублеты
( К0 , К+	– каоны,	нуклон, Ξ− ,Ξ0 -гипероны,	Т =1/ 2,Т3 = −1/ 2,+1/ 2 ),	триплеты
(π − ,π 0 ,π + –	пионы,	Σ− ,Σ0 ,Σ+ -гипероны,	Т =1,Т3 = −1,0,+1) и один	квартет

(∆− , ∆0 , ∆+ , ∆++ – резонанс, Т = 3/ 2,Т3 = −3/ 2,−1/ 2,+1/ 2,+3/ 2 ).

Закон сохранения изоспина может быть сформулирован следующим образом: при реакциях, происходящих в результате сильного взаимодействия, выполняется закон сохранения вектора изотопического спина и закон сохранения третьей компоненты вектора изоспина:

∑Ti = ∑Tj	∑T3i = ∑T3j	(7.4)
i j	; i j ;

При процессах, происходящих с участием электромагнитного и слабого взаимодействий, закон сохранения изоспина не выполняется. Рассмотрим несколько примеров, иллюстрирующих закон сохранения изоспина. Оказывается, закон сохранения изоспина запрещает такую реакцию:

d+ d →α +π 0 .

Всамом деле, изоспины дейтронов в основном состоянии равны нулю (Т = 0) .

Изоспин альфа частицы в основном состоянии тоже равен нулю. Изоспин пиона равен Т =1. Так как рассматриваемая реакция должна происходить в результате сильного взаимодействия, то закон сохранения изоспина запрещает такую реакцию и она, действительно, экспериментально не наблюдается.

Рассмотрим реакции:

p + p → d +π + и p + n → d +π 0

В первом случае изоспины систем до и после реакции одинаковы:

p p = 1/ 2,+1/ 2 1/ 2,+1/ 2 = 1,+1 ; d π + = 0,0 1,+1 = 1,+1 .

Во втором случае дело обстоит немного сложнее:

p n = 1/ 2,+1/ 2 1/ 2,−1/ 2 = (1/ 2)( 1,0 + 0,0 ) ; d π 0 = 0,0 1,0 .

В этом случае волновая функция системы p n представляет собой суперпозицию состояний с изоспинами 1,0 и 0,0 (в равных долях). При прочих равных условиях,

эффективное сечение первой реакции должно быть в два раза больше эффективного сечения второй реакции. Эксперимент дает для эффективных сечений следующие результаты: при энергии столкновения 600 МэВ σ( p + p) =(3,15 ± 0,22) миллибарн, а

σ( p + n) = (1,5 ± 0,3) миллибарн.

Характерная для слабого взаимодействия реакция: n → p + e− +ν~ иллюстрирует,

тот факт, что закон сохранения изоспина не выполняется в процессах, обусловленных слабым взаимодействием. Величина вектора изоспина сохраняет свое значение, в то время как третья компонента изменяет свое значение на единицу. Точно так же и при реакции,

происходящей под действием электромагнитного взаимодействия Σ0 → Λ0 +γ ,, изоспин

не сохраняется. В этом случае величина вектора изоспина изменяется на единицу, в то время как третья компонента изоспина сохраняет свое значение. Можно говорить о

своеобразных правилах отбора по изоспину. При слабом	взаимодействии
∆Т = 0, ∆Т3 = ±1. При электромагнитном взаимодействии ∆Т = ±1, ∆Т3	= 0 .

8. Странность. Гиперзаряд. Очарование, Прелесть и Правдивость

Впервые странные частицы были обнаружены в 1947 году Рочестером и Батлером. При столкновении π − – пионов с протонами возникали так называемые V- частицы. Эти V-

частицы возникали за время порядка 10−23 секунды (типичное время для процессов, обусловленных сильным взаимодействием), однако жили очень долго (по масштабам

ядерного времени). Время жизни этих частиц составляло ≈10−10 секунды. В одной из характерных реакций, происходящей практически мгновенно, возникало две нейтральные частицы:

π − + p → K 0 + Λ0

Через время τ ≈10−10 секунды эти частицы распались на пары заряженных частиц:

K 0 →π + +π − , Λ0 → р +π −

которые давали в магнитном поле расходящиеся треки (отсюда и название – V- частицы). Было обнаружено множество подобных реакций, в которых возникали подобные V- частицы. Такое поведение V- частиц показалось странным. Частицы, возникшие при реакции с участием сильного ядерного взаимодействия, должны бы и распадаться за те же

характерные времена τ ≈10−23 с. Однако, они живут с точки зрения ядерного времени очень долго, как будто существует какой – то запрет на процесс их немедленного распада. Полную ясность в этом вопросе внесли Гелл-Манн и Нишиджима. Они ввели новое квантовое число – странность. Это понятие стало общепринятым. Всем вновь открытым странным частицам приписывалось численная характеристика – странность S . Эталоном

странности стал К+ – каон, которому приписывалась странность +1: S(K + ) = +1.

Поскольку странные частицы возникали в результате реакций, происходящих при сильном взаимодействии, было естественно предположить, что для этого типа процессов странность должна сохраняться, В реакцию вступают нестранные частицы, странности которых равны нулю, следовательно, сумма странностей возникших странных частиц тоже должна быть равна нулю. Так можно установить странности всех наблюдаемых странных частиц. Например, реакция

π − + р → К+ + Σ−

позволяет установить, что S(Σ− ) = −1. В качестве примеров приведем еще реакции:

р + р → р+ Σ

+ К

р +π

→

р + К

~ 0

+ К

из которых можно установить, что

S(Σ

) = −1, S

~ 0

) = −1.

Таким путем были

установлены странности всех странных частиц. Из многочисленных экспериментов, в результате которых получаются странные частицы, имеем следующий результат:

S(K + ) = S(K 0 ) = +1

~ 0 = − = −

S(K ) S(K ) 1

S(Λ0 ) = S(Σ+ ) = S(Σ0 ) = S(Σ− ) = −1

S(Ξ0 ) = S(Ξ− ) = −2 .

S(Ω− ) = −3 .

Как показывает богатый экспериментальный материал, для реакций, происходящих в результате сильного ядерного взаимодействия, выполняется закон сохранения странности:

∑Si = ∑S j

i j

(Сумма странностей частиц, вступающих в реакцию равна сумме странностей частиц, получающихся в результате реакции). Для электромагнитных взаимодействий также выполняется закон сохранения странности. При ядерных слабых взаимодействиях странность не сохраняется.

Ранее мы установили связь между величиной заряда элементарной частицы и третьей компонентой изотопического спина для пионов и нуклонов (см. формулы (7.2) и (7.3)). Чем отличаются нуклоны от пионов? Нуклоны обладают барионным зарядом В =1, а для пионов он равен нулю. Воспользовавшись этим различием, можно объединить формулы (7.2) и (7.3) в одну, если вместо члена ½ в (7.2) поставить слагаемое В/2. Тогда соотношение

будет справедливо и для нуклонов и для пионов. Как следует изменить формулу (8.1), чтобы она включала и все странные частицы? Оказывается, нужно вместо барионного заряда В в формуле поставить сумму B + S . Полученная таким образом формула

Q = e(T	+	B + S	)

3	2		(8.2)

и есть формула Гелл-Манна – Нишиджимы. Сумма барионного заряда и странности называется гиперзарядом B + S = Y . Через гиперзаряд формула (8.2) примет вид:

Q = T + Y
e	3	2	(8.3)

Чтобы выяснить смысл введенного гиперзаряда, просуммируем соотношение (8.3) по всем компонентам зарядового мультиплета и поделим на число частиц в данном

мультиплете. Тогда слева будет находиться средний заряд частицы мультиплета Qe . В

правой части (8.3) будет лишь Y2 , так как сумма всех T3

мультиплета будет равна нулю, и мы получим:

Qe = Y2 .

по всем компонентам зарядового

(8.4)

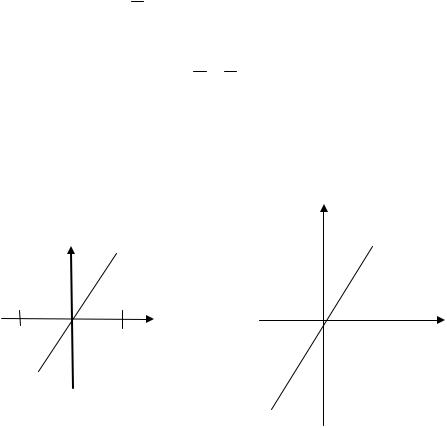
Следовательно, гиперзаряд Y равен удвоенному среднему заряду частиц зарядового мультиплета. Формула (8.4) иллюстрируется нижеследующими графиками.

К0

К+

∆−

∆0 , n

∆+ , p ∆++

π −

π +

π 0

Q / e

Σ−

Σ0

Σ+

Q / e

К−

К~ 0

Ξ−

Ξ0

Ω−

Мезоны

Барионы

Рис. 7. Иллюстрация формулы (8.4).

В 1974 году была обнаружена очередная новая частица. В одной из лабораторий ей присвоили символ J , а в конкурирующей лаборатории ей был присвоен символ ψ . Так

она и осталась существовать в таблицах под двойным символом J /ψ . Эта частица

оказалась мезоном, причем для нее не нашлось места в прежней классификации. Пришлось вводить новое квантовое свойство, очарование и присвоить соответствующее квантовое число, характеризующее это свойство – С (от английского слова charm). Кстати, сам J /ψ – мезон оказался частицей со скрытым очарованием (то есть С=0.)

Дальнейшее развитие физики элементарных частиц привело к необходимости ввести еще одно свойство – прелесть, которое количественно характеризуется величиной b (от английского слова beauty).

Наконец, самые последние исследования в физике элементарных частиц привели к необходимости ввести еще одно новое квантовое свойство – правдивость. Количественная характеристика правдивости характеризуется символом t (от английского слова truth).

При сильных и электромагнитных взаимодействиях выполняются законы сохранение очарования, прелести и правдивости:

∑Ci = ∑C j	,	∑bi = ∑bj	,	∑ti = ∑t j	(8.5)
i j	i j	i j

(Суммы очарований, прелестей и правдивостей до реакции равна их сумме после реакции). При слабых взаимодействиях эти законы сохранения не выполняются.

После появления этих свойств, приходится изменить определение гиперзаряда. Обобщенным гиперзарядом будет величина

Y = B + S + C −b + t .

Изменится так же и формула Гелл-Манна – Нишиджимы. Включающая все новые свойства частиц, обобщенная формула примет вид:

Q	= T	+	B + S + C −b + t

e	3	2	(8.6)

9. Слабые взаимодействия. Бета распад

Бета распад – это одно из возможных радиоактивных превращений, происходящих в результате слабого ядерного взаимодействия. Наиболее распространенным типом β

распада является электронный бета распад:

A X →	AY + e−	.	(9.1)
Z	Z +1

Здесь мы пишем реакцию так, как она представлялась физикам в тридцатых годах прошлого века (без указания на антинейтрино). Такая реакция будет возможна, если выполняется неравенство:

М	ядра	( AX ) > M	ядра	(	AY ) + m	e
	Z		Z +1

Прибавив к обеим частям неравенства по массе Z электронов и пренебрегая энергиями связи электронов в атомах, получим:

М	атома	( AX ) > M	атома	(	AY )	(9.2)
	Z		Z +1

Существует и позитронный бета распад, впервые наблюденный супругами Ирен и Фредериком Жолио-Кюри в 1934 году при изучении открытой ими искусственной радиоактивности:

A X →	AY + e+	.	(9.3)
Z	Z −1

Такой процесс будет возможен, если

М	ядра	( AX ) > M	ядра	(	AY ) + m	.
	Z		Z −1	e

Добавив к обеим частям неравенства по Z электронов, имеем:

М	атома	( AX ) > M	атома	(	AY ) + 2m	e	(9.4)
	Z		Z −1

Наконец, известен еще и так называемый е– захват, при котором ядро захватывает какой-либо электрон атомной оболочки. Чаще всего захватывается электрон из К – оболочки (К-захват):

		A X + e− →	AY					(9.5)
		Z			Z −1 .
Этот процесс возможен, если
	М	ядра	( AX ) + m	e	> M	ядра	(	AY ) .
		Z						Z −1
Добавив по Z-1 электрону, имеем:
M	атома	( AX ) > M	атома	(		AY )		(9.6)
	Z			Z −1

Энергия бета превращения заключена между 13,4 МэВ (125 В→126 С + е− ) и 18,61 МэВ (13 Н→23Не+ е− ). Но самым удивительным фактом является то, что спектр вылетающих

электронов – сплошной. Качественно кривая спектра бета электронов приведена на рисунке 8

εmax

Рис. 8. Качественная кривая спектра бета электронов.

Сплошной спектр вылетающих при бета – распаде электронов представляется очень странным. Если энергия бета – превращения вполне определенная, то, казалось бы, и все бета электроны должны бы иметь определенную энергию, а не любую от энергии равной нулю до максимальной. Еще более странным является тот факт, что реакции бета распада, записанные в форме (9.1). (9.3) и (9.5), указывают на нарушение закона сохранения момента импульса (спина). В самом деле, если массовое число А ядра Х четно, то до реакции мы имеем спин ядра Х целочисленный. После реакции спин ядра У тоже целочисленный. Однако, вылетающий электрон всегда уносит полуцелый момент импульса. Явное нарушение абсолютного закона сохранения момента импульса! Совершенно та же ситуация будет и при нечетном массовом числе. Эту странную ситуацию с бета – распадом подробно изучал В. Паули. Он пришел к выводу, что наряду с вылетающим электроном должна вылетать еще одна легкая нейтральная частица. Паули назвал ее маленьким нейтроном. Э.Ферми предложил назвать ее нейтрино (в итальянском языке ино есть уменьшительный суффикс). Термин нейтрино – маленький нейтрон – получил права гражданства. Нейтрино должно быть частицей с полуцелым спином. В этом случае разрешается ситуация и с законом сохранения энергии и с законом сохранения момента импульса. Сумма энергий, уносимых электроном и нейтрино, равна энергии бета – превращения. Сумма моментом импульса тоже будет сохраняться.

Ферми использовал идею существования нейтрино и предложил теорию бета распада, упрощенный вариант которой мы и рассмотрим. В теории квантовых переходов используется формула для вероятности перехода из начального состояния i в конечное k , которая носит название «золотого правила» Ферми:

	2π	ˆ	2
wi→k =	h	\|< k \| Hвзаимод \| i >\|		ρ(E)	(9.7)

Здесь i =ψi и k =ψk – волновые функции начального и конечного состояний системы, оператор Hвзаимод – оператор взаимодействия, являющийся причиной соответствующего перехода, множитель ρ(Е) – плотность энергетических состояний. Первый множитель в (9.7) есть квадрат модуля матричного элемента перехода системы из состояния i в

состояние k . Этот множитель фактически не зависит от энергии и дает правила отбора по спину. В варианте теории бета распада Ферми правило отбора очень жесткое: ∆I = 0 . В теории бета распада Гамова – Теллера, правило отбора более мягкое: ∆I = 0,±1. Нас будет

интересовать зависимость вероятности перехода от энергии, которая определяется вторым сомножителем ρ(Е) .

По	определению	ρ(E) = dN / dE ,	где	dN – число	энергетических	уровней,
приходящихся на единичный интервал энергии	dE . Число энергетических уровней мы
можем	подсчитать, поделив полный	объем	системы в	пространстве	импульсов
∫dpxe dpey dpze ∫dpνx~ dpνy~ dpνz~ ,	на минимальный объем квантового состояния в импульсном

пространстве. Согласно основному положению квантовой статистики объем квантового

состояния	вылетающих	электрона	и	антинейтрино
∆pxe ∆pey ∆pze ∆xe ∆ye ∆ze ∆pνx~ ∆pνy~ ∆pνz~ ∆xν~ ∆yν~ ∆zν~ = (2πh)6 . Если не	интересоваться, в каком

месте ядра происходит бета распад, то произведение координат электронов и антинейтрино можно заменить объемом ядра. В таком случае объем квантового состояния в пространстве импульсов будет равен: ∆pxe ∆pey ∆pze ∆pνx~ ∆pνy~ ∆pνz~ =( (2πh)6 /V 2 ) .

При вычислении интегралов по импульсам, необходимо иметь в виду, что интегрировать по импульсам антинейтрино нужно с учетом закона сохранения энергии. Сумма энергий вылетающего электрона, антинейтрино и энергии ядра отдачи должна быть равна энергии бета превращения:

Ее + Еν~ + Еотдачи = Еmax .

Ввиду большой величины массы ядра в сравнении с массой электрона и антинейтрино, энергией отдачи ядра можно пренебречь. Закон сохранения энергии можно учесть автоматически, если ввести в интеграл по импульсам антинейтрино дельта функцию Дирака δ(Еmax − Ее − Eν~ ) . Тогда число возможных квантовых состояний будет

равно

dN =	V 2		dpe dpe dpe		δ(E	− E	− E~ )dpν~ dpν~ dpν~
(2πh)6 ∫	∫	max	e
	x y z			ν	x y z

Поскольку распределение вылетающих антинейтрино по энергиям не регистрируется в экспериментах по бета – распаду, интеграл по импульсам антинейтрино необходимо брать по всем возможным импульсам вылетающих антинейтрино. Интеграл же по импульсам вылетающих электронов необходимо вычислять лишь по направлениям вылета электронов, так как в экспериментах по бета – распаду регистрируется распределение электронов по энергиям.

Заменив dpx dpy dpz на элементарный объем в пространстве импульсов в сферических переменных:

dpx dpy dpz = p2 dp sinθdθdϕ ,

замечаем, что в силу сферической симметрии подынтегральных выражений интегрирование по угловым переменных дает 4π . С учетом этого, имеем для dN следующее выражение:

	(4πV )2	2	2
dN =		pe dpe ∫δ(Emax − Ee − Eν~ ) pν~ dpν~ .
(2πh)6

Далее, необходимо при интегрировании перейти от импульсов к энергиям. Для частиц с массой покоя не равной нулю имеем закон дисперсии: Е2 = р2с2 + m2c4 , из чего

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Порогом реакции называется минимальная кинетическая энергия, которую должна иметь элементарная частица в лабораторной системе отсчёта, чтобы было возможным протекание данной ядерной реакции. Формула для расчёта:

${displaystyle T_{}={frac {(m_{b}+m_{B}-m_{a}-m_{A})(m_{b}+m_{B}+m_{a}+m_{A})c^{2}}{2m_{A}}}}$

или аналогично

${displaystyle T_{}=left|Qright|(1+{frac {m_{a}}{m_{A}}}+{frac {left|Qright|}{2m_{A}c^{2}}})}$ ,

если ${displaystyle Q<<2m_{A}c^{2}}$ , то эту формулу можно записать короче:

${displaystyle T_{}cong left|Qright|(1+{frac {m_{a}}{m_{A}}})}$ ,

где $Q$ — энергия данной реакции, ${displaystyle m_{a},m_{A},m_{b},m_{B}}$ — массы начальных и конечных частиц соответственно. Формулы также могут быть применены к любым количествам частиц в реакции.

Ссылки[править | править код]

Энергия реакции. Порог реакции Архивная копия от 17 апреля 2011 на Wayback Machine (Б. С. Ишханов, Э. И. Кэбин. Шпаргалка для отличника. Частицы и ядра)
Transforming Energy into Mass: Particle Creation Архивная копия от 24 июля 2019 на Wayback Machine (англ.)

Это статья-заготовка по физике. Помогите Википедии, дополнив эту статью, как и любую другую.

Источник

Example of pion creation[edit]

Example of antiproton creation[edit]

A more general example[edit]

References[edit]

Ссылки[править | править код]

Вам также может понравиться

Как исправить выпадающий список в эксель

Как найти номер испол производства

Как найти аккаунт гугл по электронной почте

Добавить комментарий Отменить ответ