Как найти порождающий многочлен

Время на прочтение
6 мин

Количество просмотров 60K

Код Хэмминга – не цель этой статьи. Я лишь хочу на его примере познакомить вас с самими принципами кодирования. Но здесь не будет строгих определений, математических формулировок и т.д. Эта просто неплохой трамплин для понимания более сложных блочных кодов.

Самый, пожалуй, известный код Хэмминга (7,4). Что значат эти цифры? Вторая – число бит информационного слова — то, что мы хотим передать в целости и сохранности. А первое – размер кодового слова: информация удобренная избыточностью. Кстати термины «информационное слово» и «кодовое слово», употребляются во всех 7-ми книгах по теории помехоустойчивого кодирования, которые мне довелось бегло пролистать.

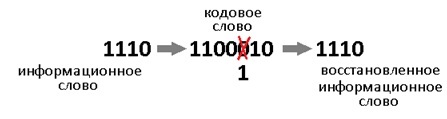
Такой код исправляет 1 ошибку. И не важно где она возникла. Избыточность несёт в себе 3 бита информации, этого достаточно, чтобы указать на одно из 7 положений ошибки или показать, что её нет. То есть ровно 8 вариантов ответов мы ждём. А 8 = 2^3, вот как всё совпало.

Чтобы получить кодовое слово, нужно информационное слово представить в виде полинома и умножить его на порождающий полином g(x). Любое число, переведя в двоичный вид, можно представить в виде полинома. Это может показаться странным и у не подготовленного читателя сразу встаёт только один вопрос «да зачем же так усложнять?». Уверяю вас, он отпадёт сам собой, когда мы получим первые результаты.

К примеру информационное слово 1010, значение каждого его разряда это коэффициент в полиноме:

Во многих книгах пишут наоборот x+x^3. Не поддавайтесь на провокацию, это вносит только путаницу, ведь в записи числа 2-ичного, 16-ричного, младшие разряды идут справа, и сдвиги мы делаем влево/вправо ориентируясь на это. А теперь давайте умножим этот полином на порождающий полином. Порождающий полином специально для Хэмминга (7,4), встречайте: g(x)=x^3+x+1. Откуда он взялся? Ну пока считайте что он дан человечеству свыше, богами (объясню позже).

Если нужно складывать коэффициенты, то делаем по модулю 2: операция сложения заменяется на логическое исключающее или (XOR), то есть x^4+x^4=0. И в конечном итоге результат перемножения как видите из 4х членов. В двоичном виде это 1001110. Итак, получили кодовое слово, которое будем передавать на сторону по зашумлённому каналу. Замете, что перемножив информационное слово (1010) на порождающий полином (1011) как обычные числа – получим другой результат 1101110. Этого нам не надо, требуется именно «полиномиальное» перемножение. Программная реализация такого умножения очень простая. Нам потребуется 2 операции XOR и 2 сдвига влево (1й из которых на один разряд, второй на два, в соответствии с g(x)=1011):

Давайте теперь специально внесём ошибку в полученное кодовое слово. Например в 3-й разряд. Получиться повреждённое слово: 1000110.

Как расшифровать сообщение и исправить ошибку? Разумеется надо «полиномиально» разделить кодовое слово на g(x). Тут я уже не буду писать иксы. Помните что вычитание по модулю 2 — это то же самое что сложение, что в свою очередь, тоже самое что исключающее или. Поехали:

В программной реализации опять же ничего сверх сложного. Делитель (1011) сдвигаем влево до самого конца на 3 разряда. И начинаем удалять (не без помощи XOR) самые левые единицы в делимом (100110), на его младшие разряды даже не смотрим. Делимое поэтапно уменьшается 100110 -> 0011110 -> 0001000 -> 0000011, когда в 4м и левее разрядах не остаётся единиц, мы останавливаемся.

Нацело разделить не получилось, значит у нас есть ошибка (ну конечно же). Результат деления в таком случае нам без надобности. Остаток от деления является синдром, его размер равен размеру избыточности, поэтому мы дописали там ноль. В данном случае содержание синдрома нам никак не помогает найти местоположение повреждения. А жаль. Но если мы возьмём любое другое информационное слово, к примеру 1100. Точно так же перемножим его на g(x), получим 1110100, внесём ошибку в тот же самый разряд 1111100. Разделим на g(x) и получим в остатке тот же самый синдром 011. И я гарантирую вам, что к такому синдрому мы придём в обще для всех кодовых слов с ошибкой в 3-м разряде. Вывод напрашивается сам собой: можно составить таблицу синдромов для всех 7 ошибок, делая каждую из них специально и считая синдром.

В результате собираем список синдромов, и то на какую болезнь он указывает:

Теперь у нас всё есть. Нашли синдром, исправили ошибку, ещё раз поделили в данном случае 1001110 на 1011 и получили в частном наше долгожданное информационное слово 1010. В остатке после исправления уже будет 000. Таблица синдромов имеет право на жизнь в случае маленьких кодов. Но для кодов, исправляющих несколько ошибок – там список синдромов разрастается как чума. Поэтому рассмотрим метод «вылавливания ошибок» не имея на руках таблицы.

Внимательный читатель заметит, что первые 3 синдрома вполне однозначно указывают на положение ошибки. Это касается только тех синдромов, где одна единица. Кол-во единиц в синдроме называют его «весом». Опять вернёмся к злосчастной ошибке в 3м разряде. Там, как вы помните был синдром 011, его вес 2, нам не повезло. Сделаем финт ушами — циклический сдвиг кодового слова вправо. Остаток от деления 0100011 / 1011 будет равен 100, это «хороший синдром», указывает что ошибка во втором разряде. Но поскольку мы сделали один сдвиг, значит и ошибка сдвинулась на 1. Вот собственно и вся хитрость. Даже в случае жуткого невезения, когда ошибка в 6м разряде, вы, обливаясь потом, после 3 мучительных делений, но всё таки находите ошибку – это победа, лишь потому, что вы не использовали таблицу синдромов.

А как насчёт других кодов Хэмминга? Я бы сказал кодов Хэмминга бесконечное множество: (7,4), (15,11), (31,26),… (2^m-1, 2^m-1-m). Размер избыточности – m. Все они исправляют 1 ошибку, с ростом информационного слова растёт избыточность. Помехоустойчивость слабеет, но в случае слабых помех код весьма экономный. Ну ладно, а как мне найти порождающую функцию например для (15,11)? Резонный вопрос. Есть теорема, гласящая: порождающий многочлен циклического кода g(x) делит (x^n+1) без остатка. Где n – нашем случае размер кодового слова. Кроме того порождающий полином должен быть простым (делиться только на 1 и на самого себя без остатка), а его степень равна размеру избыточности. Можно показать, что для Хэмминга (7,4):

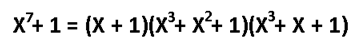
Этот код имеет целых 2 порождающих полинома. Не будет ошибкой использовать любой из них. Для остальных «хэммингов» используйте вот эту таблицу примитивных полиномов:

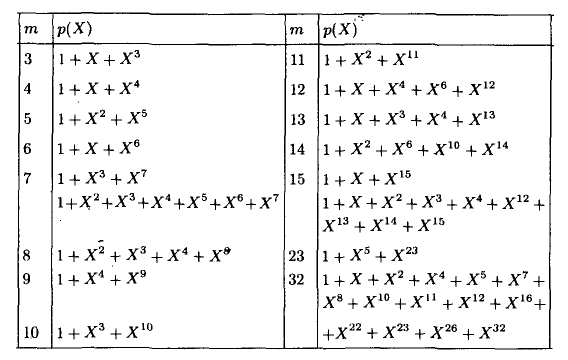
Соответственно для (15,11) порождающий многочлен g(x)=x^4+x+1. Ну а теперь переходим к десерту – к матрицам. С этого обычно начинают, но мы этим закончим. Для начала преобразую g(x) в матрицу, на которую можно умножить информационное слово, получив кодовое слово. Если g = 1011, то:

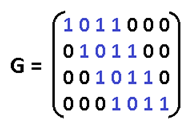
Называют её «порождающей матрицей». Дадим обозначение информационному слову d = 1010, а кодовое обозначим k, тогда:

Это довольно изящная формулировка. По быстродействию ещё быстрее, чем перемножение полиномов. Там нужно было делать сдвиги, а тут уже всё сдвинуто. Вектор d указывает нам: какие строки брать в расчёт. Самая нижняя строка матрицы – нулевая, строки нумеруются снизу вверх. Да, да, всё потому что младшие разряды располагаются справа и от этого никуда не деться. Так как d=1010, то я беру 1ю и 3ю строки, произвожу над ними операцию XOR и вуаля. Но это ещё не всё, приготовьтесь удивляться, существует ещё проверочная матрица H. Теперь перемножением вектора на матрицу мы можем получить синдром и никаких делений полиномов делать не надо.

Посмотрите на проверочную матрицу и на список синдромов, который получили выше. Это ответ на вопрос откуда берётся эта матрица. Здесь я как обычно подпортил кодовое слово в 3м разряде, и получил тот самый синдром. Поскольку сама матрица – это и есть список синдромов, то мы тут же находим положение ошибки. Но в кодах, исправляющие несколько ошибок, такой метод не прокатит. Придётся вылавливать ошибки по методу, описанному выше.

Чтобы лучше понять саму природу исправления ошибок, сгенерируем в обще все 16 кодовых слов, ведь информационное слово состоит всего из 4х бит:

Посмотрите внимательно на кодовые слова, все они, отличаются друг от друга хотя бы на 3 бита. К примеру возьмёте слово 1011000, измените в нём любой бит, скажем первый, получиться 1011010. Вы не найдёте более на него похожего слова, чем 1011000. Как видите для формирования кодового слова не обязательно производить вычисления, достаточно иметь эту таблицу в памяти, если она мала. Показанное различие в 3 бита — называется минимальное «хэммингово расстояние», оно является характеристикой блокового кода, по нему судят сколько ошибок можно исправить, а именно (d-1)/2. В более общем виде код Хэмминга можно записать так (7,4,3). Отмечу только, что Хэммингово расстояние не является разностью между размерами кодового и информационного слов. Код Голея (23,12,7) исправляет 3 ошибки. Код (48, 36, 5) использовался в сотовой связи с временным разделением каналов (стандарт IS-54). Для кодов Рида-Соломона применима та же запись, но это уже недвоичные коды.

Список используемой литературы:

1. М. Вернер. Основы кодирования (Мир программирования) — 2004
2. Р. Морелос-Сарагоса. Искусство помехоустойчивого кодирования (Мир связи) — 2006
3. Р. Блейхут. Теория и практика кодов, контролирующих ошибки — 1986

Синдром циклического кода, теорема о
синдроме циклического кода.

Пусть C – код в пространстве

,
тогда C называется циклическим если

Пример (могут просить написать):

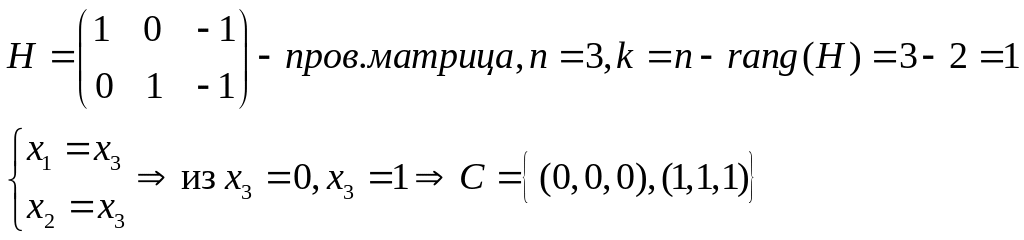
Примерами циклических кодов являются
коды Хэмминга, коды Боуза – Чоудхури –
Хоквингема (БЧХ — коды), коды Рида-Соломона.
Введем преобразование, называемое
циклическим сдвигом

.
Данное преобразование – линейное
преобразование.Циклические коды в

– это в точности все инвариантные
подпространства относительно циклического
сдвига.

Запись элементов из

в виде многочленов (описание циклических
кодов как идеалов в кольце многочленов):
Можно записать элементы поля

в виде многочленов и тогда рассматривать
циклические коды как иделы в кольце
многочленов.

– сопоставление.

Для многочленов, степень которых меньше
или равна n-1, соответствие
взаимно однозначное.

Рассмотрим множество многочленов вида

,

– поржденный им идеал в кольце многочленов

.
Рассмотрим факторкольцо:

.
Оно состоит из различных правых (левых)
смежных классов

по идеалу

.
Для удобства каждый такой класс можно
заменить на его представителя, а в
качестве различных представителей
взять многочлены из

степень которых не превышает

.
Т.о., фактор-кольцо

можно считать состоящим из многочленов
степени, не большей, чем

с коэффициентами из

.
Сложение и умножение в этом кольце
осуществляется по модулю многочлена

.
М/у элементами данного факторкольца и
элементами пространства

существует взаимнооднозначное
соответствие, причем при данном
соответствии сохраняются операции
сложения и умножения на скаляр.

Опр. Подкольцо – подмножество
кольца, которое само являющееся кольцом
относительно главных бинарных операций
кольца.

Опр. Идеал. Правый (левый) идеал –
такое подкольцо кольца, умножение всех
элементов которого справа(слева) на
элемент кольца принадлежит идеалу. Если
верны оба утверждения, множество
называется двусторонним идеалом. Если
операция коммутативна, используется
понятие идеал.

Теорема «О представлении циклического
кода в виде идеала»: Пусть С –
линейный код в

.
С является цикличным кодом тогда и
только тогда (
),
когда соответствующее ему множество
многочленов в кольце

является идеалом.

Доказательство:

Предположим, что С- циклический код:

,
соответствующий ему многочлен имеет
вид:

,
Необходимо показать что

является идеалом кольца

.
Проверим. Очевидно, что

– подкольцо, т.к.

– замкнуто по сложению, поскольку

,
то и

.
Для того, чтобы показать что произведение
элементов из

вновь
находится в

,
докажем утверждение:

Доказательство утверждения: a)

.
Т.к в кольце К

где

результат
циклического сдвига. Т.к. С- цикличен,
то и

,
то

б)

.

из свойства «а» для идеалов следует,
что

,
но тогда из свойства «б» следует, что

.
При умножении одного многочлена на
другой получим сумму указанных
произведений, каждое из которых
принадлежит I. Но так как
I замкнуто по сложению, получим что
произведение 2-х многочленов, один из
которых принадлежит кольцу К, а второй
подкольцу I лежит в I.

.
Из данного включения следует, что

является подкольцом и идеалом кольца
К. что и требовалось показать.

1)

Рассмотрим
множество

и пусть

– идеал. Необходимо показать, что код С
– цикличен. Возьмем произвольное

.
Необходимо показать, что

.
По условию:

.
Т.к.

–
идеал, то

.
Другими словами:


,
т.е.

.Что
и требовалось доказать.

Порождающий и проверочный многочлен
циклического кода.

Предположим, что код С имеет ненулевую
размерность. Среди многочленов, входящих
в С, отличных от нуля, найдем многочлен

с наименьшей степенью (таких многочленов
может быть и несколько).

Утверждение «О многочлене

»:

Доказательство: поделим многочлен

на многочлен

с остатком. Получим:

. Т.к. С – идеал, то

.
Но

;

.
В противном случае получаем противоречие
с корректностью выбора

.

Замечание: Заметим, что

,
который был описан выше, обладает
свойством:

или (что одно и то же)

,
т.е. С порождается

.
Это следует из того, что С – идеал и
последнего утверждения, в котором мы
получаем, что все многочлены из С
представимы через

.

Опр.: Многочлен

циклического кода С, описанный выше,
называется порождающим
многочленом данного кода.

Замечание: Заметим, что два различных
порождающих многочлена одного и того
же кода получаются друг из друга путем
умножения на константу. Поэтому в
качестве

берут тот, у которого старший коэффициент
равен 1.

Теорема «О порождающем многочлене»:
Пусть

– порождающий многочлен циклического
кода С в

,
тогда многочлен

делит многочлен

.

Доказательство: Поделим многочлен

на

с остатком. Получим:

.
В кольце К:



.
Поскольку

.

Эта теорема позволяет перечислять все
циклические коды определенной длинны,
указывая их порождающие многочлены.

Опр.: Пусть С – циклический код с
порождающим многочленом

и длиной кодового слова равной

,
тогда проверочным многочленом
кода С называется многочлен вида:

.

Замечание: Т.к. все порождающие
многочлены одного кода отличаются друг
от друга на константу, то и все проверочные
многочлены отличаются на константу.
Обычно, в качестве проверочного многочлена
выбирают тот, у которого коэффициент
при старшем члене равен 1.

Требование к порождающему полиному при
кодировании – его вес не должен быть
меньше минимального кодового расстояния

В теории информации циклические коды
часто записываются как

и k соответствует числу
информационных символов, а m-
проверочных

С помощью порождающего полинома
осуществляется кодирование циклическим
кодом. В частности:

• несистематическое кодирование
  осуществляется путём умножения
  кодируемого вектора на g(x): c(x)
  = u(x)g(x) – векторы сначала
  переписываются в виде соответствующих
  полиномов, а затем перемножаются, после
  чего записывается вектор, соответствующий
  ответу

• систематическое кодирование
  осуществляется путём «дописывания» к
  кодируемому слову остатка от деления
  

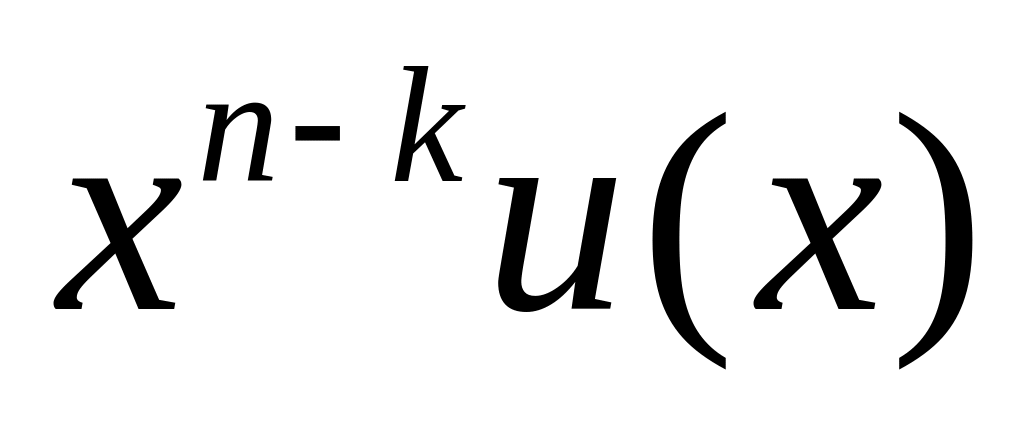
  на g(x), deg(g(x))
  = n-k,
  
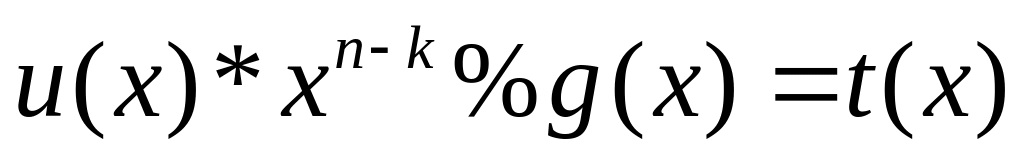
  то
  есть
  
  .

deg(u(x))=k-1;
x^n–i
– t_i(x)=ci(x)-
линейно независимые кодовые многочлены,
получаем t_i(x)
имеющий макс степень n-k-1;

,
по ним строим порождающую матрицу:

,
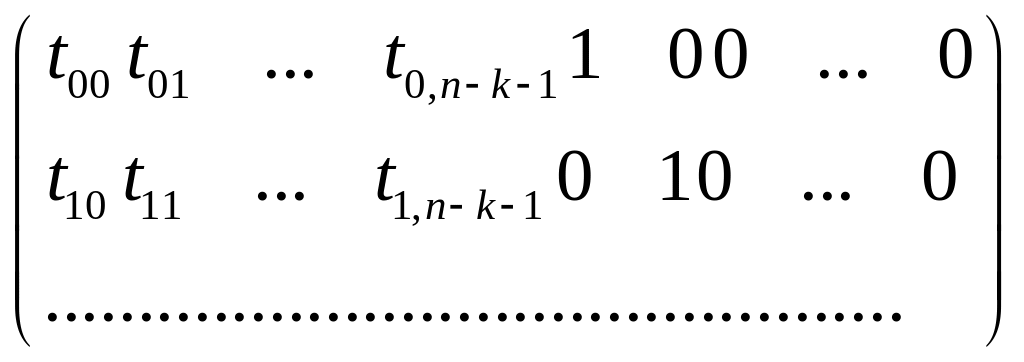
проверочная матрица строится исходя
из формулы G=[T:E]
->H=[E:T^t]

Обнаружение ошибок кодирования (при
передаче в канале с помехами)

Будем рассматривать несистематическое
кодирование. Пусть мы получили сообщение

Очевидно, что если сообщение будет
передано без ошибок

,
то для полученного кодового слова будет
выполняться

,
если же в ходе передачи возникли ошибки,
то остаток будет отличен от нуля. При
этом заметим, что так как вычисления
идут по модулю многочлена

– это и есть смысл выбора проверочного
многочлена

Теорема:

Если а(х)∈С, то
а(х)*h(x)=0;

Если а(х)
С,
то а(х)*h(x)≠0;

Доказательство:

1) а(х)∈С –>
a(x)=b(x)*g(x);

a(x)*h(x)=b(x)*g(x)*h(x)=b(x)(xⁿ+1)=0
mod(xⁿ+1);

2) а(х)

С
–> a(x)=b(x)*g(x)+r(x);

a(x)*h(x)=b(x)(xn+1)+r(x)h(x)

deg(a(x))=n-k; deg(h(x))=k; deg(r(x)h(x))<=n-1;

а(х)*h(x)=r(x)*h(x)≠0

Доказано.

Синдром
– это вектор (в указанном определении
–вектор-строка)

– определяемый через проверочную матрицу.
Можно записать соответствующий ему
многочлен

.

Учитывая, что

получим, сто синдром равен

И соответственно по синдрому можно
определить вектор ошибок. (На практике
такой поиск обычно осуществляют по
заранее составленным таблицам).

Свойства синдрома:

1)

.

2)

.

3)

.

4)

(равенство
смежных классов).

Доказательство:

1. Следует из определения проверочной
   матрицы.

2. 
   .

3. 
   .

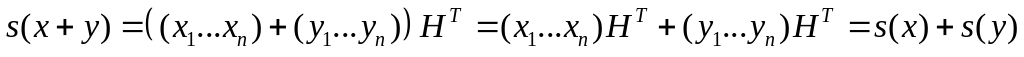
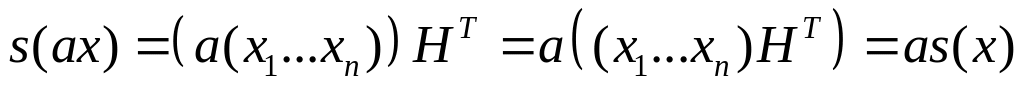
4. Используем критерий равенства правых
   смежных классов в абелевой группе (

   – группа, (С, +) – подгруппа):

.

Опр.: Пусть

–
подмножество,

(
–
непустое множество), тогда х≠0 – лидер
М, если он имеет минимальный вес Хэменга,
т.е.

.

Утверждение «О ближайшем соседе»:
Пусть С – код в

,

его
проверочная матрица.

,
тогда

будет ближайшим элементом к элементу

,
в смысле расстояния Хэменга,

элемент

будет лидером смежного класса с синдромом

.

Доказательство: Заметим, что

действительно содержится в классе,
определяемом

:

.

Пусть
х – ближайший сосед, т.е

Если
элемент

пробегает все кодовые слова, то элемент

пробегает все элементы смежного класса

,
т.е.

.
Другими словами,

лидер
смежного класса

.

Пусть

– лидер смежного класса

.
Т.е.

.
Другими словами:

.
Следовательно, х – ближайший сосед.
Утверждение доказано.

Алгоритм декодирования с помощью
синдромов и лидеров:

1. Найти проверочную матрицу для кода С.

2. Перечислить все смежный классы

   по
   

   и для каждого класса указать соответствующий
   ему синдром и выбрать какого-либо лидера
   этого класса.

3. Для полученного сообщения

   вычисляется его синдром
   
   .

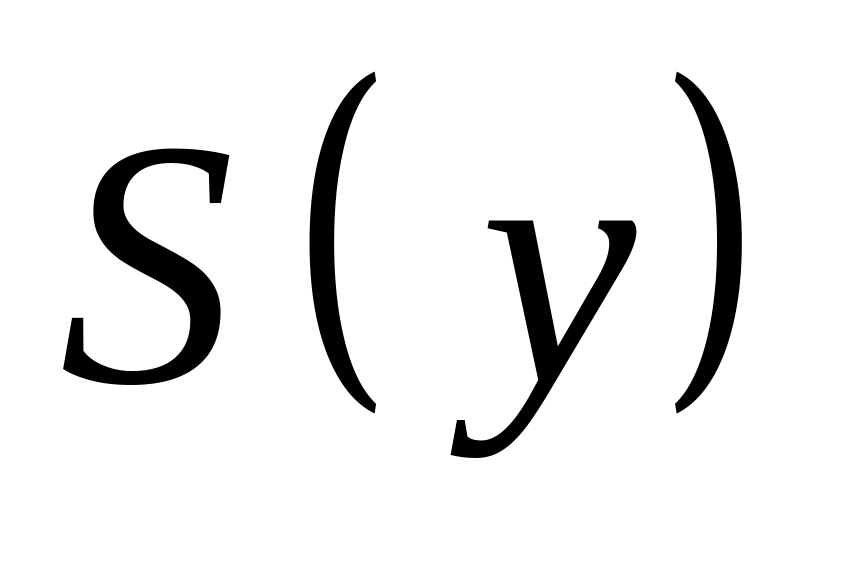
4. По полученному синдрому

   найти соответствующий ему лидер
   

5. Декодировать

   ,
   где
   

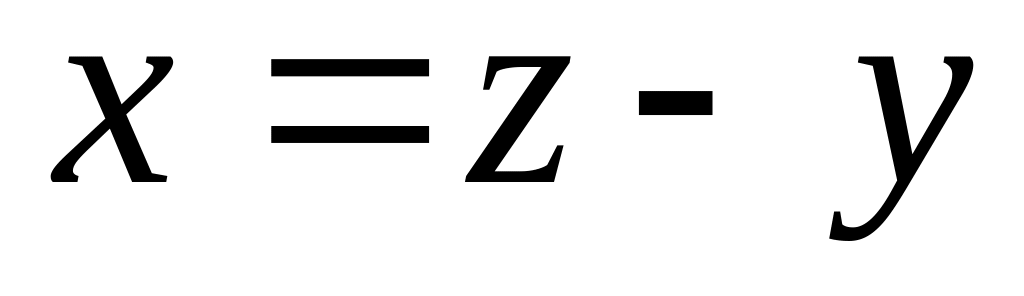
Можно написать алгоритм и для случая
использования многочленов

В этом случае процедура декодирования
имеет следующий вид:

1. Найдем синдромный многочлен

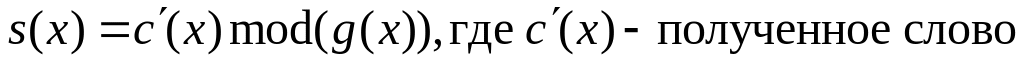
2. Для каждого
   

   вычислим
   

   до тех пор, пока не будет найден
   

   такой, что
   
   максимальное
   число ошибок, исправляемых кодом.

3. Полином ошибки есть
   

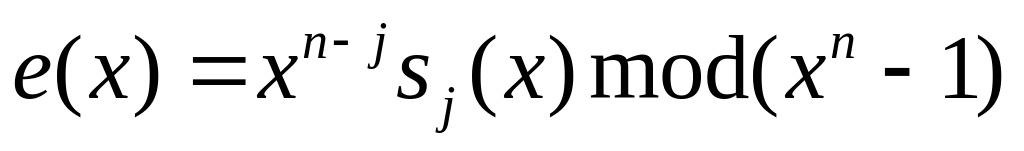
Так, для кодов Хэмминга получаемый
синдром просто совпадает с вектором
ошибок

Циклический код не обнаружит ошибок в
полученной комбинации только в том
случае, если количество ошибок таково,
что перевело одну разрешенную кодовую
комбинацию в другую( то есть полученное
нами слово так же принадлежит коду), и
не сможет исправить ошибки в том случае,
если их количество превысит число
проверочных символов.

Однако, обычно в системах связи исправление
ошибок при использовании циклических
кодов не производится, а при обнаружении
ошибок выдается запрос на повтор
испорченной ошибками комбинации

(на всякий случай – было в лекциях по
кодированию)

Теорема о синдроме циклического кода:

Пусть d* – минимальное
кодовое растояние циклического кода.
Каждому многочлену ошибок веса <

соответствует единственный синдромный
многочлен.

Доказательство:

Даны многочлены соотв векторам ошибок
e1(x), e2(x),
w(e1)<

,
w(e2)<

,
e1(x) =
c1(x)+S(x),
e2(x)=c2(x)+S(x),
e1(x)-e2(x)=c1(x)-c2(x)

e1(x)=e2(x)+c(x); w(e1(x)-e2(x))<d*;
e1-e2
->e1(x)-e2(x)=0
->e1(x)=e2(x)

Доказано.

Теорема «О порождающей матрице
циклического кода»: Пусть С –
циклический код над

с длинной кодового слова

и
порождающим многочленом

.
Тогда в качестве порождающей матрицы
кода С можно взять матрицу вида:

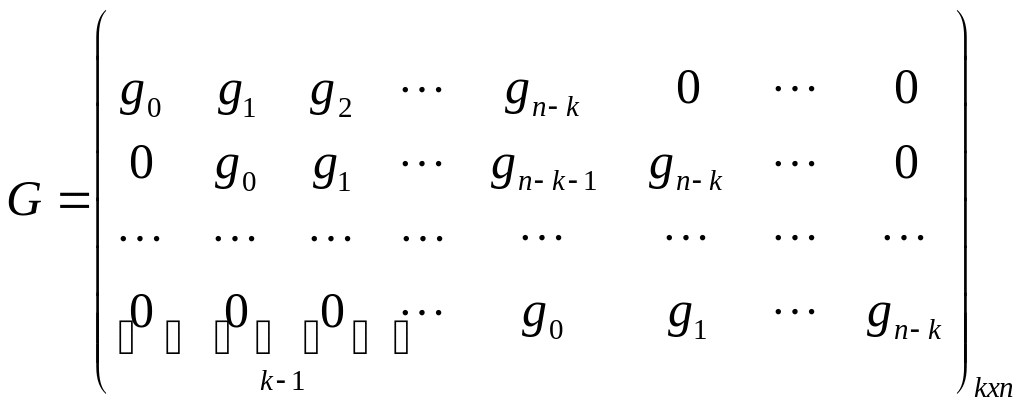
Доказательство: Для доказательства
теоремы необходимо и достаточно показать,
что вектора:

,

,

являются базисом кода С.

Запишем многочлены, которые соответствуют
данным кодовым словам:

;

;

Так как код С является идеалом, порожденным
многочленом

,
то

Покажем, что элементы

– линейно независимы. Рассмотрим линейную
комбинацию:

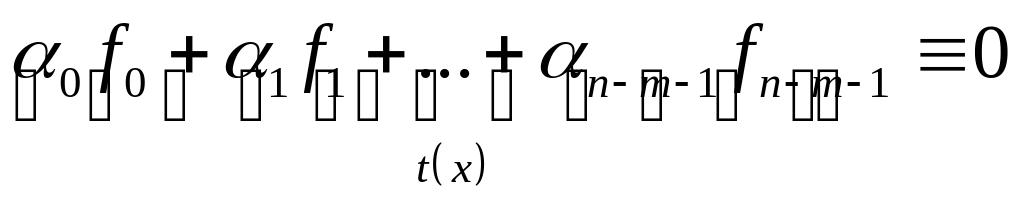
Заметим, что многочлен

имеет степень не большую, чем

,
т.к. этот многочлен тождественно равен
нулю в кольце
.
Значит мы можем сказать, что все
коэффициенты указанной линейной
комбинации равны 0. Запишем равенство
коэффициентов нулю в виде системы:

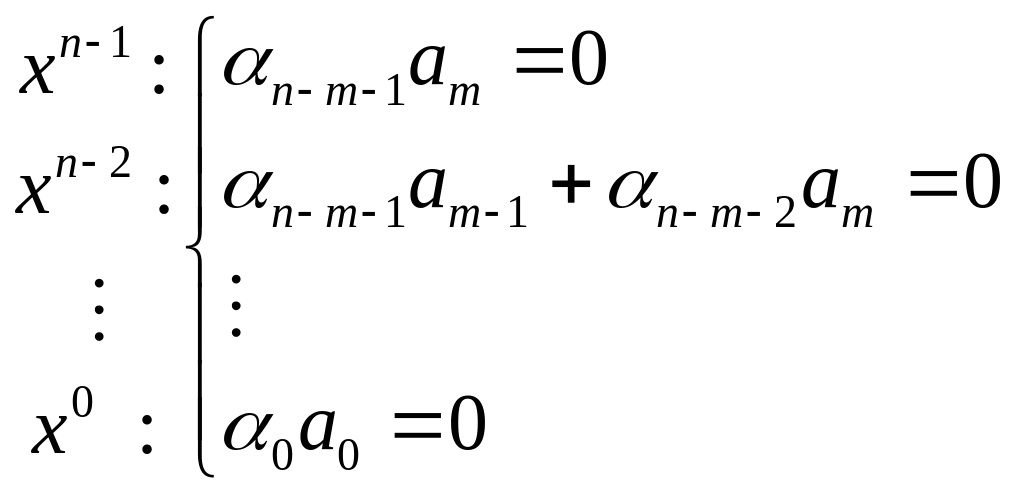
Поскольку

,
то

.
Из второго уравнения:

.
И так далее до

.
Таким образом, мы показали, что система
линейно независима. Покажем, что данная
система является полной в С. Возьмем
произвольный многочлен

.

можно выбрать таким образом, что бы он
представлялся в виде:
,
где

.
Но тогда

имеет вид:

,
где

.
Следовательно:

.
Таким образом матрица

действительно порождающая матрица.
Следствие: Пусть
циклический код С с длинной кодового
слова

и
порождающим многочленом

,
таким что:

.
Тогда

.

Теорема «О проверочной матрице
циклического кода»: Пусть
циклический код С с длинной кодового
слова

и
проверочным многочленом

,

.
Тогда в качестве проверочной матрицы
кода С можно взять матрицу вида:

Д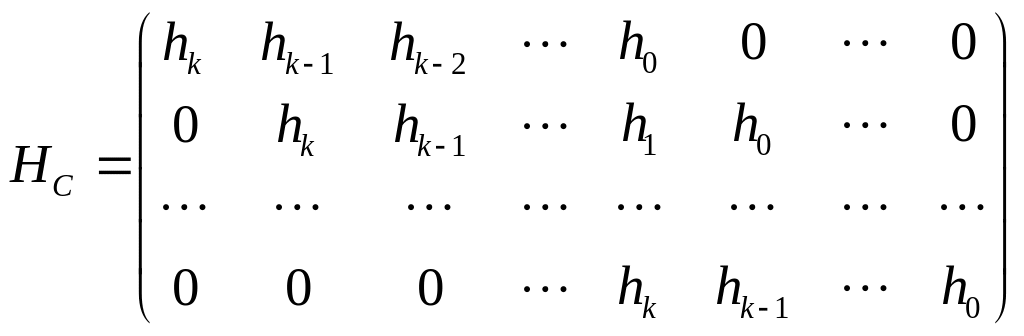
оказательство:
Т.к. проверочный многочлен

,
где

– порождающий многочлен, то:

в кольце
.
В самом деле:

в кольце, так как С – идеал. Если

делится нацело на

.
Следовательно:

.
Приравнивая к нулю коэффициенты при
соответствующих степенях в произведении

,
получим систему линейных уравнений с
матрицей

вида:

М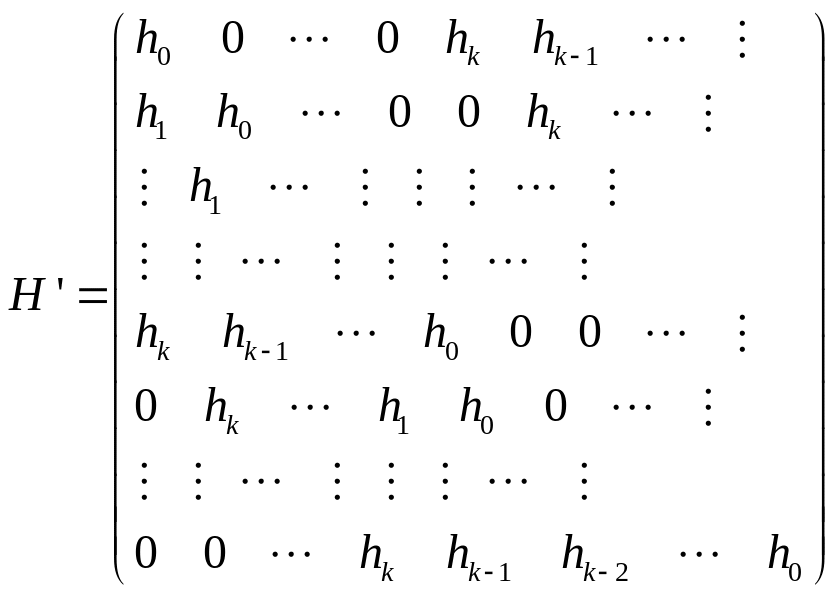
атрица

будет являться одной из проверочных
матриц для кода С. Из соображений
размерности получим:

.
Легко заметить, что последнее

строк матрицы

линейно независимы, поэтому предыдущие
строки можно отбросить и получить в
качестве проверочной матрицы матрицу
Н из условия теоремы.

20

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 28 января 2021 года; проверки требуют 2 правки.

Циклический код — линейный, блочный код, обладающий свойством цикличности, то есть каждая циклическая перестановка кодового слова также является кодовым словом. Используется для преобразования информации для защиты её от ошибок (см. Обнаружение и исправление ошибок).

Введение[править | править код]

Пусть  — слово длины n над алфавитом из элементов конечного поля и  — полином, соответствующий этому слову, от формальной переменной . Видно, что это соответствие является изоморфизмом линейных пространств. Так как «слова» состоят из букв из поля, то их можно складывать и умножать (поэлементно), причём результат будет в том же поле.
Полином, соответствующий линейной комбинации пары слов и , равен линейной комбинации полиномов этих слов .

Это позволяет рассматривать множество слов длины n над конечным полем как линейное пространство полиномов со степенью не выше n − 1 над полем .

Алгебраическое описание[править | править код]

Если  — кодовое слово, получающееся циклическим сдвигом на один разряд влево из слова , то соответствующий ему полином получается из предыдущего умножением на x:

, пользуясь тем, что

Сдвиг вправо и влево соответственно на разрядов:

Если  — произвольный полином над полем , и  — кодовое слово циклического кода, то  — тоже кодовое слово этого кода.

Порождающий полином[править | править код]

Определение

Порождающим полиномом циклического кода называется такой ненулевой полином из , степень которого наименьшая, и коэффициент при старшей степени .

Теорема 1

Если  — циклический код, и  — его порождающий полином, то степень равна , и каждое кодовое слово может быть единственным образом представлено в виде

где степень меньше или равна .

Теорема 2

 — порождающий полином циклического кода — является делителем двучлена .

Следствия

Таким образом, в качестве порождающего полинома можно выбирать любой полином делитель .
Степень выбранного полинома будет определять количество проверочных символов , число информационных символов .

Порождающая матрица[править | править код]

Полиномы линейно независимы, иначе при ненулевом , что невозможно.

Значит кодовые слова можно записывать, как и для линейных кодов, следующим образом:

где является порождающей матрицей,  — информационным полиномом.

Матрицу можно записать в символьной форме:

Проверочная матрица[править | править код]

Для каждого кодового слова циклического кода справедливо .
Поэтому проверочную матрицу можно записать как

Тогда

Кодирование[править | править код]

Несистематическое[править | править код]

При несистематическом кодировании кодовое слово получается в виде произведения информационного полинома на порождающий:

Оно может быть реализовано при помощи перемножения полиномов.

Систематическое[править | править код]

При систематическом кодировании кодовое слово формируется в виде информационного подблока и проверочного:

Пусть информационное слово образует старшие степени кодового слова, тогда

Тогда из условия следует

Это уравнение и задаёт правило систематического кодирования. Оно может быть реализовано при помощи многотактных линейных фильтров (МЛФ).

Примеры[править | править код]

Двоичный (7,4,3) код[править | править код]

В качестве делителя выберем порождающий полином третьей степени , тогда полученный код будет иметь длину , число проверочных символов (степень порождающего полинома) , число информационных символов , минимальное расстояние .

Порождающая матрица кода:

где первая строка представляет собой запись полинома коэффициентами по возрастанию степени.

Остальные строки — циклические сдвиги первой строки.

Проверочная матрица:

где i-й столбец, начиная с 1-го, представляет собой остаток от деления на полином , записанный по возрастанию степеней, начиная сверху.

Так, например, 4-й столбец получается , или в векторной записи .

Легко убедиться, что .

Двоичный (15,7,5) БЧХ код[править | править код]

В качестве порождающего полинома можно выбрать произведение двух делителей :

Тогда каждое кодовое слово можно получить с помощью произведения информационного полинома со степенью таким образом:

Например, информационному слову соответствует полином , тогда кодовое слово , или в векторном виде .

См. также[править | править код]

• Обнаружение и исправление ошибок
• Линейный код
• БЧХ код
• Конечное поле
• Многочлен над конечным полем
• Код Рида — Соломона
• Код Хэмминга

Ссылки[править | править код]

• Механизмы контроля целостности данных.

Макеты страниц