Частный
случай полос равной толщины – кольца
Ньютона –
наблюдаются, если плосковыпуклую линзу
поместить на плоскопараллельную
стеклянную пластинку (рис 3).
Если
на линзу падает пучок монохроматического
света, то световые волны, отражённые от
воздуха в точке А
и от стекла в точке В
(т.е. от
верхней и нижней границ воздушной
прослойки), оказываются когерентными
и интерферируют. Волна, отраженная от
плоской поверхности линзы, не когерентна
с ними и дает лишь равномерную засветку.
Точки, для которых толщина воздушного
зазора одинакова, располагаются на
окружностях, поэтому интерференционная
картина имеет вид чередующихся
концентрических темных и светлых колец.
Рис.3. Схема
возникновения колец Ньютона
Так как отражение
световой волны в точке В происходит от
стекла (оптически более плотной среды),
то оптическая длина пути второго луча
в точке А составит АВ + ВА + λ/2. Оптическая
длина пути первого луча в точке А равна
нулю. Поэтому
Δопт
= L2–
L1
= АВ + ВА + λ/2 = 2d
+ λ / 2
Тёмные кольца
образуются там, где оптическая разность
хода равна нечётному числу полуволн:
Δопт
= 2d
+ λ
/2 = (2m
+ 1) λ
/2,
т.е. при толщине
зазора
d
= m
λ
/2 , (8)
где
m
= 0,1,2,3… – номер кольца.
В
центре интерференционной картины
находится темный круг, соответствующий
минимуму нулевого порядка. Если rm
– радиус темного кольца под номером m,
то из треугольника AОС (см. рис.3) имеем:
rm2
=
R2
– (R
– d,)2
= 2Rd
– d
2,
(9)
где
R
– радиус кривизны линзы. Полагая величину
воздушного зазора в месте возникновения
колец малой, (т.е. пренебрегая d
2
по сравнению с 2Rd),
получим:
rm
2 = 2Rd.
.
Подставляя
сюда (8), получим
rm2
= Rmλ
(10)
Из этой формулы
видно, что зная длину волны используемого
света радиус кривизны линзы можно найти
путем измерения радиуса кольца Ньютона
и определения его порядкового номера.
Использование
формулы (10) для определения радиуса
кривизны может привести к ошибке, т.к.
в точке соприкосновения линзы и стеклянной
пластинки возможна деформация, как
линзы, так и пластинки, сравнимая по
величине с длиной волны света. Поэтому
результаты, полученные без учета этого
факта, являются неточными.
Величина
воздушного зазора оказывается меньше
теоретической величины, полученной из
рис.3, на величину суммарной деформации
стеклянной пластинки и линзы δ (рис.4).
Учитывая это, в формулу (9) вместо толщины
воздушного зазора d
необходимо подставить сумму толщины
воздушного зазора и величины суммарной
деформации линзы и стеклянной пластинки
(d
+ δ):
rm2
=
R2
– [R
–(d+
δ)]2.
Пренебрегая
малой величиной (d+
δ)2,
получаем:
rm2
= 2R(d
+ δ
)
Рис.4.
Учет деформации линзы и стеклянной
пластинки
Учитывая
(13), получим следующую формулу, для
радиусов темных колец Ньютона с учетом
суммарной деформации:
rm2
= Rmλ
+ 2Rδ
(11)
Экспериментально
удобнее вместо радиуса кольца Ньютона
измерять его диаметр (Dm
). В этом
случае формула (11) будет иметь вид:
Dm2
= 4Rmλ
+ 8Rδ,
(12)
Из
(12) видно, что квадрат диаметра кольца
Ньютона Dm2
пропорционален порядковому номеру
кольца m.
Если построить график зависимости Dm2
от m,
то экспериментальные точки должны
лежать на одной прямой, и тангенс угла
наклона этой прямой tgα
будет равен 4Rλ.
Таким образом, для нахождения радиуса
кривизны линзы необходимо, используя
график зависимости Dm2
= f(m),
найти
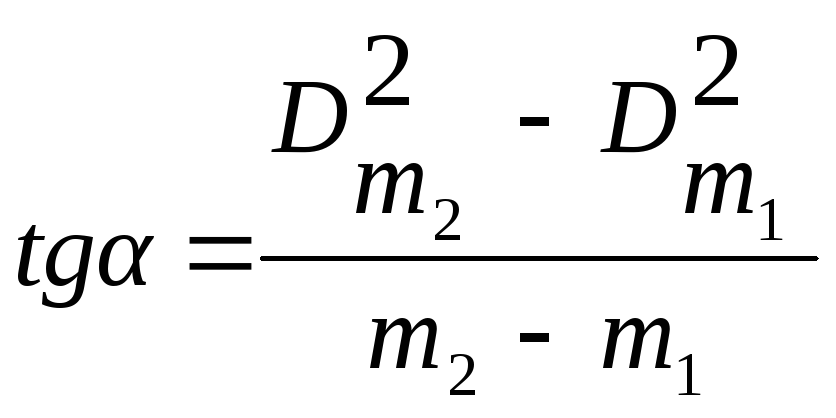
(13)
где
m1,
m2
номера колец,
D2m1
и D2m2
– их диаметры,
Радиус кривизны
линзы затем можно рассчитать по формуле
R=tgα/4λ.
(14)
В
центре линзы наблюдается круглое темное
пятно, соответствующее нулевой толщине
воздушного зазора в области деформации.
Измерив диаметр центрального темного
пятна (т.е. темного кольца, номер которого
m=0),
из (12) можно найти величину суммарной
деформации линзы и стеклянной пластинки
по формуле:
δ
= D02/
( 8R
) (15)
Соседние файлы в папке ОПТИКА Лаб.раб 2013
- #
- #
- #
- #
- #
- #
- #
- #
- #
Если плосковыпуклую линзу малой кривизны положить выпуклой поверхностью на хорошо отполированную плоскую стеклянную пластинку, то между линзой и пластинкой образуется воздушная прослойка, утолщающаяся от точки соприкосновения к краям. Если на эту систему падает свет, то части одной и той же световой волны, отраженные от границ воздушной прослойки, будут интерферировать между собой. При этом наблюдается система концентрических радужных (немонохроматический свет) или чередующихся темных и светлых (монохроматический свет) колец. Кольца Ньютона являются классическим примером полос равной толщины. Они наблюдаются и в проходящем, и в отраженном свете, причем каждому темному кольцу в отраженном свете соответствует светлое кольцо в проходящем свете. В отраженном свете картина интерференции значительно контрастнее по сравнению с картиной интерференции в проходящем свете. Кольца Ньютона представляют собой частный случай интерференции в тонких пленках. Интерферирующие лучи приобретают разность хода в воздушном зазоре между плосковыпуклой линзой радиуса кривизны и плоскопараллельной пластинкой, на которую положена линза. Картина интерференции представляет собой ряд чередующихся светлых и темных колец при нормальном падении монохроматического света на линзу.
Задача 1.
Установка для получения колец Ньютона освещается падающим нормально монохроматическим светом. Радиус четвертого темного кольца, наблюдаемого в отраженном свете, равен 4 мм. Найдите длину волны падающего света в нм, если радиус кривизны линзы м.
Свет проходит через линзу, преломляется и в очень узком воздушном промежутке между линзой и подложкой интерферирует, почему и появляются кольца Ньютона. Воздушный клин, на котором происходит интерференция, в случае, когда радиус кривизны линзы велик, имеет очень малый угол. Поэтому с большой степенью точности можно считать, что клин составлен из отдельных кусочков плоскопараллельных пластинок, и для каждого такого кусочка, характеризуемого своей толщиной , применять формулу для разности хода интерферирующих лучей:
Определим по теореме Пифагора:
Пренебрежем величиной – она очень мала, и тогда
Чтобы соблюдалось условие минимума освещенности, должно выполняться
То есть
Подставим ранее полученное выражение:
Откуда
Ответ: , 500 нм.
Задача 2.
Установка для получения колец Ньютона освещается светом с длиной волны нм, падающим по нормали к поверхности пластинки. Радиус кривизны линзы
м. Пространство между линзой и стеклянной пластинкой заполнено жидкостью. Найти показатель преломления
жидкости, если радиус третьего светлого кольца в проходящем свете
мм.
Так как радиус светлого кольца в проходящем свете соответствует радиусу темного в отраженном, то можно записать, что
Однако один из лучей проходит через жидкость, в которой его длина волны становится меньше в раз, поэтому
Или
Ответ: .
Задача 3.
Выпуклая линза с большим радиусом кривизны лежит на плоскопараллельной стеклянной пластинке и освещается нормально падающим параллельным пучком монохроматического света с длиной волны
. В воздушном зазоре между соприкасающимися поверхностями линзы и пластинки в отраженном свете наблюдаются кольца Ньютона. Найти радиусы темных колец.
Решение этой задачи аналогично первой.
Осталось подставить номер кольца.
Ответ: .
Задача 4.
Установка для получения колец Ньютона освещается падающим нормально монохроматическим светом. Радиус кривизны линзы 15 м. Наблюдение ведется в отраженном свете. Расстояние между пятым и двадцать пятым светлыми кольцами Ньютона равно 9 мм. Найти длину волны монохроматического света.
Определим радиус светлого кольца в отраженном свете. Применим формулу для разности хода интерферирующих лучей:
Определим по теореме Пифагора:
Пренебрежем величиной – она очень мала, и тогда
Чтобы соблюдалось условие максимума освещенности, должно выполняться
То есть
Подставим ранее полученное выражение:
Откуда
Обобщая информацию, сведем все в таблицу:
Радиусы колец Ньютона
Теперь решим задачу. Нам известно, что
Тогда
Или
Откуда и найдем длину волны света:
Ответ: нм.
Задача 5.
Установка для получения колец Ньютона освещается монохроматическим светом, падающим параллельно главной оптической оси линзы. Радиусы двух соседних темных колец равны 4,0 мм и 4,38 мм. Радиус кривизны линзы 6,4 м. Найдите порядковые номера колец и длину волны падающего света.
Радиус темных колец определяется формулой
Тогда следующее кольцо имеет радиус
А отношение радиусов будет равно
Тогда
Откуда
Тогда порядковый номер второго кольца – 6. А длина волны
Ответ: порядковые номера колец – 5 и 6, длина волны нм.
Кольца Ньютона
Простая интерференционная картина возникает в тонкой прослойке воздуха между стеклянной пластиной и положенной на нее плоско-выпуклой линзой, сферическая поверхность которой имеет большой радиус кривизны. Эта интерференционная картина имеет вид концентрических колец, получивших название кольца Ньютона.
Кольца Ньютона
Возьмите плоско-выпуклую линзу с малой кривизной сферической поверхности и положите ее на стеклянную пластину, как было указано выше. Внимательно разглядывая плоскую поверхность линзы (лучше через лупу), вы обнаружите в месте соприкосновения линзы и пластины темное пятно и вокруг него совокупность маленьких радужных колец. Расстояния между соседними кольцами быстро убывают с увеличением их радиуса. Это и есть кольца Ньютона. Ньютон наблюдал и исследовал их не только в белом свете, но и при освещении линзы одноцветным (монохроматическим) пучком. Оказалось, что радиусы колец одного и того же порядкового номера увеличиваются при переходе от фиолетового конца спектра к красному; красные кольца имеют максимальный радиус. Все это вы можете проверить с помощью самостоятельных наблюдений.
Но объяснить, почему возникают кольца Ньютон не смог. Удалось это Юнгу. Проследим за ходом его рассуждений. В их основе лежит предположение о том, что свет — это волны. Рассмотрим случай, когда волна определенной длины падает почти перпендикулярно на плоско-выпуклую линзу. Волна 1 появляется в результате отражения от выпуклой поверхности линзы на границе стекло — воздух, а волна 2 — в результате отражения от пластины на границе воздух — стекло. Эти волны когерентны: они имеют одинаковую длину и постоянную разность фаз, которая возникает из-за того, что волна 2 проходит больший путь, чем волна 1. Если вторая волна отстает от первой на целое число длин волн, то, складываясь, волны усиливают друг друга. Вызываемые ими колебания происходят в одной фазе.
Напротив, если вторая волна отстанет от первой на нечетное число полуволн, то колебания, вызванные ими, будут происходить в противоположных фазах и волны гасят друг друга.
Если известен радиус кривизны R поверхности линзы, то можно вычислить, на каких расстояниях от точки соприкосновения линзы со стеклянной пластиной разности хода таковы, что волны определенной длины λ гасят друг друга. Эти расстояния и являются радиусами темных колец Ньютона. Ведь линии постоянной толщины воздушной прослойки представляют собой окружности. Измерив, радиусы колец, можно вычислить длины волн.
Кольца Ньютона в отражённом свете
Длина световой волны
Длина световой волны. Для красного света измерения дают λ = 8∙10 -7 м, а для фиолетового — λ = 4∙10 -7 м. Длины волн, соответствующие другим цветам спектра, принимают промежуточные значения. Для любого цвета длина световой волны очень мала. Представьте себе среднюю морскую волну длиной в несколько метров, которая увеличилась настолько, что заняла весь Атлантический океан от берегов Америки до Европы. Длина световой волны в том же увеличении лишь ненамного превысила бы ширину этой страницы.
Явление интерференции не только доказывает наличие у света волновых свойств, но и позволяет измерить длину волны. Подобно тому, как высота звука определяется его частотой, цвет света определяется частотой колебаний или длиной волны.
Вне нас в природе нет никаких красок, есть лишь волны разной длины. Глаз — сложный физический прибор, способный обнаруживать различие в цвете, которому соответствует весьма незначительная (около 10 -6 см) разница в длине световых волн. Интересно, что большинство животных не способны различать цвета. Они всегда видят черно-белую картину.
При переходе света из одной среды в другую длина волны изменяется. Это можно обнаружить так. Заполним водой или другой прозрачной жидкостью с показателем преломления п воздушную прослойку между линзой и пластиной. Радиусы интерференционных колец уменьшатся.
Почему это происходит? Мы знаем, что при переходе света из вакуума в какую-нибудь среду скорость света уменьшается в п раз. Так как v=λv, то при этом должна уменьшиться в п раз либо частота, либо длина волны. Но радиусы колец зависят от длины волны. Следовательно, когда свет входит в среду, изменяется в п раз именно длина волны, а не частота.
Необходимы более веские доказательства того, что свет при распространении ведет себя как волна. Любому волновому движению присущи явления интерференции и дифракции. Для того чтобы быть уверенным в том, что свет имеет волновую природу, необходимо найти экспериментальные доказательства интерференции и дифракции света.
Интерференция — достаточно сложное явление . Чтобы лучше понять его суть, мы вначале остановимся на интерференции механических волн.
Сложение волн. Очень часто в среде одновременно распространяется несколько различных волн. Например, когда в комнате беседуют несколько человек, то звуковые волны накладываются друг на друга. Что при этом происходит?
Проще всего проследить за наложением механических волн, наблюдая волны на поверхности воды. Если мы бросим в воду два камня, создав этим две кольцевые волны, то нетрудно заметить, что каждая волна проходит сквозь другую и ведет себя в дальнейшем так, как будто бы другой волны совсем не существовало. Точно так же любое число звуковых волн может одновременно распространяться в воздухе, ничуть не мешая друг другу. Множество музыкальных инструментов в оркестре или голосов в хоре создают звуковые волны, одновременно улавливаемые нашим ухом. Причем ухо в состоянии отличить один звук от другого.
Теперь посмотрим более внимательно, что происходит в местах, где волны накладываются друг на друга. Наблюдая волны на поверхности воды от двух брошенных в воду камней, можно заметить, что некоторые участки поверхности не возмущены, в других же местах возмущение усилилось. Если две волны встречаются в одном месте гребнями, то в этом месте возмущение поверхности воды усиливается.
Если же, напротив, гребень одной волны встречается с впадиной другой, то поверхность воды не будет возмущена.
Вообще же в каждой точке среды колебания, вызванные двумя волнами, просто складываются. Результирующее смещение любой частицы среды представляет собой алгебраическую (т. е. с учетом их знаков) сумму смещений, которые происходили бы при распространении одной из волн в отсутствие другой.
Интерференция. Сложение в пространстве волн, при котором образуется постоянное во времени распределение амплитуд результирующих колебаний, называется интерференцией.
Выясним, при каких условиях имеет место интерференция волн. Для этого рассмотрим более подробно сложение волн, образуемых на поверхности воды.
Можно одновременно возбудить две круговые волны в ванне с помощью двух шариков, укрепленных на стержне, который совершает гармонические колебания (рис. 118). В любой точке М на поверхности воды (рис. 119) будут складываться колебания, вызванные двумя волнами (от источников O1 и О2). Амплитуды колебаний, вызванных в точке М обеими волнами, будут, вообще говоря, отличаться, так как волны проходят различные пути d1 и d2. Но если расстояние l между источниками много меньше этих путей (l « d1 и l « d2 ) , то обе амплитуды
можно считать практически одинаковыми.
Результат сложения волн, приходящих в точку M, зависит от разности фаз между ними. Пройдя различные расстояния d1 и d2, волны имеют разность хода Δd = d2—d1. Если разность хода равна длине волны λ, то вторая волна запаздывает по сравнению с первой ровно на один период (как раз за период волна проходит путь, равный длине волны). Следовательно, в этом случае гребни (как и впадины) обеих волн совпадают.
Условие максимумов. На рисунке 120 изображена зависимость от времени смещений X1 и X2 , вызванных двумя волнами при Δd= λ. Разность фаз колебаний равна нулю (или, что то же самое, 2л, так как период синуса равен 2п). В результате сложения этих колебаний возникает результирующее колебание с удвоенной амплитудой. Колебания результирующего смещения на рисунке показаны цветом (пунктир). То же самое будет происходить, если на отрезке Δd укладывается не одна, а любое целое число длин волн.
Амплитуда колебаний среды в данной точке максимальна, если разность хода двух волн, возбуждающих колебания в этой точке, равна целому числу длин волн:
Условие минимумов. Пусть теперь на отрезке Δd укладывается половина длины волны. Очевидно, что при этом вторая волна отстает от первой на половину периода. Разность фаз оказывается равной п, т. е. колебания будут происходить в противофазе. В результате сложения этих колебаний амплитуда результирующего колебания равна нулю, т. е. в рассматриваемой точке колебаний нет (рис. 121). То же самое произойдет, если на отрезке укладывается любое нечетное число полуволн.
Амплитуда колебаний среды в данной точке минимальна, если разность хода двух волн, возбуждающих колебания в этой точке, равна нечетному числу полуволн:
Если разность хода d2 — d1 принимает промежуточное значение
между λ и λ/2 , то и амплитуда результирующего колебания принимает некоторое промежуточное значение между удвоенной амплитудой и нулем. Но наиболее важно то, что Амплитуда колебаний в любой точке he меняется с течением времени. На поверхности воды возникает определенное, неизменное во времени распределение амплитуд колебаний, которое называют интерференционной картиной. На рисунке 122 показан рисунок с фотографии интерференционной картины двух круговых волн от двух источников (черные кружки). Белые участки в средней части фотографии соответствуют максимумам колебаний, а темные — минимумам.
Когерентные волны. Для образования устойчивой интерференционной картины необходимо, чтобы источники волн имели одинаковую частоту и разность фаз их колебаний была постоянной.
Источники, удовлетворяющие этим условиям, называются когерентными. Когерентными называют и созданные ими волны. Только при сложении когерентных волн образуется устойчивая интерференционная картина.
Если же разность фаз колебаний источников не остается постоянной, то в любой точке среды разность фаз колебаний, возбуждаемых двумя волнами, будет меняться. Поэтому амплитуда результирующих колебаний с течением времени изменяется. В результате максимумы и минимумы перемещаются в пространстве и интерференционная картина размывается.
Распределение энергии при интерференции. Волны несут энергию. Что же с этой энергией происходит при гашении волн друг другом? Может быть, она превращается в другие формы и в минимумах интерференционной картины выделяется тепло? Ничего подобного. Наличие минимума в данной точке интерференционной картины означает, что энергия сюда не поступает совсем. Вследствие интерференции происходит перераспределение энергии в пространстве. Она не распределяется равномерно по всем частицам среды, а концентрируется в максимумах за счет того, что в минимумы не поступает совсем.
ИНТЕРФЕРЕНЦИЯ СВЕТОВЫХ ВОЛН
Если свет представляет собой поток волн, то должно наблюдаться явление интерференции света. Однако получить интерференционную картину (чередование максимумов и минимумов освещенности) с помощью двух независимых источников света, например двух электрических лампочек, невозможно. Включение еще одной лампочки лишь увеличивает освещенность поверхности, но не создает чередования минимумов и максимумов освещенности.
Выясним, в чем причина этого и при каких условиях можно наблюдать интерференцию света.
Условие когерентности световых волн. Причина состоит в том, что световые волны, излучаемые различными источниками, не согласованы друг с другом. Для получения же устойчивой интерференционной картины нужны согласованные волны. Они должны иметь одинаковые длины волн и постоянную разность фаз в любой точке пространства. Напомним, что такие согласованные волны с одинаковыми длинами волн и постоянной разностью фаз называются когерентными.
Почти точного равенства длин волн от двух источников добиться нетрудно. Для этого достаточно использовать хорошие светофильтры, пропускающие свет в очень узком интервале длин волн. Но невозможно осуществить Постоянство разности фаз от двух независимых источников. Атомы источников излучают свет независимо друг от друга отдельными «обрывками» (цугами) синусоидальных волн, имеющими длину около метра. И такие цуги волн от обоих источников налагаются друг на друга. В результате амплитуда колебаний в любой точке пространства хаотически меняется со временем в зависимости от того, как в данный момент времени цуги волн от различных источников сдвинуты друг относительно друга по фазе. Волны от различных источников света некогерентны из-за того, что разность фаз волн не остается постоянной. Никакой устойчивой картины с определенным распределением максимумов и минимумов освещенности в пространстве не наблюдается.
Интерференция в тонких пленках. Тем не менее интерференцию света удается наблюдать. Курьез состоит в том, что ее наблюдали очень давно, но только не отдавали себе в этом отчета.
Вы тоже много раз видели интерференционную картину, когда в детстве развлекались пусканием мыльных пузырей или наблюдали за радужным переливом цветов тонкой пленки керосина или нефти на поверхности воды. «Мыльный пузырь, витая в воздухе. зажигается всеми оттенками цветов, присущими окружающим предметам. Мыльный пузырь, пожалуй, самое изысканное чудо природы» (Марк Твен). Именно интерференция света делает мыльный пузырь столь достойным восхищения.
Английский ученый Томас Юнг первым пришел к гениальной мысли о возможности объяснения цветов тонких пленок сложением волн 1 и 2 (рис. 123), одна из которых (1) отражается от наружной поверхности пленки, а вторая (2) —от внутренней. При этом происходит интерференция световых волн — сложение двух волн, вследствие которого наблюдается устойчивая во времени картина усиления или ослабления результирующих световых колебаний в различных точках пространства. Результат интерференции (усиление или ослабление результирующих колебаний) зависит от угла падения света на пленку, ее толщины и длины волны. Усиление света произойдет в том случае, если преломленная волна 2 отстанет от отраженной волны 1 на целое число длин волн. Если же вторая волна отстанет от первой на половину длины волны или на нечетное число полуволн, то произойдет ослабление света.
Когерентность волн, отраженных от наружной и внутренней поверхностей пленки, обеспечивается тем, что они являются частями одного и того же светового пучка. Цуг волн от каждого излучающего атома разделяется пленкой на два, а затем эти части сводятся вместе и интерферируют.
Юнг также понял, что различие в цвете связано с различием в длине волны (или частоте световых волн). Световым пучкам различного цвета соответствуют волны различной длины. Для взаимного усиления волн, отличающихся друг от друга длиной (углы падения предполагаются одинаковыми), требуется различная толщина пленки. Следовательно, если пленка имеет неодинаковую толщину, то при освещении ее белым светом должны появиться различные цвета.
Кольца Ньютона. Простая интерференционная картина возникает в тонкой прослойке воздуха между стеклянной пластиной и положенной на нее плоско-выпуклой линзой, сферическая поверхность которой имеет большой радиус кривизны. Эта интерференционная картина имеет вид концентрических колец, получивших название кольца Ньютона.
Возьмите плоско-выпуклую линзу с малой кривизной сферической поверхности и положите ее на стеклянную пластину. Внимательно разглядывая плоскую поверхность линзы (лучше через лупу), вы обнаружите в месте соприкосновения линзы и пластины темное пятно и вокруг него совокупность маленьких радужных колец. Расстояния между соседними кольцами быстро убывают с увеличением их радиуса (рис.111). Это и есть кольца Ньютона. Ньютон наблюдал и исследовал их не только в белом свете, но и при освещении линзы одноцветным (монохроматическим) пучком. Оказалось, что радиусы колец одного и того же порядкового номера увеличиваются при переходе от фиолетового конца спектра к красному; красные кольца имеют максимальный радиус . Все это вы можете проверить с помощью самостоятельных наблюдений.
Удовлетворительно объяснить, почему возникают кольца, Ньютон не смог. Удалось это Юнгу. Проследим за ходом его рассуждений. В их основе лежит предположение о том, что свет — это волны. Рассмотрим случай, когда волна определенной длины падает почти перпендикулярно на плоско-выпуклую линзу (рис. 124). Волна 1 появляется в результате отражения от выпуклой поверхности линзы на границе стекло — воздух, а волна 2 — в результате отражения от пластины на границе воздух — стекло. Эти волны когерентны: они имеют одинаковую длину и постоянную разность фаз, которая возникает из-за того, что волна 2 проходит больший путь, чем волна 1. Если вторая волна отстает от первой на целое число длин волн, то, складываясь, волны усиливают друг друга. Вызываемые ими колебания происходят в одной фазе.
Напротив, если вторая волна отстает от первой на нечетное число полуволн, то колебания, вызванные ими, будут происходить в противоположных фазах и волны гасят друг друга.
Если известен радиус кривизны R поверхности линзы, то можно вычислить, на каких расстояниях от точки соприкосновения линзы со стеклянной пластиной разности хода таковы, что волны определенной длины λ гасят друг друга. Эти расстояния и являются радиусами темных колец Ньютона. Ведь линии постоянной толщины воздушной прослойки представляют собой окружности. Измерив радиусы колец, можно вычислить длины волн.
Длина световой волны. Для красного света измерения дают λкр = 8•10 -7 м, а для фиолетового — λф = 4•10 -7 м. Длины волн, соответствующие другим цветам спектра, принимают промежуточные значения. Для любого цвета длина световой волны очень мала. Представьте себе среднюю морскую волну длиной в несколько метров, которая увеличилась настолько, что заняла весь Атлантический океан от берегов Америки до Европы. Длина световой волны в том же увеличении лишь ненамного превысила бы ширину этой страницы.
Явление интерференции не только доказывает наличие у света волновых свойств, но и позволяет измерить длину волны. Подобно тому как высота звука определяется его частотой, цвет света определяется частотой колебаний или длиной волны.
Вне нас в природе нет никаких красок, есть лишь волны разной длины. Глаз — сложный физический прибор, способный обнаруживать различие в цвете, которому соответствует весьма незначительная (около 10 -6 см) разница в длине световых волн. Интересно, что большинство животных неспособны различать цвета. Они всегда видят чернобелую картину. Не различают цвета также дальтоники — люди, страдающие цветовой слепотой.
При переходе света из одной среды в другую длина волны изменяется. Это можно обнаружить так. Заполним водой или другой прозрачной жидкостью с показателем преломления п воздушную прослойку между линзой и пластиной. Радиусы интерференционных колец уменьшатся.
Почему это происходит? Мы знаем, что при переходе света из вакуума в какую-нибудь среду скорость света уменьшается в n раз. Так как v = λv, то при этом должна уменьшиться в n раз либо частота, либо длина волны. Но радиусы колец зависят от длины волны. Следовательно, когда свет входит в среду, изменяется в n раз именно длина волны, а не частота.
Интерференция электромагнитных волн. На опытах с генератором СВЧ можно наблюдать интерференцию электромагнитных (радио) волн.
Генератор и приемник располагают друг против друга (рис. 125). Затем подводят снизу металлическую пластину в горизонтальном положении. Постепенно поднимая пластину, обнаруживают поочередное ослабление и усиление звука.
Явление объясняется следующим образом. Часть волны из рупора генератора непосредственно попадает в приемный рупор. Другая же ее часть отражается от металлической пластины. Меняя расположение пластины, мы изменяем разность хода прямой и отраженной волн. Вследствие этого волны либо усиливают, либо ослабляют друг друга в зависимости от того, равна ли разность хода целому числу длин волн или нечетному числу полуволн.
Наблюдение интерференции света доказывает, что свет при распространении обнаруживает волновые свойства. Интерференционные опыты позволяют измерить длину световой волны: она очень мала—от 4•10 -7 до 8•10 -7 м.
Кольца Ньютона
Если плосковыпуклую линзу малой кривизны положить выпуклой поверхностью на хорошо отполированную плоскую стеклянную пластинку, то между линзой и пластинкой образуется воздушная прослойка, утолщающаяся от точки соприкосновения к краям. Если на эту систему падает свет, то части одной и той же световой волны, отраженные от границ воздушной прослойки, будут интерферировать между собой. При этом наблюдается система концентрических радужных (немонохроматический свет) или чередующихся темных и светлых (монохроматический свет) колец. Кольца Ньютона являются классическим примером полос равной толщины. Они наблюдаются и в проходящем, и в отраженном свете, причем каждому темному кольцу в отраженном свете соответствует светлое кольцо в проходящем свете. В отраженном свете картина интерференции значительно контрастнее по сравнению с картиной интерференции в проходящем свете. Кольца Ньютона представляют собой частный случай интерференции в тонких пленках. Интерферирующие лучи приобретают разность хода в воздушном зазоре между плосковыпуклой линзой радиуса кривизны $R$ и плоскопараллельной пластинкой, на которую положена линза. Картина интерференции представляет собой ряд чередующихся светлых и темных колец при нормальном падении монохроматического света на линзу.
Задача 1. Установка для получения колец Ньютона освещается падающим нормально монохроматическим светом. Радиус четвертого темного кольца, наблюдаемого в отраженном свете, равен 4 мм. Найдите длину волны падающего света в нм, если радиус кривизны линзы $R=8$ м.
Свет проходит через линзу, преломляется и в очень узком воздушном промежутке между линзой и подложкой интерферирует, почему и появляются кольца Ньютона. Воздушный клин, на котором происходит интерференция, в случае, когда радиус кривизны линзы велик, имеет очень малый угол. Поэтому с большой степенью точности можно считать, что клин составлен из отдельных кусочков плоскопараллельных пластинок, и для каждого такого кусочка, характеризуемого своей толщиной $h$, применять формулу для разности хода интерферирующих лучей:
Определим $h$ по теореме Пифагора:
Пренебрежем величиной $h^2$ – она очень мала, и тогда
Чтобы соблюдалось условие минимума освещенности, должно выполняться
Подставим ранее полученное выражение:
Ответ: $lambda=5cdot10^$, 500 нм.
Задача 2. Установка для получения колец Ньютона освещается светом с длиной волны $lambda = 589$ нм, падающим по нормали к поверхности пластинки. Радиус кривизны линзы $R= 10$ м. Пространство между линзой и стеклянной пластинкой заполнено жидкостью. Найти показатель преломления $n$ жидкости, если радиус третьего светлого кольца в проходящем свете $r_3= 3,65$ мм.
Так как радиус светлого кольца в проходящем свете соответствует радиусу темного в отраженном, то можно записать, что
Однако один из лучей проходит через жидкость, в которой его длина волны становится меньше в $n$ раз, поэтому
Задача 3. Выпуклая линза с большим радиусом кривизны $R$ лежит на плоскопараллельной стеклянной пластинке и освещается нормально падающим параллельным пучком монохроматического света с длиной волны $lambda$. В воздушном зазоре между соприкасающимися поверхностями линзы и пластинки в отраженном свете наблюдаются кольца Ньютона. Найти радиусы темных колец.
Решение этой задачи аналогично первой.
Осталось подставить номер кольца.
Задача 4. Установка для получения колец Ньютона освещается падающим нормально монохроматическим светом. Радиус кривизны линзы 15 м. Наблюдение ведется в отраженном свете. Расстояние между пятым и двадцать пятым светлыми кольцами Ньютона равно 9 мм. Найти длину волны монохроматического света.
Определим радиус светлого кольца в отраженном свете. Применим формулу для разности хода интерферирующих лучей:
Определим $h$ по теореме Пифагора:
Пренебрежем величиной $h^2$ – она очень мала, и тогда
Чтобы соблюдалось условие максимума освещенности, должно выполняться
Подставим ранее полученное выражение:
Обобщая информацию, сведем все в таблицу:
Радиусы колец Ньютона
Теперь решим задачу. Нам известно, что
Откуда и найдем длину волны света:
Ответ: $lambda=675$ нм.
Задача 5. Установка для получения колец Ньютона освещается монохроматическим светом, падающим параллельно главной оптической оси линзы. Радиусы двух соседних темных колец равны 4,0 мм и 4,38 мм. Радиус кривизны линзы 6,4 м. Найдите порядковые номера колец и длину волны падающего света.
Радиус темных колец определяется формулой
Тогда следующее кольцо имеет радиус
А отношение радиусов будет равно
Тогда порядковый номер второго кольца – 6. А длина волны
Ответ: порядковые номера колец – 5 и 6, длина волны $lambda=500$ нм.
Глава6. Оптика (§ 28-33) >> §30 Интерференция света >> задача – 30.28
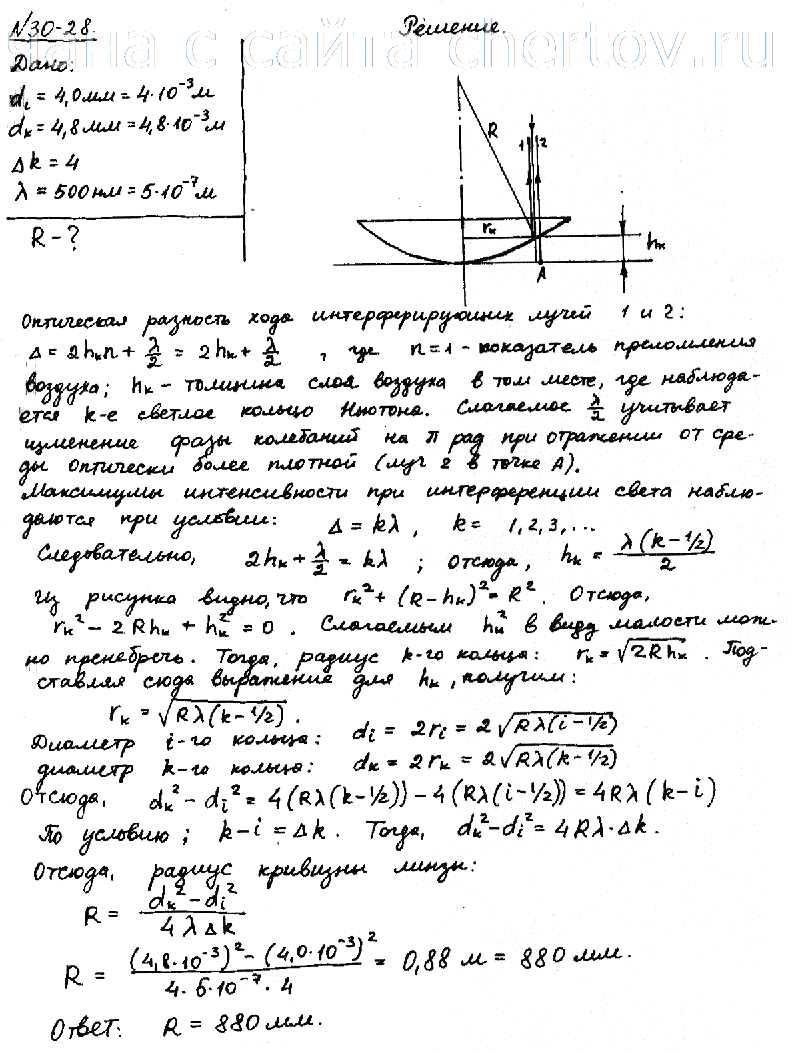
Условие:
Диаметры di и dk двух светлых колец Ньютона соответственно равны 4,0 и 4,8 мм. Порядковые номера колец не определялись, но известно, что между двумя измеренными кольцами расположено три светлых кольца. Кольца наблюдались в отраженном свете (L=500 нм). Найти радиус кривизны плосковыпуклой линзы, взятой для опыта.
При клике на картинку откроется ее увеличенная версия в новой вкладке.
Не забываем поделиться записью!
Кольца Ньютона
Простая интерференционная картина возникает в тонкой прослойке воздуха между стеклянной пластиной и положенной на нее плоско-выпуклой линзой, сферическая поверхность которой имеет большой радиус кривизны. Эта интерференционная картина имеет вид концентрических колец, получивших название кольца Ньютона.
Кольца Ньютона
Возьмите плоско-выпуклую линзу с малой кривизной сферической поверхности и положите ее на стеклянную пластину, как было указано выше. Внимательно разглядывая плоскую поверхность линзы (лучше через лупу), вы обнаружите в месте соприкосновения линзы и пластины темное пятно и вокруг него совокупность маленьких радужных колец. Расстояния между соседними кольцами быстро убывают с увеличением их радиуса. Это и есть кольца Ньютона. Ньютон наблюдал и исследовал их не только в белом свете, но и при освещении линзы одноцветным (монохроматическим) пучком. Оказалось, что радиусы колец одного и того же порядкового номера увеличиваются при переходе от фиолетового конца спектра к красному; красные кольца имеют максимальный радиус. Все это вы можете проверить с помощью самостоятельных наблюдений.
Кольца Ньютона
Но объяснить, почему возникают кольца Ньютон не смог. Удалось это Юнгу. Проследим за ходом его рассуждений. В их основе лежит предположение о том, что свет – это волны. Рассмотрим случай, когда волна определенной длины падает почти перпендикулярно на плоско-выпуклую линзу. Волна 1 появляется в результате отражения от выпуклой поверхности линзы на границе стекло – воздух, а волна 2 – в результате отражения от пластины на границе воздух – стекло. Эти волны когерентны: они имеют одинаковую длину и постоянную разность фаз, которая возникает из-за того, что волна 2 проходит больший путь, чем волна 1. Если вторая волна отстает от первой на целое число длин волн, то, складываясь, волны усиливают друг друга. Вызываемые ими колебания происходят в одной фазе.
Кольца Ньютона
Напротив, если вторая волна отстанет от первой на нечетное число полуволн, то колебания, вызванные ими, будут происходить в противоположных фазах и волны гасят друг друга.
Если известен радиус кривизны R поверхности линзы, то можно вычислить, на каких расстояниях от точки соприкосновения линзы со стеклянной пластиной разности хода таковы, что волны определенной длины λ гасят друг друга. Эти расстояния и являются радиусами темных колец Ньютона. Ведь линии постоянной толщины воздушной прослойки представляют собой окружности. Измерив, радиусы колец, можно вычислить длины волн.
Кольца Ньютона в отражённом свете
Длина световой волны
Длина световой волны. Для красного света измерения дают λ = 8∙10-7 м, а для фиолетового – λ = 4∙10-7 м. Длины волн, соответствующие другим цветам спектра, принимают промежуточные значения. Для любого цвета длина световой волны очень мала. Представьте себе среднюю морскую волну длиной в несколько метров, которая увеличилась настолько, что заняла весь Атлантический океан от берегов Америки до Европы. Длина световой волны в том же увеличении лишь ненамного превысила бы ширину этой страницы.
Явление интерференции не только доказывает наличие у света волновых свойств, но и позволяет измерить длину волны. Подобно тому, как высота звука определяется его частотой, цвет света определяется частотой колебаний или длиной волны.
Вне нас в природе нет никаких красок, есть лишь волны разной длины. Глаз – сложный физический прибор, способный обнаруживать различие в цвете, которому соответствует весьма незначительная (около 10-6 см) разница в длине световых волн. Интересно, что большинство животных не способны различать цвета. Они всегда видят черно-белую картину.
При переходе света из одной среды в другую длина волны изменяется. Это можно обнаружить так. Заполним водой или другой прозрачной жидкостью с показателем преломления п воздушную прослойку между линзой и пластиной. Радиусы интерференционных колец уменьшатся.
Почему это происходит? Мы знаем, что при переходе света из вакуума в какую-нибудь среду скорость света уменьшается в п раз. Так как v=λv, то при этом должна уменьшиться в п раз либо частота, либо длина волны. Но радиусы колец зависят от длины волны. Следовательно, когда свет входит в среду, изменяется в п раз именно длина волны, а не частота.