По поводу первой задачи: общее правило здесь такое. Если абелева группа имеет порядок $%n=p_1^{k_1}ldots p_r^{k_r}$% (число представлено в виде канонического разложения), то она разложима в прямое произведение подгрупп порядков $%p_1^{k_1}$%, … , $%p_r^{k_r}$% соответственно. Для каждого числа вида $%p^k$% надо подсчитать число абелевых групп с точностью до изоморфизма, а затем полученные числа перемножить.
Пункт а) тривиален. В пункте б) получается одна группа $%mathbb Z_2timesmathbb Z_3$%, изоморфная $%mathbb Z_6$%. В пункте в) случаев три: это $%mathbb Z_8$%, $%mathbb Z_4timesmathbb Z_2$%, $%mathbb Z_2timesmathbb Z_2timesmathbb Z_2$% (они попарно неизоморфны).
Здесь можно заметить, что число попарно неизоморфных абелевых групп порядка $%p^k$%, где $%p$% простое, равно количеству способов представить число $%k$% в виде суммы одного или нескольких натуральных слагаемых (от $%p$% оно не зависит). Скажем, для числа $%2^3$% получается три способа: 3, 2+1, 1+1+1 (порядок слагаемых роли не играет). Обозначим это число через $%f(k)$%.
В пункте г) число групп равно $%f(2)f(1)=2$% за счёт того, что $%12=2^2cdot3^1$%.
В пункте д) получится $%f(4)=5$% за счёт способов 4; 3+1; 2+2; 2+1+1; 1+1+1+1. Этим суммам соответствуют группы $%mathbb Z_{16}$%, $%mathbb Z_8timesmathbb Z_2$%, $%mathbb Z_4timesmathbb Z_4$%, $%mathbb Z_4timesmathbb Z_2timesmathbb Z_2$%, $%mathbb Z_2timesmathbb Z_2timesmathbb Z_2timesmathbb Z_2$%.
Для остальных пунктов всё аналогично: е) 3; ж) 4; з) 5.
Вторая из задача уже была здесь.
У этого термина существуют и другие значения, см. Группа.
А́белева (или коммутати́вная) гру́ппа — группа, в которой групповая операция является коммутативной; иначе говоря, группа 


Обычно для обозначения групповой операции в абелевой группе используется аддитивная запись, то есть групповая операция обозначается знаком 
Название дано в честь норвежского математика Нильса Абеля.
Примеры[править | править код]
Связанные определения[править | править код]
- По аналогии с размерностью у векторных пространств, каждая абелева группа имеет ранг. Он определяется как минимальная размерность векторного пространства над полем
рациональных чисел, в которое вкладывается фактор группы по её кручению.
Свойства[править | править код]
- Конечно порождённые абелевы группы изоморфны прямым суммам циклических групп.
- Конечные абелевы группы изоморфны прямым суммам конечных циклических групп.
- Любая абелева группа имеет естественную структуру модуля над кольцом целых чисел. Действительно, пусть
— натуральное число, а
— элемент коммутативной группы
с операцией, обозначаемой +, тогда
можно определить как
(
раз) и
.
- Утверждения и теоремы, верные для абелевых групп (то есть модулей над областью главных идеалов
), зачастую могут быть обобщены на модули над произвольной областью главных идеалов. Типичным примером является классификация конечнопорождённых абелевых групп, которую можно обобщить до классификации произвольных конечнопорождённых модулей над областью главных идеалов.
- Утверждения и теоремы, верные для абелевых групп (то есть модулей над областью главных идеалов
- Множество гомоморфизмов
всех групповых гомоморфизмов из
в
само является абелевой группой. Действительно, пусть
— два гомоморфизма групп между абелевыми группами, тогда их сумма
, заданная как
, тоже является гомоморфизмом (это неверно, если
не является коммутативной группой).
- Понятие абелевости тесно связано с понятием центра
группы
— множества, состоящего из тех её элементов, которые коммутируют с каждым элементом группы
, и играющего роль своеобразной «меры абелевости». Группа абелева тогда и только тогда, когда её центр совпадает со всей группой.
Конечные абелевы группы[править | править код]
Основополагающая теорема о структуре конечной абелевой группы утверждает, что любая конечная абелева группа может быть разложена в прямую сумму своих циклических подгрупп, порядки которых являются степенями простых чисел. Это следствие общей теоремы о структуре конечнопорождённых абелевых групп для случая, когда группа не имеет элементов бесконечного порядка.





Следовательно, можно записать абелеву группу 
двумя различными способами:
Например, 

Вариации и обобщения[править | править код]
- Дифференциальной группой называется абелева группа
, в которой задан такой эндоморфизм
, что
. Этот эндоморфизм называется дифференциалом. Элементы дифференциальных групп называются цепями, элементы ядра
— циклами, элементы образа
— границами.
- Кольцо — абелева группа, на которой задана дополнительная бинарная операция «умножения», удовлетворяющая аксиомам дистрибутивности.
- Метабелева группа — группа, коммутант которой абелев.
- Нильпотентная группа — группа, центральный ряд которой конечен.
- Разрешимая группа — группа, ряд коммутантов которой стабилизируется на тривиальной группе.
- Дедекиндова группа — группа, всякая подгруппа которой нормальна.
См. также[править | править код]
- Алгебраическая система
Примечания[править | править код]
- ↑ Абелева группа — статья из Математической энциклопедии. Ю. Л. Ершов
Литература[править | править код]
- Винберг Э. Б. Курс алгебры. — 3-е изд. — М.: Факториал Пресс, 2002. — 544 с. — 3000 экз. — ISBN 5-88688-060-7..
- Фукс Л. Бесконечные абелевы группы. — Мир, 1974.

|
Теория групп |
6 |
|||||||
|
D3 |
E |
R120 |
R240 |
R1 |
R2 |
R3 |
||
|
E |
E |
R120 |
R240 |
R1 |
R2 |
R3 |
||
|
R120 |
R120 |
R240 |
E |
R2 |
R3 |
R1 |
||
|
R240 |
R240 |
E |
R120 |
R3 |
R1 |
R2 |
||
|
R1 |
R1 |
R3 |
R2 |
E |
R240 |
R120 |
||
|
R2 |
R2 |
R1 |
R3 |
R120 |
E |
R240 |
||
|
R3 |
R3 |
R2 |
R1 |
R240 |
R120 |
E |
||
•Совокупность всех вращений относительно одной оси образуют непрерывную группу, называемую R2. Её элементы обозначим символами R(a), где a — угол поворота, находящийся в пределах 0 ≤ a < 360°. Для
этой группы таблица умножения бесконечна, поэтому группа описывается общей формулой
Поскольку результат двух последовательных поворотов вокруг одной оси не зависит от порядка поворотов, группа R2 является коммутативной. Обратный элемент в группе определеяется формулой
•Группа R3 представляет собой группу всевозможных вращений трёхмерного пространства относительно осей, проходящих через одну точку. Эта группа является группой симметрии сферы. Каждый элемент
группы R(α,β,a) задаётся тремя параметрами: α и β — эйлеровы углы, задающие положение оси, a — угол поворота.
•Группа Sn или симметрическая группа порядка n — это совокупность n! всевозможных перестановок n элементов. Перестановку удобно обозначать символом
указывающим, что элемент n при перестановке заменяется на элемент pn. Обратным элементом для элемента P будет элемент
Интересно, что группа S3 изоморфна группе D3, так как последняя содержит всевозможные преобразования, переводящие треугольник сам в себя, а преобразование треугольника можно задать различными перестановками трёх его вершин:
Абелевы группы
Абелева группа есть группа, в которой групповая операция является коммутативной; то есть группа абелева если  для любых двух элементов
для любых двух элементов  .
.
Групповая операция в абелевых группах обычно называется «сложением» и обозначается знаком 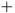 . Абелевы группы являются основой для построения более сложных объектов абстрактной алгебры, таких как кольца, поля и модули. Название дано в честь норвежского математика Абеля за его вклад в исследование групп подстановок.
. Абелевы группы являются основой для построения более сложных объектов абстрактной алгебры, таких как кольца, поля и модули. Название дано в честь норвежского математика Абеля за его вклад в исследование групп подстановок.

Примеры
•Группа параллельных переносов в линейном пространстве.
•Любая циклическая группа  . Действительно, для любых
. Действительно, для любых  и
и 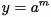 верно, что
верно, что
.
•В частности, целые числа  образуют коммутативную группу по сложению, также как и классы вычетов
образуют коммутативную группу по сложению, также как и классы вычетов
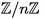 .
.
•Любое кольцо является коммутативной (абелевой) группой по своему сложению. В том числе и вещественные числа с операцией сложения.
•Обратимые элементы коммутативного кольца, в частности, ненулевые элементы любого поля, образуют абелеву группу по умножению. Например, вещественные числа, не равные нулю, с операцией умножения.
Связанные определения
•По аналогии с размерностью у векторных пространств, каждая абелева группа имеет ранг. Он определяется как минимальная размерность пространства над полем рациональных чисел, в которое вкладывается фактор группы по её кручению.
Свойства
•Конечнопорождённые абелевы группы изоморфны прямым суммам циклических групп.
•Конечные абелевы группы изоморфны прямым суммам конечных циклических групп.
•Любая абелева группа имеет естественную структуру модуля над кольцом целых чисел. Действительно,
пусть  — натуральное число, а
— натуральное число, а  — элемент коммутативной группы
— элемент коммутативной группы  с операцией, обозначаемой +, тогда
с операцией, обозначаемой +, тогда  можно определить как
можно определить как  (
(  раз) и
раз) и 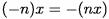 .
.
•Утверждения и теоремы, верные для абелевых групп (то есть модулей над кольцом главных идеалов  ), зачастую могут быть обобщены на модули над произвольным кольцом главных идеалов. Типичным
), зачастую могут быть обобщены на модули над произвольным кольцом главных идеалов. Типичным
примером является классификация конечнопорожденных абелевых групп.
•Множество гомоморфизмов  всех групповых гомоморфизмов из
всех групповых гомоморфизмов из  в
в  само является абелевой группой. Действительно, пусть
само является абелевой группой. Действительно, пусть  — два гомоморфизма групп между абелевыми группами, тогда их сумма
— два гомоморфизма групп между абелевыми группами, тогда их сумма  , заданная как
, заданная как  , тоже является гомоморфизмом (это неверно, если
, тоже является гомоморфизмом (это неверно, если  некоммутативная группа).
некоммутативная группа).
Конечные абелевы группы
Основополагающая теорема о структуре конечной абелевой группы утверждает, что любая конечная абелева группа может быть разложена в прямую сумму своих циклических подгрупп, порядки которых являются степенями простых чисел. Это следствие общей теоремы о структуре конечнопорождённых абелевых групп для случая, когда группа не имеет элементов бесконечного порядка.  изоморфно прямой сумме
изоморфно прямой сумме  и
и  тогда и только тогда, когда
тогда и только тогда, когда  и
и  взаимно просты.
взаимно просты.
Следовательно, можно записать абелеву группу  в форме прямой суммы
в форме прямой суммы
двумя различными способами:
•Где числа  степени простых
степени простых
•Где  делит
делит  , которое делит
, которое делит  , и так далее до
, и так далее до  .
.
Например,  может быть разложено в прямую сумму двух циклических подгрупп порядков 3 и 5:
может быть разложено в прямую сумму двух циклических подгрупп порядков 3 и 5:  . То же можно сказать про любую абелеву группу порядка пятнадцать, приходим к выводу, что все абелевы группы порядка 15 изоморфны.
. То же можно сказать про любую абелеву группу порядка пятнадцать, приходим к выводу, что все абелевы группы порядка 15 изоморфны.
For the group described by the archaic use of the related term “Abelian linear group”, see Symplectic group.
In mathematics, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on the order in which they are written. That is, the group operation is commutative. With addition as an operation, the integers and the real numbers form abelian groups, and the concept of an abelian group may be viewed as a generalization of these examples. Abelian groups are named after early 19th century mathematician Niels Henrik Abel.[1]
The concept of an abelian group underlies many fundamental algebraic structures, such as fields, rings, vector spaces, and algebras. The theory of abelian groups is generally simpler than that of their non-abelian counterparts, and finite abelian groups are very well understood and fully classified.
Definition[edit]
An abelian group is a set 








- Associativity
- For all
,
, and
in
, the equation
holds.
- Identity element
- There exists an element
in
, such that for all elements
in
, the equation
holds.
- Inverse element
- For each
in
there exists an element
in
such that
, where
is the identity element.
- Commutativity
- For all
,
in
,
.
A group in which the group operation is not commutative is called a “non-abelian group” or “non-commutative group”.[2]: 11
Facts[edit]
Notation[edit]
There are two main notational conventions for abelian groups – additive and multiplicative.
| Convention | Operation | Identity | Powers | Inverse |
|---|---|---|---|---|
| Addition |  |
0 |  |

|
| Multiplication |  or or  |
1 | 
|

|
Generally, the multiplicative notation is the usual notation for groups, while the additive notation is the usual notation for modules and rings. The additive notation may also be used to emphasize that a particular group is abelian, whenever both abelian and non-abelian groups are considered, some notable exceptions being near-rings and partially ordered groups, where an operation is written additively even when non-abelian.[3]: 28–29
Multiplication table[edit]
To verify that a finite group is abelian, a table (matrix) – known as a Cayley table – can be constructed in a similar fashion to a multiplication table.[4]: 10 If the group is 



The group is abelian if and only if this table is symmetric about the main diagonal. This is true since the group is abelian iff 




Examples[edit]
- For the integers and the operation addition
, denoted
, the operation + combines any two integers to form a third integer, addition is associative, zero is the additive identity, every integer
has an additive inverse,
, and the addition operation is commutative since
for any two integers
and
.
- Every cyclic group
is abelian, because if
,
are in
, then
. Thus the integers,
, form an abelian group under addition, as do the integers modulo
,
.
- Every ring is an abelian group with respect to its addition operation. In a commutative ring the invertible elements, or units, form an abelian multiplicative group. In particular, the real numbers are an abelian group under addition, and the nonzero real numbers are an abelian group under multiplication.
- Every subgroup of an abelian group is normal, so each subgroup gives rise to a quotient group. Subgroups, quotients, and direct sums of abelian groups are again abelian. The finite simple abelian groups are exactly the cyclic groups of prime order.[5]: 32
- The concepts of abelian group and
-module agree. More specifically, every
-module is an abelian group with its operation of addition, and every abelian group is a module over the ring of integers
in a unique way.
In general, matrices, even invertible matrices, do not form an abelian group under multiplication because matrix multiplication is generally not commutative. However, some groups of matrices are abelian groups under matrix multiplication – one example is the group of 
[edit]
Camille Jordan named abelian groups after Norwegian mathematician Niels Henrik Abel, as Abel had found that the commutativity of the group of a polynomial implies that the roots of the polynomial can be calculated by using radicals.[6]: 144–145
Properties[edit]
If 









Theorems about abelian groups (i.e. modules over the principal ideal domain 



If 






Somewhat akin to the dimension of vector spaces, every abelian group has a rank. It is defined as the maximal cardinality of a set of linearly independent (over the integers) elements of the group.[8]: 49–50 Finite abelian groups and torsion groups have rank zero, and every abelian group of rank zero is a torsion group. The integers and the rational numbers have rank one, as well as every nonzero additive subgroup of the rationals. On the other hand, the multiplicative group of the nonzero rationals has an infinite rank, as it is a free abelian group with the set of the prime numbers as a basis (this results from the fundamental theorem of arithmetic).
The center 








Finite abelian groups[edit]
Cyclic groups of integers modulo 

Any group of prime order is isomorphic to a cyclic group and therefore abelian. Any group whose order is a square of a prime number is also abelian.[10] In fact, for every prime number 



Classification[edit]
The fundamental theorem of finite abelian groups states that every finite abelian group 
The classification was proven by Leopold Kronecker in 1870, though it was not stated in modern group-theoretic terms until later, and was preceded by a similar classification of quadratic forms by Carl Friedrich Gauss in 1801; see history for details.
The cyclic group 






in either of the following canonical ways:
For example, 

For another example, every abelian group of order 8 is isomorphic to either 


See also list of small groups for finite abelian groups of order 30 or less.
Automorphisms[edit]
One can apply the fundamental theorem to count (and sometimes determine) the automorphisms of a given finite abelian group 


Given this, the fundamental theorem shows that to compute the automorphism group of 





for some 
One special case is when 






so elements of this subgroup can be viewed as comprising a vector space of dimension 


where 
In the most general case, where the 

and
then one has in particular 

One can check that this yields the orders in the previous examples as special cases (see Hillar, C., & Rhea, D.).
Finitely generated abelian groups[edit]
An abelian group A is finitely generated if it contains a finite set of elements (called generators) 
Let L be a free abelian group with basis
There is a unique group homomorphism

This homomorphism is surjective, and its kernel is finitely generated (since integers form a Noetherian ring). Consider the matrix M with integer entries, such that the entries of its jth column are the coefficients of the jth generator of the kernel. Then, the abelian group is isomorphic to the cokernel of linear map defined by M. Conversely every integer matrix defines a finitely generated abelian group.
It follows that the study of finitely generated abelian groups is totally equivalent with the study of integer matrices. In particular, changing the generating set of A is equivalent with multiplying M on the left by a unimodular matrix (that is, an invertible integer matrix whose inverse is also an integer matrix). Changing the generating set of the kernel of M is equivalent with multiplying M on the right by a unimodular matrix.
The Smith normal form of M is a matrix
where U and V are unimodular, and S is a matrix such that all non-diagonal entries are zero, the non-zero diagonal entries 


where r is the number of zero rows at the bottom of r (and also the rank of the group). This is the fundamental theorem of finitely generated abelian groups.
The existence of algorithms for Smith normal form shows that the fundamental theorem of finitely generated abelian groups is not only a theorem of abstract existence, but provides a way for computing expression of finitely generated abelian groups as direct sums.[12]: 26–27
Infinite abelian groups[edit]
The simplest infinite abelian group is the infinite cyclic group 





By contrast, classification of general infinitely generated abelian groups is far from complete. Divisible groups, i.e. abelian groups 














Two important special classes of infinite abelian groups with diametrically opposite properties are torsion groups and torsion-free groups, exemplified by the groups 

Torsion groups[edit]
An abelian group is called periodic or torsion, if every element has finite order. A direct sum of finite cyclic groups is periodic. Although the converse statement is not true in general, some special cases are known. The first and second Prüfer theorems state that if 






The cardinality of the set of direct summands isomorphic to 


Torsion-free and mixed groups[edit]
An abelian group is called torsion-free if every non-zero element has infinite order. Several classes of torsion-free abelian groups have been studied extensively:
An abelian group that is neither periodic nor torsion-free is called mixed. If 







Invariants and classification[edit]
One of the most basic invariants of an infinite abelian group 









The classification theorems for finitely generated, divisible, countable periodic, and rank 1 torsion-free abelian groups explained above were all obtained before 1950 and form a foundation of the classification of more general infinite abelian groups. Important technical tools used in classification of infinite abelian groups are pure and basic subgroups. Introduction of various invariants of torsion-free abelian groups has been one avenue of further progress. See the books by Irving Kaplansky, László Fuchs, Phillip Griffith, and David Arnold, as well as the proceedings of the conferences on Abelian Group Theory published in Lecture Notes in Mathematics for more recent findings.
Additive groups of rings[edit]
The additive group of a ring is an abelian group, but not all abelian groups are additive groups of rings (with nontrivial multiplication). Some important topics in this area of study are:
- Tensor product
- A.L.S. Corner’s results on countable torsion-free groups
- Shelah’s work to remove cardinality restrictions
- Burnside ring
Relation to other mathematical topics[edit]
Many large abelian groups possess a natural topology, which turns them into topological groups.
The collection of all abelian groups, together with the homomorphisms between them, forms the category 
Wanda Szmielew (1955) proved that the first-order theory of abelian groups, unlike its non-abelian counterpart, is decidable. Most algebraic structures other than Boolean algebras are undecidable.
There are still many areas of current research:
- Amongst torsion-free abelian groups of finite rank, only the finitely generated case and the rank 1 case are well understood;
- There are many unsolved problems in the theory of infinite-rank torsion-free abelian groups;
- While countable torsion abelian groups are well understood through simple presentations and Ulm invariants, the case of countable mixed groups is much less mature.
- Many mild extensions of the first-order theory of abelian groups are known to be undecidable.
- Finite abelian groups remain a topic of research in computational group theory.
Moreover, abelian groups of infinite order lead, quite surprisingly, to deep questions about the set theory commonly assumed to underlie all of mathematics. Take the Whitehead problem: are all Whitehead groups of infinite order also free abelian groups? In the 1970s, Saharon Shelah proved that the Whitehead problem is:
- Undecidable in ZFC (Zermelo–Fraenkel axioms), the conventional axiomatic set theory from which nearly all of present-day mathematics can be derived. The Whitehead problem is also the first question in ordinary mathematics proved undecidable in ZFC;
- Undecidable even if ZFC is augmented by taking the generalized continuum hypothesis as an axiom;
- Positively answered if ZFC is augmented with the axiom of constructibility (see statements true in L).
A note on typography[edit]
Among mathematical adjectives derived from the proper name of a mathematician, the word “abelian” is rare in that it is often spelled with a lowercase a, rather than an uppercase A, the lack of capitalization being a tacit acknowledgment not only of the degree to which Abel’s name has been institutionalized but also of how ubiquitous in modern mathematics are the concepts introduced by him.[18]
See also[edit]
- Commutator subgroup – Smallest normal subgroup by which the quotient is commutative
- Abelianization – Quotienting a group by its commutator subgroup
- Dihedral group of order 6 – Non-commutative group with 6 elements, the smallest non-abelian group
- Elementary abelian group – Commutative group in which all nonzero elements have the same order
- Grothendieck group – Abelian group extending a commutative monoid
- Pontryagin duality – Duality for locally compact abelian groups
Notes[edit]
- ^ Jacobson (2009) p. 41
- ^ Ramík, J., Pairwise Comparisons Method: Theory and Applications in Decision Making (Cham: Springer Nature Switzerland, 2020), p. 11.
- ^ Auslander, M., & Buchsbaum, D., Groups, Rings, Modules (Mineola, NY: Dover Publications, 1974), pp. 28–29.
- ^ Isaev, A. P., & Rubakov, V. A., Theory of Groups and Symmetries: Finite Groups, Lie Groups, and Lie Algebras (Singapore: World Scientific, 2018), p. 10.
- ^ Rose 2012, p. 32.
- ^ Cox, D. A., Galois Theory (Hoboken, New Jersey: John Wiley & Sons, 2004), pp. 144–145.
- ^ Eklof, Paul C., & Göbel, Rüdiger, eds., Abelian Groups and Modules: International Conference in Dublin, August 10–14, 1998 (Basel: Springer Basel AG, 1999), pp. 94–97.
- ^ Dixon, M. R., Kurdachenko, L. A., & Subbotin, I. Y., Linear Groups: The Accent on Infinite Dimensionality (Milton Park, Abingdon-on-Thames & Oxfordshire: Taylor & Francis, 2020), pp. 49–50.
- ^ Rose 2012, p. 48.
- ^ Rose 2012, p. 79.
- ^ Kurzweil, H., & Stellmacher, B., The Theory of Finite Groups: An Introduction (New York, Berlin, Heidelberg: Springer Verlag, 2004), pp. 43–54.
- ^ Finkelstein, L., & Kantor, W. M., eds., Groups and Computation II: Workshop on Groups and Computation, June 7–10, 1995 (Providence: AMS, 1997), pp. 26–27.
- ^ For example,
.
- ^ Countability assumption in the second Prüfer theorem cannot be removed: the torsion subgroup of the direct product of the cyclic groups
for all natural
is not a direct sum of cyclic groups.
- ^ Faith, C. C., Rings and Things and a Fine Array of Twentieth Century Associative Algebra (Providence: AMS, 2004), p. 6.
- ^ Albrecht, U., “Products of Slender Abelian Groups”, in Göbel, R., & Walker, E., eds., Abelian Group Theory: Proceedings of the Third Conference Held on Abelian Group Theory at Oberwolfach, August 11-17, 1985 (New York: Gordon & Breach, 1987), pp. 259–274.
- ^ Lal, R., Algebra 2: Linear Algebra, Galois Theory, Representation Theory, Group Extensions and Schur Multiplier (Berlin, Heidelberg: Springer, 2017), p. 206.
- ^ “Abel Prize Awarded: The Mathematicians’ Nobel”. Archived from the original on 31 December 2012. Retrieved 3 July 2016.
References[edit]
- Cox, David (2004). Galois Theory. Wiley-Interscience. ISBN 9781118031339. MR 2119052.
- Fuchs, László (1970). Infinite Abelian Groups. Pure and Applied Mathematics. Vol. 36-I. Academic Press. MR 0255673.
- Fuchs, László (1973). Infinite Abelian Groups. Pure and Applied Mathematics. Vol. 36-II. Academic Press. MR 0349869.
- Griffith, Phillip A. (1970). Infinite Abelian group theory. Chicago Lectures in Mathematics. University of Chicago Press. ISBN 0-226-30870-7.
- Herstein, I. N. (1975). Topics in Algebra (2nd ed.). John Wiley & Sons. ISBN 0-471-02371-X.
- Hillar, Christopher; Rhea, Darren (2007). “Automorphisms of finite abelian groups” (PDF). American Mathematical Monthly. 114 (10): 917–923. arXiv:math/0605185. Bibcode:2006math……5185H. doi:10.1080/00029890.2007.11920485. JSTOR 27642365. S2CID 1038507.
- Jacobson, Nathan (2009). Basic Algebra I (2nd ed.). Dover Publications. ISBN 978-0-486-47189-1.
- Rose, John S. (2012). A Course on Group Theory. Dover Publications. ISBN 978-0-486-68194-8. Unabridged and unaltered republication of a work first published by the Cambridge University Press, Cambridge, England, in 1978.
- Szmielew, Wanda (1955). “Elementary Properties of Abelian Groups” (PDF). Fundamenta Mathematicae. 41 (2): 203–271. doi:10.4064/fm-41-2-203-271. MR 0072131. Zbl 0248.02049.
- Robinson, Abraham; Zakon, Elias (1960). “Elementary Properties of Ordered Abelian Groups” (PDF). Transactions of the American Mathematical Society. 96 (2): 222–236. doi:10.2307/1993461. JSTOR 1993461. Archived (PDF) from the original on 2022-10-09.
External links[edit]
- “Abelian group”. Encyclopedia of Mathematics. EMS Press. 2001 [1994].















