§
1. Сравнение бесконечно малых функций
Определение
1.1. Пусть
функции α(x)
и β(x)
являются
бесконечно малыми при х а.
а.
-
Если
существует
 ,
,
то α(x)
и β(x)
называются бесконечно малыми одного
порядка при х а.
а.
-
Если
существует
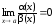 ,
,
то α(x)
называется величиной более высокого
порядка малости, чем β(x)
при х а.
а.
Обозначение:
α(x) = o(β(x))
при х а
а
(α(x)
есть о малое
от β(x)).
-
Если
не существует
 ,
,
то бесконечно малые α(x)
и β(x)
называются несравнимыми при х а.
а.
Например,
sin 2x
2x
и

– бесконечно малые одного порядка при
х 0,
0,
так как
 .
.
Функция sin 2x
2x
имеет более
высокий порядок малости, чем х
при х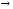 0
0
(или sin 2x=о(х)
2x=о(х)
при х 0),
0),
поскольку


Бесконечно малые

и α(x)
и β(x) = х
несравнимы при х 0,
0,
так как


а

не существует (это можно показать с
помощью определения предела функции
на языке последовательностей).
Замечание
1.1. Если
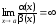 ,
,
то

Тогда β(x) = o(α(x))
при х а.
а.
Сравнить
две бесконечно малые функции – это
значит установить, что они являются
бесконечно малыми одного порядка, или
что одна из них более высокого порядка,
чем другая, или что они несравнимы. Для
этого надо найти предел их отношения,
т.е. раскрыть неопределённость
 .
.
Определение
1.2. Если
существует
 ,
,
то α(x)
и β(x)
называются эквивалентными бесконечно
малыми при х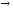 а.
а.
При
отыскании предела отношения бесконечно
малых α(x)
и β(x)
при

используется
теорема о замене эквивалентными в
отношении и таблица эквивалентных
бесконечно малых функций, так как для
α(x)
и β(x)
полезно найти эквивалентные бесконечно
малые простейшего вида С(х – а)k.
Таблица
эквивалентных бесконечно малых функций.
Пусть
функция

при
 .
.
Тогда
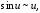

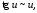
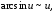



 .
.
Пример
1.1. Сравнить
бесконечно малые α(x) =
и β(x) =
при
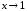 .
.
►α(x) = ~
~
 Þα(x)~
Þα(x)~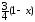
(здесь использована формула
 ,
,
где
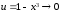
при
 ,
,
 ).
).
Имеем: β(x)= ~
~ =
=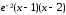 Þ
Þ ~
~ ,
,
здесь использована формула

где

при
 .
.
В результате применения теоремы о замене
эквивалентными в отношении получим:
 ¹0,
¹0,
∞. Поэтому заключаем, что α(x)
и β(x)
бесконечно малые одного порядка при
 .◄
.◄
Пример
1.2. Сравнить
бесконечно малые

и

при
 .
.
►Имеем
 ~
~ ~
~ ,
,
здесь использованы формулы:
 ,
,

и

 ,
,
где

при
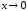 .
.
Имеем:

 .
.
Используя теорему о замене эквивалентными
в отношении, получим:
 .
.
Таким образом, α(x)
является величиной более высокого
порядка малости, чем β(х)
при х→ 0,
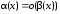
при х→ 0.◄
Пример
1.3. Сравнить
бесконечно малые α(x)
и β(x) при
при
 .
.
►Имеем
α(x) ~
~
(здесь использована формула
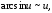
где
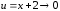
при
 ),
),
β(x) =
= ~
~
~ ~
~ ,
,
(здесь использованы формулы:


и
 ,
,
 ,
,
где
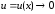
при
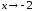 ).
).
Используя теорему о замене эквивалентными
в отношении, получим:
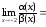
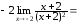
 .
.
Следовательно,

и поэтому заключаем, что β(x)
– величина более высокого порядка
малости, чем α(x)
при
 ,
,
β(x) = o(α(x))
при
 .◄
.◄
Пример
1.4. Сравнить
бесконечно малые
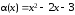
и

при
 .
.
►Заметим,
что β(x)
не эквивалентна аргументу функции
sinπx,
который не является бесконечно малым
при
 .
.
Чтобы найти эквивалентную бесконечно
малую для этой функции, сделаем замену
переменной. Пусть y = x–3,
x = y + 3,
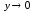
при
 .
.
Имеем:

 .
.
Так
как sin(πy + 3π) = sin(πy + 2π + π) = sin(πy + π)
= – sinπy,
то

 =
=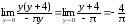 ,
,
здесь
использованы периодичность функции
синус, формулы приведения из элементарной
тригонометрии, а также соотношение

где
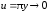
при
 .
.
Поскольку
 ,
,
то заключаем, что α(x)
и β(x)
бесконечно малые одного порядка при
 .◄
.◄
Пример
1.5. Сравнить
бесконечно малые α(x)
и α(x)
и β(x)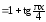 при
при
 .
.
►α(x) ~
~ ,
,
здесь использована формула

где

при
 .
.
Используя формулу для тангенса суммы
двух углов, преобразуем выражение для
β(x):
β(x) = 

Имеем:
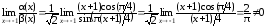 ,
,
∞, следовательно, α(x)
и β(x)
– бесконечно малые одного порядка при
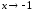 .◄
.◄
§
2. Определение порядка бесконечно малой
функции.
Определение
2.1. Пусть
функции α(x)
и β(x)
являются
бесконечно малыми при
 .
.
Бесконечно малая α(x)
называется бесконечно малой k-го
порядка по отношению к бесконечно малой
β(x)
при х а,
а,
если существует
 .
.
Так,
функция α(x) =sin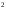 2x
2x
имеет 2-ой порядок малости относительно
β(x) =х
( )
)
при х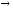 0,
0,
ибо

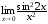
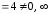 .
.
Определить
порядок малости бесконечно малой α(x)
относительно бесконечно малой β(x)
при х а
а
– значит найти число k
такое, чтобы
 .
.
При этом используется теорема о замене
эквивалентными в отношении и таблица
эквивалентных бесконечно малых функций
(§1), так как для α(x)
и β(x)
полезно найти эквивалентные бесконечно
малые вида С(х – а)k.
Пример
2.1. Определить
порядок бесконечно малой α(x) .
.
относительно бесконечно малой β(x) = х
при
 .
.
►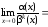

(использованы
теорема о замене эквивалентными
бесконечно малыми в отношении и формулы:
 ,
,
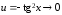 ,
,

и


при
 ).
).
Поскольку
 –
–

при
 ,
,
то порядок малости α(x)
относительно β(x)
при х 0
0
равен 2.◄
Пример
2.2. Определить
порядок бесконечно малой α(x)
) = 
относительно бесконечно малой β(x) = х
при
 .
.
►

(использованы
теорема о замене эквивалентными
бесконечно малыми в отношении и формула:
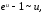

при
 ).
).
Разложив числитель на множители, получим:

 .
.
Поскольку
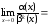 –3
–3
при
 ,
,
то порядок малости α(x)
относительно β(x)
при х 0
0
равен 2.◄
Пример
2.3. Определить
порядок бесконечно малой α(x)
относительно бесконечно малой β(x) = х
при
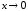 .
.
►
 .
.
Числитель разложим на множители по
формуле разность косинусов, получим:
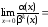
 .
.
После применения теоремы о замене
эквивалентными бесконечно малыми в
отношении и формулы:


и

при

имеем:

 .
.
Поскольку
 8
8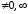
при
 ,
,
то порядок малости α(x)
относительно β(x)
при х 0
0
равен 2.◄
Пример
2.4. Определить
порядок бесконечно малой α(x)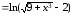 .
.
относительно бесконечно малой β(x) = х
при
 .
.
►
 .
.
Числитель заменим на эквивалентную,
получим:


(использована формула


при
 ).
).
Перенесём иррациональность из числителя
в знаменатель, умножив оба члена дроби
на выражение, сопряжённое к числителю:
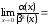
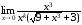 .
.
Поскольку



при
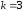 ,
,
то порядок малости α(x)
относительно β(x)
при х 0
0
равен 3.◄
Пример
2.5. Определить
порядок бесконечно малой α(x) = 
относительно бесконечно малой β(x) = х – 1
при х 1.
1.
►
 =
= =
=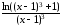
 .
.
Так как
 1,
1,
то
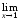
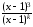 =1
=1
при
 .
.
Поэтому порядок малости α(x)
относительно β(x)
при х 1
1
равен 3.◄
Пример
2.6. Определить
порядок бесконечно малой α(x) = cos(πsinх) + 1
относительно бесконечно малой
β(x) = х – π/2
при
 .
.
►Для
α(x)
найдём эквивалентную бесконечно малую
вида С(х – π/2)k.
В результате применения формул для
половинных и дополнительных углов из
элементарной тригонометрии и формул



из таблицы эквивалентных бесконечно
малых (см. §1) для α(x)
имеем соотношение:
α(x) =
 ~
~ ~
~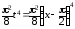 .
.
Итак,
α(x) ~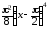
при
 .
.
Используя теорему о замене эквивалентными
в отношении, получаем:

при

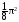

при k
= 4. Таким образом, порядок малости α(x)
относительно β(x)
при х
равен 4.◄
Пример
2.7. Определить
порядок бесконечно малой α(x)
относительно бесконечно малой β(x) = х – π
при
 .
.
►
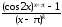 .
.
Используя основное логарифмическое
тождество, представим функцию
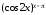
в виде:
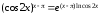 .
.
Имеем
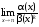 =
=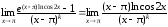 =
= =
=

(использованы теорема о замене
эквивалентными бесконечно малыми в
отношении и формулы

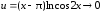
и

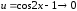
при
 .
.
Заметим, что разность
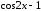
не эквивалентна
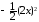
при
 ,
,
так как

не стремится к нулю при
 .
.
Чтобы найти для этой разности эквивалентную
бесконечно малую, сделаем замену
переменной: y = х – π x = y + π:
x = y + π:




 .
.
Поскольку
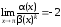
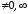
при
 ,
,
то порядок малости α(x)
относительно β(x)
при

равен 3.◄
§3.
Выделение главной части бесконечно
малой функции.
Определение
3.1. Пусть
даны функции α(x)
и β(x),
являющиеся
бесконечно малыми при х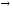 а.
а.
Функция

называется главной частью функции α(x)
при х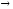 а,
а,
если α(x)
при х а
а
можно
представить в виде:
α(x) = β(x) + o(β(x)). (3.1)
Если
бесконечно малые α(x)
и β(x)
эквивалентны при х а,
а,
то для них справедливо равенство (3.1)
(свойство эквивалентных бесконечно
малых). Поэтому данная бесконечно малая
функция α(x)
при х а
а
может иметь бесчисленное множество
главных частей, так как любая бесконечно
малая функция β(x),
эквивалентная α(x),
будет её главной частью. Например,
функции х,
tg x
– главные
части функции sin x
при х 0,
0,
так как при х 0
0
справедливы утверждения: sin x~x,
sin x~tg x.
Обычно
главную часть функции α(x),
бесконечно малой при х а,
а,
находят в
наиболее
простом виде, например, в виде степенной
функции β(x) = С(х – а)k,
k > 0,
при a R
R
или
β(x) = С(1/х)k,
k > 0,
при a .
.
Найти для α(x)
такую главную часть – значит определить
константу С
и порядок k
этой функции относительно разности
x – a
или дроби 1/х.
Найти
для α(x)
главную часть простейшего вида С(х – а)k,
k > 0,
при х а
а
– это значит найти константу С
и число k
такие, чтобы
 .
.
Пример
3.1. Выделить
главную часть вида Схk
из бесконечно малой α(x) = cos2х – cos4х
при х  0.
0.
►В
результате применения формулы для
разности косинусов и формулы


из таблицы эквивалентных бесконечно
малых (см. §1) для α(x)
имеем соотношение: α(x)
 .
.
Таким образом, для α(x)
найдена эквивалентная бесконечно малая
функция 6х2,
имеющая указанный вид (С = 6,
k = 2),
следовательно, 6х2.–
главная часть α(x)
при х  0.◄
0.◄
Пример
3.2. Выделить
главную часть вида Схk
из бесконечно малой α(x) =
при х  0.
0.
► Найдём
число k
и константу С
такие, чтобы
выполнялось равенство:

 =1.
=1.
Перенесём иррациональность из числителя
в знаменатель, для этого умножим оба
члена дроби на выражение, сопряжённое
к числителю:

 =
=
 (использованы
(использованы
теорема о замене эквивалентными
бесконечно малыми в отношении и формула:


при
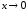 ).
).
Поскольку

при k = 2
и
 ,
,
то
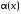 ~
~


при х  0
0
и, следовательно, функция


– главная часть бесконечно малой α(x)
при х  0.◄
0.◄
Пример
3.3. Выделить
главную часть вида С(х – 2)k
из бесконечно малой α(x)
при х  2.
2.
►В
результате применения формулы


из таблицы эквивалентных бесконечно
малых (см. §1) для α(x)
имеем соотношение:
α(x)
 .
.
Итак,
для α(x)
найдена эквивалентная бесконечно малая
функция 3(х– 1)2,
имеющая указанный вид (С = 3,
k = 2),
следовательно, 3(х–1)2–
главная часть α(x)
при х 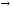 2.◄
2.◄
Пример
3.4. Выделить
главную часть вида С(х – 1)k
из бесконечно малой α(x) = cos(πex–1) + 1
при х 1.
1.
►В
результате применения формул для
половинных и дополнительных углов из
элементарной тригонометрии и формул
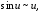

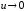
из таблицы эквивалентных бесконечно
малых (см. §1) для α(x)
имеем соотношение: α(x) = 2cos2
 = 2sin2
= 2sin2 2sin2
2sin2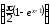
 .
.
Итак,
для α(x)
найдена эквивалентная бесконечно малая
функция
 ,
,
имеющая указанный вид (С =  ,
,
k = 2),
следовательно,

– главная часть α(x)
при х  1.◄
1.◄
Пример
3.5. Выделить
главную часть вида С(1/х)k
из бесконечно малой α(x) =
при х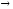
 .
.
► ,
,
α(x) =
при х

(использована формула


при х
 ).
).
Имеем



при х
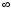 ,
,
отсюда заключаем:
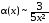
при х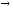
 ,
,
следовательно,

– главная часть бесконечно малой α(x)
при х
 .◄
.◄
Пример
3.6. Выделить
главную часть вида С(х – e)k
из бесконечно малой α(x) = хx – ex
при х .
.
►Используя
основное логарифмическое тождество,
представим функцию хx
в виде:
хx = exlnx.
Имеем α(x) = exlnx – ex = ex(exlnx-х–1).
В результате применения
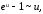

из таблицы эквивалентных бесконечно
малых (см. §1) для α(x)
получаем соотношение:
α(x) ~ ее(х(lnx – 1)) = ее+1(lnx – lne) = ее+1 ~
~
при
х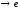 .
.
Итак, α(x) ~ 
при х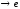 ,
,
Следовательно, ee (х–е)
– главная часть бесконечно малой α(x)
при х е.◄
е.◄
Пример
3.7. Выделить
главную часть вида Схk
из бесконечно малой α(x) = arccos(1 – x)
при х .
.
►Чтобы
найти для α(x)
эквивалентную бесконечно малую функцию
указанного вида, применим формулу

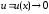 .
.
Имеем
α(x) ~sin(arccos(1 – x))
при х .
.
Преобразуем
функцию sin(arccos(1 – x)),
Используя определение арккосинуса.
Пусть arccos(1 – x) = γ,
где γ – угол или дуга такая, что
cosγ = 1 – x
и
 ,
,
тогда sin(arccos(1 – x)) = sinγ = 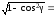
 .
.
Итак,
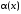 ~
~

при

и функция

– главная часть бесконечно малой α(x)
при
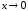 .◄
.◄
Пример
3.8. Выделить
главную часть вида

из бесконечно малой α(x) = π – 4arctg(x2 – 2x + 2)
при х .
.
►α(x)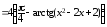 .
.
Для отыскания алгебраической функции,
эквивалентной α(x),
применим формулу

 ,
,
положив
u = 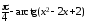 ,
,
а также формулу для разности тангенсов
двух углов из элементарной тригонометрии:
α(x)
 .
.
Итак,
α(x) ~ – 2(x – 1)2
при

и функция – 2(x – 1)2
– главная часть бесконечно малой α(x)
при
 .◄
.◄
Соседние файлы в папке Хуета
- #
- #
- #
- #
- #
- #
Содержание:
- Бесконечно малые функции одного порядка
- Бесконечно малые функции более низкого и высокого порядков
- Эквивалентные (равносильные) бесконечно малые функции
Определение
Функция $alpha(x)$ называется бесконечно малой
при $x rightarrow a$ (или в точке $x=a$ ), если
$lim _{x rightarrow a} alpha(x)=0$
Подробная теория про бесконечно малые функции по
ссылке.
Пример
Функция $alpha(x) =x^2-1$ является б.м. при
$x rightarrow 1$, так как
Бесконечно малые функции одного порядка
Пусть $alpha(x)$ и
$beta(x)$ – две б.м. функции при
$x rightarrow a$.
Определение
Функции $alpha(x)$ и
$beta(x)$ называются б.м. одного порядка малости при
$x rightarrow a$, если $lim _{x rightarrow a} frac{alpha(x)}{beta(x)}=c neq 0$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Рассмотрим функции $alpha(x)=x^{2}-1$ и $beta(x)=x-1$, которые являются б.м. при
$x rightarrow 1$:
$$lim _{x rightarrow 1} alpha(x)=lim _{x rightarrow 1}left(x^{2}-1right)=1^{2}-1=0$$
$$lim _{x rightarrow 1} beta(x)=lim _{x rightarrow 1}(x-1)=1-1=0$$
Найдем предел отношения этих функций при $x rightarrow 1$:
$$lim _{x rightarrow 1} frac{alpha(x)}{beta(x)}=lim _{x rightarrow 1} frac{x^{2}-1}{x-1}=lim _{x rightarrow 1} frac{(x-1)(x+1)}{x-1}=$$
$$=lim _{x rightarrow 1}(x+1)=1+1=2$$
Так как предел равен конечному, отличному от нуля числу, то рассматриваемые функции $alpha(x)$ и
$beta(x)$ являются б.м. одного порядка малости при
$x rightarrow 1$.
Бесконечно малые функции более низкого и высокого порядков
Определение
Если $lim _{x rightarrow a} frac{alpha(x)}{beta(x)}=0$, то
$alpha(x)$ является б.м. более высокого порядка при
$x rightarrow a$, чем
$beta(x)$, а
$beta(x)$ – б.м. более низкого порядка по сравнению с
$alpha(x)$:
$alpha(x)=o(beta(x))$ при
$x rightarrow a$.
Пример
Функция $alpha(x)=left(x^{2}-1right)^{2}$ , $left(lim _{x rightarrow 1} alpha(x)=lim _{x rightarrow 1}left(x^{2}-1right)^{2}=0right)$ является б.м. более высокого порядка, чем
функция $beta(x)=x-1$, $left(lim _{x rightarrow 1} beta(x)=lim _{x rightarrow 1}(x-1)=0right)$ в точке $x=0$, так как
$$begin{aligned}
lim _{x rightarrow 1} frac{alpha(x)}{beta(x)} &=lim _{x rightarrow 1} frac{left(x^{2}-1right)^{2}}{x-1}=lim _{x rightarrow 1} frac{(x-1)^{2}(x+1)^{2}}{x-1}=\
&=lim _{x rightarrow 1}(x-1)(x+1)^{2}=0 cdot 2=0
end{aligned}$$
Определение
Если $lim _{x rightarrow a} frac{alpha(x)}{beta(x)}=infty$, то $alpha(x)$ – б.м. низшего порядка малости при $x rightarrow a$ по сравнению с
$beta(x)$.
Пример
Рассмотрим функцию $alpha(x)=x+1$, которая является б.м. в точке $x=-1$: $lim _{x rightarrow-1} alpha(x)=lim _{x rightarrow-1}(x+1)=-1+1=0$, и б.м. в этой же точке функцию $beta(x)=(x+1)^2$: $lim _{x rightarrow-1} beta(x)=lim _{x rightarrow-1}(x+1)^{2}=(-1+1)^{2}=0$. Найдем предел частного этих функций:
$$lim _{x rightarrow-1} frac{alpha(x)}{beta(x)}=lim _{x rightarrow-1} frac{x+1}{(x+1)^{2}}=lim _{x rightarrow-1} frac{1}{x+1}=frac{1}{0}=infty$$
А поэтому, функция $alpha(x)$ является б.м.
низшего порядка малости при $x rightarrow -1$, чем функция
$beta(x)$.
Определение
Если $lim _{x rightarrow a} frac{alpha(x)}{[beta(x)]^{k}}=C$, $0 < |C| lt infty$, то $alpha(x)$ называется б.м. порядка $k$ по сравнению с
$beta(x)$ при
$x rightarrow a$.
Пример
Функция $alpha(x)=x+1$ называется б.м. порядка 2 по
сравнению с функцией $beta(x)=sqrt{x+1}$ в точке $x=-1$, так как
$$lim _{x rightarrow-1} frac{alpha(x)}{[beta(x)]^{k}}=lim _{x rightarrow-1} frac{x+1}{(sqrt{x+1})^{2}}=lim _{x rightarrow-1} frac{x+1}{x+1}=lim _{x rightarrow-1} 1=1$$
$1 neq 0$, что и требовалось доказать.
Эквивалентные (равносильные) бесконечно малые функции
Определение
Если $lim _{x rightarrow a} frac{alpha(x)}{beta(x)}=1$, то б.м. функции $alpha(x)$ и $beta(x)$ называются эквивалентными или равносильными б.м.
одного порядка при $x rightarrow a$: $alpha(x) sim beta(x)$ при $x rightarrow a$.
Пример
Функции $alpha(x)=x^4-3x+2$ и $beta(x)=x^5-4x+3$ являются эквивалентными б.м. в точке $x=1$, так как, во-первых:
$$lim _{x rightarrow 1} alpha(x)=lim _{x rightarrow 1}left(x^{4}-3 x+2right)=0$$
$$lim _{x rightarrow 1} beta(x)=lim _{x rightarrow 1}left(x^{5}-4 x+3right)=0$$
а во-вторых:
$$begin{array}{r}
lim _{x rightarrow 1} frac{alpha(x)}{beta(x)}=lim _{x rightarrow 1} frac{x^{4}-3 x+2}{x^{5}-4 x+3}= \
=lim _{x rightarrow 1} frac{(x-1)left(x^{3}+x^{2}+x-2right)}{(x-1)left(x^{4}+x^{3}+x^{2}+x-3right)}=frac{1+1+1-2}{1+1+1+1-3}=1
end{array}$$
Читать дальше: эквивалентные бесконечно малые функции, таблица эквивалентных б.м. функций.
6.6 Порядки бесконечно малых величин
Малой -го порядка малости относительно бесконечно малой величины при ,если существует конечный предел не равный нулю.
Чаще всего приходится устанавливать порядок малости бесконечно малой при относительно . Задача сводится к тому, чтобы подобрать таким образом, чтобы и были одного порядка малости.
Пример 1. Определить порядок малости функции относительно , т. е. выделить ее “главную часть”.
Ответ: Функция — бесконечно малая порядка относительно , т. е.
Пример 2. Определить порядок малости функции Относительно , т. е. выделить ее «главную часть».
Ответ: Функция бесконечно малая 2-го порядка малости относительно .
Пример 3. Установить относительный порядок малости при функций и .
Ответ: Бесконечно малая функция 2-го порядка малости относительно бесконечно малой функции .
Пример 4. Убедиться в том, что функция И при будут бесконечно малыми одного порядка.
Ответ: Функции И — бесконечно малые одного порядка, т. к. предел их отношения при равен .
Пример 5. Доказать, что при Бесконечно малые функции и будут эквивалентными.
Решение: Составляем предел отношения функций и , убеждаемся в процессе вычисления, что он равен 1, откуда делаем вывод:
Что и требовалось доказать: .
Пример 6. Найти относительный порядок малости при Двух бесконечно малых функций и .
Ответ: – бесконечно малая функция 2-го порядка относительно бесконечно малой функции .
Сравнение бесконечно малых функций. 1. Сравнить бесконечно малые функции и значит найти предел их отношения
1. Сравнить бесконечно малые функции и значит найти предел их отношения .
2. Бесконечно малые функции называются несравнимыми, если предел их отношения не существует.
Пример 1.11. Сравнить бесконечно малые функции
Находим, не существует. Следовательно, бесконечно малые функции и несравнимые.
3. Бесконечно малые функции называются одного порядка малости, если предел их отношения равен отличной от нуля конечной величине.
Пример 1.12. Сравнить бесконечно малые функции
и при х ® 2.
Следовательно, бесконечно малые функции и одного порядка малости.
4. Бесконечно малые функции называются эквивалентными, если предел их отношения равен единице.
5. Бесконечно малая функция называется более высокого порядка малости по сравнению с бесконечно малой , если предел их отношения равен нулю
Запись = о( ) означает, что более высокого порядка малости по сравнению с . (Здесь в записи используется о – буква «о» маленькая).
Пример 1.13. , .
6. Бесконечно малая функция называется n-го порядка малости по сравнению с , если , где .
Пример 1.14. Определить порядок малости по сравнению с x при .
Следовательно, бесконечно малая функция 2-го порядка малости по сравнению с x.
Теорема 1.10. Предел отношения бесконечно малых функций не изменится, если их заменить эквивалентными бесконечно малыми функциями, т. е.
О большое и о малое. Сравнение функций
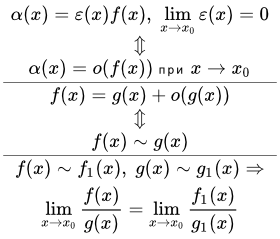
Определение о малого
Символом о малое обозначают любую бесконечно малую функцию o ( f ( x )) по сравнению с заданной функцией f ( x ) при аргументе, стремящемся к некоторому конечному или бесконечному числу x 0 .
Функция α называется бесконечно малой по сравнению с функцией f при :
при
(читается: « есть о малое от при »),
если существует такая проколотая окрестность точки , на которой
при ,
где – бесконечно малая функция при :
.
Заметим, что просто бесконечно малая функция при является бесконечно малой по сравнению с постоянной функцией, не равной нулю.
Если, в предыдущем определении, f является бесконечно малой функцией при , то говорят, что является бесконечно малой более высокого порядка, чем f при .
Определение О большого
Символом О большое обозначают любую функцию , ограниченную относительно функции при аргументе, стремящемся к некоторому конечному или бесконечному числу x 0 .
Функция f ограничена относительно функции g при x → x 0:
при
(читается: « есть О большое от при »),
если функции f и g определены на некоторой проколотой окрестности точки и существует такое число C , что на этой окрестности выполняется неравенство:
.
Можно дать еще одно эквивалентное определение О большого, которое удобно применять в некоторых задачах.
при ,
если на некоторой проколотой окрестности точки ,
,
где – функция, которая определена и ограничена на этой окрестности.
Просто ограниченная, на некоторой проколотой окрестности точки , функция является ограниченной по сравнению с постоянной функцией, не равной нулю.
Функции f и g называются функциями одного порядка при :
при ,
если и при .
Это определение также можно записать так:
.
При этом функции и определены и ограничены на некоторой проколотой окрестности точки .
Функции f и g называются эквивалентными (асимптотически равными) при :
при ,
если на некоторой проколотой окрестности точки ,
при , причем
.
Подчеркнем, что означает одну из функций, принадлежащей множеству бесконечно малых функций по сравнению с . Или это функция, о которой известно, что она является бесконечно малой. Другие свойства , в конкретном применении, не представляют интереса. Например, выражение означает, что если прибавить одну функцию из множества бесконечно малых (по сравнению с ) функций к другой функции из того же множества, то их сумма является функцией, которая также принадлежит этому множеству. Выражение означает, что , то есть что принадлежит множеству функций, бесконечно малых по сравнению с .
Определения в компактном виде
Приведенные выше определения можно дать в однообразном компактном виде.
при ;
при ;
при ;
при .
Свойства и теоремы
Теорема. Свойства о малого
1) Если , то при .
2) Если на некоторой проколотой окрестности точки , при ,
и , то
.
Пусть на некоторой проколотой окрестности точки определены функции и . Тогда при выполняются следующие соотношения.
3.1) , где c ≠ 0 – постоянная.
3.2) ;
3.3) ;
3.4) ;
3.5) , где .
Доказательство ⇓
Свойства о малого, применяемые в степенных рядах
Здесь m и n – натуральные числа, .
;
;
, если ;
;
;
;
, где ;
, где c ≠ 0 – постоянная;
.
Для доказательства этих свойств нужно выразить о малое через бесконечно малую функцию:
, где .
Свойства О большого
Пусть на некоторой проколотой окрестности точки определены функции и . Тогда при выполняются следующие соотношения;
, где c ≠ 0 – постоянная;
;
;
;
, где .
Свойства эквивалентных функций
1) Свойство симметрии. Если, при , , то .
2) Свойство транзитивности. Если, при , и , то .
3) Если , то при .
Доказательство ⇓
Теорема о связи эквивалентных функций с о малым
Для того чтобы две функции и были эквивалентными (или асимптотически равными), необходимо и достаточно чтобы при выполнялось условие:
.
Доказательство ⇓
Это свойство часто записывают так:
.
При этом говорят, что является главной частью при . При этом главная часть определена не однозначно. Любая эквивалентная функция является главной частью к исходной.
В силу свойства симметрии:
.
Теорема о замене функций эквивалентными в пределе частного
Если, при , и и существует предел
, то существует и предел
.
Доказательство ⇓
В силу свойства симметрии эквивалентных функций, если не существует один из этих пределов, то не существует и другой.
Поскольку любая функция, определенная на некоторой проколотой окрестности точки , эквивалентна самой себе, то существуют пределы
.
Заменив функции g и g 1 на 1/ g и 1/ g 1 , получим аналогичную теорему для произведения.
Если, при , и , то
.
Это означает, что если существует один предел, то существует и другой. Если не существует один из этих пределов, то не существует и второй.
Лемма. Признак функций одного порядка
Если существует конечный ненулевой предел
(Л1.1) ,
то функции f и g одного порядка при :
при .
Доказательство ⇓
Доказательство свойств и теорем
Теорема. Свойства о малого
Пусть . Это означает, что существует такая проколотая окрестность точки , на которой определено отношение и поэтому . Тогда на этой окрестности
,
где . По условию
.
Тогда .
Свойство 1) доказано.
2) Если на некоторой проколотой окрестности точки , при ,
и , то
.
Поскольку , то на рассматриваемой проколотой окрестности точки ,
.
Поскольку , то
.
Свойство 2) доказано.
Пусть на некоторой проколотой окрестности точки определены функции и . Тогда при выполняются следующие соотношения.
3.1) , где c ≠ 0 – постоянная.
3.2) ;
3.3) ;
3.4) ;
3.5) , где .
3.1). Пусть . Согласно определению о малого,
,
где . Введем функцию . Тогда
.
Поскольку , то
.
Свойство 3.1) доказано.
3.2). Докажем, что .
Пусть . Согласно определению о малого,
,
где .
Тогда ,
где . Поскольку
, то
.
Свойство 3.2) доказано.
3.3). Докажем, что .
Пусть . Согласно определению о малого,
,
где . Тогда
.
Здесь . Поскольку
,
то .
Свойство 3.3) доказано.
3.4). Докажем, что .
Пусть . Согласно определению о малого,
,
где ,
.
Согласно арифметическим свойствам предела функции,
.
Тогда .
Свойство 3.4) доказано.
3.5). Пусть при . Тогда, согласно определению о малого, ,
где . Тогда
,
где .
Поскольку и , то
.
Здесь мы воспользовались свойствами степенной функции, ее непрерывностью, теоремой о пределе непрерывной функции от функции и теоремой о пределе абсолютного значения функции.
Свойство 3.5) доказано.
Эквивалентные функции
Свойства эквивалентных функций
Все формулировки ⇑ 1) Свойство симметрии. Если, при , , то .
Поскольку при , , то согласно определению эквивалентной функции, существует такая проколотая окрестность точки , на которой
,
где .
Поскольку функция имеет отличный от нуля предел, то по теореме об ограниченности снизу функции, имеющей ненулевой предел, существует такая проколотая окрестность точки , на которой . Поэтому на этой окрестности . Следовательно, на ней определена функция . Тогда
.
Согласно теореме о пределе частного двух функций,
.
Свойство доказано.
2) Свойство транзитивности. Если, при , и , то .
Теорема о связи эквивалентных функций с о малым
Все формулировки ⇑ Для того чтобы две функции и были эквивалентными (или асимптотически равными), необходимо и достаточно чтобы при выполнялось условие:
.
1. Необходимость. Пусть функции и являются эквивалентными при . Тогда
.
Поскольку , то
.
Тогда .
Необходимость доказана.
2. Достаточность. Пусть при ,
.
Тогда , где . Отсюда
.
Поскольку , то
.
Теорема доказана.
Теорема о замене функций эквивалентными в пределе частного
Все формулировки ⇑ Если, при , и и существует предел
, то существует и предел
.
Пусть, при , и . Тогда
, где
.
Поскольку существует предел , то существует такая проколотая окрестность точки , на которой функция определена и отлична от нуля. Поскольку , то, по теореме об ограниченности снизу функции, имеющей ненулевой предел, существует такая проколотая окрестность точки , на которой и, следовательно, . Тогда существует проколотая окрестность точки , на которой функция определена и отлична от нуля и, следовательно, определено частное :
.
Применяем арифметические свойства предела функции:
.
Признак функций одного порядка
Все формулировки ⇑ Лемма
Если существует конечный ненулевой предел
(Л1.1) ,
то функции f и g одного порядка при :
при .
Поскольку существует предел (Л1.1), то по теореме о пределе абсолютного значения функции, существует предел
.
Тогда согласно определению предела функции по Коши, для любого , существует такая проколотая окрестность точки , на которой
при .
Преобразуем неравенство и подставим :
;
;
(Л1.2) .
Из второго неравенства:
,
или .
Из первого неравенства (Л1.2):
,
или .
Использованная литература.
О. И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
А. М. Дымарский. Лекции по математическому анализу. Часть 1. Москва, МФТИ, 2020.
Л. Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С. М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Порядок малости. Тема
Как определяются 1) бесконечно малые одного порядка малости, 2) эквивалентные бесконечно малые, 3) бесконечно малые более высокого порядка малости, и как сравнить порядок малости двух бесконечно малых функций.
Бесконечно малые функции, по определению, характеризуются тем, что стремятся к нулю. Но дело в том, что стремятся они с разной скоростью. Если бесконечно малая приближается к нулю быстро, то говорят, что она обладает высоким порядком малости, если медленно — то низким порядком малости.
Например, квадратичная функция в окрестности нуля обладает более высоким порядком малости, нежели линейная.
Определения, связанные с понятием порядка малости таковы:
- Если предел отношения бесконечно малых функций равен конечному числу, отличному от нуля и единицы, то говорят, что они обладают одним порядком малости.
- Если этот предел равен единице, то говорят, что они эквивалентны.
- Если же он равен нулю (или бесконечности, что, в данном контексте, одно и то же), то говорят, что одна из них обладает более высоким порядком малости.
Таким образом, прием определения порядка малости состоит в вычислении предела отношения двух бесконечно малых.
Порядок малости — это красивый термин, который часто используется в теоретических разделах математического анализа и очень редко на практике. Вам следует представлять, что такое порядок малости, чтобы понимать математические тексты.
Просмотрите видео по теме «Порядок малости». Затем перейдите к вопросам по теме «Порядок малости» и попробуйте самостоятельно сравнить порядок малости предложенных вам бесконечно малых. Наконец, проверьте себя, просмотрев ответы на вопросы по теме «Порядок малости».
Тема «Порядок малости»
Вопросы по теме «Порядок малости»
Ответы на вопросы по теме «Порядок малости»
Для того чтобы лучше разобраться с темой «Порядок малости», обязательно решите все задания.
Все лекции здесь.
Популярные сообщения из этого блога
Даны два двойных интеграла. Требуется вычислить их путем перехода к полярным координатам.
$ Общее время занятий включает в себя, помимо онлайн-занятия, несколько часов видео для предварительного изучения (которые не оплачиваются). Таким образом, занимаясь фактически 3, 4, 5 и более часов, вы оплачиваете только 2 академических часа. Это выгодно. Ознакомиться с условиями занятий
Даны два двойных интеграла. Требуется подобрать замены так, чтобы области интегрирования перешли в прямоугольники со сторонами, параллельными осям, и вычислить интегралы в новых координатах.
Сообщения без ответов | Активные темы
| Автор | Сообщение | ||
|---|---|---|---|
|
|||
|
Добрый день. Прошу помощи, очень завис, не могу разобраться. [math]sqrt{x +sqrt{ x + sqrt{ x} } }[/math] [math]slash x[/math] И как определить первого или второго или третьего порядка малости? Заранее прошу прощение за потраченное время
|
||
| Вернуться к началу |
|
||
|
wr00m |
Заголовок сообщения: Re: Определить порядок малости:
|
|
Извиняюсь,ошибся. И хочется понять получше, как определять порядки малости. Спасибо.
|
|
| Вернуться к началу |
|
|
Student Studentovich |
|
||
|
wr00m [math]sqrt{x+sqrt{x+sqrt{x}}}sim x^frac18,,,xto 0.[/math]
|
|||
| Вернуться к началу |
|
||
|
wr00m |
Заголовок сообщения: Re: Определить порядок малости:
|
|
Получается, они эквиваленты?
|
|
| Вернуться к началу |
|
|
wr00m |
Заголовок сообщения: Re: Определить порядок малости:
|
|
Какой порядок малости у функции [math]sqrt{x+sqrt{x+sqrt{x} } }[/math]?
|
|
| Вернуться к началу |
|
|
wr00m |
Заголовок сообщения: Re: Определить порядок малости:
|
|
Да-да, я тупой Я очень запутался с корневищами этими. С другими заданиями подобного рода справляюсь неплохо. Вопрос такой, вот эта штука [math]sqrt{x+sqrt{x+sqrt{x} } }[/math] равна x^1/8?
|
|
| Вернуться к началу |
|
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Определить порядок малости
в форуме Пределы числовых последовательностей и функций, Исследования функций |
lordvan |
3 |
529 |
15 окт 2015, 14:14 |
|
Определить порядок малости бмф
в форуме Пределы числовых последовательностей и функций, Исследования функций |
Enlil |
4 |
878 |
11 дек 2017, 19:38 |
|
Определить порядок малости функции
в форуме Пределы числовых последовательностей и функций, Исследования функций |
Varvara++ |
4 |
317 |
07 ноя 2018, 15:34 |
|
Определить порядок малости относительно Х при Х-> 0
в форуме Дискуссионные математические проблемы |
daria703 |
1 |
1390 |
26 янв 2015, 11:02 |
|
Определить порядок малости относительно x-1
в форуме Пределы числовых последовательностей и функций, Исследования функций |
Frud |
2 |
680 |
25 окт 2016, 15:28 |
|
о определить порядок малости относительно
в форуме Пределы числовых последовательностей и функций, Исследования функций |
evgnkjerby |
2 |
191 |
18 окт 2020, 18:56 |
|
Определить порядок малости функции относительно x, x->0
в форуме Пределы числовых последовательностей и функций, Исследования функций |
Miriam87 |
2 |
635 |
17 апр 2019, 13:24 |
|
Определить порядок малости относительно х функции
в форуме Пределы числовых последовательностей и функций, Исследования функций |
xom9ik |
3 |
1233 |
11 дек 2016, 12:25 |
|
Определить порядок малости относительно x,x→0 функции
в форуме Пределы числовых последовательностей и функций, Исследования функций |
kenar |
0 |
310 |
11 дек 2020, 19:04 |
|
Определить порядок малости функции относительно x, x->0
в форуме Пределы числовых последовательностей и функций, Исследования функций |
jannarestorana |
1 |
250 |
29 ноя 2021, 21:40 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 2 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |




