Определение частного чисел
Определение
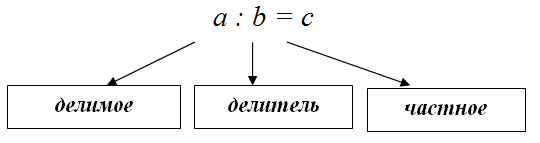
Частное чисел – это результат деления одного числа на другое. Таким образом, частное чисел
$a$ и
$b$ будет число
$c$, которое равно
$c = a : b$ . При этом число
$a$ будет делимым, а число
$b$ – делителем.
Пример
Задание. Найти частное чисел:
1) $39 : 3$ ;
4) $124 : 4$
Ответ. $39 : 3 = 13$
$124 : 4 = 31$
Для нахождения частного больших чисел или
десятичных дробей используют способ
деления в столбик.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти частное чисел:
1) $564 : 12$ ;
2) $0,567 : 0,21$
Решение. Для нахождения частного в первом примере выполним деление в столбик.
Для этого запишем делимое и делитель следующим образом
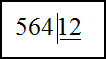
Берем первую цифру слева, она не делится на 12, значит, берем две цифры: 56 и делим их на 12 с остатком.
Возьмем по $4 : 4 cdot 12 = 48$ . Записываем 48 под 56 и находим остаток:
$56 – 48 = 8$ . Восьмерку записываем под чертой и сносим к ней следующее
число из делимого, получим 84. Делим 84 на 12, получаем 7. остаток от деления 0 и цифр в делимом больше нет. Деление окончено.
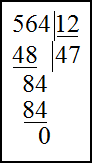
Таким образом, $564 : 12 = 47$
Для нахождения частного во втором примере, сведем деление десятичных дробей к делению десятичной дроби на целое число.
Для этого будем передвигать запятую вправо у делимого и делителя до тех пор, пока делимое не станет целым числом. Далее
запишем полученные числа в столбик, как и в первом примере:
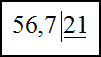
Берем в делимом первые две цифры слева и делим их на делимое с остатком. Получаем $56 : 21$ , можно взять по 2. Двойку записываем в частное.
И так как целая часть делимого закончилась, ставим в частном запятую. Умножаем $2 cdot 21 = 42$ , записываем 42 под 56 и вычитаем:
$56 – 42 = 14$ . Остаток 14 списываем к нему следующую
незадействованную цифру делимого 7. Полученное число 147 делим на 12, получаем 7. Записываем семерку в частное,
и, так как на этом делимое закончилось, а остаток после последнего деления 0, деление окончено.

Таким образом $0,567 : 0,21 = 2,7$
Ответ. $564 : 12 = 47$
$0,567 : 0,21 = 2,7$
Частное рациональных дробей находится по правилу
$$frac{m}{n}: frac{p}{q}=frac{m cdot q}{n cdot p}$$
Пример
Задание. Найти частное рациональных дробей:
1) $frac{2}{3}: frac{1}{3}$ ;
2) $1 frac{1}{14}: 1 frac{3}{7}$
Решение. 1) Воспользуемся правилом вычисления частного рациональных дробей:
$$frac{2}{3}: frac{1}{3}=frac{2 cdot 3}{3 cdot 1}=2$$
Для вычисления частного во втором примере, сначала запишем дроби в виде неправильных дробей. Для этого целую часть
умножим на знаменатель и прибавим к числителю. Затем применим правило вычисления частного рациональных дробей:
$$1 frac{1}{14}: 1 frac{3}{7}=frac{1 cdot 14+1}{14}: frac{1 cdot 7+3}{7}=frac{15}{14}: frac{10}{7}=$$
$$=frac{15 cdot 7}{14 cdot 10}=frac{15}{2 cdot 10}=frac{15}{20}=frac{3}{4}$$
Ответ. $frac{2}{3}: frac{1}{3}=2$
$1 frac{1}{14}: 1 frac{3}{7}=frac{3}{4}$
Читать дальше: что такое иррациональное число.
Все категории
- Фотография и видеосъемка
- Знания
- Другое
- Гороскопы, магия, гадания
- Общество и политика
- Образование
- Путешествия и туризм
- Искусство и культура
- Города и страны
- Строительство и ремонт
- Работа и карьера
- Спорт
- Стиль и красота
- Юридическая консультация
- Компьютеры и интернет
- Товары и услуги
- Темы для взрослых
- Семья и дом
- Животные и растения
- Еда и кулинария
- Здоровье и медицина
- Авто и мото
- Бизнес и финансы
- Философия, непознанное
- Досуг и развлечения
- Знакомства, любовь, отношения
- Наука и техника
![]()
14
1 ответ:
![]()
0
0
Порядок числа находится следующим образом:
Необходимо представить число в виде (например): 1,547*10^(x), где x – порядок числа
10^14/10^12=10^2
Порядок частного 2, либо 1, если откинуть степени 10, то то, что осталось от числа a, может быть больше того,что осталось от b и мы потеряем один порядок(пример 100/9)
Читайте также
![]()
![]()
2/3≈0,667 и 5/7≈0,714. Между ними лежит число 2*π/9≈0,698 и число 3*π/14≈0,673.
Ответ: 2*π/9 и <span>3*π/14.</span>
![]()
Если ты про графики, то там тебя это находить никто не попросит, все про них ты можешь посмотреть здесь http://www.mosrepetitor.ru/pages1/22/
![]()
Cos 27 pi/5 –
sin32pi/11 +
cos 50pi/9 +
sin 22pi/7-
Просто умнож числа на 180 и раздели а потом по кругу смотри на кругу
![]()
120 123 124 130 132 134 140 142 143 102 103 104 210 230 240 310 320 340 410 420 430
Порядок – частное
Cтраница 3
При делении двух нормализованных чисел, из которых каждое меньше 1 и больше или равно 0.1, частное будет всегда меньше 10 и больше 0.1. Если частное получается больше 1, то для его нормализации вправо порядок частного должен быть увеличен на ели-ницу, а мантисса сдвинута на один разряд вправо.
[31]
Деление чисел с плавающей запятой ведется в такой же последовательности, как и умножение. Порядок частного находится путем вычитания порядка делителя из порядка делимого.
[32]
При делении чисел следует поделить их мантиссы и из порядка делимого вычесть порядок делителя. Порядок частного или равен разности порядков делимого и делителя, или на 1 меньше-последнее, если модуль мантиссы делимого меньше модуля мантиссы делителя.
[33]
В соответствии с этими соотношениями при умножении порядки чисел складываются, а мантиссы перемножаются. При делении порядок частного определяется разностью порядков делимого и делителя, а мантисса частного равна частному от деления мантисс делимого и делителя.
[34]
Вычитание порядков с учетом знаков порядков. В результате получается порядок частного.
[35]
У машины Быстрица имеются две линейки с делениями, помещенные в прямоугольной рамке 8; одна из них подвижная и одна неподвижная. Это устройство облегчает определение порядка частного.
[36]
Причина этого исключения ясна: рассмотренный случай деления есть единственный случай деления, который может быть выполнен при обоих положениях движка. Так как для каждого из этих положений порядок частного подсчитывается по-своему, то ясно, что в одном из случаев правило окажется неверным.
[37]
Если мантисса делимого больше или равна мантиссе делителя, то порядок частного равен алгебраической разности порядков делимого и делителя плюс единица.
[38]
При делении 0 0067 на 0 0000709 применяем второе правило. Порядок делимого равен – 2, а порядок делителя – 4, поэтому порядок частного равен ( – 2) – – ( – 4 2, и в частном слева от запятой будут стоять две цифры.
[39]
Мантисса делимого равна 0 7702, а делителя-0 245607, поэтому применяем первое правило. Так как порядок делимого равен единице, а порядок делителя – четырем, то порядок частного равен 1 – 4 – f – l – – 2, поэтому в частном перед запятой будет стоять нуль, а после запятой два нуля.
[40]
При делении чисел с плавающей запятой мантисса делимого делится на мантиссу делителя, а для получения порядка частного из порядка делимого вычитается порядок делителя. При этом если мантисса делимого больше мантиссы делителя, то мантисса частного окажется больше 1 ( происходит переполнение) и ее следует сдвинуть на один разряд вправо, одновременно увеличив на единицу порядок частного.
[41]
При выполнении операции деления с числами в системе с плавающей запятой мантиссу частного определяют методами деления, указанными выше. После получения мантиссы выполняется – нормализация. Порядок частного определяется как разность порядков делимого и делителя.
[42]
При делении приближенного делимого на приближенный делитель необходимо определить порядок частного. После этого в делимом оставляют на две цифры, а в делителе на одну цифру больше, чем должно быть в частном, и выполняют действие аналогично выполнению деления на точный делитель с заданной точностью. Порядок частного равен 0 ( 2 – 2), после запятой требуется иметь две цифры, значит, частное должно состоять из трех цифр.
[43]
При выполнении операции деления чисел с, плавающей запятой сначала до – непосредственного деления выполняется, если это необходимо, нормализация мантисс. Далее по тем же алгоритмам, что и для чисел с фиксированной запятой, производится деление мантиссы делимого на мантиссу делителя и частное округляется в пределах заданной разрядности операндов. Затем находится порядок частного путем вычитания порядка делителя из порядка делимого и, наконец, нормализация результата.
[44]
Если ОД [ МА 1, то мантисса МА называется нормализованной. Поскольку порядки операндов, вообще говоря, различны, то при сложении ( вычитании) предварительно производится выравнивание порядков операндов с соответствующим сдвигом одной из мантисс, которая при этом денормализуется. При умножении порядок произведения определяется как сумма порядков сомножителей, а при делении порядок частного – как разность порядков делимого и делителя.
[45]
Страницы:
1
2
3
4
Частное чисел в математике: что это такое? В школе учат действие деление, где есть делимое, делитель и частное. Что означают эти названия? Давайте разбираться!
Содержание статьи:
Частное чисел в математике: что это такое
Однажды клоун Бим решил выучить математическое действие деление и нашел для себя в интернете вот такое определение:
Определение. Говорят, что a делится на b, если существует натуральное число с, при умножении которого на b получается а: a=b*c. При этом записывают: a:b=с, — и называют а — делимым, b — делителем, с — частным.
Как мне это понять? — задумался Бим. — Но скоро представление, пойду ребят к нам приглашать.
Как найти частное чисел
Пришли в цирк трое ребят: Вася, Коля и Оля. На входе их встречал клоун Бим, который дарил детям шарики. У него в руках было 6 шариков, но дарил он их за отгадки. Клоун спросил у ребят:
— Мне надо подарить вам шарики, какое математическое действие я буду применять?
— Деление! — быстро ответил Коля. — Ты же будешь делить шарики между нами.
Клоун хитро прищурился:
— А как называются члены деления?
— Мы недавно это изучали! — воскликнула Оля. — Всё количество шариков, которое ты будешь делить, называется делимое. У тебя сейчас 6 шариков, значит здесь делимое — 6!
— А то, на сколько ребят ты их разделишь, называется делитель, — вмешался Вася. — Нас трое ребят, значит делитель — 3!
Коля продолжил:
— У каждого из нас будет часть шариков, и результат от деления называется частным.
— Какое же здесь будет частное? — спрашивает Бим.
— Два! — не сговариваясь, хором ответили ребята.
— Правильно, каждому из вас достанется по два шарика, это и есть частное.
Ребята ответили на все вопросы Бима, и каждый получил по два шарика — как результат деления:
6 (делимое) : 3 (делитель) = 2 (частное).
Запишем цифрами:
6:3=2
В этом выражении 6 (делимое) стоит самым первым, 3 (делитель) — на втором месте. А частное (2) — после знака равенства справа.
Итак, частное — это число, которое получается в результате деления делимого на делитель.
Полное и неполное частное
А потом было замечательное представление.
В антракте дети пошли в буфет. На подносе лежало семь пирожных. Как же их разделить поровну на трёх ребят?
Друзья задумались и взяли по 2 пирожных, а последним, которое было в остатке, угостили клоуна Бима.
— Теперь я понял! — воскликнул Бим. — Если нельзя всё число пирожных поделить между ребятами без остатка, то такой результат от деления называется неполным частным. А то, что осталось после деления, так и называется остатком и записывается это вот так:
7:3=2(1)
Здесь 7 (делимое) по-прежнему стоит в начале выражения, 3 (делитель) — в середине, 2 (неполное частное) — справа. Но после неполного частного ещё пишем в скобках остаток (1).
- Полное частное — результат деления, когда делимое делится нацело на делитель (остаток равен 0, его и писать незачем).
- Неполное частное — это результат деления с остатком (когда делимое не делится нацело на делитель).
Как найти делитель
Когда дети ушли занимать свои места, буфетчица подошла к Биму и спросила:
— Я забыла, сколько было ребят. Помню только, что каждый из них съел по два пирожных, а всего им досталось 6 штук. Сколько же посетителей было у меня?
Тут в буфет заглянул дрессировщик Бом и быстренько решил эту задачку. Он разделил 6 (делимое) на 2 (частное) и получил 3 (делитель).
— Всего было трое ребят, — ответил Бом.
— Верно! — вспомнил Бим.
Для того чтобы найти делитель, надо делимое разделить на частное.
6:2=3
Здесь 6 – делимое, 2 – частное, а 3 – делитель.
Как найти делимое
— А сколько ты подарил всего шариков трём ребятам? — спросил Бом.
— Забыл, — ответил Бим. — Помню только, что детей было трое, и каждому досталось по два шарика.
Бом и говорит:
— Тогда надо 3 (делитель) умножить на 2 (частное), получится 6.
Для того чтобы найти делимое, надо делитель умножить на частное.
Запишем это цифрами:
3*2=6.
3 — наш делитель, 2 — частное, а 6 — делимое.
Проверка деления умножением
— Я что-то не пойму. Это уже умножение, а не деление! — говорит Бим. — Выходит, что деление — действие обратное умножению. То есть, мы можем проверить деление умножением?
— Да, — ответил Бом.
Деление — действие, обратное умножению. Для того чтобы проверить деление, надо провести умножение.
Заключение
А клоун для себя сделал плакаты и теперь каждый день может сразу вспомнить, что:
Определение. Говорят, что а делится на b, если существует число с, при умножении которого на b получается а: a= b*c. При этом записывают: a:b=с, — и называют а — делимым, b — делителем, с — частным.
- Деление — действие, обратное умножению;
- умножение проверяет правильность математического действия — деления;
- для того чтобы найти делимое, надо делитель умножить на частное;
- для того чтобы найти делитель, надо делимое разделить на частное.
Итак, теперь мы знаем, что же такое частное в математике. Оказывается, оно бывает полным и неполным! Кроме того, нетрудно будет найти делитель, делимое и проверить деление умножением. И если учитель спросит в школе: «Частное чисел в математике: что это такое?» — сможем ответить сразу. И пусть любой пример или задача на эту тему будет вам по плечу!
Оригинальная идея подачи материала принадлежит Стуловой Лилии Валериевне (преподаватель математики от 5 лет и старше).
Что такое частное чисел
Определение
Частное — это результат процесса деления. Делением называется такая операция, которая обратна умножению, то есть показывает, сколько одинаковых чисел способно содержаться в другом.
Буквенный вид этого действия выглядит следующим образом: a: b = c, где:
- a – это делимое (число, которое делят)
- b – это делитель (число, которым делят)
- с – это частное (результирующее число деления)
- : — арифметический знак, с помощью которого обозначается деление
Важно! Число 0 никогда не может быть делителем
Нахождение значения частного чисел
Пример:
12 : 3 = 4 (в числе 12 4 раза содержится по 3)
15 : 5 = 3 (в числе 15 5 раз содержится по 5)
Нужно знать, что правильность определения частного от деления числа всегда можно проверить путем перемножения его на делитель, либо делимое поделить на частное и получить делитель.
Например:
20 : 4 = 5
Перемножим частное двух чисел на делитель и получим делимое:
4 * 5 = 20
Разделим делимое на частное и получим делитель:
20 : 5 = 4
Таким образом, мы доказали правильность определения частного.
Что такое частное значение чисел с остатком?
Иногда при делении от делимого остается остаток, который меньше делителя, но более нуля. Приведем выражение частного чисел:
8 : 3 = 2 (ост. 2)
Это значит, что делимое 8 поделилось 2 раза по 3 и остался остаток 2, который меньше трех, но больше нуля.
Таким образом: 0 < ост. <делитель
Основные понятия о частном суммы и разности чисел
Что такое частное суммы чисел?
Определение
Частное от деления суммы чисел – это когда делимое либо делитель выступает в роли суммы двух слагаемых.
Общий вид: (a+b):(c+d), где сумма чисел (a+b) – делимое, а сумма (c+d) – делитель
Пример: (12+3):(3+2)=3
Важно, в подобных примерах последовательность решения определяется следующим образом: сначала решаются выражения в скобочках, потом выражения со знаками деления или умножения, после – вычитание или сложение.
Нет времени решать самому?
Наши эксперты помогут!
Поговорим о частном разности чисел
Аналогично, как и с частностью суммы, только в роли делимого или делителя выступает значение разности: (a-b):(c-d), где разность чисел (a-b) – делимое, а разность (c-d) – делитель
Пример нахождения разности чисел: (12-3):(5-2)=3, где
3 и 2 — это вычитаемое частное чисел
Также в математике находят сумму частного произведения чисел:
(12+3)*(1+2)=45
И произведение частного чисел:
(12*5):(5*2)=6
Основные правила при делении
- При делении одного числа на единицу – получаем в ответ делимое: 6 : 1 = 6
- При делении одного числа на само себя – получаем в ответ 1: 7 : 7 = 1
- Если произведение поделить на один из множителей, то получится другой множитель:
6*3=18, 18:6=3, 18:3=6.
При делении на десятки (10, 100…) у частной, запятой с левой стороны отделяется столько цифр, сколько нулей в делителе: 34:10=3,4, 34:100=0,34, 34:1000=0,034.

