Вещественные числа обычно представляются в виде чисел с плавающей запятой. Числа с плавающей запятой — один из возможных способов представления действительных чисел, который является компромиссом между точностью и диапазоном принимаемых значений, его можно считать аналогом экспоненциальной записи чисел, но только в памяти компьютера.
Число с плавающей запятой состоит из набора отдельных двоичных разрядов, условно разделенных на так называемые знак (англ. sign), порядок (англ. exponent) и мантиссу (англ. mantis). В наиболее распространённом формате (стандарт IEEE 754) число с плавающей запятой представляется в виде набора битов, часть из которых кодирует собой мантиссу числа, другая часть — показатель степени, и ещё один бит используется для указания знака числа ( — если число положительное, — если число отрицательное). При этом порядок записывается как целое число в коде со сдвигом, а мантисса — в нормализованном виде, своей дробной частью в двоичной системе счисления. Вот пример такого числа из двоичных разрядов:
| Знак | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Порядок | Мантисса | ||||||||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 14 | 10 | 9 | 0 |
Знак — один бит, указывающий знак всего числа с плавающей точкой. Порядок и мантисса — целые числа, которые вместе со знаком дают представление числа с плавающей запятой в следующем виде:
, где — знак, — основание, — порядок, а — мантисса.
Десятичное число, записываемое как , где — число в полуинтервале , — степень, в которой стоит множитель ; в нормализированной форме модуль будет являться мантиссой, а — порядком, а будет равно тогда и только тогда, когда принимает отрицательное значение.
Например, в числе
Порядок также иногда называют экспонентой или просто показателем степени.
При этом лишь некоторые из вещественных чисел могут быть представлены в памяти компьютера точным значением, в то время как остальные числа представляются приближёнными значениями.
Более простым вариантом представления вещественных чисел является вариант с фиксированной точкой, когда целая и вещественная части хранятся отдельно. Например, на целую часть отводится всегда бит и на дробную отводится всегда бит. Такой способ в архитектурах процессоров не присутствует. Отдаётся предпочтение числам с плавающей запятой, как компромиссу между диапазоном допустимых значений и точностью.
Содержание
- 1 Нормальная и нормализованная форма
- 2 Типы чисел с плавающей точкой (по IEEE 754)
- 2.1 Число половинной точности (Binary16, Half precision)
- 2.2 Число одинарной точности (Binary32, Single precision, float)
- 2.3 Число двойной точности (Binary64, Double precision, double)
- 2.4 Число четверной точности (Binary128, Quadruple precision)
- 2.5 Диапазон значений чисел с плавающей запятой
- 3 Особые значения чисел с плавающей точкой
- 3.1 Ноль (со знаком)
- 3.2 Неопределенность (NaN)
- 3.3 Бесконечности
- 3.4 Денормализованные числа
- 4 Действия с числами с плавающей запятой
- 4.1 Умножение и деление
- 4.2 Сложение и вычитание
- 4.3 Алгоритм получения представления вещественного числа в памяти ЭВМ
- 5 См. также
- 6 Примечания
- 7 Ссылки
- 7.1 Использованные материалы
- 7.2 Что стоит прочесть
Нормальная и нормализованная форма
Нормальной формой (англ. normal form) числа с плавающей запятой называется такая форма, в которой мантисса (без учёта знака) в десятичной системе находится на полуинтервале . Такая форма записи имеет недостаток: некоторые числа записываются неоднозначно (например, можно записать в 4 формах — , , , ), поэтому распространена также другая форма записи — нормализованная (англ. normalized), в которой мантисса десятичного числа принимает значения от (включительно) до (не включительно), а мантисса двоичного числа принимает значения от (включительно) до (не включительно). То есть в мантиссе слева от запятой до применения порядка находится ровно один знак. В такой форме любое число (кроме ) записывается единственным образом. Ноль же представить таким образом невозможно, поэтому стандарт предусматривает специальную последовательность битов для задания числа (а заодно и некоторых других полезных чисел, таких как и ).
Так как старший двоичный разряд (целая часть) мантиссы вещественного числа в нормализованном виде всегда равен «», то его можно не записывать, сэкономив таким образом один бит, что и используется в стандарте IEEE 754. В позиционных системах счисления с основанием большим, чем (в троичной, четверичной и др.), этого замечательного свойства нет (ведь целая часть там может быть не только единицей).
Типы чисел с плавающей точкой (по IEEE 754)
Число половинной точности (Binary16, Half precision)
Число́ полови́нной то́чности — компьютерный формат представления чисел, занимающий в памяти половину машинного слова (в случае 32-битного компьютера — бит или байта). В силу невысокой точности этот формат представления чисел с плавающей запятой обычно используется в видеокартах, где небольшой размер и высокая скорость работы важнее точности вычислений.
| Знак | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Порядок | Мантисса | |||||||||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 1, | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 14 | 10 | 9 | 0 |
Порядок записан со сдвигом . То есть чтобы получить актуально значение порядка нужно вычесть из него сдвиг. Сдвиг можно получить по формуле , где — число бит, отведенное на хранение порядка (в случае числа половинной точности ).
Ограничения точности
- Целые от нуля до передаются как есть.
- Целые от до округляются к ближайшему чётному целому.
- Целые от до округляются до ближайшего целого, делящегося нацело на четыре.
- Целые от до округляются до ближайшего целого, делящегося на восемь.
- Целые от до округляются до ближайшего целого, делящегося на шестнадцать.
- Целые от до округляются до ближайшего целого, делящегося на тридцать два.
Число одинарной точности (Binary32, Single precision, float)
Число́ одина́рной то́чности — компьютерный формат представления чисел, занимающий в памяти одно машинное слово (в случае 32-битного компьютера — бита или байта). Используется для работы с вещественными числами везде, где не нужна очень высокая точность.
| Знак | |||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Порядок (8 бит) | Мантисса (23+1 бита) | ||||||||||||||||||||||||||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1, | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 30 | 23 | 22 | 0 |
Порядок записан со сдвигом .
Число двойной точности (Binary64, Double precision, double)
Число́ двойно́й то́чности —
компьютерный формат представления чисел, занимающий в памяти два машинных слова (в случае 32-битного компьютера — бита или байт). Часто используется благодаря своей неплохой точности, даже несмотря на двойной расход памяти и сетевого трафика относительно чисел одинарной точности.
| Знак | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Порядок (11 бит) |
Мантисса (52+1 бит) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1, | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 62 | 52 | 51 | 0 |
Порядок записан со сдвигом .
Число четверной точности (Binary128, Quadruple precision)
Число́ четверно́й то́чности —
компьютерный формат представления чисел, занимающий в памяти четыре машинных слова (в случае 32-битного компьютера — бит или байт). Используется в случае необходимости крайне высокой точности.
| Знак | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Порядок (15 бит) |
Мантисса (112+1 бит) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1, | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 126 | 112 | 111 |
| Мантисса (112+1 бит) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 |
Порядок записан со сдвигом .
Обычно этот формат реализуется программно, случаи аппаратной реализации крайне редки. Также не гарантируется поддержка этого типа в языках программирования, хотя кое-где она и реализована (например, компилятор gcc для архитектуры x86 позволяет использовать тип __float128, являющийся программной реализацией числа с четверной точностью).
В совокупности эти факторы делают Quadruple весьма экзотичным и редко встречающимся форматом чисел с плавающей запятой.
Диапазон значений чисел с плавающей запятой
Диапазон чисел, которые можно записать данным способом, зависит от количества бит, отведённых для представления мантиссы и показателя. Пара значений показателя (когда все разряды нули и когда все разряды единицы) зарезервирована для обеспечения возможности представления специальных чисел. К ним относятся ноль, значения NaN (Not a Number, “не число”, получается как результат операций типа деления нуля на ноль) и .
Данная таблица только лишь примерно указывает границы допустимых значений, без учета возрастающей погрешности с ростом абсолютного значения и существования денормализованных чисел.
| Название в IEEE 754 | Название типа переменной в Си | Диапазон значений | Бит в мантиссе | Бит на переменную |
|---|---|---|---|---|
| Half precision | – | 6,10×10-5..65504 | 11 | 16 |
| Single presicion | float | -3,4×1038..3,4×1038 | 23 | 32 |
| Double precision | double | -1,7×10308..1,7×10308 | 53 | 64 |
| Extended precision | На некоторых архитектурах (например в сопроцессоре Intel) long double | -3,4×104932..3,4×104932 | 65 | 80 |
Особые значения чисел с плавающей точкой
Ноль (со знаком)
Как уже было оговорено выше, в нормализованной форме числа с плавающей точкой невозможно представить ноль. Поэтому для его представления зарезервированы специальные значения мантиссы и порядка — число считается нулём, если все его биты, кроме знакового, равны нулю. При этом в зависимости от значения бита знака ноль может быть как положительным, так и отрицательным.
| Знак | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Порядок | Мантисса | ||||||||||||||||
| 0/1 | 0 | 0 | 0 | 0 | 0 | 1, | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | = |
| 14 | 10 | 9 | 0 |
Арифметика нуля со знаком
Арифметика отрицательного нуля аналогична таковой для любого отрицательного числа и понятна интуитивно. Вот несколько примеров:
- (если )
- (если )
Неопределенность (NaN)
NaN — это аббревиатура от фразы “not a number“. NaN является результатом арифметических операций, если во время их выполнения произошла ошибка (примеры см. ниже). В IEEE 754 NaN представлен как число, в котором все двоичные разряды порядка — единицы, а мантисса не нулевая.
| Знак | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Порядок | Мантисса | ||||||||||||||||
| 0/1 | 1 | 1 | 1 | 1 | 1 | 1, | 0/1 | 0/1 | 0/1 | 0/1 | 0/1 | 0/1 | 0/1 | 0/1 | 0/1 | 0/1 | = |
| 14 | 10 | 9 | 0 |
Любая операция с NaN возвращает NaN. При желании в мантиссу можно записывать информацию, которую программа сможет интерпретировать. Стандартом это не оговорено и мантисса чаще всего игнорируется.
Как можно получить NaN?
- , где
Есть и другие способы получения NaN, подробности можно найти по ссылкам в соответствующем разделе.
По определению NaN ≠ NaN, поэтому, для проверки значения переменной нужно просто сравнить ее с собой.
Бесконечности
В число с плавающей запятой можно записать значение или . Как и нули со знаком, бесконечности позволяют получить хотя бы близкий к правильному результат вычисления в случае переполнения. Согласно стандарту IEEE 754 число с плавающей запятой считается равным бесконечности, если все двоичные разряды его порядка — единицы, а мантисса равна нулю. Знак бесконечности определяется знаковым битом числа.
| Знак | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Порядок | Мантисса | ||||||||||||||||
| 0/1 | 1 | 1 | 1 | 1 | 1 | 1, | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | = |
| 14 | 10 | 9 | 0 |
Получить бесконечность можно при переполнении и при делении ненулевого числа на ноль. При этом
Денормализованные числа
Денормализованные числа (англ. denormalized/subnormal numbers) – это способ увеличить количество представимых числом с плавающей запятой значений около нуля, дабы повысить точность вычислений. Каждое значение денормализованного числа меньше самого маленького нормализованного (“обычного”) значения числа с плавающей запятой.
Согласно стандарту, если порядок равен своему минимальному значению (все его биты — нули, а истинное значение порядка равно его сдвигу) и все биты мантиссы равны нулю, то это . Если же мантисса не равна нулю, то это число с порядком, на единицу большим минимального (все биты порядка, кроме младшего — нули) и данной мантиссой, целая часть которой считается равной нулю, а не единице.
То есть число с плавающей запятой, при учете вышесказанного, можно задать следующим образом:
- , если (нормализованное число)
- , если (денормализованное число)
Где — бит знака, — последовательность битов мантиссы, — значение порядка (с учетом сдвига), — минимальное значение порядка, используемое для записи чисел (1 — сдвиг) , — минимальное значение порядка, которое он в принципе может принять (все биты нули, 0 — сдвиг).
Хоть денормализованные числа и позволяют бороться с погрешностями и обрабатывать очень маленькие значения, за эти возможности приходится дорого платить. Ввиду сложности денормализованные числа крайне редко реализуют на аппаратном уровне – вместо этого используются программные реализации, работающие значительно медленнее.
В современных процессорах обработка денормализованных чисел происходит в десятки раз медленнее, чем обработка нормализованных чисел. Ниже приведена часть таблицы из статьи Isaac Dooley, Laxmikant Kale “Quantifying the Interference Caused by Subnormal Floating-Point Values”[1]
| Производитель | Процессор | Замедление (разы) |
|---|---|---|
| IBM | PowerPC 970 | 2,4 |
| AMD | Athlon | 6,0 |
| Intel | Pentium 3 | 15,8 |
| AMD | Athlon 64 | 21,4 |
| AMD | Opteron64 | 23,8 |
| Intel | Core Duo | 44,2 |
| Intel | P4 Xeon | 97,9 |
| Intel | Pentium 4 | 131,0 |
| Intel | Itanium 2 | 183,2 |
| Sun | UltraSPARC IV | 520,0 |
В таблице приведены наихудшие результаты тестирования среди всех использованных компиляторов (gcc, icc, xlc) со всеми доступными флагами оптимизации. Исследователи утверждают, что различие среднего случая с худшим незначительно.
Поскольку в стандартных форматах (одинарной и двойной точности) денормализованные числа получаются действительно очень маленькими и практически никак не влияют на результат некоторых вычислений (при этом заметно замедляя их скорость), то иногда они просто игнорируются. При этом используются два простых механизма, получивших называние Flush-to-zero (FTZ) и Denormals-are-zero (DAZ). Первый механизм заставляет операции возвращать ноль, как только становится ясно, что результат будет денормализованным. Второй механизм заставляет операции рассматривать поступающие на вход денормализованные числа как нули.
Ярким примером подобного “отсечения” денормализованных чисел могут послужить видеокарты, в которых резкое падение скорости вычислений в сотню раз недопустимо. Так же, например, в областях, связанных с обработкой звука, нет нужды в очень маленьких числах, поскольку они представляют столь тихий звук, что его не способно воспринять человеческое ухо.
В версии стандарта IEEE 754-2008 денормализованные числа (denormal или denormalized numbers) были переименованы в subnormal numbers, то есть в числа, меньшие “нормальных”. Поэтому их иногда еще называют “субнормальными“.
Действия с числами с плавающей запятой
Умножение и деление
Самыми простыми для восприятия арифметическими операциями над числами с плавающей запятой являются умножение и деление. Для того, чтобы умножить два вещественных числа в нормализованной форме необходимо перемножить их мантиссы, сложить порядки, округлить и нормализовать полученное число.
Соответственно, чтобы произвести деление нужно разделить мантиссу делимого на мантиссу делителя и вычесть из порядка делимого порядок делителя. Затем точно так же округлить мантиссу результата и привести его к нормализованной форме.
Сложение и вычитание
Идея метода сложения и вычитания чисел с плавающей точкой заключается в приведении их к одному порядку. Сначала выбирается оптимальный порядок, затем мантиссы обоих чисел представляются в соответствии с новым порядком, затем над ними производится сложение/вычитание, мантисса результата округляется и, если нужно, результат приводится к нормализированной форме. Пример:
Выполним сложение чисел с плавающей точкой и смещенным порядком в 32-х разрядном формате и . Переведем в машинный вид. Для этого сначала переведем его в двоичную систему счисления.
Нормализуем полученное двоичное число по правилам машинной арифметики.
Найдем смещенный порядок. Так как в условии говорится о 32-разрядном представлении, то смещение порядка равно .
Число отрицательное, следовательно, в бите знака будет стоять единица.
Итак, первое число в машинном 32-разрядном представлении с плавающей точкой будет иметь вид: 10000111 (жирным шрифтом выделен порядок числа, длина мантиссы — 23 бита).
Переведем второе число в машинный вид, совершая те же действия.
= ,... ... В качестве мантиссы будут сохранены первые бита после запятой т.е. . Очевидно, что порядок со смещением у второго числа будет таким же, как и у первого.
Второе число положительное, следовательно, бит знака будет содержать ноль.
Итак в машинном 32-разрядном представлении второе число будет иметь вид:
10000111 Далее в арифметических операциях будет использоваться число ,=, а не = видимо для упрощения(хотя это не совсем корректно).
Порядки у слагаемых равны, поэтому пропускаем шаг выравнивания порядков и проводим вычитание мантисс по правилам двоичной арифметики. В компьютере этим занимается арифметический сопроцессор, встроенный в центральный процессор машины.
,
Приводим полученный результат к машинному виду. Для этого мы должны внести поправку в порядок — уменьшить его на единицу. Знак результата — положительный, следовательно, бит знака содержит ноль.
10000110
Проверим правильность наших вычислений. Переведем результат в десятичное представление.
Найдем реальный порядок результата, вычтя из него значение смещения .
Следовательно, число результата будет иметь вид:
,
Результат наших вычислений верен, так как - .
Алгоритм получения представления вещественного числа в памяти ЭВМ
Покажем преобразование действительного числа для представления его в
памяти ЭВМ на примере величины типа Double.
Как видно из таблицы, величина этого типа занимает в памяти байт. На
рисунке ниже показано, как здесь представлены поля мантиссы и порядка (нумерация битов осуществляется справа налево):
| Знак | Смещённый порядок | Мантисса |
|---|---|---|
| 63 | 62..52 | 51..0 |
Можно заметить, что старший бит, отведенный под мантиссу, имеет номер
, т.е. мантисса занимает младшие бита. Черта указывает здесь на
положение двоичной запятой. Перед запятой должен стоять бит целой части
мантиссы, но поскольку она всегда равна , здесь данный бит не требуется и
соответствующий разряд отсутствует в памяти (но он подразумевается).
Значение порядка хранится здесь не как целое число, представленное в
дополнительном коде. Для упрощения вычислений и сравнения действительных
чисел значение порядка в ЭВМ хранится в виде смещенного числа, т.е. к
настоящему значению порядка перед записью его в память прибавляется
смещение. Смещение выбирается так, чтобы минимальному значению порядка
соответствовал нуль. Например, для типа Double порядок занимает бит и
имеет диапазон от до , поэтому смещение равно ()
(). Наконец, бит с номером указывает на знак числа.
Таким образом, из вышесказанного вытекает следующий алгоритм для
получения представления действительного числа в памяти ЭВМ:
- перевести модуль данного числа в двоичную систему счисления;
- нормализовать двоичное число, т.е. записать в виде M 2p, где M —
мантисса (ее целая часть равна ()) и p — порядок, записанный в
десятичной системе счисления;
- прибавить к порядку смещение и перевести смещенный порядок в двоичную
систему счисления;
- учитывая знак заданного числа (0 — положительное; 1 — отрицательное),
выписать его представление в памяти ЭВМ.
Пример. Запишем код числа ,.
- Двоичная запись модуля этого числа имеет вид .
- Имеем
.
- Получаем смещенный порядок . Далее имеем
() ().
- Окончательно
1 10000000111 0011100001010000000000000000000000000000000000000000 63 62..52 51..0
Очевидно, что более компактно полученный код стоит записать следующим
образом: C073850000000000(16).
Другой пример иллюстрирует обратный переход от кода действительного
числа к самому числу.
Пример. Пусть дан код 3FEC600000000000(16) или
- Прежде всего замечаем, что это код положительного числа, поскольку в
разряде с номером записан нуль. Получим порядок этого числа:
() (); .
- Число имеет вид , или
,.
- Переводом в десятичную систему счисления получаем ,.
| 0 | 01111111110 | 1100011000000000000000000000000000000000000000000000 |
| 63 | 62..52 | 51..0 |
См. также
- Представление символов, таблицы кодировок
- Представление целых чисел: прямой код, код со сдвигом, дополнительный код
Примечания
- ↑ Статья Isaac Dooley, Laxmikant Kale “Quantifying the Interference Caused by Subnormal Floating-Point Values” (англ.)
Ссылки
Использованные материалы
На русском
- Википедия — Экспоненциальная запись
- Википедия — Число с плавающей запятой
- Википедия — Отрицательный и положительный ноль
- Хабрахабр — статья пользователя Yruslan “Что нужно знать про арифметику с плавающей запятой”
- Статья Лапшевой Е.Е. “Машинная арифметика с вещественными числами” Статья удалена
На английском
- Wikipedia — NaN
- Wikipedia — Floating point
- Wikipedia — IEEE 754-2008
Что стоит прочесть
- Материалы по стандарту IEEE 754 (англ.)
- Русский перевод стандарта IEEE 754
Сергей Андреевич Дремук
Эксперт по предмету «Информатика»
Задать вопрос автору статьи
В $60$-х и $70$-х гг. не было единопризнанного стандарта представления чисел с плавающей запятой, из-за чего программы того времени не были переносимыми приложениями. Также большой проблемой были «странности» разных компьютеров, которые нужно было знать и учитывать при создании программ.
В $1976$ году была появилась инициатива создать единый стандарт для представления чисел с плавающей запятой, что существенно упростило работу с числами.
Вычисления компьютера ограничены его памятью, поэтому дробная часть вещественных чисел не является бесконечной и хранится в памяти с определенной точностью.
Числа в нормализованном виде чаще всего записываются только на экране компьютера, поэтому принято запятую в них заменять на точку.
Принятый способ хранения вещественных (действительных) чисел в памяти компьютера использует нормализованную (экспоненциальную) запись действительных чисел.
Сделаем домашку
с вашим ребенком за 380 ₽
Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online
Бесплатное пробное занятие
*количество мест ограничено
Для хранения вещественных чисел (как и для целых) используется двоичная система. Таким образом, число предварительно должно быть переведено двоичный код.
Нормализованная запись числа
Определение 1
Запись в виде
[a=pm mcdot q^n]
является нормализованной записью отличного от нуля действительного числа,
где $n$ — любое целое число (в том числе и ноль),
$m$ — правильная дробь в системе счисления с основой $q$, у которой первая цифра после запятой не равна нулю, то есть $frac{1}{q}le m
$m$ называется мантиссой числа, $n$ — порядком числа, $q$ — основанием системы счисления.
Пример 1
Приведем числа десятеричной системы к нормализованной записи:
[1.3579=0.13579cdot {10}^1;] [10000=0.1cdot {10}^5;] [0,123456=0.123456cdot {10}^0.]
Приведем число восьмеричной системы счисления к нормализованной записи:
${0,0000119}_8={0.119}_8cdot 8^{-4}$ (порядок записан в десятичной системе).
Приведем число двоичной системы счисления к нормализованной записи:
[{200.002}_2={0.200002}_2cdot 2^{-3}.]
«Хранение в памяти вещественных чисел» 👇
Ноль в десятичной системе будет записан в нормализованном виде следующим образом:
Определение 2
Нормализованная экспоненциальная запись (НЭЗ) числа – это запись в виде
[a=pm mcdot q^n,]
где $n$ — любое целое число (в том числе и ноль),
$m$ — правильная дробь в системе счисления с основой $q$, целая часть которой состоит из одной цифры,
$m$ –мантисса числа, а $n$ — порядок (или экспонента) числа.
Рассмотрим вышеописанные числа в нормализованной экспоненциальной записи.
Пример 2
НЭЗ десятичных чисел:
[1.3579=0.13579cdot {10}^1=1.3579cdot {10}^0;] [10000=0.1cdot {10}^5=1.0cdot {10}^4;] [0.123456=0.123456cdot {10}^0=1.23456cdot {10}^{-1}.]
НЭЗ восьмеричного числа:
[{0.0000119}_8={0.119}_8cdot 8^{-4}={1.19}_8cdot 8^{-5}.]
НЭЗ двоичного числа:
[{200.002}_2={0.200002}_2cdot 2^{-3}={2.00002}_2cdot 2^{-4}.]
Замечание 1
Обратите внимание, что в НЭЗ записи первая цифра после запятой может быть нулём, в отличие от нормализованной записи.
Хранение чисел с плавающей запятой
Для хранения вещественных чисел в памяти компьютера часть разрядов ячейки отводится для записи порядка числа, остальные — для записи мантиссы. По одному разряду в каждой группе разрядов отводится для знака порядка и знака мантиссы. Чтобы не хранить знак порядка был придуман смещенный порядок.
Если для задания порядка выделено k разрядов, то к истинному порядку (ИП) прибавляют смещение, таким образом, смещённый порядок (СП) рассчитывается по формуле:
Пример 3
Найдем смещённый порядок для истинного порядка, лежащего в диапазоне от $-127$ до $+128$.
Возьмем начальное значение ИП= $-127$:
[СП=-127+2^{8-1}-1=-127+128-1=0.]
Возьмем конечное значение ИП = $128$:
[СП=128+2^{8-1}-1=128+128-1=255.]
Таким образом, ИП, лежащий в диапазоне от $-127$ до $+128$, представляется смещённым порядком, значения которого меняются в диапазоне от $0$ до $255$.
Алгоритм представления вещественного числа:
-
Перевести число в двоичную систему счисления.
-
Привести число к нормализованной записи.
-
Найти смещённый порядок числа.
-
Поместить знак, порядок и мантиссу в соответствующие разряды.
Пример 4
Представим число $-25.625$ в $4$-байтовом представлении ($1$ бит отводится под знак числа, $8$ бит — под смещённый порядок, остальные биты — под мантиссу).
Будем действовать по алгоритму:
-
Переведем число $-25.625$ в двоичный код:
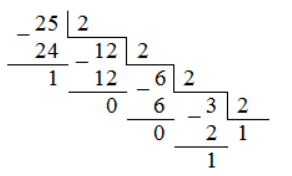
Рисунок 1.
[{25}_{10}={11001}_2]
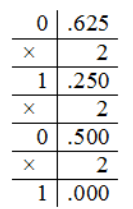
Рисунок 2.
[{25}_{10}={11001}_2] [{0.625}_{10}={0.101}_2] [{-25.625}_{10}={-11001.101}_2]
-
Приведем число к нормализованному виду:
[{-11001.101}_2={-1.1001101}_2cdot 2^4]
-
Найдем смещенный порядок числа:
[СП=127+4=131]
-
Поместим знак, порядок и мантиссу в соответствующие разряды:

Рисунок 3.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Для
представления вещественных чисел в
современных компьютерах принят способ
представления с
плавающей запятой.
Этот способ представления опирается
на нормализованную (экспоненциальную)
запись действительных чисел.
Как
и для целых чисел, при представлении
действительных чисел в компьютере чаще
всего используется двоичная система,
следовательно, предварительно десятичное
число должно быть переведено двоичную
систему.
Нормализованная запись числа.
Нормализованная
запись отличного
от нуля действительного числа – это
запись вида a= ![]() m*Pq,
m*Pq,
где q – целое число (положительное,
отрицательное или ноль), а m – правильная
P-ичная дробь, у которой первая цифра
после запятой не равна нулю, то есть ![]() .
.
При этом m называетсямантиссойчисла,
q – порядком числа.
Примеры:
-
3,1415926 =
0, 31415926 * 101; -
1000=0,1 *
104; -
0,123456789
= 0,123456789 * 100; -
0,00001078 =
0,1078 * 8-4;
(порядок записан в 10-й системе) -
1000,00012 =
0, 100000012 * 24.
Так
как число ноль не может быть записано
в нормализованной форме в том виде, в
каком она была определена, то считаем,
что нормализованная запись нуля в 10-й
системе будет такой:
0
= 0,0 * 100.
Нормализованная
экспоненциальная запись числа
– это запись вида a= ![]() m*Pq,
m*Pq,
где q – целое число (положительное,
отрицательное или ноль), а m – P-ичная
дробь, у которой целая часть состоит из
одной цифры. При этом (m-целая часть)
называется мантиссой числа,
q – порядком числа.
Представление чисел с плавающей запятой.
При
представлении чисел с плавающей запятой
часть разрядов ячейки отводится для
записи порядка числа, остальные разряды
– для записи мантиссы. По одному разряду
в каждой группе отводится для изображения
знака порядка и знака мантиссы. Для
того, чтобы не хранить знак порядка, был
придуман так называемый смещённый
порядок,
который рассчитывается по формуле
2a-1+ИП,
где a – количество разрядов, отводимых
под порядок.
Пример:
Если
истинный порядок равен -5, тогда смещённый
порядок для 4-байтового числа будет
равен 127-5=122.
Алгоритм представления числа с плавающей запятой.
-
Перевести
число из p-ичной системы счисления в
двоичную; -
представить
двоичное число в нормализованной
экспоненциальной форме; -
рассчитать
смещённый порядок числа; -
разместить
знак, порядок и мантиссу в соответствующие
разряды сетки.
Пример:
Представить
число -25,625 в машинном виде с использованием
4 байтового представления (где 1 бит
отводится под знак числа, 8 бит – под
смещённый порядок, остальные биты – под
мантиссу).

2510=1000112
0,62510=0,1012
-25,62510=
-100011,1012
2.
-100011,1012 =
-1,000111012 *
24
3.
СП=127+4=131
4.

Можно
заметить, что представление действительного
числа не очень удобно изображать в
двоичной системе, поэтому часто используют
шестнадцатеричное представление:

Окончательный
ответ: C1CD0000.
Если целые числа представлены в памяти компьютера в формате с фиксированной запятой, то для вещественных чисел такое ограничение существенно сократило бы диапазон представляемых чисел. Для вещественных чисел реализуется другой формат представления — формат с плавающей запятой. В разрядной сетке хранится запись числа, состоящая из трёх частей: знака, порядка и мантиссы. Как и в формате с фиксированной запятой, знак (0) — число положительное, (1) — отрицательное. Порядок — целое число в коде со сдвигом, а мантисса — в нормализованном виде. Порядок выбирается так, чтобы минимальному значению порядка соответствовало число (0). В этом случае хранить знак порядка не нужно.

Для числа в (32)-разрядной сетке под знак порядка отводится один бит, под значение порядка — (7) бит, под мантиссу числа со знаком — (24) бита. Так как под порядок отводится (7) бит, значит, числа могут быть представлены от (-64) до (63). То есть значение порядка должно сместиться на (64), чтобы минимальному значению порядка соответствовало число (0).
Представь данное вещественное число в виде кода в (32)-разрядной сетке:
Переведём число в шестнадцатеричную систему счисления:
.
Нормализуем:
A=7D08,816=0,7D08816×(1016)4.
Порядок смещается на
6410= 4016
; прибавляем (4), которое получилось при нормализации числа; получаем значение порядка:
px = 4416 = 0100 01002
.

Для более компактной записи используем шестнадцатеричный код:
Пример (2)
Представь данное вещественное число в виде кода в (32)-разрядной сетке:
Переведём число в шестнадцатеричную систему счисления:
A=−32008,510=−7D08,816.
Нормализуем:
A=−7D08,816=−0,7D08816×(1016)4.
Порядок смещается на
6410= 4016
; прибавляем (4), которое получилось при нормализации числа; получаем значение порядка:
px = 4416 = 0100 01002
.

Для более компактной записи используем шестнадцатеричный код:
Определи десятичное значение приведённого кода числа:
Запишем двоичный эквивалент кода:
[KB]=11000001010000000000000000000000.
Старший бит показывает, что число — отрицательное. Порядок (1) во второй слева тетраде показывает, что при нормализации значимую часть числа сдвинули на один знак вправо. Дробная часть мантиссы (01) при переводе из двоичной системы счисления в десятичную равна (1/4), или (0,25).
Таким образом:
B=−2,510(−0,2510×10101=−0,012×1021=−0,416×10161).
На чтение 4 мин Просмотров 4.1к. Опубликовано 04.07.2019
Содержание
- Содержание статьи
- Значение мантиссы
- Форма мантиссы
- Что ты хочешь узнать?
- Ответ
Содержание статьи

- Что такое мантисса
- Что такое семантика
- Что такое квинтэссенция
Значение мантиссы
Мантисса — одна из частей числа, которое представлено форматом с плавающей точкой. Второй частью этого числа является показатель степени. По сути, это дробная составляющая логарифма.
Значение мантиссы в том, что по ней находится число, которое является источником логарифма. Целая часть показывает только степень десяти или тривиальный множитель, тогда как сама мантисса показывает, какое именно число должно быть умножено на тривиальный множитель, который имеет вид 0,001 или 100.
Экспоненциальная запись представляет это в следующем виде: N = M*n^p, где мантиссой является M. Для примера можно взять число 3600 и представить его в экспоненциальной записи. Получится следующее: 3600 = 3,6*10^3. Учитывая вышесказанное, мантиссой будет являться число 3,6.
Важно понимать, что число, имеющее плавающую запятую, также имеет изменяющуюся абсолютную точность и фиксированную относительную точность. Использование чисел с плавающей запятой лучше, чем представление чисел с фиксированной запятой, так как есть возможность применения большого диапазона значений, тогда как относительная точность не меняется. Это поможет понять следующий пример: форма, имеющая фиксированную запятую, позволяет представить число, которое занимает 2 разряда после запятой и 8 разрядов в целой части, в виде 8765,43; 123456,78 и так далее. Если же брать формат, имеющий плавающую запятую, можно произвести следующую запись: 1,2345678; 0,000012345678 и так далее. Однако для того, чтобы так сделать, важно иметь двухразрядное дополнительное поле, позволяющее записать показатели степени 10, начиная от 0 и кончая 1610. Общее число разрядов составит 10, то есть 8+2.
Мантисса, как для отрицательных, так и для положительных чисел, выражается в прямом коде. Различие в знаке будет отражено лишь в значении знакового разряда. Однако мантисса числа не может превышать единицы. Обычно точка в мантиссе располагается с левой стороны от старшего разряда. Для того, чтоб получить истинное значение числа, нужно умножить мантиссу на 16 в степени порядка. Порядок, полученный этим путем, называется характеристикой. Получается, что характеристика, которая отсчитывается от 64, будет всегда положительной.
В нормальной записи мантисса числа — всегда правильная дробь. Ее запись в ячейку производится так же, как запись числа с запятой в ячейку машины. Запятая фиксируется перед первым разрядом цифрового вида.
Мантисса числа, имеющая плавающую запятую, выражается шестнадцатеричными цифрами, при этом запятая располагается слева от самой высокой цифры мантиссы
Форма мантиссы
Есть две формы, позволяющие понять место применения мантиссы. Первая — нормальная форма числа. Эта форма, которая имеет мантиссу без учета знака на полуинтервале, то есть [0; 1) (0le a
Скорость выполнения компьютером операций с числами, представленными в форме с плавающей запятой, измеряется в мегафлопcах (от англ. FLOPS — число операций с плавающей запятой в секунду) , гигафлопcах и так далее, и является одной из основных единиц измерения быстродействия вычислительных систем.
[править] Структура числа
Число с плавающей запятой состоит из:
* Мантиссы (выражающей значение числа без учёта порядка)
* Знака мантиссы (указывающего на отрицательность или положительность числа)
* Порядка (выражающего степень основания числа, на которое умножается мантисса)
* Знака порядка
[править] Нормальная форма и нормализованная форма
Что ты хочешь узнать?
Ответ

Нормализация мантиссы позволяет сэкономить один разряд в ее двоичном представлении. В обоих случаях заранее известно, что первый значащий разряд равен единице, поэтому его можно не хранить. Иногда это называется использованием неявного старшего бита.
Нормализация мантиссы результата независимо от режима не выполняется.
Нормализация мантиссы результата заключается в повторении операции сдвига мантиссы на один десятичный разряд с обнулением младшего разряда, а также в уменьшении порядка на единицу до тех пор, пока в знаковом разряде К2 ( Д9) не будет находиться наибольшая значащая цифра мантиссы. При переполнении разрядной сетки в области мантиссы выполнение этой процедуры может привести к переполнению разрядной сетки в области порядка.
00111001000100100000000000000000 — нули слева убираем:
111001000100100000000000000000 — нормализуем мантиссу:
1.11001000100100000000000000000 х 2^29.

