Что такое сортировка и зачем она нужна
Сортировка распределяет элементы в порядке, удобном для работы. Если отсортировать массив чисел в порядке убывания, то первый элемент всегда будет наибольшим, а последний наименьшим. Поэтому желательно хранить информацию упорядочено, чтобы было проще проводить над ней операции.
В данной статье вы научитесь разным техникам сортировок на языке С++. Мы затронем 7 видов:
- Пузырьковая сортировка (Bubble sort);
- Сортировка выбором (Selection sort);
- Сортировка вставками (Insertion sort);
- Быстрая сортировка (Quick sort);
- Сортировка слиянием (Merge sort);
- Сортировка Шелла (Shell sort);
- Сортировка кучей (Heap sort).
Знание этих техник поможет получить работу. На площадке LeetCode содержится более 200 задач, связанных с сортировками. 19 из них входят в топ частых вопросов на собеседованиях по алгоритмам.
1. Пузырьковая сортировка
В пузырьковой сортировке каждый элемент сравнивается со следующим. Если два таких элемента не стоят в нужном порядке, то они меняются между собой местами. В конце каждой итерации (далее называем их проходами) наибольший/наименьший элемент ставится в конец списка.
Прежде чем писать код, разберем сортировку визуально на примере массива из пяти элементов. Отсортируем его в порядке возрастания.
Проход №1
Оранжевым отмечаются элементы, которые нужно
поменять местами. Зеленые уже стоят в нужном порядке.
Наибольший элемент — число 48 — оказался в конце
списка.
Проход №2
Наибольший элемент уже занимает место в конце
массива. Чтобы поставить следующее число по убыванию, можно пройтись лишь до 4-й позиции, а не пятой.
Проход №3
Проход №4
После четвертого прохода получаем
отсортированный массив.
Функция сортировки в качестве параметров будет принимать указатель на массив и его размер. Функцией swap() элементы
меняются местами друг с другом:
#include <iostream>
using namespace std;
void bubbleSort(int list[], int listLength)
{
while(listLength--)
{
bool swapped = false;
for(int i = 0; i < listLength; i++)
{
if(list[i] > list[i + 1])
{
swap(list[i], list[i + 1]);
swapped = true;
}
}
if(swapped == false)
break;
}
}
int main()
{
int list[5] = {3,19,8,0,48};
cout << "Input array ..." << endl;
for(int i = 0; i < 5; i++)
cout << list[i] << 't';
cout << endl;
bubbleSort(list, 5);
cout << "Sorted array ..." << endl;
for(int i = 0; i < 5; i++)
cout << list[i] << 't';
cout << endl;
}
Сложность в лучшем случае: O(n).
Сложность в среднем случае: O(n2).
Сложность в худшем случае: O(n2).
2. Сортировка выбором
Ищем наименьшее значение в массиве и ставим
его на позицию, откуда начали проход. Потом двигаемся на следующую позицию.
Возьмем тот же массив из пяти элементов и отсортируем его.
Проход №1
Зеленым отмечается наименьший элемент в
подмассиве — он ставится в начало списка.
Проход №2
Число 4 — наименьшее в оставшейся части массива.
Перемещаем четверку на вторую позицию после числа 0.
Проход №3
Проход №4
Напишем функцию поиска наименьшего элемента и
используем ее в сортировке:
int findSmallestPosition(int list[], int startPosition, int listLength)
{
int smallestPosition = startPosition;
for(int i = startPosition; i < listLength; i++)
{
if(list[i] < list[smallestPosition])
smallestPosition = i;
}
return smallestPosition;
}
#include <iostream>
using namespace std;
int findSmallestPosition(int list[], int startPosition, int listLength)
{
int smallestPosition = startPosition;
for(int i = startPosition; i < listLength; i++)
{
if(list[i] < list[smallestPosition])
smallestPosition = i;
}
return smallestPosition;
}
void selectionSort(int list[], int listLength)
{
for(int i = 0; i < listLength; i++)
{
int smallestPosition = findSmallestPosition(list, i, listLength);
swap(list[i], list[smallestPosition]);
}
return;
}
int main ()
{
int list[5] = {12, 5, 48, 0, 4};
cout << "Input array ..." << endl;
for(int i = 0; i < 5; i++)
cout << list[i] << 't';
cout << endl;
selectionSort(list, 5);
cout << "Sorted array ..." << endl;
for(int i = 0; i < 5; i++)
cout << list[i] << 't';
cout << endl;
}
Сложность в любом случае: O(n2).
3. Сортировка вставками
В сортировке вставками начинаем со второго
элемента. Проверяем между собой второй элемент с первым и, если надо, меняем местами.
Сравниваем следующую пару элементов и проверяем все пары до нее.
Проход №1. Начинаем со второй позиции.
Число 12 больше 5 — элементы меняются местами.
Проход №2. Начинаем с третьей позиции.
Проверяем вторую и третью позиции. Затем
первую и вторую.
Проход №3. Начинаем с четвертой позиции.
Произошло три смены местами.
Проход №4. Начинаем с последней позиции.
Получаем отсортированный массив на выходе.
#include <iostream>
using namespace std;
void insertionSort(int list[], int listLength)
{
for(int i = 1; i < listLength; i++)
{
int j = i - 1;
while(j >= 0 && list[j] > list[j + 1])
{
swap(list[j], list[j + 1]);
cout<<"ndid";
j--;
}
}
}
int main()
{
int list[8]={3,19,8,0,48,4,5,12};
cout<<"Input array ...n";
for (int i = 0; i < 8; i++)
{
cout<<list[i]<<"t";
}
insertionSort(list, 8);
cout<<"nnSorted array ... n";
for (int i = 0; i < 8; i++)
{
cout<<list[i]<<"t";
}
return 0;
}
Сложность в лучшем случае: O(n).
Сложность в худшем случае: O(n2).
4. Быстрая сортировка
В основе быстрой сортировки лежит стратегия
«разделяй и властвуй». Задача разделяется на более мелкие подзадачи. Подзадачи
решаются отдельно, а потом решения объединяют. Точно так же, массив разделяется
на подмассивы, которые сортируются и затем сливаются в один.
В первую очередь выбираем опорный элемент.
Отметим его синим. Все значения больше опорного элемента ставятся после него,
остальные — перед.
На иллюстрации массив разделяется по опорному
элементу. В полученных массивах также выбираем опорный элемент и разделяем по
нему.
Опорным может быть любой элемент. Мы выбираем
последний в списке.
Чтобы расположить элементы большие — справа от
опорного элемента, а меньшие — слева, будем двигаться от начала списка. Если
число будет больше опорного, то оно ставится на его место, а сам опорный на
место перед ним.
Напишем функцию разделения partition(),
которая возвращает индекс опорного элемента, и используем ее в сортировке.
int partition(int list[], int start, int pivot)
{
int i = start;
while(i < pivot)
{
if(list[i] > list[pivot] && i == pivot-1)
{
swap(list[i], list[pivot]);
pivot--;
}
else if(list[i] > list[pivot])
{
swap(list[pivot - 1], list[pivot]);
swap(list[i], list[pivot]);
pivot--;
}
else i++;
}
return pivot;
}
#include <iostream>
using namespace std;
int partition(int list[], int start, int pivot)
{
int i = start;
while(i < pivot)
{
if(list[i] > list[pivot] && i == pivot-1)
{
swap(list[i], list[pivot]);
pivot--;
}
else if(list[i] > list[pivot])
{
swap(list[pivot - 1], list[pivot]);
swap(list[i], list[pivot]);
pivot--;
}
else i++;
}
return pivot;
}
void quickSort(int list[], int start, int end)
{
if(start < end)
{
int pivot = partition(list, start, end);
quickSort(list, start, pivot - 1);
quickSort(list, pivot + 1, end);
}
}
int main()
{
int list[6]={2, 12, 5, 48, 0, 4};
cout<<"Input array ...n";
for (int i = 0; i < 6; i++)
{
cout<<list[i]<<"t";
}
quickSort(list, 0, 6);
cout<<"nnSorted array ... n";
for (int i = 0; i < 6; i++)
{
cout<<list[i]<<"t";
}
return 0;
}
Сложность в лучшем случае: O(n*logn).
Сложность в худшем случае: O(n2).
5. Сортировка слиянием
Сортировка слиянием также следует стратегии
«разделяй и властвуй». Разделяем исходный массив на два равных подмассива.
Повторяем сортировку слиянием для этих двух подмассивов и объединяем обратно.
Цикл деления повторяется, пока не останется по
одному элементу в массиве. Затем объединяем, пока не образуем полный список.
Алгоритм сортировки состоит из четырех этапов:
- Найти середину массива.
- Сортировать массив от
начала до середины. - Сортировать массив от
середины до конца. - Объединить массив.
void merge(int list[],int start, int end, int mid);
void mergeSort(int list[], int start, int end)
{
int mid;
if (start < end){
mid=(start+end)/2;
mergeSort(list, start, mid);
mergeSort(list, mid+1, end);
merge(list,start,end,mid);
}
}
Для объединения напишем отдельную функцию
merge().
Алгоритм объединения массивов:
- Циклично проходим по
двум массивам.. - В объединяемый ставим тот элемент, что меньше.
- Двигаемся дальше, пока не дойдем до конца
обоих массивов.
#include <iostream>
using namespace std;
void merge(int list[],int start, int end, int mid);
void mergeSort(int list[], int start, int end)
{
int mid;
if (start < end){
mid=(start+end)/2;
mergeSort(list, start, mid);
mergeSort(list, mid+1, end);
merge(list,start,end,mid);
}
}
void merge(int list[],int start, int end, int mid)
{
int mergedList[8];
int i, j, k;
i = start;
k = start;
j = mid + 1;
while (i <= mid && j <= end) {
if (list[i] < list[j]) {
mergedList[k] = list[i];
k++;
i++;
}
else {
mergedList[k] = list[j];
k++;
j++;
}
}
while (i <= mid) {
mergedList[k] = list[i];
k++;
i++;
}
while (j <= end) {
mergedList[k] = list[j];
k++;
j++;
}
for (i = start; i < k; i++) {
list[i] = mergedList[i];
}
}
int main()
{
int list[8]={3,19,8,0,48,4,5,12};
cout<<"Input array ...n";
for (int i = 0; i < 8; i++)
{
cout<<list[i]<<"t";
}
mergeSort(list, 0, 7);
cout<<"nnSorted array ... n";
for (int i = 0; i < 8; i++)
{
cout<<list[i]<<"t";
}
}
Сложность в любом случае: O(n*logn).
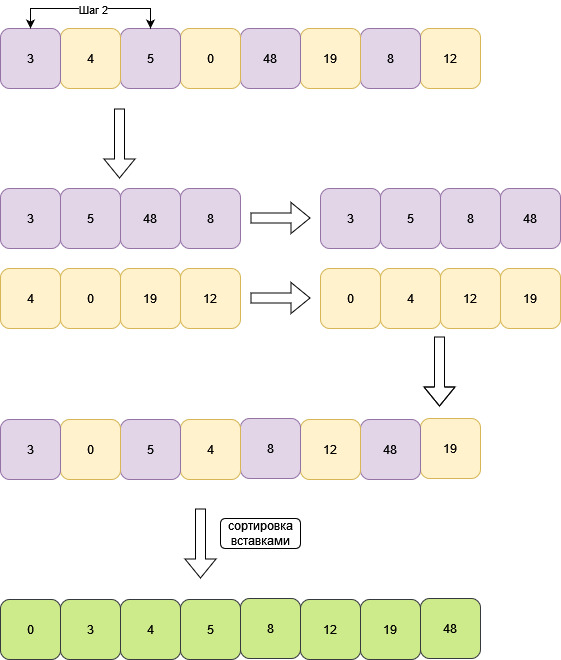
6. Сортировка Шелла
Алгоритм включает в себя сортировку вставками.
Исходный массив размером N разбивается на подмассивы с шагом N/2. Подмассивы
сортируются вставками. Затем вновь разбиваются, но уже с шагом равным N/4. Цикл
повторяется. Производим целочисленное деление шага на два каждую итерацию.
Когда шаг становится равен 1, массив просто сортируется вставками.
У массива размером с 8, первый шаг будет равен 4.
Уменьшаем шаг в два раза. Шаг равен 2.
#include <iostream>
using namespace std;
void shellSort(int list[], int listLength)
{
for(int step = listLength/2; step > 0; step /= 2)
{
for (int i = step; i < listLength; i += 1)
{
int j = i;
while(j >= step && list[j - step] > list[i])
{
swap(list[j], list[j - step]);
j-=step;
cout<<"ndid";
}
}
}
}
int main()
{
int list[8]={3,19,8,0,48,4,5,12};
cout<<"Input array ...n";
for (int i = 0; i < 8; i++)
{
cout<<list[i]<<"t";
}
shellSort(list, 8);
cout<<"nnSorted array ... n";
for (int i = 0; i < 8; i++)
{
cout<<list[i]<<"t";
}
}
Сложность в лучшем и среднем случае:
O(n*logn).
Сложность в худшем случае: O(n2).
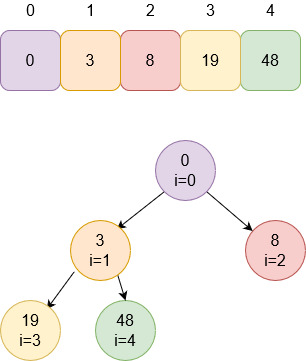
Исходный массив представляем в виде структуры
данных кучи. Куча – это один из
типов бинарного дерева.
У кучи есть следующие свойства:
- Родительский узел
всегда больше дочерних; - На i-ом слое 2i
узлов, начиная с нуля. То есть на нулевом слое 1 узел, на первом – 2 узла, на
втором – 4, и т. д. Правило для всех слоев, кроме последнего; - Слои заполняются слева направо.
После формирования кучи будем извлекать самый
старший узел и ставить на конец массива.
Алгоритм сортировки кучей:
- Формируем бинарное
дерево из массива. - Расставляем узлы в
дереве так, чтобы получилась куча (методheapify()). - Верхний элемент
помещаем в конец массива. - Возвращаемся на шаг 2, пока куча не опустеет.
Обращаться к дочерним узлам можно, зная, что
дочерние элементы i-го элемента находятся на позициях 2*i + 1 (левый узел) и
2*i + 2 (правый узел).
Изначальная куча:
Индекс с нижним левым узлом определим по
формуле n/2-1, где n – длина массива. Получается 5/2 – 1 = 2 – 1 = 1. С этого
индекса и начинаем операцию heapify(). Сравним дочерние узлы 1-й позиции.
Дочерний узел оказался больше. Меняем местами
с родителем.
Теперь проверяем родительский узел от позиции
1.
48 больше 3. Меняем местами.
После смены проверяем все дочерние узлы
элемента, который опустили. То есть для числа 3 проводим heapify(). Так как 3
меньше 19, меняем местами.
Наибольший элемент оказался наверху кучи.
Осталось поставить его в конце массива на позицию 4.
Теперь продолжаем сортировать кучу, но последний элемент игнорируем. Для
этого просто будем считать, что длина массива уменьшилась на 1.
Повторяем алгоритм сортировки, пока куча не
опустеет, и получаем отсортированный массив.
void heapify(int list[], int listLength, int root)
{
int largest = root;
int l = 2*root + 1;
int r = 2*root + 2;
if (l < listLength && list[l] > list[largest])
largest = l;
if (r < listLength && list[r] > list[largest])
largest = r;
if (largest != root)
{
swap(list[root], list[largest]);
heapify(list, listLength, largest);
}
}
#include <iostream>
using namespace std;
void heapify(int list[], int listLength, int root)
{
int largest = root;
int l = 2*root + 1;
int r = 2*root + 2;
if (l < listLength && list[l] > list[largest])
largest = l;
if (r < listLength && list[r] > list[largest])
largest = r;
if (largest != root)
{
swap(list[root], list[largest]);
heapify(list, listLength, largest);
}
}
void heapSort(int list[], int listLength)
{
for(int i = listLength / 2 - 1; i >= 0; i--)
heapify(list, listLength, i);
for(int i = listLength - 1; i >= 0; i--)
{
swap(list[0], list[i]);
heapify(list, i, 0);
}
}
int main()
{
int list[5] = {3,19,8,0,48};
cout<<"Input array ..."<<endl;
for(int i = 0; i < 5; i++)
cout << list[i] << 't';
cout << endl;
heapSort(list, 5);
cout << "Sorted array"<<endl;
for(int i = 0; i < 5; i++)
cout << list[i] << 't';
cout << endl;
}
Сложность алгоритма в любом случае: O(n*logn).
***
В этой статье мы познакомились с семью видами
сортировок, рассмотрели их выполнение и написание на С++. Попробуйте применить
новые знания в решении задачек на LeetCode или Codeforces. Понимание подобных
алгоритмов поможет в будущем пройти собеседование.
Источники:
- https://www.softwaretestinghelp.com/sorting-techniques-in-cpp/
- https://medium.com/@ssbothwell/sorting-algorithms-and-big-o-analysis-332ce7b8e3a1
- https://www.programiz.com/dsa/shell-sort
- https://www.happycoders.eu/algorithms/sorting-algorithms/
***
Материалы по теме
- Какая сортировка самая быстрая? Тестируем алгоритмы
- Пузырьковая сортировка на JavaScript
- Вводный курс по алгоритмам: от сортировок до машины Тьюринга
***
Мне сложно разобраться самостоятельно, что делать?
Алгоритмы и структуры данных действительно непростая тема для самостоятельного изучения: не у кого спросить и что-то уточнить. Поэтому мы запустили курс «Алгоритмы и структуры данных», на котором в формате еженедельных вебинаров вы:
- изучите сленг, на котором говорят все разработчики независимо от языка программирования: язык алгоритмов и структур данных;
- научитесь применять алгоритмы и структуры данных при разработке программ;
- подготовитесь к техническому собеседованию и продвинутой разработке.
Курс подходит как junior, так и middle-разработчикам.
Зарегистрируйтесь для доступа к 15+ бесплатным курсам по программированию с тренажером
Алгоритмы сортировки
—
Основы алгоритмов и структур данных
В программировании часто встречаются задачи, которые трудно решить «в лоб». Представим, что нам нужно избавиться от повторяющихся элементов в массиве. Попробуем найти все числа, которые встречаются здесь больше, чем один раз:
7, 3, 1, 9, 10, 2, 3, 6, 9, 4, 7, 5, 5, 4, 2, 8, 4, 7Чтобы это сделать, нужно написать сложный алгоритм. Можно упростить задачу и отсортировать массив. В нем повторяющиеся элементы находятся рядом, поэтому их легко обнаружить, сравнивая соседние числа:
1, 2, 2, 3, 3, 4, 4, 4, 5, 5, 6, 7, 7, 7, 8, 9, 9, 10Не удивительно, что одной из самых полезных задач в программировании считается сортировка — перестановка элементов в массиве так, чтобы они располагались в убывающем или возрастающем порядке.
Чем полезна сортировка
Познакомимся с сортировкой поближе и выясним, где она встречается в практических задачах программиста.
Посмотрим на любой интернет-магазин. В каждом разделе встречаются сотни и тысячи товаров, из которых так сложно выбрать подходящий. Чтобы пользователям было удобнее, магазин предлагает сортировку товаров по цене, по рейтингу или по популярности.
При этом покупатели выбирают сортировку по своим целям:
-
По возрастанию цены в поисках выгодных предложений
-
По убыванию цены, если готовы на дорогую покупку
Чтобы интернет-магазин умел сортировать одни и те же записи по-разному, необходима универсальная функция сортировки, о которой поговорим в конце урока.
Три алгоритма сортировки
Существуют десятки алгоритмов сортировки, но изучать все слишком долго. Чтобы не останавливаться на этой теме, мы выбрали три фундаментальных алгоритма:
-
Пузырьковая сортировка
-
Сортировка выбором
-
Быстрая сортировка
Все три алгоритма сортируют исходный массив, меняя местами его элементы и не требуя дополнительного пространства.
Эти алгоритмы помогут понять, как работает сортировка. На их примере вы изучите, какие техники программисты применяют при разработке алгоритмов.
При реализации алгоритмов мы должны помнить о вырожденных случаях — массивах, в которых один или ноль элементов. Сортировка их не меняет, но наши алгоритмы должны обрабатывать эти случаи — иначе программа завершится с ошибкой.
Пузырьковая сортировка
Один из самых простых методов — пузырьковая сортировка. Это название произошло от ассоциации с воздухом в воде: на дне пузырьки совсем маленькие, но постепенно поднимаются к поверхности, собирают кислород и увеличиваются.
Похожий принцип работает и с элементами массива при такой сортировке. Посмотрите на этот рисунок:

Мы идем по массиву и перемещаем вправо самый большой элемент из просмотренных. Так мы находим элемент со значением 10, который в итоге побеждает во всех сравнениях и оказывается в правом конце массива.
Рассмотрим механизм работы данной сортировки на реальном примере. Возьмем массив и сравним элементы попарно от начала к концу: первый со вторым, второй с третьим, третий с четвертым и так далее.
Если два соседних элемента находятся в неправильном порядке, меняем их местами. После первого прохода самый большой элемент оказывается справа — его можно больше не сравнивать и не перемещать. Далее повторяем те же действия со всеми остальными числами.
Пузырьковая сортировка реализуется в JavaScript с помощью такой функции:
const bubbleSort = (items) => {
for (let limit = items.length - 1; limit > 0; limit -= 1) {
for (let i = 0; i < limit; i += 1) {
if (items[i] > items[i + 1]) {
const temporary = items[i];
items[i] = items[i + 1];
items[i + 1] = temporary;
}
}
}
};Python
def bubble_sort(items):
for limit in range(len(items) - 1, 0, -1):
for i in range(limit):
if items[i] > items[i + 1]:
items[i], items[i + 1] = items[i + 1], items[i]PHP
<?php
function bubbleSort($items)
{
for ($limit = count($items) - 1; $limit > 0; $limit -= 1) {
for ($i = 0; $i < $limit; $i += 1) {
if ($items[$i] > $items[$i + 1]) {
$temporary = $items[$i];
$items[$i] = $items[$i + 1];
$items[$i + 1] = $temporary;
}
}
}
}Java
class App {
public static void bubbleSort(int[] items) {
for (var limit = items.length - 1; limit > 0; limit--) {
for (var i = 0; i < limit; i++) {
if (items[i] > items[i + 1]) {
var temporary = items[i];
items[i] = items[i + 1];
items[i + 1] = temporary;
}
}
}
}
}Мы видим здесь два вложенных цикла. Внешний цикл ограничивает внутренний цикл на каждом проходе. Сначала он простирается до конца массива, но после первого прохода там оказывается максимальный элемент.
Внутренний цикл на следующем проходе движется до предпоследнего элемента, а затем до пред-пред-последнего — и так до тех пор, пока не остается один элемент в левой части:
for (let limit = items.length - 1; limit > 0; limit -= 1) {
// ...
}Python
for limit in range(len(items) - 1, 0, -1):
# ...PHP
<?php
for ($limit = count(items) - 1; $limit > 0; $limit -= 1) {
// ...
}Java
for (var limit = items.length - 1; limit > 0; limit--) {
// ...
}Мы помним, что в JavaScript элементы массива нумеруются с 0 — следовательно, индекс последнего элемента массива items равен items.length - 1.
Обмен двух элементов выполняется с помощью временной переменной, которую мы назвали temporary (т.е. временная):
const temporary = items[i];
items[i] = items[i + 1];
items[i + 1] = temporary;Python
# В Python временная переменная не требуется
items[i], items[i + 1] = items[i + 1], items[i]PHP
<?php
$temporary = $items[$i];
$items[$i] = $items[$i + 1];
$items[$i + 1] = $temporary;Java
var temporary = items[i];
items[i] = items[i + 1];
items[i + 1] = temporary;На каждом шаге мы находим наибольший элемент в массиве, а последний оставшийся неизбежно оказывается наименьшим — так мы получаем упорядоченный массив. Проверим работу алгоритма:
const items = [2, 3, 4, 3, 1, 2, 4, 5, 1, 2];
bubbleSort(items);
console.log(items); // => [1, 1, 2, 2, 2, 3, 3, 4, 4, 5]Python
items = [2, 3, 4, 3, 1, 2, 4, 5, 1, 2]
bubble_sort(items)
print(items) # => [1, 1, 2, 2, 2, 3, 3, 4, 4, 5]PHP
<?php
$items = [2, 3, 4, 3, 1, 2, 4, 5, 1, 2];
bubbleSort($items);
print_r($items); // => [1, 1, 2, 2, 2, 3, 3, 4, 4, 5]Java
int[] items = {2, 3, 4, 3, 1, 2, 4, 5, 1, 2};
App.bubbleSort(items);
System.out.println(Arrays.toString(items));
// => [1, 1, 2, 2, 2, 3, 3, 4, 4, 5]При пузырьковой сортировке соседние элементы часто меняются местами, поэтому она работает довольно медленно. Чтобы сэкономить время, можно сократить количество перестановок. В этом поможет сортировка выбором.
Сортировка выбором
Этот алгоритм сначала проводит операции сравнения и находит наименьший элемент, а только потом помещает его в начало массива. После первого прохода алгоритм исключает первый элемент из рассмотрения и ищет минимальный элемент в оставшейся части массива, а затем помещаем его на второе место:

Этот алгоритм работает гораздо быстрее пузырьковой сортировки, потому что сравнений здесь столько же, а вот обмен всего один — в самом конце.
Рассмотрим функцию, реализующую сортировку выбором в Java Script:
const selectionSort = (items) => {
for (let i = 0; i < items.length - 1; i += 1) {
let indexMin = i;
for (let j = i + 1; j < items.length; j += 1) {
if (items[j] < items[indexMin]) {
indexMin = j;
}
}
const temporary = items[i];
items[i] = items[indexMin];
items[indexMin] = temporary;
}
};Python
def selection_sort(items):
for i in range(len(items) - 1):
index_min = i
for j in range(i + 1, len(items)):
if items[j] < items[index_min]:
index_min = j
items[i], items[index_min] = items[index_min], items[i]PHP
<?php
function selectionSort($items)
{
for ($i = 0; i < count($items) - 1; $i += 1) {
$indexMin = $i;
for ($j = $i + 1; $j < count(items); $j += 1) {
if ($items[$j] < $items[$indexMin]) {
$indexMin = $j;
}
}
$temporary = $items[$i];
$items[$i] = $items[$indexMin];
$items[$indexMin] = $temporary;
}
}Java
class App {
public static void selectionSort(int[] items) {
for (var i = 0; i < items.length - 1; i++) {
var indexMin = i;
for (var j = i + 1; j < items.length; j++) {
if (items[j] < items[indexMin]) {
indexMin = j;
}
}
var temporary = items[i];
items[i] = items[indexMin];
items[indexMin] = temporary;
}
}
}В реализации мы сохраняем не сам минимальный элемент, а его индекс в массиве. Это нужно потому, что в конце каждого прохода минимальный элемент записывается в начало массива. При этом элемент, который был там до этого, нужно вставить куда-то в неупорядоченную половину — легче всего просто поменять их местами.
Быстрая сортировка
Можно сделать сортировку еще быстрее, если менять местами не соседние элементы, а элементы на самом большом расстоянии друг от друга.
Возьмем для примера массив, отсортированный в порядке убывания — от больших к меньшим. Чтобы разместить элементы в порядке возрастания, надо попарно поменять их местами: первый и последний, потом второй и предпоследний, и так далее, как показано на схеме:

Сортировки массива в обратном порядке реализуется так:
let left = 0;
let right = items.length - 1;
while (left < right) {
const temporary = items[left];
items[left] = items[right];
items[right] = temporary;
left += 1;
right -= 1;
}Python
left = 0
right = len(items) - 1
while left < right:
items[left], items[right] = items[right], items[left]
left += 1
right -= 1PHP
<?php
$left = 0;
$right = count($items) - 1;
while ($left < $right) {
$temporary = $items[$left];
$items[$left] = $items[$right];
$items[$right] = $temporary;
$left += 1;
$right -= 1;
}Java
var left = 0;
var right = items.length - 1;
while (left < right) {
var temporary = items[left];
items[left] = items[right];
items[right] = temporary;
left++;
right--;
}В примере выше мы создали две переменные-указателя. Переменная left указывает на следующий элемент для обмена слева, а переменная right — справа. Для обмена используем уже знакомую временную переменную temporary:
const temporary = items[left];
items[left] = items[right];
items[right] = temporary;Python
# В Python временная переменная не требуется
items[left], items[right] = items[right], items[left]PHP
<?php
$temporary = $items[$left];
$items[$left] = $items[$right];
$items[$right] = $temporary;Java
var temporary = items[left];
items[left] = items[right];
items[right] = temporary;На каждой итерации цикла после обмена мы увеличиваем левый указатель, сдвигая его вправо, и одновременно уменьшаем правый, сдвигая влево:
Python
PHP
<?php
$left += 1;
$right -= 1;Java
Похожий подход применяется в алгоритме быстрой сортировки. Он частично упорядочивает массив, перемещая в начало маленькие элементы, а в конец — большие.
Частичное упорядочивание делается с помощью программы, похожей на пример выше. Для начала выбираем опорный элемент — это условный средний элемент, который помогает отличить маленькие элементы от больших. Затем устанавливаем два указателя на начало и конец массива.
Принцип работы быстрой сортировки
Чтобы не запутаться в алгоритме быстрой сортировки, разберем его на схематичном примере. В самом начале наш массив выглядит так:

В качестве опорного элемента выбрано число 4. Левый указатель смотрит на 5, а правый — на 3.
Далее ищем неправильный элемент слева, двигая левый указатель и пропуская элементы меньше опорного. Затем двигаем правый указатель, пропуская элементы больше опорного.
Таким образом мы ищем пару элементов, в которой левый больше правого. Когда пара найдена, меняем элементы местами. В нашем примере 5 и 3 находятся в неправильной позиции — их надо поменять:

Ищем следующую пару для обмена. Справа от 3 находится 4 — наш следующий кандидат для обмена. Обратите внимание, что 4 — опорный элемент, но он тоже принимает участие в сравнениях и обменах.
Слева от числа 5 находятся числа 6, 9 и 7. Они больше опорного элемента 4, поэтому указатель их пропускает. В итоге он останавливается на числе 2:

Меняем их местами и ищем следующую пару. Следующие кандидаты — числа 10 и 1:

Меняем их местами и останавливаемся, потому что левый и правый указатели упираются друг в друга. Мы получили частично упорядоченный массив. Разбиваем его на две части там, где указатели встретились:

Продолжаем частичное упорядочивание левой и правой половин массива. Правая половина перед упорядочиванием показана на рисунке:

Выбираем новый опорный элемент из подмассива. На этот раз это 7. Сдвигая указатели, меняем местами пары 10 и 5, а также 8 и 6. Числа 4 и 9 останутся на своих местах. Частично упорядоченный подмассив принимает такой вид:

Левый и правый указатель встречаются посередине — на числе 7. Мы снова разбиваем массив на две половины и переходим к упорядочиванию левой и правой половин.
Как реализовать быструю сортировку
Попробуем реализовать алгоритм на JavaScript. Начнем с функции частичного упорядочивания:
const partition = (items, left, right, pivot) => {
while (true) {
while (items[left] < pivot) {
left += 1;
}
while (items[right] > pivot) {
right -= 1;
}
if (left >= right) {
return right + 1;
}
const temporary = items[left];
items[left] = items[right];
items[right] = temporary;
left += 1;
right -= 1;
}
};Python
def partition(items, left, right, pivot):
while True:
while items[left] < pivot:
left += 1
while items[right] > pivot:
right -= 1
if left >= right:
return right + 1
items[left], items[right] = items[right], items[left]
left += 1
right -= 1PHP
<?php
function partition($items, $left, $right, $pivot)
{
while (true) {
while ($items[$left] < $pivot) {
$left += 1;
}
while ($items[$right] > $pivot) {
$right -= 1;
}
if ($left >= $right) {
return $right + 1;
}
const temporary = $items[$left];
$items[$left] = $items[$right];
$items[$right] = temporary;
$left += 1;
$right -= 1;
}
}Java
class App {
public static int partition(int[] items, int left, int right, int pivot) {
while (true) {
while (items[left] < pivot) {
left++;
}
while (items[right] > pivot) {
right--;
}
if (left >= right) {
return right + 1;
}
var temporary = items[left];
items[left] = items[right];
items[right] = temporary;
left++;
right--;
}
}
}В качестве параметров функция получает:
-
Массив
items -
Указатели на левую и правую часть подмассива
leftиright -
Опорный элемент для сравнения
pivot
Сначала в цикле пропускаются элементы слева, которые меньше опорного:
while (items[left] < pivot) {
left += 1;
}Python
while items[left] < pivot:
left += 1PHP
<?php
while ($items[$left] < $pivot) {
$left += 1;
}Java
while (items[left] < pivot) {
left++;
}Затем пропускаются элементы справа, которые больше опорного:
while (items[right] > pivot) {
right -= 1;
}Python
while items[right] > pivot:
right -= 1PHP
<?php
while ($items[$right] > $pivot) {
$right -= 1;
}Java
while (items[right] > pivot) {
right--;
}Если указатели встретились или зашли друг за друга, мы завершаем цикл и возвращаем место встречи в качестве результата. Нам предстоит разбить массив на два подмассива, поэтому надо решить, что именно возвращать. Мы можем сказать, что граница — это место, где заканчивается левый подмассив, или место, где начинается правый. Большой разницы здесь нет.
Решим, что функция partition возвращает индекс элемента, где начинается правый подмассив:
if (left >= right) {
return right + 1;
}Python
if left >= right:
return right + 1PHP
<?php
if ($left >= $right) {
return $right + 1;
}Java
if (left >= right) {
return right + 1;
}Если указатели остановились, то они указывают на два элемента в неверном порядке. Левый указатель смотрит на элемент, который больше опорного. При этом правый указатель смотрит на элемент, который меньше опорного.
Меняем местами и сдвигаем элементы, чтобы в следующей итерации продолжить поиск следующей неправильной пары:
const temporary = items[left];
items[left] = items[right];
items[right] = temporary;
left += 1;
right -= 1;Python
items[left], items[right] = items[right], items[left]
left += 1
right -= 1PHP
<?php
$temporary = $items[$left];
$items[$left] = $items[$right];
$items[$right] = $temporary;
$left += 1;
$right -= 1;Java
var temporary = items[left];
items[left] = items[right];
items[right] = temporary;Обычно условие завершения цикла пишут в начале (оператор while) или в конце (оператор do…while). В функции partition() условие становится известно в середине цикла.
В языках программирования нет специального синтаксиса для такой ситуации. Обычно программисты записывают бесконечный цикл с помощью конструкции while (true), а выход из цикла делают с помощью операторов break или return:
while (true) {
// ...
if (left >= right) {
return right + 1;
}
// ...
}Python
while True:
# ...
if left >= right:
return right + 1
# ...PHP
<?php
while (true) {
// ...
if ($left >= $right) {
return $right + 1;
}
// ...
}Java
while (true) {
// ...
if (left >= right) {
return right + 1;
}
// ...
}Частично упорядоченный массив нельзя назвать полностью отсортированным. Чтобы закончить сортировку, мы должны рекурсивно повторить упорядочивание для левой и правой половин массива.
Про рекурсию мы говорили на прошлом уроке. Так выглядит рекурсивный алгоритм быстрой сортировки. Он немного похож на рекурсивную функцию бинарного поиска:
const sort = (items, left, right) => {
const length = right - left + 1;
if (length < 2) {
return;
}
const pivot = items[left];
const splitIndex = partition(items, left, right, pivot);
sort(items, left, splitIndex - 1);
sort(items, splitIndex, right);
};Python
def sort(items, left, right):
length = right - left + 1
if length < 2:
return
pivot = items[left]
split_index = partition(items, left, right, pivot)
sort(items, left, split_index - 1)
sort(items, split_index, right)PHP
<?php
function sort($items, $left, $right)
{
$length = $right - $left + 1;
if ($length < 2) {
return;
}
$pivot = $items[$left];
$splitIndex = partition($items, $left, $right, $pivot);
sort($items, $left, splitIndex - 1);
sort($items, $splitIndex, $right);
}Java
class App {
public static int partition(int[] items, int left, int right, int pivot) {
// ...
}
public static void sort(int[] items, int left, int right) {
var length = right - left + 1;
if (length < 2) {
return;
}
var pivot = items[left];
var splitIndex = partition(items, left, right, pivot);
sort(items, left, splitIndex - 1);
sort(items, splitIndex, right);
}
}Для упорядочивания нужно не менее двух элементов. Поэтому мы остановим рекурсивный вызов, когда встретим пустой подмассив или подмассив с одним элементом:
const length = right - left + 1;
if (length < 2) {
return;
}Python
length = right - left + 1
if length < 2:
returnPHP
<?php
$length = $right - $left + 1;
if ($length < 2) {
return;
}Java
var length = right - left + 1;
if (length < 2) {
return;
}Функция partition возвращает индекс первого элемента в правом подмассиве. Это помогает функции sort корректно вызвать саму себя:
const splitIndex = partition(items, left, right, pivot);
sort(items, left, splitIndex - 1);
sort(items, splitIndex, right);Python
split_index = partition(items, left, right, pivot)
sort(items, left, split_index - 1)
sort(items, split_index, right)PHP
<?php
$splitIndex = partition($items, $left, $right, $pivot);
sort($items, $left, $splitIndex - 1);
sort($items, $splitIndex, $right);Java
var splitIndex = partition(items, left, right, pivot);
sort(items, left, splitIndex - 1);
sort(items, splitIndex, right);Единственный код, который вызывает вопросы — выбор опорного элемента:
const pivot = items[left];Python
PHP
<?php
$pivot = $items[$left];Java
Почему мы всегда выбираем самый левый элемент подмассива?
Средний элемент должен находиться ровно посередине отсортированного массива. В таком случае его называют медианой. Чтобы узнать медиану, нужно иметь отсортированный массив, а чтобы отсортировать массив — знать медиану. Получается замкнутый круг.
На практике необязательно делить массив ровно пополам — достаточно разбить массив на приблизительно равные части — алгоритм все равно будет работать быстро. Если элементы в массиве расположены в случайном порядке, то можно брать любой элемент по счету — в среднем массив будет всегда разбит пополам.
Можно выбрать самый левый элемент в качестве опорного элемента — как видно на примере выше, это работает.
Выше мы написали универсальную функцию, которая может сортировать отдельные подмассивы. Сложность в том, что такой функцией не очень удобно пользоваться — приходится передавать параметры left и right даже тогда, когда надо отсортировать массив целиком.
Чтобы упростить себе жизнь, напишем вспомогательную функцию, которая всегда сортирует массив целиком:
const quicksort = (items) => sort(items, 0, items.length - 1);
const items = [ 57, 10, 52, 43, 55, 93, 34, 24, 99 ];
quicksort(items);
console.log(items); // => [ 10, 24, 34, 43, 52, 55, 57, 93, 99 ]Python
def quicksort(items):
sort(items, 0, len(items) - 1)
items = [57, 10, 52, 43, 55, 93, 34, 24, 99]
quicksort(items)
print(items) # => [10, 24, 34, 43, 52, 55, 57, 93, 99]PHP
<?php
function quicksort($items)
{
return sort($items, 0, count($items) - 1);
}
$items = [ 57, 10, 52, 43, 55, 93, 34, 24, 99 ];
quicksort($items);
print_r($items); // => [ 10, 24, 34, 43, 52, 55, 57, 93, 99 ]Java
class App {
public static void quicksort(int[] items) {
return sort(items, 0, items.length - 1);
}
// ...
}
int[] items = [ 57, 10, 52, 43, 55, 93, 34, 24, 99 ];
App.quicksort(items);
System.out.println(Arrays.toString($items));
// => [ 10, 24, 34, 43, 52, 55, 57, 93, 99 ]Быстрая сортировка намного эффективнее сортировки выбором. Причем эта разница особенно видна на больших массивах. Если сортировать миллион элементов, сортировка выбором окажется медленнее в десятки тысяч раз.
Универсальная функция сортировки
Мы реализовали три функции сортировки, каждая из которых упорядочивает в возрастающем порядке элементы простых типов: чисел, дат, строк.
Вспомним пример с интернет-магазином, в котором мы сталкиваемся с более сложной задачей — сортировкой по разным атрибутам. Представим, что нам предстоит сортировать товары по трем атрибутам:
-
Название —
name -
Цена —
price -
Рейтинг —
rating
Сам массив выглядит так:
const products = [
{ name: "Телевизор", price: 100000, rating: 9.1 },
{ name: "Холодильник", price: 20000, rating: 8.3 },
{ name: "Пылесос", price: 14000, rating: 7.5 },
{ name: "Стиральная машина", price: 30000, rating: 9.2 },
{ name: "Миелофон", price: 200000, rating: 8.7 },
{ name: "Микроволновка", price: 7000, rating: 8.2 },
{ name: "Проигрыватель", price: 20000, rating: 9.0 },
{ name: "Посудомоечная машина", price: 80000, rating: 7.8 },
{ name: "Мультиварка", price: 5000, rating: 7.1 },
];Python
products = [
{"name": "Телевизор", "price": 100000, "rating": 9.1},
{"name": "Холодильник", "price": 20000, "rating": 8.3},
{"name": "Пылесос", "price": 14000, "rating": 7.5},
{"name": "Стиральная машина", "price": 30000, "rating": 9.2},
{"name": "Миелофон", "price": 200000, "rating": 8.7},
{"name": "Микроволновка", "price": 7000, "rating": 8.2},
{"name": "Проигрыватель", "price": 20000, "rating": 9.0},
{"name": "Посудомоечная машина", "price": 80000, "rating": 7.8},
{"name": "Мультиварка", "price": 5000, "rating": 7.1},
]PHP
<?php
$products = [
['name' => 'Телевизор', 'price' => 100000, 'rating' => 9.1],
['name' => 'Холодильник', 'price' => 20000, 'rating' => 8.3],
['name' => 'Пылесос', 'price' => 14000, 'rating' => 7.5],
['name' => 'Стиральная машина', 'price' => 30000, 'rating' => 9.2],
['name' => 'Миелофон', 'price' => 200000, 'rating' => 8.7],
['name' => 'Микроволновка', 'price' => 7000, 'rating' => 8.2],
['name' => 'Проигрыватель', 'price' => 20000, 'rating' => 9.0],
['name' => 'Посудомоечная машина', 'price' => 80000, 'rating' => 7.8],
['name' => 'Мультиварка', 'price' => 5000, 'rating' => 7.1],
];Java
Map[] products = {
Map.of ("name", "Телевизор", "price", 100000, "rating", 9.1),
Map.of ("name", "Холодильник", "price", 20000, "rating", 8.3),
Map.of ("name", "Пылесос", "price", 14000, "rating", 7.5),
Map.of ("name", "Стиральная машина", "price", 30000, "rating", 9.2),
Map.of ("name", "Миелофон", "price", 200000, "rating", 8.7),
Map.of ("name", "Микроволновка", "price", 7000, "rating", 8.2),
Map.of ("name", "Проигрыватель", "price", 20000, "rating", 9.0),
Map.of ("name", "Посудомоечная машина", "price", 80000, "rating", 7.8),
Map.of ("name", "Мультиварка", "price", 5000, "rating", 7.1)
};Можно реализовать несколько функций сортировки, но есть и более эффективный способ. Интернет-магазину подойдет универсальная функция сортировки.
Каждую из трех видов сортировок выше можно сделать универсальной — и тогда алгоритм сможет сортировать данные любого типа. Для этого надо добавить еще один параметр — функцию сравнения (компаратор). Универсальная функция сортировки вызывает компаратор каждый раз, когда требуется сравнить два элемента и определить, какой из них больше.
У компаратора два параметра — два элемента массива, которые надо сравнить. Если первый больше второго, компаратор возвращает 1. Если первый меньше второго, компаратор возвращает -1. Если элементы равны, компаратор возвращает 0.
Вот так будет выглядеть компаратор, сравнивающий элементы по цене:
const compareByPrice = (item1, item2) => {
if (item1.price < item2.price) {
return -1;
} else if (item1.price == item2.price) {
return 0;
} else {
return 1;
}
};Python
def compare_by_price(item1, item2):
if item1[price] < item2[price]:
return -1
elif item1[price] == item2[price]:
return 0
else:
return 1PHP
<?php
function compareByPrice($item1, $item2)
{
if ($item1['price'] < $item2['price']) {
return -1;
} else if ($item1['price'] == $item2['price']) {
return 0;
} else {
return 1;
}
}Java
public static ToIntBiFunction<Map<String, Object>, Map<String, Object>> compareByPrice = (item1, item2) -> {
var price1 = (int) item1.get("price");
var price2 = (int) item2.get("price");
if (price1 < price2) {
return -1;
} else if (price1 == price2) {
return 0;
} else {
return 1;
}
};А вот так — компаратор, сравнивающий элементы по рейтингу:
const compareByRating = (item1, item2) => {
if (item1.rating < item2.rating) {
return -1;
} else if (item1.rating == item2.rating) {
return 0;
} else {
return 1;
}
};Python
def compare_by_rating(item1, item2):
if item1[rating] < item2[rating]:
return -1
elif item1[rating] == item2[rating]:
return 0
else:
return 1PHP
<?php
function compareByRating($item1, $item2)
{
if ($item1['rating'] < $item2['rating']) {
return -1;
} else if ($item1['rating'] == $item2['rating']) {
return 0;
} else {
return 1;
}
}Java
public static ToIntBiFunction<Map<String, Object>, Map<String, Object>> compareByRating = (item1, item2) -> {
var rating1 = (double) item1.get("rating");
var rating2 = (double) item2.get("rating");
if (rating1 < rating2) {
return -1;
} else if (rating1 == rating2) {
return 0;
} else {
return 1;
}
};Универсальная функция сравнивает два элемента, но не использует операторы «больше» или «меньше». Вместо этого она вызывает компаратор и проверяет результат. Так выглядит универсальная пузырьковая сортировка:
const bubbleSort = (items, comparator) => {
for (let limit = items.length - 1; limit > 0; limit -= 1) {
for (let i = 0; i < limit; i += 1) {
if (comparator(items[i], items[i + 1]) > 0) {
const temporary = items[i];
items[i] = items[i + 1];
items[i + 1] = temporary;
}
}
}
};Python
def bubble_sort(items, comparator):
for limit in range(len(items) - 1, 0, -1):
for i in range(limit):
if comparator(items[i], items[i + 1]) > 0:
items[i], items[i + 1] = items[i + 1], items[i]PHP
<?php
function bubbleSort($items, $comparator)
{
for ($limit = count(items) - 1; $limit > 0; $limit -= 1) {
for ($i = 0; $i < $limit; $i += 1) {
if (comparator($items[$i], $items[$i + 1]) > 0) {
$temporary = $items[$i];
$items[$i] = $items[$i + 1];
$items[$i + 1] = $temporary;
}
}
}
}Java
class App {
public static void bubbleSort(Map[] items, ToIntBiFunction comparator) {
for (var limit = items.length - 1; limit > 0; limit--) {
for (var i = 0; i < limit; i++) {
if (comparator.applyAsInt(items[i], items[i + 1]) > 0) {
var temporary = items[i];
items[i] = items[i + 1];
items[i + 1] = temporary;
}
}
}
}
}Данную тему следует рассматривать в двух аспектах. Во-первых, при решении различных олимпиадных задач алгоритмы поиска приходится использовать в качестве технических элементов при реализации собственно алгоритма решения той или иной задачи. Во-вторых, задача сама по себе может требовать построения оптимального в смысле определенных требований алгоритма поиска. Подход в каждом из двух упомянутых случаев должен быть различным.
Для полноценного понимания темы рекомендую просмотреть следующие статьи:
- Анализ сложности алгоритмов. Примеры
- Примеры анализа сложности алгоритмов
- Структуры данных. Деревья
А для продолжения изучения — выбрать себе какую-нибудь книгу по алгоритмам.
Алгоритмы поиска в неупорядоченных одномерных массивах
Рассмотрим сначала нюансы реализации “технических” задач поиска, которые встречаются в различных алгоритмах. Начнем с, казалось бы, тривиальной задачи поиска элемента в неупорядоченном массиве. Во всех примерах, относящихся к поиску в одномерном массиве будем использовать следующую переменную a:
a:array[0..N] of <скалярный тип>;
при этом собственно элементы массива, которые мы будем рассматривать, пронумерованы от 1 до N, а нулевой элемент будем использовать как вспомогательный в случае необходимости. Конкретный же тип элемента в большинстве описываемых алгоритмов не важен, он может быть как любым числовым, так и символьным или даже строковым. Алгоритм поиска в массиве элемента, значение которого равно K, может выглядеть так:
i:=0;
repeat
i:=i+1
until (i=N) or (a[i]=K);
if a[i]=K then
write(i)
else
write(0)
{следующее неверно (!!!):
if i=N then
write(0)
else
write(i)
}
При отсутствии в массиве элемента с искомым значением K печатается значение нулевого индекса. Оказывается, что и такую достаточно простую программу можно упростить, заодно продемонстрировав так называемый “барьерный” метод, который часто применяется в программировании в том числе и олимпиадных задач. В данном случае он заключается в том, что мы можем занести в дополнительный элемент массива (например, нулевой) искомое значение K, избавившись тем самым в условии окончания цикла от проверки на выход за границу массива:
a[0]:=K; i:=N; while (a[i]<>K) do i:=i-1; write(i)
Эта программа не просто проще и эффективней. В ней практически невозможно сделать ошибку.
Другой полезный прием можно показать на задаче поиска максимального и минимального значения в массиве. Состоит он в том, что при любом поиске в массиве искать следует не значение искомого элемента, максимума, минимума и т.п., а его индекс. Тогда решая одну задачу, мы по сути дела решаем сразу две: определяем не только наличие искомого элемента, значение максимума или минимума, но и их местоположение в массиве. Программа при этом не только не усложняется, но зачастую становится даже короче:
imax:=1;
imin:=1;
for i:=2 to N do
if a[i]<a[imin] then
imin:=i
else
if a[i]>a[imax] then
imax:=i
Заметим, что использование в качестве начальных значений для минимума и максимума не значение первого элемента массива, а максимальное и минимальное значение в типе элементов, может привести к ошибке. Так, следующая программа не находит значение максимума для убывающего массива целых чисел (!!!):
max:=-MaxInt-1; {это минимальное число типа integer}
min:=MaxInt; {это максимальное число типа integer}
for i:=1 to N do
if a[i]<min then
min:=a[i]
else
if a[i]>max then
max:=i
Казалось бы на этом рассмотрение алгоритмов поиска в неупорядоченном массиве можно завершить. Однако именно с одновременного поиска минимума и максимума можно начать класс алгоритмов поиска, более эффективных, чем приведенные выше стандартные алгоритмы. Причем именно при решении олимпиадных задач их знание может пригодиться в первую очередь. Итак, в приведенном выше алгоритме поиска максимального и минимального элемента в массиве в худшем случае выполняется 2N – 2 сравнений. Покажем, что ту же задачу можно решить за 3*round(N/2) – 2 сравнения. Пусть у нас имеется четное число элементов. Разобьем их на пары и в каждой из N/2 пар за одно сравнение определим, какой элемент больше, а какой меньше. Тогда максимум можно искать уже любым способом только из наибольших элементов в парах, а минимум — среди наименьших. Общее число сравнений при этом равно N/2 + 2(N/2 – 1) = 3N/2 – 2. Для нечетного числа элементов — элемент, не попавший ни в одну из пар, должен участвовать как в поиске максимума, так и минимума.
Обозначение round(A)соответствует для неотрицательных чисел округлению до ближайшего целого числа, большего или равного выражению в указанных скобках, в отличие от целой части, где округление производится до ближайшего целого, меньшего или равного рассматриваемому выражению.
Еще большей эффективности можно добиться при одновременном поиске максимального и второго по величине числа. Для этого организуем поиск максимума по схеме “теннисного турнира”, а именно: разобьем элементы на пары и определим в каждой из пар больший элемент, затем разобьем на пары уже эти элементы и т.д. В “финале” и будет определен максимум. Количество сравнений в таком алгоритме, как и в традиционной схеме, равно N – 1. Однако, максимальный элемент участвовал при этом в round(log2(N)) сравнениях, причем одно из них проходило обязательно со вторым по величине элементом. Таким образом, теперь для поиска этого элемента потребуется всего round(log2(N)) – 1 сравнение. Попробуйте самостоятельно построить эффективный алгоритм для поиска уже первых трех по величите элементов.
В данном контексте можно поставить также задачу поиска i-го по счету элемента, называемого i-ой порядковой статистикой. Кроме максимума и минимума, специфической порядковой статистикой является медиана — элемент с номером (N + 1)/2 для нечетных N и два соседних элемента для четных. Конечно, задачу поиска любой порядковой статистики можно решить, предварительно отсортировав массив. Но, как будет показано ниже, оптимальные по количеству сравнений универсальные (то есть пригодные для произвольных массивов) алгоритмы сортировки выполняют порядка Nlog2N сравнений. А задачу поиска i-ой порядковой статистики можно решить, производя O(N) сравнений. Алгоритм, который гарантирует эту оценку достаточно сложен, он подробно изложен в [1, 2, 3]. Мы же приведем схему алгоритма, который в худшем случае не является линейным, однако на практике работает существенно быстрее, следовательно именно его и нужно использовать в практике реального программирования, в том числе и олимпиадных задач:
Алгоритм Выбор(A, L, R, i)
{выбирает между L-ым и R-ым элементами массива A
i-ый по счету в порядке возрастания элемент}
1. if L=R then
результат = A[L], конец;
2. Q:=L+random(R-L+1) {Q – случайный элемент между L и R}
3. Переставляем элементы от L до R в A так, чтобы сначала шли элементы, меньшие A[Q], а затем все остальные, первый элемент во второй группе обозначим K.
4. if i<=(K-L) then
Выбор(A, L, K-1, i)
else
Выбор(A, K, R, i-(K-L))
5. конец.
Оптимальную реализацию пункта 3 можно заимствовать из алгоритма так называемой быстрой сортировки (смотри по ссылкам, приведенным в начале статьи).
Наконец, рассмотрим задачу поиска в последовательности из N чисел, хранения которой не требуется вообще, следовательно ее длина может быть очень велика. Пусть известно, что в этой последовательности встречаются по одному разу все числа от 0 до N, кроме одного. Это пропущенное число и требуется найти. Вот возможное решение такой задачи:
S:=0; for i:=1 to N do begin read(a); S:=S+a end; writeln(N*(N + 1) div 2 – S)
Данную программу легко переписать так, чтобы она работала и для значений N, превосходящих максимальное представимое целое число. Для этого следует использовать переменные типа extended, а цикл for заменить на while. Используя аналогичный прием попробуйте решить следующую задачу. Пусть N — количество чисел, нечетно и известно, что среди вводимых чисел каждое имеет ровно одно, равное себе, а одно число — нет. Найдите это число. (Указание. В данном случае можно воспользоваться свойством логической функции “исключающее или”, обозначаемой в Паскале как xor: a xor b xor b = a).
Поиск в упорядоченных массивах
Под упорядоченными в дальнейшем будут пониматься неубывающие массивы, если не оговорено иное. То есть, a[1] <= a[2] <= … <= a[N].
Сначала приведем пример реализации широко известного алгоритма двоичного (бинарного) поиска элемента, равного K, в уже упорядоченном массиве. Оказывается, досрочный выход из цикла в случае нахождения элемента выигрыша по скорости практически не дает, а лишние проверки делают программу более громоздкой. Поэтому рекомендуется производить поиск, пока диапазон рассматриваемых элементов состоит более, чем из одного элемента.
L:=1; R:=N+1;
while L<R do
begin
m:=(L+R)div 2;
if a[m]<K then
L:=m+1
else
R:=m
end;
if a[m]=K then
write(m)
else
write(0)
Известно, что алгоритм бинарного поиска, аналогичный приведенному выше, но заканчивающий свою работу в случае досрочного обнаружения элемента, за Q сравнений определил, что искомым является элемент с номером I. Какова могла быть при этом размерность массива (указать все допустимые диапазоны значений N). Несмотря на кажущуюся сложность, при заданных в условии ограничениях задача решалась путем простого перебора различных значений N и обращения с каждым из этих значений к функции бинарного поиска. Конструктивный же подход к решению задачи намного сложнее. Однако и в случае подбора можно использовать немало интересных фактов. Например, длина каждого из диапазонов возможных значений N, является степенью двойки, а каждый следующий диапазон не меньше предыдущего. Это позволяет значительно сократить количество рассматриваемых значений N. Кроме того, максимальное допустимое значение для N легко найти аналитически.
Рассмотрим теперь задачу поиска в упорядоченном массиве наибольшего «равнинного» участка. То есть, требуется найти такое число p, что в массиве имеется последовательность из p равных элементов и нет последовательности из p + 1 равных по значению элементов. Оказывается, существует алгоритм решения этой задачи, количество операций в котором может оказаться существенно меньше, чем N. Так, если мы уже нашли последовательность из p1 равных между собой чисел, то другую последовательность имеет смысл теперь рассматривать только если ее длина не менее p1 + 1. Поэтому, если a[i] — первый элемент предполагаемой новой подпоследовательности, то сравнивать его надо сразу с элементом a[i+p], где p — максимальная величина для уже рассмотренных подпоследовательностей из равных элементов. Приведем фрагмент программы, решающий данную задачу. В качестве результата мы получаем длину максимальной подпоследовательности p, номер элемента, с которого эта подпоследовательность начинается, k и значение элементов в найденной подпоследовательности:
p:=1; k:=1;
i:=1; f:=false;
while i+p<=N do
if a[i+p]=a[i] then
begin
p:=p+1; f:=true
end
else
if f then
begin
k:=i; i:=i+p; f:=false
end
else
i:=i+1;
writeln(p,’ ’,k, ’ ’,a[k])
Пусть имеются три упорядоченных по алфавиту списка из фамилий людей, получающий пособие по безработице в трех различных местах. Длина каждого из списков может быть как угодно большой (каждый из списков можно хранить в отдельном файле). Известно, что по крайней мере одно лицо фигурирует во всех трех списках. Требуется написать программу поиска такого лица, порядок количества операций в которой не будет больше, чем сумма длин всех трех списков. Приведем фрагмент программы, работающий с тремя файлами, обращение к элементам которых (они могут быть любого типа, в том числе и string, к элементам которого в Паскале применимы операции сравнения, чтения и записи) из программы происходит с помощью файловых переменных x, y, z типа text:
readln(x,p); readln(y,q); readln(z,r);
while not((p=q)and(q=r)) do
begin
if p<q then
readln(x,p)
else
if q<r then
readln(y,q)
else
if r<p then
readln(z,r)
end;
writeln(p); { p=q=r }
Покажите, что для поставленной задачи чтение из файла всегда будет производиться корректно и на каждом шаге цикла значение одной из трех переменных p, q, r будет изменено. Кроме того докажите, что с помощью этой программы всегда будет найден именно минимальный из элементов, присутствующих во всех трех файлах.
Наконец, рассмотрим задачу поиска элемента, значение которого равно K, в двухмерном массиве, упорядоченном по строкам и столбцам:
a[i,j] <= a [i,j+1], a[i,j] <= a[i+1,j], 1 <= i < N, 1 <= j < M.
Данная задача решается за M + N действий, а не за M*N, как в произвольном массиве. Поиск следует начинать с элемента a[N,1]. Этот элемент самый маленький в своей строке и самый большой в своем столбце (в математике подобные элементы называют “седловыми точками”). Поэтому, если он окажется меньше, чем K, то из рассмотрения первый столбец можно исключить, а если больше — из рассмотрения исключается последняя строка и т. д. Вот возможная реализация этого алгоритма:
i:=N; j:=1;
while (i>0)and(j<M+1)and(a[i,j]<>K) do
if a[i,j]<K then
j:=j+1
else
i:=i-1;
if (i>0)and(j<M+1) then
writeln(a[i,j])
Программа могла бы быть еще короче и эффективней, если бы в ней использовался упоминавшийся выше барьерный метод. В данном случае для организации барьера требуется дополнить массив нулевой строкой и m+1-м столбцом. Во все созданные барьерные элементы следует поместить значение K. Тогда условие в цикле можно сократить до следующего: a[i,j]<>K.
Алгоритмы поиска и задачи на взвешивания
Появление подобных задач, например задачи определения фальшивой монеты, в контексте рассмотрения алгоритмов поиска не случайно. Во-первых, поиск и в этом случае осуществляется путем операций сравнения, правда, уже не только одиночных элементов, но и групп элементов между собой. Во-вторых, как будет показано ниже, в отличие от олимпиад по математике для младших школьников, задачи на взвешивания вполне можно решать конструктивно.
В качестве примера рассмотрим задачу, предлагавшуюся на теоретическом туре одной из региональных олимпиад по информатике. Пусть у нас имеется 12 монет, одна из которых фальшивая, по весу отличающаяся от остальных монет, причем неизвестно, легче она или тяжелее. Требуется за три взвешивания определить номер фальшивой монеты (попробуйте решить эту задачу самостоятельно и вы убедитесь, что это совсем не просто, а порой вообще кажется невозможным). Введем следующие обозначения. Знаком “+” будем обозначать монеты, которые во время текущего взвешивания следует положить на весы, причем, если монета на весах уже была, то на ту же самую чашу, на которой эта монета находилась во время своего предыдущего взвешивания. Знаком “-“ будем обозначать монеты, которые следует переложить на противоположную чашу весов, по отношению к той, на которой они находились (каждая в отдельности), заметим, что если монета на весах еще не была, то знак “-“ к ней применен быть не может. Наконец, знаком “0” — монеты, которые в очередном взвешивании не участвуют. Тогда, существует 14 различных способов пометки монет для трех взвешиваний:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 + + + + + + + + + 0 0 0 0 0 — первое взвешивание + + + - - - 0 0 0 + + + 0 0 — второе взвешивание + - 0 + - 0 + - 0 + - 0 + 0 — третье взвешивание
Из полученной таблицы вычеркнем 2 столбца так, чтобы в каждой из трех строк количество ненулевых элементов оказалось четным (ведь мы не можем во время одного взвешивания положить на две чаши весов нечетное число монет). Это могут быть, например, столбцы 4 и 14. Теперь будем взвешивать 12 монет так, как это записано в оставшихся 12 столбцах. То есть, в первом взвешивании будут участвовать 8 произвольных монет, во втором — три монеты следует с весов убрать, две — переложить на противоположные по отношению к первому взвешиванию чаши весов и три монеты положить на весы впервые (на свободные места так, чтобы на каждой из чаш вновь оказалось по 4 монеты). Согласно схеме проведем и третье взвешивание, опять располагая на каждой чаше весов по 4 монеты. Результат каждого взвешивания в отдельности никак не анализируется, а просто записывается. При этом равновесие на весах всегда кодируется нулем, впервые возникшее неравновесное состояние — знаком плюс, если при следующем взвешивании весы отклонятся от равновесия в ту же самую сторону, то результат такого взвешивания также кодируется плюсом, а если в другую сторону — то минусом. Например, записи “=<<” и “=>>” кодируются как “0++”, а записи “<=>” и “>=<” — как “+0-“. Так как мы не знаем, легче или тяжелее остальных монет окажется фальшивая, то нам важно как изменялось состояние весов от взвешивания к взвешиванию, а не то какая именно чаша оказывалась тяжелее, а какая легче. Поэтому два, на первый взгляд, различных результата трех взвешиваний в этом случае кодируются одинаково. После подобной записи результатов взвешиваний фальшивая монета уже фактически определена. Ею оказывается та, которой соответствует такой же столбец в таблице, как и закодированный нами результат трех взвешиваний. Для первого из примеров это монета, которая участвовала во взвешиваниях по схеме, указанной в 10-м столбце таблицы, а для второго — в 8-м. В самом деле, состояние весов в нашей задаче меняется в зависимости от того, где оказывается фальшивая монета во время каждого из взвешиваний. Поэтому монета, “поведение” которой согласуется с записанным результатом взвешиваний, такой результат и определяет.
Анализ таблицы показывает, что эту задачу можно решить не только для 12, но и для 13 монет. Для этого следует исключить из рассмотрения любой не содержащий нулей столбец, например, все тот же четвертый. В остальном все действия остаются неизменными. Для произвольного числа монет N>2 количество взвешиваний при определяется по формуле round(log3(2*N + 1)) (за одно взвешивание задача не разрешима ни для какого количества монет!!!), но подход к решению задачи при этом не изменится.
Попробуйте теперь решить задачу, которая предлагалась в 1998 году на уже упоминавшемся выше полуфинале чемпионата мира по программированию среди студенческих команд вузов. В ней также требовалось определить номер фальшивой монеты, вес которой отличался от остальных. Но все взвешивания уже были проведены, а их результаты записаны. Число взвешиваний являлось входным параметром в задаче (оно могло быть и избыточным по сравнению с описанным выше оптимальным алгоритмом определения номера фальшивой монеты). При этом в каждом из взвешиваний могло участвовать любое четное количество имеющихся монет (сколько и какие именно — известно). Результаты записывались с помощью символов “<”, “>” и “=”.
Еще одна задача на взвешивания рассмотрена в [8]. В общем случае в ней требуется найти набор из минимального количества гирь такой, что с его помощью можно взвесить любой груз, весящий целое число килограмм, в диапазоне от 1 кг до N кг. При необходимости гири можно располагать на обеих чашах весов. Так, для N=40 это гири 1, 3, 9 и 27 кг.
Поиск подстроки в строке
Формализовать эту задачу можно следующим образом. Пусть задан массив s из N элементов (строка) и массив p из M элементов (подстрока), причем 0p в s. Эта задача на практике встречается очень часто. Так, в большинстве текстовых редакторов реализована операция поиска по образцу, которая практически полностью совпадает с описанной задачей. Если размер массива s — N не превосходит 255, а тип его элементов — char, то в Турбо Паскале такой поиск можно выполнять с помощью стандартной функции Pos(p,s). Однако, в общем случае ее приходится реализовывать самостоятельно. Прямой поиск, основанный на последовательном сравнении подстроки сначала с первыми M символами строки, затем с символами с номерами 2 — M+1 и т. д., в худшем случае произведет порядка N*M сравнений. Но для этой задачи известен алгоритм Боуера и Мура, который для произвольных строк выполняет не намного более N/M сравнений. То есть разница в вычислительной сложности составляет M^2 Рассмотрим последний алгоритм, на примере которого также можно показать, что использование небольшого количества дополнительной памяти (в данном случае вспомогательного массива, размер которого равен размеру алфавита строк) позволяет существенно ускорить выполнение программы.
Перед фактическим поиском, для всех символов, которые могут встретиться в строке, вычисляется и запоминается в массиве d расстояние от самого правого вхождения этого символа в искомую подстроку до ее конца. Если же какого-то символа из алфавита строки в подстроке нет, то такое расстояние считается равным длине подстроки M. Посимвольное же сравнение подстроки с некоторым фрагментом строки начинается не с начала, а с конца искомой подстроки (образца). Если какой-либо символ образца не совпадает с соответствующим символом фрагмента строки, а х —последний символ фрагмента строки, то образец можно сдвинуть вдоль строки вправо на d[x] символов. Если большинство символов в строке отличны от символов подстроки, то сдвиг будет происходить на M элементов, что и обеспечит приведенную выше сложность алгоритма. Покажем работу алгоритма на примере поиска слова коала в строке:
кокаколулюбитикоала.
коала
коала
коала
коала
коала
Здесь выделены жирным символы, которые участвовали в сравнениях. Сдвиги определялись такими значениями массива d: d['к']=4, d['л']=1, d['ю']=5. Если бы последней в рассматриваемом фрагменте строки оказалась буква а, то величина сдвига была бы равна 2, так как в образце есть еще одна такая буква, отстоящая от конца на 2 символа, а при ее отсутствии сдвиг был бы равен 5. Приведем теперь возможную реализацию описанного алгоритма, для простоты считая, что размер подстроки не превосходит 255, что не снижает общности этой программы:
const nmax=10000;
var p:string; {подстрока}
s:array[1..nmax]of char; {строка}
d:array[char]of byte; {массив сдвигов}
c:char;
m,i,j,k:integer;
begin
…{задание строки и подстроки}
m:=length(p);{длина подстроки}
for c:=chr(0) to chr(255) do d[c]:=m;
for j:=1 to m-1 do d[p[j]]:=m-j;
{массив d определен}
i:=m+1;
repeat {выбор фрагмента в строке}
j:=m+1; k:=i;
repeat {проверка совпадения}
k:=k-1; j:=j-1
until (j<1)or(p[j]<>s[k]);
i:=i+d[s[i-1]];{сдвиг}
until (j<1)or(i>nmax+1);
if j<1 then write(k+1) else write(0)
end.
Приведенный алгоритм не дает выигрыша только в одном случае — когда количество частичных совпадений искомой подстроки с фрагментами текста достаточно велико. Это возможно, например, при чрезвычайной ограниченности алфавита, из символов которого составляются строки. Тогда следует применять алгоритм Кнута-Мориса-Пратта, или комбинацию из двух алгоритмов.
Рассмотренную проблему не следует путать с такой задачей. Пусть задан массив s из N элементов и массив p из M элементов, причем 0<M<=N. Требуется выяснить, можно ли из первого массива вычеркнуть некоторые члены так, чтобы он совпал со вторым. Число операций в данном случае имеет порядок N + M.
Часто возникает ситуация, когда в массиве
необходимо найти определённый элемент.
Типовые задачи на поиск
элемента в массиве:
·
поиск максимального или минимального
элемента;
·
поиск элемента, имеющего конкретное
значение.
Задача: Мальчики класса
решили устроить соревнование на точность. Для этого на уроке физкультуры им
всем были присвоены номера. После чего мальчики, начиная с участника с номером
один, стали бросать баскетбольный мяч в кольцо, до первого промаха каждый.
(абзац) Написать программу, которая считывает количество попаданий у каждого и
определяет номер победителя, а если их несколько, то выводит победителя с
наименьшим номером.
Очевидно,
что при решении данной задачи без использования компьютера, когда мальчики
будут бросать мяч в кольцо, мы будем действовать следующим образом:
·
запишем результат и номер первого
участника, полагая, что он победит;
·
далее, пока не закончатся участники, мы
будем делать следующее:
·
смотреть сколько раз участник попал в
кольцо;
·
если участник попал меньше или столько же
раз, как и тот, результат которого мы записали до этого – его номер мы не
записываем;
·
если участник попал в кольцо большее
количество раз, чем тот, номер которого записан, – мы зачеркнём записанный
номер и запишем новый и предположим, что этот участник победит.
Таким образом, в конце у нас будет записан номер
участника, который попал в кольцо наибольшее количество раз.
Запишем данный алгоритм в форме программы. Назовём
программу sorevnovanie.
Нам понадобится переменная n,
которая будет хранить количество участников, переменная i,
которая будет хранить номер текущего участника и переменная r, которая будет хранить номер
предполагаемого победителя. А также массив результатов a. Все данные задачи будут
принадлежать к целочисленному типу integer.
Между служебными словами begin и end запишем тело программы.
Вначале выведем на экран поясняющее сообщение о том, что это программа
определения победителя в соревнованиях по броскам мяча в корзину, а также
запрос на ввод количества участников. Считаем переменную n с переходом на следующую строку.
Запишем цикл for
i:=1
to
n
do,
в котором будут команды вывода на экран запроса на ввод результата i-того
участника, а так же считывания i-того элемента массива a.
После цикла будет следовать команда r:=1,
т. е. мы полагаем, что победит первый участник.
Далее, так как результат первого участника уже
сохранен, начнём просматривать результаты со второго. При помощи цикла for i:=2
to
n
do,
мы будем сравнивать результат предполагаемого победителя с последующими, и если
i-тый участник попал в кольцо большее
количество раз – он становится предполагаемым победителем, то есть присвоим
переменной r
значение i.
В конце выведем поясняющее сообщение с текстом «Победил участник под номером»,
и значение переменной r.
Исходный
код программы
Запустим программу на выполнение. Пусть было пятеро
участников. Первый попал в кольцо десять раз, второй – семь, третий –
одиннадцать, четвёртый – пятнадцать и пятый – восемь. Таким образом,
результатом должна быть победа четвёртого участника.
Результат
работы программы
Результат работы программы соответствует ожидаемому –
следовательно, задача решена верно.
Еще
одним типом задач являются задачи на поиск элемента в массиве по указанному
значению.
Задача: Определить, есть
ли в последовательности n
случайных
чисел от 1 до 100 число равное k. Если есть – вывести номер, под которым оно
встречается впервые, а если нет – вывести слово «Нет».
Для решения данной задачи нам понадобится
последовательность чисел, хранящаяся в массиве a, длина данной последовательности n, номер текущего элемента
последовательности i, искомое число k.
Составим блок-схему алгоритма решения данной задачи.
Для начала необходимо ввести длину последовательности
чисел, а также искомое число. Затем будут следовать циклы для генерации
последовательности случайных чисел длины n и
для вывода её элементов на экран.
Теперь перейдём к поиску. Для этого переменной i
присвоим значение 1 и будем перебирать элементы пока они не закончатся или пока
не найдём искомый. Цикл поиска будет содержать всего одну команду – увеличения i
на 1. Таким образом, в конце нам достаточно будет проверить, равен ли i-тый элемент массива a заданному k. Если равен, выведем поясняющее
сообщение «Номер искомого элемента последовательности» и значение i.
Если же не равен, выведем слово «Нет». В конце блок-схемы следует блок «Конец».
Блок-схема
алгоритма
Запишем программу по данной блок-схеме. Назовём её poisk. В разделе описания переменных будет массив из ста
элементов типа integer,
а также переменные n,
i
и k
типа integer.
Запишем тело программы. Выведем с переходом на
следующую строку поясняющее сообщение о том, что это программа поиска элемента k в
последовательности из n
случайных чисел. Теперь выведем запрос на ввод n и считаем её, то же сделаем и для k. Запишем цикл for i:=1
to
n
do,
который будет содержать команду присваивания i-тому элементу массива a, суммы случайного числа от 0 до 99 и
1. Теперь запишем такой же цикл for i:=1 to n do, который будет содержать одну
команду вывода i-того элемента массива a через пробел.
Теперь выполним поиск в последовательности случайных
чисел элемента равного k.
Для этого, согласно блок-схеме, мы будем перебирать элементы, пока они не
закончатся, или пока не найдём равный k. Для этого присвоим i:=1
и запишем цикл while
с условием i<n и a[i]<>k, содержащий команду увеличения i
на 1.
Теперь для вывода ответа мы должны перейти на
следующую строку – для этого достаточно записать оператор writeln
без параметров. Для проверки того, нашли ли мы нужный элемент, запишем условный
оператор с условием, что a[i]=k, в случае выполнения условия выведем
на экран значение i, в противном случае
выведем слово «Нет».
Исходный
код программы
Запустим программу на выполнение и введём длину
последовательности, равную 15 и k, равное 3. В
последовательности, сгенерированной программой, есть элемент равный 3 на первой
позиции, программа вывела число 1. Ещё раз запустим программу на выполнение и
введём длину последовательности, равную 10, и искомый элемент, равный 70. В
последовательности, сгенерированной программой, элемента с таким значением нет,
и программа вывела слово «Нет». Программа работает правильно. Задача решена.
Результаты
работы программы
Также при поиске удобно использовать цикл с пост
условием repeat,
который записывается в следующей форме. Записывается служебное слово repeat, после которого идёт
тело цикла, то есть последовательность команд, которая будет повторяться. После
чего записывается служебное слово until, после
которого идёт условие, при выполнении которого цикл прекратит работу. Обратим
внимание, что при записи тела цикла repeat служебных слов begin и end не требуется, а условие,
в отличии от цикла while,
проверяется после выполнения тела цикла.
Изменим текст нашей программы. До поиска элемента
программа будет такой же. Перед циклом поиска нужно присвоить переменной i
значение 0, так как условие будет проверяться уже после увеличения i
на 1. Вместо строки while
с условием запишем служебное слово repeat, а после тела цикла – служебное слово until. Цикл будет выполняться,
пока i-тый элемент массива a не будет равен k или пока i не станет равным n.
Исходный
код изменённой программы
Ещё раз запустим программу на выполнение. Введём длину
последовательности, равную 20, и k, равное 7. В сгенерированной программой
последовательности такого элемента нет, и программа вывела на экран слово
«нет». Ещё раз запустим программу на выполнение и введём длину
последовательности, равную 10 и k, равное 40. В последовательности случайных чисел
число сорок находится на второй позиции, и программа вывела на экран число 2.
Программа работает верно.
Результаты
работы изменённой программы
Важно запомнить:
Типовые задачи на поиск
элемента в массиве:
·
найти элемент, сравнивая его с другими
элементами массива;
·
найти элемент, равный определённому
значению.
В первом случае: нужно
выбрать один элемент массива, предположить его искомым и сравнить с
оставшимися, меняя в процессе предполагаемый искомый элемент.
Во втором случае:
достаточно перебирать элементы массива, пока они не закончатся или пока не
найден искомый.
Данная тема основывается на теме: Массивы. Одномерные массивы. Инициализация массива
Содержание
- 1. Нахождение сумм и произведений элементов массива. Примеры
- 2. Нахождение максимального (минимального) элемента массива. Примеры
- 3. Сортировка массива методом вставки
- 4. Поиск элемента в массиве. Примеры
- Связанные темы
Поиск на других ресурсах:
1. Нахождение сумм и произведений элементов массива. Примеры
Пример 1. Задан массив A, содержащий 100 целых чисел. Найти сумму элементов этого массива. Фрагмент кода, решающего эту задачу
// сумма элементов массива A из 100 целых чисел int A[100]; int suma; // переменная, содержащая сумму int i; // дополнительная переменная // ввод массива A // ... // Вычисление суммы suma = 0; // обнулить сумму for (i=0; i<100; i++) suma += A[i];
Перебор всех элементов массива выполняется в цикле for.
Переменная sum сохраняет результирующее значение суммы элементов массива. Переменная i есть счетчиком, определяющим индекс элемента массива A[i].
Пример 2. Задан массив B, содержащий 20 вещественных чисел. Найти сумму элементов массива, которые лежат на парных позициях. Считать, что позиции 0, 2, 4 и т.д. есть парными.
// сумма элементов массива B // лежащих на парных позициях float B[20]; float sum; // переменная, содержащая сумму int i; // дополнительная переменная // ввод массива // ... // Вычисление суммы sum = 0; // обнулить сумму for (i=0; i<20; i++) if ((i%2)==0) sum += B[i];
В этом примере выражение
(i%2)==0
определяет парную позицию (парный индекс) массива B. Если нужно взять нечетные позиции, то нужно написать
(i%2)==1
Пример 3. Задан массив, который содержит 50 целых чисел. Найти сумму положительных элементов массива.
// сумма положительных элементов массива int A[50]; int sum; // переменная, содержащая сумму int i; // дополнительная переменная // ввод массива // ... // Вычисление суммы sum = 0; // обнулить сумму for (i=0; i<50; i++) if (A[i]>0) sum = sum + A[i];
Пример 4. Задан массив из 50 целых чисел. Найти произведение элементов массива, которые есть нечетными числами.
// произведение нечетных элементов массива int A[50]; int d; // переменная, содержащая произведение int i; // вспомогательная переменная // ввод массива // ... // Вычисление произведения d = 1; // начальная установка переменной d for (i=0; i<50; i++) if ((A[i]%2)==1) d = d * A[i];
Чтобы определить, есть ли элемент массива A[i] нечетным, нужно проверить условие
(A[i]%2)==1
Если условие выполняется, то элемент массива есть нечетное число.
⇑
2. Нахождение максимального (минимального) элемента массива. Примеры
Пример 1. Задан массив из 30 вещественных чисел. Найти элемент (индекс), имеющий максимальное значение в массиве.
// поиск позиции (индекса), содержащего максимальное значение float B[30]; float max; // переменная, содержащая максимум int index; // позиция элемента, содержащего максимальное значение int i; // дополнительная переменная // ввод массива // ... // поиск максимума // установить максимум как 1-й элемент массива index = 0; max = B[0]; for (i=1; i<30; i++) if (max<B[i]) { max = B[i]; // запомнить максимум index = i; // запомнить позицию максимального элемента }
В вышеприведенном примере переменная max содержит максимальное значение. Переменная index содержит позицию элемента, который имеет максимальное значение. В начале переменной max присваивается значение первого элемента массива. Затем, начиная со второго элемента, происходит прохождение всего массива в цикле for. Одновременно проверяется условие
if (max<B[i])
Если условие выполняется (найден другой максимум), тогда новое значение максимума фиксируется в переменных max и index.
Вышеприведенный пример находит только один максимум. Однако, в массивах может быть несколько максимальных значений. В этом случае для сохранения позиций (индексов) максимальных значений нужно использовать дополнительный массив как показано в следующем примере.
Пример 2. Задан массив содержащий 50 целых чисел. Найти позицию (позиции) элемента, который имеет минимальное значение. Если таких элементов несколько, сформировать дополнительный массив индексов.
// поиск позиций (индексов), содержащих минимальное значение int A[50]; int min; // переменная, содержащая минимальное значение int INDEXES[50]; // позиции элементов, содержащих минимальное значение int n; // число одинаковых минимальных значений int i; // дополнительная переменная // ввод массива // ... // 1. Поиск минимального значения // установить минимальное значение в первом элементе массива min = A[0]; for (i=1; i<50; i++) if (min>A[i]) min = A[i]; // запомнить минимальное значение // 2. Формирование массива n = 0; // обнулить счетчик в массиве INDEXES for (i=0; i<50; i++) if (min == A[i]) { n++; // увеличить число элементов в INDEXES INDEXES[n-1] = i; // запомнить позицию } listBox1->Items->Clear(); // 3. Вывод массива INDEXES в listBox1 for (i=0; i<n; i++) listBox1->Items->Add(INDEXES[i].ToString());
В вышеприведенном листинге сначала ищется минимальное значение min.
На втором шаге формируется массив INDEXES, в котором число элементов записывается в переменную n. Происходит поиск минимального значения в массиве A с одновременным формированием массива INDEXES.
На третьем шаге приведен пример, как вывести массив INDEXES в элементе управления listBox1(ListBox).
⇑
3. Сортировка массива методом вставки
Пример. Пусть дан массив A, содержащий 10 целых чисел. Отсортировать элементы массива в нисходящем порядке с помощью метода вставки.
// сортировка массива методом вставки int A[10]; int i, j; // дополнительные переменные - счетчики int t; // дополнительная переменная // ввод массива A // ... // сортировка for (i=0; i<9; i++) for (j=i; j>=0; j--) if (A[j]<A[j+1]) { // поменять местами A[j] и A[j+1] t = A[j]; A[j] = A[j+1]; A[j+1] = t; }
⇑
4. Поиск элемента в массиве. Примеры
Пример 1. Определить, находится ли число k в массиве M состоящем из 50 целых чисел.
// определение наличия заданного числа в массиве чисел int M[50]; int i; int k; // искомое значение bool f_is; // результат поиска, true - число k есть в массиве, иначе false // ввод массива M // ... // ввод числа k // ... // поиск числа в массиве f_is = false; for (i=0; i<50; i++) if (k==M[i]) { f_is = true; // число найдено break; // выход из цикла, дальнейший поиск не имеет смысла } // вывод результата if (f_is) label1->Text = "Число " + k.ToString() + " есть в массиве M."; else label1->Text = "Числа " + k.ToString() + " нет в массиве M.";
Пример 2. Найти все позиции вхождения числа k в массиве M состоящим из 50 целых чисел.
// определение всех позиций заданного числа в массиве чисел int M[50]; // массив чисел int i; // вспомогательная переменная int k; // искомое значение int INDEXES[50]; // искомый массив позиций вхождения числа k int n; // количество найденных позиций или количество элементов в массиве INDEXES // ввод массива M // ... // ввод числа k // ... // поиск числа k в массиве M и одновременное формирование массива INDEXES n = 0; for (i=0; i<50; i++) if (k==M[i]) { // число найдено n++; INDEXES[n-1] = i; } // вывод результата в listBox1 listBox1->Items->Clear(); for (i=0; i<n; i++) listBox1->Items->Add(INDEXES[i].ToString());
⇑
Связанные темы
- Массивы. Часть 1. Определение массива в C++. Одномерные массивы. Инициализация массива
- Массивы. Часть 2. Двумерные массивы. Массивы строк. Многомерные массивы
⇑