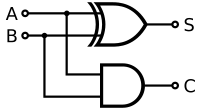Как найти порядок двоичного числа

Системы счисления в культуре
Индо-арабская
Арабская Тамильская Бирманская	Кхмерская Лаосская Монгольская Тайская
Восточноазиатские
Китайская Японская Сучжоу Корейская	Вьетнамская Счётные палочки
Алфавитные
Абджадия Армянская Ариабхата Кириллическая Греческая	Грузинская Эфиопская Еврейская Акшара-санкхья
Другие
Вавилонская Египетская Этрусская Римская Дунайская	Аттическая Кипу Майяская Эгейская Символы КППУ
Позиционные
2, 3, 4, 5, 6, 8, 10, 12, 16, 20, 60
Нега-позиционная
Симметричная
Смешанные системы
Фибоначчиева
Непозиционные
Единичная (унарная)

Двоичная система счисления — позиционная система счисления с основанием 2. Благодаря непосредственной реализации в цифровых электронных схемах на логических вентилях, двоичная система используется практически во всех современных компьютерах и прочих вычислительных электронных устройствах.

Двоичная запись чисел[править | править код]

В двоичной системе счисления числа записываются с помощью двух символов (0 и 1). Чтобы не путать, в какой системе счисления записано число, его снабжают указателем справа внизу. Например, число в десятичной системе 5₁₀, в двоичной 101₂. Иногда двоичное число обозначают префиксом 0b или символом & (амперсанд)^[1], например 0b101 или соответственно &101.

В двоичной системе счисления (как и в других системах счисления, кроме десятичной) знаки читаются по одному. Например, число 101₂ произносится «один ноль один».

Натуральные числа[править | править код]

Натуральное число, записываемое в двоичной системе счисления как , имеет значение:

где:

Отрицательные числа[править | править код]

Отрицательные двоичные числа обозначаются так же как и десятичные: знаком «−» перед числом. А именно, отрицательное целое число, записываемое в двоичной системе счисления , имеет величину:

В вычислительной технике широко используется запись отрицательных двоичных чисел в дополнительном коде.

Дробные числа[править | править код]

Дробное число, записываемое в двоичной системе счисления как , имеет величину:

где:

Сложение, вычитание и умножение двоичных чисел[править | править код]

Таблица сложения

+	0	1
0	0	1
1	1	0 (перенос 1 в старший разряд)

Таблица вычитания

–	0	1
0	0	1
1	1(заём из старшего разряда)	0

Пример сложения «столбиком» (десятичное выражение 14₁₀ + 5₁₀ = 19₁₀ в двоичном виде выглядит как 1110₂ + 101₂ = 10011₂):

+		1	1	1	0
		1	0	1
	1	0	0	1	1

Таблица умножения

×	0	1
0	0	0
1	0	1

Пример умножения «столбиком» (десятичное выражение 14₁₀ * 5₁₀ = 70₁₀ в двоичном виде выглядит как 1110₂ * 101₂ = 1000110₂):

×				1	1	1	0
				1	0	1
+				1	1	1	0
	1	1	1	0
	1	0	0	0	1	1	0

Преобразование чисел[править | править код]

Для преобразования из двоичной системы в десятичную используют следующую таблицу степеней основания 2:

1024

512

256

128

64

32

16

8

4

2

1

Начиная с цифры 1 все цифры умножаются на два.
Точка, которая стоит после 1, называется двоичной точкой.

Преобразование двоичных чисел в десятичные[править | править код]

Допустим, дано двоичное число 110001₂. Для перевода в десятичное запишите его как сумму по разрядам следующим образом:

1 * 2⁵ +
1 * 2⁴ +
0 * 2³ +
0 * 2² +
0 * 2¹ +
1 * 2⁰ = 49

То же самое чуть иначе:

1 * 32 +
1 * 16 +
0 * 8 +
0 * 4 +
0 * 2 +
1 * 1 = 49

Можно записать это в виде таблицы следующим образом:

512	256	128	64	32	16	8	4	2	1
				1	1	0	0	0	1
				+32	+16	+0	+0	+0	+1

Двигайтесь справа налево. Под каждой двоичной единицей напишите её эквивалент в строчке ниже. Сложите получившиеся десятичные числа.
Таким образом, двоичное число 110001₂ равнозначно десятичному 49₁₀.

Преобразование дробных двоичных чисел в десятичные[править | править код]

Нужно перевести число 1011010,101₂ в десятичную систему. Запишем это число следующим образом:

1 * 2⁶ +
0 * 2⁵ +
1 * 2⁴ +
1 * 2³ +
0 * 2² +
1 * 2¹ +
0 * 2⁰ +
1 * 2⁻¹ +
0 * 2⁻² +
1 * 2⁻³ = 90,625

То же самое чуть иначе:

1 * 64 +
0 * 32 +
1 * 16 +
1 * 8 +
0 * 4 +
1 * 2 +
0 * 1 +
1 * 0,5 +
0 * 0,25 +
1 * 0,125 = 90,625

Или по таблице:

64	32	16	8	4	2	1		0.5	0.25	0.125
1	0	1	1	0	1	0	,	1	0	1
+64	+0	+16	+8	+0	+2	+0		+0.5	+0	+0.125

Преобразование методом Горнера[править | править код]

Для того, чтобы преобразовывать числа из двоичной в десятичную систему данным методом, надо суммировать цифры слева направо, умножая ранее полученный результат на основу системы (в данном случае 2). Методом Горнера обычно переводят из двоичной в десятичную систему. Обратная операция затруднительна, так как требует навыков сложения и умножения в двоичной системе счисления.

Например, двоичное число 1011011₂ переводится в десятичную систему так:

0*2 + 1 = 1
1*2 + 0 = 2
2*2 + 1 = 5
5*2 + 1 = 11
11*2 + 0 = 22
22*2 + 1 = 45
45*2 + 1 = 91

То есть в десятичной системе это число будет записано как 91.

Перевод дробной части чисел методом Горнера[править | править код]

Цифры берутся из числа справа налево и делятся на основу системы счисления (2).

Например 0,1101₂

(0 + 1)/2 = 0,5
(0,5 + 0)/2 = 0,25
(0,25 + 1)/2 = 0,625
(0,625 + 1)/2 = 0,8125

Ответ: 0,1101₂= 0,8125₁₀

Преобразование десятичных чисел в двоичные[править | править код]

Допустим, нам нужно перевести число 19 в двоичное. Вы можете воспользоваться следующей процедурой :

19/2 = 9 с остатком 1
9/2 = 4 c остатком 1
4/2 = 2 без остатка 0
2/2 = 1 без остатка 0
1/2 = 0 с остатком 1

Итак, мы делим каждое частное на 2 и записываем остаток в конец двоичной записи. Продолжаем деление до тех пор, пока в частном не будет 0. Результат записываем справа налево. То есть нижняя цифра (1) будет самой левой и т. д. В результате получаем число 19 в двоичной записи: 10011.

Преобразование дробных десятичных чисел в двоичные[править | править код]

Если в исходном числе есть целая часть, то она преобразуется отдельно от дробной. Перевод дробного числа из десятичной системы счисления в двоичную осуществляется по следующему алгоритму:

• Дробь умножается на основание двоичной системы счисления (2);
• В полученном произведении выделяется целая часть, которая принимается в качестве старшего разряда числа в двоичной системе счисления;
• Алгоритм завершается, если дробная часть полученного произведения равна нулю или если достигнута требуемая точность вычислений. В противном случае вычисления продолжаются над дробной частью произведения.

Пример: Требуется перевести дробное десятичное число 206,116 в дробное двоичное число.

Перевод целой части дает 206₁₀=11001110₂ по ранее описанным алгоритмам. Дробную часть 0,116 умножаем на основание 2, занося целые части произведения в разряды после запятой искомого дробного двоичного числа:

0,116 • 2 = 0,232
0,232 • 2 = 0,464
0,464 • 2 = 0,928
0,928 • 2 = 1,856
0,856 • 2 = 1,712
0,712 • 2 = 1,424
0,424 • 2 = 0,848
0,848 • 2 = 1,696
0,696 • 2 = 1,392
0,392 • 2 = 0,784
и т. д.

Таким образом 0,116₁₀ ≈ 0,0001110110₂

Получим: 206,116₁₀ ≈ 11001110,0001110110₂

Применения[править | править код]

В цифровых устройствах[править | править код]

Двоичная система используется в цифровых устройствах, поскольку является наиболее простой и соответствует требованиям:

• Чем меньше значений существует в системе, тем проще изготовить отдельные элементы, оперирующие этими значениями. В частности, две цифры двоичной системы счисления могут быть легко представлены многими физическими явлениями: есть ток (ток больше пороговой величины) — нет тока (ток меньше пороговой величины), индукция магнитного поля больше пороговой величины или нет (индукция магнитного поля меньше пороговой величины) и т. д.
• Чем меньше количество состояний у элемента, тем выше помехоустойчивость и тем быстрее он может работать. Например, чтобы закодировать три состояния через величину напряжения, тока или индукции магнитного поля, потребуется ввести два пороговых значения и два компаратора,

В вычислительной технике широко используется запись отрицательных двоичных чисел в дополнительном коде. Например, число −5₁₀ может быть записано как −101₂ но в 32-битном компьютере будет храниться как 11111111111111111111111111111011₂.

Обобщения[править | править код]

Двоичная система счисления является комбинацией двоичной системы кодирования и показательной весовой функции с основанием равным 2. Число может быть записано в двоичном коде, а система счисления при этом может быть не двоичной, а с другим основанием. Пример: двоично-десятичное кодирование, в котором десятичные цифры записываются в двоичном виде, а система счисления — десятичная.

История[править | править код]

• Полный набор из 8 триграмм и 64 гексаграмм, аналог 3-битных и 6-битных цифр, был известен в древнем Китае в классических текстах книги Перемен. Порядок гексаграмм в книге Перемен, расположенных в соответствии со значениями соответствующих двоичных цифр (от 0 до 63), и метод их получения был разработан китайским учёным и философом Шао Юн в XI веке. Однако нет доказательств, свидетельствующих о том, что Шао Юн понимал правила двоичной арифметики, располагая двухсимвольные кортежи в лексикографическом порядке.
• Индийский математик Пингала (200 год до н. э.) разработал математические основы для описания поэзии с использованием первого известного применения двоичной системы счисления^[2][3].

• Прообразом баз данных, широко использовавшихся в Центральных Андах (Перу, Боливия) в государственных и общественных целях в I—II тысячелетии н. э., была узелковая письменность Инков — кипу, состоявшая как из числовых записей десятичной системы^[4], так и не числовых записей в двоичной системе кодирования^[5]. В кипу применялись первичные и дополнительные ключи, позиционные числа, кодирование цветом и образование серий повторяющихся данных^[6]. Кипу впервые в истории человечества использовалось для применения такого способа ведения бухгалтерского учёта, как двойная запись^[7].
• Наборы, представляющие собой комбинации двоичных цифр, использовались африканцами в традиционных гаданиях (таких как Ифа) наряду со средневековой геомантией.
• В 1605 году Френсис Бэкон описал систему, буквы алфавита которой могут быть сведены к последовательностям двоичных цифр, которые в свою очередь могут быть закодированы как едва заметные изменения шрифта в любых случайных текстах. Важным шагом в становлении общей теории двоичного кодирования является замечание о том, что указанный метод может быть использован применительно к любым объектам^[8] (см. Шифр Бэкона).

• Современная двоичная система была полностью описана Лейбницем в XVII веке в работе Explication de l’Arithmétique Binaire^[9]. В системе счисления Лейбница были использованы цифры 0 и 1, как и в современной двоичной системе. Как человек, увлекающийся китайской культурой, Лейбниц знал о книге Перемен и заметил, что гексаграммы соответствуют двоичным числам от 0 до 111111. Он восхищался тем, что это отображение является свидетельством крупных китайских достижений в философской математике того времени^[10].

• В 1854 году английский математик Джордж Буль опубликовал знаковую работу, описывающую алгебраические системы применительно к логике, которая в настоящее время известна как Булева алгебра или алгебра логики. Его логическому исчислению было суждено сыграть важную роль в разработке современных цифровых электронных схем.
• В 1937 году Клод Шеннон представил к защите кандидатскую диссертацию Символический анализ релейных и переключательных схем в MIT, в которой булева алгебра и двоичная арифметика были использованы применительно к электронным реле и переключателям. На диссертации Шеннона по существу основана вся современная цифровая техника.
• В ноябре 1937 года Джордж Штибиц, впоследствии работавший в Bell Labs, создал на базе реле компьютер «Model K» (от англ. «Kitchen», кухня, где производилась сборка), который выполнял двоичное сложение. В конце 1938 года Bell Labs развернула исследовательскую программу во главе со Штибицом. Созданный под его руководством компьютер, завершённый 8 января 1940 года, умел выполнять операции с комплексными числами. Во время демонстрации на конференции American Mathematical Society в Дартмутском колледже 11 сентября 1940 года Штибиц продемонстрировал возможность посылки команд удалённому калькулятору комплексных чисел по телефонной линии с использованием телетайпа. Это была первая попытка использования удалённой вычислительной машины посредством телефонной линии. Среди участников конференции, бывших свидетелями демонстрации, были Джон фон Нейман, Джон Мокли и Норберт Винер, впоследствии писавшие об этом в своих мемуарах.

См. также[править | править код]

• Битовые операции
• Степень двойки
• Системы счисления
• Бит
• Байт
• Единицы измерения информации
• Двоичные логические элементы
• Двоичный триггер
• Двоично-десятичный код
• Двоичное кодирование
• Азбука Морзе

Примечания[править | править код]

Ссылки[править | править код]

1. Порядковый счет в различных системах счисления.

В современной жизни мы используем позиционные системы счисления, то есть системы, в которых число, обозначаемое цифрой, зависит от положения цифры в записи числа. Поэтому в дальнейшем мы будем говорить только о них, опуская термин «позиционные».

Для того чтобы научиться переводить числа из одной системы в другую, поймем, как происходит последовательная запись чисел на примере десятичной системы.

Поскольку у нас десятичная система счисления, мы имеем 10 символов (цифр) для построения чисел. Начинаем порядковый счет: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Цифры закончились. Мы увеличиваем разрядность числа и обнуляем младший разряд: 10. Затем опять увеличиваем младший разряд, пока не закончатся все цифры: 11, 12, 13, 14, 15, 16, 17, 18, 19. Увеличиваем старший разряд на 1 и обнуляем младший: 20. Когда мы используем все цифры для обоих разрядов (получим число 99), опять увеличиваем разрядность числа и обнуляем имеющиеся разряды: 100. И так далее.

Попробуем сделать то же самое в 2-ной, 3-ной и 5-ной системах (введем обозначение для 2-ной системы, для 3-ной и т.д.):

0	0	0	0
1	1	1	1
2	10	2	2
3	11	10	3
4	100	11	4
5	101	12	10
6	110	20	11
7	111	21	12
8	1000	22	13
9	1001	100	14
10	1010	101	20
11	1011	102	21
12	1100	110	22
13	1101	111	23
14	1110	112	24
15	1111	120	30

Если система счисления имеет основание больше 10, то нам придется вводить дополнительные символы, принято вводить буквы латинского алфавита. Например, для 12-ричной системы кроме десяти цифр нам понадобятся две буквы ( и ):

0	0
1	1
2	2
3	3
4	4
5	5
6	6
7	7
8	8
9	9
10
11
12	10
13	11
14	12
15	13

 
2.Перевод из десятичной системы счисления в любую другую.

Чтобы перевести целое положительное десятичное число в систему счисления с другим основанием, нужно это число разделить на основание. Полученное частное снова разделить на основание, и дальше до тех пор, пока частное не окажется меньше основания. В результате записать в одну строку последнее частное и все остатки, начиная с последнего.

Пример 1. Переведем десятичное число 46 в двоичную систему счисления.

Пример 2. Переведем десятичное число 672 в восьмеричную систему счисления.

Пример 3. Переведем десятичное число 934 в шестнадцатеричную систему счисления.

3. Перевод из любой системы счисления в десятичную.

Для того, чтобы научиться переводить числа из любой другой системы в десятичную, проанализируем привычную нам запись десятичного числа.
Например, десятичное число 325 – это 5 единиц, 2 десятка и 3 сотни, т.е.

Точно так же обстоит дело и в других системах счисления, только умножать будем не на 10, 100 и пр., а на степени основания системы счисления. Для примера возьмем число 1201 в троичной системе счисления. Пронумеруем разряды справа налево начиная с нуля и представим наше число как сумму произведений цифры на тройку в степени разряда числа:

Это и есть десятичная запись нашего числа, т.е.

Пример 4. Переведем в десятичную систему счисления восьмеричное число 511.

Пример 5. Переведем в десятичную систему счисления шестнадцатеричное число 1151.

4. Перевод из двоичной системы в систему с основанием «степень двойки» (4, 8, 16 и т.д.).

Для преобразования двоичного числа в число с основанием «степень двойки» необходимо двоичную последовательность разбить на группы по количеству цифр равному степени справа налево и каждую группу заменить соответствующей цифрой новой системы счисления.

Например, Переведем двоичное 1100001111010110 число в восьмеричную систему. Для этого разобьем его на группы по 3 символа начиная справа (т.к. ), а затем воспользуемся таблицей соответствия и заменим каждую группу на новую цифру:

Таблицу соответствия мы научились строить в п.1.

0	0
1	1
10	2
11	3
100	4
101	5
110	6
111	7

Т.е.

Пример 6. Переведем двоичное 1100001111010110 число в шестнадцатеричную систему.

0	0
1	1
10	2
11	3
100	4
101	5
110	6
111	7
1000	8
1001	9
1010	A
1011	B
1100	C
1101	D
1110	E
1111	F

5.Перевод из системы с основанием «степень двойки» (4, 8, 16 и т.д.) в двоичную.

Этот перевод аналогичен предыдущему, выполненному в обратную сторону: каждую цифру мы заменяем группой цифр в двоичной системе из таблицы соответствия.

Пример 7. Переведем шестнадцатеричное число С3A6 в двоичную систему счисления.

Для этого каждую цифру числа заменим группой из 4 цифр (т.к. ) из таблицы соответствия, дополнив при необходимости группу нулями вначале:

Десятичное и двоичное представление чисел

Кроме цифр, в десятичной системе большое значение имеют разряды. Подсчитывая количество чего-нибудь и дойдя до самой большой из доступных нам цифр (до $9$), мы вводим второй разряд и дальше каждое последующее число формируем из двух цифр. Дойдя до $99$, мы вынуждены вводить третий разряд. В пределах трех разрядов мы можем досчитать уже до $999$ и т.д.

Таким образом, используя всего десять цифр и вводя дополнительные разряды, мы можем записывать и проводить математические операции с любыми, даже самыми большими числами.

Компьютер ведет подсчет аналогичным образом, но имеет в своем распоряжении всего две цифры – логический ноль (отсутствие у бита какого-то свойства) и логическую единицу (наличие у бита этого свойства).

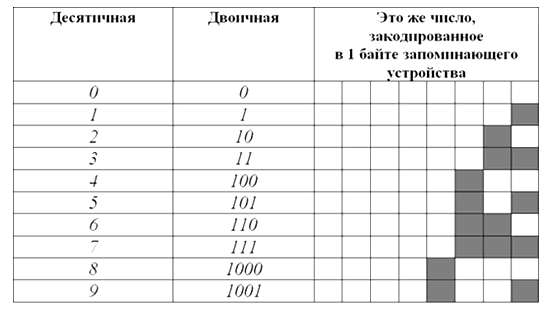
Вот таблица первых десяти чисел в каждой из этих систем счисления:

Как видите, в десятичной системе счисления для отображения любой из первых десяти цифр достаточно $1$ разряда. В двоичной системе для тех же целей потребуется уже $4$ разряда.

«Кодирование числовой информации» 👇

Соответственно, для кодирования этой же информации в виде двоичного кода нужен носитель емкостью как минимум $4$ бита ($0,5$ байта).
Человеческий мозг, привыкший к десятичной системе счисления, плохо воспринимает систему двоичную. Хотя обе они построены на одинаковых принципах и отличаются лишь количеством используемых цифр. В двоичной системе точно так же можно осуществлять любые арифметические операции с любыми числами. Главный ее минус – необходимость иметь дело с большим количеством разрядов.

Так, самое большое десятичное число, которое можно отобразить в 8 разрядах двоичной системы – $255$, в $16$ разрядах – $65535$, в $24$ разрядах – $16777215$.

Алгоритмы кодирования чисел в двоичной системе счисления

Компьютер, кодируя числа в двоичный код, основывается на двоичной системе счисления. Но, в зависимости от особенностей чисел, может использовать разные алгоритмы:

1. Небольшие целые числа без знака.

   Для сохранения каждого такого числа на запоминающем устройстве, как правило, выделяется $1$ байт ($8$ битов). Запись осуществляется в полной аналогии с двоичной системой счисления.

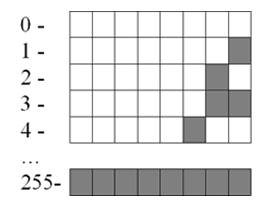
   Целые десятичные числа без знака, сохраненные на носителе в двоичном коде, будут выглядеть примерно так:

   

   Рисунок 2.

2. Большие целые числа и числа со знаком.

   Для записи каждого такого числа на запоминающем устройстве, как правило, отводится $2$-байтний блок ($16$ битов).

   Старший бит блока (тот, что крайний слева) отводится под запись знака числа и в кодировании самого числа не участвует. Если число со знаком “плюс”, этот бит остается пустым, если со знаком “минус” – в него записывается логическая единица. Число же кодируется в оставшихся 15 битах.
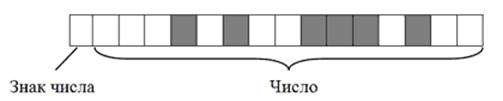
   Например, алгоритм кодирования числа $+2676$ будет следующим:

   • Перевести число $2676$ из десятичной системы счисления в двоичную. В итоге получится $101001110100$;
   • Записать полученное двоичное число в первые $15$ бит $16$-битного блока (начиная с правого края). Последний, $16$-й бит, должен остаться пустым, поскольку кодируемое число имеет знак $+$.

   В итоге $+2676$ в двоичном коде на запоминающем устройстве будет выглядеть так:

   

   Рисунок 3.

   Примечательно, что в двоичном коде присвоение числу отрицательного значения предусматривает не только изменение старшего бита. Осуществляется также инвертирование всех остальных его битов.

   Чтобы было понятно, рассмотрим алгоритм кодирования числа $-2676$:

   1. Перевести число $2676$ из десятичной системы счисления в двоичную. Получим все тоже двоичное число $101001110100$;
   2. Записать полученное двоичное число в первые $15$ бит $16$-битного блока. Затем инвертировать, то есть, изменить на противоположное, значение каждого из $15$ битов;
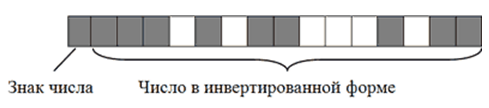
   3. Записать в $16$-й бит логическую единицу, поскольку кодируемое число имеет отрицательное значение.

   В итоге $-2676$ на запоминающем устройстве в двоичном коде будет иметь следующий вид:

   

   Рисунок 4.

   Запись отрицательных чисел в инвертированной форме позволяет заменить все операции вычитания, в которых они участвуют, операциями сложения. Это необходимо для нормальной работы компьютерного процессора.

   Максимальным десятичным числом, которое можно закодировать в $15$ битах запоминающего устройства, является $32767$. Иногда для записи чисел по этому алгоритму выделяются $4$-байтные блоки. В таком случае для кодирования каждого числа будет использоваться $31$ бит плюс $1$ бит для кодирования знака числа. Тогда максимальным десятичным числом, сохраняемым в каждую ячейку, будет $2147483647$ (со знаком плюс или минус).

3. Дробные числа со знаком.

   Дробные числа на запоминающем устройстве в двоичном коде кодируются в виде так называемых чисел с плавающей запятой (точкой). Алгоритм их кодирования сложнее, чем рассмотренные выше. Тем не менее, попытаемся разобраться.

   Для записи каждого числа с плавающей запятой компьютер чаще всего выделяет $4$-байтную ячейку ($32$ бита):

   • в старшем бите этой ячейки (тот, что крайний слева) записывается знак числа. Если число отрицательное, в этот бит записывается логическая единица, если оно со знаком “плюс” – бит остается пустым.
   • во втором слева бите аналогичным образом записывается знак порядка (что такое порядок поймете позже);
   • в следующих за ним $7$ битах записывается значение порядка.
   • в оставшихся $23$ битах записывается так называемая мантисса числа.

   

   Рисунок 5.

   Чтобы стало понятно, что такое порядок, мантисса и зачем они нужны, переведем в двоичный код десятичное число $6,25$.

   Порядок кодирования будет примерно следующим:

   1. Перевести десятичное число в двоичное (десятичное $6,25$ равно двоичному $110,01$);
   2. Определить мантиссу числа. Для этого в числе необходимо передвинуть запятую в нужном направлении, чтобы слева от нее не осталось ни одной единицы. В нашем случае запятую придется передвинуть на три знака влево. В итоге, получим мантиссу, $11001$;
   3. Определить значение и знак порядка.
      Значение порядка – это количество символов, на которое была сдвинута запятая для получения мантиссы. В нашем случае оно равно $3$ (или $11$ в двоичной форме);

   Знак порядка – это направление, в котором пришлось двигать запятую: влево – “плюс”, вправо – “минус”. В нашем примере запятая двигалась влево, поэтому знак порядка – “плюс”.

   Таким образом, порядок двоичного числа $110,01$ будет равен $+11$, а его мантисса, $11001$. В результате в двоичном коде на запоминающем устройстве это число будет записано следующим образом

   

   Рисунок 6.

A binary number is a number expressed in the base-2 numeral system or binary numeral system, a method of mathematical expression which uses only two symbols: typically “0” (zero) and “1” (one).

The base-2 numeral system is a positional notation with a radix of 2. Each digit is referred to as a bit, or binary digit. Because of its straightforward implementation in digital electronic circuitry using logic gates, the binary system is used by almost all modern computers and computer-based devices, as a preferred system of use, over various other human techniques of communication, because of the simplicity of the language and the noise immunity in physical implementation.^[1]

History[edit]

The modern binary number system was studied in Europe in the 16th and 17th centuries by Thomas Harriot, Juan Caramuel y Lobkowitz, and Gottfried Leibniz. However, systems related to binary numbers have appeared earlier in multiple cultures including ancient Egypt, China, and India. Leibniz was specifically inspired by the Chinese I Ching.

Egypt[edit]

The scribes of ancient Egypt used two different systems for their fractions, Egyptian fractions (not related to the binary number system) and Horus-Eye fractions (so called because many historians of mathematics believe that the symbols used for this system could be arranged to form the eye of Horus, although this has been disputed).^[2] Horus-Eye fractions are a binary numbering system for fractional quantities of grain, liquids, or other measures, in which a fraction of a hekat is expressed as a sum of the binary fractions 1/2, 1/4, 1/8, 1/16, 1/32, and 1/64. Early forms of this system can be found in documents from the Fifth Dynasty of Egypt, approximately 2400 BC, and its fully developed hieroglyphic form dates to the Nineteenth Dynasty of Egypt, approximately 1200 BC.^[3]

The method used for ancient Egyptian multiplication is also closely related to binary numbers. In this method, multiplying one number by a second is performed by a sequence of steps in which a value (initially the first of the two numbers) is either doubled or has the first number added back into it; the order in which these steps are to be performed is given by the binary representation of the second number. This method can be seen in use, for instance, in the Rhind Mathematical Papyrus, which dates to around 1650 BC.^[4]

China[edit]

The I Ching dates from the 9th century BC in China.^[5] The binary notation in the I Ching is used to interpret its quaternary divination technique.^[6]

It is based on taoistic duality of yin and yang.^[7] Eight trigrams (Bagua) and a set of 64 hexagrams (“sixty-four” gua), analogous to the three-bit and six-bit binary numerals, were in use at least as early as the Zhou Dynasty of ancient China.^[5]

The Song Dynasty scholar Shao Yong (1011–1077) rearranged the hexagrams in a format that resembles modern binary numbers, although he did not intend his arrangement to be used mathematically.^[6] Viewing the least significant bit on top of single hexagrams in Shao Yong’s square^[8]
and reading along rows either from bottom right to top left with solid lines as 0 and broken lines as 1 or from top left to bottom right with solid lines as 1 and broken lines as 0 hexagrams can be interpreted as sequence from 0 to 63.
^[9]

India[edit]

The Indian scholar Pingala (c. 2nd century BC) developed a binary system for describing prosody.^[10][11] He used binary numbers in the form of short and long syllables (the latter equal in length to two short syllables), making it similar to Morse code.^[12][13] They were known as laghu (light) and guru (heavy) syllables.

Pingala’s Hindu classic titled Chandaḥśāstra (8.23) describes the formation of a matrix in order to give a unique value to each meter. “Chandaḥśāstra” literally translates to science of meters in Sanskrit. The binary representations in Pingala’s system increases towards the right, and not to the left like in the binary numbers of the modern positional notation.^[12][14] In Pingala’s system, the numbers start from number one, and not zero. Four short syllables “0000” is the first pattern and corresponds to the value one. The numerical value is obtained by adding one to the sum of place values.^[15]

Other cultures[edit]

The residents of the island of Mangareva in French Polynesia were using a hybrid binary-decimal system before 1450.^[16] Slit drums with binary tones are used to encode messages across Africa and Asia.^[7]
Sets of binary combinations similar to the I Ching have also been used in traditional African divination systems such as Ifá as well as in medieval Western geomancy. The majority of Indigenous Australian languages use a base-2 system.^[17]

Western predecessors to Leibniz[edit]

In the late 13th century Ramon Llull had the ambition to account for all wisdom in every branch of human knowledge of the time. For that purpose he developed a general method or ‘Ars generalis’ based on binary combinations of a number of simple basic principles or categories, for which he has been considered a predecessor of computing science and artificial intelligence.^[18]

In 1605 Francis Bacon discussed a system whereby letters of the alphabet could be reduced to sequences of binary digits, which could then be encoded as scarcely visible variations in the font in any random text.^[19] Importantly for the general theory of binary encoding, he added that this method could be used with any objects at all: “provided those objects be capable of a twofold difference only; as by Bells, by Trumpets, by Lights and Torches, by the report of Muskets, and any instruments of like nature”.^[19] (See Bacon’s cipher.)

John Napier in 1617 described a system he called location arithmetic for doing binary calculations using a non-positional representation by letters.
Thomas Harriot investigated several positional numbering systems, including binary, but did not publish his results; they were found later among his papers.^[20]
Possibly the first publication of the system in Europe was by Juan Caramuel y Lobkowitz, in 1700.^[21]

Leibniz and the I Ching[edit]

Leibniz studied binary numbering in 1679; his work appears in his article Explication de l’Arithmétique Binaire (published in 1703).
The full title of Leibniz’s article is translated into English as the “Explanation of Binary Arithmetic, which uses only the characters 1 and 0, with some remarks on its usefulness, and on the light it throws on the ancient Chinese figures of Fu Xi”.^[22] Leibniz’s system uses 0 and 1, like the modern binary numeral system. An example of Leibniz’s binary numeral system is as follows:^[22]

0 0 0 1   numerical value 2⁰

0 0 1 0   numerical value 2¹

0 1 0 0   numerical value 2²

1 0 0 0   numerical value 2³

Leibniz interpreted the hexagrams of the I Ching as evidence of binary calculus.^[23]
As a Sinophile, Leibniz was aware of the I Ching, noted with fascination how its hexagrams correspond to the binary numbers from 0 to 111111, and concluded that this mapping was evidence of major Chinese accomplishments in the sort of philosophical mathematics he admired. The relation was a central idea to his universal concept of a language or characteristica universalis, a popular idea that would be followed closely by his successors such as Gottlob Frege and George Boole in forming modern symbolic logic.^[24]
Leibniz was first introduced to the I Ching through his contact with the French Jesuit Joachim Bouvet, who visited China in 1685 as a missionary. Leibniz saw the I Ching hexagrams as an affirmation of the universality of his own religious beliefs as a Christian.^[23] Binary numerals were central to Leibniz’s theology. He believed that binary numbers were symbolic of the Christian idea of creatio ex nihilo or creation out of nothing.^[25]

[A concept that] is not easy to impart to the pagans, is the creation ex nihilo through God’s almighty power. Now one can say that nothing in the world can better present and demonstrate this power than the origin of numbers, as it is presented here through the simple and unadorned presentation of One and Zero or Nothing.

— Leibniz’s letter to the Duke of Brunswick attached with the I Ching hexagrams^[23]

Later developments[edit]

In 1854, British mathematician George Boole published a landmark paper detailing an algebraic system of logic that would become known as Boolean algebra. His logical calculus was to become instrumental in the design of digital electronic circuitry.^[26]

In 1937, Claude Shannon produced his master’s thesis at MIT that implemented Boolean algebra and binary arithmetic using electronic relays and switches for the first time in history. Entitled A Symbolic Analysis of Relay and Switching Circuits, Shannon’s thesis essentially founded practical digital circuit design.^[27]

In November 1937, George Stibitz, then working at Bell Labs, completed a relay-based computer he dubbed the “Model K” (for “Kitchen”, where he had assembled it), which calculated using binary addition.^[28] Bell Labs authorized a full research program in late 1938 with Stibitz at the helm. Their Complex Number Computer, completed 8 January 1940, was able to calculate complex numbers. In a demonstration to the American Mathematical Society conference at Dartmouth College on 11 September 1940, Stibitz was able to send the Complex Number Calculator remote commands over telephone lines by a teletype. It was the first computing machine ever used remotely over a phone line. Some participants of the conference who witnessed the demonstration were John von Neumann, John Mauchly and Norbert Wiener, who wrote about it in his memoirs.^[29][30][31]

The Z1 computer, which was designed and built by Konrad Zuse between 1935 and 1938, used Boolean logic and binary floating point numbers.^[32]

Representation[edit]

Any number can be represented by a sequence of bits (binary digits), which in turn may be represented by any mechanism capable of being in two mutually exclusive states. Any of the following rows of symbols can be interpreted as the binary numeric value of 667:

1	0	1	0	0	1	1	0	1	1
|	―	|	―	―	|	|	―	|	|
☒	☐	☒	☐	☐	☒	☒	☐	☒	☒
y	n	y	n	n	y	y	n	y	y

The numeric value represented in each case is dependent upon the value assigned to each symbol. In the earlier days of computing, switches, punched holes and punched paper tapes were used to represent binary values.^[33] In a modern computer, the numeric values may be represented by two different voltages; on a magnetic disk, magnetic polarities may be used. A “positive”, “yes”, or “on” state is not necessarily equivalent to the numerical value of one; it depends on the architecture in use.

In keeping with customary representation of numerals using Arabic numerals, binary numbers are commonly written using the symbols 0 and 1. When written, binary numerals are often subscripted, prefixed or suffixed in order to indicate their base, or radix. The following notations are equivalent:

• 100101 binary (explicit statement of format)
• 100101b (a suffix indicating binary format; also known as Intel convention^[34][35])
• 100101B (a suffix indicating binary format)
• bin 100101 (a prefix indicating binary format)
• 100101₂ (a subscript indicating base-2 (binary) notation)
• %100101 (a prefix indicating binary format; also known as Motorola convention^[34][35])
• 0b100101 (a prefix indicating binary format, common in programming languages)
• 6b100101 (a prefix indicating number of bits in binary format, common in programming languages)
• #b100101 (a prefix indicating binary format, common in Lisp programming languages)

When spoken, binary numerals are usually read digit-by-digit, in order to distinguish them from decimal numerals. For example, the binary numeral 100 is pronounced one zero zero, rather than one hundred, to make its binary nature explicit, and for purposes of correctness. Since the binary numeral 100 represents the value four, it would be confusing to refer to the numeral as one hundred (a word that represents a completely different value, or amount). Alternatively, the binary numeral 100 can be read out as “four” (the correct value), but this does not make its binary nature explicit.

Counting in binary[edit]

Decimal number	Binary number
0	0
1	1
2	10
3	11
4	100
5	101
6	110
7	111
8	1000
9	1001
10	1010
11	1011
12	1100
13	1101
14	1110
15	1111

Counting in binary is similar to counting in any other number system. Beginning with a single digit, counting proceeds through each symbol, in increasing order. Before examining binary counting, it is useful to briefly discuss the more familiar decimal counting system as a frame of reference.

Decimal counting[edit]

Decimal counting uses the ten symbols 0 through 9. Counting begins with the incremental substitution of the least significant digit (rightmost digit) which is often called the first digit. When the available symbols for this position are exhausted, the least significant digit is reset to 0, and the next digit of higher significance (one position to the left) is incremented (overflow), and incremental substitution of the low-order digit resumes. This method of reset and overflow is repeated for each digit of significance. Counting progresses as follows:

000, 001, 002, … 007, 008, 009, (rightmost digit is reset to zero, and the digit to its left is incremented)

010, 011, 012, …

   …

090, 091, 092, … 097, 098, 099, (rightmost two digits are reset to zeroes, and next digit is incremented)

100, 101, 102, …

Binary counting[edit]

Binary counting follows the exact same procedure, and again the incremental substitution begins with the least significant digit, or bit (the rightmost one, also called the first bit), except that only the two symbols 0 and 1 are available. Thus, after a bit reaches 1 in binary, an increment resets it to 0 but also causes an increment of the next bit to the left:

0000,

0001, (rightmost bit starts over, and next digit is incremented)

0010, 0011, (rightmost two bits start over, and next bit is incremented)

0100, 0101, 0110, 0111, (rightmost three bits start over, and the next bit is incremented)

1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111 …

In the binary system, each bit represents an increasing power of 2, with the rightmost bit representing 2⁰, the next representing 2¹, then 2², and so on. The value of a binary number is the sum of the powers of 2 represented by each “1” bit. For example, the binary number 100101 is converted to decimal form as follows:

100101₂ = [ ( 1 ) × 2⁵ ] + [ ( 0 ) × 2⁴ ] + [ ( 0 ) × 2³ ] + [ ( 1 ) × 2² ] + [ ( 0 ) × 2¹ ] + [ ( 1 ) × 2⁰ ]

100101₂ = [ 1 × 32 ] + [ 0 × 16 ] + [ 0 × 8 ] + [ 1 × 4 ] + [ 0 × 2 ] + [ 1 × 1 ]

100101₂ = 37₁₀

Fractions[edit]

Fractions in binary arithmetic terminate only if 2 is the only prime factor in the denominator. As a result, 1/10 does not have a finite binary representation (10 has prime factors 2 and 5). This causes 10 × 0.1 not to precisely equal 1 in floating-point arithmetic. As an example, to interpret the binary expression for 1/3 = .010101…, this means: 1/3 = 0 × 2⁻¹ + 1 × 2⁻² + 0 × 2⁻³ + 1 × 2⁻⁴ + … = 0.3125 + … An exact value cannot be found with a sum of a finite number of inverse powers of two, the zeros and ones in the binary representation of 1/3 alternate forever.

Fraction	Decimal	Binary	Fractional approximation
1/1	1 or 0.999…	1 or 0.111…	1/2 + 1/4 + 1/8…
1/2	0.5 or 0.4999…	0.1 or 0.0111…	1/4 + 1/8 + 1/16 . . .
1/3	0.333…	0.010101…	1/4 + 1/16 + 1/64 . . .
1/4	0.25 or 0.24999…	0.01 or 0.00111…	1/8 + 1/16 + 1/32 . . .
1/5	0.2 or 0.1999…	0.00110011…	1/8 + 1/16 + 1/128 . . .
1/6	0.1666…	0.0010101…	1/8 + 1/32 + 1/128 . . .
1/7	0.142857142857…	0.001001…	1/8 + 1/64 + 1/512 . . .
1/8	0.125 or 0.124999…	0.001 or 0.000111…	1/16 + 1/32 + 1/64 . . .
1/9	0.111…	0.000111000111…	1/16 + 1/32 + 1/64 . . .
1/10	0.1 or 0.0999…	0.000110011…	1/16 + 1/32 + 1/256 . . .
1/11	0.090909…	0.00010111010001011101…	1/16 + 1/64 + 1/128 . . .
1/12	0.08333…	0.00010101…	1/16 + 1/64 + 1/256 . . .
1/13	0.076923076923…	0.000100111011000100111011…	1/16 + 1/128 + 1/256 . . .
1/14	0.0714285714285…	0.0001001001…	1/16 + 1/128 + 1/1024 . . .
1/15	0.0666…	0.00010001…	1/16 + 1/256 . . .
1/16	0.0625 or 0.0624999…	0.0001 or 0.0000111…	1/32 + 1/64 + 1/128 . . .

Binary arithmetic[edit]

Arithmetic in binary is much like arithmetic in other numeral systems. Addition, subtraction, multiplication, and division can be performed on binary numerals.

Addition[edit]

The simplest arithmetic operation in binary is addition. Adding two single-digit binary numbers is relatively simple, using a form of carrying:

0 + 0 → 0

0 + 1 → 1

1 + 0 → 1

1 + 1 → 0, carry 1 (since 1 + 1 = 2 = 0 + (1 × 2¹) )

Adding two “1” digits produces a digit “0”, while 1 will have to be added to the next column. This is similar to what happens in decimal when certain single-digit numbers are added together; if the result equals or exceeds the value of the radix (10), the digit to the left is incremented:

5 + 5 → 0, carry 1 (since 5 + 5 = 10 = 0 + (1 × 10¹) )

7 + 9 → 6, carry 1 (since 7 + 9 = 16 = 6 + (1 × 10¹) )

This is known as carrying. When the result of an addition exceeds the value of a digit, the procedure is to “carry” the excess amount divided by the radix (that is, 10/10) to the left, adding it to the next positional value. This is correct since the next position has a weight that is higher by a factor equal to the radix. Carrying works the same way in binary:

  1 1 1 1 1    (carried digits)
    0 1 1 0 1
+   1 0 1 1 1
-------------
= 1 0 0 1 0 0 = 36

In this example, two numerals are being added together: 01101₂ (13₁₀) and 10111₂ (23₁₀). The top row shows the carry bits used. Starting in the rightmost column, 1 + 1 = 10₂. The 1 is carried to the left, and the 0 is written at the bottom of the rightmost column. The second column from the right is added: 1 + 0 + 1 = 10₂ again; the 1 is carried, and 0 is written at the bottom. The third column: 1 + 1 + 1 = 11₂. This time, a 1 is carried, and a 1 is written in the bottom row. Proceeding like this gives the final answer 100100₂ (36₁₀).

When computers must add two numbers, the rule that:
x xor y = (x + y) mod 2
for any two bits x and y allows for very fast calculation, as well.

Long carry method[edit]

A simplification for many binary addition problems is the “long carry method” or “Brookhouse Method of Binary Addition”. This method is particularly when one of the numbers contains a long stretch of ones. It is based on the simple premise that under the binary system, when given a stretch of digits composed entirely of n ones (where n is any integer length), adding 1 will result in the number 1 followed by a string of n zeros. That concept follows, logically, just as in the decimal system, where adding 1 to a string of n 9s will result in the number 1 followed by a string of n 0s:

     Binary                        Decimal
    1 1 1 1 1     likewise        9 9 9 9 9
 +          1                  +          1
  ———————————                   ———————————
  1 0 0 0 0 0                   1 0 0 0 0 0

Such long strings are quite common in the binary system. From that one finds that large binary numbers can be added using two simple steps, without excessive carry operations. In the following example, two numerals are being added together: 1 1 1 0 1 1 1 1 1 0₂ (958₁₀) and 1 0 1 0 1 1 0 0 1 1₂ (691₁₀), using the traditional carry method on the left, and the long carry method on the right:

Traditional Carry Method                       Long Carry Method
                                vs.
  1 1 1   1 1 1 1 1      (carried digits)   1 ←     1 ←            carry the 1 until it is one digit past the "string" below
    1 1 1 0 1 1 1 1 1 0                       1 1 1 0 1 1 1 1 1 0  cross out the "string",
+   1 0 1 0 1 1 0 0 1 1                   +   1 0 1 0 1 1 0 0 1 1  and cross out the digit that was added to it
———————————————————————                    ——————————————————————
= 1 1 0 0 1 1 1 0 0 0 1                     1 1 0 0 1 1 1 0 0 0 1

The top row shows the carry bits used. Instead of the standard carry from one column to the next, the lowest-ordered “1” with a “1” in the corresponding place value beneath it may be added and a “1” may be carried to one digit past the end of the series. The “used” numbers must be crossed off, since they are already added. Other long strings may likewise be cancelled using the same technique. Then, simply add together any remaining digits normally. Proceeding in this manner gives the final answer of 1 1 0 0 1 1 1 0 0 0 1₂ (1649₁₀). In our simple example using small numbers, the traditional carry method required eight carry operations, yet the long carry method required only two, representing a substantial reduction of effort.

Addition table[edit]

	0	1
0	0	1
1	1	10

The binary addition table is similar, but not the same, as the truth table of the logical disjunction operation . The difference is that , while .

Subtraction[edit]

Subtraction works in much the same way:

0 − 0 → 0

0 − 1 → 1, borrow 1

1 − 0 → 1

1 − 1 → 0

Subtracting a “1” digit from a “0” digit produces the digit “1”, while 1 will have to be subtracted from the next column. This is known as borrowing. The principle is the same as for carrying. When the result of a subtraction is less than 0, the least possible value of a digit, the procedure is to “borrow” the deficit divided by the radix (that is, 10/10) from the left, subtracting it from the next positional value.

    *   * * *   (starred columns are borrowed from)
  1 1 0 1 1 1 0
−     1 0 1 1 1
----------------
= 1 0 1 0 1 1 1

  *             (starred columns are borrowed from)
  1 0 1 1 1 1 1
-   1 0 1 0 1 1
----------------
= 0 1 1 0 1 0 0

Subtracting a positive number is equivalent to adding a negative number of equal absolute value. Computers use signed number representations to handle negative numbers—most commonly the two’s complement notation. Such representations eliminate the need for a separate “subtract” operation. Using two’s complement notation subtraction can be summarized by the following formula:

A − B = A + not B + 1

Multiplication[edit]

Multiplication in binary is similar to its decimal counterpart. Two numbers A and B can be multiplied by partial products: for each digit in B, the product of that digit in A is calculated and written on a new line, shifted leftward so that its rightmost digit lines up with the digit in B that was used. The sum of all these partial products gives the final result.

Since there are only two digits in binary, there are only two possible outcomes of each partial multiplication:

• If the digit in B is 0, the partial product is also 0
• If the digit in B is 1, the partial product is equal to A

For example, the binary numbers 1011 and 1010 are multiplied as follows:

           1 0 1 1   (A)
         × 1 0 1 0   (B)
         ---------
           0 0 0 0   ← Corresponds to the rightmost 'zero' in B
   +     1 0 1 1     ← Corresponds to the next 'one' in B
   +   0 0 0 0
   + 1 0 1 1
   ---------------
   = 1 1 0 1 1 1 0

Binary numbers can also be multiplied with bits after a binary point:

               1 0 1 . 1 0 1     A (5.625 in decimal)
             × 1 1 0 . 0 1       B (6.25 in decimal)
             -------------------
                   1 . 0 1 1 0 1   ← Corresponds to a 'one' in B
     +           0 0 . 0 0 0 0     ← Corresponds to a 'zero' in B
     +         0 0 0 . 0 0 0
     +       1 0 1 1 . 0 1
     +     1 0 1 1 0 . 1
     ---------------------------
     =   1 0 0 0 1 1 . 0 0 1 0 1 (35.15625 in decimal)

See also Booth’s multiplication algorithm.

Multiplication table[edit]

	0	1
0	0	0
1	0	1

The binary multiplication table is the same as the truth table of the logical conjunction operation .

Division[edit]

Long division in binary is again similar to its decimal counterpart.

In the example below, the divisor is 101₂, or 5 in decimal, while the dividend is 11011₂, or 27 in decimal. The procedure is the same as that of decimal long division; here, the divisor 101₂ goes into the first three digits 110₂ of the dividend one time, so a “1” is written on the top line. This result is multiplied by the divisor, and subtracted from the first three digits of the dividend; the next digit (a “1”) is included to obtain a new three-digit sequence:

              1
        ___________
1 0 1   ) 1 1 0 1 1
        − 1 0 1
          -----
          0 0 1

The procedure is then repeated with the new sequence, continuing until the digits in the dividend have been exhausted:

             1 0 1
       ___________
1 0 1  ) 1 1 0 1 1
       − 1 0 1
         -----
             1 1 1
         −   1 0 1
             -----
             0 1 0

Thus, the quotient of 11011₂ divided by 101₂ is 101₂, as shown on the top line, while the remainder, shown on the bottom line, is 10₂. In decimal, this corresponds to the fact that 27 divided by 5 is 5, with a remainder of 2.

Aside from long division, one can also devise the procedure so as to allow for over-subtracting from the partial remainder at each iteration, thereby leading to alternative methods which are less systematic, but more flexible as a result.

Square root[edit]

The process of taking a binary square root digit by digit is the same as for a decimal square root and is explained here. An example is:

             1 0 0 1
            ---------
           √ 1010001
             1
            ---------
      101     01 
               0
             --------
      1001     100
                 0
             --------
      10001    10001
               10001
              -------
                   0

Bitwise operations[edit]

Though not directly related to the numerical interpretation of binary symbols, sequences of bits may be manipulated using Boolean logical operators. When a string of binary symbols is manipulated in this way, it is called a bitwise operation; the logical operators AND, OR, and XOR may be performed on corresponding bits in two binary numerals provided as input. The logical NOT operation may be performed on individual bits in a single binary numeral provided as input. Sometimes, such operations may be used as arithmetic short-cuts, and may have other computational benefits as well. For example, an arithmetic shift left of a binary number is the equivalent of multiplication by a (positive, integral) power of 2.

Conversion to and from other numeral systems[edit]

Decimal to Binary[edit]

To convert from a base-10 integer to its base-2 (binary) equivalent, the number is divided by two. The remainder is the least-significant bit. The quotient is again divided by two; its remainder becomes the next least significant bit. This process repeats until a quotient of one is reached. The sequence of remainders (including the final quotient of one) forms the binary value, as each remainder must be either zero or one when dividing by two. For example, (357)₁₀ is expressed as (101100101)_2.^[36]

Binary to Decimal[edit]

Conversion from base-2 to base-10 simply inverts the preceding algorithm. The bits of the binary number are used one by one, starting with the most significant (leftmost) bit. Beginning with the value 0, the prior value is doubled, and the next bit is then added to produce the next value. This can be organized in a multi-column table. For example, to convert 10010101101₂ to decimal:

Prior value	× 2 +	Next bit	= Next value
0	× 2 +	1	= 1
1	× 2 +	0	= 2
2	× 2 +	0	= 4
4	× 2 +	1	= 9
9	× 2 +	0	= 18
18	× 2 +	1	= 37
37	× 2 +	0	= 74
74	× 2 +	1	= 149
149	× 2 +	1	= 299
299	× 2 +	0	= 598
598	× 2 +	1	= 1197

The result is 1197₁₀. The first Prior Value of 0 is simply an initial decimal value. This method is an application of the Horner scheme.

Binary	1	0	0	1	0	1	0	1	1	0	1
Decimal	1×210 +	0×29 +	0×28 +	1×27 +	0×26 +	1×25 +	0×24 +	1×23 +	1×22 +	0×21 +	1×20 =	1197

The fractional parts of a number are converted with similar methods. They are again based on the equivalence of shifting with doubling or halving.

In a fractional binary number such as 0.11010110101₂, the first digit is , the second , etc. So if there is a 1 in the first place after the decimal, then the number is at least , and vice versa. Double that number is at least 1. This suggests the algorithm: Repeatedly double the number to be converted, record if the result is at least 1, and then throw away the integer part.

For example, , in binary, is:

Converting	Result
	0.
	0.0
	0.01
	0.010
	0.0101

Thus the repeating decimal fraction 0.3… is equivalent to the repeating binary fraction 0.01… .

Or for example, 0.1₁₀, in binary, is:

Converting	Result
0.1	0.
0.1 × 2 = 0.2 < 1	0.0
0.2 × 2 = 0.4 < 1	0.00
0.4 × 2 = 0.8 < 1	0.000
0.8 × 2 = 1.6 ≥ 1	0.0001
0.6 × 2 = 1.2 ≥ 1	0.00011
0.2 × 2 = 0.4 < 1	0.000110
0.4 × 2 = 0.8 < 1	0.0001100
0.8 × 2 = 1.6 ≥ 1	0.00011001
0.6 × 2 = 1.2 ≥ 1	0.000110011
0.2 × 2 = 0.4 < 1	0.0001100110

This is also a repeating binary fraction 0.00011… . It may come as a surprise that terminating decimal fractions can have repeating expansions in binary. It is for this reason that many are surprised to discover that 0.1 + … + 0.1, (10 additions) differs from 1 in floating point arithmetic. In fact, the only binary fractions with terminating expansions are of the form of an integer divided by a power of 2, which 1/10 is not.

The final conversion is from binary to decimal fractions. The only difficulty arises with repeating fractions, but otherwise the method is to shift the fraction to an integer, convert it as above, and then divide by the appropriate power of two in the decimal base. For example:

Another way of converting from binary to decimal, often quicker for a person familiar with hexadecimal, is to do so indirectly—first converting ( in binary) into ( in hexadecimal) and then converting ( in hexadecimal) into ( in decimal).

For very large numbers, these simple methods are inefficient because they perform a large number of multiplications or divisions where one operand is very large. A simple divide-and-conquer algorithm is more effective asymptotically: given a binary number, it is divided by 10^k, where k is chosen so that the quotient roughly equals the remainder; then each of these pieces is converted to decimal and the two are concatenated. Given a decimal number, it can be split into two pieces of about the same size, each of which is converted to binary, whereupon the first converted piece is multiplied by 10^k and added to the second converted piece, where k is the number of decimal digits in the second, least-significant piece before conversion.

Hexadecimal[edit]

0hex	=	0dec	=	0oct		0	0	0	0
1hex	=	1dec	=	1oct	0	0	0	1
2hex	=	2dec	=	2oct	0	0	1	0
3hex	=	3dec	=	3oct	0	0	1	1
4hex	=	4dec	=	4oct	0	1	0	0
5hex	=	5dec	=	5oct	0	1	0	1
6hex	=	6dec	=	6oct	0	1	1	0
7hex	=	7dec	=	7oct	0	1	1	1
8hex	=	8dec	=	10oct	1	0	0	0
9hex	=	9dec	=	11oct	1	0	0	1
Ahex	=	10dec	=	12oct	1	0	1	0
Bhex	=	11dec	=	13oct	1	0	1	1
Chex	=	12dec	=	14oct	1	1	0	0
Dhex	=	13dec	=	15oct	1	1	0	1
Ehex	=	14dec	=	16oct	1	1	1	0
Fhex	=	15dec	=	17oct	1	1	1	1

Binary may be converted to and from hexadecimal more easily. This is because the radix of the hexadecimal system (16) is a power of the radix of the binary system (2). More specifically, 16 = 2⁴, so it takes four digits of binary to represent one digit of hexadecimal, as shown in the adjacent table.

To convert a hexadecimal number into its binary equivalent, simply substitute the corresponding binary digits:

3A₁₆ = 0011 1010₂

E7₁₆ = 1110 0111₂

To convert a binary number into its hexadecimal equivalent, divide it into groups of four bits. If the number of bits isn’t a multiple of four, simply insert extra 0 bits at the left (called padding). For example:

1010010₂ = 0101 0010 grouped with padding = 52₁₆

11011101₂ = 1101 1101 grouped = DD₁₆

To convert a hexadecimal number into its decimal equivalent, multiply the decimal equivalent of each hexadecimal digit by the corresponding power of 16 and add the resulting values:

C0E7₁₆ = (12 × 16³) + (0 × 16²) + (14 × 16¹) + (7 × 16⁰) = (12 × 4096) + (0 × 256) + (14 × 16) + (7 × 1) = 49,383₁₀

Octal[edit]

Binary is also easily converted to the octal numeral system, since octal uses a radix of 8, which is a power of two (namely, 2³, so it takes exactly three binary digits to represent an octal digit). The correspondence between octal and binary numerals is the same as for the first eight digits of hexadecimal in the table above. Binary 000 is equivalent to the octal digit 0, binary 111 is equivalent to octal 7, and so forth.

Octal	Binary
0	000
1	001
2	010
3	011
4	100
5	101
6	110
7	111

Converting from octal to binary proceeds in the same fashion as it does for hexadecimal:

65₈ = 110 101₂

17₈ = 001 111₂

And from binary to octal:

101100₂ = 101 100₂ grouped = 54₈

10011₂ = 010 011₂ grouped with padding = 23₈

And from octal to decimal:

65₈ = (6 × 8¹) + (5 × 8⁰) = (6 × 8) + (5 × 1) = 53₁₀

127₈ = (1 × 8²) + (2 × 8¹) + (7 × 8⁰) = (1 × 64) + (2 × 8) + (7 × 1) = 87₁₀

Representing real numbers[edit]

Non-integers can be represented by using negative powers, which are set off from the other digits by means of a radix point (called a decimal point in the decimal system). For example, the binary number 11.01₂ means:

1 × 21	(1 × 2 = 2)	plus
1 × 20	(1 × 1 = 1)	plus
0 × 2−1	(0 × 1⁄2 = 0)	plus
1 × 2−2	(1 × 1⁄4 = 0.25)

For a total of 3.25 decimal.

All dyadic rational numbers have a terminating binary numeral—the binary representation has a finite number of terms after the radix point. Other rational numbers have binary representation, but instead of terminating, they recur, with a finite sequence of digits repeating indefinitely. For instance

The phenomenon that the binary representation of any rational is either terminating or recurring also occurs in other radix-based numeral systems. See, for instance, the explanation in decimal. Another similarity is the existence of alternative representations for any terminating representation, relying on the fact that 0.111111… is the sum of the geometric series 2⁻¹ + 2⁻² + 2⁻³ + … which is 1.

Binary numerals which neither terminate nor recur represent irrational numbers. For instance,

• 0.10100100010000100000100… does have a pattern, but it is not a fixed-length recurring pattern, so the number is irrational
• 1.0110101000001001111001100110011111110… is the binary representation of , the square root of 2, another irrational. It has no discernible pattern.

See also[edit]

• Balanced ternary
• Binary code
• Binary-coded decimal
• Finger binary
• Gray code
• IEEE 754
• Linear-feedback shift register
• Offset binary
• Quibinary
• Reduction of summands
• Redundant binary representation
• Repeating decimal
• Two’s complement

References[edit]

External links[edit]

• Binary System at cut-the-knot
• Conversion of Fractions at cut-the-knot
• Sir Francis Bacon’s BiLiteral Cypher system, predates binary number system.

Была ли эта статья полезной?