Если число имеет каноническое разложение $%n=p_1^{k_1}ldots p_r^{k_r}$%, то группа обратимых элементов кольца вычетов по модулю $%n$% изоморфна прямому произведению соответствующих групп для сомножителей: $$mathbb Z_n^{ast}congmathbb Z_{p_1^{k_1}}^{ast}timescdotstimesmathbb Z_{p_r^{k_r}}^{ast}.$$ Доказывается это при помощи китайской теоремы об остатках, и согласуется со свойством мультипликативности функции Эйлера: $%varphi(n)=varphi(p_1^{k_1})ldotsvarphi(p_r^{k_r})$%.
Применительно к данному случаю, $%|mathbb Z_{72}^{ast}|=varphi(2^3)varphi(3^2)=4cdot6=24$%, где $%|mathbb Z_8^{ast}|=4$% и $%|mathbb Z_9^{ast}|=6$%. Группа $%mathbb Z_8^{ast}={1,3,5,7}$% устроена совсем просто: каждый её элемент в квадрате равен единичному, так как $%k^2-1$% делится на $%8$% при любом нечётном $%k$%. Эта группа изоморфна произведению двух циклических групп второго порядка.
Группа $%mathbb Z_9^{ast}={1,2,4,5,7,8}$% является циклической. Чтобы не привлекать общий факт, верный для всех степеней нечётных простых чисел, просто укажем на один из образующих. Подходит число $%2$%, так как $%2^2=4ne1$% и $%2^3=8ne1$% по модулю $%9$%, то есть это элемент порядка $%6$%.
Ввиду того, что порядок элемента $%(a,b)$% прямого произведения равен НОК порядков $%a$% и $%b$%, мы заключаем, что $%g^6=1$% для всех $%ginmathbb Z_{72}$%, и максимальный порядок элемента равен $%6$%. В качестве примера подходит число, дающее при делении на $%9$% остаток $%2$%, а при делении на $%8$% — нечётный остаток. Достаточно взять элемент $%g=11$%. Вообще, элементов с таким свойством в группе всего восемь, и их нетрудно выписать в явном виде.
3.1.5 Конечные кольца и поля
Определение 3.18 Множество  с двумя алгебраическими операциями
с двумя алгебраическими операциями  ,
,  называется ассоциативным кольцом, если в нём выполняются свойства:
называется ассоциативным кольцом, если в нём выполняются свойства:
 является коммутативной группой по сложению с нейтральным элементом
является коммутативной группой по сложению с нейтральным элементом  (эта группа называется аддитивной).
(эта группа называется аддитивной).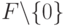 является полугруппой (обозначается
является полугруппой (обозначается 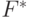 ).
).- Дистрибутивность:
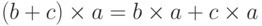 и
и 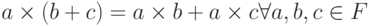 .
.
Определение 3.19 Кольца  и
и  называются изоморфными, если существует отображение
называются изоморфными, если существует отображение  , являющееся изоморфизмом аддитивных и мультипликативных групп этих колец.
, являющееся изоморфизмом аддитивных и мультипликативных групп этих колец.
Определение 3.20 Полем называется кольцо  , в котором
, в котором 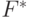 является коммутативной группой.
является коммутативной группой.
Определение 3.21 Характеристикой поля называется наименьшее такое натуральное число  , что
, что 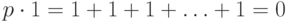 , или 0, если такого
, или 0, если такого  не существует. Характеристика поля может быть только простым числом или нулем.
не существует. Характеристика поля может быть только простым числом или нулем.
Определение 3.22 Левым (правым) идеалом кольца называется любое его подкольцо, выдерживающее умножение слева (соответственно, справа) на любой элемент кольца. Подкольцо, являющееся левым и правым идеалом, называется двусторонним идеалом, или просто идеалом.
Подкольцо  разбивает кольцо
разбивает кольцо  на классы эквивалентности:
на классы эквивалентности: 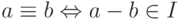 . Класс, содержащий элемент
. Класс, содержащий элемент  , можно записать в виде:
, можно записать в виде:
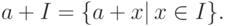
Если подкольцо является идеалом, то на множестве таких классов можно ввести операции сложения и умножения, относительно которых множество классов образует кольцо, называемое фактор-кольцом:
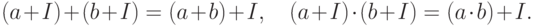
Из определения идеала следует, что результат операций не зависит от выбора представителей  ,
,  , то есть операции заданы корректно.
, то есть операции заданы корректно.
Наиболее важными для нас будут следующие кольца и поля:
- Кольцо целых чисел
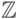 относительно обыкновенных операций сложения и умножения.
относительно обыкновенных операций сложения и умножения. - Поле рациональных чисел
 относительно операций сложения и умножения.
относительно операций сложения и умножения. - Фактор-кольцо
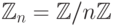 кольца целых чисел по идеалу всех чисел, кратных
кольца целых чисел по идеалу всех чисел, кратных  . Также это кольцо можно себе представлять, как кольцо целых неотрицательных чисел, меньших
. Также это кольцо можно себе представлять, как кольцо целых неотрицательных чисел, меньших  , с операцией сложения и умножения по модулю
, с операцией сложения и умножения по модулю  . Такое кольцо является полем тогда и только тогда, когда
. Такое кольцо является полем тогда и только тогда, когда  – простое число.
– простое число. - Кольцо
![F[{x_1,{dots}, x_n}]](https://intuit.ru/sites/default/files/tex_cache/5830bd1f7c4224bdde9427103672e170.png) многочленов от переменных
многочленов от переменных 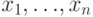 над произвольным полем
над произвольным полем  .
. - Фактор-кольцо
![F[{x}] / f(x) F[x]](https://intuit.ru/sites/default/files/tex_cache/00d09f4ebf7f7e40fc59b3267bf73e48.png) кольца многочленов над полем
кольца многочленов над полем  по идеалу, порожденному одним многочленом
по идеалу, порожденному одним многочленом 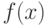 степени
степени  , то есть состоящему из всех многочленов, кратных
, то есть состоящему из всех многочленов, кратных  . Это кольцо можно также рассматривать, как кольцо многочленов степени меньше
. Это кольцо можно также рассматривать, как кольцо многочленов степени меньше  с операцией сложения и умножения по модулю
с операцией сложения и умножения по модулю  . Такое кольцо является полем тогда и только тогда, когда многочлен
. Такое кольцо является полем тогда и только тогда, когда многочлен  неприводим над
неприводим над  .
.
В криптографии нас будут интересовать больше всего конечные поля, то есть поля с конечным множеством  . Перечислим наиболее важные для нас свойства:
. Перечислим наиболее важные для нас свойства:
- Каждое конечное поле имеет простую характеристику
 .
. - Поле простого порядка не имеет подполей, и называется простым.
- Конечное поле характеристики
 содержит подполе порядка
содержит подполе порядка  .
. - Конечное поле является линейным пространством над своим простым подполем, поэтому имеет порядок
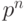 для некоторого натурального числа
для некоторого натурального числа  .
. - Мультипликативная группа конечного поля циклическая. Если поле имеет простой порядок
 , то порождающий его мультипликативную группу элемент называется примитивным корнем по модулю
, то порождающий его мультипликативную группу элемент называется примитивным корнем по модулю  .
. - Конечные поля одного порядка изоморфны.
Рассмотрим несколько связанных с кольцами вычетов задач, часто возникающих в криптографии.
Пример 3.5 Найти мультипликативный порядок элемента 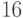 по модулю
по модулю 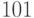 , то есть порядок элемента
, то есть порядок элемента 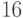 мультипликативной группы
мультипликативной группы  .
.
Решение. Поскольку число 101 простое, порядок мультипликативной группы поля  равен 100. По следствию из теоремы Лагранжа, мультипликативный порядок любого числа по модулю 101 является делителем 100, то есть одним из чисел: 1, 2, 4, 5, 10, 20, 25, 50, 100. Проверим каждое из чисел:
равен 100. По следствию из теоремы Лагранжа, мультипликативный порядок любого числа по модулю 101 является делителем 100, то есть одним из чисел: 1, 2, 4, 5, 10, 20, 25, 50, 100. Проверим каждое из чисел:
 |
1 | 2 | 4 | 5 | 10 | 20 | 25 | 50 | 100 |
|---|---|---|---|---|---|---|---|---|---|
 |
16 | 54 | 88 | 95 | 36 | 84 | 1 | – | – |
После того, как обнаружили, что 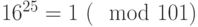 , возводить в
, возводить в 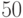 -ю и
-ю и  -ю степень излишне – видно, что наименьшая степень, в которой 16 даст единицу по модулю 101, это 25.
-ю степень излишне – видно, что наименьшая степень, в которой 16 даст единицу по модулю 101, это 25.
Пример 3.6 Найти случайный примитивный корень по модулю  .
.
Решение. Порядок мультипликативной группы поля вычетов по модулю 883 равен 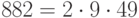 . Будем выбирать случайное число
. Будем выбирать случайное число  и возводить его в степени
и возводить его в степени  ,
,  ,
,  . Если в какой-то степени
. Если в какой-то степени  даст единицу, то его порядок меньше 882, и, следовательно, он не является примитивным корнем по модулю 883. Наоборот, порядок порождающего элемента является делителем числа 882, и если он не является делителем ни одного из чисел
даст единицу, то его порядок меньше 882, и, следовательно, он не является примитивным корнем по модулю 883. Наоборот, порядок порождающего элемента является делителем числа 882, и если он не является делителем ни одного из чисел  ,
,  ,
,  , то равен 882. В первой колонке таблицы приводятся случайно выбранные элементы
, то равен 882. В первой колонке таблицы приводятся случайно выбранные элементы  , а в следующих колонках – результаты возведения в степень.
, а в следующих колонках – результаты возведения в степень.
Итак, 326 является примитивным корнем по модулю 883.
В
теории помехоустойчивого кодирования
широко используются теория множеств,
высшая алгебра, векторные пространства
и алгебра логики. Одно из важнейших
достижений алгебры – это создание
алгебраических
систем,
использование которых позволяет
осуществить практическую реализацию
кодов. Алгебраические системы состоят
из множеств и операций над элементами
этих множеств. В теории кодирования из
алгебраических систем, в основном,
используются группы
и поля.
Группой

называется
множество элементов с определенной для
каждой пары элементов операцией
(обозначим эту операцию *), обладающее
следующими четырьмя свойствами:
1)
Замкнутость:

2)
Ассоциативность:

3)
Существование единицы:
существует
такой единичный
(нейтральный)
элемент

,
что

,
для любого
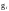
-того
элемента группы
;
4)
Существование обратного элемента:

Если
группа
содержит
конечное число элементов
,
то она называется конечной
группой, а число элементов в ней
называется
порядком
группы.
Если
конечная группа обладает свойством
коммутативности

,
то это коммутативная
(или абелева)
группа.
Если
для группы используется операция
сложения, то группа называется аддитивной,
а единичный элемент – нулем,
то есть

,
обратный элемент

,
а

.
Если
для группы используется операция
умножения, то группа называется
мультипликативной,
а единичный элемент – единицей,
т.е.

;

–
обратный элемент, а

В
группе может быть только один единичный
элемент.
Минимальная
аддитивная группа, имеет порядок 2 {0,
1}, а минимальная мультипликативная
группа – порядок 1 {1}.
Порядком
элемента аддитивной группы
называется число

,
для которого справедливо равенство

,
где

– это элемент группы. Причем всегда
.
Если

,
то
порядок элемента совпадает с порядком
группы. Элемент
в
этом случае называется примитивным
элементом.
Примитивный элемент группы позволяет
найти все элементы группы.
Порядком
элемента мультипликативной группы
называется наименьшее
удовлетворяющее условию:

,
то
– это порядок элемента
мультипликативной группы. Порядок
единичного элемента всегда равен
единице: 11=1.
Например,
имеется мультипликативная группа
относительно операции умножения по

:

Тогда:
11=11
=1
(порядок элемента 1 равен
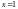
),
единичный элемент; 2222=24
=1
(порядок элемента 2 равен x=4,
а

по
),
т.е. 2 примитивный элемент; 3333=34
=1
(порядок элемента 3 равен
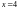
,
а

),
т.е. 3 примитивный элемент; 44=42=1
(порядок элемента 4 равен

),
т.е. 4 – это непримитивный элемент.
Подгруппа
– это подмножество

множества
(
),
такое, что
замкнуто
относительно операции множества
.
Например.
Аддитивная
группа

.
Аддитивные подгруппы:
=0
– для любой аддитивной группы;

={0,
2, 4}.
Мультипликативная
группа
Мультипликативные подгруппы:
={1}
;
={1,
4}.
Циклическая
подгруппа
(группа) состоит из степеней одного
элемента
,
если
– это порядок подгруппы. Циклическими
группами являются все мультипликативные
и аддитивные группы относительно
умножения или сложениия по модулю
простого числа(
…и
т.д.).
Полем
называется множество

,
которое является аддитивной абелевой
группой, ненулевые элементы
образуют мультипликативную группу, для
всех элементов множества выполняется
закон дистрибутивности. Характеристикой
поля
является примитивный элемент аддитивной
группы, образующей поле; примитивные
элементы мультипликативной группы
являются примитивными
элементами поля.
В
теории помехоустойчивого кодирования
используются поля с конечным числом
элементов
–
поля Галуа

.
Обозначение:
=
,
где
–
характеристика поля (должно быть простым
числом),
–
порядок расширения поля (целое число).
При этом
–простое
поле Галуа;
–
расширение поля Галуа порядка
,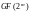
–
расширение двоичного поля Галуа порядка
.
Простое двоичное поле Галуа имеет два
элемента{0, 1}, расширение поля
имеет
элементов.
В поле
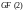
и
его расширениях сложение и умножение
выполняются по

;
если
элемент поля, то

(обратным элементом является сам
элемент).
Линейным
векторным пространством
над полем
называется
множество объектов (векторов), для
которых определены две операции:
векторное умножение и умножения вектора
на элемент поля.
Например,
если
-элемент
поля
и

–
вектор
над полем
,
тогда
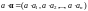
является вектором этого же пространства.
Множество
векторов

являются
линейно
независимыми и
называются базисом
векторного пространства, если

,
только когда все
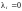
,
где

некоторые
скаляры. Векторное пространство,
содержащее нулевой вектор является
линейно зависимым.
Базис
векторного пространства порождает
–
мерное векторное пространство, объекты
которого могут быть получены линейной
комбинацией базисных векторов в виде

.
Причём в
–
мерном пространстве любое множество,
содержащее более
векторов,
является линейно зависимым. Подпространство
линейного векторного пространства
имеет размерность меньше
и должно быть замкнуто относительно
операции сложения.
Умножение
вектора на матрицу

,
где

––
вектор над полем, а матрица


Если
имеет
один столбец, то произведение скалярно.
Произведение
векторов

и
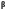
равно

,
где

– транспонированный вектор. Для
ортогональных векторов

.
Если
вектор

– элемент линейного векторного
пространства (элемент поля), то его можно
записать в виде полинома
(многочлена)

.
Если
имеется
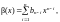
то определена операция сложения
полиномов

.
Умножение
полиномов
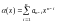
и

производится по правилам умножения в
двоичном поле

(7.12)
где

,
т.е.
-й
скаляр полинома
является, по сути, сверткой скаляров
полиномов-сомножителей.
Умножение
по модулю полинома p(x):

, (7.13)
где
–
остаток от деления произведения

на

.
Если
нельзя
представить в виде сомножителей, то
называется неприводимым
(примитивным)
полиномом.
Неприводимый полином
в
дальнейшем будем обозначать
.
Деление
полиномов по модулю полинома
:

,
(7.14)
где
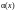
–
остаток от деления
на
полином
.
Множество
полиномов

,
где
и

,
образует поле
над
;
– производящий полином.
Пусть
производящий полином поля
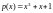
.
Тогда порядок расширения поля
определяется степенью производящего
полинома и, следовательно,

.
Количество элементов поля
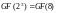
с
нулем равно 8 (аддитивная группа), без
нуля

(мультипликативная
группа).
Обозначим
примитивный элемент поля

,
который также является корнем производящего
полинома. Примитивный элемент (множество
его степеней) порождает все элементы
поля и является
первообразным корнем из единицы, т.к.

(таблица
7.3).
Т
а б л и ц а 7.3 – Элементы
поля Галуа

|
Степени |
Значения |
Полином |
Двоичная |
|
[
|
, |
|
001 010 100 011 110 111 101 001 |
Запись
элементов поля в виде полиномов удобно
использовать для сложения элементов
поля, а в виде степеней
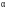
– при умножении элементов поля. Например,
сложение элементов поля:

или 011+110 = 101 =

;
умножение
элементов поля:
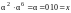
.
Заметим
также, если

–
это корень неприводимого полинома
,
то

–
также являются корнями
.
Таким образом, зная один корень, можно
определить все корни. Поэтому неприводимые
полиномы называют еще минимальными
функциями

над
полем
.
Можно
показать, что все элементы поля
и
только они являются корнями полинома
для

.
Если
–
элемент поля

,
то, подставляя этот элемент поля в
,
получаем

,
так как примитивный элемент поля в
степени

всегда равен 1. Следовательно, если корни
минимальных функций являются корнями
,
то

Это свойство широко используется при
формировании производящих полиномов
циклических кодов.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
|
0 / 0 / 0 Регистрация: 09.01.2014 Сообщений: 48 |
|
|
1 |
|
Найдите порядок элемента мультипликативной группы09.03.2014, 12:48. Показов 8608. Ответов 9
2. Найдите порядок элемента z=-0.5-sqrt(3)*i/2 мультипликативной группы С* комплексных невырожденных матриц второго порядка Заранее премного благодарен.
0 |
|
3968 / 2948 / 893 Регистрация: 19.11.2012 Сообщений: 6,061 |
|
|
09.03.2014, 17:08 |
2 |
|
РешениеПоэтому период этого элемента мультипликативной группы комплексных ЧИСЕЛ (не матриц) равен 3.
1 |
|
2662 / 1726 / 175 Регистрация: 05.06.2011 Сообщений: 4,957 |
|
|
09.03.2014, 17:37 |
3 |
|
Хм. Что, интересно, делает число в группе невырожденных матриц? И кто, кстати, сказал, что у элемента бесконечной группы непременно должен быть порядок?
0 |
|
3968 / 2948 / 893 Регистрация: 19.11.2012 Сообщений: 6,061 |
|
|
09.03.2014, 19:27 |
4 |
|
iifat, порядок (период) есть у любого элемента любой группы. Однако, элементы могут быть конечного или бесконечного порядка.
1 |
|
0 / 0 / 0 Регистрация: 09.01.2014 Сообщений: 48 |
|
|
09.03.2014, 21:09 [ТС] |
5 |
|
Поэтому период этого элемента мультипликативной группы комплексных ЧИСЕЛ (не матриц) равен 3. Можно небольшое решение, как ты пришёл к 3 степени?
0 |
|
3968 / 2948 / 893 Регистрация: 19.11.2012 Сообщений: 6,061 |
|
|
10.03.2014, 07:35 |
6 |
|
как ты пришёл к 3 степени? Лучше расскажу как можно догадаться до этого, не слишком много вычисляя.
1 |
|
0 / 0 / 0 Регистрация: 09.01.2014 Сообщений: 48 |
|
|
11.03.2014, 17:45 [ТС] |
7 |
|
Лучше расскажу как можно догадаться до этого, не слишком много вычисляя. А можно всё-таки решение? Мне просто эту работу сдавать надо, а я ещё в ней плаваю и мне нужно пошаговое решение, чтобы разобраться, но всеравно спасибо
0 |
|
3968 / 2948 / 893 Регистрация: 19.11.2012 Сообщений: 6,061 |
|
|
12.03.2014, 06:52 |
8 |
|
РешениеЧтобы вычислить период элемента x группы G, необходимо найти такое минимальное положительное целое число n, что x^n=1. В нашем случае прямые вычисления показывают, что PS Термин период элемента равносилен термину порядок элемента. Поскольку последний сильно перегружен в математике, я вслед за многими другими использую термин период. Вы используйте тот, которым пользуется ваш преподаватель. Удачи.
1 |
|
4216 / 3411 / 396 Регистрация: 15.06.2009 Сообщений: 5,818 |
|
|
12.03.2014, 14:14 |
9 |
|
Представить число в тригонометрическом виде (школьных знаний достаточно), знаки – по тригонометрическому кругу:
1 |
|
0 / 0 / 0 Регистрация: 09.01.2014 Сообщений: 48 |
|
|
12.03.2014, 15:57 [ТС] |
10 |
|
Всем огромное спасибо!
0 |
Сообщения без ответов | Активные темы
Найдите порядок элемента мультипликативной группы
Модераторы: Prokop, mad_math
| Автор | Сообщение | ||
|---|---|---|---|
|
JeRic |
Заголовок сообщения: Найдите порядок элемента мультипликативной группы
|
||
|
Найдите порядок элемента [math]z = -frac{ 1 }{ 2 }-frac{ sqrt{3}i }{ 2 }[/math] мультипликативной группы С* комплексных невырожденных матриц второго порядка Последний раз редактировалось JeRic 11 мар 2014, 16:44, всего редактировалось 2 раз(а). |
||
| Вернуться к началу |
|
||
|
JeRic |
Заголовок сообщения: Re: Найдите порядок элемента мультипликативной группы
|
|
Sonic писал(а): Задача простая, правда, совершенно неясно, зачем здесь матрицы. [math]z = -frac{ 1 }{ 2 }-frac{ sqrt{3}i }{ 2 }[/math]^3=1 Поэтому период этого элемента мультипликативной группы комплексных ЧИСЕЛ (не матриц) равен 3. Как прийти к этому я не совсем понимаю
|
|
| Вернуться к началу |
|
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Порядок элемента группы
в форуме Дискретная математика, Теория множеств и Логика |
crazymadman18 |
4 |
294 |
22 окт 2017, 21:13 |
|
Порядок элемента группы
в форуме Линейная и Абстрактная алгебра |
Smilelan |
2 |
304 |
19 янв 2018, 12:31 |
|
Доказать порядок элемента группы
в форуме Линейная и Абстрактная алгебра |
Franky163 |
1 |
293 |
09 июн 2016, 16:25 |
|
Степени элемента группы
в форуме Линейная и Абстрактная алгебра |
Knyazhskiy |
2 |
270 |
03 авг 2016, 10:31 |
|
Порядок элемента в группе
в форуме Линейная и Абстрактная алгебра |
LeF |
10 |
398 |
26 сен 2021, 09:09 |
|
Порядок элемента в группе
в форуме Линейная и Абстрактная алгебра |
antonio332 |
4 |
960 |
23 авг 2013, 19:54 |
|
Порядок группы SU(N)
в форуме Функциональный анализ, Топология и Дифференциальная геометрия |
AnnaAfraim |
0 |
71 |
22 янв 2023, 22:21 |
|
Задача на порядок каждого элемента в группе
в форуме Линейная и Абстрактная алгебра |
Nice_KF |
1 |
173 |
27 мар 2019, 17:50 |
|
Порядок фактор-группы
в форуме Линейная и Абстрактная алгебра |
AlDieRo |
1 |
140 |
14 апр 2022, 21:56 |
|
Найти порядок наибольшей p-группы
в форуме Линейная и Абстрактная алгебра |
davletova_ag |
0 |
271 |
22 май 2015, 09:38 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 3 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Powered by phpBB © 2000, 2002, 2005, 2007 phpBB Group
Вы можете создать форум бесплатно PHPBB3 на Getbb.Ru, Также возможно сделать готовый форум PHPBB2 на Mybb2.ru
Русская поддержка phpBB















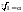





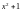

 Сообщение было отмечено JeRic как решение
Сообщение было отмечено JeRic как решение





