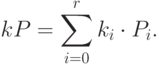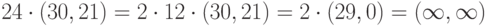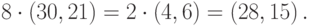Тем, кто знаком с криптографией с открытым ключом, наверно известны аббревиатуры ECC, ECDH и ECDSA. Первая — это сокращение от Elliptic Curve Cryptography (криптография на эллиптических кривых), остальные — это названия основанных на ней алгоритмов.
Сегодня криптосистемы на эллиптических кривых используются в TLS, PGP и SSH, важнейших технологиях, на которых базируются современный веб и мир ИТ. Я уже не говорю о Bitcoin и других криптовалютах.
До того, как ECC стала популярной, почти все алгоритмы с открытым ключом основывались на RSA, DSA и DH, альтернативных криптосистемах на основе модулярной арифметики. RSA и компания по-прежнему популярны, и часто используются вместе с ECC. Однако несмотря на то, что магия, лежащая в фундаменте RSA и подобных ей алгоритмов легко объяснима и понятна многим, а грубые реализации пишутся довольно просто, основы ECC всё ещё являются для большинства людей загадкой.
В этой серии статей я познакомлю вас с основами мира криптографии на эллиптических кривых. Моя цель — не создание полного и подробного руководства по ECC (в Интернете полно информации по этой теме), а простой обзор ECC и объяснение того, почему её считают безопасной. Я не буду тратить время на долгие математические доказательства или скучные подробности реализации. Также я представлю полезные примеры с визуальными интерактивными инструментами и скриптами.
В частности, я рассмотрю следующие темы:
- Эллиптические кривые над вещественными числами и групповой закон
- Эллиптические кривые над конечными полями и задача дискретного логарифмирования
- Генерирование пар ключей и два алгоритма ECC: ECDH и ECDSA
- Алгоритмы для взлома защиты ECC и сравнение с RSA
Для понимания статьи вам нужно знать основы теории множеств, геометрии и модулярной арифметики, понимать принципы симметричной и асимметричной криптографии. Наконец, вы должны чётко понимать, что такое «простая» и «сложная» задачи и их роли в криптографии.
Готовы? Приступим!
Часть 1: эллиптические кривые над вещественными числами и групповой закон
Эллиптические кривые
Во-первых: что такое эллиптическая кривая? В Wolfram MathWorld есть отличное и исчерпывающее определение. Но для нас достаточно того, что эллиптическая кривая — это просто множество точек, описываемое уравнением:
где
, (это необходимо, чтобы исключить особые кривые). Приведённое выше уравнение называется обычной формулировкой Вейерштрасса для эллиптических кривых.
Различные формы эллиптических кривых (,
изменяется от 2 до -3).
Виды особенностей: слева — кривая с точкой возврата (каспом) (). Справа — кривая с самопересечением (
). Оба этих примера не являются полноценными эллиптическими кривыми.
В зависимости от значений
и
эллиптические кривые могут принимать на плоскости разные формы. Как можно легко увидеть и проверить, эллиптические кривые симметричны относительно оси
.
Для наших целей нам также понадобится, чтобы частью кривой являлась бесконечно удалённая точка (также известная как идеальная точка). С этого момента мы будем обозначать бесконечно удалённую точку символом 0 (ноль).
Если нам требуется явным образом учитывать точку в бесконечности, то определение эллиптической кривой можно уточнить следующим образом:
Группы
В математике группа — это множество, для которого мы определили двоичную операцию, называемую «сложением» и обозначаемую символом +. Чтобы множество
было группой, сложение нужно определить таким образом, чтобы оно соответствовало четырём следующим свойствам:
- замыкание: если
и
входят в
, то
входит в
;
- ассоциативность:
;
- существует единичный элемент 0, такой, что
;
- у каждого элемента есть обратная величина, то есть: для каждого
существует такое
, что
.
Если мы добавим пятое требование:
- коммутативность:
,
то группа называется абелевой группой.
При обычной записи сложения множество целых чисел
является группой (более того, это абелева группа). Множество натуральных чисел
, однако, не является группой, потому что не удовлетворяет четвёртому свойству.
Группы удобны тем, что если мы докажем соблюдение всех четырёх свойств, то получим автоматически некоторые другие свойства «в нагрузку». Например: единичный элемент уникален; кроме того, обратные величины уникальны, то есть: для каждого
существует единственное
, такое, что
(и мы можем записать
как
). Непосредственно или косвенно эти и другие свойства групп очень пригодятся нам в будущем.
Групповой закон для эллиптических кривых
Мы можем определить группу для эллиптических кривых. А именно:
Сумма трёх точек, находящихся на одной прямой, равна 0.
Стоит учесть, что в последнем правиле нам требуются только три точки на одной прямой, и порядок расположения этих трёх точек не важен. Это значит, что если три точки
,
и
лежат на одной прямой, то
. Таким образом мы интуитивно доказали, что наш оператор + обладает свойствами ассоциативности и коммутативности: мы находимся в абелевой группе.
Пока всё идёт отлично. Но как нам вычислить сумму двух произвольных точек?
Геометрическое сложение
Благодаря тому, что мы находимся в абелевой группе, то можем записать
как
. Это уравнение в такой форме позволяет нам вывести геометрический способ вычисления суммы двух точек
и
: если мы проведём линию, проходящую через
и
, эта прямая пересечёт третью точку кривой
(это подразумевается, потому что
,
и
находятся на одной прямой). Если мы возьмём обратную величину этой точки
, мы найдём сумму
.
Проводим прямую через и
. Прямая пересекает третью точку
. Симметричная ей точка
является результатом
.
Геометрический способ работает, но требует усовершенствования. В частности, нам нужно ответить на несколько вопросов:
- Что если
или
? Разумеется, мы не сможем провести прямую (0 не находится на плоскости
). Но поскольку мы определили 0 как единичный элемент,
и
для любой
и любой
.
- Что если
? В этом случае прямая, проходящая через две точки, вертикальна, и не пересекает третью точку. Но если
является обратной величиной
, то
из определения обратной величины.
- Что если
? В этом случае через точку проходит бесконечное количество прямых. Здесь всё становится немного сложнее. Но представим, что точка
. Что произойдёт, если мы заставим
стремиться к
, всё больше приближаясь к ней?
При сближении двух точек проходящая через них прямая становится касательной к кривой.
Поскольку
стремится к
, прямая, проходящая через
и
становится касательной к кривой. В свете этого мы можем сказать, что
, где
— это точка пересечения между кривой и касательной к кривой в точке
.
- Что если
, но третьей точки
нет? В этом случае ситуация похожа на предыдущую. На самом деле, в этой ситуации прямая, проходящая через
и
, является касательной к кривой.
Если наша прямая пересекает только две точки, то это значит, что она является касательной к кривой. Легко увидеть, как результат сложения становится симметричным одной из двух точек.
Предположим, что
является точкой касания. В предыдущем случае мы записали
. Это уравнение теперь превращается в
. С другой стороны, если бы точкой касания была
, то правильным было бы уравнение
.
Геометрический способ теперь полон и учитывает все случаи. С помощью карандаша и линейки мы можем выполнить сложение всех точек любой эллиптической кривой. Если хотите попробовать, взгляните на визуальный инструмент на HTML5/JavaScript, созданный мной для вычисления сумм эллиптических кривых.
Алгебраическое сложение
Если мы хотим, чтобы сложением точек занимался компьютер, нужно превратить геометрический способ в алгебраический. Преобразование вышеизложенных правил в набор уравнений может казаться простым, но на самом деле оно довольно утомительно, потому что требует решения кубических уравнений. Поэтому я изложу только результаты.
Для начала давайте избавимся от самых раздражающих тупиковых ситуаций. Мы уже знаем, что
, и знаем, что
. Поэтому в наших уравнениях мы будем избегать этих двух случаев и рассмотрим только две ненулевые несимметричные точки
и
.
Если и
не совпадают (
), то проходящая через них прямая имеет наклон:
Пересечение этой прямой с эллиптической кривой — это третья точка
:
или, аналогично:
Поэтому
(обратите внимание на знаки и помните, что
).
Если бы нам нужно было проверить правильность результата, то пришлось бы проверить, принадлежит ли
кривой и находятся ли
,
и
на одной прямой. Проверка нахождения на одной прямой тривиальна, а проверка принадлежности
кривой — нет, потому что нам придётся решать кубическое уравнение, что совсем невесело.
Вместо этого давайте поэкспериментируем с примером: согласно визуальному инструменту, при
и
, принадлежащих кривой
, их сумма равна
. Давайте проверим, соответствует ли это уравнениям:
Да, всё верно!
Заметьте, что эти уравнения работают даже в случае, когда точка или
является точкой касания. Давайте проверим на
и
.
Мы получили результат
, который совпадает с результатом, полученным в визуальном инструменте.
К случаю нужно относиться немного иначе: уравнения для
и
остаются теми же, но с учётом того, что
нам придётся использовать для наклона другое уравнение:
Заметьте, что, как можно ожидать, это выражение для
является первой производной:
Чтобы доказать правильность этого результата, достаточно убедиться, что
принадлежит к кривой и что прямая, проходящая через
и
, имеет только два пересечения с кривой. Но мы снова не будем доказывать это и вместо этого разберём пример:
.
Что даёт нам
. Верно!
Хотя процедура получения результатов очень утомительна, наши уравнения довольно кратки. Всё это благодаря обычной формулировке Вейерштрасса: без неё эти уравнения были бы очень длинными и сложными!
Скалярное умножение
Кроме сложения, мы можем определить и другую операцию: скалярное умножение, то есть:
где
— натуральное число. Я написал визуальный инструмент и для скалярного умножения, так что можете поэкспериментировать с ним.
При записи в такой форме очевидно, что вычисление
требует
сложений. Если
состоит из
десятичных разрядов, то алгоритм будет иметь сложность
, что не очень хорошо. Но существуют и более быстрые алгоритмы.
Один из них — алгоритм удвоения-сложения. Принцип его работы проще объяснить на примере. Возьмём
. В двоичном форме оно имеет вид
. Такую двоичную форму можно представить как сумму степеней двойки:
(Мы взяли каждый двоичный разряд
и умножили на степень двойки.)
С учётом этого можно записать:
Алгоритм удвоения-сложения задаёт следующий порядок действий:
В результате мы вычислим
, выполнив всего семь удвоений и четыре сложения.
Если вам это понятно не до конца, то вот скрипт на Python, реализующий этот алгоритм:
def bits(n):
"""
Генерирует двоичные разряды n, начиная
с наименее значимого бита.
bits(151) -> 1, 1, 1, 0, 1, 0, 0, 1
"""
while n:
yield n & 1
n >>= 1
def double_and_add(n, x):
"""
Возвращает результат n * x, вычисленный
алгоритмом удвоения-сложения.
"""
result = 0
addend = x
for bit in bits(n):
if bit == 1:
result += addend
addend *= 2
return resultЕсли удвоение и сложение являются операциями
, то этот алгоритм имеет сложность
(или
, если учитывать битовую длину), что довольно неплохо. И, конечно, намного лучше, чем изначальный алгоритм
!
Логарифм
Для заданных
и
у нас есть по крайней мере один полиномиальный алгоритм вычисления
. Но как насчёт обратной задачи? Что если мы знаем
и
, а нам нужно определить
? Эта задача известна как задача логарифмирования. Мы употребляем слово «логарифм» вместо термина «деление» для согласованности с другими криптосистемами (в которых вместо умножения используется возведение в степень).
Я не знаю ни одного «простого» алгоритма для решения задачи логарифмирования, однако экспериментируя с умножением, легко обнаружить некоторые закономерности. Например, возьмём кривую
и точку
. Мы можем сразу убедиться, что если
нечётное, то
находится на кривой в левой полуплоскости; если
чётное, то
— в правой полуплоскости. Если поэкспериментировать ещё, мы, возможно, найдём и другие закономерности, которые приведут нас к написанию алгоритма для эффективного вычисления логарифма этой кривой.
Но существует вариация задачи логарифмирования: задача дискретного логарифмирования. Как мы увидим в следующей части, если уменьшить область определения эллиптических кривых, скалярное умножение остаётся «простым», а дискретный логарифм становится «сложной» задачей. Такая двойственность является ключевой особенностью криптографии на эллиптических кривых.
В следующей части мы исследуем конечные поля и задачу дискретной логарифмизации, а также примеры и инструменты для экспериментов.
Часть 2: эллиптические кривые над конечными полями и задача дискретного логарифмирования
В предыдущей части мы обсудили, как эллиптические кривые над вещественными числами можно использовать для определения групп. А именно, мы определили правило сложения точек: сумма трёх точек, лежащих на одной прямой, равна нулю (
). Мы вывели геометрический и алгебраический способы вычисления сложения точек.
Затем мы ввели понятие скалярного умножения (
) и нашли «простой» алгоритм для вычисления скалярного умножения: удвоение-сложение.
Теперь мы ограничим эллиптические кривые конечными полями, а не вещественными числами, и посмотрим, что это изменит.
Поле целых чисел по модулю p
Конечное поле — это, в первую очередь, множество конечного числа элементов. Примером конечного поля является множество целых чисел по модулю
, где
— простое число. В общем виде это записывается как
,
или
. Мы будем использовать последнюю запись.
Для полей существует две двухместные операции: сложение (+) и умножение (·). Обе они замкнуты, ассоциативны и коммутативны. Для обеих операций существует уникальный единичный элемент и для каждого элемента есть уникальный элемент обратной величины. И, наконец, умножение дистрибутивно относительно сложения:
.
Множество целых чисел по модулю состоит из всех целых чисел от 0 до
. Сложение и умножение работают как в модулярной арифметике. Вот несколько примеров операций над
:
Если эти уравнения вам незнакомы и вы хотите изучить основы модулярной арифметики, пройдите курс в Академии Хана.
Как мы уже сказали целые числа по модулю
— это поле, поэтому все перечисленные выше свойства сохраняются. Учтите, что требование того, чтобы
было простым числом, очень важно! Множество целых чисел по модулю 4 не является полем: 2 не имеет мультипликативной инверсии (т.е. уравнение
не имеет решений).
Деление по модулю p
Скоро мы определим эллиптические кривые для
, но прежде нам нужно чётко понимать, что
означает над
. Попросту говоря:
, или, прямым текстом,
в числителе и
в знаменателе равно
раз обратная величина
. Это нас не удивляет, но даёт нам простой способ выполнения деления: найти обратную величину числа, а затем выполнить простое умножение.
Вычисление обратного числа можно «просто» выполнить с помощью расширенного алгоритма Евклида, который в худшем случае имеет сложность
(или
, если мы учитываем битовую длину).
Мы не будем вдаваться в подробности расширенного алгоритма Евклида, это не входит в рамки статьи, но я представлю работающую реализацию на Python:
def extended_euclidean_algorithm(a, b):
"""
Возвращает кортеж из трёх элементов (gcd, x, y), такой, что
a * x + b * y == gcd, где gcd - наибольший
общий делитель a и b.
В этой функции реализуется расширенный алгоритм
Евклида и в худшем случае она выполняется O(log b).
"""
s, old_s = 0, 1
t, old_t = 1, 0
r, old_r = b, a
while r != 0:
quotient = old_r // r
old_r, r = r, old_r - quotient * r
old_s, s = s, old_s - quotient * s
old_t, t = t, old_t - quotient * t
return old_r, old_s, old_t
def inverse_of(n, p):
"""
Возвращает обратную величину
n по модулю p.
Эта функция возвращает такое целое число m, при котором
(n * m) % p == 1.
"""
gcd, x, y = extended_euclidean_algorithm(n, p)
assert (n * x + p * y) % p == gcd
if gcd != 1:
# Или n равно 0, или p не является простым.
raise ValueError(
'{} has no multiplicative inverse '
'modulo {}'.format(n, p))
else:
return x % pЭллиптические кривые над 
Теперь у нас есть все необходимые элементы для ограничения эллиптических кривых полем
. Множество точек, которые в предыдущей части имели следующий вид:
теперь превращаются в:
где 0 — по-прежнему точка в бесконечности, а
и
— два целых числа в
.
Кривая с
. Заметьте, что для каждого
существует максимум две точки. Также заметьте симметрию относительно
.
Кривая — особая и имеет тройную точку в
. Она не является истинной эллиптической кривой.
То, что раньше было непрерывной кривой, теперь стало множеством отдельных точек на плоскости
. Но можно доказать, что несмотря на ограничение области определения, эллиптические кривые над
всё равно создают абелеву группу.
Сложение точек
Очевидно, что нам нужно немного изменить определение сложения, чтобы оно работало для
. Для вещественных чисел мы сказали, что сумма трёх точек на одной прямой равна нулю (
). Мы можем сохранить это определение, но что значит расположение трёх точек на одной прямой над
?
Можно сказать, что три точки находятся на одной прямой, если существует прямая, соединяющая их. Разумеется, прямые над
отличаются от прямых над
. Можно сказать, что прямая над
— это множество точек
, удовлетворяющих уравнению
(это стандартное уравнение прямой с добавленной частью “
“).
Сложение точек для кривой , при
и
. Заметьте, как соединяющая точки прямая
«повторяет» себя на плоскости.
Учитывая то, что мы по-прежнему находимся в группе, сложение точек сохраняет уже известные нам свойства:
Алгебраическая сумма
Уравнения для выполнения сложений точек в точности такие же, как в предыдущей части, за исключением того, что нам нужно добавлять в конце каждого выражения “
“. Поэтому, если
,
и
, то
можно вычислить следующим способом:
Если
, то наклон
принимает форму:
Иначе, если
, мы получаем:
Уравнения не изменились, и это не совпадение: на самом деле, эти уравнения работают над любым полем, и над конечным, и над бесконечным (за исключением
и
, которые являются особыми случаями). Я чувствую, что это нужно объяснить. Но есть проблема: для доказательств группового закона обычно требуются сложные математические понятия. Однако я нашёл доказательство Стефана Фридла в котором используются только простейшие концепции. Прочитайте его, если вам интересно, почему эти уравнения работают (почти) над любым полем.
Вернёмся к кривым — мы не будем определять геометрический способ: на самом деле, с ним возникнут проблемы. Например, в предыдущей части мы сказали, что для вычисления
нам придётся взять касательную к кривой в
. Но при отсутствии непрерывности слово «касательная» теряет всякий смысл. Мы можем найти способ обойти эту и другие проблемы, однако чисто геометрический способ будет слишком сложным и совершенно непрактичным.
Вместо этого можно поэкспериментировать с интерактивным инструментом, написанным мной для выполнения сложений точек.
Порядок группы эллиптической кривой
Мы сказали, что эллиптическая кривая, определённая над конечным полем, имеет конечное количество точек. Нам нужно ответить на важный вопрос: сколько же в ней точек?
Во-первых, давайте определим, что количество точек в группе называется порядком группы.
Проверка всех возможных значений для
в интервале от 0 до
будет невыполнимым способом подсчёта точек, потому что потребует
шагов, а эта задача «сложна», если
— большое простое число.
К счастью, для вычисления порядка существует более быстрый алгоритм: алгоритм Шуфа. Я не буду вдаваться в его подробности — главное, что он выполняется за полиномиальное время, а именно этого нам и нужно.
Скалярное умножение и циклические подгруппы
Для вещественных чисел умножение можно определить как:
И, повторюсь, мы можем использовать алгоритм удвоения-сложения для выполнения умножения за
, где
— это количество бит
). Я написал интерактивный инструмент для скалярного умножения.
Умножение точек для эллиптических кривых над
обладает интересным свойством. Возьмём кривую
и точку
. Теперь вычислим все величины, кратные
:
Все значения, кратные , представляют собой пять различных точек (
,
,
,
,
), которые циклически повторяются. Легко заметить сходство между скалярным умножением для эллиптических кривых и сложением в модулярной арифметике.
Можно сразу же заметить две особенности: во-первых, значений, кратных
, всего пять: другие точки эллиптической кривой никогда ими не становятся. Во-вторых, они повторяются циклически. Можно записать:
для любого целого
. Заметьте, что благодаря оператору деления с остатком эти пять уравнений можно «ужать» в одно:
.
Более того, мы можем сразу же показать, что эти пять точек замкнуты относительно операции сложения. Что это значит: как бы я ни суммировал
,
,
,
или
, результатом всегда будет одна из этих пяти точек. И снова все остальные точки эллиптической кривой никогда не становятся результатом.
То же относится и ко всем остальным точкам, не только к
. На самом деле, если мы возьмём
в общем виде:
Что означает: если мы складываем два значения, кратных , то получаем значение, кратное
(т.е. значения, кратные
, замкнуты относительно операции сложения). Этого достаточно для того, чтобы доказать, что множество кратных
значений — это циклическая подгруппа группы, образованной эллиптической кривой.
«Подгруппа» — это группа, являющаяся подмножеством другой группы. «Циклическая подгруппа» — это подгруппа, элементы которой циклически повторяются, как мы показали в предыдущем примере. Точка
называется генератором или базовой точкой циклической подгруппы.
Циклические подгруппы — фундамент для ECC и других криптосистем. Позже я объясню, почему это так.
Порядок подгруппы
Можно задаться вопросом, каков порядок подгруппы, порождённой точкой (или, иными словами, каков порядок
). Для ответа на этот вопрос мы не можем использовать алгоритм Шуфа, потому что этот алгоритм работает только для целых эллиптических кривых, но не для подгрупп. Прежде чем приступить к решению задачи, нам нужно ещё немного информации:
- Пока мы определяли порядок как количество точек группы. Это определение по-прежнему действительно, но в циклических подгруппах мы можем дать новое аналогичное определение: порядок
— это минимальное положительное целое
, такое, что
.
На самом деле, если посмотреть на предыдущий пример, то наша подгруппа состояла из пяти точек, и
.
- Порядок
связан с порядком эллиптической кривой теоремой Лагранжа, согласно которой порядок подгруппы — это делитель порядка исходной группы.
Иными словами, если эллиптическая кривая содержит
точек, а одна из подгрупп содержит
, то
является делителем
.
Два этих факта вместе дают нам возможность определить порядок подгруппы с базовой точкой
:
- Вычисляем порядок эллиптической кривой
с помощью алгоритма Шуфа.
- Находим все делители
.
- Для каждого делителя
порядка
вычисляем
.
- Наименьшее
, такое, что
, является порядком подгруппы.
Например, кривая
над полем
имеет порядок
. Её подгруппы могут иметь порядок
,
,
,
,
,
,
или
. Если
мы подставим
, то увидим, что
,
, …,
, то есть порядок
равен
.
Учтите, что важно брать наименьший, а не случайный делитель. Если мы будем выбирать случайно, то можем получить
, что не является порядком подгруппы, но является одним из кратных.
Ещё один пример: эллиптическая кривая, определяемая уравнением
над полем
, имеет порядок
, которое является простым числом. Её подгруппы могут иметь порядок только
или
. Как вы можете догадаться, когда
, подгруппа содержит только бесконечно удалённую точку; когда
, подгруппа содержит все точки эллиптической кривой.
Поиск базовой точки
Для алгоритмов ECC требуются подгруппы с высоким порядком. Поэтому обычно выбирается эллиптическая кривая, вычисляется её порядок (
), в качестве порядка группы (
) выбирается большой делитель, а потом находится подходящая базовая точка. То есть мы не выбираем базовую точку, после чего вычисляем её порядок, а производим обратную операцию: сначала выбираем достаточно хороший порядок, а потом ищем подходящую базовую точку. Как же это сделать?
Во-первых, нужно ввести ещё одно понятие. Теорема Лагранжа подразумевает, что число всегда целое (потому что
— делитель
). Число
имеет собственное название: это кофактор подгруппы.
Теперь рассмотрим, что для каждой точки эллиптической кривой есть
. Это справедливо, потому что
— это кратное любому возможному
. Исходя из определения кофактора, мы можем записать:
Теперь допустим, что
— простое число (мы предпочитаем простые порядки по причинам, изложенным в первой части статьи). Это уравнение, записанное в такой форме, говорит нам, что точка
создаёт подгруппу порядка
(за исключением случая
, в котором подгруппа имеет порядок 1).
В свете этого мы можем определить следующий алгоритм:
- Вычисляем порядок
эллиптической кривой.
- Выбираем порядок
подгруппы. Чтобы алгоритм сработал, число должно быть простым и быть делителем
.
- Вычисляем кофактор
.
- Выбираем на кривой случайную точку
.
- Вычисляем
.
- Если
равно 0, то возвращаемся к шагу 4. В противном случае мы нашли генератор подгруппы с порядком
и кофактором
.
Заметьте, что алгоритм работает только если
простое. Если бы
не было простым, то порядок
мог быть одним из делителей
.
Дискретный логарифм
Как и в случае с непрерывными эллиптическими кривыми, теперь мы должны обсудить следующий вопрос: если мы знаем и
, то каким будет
, такое, что
?
Эта задача, известная как задача дискретного логарифмирования для эллиптических кривых, считается «сложной», для которой не обнаружено алгоритма полиномиального времени, выполняемого на классическом компьютере. Однако у этой точки зрения нет математических доказательств.
Эта задача аналогична задаче дискретного логарифмирования, используемой в других криптосистемах, таких как Digital Signature Algorithm (DSA), протокол Диффи-Хеллмана (D-H) и схема Эль-Гамаля. Названия задач совпадают неслучайно. Их разница в том, что в этих алгоритмах используется не скалярное умножение, а возведение в степень по модулю. Их задачу дискретного логарифмирования можно сформулировать так: если известны
и
, то каким будет
, такое, что
?
Обе эти задачи «дискретны», потому что в них используются конечные множества (а конкретнее — циклические подгруппы). И они являются «логарифмами», потому что аналогичны обычным логарифмам.
ECC интересна тем, что на сегодняшний момент задача дискретного логарифмирования для эллиптических кривых кажется «сложнее» по сравнению с другими схожими задачами, используемыми в криптографии. Это подразумевает, что нам потребуется меньше бит для целого
, чтобы получить тот же уровень защиты, что и в других криптосистемах, и мы это подробно рассмотрим в четвёртой, последней, части статьи.
Часть 3: ECDH и ECDSA
Параметры области определения
Алгоритмы эллиптических кривых будут работать в циклической подгруппе эллиптической кривой над конечным полем. Поэтому алгоритмам потребуются следующие параметры:
В результате параметрами области определения для алгоритмов является шестёрка .
Случайные кривые
Когда я говорил, что задача дискретного логарифмирования «сложна», я был не совсем точен. Существуют определённые классы эллиптических кривых, которые довольно слабы и позволяют использовать специальные алгоритмы для эффективного решения задачи дискретного логарифмирования. Например, все кривые, для которых
(то есть порядок конечного поля равен порядку эллиптической кривой), уязвимы к атаке Смарта, которую можно использовать для решения дискретных логарифмов за полиномиальное время на классических компьютерах.
Предположим теперь, что я дал вам параметры области определения кривой. Существует вероятность, что я обнаружил неизвестный никому новый класс слабых кривых, и, возможно, я создал «быстрый» алгоритм вычисления дискретных логарифмов для своей кривой. Как я могу убедить вас в обратном, т.е. в том, что мне неизвестно об уязвимостях? Как я могу гарантировать, что кривая «защищена» (в том смысле, что я не смогу её использовать для собственных атак)?
Чтобы решить эту проблему, иногда приходится использовать дополнительный параметр области определения: порождающее значение (seed) . Это случайное число, используемое для генерирования коэффициентов
и
или базовой точки
, или того и другого. Эти параметры генерируются вычислением хеша
. Хеши, как мы знаем, «просто» вычислить, но «сложно» реверсировать.
Простая схема генерирования случайной кривой из порождающего значения: хеш случайного числа используется для вычисления различных параметров кривой.
Если бы мы хотели сжульничать и воссоздать хеш из параметров области определения, то нам пришлось бы решать «сложную» задачу: инверсирование хеша.
Сгенерированная с помощью порождающего значения кривая называется проверяемо случайной. Принцип использования хешей для генерирования параметров известен как “nothing up my sleeve” («в рукавах ничего нет»), и широко распространён в криптографии.
Эта хитрость даёт определённую гарантию, что кривая не была специально создана таким образом, чтобы иметь известные её автору уязвимости. На самом деле, если я даю вам кривую вместе с порождающим значением, то это значит, что я не мог произвольно выбирать параметры
и
, и можно быть относительно спокойным, что я не смогу использовать специальные атаки. Причина использования слова «относительно» будет объяснена в четвёртой части.
Стандартизированный алгоритм генерирования и проверки случайных кривых описан в ANSI X9.62 и основан на SHA-1. Если интересно, можете прочитать об алгоритмах генерирования проверяемо случайных кривых в спецификации SECG (см. «Verifiably Random Curves and Base Point Generators»).
Я написал небольшой скрипт на Python, проверяющий все случайные кривые, поставляемые сейчас с OpenSSL. Крайне рекомендую посмотреть его!
Криптография на эллиптических кривых
Мы потратили много времени, но наконец добрались! Всё просто:
- Закрытый ключ — это случайное целое
, выбранное из
(где
— порядок подгруппы).
- Открытый ключ — это точка
(где
— базовая точка подгруппы).
Видите? Если мы знаем
и
(вместе с другими параметрами области определения), то найти
«просто». Но если мы знаем
и
, то поиск закрытого ключа
является «сложной» задачей, потому что требует решения задачи дискретного логарифмирования.
Теперь мы опишем два основанных на этом принципе алгоритма с открытым ключом: ECDH (Elliptic curve Diffie-Hellman, протокол Диффи-Хеллмана на эллиптических кривых), используемый для шифрования, и ECDSA (Elliptic Curve Digital Signature Algorithm), используемый для цифровых подписей.
Шифрование с помощью ECDH
ECDH — это разновидность алгоритма Диффи-Хеллмана для эллиптических кривых. На самом деле это скорее протокол согласования ключей, а не алгоритм шифрования. В сущности, это означает, что ECDH задаёт (в определённой степени) порядок генерирования ключей и обмена ими. Способ шифрования данных с помощью таких ключей мы можем выбирать сами.
Он решает следующую проблему: две стороны (обычно Алиса и Боб) хотят безопасно обмениваться информацией, чтобы третья сторона (посредник, Man In the Middle) мог перехватывать её, но не мог расшифровать. Например, это один из принципов TLS.
Вот как это работает:
- Сначала Алиса и Боб генерируют собственные закрытые и открытые ключи. У Алисы есть закрытый ключ
и открытый ключ
, у Боба есть ключи
и
. Заметьте, что и Алиса, и Боб используют одинаковые параметры области определения: одну базовую точку
на одной эллиптической кривой в одинаковом конечном поле.
- Алиса и Боб обмениваются открытыми ключами
и
по незащищённому каналу. Посредник (Man In the Middle) перехватывает
и
, но не может определить ни
, ни
, не решив задачу дискретного логарифмирования.
- Алиса вычисляет
(с помощью собственного закрытого ключа и открытого ключа Боба), а Боб вычисляет
(с помощью собственного закрытого ключа и открытого ключа Алисы). Учтите, что
одинаков и для Алисы, и для Боба. На самом деле:
Однако посреднику известны только
и
(вместе с другими параметрами области определения) и он не сможет найти общий секретный ключ
. Это известно как задача Диффи-Хеллмана, которую можно сформулировать следующим образом:
Каким будет результат
для трёх точек
,
и
?
Или, аналогично:
Каким будет результат
для трёх целых
,
и
?
(Последняя формулировка используется в исходном алгоритме Диффи-Хеллмана, основанном на модулярной арифметике.)
Протокол Диффи-Хеллмана: Алиса и Боб могут «просто» вычислить общий секретный ключ, посреднику же придётся решать «сложную» задачу.
Принцип, лежащий в основе задачи Диффи-Хеллмана, также объяснён в отличном видео Академии Хана на YouTube, в котором чуть позже объясняется алгоритм Диффи-Хеллмана в приложении к модулярной арифметике (не к эллиптическим кривым).
Задача Диффи-Хеллмана для эллиптических кривых считается «сложной». Считается, что она так же «сложна», как задача дискретного логарифмирования, но математических доказательств этому нет. Мы можем только с уверенностью сказать, что она не может быть «сложнее», потому что решение задачи логарифмирования — это способ решения задачи Диффи-Хеллмана.
Получив общий секретный ключ, Алиса и Боб могут обмениваться данными с симметричным шифрованием.
Например, они могут использовать координату
ключа
как ключ для шифрования сообщений такими безопасными шифрами, как AES или 3DES. Примерно это и делает TLS, разница в том, что TLS соединяет координату
с другими числами, относящимися к подключению, а затем вычисляет хеш получившейся строки байтов.
Эксперименты с ECDH
Я написал ещё один скрипт на Python для вычисления закрытых/открытых ключей и общих секретных ключей над эллиптической кривой.
В отличие от показанных ранее примеров, в этом скрипте используется стандартизированная кривая, а не простая кривая на небольшом поле. Я выбрал кривую secp256k1 группы SECG («Standards for Efficient Cryptography Group», основанной Certicom). Та же самая кривая используется в Bitcoin для цифровых подписей. Вот параметры области определения:
(Эти числа взяты из исходного кода OpenSSL.)
Разумеется, вы можете изменить скрипт и использовать другие кривые и параметры области определения, только обязательно используйте простые поля и обычную формулировку Вейерштрасса, иначе скрипт не будет работать.
Скрипт очень прост и содержит некоторые из описанных выше алгоритмов: сложение точек, удвоение-сложение, ECDH. Рекомендую изучить и запустить его. Он создаёт примерно такие выходные данные:
Curve: secp256k1
Alice's private key: 0xe32868331fa8ef0138de0de85478346aec5e3912b6029ae71691c384237a3eeb
Alice's public key: (0x86b1aa5120f079594348c67647679e7ac4c365b2c01330db782b0ba611c1d677, 0x5f4376a23eed633657a90f385ba21068ed7e29859a7fab09e953cc5b3e89beba)
Bob's private key: 0xcef147652aa90162e1fff9cf07f2605ea05529ca215a04350a98ecc24aa34342
Bob's public key: (0x4034127647bb7fdab7f1526c7d10be8b28174e2bba35b06ffd8a26fc2c20134a, 0x9e773199edc1ea792b150270ea3317689286c9fe239dd5b9c5cfd9e81b4b632)
Shared secret: (0x3e2ffbc3aa8a2836c1689e55cd169ba638b58a3a18803fcf7de153525b28c3cd, 0x43ca148c92af58ebdb525542488a4fe6397809200fe8c61b41a105449507083)Эфемерное ECDH
Некоторые из вас, возможно, слышали об ECDHE, а не об ECDH. «E» в ECHDE обозначает «Ephemeral» (эфемерное) и связано с тем, что передаваемые ключи временны, а не статичны.
ECDHE используется, например, в TLS, где клиент и сервер генерируют свою пару закрытого-открытого ключа на лету, при установке соединения. Затем ключи подписываются сертификатом TLS (для авторизации) и передаются между сторонами.
Подписывание с помощью ECDSA
Сценарий следующий: Алиса хочет подписать сообщение своим закрытым ключом (
), а Боб хочет проверить подпись с помощью открытого ключа Алисы (
). Никто, кроме Алисы не должен иметь возможности создать действительные подписи. Каждый должен иметь возможность проверить подписи.
Алиса и Боб снова используют одинаковые параметры области определения. Мы рассмотрим алгоритм ECDSA, разновидность Digital Signature Algorithm, применённого к эллиптическим кривым.
ECDSA работает с хешем сообщения, а не с самим сообщением. Выбор хеш-функции остаётся за нами, но, очевидно, нужно выбирать криптографическую хеш-функцию. Хеш сообщения необходимо урезать, чтобы битовая длина хеша была такой же, что и битовая длина
(порядок подгруппы). Урезанный хеш — это целое число и оно будет обозначаться как
.
Алгоритм, выполняемый Алисой для подписывания сообщения, работает следующим образом:
- Берём случайное целое
, выбранное из
(где
— это по-прежнему порядок группы).
- Вычисляем точку
(где
— базовая точка подгруппы).
- Вычисляем число
(где
— это координата
).
- Если
, то выбираем другое
и пробуем снова.
- Вычисляем
(где
— закрытый ключ Алисы, а
— мультипликативная инверсия
по модулю
).
- Если
, то выбираем другое
и пробуем снова.
Пара является подписью.
Алиса подписывает хеш с помощью закрытого ключа
и случайного
. Боб проверяет правильность подписи сообщения с помощью открытого ключа Алисы
.
Проще говоря, этот алгоритм сначала генерирует секретный ключ (
). Благодаря умножению точек (которое, как мы знаем, является «простым» в одну сторону и «сложным» в обратную) секретный ключ прячется в
. Затем
привязывается к хешу сообщения уравнением
.
Учтите, что для вычисления
мы вычислили обратную величину
по модулю
. Как было сказано в предыдущей части, это гарантировано сработает только если
— простое число. Если подгруппа имеет порядок непростого числа, ECDSA использовать не удастся. Неслучайно все стандартизированные кривые имеют простой порядок, а имеющие непростой порядок неприменимы для ECDSA.
Проверка подписей
Для проверки подписи необходим открытый ключ Алисы
, (урезанный) хеш
и, очевидно, подпись
.
- Вычисляем целое
.
- Вычисляем целое
.
- Вычисляем точку
.
Подпись действительна, только если
.
Корректность алгоритма
С первого взгляда логика алгоритма может быть неочевидной, однако если объединить все ранее записанные нами уравнения, всё становится понятнее.
Начнём с
. Из определения открытого ключа мы знаем, что
(где
— закрытый ключ). Можно записать:
С учётом определений
и
можно записать:
Здесь мы опустили “
“, как для краткости, так и потому, что циклическая подгруппа, сгенерированная точкой
, имеет порядок
, то есть часть “
” избыточна.
Ранее мы определили
. Умножив обе части уравнения уравнения на
и поделив на
, мы получаем:
. Подставляя этот результат в наше уравнение для
, получаем:
Это то же самое уравнение , которое было у нас на шаге 2 алгоритма генерирования подписи! При генерировании подписей и при их проверке мы вычисляем одну и ту же точку
, просто разными наборами уравнений. Именно поэтому алгоритм работает.
Экспериментируем с ECDSA
Разумеется, я написал скрипт на Python для генерирования и проверки подписей. Код копирует некоторые части из скрипта ECDH, в частности, параметры области определения и алгоритм генерирования пары закрытого/открытого ключей.
Вот какие выходные данные создаются этим скриптом:
Curve: secp256k1
Private key: 0x9f4c9eb899bd86e0e83ecca659602a15b2edb648e2ae4ee4a256b17bb29a1a1e
Public key: (0xabd9791437093d377ca25ea974ddc099eafa3d97c7250d2ea32af6a1556f92a, 0x3fe60f6150b6d87ae8d64b78199b13f26977407c801f233288c97ddc4acca326)
Message: b'Hello!'
Signature: (0xddcb8b5abfe46902f2ac54ab9cd5cf205e359c03fdf66ead1130826f79d45478, 0x551a5b2cd8465db43254df998ba577cb28e1ee73c5530430395e4fba96610151)
Verification: signature matches
Message: b'Hi there!'
Verification: invalid signature
Message: b'Hello!'
Public key: (0xc40572bb38dec72b82b3efb1efc8552588b8774149a32e546fb703021cf3b78a, 0x8c6e5c5a9c1ea4cad778072fe955ed1c6a2a92f516f02cab57e0ba7d0765f8bb)
Verification: invalid signatureКак видите, скрипт сначала подписывает сообщение (байтовую строку «Hello!»), а затем проверяет подпись. После чего он пробует проверить ту же подпись для другого сообщения («Hi there!») и проверка не удаётся. Наконец, он пробуем проверить проверить подпись для правильного сообщения, но с другим случайным открытым ключом, после чего проверка тоже не удаётся.
Важность k
При генерировании подписей ECDSA важно хранить секретный
по-настоящему в тайне. Если бы мы использовали одну
для всех подписей или генератор случайных чисел оказался бы в какой-нибудь степени предсказуемым, то атакующий смог бы определить закрытый ключ!
Подобную ошибку сделала Sony несколько лет назад. На игровой консоли PlayStation 3 можно было запускать игры, только подписанные Sony алгоритмом ECDSA. То есть, если бы я хотел создать новую игру для PlayStation 3, я не смог бы распространять её среди пользователей без подписи Sony. Проблема заключалась в том, что все созданные Sony подписи были сгенерированы с помощью статичного
.
(Похоже, создатели генератора случайных чисел Sony вдохновлялись или XKCD, или Дилбертом.)
В такой ситуации можно запросто восстановить закрытый ключ
Sony, купив всего две подписанные игры, после чего извлечь их хеши (
и
) и подписи (
и
) вместе с параметрами области определения. Это делается так:
Последнее уравнение позволяет нам вычислить
с помощью всего двух хешей и соответствующих им подписей. Теперь с помощью уравнения для
мы можем получить закрытый ключ:
Похожие техники можно применить, если
не статично, но каким-то образом предсказуемо.
Часть 4: алгоритмы для взлома защиты ECC и сравнение с RSA
В предыдущей части мы рассмотрели два алгоритма (ECDH and ECDSA) и разобрались, почему задача дискретного логарифмирования для эллиптических кривых играет важную роль для их безопасности. Но, если вы помните, мы сказали, что математических доказательств сложности задачи дискретного логарифмирования нет: мы полагаем, что она «сложна», но не уверены в этом. В первой части статьи мы попробовали оценить, насколько «сложна» она на практике в условиях современных технологий.
Во второй части мы попытались ответить на вопрос: зачем нам нужна криптография на эллиптических кривых, если RSA (и другие криптосистемы, основанные на модулярной арифметике) хорошо работают?
Взлом задачи дискретного логарифмирования
Теперь мы рассмотрим два наиболее эффективных алгоритма вычисления дискретных алгоритмов на эллиптической кривой: алгоритм «baby-step, giant-step» и ρ-алгоритм Полларда.
Прежде чем начать, я напомню, в чём заключается задача дискретного логарифмирования: найти для двух заданных точек и
целое число
, удовлетворяющее уравнению
. Точки принадлежат подгруппе эллиптической кривой с базовой точкой
и порядком
.
Baby-step, giant-step
Для начала приведу простое рассуждение: мы всегда можем записать любое целое
как
, где
,
и
— три произвольных целых. Например, можно записать
.
С учётом этого можно переписать уравнение задачи дискретного логарифмирования следующим образом:
Baby-step giant-step — это алгоритм «встречи посередине». В отличие от атаки перебором (при которой придётся вычислять все точки
для каждого
, пока мы не найдём
), можно вычислять «несколько» значений для
и «несколько» значений для
, пока мы не найдём соответствие. Алгоритм работает следующим образом:
- Вычисляем
- Для каждого
из
вычисляем
и сохраняем результаты в хеш-таблицу.
- Для каждого
из
:
- вычисляем
;
- вычисляем
;
- проверяем хеш-таблицу и ищем точку
, такую, что
;
- если такая точка существует, то мы нашли
.
- вычисляем
Как видите, изначально мы вычисляем точки
с небольшим инкрементом («детскими шагами» «baby step») для коэффициента
(
,
,
, …). Во второй части алгоритма мы вычисляем точки
с большим инкрементом («великанскими шагами» «giant step») для
(
,
,
, …, где
— большое число).
Алгоритм baby-step, giant-step: сначала мы вычисляем несколько точек с небольшим шагом и сохраняем их в хеш-таблице. Затем делаем великанские шаги и сравниваем новые точки с точками в хеш-таблице. Найдя соответствие, мы можем вычислить дискретный алгоритм простой перестановкой членов.
Чтобы понять, как работает алгоритм, забудем на минуту о том, что
кешируются, и возьмём уравнение
. Рассмотрим, что из этого следует:
В итоге мы проверили все точки от до
(то есть все возможные точки), выполнив не более
сложений и умножений (ровно
для «детских шагов», не более
для «великанских шагов»).
Если считать, что поиск в хеш-таблице занимает время
то легко увидеть, что этот алгоритм имеет временную и пространственную сложность
(или
, если учесть битовую длину). Это всё ещё экспоненциальное время, но оно намного лучше, чем при атаке перебором.
Baby-step giant-step на практике
Имеет смысл разобраться, что же значит сложность
на практике. Возьмём стандартизированную кривую:
prime192v1 (она же secp192r1, ansiX9p192r1). Эта кривая имеет порядок
= 0xffffffff ffffffff ffffffff 99def836 146bc9b1 b4d22831. Квадратный корень из
— это примерно 7,922816251426434 · 1028 (почти восемьдесят октиллионов [прим. пер.: по короткой шкале]).
Представим, что мы храним
точек в хеш-таблице. Предположим, что каждая точка занимает ровно 32 байта: для хеш-таблицы потребуется примерно 2,5 · 1030 байт памяти. Поискав в Интернете, можно узнать, что современная общая ёмкость накопителей всего мира имеет порядок зеттабайта (1021 байт). Это почти на десять порядков меньше, чем объём памяти, необходимый нашей хеш-таблице! Даже если бы точки занимали по 1 байт каждая, мы всё равно не смогли бы хранить их все.
Это впечатляет, и впечатляет ещё сильнее, если вспомнить, что prime192v1 — это одна из кривых с наименьшим порядком. Порядок secp521r1 (ещё одной стандартной кривой NIST) равен примерно 6,9 · 10156!
Эксперименты с baby-step giant-step
Я написал скрипт на Python, вычисляющий дискретные логарифмы с помощью алгоритма baby-step giant-step. Очевидно, что он работает только с кривыми малого порядка: не пытайтесь использовать secp521r1, если только не хотите получить MemoryError.
Скрипт выдаёт примерно такие выходные данные:
Curve: y^2 = (x^3 + 1x - 1) mod 10177
Curve order: 10331
p = (0x1, 0x1)
q = (0x1a28, 0x8fb)
325 * p = q
log(p, q) = 325
Took 105 stepsρ Полларда
ρ Полларда — это ещё один алгоритм вычисления дискретных логарифмов. Он имеет ту же асимптотическую временную сложность
, что и baby-step giant-step, но его пространственная сложность равна всего
. Если baby-step giant-step не мог решить дискретные логарифмы из-за огромных требований к памяти, может быть, ρ Полларда справится? Давайте проверим…
Для начала ещё раз напомню задачу дискретного логарифмирования: найти для заданных
и
целое
, такое, что
. В ρ-алгоритме Полларда мы будем решать немного другую задачу: найти для заданных
и
целые
,
,
и
, такие, что
.
Найдя четыре целых числа, мы сможем использовать уравнение
для вычисления
:
Теперь мы можем избавиться от
. Но прежде чем сделать это, вспомним, что наша подгруппа циклическая и имеет порядок
, то есть коэффициенты, используемые при умножении точек, берутся по модулю
:
Принцип работы ρ Полларда прост: мы определяем псевдослучайную последовательность пар . Эту последовательность пар можно использовать для генерирования последовательности точек
. Поскольку
и
являются элементами одной циклической подгруппы, последовательность точек
тоже циклическая.
Это значит, что если мы обойдём нашу псевдослучайную последовательность пар
, то рано или поздно обнаружим цикл. То есть: мы найдём пару
и другую отдельную пару
, такие, что
. Те же точки, отдельные пары: мы сможем применить приведённое выше уравнение для нахождения логарифма.
Задача заключается в следующем: как обнаружить цикл эффективным способом?
Черепаха и заяц
Для обнаружения цикла мы можем проверить все возможные значения
и
с помощью функции пересчёта пар, но при условии, что существует
таких пар, алгоритм будет иметь сложность
, что намного хуже атаки простым перебором.
Но существует и более быстрый способ: алгоритм черепахи и зайца (также известный как алгоритм нахождения цикла Флойда). На рисунке ниже показан принцип работы метода черепахи и зайца, на котором основан ρ-алгоритм Полларда.
У нас есть кривая и точки
и
. Точки принадлежат циклической подгруппе с порядком 5. Мы обходим последовательность пар с разными скоростями, пока не находим две разные пары
и
, дающих одну точку. В этом случае мы нашли пары
и
, что позволяет нам вычислить логарифм как
. И на самом деле, у нас получилось
.
В сущности, мы берём псевдослучайную последовательность пар
вместе с соответствующей последовательностью точек
. Последовательность пар
может быть или не быть циклической, но последовательность точек точно циклическая, потому что
и
сгенерированы из одной базовой точки, а из свойство подгрупп мы знаем, что не можем «сбежать» из подгруппы только скалярным умножением и сложением.
Теперь мы берём двух животных, черепаху и зайца, и заставляем обходить последовательность слева направо. Черепаха (зелёная точка на изображении) медленная и считывает каждую точку, одну за другой; заяц (красная точка) быстр и пропускает точку на каждом шаге.
Через какое-то время черепаха и заяц найдут одну точку, но с разными парами коэффициентов. Или, если выразить это уравнениями, черепаха найдёт пару
, а заяц — пару
, такие, что
.
Если случайная последовательность определяется через алгоритм (а не хранится статически), легко увидеть, что принцип работы требует всего пространства. Вычисление сложности асимптотического времени не так просто, но мы можем построить вероятностное доказательство, показывающее, что временная сложность равна
), как мы уже говорили.
Экспериментируем с ρ Полларда
Я создал скрипт на Python, вычисляющий дискретные логарифмы с помощью ρ-алгоритма Полларда. Это не реализация исходного ρ Полларда, а небольшая его вариация (я использовал более эффективный способ генерирования псевдослучайной последовательности пар). В скрипте есть полезные комментарии, так что прочитайте его, если вам интересны подробности алгоритма.
Этот скрипт, как и baby-step giant-step, работает для маленьких кривых и создаёт те же выходные данные.
Ро Полларда на практике
Мы говорили, что baby-step giant-step невозможно использовать на практике из-за огромных требований к памяти. С другой стороны, ро-алгоритм Полларда требует очень мало памяти. Насколько же он практичен?
В 1998 году Certicom начала соревнование по вычислению дискретных логарифмов на эллиптических кривых с битовой длиной от 109 до 369. На сегодняшний день успешно взломаны только кривые длиной 109 бит. Последняя успешная попытка была совершена в 2004 году. Процитируем Википедию:
Награда была вручена 8 апреля 2004 года примерно 2600 людям, которых представлял Крис Монико. Они тоже использовали разновидность распараллеленного ро-алгоритма Полларда, вычисления по которому заняли 17 месяцев календарного времени.
Как мы уже сказали, prime192v1 — это одна из «наименьших» эллиптических кривых. Мы также сказали, что ρ Полларда имеет временную сложность
. Если бы мы использовали ту же технику, что и Крис Монико (тот же алгоритм, то же оборудование и количество машин), сколько бы заняло вычисление логарифма для
prime192v1?
Полученный результат говорит сам за себя и даёт чётко понять, насколько сложно взломать дискретный логарифм с помощью таких техник.
Сравниние ρ Полларда и Baby-step giant-step
Я решил объединить скрипт baby-step giant-step, скрипт ро Полларда и скрипт перебора в четвёртый скрипт для сравнения их производительности.
Этот четвёртый скрипт вычисляет все логарифмы для всех точек на «маленькой» кривой с помощью разных алгоритмов и сообщает, сколько времени это заняло:
Curve order: 10331
Using bruteforce
Computing all logarithms: 100.00% done
Took 2m 31s (5193 steps on average)
Using babygiantstep
Computing all logarithms: 100.00% done
Took 0m 6s (152 steps on average)
Using pollardsrho
Computing all logarithms: 100.00% done
Took 0m 21s (138 steps on average)Как и можно ожидать, метод перебора чудовищно медленный по сравнению с двумя другими. Baby-step giant-step быстрее, а ро-алгоритм Полларда больше чем в три раза медленнее baby-step giant-step (хоть он и использует гораздо меньше памяти и меньшее количество шагов в среднем).
Посмотрите ещё и на количество шагов: для вычисления каждого логарифма способом перебора в среднем потребовалось 5193 шагов. 5193 очень близко к 10331 / 2 (половина порядка кривой). Baby-step giant-steps и ро Полларда использовали 152 шага и 138 шагов соответственно. Эти два числа очень близки к квадратному корню 10331 (101,64).
Дальнейшие рассуждения
В обсуждении этих алгоритмов я использовал много чисел. При их чтении важно быть внимательным: алгоритмы во многих аспектах можно сильно оптимизировать. Оборудование может улучшаться. Можно создать специализированное оборудование.
Если сегодня подход кажется непрактичным, это не значит, что его нельзя улучшить. Это также не значит, что нет других, более хороших подходов (не забывайте, что у нас нет доказательств сложности задачи дискретного логарифмирования).
Алгоритм Шора
Если современные техники неприменимы, то как насчёт техник ближайшего будущего? Ситуация вызывает всё больше беспокойства: уже существует квантовый алгоритм, способный вычислять дискретные логарифмы за полиномиальное время: алгоритм Шора со временной сложностью
и пространственной сложностью
.
Эффективность квантовых алгоритмов заключается в суперпозиции состояния. У классических компьютеров ячейки памяти (т.е. биты) могут иметь значение 1 или 0. Между ними нет промежуточных состояний. С другой стороны, ячейки памяти квантовых компьютеров (кубиты) подвержены принципу неопределённости: пока их не измерят, у них нет полностью определённого состояния. Суперпозиция состояния не значит, что каждый кубит может одновременно иметь значение 0 и 1 (как часто пишут в Интернете). Она значит, что при измерении кубита у нас есть определённая вероятность наблюдать 0 и другая вероятность наблюдать 1. Работа квантовых алгоритмов заключается в изменении вероятности каждого кубита.
Эта странность означает, что с ограниченным количеством кубитов мы можем одновременно иметь дело со множеством возможных входных данных одновременно. Например, мы можем сказать квантовому компьютеру, что существует число
, равномерно распределённое между 0 и
. При этом требуется всего
кубитов вместо
бит. Затем мы можем приказать квантовому компьютеру выполнить скалярное умножение
. В результате мы получим суперпозицию состояний, заданную всеми точками от
до
, то есть если мы теперь измерим все кубиты, то получим одну из точек от
до
с вероятностью
.
Я рассказал об этом, чтобы вы поняли всю мощь суперпозиции состояний. Алгоритм Шора работает не совсем так, на самом деле он более сложен. Его усложняет то, что хотя мы и можем «симулировать»
состояний одновременно, на каком-то этапе нам придётся снизить это количество состояний до нескольких, потому что на выходе нам нужно одно число, а не несколько (т.е., нам нужно знать один логарифм, а не множество вероятно ошибочных логарифмов).
ECC и RSA
Теперь давайте забудем о квантовых вычислениях, которые пока ещё не стали серьёзной проблемой. Я хочу ответить на следующий вопрос: зачем возиться с эллиптическими кривыми, если RSA и так работает хорошо?
Простой ответ дал NIST, представив таблицу сравнения размеров ключей RSA и ECC, необходимых для получения одинакового уровня защиты.
| Размер ключа RSA (биты) | Размер ключа ECC (биты) |
|---|---|
| 1024 | 160 |
| 2048 | 224 |
| 3072 | 256 |
| 7680 | 384 |
| 15360 | 521 |
Заметьте, что линейной связи между размерами ключей RSA и ECC нет (другими словами: если мы удваиваем размер ключа RSA, нам не нужно удваивать размер ключа ECC). Таблица говорит нам, что ECC не только использует меньше памяти, но и генерирование ключей с подписыванием в ней гораздо быстрее.
Но почему это так? Ответ заключается в том, что самые быстрые алгоритмы для вычисления дискретных алгоритмов над эллиптическими кривыми — это ρ-алгоритм Полларда и baby-step giant-step, а в случае RSA есть более быстрые алгоритмы. В частности, один из них — это общий метод решета числового поля: алгоритм для факторизации целых чисел, который можно использовать для вычисления дискретных логарифмов. Общий метод решета числового поля — это на сегодняшний день самый быстрый алгоритм для факторизации целых чисел.
Всё это относится и к другим криптосистемам, основанным на модулярной арифметике, в том числе к DSA, Диффи-Хеллману и Эль-Гамалю.
Скрытые угрозы АНБ
А теперь перейдём к сложной части. До этого момента мы обсуждали алгоритмы и математику. Настало время обсудить людей, и всё становится сложнее.
Если вы помните, в третьей части мы говорили, что некоторые классы эллиптических кривых являются слабыми, поэтому для решения проблемы получения надёжных кривых от сомнительных источников мы добавляем случайное порождающее значение (seed) к параметрам области определения. И если посмотреть на стандартные кривые NIST, можно увидеть, что они проверяемо случайны.
Если прочитать страницу Википедии о принципе “в рукавах ничего нет”, можно заметить, что:
Эти числа случайны, потому что их цифры распределены равномерно. И они не вызывают подозрений, потому что имеют обоснование.
Теперь возникает следующий вопрос: откуда берутся случайные порождающие значения для кривых NIST? Ответ: к сожалению, мы не знаем. Эти значения не имеют никакого обоснования.
Возможно ли, что NIST обнаружил «значительно большой» класс слабых эллиптических кривых, попробовал различные возможные варианты порождающих значений и нашёл уязвимую кривую? Я не могу ответить на этот вопрос, но это закономерный и важный вопрос. Мы знаем, что NIST как минимум успешно стандартизировал уязвимый генератор случайных чисел (генератор, который, как ни странно, основан на эллиптических кривых). Возможно, он успешно стандартизировал и множество слабых эллиптических кривых? Как это проверить? Да никак.
Важно понимать, что «проверяемо случайный» и «защищённый» не являются синонимами. И неважно, насколько сложна задача логарифмирования или насколько длинны ключи — если алгоритмы взломаны, то мы ничего не можем поделать.
В этом отношении RSA побеждает, потому что ей не требуются специальные параметры области определения, которые можно эксплуатировать. RSA (как и другие системы модулярной арифметики) может быть хорошей альтернативой, если мы не можем доверять властям и если мы не можем создать собственные параметры области определения. И если вам любопытно: да, TLS может использовать кривые NIST. Если вы проверите в google, то увидите, что при подключении используются ECDHE и ECDSA с сертификатом, основанным на prime256v1 (она же secp256p1).
Вот и всё!
Надеюсь, вам понравилась эта статья. Я стремился познакомить вас с основной информацией, терминологией и допущениями, необходимыми для понимания текущего состояния криптографии на эллиптических кривых. Если мне это удалось, то теперь вы сможете разобраться с существующими криптосистемами на базе ECC и расширить свои знания чтением более глубокой документации. При написании статьи я пропустил очень многие подробности и использовал упрощённую терминологию, но я чувствовал, что в противном случае вы бы не поняли информацию, изложенную в Интернете. Я считаю, что мне удалось найти хороший компромисс между простотой и полнотой информации.
Стоит однако заметить, что прочитав только эту статью, вы не сможете реализовать защищённые криптосистемы на основе ECC: обеспечение безопасности требует знания многих тонких, но важных подробностей. Вспомните требования к атаке Смарта и ошибку Sony — это два примера того, как можно создать небезопасные алгоритмы и как легко их можно эксплуатировать.
Итак, если вам интересно глубже погрузиться в мир ECC, то с чего же начать?
Во-первых, пока мы видели кривые Вейерштрасса над простыми полями, но вы должны знать, что существуют и другие виды кривых и полей, а именно:
- Кривые Коблица над двоичными полями. Это эллиптические кривые в форме
(где
— 0 или 1) над конечными полями, содержащими
элементов (где
— простое число). Они обеспечивают особо эффективное сложение точек и скалярное умножение.
Примерами стандартизированных кривых Коблица являются
nistk163,nistk283иnistk571(три кривые, определённые над полем из 163, 283 и 571 бит). - Двоичные кривые. Они очень похожи на кривые Коблица и имеют форму
(где
— целое число, часто генерируемое из случайного порождающего значения). Как подсказывает название, двоичные кривые ограничены только двоичными полями. Примерами стандартизированных кривых являются
nistb163,nistb283иnistb571.Надо сказать, что возникает всё больше подозрений в том, что кривые Коблица и двоичные кривые могут быть не так безопасны, как простые кривые.
- Кривые Эдвардса имеют вид
(где
— это 0 или 1). Они особенно интересны не только потому, что для них быстро выполняются сложение точек и скалярное умножение, но и потому, что формула сложения точек всегда одинакова, в любом случае (
,
,
, …). Эта особенность снижает возможность атак по сторонним каналам (side-channel attack), при которых атакующий измеряет время, использованное для скалярного умножения, и пытается подобрать скалярный коэффициент на основании времени для его вычисления.
Кривые Эдвардса относительно новы (впервые они были представлены в 2007 году), поэтому ни один орган, такой как Certicom или NIST, пока не стандартизировал ни одну из них.
- Curve25519 и Ed25519 — это две специальные эллиптические кривые, созданные для ECDH и варианта ECDSA соответственно. Как и кривые Эдвардса, эти две кривые быстры и помогают защищаться от атак по сторонним каналам. Как и кривые Эдвардса, эти две кривые не были пока стандартизированы и не используются в популярном ПО (за исключением OpenSSH, который поддерживает пары ключей Ed25519 с 2014 года).
Если вам интересны подробности реализации ECC, предлагаю вам почитать исходники OpenSSL и GnuTLS.
И наконец, если вам интересны математические подробности, а не безопасность и эффективность алгоритмов, то нужно знать следующее:
- Эллиптические кривые — это алгебраические многообразия рода 1.
- Бесконечно удалённые точки изучаются в проективной геометрии. Они могут быть представлены с помощью однородных координат (хотя большинство из свойств проективной геометрии не нужны для криптографии на эллиптических кривых).
И не забудьте изучить конечные поля вместе с теорией полей.
Если вас интересует эта тема, то стоит искать по таким ключевым словам.
На этом статья официально заканчивается. Благодарю за все дружественные комментарии, твиты и письма. Многие спрашивали, буду ли я писать другие статьи о близких темах. Мой ответ: возможно. Можете присылать свои предложения, но ничего не обещаю.
4.1.4 Эллиптические кривые над конечным полем
Рассмотрим эллиптические кривые над конечным полем 


или к виду (4.2) при 
Особый интерес для криптографии представляет объект, называемый эллиптический группой по модулю 

Далее мы, говоря об эллиптической кривой, если не оговорено противное, будем иметь в виду именно группу точек кривой над полем 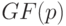


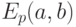
Пример 4.5 Пусть 

В этом случае 

Нас интересуют только целые значения от 
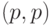

- Вычисляем значения
(табл. 4.1).
- Вычисляем значения
(табл. 4.2)
Теперь сравниваем числа в нижних строках табл. 4.1 и табл. 4.2. Число, попавшее в обе строки, определяет две точки кривой. Так, число 1 содержится и в нижней строке табл. 4.1, и в нижней строке табл. 4.2. Число 1 определяет точки 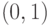

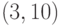
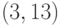
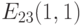


В криптографии применяются кривые, параметры которых являются большими (порядка 50 десятичных знаков) числами. В таких случаях перечисление всех точек кривой нереально за приемлемое время. Более того, даже определение количества точек кривой – весьма непростая задача.
Важной является
Теорема 4.1 (теорема Хассе) Пусть 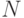


4.1.5 Генерация точек эллиптической кривой
Для нахождения случайной точки эллиптической кривой 

- Выбрать случайное
.
- Вычислить
.
- Вычислить символ Лежандра
по
.
- Если
– квадратичный невычет, перейти к пункту 1.
- Вычислить
– квадратный корень из
по модулю
(например, с помощью алгоритма Тонелли-Шенкса).
Пример 4.6 Найти случайную точку эллиптической кривой 
Решение. Пусть выбрано случайное число 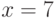

Следовательно, 


Пусть выбрано случайное число 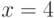

Итак, 


Имеем: 






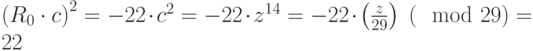
Итак, найдена точка 
4.1.6 Сложение точек кривой над конечным полем
Проиллюстрируем примерами сложение точек кривой, построенной над конечным полем.
Пример 4.7 Выбрана кривая 


Для нахождения 
Вычисляем 
Итак, мы нашли 

Таким образом, мы нашли точку 
4.1.7 Кратные точки
Данный алгоритм аналогичен алгоритму возведения в степень по модулю, см. параграф 1.2.2.
Рассмотрим алгоритм вычисления точки 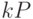

Далее, положим 

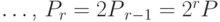
Откуда
Таким образом, мы можем вычислить 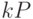

Пример 4.8 Найти 
Представляем 100 в виде 

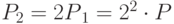

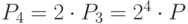


Теперь 
Мы нашли точку 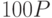
Пример 4.9 Найти точку 
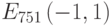
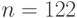

Решение.
Пример 4.10 Найти порядок точки 

Решение. По теореме Лагранжа, порядок точки является делителем 16, то есть одним из чисел 2, 4, 8, 16. Пользуясь формулами (4.2), будем последовательно удваивать точку, пока не получим нейтральный элемент группы.
Следовательно, порядок точки 
Пример 4.11 Найти порядок точки 


Решение. Порядок точки является делителем числа 48, то есть одним из чисел: 2, 4, 8, 16, 3, 6, 12, 24. Нужно попробовать умножить точку на каждое из них. Расположим делители в узлах ориентированного дерева, где каждый потомок получается из родителя выполнением одной операции сложения точек. Пример такого дерева приведён на
рис.
4.2.
Рис.
4.2.
Дерево делителей числа 48
Совершая обход этого дерева, будем получать кратные точки. Например, чтобы получить 



Заметим, что вариантов построения такого дерева может быть много. Число ребер в дереве с 10 вершинами – всегда 9, а операция удвоения точки всегда быстрее сложения произвольных двух точек. Поэтому оптимальным будет проводить вычисления по дереву на рисунке
рис.
4.3, содержащему наибольшее число удвоений.
Рис.
4.3.
Более оптимальное дерево делителей числа 48
Теперь мы знаем, что порядок точки есть делитель числа 24, поэтому нам осталось пройти только те вершины дерева, в которых записаны делители числа 24. Например, вершину 16 мы рассматривать не будем.
Итак, 24 – наименьшее число, при умножении точки на которое мы получим нейтральный элемент. Поэтому порядок точки равен 24.
Еще раз отметим, что во многих случаях определение порядка кривой является самостоятельной и весьма не простой задачей.
Список литературы
- Болоток А. А., Гашков С.Б., Фролов А. Б., Часовских А. А. Элементарное введение в эллиптическую криптографию – М.: КомКнига, 2006. – 328 с.
- Коблиц Н. Курс теории чисел и криптографии – М.: ТВП, 2003.

114 Гл. 4. Применение кривых для проверки простоты и факторизации
нам вообще не нужно будет проводить деление по модулю n. Однако Коен [89, гл. 10] все же рекомендует аффинные координаты в сочетании с усовершенствованием Монтгомери.
Замечание 4.8. Алгоритм Ленстры аналогичен (P − 1)-методу Полларда, описанному в гл. 2. В нем, так же, как и в (P − 1)-методе, возможна вторая стадия, см. [89; 192; 74].
§4.3. Вычисление порядка группы точек эллиптической кривой над конечным полем
Вычисление порядка группы точек на эллиптической кривой над конечным простым полем имеет важные приложения как в криптографии, так и в алгоритмах проверки простоты чисел, о которых будет рассказано в следующем параграфе.
Пусть p — простое число, p > 3, эллиптическая кривая E = Ea,b
над полем Z/pZ задана уравнением y2 = x3 + ax + b. Для нахождения |E(Z/pZ)| Р. Шуф в 1985 г. в работе [244] предложил алгоритм, имеющий полиномиальную сложность O(log8 p) битовых операций (см. также [245]). Дальнейшие усовершенствования алгоритма Шуфа были предложены Аткином, Элкисом, Мюллером и другими авторами, см. [65; 113; 202; 171; 245]. Это позволило на практике вычислять порядки групп точек для простых полей, число элементов которых записывается несколькими сотнями десятичных цифр; рекордное значение p равно 10499 + 153.
В данном параграфе мы опишем первоначальный алгоритм Шуфа из работы [244].
Обозначим через Z/pZ алгебраическое замыкание поля Z/pZ. Отображение Фробениуса : E(Z/pZ) → E(Z/pZ) определяется соот-
|
ношениями |
(O) = O. |
|
(x, y) = (xp, yp), |
|
|
Нетрудно доказать, что является |
гомоморфизмом и вложением |
E(Z/pZ) в себя; очевидно, что точки E(Z/pZ) остаются неподвижными при действии . Пусть
|E(Z/pZ)| = p + 1 − t,
по теореме Хассе |t| < 2√p. Целое число t называется следом отображения Фробениуса; отображение удовлетворяет уравнению
2 − t + p = 0.

|
§ 4.3. Вычисление порядка группы точек эллиптической кривой |
115 |
Для каждого натурального числа n обозначим через E[n] подгруппу E(Z/pZ), состоящую из точек, порядок которых делит n:
E[n] = {P E(Z/pZ) | nP = O}.
Теорема 4.9 (см. [256]). Если n > 1 и p не делит n, то группа E[n] изоморфна Z/pZ × Z/pZ.
Пример 4.10. Рассмотрим x1, x2, x3 — три различных корня уравнения x3 + ax + b = 0 в Z/pZ. Тогда
E[2] = {(xi, 0) : i = 1, 2, 3} {O}.
Определим многочлены n (x, y) Z/pZ [x, y], n = −1, 0, 1, 2, . . ., следующими соотношениями:
−1 (x, y) = −1, 0 (x, y) = 0, 1 (x, y) = 1, 2 (x, y) = 2y,3 (x, y) = 3x4 + 6ax2 + 12bx − a2,
4 (x, y) = 4y(x6 + 5ax4 + 20bx3 − 5a2x2 − 4abx − 8b2 − a3); далее при n 3
2n (x, y) = n (x, y) ( n+2 (x, y) n−1 (x, y)2 − n−2 (x, y) n+1 (x, y)2)/(2y), и при n 2
2n+1 (x, y) = n+2 (x, y) n (x, y)3 − n+1 (x, y)3 n−1 (x, y);
везде y2 следует заменять на x3 + ax + b.
Многочлены n (x, y) называются многочленами деления. Нетрудно доказать по индукции, что fn (x), определенные равенством
|
fn (x) = |
n (x, y)/y, |
если n четное, |
|
n (x, y), |
если n нечетное, |
являются многочленами от x, т. е. fn (x) Z/pZ [x]. Кроме того, если n— нечетно, p n, то deg fn (x) = (n2 − 1)/2.
Теорема 4.11. Пусть P = (x, y) E(Z/pZ) E[2]. Пусть n 3. Равенство nP = O выполнено тогда и только тогда, когда fn (x) = 0.
|
Теорема 4.12. Пусть |
P = (x, y) E( |
Z/pZ |
) E[2], |
n 2, причем |
|||
|
nP =/ O. Тогда |
|||||||
|
nP= x− |
n 1 (x, y) n+1 (x, y) |
n+2 (x, y) n−1 (x, y)2− n−2 |
(x, y) n+1 |
(x, y)2 |
. |
||
|
− n (x, y)2 |
, |
4y n (x, y)3 |
Далее в алгоритме Шуфа мы будем находить значение t (mod l) для небольших простых чисел l. Если таких l будет достаточно много,
8*

116 Гл. 4. Применение кривых для проверки простоты и факторизации
точнее, если Πl > 4√p, то, найдя затем по китайской теореме об остатках значение t (mod Πl), мы получим, что искомое значение t равно абсолютно наименьшему вычету в классе t (mod Πl). Это следует из теоремы Хассе (см. § 4.1). Тогда мы найдем искомое значение
|
|E(Z/pZ)| = p + 1 − t. |
случай l = 2. Согласно приведенному вы- |
|
Рассмотрим сначала |
|
|
ше примеру, в E(Z/pZ) |
найдется ненулевая точка P = (x, 0) второго |
порядка, если и только если выполнено условие НОД(xp − x, x3 + ax + b) =/ 1.
Это условие равносильно четности числа |E(Z/pZ)| что, в свою очередь, равносильно четности t, поскольку p + 1 четно. Итак, t ≡ 0 (mod 2) тогда и только тогда, когда
НОД(xp − x, x3 + ax + b) =/ 1;
в противном случае t ≡ 1 (mod 2).
Везде далее мы обозначаем через l нечетное фиксированное (небольшое) простое число, l =/ p. Реально в алгоритме следует рассматривать простые числа l порядка O(log p).
Рассмотрим группу E[l]; очевидно, что (E[l]) E[l]. Легко показать, что является изоморфизмом E[l]. Обозначим l = |E[l] . Тогда l удовлетворяет уравнению
2l − t l + p = 0.
Покажем, что если l удовлетворяет уравнению
2l − t l + p = 0
при некотором t Z, то t ≡ t (mod l). Действительно, вычитая второе уравнение из первого, получим
(t − t ) l = 0 на E[l],
откуда t ≡ t (mod l), поскольку l — изоморфизм.
Теперь нам надо найти значение , 0 l − 1, для которого2l − l + p = 0 на E[l].
Тем самым мы определим значение t (mod l). Другими словами, нам нужно найти Z/lZ, для которого на E[l] выполняется равенство2l + p = l. Случай = 0 рассматривается отдельно. Если же =/ 0, то, для
k ≡ p (mod l), 1 k l − 1,

|
§ 4.3. Вычисление порядка группы точек эллиптической кривой |
117 |
мы, по теореме 4.12, примененной к точке P = (x, y) E[l] O можем переписать наше равенство 2l (P) + pP = l (P) в виде
(xp2 , yp2) x − k−1 (x, y) k+1 (x, y) ,k (x, y)2
k+2 (x, y) k−1 (x, y)2 − k−2 (x, y) k+1 (x, y)2 =
4y k (x, y)3
= xp − −1 (x, y) +1 (x, y) p,(x, y)2
+2 (x, y) −1 (x, y)2 − −2 (x, y) +1 (x, y)2 p . 4y (x, y)3
Знак обозначает операцию сложения точек на кривой. Последнее равенство приводится к виду
H1 (x) ≡ 0 (mod fl (x)),
H2 (x) ≡ 0 (mod fl (x)),
где H1 (x), H2 (x) Z/pZ [x]. В результате перебора = 0, 1, . . . , l − 1 мы найдем истинное значение t ≡ (mod l). Так выглядит основная идея алгоритма, которую мы далее конкретизируем.
Алгоритм Шуфа.
Алгоритм находит t (mod l) для таких простых чисел l, что l > 4√p. Затем с помощью китайской теоремы об остатках находится истинное значение t. Значение t (mod 2) находим так, как было сказано выше. Пусть далее l > 2, l — фиксированное простое
число, l =/ p.
1 этап алгоритма для фиксированного l. Мы проверяем, существует ли точка P = (x, y) E[l] O такая, что
2l (P) = ±kP,
где k ≡ p (mod l), 1 k l − 1. Сначала проверяем по первой координате; это означает, что должно выполняться равенство
xp2 = x − k−1 (x, y) k+1 (x, y) .k (x, y)2
При четном k это равенство имеет вид
|
x |
p2 |
= x − |
fk−1 (x)fk+1 (x) |
, |
|
fk (x)2 (x3 + ax + b) |

118 Гл. 4. Применение кривых для проверки простоты и факторизации
а при нечетном k —
xp2 = x − fk−1 (x)fk+1 (x) (x3 + ax + b) . fk (x)2
Следовательно, по теореме 4.11 точка P = (x, y) E[l] O, удовлетворяющая соотношению 2l (P) = ±kP, существует тогда и только тогда, когда
НОД((xp2 − x)fk (x)2 (x3 + ax + b) + fk−1 (x)fk+1 (x), fl (x)) =/ 1
при четном k, и
НОД((xp2 − x)fk (x)2 + fk−1 (x)fk+1 (x) (x3 + ax + b), fl (x)) =/ 1
при нечетном k. Если же соответствующий НОД (при k четном или нечетном) равен 1, то искомое не сравнимо с 0 по модулю l. Действительно, если ≡ 0 (mod l), то
|
( l2 + k) (P) = 0 для всех P E[l], |
. |
|||||
|
а в нашем случае (при НОД = 1) |
таких точек нет, за исключением |
O |
||||
|
2 |
||||||
|
В случае неразрешимости уравнения |
l (P) |
= ±kP на E[l] O мы пере- |
||||
|
ходим на 2-й этап алгоритма. |
P E[l] O, для которой |
|||||
|
2 |
Предположим, что существует |
точка |
||||
|
l |
(P) = ±kP = ±pP. |
1случай. Если 2l (P) = −pP, то ( 2l + p)P = O. Так как ( 2 − t +
+p) (P) = O для любой точки P на кривой, то отсюда (t l) (P) = O.
Поскольку l — изоморфизм E[l], получаем, что t ≡ 0 (mod l). Таким образом, в данном случае мы нашли искомое t (mod l).
|
2 случай. Если l2 (P) = pP, то, пользуясь снова уравнением 2 − |
|||||||||
|
− t + p = 0, |
получаем соотношение (2p − t l) (P) = O. Поскольку |
||||||||
|
2pP =/ O для |
P E[l] O, то t ≡ 0 (mod l). Поэтому l (P) = |
2p |
· P |
||||||
|
t |
|||||||||
|
(здесь |
1 |
обозначает t−1 (mod l)). Применяя снова l, получим |
|||||||
|
t |
|||||||||
|
2p |
2 |
||||||||
|
pP = l2 (P) = |
l (P) = |
4p |
· P. |
||||||
|
t |
t2 |
||||||||
|
Отсюда |
p ≡ 4p2/t2 |
(mod l), |
|||||||
или t2 ≡ 4p (mod l). В частности, в этом случае p является квадратичным вычетом по модулю l.
Теперь решим уравнение w2 ≡ p (mod l) (алгоритм решения таких уравнений см. далее в главе 6; для малых l возможен перебор). Для его

|
§ 4.3. Вычисление порядка группы точек эллиптической кривой |
119 |
решения w будет выполнено сравнение t ≡ ±2w (mod l), и нам останется лишь определить истинный знак + или −.
Подставляя t ≡ ±2w (mod l) в уравнение для l, получим
2l 2w l + w2 = 0,
или ( l w)2 = 0 тождественно на E[l]. Поэтому собственное значение линейного отображения l на E[l] может быть только ±w (mod l) (если r — собственное значение, то (r w)2 ≡ 0 (mod l)). Проверку существования решения Q E[l] уравнения ( w)Q = O осуществляем так же, как выше мы осуществляли проверку существования решения уравнения 2l (P) = ±kP. Точнее, пусть Q = (x, y). Тогда для выполнения равенства l (Q) = ±wQ по первой координате должно выполняться равенство
xp = x − w−1 (x, y) w+1 (x, y) .w (x, y)2
Отсюда при w четном
|
x |
p |
= x − |
fw−1 (x)fw+1 (x) |
, |
||||
|
fw (x)2 (x3 + ax + b) |
||||||||
|
а при w нечетном |
||||||||
|
x |
p |
= x − |
fw−1 (x)fw+1 (x) (x3 + ax + b) |
. |
||||
|
fw (x)2 |
Существование такой точки Q E[l] равносильно тому, что
НОД((xp − x)fw (x)2 (x3 + ax + b) + fw−1 (x)fw+1 (x), fl (x)) =/ 1
при w четном, а при w нечетном
НОД((xp − x)fw (x)2 + fw−1 (x)fw+1 (x) (x3 + ax + b), fl (x)) =/ 1.
Если теперь такая точка Q существует (т. е. соответствующий НОД не равен 1), то надо определить знак ±w по второй координате. Если
|
(xp, yp) = l (w) = wQ = |
x − |
− |
w (x, y)2 |
2 |
, |
2 |
||||
|
w |
1 |
(x, y) w+1 |
(x, y) |
|||||||
|
w+2 (x, y) w−1 (x, y) − w−2 (x, y) w+1 |
(x, y) |
, |
||||||||
|
4y w (x, y)3 |
то отсюда
fw+2 (x) · yf2 − − fw−2 (x) · yfw+1 (x)2 yp = w 1
4y4fw (x)3

2l (P) = kP,
120 Гл. 4. Применение кривых для проверки простоты и факторизации
при w четном и
fw+2 (x) · y2f2 − − fw−2 (x) · y2fw+1 (x)2 yp = w 1 .
4yfw (x)3
при w нечетном. Пользуясь соотношением y2 = x3 + ax + b, получаем, что при w четном будет выполняться соотношение l (Q) = wQ, если
|
НОД 4fw (x)3 (x3+ax+b)p |
2 |
−fw+2 (x)fw−1 |
|
+3 |
||
|
Соответственно, при w нечетном |
||
|
НОД 4fw (x)3 (x3+ax+b)p−2 |
1−fw+2 (x)fw−1 |
|
|
В случае, когда l (Q) = −wQ, вторая |
||
|
при w четном |
+fw+2 (x)fw−1 |
|
|
НОД 4fw (x)3 (x3+ax+b)p |
2 |
|
|
+3 |
(x)fw+1 (x)2, fl (x) =/ 1.
(x)fw+1 (x)2, fl (x) =/ 1.
координата меняет знак. Тогда
(x)2−fw−2 (x)fw+1 (x)2, fl (x) =/ 1,
|
и |
1+fw+2 (x)fw−1 (x)2−fw−2 (x)fw+1 (x)2, fl (x) =/ 1. |
|||||||||
|
НОД 4fw (x)3 (x3+ax+b)p−2 |
||||||||||
|
при w нечетном. |
||||||||||
|
Теперь предположим, что не существует точки Q E[l] O такой, |
||||||||||
|
что |
l (Q) = ±wQ. Кроме |
того, мы |
находимся в условиях 2 случая, |
|||||||
|
2 |
2 |
|||||||||
|
E[l] |
O |
2 |
||||||||
|
т. е. существует P |
такая, что |
l (P) |
= kP. Покажем, что на- |
|||||||
|
ше |
предположение невозможно. |
2У |
нас |
l (P) = (±w) P; кроме того, |
||||||
|
выше мы показали, |
что |
( l w) |
P = O. Из |
этих двух соотношений |
следует, что
w2P 2w l (P) + w2P = O,
т. е. 2w2P = ±2w l (P). Так как 2w =/ 0 (mod l), то отсюда l (P) = ±wP. Мы же предположили, что для всех точек Q E[l] O (включая и P), равенство l (Q) = ±wQ невозможно. Это означает, что наше предположение было неверным.
Итак, если существует точка P E[l] O такая, что то существует и точка Q E[l] O такая, что l (Q) = ±wQ.
В итоге 1 этап алгоритма реализуется следующим образом. Если не существует точки P E[l] O, для которой 2l (P) = ±kP, то мы

|
§ 4.3. Вычисление порядка группы точек эллиптической кривой |
121 |
переходим на 2 этап алгоритма. Если же такая точка P существует (т. е. соответствующий НОД в начале описания первого этапа не
|
равен 1), то при |
p |
= −1 мы |
полагаем t ≡ 0 (mod l) |
(поскольку |
||
|
l |
||||||
|
2 |
l |
|||||
|
2 случай |
невозможен). Если же |
p |
= +1, то мы находим w Z такое, |
|||
что w ≡ p (mod l) и 0 < w < l. Затем проверяем, будет ли +w или −w собственным значением для l на E[l] (проверку осуществляем так, как это описано выше). Если ±w не является собственным значением l на E[l], то t ≡ 0 (mod l) — искомое значение, как это было объяснено выше.
Если l (Q) = wQ для некоторой точки Q E[l] O, то 2l (Q) = pQ.
Тогда, пользуясь соотношением l (Q) = 2tpQ, найденным ранее, получим
w − 2tp ≡ 0 (mod l).
Так как p ≡ w2 ≡ 0 (mod l), то отсюда t ≡ 2w (mod l) есть искомое значение t по модулю l.
Если l (Q) = −wQ для некоторой точки Q E[l] O, то аналогично получим
|
w + |
2p |
≡ 0 (mod l), |
||||
|
t |
||||||
|
откуда t ≡ −2w (mod l). |
||||||
|
Таким образом, |
если на 1 этапе окажется, что существует |
P |
||||
|
2 |
||||||
|
E[l] O, для которой |
l |
(P) = ±kP, то мы определим искомое значение |
t (mod l), и тогда 2-й этап для данного l будет не нужен.
2 этап алгоритма для фиксированного l. Пусть на 1 этапе оказалось, что не существует точки P E[l] O, для которой
2l (P) = ±kP = ±pP.
Тогда искомое значение , ≡ t (mod l), для которого на E[l] выполняется равенство
2l + p = l,
будет не равно нулю, =/ 0, как это уже показано ранее.
Далее мы перебором , 1 l −2 1 , ищем то значение, для которого соотношение
( 2l + p) (P) = ± l (P)

122 Гл. 4. Применение кривых для проверки простоты и факторизации
выполняется на E[l] тождественно. Для P = (x, y) E[l] O левая часть запишется при k ≡ p (mod l), 1 k < l в виде
(xp2 , yp2)
|
x− |
k (x, y)2 |
, |
− |
4y k (x, y)3 |
, |
||||
|
k−1 |
(x, y) k+1 |
(x, y) |
k+2 (x, y) k |
1 (x, y)2 − k−2 |
(x, y) k+1 |
(x, y)2 |
причем сложение на кривой проводится по формуле секущей, поскольку сейчас 2l (P) =/ ±pP для всех P E[l] O. Правая часть, т. е.
± l (P) = ± l ( P), имеет вид
xp − −1 (x, y) +1 (x, y) p,(x, y)2
± +2 (x, y) −1 (x, y)2 − −2 (x, y) +1 (x, y)2 p . 4y (x, y)3
Поскольку ( 2l + p) (P) = ± l (P) тождественно на E[l], нам уже не надо вычислять наибольший общий делитель с fl (x), а надо проверять делимость на fl (x). Для написания соответствующих формул надо рассмотреть четыре случая в зависимости от четности k и .
Пусть, например, k четно и четно. Тогда
|
(xp2 , yp2) |
x |
f |
fk−1 (x)fk+1 (x) |
) |
, |
fk+2 (x)fk−1 (x)2 − fk−2 (x)fk+1 (x)2 |
= |
|||||||||||
|
(x)2 ( |
3 |
4( 3 |
+ b)f |
(x)3 |
· |
y |
2 |
|||||||||||
|
− |
k |
x |
+ ax + b |
x |
+ ax 2 |
k |
||||||||||||
|
p |
f −1 (x)f +1 (x) |
p |
f +2 (x)f −1 (x) − f −2 (x)f +1 |
(x) |
p |
|||||||||||||
|
= x |
− |
, |
± |
. |
||||||||||||||
|
f (x)2 (x3 + ax + b) |
4(x3 + ax + b)f (x)3 · y |
Пользуясь соотношением y2 = x3 + ax + b, нетрудно показать, что левая часть этого равенства имеет вид
|
H2 |
(x) , |
H4 |
(x) |
· y± |
, |
||||||||||
|
H1 |
(x) |
H3 |
(x) |
1 |
|||||||||||
|
а правая часть — |
H6 |
(x) , ±H8 |
(x) |
· y± |
, |
||||||||||
|
H5 |
(x) |
H7 |
(x) |
1 |
где H1 (x), . . . , H8 (x) Z/pZ [x]. Тогда для проверки тождества
( 2l + p) (P) = ± l (P)
по первой координате нам нужно проверить, что H1 (x)H6 (x)−H5 (x)H2 (x) делится на fl (x) в Z/pZ [x]. Если это не так, то мы переходим к следующему . Если это так, то мы выбираем знак ± числа , выполняя
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Эллиптическая криптография — раздел криптографии, который изучает асимметричные криптосистемы, основанные на эллиптических кривых над конечными полями. Основное преимущество эллиптической криптографии заключается в том, что на сегодняшний день неизвестны субэкспоненциальные алгоритмы дискретного логарифмирования.
Использование эллиптических кривых для создания криптосистем было независимо друг от друга предложено Нилом Коблицем и Виктором Миллером в 1985 году[1].
Введение[править | править код]
В 1985 году независимо Нилом Коблицем и Виктором Миллером было предложено использовать в криптографии алгебраические свойства эллиптических кривых. С этого момента началось бурное развитие нового направления криптографии, для которого используется термин «криптография на эллиптических кривых». Роль основной криптографической операции выполняет операция скалярного умножения точки на эллиптической кривой на данное целое число, определяемая через операции сложения и удвоения точек эллиптической кривой. Последние, в свою очередь, выполняются на основе операций сложения, умножения и инвертирования в конечном поле, над которыми рассматривается кривая. Особый интерес к криптографии эллиптических кривых обусловлен теми преимуществами, которые дает её применение в беспроводных коммуникациях — высокое быстродействие и небольшая длина ключа[2]. Асимметричная криптография основана на сложности решения некоторых математических задач. Ранние криптосистемы с открытым ключом, такие как алгоритм RSA, криптостойки благодаря тому, что сложно разложить составное число на простые множители. При использовании алгоритмов на эллиптических кривых полагается, что не существует субэкспоненциальных алгоритмов для решения задачи дискретного логарифмирования в группах их точек. При этом порядок группы точек эллиптической кривой определяет сложность задачи. Считается, что для достижения такого же уровня криптостойкости, как и в RSA, требуются группы меньших порядков, что уменьшает затраты на хранение и передачу информации. Например, на конференции RSA 2005 Агентство национальной безопасности объявило о создании «Suite B», в котором используются исключительно алгоритмы эллиптической криптографии, причём для защиты информации, классифицируемой до «Top Secret», используются всего лишь 384-битные ключи.
Эллиптические кривые над конечными полями[править | править код]
Эллиптической кривой называется множество точек 
Это уравнение может рассматриваться над произвольными полями и, в частности, над конечными полями, представляющими для криптографии особый интерес.
В криптографии эллиптические кривые рассматриваются над двумя типами конечных полей: простыми полями нечётной характеристики (


Эллиптические кривые над полями нечётной характеристики[править | править код]
Над полем 

где 

Группой точек эллиптической кривой E над полем 


Следует отметить, что в 


Пример[править | править код]
Рассмотрим эллиптическую кривую 







Теорема Хассе[править | править код]
Теорема Хассе об эллиптических кривых утверждает, что количество точек на эллиптической кривой близко к размеру конечного поля:
что влечёт:
Эллиптические кривые над полями характеристики 2[править | править код]
Над полем характеристики 2 рассматривают два вида эллиптических кривых:
- Суперсингулярная кривая
- Несуперсингулярная кривая
Особое удобство суперсингулярных эллиптических кривых в том, что для них легко вычислить порядок, в то время как вычисление порядка несуперсингулярных кривых вызывает трудности. Суперсингулярные кривые особенно удобны для создания самодельной ЕСС (Elliptic-curve cryptography) криптосистемы. Для их использования можно обойтись без трудоёмкой процедуры вычисления порядка.
Проективные координаты[править | править код]
Для вычисления суммы пары точек на эллиптической кривой требуется не только несколько операций сложения и умножения в 



Важно отметить, что могут существовать различные именования — например, IEEE P1363-2000 называет проективными координатами то, что обычно называют координатами Якоби.
Шифрование/дешифрование с использованием эллиптических кривых[править | править код]
Первой задачей в рассматриваемой системе является шифрование открытого текста сообщения 





Как и в случае системы обмена ключами, в системе шифрования, расшифрования в качестве параметров тоже рассматривается точка 









. При этом,
— пара точек.
Заметим, что сторона 





Пользователь 










Арифметические операции с точками на эллиптической кривой не эквивалентны этим арифметическим операциям с их координатами.
Точки эллиптической кривой над конечным полем представляют собой группу[5]. Умножение сводится к многократным удвоению и суммированию.
Например, G+G ≠ 2G (), 2G + 2^115G = 2^115G + 2G (суммирование коммутативно);
2G = 2*G; 4G = 2*2G; 8G = 2*4G; 16G = 2*8G, и т. д. (для двух одинаковых точек — только операция удвоения);
25*G; 25 = 11001 (in binary); 25 = 1*2^0 + 0*2^1 + 0*2^2 + 1*2^3 + 1*2^4 = 1 + 8 + 16; 25G = 16G + 8G + G = 1*(2^4)G + 1*(2^3)G + 1*G (операция суммирования).
24G/3 = 24G * (3^-1 mod P); where 3^(-1) mod P – modular multiplicative inverse,
5G – 3G = 5G + (-3G); где -3G = nG – 3G = O – 3G – additive inverse, point opposite.
Пример[править | править код]
Рассмотрим случай 

и
.
Предположим, что пользователь 






.
Таким образом, пользователь 

Реализация шифрования[править | править код]
Конкретные реализации алгоритмов шифрования на эллиптической кривой описаны ниже. Здесь рассмотрим общие принципы эллиптической криптографии.
Набор параметров[править | править код]
Для использования эллиптической криптографии все участники должны согласовать все параметры, определяющие эллиптическую кривую, т.е. набор параметров криптографического протокола. Эллиптическая кривая определяется константами 




Итак, для поля характеристики 2 набор параметров: 



Существует несколько рекомендованных наборов параметров:
- NIST[6]
- SECG[7]
Для создания собственного набора параметров необходимо сделать следующее.
- Выбрать набор параметров.
- Найти эллиптическую кривую, удовлетворяющую этому набору параметров.
Для нахождения кривой для заданного набора параметров используются два метода.
- Выбрать случайную кривую, затем воспользоваться алгоритмом подсчета точек[8][9].
- Выбрать точки, после чего построить кривую по этим точкам, используя технику умножения.
Существует несколько классов криптографически «слабых» кривых, которых следует избегать:
Быстрая редукция (NIST-кривые)[править | править код]
Деление по модулю p (которое необходимо для операций сложения и умножения) может выполняться быстрее, если в качестве p выбрать простое число, близкое к степени числа 2.
В частности, в роли p может выступать простое число Мерсенна. Например, хорошим выбором являются 

Национальный институт стандартов и технологий (NIST) рекомендует использовать подобные простые числа в качестве p.
Ещё одним преимуществом кривых, рекомендованных NIST, является выбор значения 
Эллиптические кривые, рекомендованные NIST[править | править код]
NIST рекомендует 15 эллиптических кривых, многие из которых были получены Jerry Solinas (NSA) на базе наработок Нила Коблица[10]. В частности, FIPS 186-3[11] рекомендует 10 конечных полей. Некоторые из них:
Причём для каждого конечного поля рекомендуется одна эллиптическая кривая. Эти конечные поля и эллиптические кривые выбраны, как часто ошибочно считается, из-за высокого уровня безопасности. По заявлениям NIST, их выбор был обоснован эффективностью программной реализации[13]. Имеются сомнения в безопасности по крайней мере нескольких из них[14][15][16].
Размер ключа[править | править код]
Самым быстрым алгоритмом, решающим задачу дискретного логарифмирования на эллиптических кривых, таким как алгоритм Шенкса и ρ-метод Полларда, необходимо 

Самые сложные схемы на эллиптических кривых, публично взломанные к настоящему времени, содержали 112-битный ключ для конечного простого поля и 109-битный ключ для конечного поля характеристики 2[источник не указан 3438 дней].
В июле 2009 года кластер из более чем двухсот Sony Playstation 3 за 3,5 месяца нашел 109-битный ключ. Ключ над полем характеристики 2 был найден в апреле 2004 года, с использованием 2600 компьютеров, в течение 17 месяцев[источник не указан 3438 дней].
Аналог обмена ключами по алгоритму Диффи-Хеллмана[править | править код]
Предположим, что абоненты А и Б хотят договориться о ключе, которым будут впоследствии пользоваться в некоторой классической криптосистеме. Прежде всего, они открыто выбирают какое-либо конечное поле 










Абоненты (пользователи) А и Б первым делом открыто выбирают точку 











Чтобы образовать ключ, 



Он вычисляет 



















Пример обмена ключами по схеме Диффи-Хеллмана[править | править код]
В качестве примера возьмем
,
,
что соответствует кривой
и
.
Можно подсчитать, что 

.
Личным ключом пользователя B является 
.
Общим секретным ключом является
.
Безопасность криптографии с использованием эллиптических кривых[править | править код]
Безопасность, обеспечиваемая криптографическим подходом на основе эллиптических кривых, зависит от того, насколько трудной для решения оказывается задача определения 



К тому же, при равных длинах ключей вычислительные усилия, требуемые при использовании RSA и криптографии на основе эллиптических кривых, не сильно различаются. Таким образом, в сравнении с RSA при равных уровнях защиты явное вычислительное преимущество принадлежит криптографии на основе эллиптических кривых с более короткой длиной ключа[18].
Таблица: Вычислительные усилия, необходимые для криптоанализа при использовании эллиптических кривых и RSA
- Логарифмирование на эллиптической кривой с помощью
-метода Полларда.
| Размер ключа | MIPS-годы |
|---|---|
| 150 | 3,8 * 10^10 |
| 205 | 7,1 * 10^18 |
| 234 | 1,6 * 10^28 |
- Разложение на множители в целых числах с помощью метода решета в поле чисел общего вида.
| Размер ключа | MIPS-годы |
|---|---|
| 512 | 3 * 10^4 |
| 768 | 3 * 10^7 |
| 1024 | 3 * 10^11 |
| 1280 | 3 * 10^14 |
| 1536 | 3 * 10^16 |
| 2048 | 3 * 10^20 |
Построение электронной цифровой подписи с использованием эллиптических кривых[править | править код]
Алгоритм ECDSA (Elliptic Curve Digital Signature Algorithm) принят в качестве стандартов ANSI X9F1 и IEEE P1363.
Создание ключей[править | править код]
- Выбирается эллиптическая кривая
. Число точек на ней должно делиться на большое простое число n.
- Выбирается базовая точка
порядка
.
- Выбирается случайное число
.
- Вычисляется
.
- Закрытым ключом является d, открытым ключом — кортеж <a, b, G, n, Q>.
Создание подписи[править | править код]
- Выбирается случайное число
.
- Вычисляется
и
.
- Проверяется условие
, так как иначе подпись не будет зависеть от закрытого ключа. Если r = 0, то выбирается другое случайное число k.
- Вычисляется
.
- Вычисляется
.
- Проверяется условие
, так как в этом случае необходимого для проверки подписи числа
не существует. Если s = 0, то выбирается другое случайное число k .
Подписью для сообщения М является пара чисел (r, s).
Проверка подписи[править | править код]
- Проверим, что числа r и s принадлежат диапазону чисел (1, n). В противном случае результат проверки отрицательный, и подпись отвергается.
- Вычислить
и H(M).
- Вычислить
и
.
- Вычислить
.
- Подпись верна в том и только том случае, когда v = r[19].
Приложения[править | править код]
Большинство криптосистем современной криптографии естественным образом можно «переложить» на эллиптические кривые. Основная идея заключается в том, что известный алгоритм, используемый для конкретных конечных групп, переписывается для использования групп рациональных точек эллиптических кривых:
- алгоритм ECDSA, основывающийся на ЭЦП,
- алгоритм ECDH, основывающийся на алгоритме Диффи — Хеллмана,
- алгоритм ECMQV, основывающийся на MQV, протоколе распределения ключей Менезеса-Кью-Венстоуна,
- ГОСТ Р 34.10-2012,
- факторизация Ленстры с помощью эллиптических кривых,
- dual EC DRBG.
Необходимо отметить, что безопасность таких систем цифровой подписи опирается не только на криптостойкость алгоритмов шифрования, но и на криптостойкость используемых криптографических хеш-функций и генераторов случайных чисел.
По обзору 2013 года, чаще всего используются кривые nistp256, nistp384, nistp521, secp256k1, secp384r1, secp521r1[20].
Примечания[править | править код]
- ↑ Jeffrey Hoffstein, Jill Pipher, Joseph H. Silverman. An introduction to mathematical cryptography. — Springer, 2008. — 524 с. — (Undergraduate Texts in Mathematics). — ISBN 9780387779942.
- ↑ Болотов А. А., Гашков С. Б., Фролов А. Б., Часовских А. А.. Элементарное введение в эллиптическую криптографию. 11 с.
- ↑ Кодирование чисел в точки на эллиптической кривой в конечном поле и шифрование-дешифрование их.. Дата обращения: 29 октября 2019.
- ↑ Жданов О.Н., Золотарев В.В. Методы и средства криптографической защиты информации. 167 с.
- ↑ Эллиптическая криптография: теория. Дата обращения: 13 октября 2016.
- ↑ Recommended Elliptic Curves for Government Use
- ↑ SEC 2: Recommended Elliptic Curve Domain Parameters
- ↑ Schoof’s algorithm (недоступная ссылка)
- ↑ Schoof–Elkies–Atkin algorithm
- ↑ Neal Koblitz. Random Curves: Journeys of a Mathematician. — Springer, 2009. — С. 312-313. — 402 с. — ISBN 9783540740780.
- ↑ FIPS 186-3 Архивировано 7 октября 2013 года. // NIST, 2009; устарел в 2013 году с выходом FIPS 186-4
- ↑ Может показаться, что в этой последовательности допущена ошибка. Однако, последняя величина именно 521, а не 512 битов.
- ↑ Daniel J. Bernstein, Tanja Lange, Security dangers of the NIST curves // 2013.09.16: “Why did NIST choose these curves? * Most people we have asked: security * Actual NIST design document: eficiency” ([1])
- ↑ Daniel J. Bernstein and Tanja Lange. SafeCurves: choosing safe curves for elliptic-curve cryptography. (англ.). safecurves.cr.yp.to (18 ноября 2013). Дата обращения: 20 декабря 2013.
- ↑ Евгений Золотов. Сноуден и эллиптическое крипто: Bitcoin и TOR вне подозрений, но что с другими проектами?, Компьютерра (16 сентября 2013). Дата обращения: 20 декабря 2013.
- ↑ Dr Michael Scott, Backdoors in NIST elliptic curves Архивная копия от 20 декабря 2013 на Wayback Machine, Oct 24, 2013: “The curves themselves were suggested by Jerry Solinas who worked at the NSA.”
- ↑ Чалкин Т.А. Жданов О.Н. Применение эллиптических кривых в криптографии.
- ↑ Жданов О.Н., Золотарев В.В. Методы и средства криптографической защиты информации. 186 с.
- ↑ Ишмухаметов Ш.Т. Методы факторизации натуральных чисел.99 с.
- ↑ Bos et al, Elliptic Curve Cryptography in Practice // MSR-TR-2013-119, November 2013
Ссылки[править | править код]
- Болотов А.А., Гашков С.Б., Фролов А.Б., Часовских А.А. Алгоритмические основы эллиптической криптографии. — Москва: МЭИ, 2000. — 100 с.
- Болотов А.А., Гашков С.Б., Фролов А.Б., Часовских А.А. Элементарное введение в эллиптическую криптографию. Алгебраические и алгоритмические основы.. — Москва: КомКнига, 2006. — 328 с.
- Жданов О.Н., Золотарев В.В. Методы и средства криптографической защиты информации. — Красноярск: «Город», 2007. — 217 с.
- Ишмухаметов Ш.Т. Методы факторизации натуральных чисел. — Казань: КФУ, 2011. — 190 с.
- Koblitz N.A. Course in number theory and cryptography.. — USA: Springer-Verlag, 1994. — 235 с.
Предисловие
Полное английское название ECC – “Ellipse Curve Cryptography”.
В отличие от традиционных методов шифрования, основанных на сложности факторизации больших простых чисел, ECC генерирует ключи с помощью уравнения эллиптической кривой.
164-битный ключ ECC создает уровень безопасности, который эквивалентен уровню безопасности, обеспечиваемому 1024-битным ключом RSA, и имеет меньший объем вычислений, более высокую скорость обработки и меньшее пространство для хранения и пропускную способность передачи. В настоящее время наша странаID-карта жителя второго поколенияИспользование 256-битной криптографии с эллиптической кривой, виртуальная валютаБиткойнECC также выбран в качестве алгоритма шифрования.
Говоря с проективной плоскости
В «Элементах геометрии» древнегреческого математика Евклида было выдвинуто пять постулатов.
-
1. Прямая линия может быть проведена из любой точки в любую точку.
-
2. Ограниченная прямая линия может продолжаться.
-
3. Круг можно нарисовать с любой точкой в качестве центра и на любом расстоянии.
-
4. Все прямые углы равны.
-
5. Прямая a и две другие прямые bc пересекаются в одной плоскости. Если сумма двух внутренних углов на одной стороне a меньше двух прямых углов, две прямые bc пересекаются на этой стороне после продолжения. бесконечно.
«Геометрия» имеет только 29-е предложение
Если прямая линия пересекается с двумя параллельными прямыми линиями, образующиеся внутренние углы смещения равны, углы совмещения равны, а сумма одинаковых боковых внутренних углов равна двум прямым углам.
Пятый постулат используется только в средней школе, то есть первые 28 предложений могут быть введены, не полагаясь на пятый постулат в Geometry Original. Поэтому некоторые математики предположили, что пятый постулат нельзя рассматривать как постулат, а как теорему? Можем ли мы положиться на первые четыре постулата, чтобы доказать пятый постулат? Это самое известное в истории геометрического развития, и дискуссия о «теории параллельных линий» обсуждается более двух тысяч лет.
В 1820-х годах Лобачевский из Казанского университета в России заменил пятый постулат на «можно найти по крайней мере две разные прямые, и обе они проходят через точку P и не пересекают линию R», а затем сравнил его с лицевой стороной Евклида. Геометрия. Четыре постулата были объединены в аксиоматическую систему. После тщательных и глубоких рассуждений он придумал геометрические системы, которые были интуитивно невероятными, но логически не противоречивыми.
Такая геометрия называется геометрией Лобачевского, или для краткости геометрией Роша. Из геометрии Роша мы можем сделать вывод, что некоторые аксиомы, которые не являются логически противоречивыми, могут обеспечивать своего рода геометрию. Типы существующей неевклидовой геометрии можно резюмировать следующим образом:
1. Придерживайтесь пятого постулата и извлекайте евклидову геометрию.
2. «Можно ввести по крайней мере две параллельные прямые» – это постулат, геометрия Роговского (гиперболическая геометрия).
3. «Нельзя цитировать параллельную линию» – постулат, риманова геометрия (эллиптическая геометрия).
Слева: гиперболическая геометрия, а именно геометрия Роша; посередине: евклидова геометрия; справа: эллиптическая геометрия, а именно риманова геометрия.
Понимая неевклидову геометрию, вы можете понять пересечение параллельных линий.
Определите параллельные прямые для пересечения в бесконечной точке P∞, чтобы все прямые на плоскости были объединены и имели единственную точку пересечения.
природа:
-
1. Прямая линия имеет только одну точку бесконечности; пара параллельных прямых имеет общую точку бесконечности.
-
2. Любые две непараллельные прямые имеют разные точки бесконечности (иначе будет две точки пересечения).
-
3. Все бесконечные точки на плоскости образуют бесконечную прямую.
Проективная плоскость:Все точки на бесконечности и все обычные точки на плоскости составляют проективную плоскость.
Определение точек проективной плоскости
Для точки (x, y) на обычной плоскости, пусть x = X / Z, y = Y / Z и Z ≠ 0, тогда проекция будет точкой на проекционной плоскости. самолет (X: Y: Z)
Найдите координаты точки (1,2) в новой системе координат
∵X/Z=1 ,Y/Z=2(Z≠0)
∴X = Z, Y = 2Z ∴ Координаты (Z: 2Z: Z), Z ≠ 0
То есть (1: 2: 1) (2: 4: 2) (1.2: 2.4: 1.2) и так далее, например (Z: 2Z: Z), координаты Z ≠ 0 равны (1,2 ) в новой системе координат Координаты ниже
(2) Найдите точку бесконечности, в которой параллельные прямые L1: X + 2Y + 3Z = 0 и L2: X + 2Y + Z = 0 пересекаются
∵ L1∥L2 Итак, Z = 0, X + 2Y = 0
∴ Координаты (-2Y: Y: 0), Y ≠ 0
То есть (-2: 1: 0) (-4: 2: 0) (-2,4: 1,2: 0) и т.п. (-2Y: Y: 0), Y ≠ 0
Эллиптическая кривая
Эллиптическая кривая – это совокупность всех точек, удовлетворяющих уравнению Вейерштрасса на проективной плоскости.
[ {Y^2}Z + {a_1}XYZ + {a_3}Y{Z^2} = {X^3} + {a_2}{X^2}Z + {a_4}X{Z^2} + {a_6}{Z^3} ]
-
1 Уравнение эллиптической кривой является однородным уравнением
-
2 Каждая точка на кривой должна быть неособой (гладкой), а частные производные FX (X, Y, Z), FY (X, Y, Z), FZ (X, Y, Z) отличны от 0
-
3 Форма круговой кривой не эллиптическая. Просто потому, что уравнение описания эллиптической кривой похоже на уравнение для вычисления длины окружности эллипса.
Пример эллиптической кривой
Пример неэллиптической кривой
Эти два уравнения не являются эллиптическими кривыми, потому что они не имеют касательной в точке (0: 0: 1) (то есть в начале координат), и каждая точка, которая не удовлетворяет эллиптической кривой, должна быть невырожденной (гладкой),
Общее уравнение эллиптической кривой
Общее уравнение эллиптической кривой:
[ {y^2} + {a_1}xy + {a_3}y = {x^3} + {a_2}{x^2} + {a_4}x + {a_6} ]
Точка на бесконечность (0, Y, 0)
Нормальная точка (x, y), наклон k:
[ begin{array}{l} {F_x}left( {x,y} right) = {a_1}y – 3{x^2} – 2{a_2}x – {a_4} \ {F_y}left( {x,y} right) = 2y + {a_1}x + {a_3} \ end{array} ]
[ begin{array}{l} k = – frac{{{F_x}left( {x,y} right)}}{{{F_y}left( {x,y} right)}} = frac{{3{x^2} + 2{a_2}x + {a_4} – {a_1}y}}{{2y + {a_1}x + {a_3}}} end{array} ]
Абелева группа эллиптических кривых
Мы видели изображение эллиптической кривой, но, похоже, между точками нет связи. Можем ли мы построить алгоритм, аналогичный сложению по оси действительных чисел? Это необходимо для определения аддитивной группы эллиптической кривой, и здесь необходимо использовать абелеву группу в современной алгебре.
В математике группа – это алгебраическая структура, состоящая из набора и бинарной операции. Учитывая, что операция набора суммы (G, *) является группой, должны выполняться следующие требования.
-
Близость: ∀a, b∈G, a * b ∈ G
-
Ассоциативность: ∀a, b, c∈G, существует (ab)c = a* (b*c)
-
Единичный элемент: ョ e∈G, ∀a ∈G, существует ea = ae = a
-
Обратный элемент: ∀a ∈G, ョ b∈G такой, что ab = ba = e
В дополнение к указанным выше свойствам абелева группа также удовлетворяет аксиоме коммутативности a * b = b * a
Точно так же абелевы группы могут быть определены в эллиптических кривых.
Произвольно возьмите две точки P и Q на эллиптической кривой (если две точки P и Q совпадают, сделайте касательную к точке P), проведите прямую линию, чтобы пересечь другую точку R ‘эллиптической кривой, и проведите параллель линию оси Y, чтобы пересечь R ‘R, определить P + Q = R. Таким образом, сумма сложения также находится на эллиптической кривой, и она также имеет коммутативный и ассоциативный законы сложения.
То же добавление точки
Если складываются k идентичных точек P, это записывается как kP.
P+P+P=2P+P=3P
Эллиптическая кривая конечного поля
Эллиптическая кривая является непрерывной и не подходит для шифрования; поэтому мы должны превратить эллиптическую кривую в дискретные точки, и мы должны определить эллиптическую кривую в конечном поле.
Даем конечное поле Fp
-
В Fp 0,1,2,…, p-2, p-1 содержится p (p – простое число) элементов.
-
Добавление Fp есть a + b≡c (mod p)
-
Умножение Fp есть a × b≡c (mod p)
-
Деление Fp равно a ÷ b≡c (mod p), то есть a × b ^ (- 1) ≡c (mod p), b-1 также является целым числом от 0 до p-1, но удовлетворяет b × b -1≡1 (mod p)
-
Единичный элемент Fp равен 1, а нулевой элемент равен 0.
-
Операция в области Fp удовлетворяет закону коммутативности, закону ассоциации и закону распределения
Эллиптическая кривая Ep (a, b), p – простое число, x, y∈ [0, p-1]
[{y^2} = {x^3} + ax + bleft( {bmod p} right)]
Выберите два неотрицательных целых числа a и b, которые меньше p и удовлетворяют следующим ограничениям
[4{a^3} + 27{b^2} ne 0left( {bmod p} right)]
Эллиптическая кривая на Fp также имеет дополнение
-
1. Точка бесконечности O∞ является нулевым элементом, O∞ + O∞ = O∞, O∞ + P = P
-
2. Отрицательный элемент P (x, y) равен (x, -y mod p) = (x, p-y), существует P + (- P) = O∞
-
3. P (x1, y1), Q (x2, y2) и R (x3, y3) имеют следующие отношения:
x3≡k2-x1-x2(mod p)
y3≡k(x1-x3)-y1(mod p)
Если P = Q, то k = (3×2 + a) / 2y1mod p
Если P ≠ Q, то k = (y2-y1) / (x2-x1) mod p
Пример задачи эллиптической кривой. Для двух точек P (3,10), Q (9,7) на E23 (1,1) найти (1) -P, (2) P + Q, (3) 2P
[begin{array}{l} left( 1 right) – P = left( {3, – 10bmod 23} right) = left( {3,13} right) \ \ left( 2 right)k = frac{{7 – 10}}{{9 – 3}} = – {2^{ – 1}}bmod 23 \ 2 cdot {2^{ – 1}} = 1bmod 23 Rightarrow {2^{ – 1}} = 12 \ k = – 12bmod 23 = 11 \ P + Q = left( {{{11}^2} – 3 – 9bmod 23,11 times left( {3 – left( { – 6} right)} right)bmod 23} right) = left( {17,20} right) \ \ left( 3 right)k = frac{{3 times {3^2} + 1}}{{2 times 10}}bmod 23 = 7 cdot {5^{ – 1}}bmod 23 \ 5 cdot {5^{ – 1}} = 1bmod 23 Rightarrow {5^{ – 1}} = 14 \ k = 7 cdot 14bmod 23 = 6 \ 2P = left( {{6^2} – 3 – 3bmod 23,6 times left( {3 – 7} right)bmod 23} right) = left( {7,12} right) \ end{array} ]
добавка:
-2 ^ (- 1) mod 23 для двухчастного расчета
(1) Сначала вычислите число A, соответствующее 2 ^ (- 1), здесь2 ^ (- 1) не 2 в степени -1, а обратное 2
(2) Рассчитайте еще раз – мод 23
(1) Первый шаг расчета
Согласно правилу деления конечных полей 2 * 2 ^ (- 1) = 1 mod 23
т.е. 2A = 1 mod 23 ==> 2A = 23 + 1 ==> A = 12
(2) Второй шаг расчета
-A mod 23 ==> -12 mod 23, т.е. 23-12 = 11
Так что имейте
-2^(-1) mod 23 = 11
Порядок точки эллиптической кривой в конечном поле
Если на эллиптической кривой есть точка P, существует наименьшее натуральное число n такое, что это число умножается на nP = O∞, тогда n называется порядком P
Если n не существует, то P – бесконечный порядок
Вычислить 27P = -P = (3,13)
Таким образом, порядок 28P = O ∞ P равен 28
Эти точки образуют циклическую абелеву группу с образующей P и порядком 29. Очевидно, что распределение и порядок точек беспорядочные.
Шифрование эллиптической кривой
Рассмотрим K = kG, где K и G – точки на эллиптической кривой Ep (a, b), n – порядок G (nG = O∞), а k – целое число меньше n. Для заданных k и G легко вычислить K по правилу сложения, но, наоборот, для заданных K и G найти k очень сложно. Поскольку при фактическом использовании ECC в принципе требуется, чтобы p было достаточно большим, и n также довольно большим, невозможно вычислить n точек решения одну за другой и перечислить их в приведенной выше таблице. Это математическая основа алгоритма шифрования эллиптической кривой.
Точка G называется базовой точкой.
k (k <n) – закрытый ключ (частный ключ)
K – открытый ключ (открытый ключ)
Алгоритм безопасной связи ECC
-
1. Алиса выбирает эллиптическую кривую E и берет точку на эллиптической кривой в качестве базовой точки G. Предположим, что выбрана E29 (4,20), базовая точка G (13,23), порядок базовой точки G - это n = 37 -
2. Алиса выбирает закрытый ключ k (k <n) и генерирует открытый ключ K = kG, например 25, K = kG = 25G = (14,6) -
3. Алиса передает E и указывает K и G Бобу. -
4. После того, как Боб получает информацию, он кодирует открытый текст для передачи в точку M (метод кодирования опускается) и генерирует случайное целое число r (r <n, n - порядок G), предполагая, что r = 6, чтобы быть зашифрованным. Информация - 3, потому что M также находится в E29 (4,20), поэтому M = (3,28) -
5. Боб вычисляет точку C1 = M + rK и C2 = rG C1 = M + 6K = M + 6 * 25 * G = M + 2G = (3,28) + (27,27) = (6,12). C2 = 6G = (5,7) -
6. Боб передает С1 и С2 Алисе -
7. После получения информации Алиса вычисляет C1-kC2, результатом должна быть точка M C1-kC2 = (6,12) -25C2 = (6,12) -25 * 6G = (6,12) -2G = (6,12) - (27,27) = (6,12) + (27,2) = (3,28)
Математику можно расшифровать, потому что: C1-kC2 = M + rK-krG = M + rkG-krG-M
Технические требования ECC
Обычно эллиптическая кривая на Fp описывается как T = (p, a, b, G, n, h) p, a, b определяют эллиптическую кривую (p – простое число, операция (mod p)) G – основание point, n – порядок точки G, h – целая часть частного числа m точек, деленного на n на эллиптической кривой.
Требования к выбору параметров:
- Чем больше p, тем лучше безопасность, но это замедлит скорость вычислений.
- Около 200 бит может соответствовать общим требованиям безопасности
- n должно быть простым числом
- h≤4;p≠n×h ;pt≠1(mod n) (1≤t<20)
- 4a3+27b2≠0 (mod p)
Применение ECC
В secp256k1, выбранном системой Биткойн, параметры:
p = 0xFFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F= 2^256 − 2^32 − 2^9 − 2^8 − 2^7 − 2^6 − 2^4 − 1
a = 0, b = 7
G=(0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798, 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8)
n = 0xFFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141
h = 01
ECC vs. RSA-преимущества и недостатки
преимущество
-
Более высокие показатели безопасности
-
160-битный ECC имеет такую же степень защиты, как 1024-битный RSA и DSA.
-
Более быстрая обработка
-
Что касается скорости обработки закрытых ключей, ECC намного быстрее, чем RSA и DSA.
-
Более низкие требования к пропускной способности
-
Меньше места для хранения
-
Размер ключа и системные параметры ECC намного меньше, чем у RSA и DSA.
Недостаток
-
Сложно спроектировать, сложно реализовать
-
Если серийный номер слишком короткий, то безопасность не так совершенна, как предполагалось.




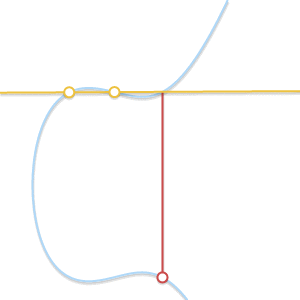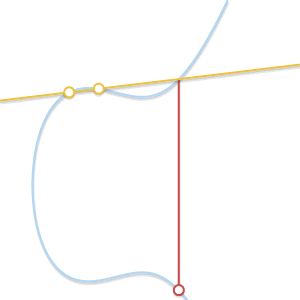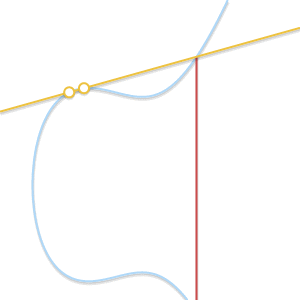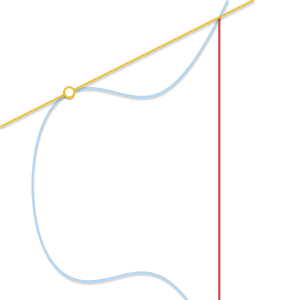

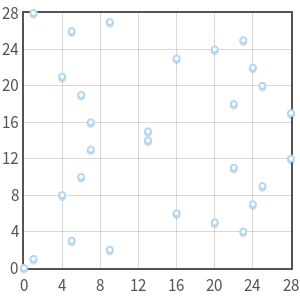

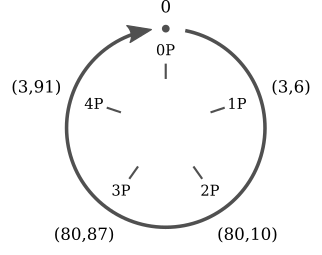
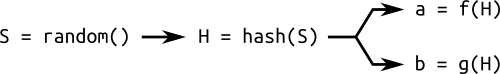

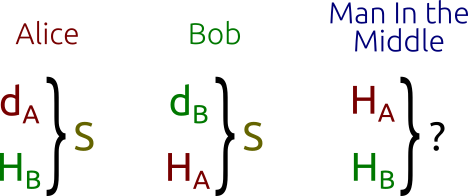

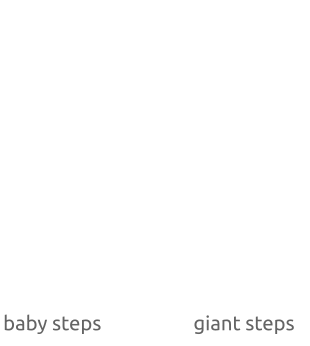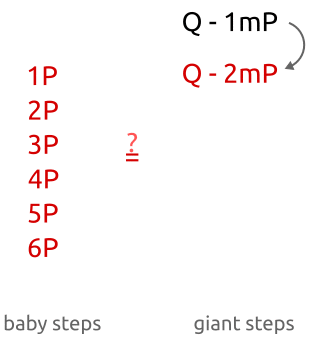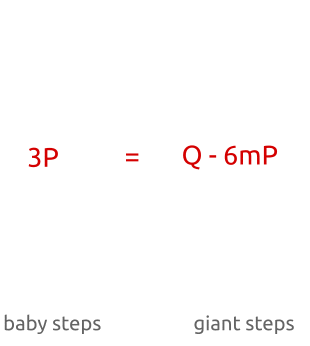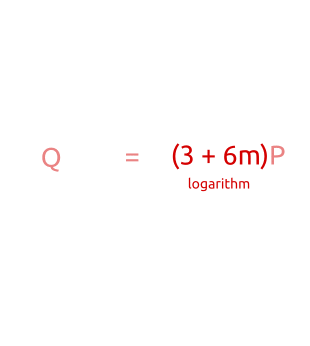


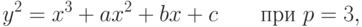
 (табл. 4.1).
(табл. 4.1).
 (табл. 4.2)
(табл. 4.2)
 .
. – квадратный корень из
– квадратный корень из