ПРОСТЫЕ ГРАФЫ (ГРАФЫ)

2.1. Способы задания
графа
Основные
способы задания графов:
-
графический;
-
с помощью множеств;
-
последовательность
степеней графа; -
матричный;
-
битовые цепочки
и таблицы инцидентности.
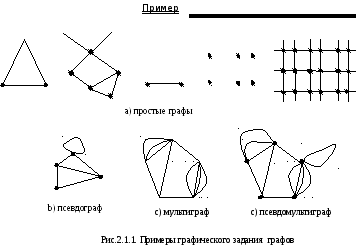
2.1.1. Графический способ
задания графа
Определения

На
плоскости (в пространстве или на объемной
фигуре) изображается некоторое количество
точек (кружков) и какое-то число отрезков,
кривых или ломаных линий соединяющих
все, или некоторые из точек.
Кружки
называются вершинами, а линии–
ребрами, а полученная геометрическая
фигура –ненаправленным графом(графом).
Замечание

Ребра показывают лишь связь
между двумя вершинами, или ее отсутствие,
однако направление этой связи (например,
передача информации, сигналов,
товаров, топлива, грузов и т.д.) в данной
модели несущественно. Вот почему
такие графы называются ненаправленными.

Ребро,
соединяющее вершину саму с собой,
называется петлей.
Несколько
ребер, соединяющих две вершины, носят
название кратных.
В
зависимости от наличия или отсутствия
петель и/или кратных ребер различают
следующие типы
ненаправленных графов:
-
Тип
Наличие
кратных реберНаличие
петельПростой
графМультиграф
Псевдограф
Псевдомультиграф
Нет
Да
Нет
Да
Нет
Нет
ДаДа
Замечание

Далее
будут рассматривать простые графы,
которые будут кратко называться графами.
2 Определения.1.2 Определение графа с помощью множеств

Множество называется
поименованным,
если каждому его элементу присвоено
имя (метка, целое число).
В дальнейшем графом
будет
называтьсяпара
разделенных поименованных множествG= (V,E) (V∩E=) и
функция преобразования:(V)Е.
Элементы множества V=V(G)
являютсявершинами графаG,
а элементы множестваE=E(G)
– егоребрами. Функция преобразования
устанавливает соответствие между
именами ребер и неупорядоченными парами
имен вершин. Поэтому ребра можно задавать
как собственными именами, так и
неупорядоченными парами имен вершин.
В дальнейшем для краткости записи
функция преобразование будет опускаться.

Определения

Граф G=(V,E)
называется пустым,
если |V(G)|≠0
, |E(G)|=0.
Нулевой граф –
это граф G=(V,E)
с |V(G)|=0
и |E(G)|=0.
Две вершины Vi
и Vk
называются смежными,
если существует ребро, соединяющее эти
вершины.
Ребра являются смежными,
если они опираются на общую вершину.
Вершина графа vи некоторое
его ребро е называютсяинцидентными,
еслиe={v,w}
илиe={w,v},
гдеw– некоторая вершина
графа.
Вершина будет изолированной, если
она не инцидентна ни с одним ребром.

Меры

-
Порядок графа|G| – число вершин графа,
|G|=|V|. -
Размер графа
||G|| – число ребер графа,
||G||=|E|.
2.1.3.
Степени вершин графа
Определения

Степенью вершины графа
Vi![]() V(G)
V(G)
(записывается как deg(Vi))
является число рёбер, смежных с вершиной
Vi.
Изолированная вершина имеет deg(Vi)=0.
Очевидно, поскольку степень
вершин задаёт число смежных вершин,
deg(Vi)>0
для всех неизолированных вершин Vi![]() V(G).
V(G).
Если граф G
имеет n
вершин, то каждая вершина в графе
максимально может иметь рёбра с другими
n-1
вершинами (кроме ребра с самой собой,
т.е. петли). Поэтому deg(Vi)![]() n-l.
n-l.
Отсюда следует оценка для любого
простого графа:
0
deg (Vi)
n-1

Меры

-
Степень
вершины deg(Vi). -
Минимальная
степень графа δ(G)=
min{deg(Vi)
| Vi V}.
V}. -
Максимальная
степень графа Δ(G)=
max{deg(Vi)
| Vi V}.
V}. -
Средняя
степень графа
d(G)
=
![]()

Лемма о рукопожатиях

Пусть
G=(V,E)
будет графом. Тогда
 2E
2E
Данное утверждение легко
получить, если отметить, что в сумму
степеней каждое ребро вносит 2
подсуммы: одну для вершины Vi,
а вторую – для вершины Vj
Важно подчеркнуть, что лемма
говорит о том, что степень
всех вершин графа всегда четна.
2.1.4.
Последовательность степеней вершин
графа
Определения

Последовательностью
степеней вершин графа
G
является последовательность его
степеней, записанная в порядке возрастания
степеней с повторами.
С помощью последовательности
степеней графа можно задавать сам граф,
но не всегда однозначно.

Определения

Последовательность
d1,d2,…,dn
неотрицательных целых чисел называется
графической,
если она представляет последовательность
степеней графа.
Из
леммы рукопожатий следует, что если
последовательность неотрицательных
чисел является графической, то сумма
элементов в этой последовательности
четна. Для простых графов наибольший
элемент графической последовательности
неотрицательных чисел равен n-1.
Теорема
Havel
–
Hakimi

П
Замечания
оследовательностьd1≥
d2≥
…≥dn≥0
неотрицательных целых чисел является
графической тогда и только тогда, когда
последовательность d2
–1, d3
– 1, …, dk+1,
dk+2,
dk+3,…,dn
(k=d1)
является графической.

1.
Важно отметить, что описатели di
являются только описателями
последовательности. Запись
последовательности в таком виде не
означает, что вершины есть {1,2,..,n} и что
d1
является степенью вершины 1 и т.д.
2.
Теорема говорит, что если заданная
последовательности является графической,
то она может быть реализована в виде
графа, в котором вершина степени d1
смежна с вершинами степени d2,
d2,…,
dk+1
(k= d1).
Это утверждение задает правило построения
графа по последовательности:
если
был построен граф с n-1
вершинами и последовательностью степеней
d2
–1, d3
– 1, …, dk+1,
dk+2,
dk+3,…,dn
(k=d1),
то добавляется новая вершина и соединяется
с вершинами степени d2
–1, d3
– 1, …, dk+1-1,
(k=d1).
Соседние файлы в папке Графы
- #
- #
- #
- #
- #
- #
This article is about sets of vertices connected by edges. For graphs of mathematical functions, see Graph of a function. For other uses, see Graph (disambiguation).

A graph with six vertices and seven edges
In discrete mathematics, and more specifically in graph theory, a graph is a structure amounting to a set of objects in which some pairs of the objects are in some sense “related”. The objects correspond to mathematical abstractions called vertices (also called nodes or points) and each of the related pairs of vertices is called an edge (also called link or line).[1] Typically, a graph is depicted in diagrammatic form as a set of dots or circles for the vertices, joined by lines or curves for the edges. Graphs are one of the objects of study in discrete mathematics.
The edges may be directed or undirected. For example, if the vertices represent people at a party, and there is an edge between two people if they shake hands, then this graph is undirected because any person A can shake hands with a person B only if B also shakes hands with A. In contrast, if an edge from a person A to a person B means that A owes money to B, then this graph is directed, because owing money is not necessarily reciprocated.
Graphs are the basic subject studied by graph theory. The word “graph” was first used in this sense by J. J. Sylvester in 1878 due to a direct relation between mathematics and chemical structure (what he called a chemico-graphical image).[2][3]
Definitions[edit]
Definitions in graph theory vary. The following are some of the more basic ways of defining graphs and related mathematical structures.
Graph[edit]

A graph with three vertices and three edges
A graph (sometimes called an undirected graph to distinguish it from a directed graph, or a simple graph to distinguish it from a multigraph)[4][5] is a pair G = (V, E), where V is a set whose elements are called vertices (singular: vertex), and E is a set of paired vertices, whose elements are called edges (sometimes links or lines).
The vertices x and y of an edge {x, y} are called the endpoints of the edge. The edge is said to join x and y and to be incident on x and y. A vertex may belong to no edge, in which case it is not joined to any other vertex.
A multigraph is a generalization that allows multiple edges to have the same pair of endpoints. In some texts, multigraphs are simply called graphs.[6][7]
Sometimes, graphs are allowed to contain loops, which are edges that join a vertex to itself. To allow loops, the pairs of vertices in E must be allowed to have the same node twice. Such generalized graphs are called graphs with loops or simply graphs when it is clear from the context that loops are allowed.
Generally, the set of vertices V is supposed to be finite; this implies that the set of edges is also finite. Infinite graphs are sometimes considered, but are more often viewed as a special kind of binary relation, as most results on finite graphs do not extend to the infinite case, or need a rather different proof.
An empty graph is a graph that has an empty set of vertices (and thus an empty set of edges). The order of a graph is its number of vertices |V|. The size of a graph is its number of edges |E|. However, in some contexts, such as for expressing the computational complexity of algorithms, the size is |V| + |E| (otherwise, a non-empty graph could have size 0). The degree or valency of a vertex is the number of edges that are incident to it; for graphs [1]with loops, a loop is counted twice.
In a graph of order n, the maximum degree of each vertex is n − 1 (or n + 1 if loops are allowed, because a loop contributes 2 to the degree), and the maximum number of edges is n(n − 1)/2 (or n(n + 1)/2 if loops are allowed).
The edges of a graph define a symmetric relation on the vertices, called the adjacency relation. Specifically, two vertices x and y are adjacent if {x, y} is an edge. A graph may be fully specified by its adjacency matrix A, which is an n × n square matrix, with Aij specifying the number of connections from vertex i to vertex j. For a simple graph, Aij is either 0, indicating disconnection, or 1, indicating connection; moreover Aii = 0 because an edge in a simple graph cannot start and end at the same vertex. Graphs with self-loops will be characterized by some or all Aii being equal to a positive integer, and multigraphs (with multiple edges between vertices) will be characterized by some or all Aij being equal to a positive integer. Undirected graphs will have a symmetric adjacency matrix (meaning Aij = Aji).
Directed graph[edit]

A directed graph with three vertices and four directed edges (the double arrow represents an edge in each direction)
A directed graph or digraph is a graph in which edges have orientations.
In one restricted but very common sense of the term,[8] a directed graph is a pair G = (V, E) comprising:
- V, a set of vertices (also called nodes or points);
- E, a set of edges (also called directed edges, directed links, directed lines, arrows, or arcs), which are ordered pairs of distinct vertices:
.
To avoid ambiguity, this type of object may be called precisely a directed simple graph.
In the edge (x, y) directed from x to y, the vertices x and y are called the endpoints of the edge, x the tail of the edge and y the head of the edge. The edge is said to join x and y and to be incident on x and on y. A vertex may exist in a graph and not belong to an edge. The edge (y, x) is called the inverted edge of (x, y). Multiple edges, not allowed under the definition above, are two or more edges with both the same tail and the same head.
In one more general sense of the term allowing multiple edges,[8] a directed graph is an ordered triple G = (V, E, ϕ) comprising:
- V, a set of vertices (also called nodes or points);
- E, a set of edges (also called directed edges, directed links, directed lines, arrows or arcs);
- ϕ, an incidence function mapping every edge to an ordered pair of vertices (that is, an edge is associated with two distinct vertices):
.
To avoid ambiguity, this type of object may be called precisely a directed multigraph.
A loop is an edge that joins a vertex to itself. Directed graphs as defined in the two definitions above cannot have loops, because a loop joining a vertex 






The edges of a directed simple graph permitting loops G is a homogeneous relation ~ on the vertices of G that is called the adjacency relation of G. Specifically, for each edge (x, y), its endpoints x and y are said to be adjacent to one another, which is denoted x ~ y.
Mixed graph[edit]
A mixed graph is a graph in which some edges may be directed and some may be undirected. It is an ordered triple G = (V, E, A) for a mixed simple graph and G = (V, E, A, ϕE, ϕA) for a mixed multigraph with V, E (the undirected edges), A (the directed edges), ϕE and ϕA defined as above. Directed and undirected graphs are special cases.
Weighted graph[edit]
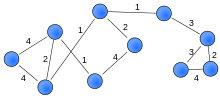
A weighted graph with ten vertices and twelve edges
A weighted graph or a network[9][10] is a graph in which a number (the weight) is assigned to each edge.[11] Such weights might represent for example costs, lengths or capacities, depending on the problem at hand. Such graphs arise in many contexts, for example in shortest path problems such as the traveling salesman problem.
Types of graphs[edit]
Oriented graph[edit]
One definition of an oriented graph is that it is a directed graph in which at most one of (x, y) and (y, x) may be edges of the graph. That is, it is a directed graph that can be formed as an orientation of an undirected (simple) graph.
Some authors use “oriented graph” to mean the same as “directed graph”. Some authors use “oriented graph” to mean any orientation of a given undirected graph or multigraph.
Regular graph[edit]
A regular graph is a graph in which each vertex has the same number of neighbours, i.e., every vertex has the same degree. A regular graph with vertices of degree k is called a k‑regular graph or regular graph of degree k.
Complete graph[edit]

A complete graph with five vertices and ten edges. Each vertex has an edge to every other vertex.
A complete graph is a graph in which each pair of vertices is joined by an edge. A complete graph contains all possible edges.
Finite graph[edit]
A finite graph is a graph in which the vertex set and the edge set are finite sets. Otherwise, it is called an infinite graph.
Most commonly in graph theory it is implied that the graphs discussed are finite. If the graphs are infinite, that is usually specifically stated.
Connected graph[edit]
In an undirected graph, an unordered pair of vertices {x, y} is called connected if a path leads from x to y. Otherwise, the unordered pair is called disconnected.
A connected graph is an undirected graph in which every unordered pair of vertices in the graph is connected. Otherwise, it is called a disconnected graph.
In a directed graph, an ordered pair of vertices (x, y) is called strongly connected if a directed path leads from x to y. Otherwise, the ordered pair is called weakly connected if an undirected path leads from x to y after replacing all of its directed edges with undirected edges. Otherwise, the ordered pair is called disconnected.
A strongly connected graph is a directed graph in which every ordered pair of vertices in the graph is strongly connected. Otherwise, it is called a weakly connected graph if every ordered pair of vertices in the graph is weakly connected. Otherwise it is called a disconnected graph.
A k-vertex-connected graph or k-edge-connected graph is a graph in which no set of k − 1 vertices (respectively, edges) exists that, when removed, disconnects the graph. A k-vertex-connected graph is often called simply a k-connected graph.
Bipartite graph[edit]
A bipartite graph is a simple graph in which the vertex set can be partitioned into two sets, W and X, so that no two vertices in W share a common edge and no two vertices in X share a common edge. Alternatively, it is a graph with a chromatic number of 2.
In a complete bipartite graph, the vertex set is the union of two disjoint sets, W and X, so that every vertex in W is adjacent to every vertex in X but there are no edges within W or X.
Path graph[edit]
A path graph or linear graph of order n ≥ 2 is a graph in which the vertices can be listed in an order v1, v2, …, vn such that the edges are the {vi, vi+1} where i = 1, 2, …, n − 1. Path graphs can be characterized as connected graphs in which the degree of all but two vertices is 2 and the degree of the two remaining vertices is 1. If a path graph occurs as a subgraph of another graph, it is a path in that graph.
Planar graph[edit]
A planar graph is a graph whose vertices and edges can be drawn in a plane such that no two of the edges intersect.
Cycle graph[edit]
A cycle graph or circular graph of order n ≥ 3 is a graph in which the vertices can be listed in an order v1, v2, …, vn such that the edges are the {vi, vi+1} where i = 1, 2, …, n − 1, plus the edge {vn, v1}. Cycle graphs can be characterized as connected graphs in which the degree of all vertices is 2. If a cycle graph occurs as a subgraph of another graph, it is a cycle or circuit in that graph.
Tree[edit]
A tree is an undirected graph in which any two vertices are connected by exactly one path, or equivalently a connected acyclic undirected graph.
A forest is an undirected graph in which any two vertices are connected by at most one path, or equivalently an acyclic undirected graph, or equivalently a disjoint union of trees.
Polytree[edit]
A polytree (or directed tree or oriented tree or singly connected network) is a directed acyclic graph (DAG) whose underlying undirected graph is a tree.
A polyforest (or directed forest or oriented forest) is a directed acyclic graph whose underlying undirected graph is a forest.
Advanced classes[edit]
More advanced kinds of graphs are:
- Petersen graph and its generalizations;
- perfect graphs;
- cographs;
- chordal graphs;
- other graphs with large automorphism groups: vertex-transitive, arc-transitive, and distance-transitive graphs;
- strongly regular graphs and their generalizations distance-regular graphs.
Properties of graphs[edit]
Two edges of a graph are called adjacent if they share a common vertex. Two edges of a directed graph are called consecutive if the head of the first one is the tail of the second one. Similarly, two vertices are called adjacent if they share a common edge (consecutive if the first one is the tail and the second one is the head of an edge), in which case the common edge is said to join the two vertices. An edge and a vertex on that edge are called incident.
The graph with only one vertex and no edges is called the trivial graph. A graph with only vertices and no edges is known as an edgeless graph. The graph with no vertices and no edges is sometimes called the null graph or empty graph, but the terminology is not consistent and not all mathematicians allow this object.
Normally, the vertices of a graph, by their nature as elements of a set, are distinguishable. This kind of graph may be called vertex-labeled. However, for many questions it is better to treat vertices as indistinguishable. (Of course, the vertices may be still distinguishable by the properties of the graph itself, e.g., by the numbers of incident edges.) The same remarks apply to edges, so graphs with labeled edges are called edge-labeled. Graphs with labels attached to edges or vertices are more generally designated as labeled. Consequently, graphs in which vertices are indistinguishable and edges are indistinguishable are called unlabeled. (In the literature, the term labeled may apply to other kinds of labeling, besides that which serves only to distinguish different vertices or edges.)
The category of all graphs is the comma category Set ↓ D where D: Set → Set is the functor taking a set s to s × s.
Examples[edit]

A graph with six vertices and seven edges
Graph operations[edit]
There are several operations that produce new graphs from initial ones, which might be classified into the following categories:
- unary operations, which create a new graph from an initial one, such as:
- edge contraction,
- line graph,
- dual graph,
- complement graph,
- graph rewriting;
- binary operations, which create a new graph from two initial ones, such as:
- disjoint union of graphs,
- cartesian product of graphs,
- tensor product of graphs,
- strong product of graphs,
- lexicographic product of graphs,
- series–parallel graphs.
Generalizations[edit]
In a hypergraph, an edge can join more than two vertices.
An undirected graph can be seen as a simplicial complex consisting of 1-simplices (the edges) and 0-simplices (the vertices). As such, complexes are generalizations of graphs since they allow for higher-dimensional simplices.
Every graph gives rise to a matroid.
In model theory, a graph is just a structure. But in that case, there is no limitation on the number of edges: it can be any cardinal number, see continuous graph.
In computational biology, power graph analysis introduces power graphs as an alternative representation of undirected graphs.
In geographic information systems, geometric networks are closely modeled after graphs, and borrow many concepts from graph theory to perform spatial analysis on road networks or utility grids.
See also[edit]
- Conceptual graph
- Graph (abstract data type)
- Graph database
- Graph drawing
- List of graph theory topics
- List of publications in graph theory
- Network theory
Notes[edit]
- ^ a b Trudeau, Richard J. (1993). Introduction to Graph Theory (Corrected, enlarged republication. ed.). New York: Dover Pub. p. 19. ISBN 978-0-486-67870-2. Archived from the original on 5 May 2019. Retrieved 8 August 2012.
A graph is an object consisting of two sets called its vertex set and its edge set.
- ^ See:
- J. J. Sylvester (February 7, 1878) “Chemistry and algebra,” Archived 2023-02-04 at the Wayback Machine Nature, 17 : 284. doi:10.1038/017284a0. From page 284: “Every invariant and covariant thus becomes expressible by a graph precisely identical with a Kekuléan diagram or chemicograph.”
- J. J. Sylvester (1878) “On an application of the new atomic theory to the graphical representation of the invariants and covariants of binary quantics, – with three appendices,” Archived 2023-02-04 at the Wayback Machine American Journal of Mathematics, Pure and Applied, 1 (1) : 64–90. doi:10.2307/2369436. JSTOR 2369436. The term “graph” first appears in this paper on page 65.
- ^ Gross, Jonathan L.; Yellen, Jay (2004). Handbook of graph theory. CRC Press. p. 35. ISBN 978-1-58488-090-5. Archived from the original on 2023-02-04. Retrieved 2016-02-16.
- ^ Bender & Williamson 2010, p. 148.
- ^ See, for instance, Iyanaga and Kawada, 69 J, p. 234 or Biggs, p. 4.
- ^ Bender & Williamson 2010, p. 149.
- ^ Graham et al., p. 5.
- ^ a b Bender & Williamson 2010, p. 161.
- ^ Strang, Gilbert (2005), Linear Algebra and Its Applications (4th ed.), Brooks Cole, ISBN 978-0-03-010567-8
- ^ Lewis, John (2013), Java Software Structures (4th ed.), Pearson, p. 405, ISBN 978-0133250121
- ^ Fletcher, Peter; Hoyle, Hughes; Patty, C. Wayne (1991). Foundations of Discrete Mathematics (International student ed.). Boston: PWS-KENT Pub. Co. p. 463. ISBN 978-0-53492-373-0.
A weighted graph is a graph in which a number w(e), called its weight, is assigned to each edge e.
- ^ Grandjean, Martin (2016). “A social network analysis of Twitter: Mapping the digital humanities community”. Cogent Arts & Humanities. 3 (1): 1171458. doi:10.1080/23311983.2016.1171458. Archived from the original on 2021-03-02. Retrieved 2019-09-16.
- ^ Pankaj Gupta, Ashish Goel, Jimmy Lin, Aneesh Sharma, Dong Wang, and Reza Bosagh Zadeh WTF: The who-to-follow system at Twitter Archived 2019-07-12 at the Wayback Machine, Proceedings of the 22nd international conference on World Wide Web. doi:10.1145/2488388.2488433.
References[edit]
- Balakrishnan, V. K. (1997). Graph Theory (1st ed.). McGraw-Hill. ISBN 978-0-07-005489-9.
- Bang-Jensen, J.; Gutin, G. (2000). Digraphs: Theory, Algorithms and Applications. Springer.
- Bender, Edward A.; Williamson, S. Gill (2010). Lists, Decisions and Graphs. With an Introduction to Probability.
- Berge, Claude (1958). Théorie des graphes et ses applications (in French). Paris: Dunod.
- Biggs, Norman (1993). Algebraic Graph Theory (2nd ed.). Cambridge University Press. ISBN 978-0-521-45897-9.
- Bollobás, Béla (2002). Modern Graph Theory (1st ed.). Springer. ISBN 978-0-387-98488-9.
- Diestel, Reinhard (2005). Graph Theory (3rd ed.). Berlin, New York: Springer-Verlag. ISBN 978-3-540-26183-4.
- Graham, R.L.; Grötschel, M.; Lovász, L. (1995). Handbook of Combinatorics. MIT Press. ISBN 978-0-262-07169-7.
- Gross, Jonathan L.; Yellen, Jay (1998). Graph Theory and Its Applications. CRC Press. ISBN 978-0-8493-3982-0.
- Gross, Jonathan L.; Yellen, Jay (2003). Handbook of Graph Theory. CRC. ISBN 978-1-58488-090-5.
- Harary, Frank (1995). Graph Theory. Addison Wesley Publishing Company. ISBN 978-0-201-41033-4.
- Iyanaga, Shôkichi; Kawada, Yukiyosi (1977). Encyclopedic Dictionary of Mathematics. MIT Press. ISBN 978-0-262-09016-2.
- Zwillinger, Daniel (2002). CRC Standard Mathematical Tables and Formulae (31st ed.). Chapman & Hall/CRC. ISBN 978-1-58488-291-6.
Further reading[edit]
- Trudeau, Richard J. (1993). Introduction to Graph Theory (Corrected, enlarged republication. ed.). New York: Dover Publications. ISBN 978-0-486-67870-2. Retrieved 8 August 2012.
External links[edit]
 Media related to Graph (discrete mathematics) at Wikimedia Commons
Media related to Graph (discrete mathematics) at Wikimedia Commons- Weisstein, Eric W. “Graph”. MathWorld.
Теория графов
В переводе с греческого граф — «пишу», «описываю». В современном мире граф описывает отношения. И наоборот: любое отношение можно описать в виде графа.
Теория графов — обширный раздел дискретной математики, в котором системно изучают свойства графов.
Теория графов широко применяется в решении экономических и управленческих задач, в программировании, химии, конструировании и изучении электрических цепей, коммуникации, психологии, социологии, лингвистике и в других областях.
Для чего строят графы: чтобы отобразить отношения на множествах. По сути, графы помогают визуально представить всяческие сложные взаимодействия: аэропорты и рейсы между ними, разные отделы в компании, молекулы в веществе.
Давайте на примере.
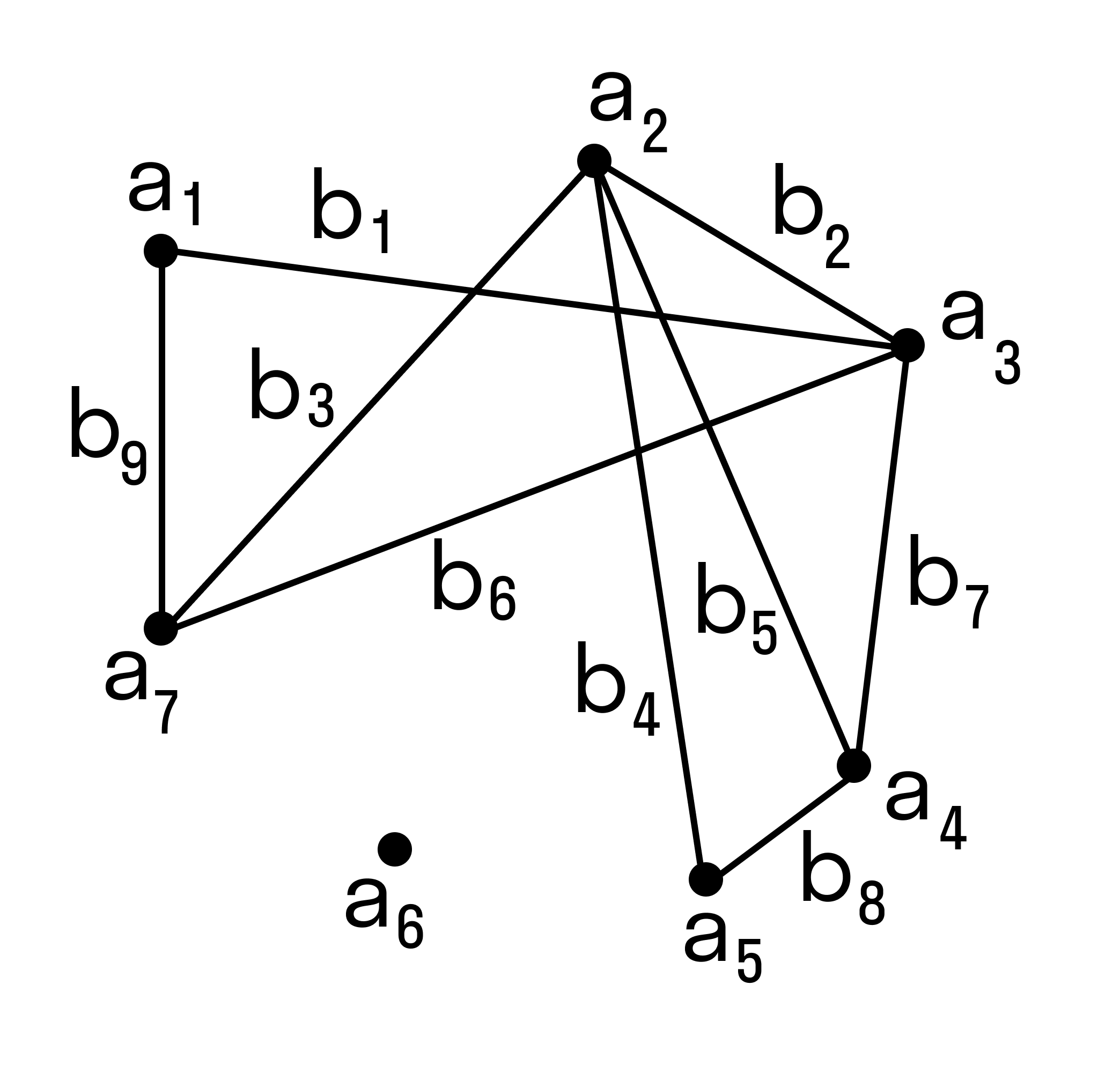
Пусть множество A = {a1, a2, … an} — это множество людей, и каждый элемент отображен в виде точки. Множество B = {b1, b2, … bm} — множество связок (прямых, дуг или отрезков).
На множестве A зададим отношение знакомства между людьми из этого множества. Строим граф из точек и связок. Связки будут связывать пары людей, знакомых между собой.
Число знакомых у одних людей может отличаться от числа знакомых у других людей, некоторые могут вовсе не быть знакомы (такие элементы будут точками, не соединёнными ни с какой другой). Так получился граф:
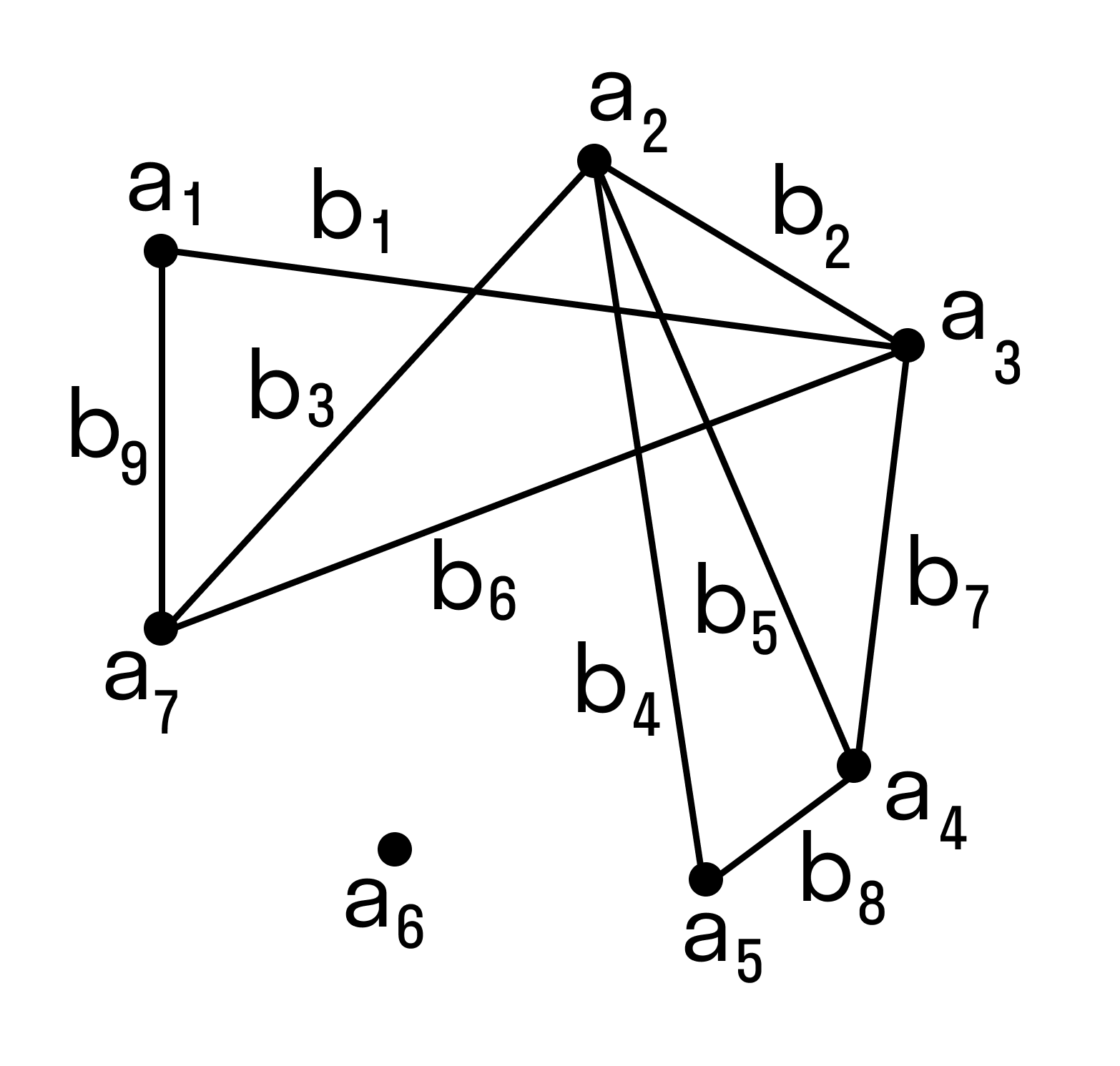
В данном случае точки — это вершины графа, а связки — рёбра графа.
Теория графов не учитывает конкретную природу множеств A и B. Существует большое количество разных задач, при решении которых можно временно забыть о содержании множеств и их элементов. Эта специфика не отражается на ходе решения задачи.
Например, вопрос в задаче стоит так: можно ли из точки A добраться до точки E, если двигаться только по соединяющим точки линиям. Когда задача решена, мы получаем решение, верное для любого содержания, которое можно смоделировать в виде графа.
Не удивительно, что теория графов — один из самых востребованных инструментов при создании искусственного интеллекта: ведь искусственный интеллект может обсудить с человеком вопросы отношений, географии или музыки, решения различных задач.
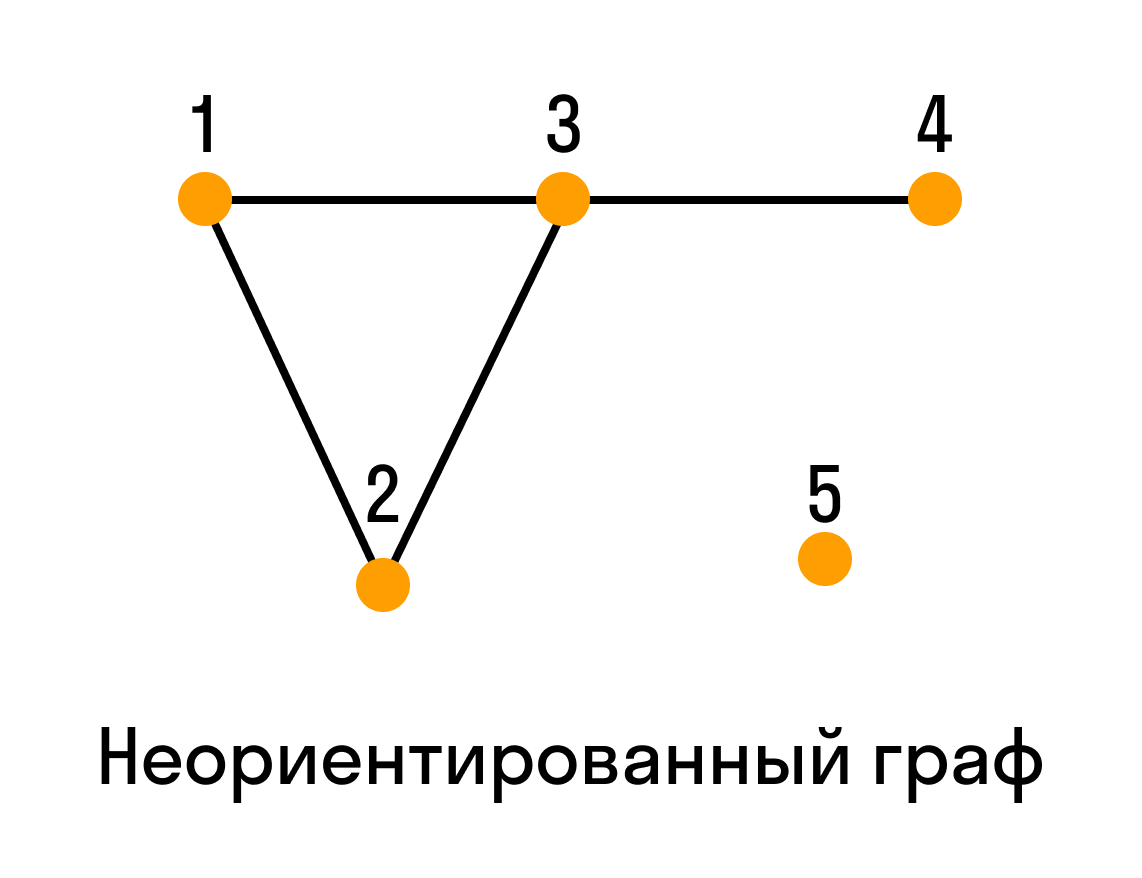
Графом называется система объектов произвольной природы (вершин) и связок (ребер), соединяющих некоторые пары этих объектов.
Пусть V — (непустое) множество вершин, элементы v ∈ V — вершины. Граф G = G(V) с множеством вершин V есть некоторое семейство пар вида: e = (a, b), где a, b ∈ V, указывающих, какие вершины остаются соединёнными. Каждая пара e = (a, b) — ребро графа. Множество U — множество ребер e графа. Вершины a и b — концевые точки ребра e.
Широкое применение теории графов в компьютерных науках и информационных технологиях можно объяснить понятием графа как структуры данных. В компьютерных науках и информационных технологиях граф можно описать, как нелинейную структуру данных.
Линейные структуры данных особенны тем, что связывают элементы отношениями по типу «простого соседства». Линейными структурами данных можно назвать массивы, таблицы, списки, очереди, стеки, строки. В нелинейных структурах данных элементы располагаются на различных уровнях иерархии и подразделяются на три вида: исходные, порожденные и подобные.
Курсы обучения математике помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас

Основные понятия теории графов
Граф — это геометрическая фигура, которая состоит из точек и линий, которые их соединяют. Точки называют вершинами графа, а линии — ребрами.
- Два ребра называются смежными, если у них есть общая вершина.
- Два ребра называются кратными, если они соединяют одну и ту же пару вершин.
- Ребро называется петлей, если его концы совпадают.
- Степенью вершины называют количество ребер, для которых она является концевой (при этом петли считают дважды).
- Вершина называется изолированной, если она не является концом ни для одного ребра.
- Вершина называется висячей, если из неё выходит ровно одно ребро.
- Граф без кратных ребер и петель называется обыкновенным.
Лемма о рукопожатиях
В любом графе сумма степеней всех вершин равна удвоенному числу ребер.
Доказательство леммы о рукопожатиях
Если ребро соединяет две различные вершины графа, то при подсчете суммы степеней вершин мы учтем это ребро дважды.
Если же ребро является петлей — при подсчете суммы степеней вершин мы также учтем его дважды (по определению степени вершины).
Из леммы о рукопожатиях следует: в любом графе число вершин нечетной степени — четно.
Пример 1. В классе 30 человек. Может ли быть так, что у 9 из них есть 3 друга в этом классе, у 11 — 4 друга, а у 10 — 5 друзей? Учесть, что дружбы взаимные.
Как рассуждаем:
Если бы это было возможно, то можно было бы нарисовать граф с 30 вершинами, 9 из которых имели бы степень 3, 11 — со степенью 4, 10 — со степенью 5. Однако у такого графа 19 нечетных вершин, что противоречит следствию из леммы о рукопожатиях.
Пример 2. Каждый из 102 учеников одной школы знаком не менее чем с 68 другими. Доказать, что среди них найдутся четверо ребят с одинаковым числом знакомых.
Как рассуждаем:
Сначала предположим противоположное. Тогда для каждого числа от 68 до 101 есть не более трех человек с таким числом знакомых. С другой стороны, у нас есть ровно 34 натуральных числа, начиная с 68 и заканчивая 101, а 102 = 34 * 3.
Это значит, что для каждого числа от 68 до 101 есть ровно три человека, имеющих такое число знакомых. Но тогда количество людей, имеющих нечетное число знакомых, нечетно. Противоречие.
Путь и цепь в графе
Путем или цепью в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершин ребром.
Циклом называют путь, в котором первая и последняя вершины совпадают.
Путь или цикл называют простым, если ребра в нем не повторяются.
Если в графе любые две вершины соединены путем, то такой граф называется связным.
Можно рассмотреть такое подмножество вершин графа, что каждые две вершины этого подмножества соединены путем, а никакая другая вершина не соединена ни с какой вершиной этого подмножества.
Каждое такое подмножество, вместе со всеми ребрами исходного графа, соединяющими вершины этого подмножества, называется компонентой связности.
Один и тот же граф можно нарисовать разными способами. Вот, например, два изображения одного и того же графа, которые различаются кривизной:
Два графа называются изоморфными, если у них поровну вершин. При этом вершины каждого графа можно занумеровать числами так, чтобы вершины первого графа были соединены ребром тогда и только тогда, когда соединены ребром соответствующие занумерованные теми же числами вершины второго графа.
Граф H, множество вершин V’ которого является подмножеством вершин V данного графа G и множество рёбер которого является подмножеством рёбер графа G соединяющими вершины из V’ называется подграфом графа G.
Визуализация графовых моделей
Визуализация — это процесс преобразования больших и сложных видов абстрактной информации в интуитивно-понятную визуальную форму. Другими словами, когда мы рисуем то, что нам непонятно — и сразу все встает на свои места.
Графы — и есть помощники в этом деле. Они помогают представить любую информацию, которую можно промоделировать в виде объектов и связей между ними.
Граф можно нарисовать на плоскости или в трехмерном пространстве. Его можно изобразить целиком, частично или иерархически.
Изобразительное соглашение — одно из основных правил, которому должно удовлетворять изображение графа, чтобы быть допустимым. Например, при изображении блок-схемы программы можно использовать соглашение о том, что все вершины должны изображаться прямоугольниками, а дуги — ломаными линиями с вертикальными и горизонтальными звеньями. При этом, конкретный вид соглашения может быть достаточно сложен и включать много деталей.
Виды изобразительных соглашений:
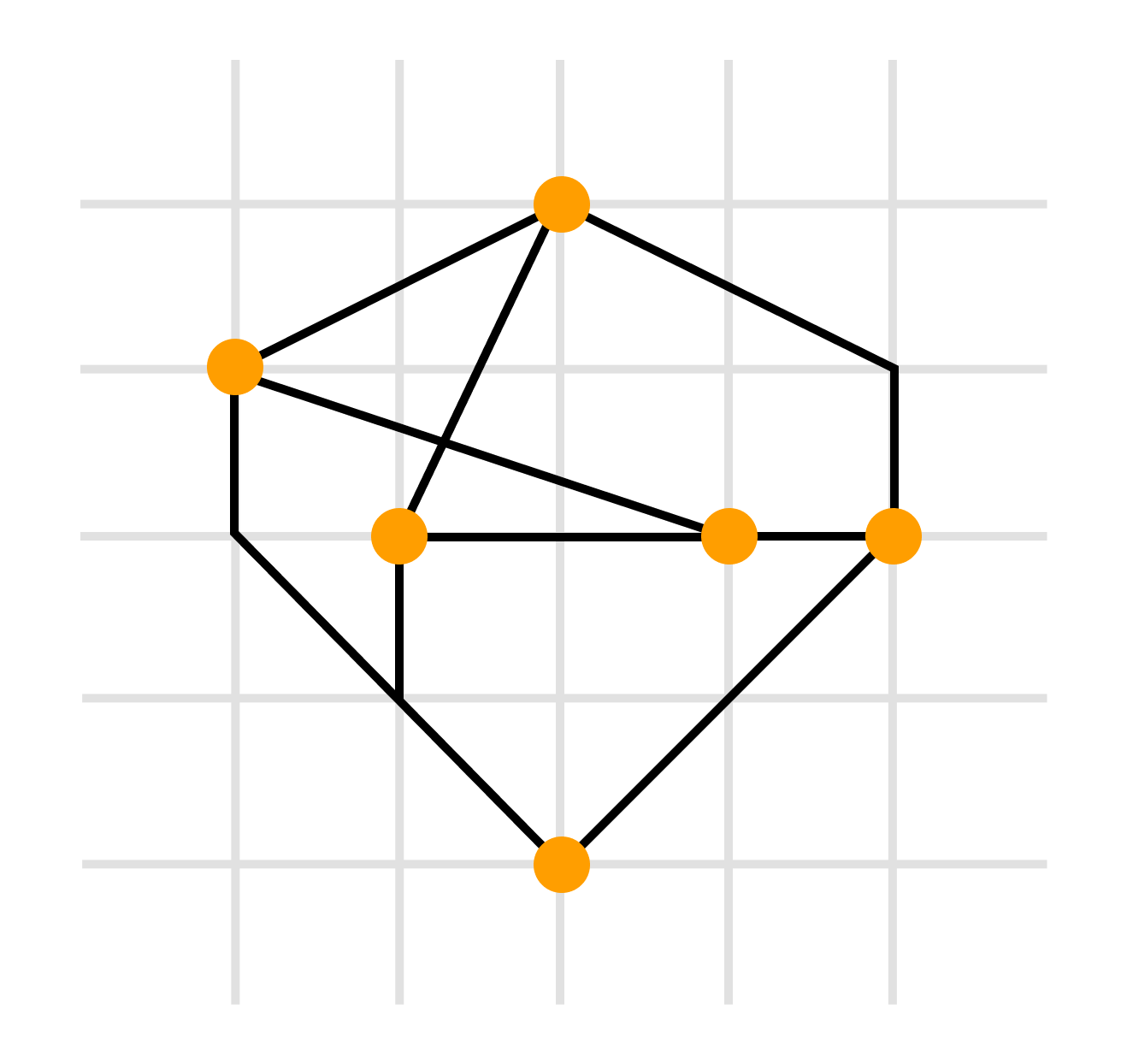
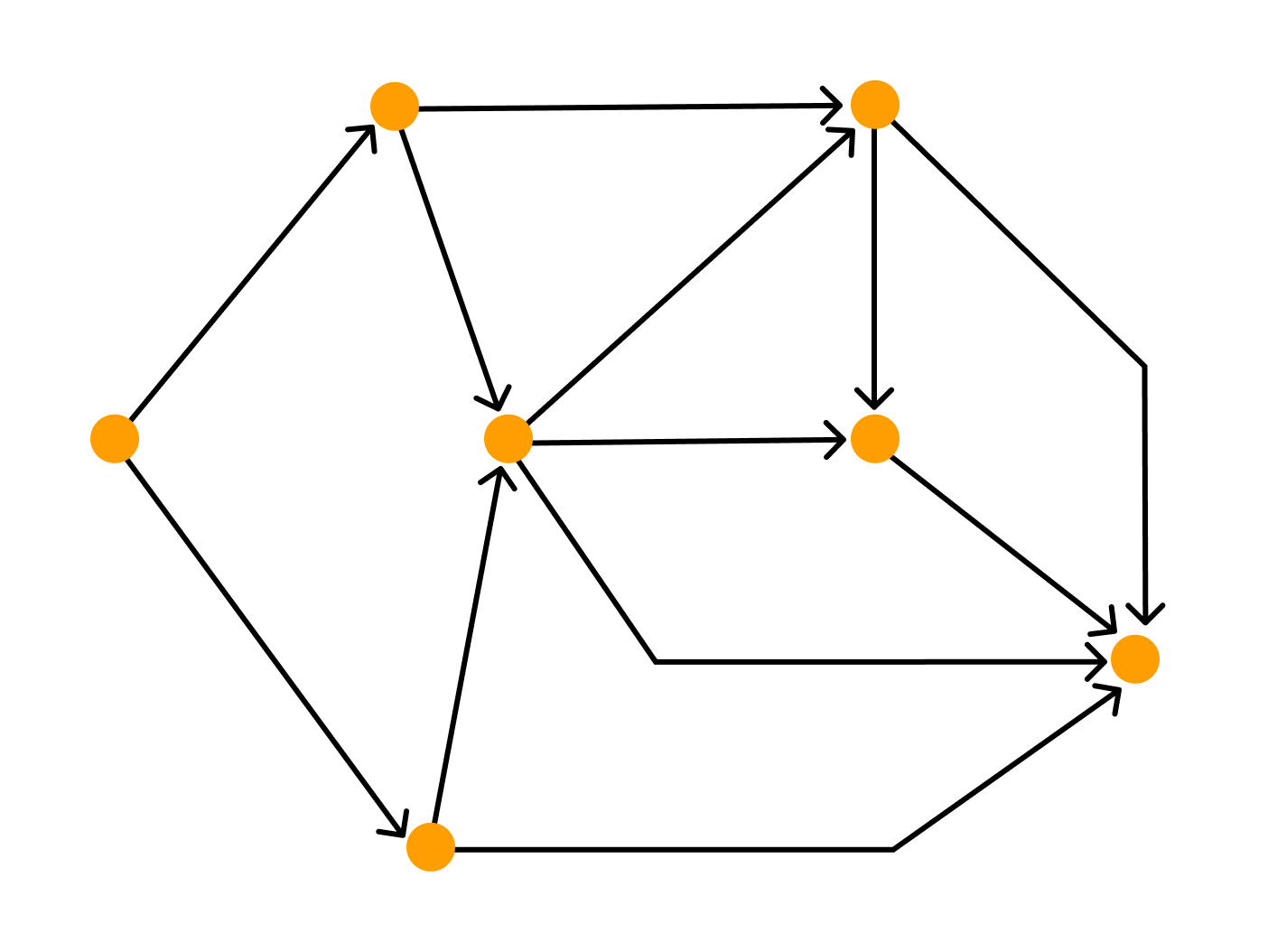
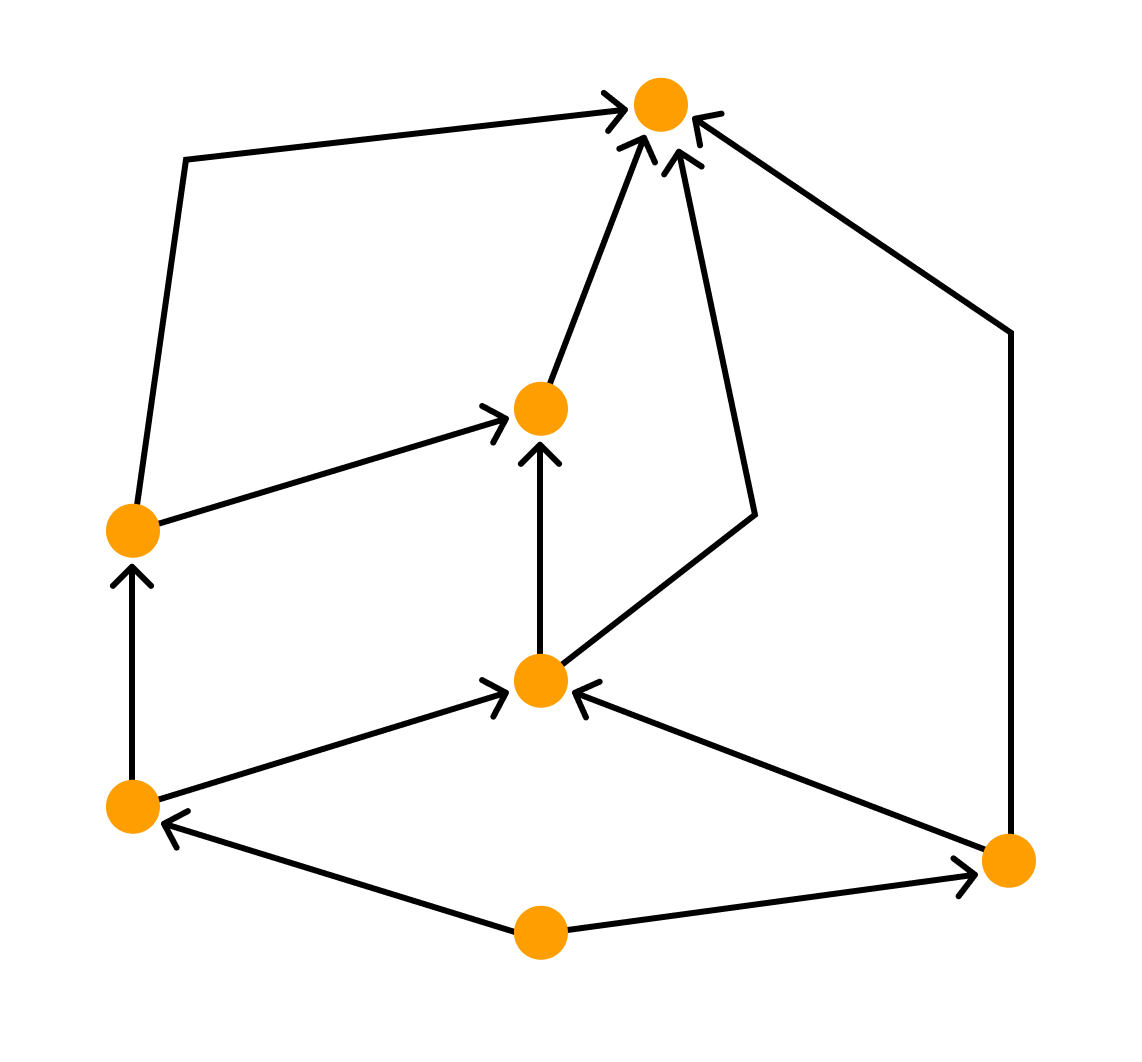
- полилинейное изображение — каждое ребро графа рисуют в виде ломаной линии
- прямолинейное изображение — каждое ребро представляют с помощью отрезка прямой
- ортогональное изображение — каждое ребро графа изображается в виде ломаной линии, состоящей из чередующихся горизонтальных и вертикальных сегментов
- сетчатое изображение — все вершины, а также все точки пересечения и сгибы ребер имеют целочисленные координаты. То есть находятся в узлах координатной сетки, образованной прямыми, параллельными координатным осям и пересекающими их в точках с целочисленными координатами
- плоское изображение предполагает отсутствие точек пересечения у линий, изображающих ребра.
- восходящее или нисходящее изображение имеет смысл по отношению к ациклическому орграфу и предполагает, что каждая дуга изображается ориентированной линией, координаты точек которой монотонно изменяются в направлении снизу вверх или сверху вниз, а также слева направо.
- Деревом называется связный граф не содержащий простых циклов.
- Деревом называется связный граф, содержащий n вершин и n – 1 ребро.
- Деревом называется связный граф, который при удалении любого ребра перестает быть связным.
- Деревом называется граф, в котором любые две вершины соединены ровно одним простым путем.
- одна вершина, у которой нет предшественников, определяет время начала работы
- одна вершина без последователей соответствует моменту завершения комплекса работ.
Виды графов
Виды графов можно определять по тому, как их построили или по свойствам вершин или ребер.
Ориентированные и неориентированные графы
Графы, в которых все ребра являются звеньями, то есть порядок двух концов ребра графа не существенен, называются неориентированными.
Графы, в которых все ребра являются дугами, то есть порядок двух концов ребра графа существенен, называются ориентированными графами или орграфами.
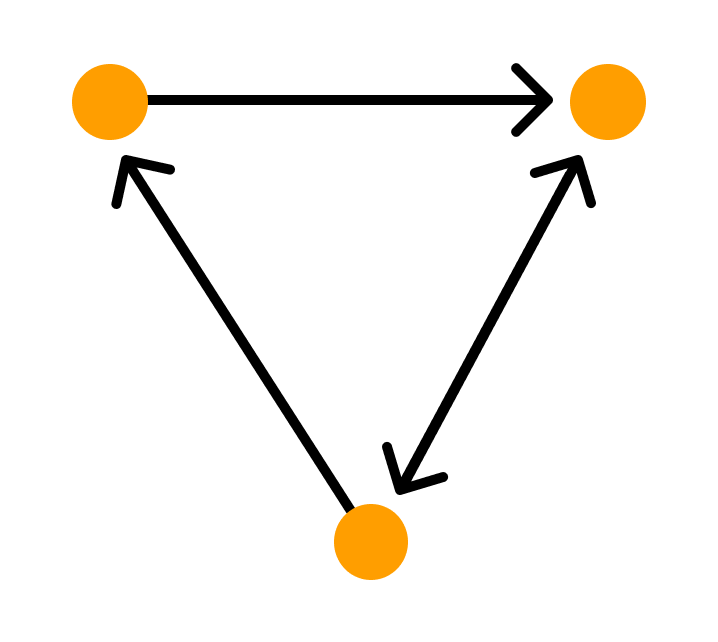
Неориентированный граф можно представить в виде ориентированного графа, если каждое его звено заменить на две дуги с противоположным направлением.
Графы с петлями, смешанные графы, пустые графы, мультиграфы, обыкновенные графы, полные графы
Если граф содержит петли — это обстоятельство важно озвучивать и добавлять к основной характеристике графа уточнение «с петлями». Если граф не содержит петель, то добавляют «без петель».
Смешанным называют граф, в котором есть ребра хотя бы двух из упомянутых трех разновидностей (звенья, дуги, петли).
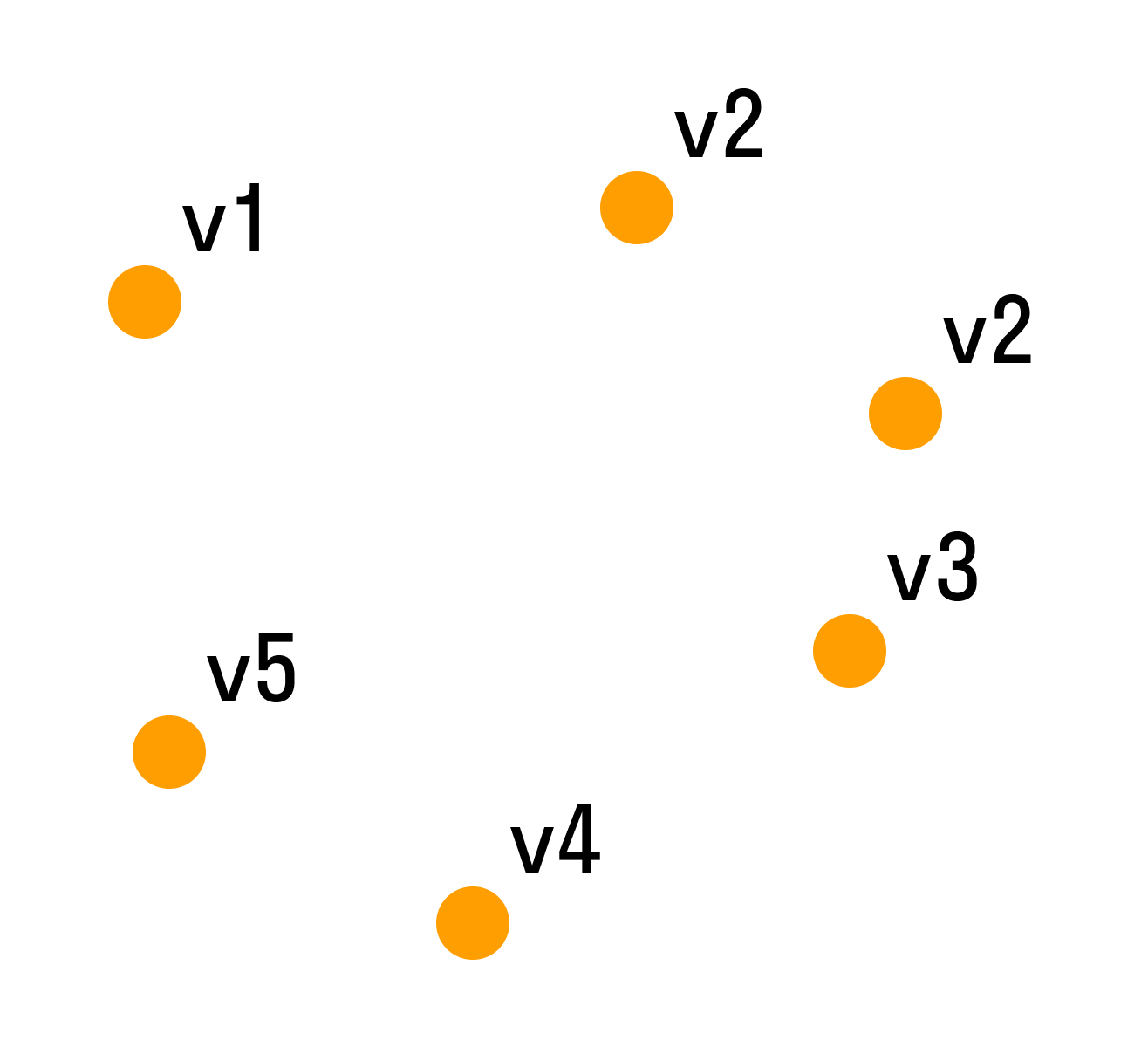
Пустой граф — это тот, что состоит только из голых вершин.
Мультиграфом — такой граф, в котором пары вершин соединены более, чем одним ребром. То есть есть кратные рёбра, но нет петель.
Граф без дуг, то есть неориентированный, без петель и кратных ребер называется обыкновенным.
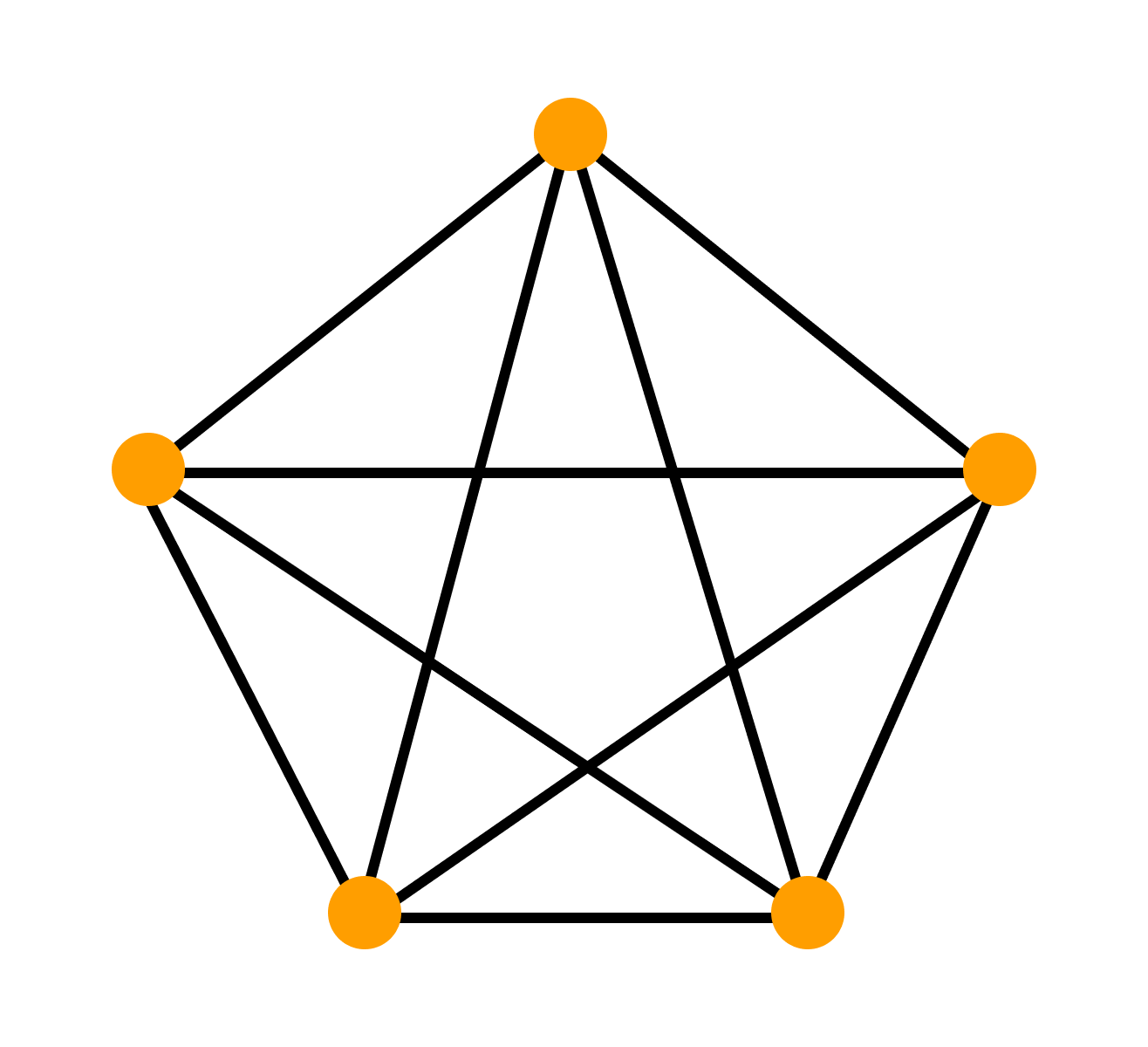
Граф называют полным, если он содержит все возможные для этого типа рёбра при неизменном множестве вершин. Так, в полном обыкновенном графе каждая пара различных вершин соединена ровно одним звеном.
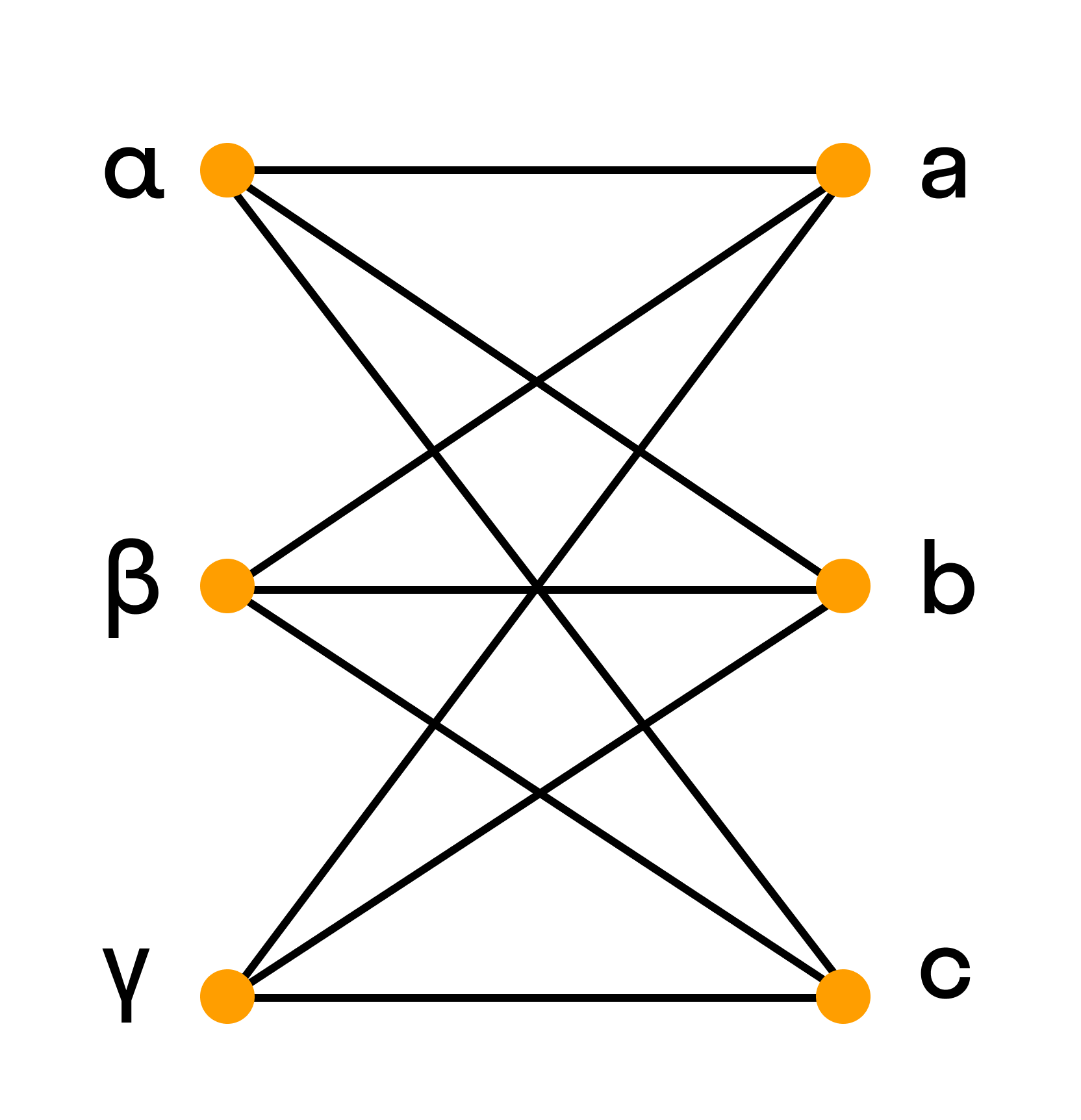
Двудольный граф
Граф называется двудольным, если множество его вершин можно разбить на два подмножества так, чтобы никакое ребро не соединяло вершины одного и того же подмножества.
Например, полный двудольный граф состоит из двух множеств вершин и из всевозможных звеньев, которые соединяют вершины одного множества с вершинами другого множества.
Эйлеров граф
Эйлеров граф отличен тем, что в нем можно обойти все вершины и при этом пройти одно ребро только один раз. В нём каждая вершина должна иметь только чётное число рёбер.
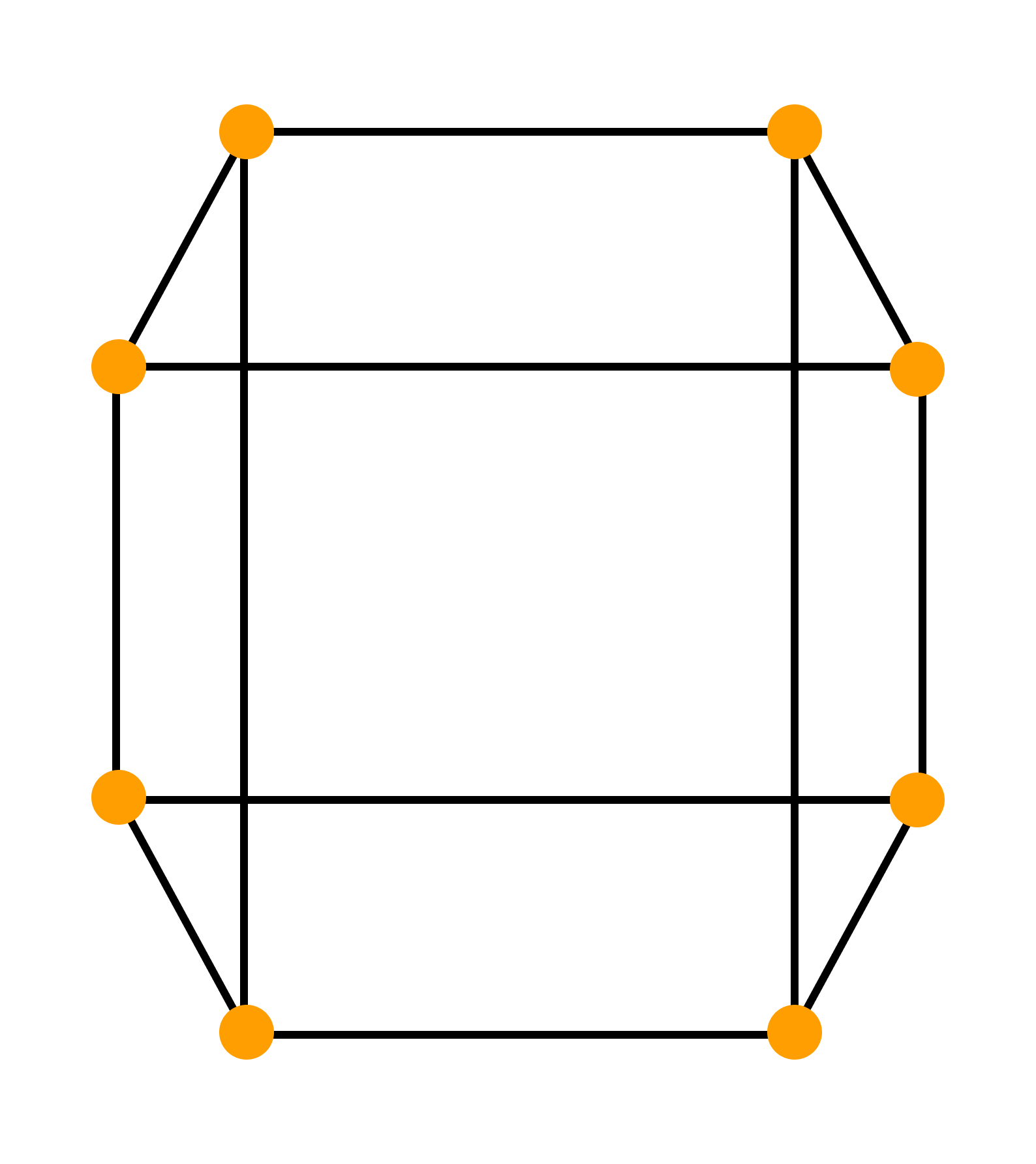
Пример. Является ли полный граф с одинаковым числом n рёбер, которым инцидентна каждая вершина, эйлеровым графом?
Ответ. Если n — нечётное число, то каждая вершина инцидентна n – 1 ребрам. В таком случае наш граф — эйлеровый.
Регулярный граф
Регулярным графом называется связный граф, все вершины которого имеют одинаковую степень k.
Число вершин регулярного графа k-й степени не может быть меньше k + 1. У регулярного графа нечётной степени может быть лишь чётное число вершин.
Пример. Построить регулярный граф, в котором самый короткий цикл имеет длину 4.
Рассуждаем так:
Чтобы длина цикла соответствовала заданному условию, нужно чтобы число вершин графа было кратно четырем. Если число вершин равно четырём — получится регулярный граф, в котором самый короткий цикл имеет длину 3.
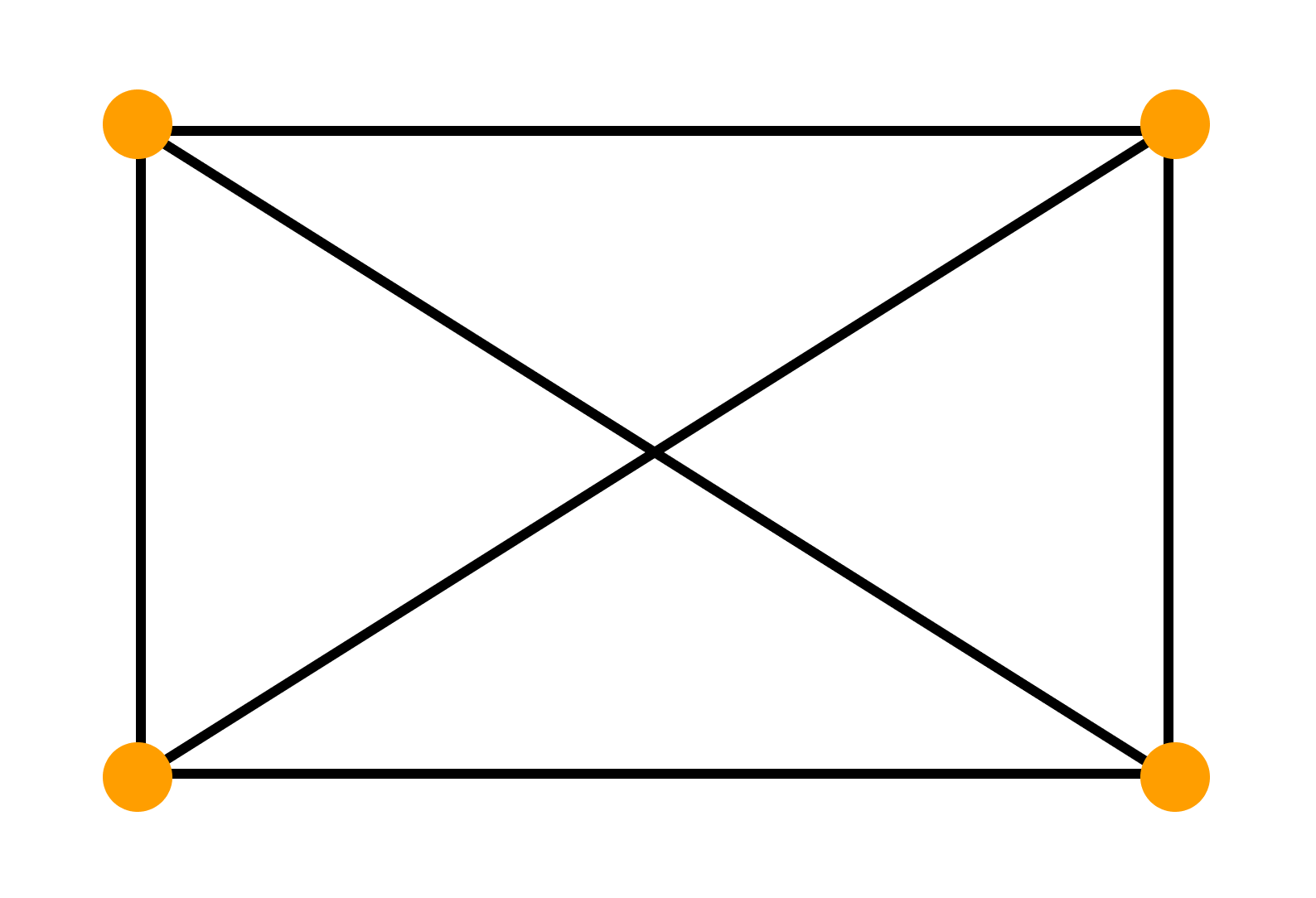
Увеличим число вершин до восьми (следующее кратное четырем число). Соединим вершины ребрами так, чтобы степени вершин были равны трём. Получаем следующий граф, удовлетворяющий условиям задачи:
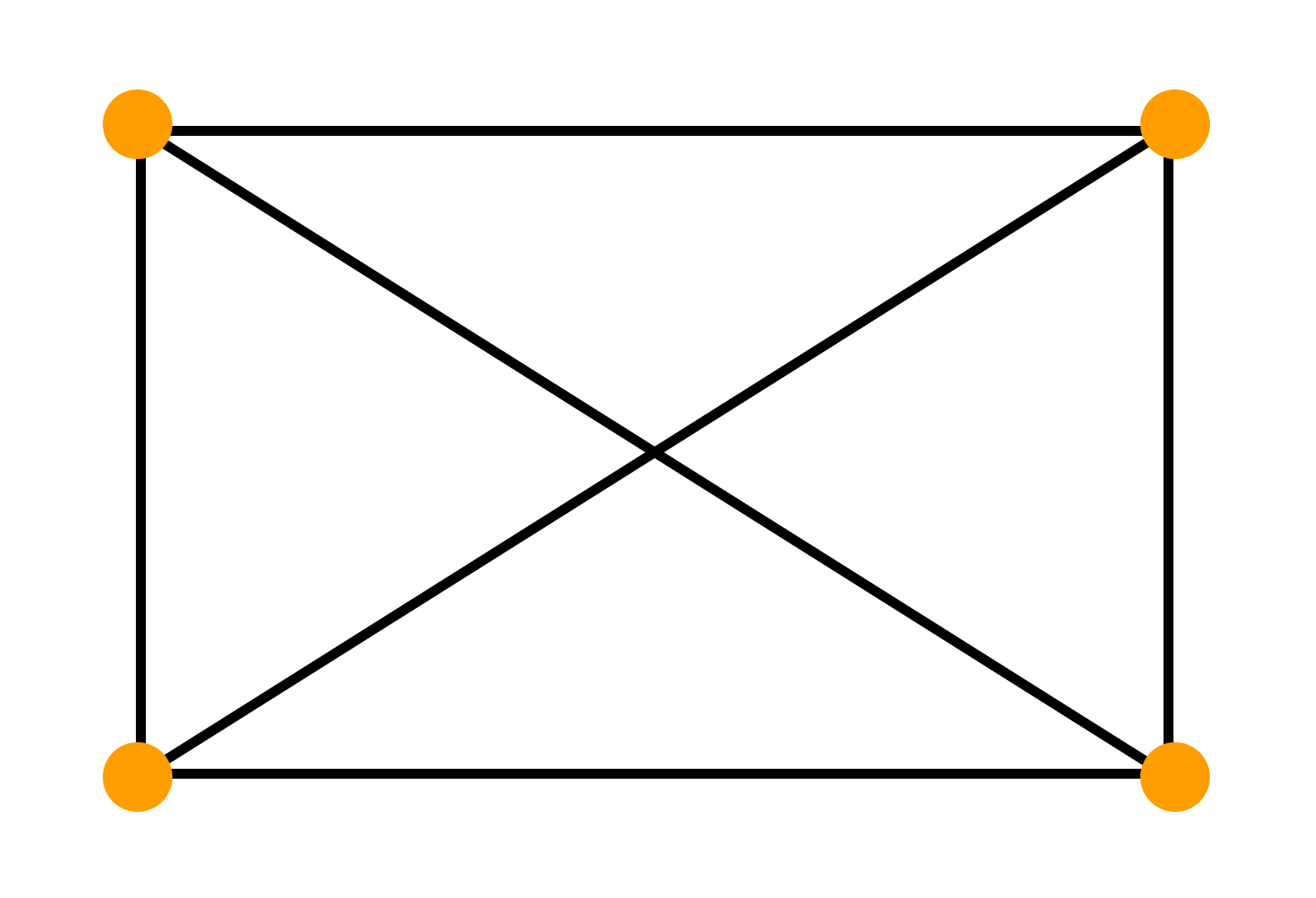
Гамильтонов граф
Гамильтоновым графом называется граф, содержащий гамильтонов цикл.
Гамильтоновым циклом называется простой цикл, который проходит через все вершины рассматриваемого графа.
Говоря проще, гамильтонов граф — это такой граф, в котором можно обойти все вершины, и каждая вершина при обходе повторяется лишь один раз.
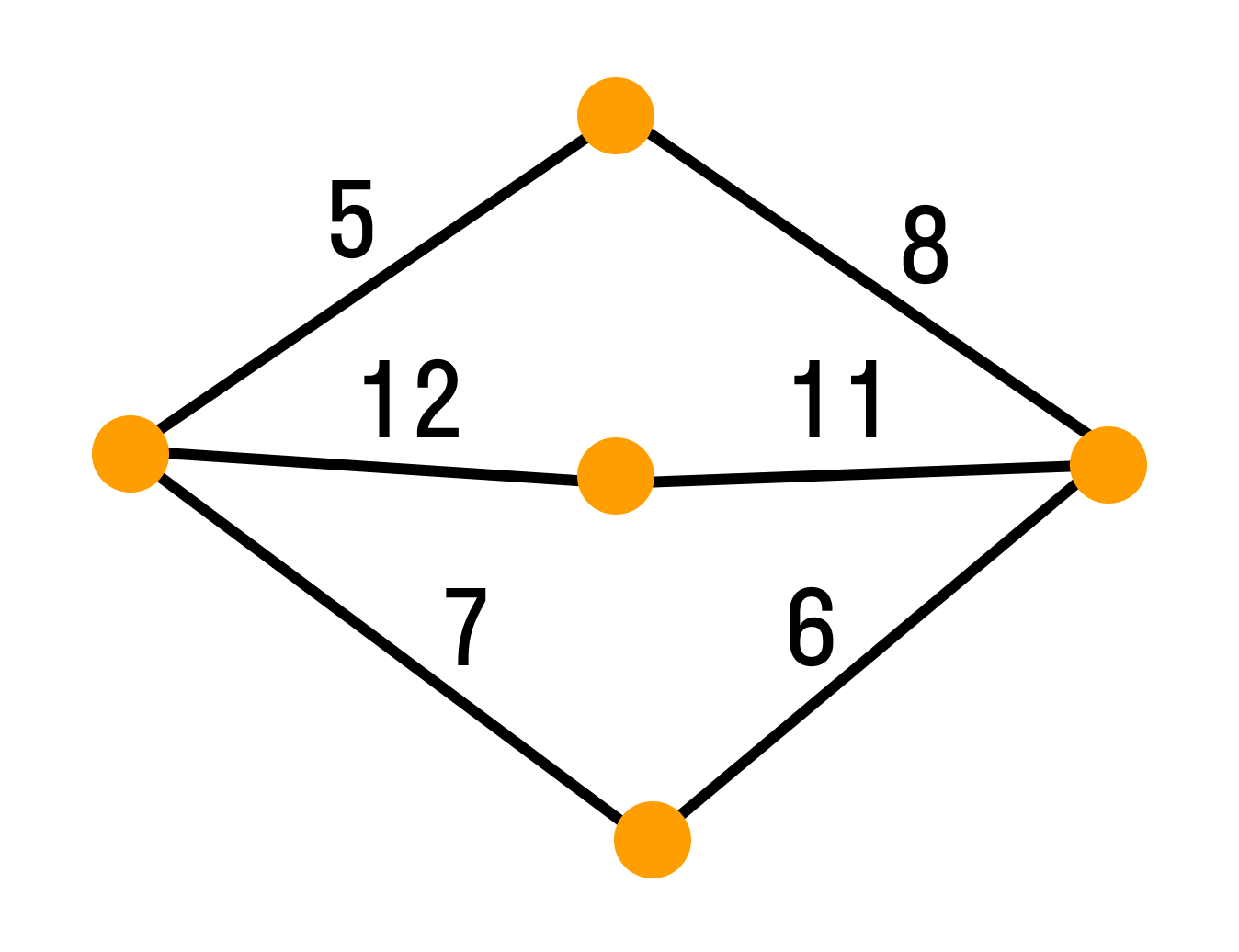
Взвешенный граф
Взвешенным графом называется граф, вершинам и/или ребрам которого присвоены «весы» — обычно некоторые числа. Пример взвешенного графа — транспортная сеть, в которой ребрам присвоены весы: они показывают стоимость перевозки груза по ребру и пропускные способности дуг.
Графы-деревья
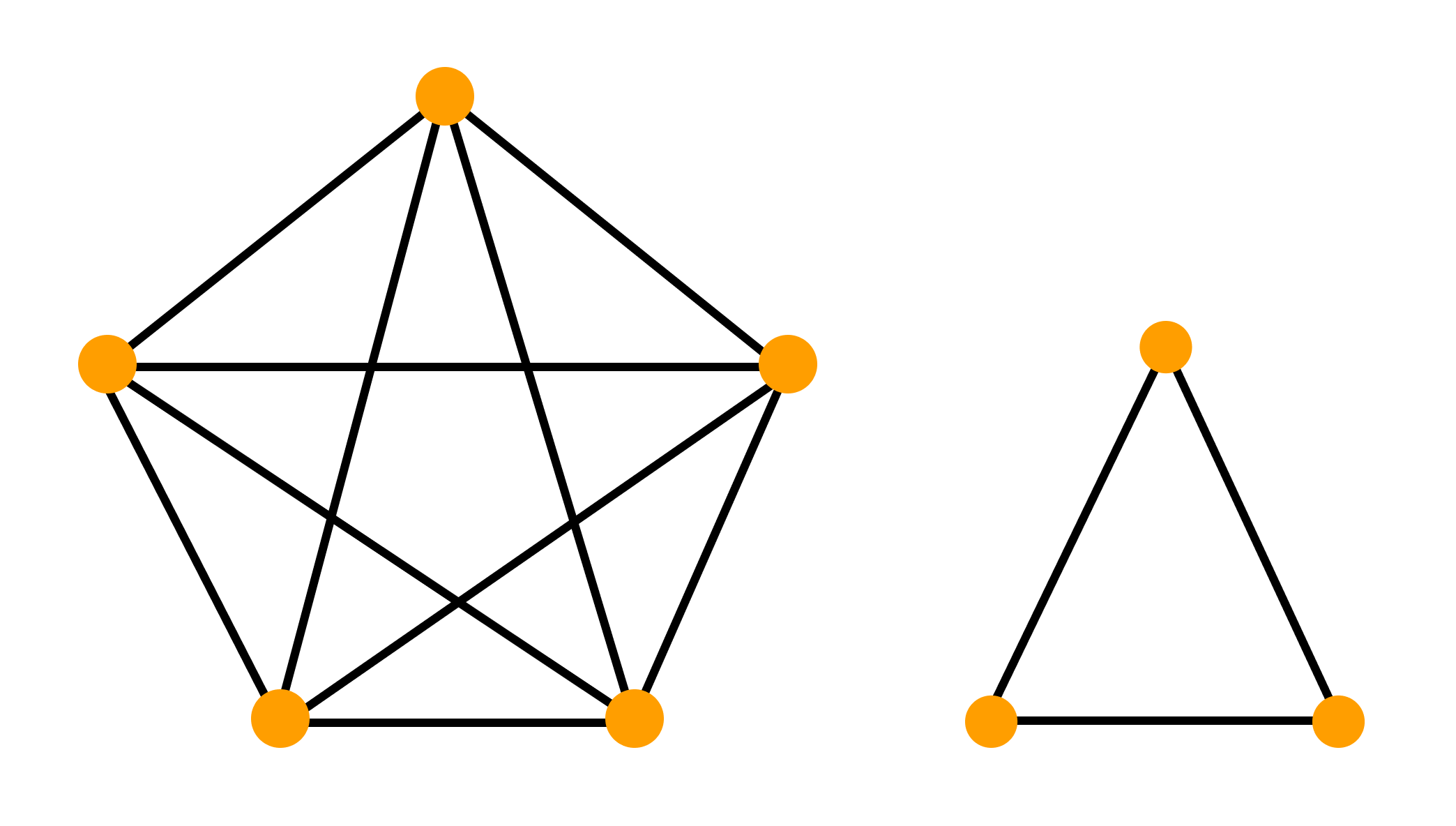
Деревом называется связный граф без циклов. Любые две вершины дерева соединены лишь одним маршрутом.
Число q ребер графа находится из соотношения q = n – 1, где n — число вершин дерева.
Приведенное соотношение выражает критическое значение числа рёбер дерева, так как, если мы присоединим к дереву ещё одно ребро — будет создан цикл. А если уберем одно ребро, то граф-дерево разделится на две компоненты. Граф, состоящий из компонент дерева, называется лесом.
Определение дерева
Деревом называется связный граф, который не содержит циклов.
Таким образом, в дереве невозможно вернуться в исходную вершину, перемещаясь по ребрам и не проходя по одному ребру два или более раз.
Циклом называется замкнутый путь, который не проходит дважды через одну и ту же вершину.
Простым путем называется путь, в котором никакое ребро не встречается дважды.
Легко проверить, что дерево — это граф, в котором любые две вершины соединены ровно одним простым путем. Если выкинуть любое ребро из дерева, то граф станет несвязным. Поэтому:
Дерево — минимальный по числу рёбер связный граф.
Висячей вершиной называется вершина, из которой выходит ровно одно ребро.
Определения дерева:
Очень часто в дереве выделяется одна вершина, которая называется корнем дерева. Дерево с выделенным корнем называют корневым или подвешенным деревом. Пример: генеалогическое дерево.
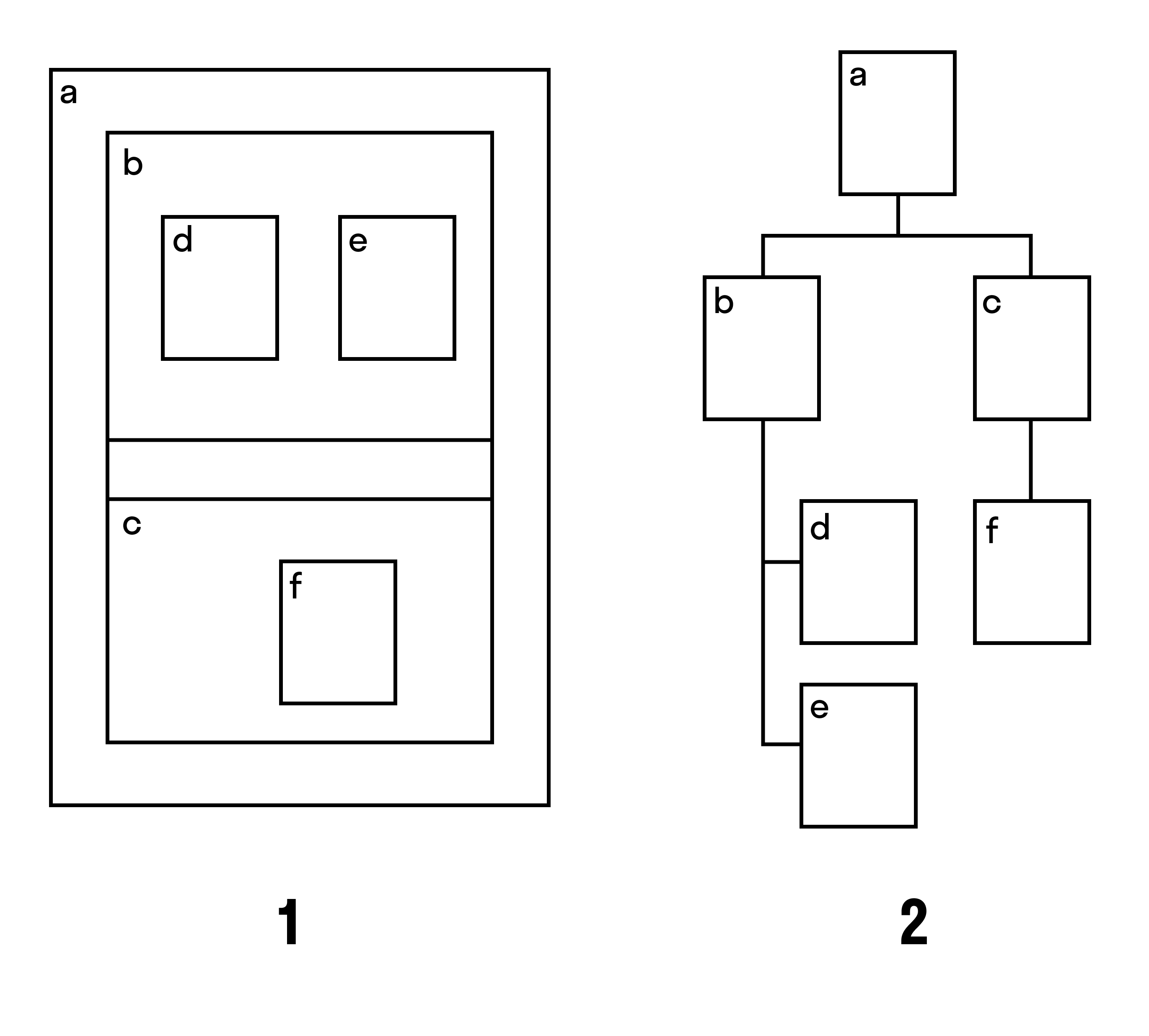
Когда изображают деревья, то часто применяют дополнительные соглашения, эстетические критерии и ограничения.
Например, при соглашении включения (рис. 1) вершины корневого дерева изображают прямоугольниками, а соглашение — опрокидывания (рис. 2) подобно классическому соглашению нисходящего плоского изображения корневого дерева. Вот так могут выглядеть разные изображения одного дерева:
Теоремы дерева и их доказательства
I теорема
В дереве с более чем одной вершиной есть висячая вершина.
Доказательство первой теоремы:
Пойдем из какой-нибудь вершины по ребрам. Так как в дереве нет циклов, то мы не вернемся в вершину, в которой уже побывали. Если у каждой вершины степень больше 1, то найдется ребро, по которому можно уйти из неё после того, как мы пришли в нее.
Но поскольку количество вершин в дереве конечно, когда-нибудь мы остановимся в некоторой вершине. Противоречие. Значит, когда-нибудь мы дойдём в висячую вершину. Если же начать идти из неё, то мы найдём вторую висячую вершину.
II теорема
В дереве число вершин на 1 больше числа ребер.
Доказательство второй теоремы:
Докажем по индукции по количеству вершин в дереве n. Если в дерево одна вершина, то факт верен. Предположим, что для всех n < k мы доказали это факт. Найдём висячую вершину.
Граф, получающийся из исходного выкидыванием висячей вершины вместе с исходящим из нее ребром, очевидно, также является деревом — и в нём меньше на одну вершину и одно ребро. Значит для исходного графа также было верно доказываемое соотношение между количеством вершин и рёбер.
Верна и обратная теорема. Если в связном графе вершин на одну больше, чем ребер, то он является деревом.
Подграф называется остовным деревом, если он является деревом и множество его вершин совпадает с множеством вершин исходного графа.
III теорема
У любого связного графа есть остовное дерево.
Доказательство третьей теоремы:
Чтобы найти остовное дерево графа G, можно найти цикл в графе G и выкинуть одно ребро цикла — потом повторить. И так пока в графе не останется циклов. Полученный граф будет связным, так как мы выкидывали рёбра, не нарушая связность, но в нём не будет циклов. Значит, он будет деревом.
Теория графов и современные прикладные задачи
На основе теории графов создали разные методы решения прикладных задач, в которых в виде графов можно моделировать сложные системы. В этих моделях узлы содержат отдельные компоненты, а ребра отражают связи между компонентами.
Графы и задача о потоках
Система водопроводных труб в виде графа выглядит так:
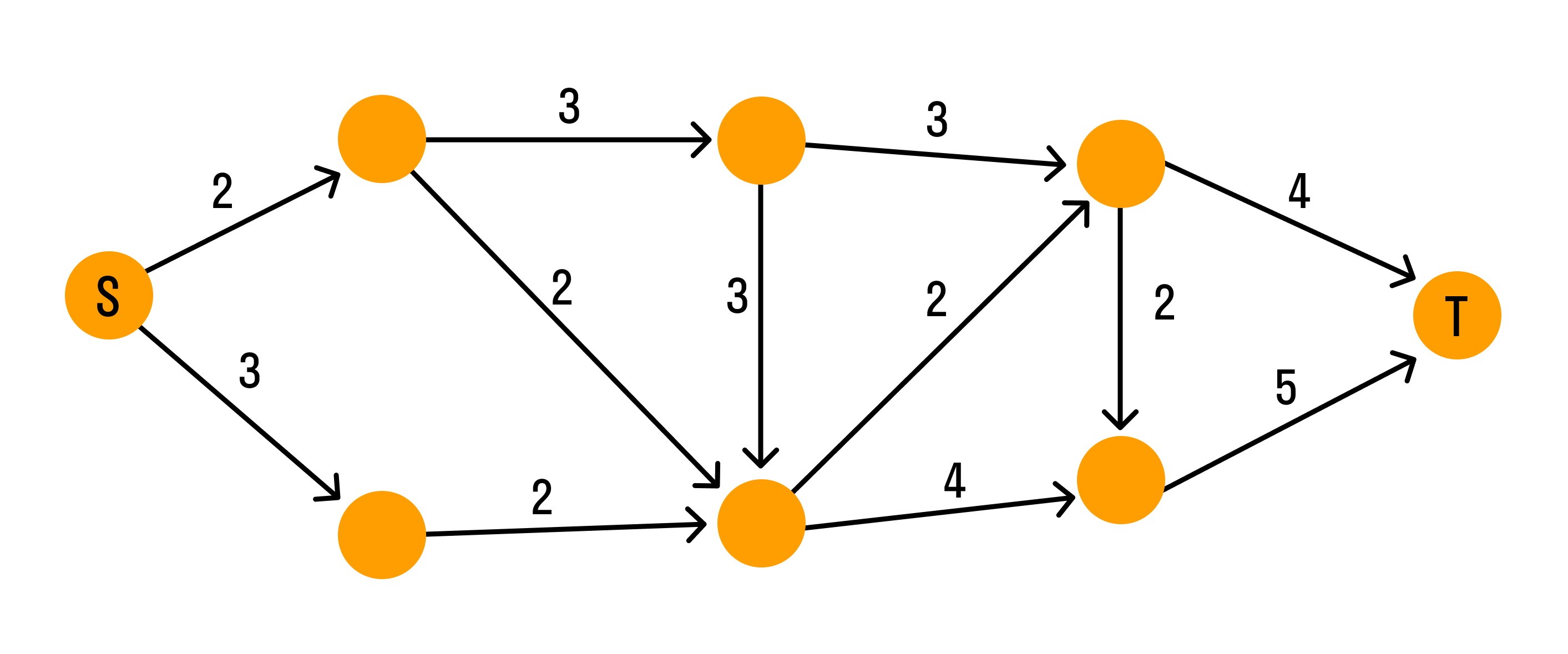
Каждая дуга графа отображает трубу. Числа над дугами (весы) — пропускная способность труб. Узлы — места соединения труб. Вода течёт по трубам только в одном направлении. Узел S — источник воды, узел T — сток.
Задача: максимизировать объём воды, протекающей от источника к стоку.
Для решения задачи о потоках можно использовать метод Форда-Фалкерсона. Идея метода в том, чтобы найти максимальный поток по шагам.
Сначала предполагают, что поток равен нулю. На каждом последующем шаге значение потока увеличивается, для чего ищут дополняющий путь, по которому поступает дополнительный поток. Эти шаги повторяют до тех пор, пока существуют дополнительные пути.
Задачу успешно применяют в различных распределенных системах: система электроснабжения, коммуникационная сеть, система железных дорог.
Графы и сетевое планирование
В задачах планирования сложных процессов, где много разных параллельных и последовательных работ, часто используют взвешенные графы. Их еще называют сетью ПЕРТ (PERT).
PERT (Program (Project) Evaluation and Review Technique) — техника оценки и анализа программ (проектов), которую используют при управлении проектами.
Сеть ПЕРТ — взвешенный ациклический ориентированный граф, в котором каждая дуга представляет работу (действие, операцию), а вес дуги — время, которое нужно на ее выполнение.
Если в сети есть дуги (a, b) и (b, c), то работа, представленная дугой (a, b), должна быть завершена до начала выполнения работы, представленной дугой (b, c). Каждая вершина (vi) представляет момент времени, к которому должны быть завершены все работы, задаваемые дугами, оканчивающимися в вершине (vi).
В таком графе:
Путь максимальной длины между этими вершинами графа называется критическим путем. Чтобы выполнить всю работу быстрее, нужно найти задачи на критическом пути и придумать, как их выполнить быстрее. Например, нанять больше людей, перепридумать процесс или ввести новые технологии.
