Порядок интерференции
Номер интерференционной полосы (от
нулевой полосы) — это порядокинтерференции. Для полосы с номером
m разность хода интерферирующих волн
равна m.
Если шумит частота света, то шумят и
длина волны, и число длин волн, которое
укладывается на оптической разности
хода для фиксированной точки экрана, и
порядок интерференции m.
Если порядок интерференции шумит на
единицу (m = 1), то на
единицу шумит и номер интерференционной
полосы для выбранной точки экрана. Этому
соответствует шумовое перемещение
интерференционной картины на расстояние,
равное ширине полосы. При таком перемещении
интерференционная картина полностью
“смазывается”. Найдем теперь, какое
изменение частоты и длины волны света
соответствует изменению порядка
интерференции на единицу.
Область высокой видности интерференционной картины при квазимонохроматическом источнике света
На границе “несмазанной” области
интерференционной картины порядок
интерференции m шумит на единицу (dm = 1).
Произведение mравно разности хода и, следовательно,
не шумит. Тогда(m)
= 0. Отсюда m+m0 иm/m/,
еслиm исчитать малыми положительными величинами.
Аналогично, из условия = c/n = const следует//,
где/— относительная ширина спектральной
линии излучения.
Из равенства m/m =/=/с учетомm = 1 получаем
два новых условия границы “несмазанной”
области интерференционной картины:
![]() =
=![]() и
и![]() =
=![]() .
.
Если теперь учесть, что порядок
интерференции — это разность хода,
выраженная в длинах волн (m = /),
то разность хода
=
![]() ,
,
определяет границу области экрана, в
которой хорошо различимы интерференционные
полосы.
Далее, для решения конкретной задачи
нужно найти область на экране, где
разность хода не превышает заданной
величины 2/.
Эта задача либо чисто геометрическая,
либо — геометрической оптики. Если
требуется найти максимальное число
наблюдаемых интерференционных полос,
то оно либо равно максимальному порядку
интерференции (m =/=/),
если наблюдаются полосы в одну сторону
от нулевой полосы, либо — вдвое больше
порядка интерференции.
Временная когерентность
Временная когерентность связана с
когерентностью вдоль луча. Когерентность
— это способность к интерференции.
Рассмотрим две точки на одном луче как
два возможных вторичных источника света
для наблюдения интерференционной
картины. При этом расстояние от каждой
из точек до мысленного экрана предполагается
одинаковым.
Возможный вариант оптической схемы
приведен на рис. 23. Здесь A и B — две
выбранные вдоль луча точки, в которые
мысленно поместим полупрозрачные
пластинки для получения интерференционной
картины на экране C. По условию задачи
AC = BC.

Рис. 23
Оптическая разность хода для
интерферирующих лучей 1 и 2, как видно
из рис. 23, равна AB. Если AB превышает
величину2/,
то, как указывалось выше, интерференционная
картина “смазывается”, и, следовательно,
вторичные источники света в точках A и
B оказываются некогерентными. Расстояние
между точками A и B, при котором это
начинает происходить, называется длиной
когерентности вдоль луча (продольной
когерентности). Обозначим его как L||,
тогда
L||=![]() .
.
Эта формула часто используется при
решении задач.
Наряду с понятием “продольная
когерентность”, используется близкое
ему понятие “временная когерентность”.
Фаза светового поля в точке A (см. рис.
23) в момент времени t равна фазе поля в
точке B в момент t+,
где— время
распространения света от A до B.
Следовательно, когерентность поля в
точках A и B в один момент времени t точно
такая же, как когерентность в одной
точке B, но в два разных момента времени
t и t+.
Время , за которое
свет проходит длину когерентности L||,
называетсявременемкогерентности.
Из известного выражения для скорости
света c/n =, получим
простое соотношение для времени
когерентности:
= L||![]() =
=![]()
![]() =
=![]()
![]() =
=![]()
![]() =
=![]() .
.
Можно посмотреть на когерентность
светового поля в точках A и B несколько
иначе. Длина волны шумит. Следовательно,
шумит число длин волн, которое укладывается
на отрезке AB. Пропорционально шумит
разность фаз в точках A и B. Результат
интерференции зависит от разности фаз.
Если разность фаз в точках A и B шумит
больше, чем на 2, то
поле в этих точках некогерентно, если
меньше, то поле когерентно. В такой форме
условие когерентности поля в точках A
и B не требует расположения этих точек
вдоль луча или рассмотрения поля в них
в один момент времени.
Подчеркнем, что условие “разность
фаз шумит больше, чем на 2”
не следует путать с условием “разность
фаз больше, чем 2”.
Соседние файлы в предмете Оптика
- #
- #
- #
- #
1. Интерференция световых волн
1.1. Интерференция от двух источников
1.2. Определим положение m-ого интерференционного максимума. Определим ширину интерференционного максимума
1.3. Интерференция на тонкой плёнке
1.4. Интерференция на клине (полосы равной толщины)
1.5. Кольца Ньютона
2. Дифракция волн
2.1. Дифракция Фраунгофера на узкой длинной щели в непрозрачном экране
2.2. Дифракция света на одномерной дифракционной решётке
2.3. Разрешающая способность дифракционной решётки
2.4. Дифракция рентгеновских лучей
3. Поляризация света
3.1. Поляризованный и естественный свет
3.2. Закон Малюса
3.3. Поляризация при отражении от диэлектриков. Закон Брюстера
3.4. Двойное лучепреломления
3.5. Искусственная оптическая анизотропия
3.6. Вращение плоскости поляризации
1. Интерференция световых волн
Интерференцией волн называется явление усиления колебаний в одних и ослабление колебаний в других точках пространства в результате наложения двух или нескольких волн, приходящих в эти точки пространства.
Для наблюдения устойчивой во времени интерференционной картины необходимы условия, при которых частоты, поляризация и разность фаз интерферирующих волн, были бы постоянными в течение всего времени наблюдения.
Интерферируют когерентные, монохроматические волны.
Когерентные волны – волны одинаковой частоты, колебания в которых отличаются постоянной разностью фаз, не изменяющейся со временем.
1.1. Интерференция от двух источников
Свет от одного источника с помощью непрозрачного экрана с двумя отверстиями даёт возможность получить два когерентных источника волн (схема Юнга). Расстояние между источниками (В, С) равно l. Длина волны, излучаемая источниками λ, расстояние до экрана, где наблюдается интерференция. О – центр экрана.
Пусть в точке М – экрана происходит наложение когерентных волн. Получим условие усиления и ослабления волнами друг друга. Расстояние от В источника до точки М – d1, от С до точки М – d2. Колебания точки М, вызываемые первым. источником волн: ![]() , а колебания, вызываемые 2-ым источником:
, а колебания, вызываемые 2-ым источником: ![]() , где А – амплитуда колебаний источников, ω – частота колебаний, k=2π/λ – βолновое число.
, где А – амплитуда колебаний источников, ω – частота колебаний, k=2π/λ – βолновое число.
Результирующее колебание точки М:
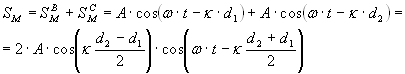 .
.
Амплитуда колебаний точки М:
AM=2Acos(k(d2-d1)/2) зависит от положения точки на экране и может быть равной 2А, если волны усиливают друг друга или нулю, если волны ослабляют друг друга.
Получим условие усиления или максимум интерференции. Чтобы АМ=2А, необходимо чтобы
|cos(k(d2-d1)/2)|=1
Это выполняется, если
![]() ;
; ![]() .
.
Значит d2-d1=±mλ.
Пусть d2-d1=Δd – разность хода интерферирующих лучей, а ΔФ=2π(d2-d1)/λ=2πΔd/λ – разность фаз интерферирующих волн, тогда
ΔΤ=2π/λ (d2-d1) =2π/λ Δd – ρоотношение между разность фаз и разность хода волн.
Если d2-d1=Δd=± mλ, γде m=0,1…, то АМ=2А и, следовательно, в этих точках пространства (экрана) наблюдается максимум интерференции. Разность фаз волн при этом будет равна ΔФ=±2πmλ/λ=±2πm.
Условие ослабления или минимум интерференции
Ам=0,
|cos(k(d2-d1)/2)|=0.
Это выполняется, если (k(d2-d1)/2)=±(2m+1)λ/2; следовательно
Δd=±(2m+1)λ/2.
Волны ослабляют друг друга, если разность хода при этом
ΔΤ=±2πmλ /(2λ)(2m+1)=±(2m+1)π,
m – называется порядком интерференционного максимума или минимума. В центре экрана наблюдается максимум нулевого порядка: d2-d1=Δd=0.
1.2. Определим положение m-ого интерференционного максимума. Определим ширину интерференционного максимума
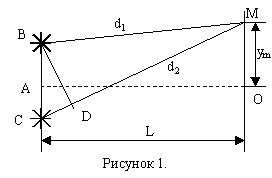
Рисунок 1. В точке М наблюдается максимум m-ого порядка. Обозначим расстояние от центра экрана до точки М – ym. Воспользуемся геометрией рисунка 1. Отрезок CD=d2-d1. Треугольники BCD и AMO – подобны. Из подобия
![]() .
.
Чтобы в точке наблюдался максимум m-ого порядка Δd=d2-d1=±mλ.
Ширина интерференционного максимума – расстояние между двумя соседними максимумами или минимумами.
Если положение m-ого максимума ym=mLλ/l, то положение (m+1)-го максимума ym+1=(m+1)Lλ/l. Тогда Δy= ym+1-ym=Lλ/l, γде Δy – ширина интерференционного максимума.
1.3. Интерференция на тонкой плёнке
На тонкую плёнку толщиной d и показателем преломления n падает монохроматический свет с длиной волны λ. Угол падения α. Среда около плёнки – воздух. Определим условие наблюдения максимума и минимума интерференции на тонкой плёнке. Интерферирующие лучи показаны на рисунке 2. Часть первого луча проходит через плёнку, преломляясь на границе раздела, отражается от нижней границы плёнки и выходит в точке С. Часть второго луча отражается от верхней поверхности плёнки и в точке С интерферирует с лучом 1. Обозначим Δ – оптическую разность хода волны.
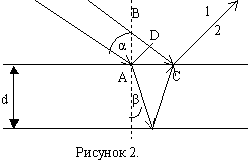
Оптическая разность хода волн 1 и 2:
Δ=n(AB+BC)-(DC+λ/2),
где n(AB+BC) – путь (оптический) первой волны,
(DC+λ/2) – путь второй волны. При отражении волны от поверхности плёнки, фаза волны меняется на π, т.к. отражение происходит от более плотной среды (nb=1);
n>nb.
Изменение фазы на π соответствует дополнительному ходу, равному λ/2.
Используя геометрию рисунка и законы преломления света, получим, что оптическая разность хода интерферирующихся волн равна:
![]() или
или ![]() ,
,
где β – угол преломления. Запишем условие усиления волнами друг друга или максимума интерференции: Δ=+– mλ. Значит:
![]() ,
,
![]() .
.
Толщина плёнки, при которой интерферирующие волны будут усиливать друг друга:
![]() ,
,
m – порядок интерференции (m=0,1,2…).
Если m=0, то
![]() – это минимальная толщина плёнки, при которой плёнка будет окрашена цветом соответствующим данной длине волн λ. Условие ослабления при интерференции или минимум интерференции:
– это минимальная толщина плёнки, при которой плёнка будет окрашена цветом соответствующим данной длине волн λ. Условие ослабления при интерференции или минимум интерференции:
Δ=(2m+1)λ/2.
![]() .
.
![]() .
.
Толщина плёнки, при которой плёнка будет казаться тёмной, т.к. наблюдается ослабление волнами друг друга, равна:
![]() , m=0,1,2…
, m=0,1,2…
1.4. Интерференция на клине (полосы равной толщины)
Две поверхности, расположение под малым углом α, образуют систему получившую название клин. Клин имеет разную толщину, а поэтому при освещении поверхности клина монохроматическим светом на поверхности клина будут наблюдаться интерференционные максимумы и минимумы (смотри интерференцию на плёнке), т.к. в одних точках поверхности толщина клина соответствует условию наблюдению максимума, а в других – условию минимума.
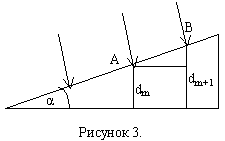
Определим ширину интерференционной полосы.
Пусть в точке А поверхности клина возникает максимум m-ого порядка. Толщина клина – dm+1. В точке В возникает максимум (m+1)-го порядка. Толщина плёнки в этом месте – dm+1. Условие наблюдения максимума при толщине dm и dm+1:
2dmn=(2m+1)λ/2; 2dm+1n=(2m+3) λ/2.
Вычтем из второго уравнения первое:
![]()
![]() .
.
dm+1-dm – разность толщины клина в местах наблюдения m-ого и (m+1)-го максимумов. На рисунке 3. Из прямоугольника:
AB=Δy=BD/sinα,
Δy – ширина интерференционной полосы
![]() .
.
Если угол при вершине мал, то ![]() ,
,
![]() , α[рад].
, α[рад].
Ширина интерференционного минимума или расстояния между соседними минимумами равна ширине интерференционного максимума.
1.5. Кольца Ньютона
Частым случаем полос равной толщины являются кольца Ньютона, которые наблюдаются в схеме, изображённой на рисунке 4.
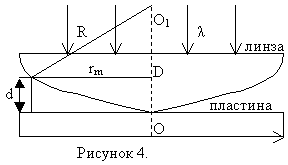
Плосковыпуклая линза с большим радиусом кривизны R выпуклой поверхностью лежит на плоской пластине и соприкасается с ней в точке О. Параллельный пучок света падает нормально на плоскую поверхность промежутка между линзой и пластиной. При наложении отраженных волн возникают интерференционные полосы равной толщины, имеющие вид колец. Вид этих колец в случае монохроматического света показан на рисунке 5.

В центре наблюдается минимум нулевого порядка (тёмное пятно). Центральный минимум окружён системой чередующихся окрашенных и тёмных колец, ширина и интенсивность которых постоянно убывает по мере удаления от центрального пятна.
Расчёт радиусом окрашенных и тёмных колец.
На рисунке 6 изображены интерферирующие волны, распространяются вдоль лучей 1 и 2.
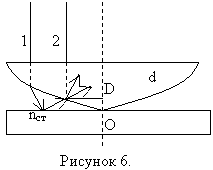
Разность хода волн равна:
![]() ,
,
где d – толщина зазора между линзой и пластиной, где наблюдается интерференция, n – показатель преломления прослойки, λ/2 – потеря полволны при отражении 1-ой волны от стеклянной пластинки (при условии n<nстекла).
Для наблюдения максимума интерференции или окрашенного кольца:
![]() ,
,
где m-ого порядка окрашенного кольца (m=1,2,3…).
Значит,![]() .
.
Для минимума интерференции ![]() , или
, или ![]() .
.
Радиус кольца определим, используя геометрию рисунка 4 OD=d. Из треугольника AO1D:
![]() .
.
Пренебрегая d2, получим: ![]() .
.
Если подставим значения d, соответствующее минимуму интерференции, получим выражение для радиуса окрашенного кольца m-ого порядка.
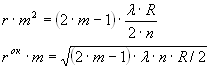
Если между линзой и пластинкой воздушная прослойка, то n=1.
2. Дифракция волн
Огибание волнами препятствий или отклонение от прямолинейного распространения в оптически неоднородной среде получило название дифракции.
Дифракция возникает при прохождении световых волн через отверстия в непрозрачных экранах, вблизи границ непрозрачных тел и т.д.
Различаются два вида дифракции световых волн: дифракция Френеля, или дифракция в расходящихся лучах, и дифракция Фраунгофера, или дифракция в параллельных лучах.
В первом случае на препятствие падает сферическая или плоская волна, а дифракционная картина наблюдается на экране, который находится позади препятствия на конечном расстоянии от него.
Во втором случае на препятствие падает плоская волна, а дифракционная картина наблюдается на экране, который находится в фокальной плоскости собирающей линзы, установленной на пути прошедшего через препятствие света.
2.1. Дифракция Фраунгофера на узкой длинной щели в непрозрачном экране
Ширина щели BC=b, длина волны, падающего света λ. Свет падает на щель нормально к её поверхности так что колебания во всех точках щели совершаются в одной фазе. О – оптический центр линзы. Дифракционная картина наблюдается на экране, который установлен в фокальной плоскости линзы. φ – угол дифракции, или угол отклонения от прямолинейного распространения падающих волн, который может принимать значения от 0 до ![]() .
.
F0 – центр дифракционной картины, где интерферируют лучи, угол дифракции которых равен нулю. В F наблюдается центральный дифракционный максимум.
Параллельные лучи BM и CN, идущие от краёв щели под углом дифракции φ, собираются линзой в побочном фокусе Fφ.
Линза обладает тем свойством, что оптические пути лучей BM и DNFφ, где D – основание перпендикуляра, опущенного из точки В на направление луча CN, одинаковы.
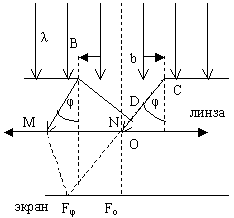
Результат интерференции в точке Fφ экрана зависит от разности хода волн 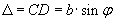 и длины волн падающего света. Щель можно разбить по ширине на зоны, которые получили название зон Френеля. Зоны имеют вид параллельных ребру В полосок, разность хода от краев которых равна λ/2.
и длины волн падающего света. Щель можно разбить по ширине на зоны, которые получили название зон Френеля. Зоны имеют вид параллельных ребру В полосок, разность хода от краев которых равна λ/2.
Число зон Френеля, укладывающихся в отверстие, равно:
![]() .
.
Все зоны излучают свет в рассматриваемом направлении с одинаковой амплитудой, причём колебания, вызываемые в точке Fφ двумя соседними зонами противоположны по фазе.
Поэтому, если число зон Френеля в отверстии чётное
![]() ,
,
где k=1,2…,
то под углом дифракции, удовлетворяющем условию, наблюдается дифракционный минимум. k – порядок дифракционного минимума.
Если число зон Френеля нечётное
![]() , где k=1,2…,
, где k=1,2…,
то под углом дифракции φ удовлетворяющему условию
![]()
наблюдается дифракционный максимум, соответствующий действию одной зоны Френеля (k – порядок дифракционного минимума).
Самый яркий центральный максимум наблюдается в главном фокусе линзы F0 (φ=0).
С ростом k ширина зон Френеля уменьшается и интенсивность максимумов быстро падает.
Амплитуда и интенсивность света в точке Fφ равны:
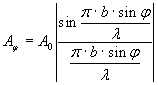 и
и 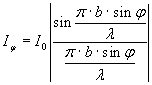 ,
,
где А0 – амплитуда, I0 – интенсивность центрального максимума (φ=0).
2.2. Дифракция света на одномерной дифракционной решётке
Одномерная дифракционная решётка представляет собой систему из большого число N одинаковых по ширине и параллельных друг другу щелей в экране, раздельных также одинаковыми по ширине непрозрачными промежутками.
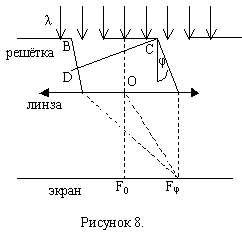
На рисунке 8 показаны только две соседние щели решётки. Величина d=a+b, называется периодом решётки (a=KC – ширина непрозрачного промежутка, b=BK – ширина щели,
![]() – ширина решётки). Если плоская монохроматическая волна с длиной λ падает на решётку нормально, то колебания во всех точках щели происходят в одинаковой фазе. Колебания, возбуждаемые в произвольной точке Fφ фокальной плоскости линзы каждой из щелей, совпадают по амплитуде, но отличаются по фазе. Для каждой пары соседних щелей сдвиг по фазе Δφ0 μежду этими колебаниями одинаков. Сдвиг по фазе зависит от разности хода волн, идущих от точек В и С под углом дифракции φ и длины волны λ.
– ширина решётки). Если плоская монохроматическая волна с длиной λ падает на решётку нормально, то колебания во всех точках щели происходят в одинаковой фазе. Колебания, возбуждаемые в произвольной точке Fφ фокальной плоскости линзы каждой из щелей, совпадают по амплитуде, но отличаются по фазе. Для каждой пары соседних щелей сдвиг по фазе Δφ0 μежду этими колебаниями одинаков. Сдвиг по фазе зависит от разности хода волн, идущих от точек В и С под углом дифракции φ и длины волны λ.
![]() ,
,
где ![]() – разность хода,
– разность хода,
D – основание перпендикуляра, опущенного из точки В на направление луча С.
![]() .
.
Условие наблюдения главных максимумов: ![]() или
или ![]() (k=1,2,3)
(k=1,2,3)
![]() ,
,
k – порядок интерференционного максимума.
Наибольший порядок спектра наблюдается под углом дифракции: ![]() ;
;
![]() ;
;
![]() ;
;
![]() ,
,
k может принимать только целые значения, поэтому результат, полученный от деления, нужно округлить до меньшего целого числа. Число максимумов наблюдаемых на экране ![]() . В центре экрана в точке F0 наблюдается центральный максимум (φ=0, k=0).
. В центре экрана в точке F0 наблюдается центральный максимум (φ=0, k=0).
Условие наблюдения главных минимумов:
![]() или
или ![]() ;
;
![]() ,
,
k – порядок главного минимума.
2.3. Разрешающая способность дифракционной решётки
Пусть на дифракционную решётку падает немонохроматический свет с длиной волны λ1 и λ2.
![]() ;
; ![]() (близкие длины волн).
(близкие длины волн).
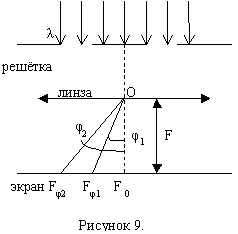
Период дифракционной решётке d, число щелей N. В спектре k-ого порядка на экране (рисунок 9) под углом φ1 наблюдается максимум для длины волны λ1, а под углом дифракции φ2 – максимум для волны с λ2. (Fφ1 θ Fφ2 – ρоответственно), максимумы для двух длин волн на экране пространственно разделены, если выполняется условие:
![]() (формула Рэлея).
(формула Рэлея).
Это условие получило название разрешающей способности дифракционной решётки. λ можно принять равным λ1 или λ2.
2.4. Дифракция рентгеновских лучей
Кристаллическую решётку твёрдых тел можно рассматривать как пространственную дифракционную решётку, период которой значительно меньше длины волны видимого света (![]() ). Для видимого света кристаллы являются оптически однородной средой.
). Для видимого света кристаллы являются оптически однородной средой.
В тоже время для рентгеновских лучей кристаллы представляют естественные кристаллические решётки (![]() ).
).
Дифракция рентгеновских лучей на кристаллах рассматривается как результат интерференции рентгеновского излучения, зеркально отражающегося от систем параллельных плоскостей, которые проходят через узлы кристаллической решётке. Расстояние d между двумя сетчатыми плоскостями называется межплоскостным расстоянием, а угол Θ между падающим лучом и плоскостью – угол скольжения. На рисунке 10 изображены две плоскости, которые проходят через углы кристаллической решётки (сетчатые или атомные плоскости).
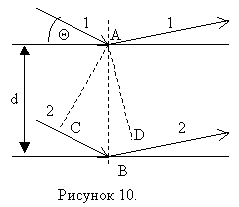
На поверхности кристалла под углом скольжения Θ падает плоская волна с длиной λ. Рентгеновские лучи не преломляются в кристалле, т.к. показатель преломления для них равен единице (примерно). Разность хода интерферирующих волн (лучи 1 и 2), отражённых от двух параллельных плоскостей равна ![]() . Отражение наблюдается в направлениях, соответствующих дифракционным максимумам, которые удовлетворяют условию Вульфа-Брэгга:
. Отражение наблюдается в направлениях, соответствующих дифракционным максимумам, которые удовлетворяют условию Вульфа-Брэгга:
![]() , m=1,2,3…
, m=1,2,3…
m – порядок дифракционного максимума
![]() ,
,
Θ – σгол скольжения для наблюдения максимума удовлетворяет этому условию.
Угол скольжения, соответствующий первому дифракционному максимуму (m=1)
![]() .
.
3. Поляризация света
3.1. Поляризованный и естественный свет
Из теории Максвелла следует, что свет является поперечной электромагнитной волной. Вектор напряжённости электрического поля (электрический или световой вектор) и вектор напряжённости магнитного поля (магнитный вектор) в световой волне колеблется в направлении перпендикулярном скорости распространения волны.
Линейно поляризованной волной называется волна, вектор ![]() которой не изменяют направление колебаний в пространстве.
которой не изменяют направление колебаний в пространстве.
Уравнение плоской монохроматической линейно-поляризованной волны, распространяющейся в направлении оси ОХ:
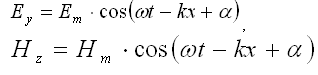 ,
,
где ω – циклическая частота, ![]() – волновое число, υ – скорость распространения волны.
– волновое число, υ – скорость распространения волны.
В каждой точке электромагнитного поля электрический вектор ![]() совершает гармонические колебания в плоскости XOY, которая называется плоскостью колебания.
совершает гармонические колебания в плоскости XOY, которая называется плоскостью колебания.
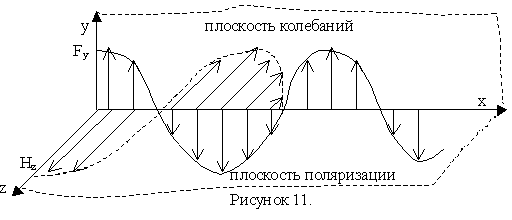
Магнитный вектор ![]() колеблется в плоскости XOZ – в плоскости поляризации.
колеблется в плоскости XOZ – в плоскости поляризации.
Световая волна со всевозможными одинаково вероятными направлениями колебаний электрического и магнитного векторов называется естественным светом.
В естественном свете плоскости поляризации меняют ориентацию в пространстве с течением времени.
Естественный свет можно представить в виде суперпозиции двух волн, которые поляризованы во взаимно-перпендикулярных плоскостях. Запишем уравнение естественного света только для электрического вектора волны:
![]() ;
;
![]() ,
,
где Ey, Ez – проекции электрического вектора ![]() на оси координат, α – сдвиг по фазе между колебаниями по Y и Z. Для естественного света Eoy=Eoz.
на оси координат, α – сдвиг по фазе между колебаниями по Y и Z. Для естественного света Eoy=Eoz.
Частично поляризованным называется свет, если в нём есть преимущественное направление колебаний вектора ![]()
(Eoy>>Eoz) или (Eoz>>Eoy).
Частично поляризованный свет можно рассматривать как смесь одновременно распространяющихся в одном и том же направлении естественного и линейно поляризованного.
Поляризацией света называется выделение линейно поляризованного света естественного или частично поляризованного. Для этой цели используются специальные устройства, называемые поляризаторами.
Для определения характера и степени поляризации используют устройства, называемые анализаторами.
Поляризатор можно использовать в качестве анализатора.
Анализатор или поляризатор условно изображают в виде решётки, “прутья” которой параллельны направлению колебаний вектора ![]() в проходящем сквозь неё свете.
в проходящем сквозь неё свете.
Если на такую решётку-анализатор падает естественный свет, то интенсивность проходящей волны не изменяется при вращении анализатора вокруг направления падающего луча вследствие того, что в естественном свете ни одно из направлений плоскости поляризации (плоскости колебаний) не является преобладающим.
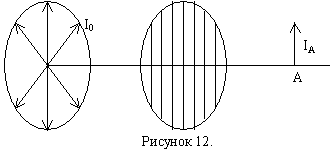
![]() ,
,
где I0 – интенсивность падающего естественного света,
k – коэффициент прозрачности анализатора,
IА – интенсивность проходящего света.
На выходе из анализатора-поляризатора имеем линейно поляризованную волну.
Если падающий свет частично поляризован, то IA при вращении анализатора изменяется в зависимости от ориентации его главной плоскости (т.е. направления прутьев) по отношению к преимущественному направлению колебаний вектора ![]() в падающем свете.
в падающем свете.
3.2. Закон Малюса
Пусть на анализатор падает линейно поляризованный свет интенсивностью I0. Оптическая ось анализатора О-О` (направление прутьев).
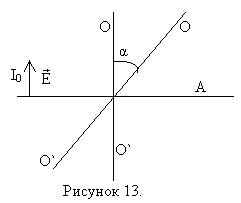
Определим интенсивность прошедшей волны в точке А, если анализатор повернуть на угол α вокруг направления распространения луча. Через анализатор пройдёт электрический вектор, величина ![]() . Т.к. интенсивность пропорциональна квадрату амплитуды, то
. Т.к. интенсивность пропорциональна квадрату амплитуды, то ![]() – это и есть закон Малюса.
– это и есть закон Малюса.
3.3. Поляризация при отражении от диэлектриков. Закон Брюстера
Направим на границу раздела двух диэлектриков (воздух, стекло) тонкий луч естественного света.
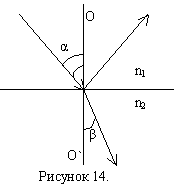
Часть световой волны отражается, а часть преломляется, распространяясь во второй среде. На рисунке: φ – угол падения луча, β – угол преломления, n2 – показатель преломления стекла, n1 – показатель преломления воздуха, n1=1.
Если на пути отражённого и преломлённого луча поставить анализатор, то можно исследовать поляризацию при отражении и преломлении.
Оказалось, что в общем случае отражённый и преломлённый лучи поляризованы частично. При некотором строго определённом для данной пары сред (диэлектриков) значение угла падения отражённый свет оказывается линейно поляризованным. Угол падения в этом случае называется углом Брюстера (φБ) или углом полной поляризации и определяется законом Брюстера:
![]() ,
,
где n21 – относительный показатель преломления среды.
3.4. Двойное лучепреломление
В оптически анизотронных кристаллах наблюдается явление двойного лучепреломления, которое состоит в том, что луч света падающий на поверхность кристалла, раздваивается на два преломлённых луча.
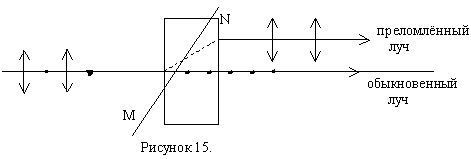
MN – оптическая ось кристалла.
Оптическая ось кристалла – направление в оптически анизотронном кристалле, вдоль которого свет распространяется, не испытывая двойного лучепреломления. Главной плоскостью или главным сечением одностороннего кристалла называется плоскость, проходящая через падающий луч и пересекающую его оптическую ось.
В одноосном кристалле один из преломлённых лучей подчиняется обычным законом преломления света. Этот луч лежит в плоскости падения. Волну, распространяющуюся вдоль направления этого луча, называют обыкновенной волной и обозначают буквой О. Показатель преломления для этой волны n0.
Вдоль второго луча распространяется необыкновенная волна. Показатель преломления луча для неё nе. угол преломления для необыкновенного луча зависит от того, как ориентирована поверхность пластинки по отношению к оптической оси кристалла MN. Угол преломления равен нулю в двух случаях:
а) если поверхность пластинки перпендикулярна к оптической оси (свет распространяется вдоль оптической оси, не испытывая двойного лучепреломления).
б) если поверхность пластинки параллельна оптической оси (свет распространяется в пластинке перпендикулярно оптической оси).
Двойное лучепреломление можно объяснить тем, что падающая на оптически анизотронный кристалл световая волна возбуждает две волны, распространяющиеся в кристалле эти по разным направлениям. В однослойном кристалле эти волны называются обыкновенными и необыкновенными волнами. Обыкновенные и необыкновенные волны линейно поляризованы во взаимно-перпендикулярных плоскостях.
В обыкновенной волне вектор ![]() направлен перпендикулярно к главной плоскости кристалла. Электрический вектор
направлен перпендикулярно к главной плоскости кристалла. Электрический вектор ![]() необыкновенной волны лежит в главной плоскости кристалла. Направления векторов
необыкновенной волны лежит в главной плоскости кристалла. Направления векторов ![]() в обыкновенных и необыкновенных волнах условно показаны на рисунке точками на обыкновенном луче и поперечными чёрточками на необыкновенном. Предполагается, что оба луча и пересекающая их оптическая ось MN кристалла лежат в плоскости рисунка.
в обыкновенных и необыкновенных волнах условно показаны на рисунке точками на обыкновенном луче и поперечными чёрточками на необыкновенном. Предполагается, что оба луча и пересекающая их оптическая ось MN кристалла лежат в плоскости рисунка.
3.5. Искусственная оптическая анизотропия
1. Оптически изотропное прозрачное вещество становится анизотропным, если его подвергнуть механической деформации. Это явление называется фотоупругостью, при одностороннем растяжении или сжатии изотропного тела вдоль оси OX оно приобретёт оптические свойства одноосного кристалла, оптическая ось которого параллельна ОХ . Разность показателей преломления обыкновенного (no) и необыкновенного (nе) лучей в направлении перпендикулярном оси ОХ, пропорциональна нормальному напряжению ![]() .
.
n0-nе=к![]()
где к- коэффициент пропорциональности, зависящий от свойств вещества.
2. Эффектом Керра называется возникновение оптической неоднородности у прозрачного изотропного диэлектрика, если его поместить во внешнее электрическое поле.
Под действием поля диэлектрик поляризуется и приобретает оптические свойства одноосного кристалла, оптическая ось которого совпадает по направлению с вектором ![]() напряженности внешнего поля.
напряженности внешнего поля.
Разность показателей преломления поляризованного диэлектрика для необыкновенного и обыкновенного лучей монохроматического света, распространяющегося перпендикулярно направлению вектора Е, удовлетворяет закону Керра.
nе-n0=Bв![]()
где ![]() -длина волны в вакууме, Вв-постоянная Керра.
-длина волны в вакууме, Вв-постоянная Керра.
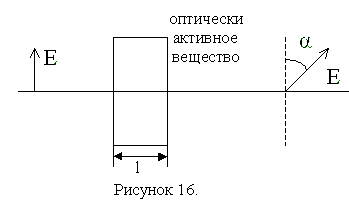
3. Эффектом Коттона-Мутона называется возникновение оптической анизотропии у некоторых изотропных вещество при помещении их в сильное внешнее магнитное поле.
В однородном магнитном поле вещество преображает оптические свойства одноосного кристалла, оптическая ось которого совпадает по направлению с вектором ![]() напряженности внешнего поля.
напряженности внешнего поля.
Разность показателей преломления вещества для необыкновенного и обыкновенного лучей монохроматического света при его распространении в направлении перпендикулярном вектору ![]() , пропорциональна
, пропорциональна ![]() .
.
![]()
с- постоянная Коттона – Мутона, ![]() -длина волны в вакууме.
-длина волны в вакууме.
3.6. Вращение плоскости поляризации
При прохождении линейно поляризованного света через некоторые вещества, называемые оптически активными, плоскость поляризации света поворачивается вокруг направления распространения луча.
Оптически активны некоторые кристалла (кварц, киноварь и др.) чистые жидкости и растворы (скипидар, раствор сахара в воде и др.)
В оптически активных кристаллах и чистых жидкостях угол поворота ![]() плоскости поляризации пропорционален толщине
плоскости поляризации пропорционален толщине ![]() слоя вещества, через который проходит свет:
слоя вещества, через который проходит свет:
![]()
Коэффициент пропорциональности ![]() называется удельным вращением, или постоянной вращения.
называется удельным вращением, или постоянной вращения.
Угол поворота плоскости поляризации при прохождении света пути ![]() в оптически активном растворе равен
в оптически активном растворе равен
![]()
С – объемно-массовая концентрация оптически активного вещества в растворе, D- плотность раствора, к=С/D- долевая концентрация по массе, ![]() – удельная вращения, зависит от природы оптически активного вещества.
– удельная вращения, зависит от природы оптически активного вещества.
Оптически неактивная среда под действием внешнего магнитного поля приобретает способность вращать плоскость поляризации света, распространяющегося вдоль направления поля.
Это явление называется эффектом Фарадея, или магнитным вращением плоскости поляризации.
![]()
где ![]() – угол поворота плоскости поляризации,
– угол поворота плоскости поляризации,
![]() -напряженность магнитного поля,
-напряженность магнитного поля,
![]() – длина пути световой волны,
– длина пути световой волны,
V – постоянная Верде.
Для интерференции света необходимым условием является получение когерентных световых пучков. В процессе его выполнения, свое применение находят различные приемы. До того времени, когда во всех приборах для наблюдения интерференции света появились лазеры, когерентные пучки получали с помощью разделения и последующего сведения световых лучей, испускаемым одним и тем же источником. На практике, это может быть осуществимо при помощи экранов и щелей, зеркал и преломляющих тел. Разберем некоторые из таких методов.

Рисунок 1
Метод Юнга и интерференция света
Первое наблюдение явления интерференции световых волн, а также и определение их длин были совершены Т. Юнгом. Роль источника света играет ярко освещенная щель S (рисунок 1), из которой световая волна попадает на две параллельные щели S, узкие равноудаленные щели S1 и S2. Исходя из этого, можно сделать вывод, что щели S1 и S2 в данной ситуации являются когерентными источниками. Интерференционная картина (область ВС) наблюдается на экране Э, установленном на определенном расстоянии параллельно S1 и S2.
Зеркала Френеля
Пара плоских соприкасающихся зеркал ОМ и ON расположены таким образом, что угол между их отражающими поверхностями, крайне близок к нулю (рис. 2). По этой причине угол j на изображении очень мал. Параллельно линии пересечения зеркал О, на некотором расстоянии r от нее, размещается прямолинейный источник света S, такой как, к примеру, узкая светящаяся щель. Зеркала отбрасывают на экран Э две цилиндрические когерентные волны, распространяющиеся так, как если бы они исходили из мнимых источников S1 и S2. Путь света от источника S к экрану Э преграждает непрозрачный экран Э1.
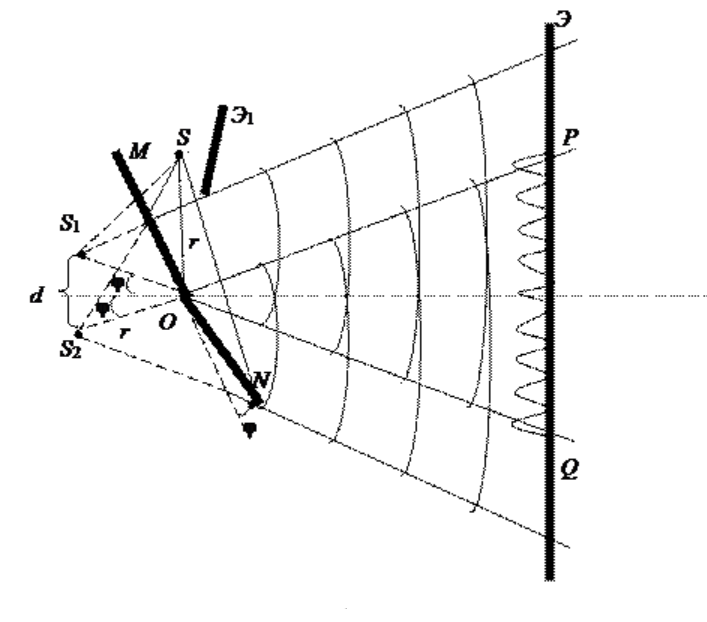
Рисунок 2
Луч OQ является отражением луча SO от зеркала ОМ, луч ОР, в свою очередь, представляет собой отражение луча SO от зеркала ON. Несложно понять, что угол между лучами ОР и OQ эквивалентен 2j. По той причине, что S1 и S2 располагаются относительно ОМ симметрично, длина отрезка OS1 равняется длине OS, другими словами r. Подобные рассуждения становятся результатом получения того же результата для отрезка OS2. Исходя из вышесказанного, можно заявить, что расстояние между источниками S1 и S2 равно d=2rsin(j)≫2pj.
Бипризма Френеля
Пара изготовленных из одного куска стекла призм с мизерным преломляющим углом q обладают одной общей гранью и называются бипризмой Френеля (рис. 3).
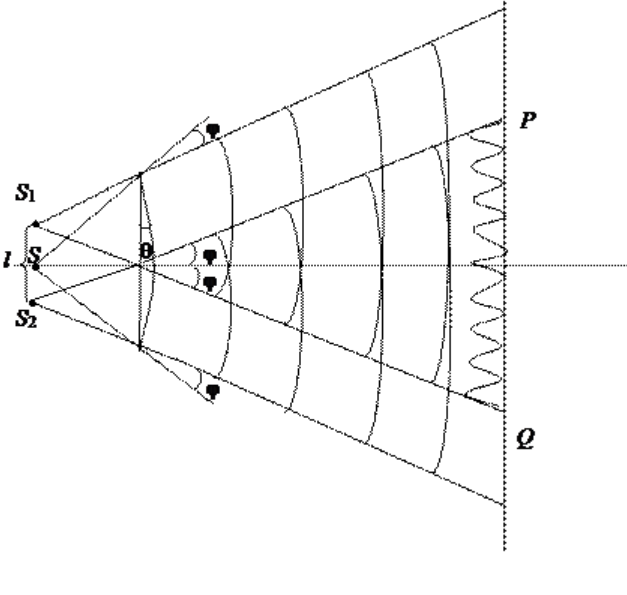
Рисунок 3
Параллельно данной грани на некотором расстоянии a от нее, находится прямолинейный источник света S. При условии, если преломляющий угол q призмы пренебрежительно мал, а углы падения лучей на грань призмы не сильно велики, то каждый луч отклоняется призмой на почти один и тот же угол, эквивалентный j=(n- l)q, где n представляет собой показатель преломления призмы. В случае, когда угол падения лучей на бипризму небольшой, все лучи отклоняются каждой из половин бипризмы на аналогичные углы. Как результат, появляется пара когерентных цилиндрических волн, испускаемых из мнимых источников S1 и S2 и принадлежащих той же плоскости, что и S.
Интерференция проявляется в качестве результата наложения двух расходящихся пучков света, расходящихся от двух когерентных источников, располагающихся на некотором расстоянии l от экрана Э, как это проиллюстрировано на рисунке 1. По данной причине порядок расчета и результат наложения волн будут абсолютно равны.
Область, в которой волны накладываются друг на друга, носит название поля интерференции.
Во всей этой области наблюдается чередование мест с максимальной и минимальной интенсивностью света. Если в поле интерференции поместить экран, то на нем будет проявляться интерференционная картина, выражающаяся в виде чередования светлых и темных полос.
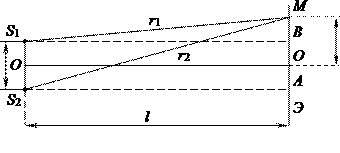
Рисунок 4
Пускай когерентные источники S1 и S2 расположены на некотором расстоянии d друг от друга, а экран Э вместе источниками находится в некой среде с абсолютным показателем преломления n.
Определим оптическую разность хода между когерентными волнами, распространяющимися от источников S1 и S2 в приведенную точку M на экране. Точка M размещена на расстоянии x от центра интерференционной картины.
∆=L2-L1=r2n-r1n=n(r2-r1),
где L2=r2n и L1=r1 n представляют собой оптические длины пути для первой и второй волн, а r2 и r1 – геометрические длины пути первой и второй волн.
Для случая треугольников S1АМ и S2ВМ будет справедливой следующая запись:
r22=l2+x+d22, r12=l2+x-d22⇒r22-r12=x+d22-x-d22⇒r2-r1r2+r1=2xd.
Так как,l≫d , можно заключить, что r2+r1≈2l, учитывая это, выражаем:
r2-r1r2+r1=2xd⇒r2-r12l=2xd⇒r2-r1=xdl.
Оптическая разность ход будет эквивалентна выражению:
∆=n(r2-r1)=nxdl.
Применяя условие интерференционных максимумов для оптической разности хода двух волн в формулу ∆=nr2-r1=nxdl, выведем координаты максимумов, другими словами, положение светлых полос, на экране
nxmaxdl=2mλ2 и xmax=mλlmd, m=0, 1, 2, 3….
В точке xmax=0 размещается максимум, соответствующий нулевой оптической разности хода. Порядок интерференции для такого максимума m=0. Он является центром интерференционной картины.
Подставляя условие интерференционных минимумов для оптической разности хода двух волн в приведенное выражение ∆=nr2-r1=nxdl, определим положение темных полос на экране или же координаты минимумов:
nxmindl=2m+1λ2 и xmin=2m+1λl2nd, m=0, 1, 2, 3…
Расстояние между двумя соседними максимумами (или минимумами), порядок m которых отличается на единицу, определяется как ширина интерференционной полосы.
∆x=xm-xm-1=mλlnd-(m-1)λlnd=λlnd.
Интерференция света
Если при наложении световых пучков интенсивность света оказывается не равной сумме интенсивностей, а периодически меняется от точки к точке, образуя систему темных и светлых линий, то говорят, что имеет место интерференция света.
Интерференция характерна для волн любой природы и сравнительно просто наблюдается на опыте для волн на поверхности воды или для звуковых волн. Наблюдать же интерференцию световых волн можно лишь при определенных условиях. Известно, что если некоторая поверхность освещается двумя лампочками, то освещенность в любой точке равна сумме освещенностей, создаваемых каждой лампочкой отдельно. В этом случае имеет место закон сложения интенсивностей, который выполняется для независимых источников света (ламп, свечей и т. п.). Однако возможны случаи, когда этот закон нарушается. Опыт показывает, что если накладываются пучки света, исходящие от одного и того же источника, но прошедшие разные оптические пути до места встречи, то при определенных условиях наложение таких пучков дает распределение интенсивности света в виде чередующихся светлых и темных полос — так называемую интерференционную картину.
Способность света давать интерференционную картину была названа когерентностью. Когерентность (от лат. cohaerens — находящийся в связи) — коррелирование протекание во времени и в пространстве нескольких колебательных или волновых процессов. Ясно, что когерентность связана со структурой света. Когерентный свет — это свет с высоко упорядоченной структурой, структура которого близка к плоской или сферической гармонической волне. В противоположность этому некогерентный свет, т. е. свет, не способный давать интерференцию и подчиняющийся закону сложения интенсивности, имеет сложную, случайную структуру светового поля, создаваемого обычными (нелазерными) источниками света. Свет таких источников образуется в результате наложения огромного числа элементарных сферических волн, испускаемых независимыми осцилляторами (атомами), и поэтому сильно отличается по своей структуре от идеальной гармонической волны. Свет имеет структуру хаотически модулированной волны. Поэтому в теории интерференции используются представление о случайном световом поле и методы статистического описания световых полей.
На опыте для наблюдения интерференции свет от одного источника нужно разделить на несколько пучков и затем наложить их друг на друга. Все существующие экспериментальные методы получения когерентных пучков из одного светового пучка можно разделить на два класса. В методе Деления волнового фронта пучок пропускается, например, через два близко расположенных отверстия в непрозрачном экране. Такой метод пригоден лишь при достаточно малых размерах источника. В другом методе пучок делился на одной или нескольких частично отражающих, частично пропускающих поверхностях. Этот метод Деления амплитуды может применяться и для протяженных источников. В зависимости от числа интерферирующих пучков различают двухлучевую и многолучевую интерференцию.
Интерференция монохроматического света
Монохроматическая идеализация оказывается достаточной для решения многих задач. В частности, при изучении явлений интерференции она пригодна для определения положения максимумов и минимумов интерференционной картины.
Рассмотрим суперпозицию двух монохроматических волн одинаковой частоты, которые возбуждают в интересующей нас точке пространства колебания одинакового направления с амплитудами А1 и А2. Если разность фаз этих колебаний равна D, то возникает результирующее колебание с амплитудой A, которую легко найти с помощью векторной (или фазовой) диаграммы (рис. 1) и теоремы косинусов:
![]() .
.
![]()


Р и с. 3.1.
Если разность фаз D постоянна во времени, то такие колебания (и волны) будут когерентными. Принимая во внимание, что интенсивность I Пропорциональна квадрату амплитуды, I~A2 , формулу перепишем так: ![]()
Последнее слагаемое в этой формуле и в называют Интерференционным слагаемым. Рассмотрим его влияние на результирующую интенсивность.
В точках пространства, где cos D > 0, I > I1 + I2; там же, где cos D < 0, I < I1 + I2. Следовательно, при суперпозиции когерентных волн происходит перераспределение интенсивности в пространстве: в одних местах возникают максимумы, в других – минимумы интенсивности, что и составляет суть явлений интерференции волн. Особенно (контрастно) отчетливо интерференция проявляемся тогда, когда I1 = I2. Тогда, согласно, I = 4I1, в максимумах и I = 0 в минимумах.
Если по каким-то причинам D непрерывно изменяется, причем так, что принимает с равной вероятностью любые значения, среднее по времени значение < cos D > = 0, последнее слагаемое в и обращается в нуль и можно записать: ![]()
Это значит, что в данном случае интенсивность результирующего колебания равна сумме интенсивностей, создаваемых каждой из волн в отдельности. Интерференция не наблюдается, а оба колебания не согласованы друг с другом и их называют некогерентными.
Общая интерференционная схема
Основной принцип любой интерференционной схемы по получению когерентных световых волн от обычных источников состоит в следующем: волну, излучаемую одним источником света, разделяют тем или иным способом на две части и затем накладывают их друг на друга подходящим способом. Образовавшиеся после разделения волны во всех схемах можно представить как бы исходящими из двух точечных источников S1 и S2 (действительных или мнимых — это не существенно). Поэтому общий подход к интерпретации получаемых результатов будет единым.
Если разность хода этих волн от источника до точки наблюдения не превышает некоторой характерной длины, то случайные изменения амплитуды и фазы световых колебаний в двух волнах происходят согласованно (когерентно) и можно будет наблюдать интерференционную картину.
Рассмотрим две волны, исходящие из когерентных источников S1 и S2 (рис.3. 2)


Р и с. 3.2
В области, где эти волны перекрываются — ее называют зоной интерференции — должна возникать система чередующихся максимумов и минимумов освещенности, которую можно наблюдать на экране.
Обозначим разность расстояний R2 и R1 от источников до интересующей нас точки М как D = R2 – R1. Эту величину называют Разностью хода. Если разность хода равна целому числу длин волн, т. е.:
![]() ,
, ![]() ,
,
Где M — порядок интерференции, то колебания, возбуждаемые в точке обеими волнами, будут происходить в фазе ![]() .
.
Таким образом, условие есть условие возникновения интерференционных максимумов.
В точках, для которых ![]() , а разность фаз
, а разность фаз ![]() , образуются минимумы.
, образуются минимумы.
В случае, когда волны от источников распространяются не в вакууме, а в среде с показателем преломления N, в формуле под D следует понимать не геометрическую, а оптическую разность хода интерферирующих волн: D = N(R2 –R1).
При этом L По-прежнему длина волны в вакууме.
Ширина интерференционной полосы
В практически важных случаях, sinQ < < 1, (рис.3. 2) и разность хода D можно записать как D ≈ QD, где D — расстояние между источниками S1 и S2. С другой стороны, Q ≈ X/![]() , где
, где ![]() расстояние от источников до экрана. Тогда для максимумов, согласно, получим:
расстояние от источников до экрана. Тогда для максимумов, согласно, получим:![]() ,откуда
,откуда ![]() .
.
В точке X = 0 расположен максимум, соответствующий нулевой разности хода. Для него порядок интерференции M = 0 . Это центр интерференционной картины. При переходе к соседнему максимуму M меняется на единицу, а X – на величину DX, которую называют шириной интерференционной полосы. Таким образом,![]() или
или ![]() ,
,
Где Y — угол, под которым видны оба источника из центра экрана, Y = D/![]() . Из формулы видно, что для увеличения ширины полосы следует увеличивать
. Из формулы видно, что для увеличения ширины полосы следует увеличивать ![]() , или уменьшать D, т. е. уменьшать угловое расстояние Y между источниками.
, или уменьшать D, т. е. уменьшать угловое расстояние Y между источниками.
Для получения более яркой интерференционной картины в качестве источников S1 и S2 используют две щели (или изображения исходного источника — щели S), и интерференционная картина будет иметь вид чередующихся светлых и темных полос, параллельных данным щелям.
Распределение интенсивности
Рассмотрим идеализированный случай, когда источники S1 и S2 строго монохроматические. В интересующую нас точку экрана колебания от этих источников будут приходить практически с одинаковой амплитудой, A1 = A2 = A0.
Тогда, согласно,![]() ,
,
Где D – разность фаз, которая зависит от разности хода D как ![]() .
.
В нашем случае, ![]() , следовательно
, следовательно ![]() .
.
Переходя к интенсивности и учитывая формулу, получим![]() ,
,
Где ![]() ; I0 – интенсивность в максимумах, в минимумах интенсивность равна нулю. Полученное идеализированное распределение интенсивности I(X) представлено на рис.3 2.
; I0 – интенсивность в максимумах, в минимумах интенсивность равна нулю. Полученное идеализированное распределение интенсивности I(X) представлено на рис.3 2.
ПОРЯДОК ИНТЕРФЕРЕНЦИИ
- ПОРЯДОК ИНТЕРФЕРЕНЦИИ
-
- ПОРЯДОК ИНТЕРФЕРЕНЦИИ
-
величина, равная разности хода интерферирующих лучей, выраженной в длинах световых волн (см. ИНТЕРФЕРЕНЦИЯ СВЕТА). Если интерферирующие пучки отражаются от к.-л. поверхности и при этом происходит изменение фазы, то в П. и. входит алгебр. сумма происходящих при этом скачков фаз, выраженная в единицах длин волн (см. ОТРАЖЕНИЕ СВЕТА). Целые и полуцелые значения П. и. соответствуют максимумам и минимумам интерференционной картины. В реальных устройствах, предназначенных для наблюдения интерференции, П. и. меняется от единиц (Френеля зеркала, Ньютона кольца, двухлучевые интерферометры) до 106 и более (эталон Фабри — Перо). Чем выше П. и., тем более монохроматичным должен быть свет для наблюдения интерференц. картины.
Физический энциклопедический словарь. — М.: Советская энциклопедия.
.
1983.- ПОРЯДОК ИНТЕРФЕРЕНЦИИ
-
– величина, равная разности хода интерферирующих лучей, выраженной в длинах световых волн. Если интерферирующие пучки отражаются от к.-л. поверхности и при этом происходит изменение фазы, то в П. и. входит алгебраич. сумма всех скачков фаз, выраженная в радианной мере (см. Отражение света). При совпадении нач. фаз источников целые значения П. и. соответствуют максимумам, а полуцелые – минимумам интерференц. картины. В реальных устройствах, предназначенных для наблюдения интерференции, П. и. меняется от единиц ( Френеля зеркала, Ньютона кольца, двухлучевые интерферометры )до
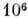 и более ( интерферометр Фабри– Перо). Чем выше П. и., тем более монохроматич-ным должен быть свет для наблюдения интерференц. картины.
и более ( интерферометр Фабри– Перо). Чем выше П. и., тем более монохроматич-ным должен быть свет для наблюдения интерференц. картины.См. также ст. Интерференция света и лит. при ней.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия.
Главный редактор А. М. Прохоров.
1988.
.
Полезное
Смотреть что такое “ПОРЯДОК ИНТЕРФЕРЕНЦИИ” в других словарях:
-
порядок интерференции — Величина, равная алгебраической сумме скачков фаз, выраженных в единицах 2я, и разности хода интерферирующих лучей, выраженной в длинах световых волн. [Сборник рекомендуемых терминов. Выпуск 79. Физическая оптика. Академия наук СССР. Комитет… … Справочник технического переводчика
-
порядок интерференции — interferencijos eilė statusas T sritis fizika atitikmenys: angl. order of interference vok. Interferenzordnung, f rus. порядок интерференции, m pranc. numéro d’ordre de la frange d’interférence, m; ordre d’interférence, m … Fizikos terminų žodynas
-
порядок интерференции — [order of interference] разность хода интерферированных лучей света, деляющая на длину их волны (Смотри Интерференция света). Чаще всего рассматривается порядки интерференции, равные целым числам (длин волн): 0, +1, ±2…, т. к. именно в этих… … Энциклопедический словарь по металлургии
-
Порядок интерференции — Разность хода интерферирующих лучей света, деленная на длину их волны (см. Интерференция света). Чаще всего рассматривают П. и., равные целым числам (длин волн): 0 ± 1, ± 2…, т.к. именно в этих случаях наиболее сильно проявляется эффект … Большая советская энциклопедия
-
порядок реакции — [reaction order] понятие химической кинетики. Порядок реакции определяется как сумма показателей степеней n1 и n2 в уравнении: r = k[A1]n1r • [A2]n2 выражающем зависимость скорости реакции r от концентраций [А1] и [A2 … Энциклопедический словарь по металлургии
-
порядок оси симметрии — [order of symmetry] число, показывающее, сколько раз в полном повороте на 360° вокруг оси симметрии кристалл или узлы кристаллической решетки совместятся. Смотри также: Порядок порядок реакции порядок интерференции … Энциклопедический словарь по металлургии
-
Порядок — [order]: Смотри также: порядок реакции порядок интерференции ближний порядок порядок оси симметрии дальний порядок … Энциклопедический словарь по металлургии
-
дальний порядок — [long range order] закономерное расположение атомов или молекул в твердых телах и жидкостях на неограниченно больших расстояниях в пределах всего макроскопического образца. Дальний порядок характерен для правильных кристаллических тел, металлов и … Энциклопедический словарь по металлургии
-
ближний порядок — [short range order] не полное статистическое распределение атомов компонентов в узлах кристаллической решетки упорядоченных твердых растворов, т.е. преимущественно окружение атома атомами другого компонента. Ближний порядок возникает в том случае … Энциклопедический словарь по металлургии
-
ИНТЕРФЕРОМЕТР — измерительный прибор, основанный на интерференции волн. Существуют И. для звук. волн и для эл. магн. волн (оптических и радиоволн). Оптич. И. применяются для измерения оптич. длин волн спектр. линий, показателей преломления прозрачных сред, абс.… … Физическая энциклопедия
