Как найти порядок комплексного числа

Числовые последовательности и ряды с комплексными членами

Последовательности комплексных чисел

Основные понятия, связанные с последовательностями комплексных чисел, вводятся так же, как в действительной области.

1. Если каждому натуральному числу n~(forall ninmathbb{N}) поставлено в соответствие комплексное число $z_n~(z_ninmathbb{C})$ , то говорят, что задана последовательность комплексных чисел (последовательность с комплексными членами): $bigl{z_nbigr}_{n=1}^{infty}$ .

2. Последовательность z_n называется ограниченной, если существует число M>0 , такое, что для любого ninmathbb{N} выполняется неравенство |z_n|<M . Последовательность, не являющаяся ограниченной, называется неограниченной: для $(forall Min mathbb{R})(exists n^0)$ , что $|z_{n^0}|>M$ .

3. Последовательность z_n называется бесконечно малой, если для любого числа varepsilon>0 найдется номер N(varepsilon) , такой, что для всех , удовлетворяющих условию n>N(varepsilon) , выполняется неравенство |z_n|<varepsiloncolon

z_n — бесконечно малая Leftrightarrow~ forall varepsilon>0~ exists N(varepsilon)colon, n>N(varepsilon),~ |z_n|<varepsilon .

Правило 1.1. Чтобы по определению доказать, что данная последовательность z_n является бесконечно малой, следует:

1) записать неравенство |z_n|<varepsilon , где — любое, varepsilon>0 ;
2) решить это неравенство относительно ;
3) из полученного решения n>N(varepsilon) , определить .

4. Последовательность z_n называется бесконечно большой, если для любого числа M~(Minmathbb{R}) найдется номер N(M) , такой, что для всех , удовлетворяющих условию n>N(M) , выполняется неравенство |z_n|>M . Геометрически это означает, что члены последовательности z_n для n>N(M) расположены в окрестности бесконечно удаленной точки, в области |z|>M .

Из определений бесконечно малой и бесконечно большой последовательностей легко установить связь между ними. Если a_n — бесконечно малая последовательность, то $z_n=frac{1}{alpha_n}$ — бесконечно большая, и наоборот, если z_n — бесконечно большая последовательность, то $alpha_n=frac{1}{z_n}$ — бесконечно малая.

5. Число A~(Aneinfty,, Ainmathbb{C}) называется пределом последовательности z_n , если последовательность alpha_n=z_n-A является бесконечно малой (обозначается $A=lim_{ntoinfty}z_n$ ):

$A=lim_{ntoinfty}z_n~ Leftrightarrow~ forall varepsilon>0~~ exists N(varepsilon)colon, |z_n-A|<varepsilon$ для n>N(varepsilon) .

Из определения получаем правило.

Правило 1.2.Чтобы доказать, что заданное число является пределом данной последовательности z_n , следует:

1) составить последовательность alpha_n=z_n-A ;
2) доказать, что alpha_n — бесконечно малая последовательность (см. правило 1.1).

6. Последовательность, имеющая предел, называется сходящейся, а последовательность, не имеющая предела, — расходящейся.

Расходящейся последовательностью является любая неограниченная последовательность, в частности бесконечно большая. Для бесконечно большой последовательности принято обозначение $lim_{ntoinfty}z_n=infty$ .

Интерпретация комплексных чисел точками сферы Римана придает этому равенству большую наглядность. Действительно, образами точек последовательности z_n на сфере Римана являются точки M_n с координатами

$xi_n=frac{x_n}{1+|z_n|^2},quad eta_n=frac{y_n}{1+|z_n|^2},quad varphi_n= frac{|z_n|^2}{1+|z_n|^2}$ , где $x_n=operatorname{Re}z_n,~ y_n=operatorname{Im} z_n$ .

Эти соотношения получаются из равенств $x=frac{xi}{1-varphi},~ y=frac{eta}{1-varphi}$ и уравнения сферы xi^2+eta^2=varphi(1-varphi) (см. замечание 1.2). Поскольку |x_n|leqslant |z_n|,~ |y_n|leqslant|z_n| , то условие $lim_{ntoinfty} z_n=infty$ означает, что последовательность точек M_n сходится к точке сферы Римана, так как при этом

$lim_{ntoinfty}xi_n=0,qquad lim_{ntoinfty}eta_n=0,qquad lim_{ntoinfty} varphi_n=1.$

Пример 1.36. Записать пять первых членов последовательностей: а) z_n= i^n ; б) omega_n=(1+i)^n .

Решение

Подставляя последовательно значения n=1,2,ldots,5 , получаем:

а) z_1=i;~~ z_2=-1;~~ z_3=-i;~~ z_4=1;~~ z_5=i ;

б) omega_1=1+i,~~ omega_2=(1+i)^2=2i,~~ omega_3=(1+i)^3= 2i(1+i)= -2+2i,

omega_4= (1+i)^4= bigl((1+i)^2bigr)^2= (2i)^2=-4,~~ omega_5=(1+i)^5= (1+i)^4(1+i)= -4-4i.

Пример 1.37. Исследовать на ограниченность последовательности: z_n=i^n,~ omega_n=(1+i)^n .

Решение. Так как |z_n|=|i^n|=1 , то для любого nin mathbb{N} выполняется, например, неравенство |z_n|<2 . По определению последовательность z_n=i^n — ограниченная.

Для второй последовательности, используя свойство модуля, находим

$|omega_n|= bigl|(1+i)^nbigr|= bigl(|1+i|bigr)^n= bigl(sqrt{2}bigr)^n.$

Далее рассматриваем неравенство $(sqrt{2})^n>M$ при любом и решаем его относительно $ncolon, nlgsqrt{2}>lg M,~ n>frac{2lg M}{lg 2}$ . В качестве n_0 можно взять любое $N(M)=frac{2lg M}{lg2}$ . По определению последовательность неограниченная.

Пример 1.38. Доказать, что последовательность z_n вида z_n= q^n является бесконечно малой, если |q|<1 , и бесконечно большой, если |q|>1 .

Решение

Пример 1.39. Применяя определение, доказать, что $lim_{ntoinfty} frac{n-2ni}{n+2}=1-2i$ .

Решение

Используем правило 1.2:

1) составляем последовательность $alpha_n= z_n-A= frac{n-2ni}{n+2}-(1-2i)= frac{4i-2}{n+2}$ ;

2) доказываем, что alpha_n — бесконечно малая. Находим $|alpha_n|= frac{|4i-2|}{n+2}= frac{sqrt{20}}{n+2}$ . Так как $lim_{ntoinfty}|alpha_n|=0$ , то |alpha_n|<varepsilon,~ n>N(varepsilon) и, следовательно, alpha_n — бесконечно малая.

Исследование сходимости последовательности комплексных чисел и нахождение ее предела (в случае сходимости) можно свести к соответствующей задаче дли последовательностей с действительными членами. А именно имеет место следующее утверждение.

Утверждение 1.2. Для сходимости последовательности z„ необходимо и достаточно, чтобы сходились две последовательности $operatorname{Re}z_n=x_n$ и $operatorname{Im}z_n=y_n$ , причем

$lim_{ntoinfty}z_n= lim_{ntoinfty}operatorname{Re}z_n+ ilim_{ntoinfty} operatorname{Im}z_n$ , иначе $lim_{ntoinfty}z_n= lim_{ntoinfty}(x_n+ iy_n)=c~ Leftrightarrow~ begin{cases}limlimits_{ntoinfty}x_n=a,\ limlimits_{ntoinfty}y_n=bend{cases} c=a+bi.$

Из утверждения 1.2 и свойств сходящихся последовательностей действительных чисел вытекают следующие свойства последовательностей с комплексными членами. Эти свойства приведем в виде утверждения.

Утверждение 1.3. Если $lim_{ntoinfty}z_n=a,~ lim_{ntoinfty}u_n=b$ , то

$lim_{ntoinfty}(z_n+u_n)=a+b;quad lim_{ntoinfty}z_ncdot u_n= acdot b;quad lim_{ntoinfty}frac{z_n}{u_n}= frac{a}{b};quad u_nne0,quad n=1,2,ldots;quad bne0.$

Пример 1.40. Вычислить предел последовательности с комплексными членами $lim_{ntoinfty}frac{2+3ni}{i-n}$ .

Решение

Первый способ. Используем утверждение 1.2. Обозначим $z_n=frac{2+3ni}{i-n}$ и найдем $x_n=operatorname{Re}z_n,~ y_n=operatorname{Im}z_n$ , выполняя операцию деления комплексных чисел:

$frac{2+3ni}{i-n}=frac{(2+3ni)(n+i)}{-(n-i)(n+i)}= frac{-n+i(3n^2+2)}{-(n^2+1)}= frac{n}{n^2+1}+ i,frac{-(3n^2+2)}{n^2+1},.$

Получаем $x_n=frac{n}{n^2+1},~ y_n=frac{-(3n^2+2)}{n^2+1}$ . Найдем пределы последовательностей действительных чисел:

$lim_{ntoinfty}frac{n}{n^2+1}=0,quad lim_{ntoinfty}frac{-(3n^2+2)}{n^2+1}=-3$ , то есть a=0,~b=-3 .

Следовательно, $lim_{ntoinfty}z_n=a+bi=-3i$ .

Второй способ. Используем утверждение 1.3, применяя соответствующие методы, как в действительном анализе. Находим

$lim_{ntoinfty}frac{2+3ni}{i-n}=lim_{ntoinfty}frac{frac{2}{n}+3i}{frac{i}{n}-1}= -3i$ , так как здесь $frac{i}{n}$ и $frac{2}{n}$ бесконечно малые.

Ряды с комплексными членами

Основные понятия, связанные с рядами в комплексной области, вводятся так же, как в действительной области.

1. Выражение вида z_1+z_2+ldots+z_n+ldots , где z_1,z_2,ldots, z_n,ldots — последовательность комплексных чисел, называется числовым рядом с комплексными членами (обозначается $sum_{n=1}^{infty}z_n$ ).

2. Сумма $z_1+z_2+ldots+z_n=sum_{k=1}^{n}z_k$ называется n-й частичной суммой ряда, обозначается S_n последовательность S_1,S_2,ldots,S_n,ldots — последовательность частичных сумм ряда.

3. Ряд $sum_{n=1}^{infty}z_n$ называется сходящимся, если сходится последовательность его частичных сумм, т.е. существует $lim_{ntoinfty}S_n$ . Этот предел называется суммой ряда:

$S=lim_{ntoinfty}S_n,~~S$ — сумма ряда; $S-S_n=sum_{k=1}^{infty} a_{n+k}$ — остаток ряда.

4. Ряд $sum_{n=1}^{infty}z_n$ называется абсолютно сходящимся, если сходится ряд, составленный из модулей его членов, т.е. ряд $sum_{n=1}^{infty}|z_n|$ . Заметим, что ряд $sum_{n=1}^{infty}|z_n|$ — ряд с действительными положительными членами.

Признаки сходимости рядов с комплексными членами

Критерий Коши. Дня сходимости ряда $sum_{n=1}^{infty}z_n$ необходимо и достаточно, чтобы для любого varepsilon>0 можно было найти N(varepsilon) , такое, что для любого n>N(varepsilon) и любого (натурального) выполнялось неравенство $|z_{n+1}+ldots+z_{n+m}|< varepsilon$ .

Необходимый признак сходимости ряда. Если ряд $sum_{n=1}^{infty}z_n$ сходится, то $lim_{ntoinfty}z_n=0$ .

Отсюда следует, что условие $lim_{ntoinfty}z_nne0$ является достаточным условием расходимости ряда $sum_{n=1}^{infty}z_n$ .

Исследование сходимости ряда с комплексными членами можно свести к соответствующей задаче для рядов с действительными членами.

Утверждение 1.4. Дня сходимости ряда с комплексными членами необходимо и достаточно, чтобы сходились два ряда с действительными членами:

$sum_{n=1}^{infty}x_n= sum_{n=1}^{infty}operatorname{Re}z_n$ и $sum_{n=1}^{infty}y_n= sum_{n=1}^{infty} operatorname{Im}z_n$ ,

причем

$sum_{n=1}^{infty}z_n=Squad Leftrightarrowquad sum_{n=1}^{infty}x_n=a,quad sum_{n=1}^{infty}y_n=b,quad S=a+bi.$

Правило 1.3. Чтобы исследовать ряд с комплексными членами на сходимость, необходимо:

1) для данного ряда $sum_{n=1}^{infty}z_n$ найти $operatorname{Re}z_n= x_n$ и $operatorname{Im}z_n=y_n$ ;

2) составить ряды $sum_{n=1}^{infty}x_n$ и $sum_{n=1}^{infty}y_n$ и исследовать их на сходимость, как ряды с действительными членами. Если оба ряда сходятся, то ряд $sum_{n=1}^{infty}z_n$ , сходящийся, если хотя бы один из рядов $sum_{n=1}^{infty}x_n$ или $sum_{n=1}^{infty}y_n$ расходится, то ряд $sum_{n=1}^{infty}z_n$ , расходящийся.

Правило 1.4. Чтобы исследовать комплексный ряд на абсолютную сходимость, необходимо:

1) составить ряд $sum_{n=1}^{infty}|z_n|$ , членами которого являются модули членов данного ряда $sum_{n=1}^{infty}z_n$ ;

2) исследовать полученный ряд на сходимость, как ряд с действительными положительными членами. Для этого могут быть использованы признаки сходимости таких рядов: признак Даламбера, Коши, признаки сравнения, интегральный признак.

Если ряд $sum_{n=1}^{infty}|z_n|$ сходится, то ряд $sum_{n=1}^{infty}z_n$ сходится абсолютно.

Если $sum_{n=1}^{infty}|z_n|$ расходится, то $sum_{n=1}^{infty}z_n$ может быть либо расходящимся, либо сходящимся; в последнем случае он называется условно сходящимся.

Признаки абсолютной сходимости рядов с комплексными членами

А. Признак Даламбера. Если $lim_{ntoinfty}left| frac{z_{n+1}}{z_n}right|=|q|<1$ , то ряд $sum_{n=1}^{infty}z_n$ сходится абсолютно.

Б. Признак Коши. Если $lim_{ntoinfty}sqrt[LARGE{n}]{|z_n|}= |q|<1$ , то ряд $sum_{n=1}^{infty}z_n$ сходится абсолютно.

В. Признак сравнения. Если forall n,~|z_n|<|alpha_n| и $sum_{n=1}^{infty} |alpha_n|$ сходится, то ряд $sum_{n=1}^{infty}z_n$ , сходится абсолютно.

Замечание 1.3. При исследовании на сходимость рядов $sum_{n=1}^{infty}z_n$ , где z_n — дробно-рациональное, или дробно-иррациональное выражение от , используется признак сравнения; при этом в качестве ряда $sum_{n=1}^{infty}|alpha_n|$ выбирается ряд вида $sum_{n=1}^{infty}frac{1}{n^{alpha}}$ , который, как доказывается в действительном анализе, сходится при alpha>1 и расходится при alphaleqslant1 .

Пример 1.41. Исследовать на сходимость ряды; в случае сходимости найти суммы рядов:

$bold{1)}~ sum_{n=1}^{infty}!left(frac{i}{2}right)^n;qquad bold{2)}~ sum_{n=1}^{infty} !left(frac{1}{3^n}+i,frac{1}{2^n}right)!.$

Решение

Пример 1.42. Исследовать на сходимость ряды:

$bold{1)}~ sum_{n=1}^{infty}frac{n^2+3in-1}{2in^2-sqrt{3}};qquad bold{2)}~ sum_{n=1}^{infty}frac{n^2+3in-1}{2in^4-sqrt{3}}.$

Решение

Для этих рядов нахождение x_n и y_n затруднительно, поэтому будем пользоваться другими признаками:

1) здесь $lim_{ntoinfty}z_n=frac{1}{2i}ne0$ , ряд расходится, так как не выполняется необходимый признак сходимости;

2) для этого ряда $lim_{ntoinfty}z_n=0$ , необходимый признак выполняется, но в силу его недостаточности требуется дальнейшее исследование. Воспользуемся замечанием 1.3. Применим признак сравнения с рядом $sum_{n=1}^{infty}frac{1}{n^2}colon$

$lim_{ntoinfty}frac{|z_n|}{1 !!not{phantom{|}}, n^2}= lim_{ntoinfty} left|frac{n^4+3in^3-n^2}{2in^4-sqrt{3}}right|= lim_{ntoinfty}frac{|n^4-n^2+3in^3|}{|sqrt{3}-2in^4|}= frac{1}{2},.$

Итак, по признаку сравнения ряд сходится абсолютно.

Пример 1.43. Доказать, что сходится абсолютно ряд $sum_{n=1}^{infty} frac{(2i)^n}{n!}$

Решение

Используя признак Даламбера, рассмотрим $lim_{ntoinfty} left|frac{z_{n+1}}{z_n}right|colon$

$lim_{ntoinfty}left|frac{(2i)^{n+1}cdot n!}{(n+1)!cdot (2i)^n}right|= lim_{ntoinfty}left|frac{2i}{n+1}right|= lim_{ntoinfty}frac{2}{n+1}=0<1.$

Так как $lim_{ntoinfty} left|frac{z_{n+1}}{z_n}right|<1$ , то ряд сходится абсолютно.

Заметим, что сходится абсолютно любой ряд вида $sum_{n=1}^{infty}frac{z^n}{n!}$ , где — любое комплексное число.

Свойства абсолютно сходящихся рядов с комплексными членами

Как и в действительной области, для абсолютно сходящихся рядов с комплексными членами справедливы те же правила действий, что и с конечными суммами.

1. В абсолютно сходящихся рядах допустима любая перестановка и группировка членов (даже бесконечного их числа).

Например, если ряд $sum_{n=1}^{infty}z_{n}$ сходится абсолютно, то сходятся и ряды, полученные группировкой членов этого ряда, например $sum_{n=1}^{infty}z_{2n}$ и $sum_{n=1}^{infty}z_{2n-1}$ — ряды членов с четными и нечетными номерами, причем $sum_{n=1}^{infty}z_{n}= sum_{n=1}^{infty}z_{2n-1}+ sum_{n=1}^{infty}z_{2n}$ .

2. Абсолютно сходящиеся ряды можно перемножать по правилу перемножения многочленов.

Пример 1.44. Найти произведение рядов $sum_{n=0}^{infty} frac{z_1^n}{n!}$ и $sum_{n=0}^{infty}frac{z_2^n}{n!}$

Решение

Как отмечено в примере 1.43, ряды вида $sum_{n=0}^{infty} frac{z^n}{n!}$ — абсолютно сходятся при любом фиксированном . Поэтому сомножителями являются абсолютно сходящиеся ряды. Перемножим их по правилу перемножения многочленов:

$begin{aligned}sum_{n=0}^{infty} frac{z_1^n}{n!}cdot sum_{n=0}^{infty} frac{z_2^n}{n!}&= !left(1+z_1+frac{z_1^2}{2!}+ldots+frac{z_1^{n-k}}{(n-k)!}+ ldots+ frac{z_1^n}{n!}+ ldotsright)! cdot! left(1+z_2+frac{z_2^2}{2!}+ldots+ frac{z_2^k}{k!}+ ldots+ frac{z_2^n}{n!}+ldotsright)!=\ &=1+(z_1+z_2)+left(frac{z_1^2}{2!}+ z_1z_2+ frac{z_2^2}{2!} right)+ldots+left(frac{z_1^n}{n!}+ frac{z_1^{n-1}z_2}{(n-1)!}+ ldots+ frac{z_1^{n-k}z_2^k}{(n-k)!k!}+ ldots+ frac{z_2^n}{n!}right)+ldots end{aligned}$

Перепишем последнее выражение следующим образом:

$1+(z_1+z_2)+ frac{1}{2!}bigl(z_1^2+2z_1z_2+z_2^2bigr)+ ldots +frac{1}{n!}bigl(z_1^n+nz_1^{n-1}z_2+ ldots+ z_2^nbigr)+ldots$

Общий член этого ряда имеет вид $frac{1}{n!}sum_{n=0}^{n}C_{n}^{k} z_{1}^{n-k}z_2^k$ , или, согласно формуле бинома Ньютона, $frac{1}{n!}(z_1+z_2)^n$ . Таким образом, окончательно получаем

$sum_{n=0}^{infty} frac{z_1^n}{n!}cdot sum_{n=0}^{infty} frac{z_2^n}{n!}= sum_{n=0}^{infty}frac{(z_1+z_2)^n}{n!},.$

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Последовательностью

комплексных чисел называется функция

,
где

– множество натуральных чисел и

– множество комплексных чисел. Соотношение

называется формулой общего члена
последовательности

Пусть дана
последовательность комплексных чисел

,
где

– некоторые действительные функции
целочисленного аргумента

Определение
4.5.1. Число

называется пределом
последовательности

,
если для любого

найдётся такой номер

,
что для всех

точки

принадлежат

-окрестности
точки

,
или, другими словами,

для

выполняется условие

при

для

выполняется условие

при

Предел
последовательности комплексных чисел
обозначается обычным образом:

.

Будем также
говорить, что последовательность

сходится к точке

Если существует
такое действительное число

,
что для всех

справедливо неравенство

,
последовательность

называется ограниченной.
Геометрически ограниченность
последовательности комплексных чисел
означает существование круга конечного
радиуса, содержащего все её члены.

Теорема 4.5.1.
Всякая сходящаяся к конечному пределу

последовательность комплексных чисел

ограничена.

Доказательство.
▶
По условию теоремы

.
Следовательно, при

выполняется неравенство

,
т.е. все члены последовательности

,
начиная с

лежат в некотором круге

конечного радиуса. Вне этого круга

могут находиться лишь точки

,

,
…,

.
Но конечное число точек

(
)
всегда можно покрыть конечным кругом

.
Построение круга

,
содержащего

,
показывает ограниченность последовательности

.
■

Теорема 4.5.2.
Последовательность

сходится к числу

тогда и только тогда, когда

и

.

Доказательство.
▶
Необходимость: Пусть

.
Это означает, что для любого

существует номер

такой, что при

выполняется неравенство

Но тогда при

заведомо одновременно выполняются
неравенства

и

,
т.е.

Достаточность:
Пусть

.
Тогда для любого

найдётся такой номер

,
что при

будут одновременно выполняться
неравенства

и

.
Оценим модуль

при

Таким образом,
при

выполняется неравенство

,
т.е.

.
■

Из теоремы 4.5.2
следует, что каждой последовательности
комплексных чисел

соответствуют две последовательности
вещественных чисел

и

.
Поэтому многие теоремы и понятия о
последовательностях, известные из
вещественного анализа, справедливы и
для последовательностей комплексных
чисел. А именно, если

и

,
то

,

,

(
).

Теорема 4.5.3.
Пусть

,

и

.
Тогда

тогда и только тогда, когда

(при соответствующем выборе аргументов).

Доказательство.
▶
Справедливость утверждения теоремы
следует из теоремы 4.5.1 и непрерывности
функций

и

,
так как

,

.
■

Пример 4.5.1.
Найти предел последовательности

,
где

произвольное конечное комплексное
число.

Решение.
Рассмотрим пределы

и

.
Находим

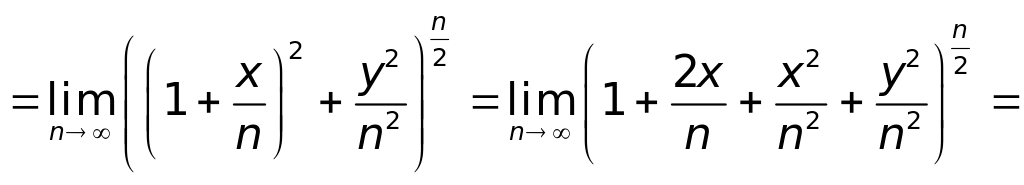
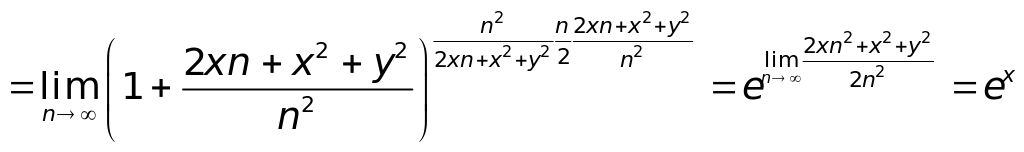
Прежде чем
вычислять предел

,
заметим, что при возведении в целую
положительную степень комплексного
числа его аргумент умножается на эту
степень. Поэтому

,

.

Находим

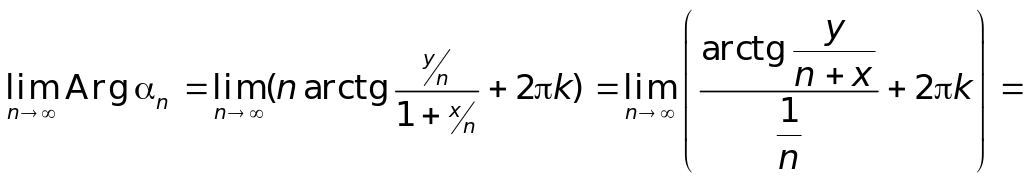
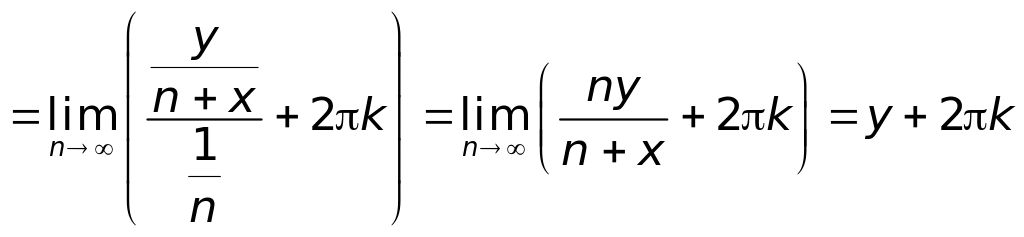
Теперь на основании
теоремы 4.5.3 можно утверждать, что

существует и справедливы равенства

,

,

.
Поэтому число

можно записать в показательной форме

.
Таким образом, имеем

Отметим, что не
имеет смысла вводить символы

или

для обозначения каких-либо комплексных
чисел, так как на расширенной комплексной
плоскости имеется только одна бесконечно
удалённая точка (см. §3). К этой точке
сходятся все последовательности
комплексных чисел

,
для которых одна из последовательностей

или обе из них являются бесконечно
большими. В этом случае записывают

.

Соседние файлы в предмете Высшая математика

#
03.02.2022375.75 Кб15.jpg
#
03.02.2022409.24 Кб26.jpg
#
03.02.2022414.94 Кб17.jpg
#
03.02.2022320.86 Кб28.jpg
#
#
#

Источник

Макеты страниц

До сих пор мы рассматривали ряды, членами которых были действительные числа или функции. Рассмотрим теперь ряды с комплексными членами. Сначала определим понятие сходимости последовательности комплексных чисел. Напомним, что если изобразить комплексные числа и на плоскости, то расстояние между полученными точками равно (рис. 3). Это позволяет ввести следующее определение.

Определение 9.1. Последовательность комплексных чисел сходится к комплексному числу если числовая последовательность сходится к нулю, т. е. если

Поскольку при имеем:

то вместо можно писать:

Докажем следующее утверждение.

Лемма 9.1. Для того чтобы последовательность комплексных чисел, где сходилась к комплексному числу необходимо

Рис. 3

и достаточно, чтобы

Доказательство. Очевидно, что

Поэтому если то и

С другой стороны, из рисунка 4 видно, что

Поэтому если т. е. если

то

А это и значит, что

Понятие предела последовательности комплексных чисел обладает обычными свойствами: если предел последовательности существует, то он однозначно определен; подпоследовательность сходящейся последовательности имеет тот же предел, что и вся последовательность, сходящаяся последовательность ограничена, т. е. существует такое А, что все

Отметим еще, что если то

Для доказательства достаточно заметить, что , и потому из вытекает, что

Рис. 4

Так же как и в случае, когда элементы ряда действительные числа, определяются понятия бесконечно малых и бесконечно больших последовательностей, доказываются свойства таких последовательностей, а также остаются справедливыми и теоремы о пределе суммы, произведения и частного.

Рассмотрим теперь ряды с комплексными членами. Как и в случае рядов с действительными членами назовем ряд с комплексными членами сходящимся, если существует предел последовательности частичных сумм этого ряда. Значение этого предела называется суммой ряда.

Из леммы 9.1 следует, что ряд где сходится в том и только в том случае, когда сходятся ряды составленные из действительных и мнимых частей членов этого ряда. При этом имеет место равенство где Поскольку вопрос о сходимости ряда сводится к вопросу о сходимости рядов с действительными членами, теоремы о сложении рядов, об умножении членов ряда на число и т. д. остаются справедливыми и в комплексном случае. Справедлив и необходимый признак сходимости: для того чтобы ряд сходился, необходимо, чтобы его общий член стремился к нулю, т. е. чтобы

Остаются в силе и теоремы об одновременной сходимости ряда и его остатков и о стремлении к нулю остатка сходящегося ряда.

Понятие абсолютной сходимости определяется для рядов с комплексными членами следующим образом:

Определение 9.2. Ряд называется абсолютно сходящимся, если сходится ряд составленный из модулей его членов.

Легко проверить, что это определение равносильно следующему:

Ряд , где называется абсолютно сходящимся, если сходятся ряды .

Для абсолютно сходящихся рядов остаются в силе теоремы о перестановке членов ряда и об умножении рядов. Доказательства этих теорем такие же, как и для рядов с действительными членами. Сохраняет силу и оценка

Для доказательства этого неравенства сначала на основании свойств модуля комплексного числа устанавливается оценка

затем устремляется к и используется теорема о пределе модуля.

Пример 9.1. Найдем предел последовательности, общий член которой

Решение. . В данном случае

причем Поэтому

Пример 9.2. Найдем предел последовательности

Решение. Вычислим Воспользуемся тем, что модуль произведения равен произведению модулей. Следовательно,

Так как

Это означает, что , таким образом, по определению предела получаем:

Пример 9.3. Напишем сумму первых членов ряда:

и, исходя из определения суммы ряда, установим, сходится ли этот ряд.

Решение.

Чтобы ответить на вопрос о сходимости ряда, запишем в следующем виде:

(см. пример 1.5), поэтому

Ряд сходится, и его сумма равна

Пример 9.4. Установим характер сходимости рядов:

Решение. Ряды и сходятся абсолютно, а потому в случае а) ряд с комплексными членами сходится абсолютно.

Ряд сходится условно, и, таким образом, в случае б) ряд с комплексными членами также сходится условно.

Вопросы для самоконтроля

(см. скан)

Упражнения

(см. скан)

Оглавление

ПРЕДИСЛОВИЕ
ВВЕДЕНИЕ
ГЛАВА 1. ОСНОВНЫЕ ПОНЯТИЯ, ФОРМУЛА И РЯД ТЕЙЛОРА
§ 1. ЧИСЛОВЫЕ РЯДЫ. СХОДИМОСТЬ И РАСХОДИМОСТЬ ЧИСЛОВОГО РЯДА
2. Сумма ряда. Сходящиеся и расходящиеся ряды.
§ 2. СВОЙСТВА СХОДЯЩИХСЯ РЯДОВ
1. Необходимый признак сходимости ряда. Остаток ряда.
§ 3. ФУНКЦИОНАЛЬНЫЕ РЯДЫ И ИХ ОБЛАСТЬ СХОДИМОСТИ
§ 4. ФОРМУЛА ТЕЙЛОРА
§ 5. РАЗЛОЖЕНИЕ ФУНКЦИЙ В РЯД ТЕЙЛОРА
1. Ряд Тейлора.
2. Разложение функции у = ln(1 + х).
3. Разложение функции у = arctg х.
4. Разложение в степенной ряд функции у = ех.
5. Разложение в степенной ряд функций y = sin x и y = cos x.
6. Разложение функции y = (1 + x)^а, где |x| < 1 и a — любое число.
7. Разложение других элементарных функций.
ЗАКЛЮЧЕНИЕ
ГЛАВА II. ЧИСЛОВЫЕ РЯДЫ
§ 6. ПРИЗНАКИ СХОДИМОСТИ ЧИСЛОВЫХ РЯДОВ С НЕОТРИЦАТЕЛЬНЫМИ ЧЛЕНАМИ
2. Признаки сходимости Даламбера и Коши.
3. Интегральный признак сходимости Коши.
4. Примеры исследования рядов на сходимость.
§ 7. СВОЙСТВА РЯДОВ С НЕОТРИЦАТЕЛЬНЫМИ ЧЛЕНАМИ
1. Перестановка членов ряда с неотрицательными членами.
2. Группировка членов и умножение рядов с неотрицательными членами.
§ 8. ЗНАКОПЕРЕМЕННЫЕ РЯДЫ
2. Абсолютно сходящиеся ряды.
3. Свойства абсолютно сходящихся рядов.
4. Свойства условно сходящихся рядов.
§ 9. ЧИСЛОВЫЕ РЯДЫ В КОМПЛЕКСНОЙ ОБЛАСТИ
ГЛАВА III. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
§ 10. ОБЛАСТЬ СХОДИМОСТИ ФУНКЦИОНАЛЬНЫХ РЯДОВ
§ 11. РАВНОМЕРНАЯ СХОДИМОСТЬ ФУНКЦИОНАЛЬНЫХ РЯДОВ
2. Чебышевское расстояние между функциями.
3. Равномерно сходящиеся функциональные последовательности.
4. Равномерно сходящиеся ряды. Признак Вейерштрасса.
5. Сохранение свойства непрерывности в случае равномерной сходимости.
§ 12. ПОЧЛЕННОЕ ИНТЕГРИРОВАНИЕ И ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИОНАЛЬНЫХ РЯДОВ
1. Почленное интегрирование функциональных рядов.
2. Почленное дифференцирование функциональных рядов.
§ 13. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ В КОМПЛЕКСНОЙ ОБЛАСТИ
1. Функции комплексного переменного.
2. Дифференцирование функций комплексного переменного.
3. Функциональные последовательности и ряды в комплексной области.
ГЛАВА IV. СТЕПЕННЫЕ РЯДЫ
§ 14. КРУГ СХОДИМОСТИ СТЕПЕННОГО РЯДА
2. Область сходимости степенного ряда. Круг и радиус сходимости.
3. Равномерная сходимость и непрерывность суммы степенного ряда.
§ 15. ПОЧЛЕННОЕ ИНТЕГРИРОВАНИЕ И ПОЧЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ СТЕПЕННЫХ РЯДОВ
1. Интегрирование и дифференцирование степенных рядов в действительной области.
2. Почленное дифференцирование рядов в комплексной области.
3. Единственность разложения функции в степенной ряд.
§ 16. ПОКАЗАТЕЛЬНЫЕ И ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ В КОМПЛЕКСНОЙ ОБЛАСТИ
1. Показательная функция в комплексной области.
2. Тригонометрические функции в комплексной области. Формулы Эйлера.
§ 17. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ РЯДОВ
1. Вычисление значений функций и интегралов.
2. Вычисление пределов.
3. Метод последовательных приближений.
ГЛАВА V. РЯДЫ ФУРЬЕ
§ 18. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ ФУНКЦИЙ
2. Скалярное произведение функций.
3. Ортонормированные системы функций.
§ 19. КОЭФФИЦИЕНТЫ ФУРЬЕ. РЯД ФУРЬЕ
2. Коэффициенты Фурье для тригонометрических систем функций.
§ 20. ЛЕММА РИМАНА
1. Кусочно гладкие функции.
2. Лемма Римана.
§ 21. ДОСТАТОЧНЫЕ УСЛОВИЯ СХОДИМОСТИ РЯДОВ ФУРЬЕ
1. Формула для частичных сумм ряда Фурье.
2. Сходимость разложения кусочно гладких функций в ряды Фурье.
3. Разложение функций, заданных на конечных промежутках, в ряд Фурье.
4. Разложение четных и нечетных функций в ряды Фурье.
5. Примеры разложения функций в ряды Фурье.
Ответы к упражнениям

Источник

Ряды с комплексными членами.

19.3.1. Числовые ряды с комплексными членами. Все основные определения сходимости, свойства сходящихся рядов, признаки сходимости для комплексных рядов ничем не отличаются от действительного случая.

19.3.1.1. Основные определения. Пусть дана бесконечная последовательность комплексных чисел . Действительную часть числа будем обозначать , мнимую – (т.е. .

Числовой ряд – запись вида .

Частичные суммы ряда:

Определение. Если существует предел S последовательности частичных сумм ряда при , являющийся собственным комплексным числом, то говорят, что ряд сходится; число S называют суммой ряда и пишут или .

Найдём действительные и мнимые части частичных сумм: , где символами и обозначены действительная и мнимая части частичной суммы. Числовая последовательность сходится тогда и только тогда, когда сходятся последовательности, составленные из её действительной и мнимой частей. Таким образом, ряд с комплексными членами сходится тогда и только тогда, когда сходятся ряды, образованные его действительной и мнимой частями.

Пример. Исследовать на сходимость ряд .

Выпишем несколько значений выражения : дальше значения периодически повторяются. Ряд из действительных частей: ; ряд из мнимых частей ; оба ряда сходятся (условно), поэтому исходный ряд сходится.