Бесконечно малая величина ![]() при
при ![]() называется бесконечно
называется бесконечно
Малой ![]() -го порядка малости относительно бесконечно малой величины
-го порядка малости относительно бесконечно малой величины ![]() при
при ![]() ,если существует конечный предел
,если существует конечный предел  не равный нулю.
не равный нулю.
Чаще всего приходится устанавливать порядок малости бесконечно малой ![]() при
при ![]() относительно
относительно ![]() . Задача сводится к тому, чтобы подобрать
. Задача сводится к тому, чтобы подобрать ![]() таким образом, чтобы
таким образом, чтобы ![]() и
и ![]() были одного порядка малости.
были одного порядка малости.
Пример 1. Определить порядок малости функции ![]() относительно
относительно ![]() , т. е. выделить ее “главную часть”.
, т. е. выделить ее “главную часть”.


Ответ: Функция ![]() – бесконечно малая порядка
– бесконечно малая порядка ![]() относительно
относительно ![]() , т. е.
, т. е. ![]()
Пример 2. Определить порядок малости функции ![]() Относительно
Относительно ![]() , т. е. выделить ее «главную часть».
, т. е. выделить ее «главную часть».


Ответ: Функция ![]() бесконечно малая 2-го порядка малости относительно
бесконечно малая 2-го порядка малости относительно ![]()
![]() .
.
Пример 3. Установить относительный порядок малости при ![]() функций
функций ![]() и
и ![]() .
.

 .
.
Ответ: Бесконечно малая функция ![]() 2-го порядка малости относительно бесконечно малой функции
2-го порядка малости относительно бесконечно малой функции ![]() .
.
Пример 4. Убедиться в том, что функция ![]() И
И ![]() при
при ![]() будут бесконечно малыми одного порядка.
будут бесконечно малыми одного порядка.
 .
.
Ответ: Функции ![]() И
И ![]() – бесконечно малые одного порядка, т. к. предел их отношения при
– бесконечно малые одного порядка, т. к. предел их отношения при ![]() равен
равен ![]() .
.
Пример 5. Доказать, что при ![]() Бесконечно малые функции
Бесконечно малые функции ![]() и
и ![]() будут эквивалентными.
будут эквивалентными.
Решение: Составляем предел отношения функций ![]() и
и ![]() , убеждаемся в процессе вычисления, что он равен 1, откуда делаем вывод:
, убеждаемся в процессе вычисления, что он равен 1, откуда делаем вывод:
![]() .
.

 .
.
Что и требовалось доказать: ![]() .
.
Пример 6. Найти относительный порядок малости при ![]() Двух бесконечно малых функций
Двух бесконечно малых функций ![]() и
и ![]() .
.


Ответ: ![]() – бесконечно малая функция 2-го порядка относительно бесконечно малой функции
– бесконечно малая функция 2-го порядка относительно бесконечно малой функции ![]() .
.
| < Предыдущая | Следующая > |
|---|
Сообщения без ответов | Активные темы
| Автор | Сообщение | ||
|---|---|---|---|
|
Lanochka |
|
||
|
Уважаемые товарищи, необходимо определить порядок малости относительно [math]x,,xto0[/math] функции [math]f(x)=7sin^2x+3x^3[/math] Заранее спасибо откликнувшимся людям, за потраченное время и силы!
|
||
| Вернуться к началу |
|
||
|
Lanochka |
Заголовок сообщения: Re: Определить порядок малости функции
|
| Вернуться к началу |
|
|
Lanochka |
Заголовок сообщения: Re: Определить порядок малости функции
|
|
вы молодец=)
|
|
| Вернуться к началу |
|
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Определить порядок малости относительно x,x→0 функции
в форуме Пределы числовых последовательностей и функций, Исследования функций |
kenar |
0 |
310 |
11 дек 2020, 19:04 |
|
Определить порядок малости функции относительно x, x->0
в форуме Пределы числовых последовательностей и функций, Исследования функций |
Miriam87 |
2 |
636 |
17 апр 2019, 13:24 |
|
Определить порядок малости функции относительно x, x->0
в форуме Пределы числовых последовательностей и функций, Исследования функций |
jannarestorana |
1 |
251 |
29 ноя 2021, 21:40 |
|
Определить порядок малости относительно х функции
в форуме Пределы числовых последовательностей и функций, Исследования функций |
xom9ik |
3 |
1233 |
11 дек 2016, 12:25 |
|
Определить порядок малости относительно Х при Х-> 0
в форуме Дискуссионные математические проблемы |
daria703 |
1 |
1390 |
26 янв 2015, 11:02 |
|
о определить порядок малости относительно
в форуме Пределы числовых последовательностей и функций, Исследования функций |
evgnkjerby |
2 |
192 |
18 окт 2020, 18:56 |
|
Определить порядок малости относительно x-1
в форуме Пределы числовых последовательностей и функций, Исследования функций |
Frud |
2 |
680 |
25 окт 2016, 15:28 |
|
Определить порядок малости функции
в форуме Пределы числовых последовательностей и функций, Исследования функций |
Varvara++ |
4 |
317 |
07 ноя 2018, 15:34 |
|
Порядок малости относительно х
в форуме Пределы числовых последовательностей и функций, Исследования функций |
alekscooper |
2 |
509 |
20 июл 2018, 13:44 |
|
Определить порядок б.м. функции относительно х
в форуме Пределы числовых последовательностей и функций, Исследования функций |
Surtr_RJ |
1 |
420 |
09 окт 2016, 15:00 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 3 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Powered by phpBB © 2000, 2002, 2005, 2007 phpBB Group
Вы можете создать форум бесплатно PHPBB3 на Getbb.Ru, Также возможно сделать готовый форум PHPBB2 на Mybb2.ru
Русская поддержка phpBB
Содержание:
- Бесконечно малые функции одного порядка
- Бесконечно малые функции более низкого и высокого порядков
- Эквивалентные (равносильные) бесконечно малые функции
Определение
Функция $alpha(x)$ называется бесконечно малой
при $x rightarrow a$ (или в точке $x=a$ ), если
$lim _{x rightarrow a} alpha(x)=0$
Подробная теория про бесконечно малые функции по
ссылке.
Пример
Функция $alpha(x) =x^2-1$ является б.м. при
$x rightarrow 1$, так как
Бесконечно малые функции одного порядка
Пусть $alpha(x)$ и
$beta(x)$ – две б.м. функции при
$x rightarrow a$.
Определение
Функции $alpha(x)$ и
$beta(x)$ называются б.м. одного порядка малости при
$x rightarrow a$, если $lim _{x rightarrow a} frac{alpha(x)}{beta(x)}=c neq 0$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Рассмотрим функции $alpha(x)=x^{2}-1$ и $beta(x)=x-1$, которые являются б.м. при
$x rightarrow 1$:
$$lim _{x rightarrow 1} alpha(x)=lim _{x rightarrow 1}left(x^{2}-1right)=1^{2}-1=0$$
$$lim _{x rightarrow 1} beta(x)=lim _{x rightarrow 1}(x-1)=1-1=0$$
Найдем предел отношения этих функций при $x rightarrow 1$:
$$lim _{x rightarrow 1} frac{alpha(x)}{beta(x)}=lim _{x rightarrow 1} frac{x^{2}-1}{x-1}=lim _{x rightarrow 1} frac{(x-1)(x+1)}{x-1}=$$
$$=lim _{x rightarrow 1}(x+1)=1+1=2$$
Так как предел равен конечному, отличному от нуля числу, то рассматриваемые функции $alpha(x)$ и
$beta(x)$ являются б.м. одного порядка малости при
$x rightarrow 1$.
Бесконечно малые функции более низкого и высокого порядков
Определение
Если $lim _{x rightarrow a} frac{alpha(x)}{beta(x)}=0$, то
$alpha(x)$ является б.м. более высокого порядка при
$x rightarrow a$, чем
$beta(x)$, а
$beta(x)$ – б.м. более низкого порядка по сравнению с
$alpha(x)$:
$alpha(x)=o(beta(x))$ при
$x rightarrow a$.
Пример
Функция $alpha(x)=left(x^{2}-1right)^{2}$ , $left(lim _{x rightarrow 1} alpha(x)=lim _{x rightarrow 1}left(x^{2}-1right)^{2}=0right)$ является б.м. более высокого порядка, чем
функция $beta(x)=x-1$, $left(lim _{x rightarrow 1} beta(x)=lim _{x rightarrow 1}(x-1)=0right)$ в точке $x=0$, так как
$$begin{aligned}
lim _{x rightarrow 1} frac{alpha(x)}{beta(x)} &=lim _{x rightarrow 1} frac{left(x^{2}-1right)^{2}}{x-1}=lim _{x rightarrow 1} frac{(x-1)^{2}(x+1)^{2}}{x-1}=\
&=lim _{x rightarrow 1}(x-1)(x+1)^{2}=0 cdot 2=0
end{aligned}$$
Определение
Если $lim _{x rightarrow a} frac{alpha(x)}{beta(x)}=infty$, то $alpha(x)$ – б.м. низшего порядка малости при $x rightarrow a$ по сравнению с
$beta(x)$.
Пример
Рассмотрим функцию $alpha(x)=x+1$, которая является б.м. в точке $x=-1$: $lim _{x rightarrow-1} alpha(x)=lim _{x rightarrow-1}(x+1)=-1+1=0$, и б.м. в этой же точке функцию $beta(x)=(x+1)^2$: $lim _{x rightarrow-1} beta(x)=lim _{x rightarrow-1}(x+1)^{2}=(-1+1)^{2}=0$. Найдем предел частного этих функций:
$$lim _{x rightarrow-1} frac{alpha(x)}{beta(x)}=lim _{x rightarrow-1} frac{x+1}{(x+1)^{2}}=lim _{x rightarrow-1} frac{1}{x+1}=frac{1}{0}=infty$$
А поэтому, функция $alpha(x)$ является б.м.
низшего порядка малости при $x rightarrow -1$, чем функция
$beta(x)$.
Определение
Если $lim _{x rightarrow a} frac{alpha(x)}{[beta(x)]^{k}}=C$, $0 < |C| lt infty$, то $alpha(x)$ называется б.м. порядка $k$ по сравнению с
$beta(x)$ при
$x rightarrow a$.
Пример
Функция $alpha(x)=x+1$ называется б.м. порядка 2 по
сравнению с функцией $beta(x)=sqrt{x+1}$ в точке $x=-1$, так как
$$lim _{x rightarrow-1} frac{alpha(x)}{[beta(x)]^{k}}=lim _{x rightarrow-1} frac{x+1}{(sqrt{x+1})^{2}}=lim _{x rightarrow-1} frac{x+1}{x+1}=lim _{x rightarrow-1} 1=1$$
$1 neq 0$, что и требовалось доказать.
Эквивалентные (равносильные) бесконечно малые функции
Определение
Если $lim _{x rightarrow a} frac{alpha(x)}{beta(x)}=1$, то б.м. функции $alpha(x)$ и $beta(x)$ называются эквивалентными или равносильными б.м.
одного порядка при $x rightarrow a$: $alpha(x) sim beta(x)$ при $x rightarrow a$.
Пример
Функции $alpha(x)=x^4-3x+2$ и $beta(x)=x^5-4x+3$ являются эквивалентными б.м. в точке $x=1$, так как, во-первых:
$$lim _{x rightarrow 1} alpha(x)=lim _{x rightarrow 1}left(x^{4}-3 x+2right)=0$$
$$lim _{x rightarrow 1} beta(x)=lim _{x rightarrow 1}left(x^{5}-4 x+3right)=0$$
а во-вторых:
$$begin{array}{r}
lim _{x rightarrow 1} frac{alpha(x)}{beta(x)}=lim _{x rightarrow 1} frac{x^{4}-3 x+2}{x^{5}-4 x+3}= \
=lim _{x rightarrow 1} frac{(x-1)left(x^{3}+x^{2}+x-2right)}{(x-1)left(x^{4}+x^{3}+x^{2}+x-3right)}=frac{1+1+1-2}{1+1+1+1-3}=1
end{array}$$
Читать дальше: эквивалентные бесконечно малые функции, таблица эквивалентных б.м. функций.
|
10 / 10 / 1 Регистрация: 17.02.2013 Сообщений: 344 |
|
|
1 |
|
Определить порядок бесконечно малой функции17.10.2013, 20:50. Показов 70189. Ответов 8
Определить порядок бесконечно малой функции Добавлено через 4 часа 24 минуты
0 |
|
4652 / 3404 / 361 Регистрация: 11.11.2010 Сообщений: 6,205 Записей в блоге: 2 |
|
|
17.10.2013, 21:14 |
2 |
|
Пусть Тогда, имеем Таким образом, функция
1 |
|
10 / 10 / 1 Регистрация: 17.02.2013 Сообщений: 344 |
|
|
17.10.2013, 21:20 [ТС] |
3 |
|
Пусть Тогда, имеем Таким образом, функция Большое спасибо, но в задании требовалось найти значение порядка малости, так чему он равен ?
0 |
|
4652 / 3404 / 361 Регистрация: 11.11.2010 Сообщений: 6,205 Записей в блоге: 2 |
|
|
17.10.2013, 21:35 |
4 |
|
Garold, единственное что могу сказать, так это то, что
0 |
|
10 / 10 / 1 Регистрация: 17.02.2013 Сообщений: 344 |
|
|
17.10.2013, 21:40 [ТС] |
5 |
|
Garold, единственное что могу сказать, так это то, что
P.S. Мне это ничего не дает.
0 |
|
Диссидент
27465 / 17154 / 3780 Регистрация: 24.12.2010 Сообщений: 38,634 |
|
|
18.10.2013, 01:03 |
6 |
|
Garold, Вам только остается пораскинуть мозгами и найти такую функцию вида f(x) = xd, что a(x)/f(x) -> 1 Добавлено через 16 минут Не по теме: Дурят вашего брата:)
2 |
|
2013 / 1342 / 382 Регистрация: 16.05.2013 Сообщений: 3,463 Записей в блоге: 6 |
|
|
18.10.2013, 09:26 |
7 |
|
Возьми наименьшую степень, и будет тебе счастие! Думаю вы заблуждаетесь уважаемый. Брать нужно наибольшую степень т.е. 3/2.
0 |
|
Диссидент
27465 / 17154 / 3780 Регистрация: 24.12.2010 Сообщений: 38,634 |
|
|
18.10.2013, 10:30 |
8 |
|
Думаю вы заблуждаетесь уважаемый. Брать нужно наибольшую степень т.е. 3/2 x + x2 – какой будет порядок?
1 |
|
2013 / 1342 / 382 Регистрация: 16.05.2013 Сообщений: 3,463 Записей в блоге: 6 |
|
|
18.10.2013, 11:06 |
9 |
|
Ай все понял. Виноват
1 |
§
1. Сравнение бесконечно малых функций
Определение
1.1. Пусть
функции α(x)
и β(x)
являются
бесконечно малыми при х а.
а.
-
Если
существует
 ,
,
то α(x)
и β(x)
называются бесконечно малыми одного
порядка при х а.
а.
-
Если
существует
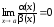 ,
,
то α(x)
называется величиной более высокого
порядка малости, чем β(x)
при х а.
а.
Обозначение:
α(x) = o(β(x))
при х а
а
(α(x)
есть о малое
от β(x)).
-
Если
не существует
 ,
,
то бесконечно малые α(x)
и β(x)
называются несравнимыми при х а.
а.
Например,
sin 2x
2x
и

– бесконечно малые одного порядка при
х 0,
0,
так как
 .
.
Функция sin 2x
2x
имеет более
высокий порядок малости, чем х
при х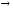 0
0
(или sin 2x=о(х)
2x=о(х)
при х 0),
0),
поскольку


Бесконечно малые

и α(x)
и β(x) = х
несравнимы при х 0,
0,
так как


а

не существует (это можно показать с
помощью определения предела функции
на языке последовательностей).
Замечание
1.1. Если
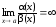 ,
,
то

Тогда β(x) = o(α(x))
при х а.
а.
Сравнить
две бесконечно малые функции – это
значит установить, что они являются
бесконечно малыми одного порядка, или
что одна из них более высокого порядка,
чем другая, или что они несравнимы. Для
этого надо найти предел их отношения,
т.е. раскрыть неопределённость
 .
.
Определение
1.2. Если
существует
 ,
,
то α(x)
и β(x)
называются эквивалентными бесконечно
малыми при х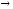 а.
а.
При
отыскании предела отношения бесконечно
малых α(x)
и β(x)
при

используется
теорема о замене эквивалентными в
отношении и таблица эквивалентных
бесконечно малых функций, так как для
α(x)
и β(x)
полезно найти эквивалентные бесконечно
малые простейшего вида С(х – а)k.
Таблица
эквивалентных бесконечно малых функций.
Пусть
функция

при
 .
.
Тогда
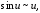

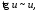
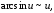



 .
.
Пример
1.1. Сравнить
бесконечно малые α(x) =
и β(x) =
при
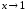 .
.
►α(x) = ~
~
 Þα(x)~
Þα(x)~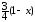
(здесь использована формула
 ,
,
где
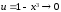
при
 ,
,
 ).
).
Имеем: β(x)= ~
~ =
=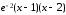 Þ
Þ ~
~ ,
,
здесь использована формула

где

при
 .
.
В результате применения теоремы о замене
эквивалентными в отношении получим:
 ¹0,
¹0,
∞. Поэтому заключаем, что α(x)
и β(x)
бесконечно малые одного порядка при
 .◄
.◄
Пример
1.2. Сравнить
бесконечно малые

и

при
 .
.
►Имеем
 ~
~ ~
~ ,
,
здесь использованы формулы:
 ,
,

и

 ,
,
где

при
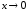 .
.
Имеем:

 .
.
Используя теорему о замене эквивалентными
в отношении, получим:
 .
.
Таким образом, α(x)
является величиной более высокого
порядка малости, чем β(х)
при х→ 0,
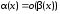
при х→ 0.◄
Пример
1.3. Сравнить
бесконечно малые α(x)
и β(x) при
при
 .
.
►Имеем
α(x) ~
~
(здесь использована формула
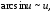
где
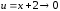
при
 ),
),
β(x) =
= ~
~
~ ~
~ ,
,
(здесь использованы формулы:


и
 ,
,
 ,
,
где
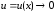
при
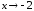 ).
).
Используя теорему о замене эквивалентными
в отношении, получим:
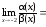
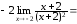
 .
.
Следовательно,

и поэтому заключаем, что β(x)
– величина более высокого порядка
малости, чем α(x)
при
 ,
,
β(x) = o(α(x))
при
 .◄
.◄
Пример
1.4. Сравнить
бесконечно малые
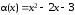
и

при
 .
.
►Заметим,
что β(x)
не эквивалентна аргументу функции
sinπx,
который не является бесконечно малым
при
 .
.
Чтобы найти эквивалентную бесконечно
малую для этой функции, сделаем замену
переменной. Пусть y = x–3,
x = y + 3,
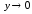
при
 .
.
Имеем:

 .
.
Так
как sin(πy + 3π) = sin(πy + 2π + π) = sin(πy + π)
= – sinπy,
то

 =
=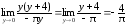 ,
,
здесь
использованы периодичность функции
синус, формулы приведения из элементарной
тригонометрии, а также соотношение

где
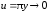
при
 .
.
Поскольку
 ,
,
то заключаем, что α(x)
и β(x)
бесконечно малые одного порядка при
 .◄
.◄
Пример
1.5. Сравнить
бесконечно малые α(x)
и α(x)
и β(x)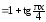 при
при
 .
.
►α(x) ~
~ ,
,
здесь использована формула

где

при
 .
.
Используя формулу для тангенса суммы
двух углов, преобразуем выражение для
β(x):
β(x) = 

Имеем:
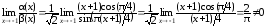 ,
,
∞, следовательно, α(x)
и β(x)
– бесконечно малые одного порядка при
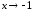 .◄
.◄
§
2. Определение порядка бесконечно малой
функции.
Определение
2.1. Пусть
функции α(x)
и β(x)
являются
бесконечно малыми при
 .
.
Бесконечно малая α(x)
называется бесконечно малой k-го
порядка по отношению к бесконечно малой
β(x)
при х а,
а,
если существует
 .
.
Так,
функция α(x) =sin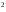 2x
2x
имеет 2-ой порядок малости относительно
β(x) =х
( )
)
при х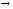 0,
0,
ибо

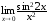
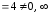 .
.
Определить
порядок малости бесконечно малой α(x)
относительно бесконечно малой β(x)
при х а
а
– значит найти число k
такое, чтобы
 .
.
При этом используется теорема о замене
эквивалентными в отношении и таблица
эквивалентных бесконечно малых функций
(§1), так как для α(x)
и β(x)
полезно найти эквивалентные бесконечно
малые вида С(х – а)k.
Пример
2.1. Определить
порядок бесконечно малой α(x) .
.
относительно бесконечно малой β(x) = х
при
 .
.
►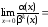

(использованы
теорема о замене эквивалентными
бесконечно малыми в отношении и формулы:
 ,
,
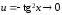 ,
,

и


при
 ).
).
Поскольку
 –
–

при
 ,
,
то порядок малости α(x)
относительно β(x)
при х 0
0
равен 2.◄
Пример
2.2. Определить
порядок бесконечно малой α(x)
) = 
относительно бесконечно малой β(x) = х
при
 .
.
►

(использованы
теорема о замене эквивалентными
бесконечно малыми в отношении и формула:
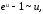

при
 ).
).
Разложив числитель на множители, получим:

 .
.
Поскольку
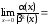 –3
–3
при
 ,
,
то порядок малости α(x)
относительно β(x)
при х 0
0
равен 2.◄
Пример
2.3. Определить
порядок бесконечно малой α(x)
относительно бесконечно малой β(x) = х
при
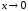 .
.
►
 .
.
Числитель разложим на множители по
формуле разность косинусов, получим:
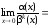
 .
.
После применения теоремы о замене
эквивалентными бесконечно малыми в
отношении и формулы:


и

при

имеем:

 .
.
Поскольку
 8
8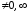
при
 ,
,
то порядок малости α(x)
относительно β(x)
при х 0
0
равен 2.◄
Пример
2.4. Определить
порядок бесконечно малой α(x)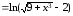 .
.
относительно бесконечно малой β(x) = х
при
 .
.
►
 .
.
Числитель заменим на эквивалентную,
получим:


(использована формула


при
 ).
).
Перенесём иррациональность из числителя
в знаменатель, умножив оба члена дроби
на выражение, сопряжённое к числителю:
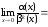
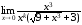 .
.
Поскольку



при
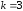 ,
,
то порядок малости α(x)
относительно β(x)
при х 0
0
равен 3.◄
Пример
2.5. Определить
порядок бесконечно малой α(x) = 
относительно бесконечно малой β(x) = х – 1
при х 1.
1.
►
 =
= =
=
 .
.
Так как
 1,
1,
то
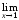
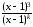 =1
=1
при
 .
.
Поэтому порядок малости α(x)
относительно β(x)
при х 1
1
равен 3.◄
Пример
2.6. Определить
порядок бесконечно малой α(x) = cos(πsinх) + 1
относительно бесконечно малой
β(x) = х – π/2
при
 .
.
►Для
α(x)
найдём эквивалентную бесконечно малую
вида С(х – π/2)k.
В результате применения формул для
половинных и дополнительных углов из
элементарной тригонометрии и формул



из таблицы эквивалентных бесконечно
малых (см. §1) для α(x)
имеем соотношение:
α(x) =
 ~
~ ~
~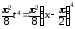 .
.
Итак,
α(x) ~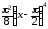
при
 .
.
Используя теорему о замене эквивалентными
в отношении, получаем:

при

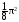

при k
= 4. Таким образом, порядок малости α(x)
относительно β(x)
при х
равен 4.◄
Пример
2.7. Определить
порядок бесконечно малой α(x)
относительно бесконечно малой β(x) = х – π
при
 .
.
►
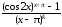 .
.
Используя основное логарифмическое
тождество, представим функцию
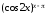
в виде:
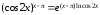 .
.
Имеем
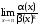 =
=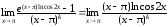 =
= =
=

(использованы теорема о замене
эквивалентными бесконечно малыми в
отношении и формулы

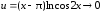
и

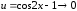
при
 .
.
Заметим, что разность
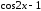
не эквивалентна
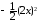
при
 ,
,
так как

не стремится к нулю при
 .
.
Чтобы найти для этой разности эквивалентную
бесконечно малую, сделаем замену
переменной: y = х – π x = y + π:
x = y + π:




 .
.
Поскольку
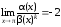
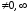
при
 ,
,
то порядок малости α(x)
относительно β(x)
при

равен 3.◄
§3.
Выделение главной части бесконечно
малой функции.
Определение
3.1. Пусть
даны функции α(x)
и β(x),
являющиеся
бесконечно малыми при х а.
а.
Функция

называется главной частью функции α(x)
при х а,
а,
если α(x)
при х а
а
можно
представить в виде:
α(x) = β(x) + o(β(x)). (3.1)
Если
бесконечно малые α(x)
и β(x)
эквивалентны при х а,
а,
то для них справедливо равенство (3.1)
(свойство эквивалентных бесконечно
малых). Поэтому данная бесконечно малая
функция α(x)
при х а
а
может иметь бесчисленное множество
главных частей, так как любая бесконечно
малая функция β(x),
эквивалентная α(x),
будет её главной частью. Например,
функции х,
tg x
– главные
части функции sin x
при х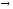 0,
0,
так как при х 0
0
справедливы утверждения: sin x~x,
sin x~tg x.
Обычно
главную часть функции α(x),
бесконечно малой при х а,
а,
находят в
наиболее
простом виде, например, в виде степенной
функции β(x) = С(х – а)k,
k > 0,
при a R
R
или
β(x) = С(1/х)k,
k > 0,
при a .
.
Найти для α(x)
такую главную часть – значит определить
константу С
и порядок k
этой функции относительно разности
x – a
или дроби 1/х.
Найти
для α(x)
главную часть простейшего вида С(х – а)k,
k > 0,
при х а
а
– это значит найти константу С
и число k
такие, чтобы
 .
.
Пример
3.1. Выделить
главную часть вида Схk
из бесконечно малой α(x) = cos2х – cos4х
при х  0.
0.
►В
результате применения формулы для
разности косинусов и формулы


из таблицы эквивалентных бесконечно
малых (см. §1) для α(x)
имеем соотношение: α(x)
 .
.
Таким образом, для α(x)
найдена эквивалентная бесконечно малая
функция 6х2,
имеющая указанный вид (С = 6,
k = 2),
следовательно, 6х2.–
главная часть α(x)
при х  0.◄
0.◄
Пример
3.2. Выделить
главную часть вида Схk
из бесконечно малой α(x) =
при х  0.
0.
► Найдём
число k
и константу С
такие, чтобы
выполнялось равенство:

 =1.
=1.
Перенесём иррациональность из числителя
в знаменатель, для этого умножим оба
члена дроби на выражение, сопряжённое
к числителю:

 =
=
 (использованы
(использованы
теорема о замене эквивалентными
бесконечно малыми в отношении и формула:


при
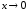 ).
).
Поскольку

при k = 2
и
 ,
,
то
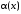 ~
~


при х  0
0
и, следовательно, функция


– главная часть бесконечно малой α(x)
при х  0.◄
0.◄
Пример
3.3. Выделить
главную часть вида С(х – 2)k
из бесконечно малой α(x)
при х  2.
2.
►В
результате применения формулы


из таблицы эквивалентных бесконечно
малых (см. §1) для α(x)
имеем соотношение:
α(x)
 .
.
Итак,
для α(x)
найдена эквивалентная бесконечно малая
функция 3(х– 1)2,
имеющая указанный вид (С = 3,
k = 2),
следовательно, 3(х–1)2–
главная часть α(x)
при х 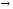 2.◄
2.◄
Пример
3.4. Выделить
главную часть вида С(х – 1)k
из бесконечно малой α(x) = cos(πex–1) + 1
при х 1.
1.
►В
результате применения формул для
половинных и дополнительных углов из
элементарной тригонометрии и формул
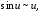

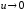
из таблицы эквивалентных бесконечно
малых (см. §1) для α(x)
имеем соотношение: α(x) = 2cos2
 = 2sin2
= 2sin2 2sin2
2sin2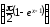
 .
.
Итак,
для α(x)
найдена эквивалентная бесконечно малая
функция
 ,
,
имеющая указанный вид (С =  ,
,
k = 2),
следовательно,

– главная часть α(x)
при х  1.◄
1.◄
Пример
3.5. Выделить
главную часть вида С(1/х)k
из бесконечно малой α(x) =
при х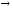
 .
.
► ,
,
α(x) =
при х

(использована формула


при х
 ).
).
Имеем



при х
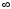 ,
,
отсюда заключаем:
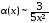
при х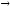
 ,
,
следовательно,

– главная часть бесконечно малой α(x)
при х
 .◄
.◄
Пример
3.6. Выделить
главную часть вида С(х – e)k
из бесконечно малой α(x) = хx – ex
при х .
.
►Используя
основное логарифмическое тождество,
представим функцию хx
в виде:
хx = exlnx.
Имеем α(x) = exlnx – ex = ex(exlnx-х–1).
В результате применения
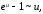

из таблицы эквивалентных бесконечно
малых (см. §1) для α(x)
получаем соотношение:
α(x) ~ ее(х(lnx – 1)) = ее+1(lnx – lne) = ее+1 ~
~
при
х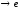 .
.
Итак, α(x) ~ 
при х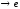 ,
,
Следовательно, ee (х–е)
– главная часть бесконечно малой α(x)
при х е.◄
е.◄
Пример
3.7. Выделить
главную часть вида Схk
из бесконечно малой α(x) = arccos(1 – x)
при х .
.
►Чтобы
найти для α(x)
эквивалентную бесконечно малую функцию
указанного вида, применим формулу

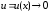 .
.
Имеем
α(x) ~sin(arccos(1 – x))
при х .
.
Преобразуем
функцию sin(arccos(1 – x)),
Используя определение арккосинуса.
Пусть arccos(1 – x) = γ,
где γ – угол или дуга такая, что
cosγ = 1 – x
и
 ,
,
тогда sin(arccos(1 – x)) = sinγ = 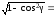
 .
.
Итак,
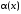 ~
~

при

и функция

– главная часть бесконечно малой α(x)
при
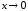 .◄
.◄
Пример
3.8. Выделить
главную часть вида

из бесконечно малой α(x) = π – 4arctg(x2 – 2x + 2)
при х .
.
►α(x)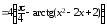 .
.
Для отыскания алгебраической функции,
эквивалентной α(x),
применим формулу

 ,
,
положив
u = 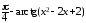 ,
,
а также формулу для разности тангенсов
двух углов из элементарной тригонометрии:
α(x)
 .
.
Итак,
α(x) ~ – 2(x – 1)2
при

и функция – 2(x – 1)2
– главная часть бесконечно малой α(x)
при
 .◄
.◄
Соседние файлы в папке Хуета
- #
- #
- #
- #
- #
- #







