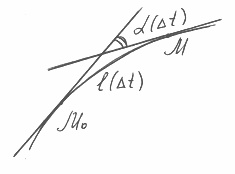
1°. Понятие порядка соприкосновения
Рассмотрим кривые 
















Определение. Будем говорить, что порядок соприкосновения кривых 



Если, кроме того,

или отношение 





Рис. 26. Кривые 


Рис. 27. Единичный вектор 



Если равенство (1) имеет место для любого 


Пример 1. Пусть 





Следовательно, порядок соприкосновения кривых 

Пример 2. Пусть 




Имеем 

Так как предел отношения – не существует (он равен бесконечности), то порядок соприкосновения кривых 

Пример 3. Пусть 


Покажем, что кривые 
В рассматриваемом случае 


то наше утверждение справедливо.
1.Понятие кривизны и ее вычисление.
Рассмотрим концентрические
окружности. Будем определять кривизну
окружности радиуса Rкак величину k=1/R.
Центром кривизны назовем центр окружности,
а ее радиус – радиусом кривизны. Обобщим
эти понятия на произвольную гладкую
кривую. Рассмотрим гладкую кривую с
параметризацией x(t),y(t),для
краткости будем использовать обозначения:
x0=x(t0),x=x(t),y0=y(t0),y=y(t),u0=x(t0),u=x(t),v0=y(t0),v=y(t).
В процессе рассмотрения
t0будет
фиксирована, а t
будет рассматриваться, как текущая
точка. Составим уравнения нормалей в
точках (x0,y0),
(x,y).

.
Найдем точку пересечения этих прямых.

Умножим первое
уравнение на u,
а второе на –vи
сложим.
(uv0 -vu0)p=u(x0-x)
+v(y0–y)откуда
.
Далее перейдем к
пределу при tt0(uu0,vv0).Получим
.
Подставляя найденной значение параметра
для предельной точки пересечения
нормалей, получим координаты предельной
точки
,
.
Полученная таким образом точка называется
центром кривизны кривой в заданной
точке, а расстояние от этой точки до
центра кривизны называется радиусом
кривизны.
.
Величина обратная радиусу кривизны
называется кривизной
.
Окружность с центром
в (X0,Y0)и радиуса R0называется
соприкасающейся окружностью.
2.Выражение центра и радиуса кривизны для явно заданной кривой.
Рассмотрим кривую , заданную в виде y=f(x),x[a,b].В качестве
параметризации выберем x=t,y=f(t),t[a,b].Тогда
,
,
.
3.Порядок соприкосновения кривых.
Пусть 1,2представлены
функциями y=f1(x),y=f2(x)и пересекаются
в точке (x0,y0).Кривые
1,2имеют порядок
соприкосновения nв точке (x0,y0),если
,
для всех k=0,1,…,n,и
.
Достаточными условиями
для того, чтобы кривые имели порядок
касания nявляются
следующие условия:
Функции n+1непрерывно
дифференцируемы в окрестности точки
x0и
,
k=0,…,n,
.
Для доказательства
обозначим f(x)=f2(x)
-f1(x).Тогда в окрестности
точки x0имеет
место разложение по формуле Тейлора с
остатком в форме Лагранжа
,
тогда

k=0,1,…,n+1.
Таким образом, будут выполнены условия
из определения порядка касания.
Ответ.
80
Конспект лекций
Логинов А.С. ЭТФ 1 семестр loginov_1999@mail.ru
Соседние файлы в папке ma
- #
- #
- #
- #
- #
- #
Соприкосновение кривых
Соприкосновение кривых (точка соприкосновения) – общая точка двух графиков функций, где обе функции имеют одинаковую касательную (одинаковый наклон).
!
Запомни
Кривые двух функций соприкосаются, если:
$f(x_C)=g(x_C)$ и
$f'(x_C)=g'(x_C)$
i
Способ
- Возьмите производные
- Приравняйте уравнения функций: $f(x_C)=g(x_C)$
- Проверьте наклоны
- Определите точку касания
Пример
Определите точку соприкосновения функции $f(x)=x^2$ и $g(x)=-x^2+4x-2$.
-
Возьмем производные
$f(x)=x^2$
$f'(x)=2x$$g(x)=-x^2+4x-2$
$g'(x)=-2x+4$ -
Приравниваем уравнения функции
Первое условие: Обе функции должны иметь общую точку.
$f(x_C)=g(x_C)$
$x^2=-x^2+4x-2quad|-x^2$
$-2x^2+4x-2=0quad|:(-2)$
$x^2-2x+1=0$Это квадратное уравнение, которое можно решить, к примеру, используя PQ формулу.
$x_{C_{1,2}} = -frac{p}{2} pmsqrt{(frac{p}{2})^2-q}$
$x_{C_{1,2}} = 1 pmsqrt{1-1}$
$x_C=color{red}{1}$ -
Проверим наклон
Второе условие: Обе функции должны иметь одинаковый наклон в точке.
$f'(x_C)=g'(x_C)$
$f'(color{red}{1})=g'(color{red}{1})$
$2cdotcolor{red}{1}=-2cdotcolor{red}{1}+4$
$2=2$
=> Функции соприкасаются в точке $x_C=1$ -
Определим точку соприкосновения
Точка соприкосновения должна быть определена: Поэтому, высчитываем y-координату с координатой основных функций.
$f(color{red}{1})=color{red}{1}^2=color{blue}{1}$
=> Точка соприкосновения: $C(color{red}{1}|color{blue}{1})$
Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте
его в существующую тему, а создайте новую в корневом разделе “Помогите решить/разобраться (М)”.
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву
, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения
и указать конкретные затруднения.
Обязательно просмотрите тему
Правила данного раздела, иначе Ваша тема может быть удалена
или перемещена в Карантин, а Вы так и не узнаете, почему.
|
|
порядок касания кривых и каков его геометрический смысл?
|
|
01/12/11 |
Объясните, пожалуйста, доходчиво, что такое порядок касания . Заранее благодарна! З. Ы.
|
|
|
|
|
ИСН |
Re: Что такое порядок касания и каков его геометрический смысл?
|
||
18/05/06 |
Обычно это объясняют на примере рельсов. Порядки выше второго, впрочем, не отличить ни глазом, ни на ощупь. Бесконечный порядок возможен, но вряд ли кому нужен.
|
||
|
|
|||
|
Ktina |
Re: Что такое порядок касания и каков его геометрический смысл?
|
|
01/12/11 |
Обычно это объясняют на примере рельсов.
|
|
|
|
|
nnosipov |
Re: Что такое порядок касания и каков его геометрический смысл?
|
||
20/12/10 |
Может ли он быть бесконечным для двух несовпадающих кривых? Вот стандартный пример:
|
||
|
|
|||
|
wallflower |
Re: Что такое порядок касания и каков его геометрический смысл?
|
|
24/12/11 |
|
|
|
|
|
Padawan |
Re: Что такое порядок касания и каков его геометрический смысл?
|
||
13/12/05 |
И ещё, где вся эта канитель применяется? Я лично применял эту канитель для вывода условий, при которых кривая, заданная кривизной и кручением, лежит на сфере. Вот в этой теме кривая на сфере.
|
||
|
|
|||
|
ИСН |
Re: Что такое порядок касания и каков его геометрический смысл?
|
||
18/05/06 |
Про дороги – ну вот topic41983.html — Ср, 2012-03-21, 20:03 — там говорят про “скачок кривизны”, а не “порядок касания”, но суть та же.
|
||
|
|
|||
|
svv |
Re: Что такое порядок касания и каков его геометрический смысл?
|
||
23/07/08 |
Пособие “Как определить порядок касания с помощью WolframAlpha (Maple, MathCAD, Mathematica, MATLAB, …)”. Даны функции Пример. Определить порядок касания кривых
Ответ: касание третьего порядка.
|
||
|
|
|||
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Кривые бывают разные.
Опр. Кривизной плоской кривой в точке М0 называется величина
В том случае, когда кривая на плоскости задана параметрически
X=x(t), y=y(t)
Порядок соприкосновения плоских кривых
Если 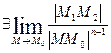
Замечание 1
Если указанный предел равен нулю, то кривые L1 и L2 имеют порядок соприкосновения выше, чем n.
Замечание 2
Если L1 и L2 имеют порядок соприкосновения выше любого значения n, то говорят, что они имеют в данной точке бесконечный прядок соприкосновения.
| < Предыдущая |
|---|


 и
и  с одной стороны, и
с одной стороны, и  и
и  и
и  и
и  . Известно, что они касаются в точке
. Известно, что они касаются в точке  , но порядок касания неизвестен, и его надо найти.
, но порядок касания неизвестен, и его надо найти. (“микроскоп”) в окрестности
(“микроскоп”) в окрестности  (“порядок увеличения микроскопа”). Последнее значение
(“порядок увеличения микроскопа”). Последнее значение  , при котором функция-микроскоп при
, при котором функция-микроскоп при  и
и  в точке
в точке  .
. для
для  :
: . При
. При  . Глубокий нуль.
. Глубокий нуль. . Нуль.
. Нуль. . Нуль.
. Нуль. . Какое-то конечное число.
. Какое-то конечное число. . Бесконечность.
. Бесконечность.