Решаем задачу нахождения длины наибольшей возрастающей подпоследовательности
Время на прочтение
7 мин
Количество просмотров 50K
Задача
“Найти длину самой большой возрастающей подпоследовательности в массиве.”
Вообще, это частный случай задачи нахождения общих элементов 2-х последовательностей, где второй последовательностью является та же самая последовательность, только отсортированная.
На пальцах
Есть последовательность:
5, 10, 6, 12, 3, 24, 7, 8
Вот примеры подпоследовательностей:
10, 3, 8
5, 6, 3
А вот примеры возрастающих подпоследовательностей:
5, 6, 7, 8
3, 7, 8
А вот примеры возрастающих подпоследовательностей наибольшей длины:
5, 6, 12, 24
5, 6, 7, 8
Да, максимальных тоже может быть много, нас интересует лишь длина.
Здесь она равна 4.
Теперь когда задача определена, решать мы ее начинаем с (сюрприз!) вычисления чисел Фибоначчи, ибо вычисление их — это самый простой алгоритм, в котором используется “динамическое программирование”. ДП — термин, который лично у меня никаких правильных ассоциаций не вызывает, я бы назвал этот подход так — “Программирование с сохранением промежуточного результата этой же задачи, но меньшей размерности”. Если же посчитать числа Фибоначчи с помощью ДП для вас проще пареной репы — смело переходите к следующей части. Сами числа Фибоначчи не имеют отношения к исходной задаче о подпоследовательностях, я просто хочу показать принцип ДП.
Последовательность Фибоначчи O(n)
Последовательность Фибоначчи популярна и окружена легендами, разглядеть ее пытаются (и надо признать, им это удается) везде, где только можно. Принцип же ее прост. n-ый элемент последовательности равен сумме n-1 и n-2 элемента. Начинается соответственно с 0 и 1.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34 …
Берем 0, прибавляем 1 — получаем 1.
Берем 1, прибавляем 1 — получаем 2.
Берем 1, прибавляем 2 — получаем, ну вы поняли, 3.
Собственно нахождение n-го элемента этой последовательности и будет нашей задачей. Решение кроется в самом определении этой последовательности. Мы заведем один мутабельный массив, в который будем сохранять промежуточные результаты вычисления чисел Фибоначчи, т.е. те самые n-1 и n-2.
Псевдокод:
int numberForIndex(int index) {
int[] numbers = [0, 1]; // мутабельный массив, можем добавлять к нему элементы
for (int i = 2; i < index + 1; i++) {
numbers[index] = numbers[i - 1] + numbers[i - 2];
}
return numbers[index];
}→ Пример решения на Objective-C
→ Тесты
Вот и всё, в этом массиве numbers вся соль ДП, это своего рода кэш (Caсhe), в который мы складываем предыдущие результаты вычисления этой же задачи, только на меньшей размерности (n-1 и n-2), что дает нам возможность за одно действие найти решение для размерности n.
Этот алгоритм работает за O(n), но использует немного дополнительной памяти — наш массив.
Вернемся к нахождению длины максимальной возрастающей подпоследовательности.
Решение за O( n ^ 2)
Рассмотрим следующую возрастающую подпоследовательность:
5, 6, 12
теперь взглянем на следующее число после последнего элемента в последовательности — это 3.
Может ли оно быть продолжением нашей последовательности? Нет. Оно меньше чем 12.
А 24 ?
Оно да, оно может.
Соответственно длина нашей последовательности равна теперь 3 + 1, а последовательность выглядит так:
5, 6, 12, 24
Вот где переиспользование предыдущих вычислений: мы знаем что у нас есть подпоследовательность 5, 6, 12, которая имеет длину 3 и теперь нам легко добавить к ней 24. Теперь у вас есть ощущение того, что мы можем это использовать, только как?
Давайте заведем еще один дополнительный массив (вот он наш cache, вот оно наше ДП), в котором будем хранить размер возрастающей подпоследовательности для n-го элемента.
Выглядеть это будет так:
Наша задача — заполнить массив counts правильными значениями. Изначально он заполнен единицами, так как каждый элемент сам по себе является минимальной возрастающей подпоследовательностью.
“Что за загадочные i и j?” — спросите вы. Это индексы итераторов по массиву, которые мы будем использовать. Изменяться они будут с помощью двух циклов, один в другом. i всегда будет меньше чем j.
Сейчас j смотрит на 10 — это наш кандидат в члены последовательностей, которые идут до него. Посмотрим туда, где i, там стоит 5.
10 больше 5 и 1 <= 1, counts[j] <= counts[i]? Да, значит counts[j] = counts[i] + 1, помните наши рассуждения в начале?
Теперь таблица выглядит так.
Смещаем j.
Промежуточные шаги, их много
Результат:
Имея перед глазами эту таблицу и понимая какие шаги нужно делать, мы теперь легко можем реализовать это в коде.
Псевдокод:
int longestIncreasingSubsequenceLength( int numbers[] ) {
if (numbers.count == 1) {
return 1;
}
int lengthOfSubsequence[] = Аrray.newArrayOfSize(numbers.count, 1);
for (int j = 1; j < numbers.count; j++) {
for (int k = 0; k < j; k++) {
if (numbers[j] > numbers[k]) {
if (lengthOfSubsequence[j] <= lengthOfSubsequence[k]) {
lengthOfSubsequence[j] = lengthOfSubsequence[k] + 1;
}
}
}
}
int maximum = 0;
for (int length in lengthOfSubsequence) {
maximum = MAX(maximum, length);
}
return maximum;
}→ Реализация на Objective-C
→ Тесты
Вы не могли не заметить два вложенных цикла в коде, а там где есть два вложенных цикла проходящих по одному массиву, есть и квадратичная сложность O(n^2), что обычно не есть хорошо.
Теперь, если вы билингвал, вы несомненно зададитесь вопросом “Can we do better?”, обычные же смертные спросят “Могу ли я придумать алгоритм, который сделает это за меньшее время?”
Ответ: “да, можете!”
Чтобы сделать это нам нужно вспомнить, что такое бинарный поиск.
Бинарный поиск O(log n)
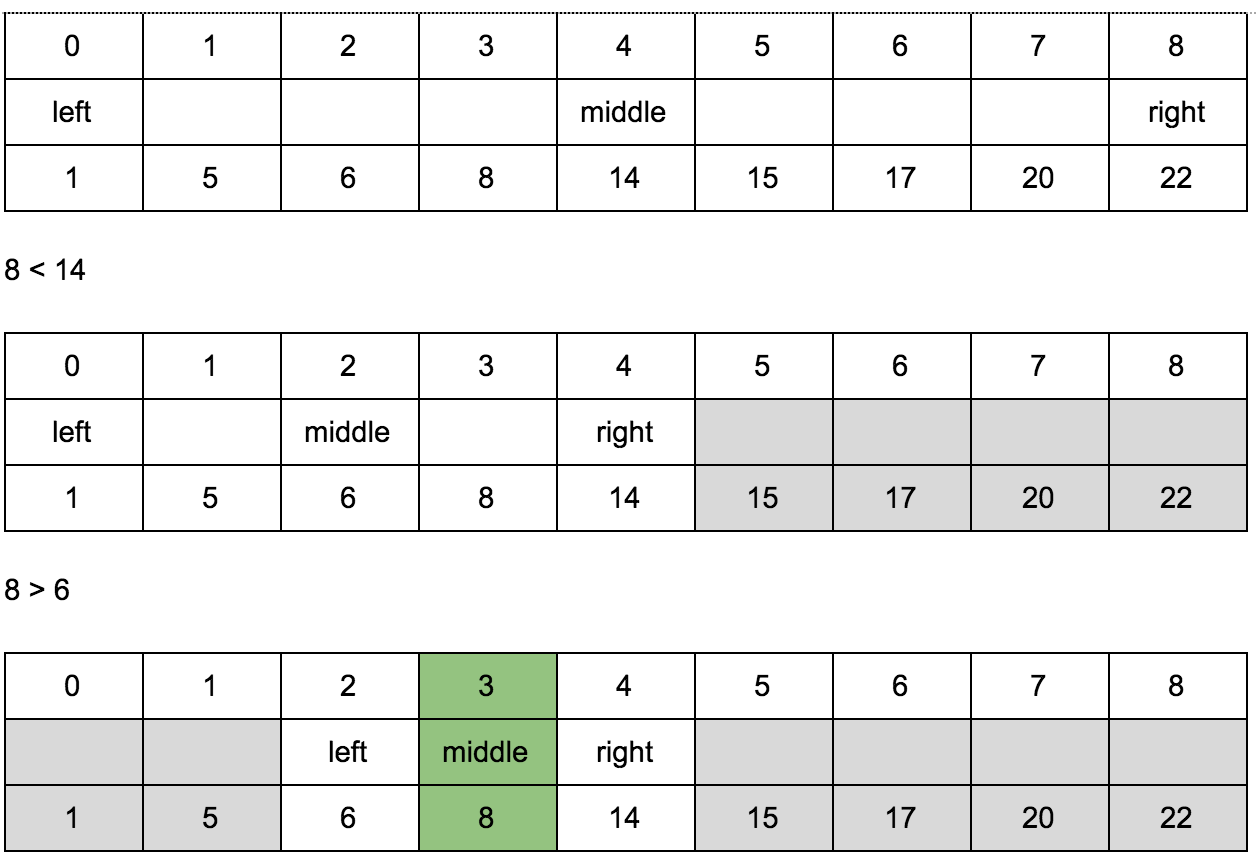
Бинарный поиск работает только на отсортированных массивах. Например, нам нужно найти позицию числа n в отсортированном массиве:
1, 5, 6, 8, 14, 15, 17, 20, 22
Зная что массив отсортирован, мы всегда можем сказать правее или левее определенного числа в массиве искомое число должно находиться.
Мы ищем позицию числа 8 в этом массиве. С какой стороны от середины массива оно будет находиться? 14 — это число в середине массива. 8 < 14 — следовательно 8 левее 14. Теперь нас больше не интересует правая часть массива, и мы можем ее отбросить и повторять ту же самую операцию вновь и вновь пока не наткнемся на 8. Как видите, нам даже не нужно проходить по всем элементам массива, сложность этого алгоритма < O( n ) и равна O (log n).
Для реализации алгоритма нам понадобятся 3 переменные для индексов: left, middle, right.
Ищем позицию числа 8.
Мы отгадали где находится 8 с трёх нот.
Псевдокод:
int binarySearch(int list [], int value) {
if !list.isEmpty {
int left = list.startIndex
int right = list.endIndex-1
while left <= right {
let middle = left + (right - left)/2
if list[middle] == value{
return middle
}
if value < list[middle]{
right = middle - 1
}
else{
left = middle + 1
}
}
}
return nil
}Решение за O (n * log n)
Теперь мы будем проходить по нашему исходному массиву при этом заполняя новый массив, в котором будет храниться возрастающая подпоследовательность. Еще один плюс этого алгоритма: он находит не только длину максимальной возрастающей подпоследовательности, но и саму подпоследовательность.
Как же двоичный поиск поможет нам в заполнении массива подпоследовательности?
С помощью этого алгоритма мы будем искать место для нового элемента в вспомогательном массиве, в котором мы храним для каждой длины подпоследовательности минимальный элемент, на котором она может заканчиваться.
Если элемент больше максимального элемента в массиве, добавляем элемент в конец. Это просто.
Если такой элемент уже существует в массиве, ничего особо не меняется. Это тоже просто.
Что нам нужно рассмотреть, так это случай когда следующий элемент меньше максимального в этом массиве. Понятно, что мы не можем его поставить в конец, и он не обязательно вообще должен являться членом именно максимальной последовательности, или наоборот, та подпоследовательность, которую мы имеем сейчас и в которую не входит этот новый элемент, может быть не максимальной.
Все это запутанно, сейчас будет проще, сведем к рассмотрению 2-х оставшихся случаев.
- Рассматриваемый элемент последовательности (x) меньше чем наибольший элемент в массиве (Nmax), но больше чем предпоследний.
- Рассматриваемый элемент меньше какого-то элемента в середине массива.
В случае 1 мы просто можем откинуть Nmax в массиве и поставим на его место x. Так как понятно, что если бы последующие элементы были бы больше чем Nmax, то они будут и больше чем x — соответственно мы не потеряем ни одного элемента.
Случай 2: для того чтобы этот случай был нам полезен, мы заведем еще один массив, в котором будем хранить размер подпоследовательности, в которой этот элемент является максимальным. Собственно этим размером и будет являться та позиция в первом вспомогательном массиве для этого элемента, которую мы найдем с помощью двоичного поиска. Когда мы найдем нужную позицию, мы проверим элемент справа от него и заменим на текущий, если текущий меньше (тут действует та же логика как и в первом случае)
Не расстраивайтесь, если не все стало понятно из этого текстового объяснения, сейчас я покажу все наглядно.
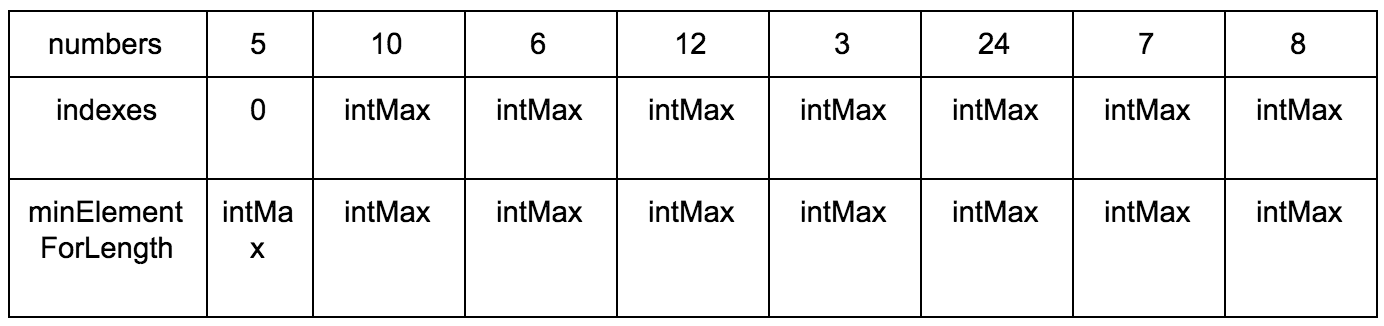
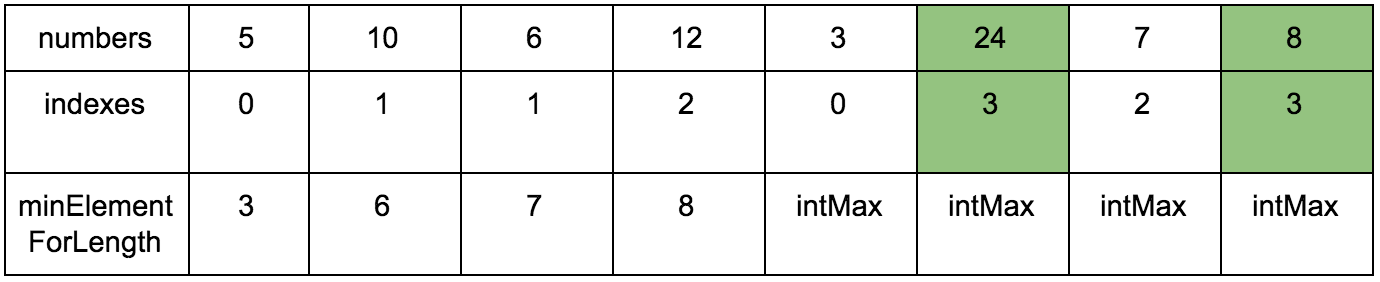
Нам нужны:
- Исходная последовательность
- Создаем мутабельный массив, где будем хранить возрастающие элементы для подпоследовательности
- Создаем мутабельный массив размеров подпоследовательности, в которой рассматриваемый элемент является максимальным.
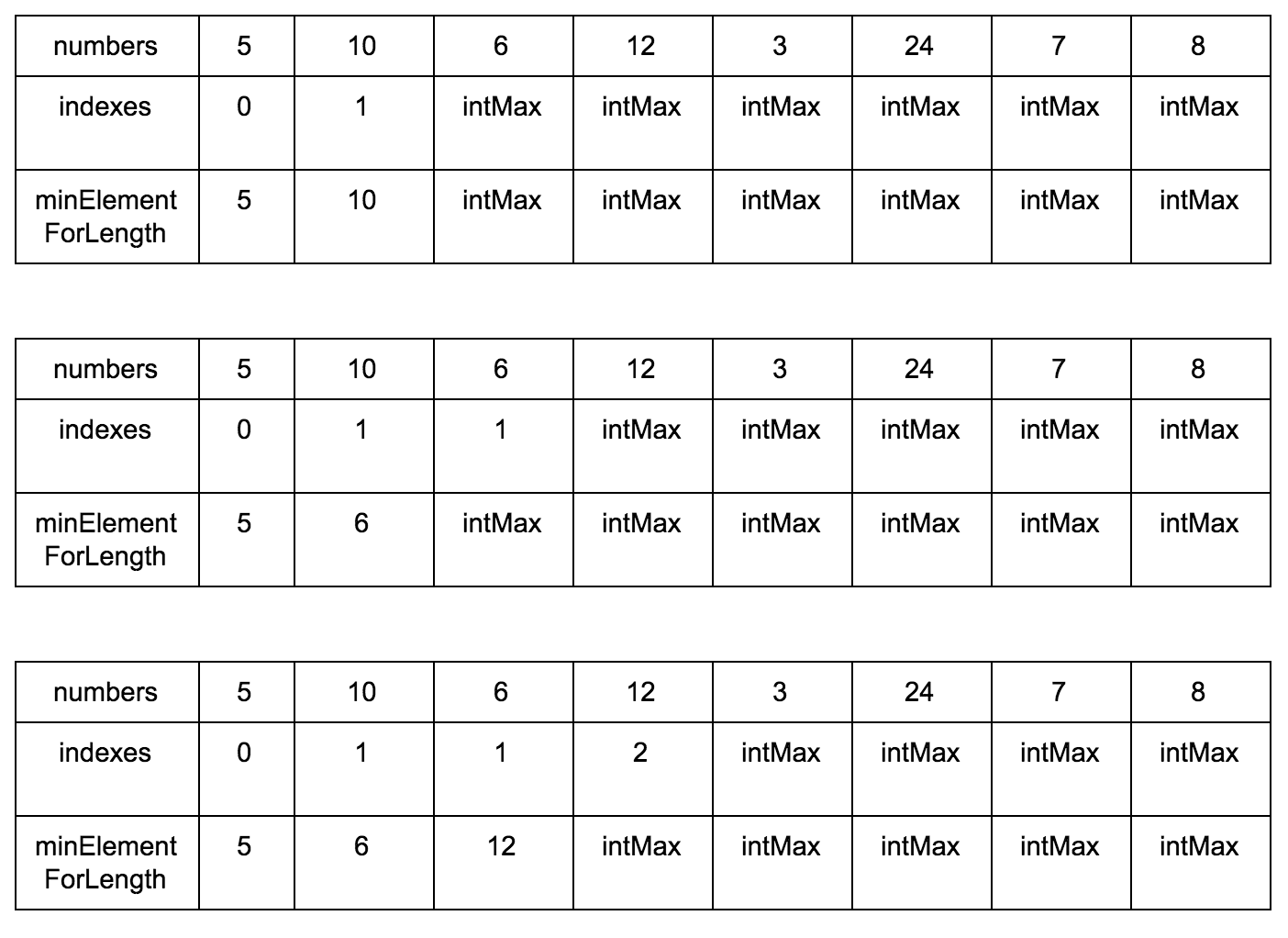
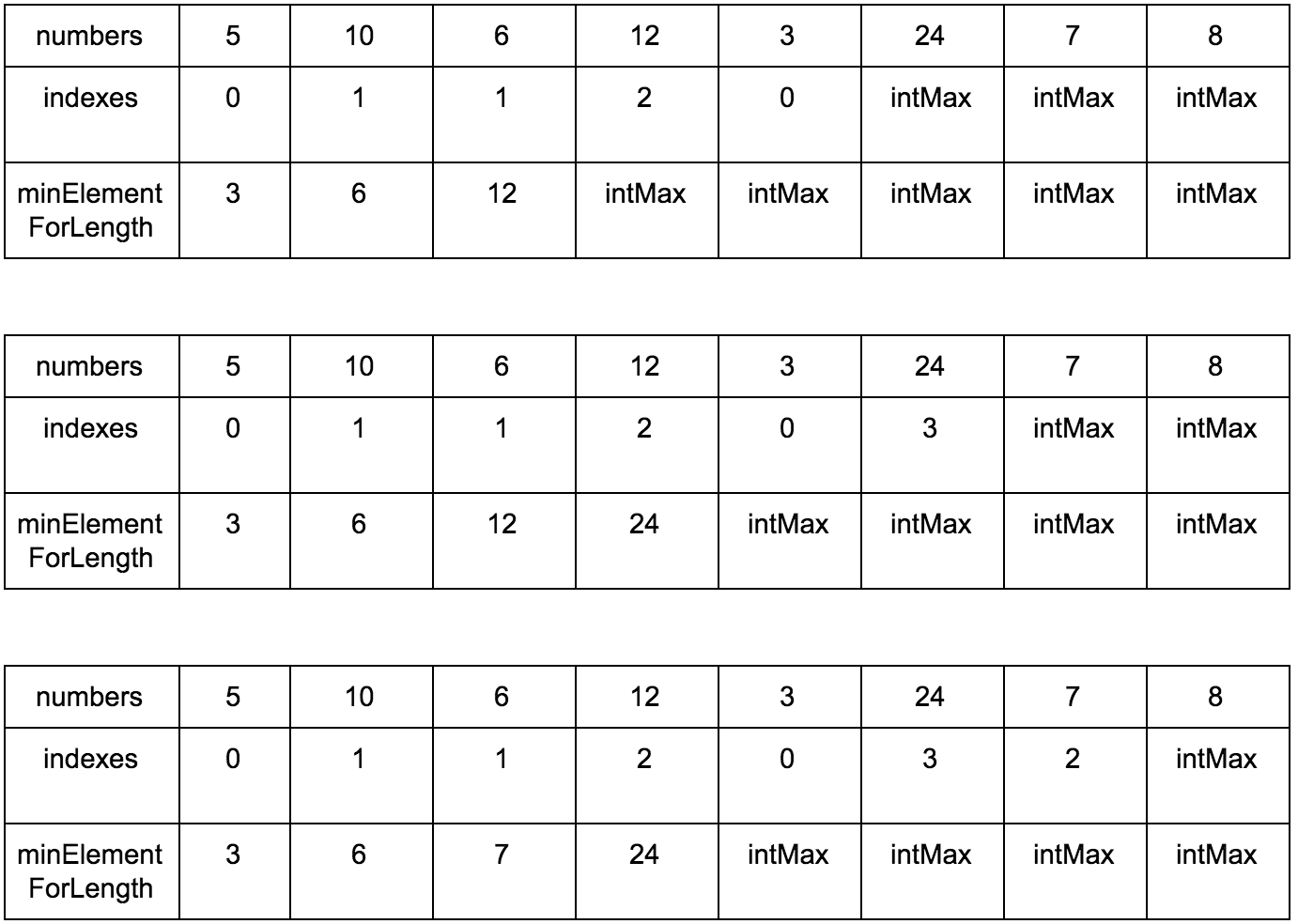
Промежуточные шаги
Результат:
Псевдокод:
int longestIncreasingSubsequenceLength(int numbers[]) {
if (numbers.count <= 1) {
return 1;
}
int lis_length = -1;
int subsequence[];
int indexes[];
for (int i = 0; i < numbers.count; ++i) {
subsequence[i] = INT_MAX;
subsequence[i] = INT_MAX;
}
subsequence[0] = numbers[0];
indexes[0] = 0;
for (int i = 1; i < numbers.count; ++i) {
indexes[i] = ceilIndex(subsequence, 0, i, numbers[i]);
if (lis_length < indexes[i]) {
lis_length = indexes[i];
}
}
return lis_length + 1;
}
int ceilIndex(int subsequence[],
int startLeft,
int startRight,
int key){
int mid = 0;
int left = startLeft;
int right = startRight;
int ceilIndex = 0;
bool ceilIndexFound = false;
for (mid = (left + right) / 2; left <= right && !ceilIndexFound; mid = (left + right) / 2) {
if (subsequence[mid] > key) {
right = mid - 1;
}
else if (subsequence[mid] == key) {
ceilIndex = mid;
ceilIndexFound = true;
}
else if (mid + 1 <= right && subsequence[mid + 1] >= key) {
subsequence[mid + 1] = key;
ceilIndex = mid + 1;
ceilIndexFound = true;
} else {
left = mid + 1;
}
}
if (!ceilIndexFound) {
if (mid == left) {
subsequence[mid] = key;
ceilIndex = mid;
}
else {
subsequence[mid + 1] = key;
ceilIndex = mid + 1;
}
}
return ceilIndex;
}→ Реализация на Objective-C
→ Тесты
Итоги
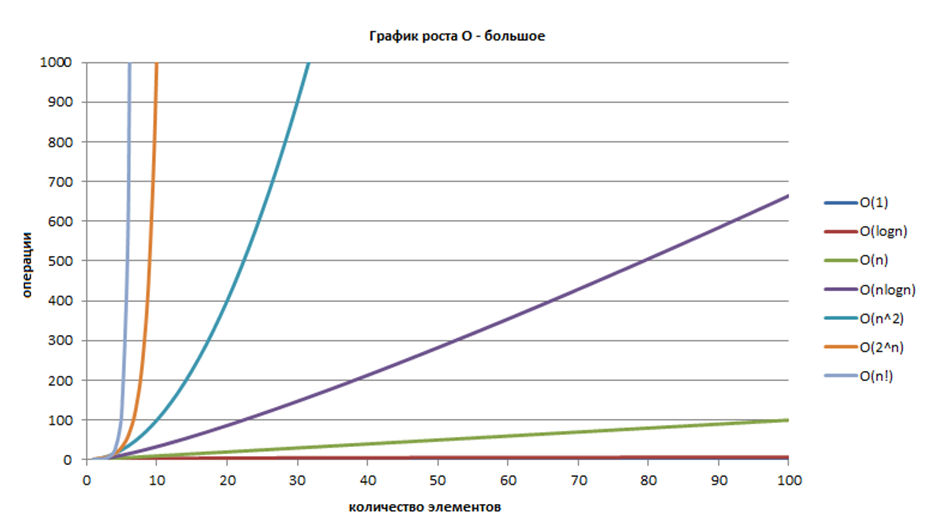
Мы с вами сейчас рассмотрели 4 алгоритма разной сложности. Это сложности, с которыми вам приходится встречаться постоянно при анализе алгоритмов:
О( log n ), О( n ), О( n * log n ), О( n ^ 2 )
Эта картинка из вот этой статьи
Еще мы рассмотрели примеры использования Динамического Программирования, тем самым расширив наш инструмент разработки и понимания алгоритмов. Эти принципы пригодятся вам при изучении других проблем.
Для лучшего понимания я рекомендую вам закодировать эти проблемы самим на привычном вам языке. А еще было бы здорово, если бы вы запостили ссылку на ваше решение в комментах.
Еще предлагаю подумать над тем как доработать последний алгоритм за O (n * log n ) так чтобы вывести еще и саму наибольшую подпоследовательность. Ответ напишите в комментах.
Всем спасибо за внимание, до новых встреч!
Ссылки:
Вопрос на Stackoverflow.com
Примеры реализации на C++ и Java
Видео с объяснением
| Задача: |
| Дан массив из чисел: . Требуется найти в этой последовательности строго возрастающую подпоследовательность наибольшей длины. |
| Определение: |
| Наибольшая возрастающая подпоследовательность (НВП) (англ. Longest increasing subsequence, LIS) строки длины — это последовательность символов строки таких, что , причем — наибольшее из возможных. |
Содержание
- 1 Решение за время O(N2)
- 1.1 Псевдокод алгоритма
- 2 Решение за O(N log N)
- 2.1 Псевдокод алгоритма
- 3 Ещё одно решение за О(N log N)
- 4 См. также
- 5 Примечания
- 6 Источники информации
Решение за время O(N2)
Построим массив , где — это длина наибольшей возрастающей подпоследовательности, оканчивающейся в элементе, с индексом . Массив будем заполнять постепенно — сначала , потом и т.д. Ответом на нашу задачу будет максимум из всех элементов массива .
Заполнение массива будет следующим: если , то искомая последовательность состоит только из числа . Если , то перед числом в подпоследовательности стоит какое-то другое число. Переберем его: это может быть любой элемент , но такой, что . Пусть на каком-то шаге нам надо посчитать очередное . Все элементы массива до него уже посчитаны. Значит наше мы можем посчитать следующим образом: при условии, что .
Пока что мы нашли лишь максимальную длину наибольшей возрастающей подпоследовательности, но саму ее мы вывести не можем. Для восстановления ответа заведем массив , где будет означать индекс в массиве , при котором достигалось наибольшее значение . Для вывода ответа будем идти от элемента с максимальным значениям по его предкам.
Псевдокод алгоритма
vector<int> findLIS(vector<int> a): int n = a.size //размер исходной последовательности int prev[0..n - 1] int d[0..n - 1] for i = 0 to n - 1 d[i] = 1 prev[i] = -1 for j = 0 to i - 1 if (a[j] < a[i] and d[j] + 1 > d[i]) d[i] = d[j] + 1 prev[i] = j pos = 0 // индекс последнего элемента НВП length = d[0] // длина НВП for i = 0 to n - 1 if d[i] > length pos = i length = d[i] // восстановление ответа vector<int> answer while pos != -1 answer.push_back(a[pos]) pos = prev[pos] reverse(answer) return answer
Решение за O(N log N)
Для более быстрого решения данной задачи построим следующую динамику: пусть — число, на которое оканчивается возрастающая последовательность длины , а если таких чисел несколько — то наименьшее из них. Изначально мы предполагаем, что , а все остальные элементы .
Заметим два важных свойства этой динамики: , для всех и каждый элемент обновляет максимум один элемент . Это означает, что при обработке очередного , мы можем за c помощью двоичного поиска в массиве найти первое число, которое больше либо равно текущего и обновить его.
Для восстановления ответа будем поддерживать заполнение двух массивов: и . В будем хранить индекс элемента, на который заканчивается оптимальная подпоследовательность длины , а в — позицию предыдущего элемента для .
Псевдокод алгоритма
vector<int> findLIS(vector<int> a): int n = a.size //размер исходной последовательности int d[0..n] int pos[0..n] int prev[0..n - 1] length = 0 pos[0] = -1 d[0] = -INF for i = 1 to n d[i] = INF for i = 0 to n - 1 j = binary_search(d, a[i]) if (d[j - 1] < a[i] and a[i] < d[j]) d[j] = a[i] pos[j] = i prev[i] = pos[j - 1] length = max(length, j) // восстановление ответа vector<int> answer p = pos[length] while p != -1 answer.push_back(a[p]) p = prev[p] reverse(answer) return answer
Ещё одно решение за О(N log N)
Существует ещё одно решение, которое позволяет нам найти длину наибольшей возрастающей подпоследовательности, но без возможности восстановления данной подпоследовательности. Для этого мы воспользуемся таблом Юнга. Оно обладает таким свойством, что длина первой строки табла и будет являться искомой величиной[1].
Само табло представляет из себя расположение различных целых чисел в массиве строк, выровненных по левому краю, где в строке содержится элементов; при этом в каждой строке элементы возрастают слева направо, а элементы каждого столбца возрастают сверху вниз. Чтобы построить табло требуется прочитать очередной элемент , если он больше либо равен , где — длина строки, то просто добавить в конец строки, если меньше, то требуется найти первый элемент , который больше данного . Поставить элемент вместо . С элементом требуется провести те же действия, что и с , только уже на строке табла.
Пример построения табла на массиве :
1. Берём элемент . Видим, что , который расположен на первой строке в ячейке с индексом . Увеличиваем и .
2. Берём элемент . Видим, что . Увеличиваем и .
3. Аналогично для элемента .
4. Берём элемент . Так как , то бинарным поиском находим нужную нам позицию , такую, что . В данном случае это
первая позиция. Присваиваем и проделываем такую же операцию, но для строки с индексом .
5. Аналогично для элемента .
6. Аналогично для элемента .
Таким образом, длина наибольшей возрастающей подпоследовательности для массива равна (например, подпоследовательность из элементов ).
См. также
- Задача о наибольшей общей подпоследовательности
- Наибольшая общая возрастающая подпоследовательность
- Задача о наибольшей общей палиндромной подпоследовательности
Примечания
- ↑ Wikipedia — Robinson–Schensted correspondence
Источники информации
- Википедия — Задача поиска наибольшей увеличивающейся подпоследовательности
- Wikipedia — Longest increasing subsequence
- Дистанционная подготовка — Наибольшая возрастающая подпоследовательность (НВП, Longest Increasing Subsequence, LIS)
- MAXimal :: algo :: Длиннейшая возрастающая подпоследовательность за O (N log N)
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 8 февраля 2015 года; проверки требуют 8 правок.
Задача поиска наибольшей увеличивающейся подпоследовательности состоит в нахождении наиболее длинной возрастающей подпоследовательности в данной последовательности элементов.
Постановка задачи[править | править код]
Отметим, подпоследовательность может и не являться подстрокой (то есть, её элементы не обязательно идут подряд в исходной последовательности). Формально, для строки x длины n необходимо найти максимальное число l и соответствующую ему возрастающую последовательность индексов 
![x[i_{{k}}]<x[i_{{k+1}}],forall {k},{mathcal {2}}{,1,..,l-1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f09a36199ec2e2a93940afacd7eab6439005ba3b)
Наибольшая увеличивающая подпоследовательность имеет применения в физике, математике, теории представления групп, теории случайных матриц. В общем случае известно решение этой задачи за время n log n в худшем случае[1].
Родственные алгоритмы[править | править код]
- Задача наибольшей увеличивающейся подпоследовательности схожа с задачей поиска наибольшей общей подпоследовательности, имеющей квадратичное динамическое решение.
- В частном случае, если строка является перестановкой 1..n, задача имеет решение за n log log n[2] с использованием деревьев ван Эмде Боаса.
- При использовании дерева, построенного для элементов алфавита, возможно решение задачи за O(n log A), где A — мощность алфавита, определяемая заранее. При реализации сбалансированными деревьями, необязательно задавать A наперёд. По очевидным причинам A ограничивается длиной строки.
- Возможно также свести задачу к поиску длиннейшего пути в ориентированном ациклическом графе, задавая рёбра между возрастающими элементами. Хотя подсчёт длиннейшего пути будет занимать линейное время от числа рёбер, в худшем случае оно может быть квадратично от длины строки.
Пример эффективного алгоритма[править | править код]
Приведем алгоритм решения задачи, работающий за O(n log n).
Для строки x будем хранить массивы M и P длины n.
M[i] содержит индекс наименьшего по величине из последних элементов возрастающих подпоследовательностей xnj длины i, ![({mathcal {8}}j,{mathcal {2}},1,..,i:x[n_{{j}}]leq ,M[i])](https://wikimedia.org/api/rest_v1/media/math/render/svg/81c7f83d08b0132275b77d92671f36eb2bab8594)
P[i] хранит индекс предшествующего символа для наидлиннейшей возрастающей подпоследовательности, оканчивающейся в i-й позиции.
На каждом шаге будем хранить текущий максимум длины подпоследовательности и соответствующий индекс конечного символа, не забывая поддерживать свойства массивов. Шаг представляет собой переход к следующему элементу строки, для каждого перехода потребуется не более логарифма времени (бинарный поиск по массиву M).
P = array of length N
M = array of length N + 1
L = 0
for i in range 0 to N-1:
lo = 1
hi = L
while lo ≤ hi:
mid = ceil((lo+hi)/2)
if X[M[mid]] < X[i]:
lo = mid+1
else:
hi = mid-1
newL = lo
P[i] = M[newL-1]
M[newL] = i
if newL > L:
L = newL
S = array of length L
k = M[L]
for i in range L-1 to 0:
S[i] = X[k]
k = P[k]
return S
Очевидно, после выполнения алгоритма, L — длина искомой подпоследовательности, сами же элементы можно получить, разворачивая P рекурсивно из элемента index.
Примечания[править | править код]
- ↑ Schensted, C. (1961). «Longest increasing and decreasing subsequences». Canadian Journal of Mathematics 13: 179—191.
- ↑ Hunt, James W. and Szymanski, Thomas G. A Fast Algorithm for Computing Longest Common Subsequences (англ.) // Commun. ACM. — ACM, 1977. — Vol. 20, no. 5. — P. 350–353. — ISSN 0001-0782.
Ссылки[править | править код]
- Наибольшая возрастающая подпоследовательность
Это довольно сложная, но очень популярная задача. Давайте решим ее на примере массива:
2 3 -8 -1 2 4 -2 3
Если рассматривать массив как содержащий чередующиеся последовательности положительных и отрицательных чисел, то не имеет смысла рассматривать части положительных или отрицательных субпоследовательностей. Почему? Включая часть отрицательной субпоследовательности, мы уменьшаем итоговое значение суммы, значит, нам не стоит включать часть отрицательной субпоследовательности вообще. Включение части положительной субпоследовательности выглядит еще более странным, поскольку включение этой субпоследовательности целиком всегда даст больший результат.
Нужно придумать алгоритм, рассматривая массив как последовательность отрицательных и положительных чисел, расположенных вперемежку.
Любое число можно представить в виде суммы субпоследовательностей положительных и отрицательных чисел. В нашем примере массив можно сократить до:
5 -9 6 -2 3
Мы еще не получили отличный алгоритм, но теперь лучше понимаем, с чем имеем дело.
Рассмотрим предыдущий массив. Нужно ли учитывать субпоследовательность {5, -9}? В сумме мы получим -4, значит, нет смысла учитывать оба этих числа, достаточно только {5}.
В каких случаях имеет смысл учитывать отрицательные числа? Только если это позволяет нам объединить две положительные субпоследовательности, сумма каждой из которых больше, чем вклад отрицательной величины.
Давайте продвигаться, начиная с первого элемента в массиве.
5 — это самая большая сумма, встретившаяся нам. Таким образом, maxsum = 5 и sum = 5. Затем мы видим следующее число (-9). Если добавить это число к sum, то получится отрицательная величина. Нет смысла расширять субпоследовательность с 5 до -9 (-9 уменьшает общую сумму до 4). Таким образом, мы просто сбрасываем значение sum.
Теперь мы дошли до следующего элемента (6). Эта субпоследовательность больше, чем 5, таким образом, мы обновляем значения maxsum и sum.
Затем мы смотрим на следующий элемент (-2). Добавление этого числа к 6 сделает sum = 4. Так как это не окончательное значение, наша субпослсдовательность выглядит как {6, -2}. Мы обновляем sum, но не maxsum.
Наконец мы смотрим па следующий элемент (3). Добавление 3 к sum (4) даст нам 7, таким образом, мы обновляем maxsum. Максимальная последовательность имеет вид {6, -2, 3}.
Когда мы работаем с развернутым массивом, логика остается такой же. Следующий код реализует этот алгоритм:
public static int getMaxSum(int[] a) {
int maxsum = 0;
int sum = 0;
for (int i = 0; i < a.lenght; i++) {
sum += a[i];
if (maxsum < sum) {
maxsum = sum;
} else if (sum < 0) {
sum = 0;
}
}
return maxsum;
}А если массив состоит из отрицательных чисел? Как действовать в этом случае? Рассмотрим простой массив {-3, -10, -5}. Можно дать три разных ответа:
• -3 (если считать, что субпоследовательность не может быть пустой);
• 0 (субпоследовательность может иметь нулевую длину);
• MINIMUM_INT (для случая ошибки).
В нашем коде был использован второй ответ (sum = 0), но в этом вопросе не существует однозначного «правильного» решения. Обсудите это с интервьюером.
Разбор задачи по книге «Карьера программиста. Как устроиться на работу в Google, Microsoft или другую ведущую IT-компанию»
Видимо я тут чего-то важного не понимаю.
#include <stdio.h>
struct range {
int start, end;
};
// inclusive range
struct range
max_gtseq (int *a, int n)
{
struct range result = {0, 0};
int max = 0, start = 0, end = 0;
for (int i = 0; i < n - 1; i++)
if (a[i] < a[i + 1])
end++;
else {
if (end - start > max) {
max = end - start;
result.start = start;
result.end = end;
}
end = start = i + 1;
}
if ((n - 1) - start > max) {
result.start = start;
result.end = n - 1;
}
return result;
}
int
main (int ac, char *av[])
{
int x[] = {1, 2, 3, 10, 1, 2, 100, 1, 2, 3, 4, 5, 6, 0}; //{10, 9, 8};
struct range r = max_gtseq(x, sizeof(x) / sizeof(x[0]));
printf ("start = %d end = %dn", r.start, r.end);
return puts("End") == EOF;
}
Неужели такой тривиальный однопроходный алгоритм не работает?