Как найти последовательность событий

Время на прочтение
5 мин

Количество просмотров 29K

Задача поиска непрерывных последовательностей событий довольно легко решается с помощью SQL. Давайте уточним, что из себя представляют эти последовательности.

Для примера возьмём Stack Overflow. Он использует клёвую систему репутации с наградами за определенные достижения. Как и во многих социальных проектах, они поощряют пользователей ежедневно посещать ресурс. Обратим внимание на эти две награды:

Нетрудно понять, что они означают. Зайдите на сайт в первый день. Затем на второй день. Затем на третий (возможно несколько раз, это не имеет значения). Не зашли на четвёртый? Начинаем считать заново.

Как отследить это с помощью SQL?

Для доступа к данным мы будем использовать Stack Exchange Data Explorer.

Обратите внимание, что мы не будем запрашивать даты посещений, так как эта информация не предоставляется. Вместо этого, давайте запросим даты размещённых пользователем сообщений.

В качестве базы данных используется SQL Server, следовательно мы можем использовать следующий запрос:

SELECT DISTINCT CAST(CreationDate AS DATE) AS date
FROM Posts
WHERE OwnerUserId = ##UserId##
ORDER BY 1

…который выдаст что-то подобное:

date          
----------
2010-11-26
2010-11-27
2010-11-29
2010-11-30
2010-12-01
2010-12-02
2010-12-03
2010-12-05
2010-12-06
2010-12-07
2010-12-08
2010-12-09
2010-12-13
2010-12-14
...
(769 rows)

(можете сделать запрос самостоятельно, здесь)

Как можно заметить, есть несколько пропусков:

date          
--------------------------------------
2010-11-26
2010-11-27 <---- Пропуск после 2 дней

2010-11-29
2010-11-30
2010-12-01
2010-12-02
2010-12-03 <---- Пропуск после 5 дней

2010-12-05
2010-12-06
2010-12-07
2010-12-08
2010-12-09 <---- Пропуск после 5 дней

2010-12-13
2010-12-14
...

Человеку легко увидеть, сколько дней подряд идут даты без пропусков. Но как сделать это посредством SQL?

Чтобы упростить задачу, давайте «сохраним» индивидуальные запросы в обобщённых табличных выражениях. Предыдущий запрос мы назовём dates:

WITH
 
  -- This table contains all the distinct date 
  -- instances in the data set
  dates(date) AS (
    SELECT DISTINCT CAST(CreationDate AS DATE)
    FROM Posts
    WHERE OwnerUserId = ##UserId##
  )
...

Теперь цель полученного запроса — поместить все последовательные даты в одну и ту же группу, чтобы мы могли объединить их. Вот как мы это сделаем:

SELECT
  COUNT(*) AS consecutiveDates,
  MIN(week) AS minDate,
  MAX(week) AS maxDate
FROM groups
GROUP BY grp -- This "grp" value will be explained later
ORDER BY 1 DESC, 2 DESC

Мы хотим объединить каждую группу «grp» и подсчитать количество дат в группе, а также найти минимум и максимум в каждой группе.

Создание групп для последовательных дат

Давайте теперь посмотрим на результат запроса, и, чтобы было понятнее, мы пронумеруем строки независимо от пропусков в датах:

row number   date          
--------------------------------
1            2010-11-26
2            2010-11-27

3            2010-11-29 <-- пропуск перед этой строкой
4            2010-11-30
5            2010-12-01
6            2010-12-02
7            2010-12-03

8            2010-12-05 <-- пропуск перед этой строкой

Как можно видеть, независимо от того, что существует разрыв между датами (две даты не являются последовательными), их номера строк по-прежнему будут последовательными. Мы можем сделать это с помощью функции ROW_NUMBER():

SELECT
  ROW_NUMBER() OVER (ORDER BY date) AS [row number],
  date
FROM dates

Теперь давайте посмотрим вот такой интересный запрос:

WITH
 
  -- This table contains all the distinct date 
  -- instances in the data set
  dates(date) AS (
    SELECT DISTINCT CAST(CreationDate AS DATE)
    FROM Posts
    WHERE OwnerUserId = ##UserId##
  ),
   
  -- Generate "groups" of dates by subtracting the
  -- date's row number (no gaps) from the date itself
  -- (with potential gaps). Whenever there is a gap,
  -- there will be a new group
  groups AS (
    SELECT
      ROW_NUMBER() OVER (ORDER BY date) AS rn,
      dateadd(day, -ROW_NUMBER() OVER (ORDER BY date), date) AS grp,
      date
    FROM dates
  )
SELECT *
FROM groups
ORDER BY rn

Приведённый выше запрос даёт нам следующий результат:

rn  grp          date          
--- ----------   ----------
1   2010-11-25   2010-11-26
2   2010-11-25   2010-11-27

3   2010-11-26   2010-11-29
4   2010-11-26   2010-11-30
5   2010-11-26   2010-12-01
6   2010-11-26   2010-12-02
7   2010-11-26   2010-12-03

8   2010-11-27   2010-12-05
9   2010-11-27   2010-12-06
10  2010-11-27   2010-12-07
11  2010-11-27   2010-12-08
12  2010-11-27   2010-12-09

13  2010-11-30   2010-12-13
14  2010-11-30   2010-12-14

(можете сделать запрос самостоятельно, здесь)

Все, что мы сделали, это вычли номер строки из дня, чтобы получить новую дату «grp». Полученная таким образом дата не имеет смысла, это просто вспомогательное значение.

Однако, мы можем гарантировать, что для последовательных дат, значение «grp» будет одинаковое, потому что для всех последовательно идущих дат, следующие два уравнения верны:

date2 - date1 = 1 // разница в днях между двумя датами
rn2 - rn1 = 1 // Разница в цифрах строк

Для непоследовательных дат, разница в номерах строк будет также 1, но разница в днях будет больше единицы. Группы теперь можно легко различить:

rn  grp          date          
--- ----------   ----------
1   2010-11-25   2010-11-26
2   2010-11-25   2010-11-27

3   2010-11-26   2010-11-29
4   2010-11-26   2010-11-30
5   2010-11-26   2010-12-01
6   2010-11-26   2010-12-02
7   2010-11-26   2010-12-03

8   2010-11-27   2010-12-05
9   2010-11-27   2010-12-06
10  2010-11-27   2010-12-07
11  2010-11-27   2010-12-08
12  2010-11-27   2010-12-09

13  2010-11-30   2010-12-13
14  2010-11-30   2010-12-14

Таким образом, финальный запрос будет следующим:

WITH
 
  -- This table contains all the distinct date 
  -- instances in the data set
  dates(date) AS (
    SELECT DISTINCT CAST(CreationDate AS DATE)
    FROM Posts
    WHERE OwnerUserId = ##UserId##
  ),
   
  -- Generate "groups" of dates by subtracting the
  -- date's row number (no gaps) from the date itself
  -- (with potential gaps). Whenever there is a gap,
  -- there will be a new group
  groups AS (
    SELECT
      ROW_NUMBER() OVER (ORDER BY date) AS rn,
      dateadd(day, -ROW_NUMBER() OVER (ORDER BY date), date) AS grp,
      date
    FROM dates
  )
SELECT
  COUNT(*) AS consecutiveDates,
  MIN(week) AS minDate,
  MAX(week) AS maxDate
FROM groups
GROUP BY grp
ORDER BY 1 DESC, 2 DESC

И его результат:

consecutiveDates minDate       maxDate       
---------------- ------------- ------------- 
14               2012-08-13    2012-08-26
14               2012-02-03    2012-02-16
10               2013-10-24    2013-11-02
10               2011-05-11    2011-05-20
9                2011-06-30    2011-07-08
7                2012-01-17    2012-01-23
7                2011-06-14    2011-06-20
6                2012-04-10    2012-04-15
6                2012-04-02    2012-04-07
6                2012-03-26    2012-03-31
6                2011-10-27    2011-11-01
6                2011-07-17    2011-07-22
6                2011-05-23    2011-05-28
...

(можете сделать запрос самостоятельно, здесь)

Бонус: найти последовательность недель

То, что мы использовали дни — это просто наш выбор. Мы взяли точное время и округлили его до дня с помощью функции CAST:

SELECT DISTINCT CAST(CreationDate AS DATE)

Если бы мы хотели узнать последовательность, например, из недель, мы могли бы округлять время до недель:

SELECT DISTINCT datepart(year, CreationDate) * 100 
              + datepart(week, CreationDate)

Этот запрос использует численное выражение года и недели и создаёт числа типа 201503 для третьей недели 2015 года. Остальная часть запроса остаётся без изменений:

WITH
  weeks(week) AS (
    SELECT DISTINCT datepart(year, CreationDate) * 100 
                  + datepart(week, CreationDate)
    FROM Posts
    WHERE OwnerUserId = ##UserId##
  ),
  groups AS (
    SELECT
      ROW_NUMBER() OVER (ORDER BY week) AS rn,
      dateadd(day, -ROW_NUMBER() OVER (ORDER BY week), week) AS grp,
      week
    FROM weeks
  )
SELECT
  COUNT(*) AS consecutiveWeeks,
  MIN(week) AS minWeek,
  MAX(week) AS maxWeek
FROM groups
GROUP BY grp
ORDER BY 1 DESC, 2 DESC

И вот что мы получим:

consecutiveWeeks minWeek maxWeek 
---------------- ------- ------- 
45               201401  201445  
29               201225  201253  
25               201114  201138  
23               201201  201223  
20               201333  201352  
16               201529  201544  
15               201305  201319  
12               201514  201525  
12               201142  201153  
9                201502  201510  
7                201447  201453  
7                201321  201327  
6                201048  201053  
4                201106  201109  
3                201329  201331  
3                201102  201104  
2                201301  201302  
2                201111  201112  
1                201512  201512  

(можете сделать запрос самостоятельно, здесь)

Неудивительно, что последовательные недели охватывают гораздо более длинные диапазоны, так как автор регулярно пишет на Stack Overflow.

Последовательность
событий. Н.А.Бернштейн.

Цель: Определить способность к
логическому мышлению, обобщению, умение понимать связь событий и строить
последовательное умозаключение.

Материал: Для проведения опыта
необходимы серии сюжетных картинок (в количестве 3-6 картин), на которых
изображены этапы какого-либо события.

Существуют серии, соответствующие по содержанию детскому возрасту
(“Волки”, “Колодец”, “Лодки” и др.), а также
серии для взрослых (“Колесо”, “Пьяница”,
“Охотник” и т. д.).

Есть несколько вариантов:

Вариант 1: Серия из 3-4 картинок,
отражающих быт детей.

Вариант 2: Серия картинок с
эмоционально – смысловым подтекстом. (Векслер, либо Бидструпа).

Инструкция: Начиная с 5ти лет
применяя серии картинок 1ого варианта. Для детей начальных классов и старше – 2
ого варианта.

Перед ребенком кладутся произвольно картинки, связанные сюжетом.
Ребенок должен понять сюжет, выстроить правильную последовательность событий и
составить по картинке рассказ.

«Посмотри, перед тобой лежат картинки, на которых нарисовано
какое-то событие, акцентируй внимание. Порядок картинок перепутан, и тебе надо
догадаться, как их поменять местами, чтобы стало ясно, что нарисовал художник.
Подумай, переложи картинки, как ты считаешь нужным, а потом составь по ним
рассказ о том событии, которое здесь изображено».

Задание состоит из двух частей:

1) выкладывание последовательности событий картинок;

2) устный рассказ по ним.

После того, как ребенок разложил все картинки, экспериментатор
записывает в протоколе (например, 5, 4, 1, 2, 3), и затем просит ребенка
рассказать по порядку о том, что получилось. Если ребенок допустил ошибки, ему
задают вопросы, цель которых помочь выявить допущенные ошибки.

Испытуемому показывают пачку перемешанных карточек и говорят:
“Вот здесь на всех рисунках изображено одно и то же событие. Нужно
разобрать, с чего все началось, что было дальше и чем дело кончилось. Вот сюда
(экспериментатор указывает место) положите первую картинку, на которой на
рисовано начало, сюда – вторую, третью…, а сюда последнюю”,

После того как больной разложил все картинки, экспериментатор
записывает в протоколе, как он разложил (например: 5, 4, 1, 2, 3), и лишь после
этого просит больного рассказать по порядку о том, что получилось. Если больной
разложил неправильно, ему задают вопросы, цель которых помочь больному
установить противоречие в его рассуждениях, выявить допущенные ошибки.

Умение ставить эти вопросы зависит от квалификации и опыта
экспериментатора. Эти вопросы и ответы больного записываются в протокол, так же
как и действия больного по исправлению раскладки картин. Если вопросами не
удается довести больного до правильного понимания последовательности
изображенных событий, экспериментатор просто показывает ему первую картинку и
предлагает снова разложить. Это вторая попытка выполнить задание. Если она тоже
безуспешна, тогда экспериментатор сам рассказывает и показывает больному
последовательность событий и, перемешав снова все карточки, предлагает ему
разложить их снова – в третий раз.

В случае, если больной лишь на третьей попытке правильно
установил. Последовательность, полезно предложить ему другую серию той же
методики, чтобы выяснить, возможен ли “перенос” с трудом усвоенного
способа рассуждений.

Обработка результатов:

Выводы об уровне развития.
Высокий – ребенок самостоятельно нашел последовательность картинок
и составил логический рассказ. При неправильно найденной последовательности
рисунков испытуемый, тем не менее, сочиняет логичную версию рассказа.
Средний – ребенок правильно нашел последовательность, но не смог
составить хорошего рассказа. Составление рассказа с помощью наводящих вопросов
экспериментатора.
Низкий – если: ребенок не смог найти последовательность картинок и
отказался от рассказа; 
– по найденной им самим последовательности картинок составил нелогичный
рассказ; 
– составленная ребенком последовательность не соответствует рассказу; 
– каждая картинка рассказывается отдельно, сама по себе, не связана с
остальными – в результате не получается рассказа;
– на каждом рисунке просто перечисляются отдельные предметы.

При истолковании результатов исследования следует обращать
внимание на то, как больной реагирует на наводящие вопросы и критические
возражения экспериментатора, “подхватывает” ли он эту помощь или не
понимает ее.

В случаях, когда при неправильном составлении последовательности
рисунка, испытуемый сочинил логическую версию рассказа, считается что задание
выполнено, верно.

Если ребенок правильно установил последовательность картинок, но
не смог составить рассказ, необходимо задать наводящие вопросы. Если не хватает
ребенку словарного запаса для объяснения, а заданий для описания, то задаются
вопросы, которые фиксируются в протоколе. В этом случае задание
выполнено на среднем уровне.

Если не смог составить рассказ даже с помощью наводящих вопросов,
то выполнение задания неудовлетворительно.

Считается, что испытуемый не справился с заданием, если:

1. Не
   смог найти последовательность событий и отказался от рассказа
2. По
   найденной им самим последовательности картинок составил нелогичный
   рассказ.
3. Составленная
   испытуемым последовательность не соответствует рассказу (но за исключением
   тех случаев, когда ребенок после наводящего вопроса меняет
   последовательность и соответствующий рассказ).
4. Каждая
   картинка описывается отдельно, сама по себе.
5. На
   каждом рисунке просто перечислены отдельные предметы.

Если 4-5 вариант, то необходима тщательная проверка
интеллектуальных способностей.

В последнее время для установления последовательности и смысла
событий используются серии, составленные из карикатур (“Дома и на
работе”, “Прошел год”, “Кто работал и кто устал”,
“Обман зрения” и т. д.). Преимущество этих серий в том, что они
труднее для понимания и пригодны для исследования более интеллектуально
развитых и сохранных больных. В то же время центр тяжести задания при
использовании этих серий как бы переносится с установления строгой
последовательности этапов события (иногда эту последовательность точно
устанавливать и не нужно) на понимание юмора, т. е. смысла карикатур в целом.

Серии последовательности событий по карикатурам используются с
некоторой модификацией порядка проведения опытов. Больному раньше предлагают
самому установить последовательность событий, а за тем, если он не может этого
выполнить, предлагают карточку с названием серии. Название составляется обычно
так, что оно как бы “проливает свет” на смысл всей серии.

Протокол

Теория вероятности — подробнее

Что такое вероятность?

Рассмотрим пример. Допустим, мы бросаем игральную кость. Что это за кость такая, знаешь? Так называют кубик с цифрами на гранях. Сколько граней, столько и цифр: от ( 1) до ( 6).

Итак, мы бросаем кость и хотим, чтобы выпало ( 5) или ( 6). И нам выпадает ( 5).

В теории вероятностей говорят, что произошло благоприятное событие.

Если бы выпало ( 6), событие тоже было бы благоприятным. Итого может произойти всего два благоприятных события.

А сколько неблагоприятных?

Раз всего возможных событий ( 6), значит, неблагоприятных из них ( 6-2=4) события (это если выпадет ( 1,text{ }2,text{ }3) или ( 4)).

Вероятностью называется отношение количества благоприятных событий к количеству всех возможных событий.

То есть вероятность показывает, какая доля из всех возможных событий приходится на благоприятные.

Обозначают вероятность латинской буквой ( p) (видимо, от английского слова probability — вероятность).

Принято измерять вероятность в процентах (см. темы «Дроби, рациональные числа» и «Проценты»).

Для этого значение вероятности нужно умножать на ( 100%).

В примере с игральной костью вероятность ( p=frac{благоприятных}{всего}=frac{2}{6}=frac{1}{3}).

А в процентах: ( p=frac{1}{3}cdot 100%=frac{100}{3}%approx 33,3%).

И еще события бывают зависимыми друг от друга и независимыми. Начнем с зависимых событий.

Зависимые события

Например, ты решил зайти к знакомому, помнишь подъезд и даже этаж на котором он живет. А вот номер и расположение квартиры забыл. И вот стоишь ты на лестничной клетке, а перед тобой ( 3) двери на выбор.

Каков шанс (вероятность) того, что если ты позвонишь в первую дверь, тебе откроет твой друг? Всего квартиры ( 3), а друг живет только за одной из них. С равным шансом мы можем выбрать любую дверь.

Но каков этот шанс?

Дверей ( 3), нужная дверь ( 1). Вероятность угадать, позвонив в первую дверь: ( frac{1}{3}). То есть один раз из трех ты точно угадаешь.

Мы хотим узнать, позвонив ( 1) раз, как часто мы будем угадывать дверь? Давай рассмотри все варианты:

1. Ты позвонил в 1-ю дверь
2. Ты позвонил в 2-ю дверь
3. Ты позвонил в 3-ю дверь

А теперь рассмотрим все варианты, где может находиться друг:

а. За 1ой дверью
б. За 2ой дверью
в. За 3ей дверью

Сопоставим все варианты в виде таблицы. Галочкой обозначены варианты, когда твой выбор совпадает с местоположением друга, крестиком – когда не совпадает.

Как видишь, всего возможно ( 9) вариантов местоположения друга и твоего выбора, в какую дверь звонить.

А благоприятных исходов всего ( 3). То есть ( 3) раза из ( 9) ты угадаешь, позвонив в дверь ( 1) раз, т.е. ( frac{3}{9}=frac{1}{3}).

Это и есть вероятность – отношение благоприятного исхода (когда твой выбор совпал с местоположение друга) к количеству возможных событий.

Определение – это и есть формула. Вероятность принято обозначать p, поэтому:

( displaystyle p=frac{text{благоприятных}}{всего})

Поскольку математики называют различные действия (у нас такое действие – это звонок в дверь) экспериментами, то результатом таких экспериментов принято называть исход.

Ну а исходы бывают благоприятные и неблагоприятные.

Давай вернемся к нашему примеру. Допустим, мы позвонили в одну из дверей, но нам открыл незнакомый человек. Мы не угадали. Какова вероятность, что если позвоним в одну из оставшихся дверей, нам откроет наш друг?

Если ты подумал, что ( displaystyle frac{1}{3}), то это ошибка. Давай разбираться.

У нас осталось две двери. Таким образом, у нас есть возможные шаги:

1. Позвонить в 1-ую дверь
2. Позвонить во 2-ую дверь

Друг, при всем этом, точно находится за одной из них (ведь за той, в которую мы звонили, его не оказалось):

а. Друг за 1-ой дверью
б. Друг за 2-ой дверью

Давай снова нарисуем таблицу:

Как видишь, всего есть ( 4) варианта, ( 2) из которых – благоприятны. То есть вероятность равна ( displaystyle frac{2}{4}=frac{1}{2}).

А почему не ( displaystyle frac{1}{3})?

Рассмотренная нами ситуация – пример зависимых событий. Первое событие – это первый звонок в дверь, второе событие – это второй звонок в дверь.

А зависимыми они называются потому что влияют на следующие действия. Ведь если бы после первого звонка в дверь нам открыл друг, то какова была бы вероятность того, что он находится за одной из двух других?

Правильно, ( 0%).

Но если есть зависимые события, то должны быть и независимые? Верно, бывают.

Правило умножения вероятностей независимых событий

Что такое независимые события ты уже знаешь.

А если нужно найти вероятность того, что два (или больше) независимых события произойдут подряд?

Можно конечно посчитать, но есть способ проще.

Допустим мы хотим знать, какова вероятность того, что бросая монетку ( 2) раза, мы два раза увидим орла?

Мы уже считали: ( p=0,25).

А если бросаем монетку ( 3) раза? Какова вероятность увидеть орла ( 3) раза подряд?

Всего возможных вариантов ( 8):

• Орел-орел-орел
• Орел-орел-решка
• Орел-решка-орел
• Орел-решка-решка
• Решка-орел-орел
• Решка-орел-решка
•  Решка-решка-орел
• Решка-решка-решка

Не знаю, как ты, но я ( 3) раза ошибся, составляя этот список. Ух! А подходит нам только ( 1) вариант (первый).

( displaystyle p=frac{{{N}_{б}}}{N}=frac{1}{8})

Для 5 бросков можешь составить список возможных исходов сам. Но математики не столь трудолюбивы, как ты.

Поэтому они сначала заметили, а потом доказали, что вероятность определенной последовательности независимых событий каждый раз уменьшается на вероятность одного события.

Другими словами,

Вероятность определенной последовательности независимых событий равна произведению вероятностей каждого из событий

Рассмотрим на примере все той же, злосчастной, монетки.

Вероятность выпадения орла в ( 1) испытании? ( displaystyle frac{1}{2}). Теперь мы бросаем монетку ( 5) раз.

Какова вероятность выпадения ( 5) раз подряд орла?

( displaystyle p=frac{1}{2}cdot frac{1}{2}cdot frac{1}{2}cdot frac{1}{2}cdot frac{1}{2}={{left( frac{1}{2} right)}^{5}}=frac{1}{32})

Это правило работает не только, если нас просят найти вероятность того, что произойдет одно и то же событие несколько раз подряд.

Если бы мы хотели найти последовательность РЕШКА-ОРЕЛ-РЕШКА, при ( 3) бросках подряд, мы поступили бы также.

Вероятность выпадения решка – ( displaystyle frac{1}{2}), орла – ( displaystyle frac{1}{2}).

Правило сложения вероятностей несовместных событий

Так стоп! Новое определение.

Несовместными называются события, которые никак не могут произойти одновременно в результате эксперимента.

Ряд несовместных событий образуют полную группу событий.

Давай разбираться. Возьмем нашу изношенную монетку и бросим её ( 3) раза. Возможные варианты:

• Орел-орел-орел
• Орел-орел-решка
• Орел-решка-орел
• Орел-решка-решка
• Решка-орел-орел
• Решка-орел-решка
•  Решка-решка-орел
• Решка-решка-решка

Так вот, несовместные события – это определенная, заданная последовательность событий. ( 1),text{ }2),text{ }3),text{ }4)ldots text{ }8)) – это несовместные события.

Вероятности несовместных событий складываются.

Если мы хотим определить, какова вероятность двух (или больше) несовместных событий, то мы складываем вероятности этих событий.

Нужно понять, что выпадение орла или решки – это два независимых события.

Если мы хотим определить, какова вероятность выпадения последовательности ( 1)) (или любой другой), то мы пользуемся правилом умножения вероятностей.

Какова вероятность выпадения при первом броске орла, а при втором и третьем решки?

( displaystyle p=frac{1}{2}cdot frac{1}{2}cdot frac{1}{2}=frac{1}{8})

Но если мы хотим узнать, какова вероятность выпадения одной из нескольких последовательностей, например, когда орел выпадет ровно ( 1) раз, т.е. варианты ( 4),text{ }6)) и ( 7)), то мы должны сложить вероятности этих последовательностей.

Правило, помогающее не запутаться, когда умножать, а когда складывать:

Опишите, что должно произойти, используя союзы «И» или «ИЛИ». Затем вместо «И» ставим знак умножения, а вместо «ИЛИ» — сложения.

Возвратимся к примеру, когда мы подбросили монетку ( 3) раза, и хотим узнать вероятность увидеть орла ( 1) раз.

Что должно произойти?

Должны выпасть:

(орел И решка И решка) ИЛИ (решка И орел И решка) ИЛИ (решка И решка И орел).

Последовательность событий. Н.А.Бернштейн.

Цель: Определить способность к логическому мышлению, обобщению, умение понимать связь событий и строить последовательное умозаключение.

Материал: Для проведения опыта необходимы серии сюжетных картинок (в количестве 3-6 картин), на которых изображены этапы какого-либо события.

Существуют серии, соответствующие по содержанию детскому возрасту (“Волки”, “Колодец”, “Лодки” и др.), а также серии для взрослых (“Колесо”, “Пьяница”, “Охотник” и т. д.).

Есть несколько вариантов:

Вариант 1: Серия из 3-4 картинок, отражающих быт детей.

Вариант 2: Серия картинок с эмоционально – смысловым подтекстом. (Векслер, либо Бидструпа).

Инструкция: Начиная с 5ти лет применяя серии картинок 1ого варианта. Для детей начальных классов и старше – 2 ого варианта.

Перед ребенком кладутся произвольно картинки, связанные сюжетом. Ребенок должен понять сюжет, выстроить правильную последовательность событий и составить по картинке рассказ.

«Посмотри, перед тобой лежат картинки, на которых нарисовано какое-то событие, акцентируй внимание. Порядок картинок перепутан, и тебе надо догадаться, как их поменять местами, чтобы стало ясно, что нарисовал художник. Подумай, переложи картинки, как ты считаешь нужным, а потом составь по ним рассказ о том событии, которое здесь изображено».

Задание состоит из двух частей:

1) выкладывание последовательности событий картинок;

2) устный рассказ по ним.

После того, как ребенок разложил все картинки, экспериментатор записывает в протоколе (например, 5, 4, 1, 2, 3), и затем просит ребенка рассказать по порядку о том, что получилось. Если ребенок допустил ошибки, ему задают вопросы, цель которых помочь выявить допущенные ошибки.

Испытуемому показывают пачку перемешанных карточек и говорят: “Вот здесь на всех рисунках изображено одно и то же событие. Нужно разобрать, с чего все началось, что было дальше и чем дело кончилось. Вот сюда (экспериментатор указывает место) положите первую картинку, на которой на рисовано начало, сюда – вторую, третью…, а сюда последнюю”,

После того как больной разложил все картинки, экспериментатор записывает в протоколе, как он разложил (например: 5, 4, 1, 2, 3), и лишь после этого просит больного рассказать по порядку о том, что получилось. Если больной разложил неправильно, ему задают вопросы, цель которых помочь больному установить противоречие в его рассуждениях, выявить допущенные ошибки.

Умение ставить эти вопросы зависит от квалификации и опыта экспериментатора. Эти вопросы и ответы больного записываются в протокол, так же как и действия больного по исправлению раскладки картин. Если вопросами не удается довести больного до правильного понимания последовательности изображенных событий, экспериментатор просто показывает ему первую картинку и предлагает снова разложить. Это вторая попытка выполнить задание. Если она тоже безуспешна, тогда экспериментатор сам рассказывает и показывает больному последовательность событий и, перемешав снова все карточки, предлагает ему разложить их снова – в третий раз.

В случае, если больной лишь на третьей попытке правильно установил. Последовательность, полезно предложить ему другую серию той же методики, чтобы выяснить, возможен ли “перенос” с трудом усвоенного способа рассуждений.

Обработка результатов:

Выводы об уровне развития.
Высокий – ребенок самостоятельно нашел последовательность картинок и составил логический рассказ. При неправильно найденной последовательности рисунков испытуемый, тем не менее, сочиняет логичную версию рассказа.
Средний – ребенок правильно нашел последовательность, но не смог составить хорошего рассказа. Составление рассказа с помощью наводящих вопросов экспериментатора.
Низкий – если: ребенок не смог найти последовательность картинок и отказался от рассказа; 
– по найденной им самим последовательности картинок составил нелогичный рассказ; 
– составленная ребенком последовательность не соответствует рассказу; 
– каждая картинка рассказывается отдельно, сама по себе, не связана с остальными – в результате не получается рассказа;
– на каждом рисунке просто перечисляются отдельные предметы.

При истолковании результатов исследования следует обращать внимание на то, как больной реагирует на наводящие вопросы и критические возражения экспериментатора, “подхватывает” ли он эту помощь или не понимает ее.

В случаях, когда при неправильном составлении последовательности рисунка, испытуемый сочинил логическую версию рассказа, считается что задание выполнено, верно.

Если ребенок правильно установил последовательность картинок, но не смог составить рассказ, необходимо задать наводящие вопросы. Если не хватает ребенку словарного запаса для объяснения, а заданий для описания, то задаются вопросы, которые фиксируются в протоколе. В этом случае задание выполнено на среднем уровне.

Если не смог составить рассказ даже с помощью наводящих вопросов, то выполнение задания неудовлетворительно.

Считается, что испытуемый не справился с заданием, если:

1. Не смог найти последовательность событий и отказался от рассказа

2. По найденной им самим последовательности картинок составил нелогичный рассказ.

3. Составленная испытуемым последовательность не соответствует рассказу (но за исключением тех случаев, когда ребенок после наводящего вопроса меняет последовательность и соответствующий рассказ).

4. Каждая картинка описывается отдельно, сама по себе.

5. На каждом рисунке просто перечислены отдельные предметы.

Если 4-5 вариант, то необходима тщательная проверка интеллектуальных способностей.

В последнее время для установления последовательности и смысла событий используются серии, составленные из карикатур (“Дома и на работе”, “Прошел год”, “Кто работал и кто устал”, “Обман зрения” и т. д.). Преимущество этих серий в том, что они труднее для понимания и пригодны для исследования более интеллектуально развитых и сохранных больных. В то же время центр тяжести задания при использовании этих серий как бы переносится с установления строгой последовательности этапов события (иногда эту последовательность точно устанавливать и не нужно) на понимание юмора, т. е. смысла карикатур в целом.

Серии последовательности событий по карикатурам используются с некоторой модификацией порядка проведения опытов. Больному раньше предлагают самому установить последовательность событий, а за тем, если он не может этого выполнить, предлагают карточку с названием серии. Название составляется обычно так, что оно как бы “проливает свет” на смысл всей серии.

Протокол

Методика «Сравнение понятий»

Методика
применяется для исследования процессов
анализа и синтеза мышления. Широко
использовалась в школе акад. В.М.
Бехтерева.

Экспериментатор
из имеющегося у него набора заготавливает
8–10 пар слов, подлежащих
сравнению.

Набор содержит
понятия разной степени общности, а также
и вовсе несравнимые понятия. Именно
несравнимые понятия оказываются иногда
очень показательными для обнаружения
расстройства мышления.

1. Утро
   – вечер 16. Ворона – воробей

2. Корова
   – лошадь 17. Волк – луна

3. Летчик
   – танкист 18. Молоко – вода

4. Лыжи
   – коньки 19. Ветер – соль

5. Трамвай
   – автобус . 20. Золото – серебро

6. Озеро
   – река 21. Сани – телега

7. Река
   – птица 22. Очки – деньги

8. Дождь
   – снег 23. Воробей – курица

9. Поезд
   – самолет 24. Кошка – яблоко

1. Ось
   – оса 25. Вечер – утро

2. Обман
   – ошибка 26. Дуб – береза

3. Стакан
   – петух 27. Голод – жажда

4. Маленькая
   девочка – большая
   кукла 28.
   Сказка – песня

5. Ботинок
   – карандаш 29. Корзина – сова

6. Яблоко
   – вишня 30. Картина – портрет

Методика апробирована,
пригодна для исследования детей и
взрослых разного образовательного
уровня. Она очень удобна при необходимости
повторных исследований испытуемых для
оценки изменчивости их состояния.

Испытуемого
просят сказать, «чем похожи и чем
отличаются» эти понятия. Записывают
все его ответы полностью. Экспериментатор
должен настаивать на том, чтобы испытуемый
обязательно раньше указывал сходство
между понятиями, а только потом различие.

Встречаются
такие пары объектов (или понятий), которые
несравнимы. В таком случае вы и должны
ответить: «Их сравнивать нельзя». Если
испытуемый сразу начинает сравнивать
эту пару – его ответ записывают, но
затем все равно дают пояснение относительно
«несравнимых» пар. В дальнейшем таких
пояснений больше не дают, а просто
регистрируют ответы испытуемых по
поводу каждой пары.

При оценке ответов
испытуемых следует учитывать, удается
ли им выделить существенные признаки
сходства и различия понятий. Неумение
выделить признаки сходства, а также
существенные признаки различия
свидетельствует о слабости обобщений
испытуемого, о склонности его к конкретному
мышлению.

Методика «Установление последовательности событий»

Методика предназначена
для выявления сообразительности, умения
понимать связь событий и строить
последовательные умозаключения.
Предложена А.Н. Бернштейном.

Для
проведения опыта необходимы серии
сюжетных картинок (в количестве 3–6
картин), на которых изображены этапы
какого-либо события.

Существуют серии,
соответствующие по содержанию детскому
возрасту, а также серии для взрослых
(см. стимульный материал).

Оригиналы этих
серий выполнены красками, но можно
пользоваться и их фотокопиями.

Испытуемому
показывают пачку перемешанных карточек
и говорят: «Вот здесь на всех рисунках
изображено одно и то же событие. Нужно
разобрать, с чего все началось, что было
дальше и чем дело кончилось. Вот сюда
(экспериментатор указывает место)
положите первую картинку, на которой
нарисовано начало, сюда – вторую,
третью…, а сюда последнюю».

После того как
испытуемый разложил все картинки,
экспериментатор записывает в протоколе,
как он разложил (например: 5, 4, 1, 2, 3), и
лишь после этого просит испытуемого
рассказать по порядку о том, что
получилось. Если он разложил неправильно,
ему задают вопросы, цель которых помочь
больному установить противоречие в его
рассуждениях, выявить допущенные ошибки.

Если
вторая попытка безуспешна, тогда
экспериментатор сам показывает
испытуемому последовательность событий
и, перемешав снова все карточки, предлагает
ему разложить их снова – в третий раз
или составить рассказ, отражающий
последовательность событий.

ФОРМА ПРОТОКОЛА

Исследование
больного, перенесшего травму

Что произошло?

Составь(те)
рассказ по картинкам и придумайте
заглавие

Составь(те)
рассказ по картинкам

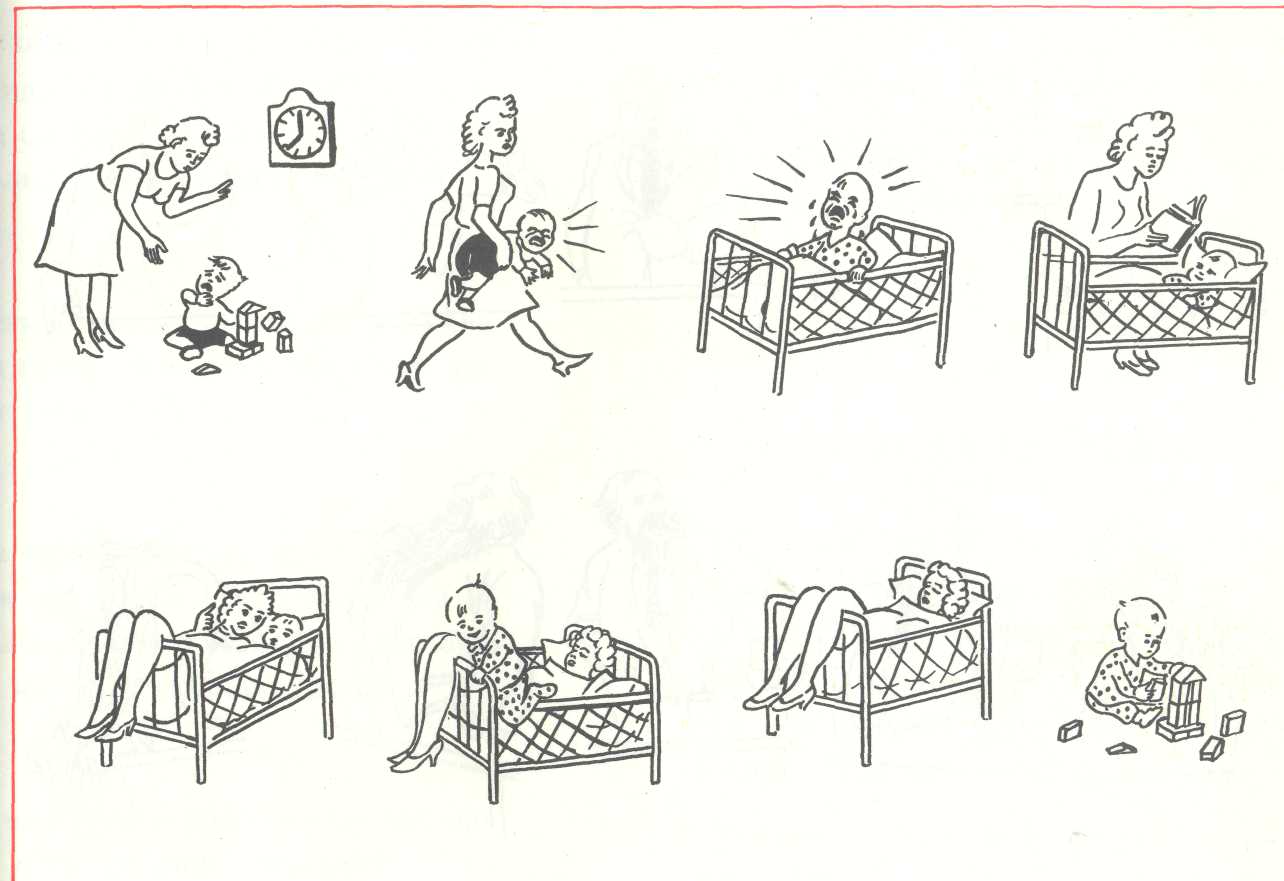
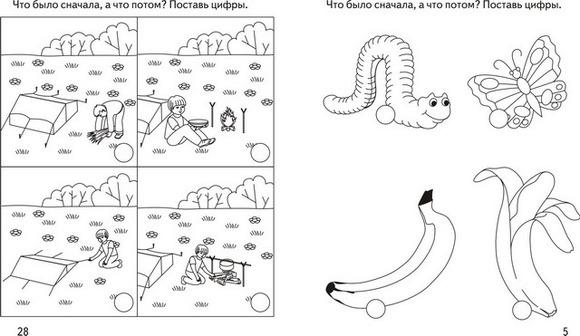
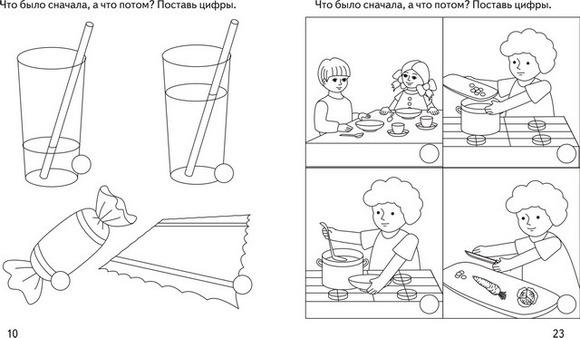
Составь(те)
рассказ по картинкам

Составь(те)
рассказ по картинкам

Интеллектуальное
недоразвитие, затрудненность осмысления,
свойственные олигофренам и больным с
органическими заболеваниями мозга,
проявляются в том, что больные, справляясь
с легкими сериями, не могут ориентироваться
в более трудных; в одной и той же серии
они, как правило, ошибаются на одной
более трудной картине.

Отчетливо
выявляются с помощью данной методики
некоторые формы инертности психических
процессов больных: разложив в первый
раз картинки неправильно, больные в
дальнейшем несколько раз подряд повторяют
ту же ошибочную версию последовательности.
Такая «склонность к застреваниям»
наблюдается при некоторых органических
заболеваниях мозга в детском, а также
в старческом возрасте.

При
истолковании результатов исследования
следует обращать внимание на то, как
больной реагирует на наводящие вопросы
и критические возражения экспериментатора,
«подхватывает» ли он эту помощь или не
понимает ее.

Значительный
интерес представляют особенности устной
речи больных, выявляющиеся во время
объяснения последовательности событий
(грамматически связная, развернутая
либо односложная, бедная, лаконичная,
либо с тенденцией к излишней детализации).

Затруднения в
установлении сюжета по серии рисунков
свидетельствуют о недостаточности
уровня процессов обобщения и отвлечения.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #