| Земля | 9,81 м/с² | 1,00 g | Солнце | 273,1 м/с² | 27,85 g |
| Луна | 1,62 м/с² | 0,165 g | Меркурий | 3,70 м/с² | 0,378 g |
| Венера | 8,88 м/с² | 0,906 g | Марс | 3,86 м/с² | 0,394 g |
| Юпитер | 24,79 м/с² | 2,528 g | Сатурн | 10,44 м/с² | 1,065 g |
| Уран | 8,86 м/с² | 0,903 g | Нептун | 11,09 м/с² | 1,131 g |
| Эрида | 0,82 ± 0,02 м/с² | 0,084 ± 0,002 g | Плутон | 0,617 м/с² | 0,063 g |
Ускоре́ние свобо́дного паде́ния (ускорение силы тяжести) — ускорение, придаваемое телу силой тяжести (или, иными словами, ускорение тела при свободном падении), при исключении из рассмотрения других сил.
В соответствии с уравнением движения тел в неинерциальных системах отсчёта[2] ускорение свободного падения численно равно силе тяжести, воздействующей на объект единичной массы.
Ускорение свободного падения на поверхности Земли g (обычно произносится как «же») варьируется от 9,780 м/с² на экваторе до 9,82 м/с² на полюсах[3]. Стандартное («нормальное») значение, принятое при построении систем единиц, составляет 9,80665 м/с²[4][5]. Стандартное значение g было определено как «среднее» в каком-то смысле на всей Земле: оно примерно равно ускорению свободного падения на широте 45,5° на уровне моря. В приблизительных расчётах его обычно округляют до 9,81, 9,8 или даже до 10 м/с².
Физическая сущность[править | править код]
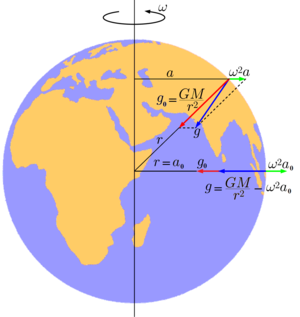
Две компоненты ускорения свободного падения на Земле
g: гравитационная (в приближении сферически симметричной зависимости плотности от расстояния от центра Земли) равна
GM/r2 и центробежная, равная
ω2a, где
a — расстояние до земной оси,
ω — угловая скорость вращения Земли.
Для определённости будем считать, что речь идёт о свободном падении на Земле. Эту величину можно представить как векторную сумму двух слагаемых: гравитационного ускорения, вызванного земным притяжением, и центробежного ускорения, связанного с вращением Земли.
Центробежное ускорение[править | править код]
Центробежное ускорение является следствием вращения Земли вокруг своей оси. Именно центробежное ускорение, вызванное вращением Земли вокруг своей оси, вносит наибольший вклад в неинерциальность системы отсчёта, связанную с Землёй. В точке, находящейся на расстоянии a от оси вращения, оно равно ω2a, где ω — угловая скорость вращения Земли, определяемая как ω = 2π/T, а Т — время одного оборота вокруг своей оси, для Земли равное 86164 секундам (звёздные сутки). Центробежное ускорение направлено по нормали к оси вращения Земли. На экваторе оно составляет 3,39636 см/с², причём на других широтах направление вектора его не совпадает с направлением вектора гравитационного ускорения, направленного к центру Земли.
Гравитационное ускорение[править | править код]
| h, км | g, м/с² | h, км | g, м/с² |
|---|---|---|---|
| 0 | 9,8066 | 20 | 9,7452 |
| 1 | 9,8036 | 50 | 9,6542 |
| 2 | 9,8005 | 80 | 9,5644 |
| 3 | 9,7974 | 100 | 9,505 |
| 4 | 9,7943 | 120 | 9,447 |
| 5 | 9,7912 | 500 | 8,45 |
| 6 | 9,7882 | 1000 | 7,36 |
| 8 | 9,7820 | 10 000 | 1,50 |
| 10 | 9,7759 | 50 000 | 0,125 |
| 15 | 9,7605 | 400 000 | 0,0025 |
В соответствии с законом всемирного тяготения, величина гравитационного ускорения на поверхности Земли или космического тела связана с его массой M следующим соотношением:
,
где G — гравитационная постоянная (6,67430[15]·10−11 м3·с−2·кг−1)[6], а r — радиус планеты. Это соотношение справедливо в предположении, что плотность вещества планеты сферически симметрична. Приведённое соотношение позволяет определить массу любого космического тела, включая Землю, зная её радиус и гравитационное ускорение на её поверхности, либо, наоборот, по известной массе и радиусу определить ускорение свободного падения на поверхности.
Исторически масса Земли была впервые определена Генри Кавендишем, который провёл первые измерения гравитационной постоянной.
Гравитационное ускорение на высоте h над поверхностью Земли (или иного космического тела) можно вычислить по формуле:
,
- где M — масса планеты.
Ускорение свободного падения на Земле[править | править код]
Ускорение свободного падения у поверхности Земли зависит от широты. Приблизительно оно может быть вычислено (в м/с²) по эмпирической формуле[7][8]:
- где
— широта рассматриваемого места,
— высота над уровнем моря в метрах.
Полученное значение лишь приблизительно совпадает с ускорением свободного падения в данном месте. При более точных расчётах необходимо использовать одну из моделей гравитационного поля Земли[en][9], дополнив её поправками, связанными с вращением Земли, приливными воздействиями.
На ускорение свободного падения влияют и другие факторы, например, атмосферное давление, которое меняется в течение суток: от атмосферного давления зависит плотность воздуха в большом объёме, а следовательно и результирующая сила тяжести, изменение которой могут зафиксировать высокочувствительные гравиметры[10].
Пространственные изменения гравитационного поля Земли (гравитационные аномалии) связаны с неоднородности плотности в её недрах, что может быть использовано для поиска залежей полезных ископаемых методами гравиразведки.
Почти везде ускорение свободного падения на экваторе ниже, чем на полюсах, за счёт центробежных сил, возникающих при вращении планеты, а также потому, что радиус r на полюсах меньше, чем на экваторе из-за сплюснутой формы планеты. Однако места экстремально низкого и высокого значения g несколько отличаются от теоретических показателей по этой модели. Так, самое низкое значение g (9,7639 м/с²) зафиксировано на горе Уаскаран в Перу в 1000 км южнее экватора, а самое большое (9,8337 м/с²) — в 100 км от Северного полюса[11].
| Ускорение свободного падения для некоторых городов | ||||
|---|---|---|---|---|
| Город | Долгота | Широта | Высота над уровнем моря, м | Ускорение свободного падения, м/с² |
| Алма-Ата | 76,85 в.д. | 43,22 с.ш. | 786 | 9.78125 |
| Берлин | 13,40 в.д. | 52,50 с.ш. | 40 | 9,81280 |
| Будапешт | 19,06 в.д. | 47,48 с.ш. | 108 | 9,80852 |
| Вашингтон | 77,01 з.д. | 38,89 с.ш. | 14 | 9,80188 |
| Вена | 16,36 в.д. | 48,21 с.ш. | 183 | 9,80860 |
| Владивосток | 131,53 в.д. | 43,06 с.ш. | 50 | 9,80424 |
| Гринвич | 0,0 в.д. | 51,48 с.ш. | 48 | 9,81188 |
| Каир | 31,28 в.д. | 30,07 с.ш. | 30 | 9,79317 |
| Киев | 30,30 в.д. | 50,27 с.ш. | 179 | 9,81054 |
| Мадрид | 3,69 в.д. | 40,41 с.ш. | 667 | 9,79981 |
| Минск | 27,55 в.д. | 53,92 с.ш. | 220 | 9,81347 |
| Москва | 37,61 в.д. | 55,75 с.ш. | 151 | 9,8154 |
| Нью-Йорк | 73,96 з.д. | 40,81 с.ш. | 38 | 9,80247 |
| Одесса | 30,73 в.д. | 46,47 с.ш. | 54 | 9.80735 |
| Осло | 10,72 в.д. | 59,91 с.ш. | 28 | 9,81927 |
| Париж | 2,34 в.д. | 48,84 с.ш. | 61 | 9,80943 |
| Прага | 14,39 в.д. | 50,09 с.ш. | 297 | 9,81014 |
| Рим | 12,99 в.д. | 41,54 с.ш. | 37 | 9,80312 |
| Стокгольм | 18,06 в.д. | 59,34 с.ш. | 45 | 9,81843 |
| Токио | 139,80 в.д. | 35,71 с.ш. | 18 | 9,79801 |
Измерение[править | править код]
Ускорение свободного падения у поверхности Земли может быть измерено посредством гравиметра. Различают две разновидности гравиметров: абсолютные и относительные. Абсолютные гравиметры измеряют ускорение свободного падения непосредственно. Относительные гравиметры, некоторые модели которых действуют по принципу пружинных весов, определяют приращение ускорения свободного падения относительно значения в некотором исходном пункте.
Ускорение свободного падения на поверхности Земли или другой планеты может быть также вычислено на основе данных о вращении планеты и её гравитационном поле. Последнее может быть определено посредством наблюдения за орбитами спутников и движения других небесных тел вблизи рассматриваемой планеты.
См. также[править | править код]
- Свободное падение
- Гравиметрия
- Гравиразведка
- Перегрузка (летательные аппараты)
Примечания[править | править код]
- ↑ У планет газовых гигантов и звёзд «поверхность» понимается как область меньших высот в атмосфере, где давление равно атмосферному давлению на Земле на уровне моря (1,013×105 Па). Также у звёзд поверхностью иногда считают поверхность фотосферы.
- ↑ Аналог уравнения второго закона Ньютона, выполняющийся для неинерциальных систем отсчёта.
- ↑ Свободное падение тел. Ускорение свободного падения. Архивировано из оригинала 20101219 года.
- ↑ Декларация III Генеральной конференции по мерам и весам (1901) (англ.). Международное бюро мер и весов. Дата обращения: 9 апреля 2013. Архивировано 8 июля 2018 года.
- ↑ Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Изд-во стандартов, 1990. — С. 237.
- ↑ CODATA Value: Newtonian constant of gravitation. physics.nist.gov. Дата обращения: 7 марта 2020. Архивировано 23 сентября 2020 года.
- ↑ Грушинский Н. П. Гравиметрия // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1988. — Т. 1: Ааронова — Бома эффект — Длинные линии. — С. 521. — 707 с. — 100 000 экз.
- ↑ Ускорение свободного падения // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга — Робертсона — Стримеры. — С. 245—246. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
- ↑ ICCEM – table of models (англ.). Дата обращения: 10 ноября 2021. Архивировано из оригинала 24 августа 2013 года.
- ↑ GRAVITY MONITORING AT OIL AND GAS FIELDS: DATA INVERSION AND ERRORS // Геология и геофизика. — 2015. — Т. 56, вып. 5. — doi:10.15372/GiG20150507. Архивировано 2 июня 2018 года.
- ↑ Перуанцам живется легче, чем полярникам? Дата обращения: 21 июля 2016. Архивировано 16 сентября 2016 года.
Литература[править | править код]
- Енохович А. С. Краткий справочник по физике. — М.: Высшая школа, 1976. — 288 с.
Ускорение свободного падения
Ускорение свободного падения — движение объекта, который получает ускорение из-за действующей на него силы тяжести; обозначается буквой g и измеряется в м/с². На поверхности Земли ускорение свободного падения примерно равно 9,81 м/с².
На полюсах (Южном и Северном) ускорение свободного падения будет больше, а на экваторе — меньше. Это происходит из-за двух фактов:
- Земля — не идеальный круг, а приплюснутый шар и её радиус на полюсах меньше, чем на экваторе (ускорение зависит от радиуса),
- центробежные силы (при вращении Земли) минимально компенсируют гравитацию больше на экваторе, чем на полюсах.
В вакууме тела падают с одинаковой скоростью потому, что ускорение свободного падения не зависит от массы.
Таблица ускорения свободного падения небесных тел
| Небесное тело | g (в м/с²) |
|---|---|
| Луна | 1,62 |
| Солнце | 274 |
| Меркурий | 3,72 |
| Венера | 8,87 |
| Земля | 9,81 |
| Марс | 3,711 |
| Юпитер | 24,79 |
| Сатурн | 10,44 |
| Уран | 8,87 |
| Нептун | 11,15 |
От чего зависит ускорение свободного падения?
Ускорение свободного падения зависит от массы планеты и радиуса планеты — чем она тяжелее, тем сильнее притягивает тела (т.е. масса тела не влияет на ускорение).
Возможно для будущих вычислений нужны будут эти данные:
- Масса Земли = 5,98 × (10^24) кг (или 5,972E24 кг)
- Радиус Земли = 6 371 км = 6,37×(10^6) м.
Как найти ускорение свободного падения?
Формула ускорения свободного падения
g — ускорение свободного падения
G — гравитационная постоянная
M — масса планеты
R — радиус планеты
Гравитационная постоянная (“G”, не путайте с “g”) — это фундаментальная физическая константа, которая примерно равна
и связывает силы гравитационного притяжения между двумя телами (G) с их массами (m1 и m2) и расстоянием между ними (R) в формуле:
Пример расчёта ускорения свободного падения (для Земли):
Вспомним формулу:
G — гравитационная постоянная
M — масса планеты
R — радиус планеты
Как узнать время падения тела?
Формула времени свободного падения (когда тело падает вертикально):
t = V / g = √(2h/g)
Где:
- t — время
- V — скорость тела
- g — ускорение ≈ 9,8 м/с²
- h — расстояние
Пример:
Высота (h) = 20 м
Нужно найти скорость и время падения.
Решение:
Формула скорости:
V0 = 0
g ≈ 9,8 м/с²
h = 20 м
V² = 0² + 2 × 9,8 м/с² × 20 м ⇔ V = √392 м/с ≈ 19,8 м/с
Зная скорость, применяем эту формулу:
t = V / g = (19,8 м/с) / (9,8 м/с²) ≈ 2,02 с
Либо используя только высоту и ускорение:
t = √(2h/g) = √(2 × 20 м / 9,8 м/с²) ≈ 2,02 с
Где нужны знания о свободном падении?
Они могут понадобиться:
- в авиации,
- в космонавтике,
- при поиске полезных ископаемых (там, где есть залежи тяжёлых ископаемых, g меняется),
- при разработке новых лыжных трамплинов и полос приземления,
- при разработке новых автомобилей (рассчитываются наилучшие показатели для экономии топлива).
Узнайте также про Закон сохранения энергии, Силу Архимеда, Законы Ньютона и Космологию.
Свободное падение — это движение тела только под действием силы тяжести.
В действительности при падении на тело действует не только сила тяжести, но и сила сопротивления воздуха. Но в ряде задач сопротивлением воздуха можно пренебречь. Воздух не оказывает значимого сопротивления падающему мячу или тяжелому грузу. Но падение пера или листа бумаги можно рассматривать только с учетом двух сил: небольшая масса тела в сочетании с большой площадью его поверхности препятствует свободному падению вниз.
Внимание!
В вакууме все тела падают с одинаковым ускорением, так как в нем отсутствует среда, которая могла бы дать сопротивление. Так, брошенные в условиях вакуума с одинаковой высоты перо и молоток приземлятся в одно и то же время!
Ускорение свободного падения
Ускорение свободного падения — векторная физическая величина. Вектор ускорения свободного падения всегда направлен вниз к центру Земли. Обозначается как g.
Единица измерения ускорения свободного падения — 1 м/с2.
Модуль ускорения свободного падения — скалярная величина. Обозначается как g. Численно равна 9,8 м/с2. При решении задач это значение округляется до целых: g = 10 м/с2.
Свободное падение
Свободное падение — частный случай равноускоренного прямолинейного движения. Если тело отпустить с некоторой высоты, оно будет падать с ускорением свободного падения без начальной скорости. Тогда его кинематические величины можно определить по следующим формулам:
Скорость
v = gt
v — скорость, g — ускорение свободного падения, t — время, в течение которого падало тело
Пример №1. Тело упало без начальной скорости с некоторой высоты. Найти его скорость в конечный момент времени t, равный 3 с.
Подставляем данные в формулу и вычисляем:
v = gt = 10∙3 = 30 (м/с).
Перемещение при свободном падении тела равно высоте, с которой оно начало падать. Высота обозначается буквой h.
Внимание! Перемещение равно высоте, с которой падало тело, только в том случае, если t — полное время падения.
Высота падения
Если известна скорость падения тела в момент времени t, перемещение (высота) определяется по следующей формуле.
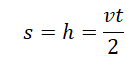
Если скорость тела в момент времени t неизвестна, но для нахождения перемещения (высоты) используется формула:
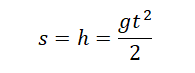
Если неизвестно время, в течение которого падало тело, но известна его конечная скорость, перемещение (высота) вычисляется по формуле:
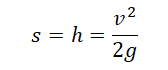
Пример №2. Тело упало с высоты 5 м. Найти его скорость в конечный момент времени.
Так как нам известна только высота, и найти нужно скорость, используем для вычислений последнюю формулу. Выразим из нее скорость:
Формула определения перемещения тела в n-ную секунду свободного падения:
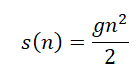
s(n) — перемещение за секунду n.
Пример №3. Определить перемещение свободно падающего тела за 3-ую секунду движения.
Движение тела, брошенного вертикально вверх
Движение тела, брошенного вертикально вверх, описывается в два этапа
Два этапа движения тела, брошенного вертикально вверхЭтап №1 — равнозамедленное движение. Тело поднимается вверх на некоторую высоту h за время t с начальной скоростью v0 и на мгновение останавливается в верхней точке, достигнув скорости v = 0 м/с. На этом участке пути векторы скорости и ускорения свободного падения направлены во взаимно противоположных направлениях (v↑↓g).
Этап №2 — равноускоренное движение. Когда тело достигает верхней точки, и его скорость равна 0, начинается свободное падение с начальной скоростью до тех пор, пока тело не упадет или не будет поймано на некоторой высоте. На этом участке пути векторы скорости и ускорения свободного падения направлены в одну сторону (v↑↑g).
Формулы для расчета параметров движения тела, брошенного вертикально вверхПеремещение тела, брошенного вертикально вверх, определяется по формуле:
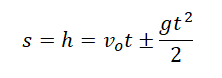
Если известна скорость в момент времени t, для определения перемещения используется следующая формула:
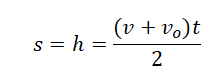
Если время движения неизвестно, для определения перемещения используется следующая формула:
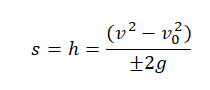
Формула определения скорости:
Какой знак выбрать — «+» или «–» — вам помогут правила:
- Если движение равнозамедленное (тело поднимается вверх), перед ускорением свободного падения в формуле нужно ставить знак «–», так как векторы скорости и ускорения противоположно направлены.
- Если движение равноускоренное (тело падает вниз), перед ускорением свободного падения в формуле нужно ставить знак «+», так как векторы скорости и ускорения сонаправлены.
Обычно тело бросают вертикально вверх с некоторой высоты. Поэтому если тело упадет на землю, высота падения будет больше высоты подъема (h2 > h1). По этой же причине время второго этапов движения тоже будет больше (t2 > t1). Если бы тело приземлилось на той же высоте, то начальная скорость движения на 1 этапе была бы равно конечной скорости движения на втором этапе. Но так как точка приземления лежит ниже высоты броска, модуль конечной скорости 2 этапа будет выше модуля начальной скорости, с которой тело было брошено вверх (v2 > v01).
Пример №4. Тело подкинули вверх на некотором расстоянии 2 м от земли, придав начальную скорость 10 м/с. Найти высоту тела относительно земли в момент, когда оно достигнет верхней точки движения.
Конечная скорость в верхней точке равна 0 м/с. Но неизвестно время. Поэтому для вычисления перемещения тела с точки броска до верхней точки найдем по этой формуле:
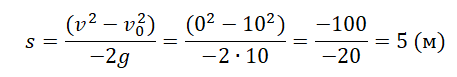
Согласно условию задачи, тело бросили на высоте 2 м от земли. Чтобы найти высоту, на которую поднялось тело относительно земли, нужно сложить эту высоту и найденное перемещение: 5 + 2 = 7 (м).
Уравнение координаты и скорости при свободном падении
Уравнение координаты при свободном падении позволяет вычислять кинематические параметры движения даже в случае, если оно меняет свое направление. Так как при вертикальном движении тело меняет свое положение лишь относительно оси ОУ, уравнение координаты при свободном падении принимает вид:
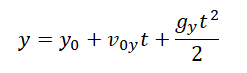
Уравнение скорости при свободном падении:
vy = v0y + gyt
Полезные факты
- В момент падения тела на землю y = 0.
- В момент броска тела от земли y0 = 0.
- Когда тело падает без начальной скорости (свободно) v0 = 0.
- Когда тело достигает наибольшей высоты v = 0.
Построение чертежа
Решать задачи на нахождение кинематических параметров движения тела, брошенного вертикально вверх, проще, если выполнить чертеж. Строится он в 3 шага.
План построения чертежа
- Чертится ось ОУ. Начало координат должно совпадать с уровнем земли или с самой нижней точки траектории.
- Отмечаются начальная и конечная координаты тела (y и y0).
- Указываются направления векторов. Нужно указать направление ускорения свободного падения, начальной и конечной скоростей.
Свободное падение на землю с некоторой высоты
Чертеж:
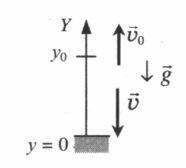
Уравнение скорости:
–v = v0 – gtпад
Уравнение координаты:
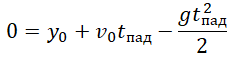
Тело подбросили от земли и поймали на некоторой высоте
Чертеж:
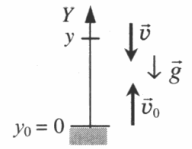Уравнение скорости:
–v = v0 – gt
Уравнение координаты:
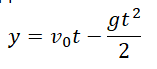
Тело подбросили от земли, на одной и той же высоте оно побывало дважды
Чертеж:
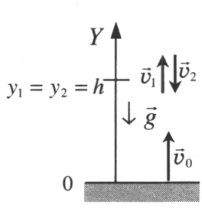
Интервал времени между моментами прохождения высоты h:
∆t = t2 – t1
Уравнение координаты для первого прохождения h:
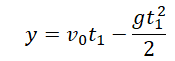
Уравнение координаты для второго прохождения h:
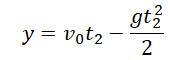
Важно! Для определения знаков проекций скорости и ускорения нужно сравнивать направления их векторов с направлением оси ОУ.
Пример №5. Тело падает из состояния покоя с высоты 50 м. На какой высоте окажется тело через 3 с падения?
Из условия задачи начальная скорость равна 0, а начальная координата — 50.
Поэтому:
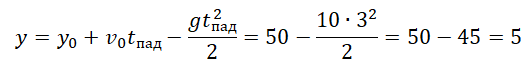
Через 3 с после падения тело окажется на высоте 5 м.
Задание EF17519
С аэростата, зависшего над Землёй, упал груз. Через 10 с он достиг поверхности Земли. На какой высоте находился аэростат? Сопротивление воздуха пренебрежимо мало.
Алгоритм решения
- Записать исходные данные.
- Сделать чертеж, иллюстрирующий ситуацию.
- Записать формулу для определения искомой величины в векторном виде.
- Записать формулу для определения искомой величины в векторном виде.
- Подставить известные данные и вычислить скорость.
Решение
Записываем исходные данные:
- Начальная скорость v0 = 0 м/с.
- Время падения t = 10 c.
Делаем чертеж:
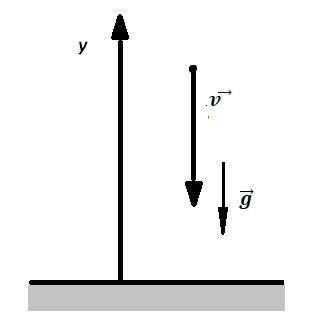
Перемещение (высота) свободно падающего тела, определяется по формуле:
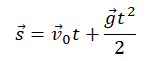
В скалярном виде эта формула примет вид:
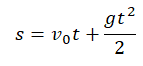
Учтем, что начальная скорость равна нулю, а ускорение свободного падения противоположно направлено оси ОУ:
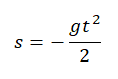
Относительно оси ОУ груз совершил отрицательное перемещение. Но высота — величина положительная. Поэтому она будет равна модулю перемещения:
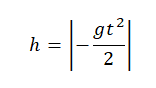
Вычисляем высоту, подставив известные данные:
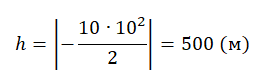
Ответ: 500
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17483
Тело брошено вертикально вверх с начальной скоростью 10 м/с. Если сопротивление воздуха пренебрежимо мало, то через одну секунду после броска скорость тела будет равна…
Алгоритм решения
- Записать исходные данные.
- Сделать чертеж, иллюстрирующий ситуацию.
- Записать формулу для определения скорости тела в векторном виде.
- Записать формулу для определения скорости тела в скалярном виде.
- Подставить известные данные и вычислить скорость.
Решение
Записываем исходные данные:
- Начальная скорость v0 = 10 м/с.
- Время движения t = 1 c.
Делаем чертеж:
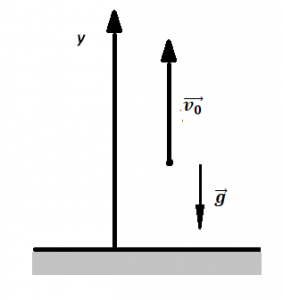
Записываем формулу для определения скорости тела в векторном виде:
v = v0 + gt
Теперь запишем эту формулу в скалярном виде. Учтем, что согласно чертежу, вектор скорости сонаправлен с осью ОУ, а вектор ускорения свободного падения направлен в противоположную сторону:
v = v0 – gt
Подставим известные данные и вычислим скорость:
v = 10 –10∙1 = 0 (м/с)
Ответ: 0
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 20.7k
Ускорение свободного падения, теория и онлайн калькуляторы
Ускорение свободного падения
Определение ускорения свободного падения
Определение
Ускорением свободного падения называют ускорение, которое телу придает сила тяжести, если другие силы на рассматриваемое тело не действуют или их
действие взаимно компенсируется.
Ускорение свободного падения обозначают буквой $g$. На поверхности Земли оно изменяется пределах от $9,78 frac{м}{с^2}$ до $9,832 frac{м}{с^2}$. На полюсах Земли ускорение свободного падения максимально, на экваторе минимально. Средним (стандартным или нормальным) значением ускорения свободного падения на Земле принято считать его величину, равную $g=9,80665 frac{м}{с^2} $. В задачах величину ускорения свободного падения считают равной $g=9,81frac{м}{с^2}$ или часто даже полагают $g=10frac{м}{с^2}$, если расчеты приблизительные.
В соответствии с обобщенным законом Галилея все тела, находящиеся в одном и том же поле тяготения падают с одинаковыми ускорениями. Это означает, что в данной точке Земли ускорение свободного падения одинаково для всех тел. Изменение величины ускорения свободного падения около поверхности Земли в зависимости от широты связано с суточным вращением нашей планеты вокруг своей оси и тем, что форма Земли отличается от формы шара (Земля сплюснута).
Зависимость ускорения свободного падения от высоты над уровнем Земли
Если суточным вращением Земли пренебречь, то сила тяжести ($P=mg$) равна по величине силе тяготения (F):
[P=mg=F=gamma frac{mM}{R^2}left(1right),]
где $M$ – масса Земли; $R$ – расстояние от центра Земли, до рассматриваемого тела; $gamma $- гравитационная постоянная. Формула (1) справедлива, если тело находится около поверхности Земли, тогда ускорение свободного падения равно:
[g=gamma frac{M}{R^2}left(2right).]
Ускорение, вычисляемое при помощи формулы (2) называют ускорением свободного падения на уровне моря.
Допустим, что тело находится на высоте $h$ над уровнем Земли, тогда сила тяжести, действующая на тело равна:
[P=gamma frac{mM}{{left(R_Z+hright)}^2}left(3right),]
где $R_Z$ – радиус Земли. В таком случае ускорение свободного падения зависит от высоты, на которой находится рассматриваемое тело:
[g=gamma frac{M}{{left(R_Z+hright)}^2}left(4right).]
Изменениями ускорения свободного падения на высотах, которые много меньше, чем радиус Земли обычно пренебрегают. При этом считают, что ускорение свободного падения постоянная величина.
Влияние вращения Земли на ускорение свободного падения
Как уже отмечалось, на ускорение свободного падения оказывает влияние вращение нашей планеты вокруг своей оси. Допустим, что тело массой $m$ находится в точке с географической широтой $varphi $. Вместе в планетой тело движется и при этом траекторией его движения является окружность радиуса $r$, равного:
[r=R_Z{cos varphi left(5right), }]
где $R_Z$ – радиус Земли. Центростремительное ускорение ($a_n$) нашего тела при этом будет составлять величину:
[a_n=frac{v^2}{r}=frac{4{pi }^2R_Z{cos varphi }}{T^2} left(6right),]
где $T$ – период вращения Земли. Силу тяготения ($F$) можно разложить на две составляющие: центростремительную силу ($F_n$) и силу тяжести ($P$). Сила тяжести везде кроме полюсов, меньше силы тяготения. Везде, кроме экватора и полюсов, сила тяжести направлена не точно в центр Земли, а немного в сторону от него.
За счет вращения Земли сила тяжести на полюсах больше, чем у экватора, наша планета сплюснута.
Ускорение свободного падения на полюсе ($g_p$) максимально. Так как центростремительное ускорение равно нулю, полярный радиус ($R_p$) минимален:
[g_p=frac{gamma M}{R^2_p}left(7right).]
Ускорение свободного падения ($g_e$) на экваторе равно разности:
[g_e=frac{gamma M}{R^2_e}-a^e_n=frac{gamma M}{R^2_e}-frac{4{pi }^2R_e}{T^2}left(8right),]
где $R_e$ – экваториальный радиус Земли. Величину $frac{gamma M}{R^2_e}$ называют напряженностью гравитационного поля Земли.
Примеры задач с решением
Пример 1
Задание. Радиус некоторой планеты равен R, ее средняя плотность составляет $rho $, считая, что масса планеты распределена равномерно, определите ускорение свободного падения около поверхности этой планеты.
Решение. Ускорение свободного падения около поверхности планеты можно найти как:
[g=gamma frac{M}{R^2}left(1.1right),]
где $R$ – радиус планеты; $M$ – масса планеты. Массу планеты найдем, считая ее шаром:
[M=frac{4}{3}pi R^3rho left(1.2right).]
Тогда ускорение свободного падения около поверхности этой планеты равно:
[g=gamma frac{frac{4}{3}pi R^3rho }{R^2}=frac{4}{3}gamma pi rho R.]
Ответ. $g=frac{4}{3}gamma pi rho R.$
Пример 2
Задание. Какова зависимость ускорения свободного падения от расстояния от центра планеты$ ( r)$, если планета – однородный шар, плотность которого равна $rho ?$ Радиус планеты R. Изобразите график $gleft(rright).$
Решение. Рассмотрим случай, когда расстояние от центра планеты меньше ее радиуса ($r$ меньше $R$) (рис.1 (а)).
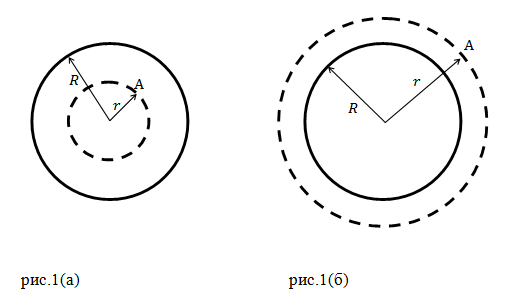
Расположим тело массы $m$ на расстоянии $r$ от центра планеты (в точке А). Тогда тело притягивается к планете с силой:
[mg=frac{gamma M’m}{r^2}left(2.1right),]
где $M’=frac{4}{3}pi r^3rho $ – масса планеты, которая ограничена сферической поверхностью радиуса $r$. При этом, ускорение свободного падения равно:
[g_1(r)=frac{gamma frac{4}{3}pi r^3rho }{r^2}=frac{4}{3}pi gamma rho r.]
Расположим материальную точку массы $m$ в точке А за пределами планеты (рис.1 (б)), тогда по закону всемирного тяготения на точечную массу действует сила, равная:
[mg=gamma frac{mM’}{r^2} left(2.2right),]
где $M’=frac{4}{3}pi R^3rho $, в этом случае ускорение свободного падения равно:
[g_2(r)=gamma frac{4}{3}pi R^3frac{rho }{r^2}.]
В результате получаем:
[left{ begin{array}{c}
g_1left(rright)=frac{4}{3}pi gamma rho r при rle R \
g_2left(rright)=gamma frac{4}{3}pi R^3frac{rho }{r^2}при rge R. end{array}
right. ]
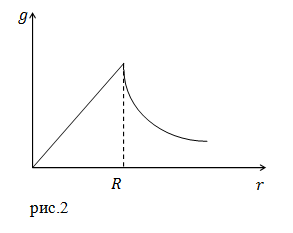
Читать дальше: центростремительное ускорение.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Свободное падение – это движение тела под действием силы тяжести. В упрощенном виде расчет производится без учета сопротивления воздуха.
На поверхности Земли ускорение свободного падения имеет величину от 9,78 м/с2 на экваторе до 9,82 м/с2 на полюсах.
Кроме того, на планете существуют места с экстремальными значениями, которые не вписываются в математическую модель. Минимум составляет
9,76 м/с2, максимум – 9,83 м/с2. Для расчетов в физике используется усредненная величина – 9,8 м/с2
Формула ускорения свободного падения:
Ускорение свободного падения вычисляется по следующей формуле:
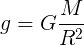
где
G – гравитационная постоянная (постоянная Ньютона), равная 6,6743015·10-11 м3/(кг*с2), или Н*м2/кг2
R – расстояние, на котором находится тело от центра планеты
M – масса планеты
Как видно из вышеприведенной формулы, значение ускорения свободного падения обратно пропорционально квадрату расстояния от центра планеты,
т.е. зависит не только от радиуса самой планеты, но от того, на какой высоте над ее поверхностью находится тело.
Поэтому для расчёта величины “g” на определенной высоте формулу можно скорректировать вот таким образом:
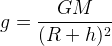
где
G – гравитационная постоянная
R – радиус планеты
h – высота над поверхностью планеты, на которой находится тело
M – масса планеты
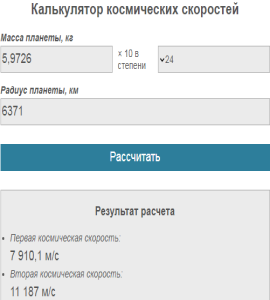
Для расчёта можно воспользоваться калькулятором, который приведен ниже.
Калькулятор ускорения свободного падения
Другие формулы
