| Квантовая механика |
|---|
|
|
Основа
|
|
Фундаментальные понятия
|
|
Эксперименты
|
|
Формулировки
|
|
Уравнения
|
|
Интерпретации
|
|
Развитие теории
|
|
Сложные темы
|
|
Известные учёные
|
|
См. также
|
| См. также: Портал:Физика |
Постоя́нная Пла́нка (квант действия) — основная константа квантовой теории, коэффициент, связывающий величину энергии кванта электромагнитного излучения с его частотой, так же как и вообще величину кванта энергии любой линейной колебательной физической системы с её частотой. Связывает энергию и импульс с частотой и пространственной частотой, действие с фазой. Является квантом момента импульса. Впервые упомянута Максом Планком в работе, посвящённой тепловому излучению, и потому названа в его честь. Обычное обозначение — латинское 
С 2019 года значение постоянной Планка считается зафиксированным и точно равным величине 
Широко используется также приведённая постоянная Планка, равная постоянной Планка, делённой на 2 π и обозначаемая как 
Дж·c =
эВ·с
Физический смысл[править | править код]
В волновой квантовой механике каждой частице ставится в соответствие волновая функция, при этом характеристики этой волны связаны с характеристиками частицы: волновой вектор 





В теоретической физике часто для упрощения внешнего вида формул используется система единиц, в которой 
Величина постоянной Планка определяет и границы применимости классической и квантовой физики. В сравнении с величиной характерных для рассматриваемой системы величин действия или момента импульса, или произведений характерного импульса на характерный размер, или характерной энергии на характерное время, — постоянная Планка показывает, насколько применима к данной физической системе классическая механика. А именно, если 



Эти оценки следуют из соотношений неопределённости Гейзенберга. В квантовой физике измеряемым физическим величинам ставятся в соответствие операторы, алгебра которых отличается от алгебры действительных чисел главным образом тем, что операторы могут не коммутировать, то есть величина 
История открытия[править | править код]
Формула Планка для теплового излучения[править | править код]
Формула Планка — выражение для спектральной плотности мощности 
Коэффициент пропорциональности в этой формуле и получил название постоянной Планка.
При этом Планк полагал, что использованная им гипотеза является не более чем удачным математическим трюком, но не является отражением непосредственно физического процесса. То есть Планк не предполагал, что электромагнитное излучение испускается в виде отдельных порций энергии (квантов), величина которых связана с частотой излучения[источник не указан 514 дней][a].
Фотоэффект[править | править код]
Фотоэффект — это испускание электронов веществом под действием света (и, вообще говоря, любого электромагнитного излучения). В конденсированных веществах (твёрдых и жидких) выделяют внешний и внутренний фотоэффект.
Фотоэффект был объяснён в 1905 году Альбертом Эйнштейном (за что в 1921 году он, благодаря номинации шведского физика Озеена, получил Нобелевскую премию) на основе гипотезы Планка о квантовой природе света. В работе Эйнштейна содержалась важная новая гипотеза — если Планк предположил, что свет излучается только квантованными порциями, то Эйнштейн уже считал, что свет и существует только в виде квантованных порций. Из закона сохранения энергии при представлении света в виде частиц (фотонов) следует формула Эйнштейна для фотоэффекта:
- где
— т. н. работа выхода (минимальная энергия, необходимая для удаления электрона из вещества),
— кинетическая энергия вылетающего электрона,
— частота падающего фотона с энергией
— постоянная Планка.
Из этой формулы следует существование красной границы фотоэффекта, то есть существование наименьшей частоты, ниже которой энергии фотона уже недостаточно для того, чтобы «выбить» электрон из тела. Суть формулы заключается в том, что энергия фотона расходуется на ионизацию атома вещества, то есть на работу, необходимую для «вырывания» электрона, а остаток переходит в кинетическую энергию электрона.
Эффект Комптона[править | править код]
Переопределение[править | править код]
На XXIV Генеральной конференции по мерам и весам (ГКМВ) 17—21 октября 2011 года была единогласно принята резолюция[2], в которой, в частности, предложено в будущей ревизии Международной системы единиц (СИ) переопределить единицы измерений СИ таким образом, чтобы постоянная Планка была равной точно 6,62606X⋅10−34 Дж·с, где Х заменяет одну или более значащих цифр, которые будут определены в дальнейшем на основании наиболее точных рекомендаций CODATA[3]. В этой же резолюции предложено таким же образом определить как точные значения постоянную Авогадро, элементарный заряд и постоянную Больцмана.
XXV ГКМВ, состоявшаяся в 2014 году, приняла решение продолжить работу по подготовке новой ревизии СИ, включающей привязку основных единиц СИ к точному значению постоянной Планка, и предварительно наметила закончить эту работу к 2018 году с тем, чтобы заменить существующую СИ обновлённым вариантом на XXVI ГКМВ[4]. В 2019 году постоянная Планка получила фиксированное значение как и постоянная Больцмана, постоянная Авогадро и другие[5].
Значения постоянной Планка[править | править код]
Ранее постоянная Планка была экспериментально измеряемой величиной, точность известного значения которой постоянно повышалась. В результате изменений СИ 2019 года было принято фиксированное точное значение постоянной Планка:
- h = 6,626 070 15 × 10−34 Дж·c[6];
- h = 6,626 070 15 × 10−27 эрг·c;
- h = 4,135 667 669… × 10−15 эВ·c[6].
Это значение является составной частью определения Международной системы единиц.
Часто применяется величина 
- ħ = 1,054 571 817… × 10−34 Дж·c[6];
- ħ = 1,054 571 817… × 10−27 эрг·c;
- ħ = 6,582 119 569… × 10−16 эВ·c[6],
называемая редуцированной (иногда рационализированной или приведённой) постоянной Планка или постоянной Дирака. Применение этого обозначения упрощает многие формулы квантовой механики, так как в эти формулы традиционная постоянная Планка часто входит в виде деленной на константу 
В ряде естественных систем единиц является единицей измерения действия[7]. В планковской системе единиц, также относящейся к естественным системам, служит в качестве одной из основных единиц системы.
Методы измерения[править | править код]
Использование законов фотоэффекта[править | править код]
При данном способе измерения постоянной Планка используется закон Эйнштейна для фотоэффекта:
- где
— максимальная кинетическая энергия вылетевших с катода фотоэлектронов,
— частота падающего света,
— т. н. работа выхода электрона.
Измерение проводится так. Сначала катод фотоэлемента облучают монохроматическим светом с частотой 
- где
— заряд электрона.
Затем тот же фотоэлемент облучают монохроматическим светом с частотой 

Почленно вычитая второе выражение из первого, получаем:
откуда следует:
Анализ спектра тормозного рентгеновского излучения[править | править код]
Этот способ считается самым точным из существующих. Используется тот факт, что частотный спектр тормозного рентгеновского излучения имеет точную верхнюю границу, называемую фиолетовой границей. Её существование вытекает из квантовых свойств электромагнитного излучения и закона сохранения энергии. Действительно,
- где
— скорость света,
— длина волны рентгеновского излучения,
— заряд электрона,
— ускоряющее напряжение между электродами рентгеновской трубки.
Тогда постоянная Планка равна:
См. также[править | править код]
- Планковские единицы
- Рациональная система единиц
Примечания[править | править код]
Комментарии[править | править код]
- ↑ Значение постоянной Планк нашел, вручную подбирая энергию пакетов и добиваясь наилучшего совпадения с экспериментальными данными[1]
Источники[править | править код]
- ↑ Каку, 2022, с. 69.
- ↑ On the possible future revision of the International System of Units, the SI. Архивная копия от 4 марта 2012 на Wayback Machine Resolution 1 of the 24th meeting of the CGPM (2011).
- ↑ Agreement to tie kilogram and friends to fundamentals — physics-math — 25 October 2011 — New Scientist. Дата обращения: 28 октября 2017. Архивировано 3 ноября 2011 года.
- ↑ On the future revision of the International System of Units, the SI (англ.). Resolution 1 of the 25th CGPM (2014). BIPM. Дата обращения: 6 июля 2017. Архивировано 14 мая 2017 года.
- ↑ The International System of Units – making measurements fundamentally better. BIPM. Дата обращения: 22 мая 2019. Архивировано из оригинала 24 мая 2019 года.
- ↑ 1 2 3 4 Fundamental Physical Constants — Complete Listing. Дата обращения: 19 июня 2011. Архивировано 8 декабря 2013 года.
- ↑ Tomilin K. A. Natural Systems of Units: To the Centenary Anniversary of the Planck System (англ.). Proc. of the XXII Internat. Workshop on high energy physics and field theory (июнь 1999). Дата обращения: 22 декабря 2016. Архивировано 12 мая 2016 года.
Литература[править | править код]
- Митио Каку. Уравнение Бога. В поисках теории всего = Michio Kaku. The God Equation: The Quest for a Theory of Everything. — М.: Альпина нон-фикшн, 2022. — 246 с. — ISBN 978-5-00139-431-0.
- John D. Barrow. The Constants of Nature; From Alpha to Omega — The Numbers that Encode the Deepest Secrets of the Universe. — Pantheon Books, 2002. — ISBN 0-37-542221-8.
- Steiner R. History and progress on accurate measurements of the Planck constant // Reports on Progress in Physics. — 2013. — Vol. 76. — P. 016101.
Ссылки[править | править код]
- Planck constant The NIST Reference on Constants, Units and Uncertainty.
- New Measurement Will Help Redefine International Unit of Mass (англ.). News. NIST (30 июня 2017). Дата обращения: 6 июля 2017.
- Measurement of the Planck constant at the National Institute of Standards and Technology from 2015 to 2017.
- Земцов Ю. К. Курс лекций по атомной физике, анализ размерностей.
For the law governing black-body radiation, see Planck’s law.
| Planck constant | |
|---|---|
|
Common symbols |
 , or , or  for the reduced Planck constant for the reduced Planck constant |
| Dimension |  |
The Planck constant, or Planck’s constant, is a fundamental physical constant of foundational importance in quantum mechanics. The constant gives the relationship between the energy of a photon and its frequency, and by the mass-energy equivalence, the relationship between mass and frequency. Specifically, a photon’s energy is equal to its frequency multiplied by the Planck constant. The constant is generally denoted by 


In metrology it is used, together with other constants, to define the kilogram, the SI unit of mass.[1] The SI units are defined in such a way that, when the Planck constant is expressed in SI units, it has the exact value 
The constant was first postulated by Max Planck in 1900 as part of a solution to the ultraviolet catastrophe. At the end of the 19th century, accurate measurements of the spectrum of black body radiation existed, but the distribution of those measurements at higher frequencies diverged significantly from what was predicted by then-existing theories. Planck empirically derived a formula for the observed spectrum. He assumed that a hypothetical electrically charged oscillator in a cavity that contained black-body radiation can only change its energy in quantized steps, and that the energies of those steps are proportional to the frequency of the oscillator’s associated electromagnetic wave.[4] He was able to calculate the proportionality constant from experimental measurements, and that constant is named in his honor.
In 1905, Albert Einstein determined a “quantum” or minimal element of the energy of the electromagnetic wave itself. The light quantum behaved in some respects as an electrically neutral particle, and was eventually called a photon. Max Planck received the 1918 Nobel Prize in Physics “in recognition of the services he rendered to the advancement of Physics by his discovery of energy quanta”.
| Constant | SI units | Units with eV |
|---|---|---|
| h | 6.62607015×10−34 J⋅Hz−1[2] | 4.135667696…×10−15 eV⋅Hz−1[5] |
| ħ | 1.054571817…×10−34 J⋅s[6] | 6.582119569…×10−16 eV⋅s[7] |
| hc | 1.98644586…×10−25 J⋅m | 1.23984198… eV⋅μm |
| ħc | 3.16152677…×10−26 J⋅m | 0.1973269804… eV⋅μm |
Origin of the constant[edit]

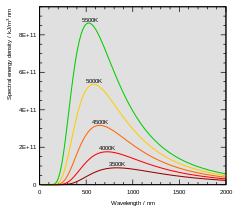
Intensity of light emitted from a black body. Each curve represents behavior at different body temperatures. The Planck constant h is used to explain the shape of these curves.
Planck’s constant was formulated as part of Max Planck’s successful effort to produce a mathematical expression that accurately predicted the observed spectral distribution of thermal radiation from a closed furnace (black-body radiation).[8] This mathematical expression is now known as Planck’s law.
In the last years of the 19th century, Max Planck was investigating the problem of black-body radiation first posed by Kirchhoff some 40 years earlier. Every physical body spontaneously and continuously emits electromagnetic radiation. There was no expression or explanation for the overall shape of the observed emission spectrum. At the time, Wien’s law fit the data for short wavelengths and high temperatures, but failed for long wavelengths.[8]: 141 Also around this time, but unknown to Planck, Lord Rayleigh had derived theoretically a formula, now known as the Rayleigh–Jeans law, that could reasonably predict long wavelengths but failed dramatically at short wavelengths.
Approaching this problem, Planck hypothesized that the equations of motion for light describe a set of harmonic oscillators, one for each possible frequency. He examined how the entropy of the oscillators varied with the temperature of the body, trying to match Wien’s law, and was able to derive an approximate mathematical function for the black-body spectrum,[4] which gave a simple empirical formula for long wavelengths.
Planck tried to find a mathematical expression that could reproduce Wien’s law (for short wavelengths) and the empirical formula (for long wavelengths). This expression included a constant, 
where 


The spectral radiance of a body, 

showing how radiated energy emitted at shorter wavelengths increases more rapidly with temperature than energy emitted at longer wavelengths.[13]
Planck’s law may also be expressed in other terms, such as the number of photons emitted at a certain wavelength, or the energy density in a volume of radiation. The SI units of 

Planck soon realized that his solution was not unique. There were several different solutions, each of which gave a different value for the entropy of the oscillators.[4] To save his theory, Planck resorted to using the then-controversial theory of statistical mechanics,[4] which he described as “an act of desperation … I was ready to sacrifice any of my previous convictions about physics[citation needed].”[14] One of his new boundary conditions was
to interpret UN [the vibrational energy of N oscillators] not as a continuous, infinitely divisible quantity, but as a discrete quantity composed of an integral number of finite equal parts. Let us call each such part the energy element ε;
— Planck, On the Law of Distribution of Energy in the Normal Spectrum[4]
With this new condition, Planck had imposed the quantization of the energy of the oscillators, “a purely formal assumption … actually I did not think much about it …” in his own words,[15] but one that would revolutionize physics. Applying this new approach to Wien’s displacement law showed that the “energy element” must be proportional to the frequency of the oscillator, the first version of what is now sometimes termed the “Planck–Einstein relation”:
Planck was able to calculate the value of 

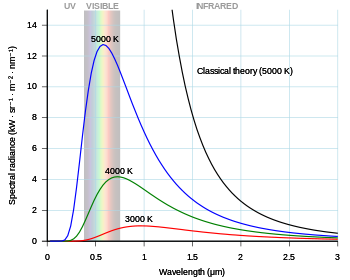
The observed Planck curves at different temperatures, and the divergence of the theoretical Rayleigh–Jeans (black) curve from the observed Planck curve at 5000K.
Development and application[edit]
The black-body problem was revisited in 1905, when Lord Rayleigh and James Jeans (on the one hand) and Albert Einstein (on the other hand) independently proved that classical electromagnetism could never account for the observed spectrum. These proofs are commonly known as the “ultraviolet catastrophe”, a name coined by Paul Ehrenfest in 1911. They contributed greatly (along with Einstein’s work on the photoelectric effect) in convincing physicists that Planck’s postulate of quantized energy levels was more than a mere mathematical formalism. The first Solvay Conference in 1911 was devoted to “the theory of radiation and quanta”.[17]
Photoelectric effect[edit]
The photoelectric effect is the emission of electrons (called “photoelectrons”) from a surface when light is shone on it. It was first observed by Alexandre Edmond Becquerel in 1839, although credit is usually reserved for Heinrich Hertz,[18] who published the first thorough investigation in 1887. Another particularly thorough investigation was published by Philipp Lenard (Lénárd Fülöp) in 1902.[19] Einstein’s 1905 paper[20] discussing the effect in terms of light quanta would earn him the Nobel Prize in 1921,[18] after his predictions had been confirmed by the experimental work of Robert Andrews Millikan.[21] The Nobel committee awarded the prize for his work on the photo-electric effect, rather than relativity, both because of a bias against purely theoretical physics not grounded in discovery or experiment, and dissent amongst its members as to the actual proof that relativity was real.[22][23]
Before Einstein’s paper, electromagnetic radiation such as visible light was considered to behave as a wave: hence the use of the terms “frequency” and “wavelength” to characterize different types of radiation. The energy transferred by a wave in a given time is called its intensity. The light from a theatre spotlight is more intense than the light from a domestic lightbulb; that is to say that the spotlight gives out more energy per unit time and per unit space (and hence consumes more electricity) than the ordinary bulb, even though the color of the light might be very similar. Other waves, such as sound or the waves crashing against a seafront, also have their intensity. However, the energy account of the photoelectric effect didn’t seem to agree with the wave description of light.
The “photoelectrons” emitted as a result of the photoelectric effect have a certain kinetic energy, which can be measured. This kinetic energy (for each photoelectron) is independent of the intensity of the light,[19] but depends linearly on the frequency;[21] and if the frequency is too low (corresponding to a photon energy that is less than the work function of the material), no photoelectrons are emitted at all, unless a plurality of photons, whose energetic sum is greater than the energy of the photoelectrons, acts virtually simultaneously (multiphoton effect).[24] Assuming the frequency is high enough to cause the photoelectric effect, a rise in intensity of the light source causes more photoelectrons to be emitted with the same kinetic energy, rather than the same number of photoelectrons to be emitted with higher kinetic energy.[19]
Einstein’s explanation for these observations was that light itself is quantized; that the energy of light is not transferred continuously as in a classical wave, but only in small “packets” or quanta. The size of these “packets” of energy, which would later be named photons, was to be the same as Planck’s “energy element”, giving the modern version of the Planck–Einstein relation:
Einstein’s postulate was later proven experimentally: the constant of proportionality between the frequency of incident light 


Atomic structure[edit]

A schematization of the Bohr model of the hydrogen atom. The transition shown from the n = 3 level to the n = 2 level gives rise to visible light of wavelength 656 nm (red), as the model predicts.
It was John William Nicholson in 1912 who introduced h-bar into the theory of the atom which was the first quantum and nuclear atom and the first to quantize angular momentum as h/2π. [25][26][27] Niels Bohr quoted him in his 1913 paper of the Bohr model of the atom.[28] The influence of the work of Nicholson’s nuclear quantum atomic model on Bohr’s model has been written about by many historians.[29][30][31]
Niels Bohr introduced the third quantized model of the atom in 1913, in an attempt to overcome a major shortcoming of Rutherford’s classical model. The first quantized model of the atom was introduced in 1910 by Arthur Erich Haas and was discussed at the 1911 Solvay conference.[32][33] In classical electrodynamics, a charge moving in a circle should radiate electromagnetic radiation. If that charge were to be an electron orbiting a nucleus, the radiation would cause it to lose energy and spiral down into the nucleus. Bohr solved this paradox with explicit reference to Planck’s work: an electron in a Bohr atom could only have certain defined energies 
where 




Bohr also introduced the quantity 


Uncertainty principle[edit]
The Planck constant also occurs in statements of Werner Heisenberg’s uncertainty principle. Given numerous particles prepared in the same state, the uncertainty in their position, 

where the uncertainty is given as the standard deviation of the measured value from its expected value. There are several other such pairs of physically measurable conjugate variables which obey a similar rule. One example is time vs. energy. The inverse relationship between the uncertainty of the two conjugate variables forces a tradeoff in quantum experiments, as measuring one quantity more precisely results in the other quantity becoming imprecise.
In addition to some assumptions underlying the interpretation of certain values in the quantum mechanical formulation, one of the fundamental cornerstones to the entire theory lies in the commutator relationship between the position operator 

where 
Photon energy[edit]
The Planck relation connects the particular photon energy E with its associated wave frequency f:
This energy is extremely small in terms of ordinarily perceived everyday objects.
Since the frequency f, wavelength λ, and speed of light c are related by 
de Broglie wavelength[edit]
In 1923, Louis de Broglie generalized the Planck–Einstein relation by postulating that the Planck constant represents the proportionality between the momentum and the quantum wavelength of not just the photon, but the quantum wavelength of any particle. This was confirmed by experiments soon afterward. This holds throughout the quantum theory, including electrodynamics. The de Broglie wavelength λ of the particle is given by
where p denotes the linear momentum of a particle, such as a photon, or any other elementary particle.
The energy of a photon with angular frequency ω = 2πf is given by
while its linear momentum relates to
where k is an angular wavenumber.
These two relations are the temporal and spatial parts of the special relativistic expression using 4-vectors.
Statistical mechanics[edit]
Classical statistical mechanics requires the existence of h (but does not define its value).[34] Eventually, following upon Planck’s discovery, it was speculated that physical action could not take on an arbitrary value, but instead was restricted to integer multiples of a very small quantity, the “[elementary] quantum of action”, now called the Planck constant.[35][note 1] This was a significant conceptual part of the so-called “old quantum theory” developed by physicists including Bohr, Sommerfeld, and Ishiwara, in which particle trajectories exist but are hidden, but quantum laws constrain them based on their action. This view has been replaced by fully modern quantum theory, in which definite trajectories of motion do not even exist; rather, the particle is represented by a wavefunction spread out in space and in time. Thus there is no value of the action as classically defined. Related to this is the concept of energy quantization which existed in old quantum theory and also exists in altered form in modern quantum physics. Classical physics cannot explain either quantization of energy or the lack of classical particle motion.
In many cases, such as for monochromatic light or for atoms, quantization of energy also implies that only certain energy levels are allowed, and values in between are forbidden.[36]
Reduced Planck constant[edit]
Implicit in the dimensions of the Planck constant is the fact that the SI unit of frequency, the hertz, represents one cycle per second. One cycle corresponds to 2π radians of phase angle.
In applications where it is natural to use the angular frequency (i.e. where the frequency is expressed in terms of radians per second instead of cycles per second or hertz) it is often useful to absorb a factor of 2π into the Planck constant. The resulting constant is called the reduced Planck constant or Dirac constant. It is equal to the Planck constant divided by 2π, and is denoted by 
Value[edit]
The Planck constant has dimensions of angular momentum. In SI units, the Planck constant is expressed with the unit joule per hertz (J⋅Hz−1) or joule-second (J⋅s).
The above values have been adopted as fixed in the 2019 redefinition of the SI base units.
Understanding the ‘fixing’ of the value of h[edit]
Since 2019, the numerical value of the Planck constant has been fixed, with a finite decimal representation. Under the present definition of the kilogram, which states that “The kilogram […] is defined by taking the fixed numerical value of h to be 6.62607015×10−34 when expressed in the unit J⋅s, which is equal to kg⋅m2⋅s−1, where the metre and the second are defined in terms of speed of light c and duration of hyperfine transition of the ground state of an unperturbed caesium-133 atom ΔνCs.”[38] This implies that mass metrology aims to find the value of one kilogram, and the kilogram is compensating. Every experiment aiming to measure the kilogram (such as the Kibble balance and the X-ray crystal density method), will essentially refine the value of a kilogram.
As an illustration of this, suppose the decision of making h to be exact was taken in 2010, when its measured value was 6.62606957×10−34 J⋅s, thus the present definition of kilogram was also enforced. In the future, the value of one kilogram must be refined to 6.62607015/6.62606957 ≈ 1.0000001 times the mass of the International Prototype of the Kilogram (IPK).
Significance of the value[edit]
The Planck constant is related to the quantization of light and matter. It can be seen as a subatomic-scale constant. In a unit system adapted to subatomic scales, the electronvolt is the appropriate unit of energy and the petahertz the appropriate unit of frequency. Atomic unit systems are based (in part) on the Planck constant. The physical meaning of the Planck constant could suggest some basic features of our physical world.
The Planck constant is one of the smallest constants used in physics. This reflects the fact that on a scale adapted to humans, where energies are typical of the order of kilojoules and times are typical of the order of seconds or minutes, the Planck constant is very small. One can regard the Planck constant to be only relevant to the microscopic scale instead of the macroscopic scale in our everyday experience.
Equivalently, the order of the Planck constant reflects the fact that everyday objects and systems are made of a large number of microscopic particles. For example, green light with a wavelength of 555 nanometres (a wavelength that can be perceived by the human eye to be green) has a frequency of 540 THz (540×1012 Hz). Each photon has an energy E = hf = 3.58×10−19 J. That is a very small amount of energy in terms of everyday experience, but everyday experience is not concerned with individual photons any more than with individual atoms or molecules. An amount of light more typical in everyday experience (though much larger than the smallest amount perceivable by the human eye) is the energy of one mole of photons; its energy can be computed by multiplying the photon energy by the Avogadro constant, NA = 6.02214076×1023 mol−1[39], with the result of 216 kJ, about the food energy in three apples.
Determination[edit]
In principle, the Planck constant can be determined by examining the spectrum of a black-body radiator or the kinetic energy of photoelectrons, and this is how its value was first calculated in the early twentieth century. In practice, these are no longer the most accurate methods.
Since the value of the Planck constant is fixed now, it is no longer determined or calculated in laboratories. Some of the practices given below to determine the Planck constant are now used to determine the mass of the kilogram. All of the methods given below except the X-ray crystal density method rely on the theoretical basis of the Josephson effect and the quantum Hall effect.
Josephson constant[edit]
The Josephson constant KJ relates the potential difference U generated by the Josephson effect at a “Josephson junction” with the frequency ν of the microwave radiation. The theoretical treatment of Josephson effect suggests very strongly that KJ = 2e/h.
The Josephson constant may be measured by comparing the potential difference generated by an array of Josephson junctions with a potential difference which is known in SI volts. The measurement of the potential difference in SI units is done by allowing an electrostatic force to cancel out a measurable gravitational force, in a Kibble balance. Assuming the validity of the theoretical treatment of the Josephson effect, KJ is related to the Planck constant by
Kibble balance[edit]
A Kibble balance (formerly known as a watt balance)[40] is an instrument for comparing two powers, one of which is measured in SI watts and the other of which is measured in conventional electrical units. From the definition of the conventional watt W90, this gives a measure of the product KJ2RK in SI units, where RK is the von Klitzing constant which appears in the quantum Hall effect. If the theoretical treatments of the Josephson effect and the quantum Hall effect are valid, and in particular assuming that RK = h/e2, the measurement of KJ2RK is a direct determination of the Planck constant.
Magnetic resonance[edit]
The gyromagnetic ratio γ of an object is the ratio of its magnetic moment to its angular momentum, which is directly related to the constant of proportionality between the frequency ν of nuclear magnetic resonance (or electron paramagnetic resonance for electrons) and the applied magnetic field B: ν = γB. It is difficult to measure gyromagnetic ratios precisely because of the difficulties in precisely measuring B, but the value for protons in water at 25 °C is known to an uncertainty of better than 10−6. The protons are said to be “shielded” from the applied magnetic field by the electrons in the water molecule, the same effect that gives rise to chemical shift in NMR spectroscopy, and this is indicated by a prime on the symbol for the gyromagnetic ratio, γ′p. The gyromagnetic ratio is related to the shielded proton magnetic moment μ′p, the spin number I (I = 1⁄2 for protons) and the reduced Planck constant.
The ratio of the shielded proton magnetic moment μ′p to the electron magnetic moment μe can be measured separately and to high precision, as the imprecisely known value of the applied magnetic field cancels itself out in taking the ratio. The value of μe in Bohr magnetons is also known: it is half the electron g-factor ge. Hence
A further complication is that the measurement of γ′p involves the measurement of an electric current: this is invariably measured in conventional amperes rather than in SI amperes, so a conversion factor is required. The symbol Γ′p-90 is used for the measured gyromagnetic ratio using conventional electrical units. In addition, there are two methods of measuring the value, a “low-field” method and a “high-field” method, and the conversion factors are different in the two cases. Only the high-field value Γ′p-90(hi) is of interest in determining the Planck constant.
Substitution gives the expression for the Planck constant in terms of Γ′p-90(hi):
Faraday constant[edit]
The Faraday constant F is the charge of one mole of electrons, equal to the Avogadro constant NA multiplied by the elementary charge e. It can be determined by careful electrolysis experiments, measuring the amount of silver dissolved from an electrode in a given time and for a given electric current. Substituting the definitions of NA and e gives the relation to the Planck constant.
X-ray crystal density[edit]
The X-ray crystal density method is primarily a method for determining the Avogadro constant NA, but as the Avogadro constant is related to the Planck constant, it also determines a value for h. The principle behind the method is to determine NA as the ratio between the volume of the unit cell of a crystal, measured by X-ray crystallography, and the molar volume of the substance. Crystals of silicon are used, as they are available in high quality and purity by the technology developed for the semiconductor industry. The unit cell volume is calculated from the spacing between two crystal planes referred to as d220. The molar volume Vm(Si) requires a knowledge of the density of the crystal and the atomic weight of the silicon used. The Planck constant is given by
Particle accelerator[edit]
The experimental measurement of the Planck constant in the Large Hadron Collider laboratory was carried out in 2011.
See also[edit]
- CODATA 2018
- International System of Units
- Introduction to quantum mechanics
- List of scientists whose names are used in physical constants
- Planck units
- Wave–particle duality
Notes[edit]
- ^ The quantum of action, a historical name for the Planck constant, should not be confused with the quantum of angular momentum, equal to the reduced Planck constant.
- ^ This value,
, is sometimes referred to as the “Dirac constant”, after Paul Dirac.[37]
References[edit]
Citations[edit]
- ^ Le Système international d’unités [The International System of Units] (PDF) (in French and English) (9th ed.), International Bureau of Weights and Measures, 2019, p. 131, ISBN 978-92-822-2272-0
- ^ a b “2018 CODATA Value: Planck constant”. The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2021-04-28.
- ^ “Resolutions of the 26th CGPM” (PDF). BIPM. 2018-11-16. Archived from the original (PDF) on 2018-11-19. Retrieved 2018-11-20.
- ^ a b c d e f Planck, Max (1901), “Ueber das Gesetz der Energieverteilung im Normalspectrum” (PDF), Ann. Phys., 309 (3): 553–63, Bibcode:1901AnP…309..553P, doi:10.1002/andp.19013090310, archived (PDF) from the original on 2012-06-10, retrieved 2008-12-15. English translation: “On the Law of Distribution of Energy in the Normal Spectrum”. Archived from the original on 2008-04-18.“. “On the Law of Distribution of Energy in the Normal Spectrum” (PDF). Archived from the original (PDF) on 2011-10-06. Retrieved 2011-10-13.
- ^ “2018 CODATA Value: Planck constant in eV/Hz”. The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2021-04-29.
- ^ “2018 CODATA Value: reduced Planck constant”. The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-08-28.
- ^ “2018 CODATA Value: reduced Planck constant in eV s”. The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2021-04-29.
- ^ a b Bitter, Francis; Medicus, Heinrich A. (1973). Fields and particles. New York: Elsevier. pp. 137–144.
- ^ Boya, Luis J. (2004). “The Thermal Radiation Formula of Planck (1900)”. arXiv:physics/0402064v1.
- ^
Planck, M. (1914). The Theory of Heat Radiation. Masius, M. (transl.) (2nd ed.). P. Blakiston’s Son. pp. 6, 168. OL 7154661M. - ^
Chandrasekhar, S. (1960) [1950]. Radiative Transfer (Revised reprint ed.). Dover. p. 8. ISBN 978-0-486-60590-6. - ^ Rybicki, G. B.; Lightman, A. P. (1979). Radiative Processes in Astrophysics. Wiley. p. 22. ISBN 978-0-471-82759-7. Archived from the original on 2020-07-27. Retrieved 2020-05-20.
- ^ Shao, Gaofeng; et al. (2019). “Improved oxidation resistance of high emissivity coatings on fibrous ceramic for reusable space systems”. Corrosion Science. 146: 233–246. arXiv:1902.03943. doi:10.1016/j.corsci.2018.11.006. S2CID 118927116.
- ^ Kragh, Helge (1 December 2000), Max Planck: the reluctant revolutionary, PhysicsWorld.com, archived from the original on 2009-01-08
- ^ Kragh, Helge (1999), Quantum Generations: A History of Physics in the Twentieth Century, Princeton University Press, p. 62, ISBN 978-0-691-09552-3, archived from the original on 2021-12-06, retrieved 2021-10-31
- ^ Planck, Max (2 June 1920), The Genesis and Present State of Development of the Quantum Theory (Nobel Lecture), archived from the original on 15 July 2011, retrieved 13 December 2008
- ^ Previous Solvay Conferences on Physics, International Solvay Institutes, archived from the original on 16 December 2008, retrieved 12 December 2008
- ^ a b See, e.g., Arrhenius, Svante (10 December 1922), Presentation speech of the 1921 Nobel Prize for Physics, archived from the original on 4 September 2011, retrieved 13 December 2008
- ^ a b c Lenard, P. (1902), “Ueber die lichtelektrische Wirkung”, Ann. Phys., 313 (5): 149–98, Bibcode:1902AnP…313..149L, doi:10.1002/andp.19023130510, archived from the original on 2019-08-18, retrieved 2019-07-03
- ^ Einstein, Albert (1905), “Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt” (PDF), Ann. Phys., 17 (6): 132–48, Bibcode:1905AnP…322..132E, doi:10.1002/andp.19053220607, archived (PDF) from the original on 2011-07-09, retrieved 2009-12-03
- ^ a b c Millikan, R. A. (1916), “A Direct Photoelectric Determination of Planck’s h“, Phys. Rev., 7 (3): 355–88, Bibcode:1916PhRv….7..355M, doi:10.1103/PhysRev.7.355
- ^ Isaacson, Walter (2007-04-10), Einstein: His Life and Universe, ISBN 978-1-4165-3932-2, archived from the original on 2020-01-09, retrieved 2021-10-31, pp. 309–314.
- ^ “The Nobel Prize in Physics 1921”. Nobelprize.org. Archived from the original on 2018-07-03. Retrieved 2014-04-23.
- ^ Smith, Richard (1962), “Two Photon Photoelectric Effect”, Physical Review, 128 (5): 2225, Bibcode:1962PhRv..128.2225S, doi:10.1103/PhysRev.128.2225.Smith, Richard (1963), “Two-Photon Photoelectric Effect”, Physical Review, 130 (6): 2599, Bibcode:1963PhRv..130.2599S, doi:10.1103/PhysRev.130.2599.4.
- ^ John Heilbron, “The path to the quantum atom,” 6 June 2013, Vol 498, NATURE, 27.
- ^ J. W. Nicholson, Month. Not. Roy. Astr. Soc. lxxii. pp. 49,130, 677, 693, 729 (1912).
- ^ The Atomic Theory of John William Nicholson, Russell McCormmach, Archive for History of Exact Sciences, Vol. 3, No. 2 (25.8.1966), pp. 160-184 (25 pages), Springer.
- ^ On the Constitution of Atoms and Molecules, Niels Bohr, Philosophical Magazine, Series 6, Volume 26 July 1913, p. 1-25
- ^ T. Hirosige and S. Nisio, “Formation of Bohr’s Theory of Atomic Constitution,” Jap. Studies Hist. Sci, No. 3 (1964), 6-28;
- ^ J. L. Heilbron, A History of Atomic Models from the Discovery of the Electron to the Beginnings of Quantum Mechanics, diss. (University of California, Berkeley, 1964).
- ^ R. McCormmach, “The Atomic Theory of John William Nicholson,” Arch. Hist. Exact Sci., 3 (1966), 160-184.
- ^ John Heilbron, “The path to the quantum atom,” 6 June 2013, Vol 498, NATURE, 29-30.
- ^ Bohr, Niels (1913), “On the Constitution of Atoms and Molecules”, Phil. Mag., 6th Series, 26 (153): 1–25, Bibcode:1913PMag…26..476B, doi:10.1080/14786441308634993, archived from the original on 2020-01-27, retrieved 2019-07-03
- ^ Giuseppe Morandi; F. Napoli; E. Ercolessi (2001), Statistical mechanics: an intermediate course, p. 84, ISBN 978-981-02-4477-4, archived from the original on 2021-12-06, retrieved 2021-10-31
- ^ ter Haar, D. (1967). The Old Quantum Theory. Pergamon Press. p. 133. ISBN 978-0-08-012101-7.
- ^ Einstein, Albert (2003), “Physics and Reality” (PDF), Daedalus, 132 (4): 24, doi:10.1162/001152603771338742, S2CID 57559543, archived from the original (PDF) on 2012-04-15,
The question is first: How can one assign a discrete succession of energy values Hσ to a system specified in the sense of classical mechanics (the energy function is a given function of the coordinates qr and the corresponding momenta pr)? The Planck constant h relates the frequency Hσ/h to the energy values Hσ. It is therefore sufficient to give to the system a succession of discrete frequency values.
- ^ P.R. Bunker; Ian M. Mills; Per Jensen (2019). “The Planck constant and its units”. Journal of Quantitative Spectroscopy & Radiative Transfer. Elsevier. 237: 106594. Bibcode:2019JQSRT.23706594B. doi:10.1016/j.jqsrt.2019.106594. S2CID 201264843.
- ^ Le Système international d’unités [The International System of Units] (PDF) (in French and English) (9th ed.), International Bureau of Weights and Measures, 2019, ISBN 978-92-822-2272-0
- ^ “2018 CODATA Value: Avogadro constant”. The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ Materese, Robin (2018-05-14). “Kilogram: The Kibble Balance”. NIST. Archived from the original on 2018-11-22. Retrieved 2018-11-13.
Sources[edit]
- Barrow, John D. (2002), The Constants of Nature; From Alpha to Omega – The Numbers that Encode the Deepest Secrets of the Universe, Pantheon Books, ISBN 978-0-375-42221-8
External links[edit]
- “The role of the Planck constant in physics” – presentation at 26th CGPM meeting at Versailles, France, November 2018 when voting took place.
формула планка
Что такое Закон Планка
Закон Планка — это уравнение, которое описывает спектральное распределение энергии излучения абсолютного черного тела. Под АЧТ подразумевается такое физическое тело, которое вне зависимости от температуры поглощает весь спектр падающего на него электромагнитного излучения во всех интервалах.
Формула закона Планка имеет вид:
(varepsilon_{nu_1T}=frac{2pinu^2}{c^2}frac{hnu}{expleft({displaystylefrac{hnu}{kT}}right)-1})
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Где h — постоянная Планка, k — постоянная Больцмана, c — скорость света, T — температура.
Это выражение было выведено Максом Планком в 1900-ом году. Это случилось после того, как он рассмотрел баланс обмена энергией между двумя разными осцилляторами: частицами вещества, которые поглощали и испускали излучение на частоте ωω, и осцилляторами, которые представляли электромагнитное поле этой же частоты.
Ученый сделал предположение, что данные осцилляторы могут находиться лишь в состояниях с дискретной энергией. Они отдают друг другу кванты энергии со значением ( Delta E=ℏomegaDelta E=ℏomega.)
Величину коэффициента пропорциональности ℏℏ между частотой электронного генератора и величиной кванта энергии Планк установил с помощью экспериментальных данных: ℏℏ=1,054·10–34 Дж·с.
Что описывает формула
Данная формула описывает излучение абсолютного черного тела.
Расчеты, которые проводят с ее помощью, совпадают с экспериментальными показателями для любых частот. В качестве частного случая в данном выражении присутствует формула Рэлея – Джинса (если (hnu<kT)).
В области больших частот (при (hnu>kT)) эта формула переходит в:
(varepsilon_{nu_1T}=frac{2pi hnu^3}{c^2}expleft(-frac{hnu}{kT}right). )
Из ФП следуют:
- закон смещения Вина;
- закон Стефана – Больцмана.
Количественное значение постоянной Планка можно найти, зная из эксперимента величины постоянных:
- k (постоянную Больцмана);
- σ (постоянную Стефана – Больцмана);
- с (скорость света в вакууме).
Таким образом, мы получим выражение:
(h=sqrt[3]{frac{2pi^5k^4}{10sigma c^2}}.)
Хотя ФП была создана, чтобы определять равновесное излучение внутри нагретого вещества, она пригодна и для описания спектрального распределения лучистой энергии, которая выпускается телами в окружающее пространство.
Пример
Например, чтобы определить температуру поверхности звезды, необходимо зарегистрировать спектр ее излучения, а затем сопоставить его с ФП.
Этим же методом можно измерять температуру тел, нагретых в земных условиях. Эта формула незаменима для раскаленных металлов и керамики, где невозможно использовать традиционные датчики теплового измерения. ФП применяют и для описания потоков лучистой энергии в эталонах яркости излучения, которые нужны для абсолютной калибровки приёмников света.
Вид формулы Планка через длину волны (λ)
ФП, записанная через длину волны, выглядит следующим образом:
(varepsilon_{lambda_1T}=frac{2pi с^2}{lambda^5}frac h{expleft({displaystylefrac{hc}{klambda T}}right)-1}.)
Зависимость спектральной плотности энергии от длины волны представлена на графике:
Насколько полезной была для вас статья?
Рейтинг: 2.25 (Голосов: 4)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
- https://ru.wikipedia.org/wiki/%D0%9F%D0%BE%D1%81%D1%82%D0%BE%D1%8F%D0%BD%D0%BD%D0%B0%D1%8F_%D0%9F%D0%BB%D0%B0%D0%BD%D0%BA%D0%B0
- http://www.astronet.ru/db/msg/1188550
| |
||||||||||||||||||
|
|
||||||||||||||||||
| Принцип неопределённости | ||||||||||||||||||
| Введение Математические основы |
||||||||||||||||||
|
||||||||||||||||||
| См. также: Портал:Физика |
Постоя́нная Пла́нка (квант действия) — основная константа квантовой теории, коэффициент, связывающий величину энергии кванта электромагнитного излучения с его частотой, так же как и вообще величину кванта энергии любой линейной колебательной физической системы с её частотой. Связывает энергию и импульс с частотой и пространственной частотой, действие с фазой. Является квантом момента импульса. Впервые упомянута Планком в работе, посвящённой тепловому излучению, и потому названа в его честь. Обычное обозначение — латинское 
Дж·c[1]
эрг·c.
эВ·c[1].
Часто применяется величина 
Дж·c[1],
эрг·c,
эВ·c[1],
называемая редуцированной (иногда рационализированной или приведённой) постоянной Планка или постоянной Дирака. Применение этого обозначения упрощает многие формулы квантовой механики, так как в эти формулы традиционная постоянная Планка входит в виде деленной на константу 
На 24-й Генеральной конференции по мерам и весам 17—21 октября 2011 года была единогласно принята резолюция[2], в которой, в частности, предложено в будущей ревизии Международной системы единиц (СИ) переопределить единицы измерений СИ таким образом, чтобы постоянная Планка была равной точно 6,62606X×10−34 Дж·с, где Х заменяет одну или более значащих цифр, которые будут определены в дальнейшем на основании наиболее точных рекомендаций CODATA[3]. В этой же резолюции предложено таким же образом определить как точные значения постоянную Авогадро, элементарный заряд и постоянную Больцмана.
Физический смысл
В квантовой механике импульс имеет физический смысл волнового вектора, энергия — частоты, а действие — фазы волны, однако традиционно (исторически) механические величины измеряются в других единицах (кг·м/с, Дж, Дж·с), чем соответствующие волновые (м−1, с−1, безразмерные единицы фазы). Постоянная Планка играет роль переводного коэффициента (всегда одного и того же), связывающего эти две системы единиц — квантовую и традиционную:
(импульс)
(энергия)
(действие)
Если бы система физических единиц формировалась уже после возникновения квантовой механики и приспосабливалась для упрощения основных теоретических формул, константа Планка вероятно просто была бы сделана равной единице, или, во всяком случае, более круглому числу. В теоретической физике очень часто для упрощения формул используется система единиц с 
.
Постоянная Планка имеет и простую оценочную роль в разграничении областей применимости классической и квантовой физики: она в сравнении с величиной характерных для рассматриваемой системы величин действия или момента импульса, или произведений характерного импульса на характерный размер, или характерной энергии на характерное время, показывает, насколько применима к данной физической системе классическая механика. А именно, если 



История открытия
Формула Планка для теплового излучения
Формула Планка — выражение для спектральной плотности мощности излучения абсолютно чёрного тела, которое было получено Максом Планком для равновесной плотности излучения 
Коэффициент пропорциональности 

Фотоэффект
Фотоэффект — это испускание электронов веществом под действием света (и, вообще говоря, любого электромагнитного излучения). В конденсированных веществах (твёрдых и жидких) выделяют внешний и внутренний фотоэффект.
Фотоэффект был объяснён в 1905 году Альбертом Эйнштейном (за что в 1921 году он, благодаря номинации шведского физика Озеена, получил Нобелевскую премию) на основе гипотезы Планка о квантовой природе света. В работе Эйнштейна содержалась важная новая гипотеза — если Планк предположил, что свет излучается только квантованными порциями, то Эйнштейн уже считал, что свет и существует только в виде квантованных порций. Из закона сохранения энергии, при представлении света в виде частиц (фотонов), следует формула Эйнштейна для фотоэффекта:
В этом случае неправильно определена кинетическая энергия электрона, так как он имеет начальную скорость движения Е = m( V +Δv)^2 / 2, где Δv – величина на которую увеличилась скорость движения электрона под действием n импульсов излучений. Разность кинетических энергий электрона равна ΔЕ = mVΔv + mΔv^2 / 2. Из этого следует, что постоянная Планка по расчётам Эйнштейна не срртветствует действительности.
- Вторая ошибка Эйштейна заключается в том, что энергия кванта излучения hυ- есть энергия излучения за 1 сек., так как υ- есть количество волн излучения за 1 сек.. Считать в этом случае квант излучения одной частицей “фотоном” не возможно, так как его масса равномерно распределена на расстоянии 300000000 м. Из формулы разности кинетических энергий электрона видим, что энергия изиеняется по квадратичной зависимости, а по формуле планка энергия излучения определяется по линейной зависимости Е = h υ. Таким образом постоянная Планка определена с ошибкой.
где 




Эффект Комптона
Методы измерения
Использование законов фотоэффекта
При данном способе измерения постоянной Планка используется закон Эйнштейна для фотоэффекта:
где 
— частота падающего света,
— т. н. работа выхода электрона.
Измерение проводится так. Сначала катод фотоэлемента облучают монохроматическим светом с частотой 
где 
Затем тот же фотоэлемент облучают монохроматическим светом с частотой 

Почленно вычитая второе выражение из первого, получаем
откуда следует
Анализ спектра тормозного рентгеновского излучения
Этот способ считается самым точным из существующих. Используется тот факт, что частотный спектр тормозного рентгеновского излучения имеет точную верхнюю границу, называемую фиолетовой границей. Её существование вытекает из квантовых свойств электромагнитного излучения и закона сохранения энергии. Действительно,
где 
— длина волны рентгеновского излучения,
— заряд электрона,
— ускоряющее напряжение между электродами рентгеновской трубки.
Тогда постоянная Планка равна
Примечания
- ↑ 1,0 1,1 1,2 1,3 Fundamental Physical Constants — Complete Listing
- ↑ On the possible future revision of the International System of Units, the SI. Resolution 1 of the 24th meeting of the CGPM (2011).
- ↑ Agreement to tie kilogram and friends to fundamentals — physics-math — 25 October 2011 — New Scientist
Литература
- John D. Barrow. The Constants of Nature; From Alpha to Omega — The Numbers that Encode the Deepest Secrets of the Universe. — Pantheon Books, 2002. — ISBN 0-37-542221-8. (см. ISBN )
- Steiner R. History and progress on accurate measurements of the Planck constant // Reports on Progress in Physics. — 2013.
Ссылки
- Ю. К. Земцов, Курс лекций по атомной физике, анализ размерностей
- История уточнения постоянной Планка
- The NIST Reference on Constants, Units and Uncertainty
Планковские единицы |
|
|---|---|
| Базовые |
Постоянная | |
| Производные |
Энергия | |
| Используются в |
Частица = |
Шаблон:Производные буквы H
|
Выделить Постоянная Планка и найти в:
|
|
|
- Страница 0 – краткая статья
- Страница 1 – энциклопедическая статья
- Разное – на страницах: 2 , 3 , 4 , 5
- Прошу вносить вашу информацию в «Постоянная Планка 1», чтобы сохранить ее
Комментарии читателей:
Материал
из свободной русской энциклопедии «Традиция»
|
Значения |
Единицы |
|
6,626 070 040(81) • 10−34 |
Дж∙c |
|
4,135 667 662(25) • 10−15 |
эВ∙c |
|
6,626 070 040(81) • 10−27 |
эрг∙c |
Постоя́нная Пла́нка, обозначаемая как h, является физической постоянной,
используемой для описания величины кванта действия в квантовой механике. Данная
постоянная впервые появилась в работах М. Планка, посвящённых тепловому
излучению, и потому названа в его честь. Она присутствует как коэффициент между
энергией E и частотой
ν фотона в формуле Планка:
![]()
Скорость
света c связана с частотой ν и длиной волны λ соотношением:
![]()
С учётом этого
соотношение Планка записывается так:
![]()
Часто
применяется величина
![]() Дж•c,
Дж•c,
![]() эрг•c,
эрг•c,
![]() эВ•c,
эВ•c,
называемая
редуцированной (или рационализированной) постоянной Планка или постоянной
Дирака.
Постоянную
Дирака удобно использовать тогда, когда применяется угловая частота ω, измеряемая в радианах за секунду,
вместо обычной частоты ν,
измеряемой количеством циклов за секунду. Так как ω = 2πν,
то справедлива формула:
![]()
Согласно
гипотезе Планка, впоследствии подтверждённой, энергия атомных состояний
является квантованной. Это приводит к тому, что нагретое вещество излучает
электромагнитные кванты или фотоны определённых частот, спектр которых зависит
от химического состава вещества.
В Юникоде
постоянная Планка занимает позицию U+210E (h), а постоянная Дирака U+210F (ħ).
Содержание
- 1 Величина
- 2 Происхождение
постоянной Планка - 2.1 Излучение
чёрного тела - 2.2 Фотоэффект
- 2.3 Структура
атома - 2.4 Принцип
неопределённости - 2.5 Спектр
тормозного рентгеновского излучения - 3 Физические
константы, связанные с постоянной Планка - 3.1 Масса
покоя электрона - 3.2 Постоянная
Авогадро - 3.3 Элементарный
заряд - 3.4 Магнетон
Бора и ядерный магнетон - 4 Определение
из экспериментов - 4.1 Постоянная
Джозефсона - 4.2 Баланс
мощности - 4.3 Магнитный
резонанс - 4.4 Постоянная
Фарадея - 4.5 Рентгеновская
плотность кристалла - 5 Постоянная
Планка в системе единиц СИ - 6 Постоянная
Планка в теории бесконечной вложенности материи - 7 См.
также - 8 Ссылки
- 9 Литература
- 10 Внешние
ссылки
Величина
Постоянная
Планка имеет размерность энергии, умноженной на время, как и размерность
действия. В международной системе единиц СИ постоянная Планка выражается в
единицах Дж•с. Такую же размерность имеет произведение импульса на расстояние в
виде Н•м•с, а также момент импульса.
Значение
постоянной Планка равно:[1]
![]() Дж•с
Дж•с ![]() эВ•с.
эВ•с.
Две цифры
между скобками обозначают неопределённость в двух последних цифрах значения
постоянной Планка (данные обновляются приблизительно каждые 4 года).
Происхождение
постоянной Планка
Излучение
чёрного тела
![]() Основная статья: Формула Планка
Основная статья: Формула Планка

![]()
Интенсивность света, излучаемая чёрным телом в зависимости от длины
волны. Кривые обозначены разным цветом и построены для разных температур тела.
Планк был первым, кто объяснил форму этих кривых
В конце
19 века Планк исследовал проблему излучения абсолютно чёрного тела, которую за
40 лет до этого сформулировал Кирхгоф. Нагретые тела светятся тем сильнее, чем
выше их температура и больше внутренняя тепловая энергия. Теплота
распределяется между всеми атомами тела, приводя их в движение друг
относительно друга и к возбуждению электронов в атомах. При переходе электронов
к устойчивым состояниям излучаются фотоны, которые могут снова поглощаться
атомами. При каждой температуре возможно состояние равновесия между излучением
и веществом, при этом доля энергии излучения в общей энергии системы зависит от
температуры. В состоянии равновесия с излучением абсолютно чёрное тело не
только поглощает всё падающее на него излучение, но и излучает само то же самое
количество энергии, по определённому закону распределения энергии по частотам.
Закон, связывающий температуру тела с мощностью общей излучаемой энергии с
единицы поверхности тела, носит название закон Стефана-Больцмана и был
установлен в 1879–1884 гг.
При
нагревании увеличивается не только общее количество излучаемой энергии, но
меняется и состав излучения. Это видно по тому, что меняется цвет нагреваемых
тел. Согласно закону смещения Вина 1893 г., основанному на принципе
адиабатического инварианта, для каждой температуры можно вычислить длину волны
излучения, при которой тело светится наиболее сильно. Вин сделал достаточно
точную оценку формы энергетического спектра чёрного тела при высоких частотах,
но не смог объяснить ни форму спектра, ни его поведение при низких частотах.
Планк
предположил, что поведение света подобно движению набора множества одинаковых
гармонических осцилляторов. Он изучал изменение энтропии этих осцилляторов в
зависимости от температуры, пытаясь обосновать закон Вина, и нашёл подходящую
математическую функцию для спектра чёрного тела. [2]
Однако
вскоре Планк понял, что кроме его решения возможны и другие, приводящие к
другим значениям энтропии осцилляторов. В результате он был вынужден
использовать вместо феноменологического подхода отвергаемую им ранее
статистическую физику, [2] что он
описывал как “акт отчаяния … Я был готов пожертвовать любыми моими
предыдущими убеждениями в физике.”[3]
Одним из новых принятых Планком условий было:
интерпретировать
UN (энергия колебаний N осцилляторов) не как
непрерывную неограниченно делимую величину, а как дискретную величину,
состоящую из суммы ограниченных равных частей. Обозначим каждую такую часть в
виде элемента энергии через ε;[2]
С этим
новым условием Планк фактически вводил квантованность энергии осцилляторов,
говоря, что это “чисто формальное предположение … на самом деле я не думал
об этом глубоко…”,[4] однако это привело к
настоящей революции в физике. Применение нового подхода к закону смещения Вина
показало, что “элемент энергии” должен быть пропорционален частоте
осциллятора. Это было первой версией того, что сейчас называется “формула
Планка”:
![]()
Планку
удалось вычислить значение h из
экспериментальных данных по излучению чёрного тела: его результат был 6,55 • 10−34
Дж•с, с точностью 1,2 % от принятого сейчас значения.[2] Он также смог впервые определить постоянную Больцмана kB из тех же данных и своей теории.[5]
До теории
Планка предполагалось, что энергия тела может быть любой, являясь непрерывной
функцией. Это эквивалентно тому, что элемент энергии ε (разность между
дозволенными уровнями энергии) равен нулю, следовательно должна быть равна нулю
и h. Исходя из этого следует
понимать утверждения о том, что “постоянная Планка равна нулю в
классической физике” или что “классическая физика является пределом
квантовой механики при устремлении постоянной Планка к нулю”. Вследствие
малости постоянной Планка она почти не проявляется в обычном человеческом опыте
и до работ Планка была незаметна.
Проблема
чёрного тела была пересмотрена в 1905 г., когда Рэлей и Джинс с одной стороны,
и Эйнштейн с другой стороны, независимо доказали, что классическая
электродинамика не может обосновать наблюдаемый спектр излучения. Это привело к
так называемой “ультрафиолетовой катастрофе”, обозначенной таким
образом Эренфестом в 1911 г. Усилия теоретиков (вместе с работой Эйнштейна по
фотоэффекту) привели к признанию того, что постулат Планка о квантовании
уровней энергии является не простым математическим формализмом, а важным элементом
представлений о физической реальности. Первый Сольвеевский конгресс в 1911 г.
был посвящён “теории радиации и квантов”.[6]
Макс Планк в 1918 г. получил Нобелевскую премию по физике “за признание
заслуг в развитии физики и открытие кванта энергии”.
Фотоэффект
![]() Основная статья: Фотоэффект
Основная статья: Фотоэффект
Фотоэффект
заключается в эмиссии электронов (называемых фотоэлектронами) с поверхности при
освещении её светом. Впервые он наблюдался Беккерелем в 1839 г., хотя обычно
упоминается Генрих Герц, [7] который
опубликовал в 1887 г. обширное исследование на эту тему. Столетов в 1888–1890
гг. сделал несколько открытий в области фотоэффекта, в том числе вывел первый
закон внешнего фотоэффекта. Другое важное исследование фотоэффекта опубликовал
Ленард в 1902 г. [8] Хотя Эйнштейн не
проводил сам экспериментов по фотоэффекту, но его работа 1905 г. [9] рассматривала эффект на основе световых квантов. Это
принесло Эйнштейну нобелевскую премию в 1921 г.[7],
когда его предсказания были подтверждены экспериментальной работой Милликена. [10] В это время теория фотоэффекта Эйнштейна
рассматривалась как более значительная, чем его теория относительности.
До работы
Эйнштейна каждое электромагнитное излучение рассматривалось в виде набора волн,
обладающих своей “частотой” и “длиной волны”. Энергия,
переносимая волной за единицу времени, называется интенсивностью. Аналогичные
параметры имеют и другие виды волн, например звуковая волна или волна на воде.
Однако перенос энергии, связанной с фотоэффектом, не согласуется с волновой
картиной света.
Кинетическая
энергия фотоэлектронов, появляющихся в фотоэффекте, может быть измерена.
Оказывается, что она не зависит от интенсивности света, [8] но зависит линейно от частоты.[10] При этом увеличение интенсивности света
приводит не к увеличению кинетической энергии фотоэлектронов, а к увеличению их
количества.[8] Если же частота слишком мала
и кинетическая энергия фотоэлектронов порядка нуля, то фотоэффект исчезает,
несмотря на значительную интенсивность света.[10]
Согласно
объяснению Эйнштейна, в данных наблюдениях проявляется квантовая природа света;
энергия света переносится малыми “пакетами” или квантами, а не в виде
непрерывной волны. Величина этих “пакетов” энергии, которые позже
назвали фотонами, была той же самой, что и у “элементов энергии”
Планка. Это привело к современному виду формулы Планка для энергии фотона:
![]()
Постулат
Эйнштейна был доказан экспериментально: постоянная пропорциональности между
частотой света ν и энергией
фотона E оказалась равной
постоянной Планка h.[10]
Структура
атома
![]() Основная статья: Постулаты Бора
Основная статья: Постулаты Бора

![]()
Схематическая модель Бора атома водорода. Показан переход электрона с
уровня n=3 на уровень n=2, приводящий к возникновению кванта
видимого света с длиной волны 656 нм (красный), в соответствии с
предсказаниями модели
Нильс Бор
представил первую квантовую модель атома в 1913 г., пытаясь избавиться от затруднений
классической модели атома Резерфорда. [11]
Согласно классической электродинамике, точечный заряд при вращении вокруг
неподвижного центра должен излучать электромагнитную энергию. Если такая
картина справедлива для электрона в атоме при его вращении вокруг ядра, то с
течением времени электрон потеряет энергию и упадёт на ядро. Для преодоления
этого парадокса Бор предложил считать, аналогично тому, как это имеет место у
фотонов, что электрон в водородоподобном атоме должен иметь квантованные
энергии En:
![]()
где R∞ есть экспериментально
определённая константа ( постоянная Ридберга в единицах обратной длины), с – скорость света, n – целое число (n = 1, 2, 3, …), Z – порядковый номер химического элемента
в таблице Менделеева, равный единице для атома водорода. Электрон, попавший на
нижний энергетический уровень (n =
1), находится в основном состоянии атома и уже не может, в силу пока не
определённых в квантовой механике причин, уменьшить свою энергию. Такой подход
позволил Бору прийти к формуле Ридберга, эмпирически описывающей спектр
излучения атома водорода, и вычислить значение постоянной Ридберга R∞ через другие фундаментальные
константы.
Бор также
ввёл величину h/2π, известную как редуцированная постоянная
Планка или постоянная Дирака ħ, как квант
момента импульса. Бор предполагал, что ħ определяет модуль момента импульса
каждого электрона в атоме. Но это оказалось неточным, несмотря на улучшения
теории Бора Зоммерфельдом и другими. Более корректной оказалась квантовая
теория, в виде матричной механики Гейзенберга в 1925 г. и в виде уравнения
Шрёдингера в 1926 г. При этом постоянная Дирака осталась фундаментальным
квантом момента импульса. Если J
есть общий момент импульса системы с инвариантностью вращения, и Jz есть момент импульса,
измеряемый вдоль выделенного направления, то эти величины могут иметь только
следующие значения: 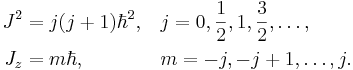
Принцип
неопределённости
Постоянная
Планка содержится также в выражении для принципа неопределённости Вернера
Гейзенберга. Если брать большое количество частиц в одном и том же состоянии,
то неопределённость в их положении Δx
, и неопределённость в их импульсе (в том же самом направлении), Δp, подчиняются соотношению:
![]()
где
неопределённость задаётся как среднеквадратическое отклонение измеряемой
величины от её математического ожидания. Существуют и другие подобные пары
физических величин, для которых справедливо соотношение неопределённостей.
В
квантовой механике постоянная Планка входит в выражение для коммутатора между
оператором положения ![]() и оператором импульса
и оператором импульса ![]() :
:
![]()
где δij
есть символ Кронекера.
Спектр
тормозного рентгеновского излучения
При
взаимодействии электронов с электростатическим полем атомных ядер возникает
тормозное излучение в виде рентгеновских квантов. Известно, что частотный
спектр тормозного рентгеновского излучения имеет точную верхнюю границу,
называемую фиолетовой границей. Её существование вытекает из квантовых свойств
электромагнитного излучения и закона сохранения энергии. Действительно,
![]()
где ![]() – скорость
– скорость
света,
![]() –
–
длина волны рентгеновского излучения,
![]() – заряд
– заряд
электрона,
![]() –
–
ускоряющее напряжение между электродами рентгеновской трубки.
Тогда
постоянная Планка будет равна:
![]()
Физические
константы, связанные с постоянной Планка
Список
констант, указанных ниже, основан на данных 2014 CODATA. [12]. Приблизительно 90 % неточности в этих
константах связаны с неточностью определения постоянной Планка, как это видно
из квадрата коэффициента корреляции Пирсона (r2 >
0,99, r > 0,995). Если
сравнивать с другими константами, постоянная Планка известна с точностью
порядка ![]() при неопределённости измерения 1σ. Эта
при неопределённости измерения 1σ. Эта
точность значительно лучше, чем у гравитационной
постоянной или у универсальной газовой постоянной.
Масса покоя
электрона
Как
правило, постоянная Ридберга R∞
(в единицах обратной длины) определяется через массу электрона
me и другие физические константы:
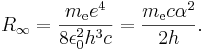
Постоянная
Ридберга может быть определена очень точно (![]() )
)
из спектра атома водорода, тогда как для массы электрона нет прямого способа
измерения. Поэтому для определения массы электрона используется формула:
![]()
где c есть скорость света и α есть постоянная
тонкой структуры. Скорость света достаточно точно определяется в системе
единиц СИ, как и постоянная тонкой структуры (![]() ).
).
Поэтому неточность определения массы электрона зависит только от неточности
постоянной Планка (r2 >
0,999).
Постоянная Авогадро
![]() Основная статья: Число Авогадро
Основная статья: Число Авогадро
Число
Авогадро NA
определяется как отношение массы одного моля электронов к массе одного
электрона. Для её нахождения нужно взять массу одного моля электронов в виде
“относительной атомной массы” электрона Ar(e), измеряемой в ловушке Пеннинга (![]() ),
),
умноженной на единицу молярной массы Mu,
которая в свою очередь определяется как 0,001 кг/моль. В результате
получается:
![]()
Зависимость
числа Авогадро от постоянной Планка (r2 >
0,999) повторяется и для других постоянных, связанных с количеством вещества,
например, для атомной единицы массы. Неопределённость в значении постоянной
Планка ограничивает значения атомных масс и частиц в единицах системы СИ, то
есть в килограммах. В то же время отношения масс частиц известны с лучшей
точностью.
Элементарный
заряд
Зоммерфельд
первоначально определял постоянную тонкой структуры α так:
![]()
где e есть элементарный электрический заряд, ε0 – электрическая постоянная (называемая также
диэлектрической проницаемостью вакуума), μ0
– магнитная постоянная или магнитная проницаемость вакуума. Последние две
постоянные имеют фиксированные значения в системе единиц СИ. Значение α может быть определено экспериментально
путём измерения g-фактора электрона ge
и последующего сравнения со значением, вытекающим из квантовой электродинамики.
В
настоящее время наиболее точное значение элементарного электрического заряда
получается из приведённой выше формулы:
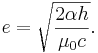
Магнетон
Бора и ядерный магнетон
![]() Основные статьи: Магнетон Бора , Ядерный магнетон
Основные статьи: Магнетон Бора , Ядерный магнетон
Магнетон
Бора и ядерный магнетон являются единицами, используемыми для описания
магнитных свойств электрона и атомных ядер соответственно. Магнетон Бора есть
магнитный момент, который ожидается у электрона, если бы он вёл себя как
вращающаяся заряженная частица согласно классической электродинамике. Его
значение выводится через постоянную Дирака, элементарный электрический заряд и
массу электрона. Все эти величины выводятся через постоянную Планка,
результирующая зависимость от h½
(r2 > 0,995)
может быть найдена с учётом формулы:
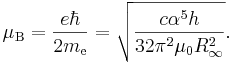
Ядерный магнетон
имеет похожее определение, с той разницей, что протон значительно массивнее
электрона. Отношение электронной относительной атомной массы к протонной
относительной атомной массе может быть определено с большой точностью (![]() ).
).
Для связи между обоими магнетонами можно записать:
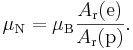
Определение
из экспериментов
|
Метод |
Значение |
Точность |
Ссылка |
|
Баланс мощности |
6,626 068 89(23) |
3,4∙10–8 |
[13] [14][15] |
|
Рентгеновская |
6,626 074 5(19) |
2,9∙10–7 |
[16] |
|
Постоянная |
6,626 067 8(27) |
4,1∙10–7 |
[17] [18] |
|
Магнитный |
6,626 072 4(57) |
8,6∙10–7 |
[19] [20] |
|
Постоянная |
6,626 065 7(88) |
1,3∙10–6 |
[21] |
|
CODATA |
6,626 |
4,4∙10–8 |
[22] |
|
Для пяти |
Постоянная
Планка может быть определена из спектра излучающего чёрного тела или
кинетической энергии фотоэлектронов, как это было сделано в начале двадцатого
века. Однако данные методы не самые точные. Значение h согласно CODATA основано на базе трёх измерений методом
баланса мощностей произведения величин KJ2RK и одного межлабораторного
измерения молярного объёма кремния,[22] в
основном методом баланса мощностей до 2007 г. в США в National Institute of
Standards and Technology (NIST).[15] Другие
измерения, указанные в таблице, не повлияли на результат из-за недостаточной
точности.
Имеются
как практические, так и теоретические трудности при определении h. Так, наиболее точные методы баланса
мощности и рентгеновской плотности кристалла не полностью согласуются друг с
другом по своим результатам. Это может быть следствием переоценки точности в
этих методах. Теоретические трудности вытекают из того, что все методы, кроме рентгеновской
плотности кристалла, основаны на теоретической базе эффекта Джозефсона и
квантового эффекта Холла. При некоторой возможной неточности этих теорий
возникнет и неточность в определении постоянной Планка. При этом полученное
значение постоянной Планка уже не может использоваться как тест для проверки
этих теорий во избежание замкнутого логического круга. Положительным моментом
является то, что имеются независимые статистические способы проверки этих
теорий.[22]
Постоянная Джозефсона
![]() Основная статья: Эффект Джозефсона
Основная статья: Эффект Джозефсона
Постоянная
Джозефсона KJ
связывает разность потенциалов U,
возникающую в эффекте Джозефсона в “контактах Джозефсона”, с частотой
ν микроволнового излучения. Из
теории достаточно строго следует выражение:
![]()
Постоянная
Джозефсона может быть измерена путём сравнения с разностью потенциалов,
возникающей в батарее контактов Джозефсона. Для измерения разности потенциалов
используется компенсация электростатической силы силой гравитации. Из теории
следует, после замены электрического заряда e
на его значение через фундаментальные постоянные (см. выше Элементарный заряд), выражение для
постоянной Планка через KJ:
![]()
Баланс
мощности
В данном
методе осуществляется сравнение двух видов мощности, одна из которых измеряется
в системе единиц СИ в ваттах, а другая измеряется в условных
электрических единицах. Из определения условного
ватта W90, он даёт
меру для произведения KJ2RK в единицах СИ, где RK есть постоянная Клитцинга,
появляющаяся в квантовом эффекте Холла. Если теоретическая трактовка эффекта
Джозефсона и квантового эффекта Холла верна, тогда RK = h/e2, и измерение KJ2RK приводит к определению
постоянной Планка:
![]()
Магнитный
резонанс
![]() Основная статья: Гиромагнитное отношение
Основная статья: Гиромагнитное отношение
Гиромагнитное
отношение γ является
коэффициентом пропорциональности между частотой ν ядерного магнитного резонанса (или электронного
парамагнитного резонанса для электронов), и приложенным магнитным полем B: ν =
γB. Хотя имеется трудность в
определении гиромагнитного отношения из-за неточности измерения B, для протонов в воде при 25 °C она
известна с лучшей точностью, чем 10–6. Протоны частично
“экранируются” от приложенного магнитного поля электронами молекул
воды. Такой же эффект приводит к химическому сдвигу в ядерно-магнитной спектроскопии, и
обозначается штрихом у символа гиромагнитного отношения, γ′p. Гиромагнитное отношение
связано с магнитным моментом экранированного протона μ′p, спиновым квантовым числом S (S=1/2
для протонов) и постоянной Дирака:
![]()
Отношение
магнитного момента экранированного протона μ′p
к магнитному моменту электрона μe
может быть измерено независимо с высокой точностью, поскольку неточность
магнитного поля на результате сказывается мало. Значение μe, выраженное в магнетонах
Бора, равно половине электронного g-фактора ge.
Следовательно,
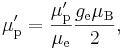
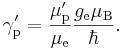
Дальнейшее
усложнение связано с тем, что для измерения γ′p
необходимо измерение электрического тока. Этот ток независимо измеряется в условных амперах, поэтому для перевода в
амперы системы СИ требуется коэффициент пересчёта. Символом Γ′p-90 обозначается измеряемое
гиромагнитное отношение в условных электрических единицах (разрешённое
использование данных единиц началось с начала 1990 г.). Эта величина может
измеряться двумя способами, методом “слабого поля” и методом
“сильного поля”, и коэффициент пересчёта в этих случаях получается
различным. Обычно для измерения постоянной Планка используется метод сильного
поля и значение Γ′p-90(hi):
![]()
После
замены получается выражение для постоянной Планка через Γ′p-90(hi):
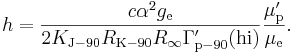
Постоянная Фарадея
![]() Основная статья: Постоянная Фарадея
Основная статья: Постоянная Фарадея
Постоянная
Фарадея F есть заряд одного моля
электронов, равный числу Авогадро NA,
умноженному на элементарный электрический заряд e. Она может быть определена при тщательных экспериментах по
электролизу, путём измерения количества серебра, перемещённого с одного
электрода на другой за данное время при заданном электрическом токе. На
практике она измеряется в условных электрических единицах, и обозначается F90. Подставляя значения NA и e, и переходя от условных электрических единиц к единицам
СИ, получают соотношение для постоянной Планка:
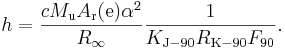
Рентгеновская
плотность кристалла
Метод рентгеновской
плотности кристалла является основным методом измерения постоянной Авогадро NA, а через неё и постоянной
Планка h. Для нахождения NA берётся отношение между
объёмом элементарной ячейки кристалла, измеряемой методом рентгеноструктурного
анализа, и молярным объёмом вещества. Используются кристаллы кремния, поскольку
они доступны с высоким качеством и чистотой благодаря технологии, развитой при
производстве полупроводников. Объём элементарной ячейки вычисляется из
пространства между двумя кристаллическими плоскостями, обозначаемыми d220. Молярный объём Vm(Si) вычисляется через
плотность кристалла и атомный вес используемого кремния. Постоянная Планка
даётся выражением:

Постоянная Планка в системе единиц СИ
![]() Основная статья: Килограмм
Основная статья: Килограмм
Как было
указано выше, численное значение постоянной Планка зависит от используемой
системы единиц. Её значение в системе единиц СИ известно с точностью 1,2∙10–8,
хотя в атомных (квантовых) единицах она определяется точно (в атомных единицах путём выбора единиц энергии и
времени можно добиться того, чтобы постоянная Дирака как редуцированная
постоянная Планка равнялась 1). Такая же ситуация имеет место в условных
электрических единицах, где постоянная Планка (записывается h90 в отличие от обозначения в
СИ) даётся выражением:
![]()
где KJ–90 и RK–90 являются точно
определёнными постоянными. Атомные единицы и условные электрические единицы
удобно использовать в соответствующих областях, так как неопределенности в окончательном
результате зависят только от неопределённостей измерений, не требуя
дополнительного и вносящего неточность коэффициента пересчёта в систему СИ.
Существует
ряд предложений по модернизации значений существующей системы базовых единиц СИ
с помощью фундаментальных физических констант.[23]
Это уже было сделано для метра, который определяется через заданное значение
скорости света. Возможной следующей единицей для пересмотра является килограмм,
чьё значение фиксируется с 1889 г. массой малого цилиндра из платиноиридиевого
сплава, хранящегося под тремя стеклянными колпаками. Имеется порядка 80 копий
таких стандартов массы, которые периодически сравниваются с международной
единицей массы. Точность вторичных эталонов изменяется со временем за счёт их использования,
вплоть до значений в десятки микрограммов. Это приблизительно соответствует
неточности в определении постоянной Планка.
На 24-й
Генеральной конференции по мерам и весам 17—21 октября 2011 года была
единогласно принята резолюция, [24] в
которой, в частности, предложено в будущей ревизии Международной системы единиц
(СИ) переопределить единицы измерений СИ таким образом, чтобы постоянная Планка
была равной точно 6,62606X• 10−34 Дж•с, где Х заменяет одну или
более значащих цифр, которые будут определены в дальнейшем на основании
наиболее точных рекомендаций CODATA. [25]. В этой
же резолюции предложено таким же образом определить как точные значения
постоянную Авогадро, элементарный заряд и постоянную Больцмана.
Постоянная
Планка в теории бесконечной вложенности материи
В отличие от атомизма, в теории бесконечной вложенности
материи отсутствуют материальные объекты – частицы с минимальной
массой или размерами. Вместо этого предполагается бесконечная делимость материи
на всё более уменьшающиеся структуры, и одновременно существование множества
объектов, по размерам значительно превышающих нашу Метагалактику. При этом
материя организуется в отдельные уровни по массам и размерам, для которых
возникает подобие уровней материи,
проявляется масштабное измерение и
осуществляется квантованность параметров
космических систем.
Так же
как постоянная Больцмана и ряд других констант, постоянная Планка отражает
свойства, присущие уровню элементарных частиц (в первую очередь нуклонам и электронам, составляющим вещество). С одной
стороны, постоянная Планка связывает энергию фотонов и их частоту; с другой
стороны, она с точностью до небольшого численного коэффициента 2π, в виде постоянной Дирака ħ задаёт единицу орбитального
момента электрона в атоме. Такая связь не случайна, поскольку при излучении из
атома электрон уменьшает свой орбитальный момент импульса, передавая его фотону
за период существования возбуждённого состояния. За один период обращения электронного
облака вокруг ядра фотон получает такую долю энергии, которая соответствует
доле переданного электроном момента импульса. Средняя частота фотона близка к
частоте вращения электрона вблизи уровня энергии, куда электрон переходит при
излучении, поскольку мощность излучения электрона быстро нарастает при
приближении к ядру.
Математически
это можно описать так. Уравнение вращательного движения имеет вид:
![]()
где K – момент
силы, L
– момент импульса. Если умножить это соотношение на приращение угла вращения ![]() и
и
учесть, что ![]() есть изменение энергии вращения электрона, а
есть изменение энергии вращения электрона, а ![]() есть угловая частота орбитального
есть угловая частота орбитального
вращения, то будет:
![]()
В этом
соотношении энергию dE
можно трактовать как приращение энергии излучаемого фотона при приращении им
момента импульса на величину dL. Для полной энергии фотона E и полного момента импульса фотона
![]() величину ω следует понимать как
величину ω следует понимать как
усреднённую угловую частоту фотона. [26] [27]
В
дополнение к корреляции свойств излучаемых фотонов и атомных электронов через
момент импульса, атомные ядра также обладают моментами импульса, выражаемыми в
единицах ħ. Можно поэтому предположить, что постоянная Планка описывает
вращательное движение элементарных частиц (спин
нуклонов, ядер и электронов, орбитальное движение электронов в атоме), и
преобразование энергии вращения и колебаний заряженных частиц в энергию
излучения. Кроме этого, основываясь на идее корпускулярно-волнового дуализма, в
квантовой механике всем частицам приписывается сопутствующая им материальная
волна де Бройля. Эта волна рассматривается в виде волны амплитуды вероятности
нахождения частицы в той или иной точке пространства. Как и для фотонов,
постоянные Планка и Дирака в таком случае становятся коэффициентами
пропорциональности для квантовой частицы, входя в выражения для импульса
частицы ![]() , для энергии E и для действия S:
, для энергии E и для действия S:
![]()
![]()
![]()
![]()
где ![]() –
–
волновой вектор, λ и ν –
длина и частота соответствующей волны, ω – угловая
частота волны, φ – фаза волны.
Если
теперь перейти к другим уровням материи, то для них также можно определить
характерные моменты импульса и соответствующие постоянные. Используя
коэффициенты подобия между уровнями материи и SPФ-симметрию,
для уровня вырожденных звёздных объектов типа нейтронных звёзд было найдено,
что h’s = h’s
= h ∙ Ф’ ∙ S’ ∙ Р’ = 3,5∙1042 Дж∙с (здесь Ф’ ∙ S’ ∙ Р’
– коэффициенты подобия по массе, скоростям
процессов и размерам соответственно). [28] [29]
Величина h’s называется звёздная постоянная
Планка. С помощью коэффициентов подобия могут быть определены
аналогичные постоянные для каждого уровня материи, как характерные моменты
импульса и действия типичных объектов на этих уровнях.
См. также
- Спин
- Введение в квантовую
механику - Планковские единицы
- Квант
- Корпускулярно-волновой
дуализм - Принцип неопределённости Гейзенберга
- Бесконечная вложенность материи
- Подобие уровней материи
- SPФ-симметрия
- Квантованность параметров космических
систем - Звёздные постоянные
- Звёздная постоянная Планка
- Звёздная постоянная Дирака
- Дискретность параметров звёзд
- Водородная система
- Длина
волны де Бройля
Ссылки
- Fundamental Physical Constants
— Complete Listing. - а б в г Planck, Max (1901), “Ueber das Gesetz der
Energieverteilung im Normalspectrum”, Ann. Phys. Vol. 309 (3), P. 553–63,
doi:10.1002/andp.19013090310, English translation: “On the Law of
Distribution of Energy in the Normal Spectrum”. - Kragh, Helge (1 December 2000), Max Planck: the reluctant revolutionary, PhysicsWorld.com.
- Kragh, Helge (1999), Quantum Generations: A History
of Physics in the Twentieth Century, Princeton University Press, p. 62, ISBN
0691095523. - Planck, Max (2 June 1920), The Genesis and Present State
of Development of the Quantum Theory (Nobel Lecture). - Previous Solvay Conferences on
Physics, International Solvay Institutes, 12 декабря 2008 г. - а б Arrhenius, Svante (10 December 1922), Presentation speech of the 1921
Noble Prize for Physics. - а б в Lenard, P. (1902), “Ueber die
lichtelektrische Wirkung”, Ann. Phys. Vol. 313 (5), P. 149–98,
doi:10.1002/andp.19023130510 - Einstein, Albert (1905), “Über einen die Erzeugung
und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt”, Ann. Phys. Vol. 17, P.
132–48, doi:10.1002/andp.19053220607. - а б в г Millikan, R. A. (1916), “A Direct
Photoelectric Determination of Planck’s h”, Phys. Rev. 7: 355–88,
doi:10.1103/PhysRev.7.355. - Bohr, Niels (1913), “On the Constitution of
Atoms and Molecules” Phil. Mag., Ser. 6, Vol. 26, P. 1–25. - Mohr, Peter J.; Newell,
David B.; Taylor, Barry N. (2015). “CODATA recommended values of the
fundamental physical constants: 2014”. Zenodo. arXiv: 1507.07956. doi: 10.5281/zenodo.22826. - Kibble, B. P.; Robinson, I. A.; Belliss, J. H.
(1990), “A Realization of the SI Watt by the NPL Moving-coil
Balance”, Metrologia, Vol. 27 (4), p.173–92,
doi:10.1088/0026-1394/27/4/002. - Steiner, R.; Newell, D.; Williams, E. (2005), “Details of the 1998 Watt
Balance Experiment Determining the Planck Constant”, J. Res. Natl. Inst. Stand.
Technol. Vol. 110 (1), P. 1–26. - а б Steiner, R. L.; Williams, E. R.; Liu, R.;
Newell, D. B. (2007), “Uncertainty Improvements of the NIST
Electronic Kilogram”, IEEE Trans. Instrum. Meas. Vol. 56 (2), P.
592–96, doi:10.1109/TIM.2007.890590. - Fujii, K.; Waseda, A.; Kuramoto, N.; Mizushima,
S.; Becker, P.; Bettin, H.; Nicolaus, A.; Kuetgens, U.; Valkiers, S.; Taylor,
P.; De Bievre, Paul; Mana, G.; Massa, E.; Matyi, R.; Kessler, E.G., Jr.;
Hanke, M. (2005), “Present state of the avogadro constant
determination from silicon crystals with natural isotopic
compositions”, IEEE Trans. Instrum. Meas. Vol. 54 (2), P. 854–59,
doi:10.1109/TIM.2004.843101. - Sienknecht, Volkmar; Funck, Torsten (1985),
“Determination of the SI Volt at the PTB”, IEEE Trans. Instrum.
Meas. Vol. 34 (2), P. 195–98, doi:10.1109/TIM.1985.4315300. Sienknecht,
V.; Funck, T. (1986), “Realization of the SI Unit Volt by Means of a
Voltage Balance”, Metrologia Vol. 22 (3), P. 209–12,
doi:10.1088/0026-1394/22/3/018. Funck, T. (1991), “Determination of
the volt with the improved PTB voltage balance”, IEEE Trans. Instrum.
Meas. Vol. 40 (2), P. 158–61, doi:10.1109/TIM.1990.1032905. - Clothier, W. K.; Sloggett, G. J.; Bairnsfather,
H.; Currey, M. F.; Benjamin, D. J. (1989), “A Determination of the
Volt”, Metrologia, Vol. 26 (1), P. 9–46,
doi:10.1088/0026-1394/26/1/003. - Kibble, B. P.; Hunt, G. J. (1979), “A
Measurement of the Gyromagnetic Ratio of the Proton in a Strong Magnetic
Field”, Metrologia, Vol. 15 (1), P. 5–30,
doi:10.1088/0026-1394/15/1/002. - Liu, R.; Liu, H.; Jin, T.; Lu, Z.; Du, X.; Xue,
S.; Kong, J.; Yu, B.; Zhou, X.; Liu, T.; Zhang, W. (1995), “A Recent
Determination for the SI Values of γ′p and 2e/h at NIM”, Acta Metrol.
Sin. Vol. 16 (3), P. 161–68. - Bower, V. E.; Davis, R. S. (1980), “The
Electrochemical Equivalent of Pure Silver: A Value of the Faraday
Constant”, J. Res. Natl. Bur. Stand. Vol. 85 (3), P. 175–91. - а б в P.J. Mohr, B.N. Taylor, and D.B. Newell (2011), “The 2010
CODATA Recommended Values of the Fundamental Physical Constants” (Web
Version 6.0). This database was developed by J. Baker, M. Douma, and S.
Kotochigova. Available: http://physics.nist.gov
[Thursday, 02-Jun-2011 21:00:12 EDT]. National Institute of Standards and
Technology, Gaithersburg, MD 20899. - 94th Meeting of the International Committee for
Weights and Measures (2005). Recommendation 1: Preparative steps
towards new definitions of the kilogram, the ampere, the kelvin and the
mole in terms of fundamental constants. - On the possible future revision
of the International System of Units, the SI. Resolution
1 of the 24th meeting of the CGPM (2011). - Agreement to tie kilogram and
friends to fundamentals — physics-math — 25 October 2011 — New Scientist. - Федосин С.Г. Физические
теории и бесконечная вложенность материи, Пермь, 2009, 844 стр., Табл.
21, Ил.41, Библ. 289 назв. ISBN 978-5-9901951-1-0 . - Fedosin S.G. The
substantial model of the photon. Journal of Fundamental and Applied
Sciences, Vol. 9, No. 1, pp. 411-467 (2017). http://dx.doi.org/10.4314/jfas.v9i1.25.
// Субстанциональная модель фотона. - Федосин С. Г. Физика
и философия подобия от преонов до метагалактик, Пермь: Стиль-МГ, 1999, 544
стр., Табл.66, Ил.93, Библ. 377 назв. ISBN 5-8131-0012-1. - Комментарии
к книге: Федосин С.Г. Физические теории и бесконечная вложенность
материи. Пермь, 2009, 844 стр., Табл. 21, Ил.41, Библ. 289 назв. ISBN
978-5-9901951-1-0.
Литература
- Barrow, John D. (2002). The Constants of Nature; From
Alpha to Omega – The Numbers that Encode the Deepest Secrets of the
Universe. Pantheon Books. ISBN 0-375-42221-8.
Внешние
ссылки
- История уточнения
постоянной Планка - The NIST Reference on Constants, Units and
Uncertainty - Quantum of Action and Quantum of Spin –
Numericana























![[{hat {p}}_{i},{hat {x}}_{j}]=-ihbar delta _{ij},](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6de152aa445b7ca6653b9dd087ad604c2b8bf0e)
































