Как найти постоянную ридберга для водорода - Сайт, где вы сможете решить свои вопросы

Постоя́нная Ри́дберга — фундаментальная физическая постоянная, используемая в формулах для расчёта уровней энергии и частот излучения атомов. Введена шведским учёным Йоханнесом Робертом Ридбергом в 1890 году при изучении спектров излучения атомов. Обозначается как ^[1]. Для тяжёлых ядер используется обозначение ${displaystyle R_{infty }}$ , для водорода — ${displaystyle R_{text{H}}}$ .

Данная константа изначально появилась как эмпирический подгоночный параметр в формуле Ридберга, описывающей спектральные серии водорода. Позже Нильс Бор показал, что её значение можно вычислить из более фундаментальных постоянных, объяснив их связь с помощью своей модели атома (модель Бора). Постоянная Ридберга является предельным значением наивысшего волнового числа любого фотона, который может быть испущен атомом водорода; с другой стороны, это волновое число фотона с наименьшей энергией, способного ионизировать атом водорода в его основном состоянии.

Также используется тесно связанная с постоянной Ридберга внесистемная единица измерения энергии, называемая просто ридберг и обозначаемая Ry. Она соответствует энергии фотона, волновое число которого равно постоянной Ридберга, то есть энергии ионизации атома водорода (в приближении бесконечно тяжёлого ядра).

По состоянию на 2012 год, постоянная Ридберга и g-фактор электрона являются наиболее точно измеренными фундаментальными физическими постоянными^[2].

Численное значение[править | править код]

Численное значение константы Ридберга, рекомендованное CODATA в 2020 году, составляет^[3]:

${displaystyle R_{infty }}$

= 10 973 731,568 160(21) м⁻¹.

Для лёгких атомов постоянная Ридберга имеет следующие значения:

Водород: R_H ≈ 10 967 758,341 м⁻¹;
Дейтерий: R_D ≈ 10 970 741,7 м⁻¹;
Гелий: R_He ≈ 10 972 226,7 м⁻¹.

Как видно, с увеличением массы ядра значение постоянной Ридберга стремится к ${displaystyle R_{infty }}$ , которая является пределом для водородоподобного атома с бесконечно тяжёлым ядром.

В атомной физике константа часто применяется в виде энергетической единицы (ридберг):

$mathrm {Ry} =Rcdot hcdot c=2pi hbar cR=me^{4}/2hbar ^{2}=e^{2}/2a_{0}$

, где $a_{0}$

— боровский радиус.

Численное значение^[4]^[5]:

Ry = 13,605 693 122 994(26) эВ = 2,179 872 361 1035(42)⋅10⁻¹⁸ Дж.

Свойства[править | править код]

Постоянная Ридберга входит в общий закон для спектральных частот следующим образом:

$nu =R{Z^{2}}left({frac {1}{n^{2}}}-{frac {1}{m^{2}}}right)$

где — волновое число (по определению, это обратная длина волны или число длин волн, укладывающихся на 1 см), Z — порядковый номер атома.

$nu ={frac {1}{lambda }}$

см⁻¹

Соответственно, выполняется

${frac {1}{lambda }}=R{Z^{2}}left({frac {1}{n^{2}}}-{frac {1}{m^{2}}}right)$

Если считать массу ядра атома бесконечно большой по сравнению с массой электрона (то есть считать, что ядро неподвижно), то постоянная Ридберга для частоты в Гц будет определяться как

$R={frac {me^{4}}{4pi chbar ^{3}}}$

в системе СГС, где и — масса и заряд электрона, — скорость света, а hbar — постоянная Дирака или приведённая постоянная Планка.

В Международной системе единиц (СИ) для частоты в Гц:

$R_{c}={frac {mk^{2}e^{4}}{4pi hbar ^{3}}}$

$R_{c}={frac {2mpi ^{2}k^{2}e^{4}}{h^{3}}}$

где $k=c^{2}times 10^{-7}$ — коэффициент из закона Кулона. Численное значение^[6]:

$R_{c}$

= 3,289 841 960 2508(64)⋅10¹⁵ Гц.

Обычно, когда говорят о постоянной Ридберга, имеют в виду постоянную, вычисленную при неподвижном ядре. При учёте движения ядра масса электрона заменяется приведённой массой электрона и ядра и тогда

${displaystyle R_{i}={frac {R_{infty }}{1+m/M_{i}}}}$

, где $M_{i}$

— масса ядра атома.

Для обычных атомов приведённая масса, выражающаяся как M_im / (M_i + m), близка к массе электрона, поскольку ${displaystyle M_{i}gg m}$ , а значит и ${displaystyle R_{i}approx R_{infty }.}$ Однако для атома позитрония, состоящего из электрона и позитрона — частиц с одинаковой массой, приведённая масса равна m / 2, и, следовательно, ${displaystyle R_{i}=R_{infty }/2.}$

См. также[править | править код]

Формула Ридберга

Примечания[править | править код]

↑ Ридберга постоянная // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. — С. 391. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
↑ Pohl R. et al. The size of the proton (англ.) // Nature. — 2010. — Vol. 466, no. 7303. — P. 213—216. — doi:10.1038/nature09250. — Bibcode: 2010Natur.466..213P. — PMID 20613837.
↑ Rydberg constant Архивная копия от 6 мая 2021 на Wayback Machine // 2020 CODATA recommended values
↑ Rydberg constant times hc in eV Архивная копия от 15 апреля 2021 на Wayback Machine // 2020 CODATA recommended values
↑ Rydberg constant times hc in J Архивная копия от 27 декабря 2011 на Wayback Machine // 2020 CODATA recommended values
↑ Rydberg constant times c in Hz Архивная копия от 25 декабря 2017 на Wayback Machine // 2020 CODATA recommended values

Литература[править | править код]

Шпольский Э. В. Атомная физика. Том 1. — М.: Наука, 1974.
Борн М. Атомная физика. — М.: Мир, 1970.
Савельев И. В. Курс общей физики. Книга 5. Квантовая оптика. Атомная физика. Физика твердого тела. Физика атомного ядра и элементарных частиц. — М.: АСТ, Астрель, 2003.

Источник

From Wikipedia, the free encyclopedia

In spectroscopy, the Rydberg constant, symbol ${displaystyle R_{infty }}$ for
heavy atoms or $R_{text{H}}$ for hydrogen, named after the Swedish physicist Johannes Rydberg, is a physical constant relating to the electromagnetic spectra of an atom. The constant first arose as an empirical fitting parameter in the Rydberg formula for the hydrogen spectral series, but Niels Bohr later showed that its value could be calculated from more fundamental constants according to his model of the atom.

Before the 2019 redefinition of the SI base units, ${displaystyle R_{infty }}$ and the electron spin g-factor were the most accurately measured physical constants.^[1]

The constant is expressed for either hydrogen as $R_{text{H}}$ , or at the limit of infinite nuclear mass as ${displaystyle R_{infty }}$ . In either case, the constant is used to express the limiting value of the highest wavenumber (inverse wavelength) of any photon that can be emitted from a hydrogen atom, or, alternatively, the wavenumber of the lowest-energy photon capable of ionizing a hydrogen atom from its ground state. The hydrogen spectral series can be expressed simply in terms of the Rydberg constant for hydrogen $R_{text{H}}$ and the Rydberg formula.

In atomic physics, Rydberg unit of energy, symbol Ry, corresponds to the energy of the photon whose wavenumber is the Rydberg constant, i.e. the ionization energy of the hydrogen atom in a simplified Bohr model.^{[citation needed]}

Value[edit]

Rydberg constant[edit]

The CODATA value is^[2]

${displaystyle R_{infty }={frac {m_{text{e}}e^{4}}{8varepsilon _{0}^{2}h^{3}c}}}$

or,

${displaystyle R_{infty }=109737,{text{cm}}^{-1}}$

where

The Rydberg constant for hydrogen may be calculated from the reduced mass of the electron:

${displaystyle R_{text{H}}=R_{infty }{frac {m_{text{p}}}{m_{text{e}}+m_{text{p}}}}approx 1.09678times 10^{7}{text{ m}}^{-1},}$

where

$m_{text{e}}$ is the mass of the electron,
$m_text{p}$ is the mass of the nucleus (a proton).

Rydberg unit of energy[edit]

The Rydberg unit of energy is equivalent to joules^[3] and electronvolts^[4] in the following manner:

${displaystyle 1 {text{Ry}}equiv hcR_{infty }={frac {m_{text{e}}e^{4}}{8varepsilon _{0}^{2}h^{2}}}={frac {e^{2}}{8pi varepsilon _{0}a_{0}}}=2.179;872;361;1035(42)times 10^{-18} {text{J}} =13.605;693;122;994(26) {text{eV}}.}$

Rydberg frequency[edit]

${displaystyle cR_{infty }=3.289;841;960;2508(64)times 10^{15} {text{Hz}}.}$

^[5]

Rydberg wavelength[edit]

${displaystyle {frac {1}{R_{infty }}}=9.112;670;505;824(17)times 10^{-8} {text{m}}}$

The angular wavelength is

${displaystyle {frac {1}{2pi R_{infty }}}=1.450;326;555;7696(28)times 10^{-8} {text{m}}}$

Occurrence in Bohr model[edit]

The Bohr model explains the atomic spectrum of hydrogen (see hydrogen spectral series) as well as various other atoms and ions. It is not perfectly accurate, but is a remarkably good approximation in many cases, and historically played an important role in the development of quantum mechanics. The Bohr model posits that electrons revolve around the atomic nucleus in a manner analogous to planets revolving around the sun.

In the simplest version of the Bohr model, the mass of the atomic nucleus is considered to be infinite compared to the mass of the electron,^[6] so that the center of mass of the system, the barycenter, lies at the center of the nucleus. This infinite mass approximation is what is alluded to with the infty subscript. The Bohr model then predicts that the wavelengths of hydrogen atomic transitions are (see Rydberg formula):

${displaystyle {frac {1}{lambda }}=mathrm {Ry} cdot {1 over hc}left({frac {1}{n_{1}^{2}}}-{frac {1}{n_{2}^{2}}}right)={frac {m_{text{e}}e^{4}}{8varepsilon _{0}^{2}h^{3}c}}left({frac {1}{n_{1}^{2}}}-{frac {1}{n_{2}^{2}}}right)}$

where n₁ and n₂ are any two different positive integers (1, 2, 3, …), and lambda is the wavelength (in vacuum) of the emitted or absorbed light.

${displaystyle {frac {1}{lambda }}=R_{M}left({frac {1}{n_{1}^{2}}}-{frac {1}{n_{2}^{2}}}right)}$

where ${displaystyle R_{M}={frac {R_{infty }}{1+{frac {m_{text{e}}}{M}}}},}$ and M is the total mass of the nucleus. This formula comes from substituting the reduced mass of the electron.

Precision measurement[edit]

The Rydberg constant is one of the most precisely determined physical constants, with a relative standard uncertainty of under 2 parts in 10¹².^[2] This precision constrains the values of the other physical constants that define it.^[7]

Since the Bohr model is not perfectly accurate, due to fine structure, hyperfine splitting, and other such effects, the Rydberg constant $R_{{infty }}$ cannot be directly measured at very high accuracy from the atomic transition frequencies of hydrogen alone. Instead, the Rydberg constant is inferred from measurements of atomic transition frequencies in three different atoms (hydrogen, deuterium, and antiprotonic helium). Detailed theoretical calculations in the framework of quantum electrodynamics are used to account for the effects of finite nuclear mass, fine structure, hyperfine splitting, and so on. Finally, the value of $R_{{infty }}$ is determined from the best fit of the measurements to the theory.^[8]

Alternative expressions[edit]

The Rydberg constant can also be expressed as in the following equations.

$R_{infty }={frac {alpha ^{2}m_{{text{e}}}c}{4pi hbar }}={frac {alpha ^{2}}{2lambda _{{{text{e}}}}}}={frac {alpha }{4pi a_{0}}}$

and in energy units

${displaystyle {text{Ry}}=hcR_{infty }={frac {1}{2}}m_{text{e}}c^{2}alpha ^{2}={frac {1}{2}}{frac {e^{4}m_{text{e}}}{(4pi varepsilon _{0})^{2}hbar ^{2}}}={frac {1}{2}}{frac {m_{text{e}}c^{2}r_{text{e}}}{a_{0}}}={frac {1}{2}}{frac {hcalpha ^{2}}{lambda _{text{e}}}}={frac {1}{2}}hf_{text{C}}alpha ^{2}={frac {1}{2}}hbar omega _{text{C}}alpha ^{2}={frac {1}{2m_{text{e}}}}left({dfrac {hbar }{a_{0}}}right)^{2}={frac {1}{2}}{frac {e^{2}}{(4pi varepsilon _{0})a_{0}}}.}$

where

$m_{text{e}}$ is the electron rest mass,
is the electric charge of the electron,
is the Planck constant,
is the reduced Planck constant,
is the speed of light in vacuum,
$varepsilon _{0}$ is the electrical field constant (permittivity) of free space,
${displaystyle alpha ={frac {1}{4pi varepsilon _{0}}}{frac {e^{2}}{hbar c}}}$ is the fine-structure constant,
$lambda _{{{text{e}}}}=h/m_{{text{e}}}c$ is the Compton wavelength of the electron,
$f_{{{text{C}}}}=m_{{{text{e}}}}c^{2}/h$ is the Compton frequency of the electron,
$omega _{{{text{C}}}}=2pi f_{{{text{C}}}}$ is the Compton angular frequency of the electron,
$a_{0}={frac {4pi varepsilon _{0}hbar ^{2}}{e^{2}m_{{{text{e}}}}}}$ is the Bohr radius,
$r_{{mathrm {e}}}={frac {1}{4pi varepsilon _{0}}}{frac {e^{2}}{m_{{{mathrm {e}}}}c^{2}}}$ is the classical electron radius.

The last expression in the first equation shows that the wavelength of light needed to ionize a hydrogen atom is 4π/α times the Bohr radius of the atom.

The second equation is relevant because its value is the coefficient for the energy of the atomic orbitals of a hydrogen atom: $E_{n}=-hcR_{infty }/n^{2}$ .

References[edit]

^ Pohl, Randolf; Antognini, Aldo; Nez, François; Amaro, Fernando D.; Biraben, François; Cardoso, João M. R.; Covita, Daniel S.; Dax, Andreas; Dhawan, Satish; Fernandes, Luis M. P.; Giesen, Adolf; Graf, Thomas; Hänsch, Theodor W.; Indelicato, Paul; Julien, Lucile; Kao, Cheng-Yang; Knowles, Paul; Le Bigot, Eric-Olivier; Liu, Yi-Wei; Lopes, José A. M.; Ludhova, Livia; Monteiro, Cristina M. B.; Mulhauser, Françoise; Nebel, Tobias; Rabinowitz, Paul; Dos Santos, Joaquim M. F.; Schaller, Lukas A.; Schuhmann, Karsten; Schwob, Catherine; Taqqu, David (2010). “The size of the proton”. Nature. 466 (7303): 213–216. Bibcode:2010Natur.466..213P. doi:10.1038/nature09250. PMID 20613837. S2CID 4424731.
^ ^a ^b “2018 CODATA Value: Rydberg constant”. The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
^ “2018 CODATA Value: Rydberg constant times hc in J”. NIST. The NIST Reference on Constants, Units, and Uncertainty. Retrieved 2020-02-06.
^ “2018 CODATA Value: Rydberg constant times hc in eV”. NIST. The NIST Reference on Constants, Units, and Uncertainty. Retrieved 2020-02-06.
^ “2018 CODATA Value: Rydberg constant times c in Hz”. NIST. The NIST Reference on Constants, Units, and Uncertainty. Retrieved 2020-02-05.
^ Coffman, Moody L. (1965). “Correction to the Rydberg Constant for Finite Nuclear Mass”. American Journal of Physics. 33 (10): 820–823. Bibcode:1965AmJPh..33..820C. doi:10.1119/1.1970992.
^ P.J. Mohr, B.N. Taylor, and D.B. Newell (2015), “The 2014 CODATA Recommended Values of the Fundamental Physical Constants” (Web Version 7.0). This database was developed by J. Baker, M. Douma, and S. Kotochigova. Available: http://physics.nist.gov/constants. National Institute of Standards and Technology, Gaithersburg, MD 20899. Link to R_∞, Link to hcR_∞. Published in Mohr, Peter J.; Taylor, Barry N.; Newell, David B. (2012). “CODATA recommended values of the fundamental physical constants: 2010”. Reviews of Modern Physics. 84 (4): 1527–1605. arXiv:1203.5425. Bibcode:2012RvMP…84.1527M. doi:10.1103/RevModPhys.84.1527. S2CID 103378639″”{{cite journal}}: CS1 maint: postscript (link) and Mohr, Peter J.; Taylor, Barry N.; Newell, David B. (2012). “CODATA Recommended Values of the Fundamental Physical Constants: 2010”. Journal of Physical and Chemical Reference Data. 41 (4): 043109. arXiv:1507.07956. Bibcode:2012JPCRD..41d3109M. doi:10.1063/1.4724320″”{{cite journal}}: CS1 maint: postscript (link).
^ Mohr, Peter J.; Taylor, Barry N.; Newell, David B. (2008). “CODATA recommended values of the fundamental physical constants: 2006”. Reviews of Modern Physics. 80 (2): 633–730. arXiv:0801.0028. Bibcode:2008RvMP…80..633M. doi:10.1103/RevModPhys.80.633.

Источник

Определение постоянной ридберга по спектру водорода

Цель
работы.
Изучение спектра водорода.

Введение

Линейчатые
спектры обусловлены испусканием
электромагнитного излучения свободными
или слабо связанными атомами. Одним из
источников такого излучения является
возбужденный газ или пар [1], [3]. В данной
работе используются газосветные трубки,
наполненные водородом и неоном.

Установлено,
что спектральные линии атомарного
водорода обнаруживают несложные
закономерности. Частоты соответствующих
линий могут быть определены по формуле



где

– частота,
c,

c
– скорость света в вакууме,

 – длина
волны,

R
– постоянная
Ридберга,

n_i, n_j
– целые числа, причем n_jможет
принимать значения

(n_i
+ 1), (n_i
+ 2), (n_i
+ 3 ), …

Из
квантовой механики известно, что атом
может обладать лишь рядом дискретных
значений энергии E₁,
E₂,
E₃
и т. д., каждое из которых определяется
главным образом квантовым числом n.
При разрешенном правилами отбора (1)
переходе атома из состояния с большей
энергией в состояние с меньшей энергией
испускается квант энергии.

Рассмотрим
переход атома из различных возбужденных
состояний на один и тот же энергетический
уровень, определяемый квантовым числом
n_i.
Совокупность спектральных линий,
отвечающая таким переходам, образует
серию. Таким образом, n_i
определяет серию. Соответственно
квантовое число n_jопределяет
энергетический уровень, с которого имел
место данный переход, т. е. линию в серии.

Различным
сериям атома водорода: Лаймана, Бальмера,
Пашена, Брэккета, Пфунда отвечают
соответственно значения
n_i
= 1, 2, 3, 4, 5.

Из
формулы (1) следует, что частоту любой
спектральной линии спектра атома
водорода можно представить как
произведение скорости света на разность
двух членов типа R/n_k².
Эти члены в спектроскопии называются
термами [3]. Иными словами,

c(T(n_i)

T(n_j)),
(2)

где

Итак,
зная систему термов для данного атома,
можно получить частоту любой спектральной
линии из соотношения (2).

Рассмотрим,
как определить частоты спектральных
линий атома водорода, принадлежащих
серии Бальмера, используя комбинационный
принцип, математическое выражение
которого представлено равенством (2).
Для серии Бальмера n_i= 2,
n_j
= 3, 4, 5… Следовательно,

3

Если
приписать n_jзначения
соответственно 3, 4, 5, 6, то из уравнения
(3) получим значения частот спектральных
линий, лежащих в видимой области и
обозначаемых в спектроскопии H_
H_
H_j,
H_..
По мере увеличения n_j
разность частот соседних линий
уменьшается, и при n_j

сами частоты стремятся к пределу

где
_гр
– частота, соответствующая границе
серии Бальмера. У каждой серии есть своя
граница, соответствующая ей частота
определяется соотношением:

Рассмотрим
физический смысл _гр
Согласно Бору, при переходе атома с
более высокого j-го
энергетического уровня на менее высокий
i-й
уровень излучается квант энергии

h
= E_j
E_i
(4)

Соответственно,
чтобы перевести электрон с уровня i
на уровень j,
необходимо сообщить ему такую же энергию.

Частота
_гр
определяет энергию (E
= h_гр),которую
надо сообщить электрону, чтобы удалить
его с уровня, определяемого числом n_iв безвоздушное
пространство за пределы атома, где его
полная энергия должна быть равна нулю.
Описанный процесс называется процессом
ионизации.

Таким
образом, E
= h_гр
представляет энергию ионизации атома
в данном состоянии. Обратный процесс –
процесс рекомбинации будет сопровождаться
излучением, частота которого _гр.

Поскольку
электрон, отделенный от атома, может
обладать произвольной кинетической
энергией Т,
то при его захвате ионом должна
освобождаться энергия (h_гр
+ T).Следовательно.
согласно второму постулату Бора (1) в
этом случае будет испускаться
электромагнитное излучение с частотой

Таким
образом, возможно излучение с частотой,
большей нежели частота границы серии,
на любую величину T/h.
Это означает, что к границе серии со
стороны высоких частот прилегает
сплошной спектр. Излучение спектров
испускания позволяет исследовать
строение атома.

Приборы
и принадлежности: монохроматор,
газосветные трубки с водородом, неоном.

Соседние файлы в папке 35 35A. 38

Источник

Введение

Квантовая теория позволила понять такие проблемы как характер взаимодействия атомов при образовании стабильных молекул, происхождение периодической системы элементов и наличие характерных электрических, магнитных, механических и оптических свойств у твёрдых тел. Однако первым шагом на этом пути было решение задачи водорода.

При рассмотрении этой задачи результаты точного квантовомеханического расчёта оказываются очень близки к результатам боровской теории водородоподобных атомов. В рамках боровской теории оптические закономерности спектров поглощения и излучения атомарного водорода имеют особенно простую и наглядную форму.

В начале кратко изложу подход к задаче водорода на основе уравнения Шредингера. Далее приведу боровское решение для движения электрона в центральном кулоновском поле атомного ядра и вытекающий из него энергетический спектр водородоподбного атома. Значительное внимание уделю принципам работы дифракционных спектральных приборов, которые отличаются от принципов работы оптических приборов, в которых в качестве диспергирующего элемента используется призма из прозрачного материала.

Цель работы состоит в освоении принципов работы дифракционного спектрометра, измерении спектра излучения дейтериевой лампы и, самое главное, определении постоянной Ридберга.

Результатом работы является вычисление постоянной Ридберга, путем исследования спектра атомарного водорода.

1.Квантовая теория атома водорода

Квантовомеханическая теория атома, стала фундаментальным вкладом в наши знания о мире. Наряду с коренной ломкой взглядов на атомные явления эта теория позволила понять такие близкие проблемы, как характер взаимодействия атомов при образовании стабильных молекул, происхождение периодической системы элементов и наличие характерных электрических, магнитных, механических и оптических свойств у твёрдых тел. Однако первым продуктивным шагом на этом пути было решение задачи водорода. Атом водорода состоит из протона с электрическим зарядом +e, в котором сосредоточена практически вся масса атома, и электрона — частицы с массой в 1836 раз меньшей и с зарядом –e, который удерживается вблизи протона электрическим полем. При таком соотношении масс можно полагать ядро совершенно неподвижным, однако, если потребуется учесть его движение, то это легко будет сделать, как и в теории Бора, путём замены массы электрона m на приведённую массу:

Потенциальная энергия электрона в водородоподобном атоме — системе с зарядом ядра Ze и движущимся вокруг него электроном — равна

где r — расстояние между неподвижным точечным ядром, расположенным в начале отсчета, и электроном.

Общий вид уравнения Шредингера для стационарных состояний имеет вид

Очевидно, что сформулированная задача имеет сферическую симметрию, поэтому решать ее целесообразно в сферических координатах, которые связаны с декартовыми координатами частицы следующими соотношениями:

Уравнение Шредингера в таком случае записывается как

Его решение стандартно, но довольно громоздко и приводит в нашем случае к результатам, близким к выводам, следующим из боровской теории.

2.Теория Бора

Для простоты Бор принял, что в атоме водорода электроны вращаются вокруг протона по окружности радиусом r с циклической частотой ω. Согласно второму закону Ньютона, мы имеем:

Бор положил, что стационарным состояниям электрона в атоме соответствует модуль механического момента, кратный постоянной Планка:

Решение уравнений (3), (4) дает выражение для радиусов круговых орбит электронов в атоме водорода:

Полная энергия электрона в атоме есть сумма кинетической и отрицательной потенциальной энергий:

Подставляя в (6) rn , получаем формулу, выражающую полную энергию электрона в атоме водорода на n‑ой стационарной орбите:

Формула (5), полученная с помощью постулатов Бора, совпадает с формулой (2), полученной с помощью решения уравнения Шредингера для атома водорода.

Однако, к сожалению, теория Бора, достаточно правильно описывая закономерности в атоме водорода и водородоподобных ионах (содержащих один электрон), даёт неправильные результаты уже для атома гелия, следующего за водородом и содержащем всего два электрона. Таким образом, теорию Бора можно рассматривать лишь как промежуточный этап на пути поиска верной теории — квантовой механики, точно описывающий закономерности микромира.

При переходе атома водорода из состояния n2 с энергией Е2 в состояние n1 с энергией Е1 излучается квант света с частотой ω, равной

Подставляя значение энергии E2 и E1 из формул (2) или (5), имеем:

Далее, вспоминая, что E2 -E1=hw, можем записать:

Формулу (10) называют обобщённой формулой Бальмера, а константу R — постоянной Ридберга.

Совокупность спектральных линий, закономерно меняющих свою интенсивность, называют спектральной серией. Предельное волновое число при называется границей серии. В видимой области спектра для водорода мы можем наблюдать только серию Бальмера: n1 = 2, n2 = 3, 4, 5, … .

В спектре излучения водорода существуют и другие серии. Это, например, серия Лаймана, все линии которой лежат в ультрафиолетовой области спектра. Для этой серии n1=1. Линии остальных серий (Пашена, Брэкета, Пфунда и др.) лежат в инфракрасной области спектра. Набор уровней энергии и возможные переходы в атоме принято показывать на энергетической диаграмме (см. рис. 2). Еn=Wn- полная энергия электрона в атоме на уровне с главным квантовым числом равном n.

Состояние атома, в котором электрон находится на низшем энергетическом уровне (для атома водорода это состояние с энергией Е1 = –13,6 эВ), называется основным. Атом без внешних возмущений может находиться в этом состоянии неопределённо долго. Энергетический уровень Е1, соответственно, является бесконечно тонким. Этот вывод вытекает непосредственно из соотношения неопределённостей:

-неопределённость значения энергии,- неопределенность времени пребывания атома в этом состоянии.

Остальные энергетические уровни являются возбужденными, так как возникают под действием внешних воздействий и могут существовать ограниченное время.

3. Описание установки и методики эксперимента

Для изучения спектра атома водорода используется спектроскоп на основе призменного монохроматора УМ-2. Схема экспериментальной установки приведена на рисунке

1- источник света, 2- входная щель спектроскопа, 3- входной объектив, 4- сложная спектральная призма, 5- микрометрический винт с отсчетным барабаном, 6- входной объектив, 7- указатель, 8- окуляр.

Свет от источника 1 через входную щель 2 и объектив 3 параллельным пучком падает на спектральную призму с высокой дисперсией 4. Призмой свет разлагается в спектр и через объектив 6 направляется в окуляр 8. При повороте призмы в центре поля зрения появляются различные участки спектра. Призму поворачивают при помощи барабана 5, на которой нанесена шкала в градусах. Вращением барабана спектральную линию подводят к стрелке указателя 7, расположенного в окуляре, и фиксируют отсчет по шкале барабана.

В работе наблюдают спектры газов в видимой области.

1. Градуируют спектроскоп по известному спектру ртути.

2. Измеряют длины волн в спектре атома водорода.

3. По измеренным длинам волн в спектре водорода определяют уровни энергии электронов, при переходах между которыми испускаются кванты света. Определяются соответствующие этим уровням квантовые числа ???????? и ????????, далее вычисляют постоянную Ридберга.

4. Основные расчетные формулы

Постоянная Ридберга (угловой коэффициент), расчёт по графику:

, где

λ – длина волны спектральных линий;

n – главное квантовое число.

Вспомогательные формулы для расчёта абсолютной погрешности постоянной Ридберга:

Угловой коэффициент прямой k= n*S3-S1S2/D

Абсолютная погрешность постоянной Ридберга, как абсолютная погрешность углового коэффициента прямой k:

, где

n – количество точек.

5. Результаты работы и их анализ

Данные градуировки спектроскопа по спектру ртути:

Градуировочный график φ(λ):

Значения длин волн λ спектральных линий водорода определяются по градуировочному графику: на оси Y откладываются значения φ, а соответствующие им значения на оси X подбираются так, чтобы точка совпала с линией. Используя график, определяем значения длин волн линий спектра водорода.

Экспериментальные данные спектра атома водорода:

Проверим справедливость формулы Бальмера. Для этого нужно построить график зависимости 1/λ(1/n2).

Данные для построения зависимости 1/λ(1/n2):

График линейной зависимости 1/λ(1/n2):

5.1 Определение постоянной Ридберга

Определяем по графику постоянную Ридберга, как угловой коэффициент линейной зависимости 1/λ(1/n2) по формуле

R = (2,445*10-6– 1,517*10-6)/( 0,111– 0,028) = 1,108*107 (м-1)

Оцениваем абсолютную погрешность R по ранее данным формулам

Ошибка определения постоянной Ридберга составила 0,98%.

Используя полученные из опыта значения длин волн построим фрагмент энергетического спектра атома водорода.

Фрагмент энергетического спектра атома водорода:

Переходы, наблюдаемые в опыте: 6s → 2p, 5s → 2p, 4s → 2p, 3s → 2p.

Заключение

В ходе работы был изучен спектр излучения атомов водорода. Был построен график линейной зависимости 1/λ(1/n2), по которому удалось определить постоянную Ридберга (R). Погрешность экспериментального определения R составила

Ошибка определения постоянной Ридберга составила 0,98%.

Постоянную Ридберга можно найти с помощью обобщенной формулы Бальмера, определив экспериментальным путем длины волн в какой-либо серии. Наиболее удобно это сделать в видимой области спектра, то есть для серии Бальмера.

В настоящей работе определяются длины волн первых четырех наиболее ярких спектральных линий этой серии, для которой i принимает значения: 3 (красная линия), 4 (голубая), 5 (фиолетовая), 6 (тёмно-фиолетовая, слаборазличимая).

Источник

Самым простым из всех атомов является атом водорода, и он выступил в свое время в качестве своеобразного тест-объекта для теории Бора. К моменту появления теории атом водорода был тщательно исследован в ходе экспериментов: имелось знание о том, что он содержит единственный электрон. Ядром атома является протон.

Определение 1

Протон – это частица с положительным зарядом, модуль которого равен модулю заряда электрона, а масса больше массы электрона в 1836 раз.

Серия Бальмера и формула Ридберга

Начало XIX века ознаменовалось открытием линейчатого спектра.

Определение 2

Линейчатый спектр – это дискретные спектральные линии в видимой области излучения атома водорода.

В последующем закономерности, в соответствии с которыми ведут себя длины волн (или частоты) линейчатого спектра, подробно в количественном отношении исследовал И. Бальмер (в 1885 г.)

Определение 3

Серия Бальмера – совокупность спектральных линий атома водорода в видимой части спектра.

Позднее подобные серии спектральных линий обнаружились в ультрафиолетовой и инфракрасной частях спектра. В 1890 г. И. Ридберг составил запись эмпирической формулы для частот спектральных линий (формула Ридберга):

νnm=R1m2-1n2.

Для серии Бальмера m = 2, n = 3, 4, 5, …. Для ультрафиолетовой серии (серия Лаймана) m = 1, n = 2, 3, 4, … .

Определение 4

Неизменяемая R в формуле для частот спектральных линий носит название постоянной Ридберга и равна: R=3,29·1015 Гц.

До того, как Бор сформулировал постулаты, вопросы, каким же образом возникают линейчатые спектры и каков смысл целых чисел, входящих в формулы спектральных линий водорода (и некоторых других атомов), оставались без ответа.

Правило квантования

Постулаты Бора задали направление для развития новой науки – квантовой физики атома. Однако в них не было «рецепта», как определить параметры стационарных состояний (орбит) и соответствующих им значений энергии En.

Бором было сформулировано правило квантования, которое приводило к соотносимым с опытом значениям энергий стационарных состояний атома водорода. Ученый выдвинул гипотезу, что момент импульса электрона, совершающего вращение вокруг ядра, может принимать лишь дискретные значения, кратные постоянной Планка.

Определение 5

Для круговых орбит правило квантования Бора имеет запись:

meνrn=nh2π (n=1, 2, 3,…).

В данном выражении me является массой электрона, υ – его скоростью, rn обозначает радиус стационарной круговой орбиты.

Правило квантования Бора дает возможность путем вычисления определить радиусы стационарных орбит электрона в атоме водорода и отыскать значения энергий. Скорость электрона, который совершает вращение по круговой орбите некоторого радиуса r в кулоновском поле ядра, записывается в виде соотношения (в соответствии с 2 законом Ньютона):

ν2=e24πε0mer.

Самой близкой к ядру орбите соответствует значение n=1.

Определение 6

Боровский радиус – это радиус первой орбиты, расположенной ближе всех к ядру электрона атома водорода, определяемый как:

r1=α0=ε0h2πmee2=5,29·10-11 м.

Радиусы последующих орбит получают возрастание пропорционально n2.

Полная механическая энергия E системы из атомного ядра и электрона, вращающегося по стационарной круговой орбите радиусом rn, имеет запись:

En=Ek+Ep=meν22-e24πε0rn.

Заметим, что Ep<0, поскольку имеет место действие сил притяжения между электроном и ядром. Подставим в это выражение записи для υ2 и rn и получаем:

En=-mee48e02h2·1n2.

Определение 7

В квантовой физике атома целое число n=1, 2, 3, … носит название главного квантового числа.

В соответствии со вторым постулатом Бора: когда электрон переходит с одной стационарной орбиты с энергией En на другую стационарную орбиту с энергией Em<En, атом испускает квант света с частотой νnm, равной ΔEnmh:

νnm=∆Enmh=mee48ε02h31m2-1n2.

Это выражение полностью идентично с эмпирической формулой Ридберга для спектральных серий атома водорода, если за постоянную R взять:

R=mee48ε02h3.

Подставим в это выражение числовые значения всех переменных, получим

R=3,29·1015 Гц.

Полученное значение отлично коррелируется с эмпирическим значением R.

На рисунке 6.3.1 проиллюстрировано образование спектральных серий в излучении атома водорода при переходе электрона с высоких стационарных орбит на более низкие.

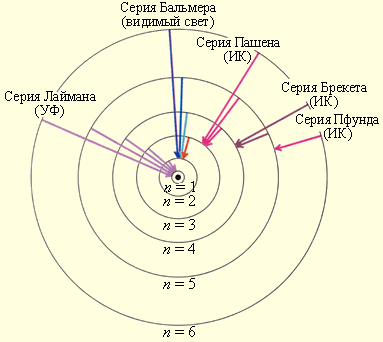
Рисунок 6.3.1. Стационарные орбиты атома водорода и образование спектральных серий.

Рисунок 6.3.2 демонстрирует диаграмму энергетических уровней атома водорода с указанием переходов для различных спектральных серий.

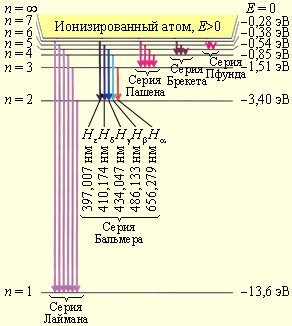
Рисунок 6.3.2. Диаграмма энергетических уровней атома водорода с указанием переходов для различных спектральных серий. Также имеется указание длин волн для первых пяти линий серии Бальмера.

Тот факт, что теория Бора для атома водорода и результаты эксперимента оказались так отлично согласованы между собой, стал весомым аргументом в пользу верности этой теории. Но при этом попытка использовать теорию применительно к более сложным атомам закончилась провалом. Бору не удалось дать физическую интерпретацию правилу квантования – это позже, спустя десятилетие, сделал де Бройль, опираясь на представления о волновых свойствах частиц. Его предположение заключалось в том, что каждая орбита в атоме водорода соответствует волне, получающей распространение по окружности около ядра атома. Стационарная орбита имеет место тогда, когда волна постоянно повторяет себя после каждого оборота вокруг ядра. Иначе говоря, стационарная орбита соответствует круговой стоячей волне де Бройля на длине орбиты (рис. 6.3.3). Такое явление подобно стационарной картине стоячих волн в струне с закрепленными концами.

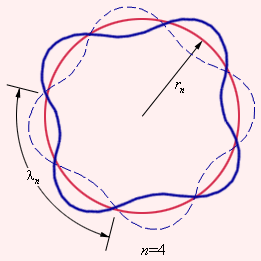
Рисунок 6.3.3. Иллюстрация идеи де Бройля возникновения стоячих волн на стационарной орбите для случая n=4.

Согласно дебройлевским идеям, в стационарном квантовом состоянии атома водорода на длине орбиты должно укладываться целое число длин волн λ:

nλn=2πrn

Если подставить сюда формулу длины волны де Бройля λ=hp, где p=meυ – импульс электрона, то:

nhneν=2πrn или meνrn=nh2π.

Итак, правило квантования Бора находится во взаимосвязи с волновыми свойствами электронов.

Вообще можно сказать, что Бор достиг поразительных успехов в попытках объяснить спектральные закономерности. Появилось утверждение, что атомы являются квантовыми системами, а энергетические уровни стационарных состояний атомов дискретны. Практически одномоментно с возникновением боровской теории экспериментально было доказано, что существуют стационарные состояния атома и квантование энергии. Дискретность энергетических состояний атома опытным путем продемонстрировали в 1913 г. Д. Франк и Г. Герц, исследуя столкновение электронов с атомами ртути. Выяснилось, что при энергии электронов менее 4,9 эВ их столкновение с атомами ртути протекает согласно закону абсолютно упругого удара. А, когда энергия электронов равна 4,9 эВ, столкновение с атомами ртути будет иметь черты неупругого удара. Таким образом, выходит, что, столкнувшись с неподвижными атомами ртути, электроны лишаются всей своей кинетической энергии, что, в свою очередь, означает факт поглощения атомами ртути энергии электрона и перевода электронов из основного состояния в первое возбужденное состояние:

E2-E1=4,9 эВ.

В соответствии с концепцией Бора, когда будет происходить обратный самопроизвольный переход атома, ртуть будет испускать кванты с частотой

ν=E2-E1h=1,2·1015 Гц.

Линия спектра с подобной частотой в самом деле нашлась в ультрафиолетовой части спектра излучения атомов ртути.

Утверждения о дискретных состояниях находились в противоречии с классической физикой, в связи с чем также возник закономерный вопрос: не опровергает ли квантовая теория законы классической физической теории.

Квантовая физика отнюдь не стремилась отменить фундаментальные основы, такие как законы сохранения энергии, импульса, электрического разряда и подобное. По сформулированному Бором принципу соответствия квантовая физика вмещает в себя классические представления, и при некоторых условиях можно заметить планомерный переход от квантовых представлений к классическим. Энергетический спектр атома водорода как раз дает нам такой пример (рис. 6.3.2): при больших квантовых числах n≫1 дискретные уровни постепенно становятся ближе, что задает плавный переход в область непрерывного спектра, вытекающего из классической физики.

Постулаты Бора со своей «половинчатостью», «полуклассикой» стали важной ступенью развития квантовых основ, введение которых в физику потребовало серьезной перестройки механики и электродинамики, произошедшей в 20-е – 30-е годы XX века.

Квантовые числа

Видение Бора о том, что существуют определенные орбиты для движения электронов в атоме, оказалось очень условным. В действительности, траектория движения электрона в атоме почти не имеет общего с движением планет или спутников. Физический смысл есть лишь в возможности обнаружить электрон в том или ином месте, и эта вероятность описывается квадратом модуля волновой функции |Ψ|2. Волновая функция Ψ служит решением базового уравнения квантовой механики – уравнения Шредингера. Выяснилось, что состояние электрона в атоме описывается целым набором квантовых чисел.

Определение 8

Основное квантовое число n – квантовое число, задающее квантование энергии атома.

Орбитальное квантовое число l – число, применяемое для квантования момента импульса.

Магнитное квантовое число m – число, применяемое для квантования проекции момента импульса.

Квантовое число m введено в связи с тем, что проекция момента импульса на любое выделенное в пространстве направление (к примеру, направление вектора B→ магнитного поля) также принимает дискретный ряд значений.

Все виды квантовых чисел (n, l, m) находятся во взаимосвязи с правилами квантования. К примеру, орбитальное квантовое число l может принимать значения целого числа от 0 до (n – 1). Магнитное квантовое число m может принимать любые значения целого числа в интервале ±l. Тогда каждому значению главного квантового числа n, описывающему состояние энергии атома, соответствует целый ряд комбинаций квантовых чисел l и m. Одновременно с этим, с каждой такой комбинацией соотносится определенное распределение вероятности |Ψ|2 обнаружения электрона в разных точках пространства («электронное облако»).

Определение 9

s-состояния (1s, 2s, …, ns, …) – это состояния, при которых орбитальное квантовое число l равно нулю.

Описываются s-состояния сферически симметричными распределениями вероятности.

Когда l>0 сферическая симметрия электронного облака нарушается.

Определение 10

p-состояния – это состояния при l=1.

d-состояния – это состояния при l=2 и т.д.

Рис. 6.3.4 иллюстрирует кривые распределения вероятности ρ (r)=4πr2|Ψ|2 обнаружения электрона в атоме водорода на разных расстояниях от ядра в состояниях 1s и 2s.

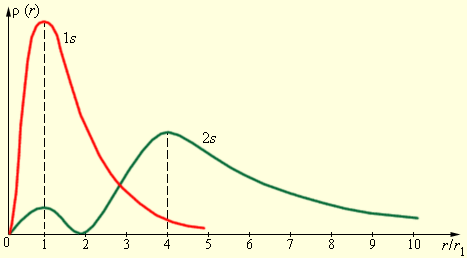
Рисунок 6.3.4. Распределение вероятности обнаружения электрона в атоме водорода в состояниях 1s и 2s. r1=5,29·10–11 м – радиус первой орбиты Бора.

На рисунке 6.3.4 наглядно продемонстрировано, что электрон в состоянии 1s (основное состояние атома водорода) имеет возможность быть обнаруженным на различных расстояниях от ядра. С самой высокой вероятностью электрон обнаружится на расстоянии, равном радиусу r1 первой боровской орбиты. Вероятность нахождения электрона в состоянии 2s достигает максимума на расстоянии r=4r1 от ядра. И в том, и в том случае атом водорода возможно представить, как сферически симметричное электронное облако, в центре которого расположено ядро.

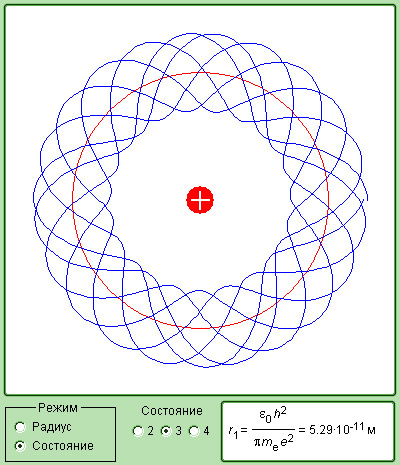
Рисунок 6.3.5. Модель квантования электронных орбит.

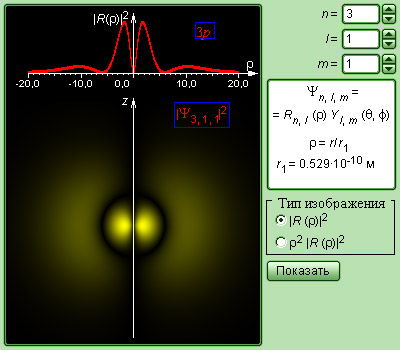
Рисунок 6.3.6. Модель атома водорода.

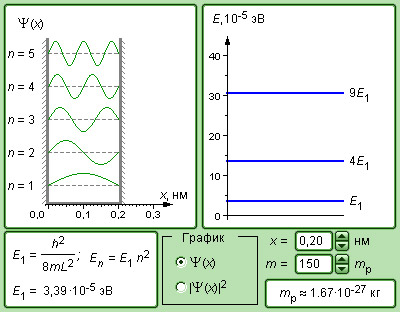
Рисунок 6.3.7. Модель частицы в потенциальной яме.

Источник

Численное значение[править | править код]

Свойства[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Value[edit]

Rydberg constant[edit]

Rydberg unit of energy[edit]

Rydberg frequency[edit]

Rydberg wavelength[edit]

Occurrence in Bohr model[edit]

Precision measurement[edit]

Alternative expressions[edit]

References[edit]

Определение постоянной ридберга по спектру водорода

Введение

Серия Бальмера и формула Ридберга

Правило квантования

Квантовые числа

Вам также может понравиться

Как найти тангенс угла в непрямоугольном треугольнике

Как найти девушку полностью голой

Стихи как найти настроение

Добавить комментарий Отменить ответ