

Зако́н Сте́фана — Бо́льцмана (закон Стефана, закон излучение Стефана — Больцмана) — интегральный закон излучения абсолютно чёрного тела. Он определяет зависимость плотности мощности излучения абсолютно чёрного тела от его температуры. В словесной форме его можно сформулировать следующим образом[1]:
Полная объёмная плотность равновесного излучения и полная испускательная способность абсолютно чёрного тела пропорциональны четвёртой степени его температуры.
Для полной испускательной способности (энергетической светимости) 
-
Закон Стефана — Больцмана
где 

-
Постоянная Стефана — Больцмана
где 


Вт / (м2 · К4).
Закон открыт сначала эмпирически Йозефом Стефаном в 1879 году, и через пять лет выведен теоретически Людвигом Больцманом в рамках термодинамики[A 1][A 2]. Больцман исходил из кинетической теории газов и цикла идеальной обратимой тепловой машины с излучением в качестве рабочего тела вместо газа. Он предполагал, что это излучение оказывает давление на стенки сосуда[4]. Это единственный важный физический закон, названный в честь словенского физика[5].
Закон говорит только об общей излучаемой энергии. Распределение энергии по спектру излучения описывается формулой Планка, в соответствии с которой в спектре имеется единственный максимум, положение которого определяется законом Вина. Используя современную формулировку, его можно вывести из закона Планка:
Применение закона к расчёту эффективной температуры поверхности Земли даёт оценочное значение, равное 249 К или −24 °C.
Общая форма[править | править код]

Увеличение мощности излучения при изменении температуры
Если замкнутую систему нагретых излучающих тел поместить в полость с идеальными отражающими стенками, то со временем установится термодинамическое равновесие между излучением и всеми телами. Температуры всех тел станут одинаковыми[6]. Равновесие достигается не только на поверхности тел, но и внутри них. Возбуждённые атомы испускают излучение, которое поглощается другими атомами среды, возбуждая их, тем самым попадая со временем на поверхность тела, с которой излучается в окружающее пространство[7]. Тепловое излучение — это равновесная форма излучения, которое однородно, изотропно, неполяризовано, обладает непрерывным спектром. Энергию r, приходящуюся на единичный диапазон частот называют спектральной испускательной способностью тела или спектральной плотностью энергетической светимости. Она зависит от частоты и температуры. При интегрировании этой величины по всему спектру получают суммарный поток энергии излучения единицы поверхности называют интегральной испускательной способностью или энергетической светимостью[8]:
Эта величина имеет размерность [Вт/м²] в единицах СИ[8]. Обычные тела поглощают частично свет падающий на них. Спектральная поглощательная способность тела характеризуется как отношение поглощённого потока падающего излучения из узкого интервала частот dΦ’ω к падающему потоку (dΦω)[9]:
Эта безразмерная величина не может быть больше единицы по определению. Если поглощение одинаково для всех частот, то такое тело называют серым. Для реальных тел поглощение зависит от частоты. В специальном случае полного поглощения падающего излучения во всём спектре говорят об абсолютно чёрном теле[10]. Его излучение имеет универсальны характер, и его энергетическая светимость пропорциональна четвёртой степени температуры[11]:
где ε — интегральная поглощательная способность тела. Для абсолютно чёрного тела ε = 1 выражение имеет специальное название: закон Стефана — Больцмана. Для многих температур металлы имеют ε = 0,1…0,4, а для окислов металлов ε = 0,5…0,9[11].
Для серых тел, закон можно записать в виде:
Однако, если коэффициент отражения зависит от длины волны 
или
В технической литературе общий закон Стефана — Больцмана обычно записывается в виде:
в основном для того, чтобы было проще вычислить где он находится 
Цвет поверхности не влияет на яркость. Белые поверхности сильно излучают. Гладкие материалы, такие как алюминий и бронза, имеют низкое сияние. Стекло пропускает коротковолновый свет, но не пропускает длинноволновое тепловое излучение.
В отличие от твёрдых тел, излучающих и поглощающих с поверхности, у газов степень поглощения зависит от толщины газового слоя и проходит по всему объёму (закон поглощения):
где 

Открытие[править | править код]


20 марта Стефан опубликовал закон в статье «О связи между тепловым излучением и температурой» (нем. Über die Beziehung zwischen der Wärmestrahlung und der Temperatur) в «Докладах заседания Венской академии наук». Статья показывает его путь к открытию закона[A 1]. Резюме рукописи содержало четыре страницы формата А4, вся статья — 61 страницу, а печатная версия — 38 страниц[12].
Ньютон обнаружил, что интенсивность лучистого потока от горячего тела пропорциональна разности температур тела и окружающей среды. Пьер Дюлонг и Алексис Пти показали, что зависимость от температуры не является линейной, и важны более высокие степени[13]. Они рассматривали теплообмен между нагретой сферической колбой и окружающими стенками сферического сосуда при комнатной температуре. Они считали, что данная установка заполненная различными газами при различных давлениях будет хорошей моделью для исследования лучистого переноса тепла. Формула для лучистой мощности, к которой они пришли, имела вид[A 3][14]
где μ — зависящая от размера тела и материала константа, a=1,0077 — не зависящая от материала константа, T — температура. Стефан понял, что пренебрегать теплопереносом в системе не следует и использовал их данные для поиска новой зависимости вида
где A — постоянная зависящая от площади поверхности тела и температура дана в Кельвинах[14].
В 1847 году Дрейпер попытался определить, при какой температуре начинает излучать нагретое тело. Он этого не наблюдал, но обнаружил, что плотность потока излучаемой энергии возрастает гораздо быстрее, чем прямо пропорционально температуре. В 1878 году Стефан прочитал работу Дрейпера о лучистой энергии[15]. В 1848 году Кельвин ввёл абсолютную шкалу температур. Стефан также использовал абсолютную температуру в своём эксперименте[16]. Густав Кирхгоф ввёл закон теплового излучения в 1859 году и доказал его в 1861 году[17].
В 1862 году он ввёл термин «излучение чёрного тела». Он сравнил излучение чёрного и других излучающих тел[4]. Он также предположил способ реализации такого излучения. Излучение чёрного тела 
Джон Тиндаль исследовал «невидимый» инфракрасный свет в 1864 году. Инфракрасные волны были открыты Уильямом Гершелем в 1800 году. Он использовал призму и с её помощью преломлял солнечный свет и использовал термометр для измерения повышения температуры за красной частью светового спектра. Он назвал эту часть спектра тепловыми лучами. Термин инфракрасный свет появился в конце XIX века. Томас Зеебек открыл явление термоэлектричества в 1821 году. Вскоре после этого, в 1835 году, Мачедонио Меллони изготовил первую термоэлектрическую батарею и открыл тепловое излучение. Было обнаружено, что новое излучение представляет собой свет, невидимый человеческому глазу, или электромагнитные волны с немного большей длиной волны, чем видимый красный свет.
В 1840 году Джон Гершель сделал первое инфракрасное изображение. Тиндаль нагрел электрическим током лампочку, в которой заменил обычную угольную нить на платиновую проволоку. Провод светился. По мере увеличения электрического тока температура провода увеличивалась и излучала всё больше и больше света. Он уловил свет линзой и призмой из каменной соли разделил излучаемый проволокой свет на радужный спектр. На место красной части поместил батарею последовательно соединенных термопар[A 4][18]. Он присоединил контакты, где ток перетекал из одного металла в другой, с внешней стороны счётчика и зачернил их. Соединения, где ток был в обратном направлении, он спрятал в корпус счётчика. Первые спаи поглощали падающий свет и нагревались, а вторые имели температуру окружающей среды. Он измерил силу тока чувствительным гальванометром[19]. Тиндаль хотел получить только приблизительный результат, а температуру проволоки не измерял. Он только указал цвет излучаемого света. Для бледно-красных отклонение гальванометра составило 10,4°, а для белых 60°. В 1864 году он опубликовал трактат «О видимом и невидимом излучении», в котором попытался ответить, как излучение красного света зависит от температуры. Немецкий перевод был опубликован в 1865 году и был прочитан Адольфом Вюльнером[A 5]. Во второе и третье издания своего учебника термодинамики «Наука о теплоте с точки зрения механической теории теплоты» включил данные Тиндаля. Он отрегулировал температуры. Хотя он полагался на измерения Дрейпера, он действовал произвольно. Книгу Вюльнера получил Стефан, который изменил температуру на абсолютную и учёл исправленное отклонение гальванометра для белого, для которого Тиндаль уже упоминал о необходимости брать удвоенное значение 122°. Таким образом, бледно-красный цвет провода имел температуру 798 К (525 °С), белый 1473 К (1200 °С). При этом Стефан предполагал, что плотность излучаемого потока энергии пропорциональна отклонению гальванометра. Он попытался записать связь между абсолютной температурой провода T и плотностью излучаемого потока энергии j в виде степенной зависимости:
Из обеих пар данных он определил отношения потоков энергии 122/10,4 = 11,731. Он достаточно точно приблизился к значению, если возводил в степень отношение соответствующих абсолютных температур 1473/798 = 1,846 в четвёртой степени: 
Его измерение было довольно точным и на 10,8 % меньше чем современное значения. Он также проверил закон по данным de la Provostaye и Desains (1846), Draper и Ericsson (1872)[A 6] и Despretz.
В 1876 году Адольфо Бартоли[en] независимо от Максвелла вывел уравнение для лучистого давления электромагнитных волн термодинамическиму методом. Он обнаружил, что с помощью движущегося зеркала тепло может передаваться от более прохладного тела к более тёплому при совершении работы. Он представил себе обратимое бесконечно малый цикл Карно, при котором энтропия не меняется, а абсолютная проделанная работа связана с давлением света на зеркало. Чтобы второй закон термодинамики работал, свет должен передавать давление на зеркало. Поэтому лучистое давление также называли «давлением Максвелла — Бартоли».
В 1880 году Крова, Андре Проспер Поль опубликовал диаграмму трёхмерного представления графика интенсивности теплового излучения в зависимости от длины волны и температуры[A 7].
Брошюры Бартоли «О движениях, вызванных теплом» и «Радиометр Крукса» остались незамеченными. Последний раз на это обратил внимание Больцман, который обобщил идею Бартоли о том, что второй закон термодинамики требует существования лучистого давления и восемью годами позже вывел этот закон термодинамическим путём[A 2]. Бартоли был близок к закону Стефана — Больцмана, но не учитывал температурную зависимость плотности потока энергии лучистого чёрного тела. Он опубликовал резюме брошюры в 1884 и 1885 годах[20][A 8]. Стефан, вероятно, не знал о размышлениях Бартоли о вакууме в радиометре с 1876 года, пока в 1883 году Бартоли не получил публичную поддержку Генри Эдди, профессора математики и астрономии в Университете Цинциннати[21].
Радо фон Кёвелигети, изучавший теоретическую физику вместе со Стефаном в Венском университете, опубликовал спектральное уравнение в 1885 году в своей первой диссертации «Теория спектра», в которой предсказал предельную энергию излучения чёрного тела. Форма кривой зависимости спектральной плотности от длины волны была очень похожа на кривую Планка:
Фон Кёвеслигети записал функциональную форму спектрального уравнения следующим образом[17]:
где 




Его спектральное уравнение имело ту же форму, что и открытое Вином в 1893 году[22][23]:
Уравнение фон Кёвеслигети даёт зависимость постоянной 
где индекс 0 обозначает сравнительный источник излучения. Лучший выбор параметра в экспоненте 
Вывод[править | править код]
Вывод из закона Планка[править | править код]
Спектральную плотность излучения абсолютно чёрного тела как функцию длины волны 
где 



Плотность светового потока определяется интегралом по всем длинам волн:[24][25]
Введя новую переменную u :
где
приходим к интегралу:
Его вычисление даёт 
см. математические подробности
Сначала полезно вычислить интеграл более общего вида:
или, что то же самое,
Так как знаменатель всегда меньше 1, его можно разложить по степеням 
В основном уравнение берётся на сумму геометрического ряда. Дробь слева представляет собой выражение для ряда, обозначаемого суммой:
это обычный множитель 
Умножение на 
становится:
Поэтому индекс повышается на сумму единиц и отбрасывается 
Вводится новая переменная:
так что:
в:
интеграл превращается в:
или:
Поскольку каждый член суммы представляет собой сходящийся интеграл, сумма может быть получена из интеграла:
Интеграл справа — это гамма-функция, 

или эквивалент:
Для целых чисел :
или
и оттуда:
Для чётных целых чисел:
где 
так что:
аналитическое значение интеграла:
где 

График зависимости плотности потока энергии 

Окончательно плотность светового потока:
и закон Стефана — Больцмана (

с константами:
и постоянная излучения :
Термодинамический вывод[править | править код]
Больцман представил себе коробку, заполненную излучением чёрного тела, и поршень на одной стенке, толкаемый радиационным давлением[26]. Из тензора напряжения Максвелла классической электродинамики следует, что лучистое давление 

Полная внутренняя энергия 

Согласно первому и второму законам термодинамики (основное термодинамическое соотношение), изменение внутренней энергии равно:
откуда следует:
Согласно термодинамическому соотношению Максвелла:
можно написать:
Поскольку лучистое давление пропорционально плотности внутренней энергии, оно зависит только от температуры, а не от объёма. Применяется следующее:
в:
так что:
После расстановки переменных:
и интегрирования:
Последними являются плотность потока энергии и закон Стефана — Больцмана:
где постоянная Стефана, выраженная через другие основные константы, взята из предыдущего вывода, поскольку постоянная Планка h неизвестна классической электродинамике. Отсюда следует, что аддитивная константа:
Оглядываясь назад, можно увидеть, что Больцману либо повезло, либо, что более вероятно, он вдохновился на сравнение результатов классического электромагнетизма с идеей о том, что излучение ведёт себя как жидкость. В то время не было возможности дать ответ на вопрос о какой-либо частице жидкости, даже эвристический, до предположения Планка и систематического исследования квантования поля излучения. С помощью размерного анализа Больцман мог заключить, что если бы постоянная Стефана зависела от других основных констант, одна из них должна была бы содержать размерность массы, которые не были известны в классической физике. В современном смысле аргумент Больцмана эквивалентен утверждению о том, что тензор электромагнитного напряжения безследовый:
Это уравнение применимо к классическому полю Максвелла, и Больцман неявно предполагал, что оно применимо и к квантованному полю. В настоящее время известно несколько примеров теорий поля, для которых тензор напряжения является бесследовым на классическом уровне, но не при правильном квантовании теории. Примерами являются электродинамика, связанная с (безмассовыми) частицами с нетривиальными явлениями поляризации вакуума и неабелевой теории взаимодействий. Действительно, закон Стефана — Больцмана в квантовой электродинамике (КЭД) неприменим при высоких температурах[27].
n-мерное пространство[править | править код]
Закон важен и в n-мерном пространстве. Лучистое давление в n-мерном пространстве равно[28]:
так что:
От ассоциации:
следует:
но:
насколько это возможно
Тот же результат получается с интегралом по частоте в законе Планка для n-мерного пространства, в противном случае с другим значением постоянной Стефана для каждого измерения. В общем, константа та же[29][30]:
Это специально для 
за 
и для 
Примеры[править | править код]
Температура поверхности Солнца[править | править код]
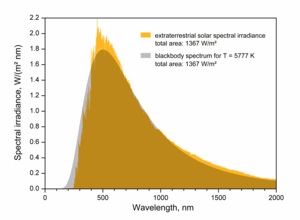
Спектр теплового излучения чёрного тела (серый по закону Планка) по сравнению со спектром Солнца на внешнем краю земной атмосферы (оранжевый). Плотность потока энергии одинакова в обоих случаях.
Используя свой закон, Стефан также определил температуру поверхности Солнца[A 1]. Он опирался на данные Жак-Луи Соре о том, что плотность потока энергии Солнца на Землю в 29 раз превышает плотность потока энергии нагретой металлической пластины. Соре измерил плотность потока энергии на Монблане. Стефан поместил круглую плитку на таком расстоянии от метра, чтобы она смотрела под тем же углом, что и Солнце. По оценкам Соре, температура плитки составит от 1900 °C до 2000 °С[A 9]. Стефан предположил, что 1/3 потока энергии Солнца удерживает атмосфера Земли. Поэтому он принял за правильный поток солнечной энергии на 3/2 большее значение, 29 · 3/2 = 43,5. Точные измерения атмосферного поглощения были сделаны только в 1888 и 1904 годах. Для температуры Стефан взял среднее значение двух предыдущих 1950 °С и для абсолютной термодинамической 2200 К. Так как 2,574 = 43,5, то из закона следует, что температура Солнца в 2,57 раза выше температуры плитки. Таким образом Стефан получил значение 5430 °С или 5703 К. Это было первое осмысленное значение температуры атмосферы Солнца.
Ему предшествовали значения от 1800 °С до 13 000 000 °С. Анджело Секки впервые назвал значение 18 000 000 °F (10 000 255 К), а позже 250 000 °F (139 144 К)[A 10]. Джон Уотерстон[en] в 1861 году и Франческо Россетти[en] в 1878 г. приводили преувеличенные значения. Россетти записал закон мощности излучения в форме[A 11]:
что дало без поправки на поглощение значение 10 238,4 К.
Ньютон определил интенсивность солнечного излучения, наблюдая за повышением температуры сухой земли при солнечном свете. В середине лета при ясной погоде на широте Лондона земля в полдень достигает 65,6 °С и 29,4 °С, так что разница составляет примерно 36,2 °С. Ньютон считал эту разницу верным показателем силы солнечного излучения. Таким образом, он показал, что комета 1680 года подвергалась воздействию температуры, в 7000 раз превышающей температуру кипения воды (212 · 7000 = 1 484 000 ° F (824,663 К)). Комета находилась в космосе на расстоянии 1/3 солнечного радиуса от поверхности Солнца. Из-за рассеивания лучей через солнечную атмосферу и на соответствующем расстоянии Джон Эрикссон сообщил о температуре солнечной фотосферы не менее 2 640 000 ° F (1 466 921 К)[A 12]. Год спустя, в 1872 году, Эрикссон пересчитал значение 4 036 000 °F (2.242.477 К)[A 6].
Дюлонг и Пти в 1817 году сообщили значение из соотношения степени охлаждения тел в вакууме 1900 °С[13]. Первое значение 1800 °С (между 1461 и 1761 °С) было определено Клодом Пулье в 1838 году из модели Дюлонга — Пти[19][A 6]. Пулье принял половину значения потока энергии Солнца. Вероятно, этот результат напомнил Стефану, что модель Дюлонга — Пти не работает при высоких температурах. Если солнечный свет собрать с помощью линзы, он может нагреть тело до температуры выше чем 1800 °С.
Излучения Солнца на его поверхность и на поверхность Земли одинаковы:
поэтому сегодняшнее расчётное значение:
где 



Температура звёзд[править | править код]
Температуру других звёзд можно определить аналогичным образом, рассматривая испускаемую энергию как излучение абсолютно чёрного тела[31]. Светимость звезды L:
r — радиус звезды и 
С помощью закона Стефана — Больцмана астрономы могут легко рассчитать радиус звезды.
Излучение Хокинга[править | править код]
Закон проявляется и в термодинамике чёрных дыр в излучении Хокинга. Температура излучения Хокинга равна:
Поверхность сферы Шварцшильда с радиусом Шварцшильда 
Таким образом, излучение чёрной дыры (при 
где 


Температура поверхности Земли[править | править код]
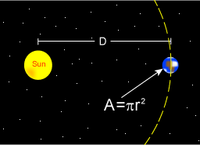
Солнечное излучение на Земле
Аналогичным образом можно рассчитать эффективную температуру поверхности Земли 
Таким образом, эффективная температура на поверхности Земли равна 6 ° С.
Приведённый выше расчет является грубым приближением, потому что по умолчанию Земля является чёрным телом. Равновесная планетарная температура имела бы одно и то же значение, если бы светимость и поглощательная способность планеты уменьшались на некую постоянную пропорцию на всех длинах волн, потому что входящие и исходящие значения всё равно были бы одинаковыми при одной и той же температуре. Однако эта температура больше не будет соответствовать определению эффективной температуры. Тот же результат получится, если предположить, что вся Земля представляет собой серое тело :
где отражательная способность и яркость одинаковы, так что отношение:
и является:
На самом деле Земля не имеет характеристик серого тела. Альбедо Земли таково, что около 30 % падающей солнечной радиации отражается обратно в космос. Из них 4 % отражённого излучения на поверхности, 20 % от облаков и 6 % выбрасывается в воздух. Если принять во внимание приведённую энергию Солнца и рассчитать температуру чёрного излучения, которое излучало бы столько энергии обратно в космос, то «эффективная температура», соответствующая такому представлению, составляет около 255 К[32].
где использовано
и является
По сравнению с 30 % отражения солнечной энергии, большее количество излучения с большими длинами волн поглощается или отражается от поверхности Земли в атмосферу и не передаётся за счёт парниковых газов, особенно: водяного пара, углекислого газа и метана[33][34]. Поскольку яркость (измеренная на более высоких длинах волн, где излучает Земля) уменьшается больше, чем поглощательная способность (измеренная на более низких длинах волн солнечного излучения), равновесная температура выше, чем показывает простое приближение чёрного тела, а не ниже. Фактическая средняя температура поверхности Земли составляет около 288 К, а не 279 К. Глобальное потепление увеличивает эту равновесную температуру из-за воздействия человека на парниковые газы. С 1880 года, когда общая равновесная температура предполагалась равной 13,6 °С, она повысилась на 0,7 °С до 14,3 °С, а плотность потока энергии глобального потепления составляет 0,02 Вт/м2[35].
Состояние радиационного равновесия Земли задаётся простой моделью нулевой траектории:
где а = 0,3 — средняя отражательная способность Земли и 
Тот же результат получается, если предположить, что атмосфера Земли является серым телом и принять во внимание её излучение 
Солнечное излучение по-разному отражается на разных длинах волн. У края атмосферы отражение в инфракрасном диапазоне равно 0,8, а у поверхности в видимом 0,2.
Плотность светового потока чёрных тел[править | править код]
В таблице приведены плотности излучаемого светового потока некоторых идеализированных чёрных тел или состояний.
 [ К ] |
 [ °С ] |
тело/состояние |  [Вт/м2 ] |
|---|---|---|---|
| 118,9 · 10−16 | Излучение Хокинга чёрной дыры с массой Солнца | 113,2 · 10−83 | |
| 0,0648 | -272 935 | световой поток, все ещё воспринимаемый человеческим глазом | 10−12[36] |
| 2,7 | -270,45 | космическая микроволновое реликтовое излучение | 3,013 · 10−6 |
| 14.01 | -259,14 | температура плавления жидкого водорода | 0,00218 |
| 184 | -89 | самая низкая измеренная температура на Земле (1983 год) | 65,0 |
| 273,15 | 0 | лёд | 315,0 |
| 288 | 15 | средняя температура на Земле | 390,1 |
| 298 | 25 | комнатная температура | 447,2 |
| 309,8 | 36,8 | средняя температура тело человека | 522,3 |
| 331 | 58 | самая высокая измеренная температура на Земле (1922 год) | 680,7 |
| 394 | 121 | Солнечное излучение на краю атмосферы | 1366 |
| 503 | 230 | горячая сварка стали | 3629,8 |
| 773 | 500 | горячий обогреватель | 20 245,6 |
| 798 | 525 | чёрное тело в точке Дрейпера | 22 994,4 |
| 1273 | 1000 | жёлтое пламя | 148 911,2 |
| 1941 г. | 1668 | расплавленный титан | 804 851,7 |
| 2041.4 | 1768,4 | расплавленная платина | 984 750,3 |
| 2773 | 2500 | лампа накаливания | 3 352 842,9 |
| 5776 | Солнечная фотосфера | 63 113 529,9 | |
| 25000 | средняя температура Вселенной через 10 000 лет после Большого взрыва | 22 150 001 850 | |
| 15,7 · 106 | Ядро Солнца | 3.445183366 · 1021 | |
| 10 · 109 | вспышка сверхновой | 567.04400475 · 1030 | |
| 140 · 1030 | Планковская температура чёрной дыры температура Вселенной 500 · 10−42 с после Большого взрыва |
217.8341047 · 10123 |
Плотность потока энергии приближения Вина[править | править код]

Плотность потока энергии в приближении Вина равна:
С той же переменной u, что и выше, интеграл переходит в:
а значение интеграла равно:
так что плотность потока энергии:
соответственно меньше.
Плотность потока энергии приближения Рэлея — Джинса[править | править код]
Плотность потока энергии в приближении Рэлея — Джинса равна:
Интеграл расходится:
так что плотность потока энергии бесконечна:
Это классический результат, согласно которому происходит непрерывный обмен энергией излучения.
Подтверждение, принятие и значение[править | править код]
Некоторые физики обвиняют Стефана в том, что его путь к открытию закона был довольно шатким. В частности, ошибкой оказалось использовать платину в качестве источника излучения абсолютно чёрного тела[37]. Было бы неправильно сказать, что он открыл закон вслепую. Многие счастливые совпадения повлияли на его целеустремленность, что часто случается со многими важными открытиями. Измерив теплопроводность, он убедился в неприменимости модель Дюлонга — Пти, использовал кинетическую теорию газов, применил абсолютную температуру[38]. В модели Дюлонга — Пти также использовалась температура по Цельсию. Вскоре после публикации статьи другие исследователи тоже начали проверять закон Стефана. Он был подтверждён Лео Гретцем в 1880 году и Кристианом Кристиансеном в 1884 году[39][40].
На момент открытия закона ещё не было до конца установлена его область применимости. В конце концов, исследователи поняли, что нужно использовать абсолютно чёрное тело. Модель чёрного тела была разработана Отто Люммером и Эрнстом Прингсгеймом в 1897 году и Фердинандом Курльбаумом в 1898 году[41]. В 1896 году Вильгельм Вин открыл закон смещения максимума спектра излучении чёрного тела. Макс Планк начал работать над излучением чёрного тела в 1894 году. Он впервые рассмотрел влияние электромагнитных волн на небольшой электрический диполь[41]. Он открыл свой закон в 1900 году, а лорд Рэлей и Джеймс Джинс представили свой закон в 1905 году на основе классической физики, который оказался аппроксимацией закона Планка. Закон Планка нельзя вывести только из уравнений электромагнитного поля, и необходимо учитывать подходы квантовой физики. Планк едва смирился с новой идеей, что излучение не может непрерывно обмениваться энергией со стенкой чёрного тела. Его формула сначала не воспринималась всерьёз, но в 1905 году Альберт Эйнштейн расширил свою идею и объяснил фотоэлектрическое явление в своей статье «Об эвристической позиции относительно происхождения и изменения света». В 1920 году Шатьендранат Бозе разработал теорию статистической фотонной механики, из которой удалось теоретически вывести закон Планка.
Значение Стефана солнечной температуры было независимо эмпирически подтверждено в 1894 году Уильямом Уилсоном и Греем с использованием гелиостата и переработанного дифференциального радиомикрометра, сделанного в 1889 году Чарльзом Бойзом. Прибор представлял собой комбинацию болометра и гальванометра. Используя нулевой метод, они сравнили солнечное излучение с излучением от электрически нагретой платиновой полосы. Они измерили эффективную температуру около 7073 К, что после нескольких поправок на поглощение в атмосфере Земли и атмосферы Солнца в 1901 году дало значение 6590 °С (6863 К)[A 13][42][43][44].
Примечания(А)[править | править код]
- ↑ 1 2 3 Stefan, 1879.
- ↑ 1 2 Boltzmann, 1884.
- ↑ Dulong, Petit, 1818.
- ↑ Tyndall, 1865b.
- ↑ Tyndall, 1865a.
- ↑ 1 2 3 Ericsson, 1872.
- ↑ Crova, 1880.
- ↑ Bartoli, 1884.
- ↑ Soret, 1872, pp. 228, 252—256.
- ↑ Young, 1880.
- ↑ Rossetti, 1878.
- ↑ Ericsson, 1871.
- ↑ Wilson, Gray, 1894.
Примечания[править | править код]
- ↑ Стефана — Больцмана закон излучения // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия (т. 1—2); Большая Российская энциклопедия (т. 3—5), 1988—1999. — ISBN 5-85270-034-7.
- ↑ Сивухин Д. В. § 118. Формула Планка // Общий курс физики. — М.: Наука, 1980. — Т. IV. Оптика. — С. 701—702. — 768 с.
- ↑ Stefan-Boltzmann constant (англ.). Fundamental Physical Constants. The NIST Reference on Constants, Units and Uncertainty. Дата обращения: 28 февраля 2018. Архивировано 29 июля 2020 года.
- ↑ 1 2 Strnad, 2006, p. 51.
- ↑ Južnič, 2004, p. 24.
- ↑ Мартинсон и Смирнов, 2004, с. 8.
- ↑ Трефил, Джеймс. Закон Стефана—Больцмана. https://elementy.ru/. Элементы. Дата обращения: 26 мая 2022. Архивировано 26 мая 2022 года.
- ↑ 1 2 Мартинсон и Смирнов, 2004, с. 9.
- ↑ Мартинсон и Смирнов, 2004, с. 10.
- ↑ Мартинсон и Смирнов, 2004, с. 11.
- ↑ 1 2 Мартинсон и Смирнов, 2004, с. 14.
- ↑ Južnič, 2004, p. 28.
- ↑ 1 2 Satterly, 1919.
- ↑ 1 2 Crepeau, 2007, с. 799.
- ↑ 1 2 Crepeau, 2007.
- ↑ Sitar, 1993, p. 80.
- ↑ 1 2 Balázs, Vargha, Zsoldos, 2008.
- ↑ Kangro, 1976, pp. 8–10.
- ↑ 1 2 Strnad, 1985, p. 48.
- ↑ Strnad, 2001, p. 149.
- ↑ Južnič, 2004, p. 29.
- ↑ Strnad, 1982, p. 8.
- ↑ Vargha, Balázs, 2008, p. 140.
- ↑ Stefan-Boltzmannov zakon (англ.). Дата обращения: 24 мая 2022. Архивировано из оригинала 23 августа 2000 года.
- ↑ Stefan-Boltzmannov zakon (англ.). PlanetPhysics.org. Дата обращения: 24 мая 2022. Архивировано из оригинала 11 сентября 2009 года.
- ↑ Cardy, 2010, p. 2.
- ↑ Cardy, 2010, p. 3.
- ↑ Giddings, 1984.
- ↑ Cardoso, de Castro, 2005, p. 563.
- ↑ Gonzalez-Ayala, Angulo-Brown, 2015.
- ↑ Izsev zvezd (англ.). Australian Telescope Outreach and Education. Дата обращения: 13 августа 2006. Архивировано 9 августа 2014 года.
- ↑ Kreith, 2000.
- ↑ Das, 1996.
- ↑ Cole, Woolfson, 2002.
- ↑ Nordell, 2003, p. 310.
- ↑ Strnad, 1978, p. 523.
- ↑ Dougal, 1979, p. 234.
- ↑ Strnad, 1990, p. 192.
- ↑ Sitar, 1993, p. 83.
- ↑ Južnič, 2004, p. 30.
- ↑ 1 2 Strnad, 1982, p. 3.
- ↑ Petrovay, 2020.
- ↑ Leaney, 2009.
- ↑ Butler, Elliottt, 1993.
Источники[править | править код]
- Balázs, Lajos G.; Vargha, Magda; Zsoldos, Endre (julij 2008). “Rado Köveslighety’s spectroscopic work”. Journal of Astronomical History and Heritage. 11 (2): 124—133. Bibcode:2008JAHH…11..124B. ISSN 1440-2807.
- Bartoli, Adolfo (1884). “Il calorico raggiante e il secondo principio di termodynamica” [Лучистое тепло и второй закон термодинамики] (PDF). Il Nuovo Cimento (1877-1894) [итал.]. 15: 196—202.
- Boltzmann, Ludwig Edward (1884). “Ableitung des Stefan’schen Gesetzes, betreffend die Abhängigkeit der Wärmestrahlung von der Temperatur aus der electromagnetischen Lichttheorie” [Вывод закона Стефана о зависимости теплового излучения от температуры из электромагнитной теории света]. Annalen der Physik und Chemie [нем.]. 22: 291—294. DOI:10.1002/andp.18842580616.
- Butler, C. J.; Elliottt, I. (1993). “Biographical and Historical Notes on the Pioneers of Photometry in Ireland”. DOI:10.1017/S0252921100007326.
- Cardoso, Tatiana R.; de Castro, Antonio S. (2005). “The blackbody radiation in a D-dimensional universes” (PDF). Revista Brasileira de Ensino de Física. 27 (4): 559—563. DOI:10.1590/S1806-11172005000400007.
- Cardy, John (2010). “The Ubiquitous ‘c’: from the Stefan-Boltzmann Law to Quantum Information”. Boltzmann Medal Lecture. Cairns. arXiv:1008.2331.
- Cole, George H. A.; Woolfson, Michael M. (2002). “Planetary Science: The Science of Planets Around Stars” (1 ed.). Institute of Physics Publishing: 36—37, 380—382. ISBN 0-7503-0815-X.
- Crepeau, John C. (2007). “Josef Stefan: His life and legacy in the thermal sciences”. Experimental Thermal and Fluid Science. 31: 795—803. DOI:10.1016/j.expthermflusci.2006.08.005.
- Crepeau, John C. (2009). “A brief history of the T4 radiation law” (PDF). 2009 ASME Summer Heat Transfer Conference.
- Crova, André-Prosper-Paul (1880). “Étude des radiations émises par les corps incandescents. Mesure optique des hautes températures” [Изучение излучения, испускаемого раскаленными телами. Оптическое измерение высоких температур]. Annales de chimie et de physique. Série 5 [фр.]. 19: 472—550.
- Das, P. K. (1996). “The Earth’s Changing Climate” (PDF). Resonance. 1 (3): 54—65.
- Dougal, R. C. (1979). “The centenary of the fourth-power law”. Phys. Educ. 14: 234—238.
- Dulong, P. L.; Petit, A. T. (1818). “Des Recherches sur la Mesure des Tempe´ratures et sur les Lois de la communication de la chaleur” [Исследование по измерению температуры и законам тепловой связи]. Annales de Chimie et de Physique. 7: 225—264.
- Ericsson, John (1871). “The temperature produced by solar radiation” [Температура, создаваемая солнечным излучением]. Nature [англ.]. 5: 46—48.
- Ericsson, John (1872). “The temperature of the surface of the sun” [Температура поверхности солнца]. Nature [англ.]. 5: 505—507.
- Giddings, Steven B. (1984). “Incoherent radiation in an n‐dimensional space”. American Journal of Physics. 52: 1125. Bibcode:1984AmJPh..52.1125G. DOI:10.1119/1.13741.
- Gonzalez-Ayala, Julian; Angulo-Brown, F. (2015). “Is the 3 + 1) − d nature of the universe a thermodynamic necessity?”. arXiv:1502.01843 [gr-qc].
- Južnič, Stanislav (2004). “Raziskovanje vakuuma na (dunajskem) fizikalnem inštitutu Jožefa Stefana : (ob stopetindvajsetletnici Stefanovega zakona)” [Вакуумные исследования в Физическом институте Йозефа Стефана (Вена): (к 125-й годовщине смерти Стефана)]. Vakuumist. 2 (4): 24—32. 18917159.
- Kangro, Hans (1976). “Early History of Planck’s Radiation Law”. Taylor & Francis. ISBN 0-85066-063-7.
- Kreith, Frank (2000). “The CRC Handbook of Thermal Engineering”. CRC Press/Springer. ISBN 3540663495.
- Leaney, Enda (2009). “Ireland’s national biographical dictionary”.
- Nordell, Bo (2003). “Thermal pollution causes global warming” (PDF). Global and Planetary Change. 38 (3—4): 305—312. DOI:10.1016/S0921-8181(03)00113-9.
- Pérez-Madrid, Agustin; Rubí, J. Miguel; Lapas, Luciano C. (2010-02-10). “Nonequilibrium Stefan-Boltzmann law”. Journal of Non-Equilibrium Thermodynamics. 35 (3). arXiv:1002.0794. DOI:10.1515/JNETDY.2010.017.
- Petrovay, Kristóf (2020). “The Determination of Stellar Temperatures from Baron B. Harkányi to the Gaia Mission”. Journal for the History of Astronomy. 51 (2): 152—152. arXiv:2003.08092. DOI:10.1177/0021828620918961.
- Poynting, John Henry (1904). “Radiation in the Solar System”. Nature. 70: 512—515.
- Rossetti, Francesco (1878). “Indagini sperimentali sulla temperatura del Sole” [Экспериментальные исследования температуры Солнца]. Atti della Realle Accademia dei Lincei. Memorie della Classe di scienze fisiche, matematiche e naturali (1877-1878, Serie 3) [итал.]. 275 (2): 169—201.
- Satterly, John (1919). “Radiation and the Temperature of the Sun”. Journal of the Royal Astronomical Society of Canada. 13 (2): 33—44. Bibcode:1919JRASC..13…33S.
- Sitar, Sandi (1993). “Jožef Stefan : pesnik in fizik : ob stoletnici smrti”. Ljubljana: Park.
- Soret, M. J.-L. (1872). “Comparaison des intensités calorifiques du rayonnement solaire et du rayonnement d’un corps chauffé à la lampe oxyhydrique” [Сравнение теплотворных способностей солнечного излучения и излучения тела, нагретого кислородно-водородной лампой]. Archives des sciences physiques et naturelles, Ser.2. 43-45: 220.
- Stefan, Jožef (1879). “Über die Beziehung zwischen der Wärmestrahlung und der Temperatur” [О связи между тепловым излучением и температурой] (PDF). SAW [нем.]. 79 (II): 391—428.
- Strnad, Janez (1978). “Fizika, 2. del, Elektrika, Optika”. Ljubljana: DZS: 524.
- Strnad, Janez (1979). “Sto let Stefanovega zakona”. Obzornik za matematiko in fiziko. 26 (3): 65—73. (PACS 01.65.+g).
- Strnad, Janez (1982). “Začetki kvantne fizike: od kvanta do snovnega valovanja” (Presekova knjižnica; 9 ed.). Ljubljana: DMFA: 1—48.
- Strnad, Janez (1985). “Jožef Stefan, Ob stopetdesetletnici rojstva” (Presekova knjižnica; 24 ed.). Ljubljana: DMFA: 1—64.
- Strnad, Janez (1990). “Zgodbe iz fizike”. Ljubljana: Slovenska matica.
- Strnad, Janez (2001). “Sevalni tlak in P. N. Lebedev”. Obzornik za matematiko in fiziko. 48 (5): 148—153. (PACS 01.60, 33.80.P).
- Strnad, Janez (2006). “Planckov začetek kvantne fizike”. Obzornik za matematiko in fiziko. 53 (2): 51—63. (PACS 01.65.+g).
- Tyndall, John (1865a). “Über leuchtende und dunkle Strahlung” [О светящемся и тёмном излучении]. Annalen der Physik und Chemie [нем.]. 200: 36—53.
- Tyndall, John (1865b). “Heat considered as a Mode of Motion” [Теплота как способ движения] (PDF) [англ.]. D. Appleton & Company.
- Vargha, Magda; Balázs, Lajos G. (2008). “Kovesligethy’s spectroscopic studies” (PDF). Communications in Asteroseismology. 149: 136—142.
- Wilson, William Edward; Gray, P. E. (1894). “Experimental Investigations on the Effective Temperature of the Sun” [Экспериментальные исследования эффективной температуры Солнца]. Proceedings of the Royal Society of London Series I [англ.]. 55: 250—251.
- Wilson, William Edward (1900). “Astronomical and physical researches made at Mr. Wilson’s Observatory, Daramona, Westmeath” (PDF).
- Young, Charles Augustus (1880). “The Sun’s Heat” [Солнечное тепло]. Popular Science Monthly [англ.]. 18.
- Мартинсон, Л. К.; Смирнов, Е. В. Квантовая теория. — М.: Изд-во МГТУ им. Н. Э. Баумана, 2004. — 496 с. — ISBN 5703824389.
Действие закона Стефана-Больцмана
Закон Стефана-Больцмана: совместимость абсолютно черного тела пропорциональна четвертой степени его температуры.
Тела, нагретые до какой-то температуры, способны излучать энергию. Она состоит из электромагнитных волн с различной длиной. Выражение «раскален докрасна» означает, что температура объекта настолько велика, что тепловое излучение происходит в видимой, световой области спектра. При рассмотрении тел на атомарном уровне возбужденные атомы испускают фотоны, которые формируют излучение.
Действие закона Стефана-Больцмана можно объяснить с помощью рассмотрения атома, который излучает свет в недрах Солнца. Свет будет поглощен мгновенно другим атомом и излучен им повторно. Таким образом, потенциальный свет будет перемещаться между атомами по цепочке. Для такой системы характерно энергетическое равновесие.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Равновесному состоянию можно дать следующее обозначение:
- Свет со строго определенной частотой будет поглощен одним атомом в одной точке.
- Одновременно будет наблюдаться испускание света с такой же частотой другим атомом в другой точке.
- Показатели интенсивности света каждой длины волны спектра остаются стабильными.
Внутри Солнца наблюдается падение температуры с удалением от центра звезды. Если двигаться на поверхность, то можно отметить более высокие температуры светового излучения по сравнению с температурой окружающей среды, соответствующие определенному спектру. В итоге, повторное излучение, исходя из закона Стефана-Больцмана, характеризуется более низкими энергиями и частотами.
Однако, согласно закону сохранения энергии, количество излучаемых фотонов будет увеличиваться. Таким образом, на момент достижения излучением поверхности звезды спектральное распределение будет определено в соответствии с температурой поверхности Солнца, то есть около 5 800 К, а не температурой центра Солнца, которая составляет примерно 15 000 000 К.
История открытия
Данная закономерность была сформулирована в 1879 году физиком из Австрии Йозефом Стефаном. Основанием для открытия послужили экспериментальные измерения. Непосредственно сами опыты были проведены ирландским физиком Джоном Тиндалем.
В 1884 году Людвиг Больцман проводил теоретические исследования с применением термодинамики. В результате ученый пришел к этому закону изучения черного тела. Рассуждения Больцмана были построены на изучении некого идеального двигателя, в качестве энергетического источника которого использовался свет. Экспериментально подтвержденный закон был опубликован Стефаном в статье с названием «Об отношении между излучением и абсолютной температурой», которая была включена в одну из брошюр Академии наук Вены.
Концепция черного тела
Черное тело — теоретический объект, обладающий способностью к поглощению абсолютно всей электромагнитной энергии, попадающей на его поверхность.
Закономерность Стефана-Больцмана справедлива при условии наблюдения за абсолютно черным телом, которое поглощает излучение, попадающее на поверхность, в полном объеме. В реальном мире физические объекты способны поглощать лишь какую-то часть лучевой энергии. Остальное излучение отражается от их поверхности.
Следует отметить, что закон, исходя из которого удельная мощность излучения с их поверхности пропорциональна Т4, работает и при реальных условиях. Только в данной ситуации необходимо постоянную Больцмана заменить на другой коэффициент, отражающий характеристики реального физического объекта. Определить такую константу можно с помощью эксперимента.
Математическая формула закона излучения
Энергия, поступая к поверхности Солнца или любого другого горячего объекта, отражается от него в виде излучения. Определить характер излученной энергии позволяет закон Стефана-Больцмана. В виде формулы закономерность записывают в следующем виде:
(E=sigma T^{4})
Где Т является температурой и измеряется в Кельвинах, σ представляет собой постоянную Больцмана.
Согласно уравнению, можно сделать вывод, что повышение температуры сопровождается увеличением светимости тела в значительно большей степени. При повышении температуры объекта в 2 раза, его светимость увеличится в 16 раз.
Использование закона Стефана-Больцмана
Йозеф Стефан применил самостоятельно открытый закон на практике. С помощью выведенной закономерности ученому удалось определить температуру, которой обладает поверхность Солнца. Стефан использовал данные Чарльза Сорета, в которых указано, что величина плотности потока солнечной энергии в 29 раз превышает аналогичные показатели электромагнитного излучения нагретой пластины из металла. Ученый разместил пластину от датчика электромагнитного излучения под тем же углом, под которым видно Солнце с нашей планеты. Результаты эксперимента Сорета оценивали температуру пластины в 1900-2000 градусов.
В опыте Йозефа Стефана было учтено, что солнечное излучение поглощается атмосферой на Земле. По его предположению, поток энергии от звезды в реальных условиях в 43,5 раз превышает аналогичные показатели нагретой пластины. Данное исследование послужило началом для ряда экспериментов по измерению точного атмосферного поглощения энергии от Солнца, которые проводились в период с 1888 по 1904 года.
Исходя из закона Стефана-Больцмана, достаточно просто прийти к выводу, что температура на поверхности нашей звезды превышает температуру металлической пластины в 2,57 раза. Расчет выполняется с помощью извлечения корня четвертой степени от отношения потоков энергии Солнца и пластины. По итогам эксперимента Стефан вычислил, что температура поверхности звезды составляет 5712 К. Стоит отметить, что по современным данным данный показатель равен 5780 К.
|
ОПРЕДЕЛЕНИЕ ПОСТОЯННОЙ СТЕФАНА-БОЛЬЦМАНА Цель работы: изучение Приборы и принадлежности: 1. ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ Тепловым или температурным излучением называется Тепловое излучение относится к равновесному. Если на тело Основными характеристиками теплового излучения являются Энергетическая светимость тела Rт – это полная энергия, испускаемая единицей площади
Лучеиспускательная (излучательная) способность
Эта величина является функцией длины волны (частоты) и температуры
Лучепоглощательная способность тела аν,Т (аλ,Т)
где dWпогл – энергия, Лучеиспускательная rλ,Т и лучепоглощательная аλ,Т способности зависят не только от длины волны (частоты) |
|||||||||||||||||||||||||||||||||
|
Тело, поглощающее всю падающую
|
|||||||||||||||||||||||||||||||||
|
Для разных тел величины |
|||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
|
где f (ν, Т) Применим закон Кирхгофа к
где εν,Т – лучеиспускательная f (ν, Т) = εν,Т. (7) Установлены следующие законы Закон Стефана–Больцмана: энергетическая светимость абсолютно |
|||||||||||||||||||||||||||||||||
|
где Закон смещения Вина (первый закон): длина волны λ0, на которую
где Выражение (9) потому называют |
|||||||||||||||||||||||||||||||||
|
На рис. 2 изображены кривые распределения энергии излучения |
|||||||||||||||||||||||||||||||||
|
где в/ = 1,29 · 10-5 Вт/(м3 · К5) Для объяснения законов теплового
где Планк на основе квантовых
где с – скорость света в вакууме; k Интегрируя функцию Планка (12)
Если взять производную по λ от функции Планка (13) и Рассмотренные закономерности |
|||||||||||||||||||||||||||||||||
|
2. ОПИСАНИЕ РАБОЧЕЙ УСТАНОВКИ Если излучение происходит в
где Т – температура тела; Т0 Измерение температуры тела в Комплект оптического пирометра с Внешний вид пирометра изображен Оптическая схема пирометра с В фокусе объектива 1 (см. рис. 4) помещена электрическая |
|||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
Рис. 3 |
|||||||||||||||||||||||||||||||||
|
Лампочка 2 питается током от аккумуляторной батареи. Накал нити регулируется |
|||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
Рис. 4 |
|||||||||||||||||||||||||||||||||
|
Если исследуемая поверхность не
|
|||||||||||||||||||||||||||||||||
|
Для данной температуры tярк, которая
Окончательно
|
|||||||||||||||||||||||||||||||||
|
где Т – действительная Задачей данной работы является В нашей работе нагретым телом,
где S – общая поверхность раскаленного Из формулы (18)
где Р – мощность, По формуле (19) определяют σ. Постоянную Планка h определяют из формулы
полученной в квантовой теории
где |
|||||||||||||||||||||||||||||||||
|
3. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 3.1. Собирают электрическую цепь (рис. 6), но не 3.2. Подключают к блоку питания, соединяя клеммы 3.3. Перемещая окуляр пирометра, устанавливают его так, 3.4. Вводят красный светофильтр (см. рис. 3).
3.6. Вращая кольцо пирометра, изменяют яркость нити 3.7. Так как волосок 3.8. Опыт повторяют три раза для различных значений мощности |
|||||||||||||||||||||||||||||||||
|
Форма |
|||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||
|
3.9. По 3.10. Используя 3.11. Оценивают погрешность ВОПРОСЫ
|
Светимость абсолютно черного тела пропорциональна четвертой степени его температуры.
Нагретые тела излучают энергию в виде электромагнитных волн различной длины. Когда мы говорим, что тело «раскалено докрасна», это значит, что его температура достаточно высока, чтобы тепловое излучение происходило в видимой, световой части спектра. На атомарном уровне излучение становится следствием испускания фотонов возбужденными атомами (см. Излучение черного тела). Закон, описывающий зависимость энергии теплового излучения от температуры, был получен на основе анализа экспериментальных данных австрийским физиком Йозефом Стефаном и теоретически обоснован также австрийцем Людвигом Больцманом (см. Постоянная Больцмана).
Чтобы понять, как действует этот закон, представьте себе атом, излучающий свет в недрах Солнца. Свет тут же поглощается другим атомом, излучается им повторно — и таким образом передается по цепочке от атома к атому, благодаря чему вся система находится в состоянии энергетического равновесия. В равновесном состоянии свет строго определенной частоты поглощается одним атомом в одном месте одновременно с испусканием света той же частоты другим атомом в другом месте. В результате интенсивность света каждой длины волны спектра остается неизменной.
Температура внутри Солнца падает по мере удаления от его центра. Поэтому, по мере движения по направлению к поверхности, спектр светового излучения оказывается соответствующим более высоким температурам, чем температура окружающий среды. В результате, при повторном излучении, согласно закону Стефана—Больцмана, оно будет происходить на более низких энергиях и частотах, но при этом, в силу закона сохранения энергии, будет излучаться большее число фотонов. Таким образом, к моменту достижения им поверхности спектральное распределение будет соответствовать температуре поверхности Солнца (около 5 800 К), а не температуре в центре Солнца (около 15 000 000 К).
Энергия, поступившая к поверхности Солнца (или к поверхности любого горячего объекта), покидает его в виде излучения. Закон Стефана—Больцмана как раз и говорит нам, какова излученная энергия. Этот закон записывается так:
E = σT 4
где Т — температура (в кельвинах), а σ — постоянная Больцмана. Из формулы видно, что при повышении температуры светимость тела не просто возрастает — она возрастает в значительно большей степени. Увеличьте температуру вдвое, и светимость возрастет в 16 раз!
Итак, согласно этому закону любое тело, имеющее температуру выше абсолютного нуля, излучает энергию. Так почему, спрашивается, все тела давно не остыли до абсолютного нуля? Почему, скажем, лично ваше тело, постоянно излучая тепловую энергию в инфракрасном диапазоне, характерном для температуры человеческого тела (чуть больше 300 К), не остывает?
Ответ на этот вопрос, на самом деле, состоит из двух частей. Во-первых, с пищей вы получаете энергию извне, которая в процессе метаболического усвоения пищевых калорий организмом преобразуется в тепловую энергию, восполняющую потери вашим телом энергии в силу закона Стефана—Больцмана. Умершее теплокровное весьма быстро остывает до температуры окружающей среды, поскольку энергетическая подпитка его тела прекращается.
Еще важнее, однако, тот факт, что закон распространяется на все без исключения тела с температурой выше абсолютного нуля. Поэтому, отдавая свою тепловую энергию окружающей среде, не забывайте, что и тела, которым вы отдаете энергию, — например, мебель, стены, воздух, — в свою очередь излучают тепловую энергию, и она передается вам. Если окружающая среда холоднее вашего тела (как чаще всего бывает), ее тепловое излучение компенсирует лишь часть тепловых потерь вашего организма, и он восполняет дефицит за счет внутренних ресурсов. Если же температура окружающей среды близка к температуре вашего тела или выше нее, вам не удастся избавиться от избытка энергии, выделяющейся в вашем организме в процессе метаболизма посредством излучения. И тут включается второй механизм. Вы начинаете потеть, и вместе с капельками пота через кожу покидают ваше тело излишки теплоты.
В вышеприведенной формулировке закон Стефана—Больцмана распространяется только на абсолютно черное тело, поглощающее всё попадающее на его поверхность излучение. Реальные физические тела поглощают лишь часть лучевой энергии, а оставшаяся часть ими отражается, однако закономерность, согласно которой удельная мощность излучения с их поверхности пропорциональна Т 4, как правило, сохраняется и в этом случае, однако постоянную Больцмана в этом случае приходится заменять на другой коэффициент, который будет отражать свойства реального физического тела. Такие константы обычно определяются экспериментальным путем.







![{displaystyle {frac {mathrm {d} j^{star }}{mathrm {d} lambda }}=left[1-a(lambda )right]left({frac {mathrm {d} j^{star }}{mathrm {d} lambda }}right)_{0}!,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d2b3971a088c596c1419c54f3784b8337da5fec)



























































![{displaystyle mathrm {const.} =ln {frac {2pi ^{5}k_{rm {B}}^{4}}{15h^{3}c_{0}^{3}}}=-36,204022,ln left[mathrm {J/(m^{3},K^{4})} right]!,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c7ae0a2d5393a96b5f2c0ce957301f242a85baa)















![{displaystyle T_{odot }={sqrt[{4}]{frac {j_{odot }4pi a_{0}^{2}}{sigma 4pi r_{odot }^{2}}}}={sqrt[{4}]{frac {j_{odot }a_{0}^{2}}{sigma r_{odot }^{2}}}}={sqrt[{4}]{frac {1366cdot 149597870691^{2}}{5{,}670400cdot 10^{-8},cdot ,(6{,}960cdot 10^{8})^{2}}}}=5775,9 mathrm {K} !,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/052cbd1686c2d3809affa52a8aa60922a28ab129)








![{displaystyle T_{{rm {Z}},0}={sqrt[{4}]{frac {j_{odot }}{4sigma }}}=T_{odot }{sqrt {frac {r_{odot }}{2a_{0}}}}!,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d4ec02f387797b66929bab6dffcb1aa6ec0bea2)


![{displaystyle T_{{rm {Z}},1}={sqrt[{4}]{frac {(1-a)j_{odot }}{4sigma }}}={sqrt[{4}]{frac {(1-0,3)cdot 1366}{4cdot 5{,}670400cdot 10^{-8}}}}approx 255;{rm {K}}!,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae39edce62bac1bd2e845ae82753a694aad7f553)

![{displaystyle T_{{rm {Z}},2}={sqrt[{4}]{frac {(1-a)j_{odot }}{4varepsilon sigma }}}={sqrt[{4}]{frac {(1-0,3)cdot 1366}{4cdot 0,612cdot 5{,}670400cdot 10^{-8}}}}approx 288;{rm {K}}!,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6bdde69d0a492f68acc42b423c61804fea75475d)
![{displaystyle T_{{rm {Z}},2}=T_{{rm {Z}},1}{sqrt[{4}]{frac {2}{2-varepsilon _{o}}}}=T_{{rm {Z}},1}{sqrt[{4}]{frac {1}{varepsilon }}}=255cdot {sqrt[{4}]{frac {2}{2-0,776}}}=255cdot {sqrt[{4}]{frac {1}{0,612}}}approx 288;{rm {K}}!,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f16ffe4409e405756581af9e70c29bc1bbf8f75)












 Моделью
Моделью










 Эта
Эта
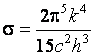

 3.5. Замыкают цепь лампы накаливания (см.
3.5. Замыкают цепь лампы накаливания (см.