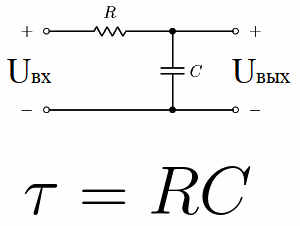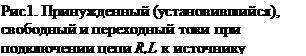Электрическая цепь RC
Рассмотрим ток в электрической цепи, состоящей из конденсатора ёмкостью C и резистора сопротивлением R, соединённых параллельно.
Значение тока заряда или разряда конденсатора определится выражением I = C(dU/dt), а значение тока в резисторе,
согласно закону Ома, составит U/R, где U – напряжение заряда конденсатора.
Из рисунка видно, что электрический ток I в элементах C и R цепи будет иметь одинаковое значение и
противоположное направление, согласно закону Кирхгофа. Следовательно, его можно выразить следующим образом:
Решаем дифференциальное уравнение C(dU/dt)= -U/R

Из таблицы интегралов здесь используем преобразование
Получаем общий интеграл уравнения: ln|U| = – t/RC + Const.
Выразим из него напряжение U потенцированием: U = e-t/RC * eConst.
Решение примет вид:
U = e-t/RC * Const.
Здесь Const – константа, величина, определяемая начальными условиями.
Следовательно, напряжение U заряда или разряда конденсатора будет меняться во времени по экспоненциальному закону
e-t/RC.
Экспонента – функция exp(x) = ex
e – Математическая константа, приблизительно равная 2.718281828…
Постоянная времени τ
Если конденсатор емкостью C последовательно с резистором сопротивлением R подключить к источнику постоянного напряжения U,
в цепи пойдёт ток, который за любое время t зарядит конденсатор до значения UC и определится выражением:

Тогда напряжение UC на выводах конденсатора будет увеличиваться от нуля до значения U по экспоненте:
UC = U(1 – e-t/RC)
При t = RC, напряжение на конденсаторе составит UC = U(1 – e-1) = U(1 – 1/e) .
Время, численно равное произведению RC, называется постоянной времени цепи RC и обозначается греческой буквой τ.
Постоянная времени τ = RC
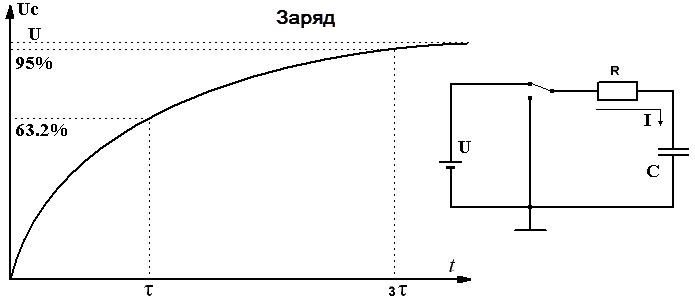
За время τ конденсатор зарядится до (1 – 1/e)*100% ≈ 63,2% значения U.
За время 3τ напряжение составит (1 – 1/e3)*100% ≈ 95% значения U.
За время 5τ напряжение возрастёт до (1 – 1/e5)*100% ≈ 99% значения U.
Если к конденсатору емкостью C, заряженному до напряжения U, параллельно подключить резистор сопротивлением R,
тогда в цепи пойдёт ток разряда конденсатора.
Напряжение на конденсаторе при разряде будет составлять UC = Ue-t/τ = U/et/τ.
За время τ напряжение на конденсаторе уменьшится до значения U/e, что составит 1/e*100% ≈ 36.8% значения U.
За время 3τ конденсатор разрядится до (1/e3)*100% ≈ 5% от значения U.
За время 5τ до (1/e5)*100% ≈ 1% значения U.
Параметр τ широко применяется при расчётах RC-фильтров различных электронных цепей и узлов.
Замечания и предложения принимаются и приветствуются!
Есть простейшая схема состоящая из источника питания с напряжением 10V, кнопки, резистора сопротивлением 1кОм и конденсатора ёмкостью 1000мфк. Сочетание конденсатора и резистора называется резистивно-емкостной цепочкой (или RC-цепь, R – резистор, С-конденсатор). Через какое время после нажатия на кнопку напряжение на конденсаторе сможет достичь значения напряжения источника питания?
Для ответа на этот вопрос необходимо построить график изменения напряжения на конденсаторе в зависимости от времени. Делать это с помощью вольтметра не очень удобно, поэтому я воспользуюсь платой Arduino и модулем цифрового вольтметра INA219 из прошлой статьи. (перед проведением опыта конденсатор необходимо полностью разрядить перемкнув его выводы перемычкой)!
Скетч который в данном случае cможет заменить осциллограф состоит из 3 строк кода (строим график только если напряжение на конденсаторе больше 0.1V и прекращаем строить если больше 9.9V)
Открываем плоттер порта в среде Arduino IDE, “клацаем” кнопку и на выходе получаем симпатичную картинку.
Осталось проанализировать получившийся график.
Из графика хорошо видно, что скорость зарядки конденсатора падает по мере роста на нем напряжения.
Если представить, что резистор это вентиль, ограничивающий поток воды, а конденсатор это резиновый шарик, который будет наполняться – то если
закрыть вентиль до такой степени, что вода будет просачиваться по каплям – шарик будет заполняться очень долго.
По мере того как шарик наполняется, оболочка растягивается, оказывая большее давление на его содержимое. С увеличением давления внутри шарика, оно выталкивает входящий поток воды и следовательно с течением времени вода будет заполнять шарик все медленнее. Если предположить, что шарик не лопнет – процесс закончится когда давление внутри шарика сравняется с давлением воды в трубе.
Похожие процессы происходят в конденсаторе. Сначала электроны стремительно поступают, но по мере заполнения пространства новоприбывшим требуется больше времени на поиск свободного места. Процесс заряда становится все более медленным и медленным, а на самом деле теоретически никогда не сравняется с подаваемым на него напряжением.
Скорость с которой заряжается конденсатор зависит от параметра – постоянная времени.
TC = R * C
- TC – постоянная времени в секундах
- С – емкость конденсатора в фарадах
- R – сопротивление в омах
Для нашего примера:
TC = 1 кОм * 1000мкф = 1000 Ом * 0.001Ф = 1с.
Постоянная времени RC цепи ТС это время (сек) необходимое конденсатору для того, чтобы напряжение на нем составило 63% от подаваемого напряжения, если заряд начинался с нулевого значения.
Для нашего случая в первую секунду конденсатор должен будет зарядиться до значения:
10V / 100 * 63 = 6.3V
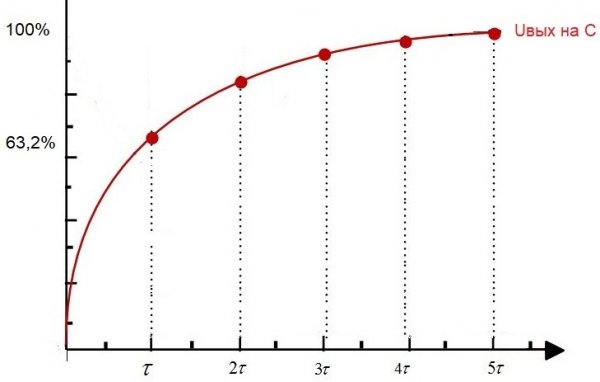
А дальше смотрим картинку:
Считаем:
Первая секунда:
10*0.63 = 6.3V
Вторая секунда:
10 – 6.3 = 3.7
3.7 * 0.63 = 2.33
6.3 + 2.33 = 8.63V
Третья секунда:
10 – 8.63=1.37
1.37 * 0.63 = 0.86
8.63 + 0.86 = 9.49V
Четвертая секунда:
10 – 9.49 = 0.51
0.51 * 0.63 = 0.32
9.49 + 0.32 = 9.81V
Пятая секунда:
10 – 9.81 = 0.19
0.19 * 0.63 = 0.11
9.81 + 0.11 = 9.92V
В мире идеальных компонентов процесс заряда будет продолжаться бесконечно. В реальных условиях считается, что по истечении временного интервала, равного 5 постоянным времени, заряд конденсатора приблизится к 100% и можно считать процесс завершенным.
Если вы еще раз обратите внимание на мой реальный график – цифры будут несколько отличаться от расчетных. Здесь много причин влияющих на результат измерений: номинал резистора не ровно 1000 Ом, емкость конденсатора не ровно 1000 микрофарад, сопротивление контактов макетной платы, внутреннее сопротивление вольтметра INA219, небольшой ток утечки присущий любому электролиту, помехи от ПК и много чего другого. Тем не менее Arduino остановило отрисовку графика ровно через 5 секунд, и окончательный расчёт времени зарядки конденсатора достаточно простой:
T = 5*R*C = 5 * 1000 Ом * 0.001 Ф = 5 сек.
что для практических целей необходимо и достаточно.
Полный список всех статей на канале доступен по этой ссылке:
Если информация была полезной не забудьте подписаться и поставить лайк. Всем удачи!
Лабораторная работа № 6
Цель
работы: изучение
процессов при замыкании и размыкании
электрической цепи, имеющей индуктивность
и сопротивление; определение постоянной
времени
-цепи.
Приборы
и материалы:
лабораторный стенд, имеющий набор
объектов на плате, генератор сигналов,
осциллограф, набор соединительных
проводов.
1. Краткая теория
Электрический ток, текущий в любом
контуре, создает пронизывающий этот
контур магнитный поток. При изменениях
силы тока изменяется также и магнитный
поток, вследствие чего в контуре возникает
ЭДС самоиндукции
.
Это приводит к тому, что установление
тока при замыкании цепи и убывание тока
при размыкании цепи происходит не
мгновенно, а постепенно.
Рассмотрим
цепь с не зависящей от силы тока
индуктивностью
,
сопротивлением
и источником тока
(рис. 6.1). Такая цепь называется
-цепью.
В литературе [1]
показано, что при подключении к цепи
источника тока функция, описывающая
нарастание тока, имеет вид:
. (6.1)
А
функция, описывающая убывание тока
после отключения источника тока:
.
(6.2)
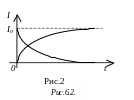
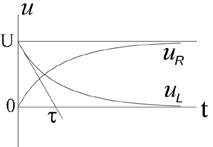
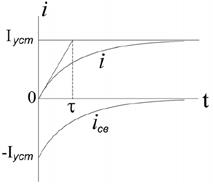
Графики возрастания и убывания тока
при замыкании и размыкании цепи приведены
на рис. 6.2. Скорость возрастания или
убывания тока характеризуется величиной,
имеющей размерность времени:
,
(6.3)
которую называют постоянной времени
–цепи.
Заменив в (6.1) и в (6.2)
через
,
получим:
, (6.4)
. (6.5)
В соответствии с формулой (6.5)
есть время, в течение которого сила тока
уменьшается в
раз. Из (6.3) и (6.5) видно, что чем больше
индуктивность цепи
и меньше ее сопротивление
,
тем больше постоянная времени
и тем медленнее спадает ток в цепи.
2. Методика выполнения работы
В данной работе к
-цепи
в качестве источника тока подключается
генератор прямоугольных импульсов. В
результате этого, действие переднего
фронта прямоугольного импульса аналогично
подключению к цепи источника
,
а действие заднего фронта – отключению
от цепи источника
.
В соответствии с выше сказанным, сигнал
будет иметь не строго прямоугольную
форму. Его передний фронт будет описываться
выражением (6.4), а задний фронт – выражением
(6.5).
В работе, используя изображения импульса
на экране осциллографа, измеряется
напряжение на сопротивлении
как функция времени
:
для переднего и заднего фронтов импульса.
Используя (6.4), (6.5) и закон Ома, можно
получить следующие выражения:
, (6.6)
. (6.7)
Построив графики функции
и
от времени
,
находят тангенс угла наклона каждого
из графиков
и в обоих случаях определяют постоянную
времени
.
Сравнивают полученные результаты.
3. Выполнение упражнений и обработка результатов измерений Задание. Определить постоянную времени -цепи.
1. Подготовка экспериментальной
установки к работе
Перед началом измерений следует
ознакомиться с работой генератора
сигналов и электронного осциллографа.
1
.1.
Соберите электрическую схему (рис.6.3),
состоящую из генератора сигналов
,
катушки индуктивности
,
резистора
и осциллографа. Резистор и катушка
индуктивности входят в состав
соответственно магазина сопротивлений
и магазина индуктивностей, находящихся
на плате лабораторного стенда. Используя
ручки регулировки генератора сигналов,
подготовьте его к работе в качестве
источника прямоугольных импульсов.
Значения сопротивления
,
индуктивности
и частоты сигналов генератора указываются
преподавателем.
1.2. После проверки электрической схемы
преподавателем или инженером приступите
к выполнению задания.
2. Определение постоянной времени
-цепи
2.1. Включите осциллограф и генератор
сигналов. Дайте приборам прогреться
около 5 минут.
2.2. Используя ручки регулировки генератора
сигналов и органов управления
осциллографом, добейтесь устойчивого
изображения сигнала на экране осциллографа.
2.3. Зарисуйте осциллограмму.
2.4. По экрану осциллографа произведите
измерения напряжения
в различные моменты времени для переднего
и заднего фронта импульса (по 10 точек
для каждого фронта импульса). Точки
следует брать в наиболее искривленных
участках осциллограммы. Результаты
измерений занести в таблицу 6.1. Следует
отметить, что для начального момента
времени
=0
имеем: в случае переднего фронта импульса
=0
и
=0;
в случае заднего фронта импульса
=
и
=0.
Таблица
6.1
|
№ п/п |
Для переднего |
Для заднего фронта |
||||||
|
, |
, мс |
, |
, |
, мс |
, |
|||
2.4. Постройте графики зависимостей
для переднего фронта и
для заднего фронта импульса.
2.5. По построенным графикам определите
постоянные времени
для переднего фронта и для заднего
фронта импульса, как величины обратные
тангенсам углов наклона полученных
прямых. Сравните полученные значения
между собой и со значением, рассчитанным
по формуле:
.
2.6. Оставив неизменным значение
индуктивности, повторить измерения еще
для трех сопротивлений отличных от
первоначального значения.
2.7. Оставив неизменным первоначальное
значение сопротивления, повторить
измерения еще для трех катушек, значения
индуктивностей которых отличны от
первоначального.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
how can ı fınd tıme constant in graph with use cursor
Move your cursor to the point in the red circle below: –
That’s equivalent to 1 time constant as per the purple trace in the graph below: –
Image from Electronics Tutorials.
And, from your graph I estimate the time constant to be 0.5 μs whereas, in your circuit it is clearly numerically 0.44 μs: –
So, move your cursors to where I suggest and, get better numbers than those I had available.
What Scott is alluding to in comments is worth putting in the answer: –
So, both the initial slope of current and the 37% decay point predict the time constant.
На чтение 14 мин Просмотров 3 Опубликовано 11 апреля 2023 Обновлено 11 апреля 2023
Содержание
- Постоянная времени электрической цепи — что это такое и где используется
- Постоянная времени цепи RC
- Электрическая цепь RC
- Постоянная времени τ
- Постоянная времени на графике
- Электрическая цепь RC
- Постоянная времени τ
- Электрическая цепь RC
- Постоянная времени τ
Постоянная времени электрической цепи — что это такое и где используется
Природе свойственны периодические процессы: день сменяет ночь, теплое время года сменяется холодным и т. д. Период этих событий почти постоянен и поэтому может быть строго определен. Кроме того, мы вправе утверждать, что приведенные в качестве примера периодические природные процессы не являются затухающими, по крайней мере по отношению к продолжительности жизни одного человека.
Однако в технике, а в электротехнике и в электронике — особенно, далеко не все процессы являются периодическими и незатухающими. Обычно какой-нибудь электромагнитный процесс сначала возрастает, а затем убывает. Часто дело ограничивается лишь фазой начала колебания, которое так и не успевает толком набрать размах.
Сплошь и рядом в электротехнике можно встретить так называемые экспоненциальные переходные процессы, суть которых заключается в том, что система просто стремится придти к какому-то равновесному состоянию, которое в конце концов выглядит как состояние покоя. Такой переходный процесс может быть как нарастающим, так и спадающим.
Внешняя сила сначала выводят динамическую систему из состояния равновесия, а затем не препятствует естественному возврату данной системы к ее исходному состоянию. Эта последняя фаза и есть так называемый переходный процесс, которому свойственна определенная длительность. Кроме того процесс выведения системы из равновесия также является переходным процессом с характерной длительностью.
Так или иначе, постоянной времени переходного процесса мы называем его временную характеристику, определяющую время, через которое некоторый параметр данного процесса изменится в «е» раз, то есть увеличится или уменьшится примерно в 2,718 раз по сравнению с состоянием, принятым за исходное.
Рассмотрим для примера электрическую цепь, состоящую из источника постоянного напряжения, конденсатора и резистора. Подобного рода цепь, где резистор включен последовательно с конденсатором, называется интегрирующей RC-цепью.
Если в начальный момент времени подать на такую цепь питание, то есть установить на входе некоторое постоянное напряжение Uвх, то Uвых — напряжение на конденсаторе, начнет по экспоненте нарастать.
Через время t1 напряжение на конденсаторе достигнет 63,2% от напряжения на входе. Так вот, промежуток времени от начального момента до t1 – это и будет постоянная времени данной RC-цепи.
Данную константу цепи называют «тау», она измеряется в секундах, а обозначают ее соответствующей греческой буквой. Численно для RC-цепи она равна R*C, где R выражается в омах, а С — в фарадах.
Интегрирующие RC-цепи применяются в электронике в качестве фильтров нижних частот, когда более высокие частоты необходимо отсечь (подавить), а более низкие — пропустить.
Практически механизм такой фильтрации зиждиться на следующем принципе. Для переменного тока конденсатор выступает как емкостное сопротивление, значение которого обратно пропорционально частоте, то есть чем выше частота — тем меньшим будет реактивное сопротивление конденсатора в омах.
Следовательно, если пропустить через RC-цепь переменный ток, то, как на плечах делителя напряжения, на конденсаторе упадет определенное напряжение, пропорциональное его емкостному сопротивлению на частоте пропускаемого тока.
Если известна частота среза и амплитуда входного переменного сигнала, то для разработчика не составит труда подобрать такие конденсатор и резистор в RC-цепь, чтобы минимальное (граничное) напряжение (для частоты среза — верхней частотной границы) приходилось на конденсатор как на реактивное сопротивление, входящее в состав делителя в совокупности с резистором.
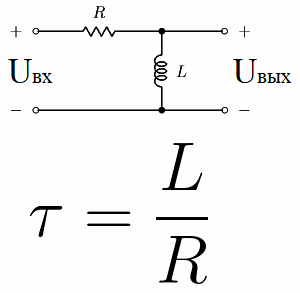
Теперь рассмотрим так называемую дифференцирующую цепь. Это цепь, состоящая из последовательно соединенных резистора и катушки индуктивности, RL-цепь. Ее постоянная времени численно равна L/R, где L – индуктивность катушки в генри, а R – сопротивление резистора в омах.
Если к такой цепи приложить постоянное напряжение от источника, то через время тау напряжение на катушке уменьшится по сравнению с U вх на 63,2%, то есть в полном соответствии со значением постоянной времени для данной электрической цепи.
В цепях переменного тока (переменных сигналов) LR-цепи применяются в качестве фильтров верхних частот, когда низкие частоты необходимо отсечь (подавить), а частоты выше (выше частоты среза — нижней частотной границы)— пропустить. Так вот, индуктивное сопротивление катушки тем больше, чем выше частота.
Как и в случае с рассмотренной выше RC-цепью, здесь используется принцип делителя напряжения. Ток более высокой частоты, пропускаемый через RL-цепь, вызовет большее падение напряжения на индуктивности L, как на индуктивном сопротивлении, входящем в состав делителя напряжения в совокупности с резистором. Задача разработчика — подобрать такие R и L, чтобы минимальное (граничное) напряжение на катушке получалось как раз на частоте среза.
Источник
Постоянная времени цепи RC
Электрическая цепь RC
Рассмотрим ток в электрической цепи, состоящей из конденсатора ёмкостью C и резистора сопротивлением R, соединённых параллельно.
Значение тока заряда или разряда конденсатора определится выражением I = C(dU/dt), а значение тока в резисторе, согласно закону Ома, составит U/R, где U — напряжение заряда конденсатора.
Из рисунка видно, что электрический ток I в элементах C и R цепи будет иметь одинаковое значение и противоположное направление, согласно закону Кирхгофа. Следовательно, его можно выразить следующим образом:
Решаем дифференциальное уравнение C(dU/dt)= -U/R

Из таблицы интегралов здесь используем преобразование
Получаем общий интеграл уравнения: ln|U| = — t/RC + Const.
Выразим из него напряжение U потенцированием: U = e -t /RC * e Const .
Решение примет вид:
Здесь Const — константа, величина, определяемая начальными условиями.
Следовательно, напряжение U заряда или разряда конденсатора будет меняться во времени по экспоненциальному закону e -t /RC .
Экспонента — функция exp(x) = e x
e – Математическая константа, приблизительно равная 2.718281828.
Постоянная времени τ
Если конденсатор емкостью C последовательно с резистором сопротивлением R подключить к источнику постоянного напряжения U, в цепи пойдёт ток, который за любое время t зарядит конденсатор до значения UC и определится выражением:
Тогда напряжение UC на выводах конденсатора будет увеличиваться от нуля до значения U по экспоненте:
При t = RC, напряжение на конденсаторе составит UC = U(1 — e -1 ) = U(1 — 1/e) .
Время, численно равное произведению RC, называется постоянной времени цепи RC и обозначается греческой буквой τ.
За время τ конденсатор зарядится до (1 — 1/e)*100% ≈ 63,2% значения U.
За время 3τ напряжение составит (1 — 1/e 3 )*100% ≈ 95% значения U.
За время 5τ напряжение возрастёт до (1 — 1/e 5 )*100% ≈ 99% значения U.
Если к конденсатору емкостью C, заряженному до напряжения U, параллельно подключить резистор сопротивлением R, тогда в цепи пойдёт ток разряда конденсатора.
Напряжение на конденсаторе при разряде будет составлять UC = Ue -t/τ = U/e t/τ .
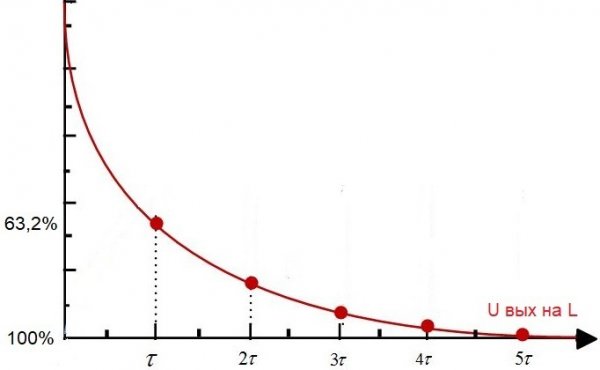
За время τ напряжение на конденсаторе уменьшится до значения U/e, что составит 1/e*100% ≈ 36.8% значения U.
За время 3τ конденсатор разрядится до (1/e 3 )*100% ≈ 5% от значения U.
За время 5τ до (1/e 5 )*100% ≈ 1% значения U.
Параметр τ широко применяется при расчётах RC-фильтров различных электронных цепей и узлов.
Замечания и предложения принимаются и приветствуются!
Источник
Постоянная времени на графике
Электрическая цепь RC
Рассмотрим ток в электрической цепи, состоящей из конденсатора ёмкостью C и резистора сопротивлением R, соединённых параллельно.
Значение тока заряда или разряда конденсатора определится выражением I = C(dU/dt), а значение тока в резисторе, согласно закону Ома, составит U/R, где U — напряжение заряда конденсатора.
Из рисунка видно, что электрический ток I в элементах C и R цепи будет иметь одинаковое значение и противоположное направление, согласно закону Кирхгофа. Следовательно, его можно выразить следующим образом:
Решаем дифференциальное уравнение C(dU/dt)= -U/R

Из таблицы интегралов здесь используем преобразование
Получаем общий интеграл уравнения: ln|U| = — t/RC + Const.
Выразим из него напряжение U потенцированием: U = e -t /RC * e Const .
Решение примет вид:
Здесь Const — константа, величина, определяемая начальными условиями.
Следовательно, напряжение U заряда или разряда конденсатора будет меняться во времени по экспоненциальному закону e -t /RC .
Экспонента — функция exp(x) = e x
e – Математическая константа, приблизительно равная 2.718281828.
Постоянная времени τ
Если конденсатор емкостью C последовательно с резистором сопротивлением R подключить к источнику постоянного напряжения U, в цепи пойдёт ток, который за любое время t зарядит конденсатор до значения UC и определится выражением:
Тогда напряжение UC на выводах конденсатора будет увеличиваться от нуля до значения U по экспоненте:
При t = RC, напряжение на конденсаторе составит UC = U(1 — e -1 ) = U(1 — 1/e) .
Время, численно равное произведению RC, называется постоянной времени цепи RC и обозначается греческой буквой τ.
За время τ конденсатор зарядится до (1 — 1/e)*100% ≈ 63,2% значения U.
За время 3τ напряжение составит (1 — 1/e 3 )*100% ≈ 95% значения U.
За время 5τ напряжение возрастёт до (1 — 1/e 5 )*100% ≈ 99% значения U.
Если к конденсатору емкостью C, заряженному до напряжения U, параллельно подключить резистор сопротивлением R, тогда в цепи пойдёт ток разряда конденсатора.
Напряжение на конденсаторе при разряде будет составлять UC = Ue -t/τ = U/e t/τ .
За время τ напряжение на конденсаторе уменьшится до значения U/e, что составит 1/e*100% ≈ 36.8% значения U.
За время 3τ конденсатор разрядится до (1/e 3 )*100% ≈ 5% от значения U.
За время 5τ до (1/e 5 )*100% ≈ 1% значения U.
Параметр τ широко применяется при расчётах RC-фильтров различных электронных цепей и узлов.
Замечания и предложения принимаются и приветствуются!
Электрическая цепь RC
Рассмотрим ток в электрической цепи, состоящей из конденсатора ёмкостью C и резистора сопротивлением R, соединённых параллельно.
Значение тока заряда или разряда конденсатора определится выражением I = C(dU/dt), а значение тока в резисторе, согласно закону Ома, составит U/R, где U — напряжение заряда конденсатора.
Из рисунка видно, что электрический ток I в элементах C и R цепи будет иметь одинаковое значение и противоположное направление, согласно закону Кирхгофа. Следовательно, его можно выразить следующим образом:
Решаем дифференциальное уравнение C(dU/dt)= -U/R

Из таблицы интегралов здесь используем преобразование
Получаем общий интеграл уравнения: ln|U| = — t/RC + Const.
Выразим из него напряжение U потенцированием: U = e -t /RC * e Const .
Решение примет вид:
Здесь Const — константа, величина, определяемая начальными условиями.
Следовательно, напряжение U заряда или разряда конденсатора будет меняться во времени по экспоненциальному закону e -t /RC .
Экспонента — функция exp(x) = e x
e – Математическая константа, приблизительно равная 2.718281828.
Постоянная времени τ
Если конденсатор емкостью C последовательно с резистором сопротивлением R подключить к источнику постоянного напряжения U, в цепи пойдёт ток, который за любое время t зарядит конденсатор до значения UC и определится выражением:
Тогда напряжение UC на выводах конденсатора будет увеличиваться от нуля до значения U по экспоненте:
При t = RC, напряжение на конденсаторе составит UC = U(1 — e -1 ) = U(1 — 1/e) .
Время, численно равное произведению RC, называется постоянной времени цепи RC и обозначается греческой буквой τ.
За время τ конденсатор зарядится до (1 — 1/e)*100% ≈ 63,2% значения U.
За время 3τ напряжение составит (1 — 1/e 3 )*100% ≈ 95% значения U.
За время 5τ напряжение возрастёт до (1 — 1/e 5 )*100% ≈ 99% значения U.
Если к конденсатору емкостью C, заряженному до напряжения U, параллельно подключить резистор сопротивлением R, тогда в цепи пойдёт ток разряда конденсатора.
Напряжение на конденсаторе при разряде будет составлять UC = Ue -t/τ = U/e t/τ .
За время τ напряжение на конденсаторе уменьшится до значения U/e, что составит 1/e*100% ≈ 36.8% значения U.
За время 3τ конденсатор разрядится до (1/e 3 )*100% ≈ 5% от значения U.
За время 5τ до (1/e 5 )*100% ≈ 1% значения U.
Параметр τ широко применяется при расчётах RC-фильтров различных электронных цепей и узлов.
Замечания и предложения принимаются и приветствуются!
Переходные процессы в электрических цепях, явления, возникающие при переходе от одного режима работы электрической цепи к другому, отличающемуся от предыдущего амплитудой, фазой, формой или частотой действующего в цепи напряжения, значениями параметров или конфигурацией цепи. П. п. возникают главным образом при коммутациях в электрических цепях и обусловлены тем, что ток, проходящий через катушку индуктивности, и напряжение на конденсаторе не могут изменяться скачком, то есть энергия электрического и магнитного полей в ёмкостных и индуктивных элементах цепи не может изменяться мгновенно.


Общие принципы исследования переходных процессов. Законы коммутации
Переходным режимом или переходным процессом в электрической цепи называют режим, при котором параметры элементов или параметры токов и напряжений изменяются в функции времени. Изменение параметров электрической цепи может происходить только за конечный промежуток времени, т.к. оно связано с изменением количества энергии, запасенной в электрических и магнитных полях. Однако при анализе переходных процессов обычно пренебрегают существованием электрических или магнитных полей на том или ином участке цепи, считая что ток или напряжение мгновенно изменяются на некоторую конечную величину. Процесс скачкообразного (мгновенного) изменения какого-либо параметра электрической цепи называется коммутацией. При анализе переходных процессов отсчет времени принято производить от этого момента.
Обычно процесс коммутации на электрической схеме изображается идеальным ключевым элементом.
1) в замкнутом состоянии обладает нулевым сопротивлением и эквивалентен идеальному проводнику;
2)в разомкнутом состоянии обладает бесконечно большим сопротивлением и эквивалентен разрыву цепи;
3) переходит из одного состояния в другое за бесконечно малый промежуток времени (мгновенно).
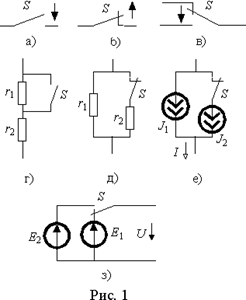
На рис. 1 г) и д) показаны примеры реализации с помощью ключей мгновенного изменения сопротивления. В первом случае значение сопротивления при коммутации изменяется от r1+r2 до r2, а во втором — от r1r2/( r1+r2) до r1. Аналогично с помощью ключей можно скачкообразно изменять ток и напряжение источников. На рис. 1 е) ток I скачком изменяется от J1+J2 до J1, а на рис. 1 з) напряжение U при коммутации изменяется от E1 до E2 .
мгновенное изменение тока в индуктивности iL или напряжения на емкости uC должны создавать бесконечно большое напряжение или ток на соответствующем участке цепи, нарушающие законы Кирхгофа. Но законы Кирхгофа не могут нарушаться в принципе, т.к. они являются одной из форм закона сохранения энергии. Следовательно, скачкообразное изменение рассмотренных параметров невозможно, что формулируется в виде
законов коммутации :
I) мгновенное изменение тока в индуктивности невозможно, поэтому ток в ней до и первый момент после коммутации одинаковы, т.е. iL(0- ) = iL(0+);
II) мгновенное изменение напряжения на емкости невозможно, поэтому напряжение на ней до и в первый момент после коммутации одинаковы, т.е. uC(0- ) = uC(0+).
В теории переходных процессов под i(0- ) понимают значение некоторой величины в момент времени непосредственно предшествующий коммутации, а под i(0+) — значение этой величины в момент времени непосредственно следующий за коммутацией.
В простейшем случае переходному процессу предшествует установившийся режим и заканчивается он также установившимся режимом.
Как известно, напряжения и токи в индуктивностях и емкостях являются производными и интегралами соответствующих величин. Поэтому уравнения Кирхгофа для электрической цепи содержащей реактивные элементы будут дифференциальными или интегро-дифференциальными и задачей анализа переходных процессов является их решение.
Постоянная времени – это время, в течение которого свободная составляющая процесса уменьшается в е = 2,72 раза по сравнению с начальным значением.
Нарастание тока происходит тем быстрее, чем меньше постоянная времени 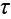
Не нашли то, что искали? Воспользуйтесь поиском:
Источник