Как найти постоянные ван дер ваальса найти

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 17 ноября 2022 года; проверки требует 1 правка.

Уравне́ние Ван-дер-Ва́альса (или уравне́ние Ван дер Ва́альса^{[К 1]}) — уравнение, связывающее основные термодинамические величины в модели газа Ван-дер-Ваальса.

Хотя модель идеального газа хорошо описывает поведение реальных газов при низких давлениях и высоких температурах, в других условиях её соответствие с опытом гораздо хуже. В частности, это проявляется в том, что реальные газы могут быть переведены в жидкое и даже в твёрдое состояние, а идеальные — не могут.

Для более точного описания поведения реальных газов при низких температурах была создана модель газа Ван-дер-Ваальса, учитывающая силы межмолекулярного взаимодействия. В этой модели внутренняя энергия становится функцией не только температуры, но и объёма.

Уравнение Ван-дер-Ваальса — это одно из широко известных приближённых уравнений состояния, описывающее свойства реального газа, имеющее компактную форму и учитывающее основные характеристики газа с межмолекулярным взаимодействием^[7].

Уравнение состояния[править | править код]

Изотермы газа ван дер Ваальса:
P — давление;
V — объём;
K — критическая точка;
abKcd — бинодаль (граница области двухфазного равновесия; область под колоколом бинодали — область двухфазного равновесия жидкость — пар);
eKf — спинодаль (граница между областями метастабильных и термодинамически неустойчивых состояний; область под колоколом спинодали — нереализуемые состояния);
bc — коннода (линия конденсации);
abKe — область перегретой жидкости;
dcKf — область переохлаждённого пара;
площади закрашенных фигур под изобарой bc и над ней равны (правило Максвелла, 1875)

Термическим уравнением состояния (или, часто, просто уравнением состояния) называется связь между давлением, объёмом и температурой.

Для одного моля газа Ван-дер-Ваальса оно имеет вид:

$left(p+{frac {a}{V_{m}^{2}}}right)(V_{m}-b)=RT,$

где

Видно, что это уравнение фактически является уравнением состояния идеального газа с двумя поправками. Поправка учитывает силы притяжения между молекулами (давление на стенку уменьшается, так как есть силы, втягивающие молекулы приграничного слоя внутрь), поправка — суммарный объём молекул газа.

Для молей газа Ван-дер-Ваальса уравнение состояния выглядит так:

$left(p+{frac {anu ^{2}}{V^{2}}}right)left({V}-{bnu }right)=nu RT,$

где

— объём.

Из рисунка, на котором изображены изотермы газа Ван-дер-Ваальса, видно, что ниже некоторой температуры зависимость перестаёт быть монотонной: образуется петля Ван-дер-Ваальса, в которой увеличению давления соответствует увеличение объёма, что противоречит законам термодинамики. Появление петли означает, что уравнение Ван-дер-Ваальса в данной области изменения и перестаёт описывать действительную ситуацию, когда имеет место фазовый переход газ — жидкость и реальная изотерма представляет собой отрезок прямой — конноду (ноду), соединяющую две фигуративные точки на бинодали.

Вывод уравнения[править | править код]

Наиболее известны два способа получения уравнения: традиционный вывод самого Ван-дер-Ваальса и вывод методами статистической физики.

Традиционный вывод[править | править код]

Рассмотрим сначала газ, в котором частицы не взаимодействуют друг с другом, такой газ удовлетворяет уравнению состояния идеального газа:

$p={frac {RT}{V_{{mathrm {m}}}}}.$

Далее предположим, что частицы данного газа являются упругими сферами одинакового радиуса . Так как газ находится в сосуде конечного объёма, то пространство, где могут перемещаться частицы, будет несколько меньше. В исходной формуле следует вычесть из всего объёма некую его часть , которая, вообще говоря, зависит только от вещества, из которого состоит газ. Таким образом, получается следующее уравнение:

$p={frac {RT}{V_{{mathrm {m}}}-b}}.$

Вычитаемый объём не будет в точности равен суммарному объёму всех частиц. Если частицы считать твёрдыми и абсолютно упругими шариками, то вычитаемый объём будет примерно в четыре раза больше. Это легко объясняется тем, что центры упругих шаров не могут приближаться на расстояние ближе .

Далее Ван-дер-Ваальс рассматривает силы притяжения между частицами газа и делает следующие допущения:

Частицы распределены равномерно по всему объёму.
Силы притяжения стенок сосуда не учитываются, что в общем случае неверно.
Частицы, находящиеся внутри сосуда и непосредственно у стенок, ощущают притяжение по-разному: внутри сосуда действующие силы притяжения других частиц компенсируют друг друга.

Таким образом, для частиц внутри сосуда силы притяжения не учитываются. Частицы, находящиеся непосредственно у края сосуда, затягиваются внутрь силой, пропорциональной концентрации:

$n=N_{{mathrm {A}}}/V_{{mathrm {m}}}$

Число частиц, которые находятся непосредственно у стенок, в свою очередь тоже предполагается пропорциональным концентрации . Можно считать, что давление на стенки сосуда меньше на некоторую величину, обратно пропорциональную квадрату объёма:

${displaystyle p={frac {RT}{V_{mathrm {m} }-b}}-{frac {a}{V_{mathrm {m} }^{2}}}.}$

Окончательное уравнение:

$left(p+{frac {a}{V_{{mathrm {m}}}^{2}}}right)(V_{{mathrm {m}}}-b)=RT.$

Внутренняя энергия газа Ван-дер-Ваальса[править | править код]

Потенциальная энергия межмолекулярных сил взаимодействия вычисляется как работа, которую совершают эти силы при разведении молекул на бесконечность:

${displaystyle U_{p}=int limits _{V}^{mathcal {infty }}left(-{frac {nu ^{2}a}{V^{2}}}right),dV={frac {nu ^{2}a}{V}}{Bigr |}_{V}^{mathcal {infty }}=-{frac {nu ^{2}a}{V}}.}$

Внутренняя энергия газа Ван-дер-Ваальса складывается из его кинетической энергии (энергии теплового движения молекул) и только что нами посчитанной потенциальной. Так, для одного моля газа:

${displaystyle U=C_{V}T-{frac {nu ^{2}a}{V}},}$

где C_V — молярная теплоёмкость при постоянном объёме, которая предполагается не зависящей от температуры.

Адиабата[править | править код]

Уравнение адиабаты для газа Ван-дер-Ваальса:

${displaystyle Tcdot (V-b)^{n-1}={text{const}},}$

где ${displaystyle n=1-{frac {R}{C-C_{V}}}.}$

Критические параметры[править | править код]

Критическими параметрами газа называются значения его макропараметров (давления, объёма и температуры) в критической точке, то есть в таком состоянии, когда жидкая и газообразная фазы вещества неразличимы. Найдём эти параметры для газа Ван-дер-Ваальса, для чего преобразуем уравнение состояния:

${displaystyle left(p+{frac {a}{V^{2}}}right)(V-b)=RT,}$

${displaystyle left(V^{2}+{frac {a}{p}}right)(V-b)={frac {V^{2}RT}{p}}.}$

Мы получили уравнение третьей степени относительно

${displaystyle V^{3}-left({frac {RT}{p}}+bright)V^{2}+{frac {a}{p}}V-{frac {ab}{p}}=0.}$

В критической точке все три корня уравнения сливаются в один, поэтому предыдущее уравнение эквивалентно следующему:

${displaystyle left(V-V_{crit}right)^{3}=0,}$

${displaystyle V^{3}-3V_{crit}V^{2}+3{V_{crit}}^{2}V-{V_{crit}}^{3}=0.}$

Приравняв коэффициенты при соответствующих степенях , получим равенства:

${displaystyle {frac {RT_{crit}}{p_{crit}}}+b=3V_{crit},}$

${displaystyle {frac {a}{p_{crit}}}=3{V_{crit}}^{2},}$

${displaystyle {frac {ab}{p_{crit}}}={V_{crit}}^{3}.}$

Из них вычислим значения критических параметров

${displaystyle V_{crit}=3b,}$

${displaystyle p_{crit}={frac {a}{27b^{2}}},}$

${displaystyle T_{crit}={frac {8a}{27bR}}}$

и критического коэффициента:

${displaystyle k_{crit}={frac {RT_{crit}}{p_{crit}V_{crit}}}={frac {8}{3}}.}$

Приведённые параметры[править | править код]

Приведённые параметры определяются как отношения

${displaystyle varphi ={frac {V}{V_{crit}}},qquad pi ={frac {p}{p_{crit}}},qquad tau ={frac {T}{T_{crit}}}.}$

Если подставить в уравнение Ван-дер-Ваальса ${displaystyle V=varphi V_{crit},}$ ${displaystyle p=pi p_{crit},}$ ${displaystyle T=tau T_{crit},}$ получится приведённое уравнение состояния (для моль).

${displaystyle left(pi +{frac {3}{{varphi }^{2}}}right)left(varphi -{frac {1}{3}}right)={frac {8}{3}}tau .}$

Если вещества обладают двумя одинаковыми приведёнными параметрами из трёх, то и третьи приведённые параметры у них совпадают.

Недостатки уравнения Ван-дер-Ваальса[править | править код]

Уравнение Ван-дер-Ваальса более точно описывает поведение реальных газов, чем уравнение состояния идеального газа, но вместе с тем не является абсолютно адекватной моделью. Его недостатки ^[8]:

1. Для реальных веществ ${displaystyle k_{crit}>2{,}67.}$

2. Для реальных веществ ${displaystyle V_{crit}not =3b}$

(скорее,

3. Уравнение Ван-дер-Ваальса расходится с экспериментом в области двухфазных состояний.

Константы Ван-дер-Ваальса для некоторых газов[править | править код]

Константы Ван-дер-Ваальса^[9]

Вещество	a, Па·м⁶·моль⁻²	b, 10⁻⁶ м³·моль⁻¹
Азот N₂	0,1370	38,7
Аммиак NH₃	0,4225	37,1
Аргон Ar	0,1355	32,0
Ацетилен C₂H₂	0,4516	52,2
Бром Br₂	0,975	59,1
Бромоводород HBr	0,4500	44,2
Бутан C₄H₁₀	1,389	116,4
Водород H₂	0,02452	26,5
Вода H₂O	0,5537	30,5
Гексафторид серы SF₆	0,7857	87,9
Гелий He	0,00346	23,8
Гидразин N₂H₄	0,846	46,2
Кислород O₂	0,1382	31,9
Криптон Kr	0,5193	10,6
Ксенон Xe	0,4192	51,6
Метан CH₄	0,2303	43,1
Неон Ne	0,0208	16,7
Озон O₃	0,3570	48,7
Окись углерода CO	0,1472	39,5
Пропан C₃H₈	0,939	90,5
Сернистый ангидрид SO₂	0,6865	56,8
Сероводород H₂S	0,4544	43,4
Углекислый газ CO₂	0,3658	42,9
Фтор F₂	0,1171	29,0
Фтороводород HF	0,9565	73,9
Хлор Cl₂	0,6343	54,2
Хлороводород HCl	0,3700	40,6
Циановодород HCN	1,129	88,1
Этан C₂H₆	0,5580	65,1
Этилен C₂H₄	0,4612	58,2

См. также[править | править код]

Уравнение состояния идеального газа
Уравнение Дитеричи
Критическая точка
Вириальное разложение

Примечания[править | править код]

Комментарии[править | править код]

↑ В большинстве современных словарей, руководств и энциклопедий название уравнения приводится в виде «уравнение Ван-дер-Ваальса»^[1]^[2]^[3]^[4]^[5]. Вместе с тем в Большой российской энциклопедии уравнение называется «уравнение Ван дер Ваальса»^[6].

Источники[править | править код]

↑ Русский орфографический словарь: около 200 000 слов / Российская академия наук. Институт русского языка им. В. В. Виноградова / Под. ред. В. В. Лопатина, О. Е. Ивановой. — 4-е изд., испр. и доп. — М.: АСТ-Пресс Книга, 2013. — С. 68. — 896 с. — (Фундаментальные словари русского языка). — ISBN 978-5-462-01272-3.
↑ Мильчин А. Э., Чельцова Л. К. Артикли, предлоги, частицы ван, да, дас, де, дель, дер, ди, дос, дю, ла, ле, фон и т. п. в западноевропейских фамилиях и именах // Справочник издателя и автора. Редакционно-издательское оформление издания. — 2-е изд., испр. и доп.. — М.: Олма-Пресс, 2003. — 800 с. — 3000 экз. — ISBN 5-224-04565-7.
↑ Любитов Ю. Н. Ван-дер-Ваальса уравнение // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1988. — Т. 1. — С. 240. — 704 с. — 100 000 экз.
↑ Анисимов М. А. Ван-дер-Ваальса уравнение // Химическая энциклопедия / Гл. ред. И. Л. Кнунянц. — М.: «Советская энциклопедия», 1988. — Т. 1. — С. 352.
↑ Лопаткин А. А. Ван-дер-Ваальса уравнение // Большая Советская энциклопедия / Гл. ред. А. М. Прохоров. — М.: «Советская энциклопедия», 1971. — Т. 4.
↑ Башкиров А. Г. Ван дер Ваальса уравнение // Большая Российская энциклопедия / Гл. ред. Ю. С. Осипов. — М., 2006. — Т. 4. — С. 579. — 750 с. — 65 000 экз. — ISBN 5-85270-333-8.
↑ Матвеев, 1981.
↑ Матвеев, 1981, с. 245.
↑ CRC Handbook of Chemistry and Physics / D. R. Lide (Ed.). — 90th edition. — CRC Press; Taylor and Francis, 2009. — P. 6-33. — 2828 p. — ISBN 1420090844.

Литература[править | править код]

Сивухин Д. В. Общий курс физики. — М.: Наука, 1975. — Т. II. Термодинамика и молекулярная физика. — 519 с.
Матвеев А. Н. Молекулярная физика. — М.: Высшая школа, 1981. — С. 237—253. — 400 с.
Atkins P. W., De Paula J. Physical Chemistry. — W. H. Freeman, 2010. — Т. 1. — ISBN 9780199593361.
Иванов В. К. Курс общей физики. Молекулярная физика. Дата обращения: 6 ноября 2012. Архивировано из оригинала 24 января 2010 года. (4.1. Взаимодействие молекул газа. Уравнение Ван-дер-Ваальса)

Источник

Из
множества различных уравнений,
предложенных для реального газа, наиболее
простым и точным является уравнение
Ван-дер-Ваальса. В модели реального газа
Ван-дер-Ваальса молекулы рассматриваются
как абсолютно твердые шарики с эффективным
диаметром d,
между которыми действуют силы взаимного
притяжения и отталкивания.

Уравнение
Ван-дер-Ваальса является приближенным,
так как не существует точного способа
вычисления сил взаимодействия между
молекулами. Уравнение Ван-дер-Ваальса
сводится к поправкам к уравнению
идеального газа и для 1 моля имеет вид

^,
⁽⁸⁰⁾

где
a
и b
– постоянные
Ван-дер-Ваальса,
определяемые экспериментально для
каждого газа, V_М
– объём 1 моля.

Поправка

называетсявнутренним
давлением
и характеризует добавку к внешнему
давлению, обусловленную взаимным
притяжением
молекул. Из-за притяжения молекул газ
как бы сжимает сам себя и поэтому поправка
в формуле (80) приводится с «плюсом».

Поправка
b
= 4 N_AV_МОЛ
равна учетверённому значению собственного
объёма всех молекул,
где N_A
– число Авогадро (так как взят 1 моль
газа), V_МОЛ
– объём одной молекулы. Если, например,
в сосуде находятся две молекулы, то
центр любой из них не может приблизиться
к центру другой молекулы на расстояние,
меньшее диаметра d
молекулы (рис. 13). Это означает, что для
центров обеих молекул оказывается
недоступным для движения сферический
объём радиуса d,
т.е. объём, равный 8 объёмам молекулы или
учетверённому объёму молекулы в расчете
на одну молекулу. Поэтому в уравнении
Ван-дер-Ваальса вместо полного объёма
сосуда стоит «свободный» для движения
объём, который получается вычитанием
собственного объёма молекул.

Уравнение
Ван-дер-Ваальса – это уравнение третьей
степени относительноV.
Поэтому изотерма
Ван-дер-Ваальса
при температуре ниже критической
будет иметь вид, показанный на рис. 39.
Как видно, она отличается от изотермы
реального газа (пунктир). Однако при
некоторых условиях участки 1–2 и 3–4
могут наблюдаться в эксперименте. Это
так называемые метастабильные
состояния
(очень неустойчивые). На участке 1–2
можно получить пересыщенный
пар (применяется
в камере Вильсона). На участке 3–4
реализуется перегретая
жидкость
(применяется в пузырьковой камере).

Семейство
изотерм Ван-дер-Ваальса показано на
рис. 40. Постоянные Ван-дер-Ваальса можно
найти из критических параметров р_К,
Т_К,
V_К.
Как видно из рис. 40, критическая точка
К является точкой перегиба изотермы,
поскольку в ней совмещаются и минимумы,
и максимумы. Следовательно, в критической
точке и первая, и вторая производные
будут равны нулю. Если решить уравнение
Ван-дер-Ваальса относительно давления
р:

а
затем взять первую и вторую производные
и приравнять их к нулю, то можно получить
связь постоянных Ван-дер-Ваальса и
критических параметров:

Чтобы
написать уравнение Ван-дер-Ваальса для
произвольного числа молей ,
нужно учесть, что 
молей газа занимают в 
раз больший объем V
= V_M
.
Подставим в уравнение (80) выражение V_M
= V/,
а затем умножим обе части равенства на
.
Получаем уравнение Ван-дер-Ваальса для
произвольного числа молей:

^.
⁽⁸¹⁾

При
сильном разряжении газа, когда
взаимодействием между молекулами можно
пренебречь, уравнение Ван-дер-Ваальса
переходит в уравнение Менделеева-Клапейрона.

Внутренняя
энергия газа Ван-дер-Ваальса
должна включать кроме кинетической
энергии молекул (которую мы раньше
определили для идеального газа) и энергию
взаимодействия между молекулами. Для
вывода формулы воспользуемся тем, что
работа, совершаемая при расширении газа
против сил взаимного притяжения молекул,
равна изменению потенциальной энергии
dA
= dE_P.
Силы взаимного притяжения учтены в
уравнении Ван-дер-Ваальса с помощью
добавки к давлению
.
Работа равна:

Внутренняя
энергия газа Ван-дер-Ваальса равна сумме
кинетической и потенциальной энергий:

Найдем
постоянную интегрирования. Если газ
расширяется, то силами взаимодействия
в разряженном газе можно пренебречь и
получается идеальный газ. Значит, при
стремлении объёма газа к бесконечности
формула для внутренней энергии газа
Ван-дер-Ваальса должна переходить в
формулу для внутренней энергии идеального
газа. Второе слагаемое в формуле
внутренней энергии газа Ван-дер-Ваальса
стремится к нулю при стремлении объёма
к бесконечности. Поэтому постоянную
интегрирования также следует положить
равной нулю. В итоге имеем формулу
для внутренней
энергии газа Ван-дер-Ваальса:

^.
⁽⁸²⁾

Таким
образом, внутренняя энергия газа
Ван-дер-Ваальса зависит не только от
температуры, но и от объёма газа.

ТРИЗ-задание
26. Опоздание на 40 лет

«Изобретения
всегда опаздывают», – это первая фраза,
произнесённая Г.С. Альтшуллером в
фильме «Алгоритм изобретений» (студия
«Центрнаучфильм», 1974 г.). Данное
высказывание можно подтвердить примером
из области детекторов заряженных частиц.
Вкамере
Вильсона,
изобретённой в 1912 г., рабочим веществом
является переохлаждённый (пересыщенный)
пар. Регистрируемая заряженная частица
конденсирует пар на своём пути, оставляя
след (трек) из мелких капель жидкости.
В 1952 г.
Д. Глезер
(США) изобрёл
пузырьковую камеру.
В ней трек заряженной частицы образуется
пузырьками пара в перегретой (выше точки
кипения) жидкости. За эти два изобретения
были получены две Нобелевские премии:
Ч. Вильсоном – в 1927 г., Д. Глезером – в
1960 г. Вопрос: с учётом принципов работы
камер какой изобретательский приём
позволил бы ещё в 1912 г. получить идею
пузырьковой камеры?

Соседние файлы в папке папа Жужа

Источник

Наталья Николаевна Пушкина

Эксперт по предмету «Физика»

Задать вопрос автору статьи

Что такое реальный газ

Реальным газом называют газ, между молекулами которого существуют заметные силы взаимодействия. В неидеальных, газах под высоким давлением, газах с большой плотностью взаимодействие молекул велико и его необходимо учитывать. Силы притяжения играют наиболее существенную роль на больших расстояниях между молекулами. Расстояние уменьшается, силы притяжения растут, но до определенного предела, затем они начинают уменьшаться и переходят в силы отталкивания. Притяжение и отталкивание молекул можно разделить и рассматривать и учитывать отдельно друг от друга.

Уравнение Ван-дер-Ваальса

Уравнение Ван-дер-Ваальса, описывающее состояние 1 моля реального газа, имеет вид:

Уравнение Ван-дер-Ваальса

[left(p+frac{a}{V^2_{mu }}right)left(V_{mu }-bright)=RT left(1right),]

где${ V}_{mu }$- молярный объем газа, $frac{a}{V^2_{mu }}$- внутреннее давление, обусловленное силами притяжения между молекулами, b — поправка на собственный объем молекул, которая учитывает действие сил отталкивания между молекулами, причем

[b=N_Afrac{2}{3}pi d^3(2),]

где d- диаметр молекулы,

величина a вычисляется по формуле:

[a=-2pi N^2_Aintnolimits^{infty }_d{W_pleft(rright)r^2dr left(3right),}]

где $W_pleft(rright)$- потенциальная энергия притяжения двух молекул. Необходимо заметить, что газовая постоянная имеет индивидуальное значение для каждого вещества. Она отличается от молярной газовой постоянной, причем она меньше, что говорит об объединении молекул вещества в комплексы около критического состояния. Вдали от критических состояний можно использовать универсальную газовую постоянную.

С увеличением объема роль поправок в уравнении (1) становится менее существенной. И в пределе уравнение (1) переходит в уравнение состояния идеального газа для 1 моля (4):

[pV=RT (4)]

Уравнение (4) — уравнение Менделеева — Клайперона, где m- масса газа, $R=8,31 frac{Дж}{мольcdot К}$- универсальная газовая постоянная.

Это согласуется с тем фактом, что при уменьшении плотности реальные газы по своим свойствам приближаются к идеальным.

Уравнение (1) может быть записано в вириальной форме:

[{pV}_m=RT+frac{RTb’-a’}{V_m}+RTsumlimits^{infty }_{n=2}{frac{{b’}^n}{V^n_m}} left(5right),]

где $V_m=frac{V}{nu }.$

Для анализа изотерм уравнение (1) удобнее представить в виде:

[V^3_m-left(b’+frac{RT}{p}right)V^2_m+frac{a’V_m}{p}-frac{a’b}{p}=0left(6right).]

Рассматриваемое уравнение может описывать и свойства жидкости, например плохую ее сжимаемость.

На рис.1 изображена изотерма Ван-дер-Ваальса для некоторого постоянного значения температуры T, построенная из соответствующего уравнения.

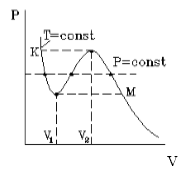
Рис.1

Такая зависимость на практике невозможна. Опыт показывает, что график должен иметь вид рис.2 то есть существуют области, в которых при изменении объема давление неизменно. В некоторых отрезках график изотермы параллелен оси V (рис 2). Это область фазового перехода. Жидкость и газ существую одновременно.

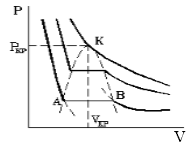
Рис.2

По мере увеличения температуры участок, отражающий состояние нахождения газа одновременно в двух фазах на графиках p(V), сужается и превращается в точку (рис. 2). Это особая точка К, в которой пропадает различие между жидкостью и паром. Это так называемая критическая точка.

«Уравнение Ван-дер-Ваальса» 👇

Вывод

Итак, уравнение Ван-дер-Ваальса описывает поведение газов близких к реальным. Их можно применить к газообразной и жидкой фазам вещества. Эти уравнения отражают существование фазового перехода газ — жидкость. Показывают наличие критической точки перехода. Однако абсолютно точных количественных результатов расчеты, в которых используются вышеназванные уравнения, не дают.

Пример 1

Задание: Газ в количестве 1 моль находится в сосуде объемом V л при температуре $T_1$ давление газа $p_1$, а при $T_2$ давление газа $p_2$. Найти постоянные Ван-дер-Ваальса.

Решение:

Запишем уравнение Ван-дер-Ваальса для одного моля реального газа для состояний 1 и 2:

[left(p_1+frac{a}{V^2_{mu }}right)left(V_{mu }-bright)=RT_1 left(1.1right).]

[left(p_2+frac{a}{V^2_{mu }}right)left(V_{mu }-bright)=RT_2 left(1.2right).]

Раскроем скобки в (1.1):

[p_1V_{mu }+frac{a}{V_{mu }}-p_1b-frac{ab}{V^2_{mu }}=RT_1 left(1.3right).]

[p_2V_{mu }+frac{a}{V_{mu }}-p_2b-frac{ab}{V^2_{mu }}=RT_2left(1.4right).]

Вычтем $left(1.4right). из left(1.3right):$

[p_1V_{mu }+frac{a}{V_{mu }}-p_1b-frac{ab}{V^2_{mu }}-p_2V_{mu }-frac{a}{V_{mu }}+p_2b+frac{ab}{V^2_{mu }}=RT_1-RT_2to ]

[p_1V_{mu }-p_1b-p_2V_{mu }{+p}_2b=RT_1-RT_2]

[-p_1b{+p}_2b=RT_1-RT_2-p_1V_{mu }+p_2V_{mu }to b=frac{RT_1-RT_2-p_1V_{mu }+p_2V_{mu }}{p_2-p_1}left(1.5right).]

Выразим a из (1.1):

[aleft(frac{1}{V_{mu }}-frac{b}{V^2_{mu }}right)=RT_1-p_1V_{mu }+p_1bto a=frac{RT_1-p_1V_{mu }+p_1b}{left(frac{1}{V_{mu }}-frac{b}{V^2_{mu }}right)}]

Ответ: $b=frac{RT_1-RT_2-p_1V_{mu }+p_2V_{mu }}{p_2-p_1}, a=frac{RT_1-p_1V_{mu }+p_1b}{left(frac{1}{V_{mu }}-frac{b}{V^2_{mu }}right)}$.

Пример 2

Задание: Для реального газа, используя уравнение Ван-дер-Ваальса, получите уравнение адиабаты в параметрах V и T.

Решение:

Запишем первое начало термодинамики:

[delta Q=dU+partial A=0 left( 2.1right)]

Так как процесс адиабатный, то он идет теплообмена. Перепишем уравнение (2.1) для ван-дер-ваальсовского газа, зная, что:

[dU=frac{i}{2}nu RdT-frac{a}{V+dV}+frac{a}{V}=frac{i}{2}nu RdT+frac{adV}{V^2} (2.2)]

получим:

[0=pdV+frac{i}{2}nu RdT+frac{adV}{V^2} (2.3)]

[0=(p+frac{a}{V^2})dV+frac{i}{2}nu RdT (2.4)]

Из уравнения Ван-дер-Ваальса:

[left(p+frac{a}{V^2}right)left(V-bright)=RT to p+frac{a}{V^2}=frac{RT}{left(V-bright)} left(2.5right)]

Подставим (2.5) в (2.4), разделим переменные:

[frac{RT}{left(V-bright)}dV+frac{i}{2}nu RdT =0to frac{Rd(V-b)}{left(V-bright)}=-frac{i}{2}nu Rfrac{dT}{T}(2.6) ]

[frac{d(V-b)}{frac{i}{2}nu left(V-bright)}=-frac{dT}{T}(2.7) ]

Проинтегрируем (2.7):

ln$left({left(V-bright)}^{frac{i}{2}nu }Tright)=0to {left(V-bright)}^{frac{i}{2}nu }T=const.$

Ответ: Уравнение адиабаты для заданного случая имеет вид: ${left(V-bright)}^{frac{i}{2}nu }T=const.$

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

In chemistry and thermodynamics, the Van der Waals equation (or Van der Waals equation of state) is an equation of state which extends the ideal gas law to include the effects of interaction between molecules of a gas, as well as accounting for the finite size of the molecules.

The ideal gas law treats gas molecules as point particles that interact with their containers but not each other, meaning they neither take up space nor change kinetic energy during collisions (i.e. all collisions are perfectly elastic).^[1] The ideal gas law states that the volume V occupied by n moles of any gas has a pressure P at temperature T given by the following relationship, where R is the gas constant:

To account for the volume occupied by real gas molecules, the Van der Waals equation replaces V/n in the ideal gas law with ${displaystyle (V_{m}-b)}$ , where V_m is the molar volume of the gas and b is the volume occupied by the molecules of one mole:^[1]

${displaystyle P(V_{m}-b)=RT}$

Van der Waals equation on a wall in Leiden

The second modification made to the ideal gas law accounts for interaction between molecules of the gas. The Van der Waals equation includes intermolecular interaction by adding to the observed pressure P in the equation of state a term of the form ${displaystyle a/V_{m}^{2}}$ , where a is a constant whose value depends on the gas.

The complete Van der Waals equation is therefore:^[1]

${displaystyle left(P+a{frac {1}{V_{m}^{2}}}right)(V_{m}-b)=RT}$

For n moles of gas, it can also be written as:

${displaystyle left(P+a{frac {n^{2}}{V^{2}}}right)(V-nb)=nRT}$

When the molar volume V_m is large, b becomes negligible in comparison with V_m, a/V_m² becomes negligible with respect to P, and the Van der Waals equation reduces to the ideal gas law, PV_m=RT.^[1]

This equation approximates the behavior of real fluids above their critical temperatures and is qualitatively reasonable for their liquid and low-pressure gaseous states at low temperatures. However, near the phase transitions between gas and liquid, in the range of p, V, and T where the liquid phase and the gas phase are in equilibrium, the Van der Waals equation fails to accurately model observed experimental behavior. In particular, p is a constant function of V at given temperatures in these regions. As such, the Van der Waals model is not useful for calculations intended to predict real behavior in regions near critical points. Corrections to address these predictive deficiencies include the equal area rule and the principle of corresponding states.

The equation was named for its developer, the Dutch physicist Johannes Diderik van der Waals.

Overview and history[edit]

This section needs expansion with: a proper lay explanation of the equation and the history and context of its discovery. You can help by adding to it. (June 2015)

The Van der Waals equation is a thermodynamic equation of state based on the theory that fluids are composed of particles with non-zero volumes, and subject to a (not necessarily pairwise) inter-particle attractive force.^{[citation needed]} It was based on work in theoretical physical chemistry performed in the late 19th century by Johannes Diderik van der Waals, who did related work on the attractive force that also bears his name.^{[citation needed]} The equation is known to be based on a traditional set of derivations deriving from Van der Waals’ and related efforts,^{[citation needed]} as well as a set of derivation based in statistical thermodynamics,^{[citation needed]} see below.

Van der Waals’ early interests were primarily in the field of thermodynamics, where a first influence was Rudolf Clausius’s published work on heat in 1857; other significant influences were the writings by James Clerk Maxwell, Ludwig Boltzmann, and Willard Gibbs.^[2] After initial pursuit of teaching credentials, Van der Waals’ undergraduate coursework in mathematics and physics at the University of Leiden in the Netherlands led (with significant hurdles) to his acceptance for doctoral studies at Leiden under Pieter Rijke. While his dissertation helps to explain the experimental observation in 1869 by Irish professor of chemistry Thomas Andrews (Queen’s University Belfast) of the existence of a critical point in fluids,^[3]^{[non-primary source needed]} science historian Martin J. Klein states that it is not clear whether Van der Waals was aware of Andrews’ results when he began his doctorate work.^[4]

Van der Waals’ doctoral research culminated in an 1873 dissertation that provided a semi-quantitative theory describing the gas-liquid change of state and the origin of a critical temperature, Over de Continuïteit van den Gas- en Vloeistoftoestand (Dutch; in English, On the Continuity of the Gas and Liquid State). It was in this dissertation that the first derivations of what we now refer to as the Van der Waals equation appeared.^[5] James Clerk Maxwell reviewed and lauded its published content in the British science journal Nature,^[6]^[7] and Van der Waals began independent work that would result in his receipt of the Nobel Prize in 1910, which emphasized the contribution of his formulation of this “equation of state for gases and liquids”.^[2]

Equation[edit]

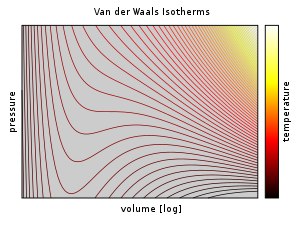
Van der Waals isotherms.^{[citation needed]} The model correctly predicts a mostly incompressible liquid phase, but the oscillations in the phase transition zone do not fit experimental data.

Van der Waals isotherms and oscillations, temperatures, T, below and above T_C.^{[citation needed]} Shown in this PV diagram are a series of 5 isotherms for temperatures ranging from below (blue) to above (red) T_C (the critical temperature), where the upward arise and downward dip in the isotherm predicted by the Van der Waals equation (the “oscillation”, especially evident for the two isotherms for values of T < T_C) is evident in the region of the gas-liquid phase transition.

The equation relates four state variables: the pressure of the fluid p, the total volume of the fluid’s container V, the number of particles N, and the absolute temperature of the system T.

The intensive, microscopic form of the equation is:

${displaystyle left(p+{frac {a'}{v^{2}}}right)left(v-b'right)=k_{text{B}}T}$

^[2]

where

is the volume of the container occupied by each particle (not the velocity of a particle), and k_B is the Boltzmann constant. It introduces two new parameters: a′, a measure of the average attraction between particles, and b′, the volume excluded from v by one particle.

The equation can be also written in extensive, molar form:

$left(p+{frac {n^{2}a}{V^{2}}}right)left(V-nbright)=nRT$

^[8]

or also:

${displaystyle p={frac {RT}{V_{m}-b}}-{frac {a}{V_{m}^{2}}}}$

where

$a=N_{A}^{2}a'$

is a measure of the average attraction between particles,

${displaystyle b=N_{text{A}}b'}$

is the volume excluded by a mole of particles,

${displaystyle n=N/N_{text{A}}}$

is the number of moles,

${displaystyle R=N_{text{A}}k_{text{B}}}$

is the universal gas constant, k_B is the Boltzmann constant, and N_A is the Avogadro constant,

${displaystyle V_{m}={frac {V}{n}}=vN_{A}}$

is the specific molar volume.

Also the constant a, b can be expressed in terms of the critical constants:

${displaystyle a={frac {27}{64}}{frac {R^{2}T_{c}^{2}}{P_{c}}}}$

${displaystyle b={frac {1}{8}}{frac {RT_{c}}{P_{c}}}}$

And the critical constants can be expressed in terms of a, b:

${displaystyle P_{c}={frac {a}{27b^{2}}}}$

${displaystyle T_{c}={frac {8a}{27bR}}}$

${displaystyle V_{m,c}=3b}$

A careful distinction must be drawn between the volume available to a particle and the volume of a particle.^{[according to whom?]} In the intensive equation, v equals the total space available to each particle, while the parameter b′ is proportional to the proper volume of a single particle – the volume bounded by the atomic radius. This is subtracted from v because of the space taken up by one particle.^{[citation needed]} In Van der Waals’ original derivation, given below, b’ is four times the proper volume of the particle. Observe further that the pressure p goes to infinity when the container is completely filled with particles so that there is no void space left for the particles to move; this occurs when V = nb.^[9]

Gas mixture[edit]

If a mixture of gases is being considered, and each gas has its own (attraction between molecules) and (volume occupied by molecules) values, then and for the mixture can be calculated as

= total number of moles of gas present,

for each

, $m_{i}$

= number of moles of gas

present, and ${displaystyle x_{i}={frac {m_{i}}{m}}}$

${displaystyle a=sum _{i=1}^{i=n}sum _{j=1}^{i=n}(x_{i}x_{j}{sqrt {a_{i}a_{j}}})}$

^[10]^[11]

${displaystyle b=sum _{i=1}^{i=n}sum _{j=1}^{i=n}(x_{i}x_{j}{sqrt {b_{i}b_{j}}})}$

^[10]^[11]

and the rule of adding partial pressures becomes invalid if the numerical result of the equation ${displaystyle left(p+({n^{2}a}/{V^{2}})right)left(V-nbright)=nRT}$ is significantly different from the ideal gas equation pV=nRT .

Reduced form[edit]

The Van der Waals equation can also be expressed in terms of reduced properties:

${displaystyle left(P_{r}+{frac {3}{V_{r}^{2}}}right)left(V_{r}-{frac {1}{3}}right)={frac {8}{3}}T_{r}}$

The equation in reduced form is exactly the same for every gas, this is consistent with the Theorem of corresponding states.

This yields a critical compressibility factor of 3/8. Reasons for modification of ideal gas equation: The equation state for ideal gas is PV=RT. In the derivation of ideal gas laws on the basis of kinetic theory of gases some assumption have been made.

Compressibility factor[edit]

The compressibility factor for the Van der Waals equation is:

${displaystyle Z={frac {PV_{m}}{RT}}={frac {V_{m}}{V_{m}-b}}-{frac {a}{V_{m}RT}}}$

Or in reduced form by substitution of ${displaystyle P_{r}=P/P_{c},T_{r}=T/T_{c},V_{r}=V_{m}/V_{c}}$ :

${displaystyle Z={frac {V_{r}}{V_{r}-{frac {1}{3}}}}-{frac {9}{8V_{r}T_{r}}}}$

At the critical point:

${displaystyle Z_{c}={frac {P_{c}V_{c}}{RT_{c}}}={frac {3}{8}}=0.375}$

Validity[edit]

The Van der Waals equation is mathematically simple, but it nevertheless predicts the experimentally observed transition between vapor and liquid, and predicts critical behaviour.^[12]^: 289 It also adequately predicts and explains the Joule–Thomson effect (temperature change during adiabatic expansion), which is not possible in ideal gas.

Above the critical temperature, T_C, the Van der Waals equation is an improvement over the ideal gas law, and for lower temperatures, i.e., T < T_C, the equation is also qualitatively reasonable for the liquid and low-pressure gaseous states; however, with respect to the first-order phase transition, i.e., the range of (p, V, T) where a liquid phase and a gas phase would be in equilibrium, the equation appears to fail to predict observed experimental behaviour, in the sense that p is typically observed to be constant as a function of V for a given temperature in the two-phase region. This apparent discrepancy is resolved in the context of vapour–liquid equilibrium: at a particular temperature, there exist two points on the Van der Waals isotherm that have the same chemical potential, and thus a system in thermodynamic equilibrium will appear to traverse a straight line on the p–V diagram as the ratio of vapour to liquid changes. However, in such a system, there are really only two points present (the liquid and the vapour) rather than a series of states connected by a line, so connecting the locus of points is incorrect: it is not an equation of multiple states, but an equation of (a single) state. It is indeed possible to compress a gas beyond the point at which it would typically condense, given the right conditions, and it is also possible to expand a liquid beyond the point at which it would usually boil. Such states are called “metastable” states. Such behaviour is qualitatively (though perhaps not quantitatively) predicted by the Van der Waals equation of state.^[13]

However, the values of physical quantities as predicted with the Van der Waals equation of state “are in very poor agreement with experiment”, so the model’s utility is limited to qualitative rather than quantitative purposes.^[12]^: 289 Empirically-based corrections can easily be inserted into the Van der Waals model (see Maxwell’s correction, below), but in so doing, the modified expression is no longer as simple an analytical model; in this regard, other models, such as those based on the principle of corresponding states, achieve a better fit with roughly the same work.^{[citation needed]}
Even with its acknowledged shortcomings, the pervasive use of the Van der Waals equation in standard university physical chemistry textbooks makes clear its importance as a pedagogic tool to aid understanding fundamental physical chemistry ideas involved in developing theories of vapour–liquid behavior and equations of state.^[14]^[15]^[16] In addition, other (more accurate) equations of state such as the Redlich–Kwong and Peng–Robinson equation of state are essentially modifications of the Van der Waals equation of state.

Derivation[edit]

Textbooks in physical chemistry generally give two derivations of the title equation.^[who?] One is the conventional derivation that goes back to Van der Waals, a mechanical equation of state that cannot be used to specify all thermodynamic functions; the other is a statistical mechanics derivation that makes explicit the intermolecular potential neglected in the first derivation.^{[citation needed]} A particular advantage of the statistical mechanical derivation is that it yields the partition function for the system, and allows all thermodynamic functions to be specified (including the mechanical equation of state).^{[citation needed]}

Conventional derivation[edit]

Consider one mole of gas composed of non-interacting point particles that satisfy the ideal gas law:(see any standard Physical Chemistry text, op. cit.)

$p = frac{RT}{V_mathrm{m}}.$

Next, assume that all particles are hard spheres of the same finite radius r (the Van der Waals radius). The effect of the finite volume of the particles is to decrease the available void space in which the particles are free to move. We must replace V by V − b, where b is called the excluded volume (per mole) or “co-volume”. The corrected equation becomes

$p={frac {RT}{V_{mathrm {m} }-b}}.$

The excluded volume is not just equal to the volume occupied by the solid, finite-sized particles, but actually four times the total molecular volume for one mole of a Van der waals’ gas. To see this, we must realize that a particle is surrounded by a sphere of radius 2r (two times the original radius) that is forbidden for the centers of the other particles. If the distance between two particle centers were to be smaller than 2r, it would mean that the two particles penetrate each other, which, by definition, hard spheres are unable to do.

The excluded volume for the two particles (of average diameter d or radius r) is

$b'_{2}=4pi d^{3}/3=8times (4pi r^{3}/3)$

which, divided by two (the number of colliding particles), gives the excluded volume per particle:

$b'=b'_{2}/2quad rightarrow quad b'=4times (4pi r^{3}/3)$

So b′ is four times the proper volume of the particle. It was a point of concern to Van der Waals that the factor four yields an upper bound; empirical values for b′ are usually lower. Of course, molecules are not infinitely hard, as Van der Waals thought, and are often fairly soft. To obtain the excluded volume per mole we just need to multiply by the number of molecules in a mole, i.e. by the avogadro number:

$b=N_{A}b'$

Next, we introduce a (not necessarily pairwise) attractive force between the particles. Van der Waals assumed that, notwithstanding the existence of this force, the density of the fluid is homogeneous; furthermore, he assumed that the range of the attractive force is so small that the great majority of the particles do not feel that the container is of finite size.^{[citation needed]} Given the homogeneity of the fluid, the bulk of the particles do not experience a net force pulling them to the right or to the left. This is different for the particles in surface layers directly adjacent to the walls. They feel a net force from the bulk particles pulling them into the container, because this force is not compensated by particles on the side where the wall is (another assumption here is that there is no interaction between walls and particles, which is not true, as can be seen from the phenomenon of droplet formation; most types of liquid show adhesion). This net force decreases the force exerted onto the wall by the particles in the surface layer. The net force on a surface particle, pulling it into the container, is proportional to the number density. On considering one mole of gas, the number of particles will be N_A

$C=N_{mathrm {A} }/V_{mathrm {m} }$

The number of particles in the surface layers is, again by assuming homogeneity, also proportional to the density. In total, the force on the walls is decreased by a factor proportional to the square of the density, and the pressure (force per unit surface) is decreased by

${displaystyle a'C^{2}=a'left({frac {N_{mathrm {A} }}{V_{mathrm {m} }}}right)^{2}={frac {a}{V_{mathrm {m} }^{2}}}}$

so that

$p={frac {RT}{V_{mathrm {m} }-b}}-{frac {a}{V_{mathrm {m} }^{2}}}Rightarrow left(p+{frac {a}{V_{mathrm {m} }^{2}}}right)(V_{mathrm {m} }-b)=RT.$

Upon writing n for the number of moles and nV_m = V, the equation obtains the second form given above,

$left(p+{frac {n^{2}a}{V^{2}}}right)(V-nb)=nRT.$

It is of some historical interest to point out that Van der Waals, in his Nobel prize lecture, gave credit to Laplace for the argument that pressure is reduced proportional to the square of the density.^{[citation needed]}

Statistical thermodynamics derivation[edit]

The canonical partition function Z of an ideal gas consisting of N = nN_A identical (non-interacting) particles, is:^[17]^[18]

${displaystyle Z={frac {z^{N}}{N!}}quad {hbox{with}}quad z={frac {V}{Lambda ^{3}}}}$

where Lambda is the thermal de Broglie wavelength,

$Lambda ={sqrt {frac {h^{2}}{2pi mkT}}}$

with the usual definitions: h is the Planck constant, m the mass of a particle, k the Boltzmann constant and T the absolute temperature. In an ideal gas z is the partition function of a single particle in a container of volume V. In order to derive the Van der Waals equation we assume now that each particle moves independently in an average potential field offered by the other particles. The averaging over the particles is easy because we will assume that the particle density of the Van der Waals fluid is homogeneous.
The interaction between a pair of particles, which are hard spheres, is taken to be

$u(r)={begin{cases}infty &{hbox{when}}quad r<d,\-epsilon left({frac {d}{r}}right)^{6}&{hbox{when}}quad rgeq d,end{cases}}$

r is the distance between the centers of the spheres and d is the distance where the hard spheres touch each other (twice the Van der Waals radius). The depth of the Van der Waals well is epsilon .

Because the particles are not coupled under the mean field Hamiltonian, the mean field approximation of the total partition function still factorizes,

${displaystyle Z=z^{N}/N!}$

but the intermolecular potential necessitates two modifications to z. First, because of the finite size of the particles, not all of V is available, but only V − Nb’, where (just as in the conventional derivation above)

$b'=2pi d^{3}/3$

Second, we insert a Boltzmann factor
exp[ – ϕ/2kT] to take care of the average intermolecular potential. We divide here the potential by two because this interaction energy is shared between two particles. Thus

${displaystyle z={frac {(V-Nb'),e^{-phi /(2kT)}}{Lambda ^{3}}}.}$

The total attraction felt by a single particle is

$phi =int _{d}^{infty }u(r){frac {N}{V}}4pi r^{2}dr,$

where we assumed that in a shell of thickness dr there are N/V 4π r²dr particles. This is a mean field approximation; the position of the particles is averaged. In reality the density close to the particle is different than far away as can be described by a pair correlation function. Furthermore, it is neglected that the fluid is enclosed
between walls. Performing the integral we get

$phi =-2a'{frac {N}{V}}quad {hbox{with}}quad a'=epsilon {frac {2pi d^{3}}{3}}=epsilon b'.$

Hence, we obtain,

${displaystyle ln Z=Nln {(V-Nb')}+{frac {N^{2}a'}{VkT}}-Nln {(Lambda ^{3})}-ln {N!}}$

From statistical thermodynamics we know that

${displaystyle p=kT{frac {partial ln Z}{partial V}}}$

so that we only have to differentiate the terms containing . We get

$p={frac {NkT}{V-Nb'}}-{frac {N^{2}a'}{V^{2}}}Rightarrow left(p+{frac {N^{2}a'}{V^{2}}}right)(V-Nb')=NkTRightarrow left(p+{frac {n^{2}a}{V^{2}}}right)(V-nb)=nRT.$

Maxwell equal area rule[edit]

Van der Waals isotherm oscillation and Maxwell’s equal areas.^[19] Maxwell’s rule eliminates the oscillating behavior of the isotherm in the phase transition zone by defining it as a certain isobar in that zone. The above isotherm is for a reduced temperature of T_R=0.9. The Maxwell correction is at a vapor pressure of p_V≈0.64700 between the reduced volume of the pure liquid V_L≈0.60340 and the pure gas V_G≈2.3488 at the vapor pressure.

Below the critical temperature, the Van der Waals equation seems to predict qualitatively incorrect relationships. Unlike for ideal gases, the p-V isotherms oscillate with a relative minimum (d) and a relative maximum (e). Any pressure between p_d and p_e appears to have 3 values for the volume, contradicting the experimental observation that two state variables completely determine a one-component system’s state.^[19] Moreover, the isothermal compressibility is negative between d and e (equivalently $scriptstyle left({{partial P}/{partial V}}right)_{T,N}>0$ ), which cannot describe a system at equilibrium.^[20]

To address these problems, James Clerk Maxwell replaced the isotherm between points a and c with a horizontal line positioned so that the areas of the two shaded regions would be equal (replacing the a–d–b–e–c)^[20] curve with a straight line from a to c); this portion of the isotherm corresponds to the liquid-vapor equilibrium. The regions of the isotherm from a–d and from c–e are interpreted as metastable states of super-heated liquid and super-cooled vapor, respectively.^[21]^[22] The equal area rule can be expressed as:

${displaystyle p_{V}(V_{G}-V_{L})=int _{V_{L}}^{V_{G}}p,dV}$

where p_V is the vapor pressure (flat portion of the curve), V_L is the volume of the pure liquid phase at point a on the diagram, and V_G is the volume of the pure gas phase at point c on the diagram.^{[citation needed]} A two-phase mixture at p_V will occupy a total volume between V_L and V_G, as determined by Maxwell’s lever rule.

Maxwell justified the rule based on the fact that the area on a pV diagram corresponds to mechanical work, saying that work done on the system in going from c to b should equal work released on going from a to b. This is because the change in free energy A(T,V) equals the work done during a reversible process, and, as a state variable, the free energy must be path-independent. In particular, the value of A at point b should be the same regardless of whether the path taken is from left or right across the horizontal isobar, or follows the original Van der Waals isotherm.^{[citation needed]}

This derivation is not entirely rigorous, since it requires a reversible path through a region of thermodynamic instability, while b is unstable.^{[clarification needed]}^{[citation needed]} Nevertheless, modern derivations from chemical potential reach the same conclusion, and it remains a necessary modification to the Van der Waals and to any other analytic equation of state.^[19]

From chemical potential[edit]

The Maxwell equal area rule can also be derived from an assumption of equal chemical potential μ of coexisting liquid and vapour phases.^[23]^{[non-primary source needed]} On the isotherm shown in the above plot, points a and c are the only pair of points which fulfill the equilibrium condition of having equal pressure, temperature and chemical potential. It follows that systems with volumes intermediate between these two points will consist of a mixture of the pure liquid and gas with specific volumes equal to the pure liquid and gas phases at points a and c.

The Van der Waals equation may be solved for V_G and V_L as functions of the temperature and the vapor pressure p_V.^{[citation needed]} Since:^{[according to whom?]}

${displaystyle p=-left({frac {partial A}{partial V}}right)_{T,N}}$

where A is the Helmholtz free energy, it follows that the equal area rule can be expressed as:

${displaystyle p_{V}={frac {A(V_{L},T,N)-A(V_{G},T,N)}{V_{G}-V_{L}}}}$

Since the gas and liquid volumes are functions of p_V and T only, this equation is then solved numerically to obtain p_V as a function of temperature (and number of particles N), which may then be used to determine the gas and liquid volumes.^{[citation needed]}

Locus of coexistence for two phases of Van der Waals fluid

A pseudo-3D plot of the locus of liquid and vapor volumes versus temperature and pressure is shown
in the accompanying figure. One sees that the two locii meet at the critical point (1,1,1) smoothly. An isotherm of the Van der Waals fluid taken at T _r = 0.90 is also shown where the intersections of the isotherm with the loci illustrate the construct’s requirement that the two areas (red and blue, shown) are equal.

Other parameters, forms and applications[edit]

Other thermodynamic parameters[edit]

We reiterate that the extensive volume V is related to the volume per particle v=V/N where N = nN_A is the number of particles in the system.
The equation of state does not give us all the thermodynamic parameters of the system. We can take the equation for the Helmholtz energy A ^[24]

From the equation derived above for lnQ, we find

$A(T,V,N)=-NkTleft[1+ln left({frac {(V-Nb')T^{3/2}}{NPhi }}right)right]-{frac {a'N^{2}}{V}}.$

Where Φ is an undetermined constant, which may be taken from the Sackur–Tetrode equation for an ideal gas to be:

$Phi =T^{3/2}Lambda ^{3}=left({frac {h}{sqrt {2pi mk}}}right)^{3}$

This equation expresses A in terms of its natural variables V and T , and therefore gives us all thermodynamic information about the system. The mechanical equation of state was already derived above

${displaystyle p=-left({frac {partial A}{partial V}}right)_{N,T}={frac {NkT}{V-Nb'}}-{frac {a'N^{2}}{V^{2}}}.}$

The entropy equation of state yields the entropy (S )

${displaystyle S=-left({frac {partial A}{partial T}}right)_{N,V}=Nkleft[ln left({frac {(V-Nb')T^{3/2}}{NPhi }}right)+{frac {5}{2}}right]}$

from which we can calculate the internal energy

$U=A+TS={frac {3}{2}},NkT-{frac {a'N^{2}}{V}}.$

Similar equations can be written for the other thermodynamic potential and the chemical potential, but expressing any potential as a function of pressure p will require the solution of a third-order polynomial, which yields a complicated expression. Therefore, expressing the enthalpy and the Gibbs energy as functions of their natural variables will be complicated.

Reduced form[edit]

Although the material constant a and b in the usual form of the Van der Waals equation differs for every single fluid considered, the equation can be recast into an invariant form applicable to all fluids.

Defining the following reduced variables (f_R, f_C are the reduced and critical variable versions of f, respectively),

$p_{R}={frac {p}{p_{C}}},qquad v_{R}={frac {v}{v_{C}}},quad {hbox{and}}quad T_{R}={frac {T}{T_{C}}}$

where

$p_C=frac{a'}{27b'^2}, qquad displaystyle{v_C=3b'},quadhbox{and}quad kT_C=frac{8a'}{27b'}$

as shown by Salzman.^[25]

The first form of the Van der Waals equation of state given above can be recast in the following reduced form:

${displaystyle left(p_{R}+{frac {3}{v_{R}^{2}}}right)(3v_{R}-1)=(8T_{R}}$

)

This equation is invariant for all fluids; that is, the same reduced form equation of state applies, no matter what a and b may be for the particular fluid.

This invariance may also be understood in terms of the principle of corresponding states. If two fluids have the same reduced pressure, reduced volume, and reduced temperature, we say that their states are corresponding. The states of two fluids may be corresponding even if their measured pressure, volume, and temperature are very different. If the two fluids’ states are corresponding, they exist in the same regime of the reduced form equation of state. Therefore, they will respond to changes in roughly the same way, even though their measurable physical characteristics may differ significantly.

Cubic equation[edit]

The Van der Waals equation is a cubic equation of state; in the reduced formulation the cubic equation is:

${v_{R}^{3}}-{frac {1}{3}}left({1+{frac {8T_{R}}{p_{R}}}}right){v_{R}^{2}}+{frac {3}{p_{R}}}v_{R}-{frac {1}{p_{R}}}=0$

At the critical temperature, where $T_{R}=p_{R}=1$ we get as expected

${displaystyle {v_{R}^{3}}-3v_{R}^{2}+3v_{R}-1=left(v_{R}-1right)^{3}=0quad Longleftrightarrow quad v_{R}=1}$

For T_R < 1, there are 3 values for v_R.
For T_R > 1, there is 1 real value for v_R.

The solution of this equation for the case where there are three separate roots may be found at Maxwell construction.

Application to compressible fluids[edit]

The equation is also usable as a PVT equation for compressible fluids (e.g. polymers). In this case specific volume changes are small and it can be written in a simplified form:

where p is the pressure, V is specific volume, T is the temperature and A, B, C are parameters.

References[edit]

^ ^a ^b ^c ^d Silbey, Robert J.; Alberty, Robert A.; Bawendi, Moungi G. (2004). Physical Chemistry (4th ed.). Wiley. ISBN 978-0471215042.
^ ^a ^b ^c “J. D. Van der Waals, The equation of state for gases and liquids: Nobel Lecture, December 12, 1910” (PDF). Nobel Lectures, Physics 1901–1921. Amsterdam: Elsevier Publishing Company. 1967. pp. 254–265. Archived (PDF) from the original on 10 April 2020.
^ Andrews, T. (1869). “The Bakerian Lecture: On the Gaseous State of Matter”. Philosophical Transactions of the Royal Society of London. 159: 575–590. doi:10.1098/rstl.1869.0021.
^ Klein, M. J. (1974). “The Historical Origins of the Van der Waals Equation”. Physica. 73 (1): 31. Bibcode:1974Phy….73…28K. doi:10.1016/0031-8914(74)90224-9.
^ Van der Waals, J. D. (1873). Over de Continuiteit van den Gas- en Vloeistoftoestand [About the Continuity of the Gas and Fluid States] (in Dutch). University of Leiden.
^ Clerk-Maxwell, J. (1874). “Over de Continuiteit van den Gas- en Vloeistoftoestand. Academisch Proefschrift”. Nature. 10 (259): 477–480. Bibcode:1874Natur..10..477C. doi:10.1038/010477a0. S2CID 4046639.
^ Maxwell, J.C. (1890). “LXIX. Van der Waals on the Continuity of the Gaseous and Liquid States”. In Niven, W. D. (ed.). The Scientific Papers of James Clerk Maxwell, Vol. II. Cambridge University Press. pp. 407–415.
^ Chang, Raymond (2014). Physical Chemistry for the Chemical Sciences. University Science Books. p. 14. ISBN 978-1891389696.
^ “Deviations from Ideal Gas Law Behavior”. Bodner Research Web. Purdue University, College of Science, Division of Chemical Education. 2004.
^ ^a ^b Hewitt, Nigel. “Who was Van der Waals anyway and what has he to do with my Nitrox fill?”. Maths for Divers.
^ ^a ^b Lindsey, Brice, “Mixing Rules for Simple Equations of State”, Intermolecular Potentials and the Evaluation of Second Virial Coefficient
^ ^a ^b Hill, Terrell L. (2012) [1960]. An Introduction to Statistical Thermodynamics. Dover Books on Physics. Chicago: R.R. Donnelly (Courier/Dover). ISBN 978-0486130903.. Note, this Donnelly edition is a reprint of the 1986 Dover edition, which itself reprinted the 1962 corrected version of the original 1960 text (Addison Wesley Series in Chemistry, Francis T. Bonner & George C. Pimentel, Eds., Reading, MS: Addison-Wesley).
^ Sandler, S. I. (1999). Chemical and Engineering Thermodynamics (Third ed.). New York: Wiley. p. 273.
^ Atkins, Peter; de Paula, Julio (2006). Physical Chemistry (8th ed.). New York: Macmillan. pp. 17–22, 104 fwd, 632–641. ISBN 0716787598.
^ Berry, R. Stephen; Rice, Stuart A.; Ross, John (2000). Physical Chemistry. Oxford: Oxford University Press. pp. 298–306 and passim. ISBN 0195105893.
^ Dill, Ken A.; Bromberg, Sarina (2003). Molecular Driving Forces: Statistical Thermodynamics in Chemistry and Biology. New York: Garland Science. pp. 457–462. ISBN 0815320515.
^ Hill, Terrell L. (1960). An Introduction to Statistical Thermodynamics. Courier Corporation. p. 77.
^ Denker, John (2014). “Chapter 26.9, Derivation: Particle in a Box”. Modern Thermodynamics. CreateSpace Independent Publishing Platform. ISBN 978-1502530356.
^ ^a ^b ^c Sandler, Stanley I. (2006). Chemical, Biochemical, and Engineering Thermodynamics (4th ed.). New York: John Wiley & Sons. p. 284. ISBN 978-0-471-66174-0.
^ ^a ^b Sandler (2006), p. 287.
^ Clerk-Maxwell, J. (1875). “On the Dynamical Evidence of the Molecular Constitution of Bodies”. Nature. 11 (279): 357–359. Bibcode:1875Natur..11..357C. doi:10.1038/011357a0. ISSN 0028-0836.
^ Maxwell (1890), “LXXI. On the Dynamical Evidence of the Molecular Constitution of Bodies”, pp. 418–438.
^ Elhassan, A. E.; Craven, R.J.B.; de Reuck, K. M. (1997). “The area method for pure fluids and an analysis of the two-phase region”. Fluid Phase Equilibria. 130 (1–2): 167–187. doi:10.1016/S0378-3812(96)03222-0.
^ Gershenson, Michael (n.d.), “Lecture 16. The Van der Waals Gas (Ch. 5)” (PDF), Slide set from prior teaching of PHYS 351, Thermal Physics (Statistics and Thermodynamics), Rutgers University, Department of Physics and Astronomy, retrieved 25 June 2015. Possibly sourced from Schroeder, Daniel V. (2013). An Introduction to Thermal Physics. New York: Pearson Education. ISBN 978-1292026213.
^ Salzman, W. R. (8 July 2004). “Critical Constants of the Van der Waals Gas”. Chemical Thermodynamics. Department of Astronomy, Arizona State University. Archived from the original on 29 July 2015. Retrieved 7 July 2015.

Further reading[edit]

Chandler, David (1987). Introduction to Modern Statistical Mechanics. Oxford: Oxford University Press. pp. 287–295. ISBN 0195042778.
Cross, Michael (2004), “Lecture 3: First Order Phase Transitions” (PDF), Physics 127: Statistical Physics, Second Term, Pasadena, California: Division of Physics, Mathematics, and Astronomy, California Institute of Technology.
Dalgarno, A.; Davison, W.D. (1966). “The Calculation of Van Der Waals Interactions”. Advances in Atomic and Molecular Physics. 2: 1–32. Bibcode:1966AdAMP…2….1D. doi:10.1016/S0065-2199(08)60216-X. ISBN 9780120038022.
Kittel, Charles; Kroemer, Herbert (1980). Thermal Physics (Revised ed.). New York: Macmillan. pp. 287–295. ISBN 0716710889.

Источник

Библиографическое описание:

Ковальчук, Е. М. Уравнение Ван-дер-Ваальса / Е. М. Ковальчук, А. В. Чаленко. — Текст : непосредственный // Юный ученый. — 2019. — № 2 (22). — С. 36-41. — URL: https://moluch.ru/young/archive/22/1387/ (дата обращения: 21.05.2023).

Уравнение Ван-дер-Ваальса является простейшей формой уравнения состояния реальных газов, которое качественно правильно описывает поведение реального газа, включая фазовые переходы.

Рассмотрим простой метод получения уравнения Ван-дер-Ваальса [1].

Известно, что по мере увеличения плотности газа, его свойства все более отклоняются от свойств идеального газа и, в конце концов, наступает его конденсация в жидкость. Эти явления связаны со сложными молекулярными взаимодействиями и нет способа, которым можно было бы учесть эти взаимодействия количественным образом с тем, чтобы теоретически построить уточное уравнение состояния вещества. Тогда можно построить уравнение состояния, учитывающее основные качественные особенности молекулярного взаимодействия. Рассмотрим кратко эти особенности.

Особенности молекулярного взаимодействия

Силы взаимодействия между атомами, приводящие к образованию молекул, имеют в основном электрическое происхождение. Но образование молекул, как и структура атомов, относится к категории квантовых явлений, которые не могут быть объяснены в рамках классической механики.

Простейшей молекулой является двухатомная молекула, состоящая из двух атомов — одинаковых или различных. Взаимодействие атомов, приводящее к образованию такой молекулы, описывается потенциальной энергией, график которой изображен на рис. 1. На этом графике отложена потенциальная энергия взаимодействия двух атомов как функция расстояния между ними (точнее, расстояния между ядрами атомов). Эта функция имеет довольно глубокий и резкий минимум при некотором значении . На меньших расстояниях кривая очень круто поднимается вверх. Эта область соответствует сильному отталкиванию атомов, обусловленному в основном кулоновским отталкиванием сближающихся ядер. Более строгое объяснение природы отталкивания учитывает перекрытие электронных облаков атомов при их сближении и возникновение отталкивания за счет повышения энергии системы, вызванного переходом электронов на более высокие энергетические уровни за счет действия принципа Паули.

На больших расстояниях атомы притягиваются. Природа сил притяжения связана с взаимодействием электрических моментов, которые атомы наводят друг на друге.

Расстояние отвечает устойчивому равновесному взаимному положению ядер в молекуле. В действительности ядра не занимают строго эти положения, а совершают около них колебания. Амплитуда этих колебаний обычно мала. Глубина потенциальной ямы характеризует прочность связи атомов в молекуле. Различные молекулы тоже взаимодействуют друг с другом. Это взаимодействие называют ван-дер-ваальсовым, в отличие от химического взаимодействия атомов, приводящего к образованию молекул.

Взаимодействие молекул нельзя, вообще говоря, изобразить просто в виде кривой , как в случае атомов. Это связано с тем, что взаимное расположение молекул характеризуется большим числом параметров. Так, наряду с расстоянием между молекулами существенна также и их взаимная ориентация. Но если представить себе взаимодействие молекул как бы усредненным по всем возможным их ориентациям, то оно тоже может быть изображено в виде такой кривой.

Рис. 1 Потенциальная энергия взаимодействия двух атомов как функция расстояния между ними

Эта кривая похожа на кривую взаимодействия атомов в молекуле в том отношении, что на больших расстояниях все молекулы притягиваются друг к другу, а на малых расстояниях — отталкиваются. Силы притяжения между молекулами быстро убывают с увеличением расстояния между ними. Еще быстрее происходит увеличение сил отталкивания при сближении молекул. Можно себе представить, что при сближении молекулы ведут себя как твердые, взаимно не проникающие тела. Глубина же минимума на кривой ван-дер-ваальсовского взаимодействия очень мала. Она измеряется несколькими десятыми или даже сотыми долями электрон-вольта, в то время как глубина потенциальной ямы на кривой химического взаимодействия между атомами составляет несколько электрон-вольт.

Другое существенное отличие между обоими видами взаимодействия состоит в том, что ван-дер-ваальсовы силы, в отличие от химических, не обладают свойством насыщаемости. Ван-дер-ваальсово взаимодействие существует между всеми молекулами, так что если две молекулы сближаются друг с другом благодаря этому взаимодействию, то они продолжают притягивать и другие молекулы. Поэтому силы молекулярного взаимодействия не приводят к образованию «сверхмолекул», а только содействуют общему стремлению молекул сблизиться друг с другом. Это стремление осуществляется при переходе вещества в конденсированное состояние — жидкое или твердое.

Получение уравнения Ван-дер-Ваальса

Быстро возрастающие на малых расстояниях силы отталкивания означают, грубо говоря, что молекулы как бы занимают некоторый определенный объем, дальше которого газ не может быть сжат. Другое основное свойство взаимодействия молекул заключается в притяжении на больших расстояниях. Это притяжение очень существенно, поскольку именно оно приводит к конденсации газа в жидкость.

Начнем с того, что учтем в уравнении состояния (для одного моля вещества) ограниченную сжимаемость газа. Для этого надо в уравнении идеального газа

(1)

заменить объем разностью , где –характерная для данного газа положительная постоянная, учитывающая размеры молекул и занимаемый молекулами объем. Конечность размеров молекул приводит к уменьшению объема, доступного для их движения. Эти соображения приводят к уравнению

. (2)

Из него следует, что объем не может быть сделан меньшим, чем , поскольку при давление обращается в бесконечность. Учтем теперь притяжение молекул. Это притяжение должно приводить к уменьшению давления газа, поскольку на каждую молекулу, находящуюся вблизи стенки сосуда, будет действовать со стороны остальных молекул сила, направленная внутрь сосуда. В грубом приближении эта сила будет пропорциональна числу молекул в единице объема, т. е. плотности газа. С другой стороны, давление само пропорционально этому же числу. Поэтому общее уменьшение давления, связанное с взаимным притяжением молекул, будет пропорционально квадрату плотности газа, т. е. обратно пропорционально квадрату его объема.

В соответствии с этими соображениями, вычтем из предыдущего выражения для давления член вида , где – некоторая новая постоянная, характеризующая силы молекулярного притяжения. Таким образом, получим уравнение Ван-дер-Ваальса:

, (3)

или, в несколько другом виде

. (3*)

При большом разрежении газа (большие объемы ) величинами и можно пренебречь, и уравнение Ван-дер-Ваальса возвращаемся к уравнению состояния идеального газа.

Для проведения количественных расчетов на основе уравнения Ван-дер-Ваальса необходимо определить величины постоянных и . Простейшим вариантом является определение этих постоянных из соотношений, связывающих их с критическими параметрами вещества — температурой, давлением и объемом в критической точке. Величины постоянных являются функциями температуры и подобрать их таким образом, чтобы получить согласие с экспериментальными данными во всем диапазоне параметров невозможно [2, 3]. Поэтому уравнение Ван-дер-Ваальса используется в основном для качественного анализа поведения вещества.

Принципиальное значение уравнения Ван-дер-Ваальса определяется следующими обстоятельствами:

1) Уравнение было получено из модельных представлений о свойствах реальных газов и жидкостей, а не явилось результатом эмпирического подбора функции , описывающей свойства реальных газов.

2) Уравнение долго рассматривалось как некоторое исходное уравнение состояния реальных газов, на основе которого было построено много других уравнений состояния.

3) С помощью уравнения Ван-дер-Ваальса впервые удалось описать явление перехода газа в жидкость и проанализировать критические явления. В этом отношении уравнение Ван-дер-Ваальса имеет преимущество даже перед более точными уравнениями в вириальной форме.

Аналитическое исследование свойств газа Ван-дер-Ваальса

Для исследования поведения газа, описываемого уравнением Ван-дер-Ваальса, рассмотрим определяемые этим уравнением изотермы, т. е. кривые зависимости давления от объема при постоянных значениях температуры. С этой целью перепишем уравнение Ван-дер-Ваальса в виде

. (1.4)

При фиксированных значениях и это — уравнение третьей степени относительно переменной . Как известно, уравнение третьей степени имеет три корня, из них вещественными могут быть либо все три, либо только один. Физический смысл имеют только вещественные и положительные корни (объем ). Отметим, что уравнение не может иметь отрицательных вещественных корней, т. к. в этом случае все слагаемые имели бы отрицательный знак и не могли бы в сумме дать ноль. Отметим, что заданным значениям давления и температуры по уравнению Ван-дер-Ваальса соответствуют либо три различных значения объема, либо только одно.

Второй случай имеет место при достаточно высоких температурах. Соответствующие изотермы отличаются от изотерм идеального газа лишь некоторым изменением их формы, но остаются монотонно спадающими кривыми. При более низких температурах изотермы имеют максимум и минимум, так что для каждой из них существуют такие интервалы давлений, в которых кривая определяет три различных значения . На рис. 2 изображена одна из таких изотерм. Разберем физический смысл различных ее участков.

Рис. 2 Изотерма уравнения Ван-дер-Ваальса

На участках и зависимость давления от объема имеет нормальный характер, т. е. давление возрастает при уменьшении объема. Участок же соответствовал бы неестественному положению, когда сжатие вещества приводило бы к уменьшению давления. Такие состояния не могут осуществляться в природе.

Наличие заведомо неосуществимого участка изотермы означает, что при постепенном изменении объема вещество не может оставаться все время в виде однородной среды. В некоторый момент времени должно наступать скачкообразное изменение состояния и распад вещества на две фазы. Другими словами, истинная изотерма будет иметь вид ломаной линии , как показано на рис. 3. Часть ее отвечает газообразному состоянию вещества, а часть — жидкому состоянию. Горизонтальный же прямолинейный отрезок соответствует двухфазным состояниям — переходу газа в жидкость, происходящему (при заданной температуре) при определенном постоянном давлении.

Рис. 3 Изотерма уравнения Ван-дер-Ваальса и изотерма реального газа

Что касается участков изотермы и , то они отвечают метастабильным состояниям — переохлажденному пару и перегретой жидкости. Видно, что существуют определенные границы (изображаемые точками и ), дальше которых переохлаждение пара или перегрев жидкости вообще невозможны.

При повышении температуры прямолинейный участок изотермы уменьшается и при критической температуре стягивается в одну точку. Проходящая через эту точку изотерма разделяет изотермы обоих типов: монотонные изотермы и изотермы с максимумами и минимумами, на которых неизбежно распадение вещества на две фазы.

Если соединить между собой точки начала и конца прямолинейных отрезков изотерм, то получающаяся кривая представит собой кривую фазового равновесия жидкости и пара на диаграмме , . Максимум этой кривой есть критическая точка. В этом состоянии система с макроскопической точки зрения представляет собой одну фазу.

В критической точке сливаются в одну три точки, в которых прямолинейный участок пересекает изотеру Ван-дер-Ваальса. Отсюда следует, что касательная к изотерме в критической точке имеет горизонтальное направление, т. е. обращается в ноль производная от давления по объему (при постоянной температуре):

. (5)

Величина, обратная этой производной, есть сжимаемость вещества. Таким образом, в критической точке сжимаемость вещества обращается в бесконечность. Отметим, что параметры уравнения Ван-дер-Ваальса и можно найти, зная давление, объем и температуру в критической точке. Для нахождения критических параметров , , заметим, что уравнение Ван-дер-Ваальса в критической точке можно записать в виде

. (6)

Поскольку в этом случае все три корня совпадают и равны , уравнение должно приводиться к виду:

. (7)

Возводя в куб и сравнивая коэффициенты двух последних уравнений, получим три уравнения: , , .

Решая их, найдем

, , . (8)

К тем же результатам можно прийти, заметив, что критическая точка является точкой перегиба изотермы, поэтому, кроме первой производной в ней должна обращаться в ноль и вторая производная давления по объему:

, . (9)

Вычисляя эти производные из уравнения Ван-дер-Ваальса и, решая полученную систему уравнений, придем к тем же результатам. И наоборот, зная из эксперимента критические параметры вещества, можно определить постоянные Ван-дер-Ваальса:

, . (10)

Одним из параметров, характеризующих качество уравнения состояния реального газа, является вычисленный на его основе критический коэффициент :

. (11)

Подставляя сюда полученные выше выражения критических параметров через постоянные Ван-дер-Ваальса, получим . Таким образом, критический коэффициент получается одинаковым для всех веществ. В действительности для разных веществ имеет различные значения, причем они всегда больше 2,67 и имеют в среднем значение 3,7.

Литература:

Ландау Л. Д., Лифшиц Е. М. Курс общей физики. Механика и молекулярная физика. — М.: Наука, 1965. — 384 с.
Таблицы физических величин. Справочник. Под ред. акад. И. К. Кикоина. –М.: Атомиздат, 1976. — 1008 с.
Каханер Д., Моулер К., Нэш С. Численные методы и математическое обеспечение: Пер. с англ. — М.: Мир, 1998. — 575 с.

Основные термины (генерируются автоматически): уравнение, молекула, идеальный газ, уравнение состояния, объем, молекулярное взаимодействие, реальный газ, образование молекул, давление, изотерм.

Источник

Уравнение состояния[править | править код]

Вывод уравнения[править | править код]

Традиционный вывод[править | править код]

Внутренняя энергия газа Ван-дер-Ваальса[править | править код]

Адиабата[править | править код]

Критические параметры[править | править код]

Приведённые параметры[править | править код]

Недостатки уравнения Ван-дер-Ваальса[править | править код]

Константы Ван-дер-Ваальса для некоторых газов[править | править код]

См. также[править | править код]

Примечания[править | править код]

Комментарии[править | править код]

Источники[править | править код]

Литература[править | править код]

Что такое реальный газ

Уравнение Ван-дер-Ваальса

Overview and history[edit]

Equation[edit]

Gas mixture[edit]

Reduced form[edit]

Compressibility factor[edit]

Validity[edit]

Derivation[edit]

Conventional derivation[edit]

Statistical thermodynamics derivation[edit]

Maxwell equal area rule[edit]

From chemical potential[edit]

Other parameters, forms and applications[edit]

Other thermodynamic parameters[edit]

Reduced form[edit]

Cubic equation[edit]

Application to compressible fluids[edit]

See also[edit]

References[edit]

Further reading[edit]

Библиографическое описание:

Добавить комментарий Отменить ответ

Уравнение состояния[править | править код]

Вывод уравнения[править | править код]

Традиционный вывод[править | править код]

Внутренняя энергия газа Ван-дер-Ваальса[править | править код]

Адиабата[править | править код]

Критические параметры[править | править код]

Приведённые параметры[править | править код]

Недостатки уравнения Ван-дер-Ваальса[править | править код]

Константы Ван-дер-Ваальса для некоторых газов[править | править код]

См. также[править | править код]

Примечания[править | править код]

Комментарии[править | править код]

Источники[править | править код]

Литература[править | править код]

Что такое реальный газ

Уравнение Ван-дер-Ваальса

Overview and history[edit]

Equation[edit]

Gas mixture[edit]

Reduced form[edit]

Compressibility factor[edit]

Validity[edit]

Derivation[edit]

Conventional derivation[edit]

Statistical thermodynamics derivation[edit]

Maxwell equal area rule[edit]

From chemical potential[edit]

Other parameters, forms and applications[edit]

Other thermodynamic parameters[edit]

Reduced form[edit]

Cubic equation[edit]

Application to compressible fluids[edit]

See also[edit]

References[edit]

Further reading[edit]

Библиографическое описание:

Вам также может понравиться

Как найти снайпера в игре снайпер

Субнаутика как найти острова

Как найти элемент площади поверхности

Добавить комментарий Отменить ответ