Для
того, чтобы определить ЛАХ последовательного
корректирующего устройства, из ординат
желаемой ЛАХ вычитаются ординаты ЛАХ
нескорректированной системы, то есть:
![]()
Вычитание ЛАХ
производится графически. Из полученного
графического изображения ЛАХ
последовательной коррекции определяется
ее передаточная функция:
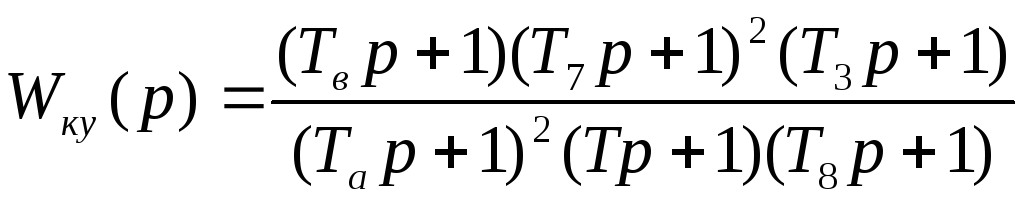 ,
,
где
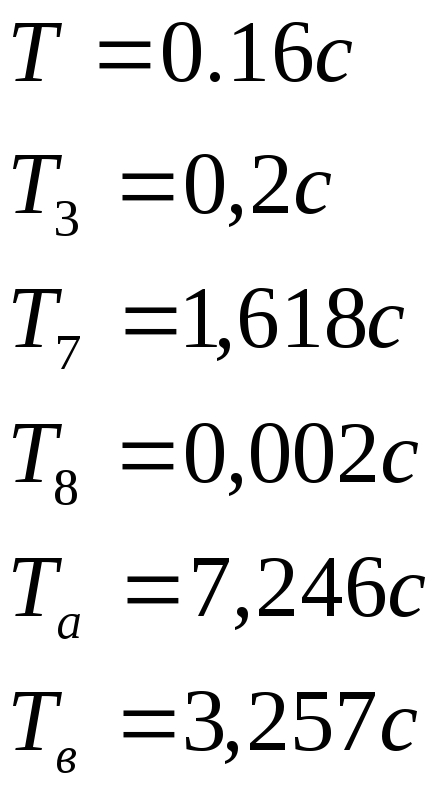
Реализовать
последовательное корректирующее
устройство с данной передаточной
функцией вполне возможно, так как степени
числителя и знаменателя равны 4.
Определим место
последовательного корректирующего
устройства:

Рисунок 10 – Структурная
схема САУ с последовательным КУ
Найдем ПФ скорректированной
САУ:
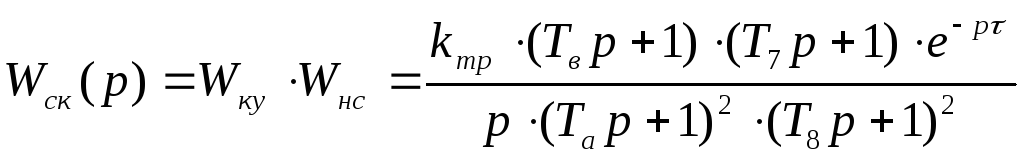
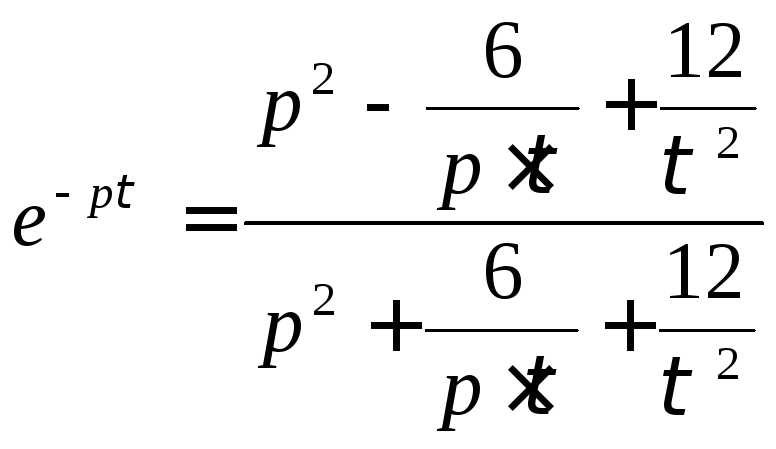
Построим
ФЧХ скорректированной САУ, используя
программуMathLAB7.3.0.
Алгоритм ввода данных имеет следующий
листинг:
>> k=192.308
k=
192.3080
>> Ta=7.246
Ta=
7.2460
>> T8=0.002
T8
=
0.0020
>> Tv=3.257
Tv =
3.2570
>> T7=1.618
T7 =
1.6180
>> tau=0.007
tau =
0.0070
>>w1=tf([k*Tv*T7,Tv*k+k*T7,k+12*k*Tv*T7/tau^2,12*Tv*k/tau^2+12*T7*k/tau^2-6*k*Tv*T7/tau,12*k/tau^2-6*Tv*k/tau+6*T7*k/tau,-6*k/tau],[Ta^2*T8^2,2*T8*Ta^2+2*Ta*T8^2,Ta^2+T8^2+4*Ta*T8+12*Ta^2*T8^2/tau^2,2*Ta+2*T8+6*Ta^2*T8^2/tau+24*T8*Ta^2/tau^2+24*Ta*T8^2/tau^2,1+12*T8*Ta^2/tau+12*Ta*T8^2/tau+12*Ta^2/tau^2+12*T8^2/tau^2+48*Ta*T8/tau^2,6*Ta^2/tau+6*T8^2/tau+24*Ta*T8/tau+24*Ta/tau^2+24*T8/tau^2,12*Ta/tau+12*T8/tau+12/tau^2,6/tau,0])
Transfer function:
1013 s^5 + 937.5 s^4 + 2.482e008 s^3 + 2.287e008
s^2 + 4.683e007 s- -1.648e005
——————————————————————————————–
0.00021 s^8 + 0.2101 s^7 + 104 s^6 + 5.146e004 s^5
+ 1.287e007 s^4 +3.595e006s^3 + 2.573e005 s^2 + 857.1 s
>> margin(w1);grid
Имеем
следующие данные:
|
|
|
|
|
-1.01 |
0.0969 |
-494 |
|
-0.76 |
0.173 |
-512 |
|
-0.56 |
0.272 |
-517 |
|
-0.38 |
0.413 |
-513 |
|
-0.13 |
0.737 |
-497 |
|
0.12 |
1.32 |
-480 |
|
0.37 |
2.35 |
-468 |
|
0.62 |
4.19 |
-461 |
|
0.87 |
7.49 |
-457 |
|
1.13 |
13.4 |
-456 |
|
1.25 |
17.9 |
-456 |
|
1.5 |
31.9 |
-459 |
|
1.75 |
56.9 |
-464 |
|
2 |
100 |
-473 |

Рисунок 11 – ЛАХ и ЛФХ
скорректированной САУ
3.4 Определение операторной передаточной функции и постоянных времени корректирующей обратной связи.
Корректирующая
обратная связь (в дальнейшем КОС)
позволяет скорректировать систему
путем охвата обратной связью с
определенными звеньями некоторой части
системы (или всей системы). Принципиальный
вид структурной схемы с КОС следующий:
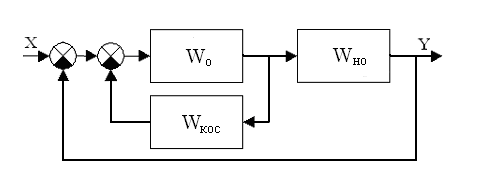
Рисунок
12 – Общий вид схемы с КОС
Для
дальнейшего определения ЛАХ КОС запишем
следующее условие:
![]()
Таким
образом, сначала необходимо из ЛАХ
нескорректированной системы отнять
желаемую ЛАХ и из этой разности, отняв
ЛАХ охватываемой части найти ЛАХ КОС,
то есть:
![]() .
.
Охватим регулятор
корректирующей обратной связью. Схема
имеет вид:
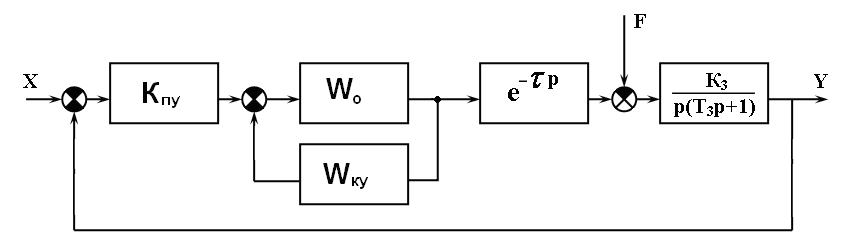
Рисунок
13 – Структурная схема САУ с КОС
Охваченная часть будет
представлять собой два инерционных
звена и одно форсирующее звено, то есть:
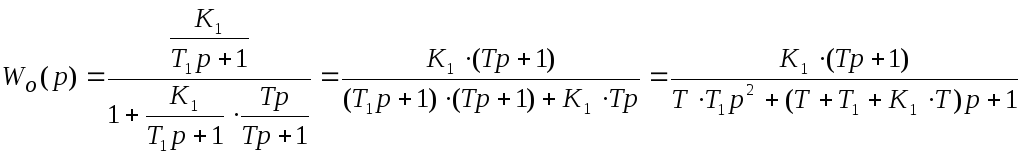
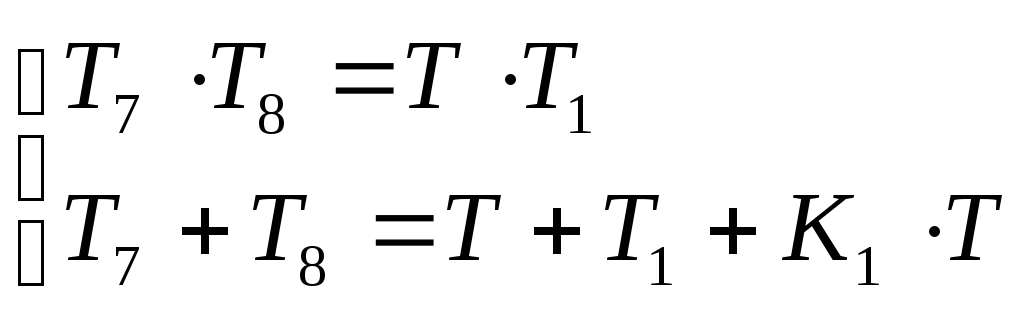
В итоге получаем:
![]() ,
,
где
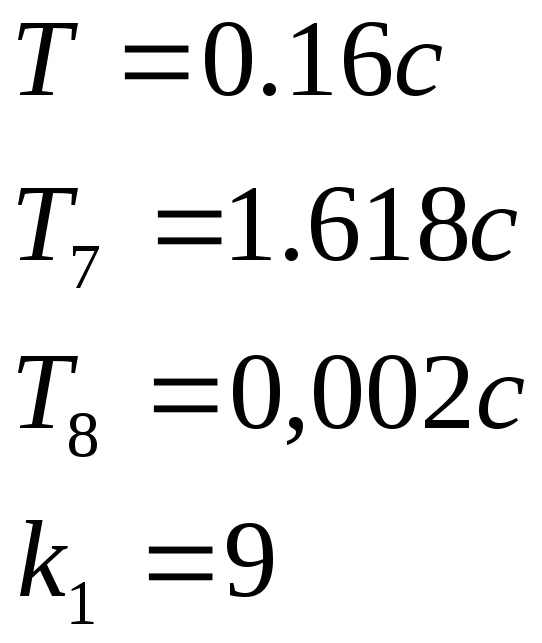
ЛАХ
данного охваченного участка, проходит
через точку
![]()
на оси ординат с наклоном
![]() ,
,
затем в точке
![]() (по
(по
логарифмической шкале
![]() )
)
она претерпевает излом на
![]() ,
,
что и характерно для инерционного звена.
Далее в точке
![]() (по
(по
логарифмической шкале
![]() )
)
она выравнивается на![]() ,
,
и в точке
![]() (по логарифмической шкале
(по логарифмической шкале
![]() )
)
она снова ломается на![]() .
.
Желаемую
ЛАХ в низкочастотной области при
![]() оставим под наклоном
оставим под наклоном![]() ,
,
а при![]() сломаем на
сломаем на![]() ,
,
на высокочастотной области оставим
желаемую ЛАХ под наклоном![]() ,
,
то есть не будем ломать ее как в предыдущем
случае для последовательного КУ на![]() .
.
При этом изменится ее передаточная
функция и ФЧХ.
Передаточная
функция желаемой ЛАХ для КОС будет
выглядеть следующим образом:
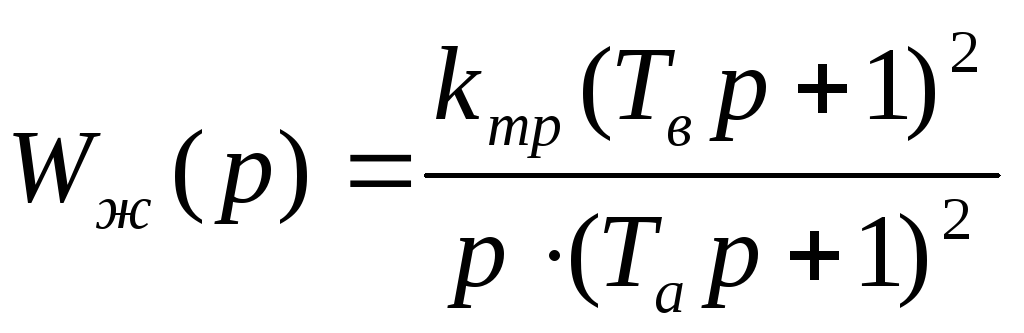
Для
построения ФЧХ воспользуемся программой
MathLAB7.3.0. Алгоритм ввода
данных имеет следующий листинг:
>>
Ta=12.7
Ta =
12.7000
>>
Tv=5.52
Tv
=
5.5200
>>
k=192.308
k =
192.3080
>>
w=tf([k*Tv^2,2*Tv*k, k],[Ta^2,2*Ta,1,0])
Transfer function:
5860 s^2 + 2123 s +
192.3
————————-
161.3 s^3 + 25.4 s^2 +
s
>> bode(w)
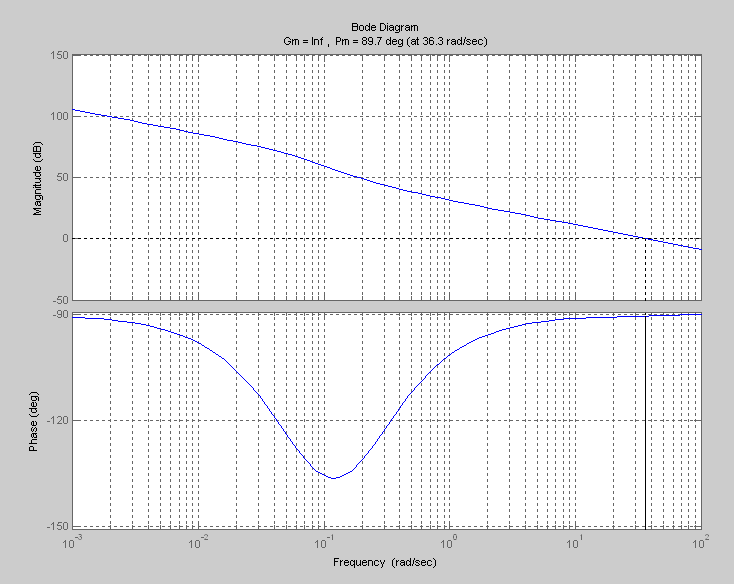
Рисунок 14 – желаемаяЛАХ и ЛФХдля КОС
ФЧХ
не пересекает линию -,
следовательно имеется бесконечный
запас устойчивости по фазе.
Определив
желаемую ЛАХ и отняв последовательно
из ЛАХ нескорректированной системы
желаемую ЛАХ и от этой разницы ЛАХ
охваченной части в соответствии с
формулой
![]() ,
,
получаем ЛАХ корректирующей обратной
связи. Передаточная функция КОС:
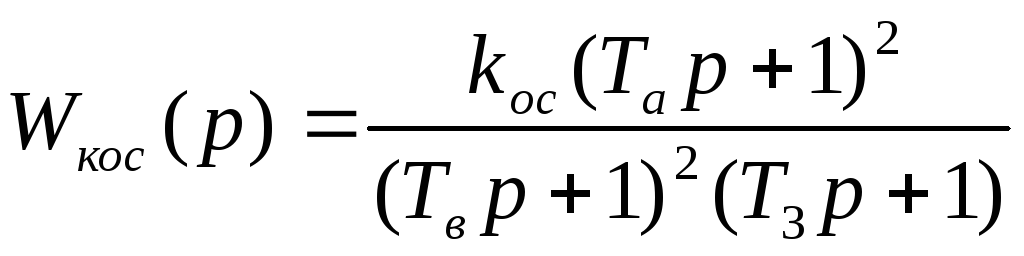 .
.
Степень
числителя равна 2, степень знаменателя
– 3, следовательно,
реализация такого
устройства возможна.
Найдем
ПФ и построим ФЧХ скорректированной
САУ. Передаточная функция будет иметь
вид (исходя из рисунка 13):
![]()
Для
построения ФЧХ воспользуемся программой
MathLAB7.3.0. Алгоритм ввода
данных имеет следующий листинг:
>> Ta=12.7
Ta =
12.7000
>> Tv=5.52
Tv =
5.5200
>> T=0.16
T =
0.1600
>> T7=1.618
T7 =
1.6180
>> T3=0.2
T3 =
0.2000
>> T8=0.002
T8 =
0.0020
>> kpu=7.122
kpu =
7.1220
>> k3=3
k3 =
3
>> k1=9
k1 =
9
>> kos=0.112
kos =
0.1120
>> tau=0.007
tau =
0.0070
w3=tf([kpu*k3,0,12*kpu*k3/tau^2,-kpu*k3*6/tau],[T3,1,12*T3/tau^2,6*T3/tau+12/tau^2,6/tau,0])
Transfer function:
21.37 s^3 + 5.232e006 s – 1.831e004
——————————————————-
0.2s^5+s^4+4.898e004s^3+2.451e005s^2+857.1s
w2=tf([kos*Ta^2,2*kos*Ta,kos],[T3*Tv^2,Tv^2+2*Tv*T3,2*Tv+T3,1])
Transfer function:
18.06 s^2 + 2.845 s + 0.112
———————————–
6.094 s^3 + 32.68 s^2 + 11.24 s + 1
w1=tf([k1*T,k1],[T7*T8,T7+T8,1])
Transfer function:
1.44 s + 9
————————-
0.003236 s^2 + 1.62 s + 1
>> w4=w3*w1/(1+w1*w2)
Transfer function:
0.6067 s^9 + 310.8 s^8 + 1.523e005 s^7 + 7.612e007
s^6 + 9.147e008 s^5 + 3.162e009 s^4 + 2.482e009 s^3 + 6.044e008 s^2 +
4.495e007 s – 1.648e005
——————————————————————————————–
1.276e-005 s^12 + 0.01291 s^11 + 6.482 s^10 + 3208
s^9 + 8.222e005 s^8 + 1.131e007 s^7 + 5.785e007 s^6 + 1.211e008 s^5 +
7.108e007 s^4 + 1.06e007 s^3 + 5.28e005 s^2 + 1721 s
>> margin(w4);grid
Имеем
следующие данные:
|
|
|
|
|
-1.01 |
0.0976 |
-479 |
|
-0.78 |
0.166 |
-485 |
|
-0.63 |
0.233 |
-483 |
|
-0.38 |
0.415 |
-477 |
|
-0.13 |
0.741 |
-473 |
|
-0.004 |
0.99 |
-474 |
|
0.25 |
1.77 |
-480 |
|
0.49 |
3.15 |
-495 |
|
0.75 |
5.63 |
-513 |
|
1 |
10 |
-527 |
|
1.25 |
17.9 |
-535 |
|
1.5 |
32 |
-540 |
|
1.76 |
57.1 |
-545 |
|
2 |
100 |
-550 |
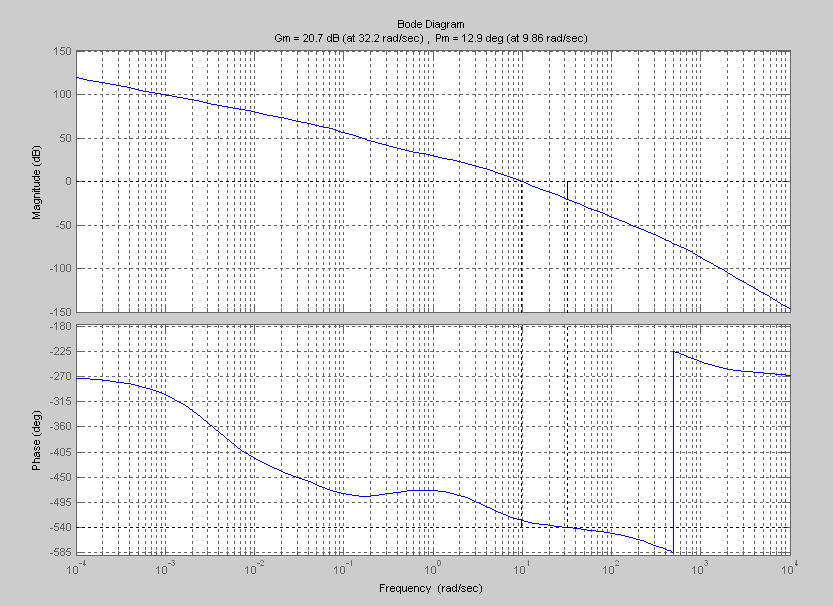
Рисунок
14.1 – ЛАХ и ЛФХ скорректированной САУ
Соседние файлы в папке курсовая работа
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Постоянная времени (греч. (Тау) или ) является характеристической величиной линейной динамической системы , которая описывается обыкновенным дифференциальным уравнением или соответствующей передаточной функцией. Он имеет измерение времени; его единицей измерения обычно является секунда.


Функциональная схема элемента ПТ 1
после скачка входа.
Динамическая система – это функциональный блок для обработки и передачи сигналов; системная входная переменная определяется как причина, а системная выходная переменная – как временное следствие. Типичными входными сигналами для проверки поведения системы являются импульсная функция , ступенчатая функция и функция нарастания .
В электротехнике обычно известно поведение во времени элемента задержки первого порядка (например, RC-элемента – фильтра нижних частот ) с переходной характеристикой с экспоненциальной асимптотикой. Постоянная времени определяет курс во времени. По истечении примерно 3-х постоянных времени выходной сигнал достигает примерно 95% от размера входного сигнала при увеличении коэффициента усиления системы .
В основном, ход выходного сигнала системы передачи любого порядка зависит от типа системы передачи и входного сигнала и не относится только к элементам ( элементам) временной задержки .
Термин постоянная времени является результатом описания линейной динамической системы с помощью обыкновенного дифференциального уравнения с постоянными коэффициентами . Чтобы упростить вычисление зависящего от времени поведения системы, дифференциальное уравнение, описывающее систему, подвергается преобразованию Лапласа, и на основании этого отношение сигналов формируется как передаточная функция .
Передаточная функция в представлении постоянной времени возникает следующим образом:
- Преобразование Лапласа обыкновенного дифференциального уравнения высшего порядка,
- Формирование передаточной функции .
- Полюса и нули передаточной функции являются наиболее важными параметрами поведения системы.
- Факторизуя многочлены в представлении полюс-нуль:
- Преобразование представления полюс-нуль числовыми значениями полюсов и нулей в представление постоянной времени,
- Значения полюсов и нулей линейного множителя могут принимать три формы: ноль, отрицательное действительное, отрицательное сопряженное комплексное.
- Это означает, что в числителе и знаменателе передаточной функции могут возникать различные основные формы линейных факторов и факторов 2-го порядка с различным поведением системы.
-
.
Постоянная времени соответствует коэффициенту перед комплексной переменной Лапласа . Они , как правило , рассчитывается с обратной отрицательной действительной полюса или нуля в знаменателе многочлена или числитель полинома передаточной функции , как:
-
или .
Определение постоянных времени по полиномам линейной динамической системы передачи высшего порядка
Системные описания через передаточные функции могут возникать из:
- Преобразование Лапласа обыкновенного дифференциального уравнения, описывающего систему, в передаточную функцию,
- Сложные делители напряжения с безреакционным соотношением импедансов (пример: операционный усилитель с RC-цепочкой ),
- Идентификация системы с помощью ступенчатой или импульсной характеристики.
Для облегчения вычислений и понимания описывающее систему обыкновенное дифференциальное уравнение подвергается преобразованию Лапласа и, следовательно, может быть вычислено алгебраически . Согласно теореме дифференцирования Лапласа, А первый порядок производная дифференциального уравнения заменяется переменным Лаплас в качестве комплексной частоты . Высшие производные n-го порядка находятся в соответствии с атомным номером путем замены.
Пример обыкновенного дифференциального уравнения высшего порядка системы передачи с постоянными коэффициентами и :
Эта общая форма дифференциального уравнения подвергается преобразованию Лапласа:
-
.
Передаточная функция получается путем применения теоремы о дифференцировании Лапласа к обыкновенному дифференциальному уравнению, описывающему систему . Путем определения полюса и нуля числителя и полинома знаменателя создается факториальное представление (линейные коэффициенты) передаточной функции.
Передаточная функция G (s) формируется из отношения выходной переменной к входной. Не должно быть начальных значений внутреннего накопителя энергии ( представления в пространстве состояний ) системы.
Переменная Лапласа является независимой переменной в комплексной частотной области (область изображения, s-область) с действительной и мнимой частью. Он допускает любые алгебраические операции в s-области, но является только символом завершенного преобразования Лапласа и не содержит числового значения. Показатели s соответствуют степени производной дифференциалов .
Для определения элементарных индивидуальных систем передаточной функции G (s) более высокого порядка полиномы числителя и знаменателя факторизируются путем определения нулей.
Если доступны числовые значения коэффициентов, полюсы и нули можно вычислить с помощью различных методов. Для этого подходит так называемая формула pq для систем 2-го порядка. Доступные в Интернете готовые программы для систем до 4-го порядка можно использовать с вызовом: «Определить нули (решения) многочленов».
Полюса (нули в знаменателе) и нули (нули в числителе) передаточной функции являются наиболее важными параметрами поведения системы. Они либо равны нулю (отсутствует конечный член дифференциального уравнения), либо вещественны [ ]; и [ ] или комплексно сопряженные [ ] и [ ].
Для определения постоянных времени полиномы передаточной функции разбиваются на линейные множители и множители 2-го порядка путем определения нулей. Если числовые значения даны для коэффициентов многочленов, многочлены могут быть факторизованы путем определения корней.
Разложение полиномов числителя и знаменателя более высокого порядка по полюсам и нулям приводит к множеству линейных множителей и множеству множителей 2-го порядка. В качестве предпосылки для этого многочлены не должны иметь пробелов в порядке элементов суммы согласно порядковому номеру.
Если эти факторы определены как независимые индивидуальные передаточные функции, в зависимости от типа полюсов и нулей возникают следующие элементарные передаточные функции:
Пример передаточной функции с полиномиальным представлением, представлением полюс-нуль и представлением постоянной времени:
-
.
Постоянные времени элементарных индивидуальных систем в числителе и знаменателе передаточной функции
Разложение полинома знаменателя приводит к отдельным системам с запаздыванием (линейные факторы) и факторам запаздывания 2-го порядка. Разложение полинома числителя приводит к дифференцированию отдельных систем (линейных факторов) и дифференцирующих факторов 2-го порядка. В сочетании с запаздывающими системами знаменателя последние не влияют на поведение во времени, а только на амплитуды сигналов .
- Постоянные времени линейных факторов как переменных с полюсами и нулями, равными нулю:
- Эти линейные множители возникают в результате преобразования Лапласа обыкновенного дифференциального уравнения, описывающего систему, конечные члены которого отсутствуют или отсутствуют.
- Член продукта становится числителем и знаменателем соответственно . Постоянные времени для элемента I и для элемента D, показанные в таблице ниже в следующем разделе , взяты из определения контроллера . На самом деле они соответствуют коэффициентам пропорциональности или имеют рейтинг 1, если не указаны другие числовые значения.
- Постоянная времени линейных факторов с полюсами и нулями одинакова :
- Определение постоянная времени в -Члене или -Член рассчитывается как следует из полюсов и нулей для числовых значений с отрицательными вещественными частями .
- Пример определения постоянной времени из линейного коэффициента счетчика:
-
.
-
- Постоянное время , как правило , вычисляются из обратной величины (обратная величина) от отрицательного действительного нулевого или в знаменателе полином или числитель полинома передаточной функции , как:
-
или .
-
- Постоянные времени множителя второго порядка с комплексно сопряженными полюсами и нулями:
- Факторы второго порядка возникают из представления полюс-нуль с отрицательными комплексно сопряженными полюсами и нулями. Если [ ] или [ ] заменяется на комплексно сопряженный ноль из нулевого представления , представление постоянной времени создается возведением в квадрат, чтобы избежать мнимых величин:
- Фактор 2-го порядка в представлении полюс-ноль после возведения в квадрат:
- Нормальная форма постоянная времени представления результатов второго фактора порядка с:
- Заключение:
Установление и поведение элементарных индивидуальных систем
Назначив эти коэффициенты в числителе и знаменателе передаточных функций, следующие 6 различных стабильных элементарных систем могут возникнуть индивидуально или несколько раз:
| обозначение | I-ссылка | D ссылка |
 -Элемент -Элемент |
 -Элемент -Элемент |
 -Ссылка (вибрирующая ссылка) -Ссылка (вибрирующая ссылка) |
 -Элемент -Элемент
|
|---|---|---|---|---|---|---|
| Полюсные нули |  |
 |
 |
 |
 |

|
| Функция передачи |  |
 |
 |
 |
 |

|
В представлении постоянной времени постоянная времени соответствует коэффициенту перед комплексной переменной Лапласа .
Расчет временного поведения всей системы передачи всегда требует, чтобы количество факторов в знаменателе всегда было равно или больше, чем количество факторов в числителе .
Дифференцирующие элементы могут полностью компенсировать поведение замедляющих элементов во времени с теми же постоянными времени. То же самое, конечно, относится к ссылкам и ссылкам.

Переходная характеристика различных элементарных систем передачи.
Тестовые сигналы для проверки поведения системы:
Общие тестовые сигналы для систем передачи: ступенчатая функция, функция возврата, импульсная функция, функция нарастания и синусоидальная функция . Эти сигналы также преобразуются по Лапласу из временной области в область изображения. См. Определение тестовых сигналов в следующем разделе.
Временной ход дифференцирующих передаточных элементов:
Временное поведение переходной характеристики или импульсной характеристики дифференцирующей системы полинома числителя не может быть представлено графически только потому, что изменение выходного сигнала происходит во временной области . Временное поведение дифференцирующей системы может быть представлено только графически с входным сигналом в виде функции нарастания. Дифференцирующие системы без так называемых запаздывающих паразитных элементов технически не могут быть изготовлены в виде оборудования. Требуемая паразитная постоянная времени элемента задержки времени должна быть намного меньше постоянной времени элемента или элемента.
Временной ход передаточных элементов с комплексно сопряженными полюсами ( элементами):
Эти передаточные элементы 2-го порядка содержат двойные полюса в диапазоне s . В зависимости от величины демпфирования , когда система возбуждается любым входным сигналом, возникает затухающая, колеблющаяся выходная переменная. Переходная характеристика часто представляется как характерное поведение, при котором выходная переменная экспоненциально асимптотически достигает конечного значения с наложением вибрации.
В эти системы можно разбить на две части.
Постоянные времени, связанные с системой, имеют квадратную форму.
Системы передачи с линейными коэффициентами или коэффициентами 2-го порядка с положительной действительной частью полюсов:
Положительные действительные части полюсов и нулей приводят к отрицательным постоянным времени.
Передаточные элементы с положительными полюсами образуют нестабильные нелинейные передаточные функции, которые могут быть достигнуты с помощью z. B. можно назвать «нестабильными членами T1» или «нестабильными членами T2». Им также можно назначить постоянные времени. Выходной сигнал этих систем экспоненциально увеличивается после любого положительного входного сигнала до предела и возвращается только тогда, когда входной сигнал становится отрицательным ( эффект обратной связи ). (Подробнее см. Управляемая система № Характеристика контролируемых систем )
Расчет временного поведения передаточных функций
-
Обратное преобразование Лапласа: поведение системы на выходе любой системы передачи во временной области зависит от передаточной функции и типа входного сигнала . Обратное преобразование Лапласа можно использовать для определения поведения времени с использованием таблиц преобразования Лапласа и условия поиска:
- Если это нормализованная ступенчатая функция входного сигнала , то есть .
-
Численный расчет: с помощью числовой математики путем расчета разностных уравнений выходные сигналы могут быть рассчитаны как пронумерованные последовательные уравнения динамической системы для заданных входных сигналов . Постоянные времени в разностных уравнениях определяют поведение отдельных систем.
- Разностные уравнения, аппроксимируя непрерывную функцию, постепенно вычисляют последовательность значений со следующими элементами для небольшого интервала, последовательность значений в точке , посредством чего вычисленные значения нумеруются .
Тестовые сигналы

Переходные характеристики от 4-х разъединенных последовательно соединенных элементов PT1, каждый с одинаковыми временными константами.
Непериодические (детерминированные) тестовые сигналы имеют центральное значение в теории систем. С их помощью можно протестировать трансмиссионную систему, проверить ее устойчивость или определить свойства.
Чтобы вычислить поведение системы передачи во времени, преобразованные тестовые сигналы могут быть умножены в области изображения вместо передаточной функции системы . Для обратного преобразования из во временную область желаемое уравнение отклика системы может быть найдено с помощью таблиц преобразования Лапласа.

Импульсные характеристики от 4 последовательно соединенных развязанных элементов PT1, каждый с одинаковыми постоянными времени.
Общим для тестовых сигналов является то, что они начинаются в определенный момент времени и имеют амплитуду = 0 атм. Чтобы различать функции сигналов, они обозначаются символами δ ( импульс ), Ϭ ( скачок ), a (подъем) и s ( синус ).
Тестовые сигналы представлены как входная переменная и как переменная, преобразованная по Лапласу, как показано ниже.
| Срок действия тестового сигнала u (t) |
Область изображения входного сигнала |
Ответ системы y (t) |
|---|---|---|
Импульсная функция δ или функция удара, дельта-импульс |
 |
Импульсная характеристика или весовая функция |
| Ступенчатая функция σ |
 |
Переходная характеристика или переходная функция |
| Увеличение функции или рампы |
 |
Отклик на повышение или отклик на повышение |
| Синусоидальная функция s (периодический сигнал) |
 |
Частотный отклик |
Основы определения постоянных времени из обыкновенного дифференциального уравнения первого порядка
Линейное обыкновенное дифференциальное уравнение 1-го порядка с постоянными коэффициентами и гласит:
-
.
Постоянная времени уже может быть вычислена из этой формы дифференциального уравнения.
В общем, высшая производная дифференциального уравнения используется для определения нулей, в этом случае все члены уравнения делятся на соответствующий коэффициент . Таким образом, новое математически идентичное дифференциальное уравнение гласит:
-
.
Передаточная функция G (s) этого дифференциального уравнения читается для начальных условий, равных нулю, после применения теоремы о дифференцировании Лапласа:
-
.
Передаточная функция в представлении постоянной времени получается из отношения выходной переменной к входной :
-
.
При такой форме передаточной функции постоянная времени может быть считана непосредственно как коэффициент перед переменной Лапласа с отношением коэффициентов .
Если вы вставите для и в уравнение передаточной функции, вы получите нормальную форму передаточной функции элемента ( элемента) задержки в представлении постоянной времени:
Построение обыкновенного дифференциального уравнения первого порядка из аппаратного ФНЧ.
Элемент задержки ( элемент PT1 ), описываемый обыкновенным дифференциальным уравнением первого порядка, чаще всего встречается в природе и в технике. Возникает з. B. Когда тепло течет в среду или к RC-элементу прикладывается электрическое напряжение . Всегда интересно, как выходная переменная системы ведет себя как функция времени для данной входной переменной. Поведение системы особенно ясно для данной входной переменной как ступенчатой функции.
Самая известная динамическая система в электротехнике, которая описывается обыкновенным дифференциальным уравнением первого порядка, – это RC-элемент в виде цепи резистор-конденсатор с постоянной времени .

Простой RC-фильтр нижних частот с
U e : входное напряжение
U a : выходное напряжение
Общее математическое описание RC-элемента является результатом применения законов Кирхгофа .
Для аппаратной модели в качестве фильтра нижних частот применяется сеточное уравнение напряжений:
-
.
Это входная переменная, желаемый выходной размер. Если уравнение для зарядного тока вставить в приведенное выше уравнение для падения напряжения при R , дифференциальное уравнение RC-элемента создается как низкочастотный:
Если используются обычные имена сигналов из теории систем, новые имена сигналов представляют собой обыкновенное дифференциальное уравнение: и .
Не существует полинома числителя и знаменателя для дифференциального уравнения первого порядка и соответствующей передаточной функции . Это уже линейный множитель в знаменателе передаточной функции. Следовательно, ноль не имеет значения.
В обычном представлении дифференциального уравнения высшая производная коэффициентов остается свободной путем деления всех членов уравнения на соответствующий коэффициент (здесь ). Таким образом, новое математически идентичное дифференциальное уравнение гласит:
Передаточная функция G (s) этого дифференциального уравнения читается для начальных условий, равных нулю, согласно теореме дифференцирования:
-
.
Суммированная как отношение выходных переменных к входной, передаточная функция приводит к представлению постоянной времени:
-
.
Коэффициент перед переменной Лапласа соответствует постоянной времени .
Построение передаточной функции фильтра ( элемента) нижних частот через соотношение комплексных сопротивлений.

В отличие от передаточной функции , частотная характеристика может быть измерена с помощью линейной передаточной системы. Частотная характеристика – это частный случай передаточной функции. Передаточную функцию можно преобразовать в частотную характеристику с идентичными коэффициентами (постоянными времени) в любое время. Генезис АЧХ и передаточная функция различны, написание может оставаться идентичным.

В показанной RC-цепи отношение выходного напряжения к входному также можно определить как отношение выходного импеданса к входному. Если установить емкость с комплексным сопротивлением, для комплексного отношения сопротивлений как передаточной функции будут получены следующие результаты :
Результат соответствует члену, полученному из дифференциального уравнения .
Создание передаточной функции для высокого проходного отношения комплексных сопротивлений.
Если емкость C заменяется индуктивностью L в RC-цепи, создается фильтр верхних частот первого порядка при рассмотрении входных и выходных напряжений системы. В случае высокочастотных входных сигналов индуктивность имеет высокое комплексное сопротивление. С падением частоты индуктивное сопротивление падает.
В показанной LC-схеме отношение выходного напряжения к входному также можно определить как отношение выходного импеданса к входному. Если установить для индуктивности с комплексным сопротивлением, следующие результаты для комплексного отношения сопротивлений как передаточной функции :
Передаточная функция элемента RL следующая :
Результат соответствует последовательному соединению -link с D-link. Для нормализованного входного шага выходной сигнал перескакивает в момент времени до , а затем экспоненциально асимптотически падает до значения .
Временное поведение, связанное с этой передаточной функцией, соответствует скачку входа:
Стандартное уравнение применяется к входному скачку ; .
Расчет временного поведения элемента после входного скачка

Временной ход переходной характеристики элемента с постоянной времени T = 1, K = 1.
Часто выходная переменная передаточной функции элемента (= элемент) представлена как переходная характеристика во временной области . Нормализуется скачок является преобразование Лапласа: .
Таким образом, передаточная функция и переходная характеристика:
-
.
Возможно существующий коэффициент усиления не может быть преобразован. Он также не появляется в соответствующих таблицах преобразования Лапласа обратного преобразования и может быть принят без изменений во временной области.
Решение во временной области переходной характеристики получается из таблиц соответствия таблиц преобразования Лапласа для выражения:
-
:
дает временное поведение элемента задержки с добавленным коэффициентом усиления .
-
)
Стандартизировано уравнение применимо к входной скачке к . .
Время поведение перейти обратно
-
Стандартизированное уравнение применяется к доходности от до .
Выходные значения элемента перехода и возврата для одной-пяти постоянных времени:
| Постоянная времени T | Скачок реакции на скачок : в [%]  |
Возврат ступенчатого отклика : в [%]  |
|---|---|---|
| T легко | 63,2 | 36,8 |
 |
86,5 | 13,5 |
 |
95,0 | 5.0 |
 |
98,2 | 1,8 |
 |
99,3 | 0,7 |
Это стандартизированное уравнение применяется к входному скачку . – коэффициент усиления .
Пример расчета для определения постоянных времени обыкновенного дифференциального уравнения 2-го порядка
-
Дано: дифференциальное уравнение временного элемента 2-го порядка без дифференциалов входной переменной .
Требуются: передаточная функция, полюса, постоянные времени.
Применение преобразования Лапласа дифференциального уравнения согласно теореме дифференцирования:
-
.
Формирование передаточной функции и освобождение от высшей преобразованной производной
:
-
.
Даны числовые значения :
и для .
Таким образом, передаточная функция и исключение самого высокого показателя степени (уравнение, деленное на ) выглядят следующим образом :
-
.
В Интернете (Google) есть программы, которые могут вычислять нули многочленов до 4-го порядка.
Так называемая формула pq может использоваться для решения нулей (полюсов) многочлена 2-го порядка:
- Полином:
-
.
Это позволяет факторизовать полином и передаточную функцию в представлении постоянной времени.
-
.
Эти уравнения алгебраически идентичны.
Результат:
Двухзвенная система передачи содержит постоянные времени .
Аппаратное моделирование этой системы с двумя последовательно включенными RC-элементами требует развязки без нагрузки.
Аннотация:
Расчет временного поведения передаточной функции более высокого порядка сложной динамической системы для заданной входной переменной состоит из:
Стандартизированные постоянные времени и частоты переходов фильтров
| Постоянная времени τ в мкс |
Частота кроссовера f c в Гц |
Стандарт эквализации |
|---|---|---|
| 7958 | 20-е | RIAA |
| 3183 | 50 | RIAA, NAB |
| 1592 | 100 | – |
| 318 | 500 | RIAA |
| 200 | 796 | – |
| 140 | 1137 | – |
| 120 | 1326 | MC |
| 100 | 1592 | – |
| 90 | 1768 | MC |
| 75 | 2122 | RIAA, FM США |
| 50 | 3183 | NAB, PCM, FM Европа |
| 35 год | 4547 | DIN |
| 25-е | 6366 | – |
| 17,5 | 9095 | AES |
| 15-е | 10610 | PCM |
Индивидуальные доказательства
- ↑ Автор: Ян Лунзе / Control Engineering 1; Springer Vieweg, Берлин, 8-е издание, 2014 г., ISBN 978-3-642-53943-5 ; Основная глава: передаточная функция, подраздел: постоянные времени передаточной функции.
- ↑ Автор: Ян Лунзе / Control Engineering 1; Springer Vieweg, Берлин, 8-е издание, 2014 г., ISBN 978-3-642-53943-5 ; Глава: Описание анализа линейных систем в частотной области.
литература
- Хольгер Лутц, Вольфганг Вендт: Карманный справочник по технике управления с MATLAB и Simulink. 12-е издание. Verlag Europa-Lehrmittel, 2021, ISBN 978-3-8085-5870-6 .
- Ян Лунзе: Техника управления 1. 6. Издание. Springer Verlag, Берлин 2007, ISBN 978-3-540-70790-5 . Техника управления 2-е 4-е издание. Springer Verlag, Берлин 2006 г., ISBN 978-3-540-32335-8 .
- Майкл Лэйбл: Механические величины, измеряемые электрически. Основы и примеры технической реализации. 7-е издание. Эксперт Verlag, Реннинген 1980, ISBN 3-8167-2892-8 .
- Вольфганг Шнайдер: Практическая техника управления. Учебник и тетрадь для инженеров-неэлектриков. 3. Издание. Vieweg + Teubner Verlag, Висбаден, 2008 г., ISBN 978-3-528-24662-4 .
- Вальтер Касперс, Ханс-Юрген Кюфнер: Измерение контроля, контроль. 3. Издание. Friedrich Vieweg & Sohn Verlag, Wiesbaden 1984, ISBN 3-528-24062-8 .
- Дэвид Халлидей, Роберт Резник, Джерл Уокер: Физика . Выпуск для бакалавров, 2-е издание. John Wiley & Sons Verlag, Weinheim 2013, ISBN 978-3-527-41181-8 .
Смотри тоже
- Сигмовидная функция
- Высокая частота
- НЧ
- Bandpass
- Bandstop
- Режущая характеристика
- Время отдыха
- Расслабление (наука)
веб ссылки
- Постоянная времени и частота кроссовера (частота среза) (файл PDF; 228 кБ)
- Амплитудно-частотная характеристика и эквализация – расчет постоянной времени и частоты среза
2. Математическое описание систем автоматического управления ч. 2.9 — 2.13
Лекции по курсу «Управление Техническими Системами», читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки», факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность.
Данные лекции только готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.
В предыдущих сериях:
В это части будут рассмотрены:
2.9. Использование обратных преобразований Лапласа для решения уравнений динамики САР (звена).
2.10. Весовая и переходная функции звена (системы).
2.11. Определение переходного процесса в системе (САР) (звене) через весовую и переходную функции.
2.12. Mетод переменных состояния.
2.13. Переход от описания переменных «вход-выход» к переменным состояния.
Попробуем применить, полученные знания на практике, создавая и сравнивая расчетные модели в разных видах. Будет интересно познавательно и жестко.

2.9. Использование обратных преобразований Лапласа для решения уравнений динамики САР (звена)
Рассмотрим динамическое звено САР изображенное на рисунке 2.9.1
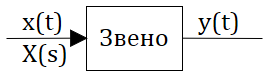
Предположим, что уравнение динамики имеет вид:
где: — постоянные времени;
— коэффициент усиления.
Пусть известны отображения:
Найдем изображения для производных:
Подставим полученные выражения в уравнение динамики и получим уравнение динамики в изображениях:
B(s) — слагаемое, которое определяется начальными условиями, при нулевых начальных условиях B(s)=0.
W(s) — передаточная функция.
Передаточной функцией САР (звена) называется отношение изображений выходного сигнала к входному воздействию при нулевых н.у.
После того, как в явном виде найдено изображение для неизвестной выходной величины, нахождение оригинала не представляет сложностей. Либо по формуле Хэвисайда, либо разложением на элементарные дроби, либо по таблице из справочника.
Пример
Построить выходной сигнал звена САР при единичном входном воздействии и нулевых начальных условиях, если уравнение динамики звена имеет следующий вид:
входное воздействие: — единичное ступенчатое воздействие.
Выполним преобразование Лапласа:
Подставим в уравнение динамики и получим уравнение динамики в изображениях:
Для получения выходного сигнала из уравнения в изображениях выполним обратное преобразования Лапласа:
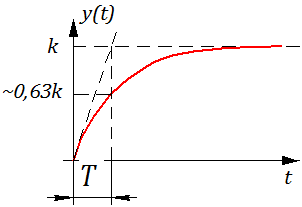
2.10. Весовая и переходная функции звена (системы).
Определение: Весовой функцией звена (системы) называется реакция системы при нулевых н.у. на единичное импульсное воздействие.
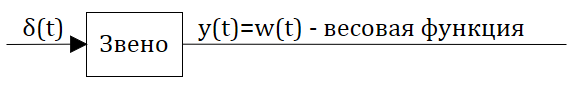
Определение: Переходной функцией звена (системы) при н.у. называется реакция на единичное ступенчатое воздействие.
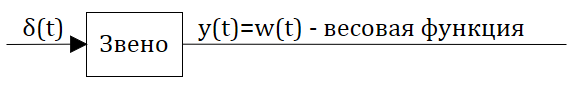
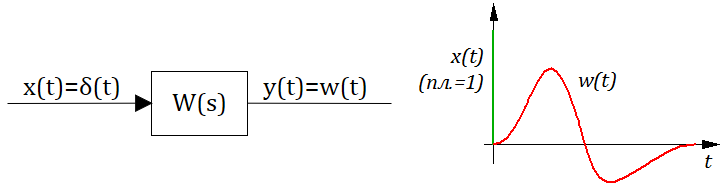
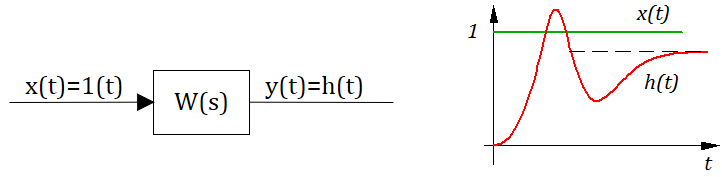
На этом месте можно вспомнить, что преобразование Лапласа это интеграл от 0 до бесконечности по времени (см. предыдущий текст), а импульсное воздействие при таком интегрировании превращается в 1 тогда в изображениях получаем что:
Передаточная функция играет роль изображения реакции звена или системы на единичное импульсное воздействие.
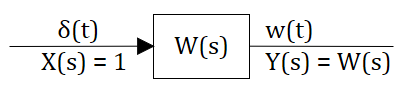
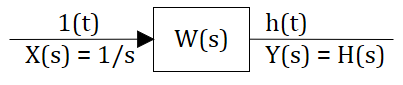
Для единичного ступенчатого воздействия преобразование Лапласа тоже известно (см. предыдущий текст):
тогда в изображениях получаем, что реакция системы на ступенчатое воздействие, рассчитывается так:
Реакция системы на единичное ступенчатое воздействие рассчитывается обратным преобразованием Лапласа:
2.11. Определение переходного процесса в системе (САР) (звене) через весовую и переходную функции. Формула Дюамеля-Карсона
Предположим, что на вход системы поступает произвольное воздействие x(t), заранее известное. Найти реакцию системы y(t), если известны входное воздействие x(t) и весовая функция w(t).
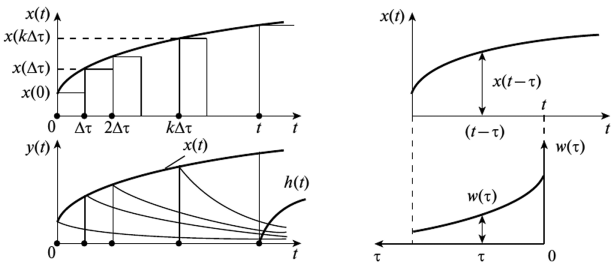
Представим, что входное воздействие представляет собой последовательность прямоугольных импульсов до времени t и ступеньки высотой x(t) в момент времени t. см.рис. 2.11 Для каждого импульса мы можем записать реакцию системы через весовую функциию:
где:
— значение отклика по завершению предыущего импульса;
— время завершения текущего импульса;
— значение весовой функции в начале текущего импульса.
Тогда для определения занчения отклика в произвольный момент времени необходимо сложить все импульсы и ступенчатое воздействие в момент времени t:
Переходя к пределам
если перейти от t к бесконечности мы получим формулу интеграла Дюамеля-Карсона, или по другому «интеграла свертки» который обеспечивает вычисление оригинала функции по произвдению изображения двух функций:
где — вспомогательное время
Для вывода аналогичной зависмости от переходной функции вспомним что изображение весовой и переходной функции связаны соотношением: запишем выражение изображения для отклика в операторной форме:
Используя интеграл свертки получаем, что при известной переходной функции (h(t)) и известному входному воздействию х(t) выходное воздействие рассчитывается как:
2.12. Mетод переменных состояния.
До этого мы рассматривали системы с одной передаточной функцией, но жизнь всегда сложнее и как правило в системах есть несколько передаточных функций несколько входных воздейстий и несколько реакций системы. (см. рис. 2.12.1)
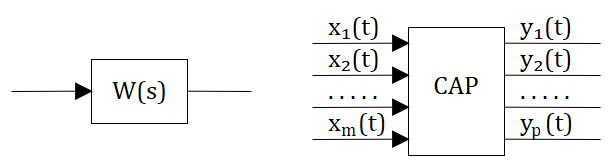
В этом случае наиболее удобной формой пердставления систем для их анализа и расчета оказался метод переменных состояния. Для этого метода, вместо передаточных функций связывающих вход с выходом используются дополнительные переменные состояния, которые описывают систему. В этом случае можно говорить, что состояние системы — это та минимальная информация о прошлом, которая необходима для полного описания будущего поведения (т.е. выходов) системы, если поведение ее входов известно. см. рис. 2.12.2
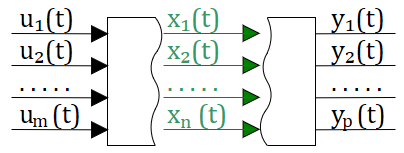
В методе состояний, производные всех переменных состояния, в общем случае зависит от всех переменных и всех входных воздействия, и могут быть записаны в представленной ниже системы обыкновенных дифференциальных уравнений (ОДУ) первой степени. Эта система уравнений называю системой ОДУ в форме Коши:
Выход из системы зависит от переменных состояния и, в общем случае от входных воздействий и описывается следующей системой уравнений:
где:
n — количество перемнных состояния,
m — количество входных воздействий,
p — количество выходных переменных;
Данная система уравнений может быть записана в матричной форме:
где:
— вектор входа (или вектор управления);
— вектор столбец производных переменных состояния;
— вектор столбец переменных состояния;
— вектор выхода;
— собственная матрица системы [n x n],
— постоянные коэффициенты;
— матрица входа [n x m],
— постоянные коэффициенты;
— матрица выхода а [p x n],
— постоянные коэффициенты;
— матрица обхода [p x m],
— постоянные коэффициенты;
В нашем случае почти всегда все элементы матрицы D будут нулевыми: D = 0.
Такое описание системы позволяет с одной стороны стандартным образом описывать различные технические системы. Явная формула для расчета производных позволяет достаточно просто осуществлять численное интегрирование по времени. И это используется в различных программах моделирования
Другое использование данного представления для простых систем, описанных в переменных «вход-выход», зачастую позволяет устранить технические трудности, связанные с решением ОДУ высокой степени.
Еще одним преимуществом данного описания, является то, что уравнения в форме Коши можно получить из законов физики
Пример решения задачи в форме коши.
Рассмотрим задачу моделирования гидравлического привода, при следующих условиях:
Дано:
Цилиндрический плунжер диаметром 10 мм, с приведенной массой 100 кг, работает на пружину жесткостью 200 Н/мм и демпфер с коэффициентом вязкого трения — 1000 Н/(м/с). Полость начальным объемом 20 см 3 соединяется с источником давлния дросселем диаметром диаметр которого 0,2 мм. Коэффициент расхода дросселя 0.62. Плотность рабочей жидкости ρ = 850 кг/м 3 .
Определить:
Перемещение дросселя, если в источнике давление происходит скачек 200 бар. см. рис. 2.12.13
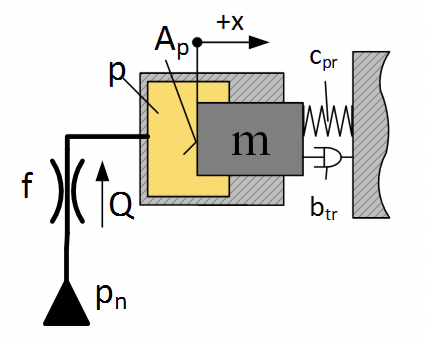
Уравенение движение плунжера:
Где: – площадь плунжера, – жесткость пружины, – коэффициент вязкого трения, p – давление в камере.
Поскольку дифференциальное движения это уравнение второго порядка, превратим его в систему из двух уравнений первого порядка, добавив новую переменную — скорость , тогда
Уравнение давления в камере, для упрощения принимаем что изменениям объема камеры из-за перемещения плунжера можно пренебречь:
Где: Q – расход в камеру, V — объем камеры.
Расход через дроссель:
Где: f– площадь дросселя, – давление в источнике, p – давление в камере.
Уравнение дросселя не линейное, по условию задачи, давление входное изменяется скачком, от 0 до 200 бар, проведем линеаризацию в окрестности точки давления 100 бар тогда:
Подставляем линеаризованную формул расхода в формулу давления:
Таким образом общая система уравнений в форме Коши, для рис 2.12.3 привода принимает вид:
Матрицы A, B, С, В для матричной формы системы уравнений принимают вид:
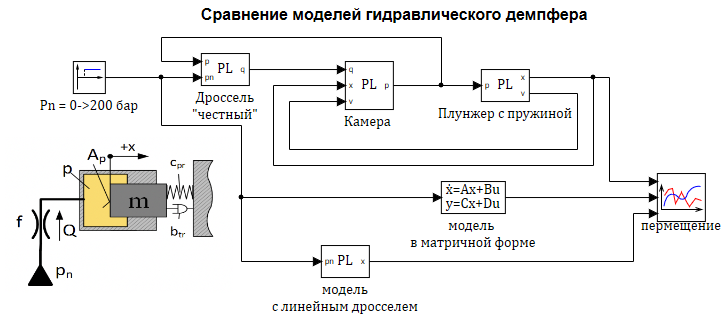
Проверим моделированием в SimInTech составленную модель. На рисунке 2.12.13 представлена расчетная схема содержащая три модели:
1 — «Честная» модель со всеми уравнениями без упрощений.
2 — Модель в блоке «Переменные состояние» (в матричной форме).
3 — Модель в динамическом блоке с линеаризованным дросселем.
Все условия задачи задаются как глобальные константы проекта, в главном скрипте проекта, там же расчитываются на этапе инициализации расчета, площади плунжера и проходного сечения дросселя см. рис. 2.12.5:
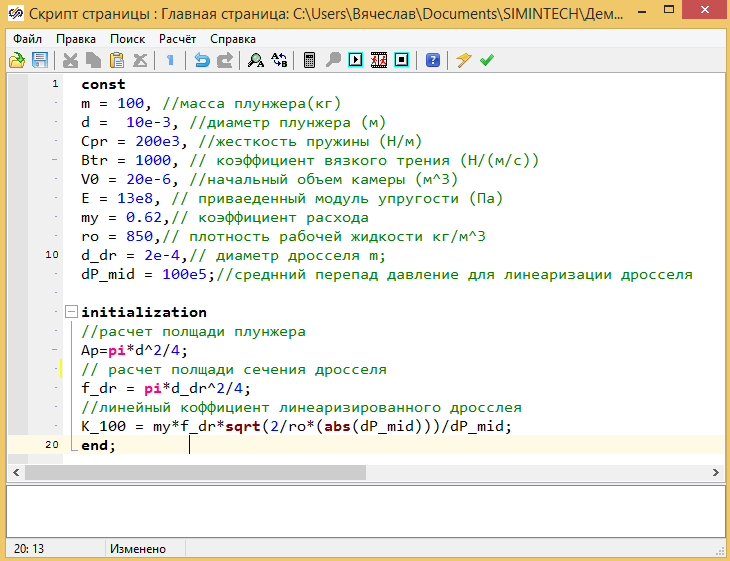
Рисунок 2.12.5 Глобальный скрипт проекта.
Модель на внутреннем языке программирования представлена на рис. 2.12.6. В данной модели используется описание модели в форме Коши. Так же выполняется учет изменения объема дросселя на каждом шаге расчета, за счет перемещения плунжера (Vk = V0+Ap*x.)
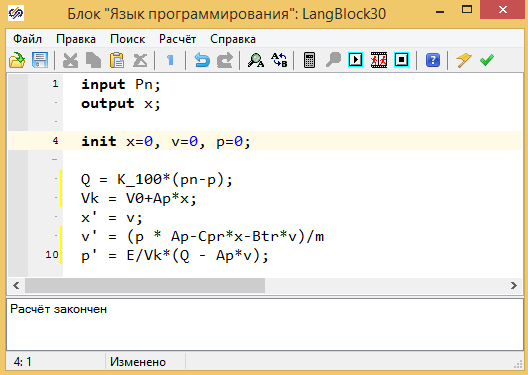
Рисунок 2.12.6 Скрипт расчета модели в форме Коши.
Модель в матричном форме задается с использованием глобальных констант в виде формул. (Матрица в SimInTech задается в виде последовательности из ее столбцов) см. рис. 2.12.7
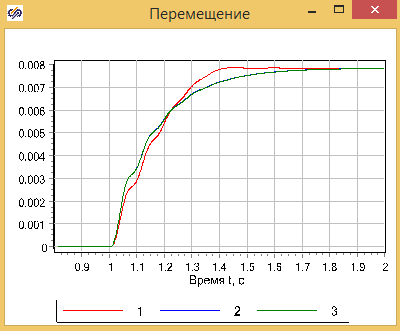
Результаты расчета показывают, что модель в матричной форме и модель на скриптовом языке в форме Коши, практически полностью совпадают, это означает, что учет изменения объема полости практически не влияют на результаты. Кривые 2 и З совпадают.
Процедура линеаризация расхода через дроссель вызывает заметное отличие в результатах. 1-й график c «честной» моделью дросселя, отличается от графиков 2 и 3. (см. рис. 2.12.8)
Сравним полученные модели, с моделью созданной из библиотечных блоков SimInTech, в которых учитываются так же изменение свойств реальной рабочей жидкости — масла АМГ-10. Сама модель представлена на рис. 2.12.9, набор графиков на рисунке 2.12.10
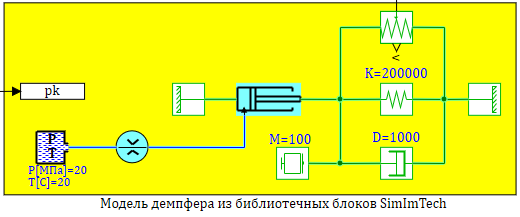
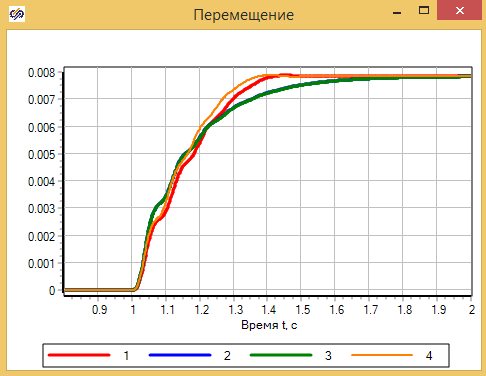
На графиках видно, что уточненная модель отличается от предыдущих, однако погрешность модели составлят наших упрощенных моделей составляют примерно 10%, в лишь в некоторые моменты времени.
2.13. Переход от описания переменных «вход-выход» к переменным состояния и обратно
Рассмотрим несколько вариантов перехода от описания «вход-выход», к переменным состояния:
Вариант прехода зависит от правой части уравнения с переменными «вход-выход»:
2.13.1. Правая часть содержит только b0*u(t)
В этом варианте, в уравнениях в правой части отсутствуют члены с производными входной величины u(t). Пример с плунжером выше так же относится к этому варианту.
Что бы продемонстрировать технологию перехода рассмотрим следующее уровнение:
Для перехода к форме Коши ведем новые переменные:
И перепишем уравнение относительно y”'(t):
Используя эти переменные можно перейти от дифференциального уравнения 3-го прядка, к системе из 3-х уравнений первого порядка в форме Коши:
Соотвественно матрицы для матричного вида уравнений в переменных сосотяния:
2.13.2. Правая часть общего вида
Более сложный случай, когда в уравнениях есть производные от входных воздействий и уравнение в общем случае выглядит так:
Сделаем преобразования: перейдем к уравнениям динамики в изображениях:
Тогда можно представить уравнение в изображениях в виде:
Разделим уравнение в изображениях на произведение полиномов , получим:
Где: — некоторая комплексная величина (отношение двух комплексных величин). Можно считать, что отображение величины . Тогда входная величина может быть в изображениях представлена как:
Вренемся к оригиналу от изображений получим: ,
где: — дифференциальный оператор.
А это дифференциальное уравнение n-го порядка мы можем преобразовать к системе из n дифференциальных уравнений первого порядка, как это мы делали выше:
Таким образом, мы получили систему уравнение в форе Коши, относительно переменных состояния :
А регулируемую величину (выход системы) мы так же можем выразить через эти переменные, в изображениях:
Перейдем от изображения к оригиналам:
Если обозначить вектор , то мы получим уравнения переменных состояниях в матричной форме, где D = 0:
Пример:
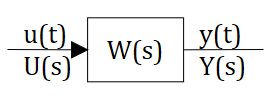
Рисунок 2.13.1 Передаточная функция.
Имеется передаточная функция (рис. 2.13.1) в изображениях :
Необходимо преобразовать передаточную функцию к системе уравнений в форме Коши
В изображения реакция системы связана с входным воздействие соотношением:
Разделим в последнем правую и левую часть на произведения , и введем новую перменную :
Полиномы N(s) и L(s) равны:
Перейдем в последнем выражении от изображения к оригиналам и ведем новые переменные (состояния):
Переходим от уравнения третьего порядка к системе трех уравнений первого порядка:
Или в матричной форме:
Для получения второго матричного уравнения воспользуемся соотношением для новых переменных в отображениях:
Перейдем от изображений к оригиналу:
Таким образом второе уравнение матричной системы выглядит так:
Проверим в SimInTech сравнив передаточную функцию и блок переменных состояния, и убедимся, что графики совпадают см. рис. 2.13.2
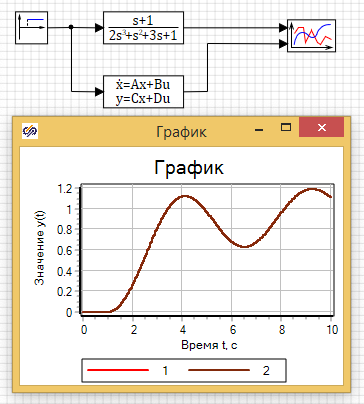
Рисунок 2.13.2 Сравнение переходного процеса у блока передаточной функции и блока переменных состояния.
Апериодическое (инерционное, статическое) звено. Передаточная функция и уравнения

Дифференциальное уравнение, описывающее взаимосвязь входного и выходного сигналов апериодического типового динамического звена (ТДЗ), можно представить в следующем виде:

Где: k – коэффициент передачи, Т0 – постоянная времени.
Дифференциальное уравнение является не самой удобной формой представления математической модели объекта или звена. Это связано с тем, что решения любого дифференциального уравнения довольно сложная вычислительная процедура. Более удобна и, соответственно чаще используемая, математическая модель объекта, записанная в виде передаточной функции.
Передаточная функция – это преобразованное по Лапласу исходное дифференциальное уравнение, то есть уравнение, записанное в виде преобразованных по Лапласу выходного и входного сигналов объекта (звена).
Исходное дифференциальное уравнение в преобразовании Лапласа называют оригиналом, а записанное в операторной форме преобразованное уравнение – его изображением. Суть преобразования Лапласа заключается в замене на функции комплексных переменных Хвых(р) и Хвх(р) функций вещественных переменных Хвых(τ) и Хвх(τ), где р – оператор Лапласа (комплексное число р = ±m±in). Данные функции связываются между собой интегралом Лапласа:

Для большинства используемых в ТДЗ дифференциальных уравнений, чисто формальным условием перехода от оригинала к изображению будут представленные ниже замены:

Использовав приведенное выше условие довольно легко получить изображение, то есть перейти к операторной форме записи дифференциального уравнения апериодического звена.
Оригинал дифференциального уравнения апериодического звена имеет следующий вид:

Операторная форма записи (изображения) уравнения апериодического звена:

Огромным преимуществом данного преобразования является то, что записанное в операторной форме исходное дифференциальное уравнения становится алгебраическим. Но стоит отметить, что если бы все дифференциальные уравнения можно было бы преобразовать по Лапласу, то в математике произошла бы революция, так как решение алгебраических уравнение значительно проще дифференциальных. К сожалению, такое преобразование возможно лишь для ограниченного количества уравнений, в том числе для уравнений типовых динамических звеньев (ТДЗ).
Поскольку уравнение апериодического звена приняло вид алгебраического, то его можно записать следующим образом:

Из полученного выражения достаточно легко выделить отношение Хвых(р) / Хвх(р), которое называется передаточной функцией и для апериодического звена имеет вид:

У каждого типового динамического звена присутствует ряд типовых частотных характеристик: амплитудно-частотную (АЧХ), фазочастотную (ФЧХ), амплитудно-фазовую частотную (АФЧХ или АФХ), логарифмическую амплитудно-частотную (ЛАЧХ), логарифмическую фазочастотную (ЛФЧХ).
На практике чаще всего используется АФЧХ или АФХ.
Амплитудно-фазовая характеристика это вектор, а график АФХ – годограф этого вектора, то есть кривая на комплексной плоскости, которую описывает конец вектора при изменении частоты ω от 0 до ∞. Вектор характеризуется двумя величинами – длина (скаляр или вектор по модулю) и направление (градиент).
Вектор аналитически можно записать в виде двух проекций на действительную и мнимую оси, и выразить эти проекции через угол α:

После использования формулы Эйлера:

Где |W| — длина вектора или вектор по модулю, i – мнимое число:

Аналитическое выражение для любого вектора АФХ любого типичного динамического звена легко получить из передаточной функции, заменив в ней оператор Лапласа р на выражение iω. Где ω – частота колебаний (ω = 2π/Т), Т – период колебаний.
Для апериодического звена амплитудно-фазовая частотная характеристика (АФХ) имеет вид:

Для записи вектора АФХ в виде проекций на действительную и мнимую ось необходимо произвести следующие преобразования:

Изменяя частоту ω от 0 до ∞ можно построить на комплексной плоскости годораф (график вектора АФХ), представляющий из себя полуокружность (рисунок а)), которая располагается в четвертом квадранте комплексной плоскости. Диаметр полуокружности равен коэффициенту k.

На рисунке б) показана типовая переходная функция апериодического звена. Как видно из графика, она изменяется по экспоненциальному закону. У любой экспоненты есть одно прекрасное свойство – если к любой ее точке провести касательную, а затем точку пересечения касательной с асимптотой и точку касания спроецировать на ось времени, то получится один и тот же отрезок времени на оси времени. Эта проекция, которую называют постоянной времени, соответствует значению коэффициента Т0 в АФХ и передаточной функции апериодического звена, а ордината асимптоты, к которой стремится экспонента, соответствует коэффициенту k в передаточной функции. Таким образом, по переходной характеристике апериодического звена довольно легко найти коэффициенты Т0 и k в передаточной функции звена.
Физическим примером апериодического звена может быть конденсатор, при подаче напряжения на который заряд происходит не мгновенно, а с определенной задержкой, или же электродвигатель, который при подаче питания разгоняется не мгновенно, а через какое-то время t. На рисунке в) показан пример установки, которую также можно считать апериодическим звеном (вода – заполняющая бак).
В бак поступает определенное количество воды с расходом Q1. В то же время из бака вытекает вода с расходом Q2. Регулируемый параметр в этой системе Хвых – уровень воды в баке H.
При подаче единичного скачка Q1 (открыли входной вентиль) уровень воды H в баке повышается. При этом растет гиростатическое давление и возрастает Q2. Через некоторое время уровень воды H в баке стабилизируется (экспонента приближается к асимптоте). Способность самостоятельно восстанавливать равновесие, которое присуща объектам, аппроксимируемым апериодическим звеном, за счет стока или притока вещества или энергии называют самовыравниванием. Количество самовыравнивания определяет коэффициент р, равный обратному значению коэффициента k в передаточной функции звена, то есть р = 1/k.
В литературе объекты с передаточной функцией апериодического звена называют статическими.
Примеры решения задач по ТАУ

Здравствуйте на этой странице я собрала теорию и практику с примерами решения задач по предмету теория автоматического управления с решением по каждой теме, чтобы вы смогли освежить знания!
Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!

ТАУ
Теория автоматического управления является основной общепрофессиональной дисциплиной направления подготовки дипломированного специалиста «Автоматизированные технологии и производства».
Основной целью автоматизации является исключение непосредственного участия человека в управлении производственными процессами и другими техническими объектами.
В настоящее время автоматизация технологических процессов представляет собой одно из важнейших средств роста эффективности производства, интенсификации развития народного хозяйства. Таким образом, задача изучения дисциплины «Теория автоматического управления» состоит в освоении основных принципов построения и функционирования автоматических систем управления на базе современных математических методов и технических средств.
Построение структурных схем и сигнальных графов автоматических систем
В теории систем автоматического управления (САУ) широко используют понятие звена, под которым понимают некоторый физический элемент системы (усилитель, двигатель, датчик и т. п.) либо формально выделенную часть математической модели системы (например, уравнение равновесия напряжений якорной цепи двигателя), для которых указаны входные (одна или несколько) и выходная (обычно одна) переменные. При этом говорят, что звено преобразует входные переменные, т. е. приложенные к звену внешние воздействия, в выходную переменную — реакцию. В математическом плане обобщением понятий САУ и звена САУ является понятие динамической системы.
Возможно эта страница вам будет полезна:
Дифференциальное уравнение (ДУ) линейной динамической системы с одним входом и одним выходом записывается в классической форме следующим образом:
Здесь 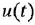 и
и 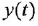 — входная и выходная переменные системы (в дальнейшем зависимость от
— входная и выходная переменные системы (в дальнейшем зависимость от 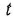 часто будем опускать);
часто будем опускать); 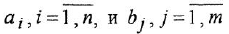 -постоянные вещественные коэффициенты;
-постоянные вещественные коэффициенты; 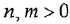 — целые числа (
— целые числа ( 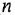 — порядок системы), причем
— порядок системы), причем 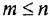 . То же уравнение в операторной форме имеет вид
. То же уравнение в операторной форме имеет вид
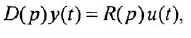
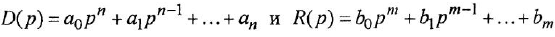
полиномы степеней, соответственно, 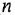 и
и 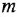 от оператора дифференцирования
от оператора дифференцирования 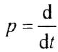 определяемого для любой дифференцируемой функции
определяемого для любой дифференцируемой функции 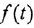 следующим образом:
следующим образом:
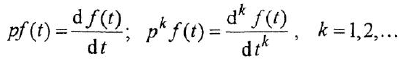
Определим формально операторную передаточную функцию (ОПФ) 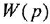 соотношением
соотношением 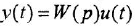 . Тогда в силу уравнения (1 2) имеем
. Тогда в силу уравнения (1 2) имеем
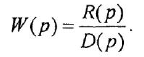
Преобразование ДУ (1.1) по Лапласу при нулевых начальных условиях (ННУ) дает
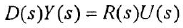
(использована теорема об изображении производной при ННУ: если
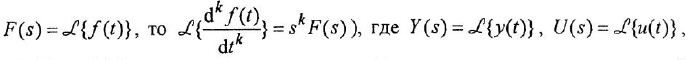
a 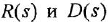 — уже не операторные, а обычные полиномы от комплексной переменной
— уже не операторные, а обычные полиномы от комплексной переменной 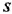 ).
).
Передаточной функцией (ПФ) 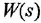 системы, описываемой ДУ (1.1) или (1.2), называется отношение изображений по Лапласу выходной и входной переменных при ННУ:
системы, описываемой ДУ (1.1) или (1.2), называется отношение изображений по Лапласу выходной и входной переменных при ННУ:
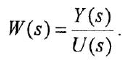
Отсюда в силу уравнения (1.4) и с учетом (1.3) получаем:
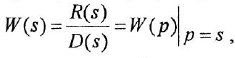
т. е. ПФ совпадает с ОПФ с точностью до обозначения аргумента
В связи с этим в дальнейшем будем использовать одно и го же обозначение, например 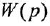 , как для ПФ, так и для ОПФ, понимая под символом
, как для ПФ, так и для ОПФ, понимая под символом 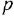 в первом случае (когда ДУ рассматривается в комплексной области) комплексную переменную, а во втором (при рассмотрении ДУ во временной области) — оператор дифференцирования
в первом случае (когда ДУ рассматривается в комплексной области) комплексную переменную, а во втором (при рассмотрении ДУ во временной области) — оператор дифференцирования 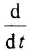 . Иногда, если это не будет приводить к разночтениям, и сами уравнения (12) или (1.4) будем записывать одинаково — в виде
. Иногда, если это не будет приводить к разночтениям, и сами уравнения (12) или (1.4) будем записывать одинаково — в виде 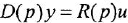 , т. е. без указания у функций
, т. е. без указания у функций 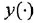 и
и 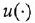 их аргументов
их аргументов 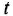 или
или 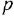 (тем самым допуская возможность толкования этого уравнения в обеих областях) и даже, несмотря на некоторую нестрогость, обозначая одинаковыми буквами как сами переменные, так и их изображения.
(тем самым допуская возможность толкования этого уравнения в обеих областях) и даже, несмотря на некоторую нестрогость, обозначая одинаковыми буквами как сами переменные, так и их изображения.
С учетом сказанного рекомендуется следующая методика нахождения ПФ поДУ( 1.1), не требующая применения преобразования Лапласа:
Если система имеет несколько входов и/или выходов, т. е. является многомерной, то уместно говорить о множестве передаточных функций, связывающих каждый вход 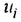 с каждым выходом
с каждым выходом 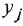 : I
: I
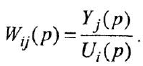
Все они имеют один и тот же знаменатель (если не производить сокращения одинаковых нулей и полюсов) и, в общем случае, разные числители:
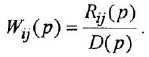
Теперь приведем передаточные функции наиболее важных типовых звеньев систем автоматического управления. 1 Пропорциональное звено:
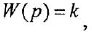
где 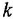 — коэффициент передачи (обычно
— коэффициент передачи (обычно 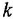 > 0).
> 0).
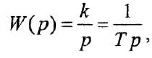
где 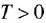 — постоянная времени.
— постоянная времени.
В качестве обобщения можно рассматривать интегрирующее звено произвольного порядка:
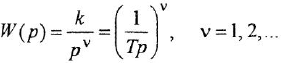
- Дифференцирующее звено:
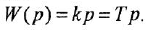
Обобщенное дифференцирующее звено:
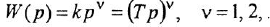
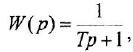
где 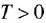 — постоянная времени.
— постоянная времени.
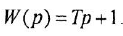
- Апериодическое звено 2-го порядка:
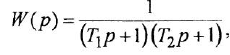
где 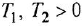 — постоянные времени. 7 Колебательное звено
— постоянные времени. 7 Колебательное звено
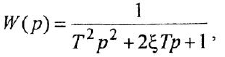
где 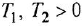 — постоянная времени;
— постоянная времени; 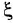 — коэффициент затухания (0
— коэффициент затухания (0 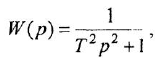
где 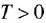 — постоянная времени.
— постоянная времени.
Часто в передаточных функциях звеньев 4, 6, 7 и 8 вместо единицы пишут коэффициент передачи к.
Построение структурных схем и М-графов динамических систем
При анализе и синтезе систем автоматического управления часто прибегают к графическом)’ изображению уравнений, описывающих систему. Для этой цели обычно используют структурные схемы и, реже, сигнальные графы В структурной схеме переменные обозначаются отрезками прямых или ломаными линиями, оканчивающимися стрелками В графе каждой переменной соответствует некоторая вершина. Мы будем рассматривать только одну разновидность сигнальных графов, а именно граф Мейсона (Мэзона), или, короче, М-граф
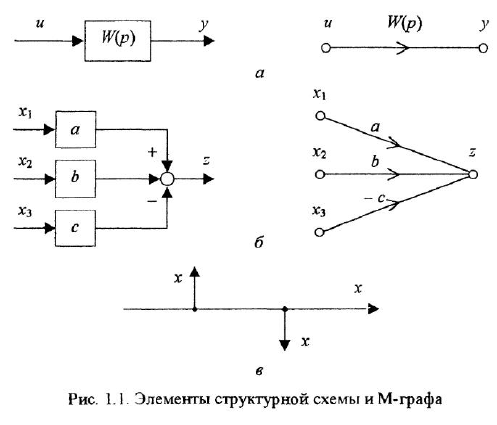
Уравнение звена вила 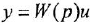 изображается в виде структурной схемы и М-графа так, как показано на рис. 1.1, а (напоминаем, что мы намеренно не делаем различия между записью уравнений во временной и комплексной областях). На структурных схемах внутри прямоугольных блоков, изображающих звенья системы, могут записываться не только передаточные функции или ОПФ, но и коэффициенты передачи, матрицы, обозначения функциональных зависимостей, в том числе графические, и другие разновидности математических характеристик звеньев. Их мы будем обозначать общим термином «передача» Изображенная на рис. 1.1, а структурная схема трактуется единственным образом: выходная переменная звена равна входной переменной, умноженной на передачу звена. В М-графе передача записывается над дугой, при этом переменная, соответствующая вершине-стоку, равна переменной, отождествляемой с вершиной-истоком, умноженной на передачу дуги. Дуга графа может иметь вид собственно дуги либо прямолинейного отрезка, снабженных стрелкой.
изображается в виде структурной схемы и М-графа так, как показано на рис. 1.1, а (напоминаем, что мы намеренно не делаем различия между записью уравнений во временной и комплексной областях). На структурных схемах внутри прямоугольных блоков, изображающих звенья системы, могут записываться не только передаточные функции или ОПФ, но и коэффициенты передачи, матрицы, обозначения функциональных зависимостей, в том числе графические, и другие разновидности математических характеристик звеньев. Их мы будем обозначать общим термином «передача» Изображенная на рис. 1.1, а структурная схема трактуется единственным образом: выходная переменная звена равна входной переменной, умноженной на передачу звена. В М-графе передача записывается над дугой, при этом переменная, соответствующая вершине-стоку, равна переменной, отождествляемой с вершиной-истоком, умноженной на передачу дуги. Дуга графа может иметь вид собственно дуги либо прямолинейного отрезка, снабженных стрелкой.
В вершину графа могут входить несколько дуг. В этом случае действует следующее соглашение: переменная, отождествляемая с вершиной, в которую входят дуги, равна взвешенной сумме переменных, соответствующих вершинам, из которых эти дуги исходят, причем в качестве весовых коэффициентов выступают передачи дуг. Так, М-граф, приведенный на рис. 11,6, соответствует уравнению 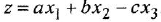 . В структурных схемах для обозначения операции алгебраического суммирования применяют специальный элемент — сумматор, изображаемый в виде кружка (см. рис. 1.1, б, где рядом с графом приведена структурная схема, соответствующая тому же уравнению). Сумматор может иметь любое число входных переменных (знак, с которым переменная входит в алгебраическую сумму, указывается рядом с соответствующей стрелкой) и только одну выходную переменную
. В структурных схемах для обозначения операции алгебраического суммирования применяют специальный элемент — сумматор, изображаемый в виде кружка (см. рис. 1.1, б, где рядом с графом приведена структурная схема, соответствующая тому же уравнению). Сумматор может иметь любое число входных переменных (знак, с которым переменная входит в алгебраическую сумму, указывается рядом с соответствующей стрелкой) и только одну выходную переменную
Часто одна и та же переменная входит в несколько уравнений Чтобы в структурной схеме иметь возможность использовать какую-либо переменную в качестве входа сразу нескольких звеньев, применяют специализированный элемент — отвод. Это линия, отходящая от основной в какой-либо точке и обозначающая ту же переменную, что и основная линия (см. рис. 1.1, в, где показаны два отвода). Начало отвода отмечается «жирной» точкой.
Если в структурной схеме имеется горизонтальная цепочка звеньев, чередующихся с сумматорами, то обычно знаки «плюс» или «минус» ставят не у всех стрелок, входящих в сумматоры, а только у тех, которые подходят к данной цепочке извне (см., например, три сумматора между переменными 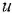 и
и 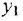 на рис. 2.2, а), — если, конечно, переменные, изображенные горизонтальными стрелками, входят в алгебраическую сумму со знаком «плюс».
на рис. 2.2, а), — если, конечно, переменные, изображенные горизонтальными стрелками, входят в алгебраическую сумму со знаком «плюс».
Пусть система задана некоторым числом алгебраических и дифференциальных уравнений. Чтобы построить по ним структурную схему и М-граф системы, рекомендуется выполнить следующие действия:
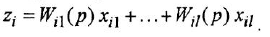
При этом выражения 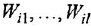 окажутся не чем иным, как передаточными функциями (иначе: ОПФ), связывающими входы звена с его выходом.
окажутся не чем иным, как передаточными функциями (иначе: ОПФ), связывающими входы звена с его выходом.
- По каждому уравнению вида (1.15) изобразить М-граф, для чего:
а) нанести на рисунок вершины, соответствующие переменным 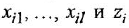 ;
;
б) из каждой вершины 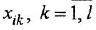 , провести в вершину
, провести в вершину 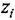 дугу со стрелкой и написать рядом с ней соответствующую передачу
дугу со стрелкой и написать рядом с ней соответствующую передачу 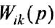 .
.
Поскольку правая часть уравнения (1.15) представляет собой алгебраическую сумму, для изображения соответствующей структурной схемы необходим сумматор. В результате получается схема, подобная той, что показана на рис. 11, б Таким образом, если звено имеет один вход, то ему соответствуют структурная схема и М-граф аналогичные тем, что приведены на рис. 1.1, в Нел и же входов несколько, то звену (уравнению) соответствует структурная схема и граф, содержащие несколько звеньев (дуг), причем в структурной схеме обязательно появится сумматор
Уравнения, по которым строится структурная схема или граф, связаны между собой, так как содержат общие переменные Это должно быть ясно отражено и в самой схеме (графе), а именно: в графе не должно быть двух вершин с одинаковыми именами переменных, а в структурной схеме линии, соответствующие одной и той же переменной, должны либо совпадать (так что выход одного звена является входом другого), либо выступать одна по отношению к другой как основная линия и отвод.
Нецелесообразно изображать систему исходных уравнений в виде набора отдельных фрагментов структурной схемы: после этого все равно придется проводить между ними линии связи.
Удобнее рисовать схему (граф) последовательно, используя то обстоятельство, что входными переменными любого звена являются, как правило, выходные переменные других звеньев.
Конечно, входами могут быть и внешние воздействия рассматриваемой системы, т. е независимые переменные, не являющиеся выходами каких-либо звеньев на структурной схеме таким переменным соответствуют стрелки, не исходящие ни из каких звеньев, а в графе — вершины, не имеющие входящих дуг.
В детализированной структурной схеме (ДСС) [3] используются только элементарные звенья — пропорциональные, интегрирующие и дифференцирующие, а также сумматоры. Если для всех передаточных функций системы, связывающих каждый вход с каждым выходом, выполнено условие реализуемости (степень полинома числителя не превышает степени полинома знаменателя), то система может быть описана в виде ДСС, состоящей только из безынерционных (пропорциональных и суммирующих) и интегрирующих звеньев [4]. Для этого рекомендуется пользоваться следующей методикой:
- Представить математическую модель системы
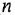 -го порядка в виде совокупности дифференциальных уравнений 1-го порядка (один из способов сделать это состоит в построении гак называемых канонических форм уравнений состояния [3D и, возможно, еще ряда алгебраических уравнений:
-го порядка в виде совокупности дифференциальных уравнений 1-го порядка (один из способов сделать это состоит в построении гак называемых канонических форм уравнений состояния [3D и, возможно, еще ряда алгебраических уравнений:
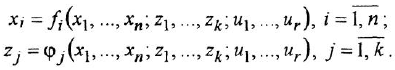
Здесь 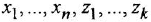 — внутренние переменные системы;
— внутренние переменные системы; 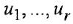 — внешние воздействия;
— внешние воздействия; 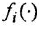 и
и 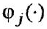 — линейные функции своих аргументов.
— линейные функции своих аргументов.
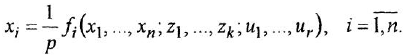
Предостережение. Переходя от уравнения (1.17) к уравнению (1.18), не следует приводить подобные члены, содержащие переменную 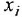 , иначе структурная схема, построенная по такому уравнению, не будет детализированной. Таким образом, переменная
, иначе структурная схема, построенная по такому уравнению, не будет детализированной. Таким образом, переменная 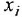 может одновременно присутствовать как в левой, так и в правой частях уравнения (1.18), что на рис. 1.2 показано пунктиром. Не следует также раскрывать скобки в (1.18): это приведет к появлению выражения
может одновременно присутствовать как в левой, так и в правой частях уравнения (1.18), что на рис. 1.2 показано пунктиром. Не следует также раскрывать скобки в (1.18): это приведет к появлению выражения 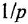 во всех слагаемых правой части и создаст иллюзию повышения порядка динамической системы.
во всех слагаемых правой части и создаст иллюзию повышения порядка динамической системы.
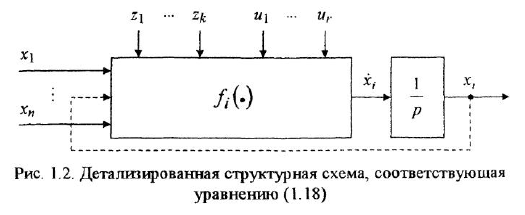
- По уравнениям (1.17), (1.18) изобразить ДСС, принимая во внимание, что уравнению (1.18) соответствует схема, показанная на рис 1.2.
Сформулированная методика сохраняет силу и при построении детализированного М-графа. Имеется, однако, тонкость: чтобы графически изобразить 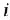 -е уравнение в (1.18), необходимо задать не только вершины, соответствующие переменным
-е уравнение в (1.18), необходимо задать не только вершины, соответствующие переменным 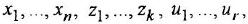 , но и вершину для переменной
, но и вершину для переменной 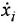 или пропорциональной ей величины (см задачу 1 5).
или пропорциональной ей величины (см задачу 1 5).
Пример №1.1.
Записать в самом общем виде уравнение, выражающее зависимость выходной величины у линейной динамической системы от входных величин 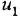 и
и 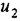 , введя необходимые обозначения передаточных функций По уравнению построить структурную схему и М-граф.
, введя необходимые обозначения передаточных функций По уравнению построить структурную схему и М-граф.
Решение:
Обозначим передаточные функции, связывающие выход с каждым из входов, как 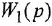 и
и 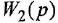 . Тогда на основании свойства линейности искомое уравнение имеет вид
. Тогда на основании свойства линейности искомое уравнение имеет вид 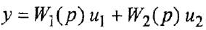 . Структурная схема и М-граф показаны на рис. 1.3.
. Структурная схема и М-граф показаны на рис. 1.3.
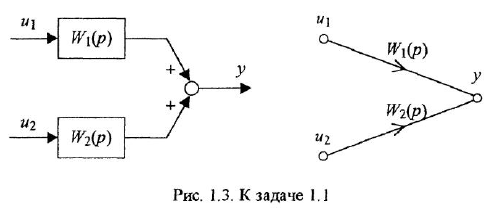
Пример №1.2.
Определить ПФ системы с одним входом 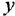 и одним выходом и по ее дифференциальному уравнению
и одним выходом и по ее дифференциальному уравнению
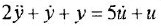
Решение:
Производя замену 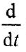 на
на 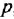 , записываем дифференциальное уравнение в операторной форме:
, записываем дифференциальное уравнение в операторной форме:
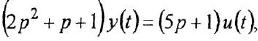
после чего переходим в комплексную область:
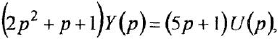
откуда получается искомая ПФ
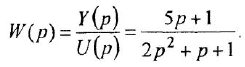
Пример №1.3.
По передаточной функции
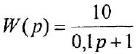
системы с одним входом и одним выходом записать ее дифференциальное уравнение.
Решение:
Обозначив выходную и входную переменные системы как 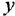 и
и 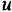 , запишем, согласно определению передаточной функции, равенство
, запишем, согласно определению передаточной функции, равенство
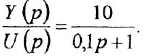
Освобождаясь от дробей и заменяя 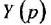 и
и 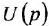 , соответственно, на
, соответственно, на 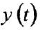 и
и 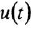 , получаем ДУ в операторной форме
, получаем ДУ в операторной форме 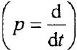 :
:
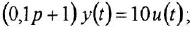
и в классической:
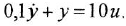
Пример №1.4.
Изобразить структурную схему следящей системы по приведенным ниже уравнениям ее функциональных элементов:
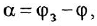
где 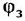 и
и 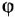 — заданное и действительное значения углового положения исполнительной оси;
— заданное и действительное значения углового положения исполнительной оси; 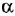 — угловое рассогласование (ошибка).
— угловое рассогласование (ошибка).
• Регулятор и усилительно-преобразовательное устройство:
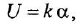
где 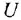 — напряжение, приложенное к якорю двигателя,
— напряжение, приложенное к якорю двигателя, 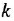 — коэффициент.
— коэффициент.
• Двигатель постоянного тока.
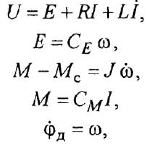
где 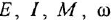 и
и 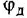 — ЭДС, ток, электромагнитный момент, угловая скорость и угловое положение вала двигателя;
— ЭДС, ток, электромагнитный момент, угловая скорость и угловое положение вала двигателя; 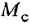 — момент сопротивления,
— момент сопротивления, 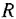 и
и 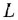 — активное сопротивление и индуктивность якорной цепи,
— активное сопротивление и индуктивность якорной цепи, 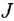 — суммарный момент инерции ротора двигателя, редуктора и исполнительного механизма, приведенный к валу двигателя;
— суммарный момент инерции ротора двигателя, редуктора и исполнительного механизма, приведенный к валу двигателя; 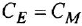 — константы.
— константы.
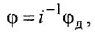
где 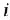 — передаточное отношение редуктора
— передаточное отношение редуктора
Решение:
Структурная схема, построенная по уравнениям (1.19)-(1 26), показана на рис. 1.4. На ней для большей ясности рядом со звеньями написаны номера соответствующих уравнений. Последовательность изображения уравнений может быть, например, следующей: (1.19)-(1.21), (1.24), (1.23), (1.22), (1.25), (1.26).
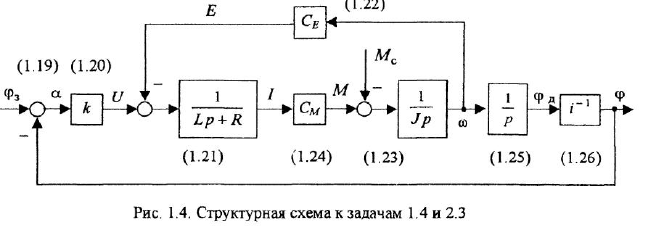
Графическое изображение уравнений (1.20), (1.22) и (1 24) затруднений не вызывает — это пропорциональные звенья. Наличие разности в правой части уравнения (1.19) указывает на то, что необходим сумматор с двумя входами Во всех дифференциальных уравнениях заменяем 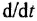 на
на 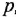 , после чего разрешаем эти уравнения относительно переменных, выбранных в качестве выходных. Чтобы избежать появления дифференцирующих звеньев, необходимо сделать выходными величины, стоящие в уравнениях под знаком производной, т. е.
, после чего разрешаем эти уравнения относительно переменных, выбранных в качестве выходных. Чтобы избежать появления дифференцирующих звеньев, необходимо сделать выходными величины, стоящие в уравнениях под знаком производной, т. е. 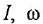 и
и 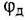 . Тогда уравнения (1.23) и (1.24) примут вид
. Тогда уравнения (1.23) и (1.24) примут вид
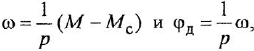
т. е им будут соответствовать интегрирующие звенья с передачей 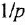 , причем для первого звена входная величина
, причем для первого звена входная величина 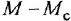 должна быть сформирована из переменных
должна быть сформирована из переменных 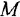 и
и 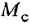 с помощью сумматора
с помощью сумматора
Наибольшую трудность вызывает графическая интерпретация уравнения якорной цепи двигателя (1.21). После замены 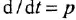 возможны три основных варианта записи этого уравнения, один из них рассмотрен в задаче 1 5, а еще два приведены ниже:
возможны три основных варианта записи этого уравнения, один из них рассмотрен в задаче 1 5, а еще два приведены ниже:
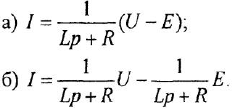
Первый из приведенных вариантов предпочтителен, поскольку в этом случае, во-первых, в структурной схеме будет на одно звено меньше, а во-вторых, последний вариант создает иллюзию того, что порядок системы на единицу выше, чем на самом деле
Замечание. Передаточную функцию
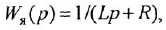
связывающую переменные 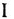 и
и 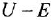 , уместно назвать передаточной функцией якорной двигателя При необходимости ее легко можно преобразовать к стандартной форме ПФ апериодического звена 1-го порядка:
, уместно назвать передаточной функцией якорной двигателя При необходимости ее легко можно преобразовать к стандартной форме ПФ апериодического звена 1-го порядка:
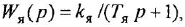
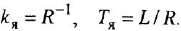
Возможно эта страница вам будет полезна:
Пример №1.5.
По уравнению (1.21) изобразить ДОС и детализированный граф.
Решение:
Перепишем (1.21) в форме уравнения (116): 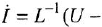
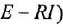 . Далее, заменив
. Далее, заменив 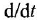 переменной
переменной 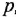 , представим это уравнение в операторной форме (1.18):
, представим это уравнение в операторной форме (1.18):
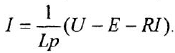
Заметим, что переменная 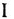 присутствует в обеих частях уравнения, но как раз or приведения подобных мы уже предостерегали. ДСС, являющаяся решением задачи, показана на рис. 1.5, а (сравните с аналогичным фрагментом схемы рис. 1.4, не являющимся ДСС).
присутствует в обеих частях уравнения, но как раз or приведения подобных мы уже предостерегали. ДСС, являющаяся решением задачи, показана на рис. 1.5, а (сравните с аналогичным фрагментом схемы рис. 1.4, не являющимся ДСС).
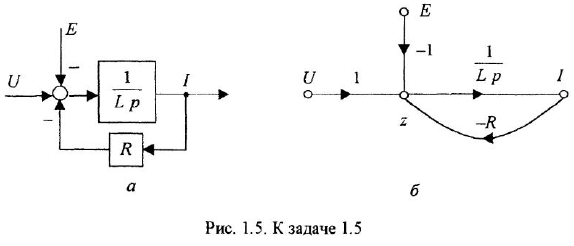
Чтобы изобразить М-граф, нанесем на рисунок вершины для переменных
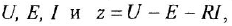
после чего проведем ребра с соответствующими передачами. Результат показан на рис. 1.5, б.
Полезно сравнить структурную схему и М-граф, соответствующие одному и тому же уравнению. Это, во-первых, поможет читателю в дальнейшем избежать распространенной ошибки — смешивания в одном рисунке элементов структурной схемы и графа, а во-вторых, позволит ему при необходимости легко изобразить по М-графу соответствующую структурную схему, и наоборот.
Анализ структурных схем. Передаточные функции типовых соединений звеньев САУ
Типовыми соединениями звеньев в структурных схемах являются последовательное (рис. 2.1, д), параллельное, или согласно-параллельное (рис. 2.1,6), и соединение с обратной связью, или встречно-параллельное (рис. 2.1, в). Каждое из этих соединений можно рассматривать как одно звено, считая его входной и выходной величинами, соответственно, переменные  и
и 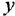 (рис 2.1,г).
(рис 2.1,г).
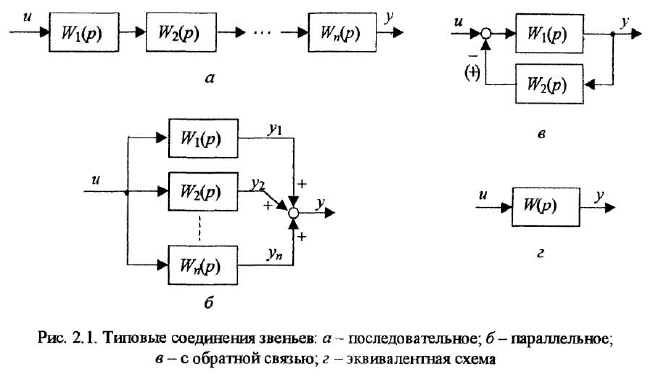
Необходимо твердо усвоить формулы для определения передаточной функции
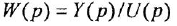
типового соединения по передаточным функциям звеньев, образующих это соединение:
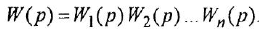
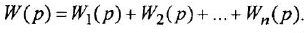
(Если какая-либо из переменных 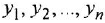 на рис. 2.1, б входит в сумматор со знаком «минус», то и в формуле (2 2) соответствующее слагаемое должно быть взято со знаком «минус».)
на рис. 2.1, б входит в сумматор со знаком «минус», то и в формуле (2 2) соответствующее слагаемое должно быть взято со знаком «минус».)
• Соединение с обратной связью:
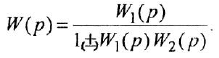
В последней формуле необходимо выбирать знак «плюс» в случае отрицательной обратной связи и «минус» — в случае положительной. Отметим, что в этой формуле выражение 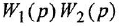 , т. е. произведение передач прямой и обратной связей, называется передаточной функцией разомкнутого контура, а само выражение (2.3) — передаточной функцией замкнутого контура.
, т. е. произведение передач прямой и обратной связей, называется передаточной функцией разомкнутого контура, а само выражение (2.3) — передаточной функцией замкнутого контура.
Если структурная схема содержит только типовые соединения, то, как бы сложна ни была эта схема, по ней всегда можно определить передаточную функцию, связывающую заданные переменные, путем последовательного применения формул (2.1)-(2.3). Если же, кроме типовых, есть соединения с более сложной топологией (подробнее об этом см. в 3 1), то необходимо либо использовать теорему Мейсона, рассматриваемую в 2.2, либо применить метод эквивалентных структурных преобразований, излагаемый в 3.1
Теорема Мейсона (Мэзона)
Теорема Мейсона позволяет определить передаточную функцию, связывающую любые две переменные структурной схемы или М-графа. Поскольку первоначально теорема была сформулирована для графов, а затем распространена на структурные схемы, уточним некоторые топологические термины, знание которых необходимо для правильного применения этой теоремы.
Маршрутом в теории графов называют последовательность ребер, в которой соседние ребра инцидентны одной и той же вершине (напомним, что вершина 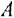 и ребро
и ребро 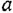 называются инцидентными друг другу, если вершина
называются инцидентными друг другу, если вершина 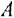 является концом ребра
является концом ребра 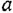 , например, на рис 1.1,6 вершина
, например, на рис 1.1,6 вершина 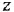 инцидентна всем трем ребрам графа, а вершина
инцидентна всем трем ребрам графа, а вершина 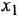 не инцидентна ребрам с передачами
не инцидентна ребрам с передачами 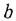 и
и 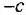 ). Таким образом, геометрически маршрут представляет собой непрерывную цепочку ребер. В направленных графах, каковыми являются М-графы, при «обходе» маршрута направления всех ребер, образующих маршрут, должны совпадать с направлением обхода. Например, в графе на рис. 2.2, б последовательность ребер с передачами
). Таким образом, геометрически маршрут представляет собой непрерывную цепочку ребер. В направленных графах, каковыми являются М-графы, при «обходе» маршрута направления всех ребер, образующих маршрут, должны совпадать с направлением обхода. Например, в графе на рис. 2.2, б последовательность ребер с передачами 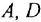 и 1, соединяющая вершины
и 1, соединяющая вершины 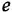 и
и 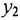 , является маршрутом, а последовательность
, является маршрутом, а последовательность 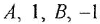 — не является, поскольку направление ребра 1 противоположно направлению обхода указанной последовательности ребер.
— не является, поскольку направление ребра 1 противоположно направлению обхода указанной последовательности ребер.
Путь — это маршрут без повторяющихся ребер и вершин На рис. 2.2, б последовательность ребер с передачами 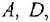 1 (вверх),
1 (вверх), 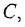 1,-1 — это маршрут, но не путь, поскольку вершина
1,-1 — это маршрут, но не путь, поскольку вершина 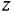 проходится дважды В структурной схеме путем называют направленную последовательность звеньев, в которой ни одна переменная не встречается более одного раза [3].
проходится дважды В структурной схеме путем называют направленную последовательность звеньев, в которой ни одна переменная не встречается более одного раза [3].
Передачей пути называется произведение передач всех звеньев (в графе — ребер), образующих этот путь, причем необходимо учитывать и знаки, с ко-
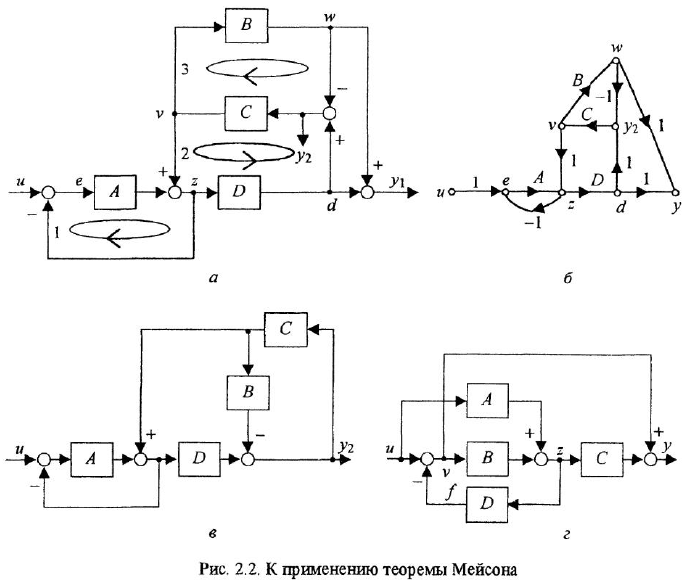
торыми переменные данного пути входят в сумматоры, встречающиеся на этом пути. Па рис 2.2, а, б путь между переменными 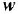 и
и 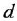 имеет передачу
имеет передачу 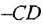 .
.
Контуром как в графе, так и в структурной схеме называют замкнутый путь. Для графа это означает, что начальная и конечная вершины пути совпадают.
Передача контура — это произведение передач всех звеньев (или ребер), образующих контур, с учетом знаков в сумматорах Например, контур в графе на рис. 1.5, б имеет передачу 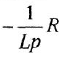 . Предостережем от распространенной ошибки: иногда вместо передачи контура записывают передаточную функцию замкнутого контура вида (2.3); на самом деле передача контура есть, по существу, передаточная функция разомкнутого контура, но с учетом знака обратной связи.
. Предостережем от распространенной ошибки: иногда вместо передачи контура записывают передаточную функцию замкнутого контура вида (2.3); на самом деле передача контура есть, по существу, передаточная функция разомкнутого контура, но с учетом знака обратной связи.
Говорят, что контур не касается другого контура или пути, если он не имеет с ним общих переменных. На рис 2.2, а, б контур с передачей 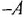 не касается контура с передачей
не касается контура с передачей 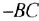 , и, наоборот, касается контура с передачей
, и, наоборот, касается контура с передачей 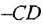 , поскольку имеет с ним общую переменную
, поскольку имеет с ним общую переменную 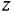 .
.
Согласно теореме Мейсона, передача, связывающая некоторую «входную» переменную 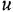 (обычно это внешнее воздействие) с некоторой «выходной» переменной
(обычно это внешнее воздействие) с некоторой «выходной» переменной 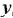 , определяется формулой
, определяется формулой
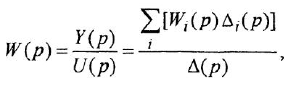
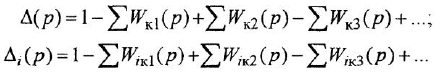
Обозначения, использованные в формулах (2.4)-(2.6), имеют следующий смысл: 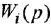 — передача
— передача 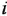 -го пути от
-го пути от 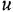 к
к 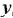 ;
; 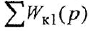 — сумма передач всех контуров;
— сумма передач всех контуров; 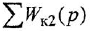 — сумма произведений передач всех не касающихся друг друга контуров, взятых по два;
— сумма произведений передач всех не касающихся друг друга контуров, взятых по два; 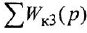 — сумма произведений передач всех не касающихся друг друга контуров, взятых по три, и т. д.;
— сумма произведений передач всех не касающихся друг друга контуров, взятых по три, и т. д.; 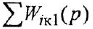 сумма передач всех контуров, не касающихся
сумма передач всех контуров, не касающихся 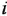 -го пути;
-го пути; 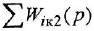 — сумма произведений передач всех контуров, не касающихся
— сумма произведений передач всех контуров, не касающихся 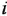 -го пути и друг друга, взятых по два;
-го пути и друг друга, взятых по два; 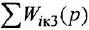 — сумма произведений передач всех контуров, не касающихся
— сумма произведений передач всех контуров, не касающихся 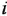 -го пути и друг друга, взятых но три, и т. д.
-го пути и друг друга, взятых но три, и т. д.
Заметим, что два пути или два контура могут частично совпадать; тем не менее, если они различаются хотя бы одним звеном (ребром), то это рахпич-ные пути или контуры.
Решение любой задачи, требующей применения теоремы Мейсона, следует начинать с анализа структурной схемы или М-графа. Если схема сложна, то рекомендуется сначала выписать передачи всех путей, связывающих заданные переменные, и передачи всех контуров, отметив специально «некасающиеся» контуры После этого можно непосредственно записывать искомую передаточную функцию в соответствии с формулами (2 4)-(2.6).
Хотя при определении передаточных функций по теореме Мейсона в качестве входной переменной практически всегда выступает какое-либо внешнее воздействие, ничто не мешает применять эту теорему в ситуации, когда входом является некоторая «внутренняя» переменная структурной схемы. В этом случае надо лишь «усечь» схему, исключив из нее все пути, направленные к указанной входной переменной от заданного выхода и от внешних входных воздействий.
Удобство теоремы Мейсона заключается в возможности быстро записать требуемую передаточную функцию без многократного перерисовывания структурной схемы, что часто бывает необходимо в случае применения альтернативного метода структурных преобразований (см. 3.1) Вместе с тем, с ростом сложности схемы резко возрастает опасность «пропустить» при ее анализе какой-нибудь путь или контур либо не заметить факта «некасания» Поэтому в целом метод структурных преобразований считается более надежным способом определения передаточной функции по структурной схеме
Анализ установившегося режима по структурной схеме при постоянных входных воздействиях
Для исследования динамических систем, в том числе на ЭВМ, бывает важно уметь анализировать установившийся режим при постоянных внешних воздействиях Это можно делать различными способами — например, с помощью алгебраических методов пространства состояний. Здесь мы рассмотрим простой способ, позволяющий определить установившиеся значения всех переменных системы по структурной схеме.
Пусть система асимптотически устойчива (изложение методов анализа устойчивости выходит за рамки данного учебного пособия) Тогда, если все входные (внешние) воздействия постоянны, то с течением времени (теоретически — при 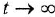 ) все переменные системы примут постоянные значения Из этого факта вытекают важные следствия.
) все переменные системы примут постоянные значения Из этого факта вытекают важные следствия.
- Если схема содержит интегрирующее звено, описываемое, как известно, уравнением
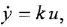 , то из
, то из 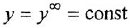 (индекс
(индекс 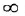 служит обозначением установившегося режима) следует, что
служит обозначением установившегося режима) следует, что 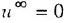 . Таким образом, в асимптотически устойчивой системе с постоянными внешними воздействиями входные переменные всех интегрирующих звеньев в установитиемся режиме равны нулю.
. Таким образом, в асимптотически устойчивой системе с постоянными внешними воздействиями входные переменные всех интегрирующих звеньев в установитиемся режиме равны нулю.
2 Если в схеме имеется дифференцирующее звено, описываемое уравнением 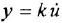 , то из
, то из 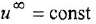 следует
следует 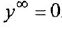 . Следовательно, в асимптотически устойчивой системе с постоянными внешними воздействиями выходы всех дифференцирующих звеньев в установившемся режиме равны нулю. По этой же причине выход форсирующего звена (см. передаточную функцию (1.11)) принимает постоянное значение, равное его входу.
. Следовательно, в асимптотически устойчивой системе с постоянными внешними воздействиями выходы всех дифференцирующих звеньев в установившемся режиме равны нулю. По этой же причине выход форсирующего звена (см. передаточную функцию (1.11)) принимает постоянное значение, равное его входу.
Большинство звеньев структурной схемы — это позиционные звенья, описываемые передаточными функциями (1.5), (I 10), (1 12) и (I 13), причем в трех последних в общем случае присутствует коэффициент передачи 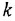 .
.
Коэффициент передачи к звена (системы) может быть определен двояко:
а) 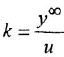 , т. е. как отношение установившейся реакции
, т. е. как отношение установившейся реакции 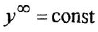 к постоянному входному воздействию
к постоянному входному воздействию 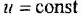 , если система асимптотически устойчива;
, если система асимптотически устойчива;
б) 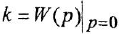 , если это выражение имеет смысл (определено).
, если это выражение имеет смысл (определено).
Последнее выражение — это одновременно и практический способ определения коэффициента передачи.
Общим свойством позиционных звеньев является то, что при подаче на вход такого звена постоянной величины на его выходе с течением времени также устанавливается постоянное значение. ПФ позиционного звена в установившемся режиме вырождается в коэффициент передачи 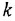 (т. е в ПФ можно положить
(т. е в ПФ можно положить 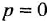 ), поэтому в установившемся режиме вход и выход пропорционального, апериодических 1-го и 2-го порядков и колебательного звеньев связаны соотношением
), поэтому в установившемся режиме вход и выход пропорционального, апериодических 1-го и 2-го порядков и колебательного звеньев связаны соотношением 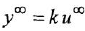 .
.
Консервативное звено с ПФ (1.14) также относится к позиционным, но, в отличие от остальных, не является асимптотически устойчивым. При наличии в схеме консервативного звена (или эквивалентного ему встречно-параллельного соединения интегрирующего звена 2-го порядка и пропорционального звена) в системе в установившемся режиме будут наблюдаться незатухающие колебания, т. е. по крайней мере некоторые переменные будут изменяться по гармоническому закону. Анализ такого установившегося режима выходит за рамки излагаемого здесь метода.
В заключение отметим, что отводы по переменным, установившиеся значения которых равны нулю, при анализе установившегося режима можно не учитывать.
Возможно эта страница вам будет полезна:
Пример №2.1.
По структурной схеме (рис 2.3, а) определить передаточные функции 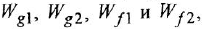 , связывающие выходы
, связывающие выходы 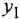 и
и 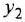 с внешними воздействиями
с внешними воздействиями 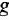 и
и 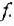
Решение:
Сначала найдем ПФ 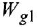 , при этом вход
, при этом вход 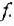 учитывать не надо. Данная схема содержит только типовые соединения. Звенья с передачами
учитывать не надо. Данная схема содержит только типовые соединения. Звенья с передачами 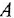 и
и 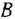 образуют соединение с обратной связью, причем положительной. Будем рассматривать это соединение как одно звено с ПФ
образуют соединение с обратной связью, причем положительной. Будем рассматривать это соединение как одно звено с ПФ 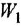 , определяемой согласно формуле (2.3) как
, определяемой согласно формуле (2.3) как 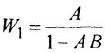 . Звенья с передачами
. Звенья с передачами 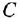 и
и 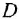 образуют
образуют
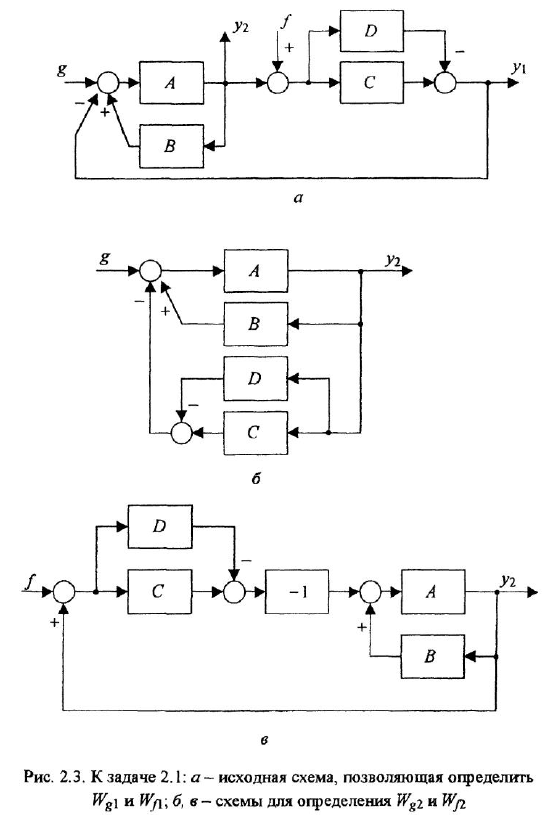
согласно-параллельное соединение; в соответствии с формулой (2.2) его 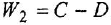 . Эквивалентные звенья с передачами
. Эквивалентные звенья с передачами 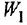 и
и 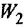 образуют последовательное соединение, ПФ которого на основании (2.1) есть
образуют последовательное соединение, ПФ которого на основании (2.1) есть 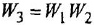 . Таким образом, схема сводится к одноконтурной системе с единичной отрицательной обратной связью и передачей прямой связи
. Таким образом, схема сводится к одноконтурной системе с единичной отрицательной обратной связью и передачей прямой связи 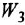 . Поэтому ПФ
. Поэтому ПФ 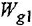 записывается по формуле (2 3) как
записывается по формуле (2 3) как 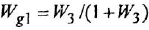 , или, с учетом введенных обозначений.
, или, с учетом введенных обозначений.
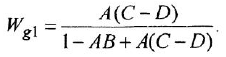
Для сравнения получим искомую ПФ иначе — с помощью теоремы Мейсона. От 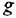 к
к 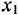 ведут два пути — с передачами
ведут два пути — с передачами 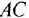 и
и 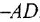 . Схема содержит три контура, имеющие передачи
. Схема содержит три контура, имеющие передачи 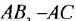 и
и 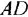 (последняя получилась такой в результате сокращения двух минусов). Контуры, не касающиеся какого-либо пути или другого контура, отсутствуют. В результате согласно формулам (2.4)-(2.6) находим:
(последняя получилась такой в результате сокращения двух минусов). Контуры, не касающиеся какого-либо пути или другого контура, отсутствуют. В результате согласно формулам (2.4)-(2.6) находим:
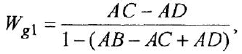
что, разумеется, совпадает с ранее полученным выражением.
Чтобы найти ПФ 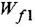 , следует не только помнить о необходимости рассматривать каждое из типовых соединений как одно звено, но и ясно представлять себе общую структуру системы с обратной связью. Внешнее воздействие
, следует не только помнить о необходимости рассматривать каждое из типовых соединений как одно звено, но и ясно представлять себе общую структуру системы с обратной связью. Внешнее воздействие 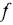 приложено к сумматору (вид схемы на рис. 2.3, а позволяет предположить, что
приложено к сумматору (вид схемы на рис. 2.3, а позволяет предположить, что 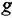 — это задающее воздействие, а
— это задающее воздействие, а 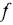 — возмущающее; исходя из этого, первый сумматор можно назвать элементом сравнения, второй же, к которому приложено возмущение, называть так нежелательно), и та часть схемы, которая заключена между этим сумматором и выходом
— возмущающее; исходя из этого, первый сумматор можно назвать элементом сравнения, второй же, к которому приложено возмущение, называть так нежелательно), и та часть схемы, которая заключена между этим сумматором и выходом 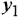 (ее передача равна
(ее передача равна 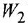 ), представляет собой прямую связь, а остальные звенья образуют обратную связь. Поскольку воздействие
), представляет собой прямую связь, а остальные звенья образуют обратную связь. Поскольку воздействие 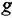 не учитываем, то знак подходящей к элементу сравнения отрицательной связи по переменной
не учитываем, то знак подходящей к элементу сравнения отрицательной связи по переменной 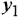 следует учесть отдельно в виде звена с передачей -1, стоящего перед встречно-параллельным соединением, имеющим передачу
следует учесть отдельно в виде звена с передачей -1, стоящего перед встречно-параллельным соединением, имеющим передачу 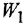 . Следовательно, результирующая передача звеньев, стоящих в обратной связи, равна —
. Следовательно, результирующая передача звеньев, стоящих в обратной связи, равна — 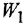 , но сама обратная связь формально является положительной, поскольку она подходит к сумматору, к которому приложено воздействие
, но сама обратная связь формально является положительной, поскольку она подходит к сумматору, к которому приложено воздействие 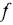 со знаком «плюс». В силу этого при определении
со знаком «плюс». В силу этого при определении 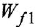 в формуле (2.3) следует выбрать знак «минус»:
в формуле (2.3) следует выбрать знак «минус»:
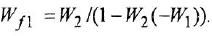
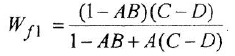
До сих пор на структурных схемах выходная величина всегда изображалась стрелкой, заканчивающей горизонтальную цепочку звеньев, берущую начало от места приложения задающего воздействия. Если же в качестве выхода рассматривается какая-либо «внутренняя» переменная (в данной задаче — 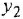 ), то в большинстве случаев, если не предполагается использовать теорему Мейсона, структурную схему целесообразно, а чаще всего даже необходимо, перерисовать так, чтобы образовалась указанная цепочка, началом которой являлось бы рассматриваемое внешнее воздействие, а концом — данная выходная переменная. Если таких цепочек в исходной схеме несколько, удобно взять самую длинную из них. После этого остается дополнить цепочку остальными элементами схемы — так, чтобы в итоге получилась структурная схема, топологически эквивалентная исходной, т. е. сохраняющая способ соединения звеньев друг с другом. На рис. 2.3, б и в показаны две такие схемы, нарисованные для случаев, когда входами системы являются, соответственно, переменные
), то в большинстве случаев, если не предполагается использовать теорему Мейсона, структурную схему целесообразно, а чаще всего даже необходимо, перерисовать так, чтобы образовалась указанная цепочка, началом которой являлось бы рассматриваемое внешнее воздействие, а концом — данная выходная переменная. Если таких цепочек в исходной схеме несколько, удобно взять самую длинную из них. После этого остается дополнить цепочку остальными элементами схемы — так, чтобы в итоге получилась структурная схема, топологически эквивалентная исходной, т. е. сохраняющая способ соединения звеньев друг с другом. На рис. 2.3, б и в показаны две такие схемы, нарисованные для случаев, когда входами системы являются, соответственно, переменные 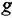 и
и 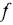 , а выходом —
, а выходом — 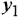 (в принципе, первую из схем можно было бы и не изображать, поскольку понять ее структуру непосредственно по исходной схеме ничуть не сложнее, чем в только что рассмотренной задаче нахождения ПФ
(в принципе, первую из схем можно было бы и не изображать, поскольку понять ее структуру непосредственно по исходной схеме ничуть не сложнее, чем в только что рассмотренной задаче нахождения ПФ 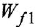 ). Обе схемы в целом представляют собой систему с обратной связью и содержат только типовые соединения: звенья с передачами
). Обе схемы в целом представляют собой систему с обратной связью и содержат только типовые соединения: звенья с передачами 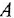 и
и 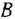 образуют встречно-параллельное соединение, а звенья с передачами
образуют встречно-параллельное соединение, а звенья с передачами 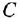 и
и 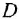 — согласно-параллельное. На рис. 2.3, б передача прямой связи равна
— согласно-параллельное. На рис. 2.3, б передача прямой связи равна
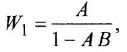
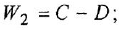
на рис. 2.3, в прямая связь имеет передачу — 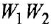 , обратная связь является единичной и, формально, положительной.
, обратная связь является единичной и, формально, положительной.
С учетом сказанного, легко записать искомые ПФ
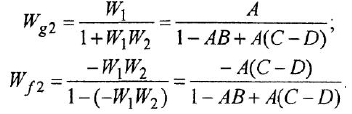
Обращаем внимание читателя на то, что все четыре найденные передаточные функции имеют, как это всегда и должно быть, одинаковые знаменатели.
Чтобы найти ПФ 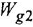 и
и 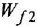 с помощью теоремы Мейсона, нет необходимости перерисовывать схему рис. 2 3, а. Предоставляем читателю возможность решить задачу этим способом самостоятельно.
с помощью теоремы Мейсона, нет необходимости перерисовывать схему рис. 2 3, а. Предоставляем читателю возможность решить задачу этим способом самостоятельно.
Пример №2.2.
С помощью теоремы Мейсона по структурной схеме или М-графу, изображенным на рис. 2.2, а и б, определить передаточные функции 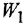 и
и 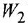 , связывающие вход
, связывающие вход 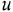 с выходами, соответственно,
с выходами, соответственно, 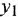 и
и 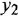 .
.
Решение:
Определим ПФ 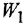 . От
. От 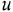 к
к 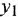 ведут два пути — с передачами, соответственно,
ведут два пути — с передачами, соответственно, 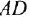 и
и 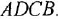 . В схеме (графе) три контура (на рис. 2.2, а они показаны дугами и пронумерованы): контур 1 имеет передачу —
. В схеме (графе) три контура (на рис. 2.2, а они показаны дугами и пронумерованы): контур 1 имеет передачу —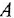 , контур 2 — передачу
, контур 2 — передачу 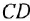 контур 3 — передачу
контур 3 — передачу 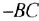 , при этом 1 -й и 3-й контуры друг друга не касаются, кроме того, 3-й контур не касается 1-го пути После такого анализа не составляет труда записать искомую передаточную функцию
, при этом 1 -й и 3-й контуры друг друга не касаются, кроме того, 3-й контур не касается 1-го пути После такого анализа не составляет труда записать искомую передаточную функцию
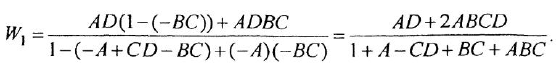
При нахождении 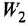 учтем, что знаменатель у этой ПФ тот же, что и у ПФ
учтем, что знаменатель у этой ПФ тот же, что и у ПФ 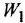 поскольку он определяется, согласно выражению (2.5), только контурами схемы (графа). От
поскольку он определяется, согласно выражению (2.5), только контурами схемы (графа). От 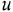 к
к 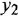 ведет единственный путь, его передача равна
ведет единственный путь, его передача равна 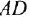 . Все три контура касаются этого пути. С учетом этого находим:
. Все три контура касаются этого пути. С учетом этого находим:
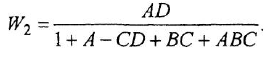
Пример №2.3.
С помощью теоремы Мейсона определить передачу между переменными 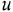 и
и 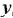 структурной схемы, изображенной на рис. 2.2, г.
структурной схемы, изображенной на рис. 2.2, г.
Решение:
В схеме только один контур, но четыре пути: с передачами, соответственно, 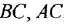 , 1 и —
, 1 и — 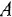 (последний путь топологически наиболее сложен, он включает- в себя прямую связь с передачей
(последний путь топологически наиболее сложен, он включает- в себя прямую связь с передачей 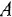 , далее — единичную отрицательную обратную связь и, наконец, единичную прямую связь; полезно убедиться в том, что он полностью удовлетворяет данному ранее определению пути — при его обходе ни одна переменная не встречается дважды, а сам обход происходит только в направлении стрелок). Поскольку контур касается всех путей, искомая передаточная функция записывается предельно просто:
, далее — единичную отрицательную обратную связь и, наконец, единичную прямую связь; полезно убедиться в том, что он полностью удовлетворяет данному ранее определению пути — при его обходе ни одна переменная не встречается дважды, а сам обход происходит только в направлении стрелок). Поскольку контур касается всех путей, искомая передаточная функция записывается предельно просто:
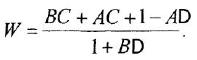
Возможно эта страница вам будет полезна:
Преобразование структурных схем. Эквивалентные структурные преобразования
Если в структурной схеме имеются не только типовые соединения звеньев (см. 2.1), но и другие, более сложные, то при необходимости определить передаточную функцию, связывающую заданные переменные, можно поступить различным образом: воспользоваться теоремой Мейсона (о ее достоинствах и недостатках было сказано ранее) либо применить метод эквивалентных преобразований структурных схем (короче — метод структурных преобразований), излагаемый далее. Этот метод, как показывает практика преподавания, не так легок для начального освоения, как теорема Мейсона, и даже может показаться громоздким, но в действительности после приобретения необходимых навыков становится удобным, эффективным и надежным инструментом анализа систем. Знание этого метода обязательно для специалиста в области автоматического управления. Рассмотрим сущность метода эквивалентных структурных преобразований.
Обычно в схеме можно выделить две части, не обязательно компактные одна состоит только из типовых соединений, к которым, следовательно, сразу могут быть применены формулы (2 1)—(2.3) для определения передаточных функций, другая же — назовем ее преобразуемой частью — содержит различного рода нетиповые соединения звеньев. В чем особенность таких соединений, и почему они являются предметом специального рассмотрения0
На рис 3.1, а показана структурная схема, в которой вообще нет типовых соединений. Если бы в этой схеме отсутствоват отвод «*» (конечно, вместе с сумматором  ), то это была бы обычная, «типовая» схема, содержащая всгречно-параллельное и последовательное соединения (То же самое можно сказать и о случае, когда в схеме не было бы отвода «**».) Наличие этого отвода не позволяет «свернуть» встречно-параллельное соединение звеньев с передачами
), то это была бы обычная, «типовая» схема, содержащая всгречно-параллельное и последовательное соединения (То же самое можно сказать и о случае, когда в схеме не было бы отвода «**».) Наличие этого отвода не позволяет «свернуть» встречно-параллельное соединение звеньев с передачами 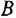 и
и 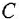 в одно звено, так как в новом звене перестанет существовать переменная
в одно звено, так как в новом звене перестанет существовать переменная 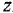 , по которой и сделан отвод.
, по которой и сделан отвод.
Возникает вопрос: нельзя ли заменить эту схему другой так, чтобы ее передаточная функция не изменилась, но отвод «*» шел не с выхода звена с передачей 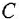 , а с его входа (в этом случае упомянутое встречно-параллельное соединение беспрепятственно «сворачивается» в одно звено)? Положительный ответ на этот вопрос как раз и составляет сущность структурных преобразований вообще и преобразования рассматриваемой схемы в частности Для данного примера результат преобразования представлен на рис 3.1, б (метод его получения будет рассмотрен позднее). Ценой некоторого усложнения схемы (добавилось одно звено) достигнута главная цель — точка отвода перенесена через звено. Заметим, что схема теперь содержит только типовые
, а с его входа (в этом случае упомянутое встречно-параллельное соединение беспрепятственно «сворачивается» в одно звено)? Положительный ответ на этот вопрос как раз и составляет сущность структурных преобразований вообще и преобразования рассматриваемой схемы в частности Для данного примера результат преобразования представлен на рис 3.1, б (метод его получения будет рассмотрен позднее). Ценой некоторого усложнения схемы (добавилось одно звено) достигнута главная цель — точка отвода перенесена через звено. Заметим, что схема теперь содержит только типовые
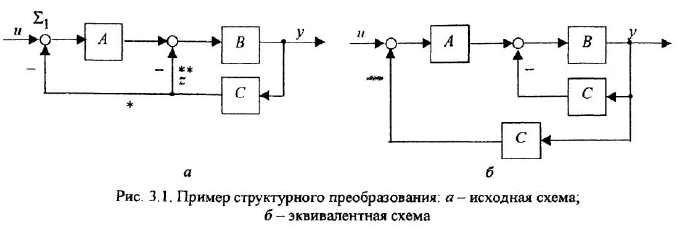
соединения, а передаточная функция, связывающая переменные 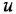 и
и 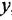 , в результате преобразования не изменилась (ПФ исходной схемы легко найти по теореме Мейсона, а ПФ преобразованной — по формулам (2.1)-(2 3)). Можно сказать и иначе: уравнения, связывающие входную и выходную переменные в рассматриваемых схемах, совпадают с точностью до тождественности алгебраических выражений.
, в результате преобразования не изменилась (ПФ исходной схемы легко найти по теореме Мейсона, а ПФ преобразованной — по формулам (2.1)-(2 3)). Можно сказать и иначе: уравнения, связывающие входную и выходную переменные в рассматриваемых схемах, совпадают с точностью до тождественности алгебраических выражений.
Приведение схемы к типовому виду осуществляется выполнением некоторого количества операций преобразования. После выполнения любой из этих операций новая схема должна в определенном смысле быть эквивалентна предыдущей Пусть та часть (фрагмент) структурной схемы, над которой совершается операция преобразования, имеет 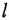 входных переменных
входных переменных 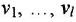 и
и 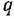 выходных
выходных  . Тогда критерий эквивалентности исходной и преобразованной схем (фрагментов) может быть сформулирован следующим образом: операция преобразования не должна изменять ни одной из передаточных функций
. Тогда критерий эквивалентности исходной и преобразованной схем (фрагментов) может быть сформулирован следующим образом: операция преобразования не должна изменять ни одной из передаточных функций
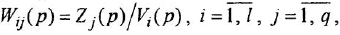
связывающих каждый вход 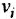 с каждым выходом
с каждым выходом 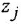 . Соблюдение условия эквивалентности при выполнении преобразований отдельных частей структурной схемы гарантирует, что и вся схема на любом этапе ее преобразования будет удовлетворять этому условию.
. Соблюдение условия эквивалентности при выполнении преобразований отдельных частей структурной схемы гарантирует, что и вся схема на любом этапе ее преобразования будет удовлетворять этому условию.
В табл. 3.1 приведены правила, по которым выполняются структурные преобразования. Подавляющее большинство приведенных здесь операций -это различного рода перестановки: звеньев, сумматоров и отводов. Для пояснения каждой операции в соответствующей горизонтальной графе показаны две схемы: исходная и эквивалентная ей преобразованная Однако как раз в силу эквивалентности всех преобразований каждую пару схем можно просматривать и в обратном порядке, считая эквивалентную схему исходной Например, операция 3 носит двойственный характер: сумматоры можно объединять и, наоборот, разделять.
При начальном изучении табл. 3.1 полезно убедиться в корректности каждой операции. Для этого рекомендуется проверить совпадение передаточных функций, связывающих каждый вход с каждым выходом в исходной
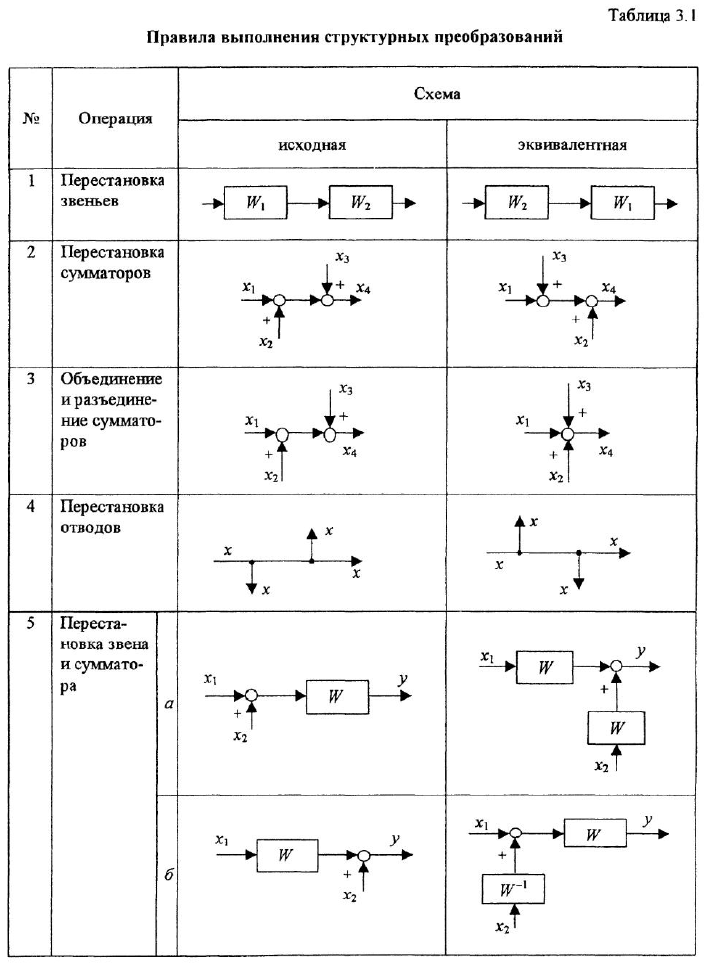
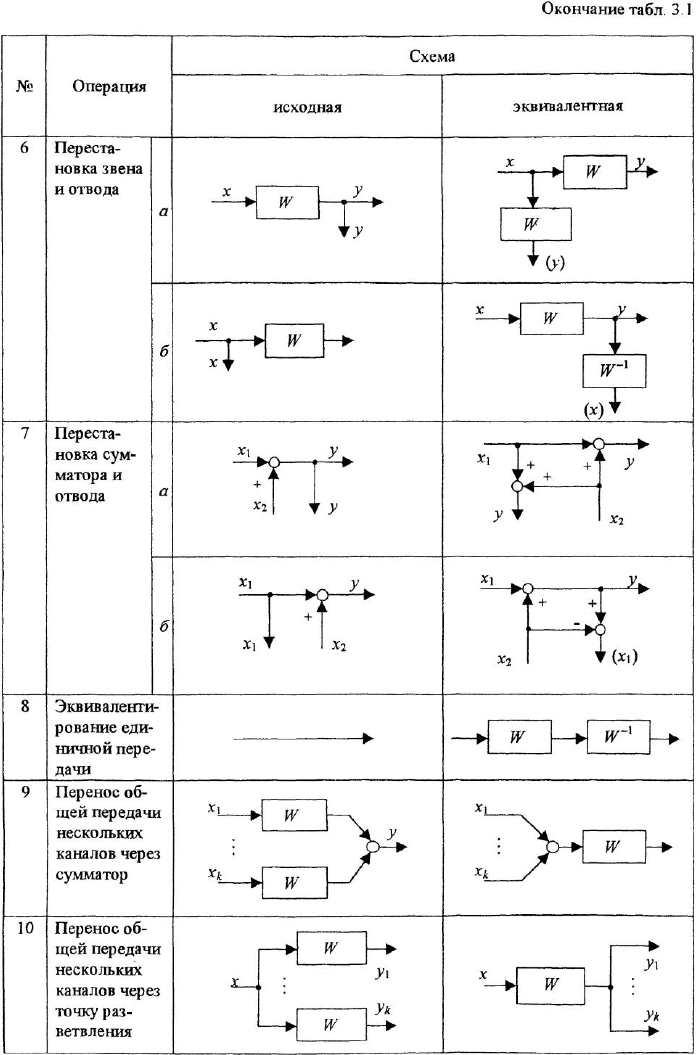
и эквивалентной схемах. Чтобы получить требуемую ПФ, необходимо просто «пройти» вдоль пути, связывающего данный вход с данным выходом, перемножая передачи всех звеньев этого пути и учитывая знаки в сумматорах. Можно поступить и иначе, в обеих схемах для каждой выходной переменной записать уравнение, описывающее зависимость этой переменной от всех входных переменных, после чего сравнить эти уравнения.
Особо подчеркнем следующее обстоятельство: приведенные в табл 3.1 правила выполнения операций не предназначены для запоминания. Необходимо просто понять логику построения эквивалентной схемы по имеющейся исходной и всякий раз при решении конкретной задачи поступать аналогично.
Рассмотрим теперь правила выполнения отдельных операций Все множество приведенных в табл. 3.1 операций можно условно разделить на три группы Первую из них составляют простейшие операции 1-4, которые вряд ли нуждаются в пояснениях.
Группу основных операций составляют операции 5-7. Именно они являются главным инструментом преобразования структурных схем. Рассмотрим перестановку звена и сумматора — например, в случае, когда сумматор стоит перед звеном (в табл. 3.1 — операция 5, вариант а). Если просто поменять местами сумматор и звено с передачей  , то полученная схема не будет эквивалентна исходной: в то время как по входу
, то полученная схема не будет эквивалентна исходной: в то время как по входу 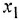 передача не изменяется и равна
передача не изменяется и равна  , по входу
, по входу 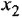 в исходной схеме передача равна
в исходной схеме передача равна  , а в преобразованной — единице. Следовательно, для того чтобы обеспечить эквивалентность, необходимо в связь по переменной
, а в преобразованной — единице. Следовательно, для того чтобы обеспечить эквивалентность, необходимо в связь по переменной 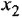 вставить дополнительное звено с передачей
вставить дополнительное звено с передачей  .
.
Аналогично рассуждаем при обосновании правила перестановки звена и отвода. Рассмотрим операцию 6, вариант а. Просто поменять местами звено и отвод нельзя: в этом случае отвод будет по переменной 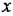 , а надо — по переменной
, а надо — по переменной 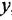 . А поскольку
. А поскольку 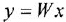 , то в отвод необходимо вставить звено с передачей
, то в отвод необходимо вставить звено с передачей  .
.
Перестановка сумматора и отвода — наиболее сложная из операций преобразования структурных схем, и ее по возможности следует избегать. Здесь тоже есть два варианта взаимного расположения переставляемых элементов (варианты а и б операции 7 в табл. 3.1) В связи с этим следует со всей определенностью сказать, что объективная необходимость в выполнении перестановки по варианту б встречается крайне редко Бели при анализе конкретной схемы выясняется, что без перестановки сумматора и отвода обойтись нельзя, то необходимо, прежде всего, искать возможность выполнить перестановку по варианту а, такая возможность, скорее всего, существует.
Обращаем внимание на то, что, согласно правилу выполнения данной операции, в эквивалентной схеме вместо отвода по переменной 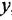 , равной сумме (или в других случаях — разности) переменных
, равной сумме (или в других случаях — разности) переменных 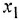 и
и 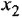 , появляются два отвода — по каждой из указанных переменных, а также дополнительный сумматор. Таким образом, схема усложнилась, и требуется еще ряд преобразований, чтобы ее упростить. (Принцип здесь таков: выходящая из дополнительного сумматора связь, хотя бы и пройдя через промежуточные звенья, обязательно заканчивается в каком-нибудь сумматоре; следовательно, дополнительный сумматор можно объединить с этим сумматором, если до этого поменять местами указанные промежуточные звенья и дополнительный сумматор.)
, появляются два отвода — по каждой из указанных переменных, а также дополнительный сумматор. Таким образом, схема усложнилась, и требуется еще ряд преобразований, чтобы ее упростить. (Принцип здесь таков: выходящая из дополнительного сумматора связь, хотя бы и пройдя через промежуточные звенья, обязательно заканчивается в каком-нибудь сумматоре; следовательно, дополнительный сумматор можно объединить с этим сумматором, если до этого поменять местами указанные промежуточные звенья и дополнительный сумматор.)
Однако, оказывается, перестановку сумматора и отвода можно выполнить гораздо более простым способом, исключающим появление дополнительного сумматора, а значит, и не требующим последующих операций по упрощению схемы. Суть этого способа (отразить его в табл. 3.1 не представляется возможным) состоит в следующем. В исходной системе отвод по переменной у, или в данном случае удобнее сказать — сама переменная 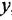 , в конце концов «приходит» в некоторый сумматор, пройдя в общем случае через какие-то промежуточные звенья (обозначим их эквивалентную передачу как
, в конце концов «приходит» в некоторый сумматор, пройдя в общем случае через какие-то промежуточные звенья (обозначим их эквивалентную передачу как  ). Но поскольку переменная у есть сумма переменных
). Но поскольку переменная у есть сумма переменных 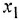 и
и 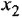 , то, согласно принципу суперпозиции, можно считать, что каждая из этих переменных, пройдя через эквивалентное звено с передачей
, то, согласно принципу суперпозиции, можно считать, что каждая из этих переменных, пройдя через эквивалентное звено с передачей  , «приходит» в указанный сумматор. Следовательно, в преобразованной схеме нужно вместо отвода по у просто сделать два отвода — по переменным
, «приходит» в указанный сумматор. Следовательно, в преобразованной схеме нужно вместо отвода по у просто сделать два отвода — по переменным 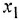 и
и 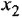 — и провести эти новые связи в упомянутый сумматор, вставив в каждую из них звено с передачей
— и провести эти новые связи в упомянутый сумматор, вставив в каждую из них звено с передачей  . Этот прием подробно разъясняется в задаче 3.2.
. Этот прием подробно разъясняется в задаче 3.2.
Последнюю группу в табл. 3.1 составляют операции 8-10, которые можно назвать вспомогательными. Справедливость операций 8^и 10 очевидна, при этом заметим, что величины  , по существу, представляют собой одну и ту же переменную. Операция 9 по сути является графической интерпретацией свойства дистрибутивности сложения и умножения:
, по существу, представляют собой одну и ту же переменную. Операция 9 по сути является графической интерпретацией свойства дистрибутивности сложения и умножения:
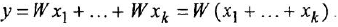
В чем польза трех последних операций? Рассмотрим более внимательно операцию 9. Ее смысл заключается в возможности выноса общей передачи из нескольких суммирующихся каналов (имеются в виду линии, входящие в сумматор) в канон за сумматором. Очевидно, что это упрощает схему, особенно если число входящих в сумматор каналов велико. Однако, возможно, еще большая польза этой операции состоит в другом. Если, наоборот, эквивалентную схему принять за исходную, то операция 9 трактуется по-другому: передачу звена, расположенного за сумматором, можно поместить в каждый из суммирующихся каналов Это позволяет иначе взглятть на уже рассмотренную операцию 5 перестановки звена и сумматора (в варианте а). Очевидно, что она полностью совпадает с операцией 9, и, следовательно, если в схеме последовательно расположены сумматор и звено, то операцию 5 над ними можно трактовать уже не как взаимную перестановку, а как «ввод» звена в каждый из каналов — это правило легко запоминается учащимися
Аналогично обстоит дело с операцией 10. Если рассматривать приведенную в табл 3.1 пару схем слева направо, то правило звучит так: общую передачу всех связей, отходящих от точки разветвления, можно внести в связь перед этой точкой. Рассматривая эти же схемы в обратном порядке, можно прийти к следующему выводу: передачу звена, стоящего до точки разветвления, можно внести во все отходящие от этой точки связи. Знание этого правила позволяет, не задумываясь, выполнять операцию 6 перестановки звена и отвода (вариант а).
Операция 8 удобна тем, что позволяет искусственно создать в какой-либо связи звено с требуемой передачей — чтобы получить возможность вынести эту передачу из двух или более связей, т. е. выполнить операцию 9 или 10.
В заключение укажем на еще одно правило, которое бывает полезно при упрощении схем и выполнении других процедур их преобразования к заданному виду: уравнения, описывающие систему, не изменятся, если в структурной схеме у всех переменных, связанных с каким-либо сумматором, изменить знак на противоположный. Другими словами, можно изменить знаки у всех стрелок, входящих в сумматор, и поставить звено с передачей -1 в связь, выходящую из сумматора. Эта операция, по существу, является частным случаем операции 9 при  =-1.
=-1.
Знание правил структурных преобразований не дает, однако, ответа на вопрос, в каком порядке следует преобразовывать схему к типовому виду при решении конкретной задачи. Ответить определенно на него невозможно, поскольку задачи такого типа решаются, как правило, не единственным образом То, какие именно операции и в какой последовательности будут использованы, зависит как от многообразия вариантов решения, так и от опыта и, не в последнюю очередь, от личных предпочтений специалиста, выполняющего структурные преобразования. Нет нужды доказывать, что при наличии нескольких возможных алгоритмов решения задачи необходимо выбирать наиболее простой.
Несмотря на сказанное, некоторые общие рекомендации относительно алгоритма преобразования структурных схем все же можно дать. Прежде всего, необходимо каждое имеющееся в схеме типовое соединение звеньев заменить эквивалентным звеном, снабдив его обозначением соответствующей передаточной функции. Затем целесообразно выполнить операции перестановки звена и отвода или/и звена и сумматора (как уже указывалось, операцию перестановки сумматора и отвода без необходимости применять не следует), чтобы в результате образовались новые типовые соединения. Их нужно опять заменить эквивалентными звеньями и т. д. Рекомендуется после каждого этапа преобразований перерисовывать схему с новыми обозначениями.
Возможно эта страница вам будет полезна:
Операция инверсии
Полезным видом структурно-топологических преобразований является операция инверсии. Ее применяют
- а) для приведения структурной схемы к виду, удобному для цифрового и аналогового моделирования, путем устранения дифференцирующих звеньев,
- б) при анализе установившихся режимов для устранения некорректности типа деления на ноль (в передаточных функциях вида /р при р-> 0),
- в) для получения из схемы общего вида некоторых частных структурных схем путем предельного перехода при стремлении какого-либо параметра к бесконечности или к нулю.
Различают инверсию пути и контура. Главной чертой этих операций является изменение направления пути (контура) на противоположное
Рассмотрим операцию инверсии пути. Чтобы излагаемое далее правило было более понятно, проиллюстрируем его примером. Пусть требуется про-инвертировать путь между переменными 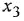 и
и 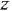 в схеме на рис. 1.1,6. Этот путь включает в себя звено с передачей
в схеме на рис. 1.1,6. Этот путь включает в себя звено с передачей 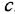 , сумматор (перед ним необходимо мысленно поместить звено с передачей -1, учитывающее знак при суммировании) и, разумеется, все линии связи, в том числе стрелки, соответствующие переменным
, сумматор (перед ним необходимо мысленно поместить звено с передачей -1, учитывающее знак при суммировании) и, разумеется, все линии связи, в том числе стрелки, соответствующие переменным 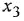 и
и 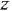 . Вообще говоря, при решении задач, по крайней мере на этапе освоения данной операции, полезно каким-либо образом выделять инвертируемый путь. Это помогает избежать распространенных ошибок, когда к рассматриваемому пути по невнимательности относят элементы, на самом деле ему не принадлежащие, и, наоборот, упускают из виду неотъемлемые элементы данного пути. В связи с этим обращаем особое внимание на то, что отводы, отходящие от пути в точках разветвления, а также связи (стрелки), подходящие к пути в сумматорах, не являются элементами этого пути
. Вообще говоря, при решении задач, по крайней мере на этапе освоения данной операции, полезно каким-либо образом выделять инвертируемый путь. Это помогает избежать распространенных ошибок, когда к рассматриваемому пути по невнимательности относят элементы, на самом деле ему не принадлежащие, и, наоборот, упускают из виду неотъемлемые элементы данного пути. В связи с этим обращаем особое внимание на то, что отводы, отходящие от пути в точках разветвления, а также связи (стрелки), подходящие к пути в сумматорах, не являются элементами этого пути
Для рассматриваемого примера результат инверсии показан па рис 3.2, а. Сравнение этой схемы с исходной позволяет лучше усвоить излагаемое далее правило инверсии пути.
Чтобы проинвертировать некоторый путь между двумя переменными структурной схемы, необходимо изменить:
1) направление пути на противоположное;
2) передачи всех звеньев этого пути — на обратные;
3) знаки всех воздействий, подходящих к данному пути, — на противоположные.
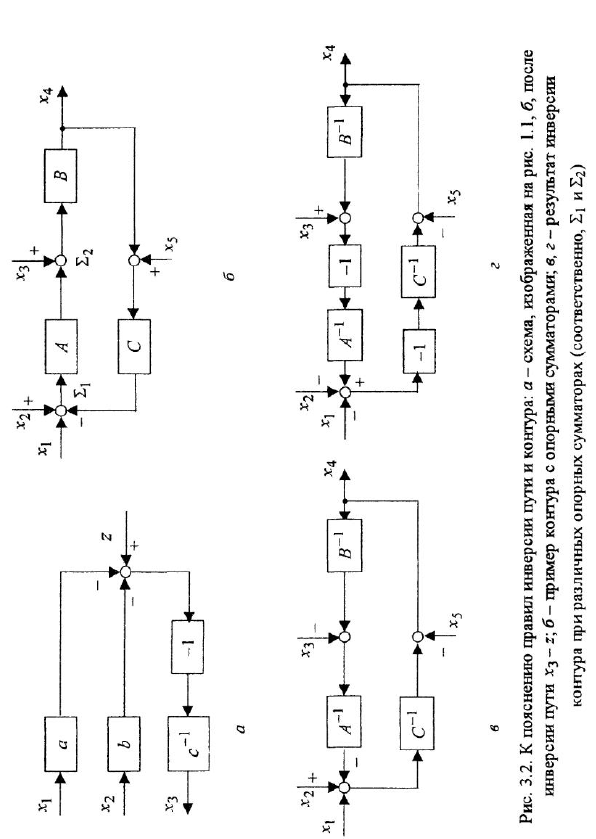
Это правило можно рассматривать как алгоритм выполнения данной операции. На первом этапе следует перерисовать схему, изменив направления всех стрелок рассматриваемого пути (и только его!) и пока воздержавшись от записи передач внутри графических изображений звеньев. Далее необходимо записать эти передачи как обратные исходным, причем, если на инвертируемом пути встречаются сумматор и принадлежащая этому же пути стрелка, входящая в сумматор со знаком «минус», то последний следует интерпретировать как звено с передачей -1. В заключение меняют на противоположные знаки, с которыми к рассматриваемому пути подходят (в сумматорах) внешние воздействия, в том числе воздействия от остальной части схемы.
Заметим, что с математической точки зрения инверсия пути соответствует разрешению алгебраического уравнения, описывающего данный путь, относительно новой переменной.
Так, в рассмотренном примере исходной и преобразованной схемам соответствуют следующие два варианта одного и того же уравнения:
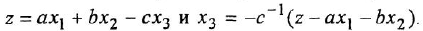
Инверсия контура в практическом плане является наиболее важной из двух рассматриваемых здесь операций. Именно она является инструментом решения задач, перечисленных в начале раздела.
Чтобы проинвертировать некоторый контур структурной схемы, необходимо:
1) любой сумматор этого контура принять за опорный (обозначим его 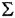 ) и любую переменную контура — за выходную (обозначим ее у), тогда путь от
) и любую переменную контура — за выходную (обозначим ее у), тогда путь от 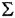 к
к 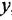 будем считать прямой связью, а путь от
будем считать прямой связью, а путь от 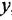 к
к 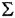 — обратной связью;
— обратной связью;
2) направление контура изменить на противоположное; в результате этого прямая связь становится обратной, а обратная — прямой;
3) передачи всех звеньев контура изменить на обратные (как-уже пояснялось, знаки «минус» при входящих в сумматоры стрелках данного контура тоже необходимо рассматривать как звенья этого контура, имеющие передачу -1);
4) знаки прямой и обратной связей изменить на противоположные, вставив звено с передачей -1 непосредственно у опорного сумматора;
5) знаки всех воздействий, подходящих к данному контуру извне, за исключением воздействий, приложенных к опорному сумматору, заменить на противоположные.
Применение этого правила проиллюстрируем на примере контура, изображенного на рис. 3.2, б Рассмотрим два варианта назначения опорного сумматора (приводящие, таким образом, к двум вариантам решения) — они обозначены на схеме как 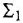 и
и 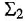 . Выходной переменной все время будем считать
. Выходной переменной все время будем считать 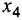 . Сначала изменим на противоположное направление всех стрелок в контуре (обращаем внимание на то, что одна из стрелок, изображающих переменную
. Сначала изменим на противоположное направление всех стрелок в контуре (обращаем внимание на то, что одна из стрелок, изображающих переменную 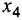 , а именно — стрелка, направленная вправо от точки разветвления, не изменила своего направления, поскольку не принадлежит этому кон-туру). Далее передачи
, а именно — стрелка, направленная вправо от точки разветвления, не изменила своего направления, поскольку не принадлежит этому кон-туру). Далее передачи 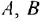 и
и  меняем на обратные. Минус у стрелки, входящей в сумматор
меняем на обратные. Минус у стрелки, входящей в сумматор 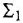 , будем считать звеном с передачей -1, но, как увидим позднее, в зависимости от варианта выбора опорного сумматора это звено будет либо изображено, либо нет.
, будем считать звеном с передачей -1, но, как увидим позднее, в зависимости от варианта выбора опорного сумматора это звено будет либо изображено, либо нет.
Пусть опорным является сумматор 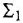 . Чтобы изменить, согласно 4-му шагу алгоритма, знак прямой связи (она теперь становится обратной), необходимо на схеме рис. 3.2, в вставить звено с передачей -1 в эту связь непосредственно справа от опорного сумматора. Вместо этого выполним эквивалентное действие — поставим знак «минус» у стрелки, входящей в этот сумматор справа. Нужно также изменить и знак обратной связи (становящейся, напротив, прямой), поэтому на схеме рис. 3.2, в на выходе опорного сумматора, где мыслилось звено с передачей -1, это звено теперь не изображаем В заключение меняем знаки, с которыми воздействия
. Чтобы изменить, согласно 4-му шагу алгоритма, знак прямой связи (она теперь становится обратной), необходимо на схеме рис. 3.2, в вставить звено с передачей -1 в эту связь непосредственно справа от опорного сумматора. Вместо этого выполним эквивалентное действие — поставим знак «минус» у стрелки, входящей в этот сумматор справа. Нужно также изменить и знак обратной связи (становящейся, напротив, прямой), поэтому на схеме рис. 3.2, в на выходе опорного сумматора, где мыслилось звено с передачей -1, это звено теперь не изображаем В заключение меняем знаки, с которыми воздействия 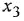 и
и 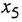 подходят к данному контуру; при воздействиях
подходят к данному контуру; при воздействиях 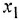 и
и 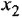 знаки сохраняются, так как они приложены в опорном сумматоре.
знаки сохраняются, так как они приложены в опорном сумматоре.
Теперь рассмотрим вариант с опорным сумматором 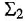 . Для изменения знака прямой связи (превращающейся на рис 3.2, г в обратную) ставим справа от этого сумматора знак «минус» при входящей стрелке. А для изменения знака обратной связи звено с передачей -1 помещаем на выход опорного сумматора У воздействий
. Для изменения знака прямой связи (превращающейся на рис 3.2, г в обратную) ставим справа от этого сумматора знак «минус» при входящей стрелке. А для изменения знака обратной связи звено с передачей -1 помещаем на выход опорного сумматора У воздействий 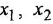 и
и 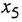 меняем знак. Напротив, знак при переменной
меняем знак. Напротив, знак при переменной 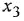 , как приложенной к опорному сумматору, сохраняем прежним
, как приложенной к опорному сумматору, сохраняем прежним
Хотя выбор различных опорных сумматоров привел к различным структурным схемам, эти схемы легко получаются одна из другой изменением знаков всех переменных в сумматорах 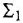 и
и 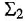 . Заметим также, что все переменные системы после инверсии сохранили свои позиции на схеме.
. Заметим также, что все переменные системы после инверсии сохранили свои позиции на схеме.
Если требуется привести структурную схему к виду, удобному для моделирования, путем устранения имеющихся в ней дифференцирующих звеньев, то эту задачу можно решить с помощью операции инверсии контура в том случае, если инвертируемый контур не содержит интегрирующих звеньев. В противном случае при замене передач звеньев кон тура на обратные интегрирующие звенья превратятся в дифференцирующие. В такой ситуации делу могут помочь структурные преобразования, а в сложных случаях — применение методов пространства состояний (канонических форм, которые всегда приводят к структурным схемам без дифференциаторов [3]).
Пример №3.1.
По структурной схеме, изображенной на рис 3.1, а, определить передаточную функцию, связывающую переменные 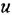 и
и 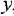 , с помощью структурных преобразований: а) путем переноса отвода «*» через звено с передачей
, с помощью структурных преобразований: а) путем переноса отвода «*» через звено с передачей  ; б) с использованием перестановки сумматора
; б) с использованием перестановки сумматора 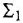 и звена с передачей
и звена с передачей 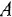 .
.
Решение:
На рис. 3.1,6 показан результат решения задачи первым способом. Чтобы получить его, необходимо сначала перерисовать без каких-либо изменений ту часть схемы, которая не подвергается операции преобразования. В данном случае это вся схема за исключением отвода «». Специально обращаем внимание на то, что звено с передачей  никуда не «исчезнет» из-за того, что через него будет перенесен отвод; точно так же отвод этот, откуда бы он ни начинался, должен закончиться в сумматоре
никуда не «исчезнет» из-за того, что через него будет перенесен отвод; точно так же отвод этот, откуда бы он ни начинался, должен закончиться в сумматоре 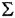 , который, таким образом, тоже остается на прежнем месте. Итак, положения начала и конца связи «*» известны Чтобы определить ее передачу, рассуждаем следующим образом: указанный отвод отождествляется с переменной
, который, таким образом, тоже остается на прежнем месте. Итак, положения начала и конца связи «*» известны Чтобы определить ее передачу, рассуждаем следующим образом: указанный отвод отождествляется с переменной 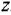 , но в новой схеме он берется по переменной
, но в новой схеме он берется по переменной  ; а поскольку
; а поскольку  , то в рассматриваемую связь необходимо вставить звено с передачей
, то в рассматриваемую связь необходимо вставить звено с передачей  . Возможно, более простым может показаться другой способ рассуждений: согласно правилу выполнения операции 10 (см. табл 3.1), передачу
. Возможно, более простым может показаться другой способ рассуждений: согласно правилу выполнения операции 10 (см. табл 3.1), передачу  звена, стоящего до точки разветвления, можно перенести в обе связи, отходящие от этой точки Поскольку теперь схема содержит только типовые соединения звеньев — встречно-параллельное (дважды) и последовательное, — то по формулам (2.3) и (2.1) определяем искомую передаточную функцию:
звена, стоящего до точки разветвления, можно перенести в обе связи, отходящие от этой точки Поскольку теперь схема содержит только типовые соединения звеньев — встречно-параллельное (дважды) и последовательное, — то по формулам (2.3) и (2.1) определяем искомую передаточную функцию:
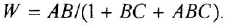
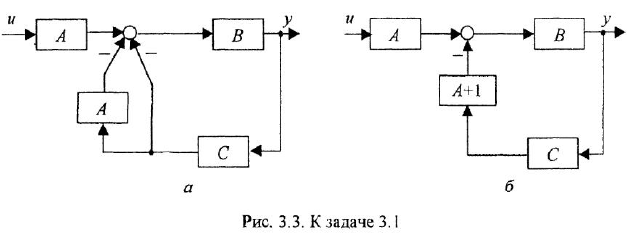
Для решения вторым способом удобно воспользоваться операцией 9 (см. табл. 3.1): убрав звено с передачей  из связи, выходящей из сумматора
из связи, выходящей из сумматора 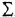 , вставить такое же звено в каждую из связей, входящих в этот сумматор. После этого оба сумматора рассматриваемой схемы оказываются рядом, и, следовательно, их можно объединить. В итоге получается схема, изображенная на рис. 3.3, а В принципе, никаких преобразований больше не требуется. Чтобы записать передаточную функцию, необходимо только понимать, что между точкой разветвления и сумматором образовалось согласно-параллельное соединение звеньев с передачами
, вставить такое же звено в каждую из связей, входящих в этот сумматор. После этого оба сумматора рассматриваемой схемы оказываются рядом, и, следовательно, их можно объединить. В итоге получается схема, изображенная на рис. 3.3, а В принципе, никаких преобразований больше не требуется. Чтобы записать передаточную функцию, необходимо только понимать, что между точкой разветвления и сумматором образовалось согласно-параллельное соединение звеньев с передачами  и 1, поэтому его можно заменить эквивалентным звеном с передачей
и 1, поэтому его можно заменить эквивалентным звеном с передачей  +1, при этом оба минуса можно заменить одним, как показано на рис 3.3, б. Передаточная функция, записанная по последней схеме, разумеется, совпадает с найденной ранее. Представляется, что решение первым способом является более простым.
+1, при этом оба минуса можно заменить одним, как показано на рис 3.3, б. Передаточная функция, записанная по последней схеме, разумеется, совпадает с найденной ранее. Представляется, что решение первым способом является более простым.
Пример №3.2.
По схеме, изображенной на рис. 2.2, г, определить передаточную функцию от и к у методом структурных преобразований
Решение:
Данная схема является примером случая, когда нельзя обойтись без операции перестановки сумматора и отвода Наиболее быстро задача решается взаимной перестановкой первого (слева) сумматора и отвода по переменной 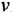 . Выполним эту операцию не по образцу из табл. 3.1, а рекомендованным при ее обсуждении более простым способом. Поскольку отвод по переменной
. Выполним эту операцию не по образцу из табл. 3.1, а рекомендованным при ее обсуждении более простым способом. Поскольку отвод по переменной 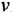 заканчивается в третьем сумматоре, а сама величина
заканчивается в третьем сумматоре, а сама величина 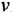 является разностью переменных
является разностью переменных 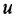 и
и 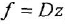 , то можно вместо отвода по
, то можно вместо отвода по 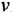 сделать отводы по переменным
сделать отводы по переменным 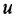 и
и 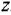 и провести их к тому же сумматору. Остается только определить передачи новых связей. В исходной схеме путь от
и провести их к тому же сумматору. Остается только определить передачи новых связей. В исходной схеме путь от 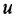 к
к 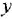 имеет передачу 1, а путь от
имеет передачу 1, а путь от 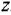 к
к 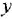 — передачу —
— передачу — 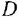 Поэтому первая из новых связей (по
Поэтому первая из новых связей (по 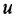 ) будет единичной, а во вторую (по
) будет единичной, а во вторую (по 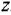 ) необходимо ввести звено с передачей —
) необходимо ввести звено с передачей —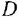 . Результат показан на рис 3 4, а. Звенья с передачами
. Результат показан на рис 3 4, а. Звенья с передачами  и —
и — 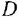 образуют параллельное соединение с эквивалентной передачей
образуют параллельное соединение с эквивалентной передачей  —
— 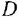 . Часть схемы, содержащая звенья с передачами
. Часть схемы, содержащая звенья с передачами 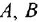 и
и 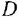 , еще не приведена к типовому виду (заметим, кстати, что структура этой части схемы, заключенной
, еще не приведена к типовому виду (заметим, кстати, что структура этой части схемы, заключенной
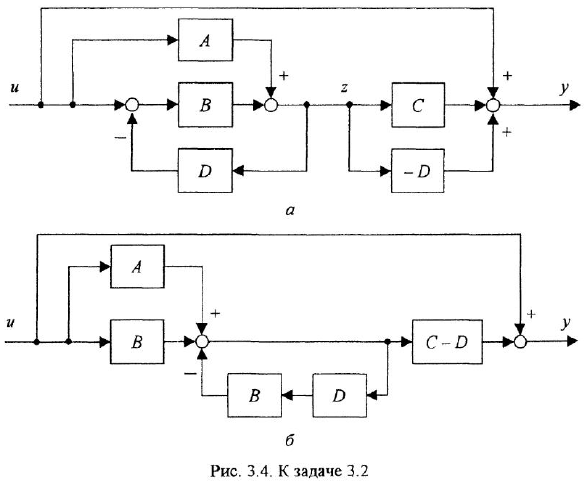
между переменными 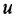 и
и 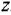 , характерна для многих задач на структурные преобразования). Поменяв местами первый сумматор и звено с передачей В и объединив затем оказавшиеся рядом сумматоры, приходим к структурной схеме, приведенной на рис. 3.4, б. Поскольку схема стала типовой (обращаем внимание на то, что в ней две связи имеют передачу 1), по формулам (2.1.)-(2.3) определяем передаточную функцию:
, характерна для многих задач на структурные преобразования). Поменяв местами первый сумматор и звено с передачей В и объединив затем оказавшиеся рядом сумматоры, приходим к структурной схеме, приведенной на рис. 3.4, б. Поскольку схема стала типовой (обращаем внимание на то, что в ней две связи имеют передачу 1), по формулам (2.1.)-(2.3) определяем передаточную функцию:
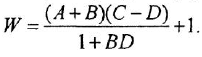
Это выражение после упрощения совпадает с найденным в задаче 2.3
Пример №3.3.
По структурным схемам, приведенным на рис. 2.2, а и в, определить методом структурных преобразований передаточные функции 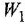 и
и 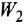 связывающие вход
связывающие вход 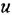 с выходами, соответственно,
с выходами, соответственно, 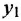 и
и 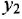 (сравните с задачей 2.2).
(сравните с задачей 2.2).
Решение:
Главную трудность при нахождении ПФ 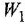 представляет наличие отвода «*» по переменной
представляет наличие отвода «*» по переменной 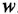 . Перенесем его через звено с передачей
. Перенесем его через звено с передачей 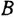 в точку разветвления связи по переменной
в точку разветвления связи по переменной 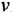 . Тогда между переменными
. Тогда между переменными 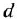 и
и 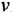 окажется заключено встречно-параллельное соединение звеньев с передачами
окажется заключено встречно-параллельное соединение звеньев с передачами 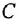 и
и 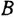 (обратная связь — отрицательная), передача которого равна, следовательно,
(обратная связь — отрицательная), передача которого равна, следовательно,
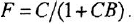
Одновременно сделаем перестановку крайнего левого сумматора и звена с передачей  , после чего объединим сумматоры. Итогом этих преобразований является схема, изображенная на рис 3 5, а. Предлагаем читателю завершить приведение ее к типовому виду самостоятельно. Для этого необходимо только перенести отвод, идущий из точки о на вход звена с передачей
, после чего объединим сумматоры. Итогом этих преобразований является схема, изображенная на рис 3 5, а. Предлагаем читателю завершить приведение ее к типовому виду самостоятельно. Для этого необходимо только перенести отвод, идущий из точки о на вход звена с передачей 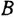 , через звено с передачей
, через звено с передачей 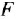 в точку
в точку 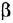 . В результате получается следующая структура: звено с единичной передачей охвачено отрицательной обратной связью с передачей
. В результате получается следующая структура: звено с единичной передачей охвачено отрицательной обратной связью с передачей  ; этот контур, в свою очередь, образует последовательное соединение со звеном
; этот контур, в свою очередь, образует последовательное соединение со звеном 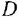 , охваченное далее положительной обратной связью с передачей
, охваченное далее положительной обратной связью с передачей 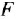 , наконец, это соединение включено последовательно со звеньями, имеющими передачи
, наконец, это соединение включено последовательно со звеньями, имеющими передачи  и
и 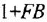 . С учетом сказанного, передаточная функция от
. С учетом сказанного, передаточная функция от 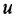 к
к 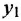 получается равной
получается равной
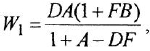
что после подстановки выражения для 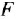 дает ответ, совпадающий с найденным в задаче 2.2.
дает ответ, совпадающий с найденным в задаче 2.2.
Преобразования схемы на рис. 2.2, в, необходимые для нахождения ПФ 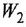 , частично совпадают с только что описанными, а именно: перестановка левого сумматора и звена с передачей
, частично совпадают с только что описанными, а именно: перестановка левого сумматора и звена с передачей  позволяет получить встречно-параллельное (с отрицательной обратной связью) соединение звеньев с передачами 1 и
позволяет получить встречно-параллельное (с отрицательной обратной связью) соединение звеньев с передачами 1 и  . Кроме этого, надо перенести отвод, идущий к звену с передачей
. Кроме этого, надо перенести отвод, идущий к звену с передачей 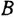 , на вход звена с передачей
, на вход звена с передачей 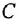 . По преобразованной схеме (рис. 3.5, б) записываем:
. По преобразованной схеме (рис. 3.5, б) записываем:
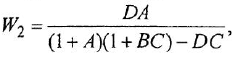
что совпадает с ПФ в задаче 2.2.
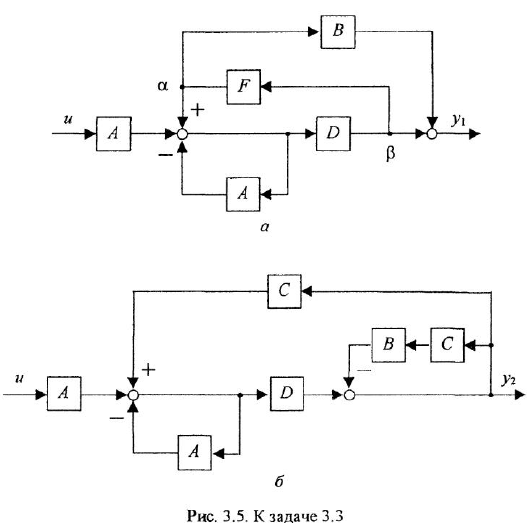
Пример №3.4.
Выполнить инверсию контура 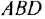 на рис. 3.6, а.
на рис. 3.6, а.
Решение:
Примем левый сумматор за опорный, а переменную 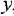 — за выходную. Схема с проинвертированным контуром приведена на рис. 3.6, б. При желании ее можно изобразить более привычным образом, проведя горизонтально единичную прямую связь вправо от опорного сумматора; звенья же с передачами
— за выходную. Схема с проинвертированным контуром приведена на рис. 3.6, б. При желании ее можно изобразить более привычным образом, проведя горизонтально единичную прямую связь вправо от опорного сумматора; звенья же с передачами 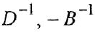 (охвачено местной отрицательной обратной связью с передачей
(охвачено местной отрицательной обратной связью с передачей 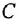 ) и
) и 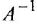 войдут в обратную связь. Поясним основные этапы выполнения инверсии. При замене передач всех звеньев контура на обратные учитываем минус при связи, выходящей из звена с передачей
войдут в обратную связь. Поясним основные этапы выполнения инверсии. При замене передач всех звеньев контура на обратные учитываем минус при связи, выходящей из звена с передачей 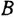 . Что касается минуса при единичной обратной связи, то при инверсии он исчезает, поскольку знак обратной связи должен быть заменен на противоположный. А для замены знака прямой связи ставим минус при стрелке, выходящей из звена с передачей
. Что касается минуса при единичной обратной связи, то при инверсии он исчезает, поскольку знак обратной связи должен быть заменен на противоположный. А для замены знака прямой связи ставим минус при стрелке, выходящей из звена с передачей  . Знак при внешнем воздействии и не меняем, поскольку оно приложено в опорном сумматоре. Выходная переменная звена с передачей
. Знак при внешнем воздействии и не меняем, поскольку оно приложено в опорном сумматоре. Выходная переменная звена с передачей 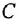 является для данного контура вторым внешним воздействием, и знак, с которым оно приложено ко второму, не опорному, сумматору, изменен на противоположный
является для данного контура вторым внешним воздействием, и знак, с которым оно приложено ко второму, не опорному, сумматору, изменен на противоположный
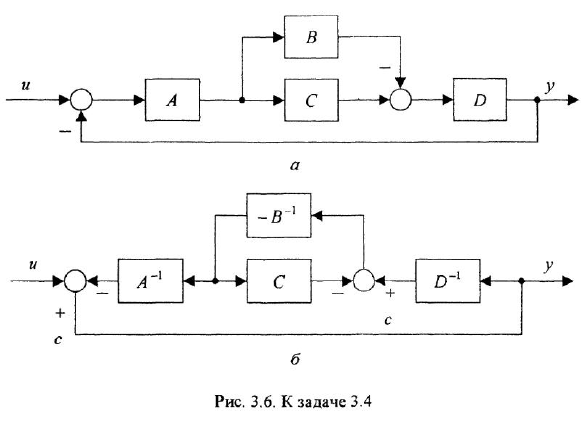
Полезно убедиться, что передаточная функция системы после инверсии не изменилась.
Пример №3.5.
В структурной схеме, изображенной на рис. 2.1, в, с помощью эквивалентных структурных преобразований сделать обратную связь единичной.
Решение:
Задача предназначена для самостоятельного решения Рекомендуется использовать операции 8 и 10 из табл. 3.1.
Пример №3.6.
На рис. 3.7, а показана упрошенная структурная схема системы автоматического регулирования скорости электродвигателя постоянного тока, соединенного с рабочим механизмом упругой механической связью, имеющей жесткость с. Требуется с помощью операции инверсии контура: а) получить частную схему для случая жесткой связи двигателя с механизмом 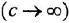 ; б) определить уравнение, связывающее установившуюся ошибку по скорости
; б) определить уравнение, связывающее установившуюся ошибку по скорости 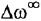 с постоянным моментом сопротивления
с постоянным моментом сопротивления 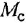 .
.
Пояснение Кроме названных, в схеме имеются следующие переменные: 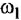 и
и 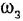 — угловые скорости двигателя и механизма;
— угловые скорости двигателя и механизма; 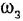 — задающее воздействие по скорости (здесь полагается постоянным);
— задающее воздействие по скорости (здесь полагается постоянным); 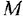 — электромагнитный момент двигателя;
— электромагнитный момент двигателя; 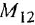 — момент сил упругости Параметры системы:
— момент сил упругости Параметры системы: 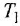 и
и 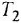 — «механические» постоянные времени двигателя и механизма;
— «механические» постоянные времени двигателя и механизма; 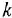 — коэффициент, упрощенно описывающий регулятор скорости и внутренний контур регулирования тока двигателя.
— коэффициент, упрощенно описывающий регулятор скорости и внутренний контур регулирования тока двигателя.
Решение:
Проинвертируем контур, содержащий звенья с передачами 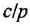 и
и 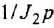 , приняв левый сумматор за опорный. С этой целью указанные передачи превратим в обратные, знак, с которым переменная
, приняв левый сумматор за опорный. С этой целью указанные передачи превратим в обратные, знак, с которым переменная 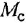 входит в сумматор, изменим на «плюс» и с обеих сторон опорного сумматора (в начале прямой связи и в конце обратной связи) также поменяем знаки. После этого учтем условие
входит в сумматор, изменим на «плюс» и с обеих сторон опорного сумматора (в начале прямой связи и в конце обратной связи) также поменяем знаки. После этого учтем условие 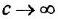 да: передача
да: передача 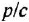 станет нулевой, что эквивалентно разрыву данной связи, а следовательно, перестает существовать сумматор, принятый за опорный. Результатом описанных действий является схема, показанная на рис. 3.7, б. Обратим внимание читателя на то, что, согласно схеме, угловые скорости
станет нулевой, что эквивалентно разрыву данной связи, а следовательно, перестает существовать сумматор, принятый за опорный. Результатом описанных действий является схема, показанная на рис. 3.7, б. Обратим внимание читателя на то, что, согласно схеме, угловые скорости 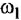 и
и 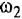 двух вращающихся масс теперь совпадают, а это соответствует абсолютно жесткой связи между этими массами. Чтобы придать структурной схеме окончательный вид, объединим два правых сумматора, приняв во внимание, что соединяющая их связь имеет передачу -1. В результате внешнее воздействие
двух вращающихся масс теперь совпадают, а это соответствует абсолютно жесткой связи между этими массами. Чтобы придать структурной схеме окончательный вид, объединим два правых сумматора, приняв во внимание, что соединяющая их связь имеет передачу -1. В результате внешнее воздействие 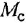 оказывается приложенным со знаком «минус», а звенья с передачами
оказывается приложенным со знаком «минус», а звенья с передачами 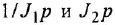 образуют соединение с отрица-
образуют соединение с отрица-
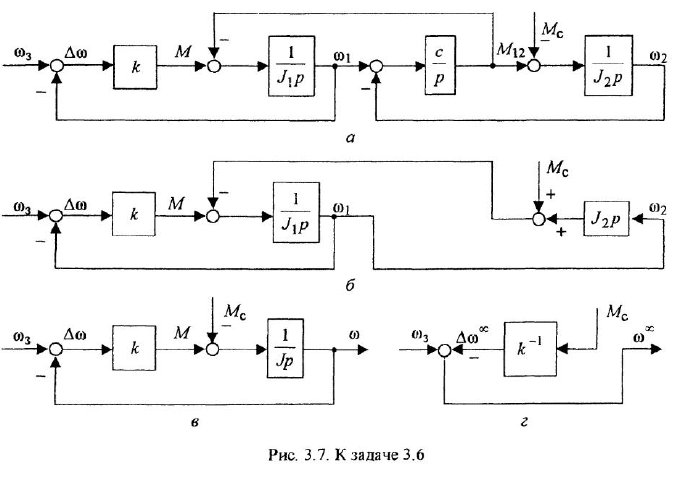
тельной обратной связью, передача которого есть 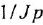 , где
, где 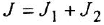 -суммарный момент инерции двигателя и механизма (рис. 3.7, в). Это полностью соответствует физике явления, поскольку в случае абсолютно жесткой связи двигателя и механизма последние должны рассматриваться как одно целое.
-суммарный момент инерции двигателя и механизма (рис. 3.7, в). Это полностью соответствует физике явления, поскольку в случае абсолютно жесткой связи двигателя и механизма последние должны рассматриваться как одно целое.
Чтобы решить вторую часть задачи, выполним инверсию полученного контура (ввиду простоты эту операцию не поясняем). Для перехода к схеме установившегося режима достаточно заменить обозначения переменных на установившиеся значения и принять 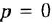 , в результате чего передача
, в результате чего передача 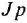 становится нулевой и данная связь разрывается (рис. 3.7, г). По структурной схеме записываем искомое уравнение:
становится нулевой и данная связь разрывается (рис. 3.7, г). По структурной схеме записываем искомое уравнение:
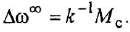
Пример №3.7.
Структурную схему, изображенную на рис. 3.8, привести к виду, удобному для моделирования, устранив дифференцирующее звено.
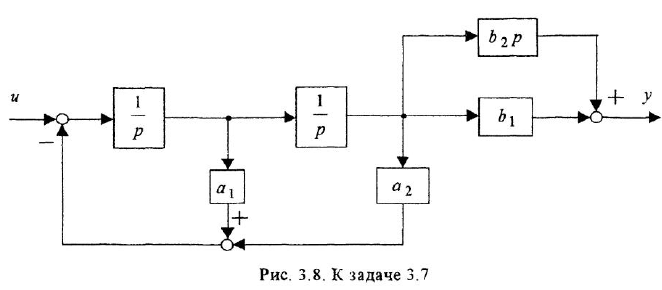
Решение:
Задача решается путем переноса отвода, идущего на вход звена с передачей 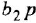 , через интегрирующее звено.
, через интегрирующее звено.
Построение и анализ логарифмических частотных характеристик. Логарифмические частотные характеристики
Математический аппарат частотных характеристик, в особенности — логарифмических частотных характеристик, является весьма эффективным инструментом анализа и синтеза автоматических систем, даже несмотря на наличие мощных методов так называемой «современной теории управления» (методов пространства состояний, вход-выходного подхода и др.) и огромные возможности вычислительной техники. Частотные характеристики благодаря сочетанию строгости, простоты, наглядности и информативности не только являются удобным средством в руках инженера и исследователя, но и, после приобретения достаточного опыта, вырабатывают у специалиста интуицию, необходимую для приближенной оценки динамических свойств систем и поиска методов их улучшения.
Как известно, частотная передаточная функция (ЧПФ) 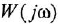 получается из передаточной функции
получается из передаточной функции 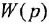 подстановкой р = уш. Годограф функции
подстановкой р = уш. Годограф функции 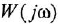 при изменении аргумента
при изменении аргумента 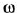 от 0 до
от 0 до 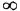 называется амплитудно-фазовой частотной характеристикой (АФХ). Если ЧПФ представлена в показательной форме
называется амплитудно-фазовой частотной характеристикой (АФХ). Если ЧПФ представлена в показательной форме
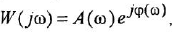
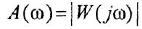
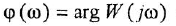
называются, соответственно, амплитудной (АЧХ) и фазовой (ФЧХ) частотными характеристиками. Если же ЧПФ представлена в алгебраической форме
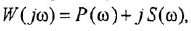
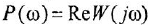
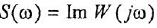
называются, соответственно, вещественной (ВЧХ) и мнимой (МЧХ) частотными характеристиками.
Чтобы построить АФХ, необходимо
1) записать аналитические выражения для 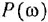 и
и 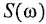 ;
;
2) задавая некоторые характерные значения 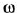 , определить соответствующие им значения
, определить соответствующие им значения 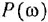 и
и 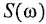 (кроме значений 0 и
(кроме значений 0 и 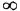 , необходимо выбирать такие значения частоты, которые позволяют выявить перемену знаков в выражениях
, необходимо выбирать такие значения частоты, которые позволяют выявить перемену знаков в выражениях 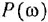 и
и 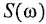 , т. е переход АФХ в новый квадрант комплексной плоскости; собственно говоря, в этих промежуточных точках нет нужды вычислять значения
, т. е переход АФХ в новый квадрант комплексной плоскости; собственно говоря, в этих промежуточных точках нет нужды вычислять значения 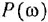 и
и 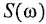 , достаточно определить их знак); свести результаты в таблицу;
, достаточно определить их знак); свести результаты в таблицу;
3) задав на комплексной плоскости систему координатных осей 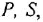 по данным таблицы построить АФХ; отметить на ней направление возрастания частоты.
по данным таблицы построить АФХ; отметить на ней направление возрастания частоты.
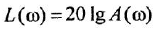
называется логарифмической амплитудной частотной характеристикой (ЛAX) и графически изображается как функция частоты 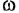 [рад/с], откладываемой по оси абсцисс в логарифмическом масштабе, т. е., фактически, как функция безразмерной переменной
[рад/с], откладываемой по оси абсцисс в логарифмическом масштабе, т. е., фактически, как функция безразмерной переменной 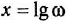 , откладываемой в равномерном масштабе. Значения
, откладываемой в равномерном масштабе. Значения 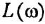 измеряются в децибелах (дБ) и откладываются по оси ординат в равномерном масштабе. ФЧХ, изображаемая как функция частоты, откладываемой в логарифмическом масштабе, называется логарифмической фазовой частотной характеристикой (ЛФХ). Ее значения измеряются в градусах или радианах. ЛАХ и ЛФХ называются логарифмическими частотными характеристиками (ЛЧХ).
измеряются в децибелах (дБ) и откладываются по оси ординат в равномерном масштабе. ФЧХ, изображаемая как функция частоты, откладываемой в логарифмическом масштабе, называется логарифмической фазовой частотной характеристикой (ЛФХ). Ее значения измеряются в градусах или радианах. ЛАХ и ЛФХ называются логарифмическими частотными характеристиками (ЛЧХ).
Любой интервал частот 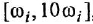 , граничные частоты которого различаются в 10 раз, называется декадой. Ширина декады
, граничные частоты которого различаются в 10 раз, называется декадой. Ширина декады
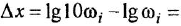
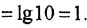
На рис. 4.1 изображена система координат, которой пользуются при построении ЛЧХ. На ней показан пример оцифровки осей, причем для оси абсцисс даны два варианта оцифровки, используемые в литературе: снизу от оси — для  в радианах в секунду (сокращенно
в радианах в секунду (сокращенно  ) и сверху — для
) и сверху — для 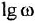 (это безразмерная величина, иногда условно считают, что она измеряется в декадах) Как правило, мы будем давать оцифровку для самой частоты. Ось ординат чаще всего проводят через точку, соответствующую частоте 1 рад/с, хотя это и не обязательно; иногда мы при изображении ЛЧХ вообще не будем проводить ось ординат.
(это безразмерная величина, иногда условно считают, что она измеряется в декадах) Как правило, мы будем давать оцифровку для самой частоты. Ось ординат чаще всего проводят через точку, соответствующую частоте 1 рад/с, хотя это и не обязательно; иногда мы при изображении ЛЧХ вообще не будем проводить ось ординат.
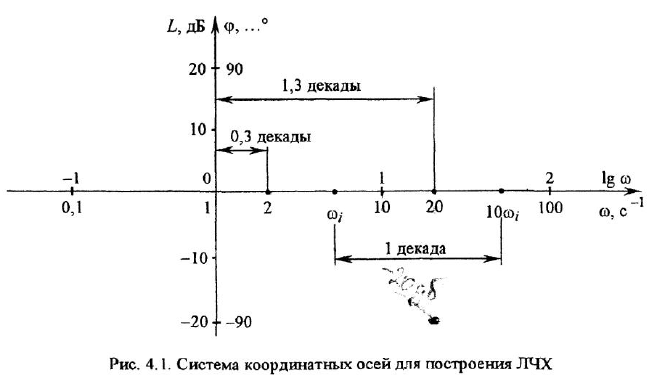
Необходимо уметь правильно отмечать на оси абсцисс точки, соответствующие конкретным значениям частоты. Пусть, например, требуется нанести на ось частот две точки: 2  и 20
и 20  . Логарифмируя эти числа, получаем 0,3 и 1,3. Это означает, что указанные точки отстоят от точки с оцифровкой 1
. Логарифмируя эти числа, получаем 0,3 и 1,3. Это означает, что указанные точки отстоят от точки с оцифровкой 1  (или 0 для
(или 0 для 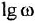 ) на расстояние, соответственно, в 0,3 и 1,3 декады (см рис. 4.1). Однако удобнее координаты второй точки находить иначе. Поскольку точка 20
) на расстояние, соответственно, в 0,3 и 1,3 декады (см рис. 4.1). Однако удобнее координаты второй точки находить иначе. Поскольку точка 20  занимает в пределах второй (если вести отсчет от точки 1
занимает в пределах второй (если вести отсчет от точки 1  ) декады точно такую же позицию, что и точка 2
) декады точно такую же позицию, что и точка 2  в пределах первой декады, то можно брать логарифм не от 20, а от 2, после чего откладывать отрезок длиной 0,3 декады уже от точки 10
в пределах первой декады, то можно брать логарифм не от 20, а от 2, после чего откладывать отрезок длиной 0,3 декады уже от точки 10  .
.
Также необходимо уметь строить в принятом масштабе наклонные участки асимптотических ЛАХ, т е. отрезки прямых, имеющих стандартные коэффициенты наклона Например, чтобы через данную точку провести прямую, имеющую коэффициент наклона -20 дБ/дек, следует найти вторую точку, отстоящую от заданной на 1 декаду вправо и на 20 дБ вниз (либо, наоборот, на 1 декаду влево и на 20 дБ вверх), после чего соединить обе точки отрезком прямой. Коэффициенты наклона 0, ±20 дБ/дек, ±40 дБ/дек… сокращенно обозначают 0, ±1, ±2 . ..
При изучении теории автоматического управления обязательным является знание логарифмических частотных характеристик типовых звеньев САУ, перечисленных в 1.1. Этот материал можно найти в любом учебнике по теории автоматического управления Здесь мы, не приводя графиков ЛЧХ типовых звеньев, отметим их существенные особенности, знание которых облегчает усвоение этого материала.
Общей чертой трех типов звеньев — пропориионального с ПФ (1 5), интегрирующего и дифференцирующего (произвольного порядка), описываемых передаточными функциями (1.7) и (1.9), — является то, что для них как ЛАХ, так и ЛФХ представляют собой прямые При этом ЛАХ пропорционального звена — горизонтальная прямая с ординатой 20 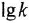 [дБ], а ЛФХ -прямая, совпадающая с осью частот. ЛАХ обобщенных интегрирующего и дифференцирующего звеньев — это прямые, имеющие коэффициенты наклона, соответственно, -20
[дБ], а ЛФХ -прямая, совпадающая с осью частот. ЛАХ обобщенных интегрирующего и дифференцирующего звеньев — это прямые, имеющие коэффициенты наклона, соответственно, -20 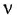 дБ/дек и 20
дБ/дек и 20 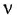 дБ/дек (сокращенно —
дБ/дек (сокращенно — 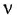 и
и 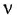 ), каждая из которых проходит через две характерные точки, описываемые формально одними и теми же выражениями для интегрирующего и дифференцирующего звеньев:
), каждая из которых проходит через две характерные точки, описываемые формально одними и теми же выражениями для интегрирующего и дифференцирующего звеньев:
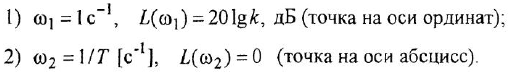
Каждая из этих точек соответствует своей, одной из двух форм записи передаточных функций (1.7) и (1.9) — с использованием коэффициента 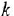 или постоянной времени
или постоянной времени 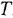 Если необходимо построить ЛАХ обобщенного интегрирующего или дифференцирующего звена, то следует определить координаты одной из указанных точек (ее выбирают в зависимости от того, к какой форме записи проще приводится заданная передаточная функция) и провести через нее прямую с нужным коэффициентом наклона. Что касается фазовых характеристик указанных звеньев, то это горизонтальные прямые с ординатой -90°
Если необходимо построить ЛАХ обобщенного интегрирующего или дифференцирующего звена, то следует определить координаты одной из указанных точек (ее выбирают в зависимости от того, к какой форме записи проще приводится заданная передаточная функция) и провести через нее прямую с нужным коэффициентом наклона. Что касается фазовых характеристик указанных звеньев, то это горизонтальные прямые с ординатой -90° 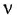 для интегрирующего звена и 90°
для интегрирующего звена и 90° 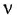 — для дифференцирующего Обращаем внимание на полное соответствие (точнее, пропорциональность) между коэффициентом наклона ЛAX и ординатой ЛФХ для всех трех рассмотренных звеньев.
— для дифференцирующего Обращаем внимание на полное соответствие (точнее, пропорциональность) между коэффициентом наклона ЛAX и ординатой ЛФХ для всех трех рассмотренных звеньев.
С остальными из перечисленных в 1.1 типовых звеньев дело обстоит сложнее. Для каждого из них различают два вида ЛАХ — точную, описываемую выражением (4.1), и асимптотическую. При компьютерном моделировании САУ с помощью специализированных математических пакетов, например Control System Toolbox системы Matlab, мы имеем возможность рассчитывать и видеть на экране график именно точной ЛАХ исследуемой системы. Однако в практике предварительного инженерного анализа систем и оценки вариантов закона управления обычно имеют дело с асимптотическими ЛАХ, широкое применение которых объясняется простотой их построения даже для весьма сложных систем и богатством заключенной в них информации.
Асимптотическая логарифмическая амплитудная частотная характеристика — это ломаная, отрезки которой являются асимптотами для точной ЛАХ. Для звеньев, описываемых передаточными функциями (1.10), (1.11), (1 13) и (1 14) (апериодическое звено 2-го порядка мы исключаем из рассмотрения, поскольку оно заменяется последовательным соединением двух апериодических звеньев 1-го порядка), асимптотическая ЛАХ состоит из двух асимптот: низкочастотной (к ней точная ЛАХ приближается при 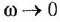 ) и высокочастотной (то же при
) и высокочастотной (то же при 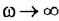 ). Соединение (сопряжение) двух асимптот происходит на частоте сопряжения, которая для всех рассматриваемых звеньев равна
). Соединение (сопряжение) двух асимптот происходит на частоте сопряжения, которая для всех рассматриваемых звеньев равна 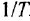 . Низкочастотной асимптотой для всех звеньев выступает горизонтальная прямая с ординатой 20
. Низкочастотной асимптотой для всех звеньев выступает горизонтальная прямая с ординатой 20 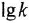 где
где 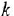 — коэффициент передачи звена, в общем случае присутствующий в числителе передаточных функций (1 10), (1 13) и (1.14) (для форсирующего звена
— коэффициент передачи звена, в общем случае присутствующий в числителе передаточных функций (1 10), (1 13) и (1.14) (для форсирующего звена 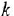 -1). Высокочастотная асимптота ЛАХ рассматриваемых звеньев представляет собой прямую, коэффициент наклона которой определяется тем, в числителе или в знаменателе передаточной функции находится полином от переменной
-1). Высокочастотная асимптота ЛАХ рассматриваемых звеньев представляет собой прямую, коэффициент наклона которой определяется тем, в числителе или в знаменателе передаточной функции находится полином от переменной 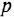 и какова степень этого полинома. У апериодического и форсирующего звеньев полиномы имеют первую степень, поэтому наклон асимптоты составляет 20 дБ/дек, для звеньев 2-го порядка — колебательного и консервативного — он равен 40 дБ/дек. В ПФ форсирующего звена полином находится в числителе, поэтому коэффициент наклона положителен; у остальных звеньев он отрицателен Заметим, что асимптотические ЛАХ колебательного и консервативного звеньев совпадают
и какова степень этого полинома. У апериодического и форсирующего звеньев полиномы имеют первую степень, поэтому наклон асимптоты составляет 20 дБ/дек, для звеньев 2-го порядка — колебательного и консервативного — он равен 40 дБ/дек. В ПФ форсирующего звена полином находится в числителе, поэтому коэффициент наклона положителен; у остальных звеньев он отрицателен Заметим, что асимптотические ЛАХ колебательного и консервативного звеньев совпадают
Фазовые характеристики трех звеньев графически представляют собой плавные кривые; они являются следующими функциями частоты: 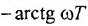 для апериодического звена,
для апериодического звена, 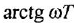 — для форсирующего и
— для форсирующего и 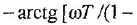
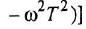 — для колебательного; ЛФХ консервативного звена — это разрывная по
— для колебательного; ЛФХ консервативного звена — это разрывная по 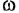 функция: 0 при
функция: 0 при 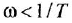 и 180° при
и 180° при 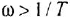 . Первые три ЛФХ имеют асимптоты: низкочастотная совпадает с осью абсцисс, высокочастотная является горизонтальной прямой с ординатой -180°, дня консервативного звена указанные асимптоты как раз и составляют точную ЛФХ. Для всех названных звеньев имеется полное соответствие между коэффициентами наклона асимптот ЛАХ и ординатами соответствующих асимптот ЛФХ. На частоте сопряжения первые три ЛФХ принимают среднее из асимптотических значений При эскизном построении ЛФХ апериодического, форсирующего и колебательного звеньев следует иметь в виду, что уже на расстоянии 1 декады влево и вправо от частоты сопряжения значения этих ЛФХ мало отличаются от асимптотических значений (например, для апериодического и форсирующего звеньев — на 5,7°).
. Первые три ЛФХ имеют асимптоты: низкочастотная совпадает с осью абсцисс, высокочастотная является горизонтальной прямой с ординатой -180°, дня консервативного звена указанные асимптоты как раз и составляют точную ЛФХ. Для всех названных звеньев имеется полное соответствие между коэффициентами наклона асимптот ЛАХ и ординатами соответствующих асимптот ЛФХ. На частоте сопряжения первые три ЛФХ принимают среднее из асимптотических значений При эскизном построении ЛФХ апериодического, форсирующего и колебательного звеньев следует иметь в виду, что уже на расстоянии 1 декады влево и вправо от частоты сопряжения значения этих ЛФХ мало отличаются от асимптотических значений (например, для апериодического и форсирующего звеньев — на 5,7°).
Заметам, что передаточные функции (1 10) и (1.11) апериодического и форсирующего звеньев являются взаимно обратными. Как следствие, их ЛЧХ симметричны друг другу относительно оси частот. То же самое можно сказать об ЛЧХ дифференцирующего и интегрирующего звеньев. В связи с этим набор «типовых» передаточных функций можно расширить, введя в него функции, обратные передаточным функциям (1 13) и (1 14) колебательного и консервативного звеньев. Соответственно, ЛЧХ таких звеньев будут зеркальным отображением ЛЧХ указанных звеньев. Такой расширенный набор позволяет почти любую передаточную функцию, не являющуюся типовой, представить в виде произведения типовых передаточных функций
В процессе анализа САУ часто возникает необходимость в построении ЛЧХ систем с довольно сложной структурой Будем предполагать, что структурная схема системы уже преобразована так, что содержит только типовые соединения Следовательно, возникает задача построения ЛЧХ типовых соединений звеньев по известным ЛЧХ самих этих звеньев
Рассмотрим последовательное соединение Основной результат состоит в том, что как ЛАХ, так и ЛФХ последовательного соединения звеньев могут быть получены суммированием соответствующих характеристик звеньев, образующих это соединение (уточним, что нас интересует, главным образом, графическое сложение частотных характеристик). Это позволяет сравнительно легко строить ЛЧХ длинных цепочек звеньев
На данный результат можно посмотреть и с другой стороны. Среди звеньев структурной схемы могут оказаться и такие, передаточные функции которых не совпадают ни с одной из рассмотренных ранее передаточных функций типовых звеньев. Однако в большинстве случаев такая «сложная» передаточная функция всегда может быть представлена в виде произведения типовых передаточных функций, а значит, ее можно рассматривать как ПФ последовательного соединения типовых звеньев, что позволяет строить ЛЧХ по такой ПФ суммированием «типовых» составляющих.
Несмотря на ясность изложенного подхода, необходимо сделать существенную оговорку. Основные преимущества метода ЛЧХ связаны, в первую очередь, с простотой ручного построения асимптотических ЛАХ типовых звеньев САУ и, как следствие, систем в целом (мы говорим именно о ручном построении как основе предварительных, прикидочных расчетов автоматических систем; впрочем, очень часто расчеты, выполненные с помощью ЛЧХ, являются весьма точными). В отличие от асимптотических ЛАХ, которые можно строить вполне точно с соблюдением необходимых масштабов, фазовые характеристики большинства даже типовых звеньев и тем более их последовательных соединений могут быть построены вручную только эскизно, поскольку описываются не очень простыми выражениями. Если бы оказалось, что для анализа каких-либо свойств системы необходимо точное построение ее ЛФХ, то это свело бы на нет преимущества использования аппарата асимптотических ЛАХ. К счастью, большинство систем, с которыми приходится иметь дело, относятся к так называемым минимально-фазовым системам, для которых существует однозначная связь между амплитудной и фазовой частотными характеристиками и, следовательно, можно обойтись построением только ЛАХ — если, конечно, имеется возможность на любом этапе расчета восстановить (в случае необходимости) ЛФХ по имеющейся ЛАХ или хотя бы оценить значение фазы в любой точке ЛАХ (подробно об этом говорится в 4 2).
Таким образом, наибольшее значение для практики анапиза и синтеза автоматических систем имеет построение асимптотических ЛАХ типовых соединений звеньев. Для последовательного соединения или, что равнозначно, для передаточной функции сложного вида результирующая ЛАХ может быть найдена, как уже было сказано, простым суммированием составляющих, соответствующих передаточным функциям отдельных звеньев или сомножителям сложной передаточной функции. Однако на практике этот способ применяется редко. Более эффективной является специальная методика, позволяющая строить результирующую ЛАХ по передаточной функции сложного вида без предварительного изображения отдельных составляющих. Методика базируется том факте, что ЛАХ пропорционального, интегрирующего и дифференцирующего звеньев являются бесконечными прямыми и, следовательно, вносят свой вклад в результирующую ЛАХ во всем диапазоне частот, в то время как влияние асимптотических ЛАХ звеньев других типов начинается только с соответствующей частоты сопряжения (если рассматривать весь частотный диапазон слева направо), поскольку их низкочастотные асимптоты, если полагать коэффициент передачи этих звеньев равным единице, совпадают с осью абсцисс.
Пусть передаточная функция имеет следующий вид (или приведена к таковому):
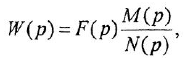
где функция 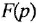 представляет собой одно из следующих выражений:
представляет собой одно из следующих выражений:
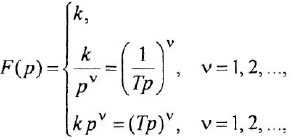
a 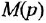 и
и 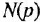 — выражения, представляющие собой произведения сомножителей вида
— выражения, представляющие собой произведения сомножителей вида
[spoiler title=”источники:”]
http://elenergi.ru/aperiodicheskoe-zveno.html
http://lfirmal.com/primery-resheniya-zadach-po-tau/
[/spoiler]
Макеты страниц
Связь между входной и выходной величинами в системе с переменными параметрами определяется интегральной зависимостью (13.9):

Предположим, что к входному сигналу  можно применить преобразование Фурье (7.15). Тогда его можно представить в виде (7.16):
можно применить преобразование Фурье (7.15). Тогда его можно представить в виде (7.16):

Объединяя записанные выше две формулы, получаем

Здесь в первом интеграле нижний предел взят равным  Это отражает тот факт, что входное воздействие может начаться в любой момент времени при
Это отражает тот факт, что входное воздействие может начаться в любой момент времени при  в том числе и при
в том числе и при  Меняя в (13.56) порядок интегрирования и умножая правую часть на
Меняя в (13.56) порядок интегрирования и умножая правую часть на  получаем
получаем

Здесь введена частотная передаточная функция системы с переменными параметрами

Ее можно представить также в следующем виде:

где  — реверс-смещение, а
— реверс-смещение, а  — сопряженная функция веса (13.7).
— сопряженная функция веса (13.7).
Величина, находящаяся в правой части (13.57) под знаком интеграла, представляет собой изображение Фурье функции времени  Поэтому вместо (13.57) можно записать
Поэтому вместо (13.57) можно записать

Таким образом, изображение Фурье выходной величины системы с переменными параметрами можно представить как изображение Фурье входной величины, умноженное на частотную передаточную функцию. Разница по сравнению с системой, имеющей постоянные параметры, заключается в том, что выражение (13.60) записано для некоторого фиксированного момента времени  . В связи с этим в частотную передаточную функцию
. В связи с этим в частотную передаточную функцию  входит параметр
входит параметр  вследствие чего она называется параметрической частотной передаточной функцией.
вследствие чего она называется параметрической частотной передаточной функцией.
Переходя в формуле (13.57) к преобразованию Лапласа, получим

где параметрическая передаточная функция

Отыскание параметрической передаточной функции.
Использование интегральной связи (13.62) для нахождения параметрической передаточной функции является нерациональным, так как требует знания функции веса, что усложняет задачу. Более удобно находить параметрическую передаточную функцию непосредственно из исходного дифференциального уравнения (13.1). Положим в нем  Тогда решение этого уравнения будет соответствовать функции веса
Тогда решение этого уравнения будет соответствовать функции веса  Подставим эти значения
Подставим эти значения

Умножим левую и правую части (13.63) на  и проинтегрируем по
и проинтегрируем по  в пределах от
в пределах от  до
до 

На основании (13.62) величины, находящиеся в квадратных скобках, можно представить в следующем виде:

В результате вместо (13.64) можно записать

Продифференцировав левую часть и сократив на  получим
получим

Здесь введены обозначения:

Таким образом, параметрическая передаточная функция может быть получена в результате решения дифференциального уравнения с переменными коэффициентами (13.66).
Заметим, что в системах с постоянными параметрами передаточная функция не зависит от времени и уравнение (13.66) приобретает вид

Передаточная функция в случае постоянства параметров будет

В случае переменных параметров уравнение (13.66) может быть решено методом последовательных приближений [118]. Для этого представим его в виде

Будем искать решение в виде ряда

Первое приближение можно получить, положив  в (13.70):
в (13.70):

Это будет передаточная функция системы с «замороженными» коэффициентами.
Для вычисления первой поправки  подставим полученное из (13.73) первое приближение в правую часть (13.70). Тогда получим для первой поправки
подставим полученное из (13.73) первое приближение в правую часть (13.70). Тогда получим для первой поправки

Формула для  поправки будет иметь вид
поправки будет иметь вид

Таким образом, последующий член ряда (13.72) получается посредством дифференцирования предыдущего члена в соответствии с (13.71) и подстановки его в (13.75).
Ряд (13.72) сходится тем быстрее, чем медленнее изменяются коэффициенты исходного дифференциального уравнения (13.1).
По найденной функции  может быть получена параметрическая частотная передаточная функция
может быть получена параметрическая частотная передаточная функция  подстановкой
подстановкой 
Использование параметрических передаточных функций.
В соответствии с формулой (13.61) изображение Лапласа выходной величины системы с переменными параметрами можно найти как произведение изображения воздействия на параметрическую передаточную функцию:

Это дает возможность находить переходные процессы в системе с переменными параметрами посредством использования преобразования Лапласа (или Карсона — Хевисайда). Для этой цели по формуле (13.76) отыскивается изображение выходной величины, а затем делается переход к оригиналу 
Для этой цели могут использоваться существующие таблицы изображений Лапласа функций времени. Так, например, пусть изображение выходной величины равно

Полагая в этом выражении время  фиксированным параметром, по таблице (см., например, табл. 7.2) находим
фиксированным параметром, по таблице (см., например, табл. 7.2) находим

Если изображение представляет собой сложную дробно-рациональную функцию, то можно использовать теорему разложения (см. § 7.4). При отсутствии нулевых корней знаменателя изображения

аналогично формуле (7.37) получаем

При наличии одного нулевого корня знаменателя изображения

аналогично формуле (7.39) получаем

В формулах (13.78) и (13.80) корни знаменателя предполагаются некратными.
Для построения переходного процесса может также использоваться вещественная частотная характеристика (см. § 7.5). Для общего случая воздействия произвольной формы из (13.57), аналогично проделанному в § 7.5, можно получить расчетную формулу, являющуюся обобщением формулы (7.52):

где  — вещественная часть частотного изображения искомой функции
— вещественная часть частотного изображения искомой функции  полученного подстановкой в преобразование Карсона — Хевисайда
полученного подстановкой в преобразование Карсона — Хевисайда 
В частном случае, когда входное воздействие представляет собой единичную ступенчатую функцию, из (13.57), аналогично проделанному в § 7.5 получается расчетная формула, являющаяся обобщением формулы (7.53) для переходной функции рассматриваемой динамической системы:

где  — вещественная часть параметрической частотной передаточной функции (13.58).
— вещественная часть параметрической частотной передаточной функции (13.58).

Рис. 13.7.
Построение переходного процесса проводится, аналогично изложенному в § 7.5, по  -функциям. Разница будет заключаться в том, что построение переходного процесса будет справедливым только для того момента времени
-функциям. Разница будет заключаться в том, что построение переходного процесса будет справедливым только для того момента времени  который вошел в качестве параметра в параметрическую передаточную функцию. Поэтому необходимо построить серию кривых (рис. 13.7) для различных фиксированных моментов времени
который вошел в качестве параметра в параметрическую передаточную функцию. Поэтому необходимо построить серию кривых (рис. 13.7) для различных фиксированных моментов времени  и т. д., а затем через точки, соответствующие этим значениям времени, провести плавную кривую.
и т. д., а затем через точки, соответствующие этим значениям времени, провести плавную кривую.
Указанное обстоятельство значительно увеличивает объем вычислительной работы по сравнению с построением кривой переходного процесса в системе с постоянными параметрами.
Глава 5. Типовые звенья САР
С целью упрощения анализа и моделирования САР сложные передаточные функции представляют в виде комбинаций простых – элементарных – передаточных функций. Эту операцию называют декомпозицией передаточной функции.
Объкты, описываемые элементарными передаточными функциями, называют элементарными звеньями. Всего существует 6 типов линейных элементарных звеньев:
– пропорциональное;
– инерционное;
– интегрирующее;
– дифференцирующее;
– колебательное;
– звено запаздывания.
Структурную схему линейной системы любой сложности можно представить в виде соединений (последовательных, параллельных, обратных связей) этих шести элементарных звеньев. Данные звенья всегда используются при описании САР, поэтому их называют типовыми. Также к типовым относят и некоторые наиболее распространенные комбинации элементарных звеньев, такие типовые неэлементарные звенья мы рассмотрим в конце данной главы.
5.1. Пропорциональное звено
Пропорциональное (также усилительное или безынерционное) звено. Связь между выходной и входной величинами определяется алгебраическим уравнением:

где K – коэффициент усиления звена.
Примером усилительного звена может служить рычажная передача (рис. 28):

Рис. 28. Пример усилительного звена
Передаточная функция и амплитудно-фазовая характеристика (АФХ) звена (рис. 29):

5.2. Инерционное звено
Апериодическое (инерционное) звено. Зависимость между входом и выходом апериодического звена описывается дифференциальным уравнением первого порядка:

где Т – постоянная времени звена; K – коэффициент усиления звена.
Передаточная функция:


Рис. 30. Характеристики апериодического звена:
а – временнáя характеристика; б – АФХ
Решение исходного уравнения (44) дает:

При единичном воздействии
кривая разгона апериодического звена (рис. 31):

Рис. 31. Кривая разгона апериодического звена при Хвх = 1
Постоянная времени T апериодического звена определяется по тангенсу угла наклона касательной a к кривой разгона при t = 0:

Постоянная времени T – время, за которое выходная величина достигла бы своего установившегося значения, если бы она изменялась с постоянной скоростью, равной скорости в начальный момент.
Примером апериодического звена может служить аппарат со свободным сливом жидкости (рис. 33,б).
5.3. Интегрирующее звено
Зависимость между входом и выходом интегрирующего звена описывается уравнением:

где K – коэффициент усиления звена.


Амплитудно-фазовая характеристика (рис. 32,б):


Примером интегрирующего звена может служить емкость, из которой жидкость откачивается насосом (рис. 33,а), а примером апериодического звена – емкость, из которой жидкость вытекает под действием силы тяжести (рис. 33,б). В случае нарушения равенства Fпр ≠ Fст (рис. 33,а) уровень начнет меняться либо до полного опорожнения сборника, либо до перелива сборника. Это объект без самовыравнивания (интегрирующее звено).
Если жидкость вытекает из отверстия под действием силы тяжести, то такой объект обладает свойством самовыравнивания (рис. 33,б). При небольшом изменении уровня можно принимать, что изменение уровня описывается уравнением апериодического звена (44).

Рис. 33. Примеры объектов:
а – без самовыравнивания; б – с самовыравниванием
5.4. Дифференцирующее звено
Связь между входной и выходной величинами идеального дифференцирующего звена имеет вид:


где K – коэффициент усиления звена.
Передаточная функция:

Амплитудно-фазовая характеристика (рис. 34):


Рис. 34. АФХ идеального дифференцирующего звена
Следует обратить внимание, что фазочастотная характеристика ф=П/2
всегда положительна, т. е. идеальное дифференцирующее звено на выходе создает опережение входного сигнала при всех частотах w. В математическом аспекте это возможно, но совершенно невозможно с точки зрения материального и теплового балансов. Поэтому идеальное дифференцирующее звено реализовать невозможно и практически применяют звенья, обеспечивающие приближенно дифференцирующее действие (см. раздел «Неэлементарные звенья»).
5.5. Колебательное звено
Связь между входной и выходной величинами определяется уравнением второго порядка:




Соотношение Т2/Т1 определяет, какие корни имеет знаменатель передаточной функции W(p):

Корни этого квадратного уравнения находятся по формуле:

Переходный процесс будет колебательным, если корни уравнения комплексные. Это будет при



корни уравнения будут действительными, т. е. переходный процесс не колебательный. Звено, описываемое таким уравнением, не является колебательным и может быть представлено как два последовательно включенных апериодических звена (см. раздел «Неэлементарные звенья»).

Рис. 36. Кривые разгона (а) и АФХ (б) колебательного звена


Заменив T1 на единственную постоянную времени колебательного звена T, получим следующее выражение для передаточной функции колебательного звена (58):

Параметр ξ называют декрементом затухания. Звено будет обладать колебательными свойствами только при выполнении условия

Если декремент затухания равен нулю, получим частный случай колебательного звена, который носит отдельное название – консервативное звено. Его передаточная функция равна

5.6. Звено запаздывания
Выходная величина равна входной, но отстоит от нее на время t:

Примерами звеньев чистого запаздывания служат транспортеры, трубопроводы и т. д.
5.7. Неэлементарные звенья
5.7.1. Апериодическое звено 2-го порядка
Апериодическое звено 2-го порядка получается при последовательном соединении двух инерционных (апериодических) элементарных звеньев. Дифференциальное уравнение звена:


при отношении постоянных времени:

При Т2/Т1<2 корни уравнения будут комплексными, и звено превращается в колебательное.
5.7.2. Реальное дифференцирующее звено
Поэтому идеальное дифференцирующее звено реализовать невозможно и практически применяют звенья, обеспечивающие приближенно дифференцирующее действие.

Рис. 35. Характеристики реального дифференцирующего звена
а – временнáя характеристика; б – АФХ
Уравнение реального дифференцирующего звена представляет собой комбинацию из апериодического и дифференцирующего звеньев и имеет вид:











































![{ displaystyle [s ^ {2} -2 cdot delta cdot s + delta ^ {2} + omega ^ {2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/551fbde92c8ece8df34728c9909a0b6467b4fd80)

![{ displaystyle [T ^ {2} cdot s ^ {2} + 2DT cdot s + 1] qquad D = { text {Степень демпфирования}} 0 <D <1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd3c65f385e61134d1dca1f3a6d0fbee6c7555b9)

















![k = [0,1,2,3, точки]](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9fe1599c4eb24c9a688785ec976333a50a69a07)

![{ displaystyle y _ {(k)} = [y _ {(0)}, y _ {(1)}, y _ {(2)}, y _ {(3)} точки]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac7b4fa2182ad83a16c92a856c324845e21c684c)
![{ Displaystyle х _ {(к)} = [х _ {(0)}, х _ {(1)}, х _ {(2)}, х _ {(3)} точки]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2f512e06a2bf097e9c59973ec082f87e50bfb63)















































