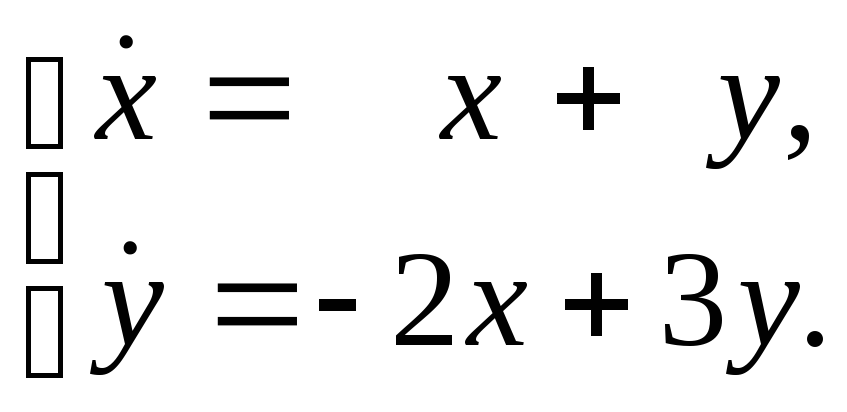where d is a constant coefficient, p≫1 is a positive integer (generally p≠n), and a dot denotes differentiation with respect to time, t.
From: Encyclopedia of Vibration, 2001
Ordinary Differential Equations
Ilpo Laine, in Handbook of Differential Equations: Ordinary Differential Equations, 2008
1.4.2 A non-linear case: a glimpse at the Briot–Bouquet theory
As an example of a non-linear case, we first consider
(1.4.29)zw′=λw+p10z+∑j,k=1∞pjkzjwk,λ∈C
with constant coefficients. This is the most simple case of what are usually called as Briot–Bouquet equations.
THEOREM 1.4.1
If λ ∈ ℂℕ, then (1.4.29) admits a local analytic solution in a neighborhood of z = 0. The solution satisfying the initial condition w(0) = 0 is unique.
PROOF
For a proof based on the Cauchy majorant method, see [74], pp. 55–56.
This theorem is a special case of more general systems of differential equations having a singular point of regular type at z = 0. We may write such a system in the form
(1.4.30)zyj′=fjz,y1,…yn,j=1,…,n,
where the right-hand sides fj(z, y1, …, yn) = fj(z, y) are analytic around (z, y) = (0, 0), and assume that the initial conditions fj(0,0) = 0 are satisfied for j = 1, …, n. Systems of this type are called Briot–Bouquet systems. Of course, we may write (1.4.30) in vectorial form as
(1.4.31)zY′=FzY,
where Y = t(y) ∈ ℂn and F(z,Y) = t(f1(z,Y), …, fn(z,Y)). Denoting K ≔ (k1, …, kn) ∈ (ℕ ∪ {0})n, |K| ≔ k1 + ⋯ + kn, AjK ≔ t(ajK(1), …, ajK(n)) ∈ ℂn, ||Y|| ≔ maxj|yj| and YK≔y1k1⋯ynkn, the power series expansion
(1.4.32)FzY=∑j+K≥1AjKzjYK
converges in some domain around the origin, say |z| < r0, ‖Y‖ < R0. Then we obtain the following
THEOREM 1.4.2
If none of the eigenvalues of the matrix
A=∂f1∂y100⋯∂f1∂yn00⋮⋮∂fn∂y100⋯∂fn∂yn00
is a natural number, then Eq. (1.4.31) admits a unique solution of the form
(1.4.33)Yz=∑j=1∞Cjzj,Cj∈Cn,
analytic in a neighborhood of the origin.
PROOF
See [97], pp. 261–263.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/S1874572508800089
Transient analysis of solids and structures
Sinan Muftu, in Finite Element Method, 2022
12.4.2 Free vibration problem
The constant coefficients of Eq. (12.45) can be found by using the initial conditions. By using Eq. (12.45) we can express the initial conditions as follows:
(12.46a)v(x,0)=∑k=1∞D2kcos(aβk2t)sin(βkx)=v(0)(x)
(12.46b)∂v∂t(x,0)=∑n=1∞D1kaβk2cos(aβk2t)sin(βkx)=v˙(0)(x)
Let’s next multiply these equations by sin(βmx) and integrate through the domain. This gives,
(12.47a)∫0L(∑k=1∞D2ksin(βmx)sin(βkx))dx=∫0Lsin(βmx)v(0)(x)dx
(12.47b)∫0L(∑k=1∞D1kaβk2sin(βmx)sin(βkx))dx=∫0Lsin(βmx)v˙(0)(x)dx
Before proceeding to evaluate these integrals let’s recall the orthogonality condition for the sine function [2],
(12.48)∫0Lsin(βmx)sin(βkx)dx={L2fork=m0fork≠m
Thus by using the orthogonality condition in Eq. (12.47) we can find the coefficients D2k and D1k as follows:
(12.49a)D2k=2L∫0Lv(0)sin(βkx)dx
(12.49b)D1k=2L∫0Lv˙(0)aβk2sin(βkx)dx
In this example the simple-support conditions lead to relatively simple mode shapes given in Eq. (12.39). It can be shown that the mode shapes that arise from more general boundary conditions are also orthonormal [4].
Let’s next consider the initial conditions shown in Fig. 12.6,
(12.50)att=0,v(0)=V(0)sinπxLandv˙(0)=0
where V(0) is the amplitude of the initial displacement of the beam. By recalling βk=kπx/L the coefficients D1k and D2k of the solution Eq. (12.45) can be found from Eq. (12.49a) as follows:
(12.51)D1k=0andD2k=2L∫0LV(0)sinπxLsin(kπxL)dx
Integration of this equation shows that only the case k=1 is nonzero due to the orthogonality condition given in Eq. (12.48) above. Thus, we find the coefficients of Eq. (12.45) as follows:
(12.52a)D1k=0,fork≥1
(12.52b)D2(1)=V(0),andD2k=0fork≥2
The free vibration of an undamped Euler–Bernoulli beam subjected to an initial displacement of the half-sine shape can then be stated by using Eqs. (12.45) and (12.52a) as follows:
(12.53)v(x,t)=V(0)sin(β1x)cos(aβ12t)
where β1=π/L and a=(EI/ρA)1/2. The analytical solution given by Eq. (12.53) is plotted in Fig. 12.7B.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780128211274000074
Calculus
Seifedine Kadry, in Mathematical Formulas for Industrial and Mechanical Engineering, 2014
5.37 Second-Order Differential Equations
Homogeneous linear equation with constant coefficients: y″+by′+cy=0. The characteristic equation is λ2+bλ+c=0.
-
If λ1≠λ2 (distinct real roots) then y=c1eλ1x+c2eλ2x.
-
If λ1=λ2 (repeated roots) then y=c1eλ1x+c2xeλ1x.
-
If λ1=α+βiandλ2=α−βi are complex numbers (distinct real roots) then y=eαx(c1cosβx+c2sinβx).
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780124201316000051
Differential Equations
Robert G. Mortimer, S.M. Blinder, in Mathematics for Physical Chemistry (Fifth Edition), 2024
12.2.1.2 Solution of the Equation of Motion
A homogeneous ordinary linear differential equation with constant coefficients can be solved by the following method:
- 1.
-
Assume the trial solution
(12.17)z(t)=eλt
where λ is a constant. A trial solution is what the name implies.
- 2.
-
Substitute the trail solution into the equation and produce an algebraic equation in λ called the characteristic equation.
- 3.
-
Find the values of λ that satisfy the characteristic equation. For an equation of order n, there will be n values of λ, where n is the order of the equation. Call these values λ1,λ2,…,λn. These values produce n versions of the trial solution that satisfy the equation.
- 4.
-
Write the solution as a linear combination
(12.18)z(t)=c1eλ1t+c2eλ2t+⋯+cneλnt
Before tackling the equation of motion for the harmonic oscillator we look at some other equations:
Example 12.2
Find a solution to the differential equation
d2ydx2+dydx−2y=0
Substitution of the trial solution y=eλx gives the equation
λ2eλx+λeλx−2eλx=0
Division by eλx gives the characteristic equation.
λ2+λ−2=0
The solutions to this equation are
λ=1,λ=−2
The solution to the differential equation is
y(x)=c1ex+c2e−2x
where c10 and c2 are constants.
The solution in the previous example is a family of solutions, one solution for each set of values for c1 and c2. A solution to a linear differential equation of order n that contains n arbitrary constants is known to be a general solution, which is a family of functions that includes almost every solution to the differential equation. Our solution is a general solution, since it contains two arbitrary constants. A solution to a differential equation that contains no arbitrary constants is called a particular solution.
Exercise 12.2
Find the general solution to the differential equation
d2ydx2−3dydx+2y=0
We frequently have additional information that will enable us to pick a particular solution out of a family of solutions. Such information consists of knowledge of boundary conditions and initial conditions. Boundary conditions arise from physical requirements on the solution, such as conditions that apply to the boundaries of the region in space where the solution applies. Initial conditions arise from knowledge of the state of the system at some initial time.
Exercise 12.3
Find the general solution to the differential equation
d2ydx2−3dydx+2y=0
We now solve the equation of motion of the harmonic oscillator, Eq. (12.14). We substitute the trial solution into the equation:
(12.19)d2eλtdt2+kmeλt=0
(12.20)λ2eλt+kmeλt=0
Division by eλt gives the characteristic equation
(12.21)λ2+km=0
The solution of the characteristic equation is
(12.22)λ=±i(km)1/2
where i=−1, the imaginary unit.
The general solution is
(12.23)z=z(t)=c1exp[+i(km)1/2t]+c2exp[−i(km)1/2t]
where c1 and c2 are arbitrary constants. The solution must be real, because imaginary and complex numbers cannot represent physically measurable quantities. From a trigonometric identity
(12.24)eiωt=cos(ωt)+isin(ωt)
we can write
(12.25)z=c1[cos(ωt)+isin(ωt)]+c2[cos(ωt)−isin(ωt)]
where we let
ω=(km)1/2
If we let c1+c2=b1 and i(c1−c2)=b2, then
(12.26)z=b1cos(ωt)+b2sin(ωt)
Although the solutions in Eqs. (12.23) and (12.26) look different, they are equivalent to each other.
Exercise 12.4
Show that the function of Eq. (12.26) satisfies Eq. (12.14).
To obtain a particular solution, we require some Initial conditions. Assume that we have the conditions at t=0:
(12.27)z(0)=0
(12.28)vz(0)=v0
where v0 is a constant.
We require one initial condition to evaluate each arbitrary constant, so these two initial conditions will enable to evaluate both arbitrary constants in the general solution. For our initial conditions, b1 must vanish:
(12.29)z(0)=b1cos(0)+b2sin(0)=b1=0
The position is given by
(12.30)z(t)=b2sin(ωt)
The velocity is given by
(12.31)vz(t)=dzdt=b2ωcos(ωt)
so that
vz(0)=b2ωcos(0)=b2ω
This gives
(12.32)b2=v0ω
Our particular solution is
(12.33)z(t)=(v0ω)sin(ωt)
as depicted in Fig. 12.1.
Figure 12.1. The position and velocity of a harmonic oscillator as functions of time.
The motion given by this solution is called uniform harmonic motion. It is periodic, repeating itself over and over. During one period, the argument of the sine changes by 2π, so that if τ is the period (the length of time required for one cycle of the motion),
(12.34)2π=ωτ=(km)1/2τ
The period is given by
(12.35)τ=2π(mk)1/2
The reciprocal of the period is called the frequency, denoted by ν.
(12.36)v=12πkm=ω2π
The frequency gives the number of oscillations per second. The circular frequency ω gives the rate of change of the argument of the sine or cosine function in radians per second.
Example 12.3
A mass of
is suspended from a spring with a spring constant
. Find the frequency and period of oscillation.
The solution of the equation of motion of the harmonic oscillator illustrates a general property of classical equations of motion If the equation of motion and the initial conditions are known, the motion of the system is determined as a function of time. We say that classical equations of motion are deterministic.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B978044318945600017X
Second- and higher-order equations
Henry J. Ricardo, in A Modern Introduction to Differential Equations (Third Edition), 2021
4.2.1 The structure of solutions
If we take the same RLC circuit that we considered at the beginning of the preceding section and hook up a generator supplying alternating current to it, Kirchhoff’s Voltage Law will now take the form Ld2Idt2+RdIdt+1CI=dEdt, where E is the applied nonconstant voltage. An equation of this kind is called a nonhomogeneous second-order linear equation with constant coefficients. (The nonzero right-hand side of such an equation is often called the forcing function or the input. The solution of the equation is the output. See Section 2.2.)
To get a handle on solving a nonhomogeneous linear equation with constant coefficients, let’s think a bit about the difference between a nonhomogeneous equation
(4.2.1)ay″+by′+cy=f(t)
and its associated homogeneous equation ay″+by′+cy=0. If y is the general solution of the homogeneous system, then y doesn’t quite “reach” all the way to f(t) under the transformation L(y)=ay″+by′+cy. It stops short at 0. Perhaps we could enhance the solution y in some way so that operating on this new function does give us all of f. We have to be able to capture the “leftover” term f(t).
For nonhomogeneous second-order equations with constant coefficients, the proper form of the Superposition Principle is the following:
If y1 is a solution of ay″+by′+cy=f1(t) and y2 is a solution of ay″+by′+cy=f2(t), then y=c1y1+c2y2 is a solution of ay″+by′+cy=c1f1(t)+c2f2(t) for any constants c1 and c2.
From the Superposition Principle follows a fundamental truth about the solutions of linear equations with constant coefficients:
The general solution, yGNH, of a linear nonhomogeneous equation ay″+by′+cy=f(t) is obtained by finding a particular solution, yPNH, of the nonhomogeneous equation and adding it to the general solution, yGH, of the associated homogeneous equation: yGNH=yGH+yPNH.
We can prove this easily using operator notation, in which L(y)=ay″+by′+cy:
- 1.
-
First note that L(yGH)=0 and L(yPNH)=f(t) by definition.
- 2.
-
Then if y=yGH+yPNH, we have L(y)=L(yGH+yPNH)=L(yGH)+L(yPNH)=0+f(t)=f(t), so y is a solution of Eq. (4.2.1).
- 3.
-
Now we must show that every solution of Eq. (4.2.1) has the form y=yGH+yPNH. To do this, we assume that y* is an arbitrary solution of L(y)=f(t) and yPNH is a particular solution of L(y)=f(t). If we let z=y⁎−yPNH, then
L(z)=L(y⁎−yp)=L(y⁎)−L(yp)=f(t)−f(t)=0,
which shows that z is a solution to the homogeneous equation L(y)=0. Because z=y⁎−yPNH, it follows that y⁎=z+yPNH. Since y⁎ is an arbitrary solution of the nonhomogeneous equation, the expression z+yPNH includes all solutions. (See Problem 23 of Exercises 1.3 and Problem 35 of Exercises 2.2 for related results.)
Let’s go through a few simple examples to develop some intuition for the solutions of nonhomogeneous equations.
Example 4.2.1 Solving a Nonhomogeneous Equation
If we are given the nonhomogeneous equation y″+4y′+5y=10e−2xcosx, the general solution will be made up of the general solution of the associated homogeneous equation and a particular solution of the nonhomogeneous equation: yGNH=yGH+yPNH. The characteristic equation λ2+4λ+5=0 has roots −2±i, so we know that yGH=e−2x(c1cosx+c2sinx). We can verify that a particular solution of the nonhomogeneous equation is 5xe−2xsinx. Therefore, the general solution of the nonhomogeneous equation is y=e−2x(c1cosx+c2sinx)+5xe−2xsinx.
In the preceding example, a particular solution appeared magically. The next example hints at how we may find yPNH by examining the forcing function on the right-hand side of the equation. Sections 4.3 and 4.4 will provide systematic procedures for determining a particular solution of a nonhomogeneous equation.
Example 4.2.2 Solving a Nonhomogeneous Equation
Suppose we want to find the general solution of y″+3y′+2y=12et. Because the characteristic equation of the associated homogeneous equation is λ2+3λ+2=0, with roots −1 and −2, we know that the general solution of the homogeneous equation is yGH=c1e−t+c2e−2t.
Now we look carefully at the form of the nonhomogeneous equation. In looking for a particular solution yPNH, we can ignore any terms of the form e−t or e−2t because they are part of the homogeneous solution and won’t contribute anything new. But somehow, after differentiations and additions, we have to wind up with the term 12et. We guess that y=cet for some undetermined constant c. Substituting this expression into the left-hand side of the nonhomogeneous equation, we get (cet)+3(cet)+2(cet)=6cet. If we choose c=2, then yPNH=2et is a particular solution of the nonhomogeneous equation.
Putting these two components together, we can write the general solution of the nonhomogeneous equation as yGNH=yGH+yPNH=c1e−t+c2e−2t+2et.
The intelligent guessing used in the preceding example can be formalized into the method of undetermined coefficients, which will be discussed in the next section. But, as we’ll see, this method is effective only when the forcing function f(t) in the equation ay″+by′+cy=f(t) is of a special type.
Exercises 4.2
A
For each of the nonhomogeneous differential equations in Problems 1–5, verify that the given function yp is a particular solution.
- 1.
-
y″+3y′+4y=3x+2; yp=34x−116
- 2.
-
y″−4y=2e3x; yp=35e3x
- 3.
-
3y″+y′−2y=2cosx; yp=−513cosx+113sinx
- 4.
-
y″+5y′+6y=x2+2x; yp=16×2+118x−11108
- 5.
-
y″+y=sinx; yp=−12xcosx
- 6.
-
If x1(t)=12et is a solution of x¨+x˙=et and x2(t)=−te−t is a solution of x¨+x˙=e−t, find a particular solution of x¨+x˙=et+e−t and verify that your solution is correct.
- 7.
-
Given that yp=x2 is a solution of y″+y′−2y=2(1+x−x2), use the Superposition Principle to find a particular solution of y″+y′−2y=6(1+x−x2) and verify that your solution is correct.
- 8.
-
If y1=1+x is a solution of y″−y′+y=x and y2=e2x is a solution of y″−y′+y=3e2x, find a particular solution of y″−y′+y=−2x+4e2x. Verify that your solution is correct.
B
- 9.
-
Find the general solution of the equation given in Problem 1.
- 10.
-
Find the general solution of the equation given in Problem 2.
- 11.
-
Find the general solution of the equation given in Problem 3.
- 12.
-
Find the general solution of the equation given in Problem 4.
- 13.
-
Find the general solution of the equation given in Problem 5.
- 14.
-
Find the general solution of the equation y″+y′−2y=6(1+x−x2) given in Problem 7.
- 15.
-
Find the general solution of the equation x¨+x˙=et+e−t given in Problem 6.
- 16.
-
Find the form of a particular solution of y″−y=x by intelligent guessing and use this information to solve the IVP y″−y=x, y(0)=y′(0)=0.
C
- 17.
-
Suppose x(t) satisfies the IVP
x¨+π2x=f(t)={π2,0≤t≤10,t>1
with x(0)=1 and x˙(0)=0. Determine the continuously differentiable solution for t≥0. (This means that the solution has a continuous derivative function. Note that it will have a discontinuous second derivative at t=1.)
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780128182178000117
Ordinary differential equations
Brent J. Lewis, … Andrew A. Prudil, in Advanced Mathematics for Engineering Students, 2022
Method of undetermined coefficients
This method applies to the equation with constant coefficients
(2.62)
where r(x) is of a special form as detailed in the following rules:
- (a)
-
Basic rule. If r(x) in Eq. (2.62) is one of the functions in the first column of Table 2.4, choose the corresponding function for yp and determine its undetermined coefficients by substitution into Eq. (2.62).
Table 2.4. Choice for the yp function.
Term in r(x) Choice for yp keγx Ceγx kxn (n = 0,1,…) Knxn + Kn−1xn−1 + … + K1x + Ko kcosωxksinωx }Kcosωx+Msinωx keαxcosωxkeαxsinωx }eαx(Kcosωx+Msinωx) - (b)
-
Modification rule. If the choice for yp is also a solution of the homogeneous equation corresponding to Eq. (2.62), then multiply the choice for yp by x (or x2 if this solution corresponds to a double root of the characteristic equation of the homogeneous equation).
- (c)
-
Sum rule. If r(x) is a sum of functions in several lines of Table 2.4, then choose for yp the corresponding sum of functions.
Example 2.2.12
(rule a) Solve y″+5y=25×2.
Solution. Using Table 2.4, yp=K2x2+K1x+Ko, yielding yp″=2K2. Therefore, 2K2+5(K2x2+K1x+Ko)=25×2. Equating coefficients on both sides gives 5K2=25, 5K1=0, 2K2+5Ko=0, so that K2=5, K1=0, and Ko=−2. Therefore, yp=5×2−2. Thus, the general solution is given by y=yh+yp=Acos5x+Bsin5x+5×2−2. [answer]
Example 2.2.13
(rule b) Solve y″−y=e−x.
Solution. The characteristic equation (λ2−1)=(λ−1)(λ+1)=0 has the roots 1 and −1, so that yh=c1ex+c2e−x. Normally Table 2.4 suggests yp=Ce−x (which is already a solution of the homogeneous equation). Thus, rule (b) applies, where yp=Cxe−x. As such, yp′=C(e−x−xe−x) and yp″=C(−2e−x+xe−x). Substituting these expressions into the differential equation gives
. Simplifying, one obtains C=−1/2. Thus, the general solution is given by y=c1ex+c2e−x−12xe−x. [answer]
Example 2.2.14
(rules b and c) Solve y″+2y′+y=e−x−x, y(0)=0, y′(0)=0.
Solution. The characteristic equation λ2+2λ+1=(λ+1)2=0 has a double root λ=−1. Hence, yh=(c1+c2x)e−x (see Section 2.2.2). For the x-term on the right-hand side, Table 2.4 suggests the choice K1x+Ko. However, since λ=−1 is a double root, rule b suggests the choice Cx2e−x (instead of Ce−x) so that yp=K1x+Ko+Cx2e−x. As such, yp″+2yp′+yp=2Ce−x+K1x+(2K1+Ko)=e−x−x, which implies C=12, K1=−1 and Ko=2. The general solution is y=yh+yp=(c1+c2x)e−x+12x2e−x+2−x.
For the initial conditions, y′=(−c1+c2−c2x)e−x+(x−12×2)e−x−1.
Therefore, y(0)=c1+2=0 (so that c1=−2) and y′(0)=−c1+c2−1=0 (so that c2=−1). Thus, y=−(2+x)e−x+12x2e−x+(2−x). [answer]
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780128236819000101
Differential — Difference Equations
KENNETH L. COOKE, in International Symposium on Nonlinear Differential Equations and Nonlinear Mechanics, 1963
4 Exponential Solutions
One method of obtaining solutions of equations with constant coefficients is the method of exponential solutions. For example, the function u(t) = exp (st) is a solution of the equation
(4.1)u′(t)=cu(t−1)
provided s is a root of the characteristic equation
(4.2)s=ce−s
By combining such solutions, one can obtain more general solutions in series form.
In general the transcendental characteristic equations which are encountered have infinitely many roots, and there are questions of convergence of series of solutions. Also, it becomes somewhat difficult to determine the coefficients entering into the series from the initial function g(t). One of the best ways of handling this problem is by means of the Laplace transform, as we shall explain below.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123956514500222
FORMS OF DIMENSIONLESS RELATIONS
In Applied Dimensional Analysis and Modeling (Second Edition), 2007
The Heuristic Reasoning Method.
Very often the constant exponents—and rarely even the constant coefficient (Example 13-16)—of a monomial can be found merely by heuristic reasoning. This way at the most we only have to determine the single constant coefficient, an activity which requires only one measurement, regardless of the number of dimensionless variables in the relation. It must be mentioned, though, that this reasoning does sometimes call for rather high levels of sophistication, imagination, an inquisitive if not iconoclastic mind, and perhaps some knowledge of the relevant physical laws.
The following examples demonstrate this process and its beneficial and powerful results.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123706201500198
Functional Equations in Applied Sciences
In Mathematics in Science and Engineering, 2005
3.8.1 Solution of the homogeneous equation
In order to find the general solution of the constant coefficients homogeneous Equation (Equation (3.30) with h(x) = 0) we solve its associated characteristic equation
(3.31)∑k=0nakzn−k=0,
and we distinguish the following four cases:
- •
-
Single real roots:
If z1 is a single real root of (3.31), then its additive contribution to the general solution of (3.30) is
C1z1x. - •
-
Multiple real roots:
If z1 is a multiple root with multiplicity index p, then its additive contribution to the general solution is
(C1xp−1+C2xp−2+⋯+Cp)z1x. - •
-
Pairs of conjugate complex roots:
If z1 = ρ(cos α+i sin α) is a single complex root of (3.31), then the additive contribution of the pair of z1 and its conjugate to the general solution of (3.30) is ρx[A cos (αx) + B sin (αx)].
- •
-
Pairs of multiple conjugate roots:
If z1 = ρ(cos α + i sin α) is a multiple complex root of (3.31) with multiplicity index p, then the additive contribution of the pair of z1 and its conjugate to the general solution of (3.30) is
(3.32)ρx[(A1xp−1+A2xp−2+…+Ap)cos(αx)+ +(B1xp−1+B2xp−2+…+Bp)sin(αx))].
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/S0076539205800062
Differential Equations
S.M. Blinder, in Guide to Essential Math (Second Edition), 2013
8.4 Second-Order Differential Equations
We will consider here linear second-order equations with constant coefficients, in which the functions p(x) and q(x) in Eq. (8.2) are constants. The more general case gives rise to special functions, several of which we will encounter later as solutions of partial differential equations. The homogeneous equation, with f(x)=0, can be written
(8.55)d2ydx2+a1dydx+a2y=0.
It is convenient to define the differential operator
(8.56)D≡ddx
in terms of which
(8.57)Dy=dydxandD2y=d2ydx2.
The differential equation (8.55) is then written
(8.58)D2y+a1Dy+a2y=0,
or, in factored form,
(8.59)(D-r1)(D-r2)y=(D-r2)(D-r1)y=0,
where r1,r2 are the roots of the auxilliary equation
(8.60)r2+a1r+a2=0.
The solutions of the two first-order equations
(8.61)(D-r1)y=0ordydx+r1y=0
give
(8.62)y=conster1x,
while
(8.63)(D-r2)y=0ordydx+r2y=0
gives
(8.64)y=conster2x.
Clearly, these are also solutions to Eq. (8.59). The general solution is the linear combination
(8.65)y(x)=c1er1x+c2er2x.
In the case that r1=r2=r, one solution is apparently lost. We can recover a second solution by considering the limit:
(8.66)limr1→r2er2x-er1xr2-r1=∂∂rerx=xerx.
(Remember that the partial derivative ∂/∂r does the same thing as d/dr, with every other variable held constant.) Thus the general solution for this case becomes
(8.67)y(x)=c1erx+c2xerx.
When r1 and r2 are imaginary numbers, say ik and -ik, the solution (8.65) contains complex exponentials. Since, by Euler’s theorem, these can be expressed as sums and difference of sine and cosine, we can write
(8.68)y(x)=c1coskx+c2sinkx.
Many applications in physics, chemistry, and engineering involve a simple differential equation, either
(8.69)y″(x)+k2y(x)=0ory″(x)-k2y(x)=0.
The first equation has trigonometric solutions coskx and sinkx, while the second has exponential solutions ekx and e-kx. These results can be easily verified by “reverse engineering.” For example, assuming that y(x)=coskx, then y′(x)=-ksinkx and y″(x)=-k2coskx. It follows that y″(x)+k2y(x)=0.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780124071636000084
Ниже разберем способы, как решить линейные однородные и неоднородные дифференциальные уравнения порядка выше второго, имеющих постоянные коэффициенты. Подобные уравнения представлены записями y(n)+fn-1·y(n-1)+…+f1·y’+f0·y=0 и y(n)+fn-1·y(n-1)+…+f1·y’+f0·y=f(x), в которых f0, f1,…, fn-1 – являются действительными числами, а функция f(x) является непрерывной на интервале интегрирования X.
Оговоримся, что аналитическое решение подобных уравнений иногда неосуществимо, тогда используются приближенные методы. Но, конечно, некоторые случаи дают возможность определить общее решение.
Общее решение ЛОДУ и ЛДНУ
Мы зададим формулировку двух теорем, показывающих, какого вида общих решений ЛОДУ и ЛНДУ n-ого порядка следует искать.
Общим решением y0 ЛОДУ y(n)+fn-1·y(n-1)+…+f1·y’+f0·y=0 на интервале
X (коэффициенты f0(x), f1(x),…, fn-1(x) непрерывны на X) будет линейная комбинация
n линейно независимых частных решений ЛОДУ yj, j=1, 2,…, n, содержащая произвольные постоянные коэффициенты Cj, j=1, 2,…, n, то есть y0=∑j=1nCj·yj.
Общим решением y ЛНДУ y(n)+fn-1·y(n-1)+…+f1·y’+f0·y=f(x) на интервале X (коэффициенты f0(x), f1(x),…, fn-1(x) непрерывны на X ) и функцией f(x) будет являться сумма y=y0+y~, где y0 – общее решение соответствующего ЛОДУ y(n)+fn-1·y(n-1)+…+f1·y’+f0·y=0, а y~ – некоторое частное решение исходного ЛНДУ.
Итак, общее решение линейного неоднородного дифференциального уравнения, содержащего постоянные коэффициенты y(n)+fn-1·y(n-1)+…+f1·y’+f0·y=f(x), нужно искать, как y=y0+y~, где y~ – некоторое его частное решение, а y0=∑j=1nCj·yj – общее решение соответствующего однородного дифференциального уравнения y(n)+fn-1·y(n-1)+…+f1·y’+f0·y=0.
В первую очередь рассмотрим, как осуществлять нахождение y0=∑j=1nCj·yj – общее решение ЛОДУ n-ого порядка с постоянными коэффициентами, а потом научимся определять частное решение y~ линейного неоднородного дифференциального уравнения n-ого порядка при постоянных коэффициентах.
Алгебраическое уравнение n-ого порядка kn+fn-1·kn-1+…+f1·k+f0=0 носит название характеристического уравнения линейного однородного дифференциального уравнения n-ого порядка, содержащего постоянные коэффициенты, записи y(n)+fn-1·y(n-1)+…+f1·y’+f0·y=0.
Возможно определить n частных линейно независимых решений y1, y2,…, yn исходного ЛОДУ, исходя из значений найденных n корней характеристического уравнения k1, k2,…, kn.
Методы решения ЛОДУ и ЛНДУ
Укажем все существующие варианты и приведем примеры на каждый.
- Когда все решения k1, k2,…, kn характеристического уравнения kn+fn-1·kn-1+…+f1·k+f0=0 действительны и различны, линейно независимые частные решения будут выглядеть так:
y1=ek1·x, y2=ek2·x,…, yn=ekn·x. Общее же решение ЛОДУ n-ого порядка при постоянных коэффициентах запишем как: y0=C1·ek1·x+C2·ek2·x+…+Cn·ekn·x.
Задано ЛОДУ третьего порядка, содержащее постоянные коэффициенты y”’-3y”-y’+3y=0. Определите его общее решение.
Решение
Cоставим характеристическое уравнение и найдем его корни, разложив предварительно многочлен из левой части равенства на множители, используя метод группировки:
k3-3k2-k+3=0k2(k-3)-(k-3)=0(k2-1)(k-3)=0k1=-1, k2=1, k3=3
Ответ: найденные корни являются действительными и различными, значит общее решение ЛОДУ третьего порядка с постоянными коэффициентами запишем как: y0=C1·e-x+C2ex+C3·e3x.
- Когда решения характеристического уравнения являются действительными и одинаковыми ( k1=k2=…=kn=k0), линейно независимые частные решения линейного однородного дифференциального уравнения n-ого порядка с постоянными коэффициентами буду иметь вид: y1=ek0·x, y2=x·ek0·x,…, yn=xn-1·ek0·x.
Общее же решение ЛОДУ будет выглядеть так:
y0=C1·ek0·x+C2·ek0·x+…+Cn·xn-1·ek0·x==ek0·x·C1+C2·x+…+Cn·xn-1
Задано дифференциальное уравнение: y(4)-8k(3)+24y”-32y’+16y=0. Необходимо определить его общее решение.
Решение
Составим характеристическое уравнение заданного ЛОДУ: k4-8k3+24k2-32k+16=0.
Преобразуем данное характеристическое уравнение, используя формулу бинома Ньютона, оно примет вид: k-24=0. Отсюда мы выделим его четырехкратный корень k0 = 2.
Ответ: общим решением заданного ЛОДУ станет: y0=e2x·C1+C2·x+C3·x2+C4·x3
- Когда решения характеристического уравнения линейного однородного дифференциального уравнения n-ого порядка при постоянных коэффициентах – различные комплексно сопряженные пары α1±i·β1, α2±i·β2,…, αm±i·βm, n=2m, линейно независимые частные решения такого ЛОДУ будут иметь вид:
y1=eα1x·cos β1x, y2=eα1x·sin β1x,y3=eα2x·cos β2x, y4=eα2x·sin β2x,…yn-1=eαmx·cos βmx, yn=eαmx·sin βmx
Общее же решение запишем так:
y0=eα1x·C1·cosβ1x+C2·sinβ1x++eα2x·C3·cosβ2x+C4·sinβ2x+…++eαmx·Cn-1·cosβmx+Cn·sinβmx
Задано ЛОДУ четвертого порядка при постоянных коэффициентах y(4)-6y(3)+14y”-6y’+13y=0. Необходимо его проинтегрировать.
Решение
Составим характеристическое уравнение заданного ЛОДУ: k4-6k3+14k2-6k+13=0. Осуществим преобразования и группировки:
k4-6k3+14k2-6k+13=0k4+k2-6k3+k+13k2+1=0k2+1k2-6k+13=0
Из полученного результата несложно записать две пары комплексно сопряженных корней k1,2=±i и k3,4=3±2·i.
Ответ: общее решение заданного линейного однородного дифференциального уравнения n-ого порядка с постоянными коэффициентами запишется как:
y0=e0·C1·cos x+C2·sin x+e3x·C3·cos 2x+C4·sin 2x==C1·cos x+C2·sin x+e3x·C3·cos 2x+C4·sin 2x
- Когда решения характеристического уравнения – это совпадающие комплексно сопряженные пары α±i·β, линейно независимыми частными решениями линейного однородного дифференциального уравнения n-ого порядка с постоянными коэффициентами будут записи:
y1=eα·x·cos β x, y2=eα·x·sin β x,y3=eα·x·x·cos β x, y4=eα·x·x·sin β x,…yn-1=eα·x·xm-1·cos β x, yn=eα·x·xm-1·sin β x
Общим решением ЛОДУ будет:
y0=eα·x·C1·cosβ x+C2·sinβ x++eα·x·x·C4·cosβ x+C3·sinβ x+…++eα·x·xm-1·Cn-1·cosβ x+Cn·sinβ x==eα·x·cosβ x·C1+C3·x+…+Cn-1·xm-1++eα·x·sin β x·C2+C4·x+…+Cn·xm-1
Задано линейное однородное дифференциальное уравнение с постоянными коэффициентами y(4)-4y(3)+14y”-20y’+25y=0. Необходимо определить его общее решение.
Решение
Составим запись характеристического уравнения, заданного ЛОДУ, и определим его корни:
k4-4k3+14k2-20k+25=0k4-4k3+4k2+10k2-20k+25=0(k2-2k)2+10(k2-2k)+25=0(k2-2k+5)2=0D=-22-4·1·5=-16k1, 2=k3, 4=2±-162=1±2·i
Таким образом, решением характеристического уравнения будет двукратная комплексно сопряженная пара α±β·i=1±2·i.
Ответ: общее решение заданного ЛОДУ: y0=ex·cos 2x·(C1+C3·x)+ex·sin 2x·(C2+C4·x)
- Встречаются различные комбинации указанных случаев: некоторые корни характеристического уравнения ЛОДУ n-ого порядка с постоянными коэффициентами являются действительными и различными, некоторые – действительными и совпадающими, а какие-то – комплексно сопряженными парами или совпадающими комплексно сопряженными парами.
Задано дифференциальное уравнение y(5)-9y(4)+41(3)+35y”-424y’+492y=0. Необходимо определить его общее решение.
Решение
Составим характеристическое уравнение заданного ЛОДУ: k5-9k4+41k3+35k2-424k+492=0.
Левая часть содержит многочлен, который возможно разложить на множители. В числе делителей свободного члена определяем двукратный корень k1=k2=2 и корень k3=-3.
На основе схемы Горнера получим разложение: k5-9k4+41k3+35k2-424k+492=k+3k-22k2-8k+41.
Квадратное уравнение k2-8k+41=0 дает нам оставшиеся корни k4, 5=4±5·i.
Ответ: общим решением заданного ЛОДУ с постоянными коэффициентами будет: y0=e2x·C1+C2x+C3·e-3x+e4x·C4·cos 5x+C5·sin 5x
Таким образом, мы рассмотрели основные случаи, когда возможно определить y0 – общее решение ЛОДУ n-ого порядка с постоянными коэффициентами.
Следующее, что мы разберем – это ответ на вопрос, как решить линейное неоднородное дифференциальное уравнение n-ого порядка с постоянными коэффициентами записи y(n)+fn-1·y(n-1)+…+f1·y’+f0·y=f(x).
Общее решение в таком случае составляется как сумма общего решения соответствующего ЛОДУ и частного решения исходного ЛНДУ: y=y0+y~. Поскольку мы уже умеем определять y0, остается разобраться с нахождением y~, т.е. частного решения ЛНДУ порядка n с постоянными коэффициентами.
Приведем все способы нахождения y~ согласно тому, какой вид имеет функция f(x), находящаяся в правой части рассматриваемого ЛНДУ.
- Когда f(x) представлена в виде многочлена n-ой степени f(x) = Pn(x), частным решением ЛНДУ станет: y~=Qn(x)·xγ. Здесь Qn(x) является многочленом степени n, а r – указывает, сколько корней характеристического уравнения равно нулю.
- Когда функция f(x) представлена в виде произведения многочлена степени n и экспоненты f(x)=Pn(x)·eα·x, частным решением ЛНДУ второго порядка станет: y~=eα·x·Qn(x)·xγ. Здесь Qn(x) является многочленом n-ой степени, r указывает, сколько корней характеристического уравнения равно α.
- Когда функция f(x) записана как f(x)=A1cos(βx)+B1sin(βx), где А1 и В1 – числа, частным решением ЛНДУ станет запись y~=Acosβx+Bsinβx·xγ. Здесь где А и В являются неопределенными коэффициентами, r – указывает, сколько комплексно сопряженных пар корней характеристического уравнения равно ±iβ.
- Когда f(x)=eαx·Pn(x)sinβx+Qkxcosβx, то y~=eαx·Lmxsinβx+Nmxcosβx·xγ, где r – указывает, сколько комплексно сопряженных пар корней характеристического уравнения равно α±iβ, Pn(x), Qk(x), Lm(x) и Nm(x) являются многочленами степени n, k, m и m соответственно, m=max(n,k).
Коэффициенты, которые неизвестны, определяются из равенства y~(n)+fn-1·y~(n-1)+…+f1y~’+f0·y~=f(x)
Подробности нахождения решений уравнений в каждом из указанных случаев можно изучить в статье линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами, поскольку схемы решения ЛНДУ степени выше второй полностью совпадают.
Когда функция f(x) имеет любой иной вид, общее решение ЛНДУ возможно определить, используя метод вариации произвольных постоянных. Его разберем подробнее.
Пусть нам заданы yj, j=1,2,…, n – n линейно независимые частные решения соответствующего ЛОДУ, тогда, используя различные вариации произвольных постоянных, общим решением ЛНДУ
n-ого порядка с постоянными коэффициентами будет запись: н=∑j=1nCj(x)·yj. В нахождении производных функций Cj(x), j=1, 2,…, n поможет система уравнений:
∑j=1nCj'(x)·yj=0∑j=1nCj'(x)·y’j=0∑j=1nCj'(x)·y”j=0…∑j=1nCj'(x)·yj(n-2)=0∑j=1nCj'(x)·yj(n-1)=0
а собственно функции Cj(x), j=1, 2,…, n найдем при последующем интегрировании.
Разберем пример.
Задано ЛНДУ с постоянными коэффициентами: y”’-5y”+6y’=2x. Необходимо найти его общее решение.
Решение
Составим характеристическое уравнение: k3-5k2+6k=0. Корни данного уравнения: k1=0, k2=2 и k3=3. Таким образом, общим решением ЛОДУ будет запись: y0=C1+C2·e2x+C3·e3x, а частные линейно независимые решения это: y1=1, y2=e2x, y3=e3x.
Варьируем произвольные постоянные: y=C1(x)+C2(x)·e2x+C3(x)·e3x.
Чтобы определить C1(x), C2(x) и C3(x), составим систему уравнений:
C’1(x)·y1+C’2(x)·y2+C’3(x)·y3=0C’1(x)·y’1+C’2(x)·y’2+C’3(x)·y’3=0C’1(x)·y”1+C’2(x)·y”2+C’3(x)·y”3=2x⇔C’1(x)·1+C’2x·e2x’+C’3(x)·y3=0C’1(x)·1’+C’2x·e2x’+C’3(x)·e3x’=0C’1(x)·1”+C’2x·e2x”+C’3(x)·e3x”=2x⇔C’1(x)·1+C’2x·e2x+C’3(x)·e3x=0C’1(x)·0+C’2(x)·2e2x+C’3(x)·3e3x=0C’1(x)·0+C’2(x)·4e2x+C’3(x)·9e3x=2x
Решаем, используя метод Крамера:
∆=1e2xe3x02e2x3e3x04e2x9e3x=18e2x·e3x-12e2x·e3x=6e5x∆C1′(x)=0e2xe3x02e2x3e3x2x4e2x9e3x=e5x·2x⇒C’1(x)=∆C1′(x)∆=e5x·2x6e5x=16·2x∆C2′(x)=10e3x003e3x02x9e3x=-3ex·2x⇒C’2(x)=∆C2′(x)∆=-3e3x·2x6e5x=-12·e-2x·2x∆C3′(x)=1e2x002e2x004e2x2x=2e2x·2x⇒C’3(x)=∆C3′(x)∆=2e2x·2x6e5x=13·e-3x·2x
Интегрируем C’1(x)=16·2x с помощью таблицы первообразных, а
C’2(x)=-12·e-2x·2x и C’3(x)=13·e-3x·2x при помощи метода интегрирования по частям, получим:
C1(x)=16·∫2xdx=16·2xln 2+C4C2(x)=-12·∫e-2x·2xdx=-12·e-2x·2xln 2-2+C5C3(x)=13·∫e-3x·2xdx=13·e-3x·2xln 2-3+C6
Ответ: искомым общим решением заданного ЛОДУ с постоянными коэффициентами будет:
y=C1(x)+C2(x)·e2x+C3(x)·e3x==16·2xln 2+C4+-12·e-2x·2xln 2-2+C5·e2x++13·e-3x·2xln 2-3+C6·e3x
где C4, C5 и C6 – произвольные постоянные.
Линейная
однородная система с постоянными
коэффициентами
имеет вид

где
постоянные действительные числа. В
матричном виде система записывается
так:
(23)
где

однородных уравнений с постоянными
коэффициентами, т.е. попробуем найти
решения вида(
постоянный вектор,
постоянное число), а затем из этих решений
составить общее решение системы.
Продифференцируем функциюПодставим это выражение в уравнение
(23):Сократив на
будем иметь:
Это равенство означает, что
собственный
вектор
матрицы
а
еёсобственное
значение.
Как известно из линейной алгебры,
собственные значения матрицы могут
быть найдены из характеристического
уравнения
(24)
где
единичная
-матрица,
а собственные векторы находятся мз
системы линейных уравнений
(25)
Уравнение
(24) и систему (25) можно записать в
развёрнутом виде:


Предположим,
что имеет место “самый хороший” случай:
корни
характеристического уравнения
действительны и различны.
В этом случае, решив для каждого
систему уравнений (27), мы получим
линейно независимых собственных векторов
Эти векторы определяют
линейно независимых вектор-функций
являющихся решениями системы (22), а
значит, образующими фундаментальную
систему решений этой системы. Таким
образом, общее решение системы (22) имеет
вид
(28)
где
произвольные постоянные. Рассмотрим
пример.
Пример
1. Система
Найдём
все решения этой системы. Вначале запишем
эту систему в матричном виде:
Составим характеристическое уравнение:

откуда
Найдём теперь собственные векторы. Для
надо решить систему

решить систему



решения нашей системы:
где
произвольные постоянные. От векторной
формы общего решения можно перейти к
обычной форме:
Предположим,
что характеристическое уравнение имеет
кратный
корень
В этом случае, как и в случае простых
корней, мы находим собственные векторы
из системы (27), и если окажется, что
существуетлинейно независимых собственных
векторов, то общее решение системы также
запишется в виде (28). Если же собственных
векторов “не хватает” до базиса
пространствато можно искать решения системы в виде
и т.д. Для матриц больших размеров такой
метод является неприемлемым, и
фундаментальную систему решений системы
(23) находят, приводя матрицукжордановой
нормальной форме.
Мы этот метод рассматривать не будем,
а ограничимся матрицами небольших
размеров.
Пример
2. Система
Найдём
все решения этой системы. Характеристическое
уравнение

корни
Для собственных векторов с
мы имеем систему

собственных вектора:

находятся из системы

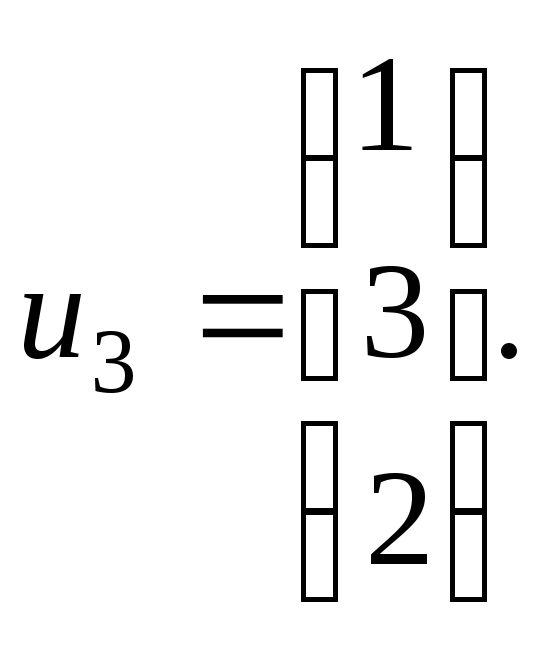
линейно независимы, то мы можем с их
помощью записать общее решение системы:
Пример
3. Система
Характеристическое
уравнение

Для собственных векторов с
мы имеем систему

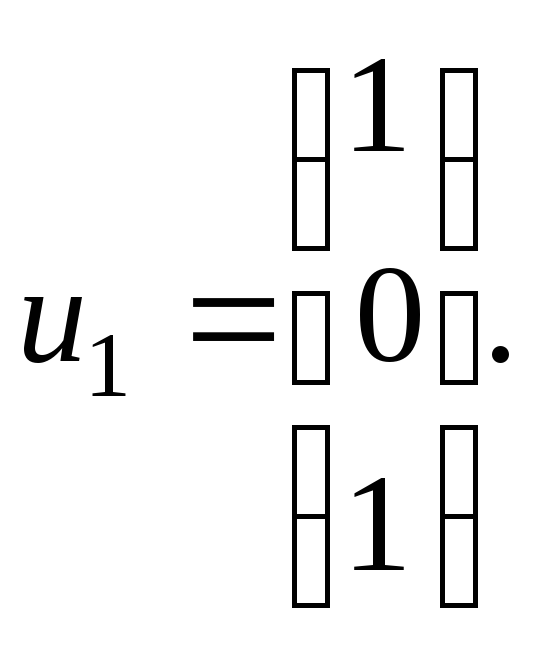
имеем систему

где

не составляют базиса пространства
Поэтому будем искать решения системы
дифференциальных уравнений, имеющие
видгде
постоянные векторы. В нашем примере
но мы проделаем выкладки для произвольного
Имеем:
Подставим в систему дифференциальных
уравнений:Отсюда следует, что
Таким
образом,
собственный вектор. Вектор
удовлетворяющий уравнению
в линейной алгебре называюткорневым
вектором.
В нашем примере

мы имеем систему
т.е.

векторЗначит,

уравнений. Итак, теперь найдены три
линейно независимых решения системы
дифференциальных уравнений, поэтому
мы можем написать её общее решение:
Наконец,
выясним, как найти решения системы (23),
соответствующие комплексным
собственным значениям матрицы А.
Пусть
комплексный корень характеристического
уравнения, асоответствующий ему собственный вектор.
Имеем:Тогда
комплексное решение системы (23). Пусть
где
действительные вектор-функции. Так как
то
и мы получаем:
и
Таким образом, вектор-функции
и
тоже решения системы.
Проиллюстрируем
эти рассуждения примером.
Пример
4. Система
Чтобы
решить систему, вначале составим
характеристическое уравнение:
Отсюда
а значит,
Собственный вектор, соответствующий
собственному значениюнайдём из системы
т.е.

Следовательно,

в вектор-функциидействительную часть от мнимой:
Отсюда
получаем:

системы:
Подведём
итог рассуждениям этого параграфа,
сформулировав теорему. Недоказанным в
этой теореме останется лишь утверждение
(г) и метод нахождения решений в случае
отсутствия базиса из собственных
векторов. Эти недостающие детали можно
найти в более подробных учебниках по
дифференциальным уравнениям.
Теорема.
Решения системы дифференциальных
уравнений
с постоянными коэффициентами могут
быть получены следующим образом:
(а)
если корни
характеристического уравнения
действительны и различны, то общее
решение системы имеет вид
где
собственные векторы, соответствующие
собственным значенияма
произвольные постоянные;
(б)
если корни характеристического уравнения
действительные, не обязательно различные,
но существует базиспространства
состоящий из собственных векторов
(соответствующих числам),
то также
(в)
если
комплексный корень характеристического
уравнения исоответствующий собственный вектор,
то вектор-функциии
являются решениями системы дифференциальных
уравнений;
(г)
если
кратный корень характеристического
уравнения, то ему соответствует решение
системы, имеющее вида если
комплексный корень, то следует взять
и
Соседние файлы в папке Прокофьев
- #
- #
- #
- #
- #
- #
- #
Постоянный коэффициент
Cтраница 1
Постоянный коэффициент е в правой части уравнения ( 83) имеет размерность 1 / с. Его называют скоростью разгона объекта, под которой понимается скорость изменения выходной величины ф при предварительном скачкообразном изменении входной величины ц, равном единице.
[1]
Постоянный коэффициент Т0 при первой производной в левой части уравнений ( 95) и ( 96) имеет размерность времени и называется постоянной времени. Под постоянной времени объекта понимается время, в течение которого параметр объекта в случае скачкообразного возмущения достигнет нового равновесного состояния при условии, что параметр изменяется с постоянной скоростью, равной скорости в момент возмущения.
[2]
Постоянные коэффициенты этой функции определяются экспериментально. Многие гиперупругие тела незначительно изменяют свой объем при деформировании.
[3]
Постоянный коэффициент kw в формуле (4.12) обычно называют ветровым коэффициентом и принимают равным отношению скорости поверхностного течения к скорости ветра. Числовое значение kw получают как среднее арифметическое из большого количества результатов произведенных в натуре измерений.
[4]
Постоянные коэффициенты С зависят только от отношения с толщины стенки к диаметру оболочки и могут быть найдены без особых трудностей ( многие из этих – коэффициентов равны нулю) путем подстановки упомянутых выше представлений для перемещений в основные уравнения, приведения подобных членов и решения пблучающихся в результате алгебраических уравнений.
[5]
Постоянный коэффициент 48 80 был выведен как теплота полного сгорания угля, считая на один грамматом кислорода, а коэффициент 10 60 – как теплота конденсации образующихся водяных паров в жидкую воду.
[6]
Постоянные коэффициенты здесь имеют размерность сопротивлений и поэтому данная система уравнений называется системой г-параметров.
[8]
Постоянный коэффициент г, характерный для данного вещества, называют удельной рефракцией.
[9]
Постоянные коэффициенты В, С и D должны определяться из экспериментальных данных.
[10]
Постоянные коэффициенты Ь0 ется следующим образом.
[12]
Постоянные коэффициенты V0 и m определяются по двум точкам а и б, произвольно взятым на прямолинейной части графика ( см. рис. VII.
[13]
Постоянные коэффициенты at, bt и с / определяются из условия наибольшего соответствия формулы заданному участку характеристики. Если переходный процесс происходит на некоторой ветви частного цикла перемагничивания, то в аналитическое выражение необходимо ввести постоянную составляющую тока или магнитного потока.
[14]
Постоянный коэффициент К имеет размерность расстояния и называется длиной волны. Если мысленно представить себе электромагнитное поле застывшим во времени, то его изменение по дальности будет происходить с периодом К, то есть вдоль направления распространения поле имеет волновой характер.
[15]
Страницы:
1
2
3
4