 Этот урок будет посвящён многопосылочным умозаключениям. Так же как и в случае однопосылочных умозаключений, вся необходимая информация в скрытом виде будет присутствовать уже в посылках. Однако, поскольку посылок теперь будет много, то способы её извлечения становятся более сложными, а потому и добытая в заключении информация не будет казаться тривиальной. Кроме того, нужно отметить, что существует много разных видов многопосылочных умозаключений.
Этот урок будет посвящён многопосылочным умозаключениям. Так же как и в случае однопосылочных умозаключений, вся необходимая информация в скрытом виде будет присутствовать уже в посылках. Однако, поскольку посылок теперь будет много, то способы её извлечения становятся более сложными, а потому и добытая в заключении информация не будет казаться тривиальной. Кроме того, нужно отметить, что существует много разных видов многопосылочных умозаключений.
Мы с вами сосредоточимся только на силлогизмах. Они отличаются тем, что и в посылках и в заключении имеют категорические атрибутивные высказывания и на основании наличия или отсутствия каких-то свойств у объектов позволяют сделать вывод о наличии или отсутствии у них других свойств.
Содержание:
- Простой категорический силлогизм
- Правила терминов
- Задачи Эйнштейна
- Энтимемы
- Сориты
- Упражнения
- Проверочные вопросы на усвоение материала
Простой категорический силлогизм
Простой категорический силлогизм – это одно из наиболее простых и часто встречающихся умозаключений. Он состоит из двух посылок. В первой посылке говорится об отношении терминов А и В, во второй – об отношениях терминов В и С. На основании этого делается вывод об отношении терминов А и С. Такой вывод возможен потому, что обе посылки содержат общий термин В, который опосредует отношение между терминами А и С.
Приведём пример:
- Все рыбы не могут жить без воды.
- Все акулы – это рыбы.
- Следовательно, все акулы не могут жить без воды.
В данном случае, термин «рыбы» – это общий термин для двух посылок, и он помогает связать термины «акулы» и «существа, способные жить без воды». Общий термин для двух посылок принято называть средним термином. Субъект заключения (в нашем примере это «акулы») называют меньшим термином. Предикат заключения («существа, способные жить без воды») называют бóльшим термином. Соответственно, посылку, содержащую меньший термин, называют меньшей посылкой («Все акулы – это рыбы»), а посылку, содержащую больший термин, – бóльшей посылкой («Все рыбы не могут жить без воды»).
Фигура – это форма простого категорического силлогизма, которая определяется расположением среднего термина.
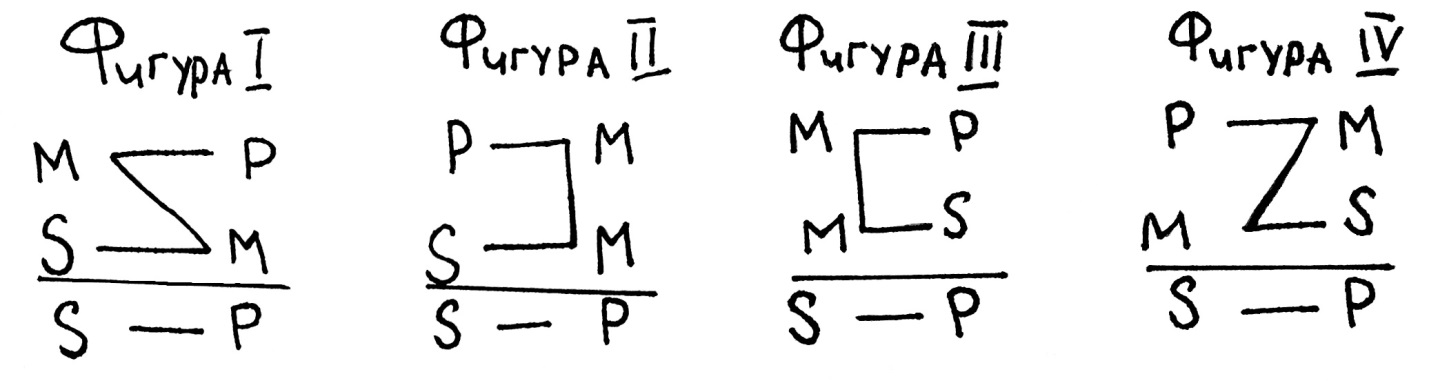
Сверху расположена большая посылка, за ней следует меньшая посылка, под чертой находится заключение. Буквой S обозначен меньший термин, буквой P – больший термин, буквой М – средний термин.
Далее, фигуры могут наполняться разным содержанием, то есть на место посылок и заключений могут подставляться разные типы категорических атрибутивных высказываний. Например:
- Всякий М есть P
- Всякий S есть М
- Всякий S есть P
или:
- Ни один М не есть P
- Некоторые М есть S
- Некоторые S не есть P
Эти различные сочетания высказываний в фигурах образуют так называемые модусы. Каждая фигура имеет 64 модуса, таким образом, на все четыре фигуры приходятся всего 256 модусов. Если подумать обо всём многообразии умозаключений, имеющих форму силлогизмов, то 256 модусов – это не так уж и много. Кроме того, далеко не все модусы образуют правильные умозаключения, то есть существуют такие модусы, которые при истинности посылок не гарантируют истинности умозаключения. Такие модусы называются неправильными. Правильными же называются те модусы, с помощью которых из истинных посылок мы всегда получаем истинное заключение. Всего существует 24 правильных модуса – по шесть на каждую фигуру. Это означает, что во всей классической силлогистике, которая исчерпывает львиную долю рассуждений, производимых людьми, существует всего 24 вида правильных умозаключений. Это очень маленькое число, поэтому правильные модусы не так уж и сложно запомнить.
Каждый из этих модусов ещё в Средние века получил особое мнемоническое наименование. Каждый тип категорического атрибутивного высказывания был обозначен с помощью всего одной буквы. Высказывания типа «Все S есть P» обозначили буквой «а», первой буквой в латинском слове «affirmo» («утверждаю»), и их запись превратилась в «SaP». Высказывания вида «Некоторые S есть P» записывались с помощью буквы «i», второй гласной в слове «affirmо», поэтому они выглядели как «SiP». Высказывания формы «Ни один S не есть P» обозначили буквой «е», первой гласной в латинском слове «nego» («отрицаю»), их стали записывать в виде «SeP». Как вы, наверное, уже догадались высказывания типа «Некоторые S не есть P» обозначили буквой «о», второй гласной в слове «nego», их формальная запись выглядела как «SoP». Поэтому модусы правильных силлогизмов традиционно обозначаются именно с помощью этих четырёх букв, которые для удобства запоминания представлены в виде слов. Таблица всех правильных модусов выглядит так:
|
Фигура I |
Фигура II |
Фигура III |
Фигура IV |
|
Barbara (aaa) Celarent (eae) Darii (aii) Ferio (eio) Barbari (aai) Celaront (eao) |
Baroko (aoo) Cesare (eae) Camestres (aee) Festino (eio) Camestrop (aeo) Cesaro (eao) |
Bocardo (oao) Disamis (iai) Datisi (aii) Ferison (eio) Darapti (aai) Felapton (eao) |
Camenos (aeo) Dimaris (iai) Camenes (aee) Fresison (eio) Bramantip (aai) Fesapo (eao) |
К примеру, модус второй фигуры Cesare (eae) в развёрнутом виде будет выглядеть так:
- Ни один P не есть М
- Все S есть М
- Ни один S не есть P
Хотя 24 модуса – это совсем не много и в таблице можно усмотреть некоторые регулярности (например, для всех фигур верны модусы eao и eio), запомнить её всё равно сложно. К счастью, это совсем и необязательно. Для проверки силлогизмов можно также пользоваться модельными схемами. Только в отличие от тех схем, которые мы строили раньше, на них уже должно присутствовать не два, а три термина: S, P, M.
Давайте возьмём модус четвёртой фигуры Bramantip (aai) и проверим его с помощью модельных схем.
- Всякий P есть М
- Всякий М есть S
- Некоторые S есть P
Сначала нужно найти такие модельные схемы, при которых обе посылки будут одновременно истинными. Таких схем всего четыре:
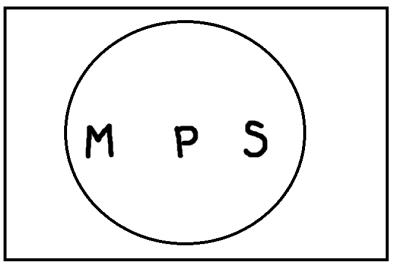
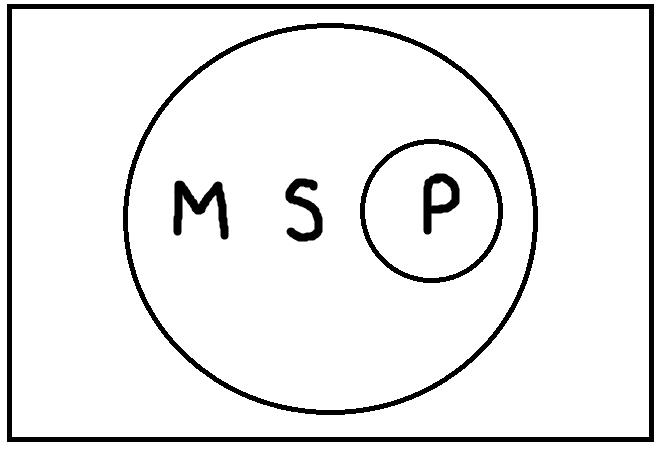
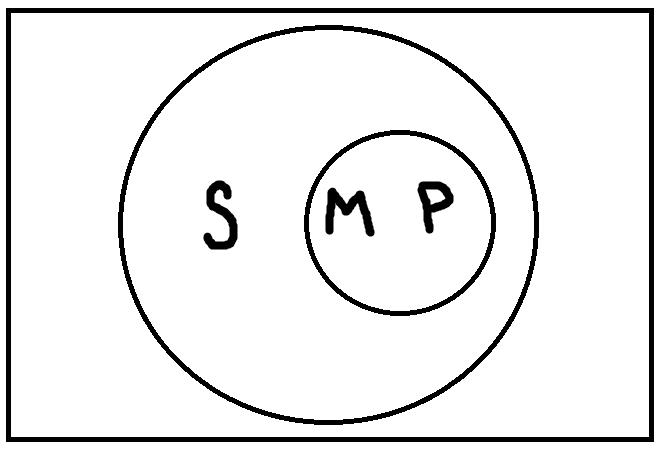
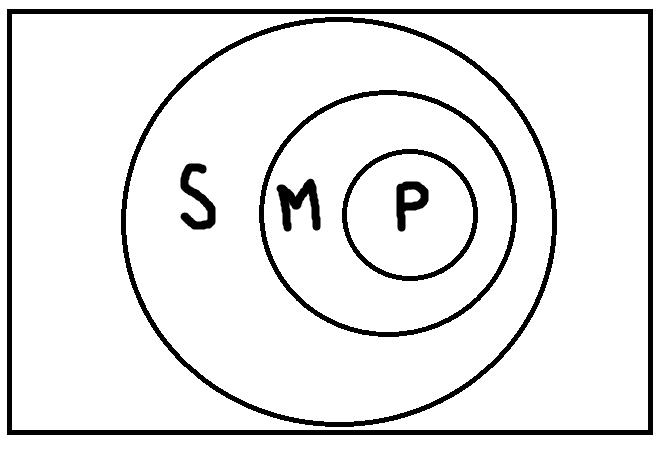
Теперь на каждой из этих схем мы должны проверить, верно ли будет высказывание «Некоторые S есть P», представляющее заключение. В результате проверки, мы обнаруживаем, что на каждой схеме это высказывание будет верным. Таким образом, умозаключение по модусу Bramantip (aai) четвёртой фигуры правильное. Если бы была хотя бы одна схема, на которой это высказывание было бы ложным, то умозаключение было бы неправильным.
Метод проверки силлогизмов с помощью модельных схем хорош, так как он позволяет представить отношения между терминами наглядно. Однако для некоторых посылок могут оказаться верными очень много схем сразу. В результате их построение и проверка будут представлять собой трудоёмкую и отнимающую много времени задачу. Таким образом, метод модельных схем не всегда удобен.
Поэтому логики разработали ещё один метод для определения, правильный силлогизм или нет. Этот метод называется синтаксическим и представляет собой два перечня правил (правила терминов и правила посылок), при соблюдении которых силлогизм будет верным.
Модус простого категорического силлогизма является правильным, если он удовлетворяет следующим условиям:
Правила терминов
- Простой категорический силлогизм должен включать только три термина.
- Средний термин должен быть распределён хотя бы в одной из посылок.
- Если больший или меньший термин не распределён в посылке, то он должен быть нераспределён и в заключении.
Правила посылок:
- Хотя бы одна из посылок должна быть утвердительной.
- Если обе посылки являются утвердительными, то и заключение должно быть утвердительным.
- Если одна из посылок отрицательная, то и заключение должно быть отрицательным.
Правила посылок понятны, а правила терминов требуют некоторых пояснений. Начнём с правила о трёх терминах. Хотя оно кажется очевидным, оно довольно часто нарушается вследствие так называемой подмены терминов. Посмотрите на следующий силлогизм:
- Золото – элемент 11 группы, шестого периода периодической системы химических элементов Д. И. Менделеева, с атомным номером 79.
- Молчание – золото.
- Молчание – элемент 11 группы, шестого периода периодической системы химических элементов Д. И. Менделеева, с атомным номером 79.
Прежде всего, если вы помните фигуры и правильные модусы, вы сразу можете сказать, что этот силлогизм неправильный, так как он относится ко второй фигуре и имеет модус aaa, который не принадлежит к списку правильных модусов для этой фигуры. Но если вы их не помните, всё равно вы можете выявить его ложность, потому что здесь явно присутствует четыре термина, вместо трёх. Термин «золото» употребляется в двух совершенно различных смыслах: как химический элемент и как нечто, обладающее ценностью. Посмотрим на более сложный пример:
- Все книги из собрания Российской государственной библиотеки нельзя прочитать за целую жизнь.
- «Отцы и дети» Ивана Тургенева – книга из собрания Российской государственной библиотеки.
- «Отцы и дети» Ивана Тургенева нельзя прочитать за целую жизнь.
Кажется, что этот силлогизм соответствует модусу Barbara первой фигуры. Однако посылки истинны, а заключение ложно.
Если бы мы заменили слово «все» на слова «каждый в отдельности», то первая посылка попросту стала бы ложной: «Каждую в отдельности книгу из собрания Российской государственной библиотеки нельзя прочитать за целую жизнь». Таким образом, мы получаем четыре термина вместо трёх, а потому это умозаключение ложно.
Теперь перейдём к правилам о распределённости терминов. Для начала объясним, что это за характеристика. Термин называют распределённым, если в высказывании речь идёт обо всех объектах, входящих в его объём. Соответственно, термин не распределён, если в высказывании речь идёт не обо всех объектах, составляющих его объём. Грубо говоря, термин распределён, если мы говорим обо всех предметах, и не распределён, если мы говорим только о некоторых предметах, о части объёма термина.
Давайте возьмём типы высказываний и посмотрим, какие термины в них распределены, а какие нет. Распределённый термин отмечается знаком «+», нераспределённый – знаком «–».
Все S+ есть P–.
Ни один S+ не есть P+.
Некоторые S– есть P–.
Некоторые S– не есть P+.
а+ есть P–.
a+ не есть P+.
Как видно, субъект всегда распределён в общих и единичных высказываниях, но не распределён в частных. Предикат всегда распределён в отрицательных высказываниях, но не распределён в утвердительных. Если теперь перенести это на наши правила для терминов, то получается, что средний термин хотя бы в одной из посылок должен быть взят во всём своём объёме.
- Пингвины – это птицы.
- Некоторые птицы не умеют летать.
- Пингвины не умеют летать.
Хотя и высказывания над чертой и высказывание под чертой истинны, умозаключение как таковое здесь отсутствует. Здесь нет логического перехода от посылок к заключению. И это можно легко выявить, так как средний термин «птицы» ни разу не берётся во всём своём объёме.
Что касается третьего правила терминов, если в посылках речь идёт только о части объектов из объёма терминов, то в заключении мы не можем ничего утверждать обо всех объектах объёма терминов. Мы не можем перейти от части к целому. Кстати, обратный переход возможен: если мы говорим обо всех элементах объёма терминов, то мы можем сделать заключение о части из них.
Задачи Эйнштейна
Эта игра является нашей версией всемирно известной «загадки Эйнштейна», в которой 5 иностранцев живут на 5 улицах, едят 5 видов еды и т.д. Подробнее про эту задачу написано здесь. В подобных заданиях вам нужно сделать правильное умозаключение на основе имеющихся посылок, которых, на первый взгляд, для этого недостаточно.
Энтимемы
Во время реальных дискуссий и споров мы довольно часто опускаем те или иные части рассуждения. Это приводит к возникновению энтимем. Энтимема – это сокращённая форма умозаключения, в которой пропущены посылки или заключение. Важно не путать энтимемы с однопосылочными умозаключениями. Энтимема – это именно многопосылочное умозаключение, просто его части в силу тех или иных причин опущены. Иногда такие пропуски оправданы, так как оба собеседника хорошо разбираются в проблеме, и им нет нужды проговаривать все шаги. Между тем, недобросовестные собеседники могут специально пользоваться энтимемами, чтобы затемнить и запутать своё рассуждение и скрыть свои истинные аргументы или выводы. Поэтому необходимо уметь отличать корректные энтимемы от некорректных. Энтимема называется корректной, если она может быть восстановлена в виде правильного модуса категорического силлогизма, и если все пропущенные посылки оказываются истинными.
Поговорим о том, как восстановить энтимему до полного силлогизма. В первую очередь нужно понять, что именно пропущено. Для этого нужно обратить внимание на слова-маркеры, обозначающие причинно-следственные связи: «таким образом», «следовательно», «так как», «потому что», «в результате» и т.д. К примеру, возьмём рассуждение: «Золото – это драгоценный металл, потому что оно практически не окисляется на воздухе». Здесь заключением является высказывание «Золото – это драгоценный металл». Одна из посылок: «Золото практически не окисляется на воздухе». Ещё одна посылка пропущена. Нужно сказать, что чаще всего пропускают именно одну из посылок. Довольно странно, если в рассуждении отсутствует самое важное – вывод.
Итак, мы установили, что именно пропущено. В нашем примере – это посылка. Большая это посылка или меньшая? Как вы помните, меньшая посылка содержит субъект заключения («золото»), а большая – предикат заключения («драгоценный металл»). Посылка, содержащая субъект заключения нам уже известна: «Золото практически не окисляется на воздухе». Значит, нам известна меньшая посылка, и не известна большая. Кроме того, благодаря известной посылке, мы можем установить и средний термин: «металлы, которые практически не окисляются на воздухе», – тот термин, который не содержится в заключении.
Теперь располагаем известную нам информацию в форме силлогизма:
- 1.
- 2. Золото практически не окисляется на воздухе.
- 3. Золото – это драгоценный металл.
Или в виде схемы:
- 1.
- 2. SaМ
- 3. SaP
В большей посылке должны находиться предикат заключения и средний термин: «драгоценные металлы» (P) и «металлы, которые окисляются на воздухе» (M). Здесь возможны два варианта:
- 1. P M
- 2. SaМ
- 3. SaP
Или:
- 1. М P
- 2. SaМ
- 3. SaP
Значит, возможен силлогизм либо второй фигуры, либо первой фигуры. Теперь смотрим на нашу табличку с правильными модусами силлогизмов. Во второй фигуре вообще нет правильных модусов, где в заключении стояло бы высказывание типа а. В первой фигуре есть только один такой модус – Barbara. Достраиваем наш силлогизм:
- 1. МаP
- 2. SaМ
- 3. SaP
Или:
- 1. Все металлы, которые практически не окисляются на воздухе, являются драгоценными.
- 2. Золото практически не окисляется на воздухе.
- 3. Золото – драгоценный металл.
Теперь проверяем, истинна ли наша восстановленная посылка. В нашем случае она истинна, поэтому энтимема была правильной.
Сориты
Термином «сориты» пользовался Льюис Кэррол для обозначения сложных силлогизмов, которые имеют более чем две посылки. По большому счёту, сорит представляет собой гибрид силлогизма и энтимемы. Он устроен следующим образом: дано множество посылок, из каждой пары посылок делаются промежуточные выводы, которые обычно опускаются, к промежуточным выводам присоединяются новые посылки, из них делаются новые промежуточные выводы, к которым опять присоединяются новые посылки и так далее, пока мы не переберём все имеющиеся посылки и не дойдём до окончательного заключения. В принципе подобным образом люди и рассуждают в повседневной жизни. Поэтому очень важно уметь решать сориты и оценивать, правильны они или нет.
Мы приведём пример сорита из книги Льюиса Кэррола «История с узелками»:
1. Все полисмены из нашей округи ужинают у нашей кухарки.
2. Человек с длинными волосами не может не быть поэтом.
3. Амос Джадд никогда не сидел в тюрьме.
4. Все кузены нашей кухарки любят холодную баранину.
5. В этой округе нет других поэтов, кроме полисменов.
6. С нашей кухаркой не ужинает никто, кроме её кузенов.
7. Все люди с короткими волосами сидели в тюрьме.
8. Амос Джадд любит холодную баранину.
Над чертой находятся посылки, под чертой – заключение.
Как же нужно решать и проверять сориты? Дадим пошаговую инструкцию. Во-первых, необходимо привести все посылки в более или менее стандартную форму:
1. Все полисмены из нашей округи ужинают у нашей кухарки.
2. Все люди с длинными волосами являются поэтами.
3. Амос Джадд не сидел в тюрьме.
4. Все кузены нашей кухарки любят холодную баранину.
5. Все поэты из нашего округа являются полисменами.
6. Все люди, ужинающие с нашей кухаркой, приходятся ей кузенами.
7. Все люди с короткими волосами сидели в тюрьме.
Теперь нужно взять две исходные посылки. По большому счёту, неважно, с каких именно посылок вы начнёте. Главное, чтобы ваши исходные посылки вместе содержали всего три термина. Это означает, что мы не можем взять посылки «Амос Джадд не сидел в тюрьме» и «Все кузены нашей кухарки любят холодную баранину». В них входят четыре разных термина, а потому мы не можем сделать из них никакого заключения. Я в качестве исходных возьму посылки 7 и 3 и сделаю из них вывод по правилам для простых категорических силлогизмов.
- 1. Все люди с короткими волосами сидели в тюрьме.
- 2. Амос Джадд не сидел в тюрьме.
- 3. Амос Джадд не является человеком с короткими волосами.
Этот силлогизм соответствует модусу Camestres (aee) второй фигуры. Теперь для удобства я переформулирую наш промежуточный вывод следующим образом: «Амос Джадд является человеком с длинными волосами». Этот промежуточный вывод я соединяю с посылкой номер 2:
- 1. Все люди с длинными волосами являются поэтами.
- 2. Амос Джадд является человеком с длинными волосами.
- 3. Амос Джадд является поэтом.
Этот силлогизм соответствует модусу Barbara (aaa) первой фигуры. Теперь я присоединяю этот промежуточный вывод к посылке номер 5:
- 1. Все поэты из нашего округа являются полисменами.
- 2. Амос Джадд является поэтом.
- 3. Амос Джадд является полисменом.
Этот силлогизм опять же соответствует модусу Barbara (aaa) первой фигуры. Присоединяем промежуточный вывод к посылке номер 1:
- 1. Все полисмены из нашей округи ужинают у нашей кухарки.
- 2. Амос Джадд является полисменом.
- 3. Амос Джадд ужинает у нашей кухарки.
Это силлогизм, как вы уже, наверное, заметили, тоже представляет собой модус Barbara (aaa) первой фигуры. Присоединяем этот вывод к посылке номер 6:
- 1. Все люди, ужинающие с нашей кухаркой, приходятся ей кузенами.
- 2. Амос Джадд ужинает у нашей кухарки.
- 3. Амос Джадд приходится кузеном нашей кухарке.
Опять Barbara, которая является одним из самых распространённых модусов. Присоединяем к нашему последнему промежуточному выводу последнюю посылку номер 4:
- 1. Все кузены нашей кухарки любят холодную баранину.
- 2. Амос Джадд приходится кузеном нашей кухарке.
- 3. Амос Джадд любит холодную баранину.
Итак, с помощью всё того же модуса Barbara мы получили наше заключение: «Амос Джадд любит холодную баранину». Таким образом, сориты решаются и проверяются с помощью пошагового разделения на простые категорические силлогизмы. В нашем примере сорит оказался правильным, но возможны и обратные ситуации. Существует два условия корректности соритов. Во-первых, каждый сорит должен разбиваться на последовательность правильных модусов силлогизмов. Во-вторых, заключение, которое вы получаете, когда все посылки исчерпаны, должно совпасть с заключением сорита. Это условие действует в тех случаях, когда вы имеете дело с чужим рассуждением, в котором уже присутствует какое-то заключение.
Итак, мы рассмотрели различные многопосылочные умозаключения на примере простых категорических силлогизмов, энтимем и соритов. По большому счёту, если вы знаете, как иметь с ними дело, то вы вооружены для любых дискуссий с любыми противниками. Единственное, что может на данный момент вызывать некоторое недовольство, это необходимость тратить много времени на проверку правильности умозаключений. Не стоит расстраиваться по этому поводу: лучше выглядеть тугодумом, который рассуждает правильно, чем блестящим демагогом, который не замечает своих и чужих ошибок. Тем более, с накоплением опыта внимательного отношения к умозаключениям у вас появится чутьё, автоматический навык, позволяющий быстро отделять корректные рассуждения от некорректных. Поэтому упражнений к этому уроку будет много, чтобы у вас была возможность набить руку.
Упражнения
Упражнения 1, 2 и 3 взяты из книги Льюиса Кэррола «История с узелками», М.: Мир, 1973.
Упражнение 1
Сделайте заключения из следующих посылок по правилам для простого категорического силлогизма. Помните, что простой категорический силлогизм должен содержать только три термина. Не забывайте приводить высказывания к стандартному виду.
1
- Зонтик – очень нужная вещь в путешествии.
- Отправляясь в путешествие, всё лишнее следует оставлять дома.
- ?
2
- Музыка, которую можно услышать, вызывает колебания воздуха.
- Музыка, которую нельзя услышать, не стоит того, чтобы за неё платили деньги.
- ?
3
- Ни один француз не любит пудинга.
- Все англичане любят пудинг.
- ?
4
- Ни один старый скряга не жизнерадостен.
- Некоторые старые скряги тощи.
- ?
5
- Все непрожорливые кролики чёрные.
- Ни один старый кролик не склонен к воздержанию в пище.
- ?
6
- Ничто разумное никогда не ставило меня в тупик.
- Логика ставит меня в тупик.
- ?
7
- Ни в одной из исследованных до сих пор стран не обитают драконы.
- Неисследованные страны пленяют воображение.
- ?
8
- Некоторые сны ужасны.
- Ни один барашек не внушает ужаса.
- ?
9
- Ни одному лысому созданию не нужна расчёска.
- Ни у одной ящерицы нет волос.
- ?
10
- Все яйца можно разбить.
- Некоторые яйца сварены вкрутую.
- ?
Упражнение 2
Проверьте, правильны ли следующие рассуждения. Попробуйте разные способы проверки. Не забывайте ставить большую посылку на первую строку.
1
- Словари полезны.
- Полезные книги высоко ценятся.
- Словари высоко ценятся.
2
- Золото тяжёлое.
- Ничто, кроме золота, не сможет заставить его замолчать.
- Ничто лёгкое не сможет заставить его замолчать.
3
- Некоторые галстуки безвкусны.
- Всё, сделанное со вкусом, приводит меня в восторг.
- Я не в восторге от некоторых галстуков.
4
- Ни одно ископаемое животное не может быть несчастно в любви.
- Устрица может быть несчастна в любви.
- Устрицы – не ископаемые животные.
5
- Ни одна горячая сдоба не полезна.
- Все булочки с изюмом неполезны.
- Булочки с изюмом – не сдоба.
6
- Некоторые подушки мягкие.
- Ни одна кочерга не мягкая.
- Некоторые кочерги – не подушки.
7
- Скучные люди невыносимы.
- Ни одного скучного человека не упрашивают остаться, когда он собирается уходить из гостей.
- Ни одного невыносимого человека не упрашивают остаться, когда он собирается уходить из гостей.
8
- Ни одна лягушка не имеет поэтической внешности.
- Некоторые утки выглядят прозаично.
- Некоторые утки – не лягушки.
9
- Все разумные люди ходят ногами.
- Все неразумные люди ходят на голове.
- Ни один человек не ходит на голове и ногах.
Упражнение 3
Найдите заключения следующих соритов.
1
- Малые дети неразумны.
- Тот, кто может укрощать крокодилов, заслуживает уважения.
- Неразумные люди не заслуживают уважения.
2
- Ни одна утка не танцует вальс.
- Ни один офицер не откажется потанцевать вальс.
- У меня нет другой птицы, кроме уток.
3
- Всякий, кто находится в здравом уме, может заниматься логикой.
- Ни один лунатик не может быть присяжным заседателем.
- Ни один из ваших сыновей не может заниматься логикой.
4
- В этой коробке нет моих карандашей.
- Ни один из моих леденцов – не сигара.
- Вся моя собственность, не находящаяся в этой коробке, состоит из сигар.
5
- Ни один терьер не блуждает среди знаков Зодиака.
- То, что не блуждает среди знаков Зодиака, не может быть кометой.
- Только у терьера хвост колечком.
6
- Никто не станет выписывать газету «Таймс», если он не получил хорошего образования.
- Ни один дикобраз не умеет читать.
- Те, кто не умеет читать, не получили хорошего образования.
7
- Никто их тех, кто действительно ценит Бетховена, не станет шуметь во время исполнения «Лунной сонаты».
- Морские свинки безнадёжно невежественны в музыке.
- Те, кто безнадёжно невежественен в музыке, не станут соблюдать тишину во время исполнения «Лунной сонаты».
8
- Вещи, продаваемые на улице, не имеют особой ценности.
- Только дрянь можно купить за грош.
- Яйца большой гагарки представляют большую ценность.
- Лишь то, что продаётся на улице, и есть настоящая дрянь.
9
- Те, кто нарушает свои обещания, не заслуживают доверия.
- Любители выпить очень общительны.
- Человек, выполняющий свои обещания, честен.
- Ни один трезвенник не ростовщик.
- Тому, кто очень общителен, всегда можно верить.
10
- Любая мысль, которую нельзя выразить в виде силлогизма, поистине смешна.
- Моя мечта о сдобных булочках не стоит того, чтобы её записывать на бумаге.
- Ни одну мою несбыточную мечту нельзя выразить в виде силлогизма.
- Мне не приходило в голову ни одной действительно смешной мысли, о которой я бы не сообщим своему другу.
- Я только и мечтаю, что о сдобных булочках.
- Я никогда не высказывал своему другу ни одной мысли, если она не стоила того, чтобы её записать на бумаге.
Упражнение 4
Проверьте правильность следующих энтимем.
- Барсик – не законопослушный кот, потому что он украл у меня сосиску.
- Ртуть жидкая, следовательно, она не может быть металлом.
- Ни один послушный ребёнок не устраивает истерик по пустякам. Поэтому Толя – непослушный ребёнок.
- Некоторые женщины глупы, значит, некоторые мужчины могут этим воспользоваться.
- Все девушки хотят выйти замуж, так как каждая из них мечтает о пышном белом платье.
- Ни один студент не хочет получить двойку на экзамене, вот почему все студенты – ботаники.
- Некто украл у меня кошелёк, поэтому у меня совсем не осталось денег.
- Павлины – самовлюблённые птицы, потому что у них большой красивый хвост.
Проверьте свои знания
Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.
← 6 Умозаключения8 Типы рассуждений →
Юлия Валерьевна Шульгина
Эксперт по предмету «Логика»
преподавательский стаж — 10 лет
Задать вопрос автору статьи
Большая и меньшая посылки как части силлогизма
Определение 1
Большая и меньшая посылки – это суждения, содержащие исходную информацию для формирования заключения в силлогизме.
Силлогизм – это одна из важнейших для логики форм умозаключения; точнее говоря, дедуктивного умозаключения.
Определение 2
Силлогизм – это форма умозаключения, предусматривающая вывод из двух суждений третьего (с необходимостью).
В силлогизме по крайней мере одно из исходных суждений (посылок) должно носить общий характер (общеутвердительный или общеотрицательный), поэтому умозаключение ведется от общего. Полученное суждение не может быть более общим, чем исходные.

Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Пример силлогизма:
Пример 1
Все смартфоны – сложные технические изделия.
FJ42 – смартфон.
FJ42 – сложное техническое изделие.
На этом примере наглядно продемонстрировано, как из двух суждений с необходимостью выводится третьей. При этом истинность исходных суждений остается за кадром. В силлогизме считается, что они уже допущены, что позволяет осуществить вывод нового суждения.
Основные части силлогизма:
- посылки (предпосылки) – исходные суждения,
- заключение – новое суждение, полученное путем сопоставления посылок.
Понятия, входящие в состав указанных суждений, называют терминами. Их должно быть ровно три:
- меньший термин является подлежащим (субъектом) в заключении и входит (как подлежащее или сказуемое) в меньшую посылку;
- средний термин входит в две посылки (может быть подлежащим или сказуемым в каждой из них), но отсутствует в заключении;
- больший термин является сказуемым (предикатом) в заключении и входит в большую посылку (может быть в ней подлежащим или сказуемым).
« Большая и меньшая посылки» 👇
Обозначение «больший» и «меньший» для терминов связано с их ролью и объемом. В типичном случае силлогистического вывода на долю предиката заключения приходится самый большой объем, а на долю субъекта – самый маленький. Это может быть продемонстрировано схемой. Средний термин называют так по двум причинам:
- он имеет средний объем (больше меньшего термина, но меньше большего);
- он служит связующим звеном для большего и меньшего термина, обеспечивает их сравнение. Напрямую эти термины не сравниваются – только посредством среднего термина.
В рассмотренном примере самый большой объем имеет понятие «сложные технические изделия». В эту категорию входят не только смартфоны (средний термин), но и телевизоры, ноутбуки и т. д. Только часть сложных технических изделий – это смартфоны. Аналогично с конкретной моделью FJ42 (меньший термин) – смартфоны бывают и других моделей.
Названия суждений определяются входящими в них терминами:
- то суждение, в которое входит больший термин, называется большим;
- то суждение, в которое входит меньший термин, называется меньшим.
Аксиома силлогизма
Силлогизм описывается формой и содержанием:
- под содержанием понимают термины, имеющиеся в силлогизме,
- под формой понимают связь, придаваемую терминам посылок.
Истинность или ложность конкретных посылок имеет вторичное значение и не является предметом исследования. С точки зрения силлогистики важно только корректное построение умозаключения, правильная связь между большим и меньшим терминами. Бывает, что посылки ложные, но при исключении среднего термина получается истинное заключение (хотя гарантировать этого нельзя в общем случае).
Пример получения истинного заключения из ложных посылок:
Пример 2
Все дорожные знаки красные.
«Проезд запрещен» – дорожный знак.
Знак «Проезд запрещен» красный.
Здесь большая посылка ложная (бывают знаки и других цветов), но вывод истинный. Но если бы в меньшей посылке взяли другой знак (например, зеленый знак «автомагистраль»), правильным образом построенный вывод («Знак «автомагистраль» красный») был бы ложным.
Умозаключение силлогизма таково, что при допущении посылок заключение вытекает из них необходимым образом. Необходимость обосновывается следующим положением, называемым аксиомой силлогизма: «Если одна вещь полностью находится в другой, а эта другая вещь полностью находится вне третьей, то первая тоже находится вне третьей». Точно так же, если вторая вещь находится внутри третьей, то и первая находится внутри третьей. Иными словами, все, утверждаемое относительно класса вещей, утверждается и для каждой вещи из этого класса; все, отрицаемое относительно класса вещей, отрицается и для каждого элемента этого класса. Очевидность этого положения позволяет называть его аксиомой. На нем базируется необходимость заключения силлогизма на основании данных посылок.
Правила построения большей и меньшей посылок
Чтобы силлогизм был правильным, его посылки и заключение должны строиться с соблюдением определенных правил:
- хотя бы в одной из посылок средний термин должен браться в полном объеме;
- если в посылке термин взят не в полном объеме, также частично он должен быть взят и в заключении;
- если обе посылки отрицательны, заключение не может быть получено;
- если обе посылки частные, заключение не может быть получено;
- при наличии частной посылки заключение будет частным;
- при наличии отрицательной посылки заключение будет отрицательным;
-
силлогизм должен содержать ровно три термина. При этом один из терминов должен входить в обе посылки (это должен быть неизменный термин), и по одному термину в посылках должны различаться.
Если большая и меньшая посылка содержат всего два термина, построить заключение не удастся (не будет возможности получить какую-то новую информацию):
Все груши – это фрукты.
Некоторые фрукты – груши.
Если в посылках будет четыре термина, они не будут содержать необходимой связи для построения заключения. Часто встречается ошибка учетверения терминов, когда средний термин выражается одним словом, но имеющим разные значения (обычно прямое и переносное):
Пример 3
Все проводники должны сдавать экзамен на знание транспортной безопасности.
Все металлы – проводники.
Все металлы должны сдавать экзамен на знание транспортной безопасности.
Здесь в большей посылке идет речь о проводниках как профессии, а в меньшей – о проводящих электрический ток веществах.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Определение силлогизма. Мы рассмотрели непосредственные умозаключения, теперь перейдём к рассмотрению посредственных умозаключений и из них прежде всего рассмотрим дедуктивные умозаключения. Дедуктивные умозаключения принимают формы силлогизма. Силлогизм есть такая форма умозаключения, в которой из двух суждений необходимо вытекает третье, причём одно из двух данных суждений является обще-утвердительным или обще-отрицательным. Силлогизм, таким образом, представляет собой умозаключение от общего. Полученное суждение ни в коем случае не будет более общим, чем суждения, из которых оно выводится.
Например, нам даются два суждения:
Все растения суть организмы.
Сосны суть растения.
Из них следует, что «сосны суть организмы».
Этот пример показывает, что, если нам даются два суждения, из них необходимо получается новое суждение. Мы не входим в рассмотрение того, истинны ли эти суждения или нет, но раз только мы допустим их, то тотчас же необходимо следует новое суждение.
Части силлогизма. Данные суждения называются предпосылками или посылками (praemissae), а новое суждение, которое получается из сопоставления посылок, называется заключением (conclusio). Те понятия, которые входят в заключение и предпосылки, называются терминами (termini). Подлежащее заключения («сосны») называется меньшим термином (terminus minor), сказуемое заключения («организмы») называется большим термином (terminus major), а термин «растение», который не входит в заключение, называется средним термином (terminus medius). Обозначение, терминов большими или меньшими находится зависимости от того, какой объём им присущ в одном из типичных случаев силлогистического вывода, как в только что приведённом. Самый больший объём приходится на долю сказуемого («организмы»), самый меньший – на долю меньшего термина, подлежащего заключения («сосны»), а средний – на долю среднего термина («растения»), который не входит в заключение. Это наглядно обнаруживается, если изобразить отношение между терминами схематически. На рис. 19 S обозначает меньший термин, M – средний, P – больший.
Средний термин называется средним также потому, что он служит посредствующим связующим элементом между большим и меньшим терминами. Средний термин служит для сравнения большего термина с меньшим. Сами по себе эти термины не могут быть сравниваемы. Сравнение может происходить через посредство среднего термина. Мы не могли бы связать термин «сосны» с термином «организмы», если бы у нас не было термина «растения», который связывается, с одной стороны, с термином «организмы», с другой стороны, с термином «сосны» и, таким образом, служит связующим звеном между термином «сосны» и термином «организмы».
Суждение, в которое входит больший термин, называется большей посылкой ; суждение, в которое входит меньший термин, называется меньшей посылкой.
Форма и содержание силлогизма. В силлогизме нужно отличать содержание от формы. Содержание – это термины, которые имеются налицо. Форма есть связь, которая придаётся нами терминам посылок. В силлогизме мы можем не обращать никакого внимания на истинность или ложность посылок. Для нас важно только сделать правильный вывод, совершить правильное умозаключение, правильно связать больший термин с меньшим, а это и есть форма силлогизма. Поэтому иногда посылки могут быть ложными, а заключение будет всё-таки истинным, как это можно видеть из следующего силлогизма, посылки которого состоят из очевидно ложных суждений:
Львы суть травоядные.
Коровы суть львы.
Коровы суть травоядные.
Аксиома силлогизма. Силлогистическое умозаключение таково, что раз мы допустили посылки, то из них необходимо будет вытекать заключение. Но почему же происходит то, что при наличности известных посылок заключение вытекает из них необходимо? Такого рода отношение между посылками и заключением объясняется следующим положением: «если одна вещь находится в другой, а эта другая находится в третьей, то первая находится в третьей», или «если одна вещь находится в другой, а эта другая находится вне третьей, то и первая также находится вне третьей». Это положение, которое называется аксиомой силлогизма, можно, иллюстрировать при помощи следующей схемы:
Если A находится в B, а B находится в C, то, следовательно, A находится в C. Далее, если A находится в B, но B находится вне C, то A также находится вне C.
Наиболее общая формула этой аксиомы называется в логике dictum de omni et de nullo. Полное выражение этой аксиомы будет: «quidquid de omni valet, valet etiam de quibusdam et de singulis. Quidquid de nullo valet, nec de quibusdam valet, nec de singulis». Смысл этой аксиомы заключается в следующем: всё, что утверждается относительно целого класса, утверждается и относительно каждой вещи, которая содержится в этом классе, и наоборот: всё, что отрицается относительно целого класса, отрицается относительно всего, что содержится в этом классе. Это положение называется аксиомой, потому что оно очевидно; аксиомой же силлогизма оно называется потому, что на нём основывается необходимость вывода заключения силлогизма из данных предпосылок.
Правила силлогизма. Рассмотрим, какие правила мы должны соблюсти при построении силлогизма, чтобы он был правилен, или, другими словами, каким условиям должен удовлетворять силлогизм, чтобы заключение было правильно. Первое правило:
1. Во всяком силлогизме должно быть не менее и не более трёх терминов.
Если даётся более трёх терминов, то силлогистического соединения получиться не может. Если мы возьмём такой пример:
Все ораторы тщеславны.
Цицерон был государственный человек.
то в данных двух суждениях четыре термина, и вывода сделать нельзя. Если бы второе суждение было: «Цицерон оратор», то можно было бы сделать вполне определённый вывод, потому что тогда в силлогизме было бы три термина.
Иногда в силлогизме бывает четыре термина, а на первый взгляд кажется, что их только три. Это происходит вследствие двусмысленности терминов. Вот пример:
Лук есть оружие дикарей.
Это растение есть лук.
Это растение есть оружие дикарей.
Ошибка в этом случае происходит вследствие того, что средний термин в большей посылке употреблён не в том же смысле, в каком он употреблён в меньшей посылке. Таким образом, в силлогизме вместо трёх терминов получается четыре. Такая погрешность называется quaternio terminorum (учетверение терминов).
Второе правило силлогизма формулируется следующим образом:
2. Во всяком силлогизме должно быть не более и не менее трёх суждений.
Это оттого, что при трёх терминах может быть только три суждения. В самом деле, если у нас есть три термина, два из которых должны входить в состав того или другого суждения, причём одна и та же пара терминов не должна повторяться, то ясно, что при трёх терминах можно получить только три суждения.
3. Средний термин должен быть взят по крайней мере в одной из посылок во всём объёме. Для пояснения этого правила возьмём пример:
Все французы суть европейцы.
Все парижане суть европейцы.
Из этих двух посылок нельзя сделать никакого заключения. Но если бы средний термин мы взяли хоть в одной посылке во всём объёме, то заключение было бы возможно сделать. Например:
Все французы суть европейцы.
Все европейцы суть грамотны.
Следовательно, все французы суть грамотны.
Возьмём ещё пример:
Все натуралисты наблюдательны.
N наблюдателен.
Следовательно, N натуралист.
Так как термин «наблюдателен» взят не во всём объёме, то в класс наблюдательных кроме натуралистов могут входить и историки, и художники, и т.п. Следовательно, N может быть наблюдателен и в то же время находиться вне круга натуралистов, как это можно видеть на прилагаемой схеме (рис. 20).
Если бы было сказано:
Все наблюдательные люди суть натуралисты.
N наблюдателен.
Следовательно, N натуралист. –
то такой вывод был бы правилен.
В первом случае средний термин ни в одной из посылок не взят во всём объёме. Вследствие этого получается неопределённость. А именно: может случиться, что мы один раз берём одну часть среднего термина, а другой раз – другую, как это можно видеть на схеме. Между тем, если средний термин взят хоть один раз во всём объёме, то мы и в большей и в меньшей посылке будем иметь дело с одним и тем же.
Если вообще средний термин взят хоть в одной посылке во всём объёме, тогда имеется налицо то, что связывает больший термин с меньшим термином. Если же он не входит ни в большую посылку, ни в меньшую во всём объёме, то он не может выполнять своего назначения – быть соединительным звеном, потому что в таком случае больший или меньший термин относятся к чему-либо неопределённому, как в приведённом выше случае: N может быть внутри круга натуралистов, но может быть и вне этого круга. Вследствие этого не может получиться определённого заключения. Поэтому средний термин хоть в одной из посылок должен быть взят во всём объёме.
4. Термины, не взятые в посылках во всём объёме, не могут быть и в заключении взяты во всём объёме.
Для пояснения этого правила возьмём следующий пример:
Все преступники заслуживают наказания.
Некоторые англичане суть преступники.
Все англичане заслуживают наказания.
Очевидная ошибка в этом силлогизме получается вследствие того, что мы в заключении термин «англичане» берём во всём объёме, между тем как в посылке этот термин взят не во всём объёме. Мы бы сделали правильное заключение, если бы сказали: «некоторые англичане заслуживают наказания».
Возьмём другой пример, где ошибка не так очевидна:
Все историки беспристрастны.
Натуралисты не суть историки.
Натуралисты не суть беспристрастны.
Чтобы видеть, правилен ли этот вывод, изобразим силлогизм символически (рис. 21).
Историки (M) находятся в P (беспристрастные). О натуралистах сказано, что они не суть историки. Мы, следовательно, не имеем права помещать их в круге M; поэтому натуралистов мы можем поместить где угодно, лишь бы не в круге M, а если так, то, помещая S вне M, мы можем его поместить всё-таки в круге P. Вследствие этого может оказаться, что «натуралисты беспристрастны». В большей посылке термин «беспристрастный» взят не во всём объёме, так что историки должны составлять только часть тех, которые беспристрастны, а потому мы не имеем права исключать из числа беспристрастных и натуралистов. Ошибка в этом силлогизме получилась оттого, что в большей посылке термин «беспристрастный», как сказуемое обще-утвердительного суждения, взят не во всём объёме, между тем как в заключении, как сказуемое обще-отрицательного суждения, он взят во всём объёме. Другими словами, мы один раз говорим не обо всех, а другой раз обо всех. Такая ошибка называется ошибкой illiciti processi, недозволительное расширение большего термина, как в данном примере; недозволительное расширение меньшего термина мы имели в первом примере.
5. Из двух отрицательных суждений нельзя вывести никакого заключения. Возьмём пример, чтобы пояснить это правило:
Химия не есть гуманитарная наука.
Математика не есть химия.
Что следует из этих посылок? Обозначим (рис. 22) «химия» посредством M, «гуманитарные науки» – посредством P, «математика» – посредством S:
M должно быть вне P, S должно быть вне M. Как легко видеть, средний термин в этом силлогизме не связывает больший термин с меньшим, потому что он находится вне большего и меньшего терминов. Если M не соединено с P, а S не соединено с M, то S не может быть соединено с P, т.е. через средний термин нельзя установить никакой связи между большим и меньшим терминами.
6. Если одна из посылок отрицательна, то заключение должно быть также отрицательно, и наоборот, для получения отрицательного заключения необходимо, чтобы одна из посылок была отрицательна. Возьмём пример:
Ни одно M не есть P.
Все S суть M.
Раз P находится вне среднего термина M, то, очевидно, S, которое находится в M, не свяжется с P, а потому получится отрицательное заключение.
Таким образом, если у нас есть две посылки, из которых одна отрицательна, то мы не можем сделать утвердительного заключения.
7. Из двух частных суждений нельзя сделать никакого заключения.
Это ясно из предыдущих правил. Предположим, что эти частные суждения будут I и I; тогда окажется, что средний термин в обеих посылках будет не распределён как подлежащее и сказуемое частно-утвердительного суждения. Если мы будем стараться вывести заключение, то мы нарушим третье правило. В самом деле, пусть эти посылки будут:
Некоторые M суть P.
Некоторые S суть M.
В обоих этих суждениях средний термин не распределён. Следовательно, заключение не следует необходимо. Возьмём суждения I и O, например:
Некоторые M суть P.
Некоторые S не суть M.
Так как здесь одна посылка отрицательная, то и сказуемое P заключения должно быть распределено, между тем как в данных посылках P как сказуемое частно-утвердительного суждения не распределено. Следовательно, попытка сделать заключение нарушала бы правило 4.
Наконец, правило 8 формулируется так:
8. Если одна из посылок есть суждение частное, то и заключение также должно быть частным.
Если мы желаем получить общее заключение в том случае, когда в силлогизме одна из посылок частная, то нарушается третье или четвёртое правило.
В самом деле, пусть мы имеем силлогизм:
Все M суть P.
Некоторые S суть M.
Все S суть P.
В этом силлогизме нарушается правило 4. Или пусть мы имеем силлогизм:
Некоторые M суть P. Все S суть M.
Все S суть P.
В этом силлогизме нарушается правило 3.
Вопросы для повторения
Как определяется силлогизм? Какие части мы различаем в силлогизме? Какое различие между формой и содержанием силлогизма? В чём заключается аксиома силлогизма? Перечислите правила силлогизма и объясните при помощи примеров их применение.
§ 3. ПРОСТОЙ КАТЕГОРИЧЕСКИЙ СИЛЛОГИЗМ
1. Состав простого категорического силлогизма
Широко распространенным видом опосредованных умозаключений является категорический силлогизм[32]. Он состоит из трех категорических суждений, два из которых являются посылками, а третье — заключением. Например:
1. Обвиняемый (М) имеет право на защиту (Р).
2. Бобров (S) — обвиняемый (М).
____________________
3. Бобров (S) имеет право на защиту (Р).
В отличие от терминов суждения — субъекта (S) и предиката (Р) — понятия, входящие в состав силлогизма, называются терминами силлогизма. Различают меньший, больший и средний термины.
Меньшим термином силлогизма называется понятие, которое в заключении является субъектом (в нашем примере понятие «Бобров»). Б?льшим термином силлогизма называется понятие, которое в заключении является предикатом («имеет право на защиту»). Меньший и больший термины называются крайними и обозначаются соответственно латинскими буквами S (меньший термин) и Р (больший термин).
Каждый из крайних терминов входит не только в заключение, но и в одну из посылок. Посылка, в которую входит меньший термин, называется меньшей посылкой, посылка в которую входит больший термин, называется большей посылкой. В нашем примере большей посылкой будет первое суждение (1), меньшей — второе суждение (2).
Для удобства анализа силлогизма посылки принято располагать в определенной последовательности: б?льшую — на первом месте, меньшую — на втором. Под чертой записывают заключение.
Однако в рассуждении меньшая посылка может находиться на первом месте, а б?льшая — на втором. Иногда посылки стоят после заключения.
Посылки различаются не их местом в силлогизме, а входящими в них терминами.
Вывод в силлогизме был бы невозможен, если бы в нем не было среднего термина. Средним термином силлогизма называется понятие, входящее в обе посылки и отсутствующее в заключении (в нашем примере — «обвиняемый»). Средний термин обозначается латинской буквой М (от латинского medius — «средний»).
Средний термин связывает два крайних термина. Отношение крайних терминов (субъекта и предиката) устанавливается благодаря их отношению к среднему термину.
Итак, простой категорический силлогизм — это умозаключение об отношении двух крайних терминов на основании их отношения к среднему термину.
2. Аксиома силлогизма
Правомерность вывода, т. е. логического перехода от посылок к заключению, в категорическом силлогизме основывается на положении (аксиоме силлогизма): все, что утверждается или отрицается относительно всех предметов некоторого класса, утверждается или отрицается относительно каждого предмета и любой части предметов этого класса[33].
В приведенном примере — все, что утверждается относительно всех обвиняемых, утверждается и относительно конкретного обвиняемого (см. в круговых схему 31).
Рассмотрим силлогизм:
Обвиняемый (М) не обязан доказывать свою невиновность (Р).
Куницын (S) — обвиняемый (М).
__________________
Куницын (S) не обязан доказывать свою невиновность (Р).
В этом силлогизме все, что отрицается относительно каждого обвиняемого, отрицается и относительно конкретного лица (схема 32).

Схема 31

Схема 32
Вопросы для самопроверки
1. Какое умозаключение называется простым категорическим силлогизмом? Приведите его определение.
2. Какие термины входят в состав категорического силлогизма? Какая посылка называется большей и какая — меньшей?
3. Какая аксиома обосновывает вывод в категорическом силлогизме? Как она формулируется?
3. Общие правила категорического силлогизма
Из истинных посылок не всегда можно получить истинное заключение. Его истинность обусловлена правилами силлогизма. Этих правил пять: три относятся к терминам и два — к посылкам.
Правила терминов.
1-е правило: в силлогизме должно быть только три термина. Вывод в силлогизме основан на отношении двух крайних терминов к среднему, поэтому в нем не может быть ни меньше, ни больше трех терминов. Нарушение этого правила связано с отождествлением разных понятий, которые принимаются за одно и рассматриваются как средний термин. Эта ошибка основана на нарушении требований закона тождества и называется учетверением терминов.
Нельзя, например, получить заключение из посылок: «Законы не создаются людьми» и «Закон — это нормативный акт, принятый высшим органом государственной власти», так как вместо трех терминов мы имеем дело с четырьмя: в первой посылке имеются в виду объективные законы, существующие независимо от людей, во второй — юридический закон, устанавливаемый государством. Это два разных понятия, которые не могут связать крайние термины.
2-е правило: средний термин должен быть распределен хотя бы в одной из посылок[34]. Если средний термин не распределен ни в одной из посылок, то связь между крайними терминами остается неопределенной.
Например, в посылках «Некоторые юристы (М—) — члены коллегии адвокатов (Р)», «Все сотрудники нашего коллектива (S) — юристы (М—)» средний термин (М) не распределен в большей посылке, так как является субъектом частного суждения, и не распределен в меньшей посылке как предикат утвердительного суждения. Следовательно, средний термин не распределен ни в одной из посылок, поэтому необходимую связь между крайними терминами (S и Р) установить нельзя, что видно из схемы 33, на которой изображены три возможных случая: 1) «Ни один сотрудник нашего коллектива не является членом коллегии адвокатов» (S1); 2) «Некоторые сотрудники нашего коллектива — члены коллегии адвокатов» (S2); 3) «Все сотрудники нашего коллектива члены коллегии адвокатов» (S3).
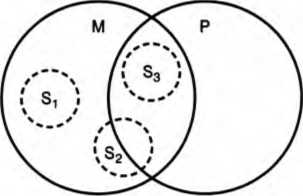
Схема 33
3-е правило: термин, не распределенный в посылке, не может быть распределен и в заключении.
Например:
Нравственные нормы (М) не санкционируются государством (Р+).
Нравственные нормы (М) — формы социальной регуляции (S—).
_____________________
Некоторые формы социальной регуляции (S—) не санкционируются государством (Р+).
Меньший термин (S) не распределен в посылке (как предикат утвердительного суждения), поэтому он не распределен и в заключении (как субъект частного суждения). Делать вывод с распределенным субъектом в форме общего суждения («Ни одна форма социальной регуляции не санкционируется государством») это правило запрещает.
Ошибка, связанная с нарушением правила распределенности крайних терминов, называется незаконным расширением меньшего (или большего) термина.
Правила посылок.
1-е правило: хотя бы одна из посылок должна быть утвердительным суждением.
Из этого правила следует:
а) Из двух отрицательных посылок заключение с необходимостью не следует.
Например, из посылок «Студенты нашего института (М) не изучают биологию (Р)», «Сотрудники НИИ (S) не являются студентами нашего института (М)» нельзя получить необходимого заключения, так как оба крайних термина (S и Р) исключаются из среднего. Поэтому средний термин не может установить определенного отношения между крайними терминами. В заключении меньший термин (М) может полностью или частично входить в объем большего термина (Р) или полностью исключаться из него. В соответствии с этим возможны три случая: 1) «Ни один сотрудник НИИ не изучает биологию (S1); 2) «Некоторые сотрудники НИИ изучают биологию» (S2); 3) «Все сотрудники НИИ изучают биологию» (S3) (схема 34).
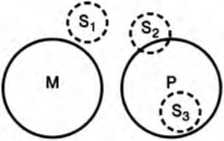
Схема 34

Схема 35
б) Если одна из посылок — отрицательное суждение, то и заключение должно быть отрицательным.
Например:
Судья, являющийся родственником потерпевшего (М), не может участвовать в рассмотрении дела (Р).
Судья К. — родственник потерпевшего (М).
____________________
Судья К. (S) не может участвовать в рассмотрении дела (Р).
Этот пример показывает, что в силлогизме с одной отрицательной посылкой средний термин исключается из объема крайнего термина (в данном случае — большего), поэтому объем крайнего термина, который входит в объем среднего, исключается из объема другого крайнего термина (схема 35).
2-е правило: хотя бы одна из посылок должна быть общим суждением.
Из правила следует:
а) Из двух частных посылок заключение с необходимостью не следует.
Если обе посылки — частноугвердительные суждения (II), то вывод сделать нельзя согласно 2-му правилу терминов: в частноутвердительном суждении ни субъект, ни предикат не распределены, поэтому и средний термин не распределен ни в одной из посылок.
Если обе посылки — частноотрицательные суждения (ОО), то вывод сделать нельзя согласно 1-му правилу посылок.
Если одна посылка — частноугвердительная, а другая — частноотрицательная (IO или OI), то в таком силлогизме распределенным будет только один термин — предикат частноотрицательного суждения (1). Если этим термином будет средний, то вывода сделать нельзя, так, согласно 2-му правилу посылок, заключение должно быть отрицательным. Но в этом случае предикат заключения должен быть распределен, что противоречит 3-му правилу терминов: больший термин, не распределенный в посылке, окажется распределенным в заключении; если же больший термин распределен (2), то вывода не следует согласно 2-му правилу терминов.
1) Некоторые М(—) есть Р(-).
Некоторые S(-) не есть М(+).
2) Некоторые М(-) не есть Р(+).
Некоторые S(-) есть М(-).
Ни один из этих случаев не дает необходимых заключений, в чем легко убедиться, подобрав соответствующие примеры.
б) Если одна из посылок — частное суждение, то и заключение должно быть частным.
Если одна посылка общеугвердительная, а другая — частноутвердительная (AI, IA), то в них распределен только один термин — субъект общеугвердительного суждения.
Согласно 2-му правилу терминов, это должен быть средний термин. Но в таком случае два крайних термина, в том числе меньший, не будут распределены. Поэтому в соответствии с 3-м правилом терминов меньший термин не будет распределен в заключении, которое будет частным суждением. Например:
Все студенты нашего института (М+) изучают логику (Р—).
Некоторые сотрудники милиции (S—) — студенты нашего института (М—).
_________________________
Некоторые сотрудники милиции (S—) изучают логику (Р—).
Если одна из посылок утвердительная, а другая — отрицательная, причем одна из них частная (EI, АО, ОА), то распределенными окажутся два термина: субъект и предикат общеотрицательного суждения (EI) или субъект общего и предикат частного суждения (АО, ОА). Но в том и другом случае, согласно 2-му правилу посылок, заключение будет отрицательным, т. е. суждением с распределенным предикатом. Атак как вторым распределенным термином должен быть средний (2-е правило терминов), то меньший термин в заключении окажется нераспределенным, т. е. заключение будет частным. Например:
Все врачи (Р+) имеют медицинское образование (М—).
Некоторые из присутствующих (S—) не имеют медицинского образования (М+).
_____________________
Некоторые из присутствующих (S—) не врачи (Р+).
Вопросы для самопроверки
1. Назовите правила терминов и посылок простого категорического силлогизма.
2. К каким логическим ошибкам ведет нарушение правил?
4. Фигуры категорического силлогизма. Правила фигур
В посылках простого категорического силлогизма средний термин может занимать место субъекта или предиката. В зависимости от этого различают четыре разновидности силлогизма, которые называют фигурами (схема 36).

Схема 36
В первой фигуре средний термин занимает место субъекта в большей и место предиката в меньшей посылках.
Во второй фигуре — место предиката в обеих посылках.
В третьей фигуре — место субъекта в обеих посылках.
В четвертой фигуре — место предиката в большей и место субъекта в меньшей посылках.
Эти фигуры исчерпывают все возможные комбинации терминов.
Фигуры силлогизма — это его разновидности, различающиеся положением среднего термина в посылках.
Каждая фигура имеет свои особые правила, которые выводятся из общих.
Правила 1-й фигуры:
1. Б?льшая посылка — общее суждение.
2. Меньшая посылка — утвердительное суждение.
Докажем сначала 2-е правило. Если меньшая посылка будет отрицательным суждением, то согласно 2-му правилу посылок заключение также будет отрицательным, в котором Р распределен. Но тогда он будет распределен и в большей посылке, которая также должна быть отрицательным суждением (в утвердительном суждении Р не распределен), а это противоречит 1-му правилу посылок. Если же большая посылка будет утвердительным суждением, то Р будет не распределен.
Но тогда он не будет распределен и в заключении (согласно 3-му правилу терминов). Заключение с нераспределенным Р может быть только утвердительным суждением, так как в отрицательном суждении Р распределен. А это значит, что и меньшая посылка — утвердительное суждение, так как в противном случае заключение будет отрицательным.
Теперь докажем 1-е правило. Так как средний термин в этой фигуре занимает место субъекта в большей и место предиката в меньшей посылке, то, согласно 2-му правилу терминов, он должен быть распределен хотя бы в одной из посылок. Но меньшая посылка — утвердительное суждение. Значит, средний термин в ней не распределен. Но в таком случае он должен быть распределен в большей посылке, а для этого она должна быть общим суждением (в частной посылке субъект не распределен).
1-я фигура дает любые заключения: общеутвердительные, общеотрицательные, частноутвердительные и частноотрицательные, что определяет ее познавательное значение и широкое применение в рассуждениях.
1-я фигура — наиболее типичная форма дедуктивного умозаключения. Из общего положения, выражающего нередко закон науки, правовую норму, делается вывод об отдельном факте, единичном случае, конкретном лице. Широко применяется эта фигура в судебной практике. Юридическая оценка (квалификация) правовых явлений, применение нормы права к отдельному случаю, назначение наказания за преступление, совершенное конкретным лицом, и другие судебные решения принимают логическую форму 1-й фигуры силлогизма.
Например:
Все лица, лишенные свободы (М), имеют право на гуманное обращение и уважение достоинства, присущего человеческой личности (Р)[35].
Н. (S) лишен свободы (М).
______________________
Н. (S) имеет право на гуманное обращение и уважение достоинства, присущего человеческой личности (Р).
Правила 2-й фигуры:
1. Б?льшая посылка — общее суждение.
2. Одна из посылок — отрицательное суждение.
Второе правило фигуры выводится из 2-го правила терминов (средний термин должен быть распределен хотя бы в одной из посылок). Но так как средний термин занимает место предиката в обеих посылках, то одна из них должна быть отрицательным суждением с распределенным предикатом.
Если одна из посылок—отрицательное суждение, то и заключение должно быть отрицательным (суждение с распределенным предикатом). Но в этом случае предикат заключения (больший термин) должен быть распределен и в большей посылке, где он занимает место субъекта суждения. Такой посылкой должно быть общее суждение, в котором субъект распределен. Значит, большая посылка должна быть общим суждением.
2-я фигура применяется, когда необходимо показать, что отдельный случай (конкретное лицо, факт, явление) не может быть подведен под общее положение. Этот случай исключается из числа предметов, о которых сказано в большей посылке. В судебной практике 2-я фигура используется для заключений об отсутствии состава преступления в данном конкретном случае, для опровержения положений, противоречащих тому, о чем говорится в посылке, выражающей общее положение.
Например:
Подстрекателем (Р) признается лицо, склонившее другое лицо к совершению преступления (М).
Н. (S) не признается лицом, склонившим другое лицо к совершению преступления (М).
__________________
Н. (S) не является подстрекателем (Р).
Правила 3-й фигуры:
1. Меньшая посылка — утвердительное суждение.
2. Заключение — частное суждение.
1-е правило доказывается так же, как 2-е правило 1-й фигуры. Но если меньшая посылка — утвердительное суждение, то его предикат (меньший термин силлогизма) не распределен. Термин, не распределенный в посылке, не может быть распределен в заключении. Значит, заключение должно быть частным суждением.
Давая только частные заключения, 3-я фигура применяется чаще всего для установления частичной совместимости признаков, относящихся к одному предмету. Например:
Осмотр места происшествия (М) имеет одной из своих задач обнаружение следов преступления (Р).
Осмотр места происшествия (М) — следственное действие (S).
_____________________
Некоторые следственные действия (S) имеют одной из своих задач обнаружение следов преступления (Р).
В практике рассуждения 3-я фигура применяется сравнительно редко.
4-я фигура силлогизма также имеет свои правила. Однако выведение заключения из посылок по этой фигуре не характерно для естественного процесса рассуждения. Например:
Захват заложника (Р) — преступление против общественной безопасности (М).
Преступление против общественной безопасности (М) — общественно опасное деяние, предусмотренное Особенной частью Уголовного кодекса (S).
_____________________________
Некоторые общественно опасные деяния, предусмотренные Особенной частью Уголовного кодекса (S), являются захватом заложника (Р).
Такой ход рассуждения представляется в известной мере искусственным, на практике выводы в подобных случаях делаются обычно по 1-й фигуре:
Преступления против общественной безопасности (М) — общественно опасные деяния, предусмотренные Особенной частью Уголовного кодекса (Р).
Захват заложника (S) — преступление против общественной безопасности (М).
_____________________________
Захват заложника (S) — общественно опасное деяние, предусмотренное Особенной частью Уголовного кодекса (Р).
Так как ход рассуждения по 4-й фигуре не типичен для процесса мышления, правила этой фигуры нами не рассматриваются.
5. Модусы силлогизма
Посылками силлогизма могут быть суждения, различные по качеству и количеству: общеутвердительные (А), общеотрицательные (Е), частноутвердительные (I) и частноотрицательные (О).
Разновидности силлогизма, различающиеся количественными и качественными характеристиками посылок, называются модусами простого категорического силлогизма.
Так как каждая посылка может быть любым из четырех суждений, число возможных комбинаций посылок в каждой фигуре равно 24, т. е. 16:

Очевидно, в четырех фигурах число комбинаций равно 64.
Однако не все модусы согласуются с общими правилами силлогизма. Например, модусы, заключенные в скобках, противоречат 1-му и 2-му правилам посылок, модус IA не проходит по первой и второй фигурам, так как противоречит 2-му правилу терминов, и т. д. Поэтому, отобрав только те модусы, которые согласуются с общими правилами силлогизма, получим 19 модусов, которые называются правильными. Их принято записывать вместе с заключением:

Правильные модусы можно вывести, исключив комбинации посылок, не соответствующие общим правилам, и те, которые не соответствуют правилам фигур[36].
Вопросы для самопроверки
1. Что такое фигура силлогизма? Какое место занимает в них средний термин?
2. Дайте характеристику 1-й, 2-й и 3-й фигурам.
3. Каким особым правилам подчиняются фигуры силлогизма?
4. Что называется модусом силлогизма?
6. Категорический силлогизм с выделяющими суждениями
Правила силлогизма сформулированы для силлогистических умозаключений, не включающих в качестве посылок выделяющие суждения. Если же такие посылки есть, то эти силлогизмы не подчиняются некоторым общим правилам, а также особым правилам фигур.
Рассмотрим наиболее распространенные случаи.
1. Вывод из двух частных посылок.
Некоторые адвокаты (М-) — выпускники Московского университета (Р—).
Некоторые юристы (S—) — адвокаты (М+).
________________________
Некоторые юристы (S—) — выпускники Московского университета (Р—).
В этом примере меньшая посылка — частноутвердительное выделяющее суждение («Некоторые юристы, и только юристы, являются адвокатами») с распределенным предикатом (средним термином силлогизма). Так как средний термин в одной из посылок распределен, заключение из двух частных посылок следует с необходимостью. Легко проверить, что все другие общие правила силлогизма соблюдаются.
2. Вывод по 1-й фигуре, в которой б?льшая посылка — частное суждение.
Необходимость вывода в этом силлогизме может быть показана на приведенном примере: средний термин в меньшей посылке распределен.
3. Одна из посылок — частное суждение, заключение — общее суждение.
Некоторые юристы (Р+) — следователи (М+).
Все участники совещания (S+) — следователи (М—).
________________________
Все участники совещания (S+) — юристы (Р-).
Б?льшая посылка в этом примере — частноутвердительное выделяющее суждение с распределенным предикатом — средним термином силлогизма.
4. Вывод по 2-й фигуре из двух утвердительных посылок.
Приведенный пример показывает, что вывод по 2-й фигуре следует с необходимостью, так как средний термин в одной из посылок распределен.
5. Вывод по 1-й фигуре, в которой меньшая посылка — отрицательное суждение.
Лицо, совершившее преступление (М+), привлекается к уголовной ответственности (Р+).
Н. (S+) не совершил преступления (М+).
_____________________
Н. (S+) не привлекается к уголовной ответственности (Р+).
Вывод следует с необходимостью, так как б?льшая посылка — общеутвердительное выделяющее суждение с распределенным предикатом. Предикат — больший термин силлогизма — распределен в посылке и в заключении.
Рассмотренные примеры показывают, что силлогизмы, в состав которых входят выделяющие суждения, подчиняются не всем правилам. Это обусловлено особенностью выделяющих суждений, распределенностью их терминов. Поэтому, устанавливая логическую необходимость вывода в силлогизме с выделяющим суждением, необходимо иметь в виду эту особенность. Целесообразно проверять правильность вывода с помощью круговых схем.
В некоторых случаях большей посылкой силлогизма является определение через род и видовое отличие. Так как такое определение подчиняется правилу соразмерности, оно выражается в форме общеутвердительною выделяющего суждения, оба термина которого распределены. А это значит, что на силлогизм, большей посылкой которого является определение, также не распространяются некоторые правила.
Такие силлогизмы используются в судебной практике, в частности при квалификации преступлений. Например:
Хулиганство (Р+) — это умышленные действия, грубо нарушающие общественный порядок и выражающие явное неуважение к обществу (М+).
Действия Н. (S+) являются умышленными, грубо нарушающими общественный порядок и выражающими явное неуважение к обществу (М—).
____________________
Действия Н. (S) являются хулиганством (Р).
Заключение получено из двух утвердительных посылок по 2-й фигуре.
Вопросы для самопроверки
1. Как распределены термины в общеутвердительных, общеотрицательных, частноутвердительных и частноотрицательных выделяющих суждениях?
2. Почему силлогизмы с выделяющими посылками не подчиняются некоторым правилам?
Данный текст является ознакомительным фрагментом.
Читайте также
3.3. Простой, или категорический силлогизм
3.3. Простой, или категорический силлогизм
Рассмотренные в предыдущем параграфе дедуктивные умозаключения также называются силлогизмами. Существует несколько видов силлогизмов. Первый из них называется простым, или категорическим, потому что все суждения, входящие в
1. Простой категорический силлогизм
1. Простой категорический силлогизм
Наиболее распространенной и важной формой опосредованного умозаключения из простых атрибутивных суждений выступает простой категорический силлогизм (от греч. syllogismos — умозаключение, выведение). Приводившийся выше пример с Сократом
2. Сложный категорический силлогизм
2. Сложный категорический силлогизм
Умозаключение из атрибутивных (категорических) суждений далеко не всегда облекается в форму простого силлогизма, включающего лишь две посылки. Оно может принимать форму и сложного категорического силлогизма, состоящего из нескольких
1. Простой категорический силлогизм
1. Простой категорический силлогизм
Структура простого категорического силлогизма1. Выделите структуру (посылки и заключение, больший, меньший и средний термины, б?льшую и меньшую посылку) простого категорического силлогизма в следующем примере:«Все таможенники —
2. Сложный категорический силлогизм
2. Сложный категорический силлогизм
1. Из следующих силлогизмов, связанных между собой, постройте сорит:«Все юристы имеют специальное образование.Все адвокаты — юристы.Следовательно, все адвокаты имеют специальное образование». «Все адвокаты имеют специальное
Глава IV. Категорический силлогизм
Глава IV. Категорический силлогизм
§ 1. Определение категорического силлогизма
Рассмотрим суждение «Том Муни представляет опасность для общества». Что может послужить адекватным основанием для этого суждения? Например, аргумент можно выстроить следующим образом: «Все
Глава IV. Категорический силлогизм
Глава IV. Категорический силлогизм
1. Первые четыре аксиомы категорического силлогизма не являются независимыми друг от друга. Докажите вторую, третью и четвертую аксиомы, допустив первую аксиому вместе с общим принципом контрапозиции, а также процессами обращения и
40. Понятие силлогизма. Простой категорический силлогизм
40. Понятие силлогизма. Простой категорический силлогизм
Слово «силлогизм» произошло от греческого syllogysmos, что означает «вывод». Очевидно, что силлогизм – это выведение следствия, заключения из определенных посылок. Силлогизм бывает простым, сложным, сокращенным и
41. Сложный силлогизм. Сокращенный силлогизм
41. Сложный силлогизм. Сокращенный силлогизм
В мышлении мы оперируем понятиями, суждениями и умозаключениями, в том числе и силлогизмами. Как и суждения, силлогизм может быть простым (рассмотрен выше) и сложным. Конечно, слово «сложный» не стоит понимать в обычном смысле
VI. Простой и сложный труд
VI. Простой и сложный труд
Г-н Дюринг открыл у Маркса очень грубую экономическую ошибку, достойную ученика младшего класса и в то же время заключающую в себе общественно-опасную социалистическую ересь.
Теория стоимости Маркса представляет собой «не более как обычное…
1. Понятие силлогизма. Простой категорический силлогизм
1. Понятие силлогизма. Простой категорический силлогизм
Слово «силлогизм» произошло от греческого syllogysmos, что означает «вывод». Очевидно, что силлогизм — это выведение следствия, заключения из определенных посылок. Силлогизм бывает простым, сложным, сокращенным и
Простой род (76–90)
Простой род (76–90)
Прежде всего должны мы изобразить того оратора, за кем одним признают иные имя аттического.(76) Он скромен, невысокого полета, подражает повседневной речи и отличается от человека неречистого больше по существу, чем по виду. Поэтому слушатели, как бы ни
3. Простой разговор
3. Простой разговор
Одно из многих препятствий в изучении искусства жить — это сведение всего к тривиальному разговору.Что такое тривиальный? Дословно означает «имеющий общее место» (от латинского trivia — точка пересечения трех дорог); он обычно отличается пустотой,
Простой (Simle)
Простой (Simle)
Неделимый, не поддающийся разъятию на составные части (Лейбниц называет простым то, что не имеет частей). Слово «простой» в расширительном значении употребляется также для обозначения того, что легко поддается пониманию или выполнению. Возможно, отсюда
Формальная логика есть не что иное, как учение о свойствах, общих всякой классификации, — разъясняет Анри Пуанкаре. — Она учит нас, что два солдата, являющихся частью одного полка, тем самым принадлежат к одной и той же бригаде, следовательно, к одной и той же дивизии; к этому-то и сводится вся теория силлогизмов[1].
Простой категорический силлоги́зм (др.-греч. συλ-λογισμός «подытоживание, подсчёт, умозаключение» от συλ- (συν-) «вместе» + λογισμός «счёт, подсчёт; рассуждение, размышление») — дедуктивное умозаключение, состоящее из трёх простых атрибутивных суждений: двух посылок и одного заключения.
Пример силлогизма:
| Всякий человек смертен. | |
| Сократ — человек. | |
| След.: | Сократ смертен. |
Структура простого категорического силлогизма[править | править код]
Простой категорический силлогизм состоит из трех простых атрибутивных суждений (посылок и заключения) и включает в себя три понятия — «термины простого категорического силлогизма».
Термины:
- M — средний термин: входит в обе посылки, но не входит в заключение;
- S — меньший термин: субъект заключения;
- P — больший термин: предикат заключения.
Больший и меньший термины также называются крайними.
Посылки:
- Бóльшая посылка — посылка, содержащая P — предикат заключения. Записывается первой.
- Меньшая посылка — посылка, содержащая S — субъект заключения. Записывается второй.
Общие правила простого категорического силлогизма[править | править код]
Правила терминов[править | править код]
- В каждом силлогизме должно быть ровно три термина.
- Средний термин должен быть распределён хотя бы в одной из посылок.
- Крайний термин, не распределённый в посылке, не должен быть распределён в заключении.
Тут “распределен” значит “используется во всей полноте”, т.е., суждение касается всех значений термина (напр., “все люди”, “ни одна рептилия”).
Правила посылок[править | править код]
- Должна быть хотя бы одна общая посылка (из двух частных вывода нет).
- Если одна из посылок частная, то заключение должно быть тоже частным.
- Должна быть хотя бы одна утвердительная посылка (из двух отрицательных вывода нет).
- Если одна из посылок отрицательная, то заключение должно быть тоже отрицательным.
- Если обе посылки утвердительные, то и заключение должно быть утвердительным.
Фигуры и модусы[править | править код]
Фигурами силлогизма называются формы силлогизма, отличающиеся расположением среднего термина в посылках:
| Фигура 1 | Фигура 2 | Фигура 3 | Фигура 4 | |||||
| Бо́льшая посылка: | M—P | P—M | M—P | P—M | ||||
| Меньшая посылка: | S—M | S—M | M—S | M—S | ||||
| Заключение: | S—P | S—P | S—P | S—P |
Каждой фигуре отвечают модусы — формы силлогизма, различающиеся количеством и качеством посылок и заключения.
Например, в силлогизме:
| Все небесные тела движутся. | |
| Все планеты — это небесные тела. | |
| Все планеты движутся. |
Бóльшая посылка является простым суждением вида a (общеутвердительным), меньшая посылка — это тоже простое суждение вида a, и вывод в данном случае представляет собой простое суждение вида a. Поэтому рассмотренный силлогизм имеет модус aaa фигуры 1.
Силлогизм:
| Все журналы — периодические издания. | |
| Все книги не являются периодическими изданиями. | |
| Все книги не являются журналами. |
имеет модус aee фигуры 2.
Силлогизм:
| Все углероды — простые тела. | |
| Все углероды электропроводны. | |
| Некоторые электропроводники — простые тела. |
имеет модус aai фигуры 3.
Всего модусов во всех четырёх фигурах, то есть возможных комбинаций простых суждений в силлогизме, — 256. В каждой фигуре 64 модуса. Однако из всех этих 256 модусов только 24 (19 сильных и 5 слабых) дают достоверные выводы: из истинных посылок выводится необходимо истинное заключение. Заключение сделанное по остальным модусам может оказаться как истинным так и ложным; истинность будет зависеть исключительно от конкретного содержания посылок и заключения.
Модусы изучались ещё средневековыми школами, и для правильных модусов каждой фигуры были придуманы мнемонические имена:
| Фигура 1 | Фигура 2 | Фигура 3 | Фигура 4 | |||
| Barbara | Cesare | Darapti | Bramantip | |||
| Celarent | Camestres | Disamis | Camenes | |||
| Darii | Festino | Datisi | Dimaris | |||
| Ferio | Baroco | Felapton | Fesapo | |||
| Barbari | Cesaro | Bocardo | Fresison | |||
| Celaront | Camestros | Ferison | Camenos |
Здесь и выше гласные буквы жирным шрифтом означают тип суждения:
- a – общеутвердительное (все животные смертны),
- е – общеотрицательное (ни одна змея не имеет меха),
- i – частноутвердительное (некоторые домашние животные – котята),
- o – частноотрицательное (некоторые змеи не имеют меха).
a и i – первая и вторая гласные буквы в слове affirmo (утверждаю, лат.), буквы e и o – аналогично в слове nego (отрицаю, лат.).
Курсивом выделены слабые модусы — модусы которые содержат частное заключение при возможности общего.
Слабые модусы, а также модусы Felapton, Darapti, Fesapo и Bramantip, предполагают непустоту классов, с которыми оперируют силлогизмы (пример Б. Рассела: Все золотые горы — золотые. Все золотые горы — горы. По модусу Darapti отсюда должно следовать: Некоторые горы золотые; однако такое умозаключение неверно, если класс золотых гор пуст).
Примеры силлогизмов каждого типа.
Barbara
| Все животные смертны. | |
| Все люди — животные. | |
| Все люди смертны. |
Celarent
| Ни одна рептилия не имеет меха. | |
| Все змеи — рептилии. | |
| Ни одна змея не имеет меха. |
Darii
| Все котята игривы. | |
| Некоторые домашние животные — котята. | |
| Некоторые домашние животные игривы. |
Ferio
| Ни одна домашняя работа не весела. | |
| Некоторое чтение — домашняя работа. | |
| Некоторое чтение не весело. |
Barbari
| Все животные смертны. | |
| Все люди — животные. | |
| Некоторые люди смертны. |
Celaront
| Ни одна рептилия не имеет меха. | |
| Все змеи — рептилии. | |
| Некоторые змеи не имеют меха. |
Cesare
| Ни одна здоровая еда не полнит. | |
| Все торты полнят. | |
| Ни один торт — не здоровая еда. |
Camestres
| Все лошади имеют вздутие живота. | |
| Ни один человек не имеет вздутия живота. | |
| Ни один человек — не лошадь. |
Festino
| Ни один ленивый человек не сдаёт экзамены. | |
| Некоторые студенты сдают экзамены. | |
| Некоторые студенты не ленивы. |
Baroco
| Все информативные вещи полезны. | |
| Некоторые сайты не полезны. | |
| Некоторые сайты не информативны. |
Cesaro
| Ни одна здоровая еда не полнит. | |
| Все торты полнят. | |
| Некоторые торты — не здоровая еда. |
Camestros
| Все лошади имеют вздутие живота. | |
| Ни один человек не имеет вздутия живота. | |
| Некоторые люди — не лошади. |
Darapti
| Все фрукты питательны. | |
| Все фрукты вкусны. | |
| Некоторые вкусные продукты питательны. |
Disamis
| Некоторые кружки красивы. | |
| Все кружки полезны. | |
| Некоторые полезные вещи красивы. |
Datisi
| Все прилежные мальчики в этой школе рыжие. | |
| Некоторые прилежные мальчики в этой школе — пансионеры. | |
| Некоторые пансионеры в этой школе рыжие. |
Felapton
| Ни один кувшин в этом шкафу не нов. | |
| Все кувшины в этом шкафу треснутые. | |
| Некоторые треснутые вещи в этом шкафу не новы. |
Bocardo
| Некоторые кошки не имеют хвоста. | |
| Все кошки — млекопитающие. | |
| Некоторые млекопитающие не имеют хвоста. |
Ferison
| Ни одно дерево не съедобно. | |
| Некоторые деревья зелёные. | |
| Некоторые зелёные вещи не съедобны. |
Bramantip
| Все яблоки в моём саду полезны. | |
| Все полезные фрукты зрелы. | |
| Некоторые зрелые фрукты — яблоки в моём саду. |
Camenes
| Все яркие цветы ароматны. | |
| Ни один ароматный цветок не выращен в помещении. | |
| Ни один выращенный в помещении цветок не ярок. |
Dimaris
| Некоторые небольшие птицы питаются мёдом. | |
| Все питающиеся мёдом птицы цветные. | |
| Некоторые цветные птицы небольшие. |
Fesapo
| Ни один человек не совершенен. | |
| Все совершенные существа мифические. | |
| Некоторые мифические существа — не люди. |
Fresison
| Ни один компетентный человек не ошибается. | |
| Некоторые ошибающиеся люди работают здесь. | |
| Некоторые работающие здесь люди некомпетентны. |
Camenos
| Все яркие цветы ароматны. | |
| Ни один ароматный цветок не выращен в помещении. | |
| Некоторые выращенные в помещении цветы не ярки. |
В соответствии с правилами, формы могут быть преобразованы в другие формы, и все формы могут быть преобразованы в одну из форм первой фигуры.
История[править | править код]
Учение о силлогизме впервые изложено у Аристотеля в его «Первой аналитике». Он говорит лишь о трёх фигурах категорического силлогизма, не упоминая о возможной четвёртой. Особенно подробно он рассматривает роль модальности суждений в процессе умозаключения. Преемник Аристотеля, основатель ботаники Теофраст, по словам Александра Афродизийского (в его комментарии к первой «Аналитике» Аристотеля), прибавил ещё пять модусов (modi) к первой фигуре силлогизма; эти пять модусов впоследствии были выделены Клавдием Галеном (жившим во II-м в. н. э.) в особую четвёртую фигуру. Кроме того, Теофраст и его ученик Евдем занялись анализом условного и разделительного силлогизмов. Они допустили пять видов умозаключений: два из них соответствуют условному силлогизму, а три — разделительному, который они рассматривали как видоизменение условного силлогизма. Этим и заканчивается развитие учения о силлогизме в древности, если не считать того добавления, которое сделали стоики в учении об условном силлогизме. По словам Секста Эмпирика, стоики признавали некоторые виды условного и разделительного силлогизма αναπόδεικτοι, то есть не нуждающимися в доказательствах, и рассматривали их как прототипы силлогизма (как, например, смотрит на силлогизм Зигварт). Стоики признавали пять видов подобных силлогизмов, совпадающих с Теофрастовыми. Секст Эмпирик приводит следующие примеры для этих пяти видов:
- Если наступил день, то имеется свет; но теперь день, следовательно, имеется свет.
- Если наступил день, то имеется свет, но света нет, следовательно, нет и дня.
- Не может быть (одновременно) дня и ночи, но день наступил, следовательно, нет ночи.
- Может быть или день, или ночь, но теперь день, следовательно, нет ночи.
- Может быть или день, или ночь, но ночи нет, следовательно, теперь день.
У Секста Эмпирика и скептиков вообще мы встречаемся и с критикой силлогизма, но цель критики — доказательство невозможности доказательства вообще, в том числе и силлогистического. Схоластическая логика ничего существенного не добавила к учению о силлогизмах; она лишь порвала ту связь с теорией познания, которая существовала у Аристотеля и тем превратила логику в чисто формальное учение. Образцовым руководством логики в средние века было сочинение Марциана Капеллы, образцовым комментарием — сочинения Боэция. Некоторые из комментариев Боэция занимаются специально учением о силлогизмах, например «Introductio ad categoricos syllogismos», «De syllogismo categorico» и «De syllogismo hypothetico». Сочинения Боэция имеют некоторое историческое значение; они способствовали также установлению логической терминологии. Но в то же самое время именно Боэций придал учениям логическим характер чисто формальный.

Из эпохи схоластической философии по отношению к учению о силлогизме внимания заслуживает Фома Аквинский (ум. 1274), в особенности его подробный анализ ложных умозаключений («De fallaciis»). Сочинение по логике, имевшее некоторое историческое значение, принадлежит византийцу Михаилу Пселлу. Он предложил так называемый «логический квадрат», в коем наглядно выражается отношение различных видов суждений. Ему принадлежат названия различных modi (греч. τρόποι) фигур. Эти названия, латинизированные, перешли в западную логическую литературу.
Михаил Пселл, следуя Теофрасту, пять modi четвёртой фигуры относил к первой. Название видов имело у него в виду мнемонические цели. Ему же принадлежит и общеупотребительное обозначение буквами количества и качества суждений (а, е, i, о). Учения логические у Пселла носят формальный характер. Сочинение Пселла было переведено Уильямом из Шервуда и получило распространение благодаря переделке Петра Испанского (папы Иоанна XXI). У Петра Испанского в его учебнике заметно то же стремление к мнемотехническим правилам. Латинские названия видов фигур, приводимые в формальных логиках, взяты у Петра Испанского. Пётр Испанский и Михаил Пселл представляют собой расцвет формальной логики в средневековой философии. С эпохи Возрождения начинается критика формальной логики и силлогистического формализма.
Первым серьёзным критиком Аристотелевской логики был Пьер Рамэ, погибший во время Варфоломеевой ночи. Во второй части его «Диалектики» говорится о силлогизме; учение его о силлогизме, однако, существенных отступлений от Аристотеля не представляет. Начиная с Бэкона и Декарта философия идёт по новым путям и отстаивает методы исследования: непригодность силлогистического метода в смысле метода получения нового знания становится всё более и более очевидной.
Тем не менее, решение силлогизмов составляет важнейшую часть любого учебника по традиционной логике.[2] Несмотря на то, что использование силлогизмов само по себе не даёт новое знание, использование правил построения силлогизмов позволяет избежать логических ошибок, софизмов, в рамках имеющегося знания (см. Демагогия).
Силлогизм в современной логике[править | править код]
Силлогизм преобладал в логике до XIX века и имел ограниченное приложение в частности из-за привязки к категорическому силлогизму. Заменой аристотелевской силлогистике служит более простая логика первого порядка.
См. также[править | править код]
- Дедуктивное умозаключение
- Силлогистические теории
- Софизм
- Сорит
- Энтимема
- Силлогистика
Примечания[править | править код]
- ↑ Салин Ю. С. Эволюционный тупик Архивная копия от 11 февраля 2015 на Wayback Machine
- ↑ Светлов В.А. Практическая логика. — Изд. 3-е, испр. и доп.. — СПб.: “Росток”, 2003. — С. 191. — 688 с.
Литература[править | править код]
- Радлов Э. Л. Силлогизм // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
Ссылки[править | править код]
- Логический квадрат М. Пселл
