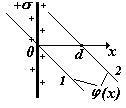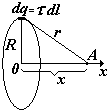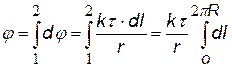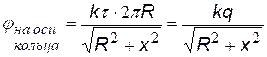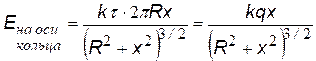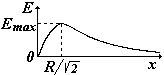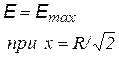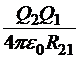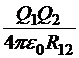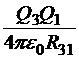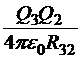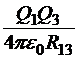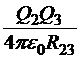Рассмотрим
вычисление потенциала поля, созданного
некоторыми заряженными телами.
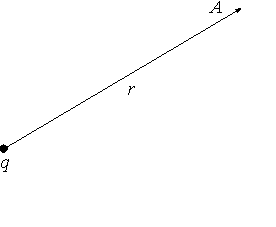
Рис.3.
Расположение точки наблюдения А по
отношению к точечному источнику поля
q
1.
Пример
Точечный
заряд.
Используя соотношения (1) и (4) и совмещая
точку 1 с точкой наблюдения А
(рис.3), а точку 2 удаляя на бесконечность,
получим
![]() (7)
(7)
Замечание.
До сих пор использовалось понятие
векторного поля – поля векторов
![]() (каждой точке пространства ставится в
(каждой точке пространства ставится в
соответствие вектор![]() ).
).
Представление о потенциале
![]() как
как
функции точки пространства позволяет
ввести понятие скалярного поля – поля
чисел
![]()
(каждой точке пространства ставится в
соответствие, с точностью до произвольной
аддитивной постоянной, число
![]() ).
).
Поэтому в дальнейшем кроме понятий
электростатическое поле и поле
![]() ,
,
будем использовать понятие поля![]() .
.
2.Пример. Найдем потенциал бесконечной однородно заряженной с линейной плотностью нити.
Наша задача найти
![]()
как функцию
![]() .
.
К
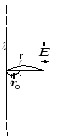 ак
ак
уже было показано для бесконечно длинной
нити:![]() .
.
Выберем где-нибудь
точку из которой мы стартуем, к примеру
в точке
![]() ,
,
то
![]() .
.
Договоримся, что
в точке старта потенциал равен нулю:
![]() ,
,
тогда
![]() .
.
Это при такой
нормировке. Если в такой задаче нормировать
![]() ,
,
то получим![]() ,то
,то
есть все потенциалы во всех точках
бесконечно большие. Кому нужна такая
нормировка? Если Вас интересует какой-то
конкретный пространственный диапазон,
то нормировать надо где-то вблизи этой
области, тогда все потенциалами будут
конечными приятными числами. От
бесконечной нити нельзя уйти на
бесконечность, по этой же причине не
следует ожидать хорошего результата
от![]() как суммы потенциалов точечных фрагментов
как суммы потенциалов точечных фрагментов
нити, каждый из которых нормирован
условием![]() .
.
3.Пример. Потенциал поля точечного диполя (первый способ).
И так,
так,
мы рассматриваем точечный диполь и
точку наблюдения достаточно далеко от
этой нашей гантельки.
Давайте искать
потенциал этой точки наблюдения.
Во первых, принцип
суперпозиции.
![]()
Во-вторых, как
известно
![]()
![]() .
.
Учтя, что
![]() есть проекция вектора
есть проекция вектора![]() на
на![]() и то, что расстояние до диполя очень
и то, что расстояние до диполя очень
велико, то
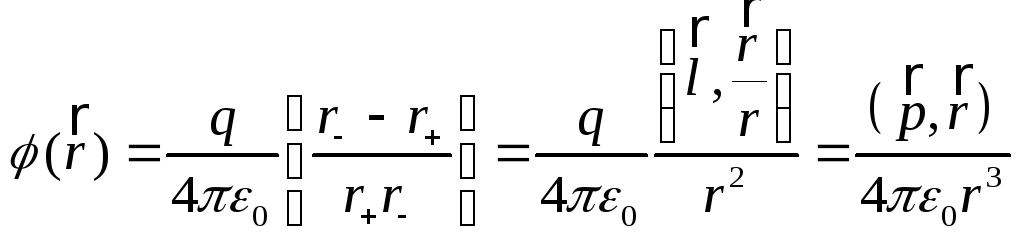
Потенциал поля точечного диполя (второй способ).
Используем готовую
формулу для напряженности поля:
![]() .
.
Вот такое выражение мы с вами в свое
время вывели. Обопремся на него.
![]()
Д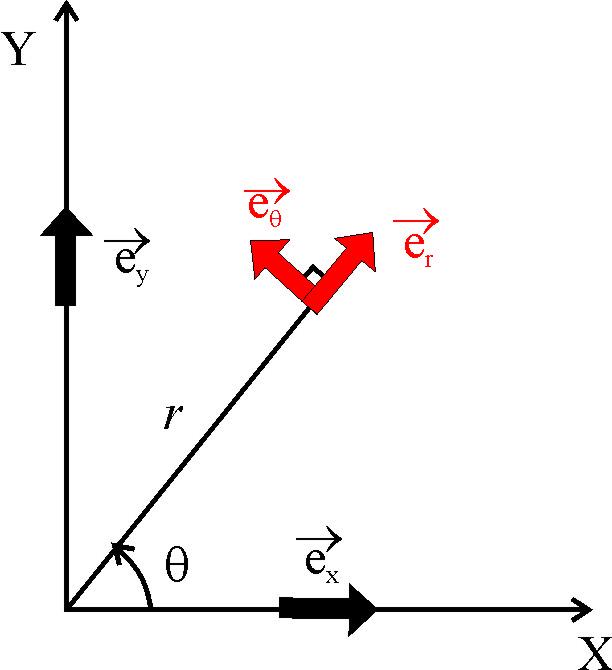 авайте
авайте
выберем такое направление, чтобы нам
было удобно вычислять этот интеграл,
так как поле потенциальное, то результат
не будет зависеть от вида траектории.
Ориентация диполя, направление движения
и вектор![]() показаны
показаны
на рисунке. С учетом некоторых соотношений
(5) примет вид:
![]()
Определение
вектора
![]() точечного
точечного
диполя из
![]() в
в
полярной системе координат.
![]() Оператор
Оператор
![]() запишется в полярной системе координат
запишется в полярной системе координат
так:
![]()
Ортыкоординатных
осей декартовой и полярной систем
координат (см.рис.)
4.Пример
См. Иродов задача
3.38. (часть2)
Показать, что
потенциал диполя с электрическим
моментом может быть представлен как![]() ,
,
где![]() –радиус
–радиус
вектор. Найти с помощью этого выражения
модуль напряженности электрического
поля диполя как функцию![]() и
и![]() .
.
![]() –
–
это уже показали выше, отсюда, раскрывая
скалярное произведение и продифференцировав
формулу для потенциала, мы получим
![]() .
.
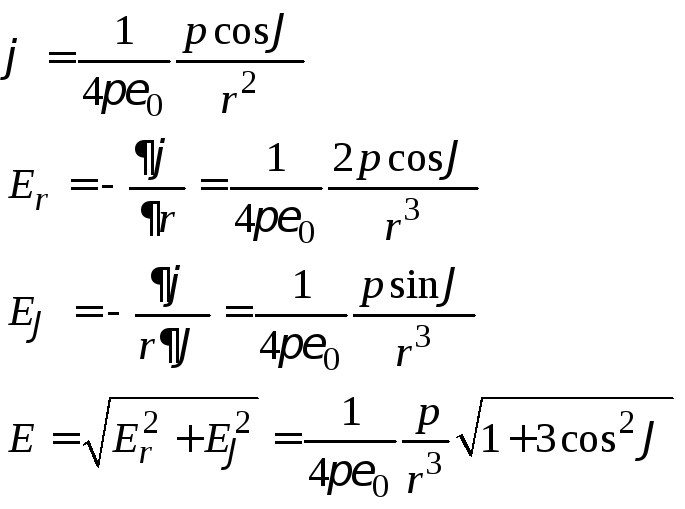
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Будем рассматривать только случаи, когда напряженность и потенциал зависят только от одной координаты х или радиальной координаты r
для сферически или цилиндрически симметричных тел. Разность потенциалов связана с напряженностью в этом случае как (см. формулу (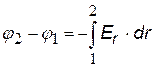 )):
)):
|
|
Связь разности потенциалов с напряженностью для случая одной переменной х или r (математически это уравнение однотипно с ( |
Из уравнений (ª) или (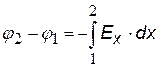 ) можно найти разность потенциалов, если известна функция Е(r) или Е(r). Чтобы получить формулу для потенциала, следует выбрать уровень нулевого потенциала (так же, как в случае потенциальной энергии – см. механику). Обычно принимают j = 0 на бесконечности, но для поля нити это невозможно (см. ниже).
) можно найти разность потенциалов, если известна функция Е(r) или Е(r). Чтобы получить формулу для потенциала, следует выбрать уровень нулевого потенциала (так же, как в случае потенциальной энергии – см. механику). Обычно принимают j = 0 на бесконечности, но для поля нити это невозможно (см. ниже).
1) Точечный заряд.
Подставим в формулу (ª) выражение для напряженности поля точечного заряда. 1 и 2 – любые две точки на радиальной оси координат r. Примем j 1 = 0 при
r1 ®¥, заменим j 2 ® j , r2
®r получим j (r).
2).Сфера радиуса R, заряженная с поверхностной плотностью заряда s (Кл/м2).
Полный заряд на сфере q = s×4p×R2 . Будем рассматривать две области:1) ![]() – выбираем две любые точки 1 и 2 в этой области и 2)
– выбираем две любые точки 1 и 2 в этой области и 2) ![]() также выбираем две любые точки уже в этой области. Потенциал должен быть непрерывной функцией, в отличие от напряженности он не может иметь разрывов в данной точке, т.к. по смыслу j – потенциальная энергия единичного положительного заряда, а двух энергий у одного заряда в одной точке данного поля не может быть.
также выбираем две любые точки уже в этой области. Потенциал должен быть непрерывной функцией, в отличие от напряженности он не может иметь разрывов в данной точке, т.к. по смыслу j – потенциальная энергия единичного положительного заряда, а двух энергий у одного заряда в одной точке данного поля не может быть.
|
|
Подставим в (ª) Е поля сферы. Для |
|
Внимание! Если вам нужна помощь в написании работы, то рекомендуем обратиться к |
|
|
|
|
|
|
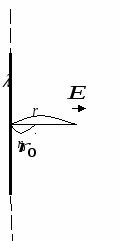
3)Бесконечно длинная нить, заряженная с линейной плотностью заряда t.
Выберем на оси радиальных координат r две любые точки с координатами r1
и r2.
(см. рис.). Подставим в (ª) напряженность поля длинной нити и проинтегрируем.
|
|
В этом случае принять j = 0 на бесконечности нельзя (см. график ln x), поэтому выбираем j = 0 в некоторой произвольной точке с координатой ro. Т.е. примем
заменим j 2 ® j , r2 ®r получим j (r) |
|
|
j = 0 при r |
|
|
4)Бесконечно протяженная плоскость, равномерно заряженная с поверхностной плотностью заряда s (Кл/м2). Выберем на оси координат х
две произвольные точки х1 и х2 .). Используем формулу связи Е и j (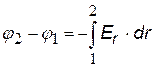 ), подставим выражение для напряженности поля бесконечной плоскости.
), подставим выражение для напряженности поля бесконечной плоскости.
|
|
Чтобы получить выражение для потенциала примем 1)j х1 = 0 и 2) j 1 = 0 при х1 = d (d – произвольная точка на оси х) |
|
1) 2) |
|
Следует иметь в виду, что формулы для Е и j в случаях плоскости, нити, цилиндра применимы только на расстояниях от них, существенно меньших размеров этих тел. В действительности при учете краевых эффектов поля становятся более сложными.
Во всех случаях, задавая нулевой уровень потенциала j = 0 в различных точках, мы можем получить сколько угодно формул для потенциала данного поля. Потенциальные кривые (или прямые), т.е. графики j(r)или j(х) при этом будут перемещаться по вертикали параллельно самим себе. В принципе, неважно, где выбрать нулевой уровень потенциала, т.к. во всех задачах имеет значение не сам потенциал, а его изменение
Так как потенциал – скалярная величина, а напряженность – вектор, то значительно проще найти сначала зависимость j(r) или
j(х), затем дифференцируя, получить формулу для Е(r)или
Е (х).
В качестве примера найдем потенциал поля на оси тонкого кольца, равномерно заряженного с линейной плотностью t, а затем Е (х).Для этого выделим в кольце бесконечно малый элемент dl с зарядом dq = t×dl (см. рис.) В некоторой точке A потенциал складывается из потенциалов, создаваемых всеми элементами кольца.
|
|
потенциал поля элементарного заряда dq (j¥ = 0) |
|
||
|
|
«суммируя» (интегрируя) потенциалы от всех элементов кольца, получим формулу для j (х). |
|||
|
|
Дифференцируя по х, найдем напряженность Е(х) |
|||
|
|
|
|
||
Получить выполненную работу или консультацию специалиста по вашему
учебному проекту
Узнать стоимость
следовательно, потенциал внутри сферы будет совпадать с потенциалом поверхности, то есть в данном случае это будет эквипотенциальный объём. Теперь сформулируем вывод:
на поверхности и за пределами равномерно заряженной сферы потенциал электростатического поля ничем не отличается от потенциала поля точечного заряда, помещённого в центр сферы и равного заряду сферы; внутри сферы потенциал постоянный и равен потенциалу на поверхности.
14.5.3. Однородное поле
Начало отсчёта потенциала берём на месте плоскости заряда (рис.14.8). Поскольку распределение заряда безгранично, выбор начала отсчёта потенциала на бесконечности приведёт к расходимости в интеграле. Поэтому так делать в этом случае нельзя.
15.5.4. Прямая бесконечная однородно заряженная нить
Это тоже неограниченное в пространстве распределение заряда. На бесконечном удалении брать нельзя, но и на самой нити − тоже, так как в этом случае тоже получится расходимость. Начало отсчёта берём на расстоянии от нити, равном 1м. Обозначим расстояние от нити r.
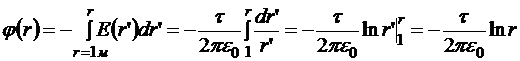 ;
;
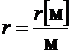 − безразмерное.
− безразмерное.
 Рис.14.10
Рис.14.10
§14.6. Энергия системы точечных зарядов
До сих пор мы рассматривали потенциальную энергию пробного заряда в поле источников. Теперь мы ставим вопрос об энергии, которой обладает система источников сама по себе. Есть эта энергия или её нет? Ответ на этот вопрос является одновременно ответом на вопрос: а нужно ли было совершить работу для создания этой системы, поскольку из закона изменения механической энергии в отсутствии внешних потенциальных полей следует
![]()
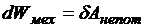 .
.
В нашем случае работу непотенциальных сил должны выполнять внешние по отношению к системе силы. Кроме этого, мы будем рассматривать только неподвижные заряды, и до воздействия внешних сил, и тогда, когда заряды уже собраны в систему. Поэтому изменение механической энергии будет совпадать с изменением потенциальной энергии взаимного расположения источников. Тогда закон изменения механической энергии примет вид:
![]()
В интегральной форме:
![]()
Очевидно, что конфигурация бесконечного удаления источников друг от друга может считаться началом отсчёта потенциальной энергии. Поэтому из последнего соотношения получим способ для определения потенциальной энергии взаимного расположения источников или энергии системы точечных зарядов:
![]() .
.
Здесь под Авнеш нужно понимать работу внешних сил по сведению точечных источников в данную конфигурацию из конфигурации их бесконечного удаления друг от друга.
Рассмотрим систему двух точечных источников Q1 и Q2, отстоящих друг от друга на расстояние R12. Работа внешних сил по сближению их из бесконечного удаления до указанного расстояния не должна зависеть от способа сближения. Поэтому мы в праве выбрать тот способ сближения, который наиболее удобен с точки зрения вычислений. Это способ, когда один заряд неподвижен и может играть роль источника, а второй перемещается по направлению к первому и играет роль пробного заряда. Тогда потенциальная энергия конфигурации — это потенциальная энергия пробного заряда в поле источника, то есть
Хотя, для получения этого результата мы отдали роль источника заряду Q1, а пробного − заряду Q2, выражение показывает, что оба заряда, на самом деле равноправны.
Можно нарисовать матрицу 2´2, номера столбцов которой будут, например, номерами возможных источников, а номера строк − номерами возможных пробных зарядов:
|
1 |
2 |
|
|
1 |
|
|
|
2 |
|
Для краткости обозначим: 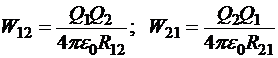 .Тогда можно записать, что
.Тогда можно записать, что ![]() , или
, или 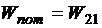 , но можно и так:
, но можно и так:
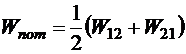
Установив в нужном месте заряды Q1 и Q2, будем приближать к ним заряд Q3, создавая систему из трёх зарядов. Очевидно, что к уже сделанной работе мы добавим слагаемые 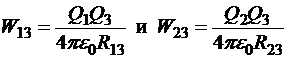 , которые получаются, если заряд Q3 играет роль пробного в поле источников Q1 и Q2. Но в результате мы можем записать матрицу, в которой уже три заряда могут получить роли как пробных, так и источников:
, которые получаются, если заряд Q3 играет роль пробного в поле источников Q1 и Q2. Но в результате мы можем записать матрицу, в которой уже три заряда могут получить роли как пробных, так и источников:
|
1 |
2 |
3 |
|
|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
Теперь энергию системы можно записать как
![]() .
.
А можно как
![]()
Иными словами, для получения системы мы можем суммировать все поддиагональные ячейки, можем суммировать все наддиагональные ячейки. Результат не изменится, так как матрица транспонированная. А можем суммировать все недиагональные ячейки и делить результат пополам. В последнем способе слагаемые можно расставлять множеством способов. Можно так:
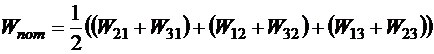 ,
,
то есть суммы каждой строки мы суммировали по всем строкам.
Рассмотрим физический смысл суммы по одной строке, например, по первой:
![]() .
.
Это произведение первого заряда на потенциал, созданный на его месте всеми зарядами кроме него. Тогда способ суммирования сумм каждой строки по всем строкам можно записать так:
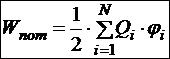
Потенциальная энергия системы зарядов равна полусумме произведений каждого заряда на потенциал, создаваемый на его месте всеми остальными зарядами, кроме него.
Такое представление энергии системы зарядов полезно тем, что позволяет сделать обобщение на случай непрерывного распределения заряда: очевидно, что дискретное суммирование будет заменено интегрированием. Кроме этого, точечный заряд ![]() является элементарным, то есть пренебрежимо малым по сравнению с полным зарядом системы (в выражении элементарного заряда dV − объём, занимаемый этим зарядом, в котором и создаётся потенциал ). Значит, в выражении
является элементарным, то есть пренебрежимо малым по сравнению с полным зарядом системы (в выражении элементарного заряда dV − объём, занимаемый этим зарядом, в котором и создаётся потенциал ). Значит, в выражении
Подборка по базе: Лабораторная работа №3 %22Исследование интегральных характеристи, Значительно скромнее выглядит научный потенциал.docx, Концепции поражения АУГ потенциального противника.docx, 10 шагов к развитию лидерского потенциала (Автосохраненный).docx, Энергия-кинетическая и потенциальная.docx, Воспитательный потенциал уроков ОБЖ, как необходимость повышения, Электрохимия потенциал қатары.docx, _О реализации федерального проекта Развитие кадрового потенциала, 17. Достоинства и недостатки плановой экономики. Потенциал и реа, разность потенциалов.docx
2. Потенциал электростатического поля.
(«Пионером» в этой области считается Лагранж, который
в 1777 году впервые ввел понятие потенциала для гравитационного поля).
2.1. Работа сил электростатического поля по переносу точечного заряда.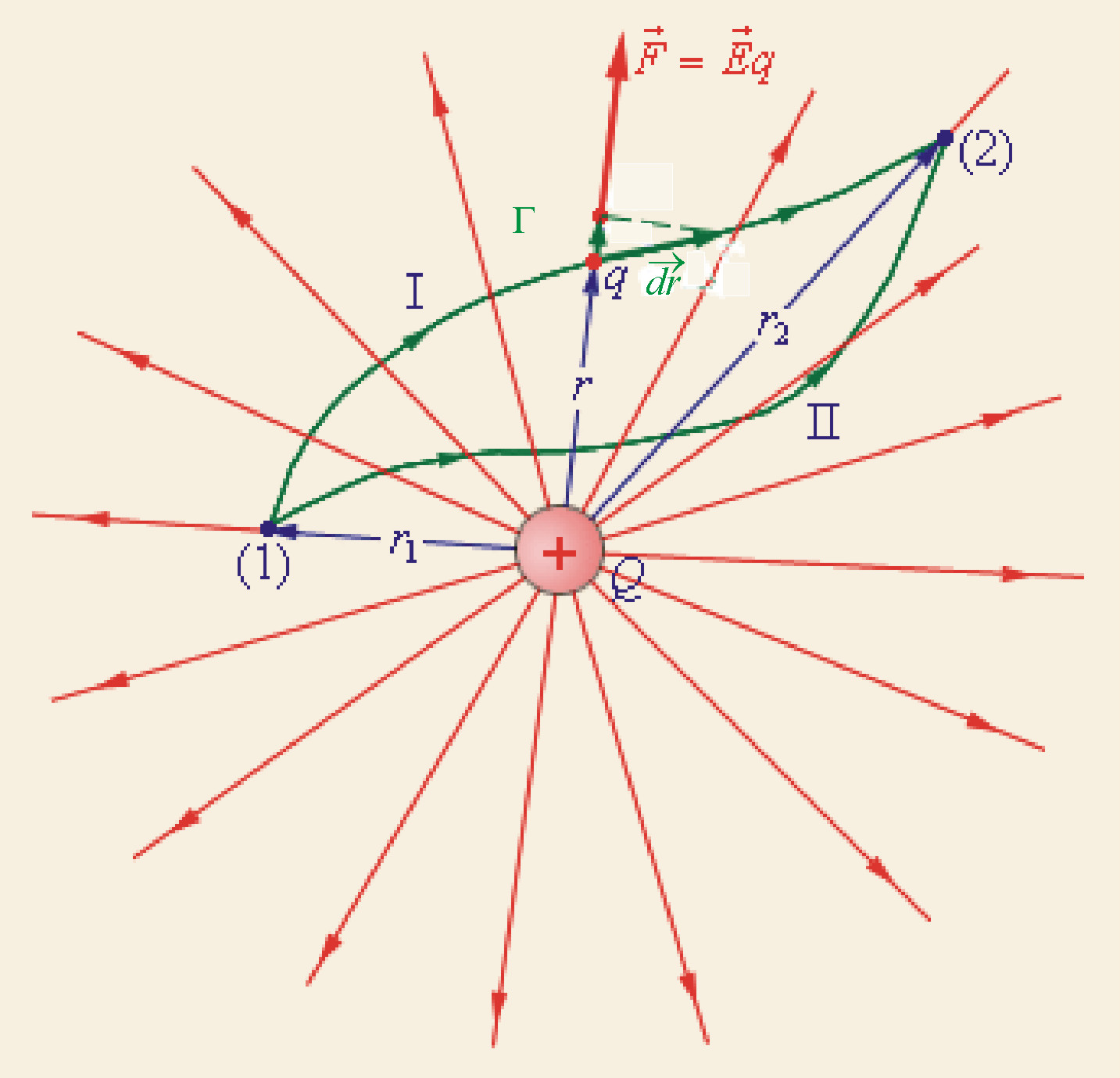
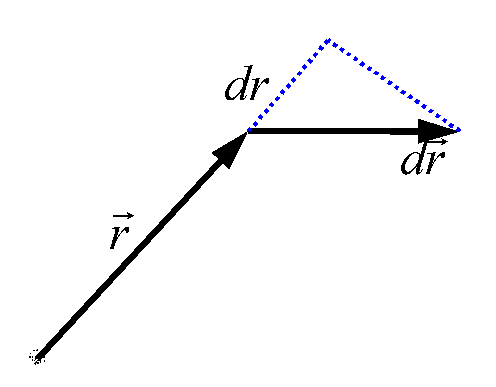
Пробный (положительный и очень маленький по размеру – это определение пробного заряда) заряд q
медленно (квазистатически – заряд находится почти в покое) перемещаем по пути Г («гамма-большое») из 1 в 2 в электростатическом поле точечного статического заряда Q. Найдем элементарную работу сил электростатического поля этого заряда по перемещению заряда q:
Как известно из курса механики
Элементарная работа силы ![]() :
: ![]() где
где ![]() – элементарное перемещение точки приложения силы
– элементарное перемещение точки приложения силы ![]() .
.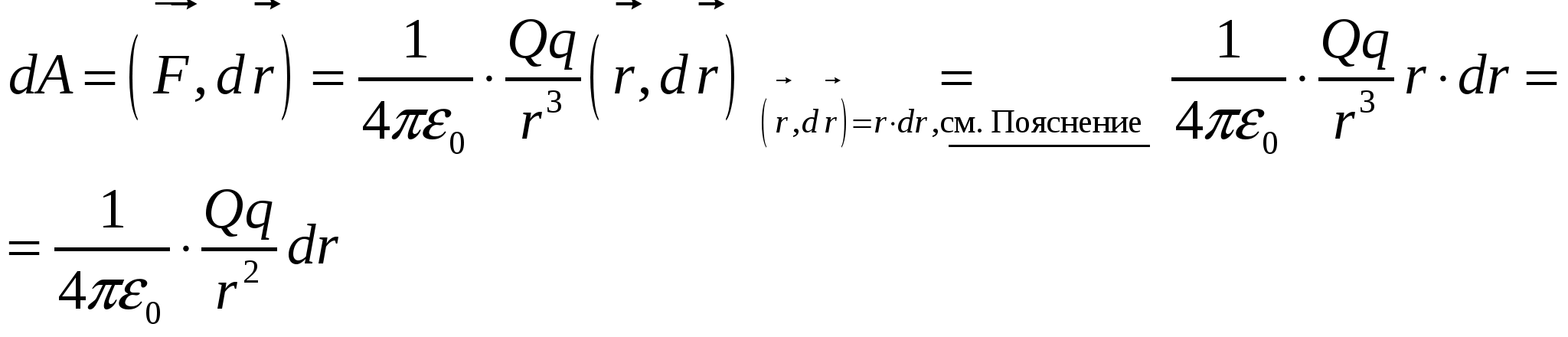
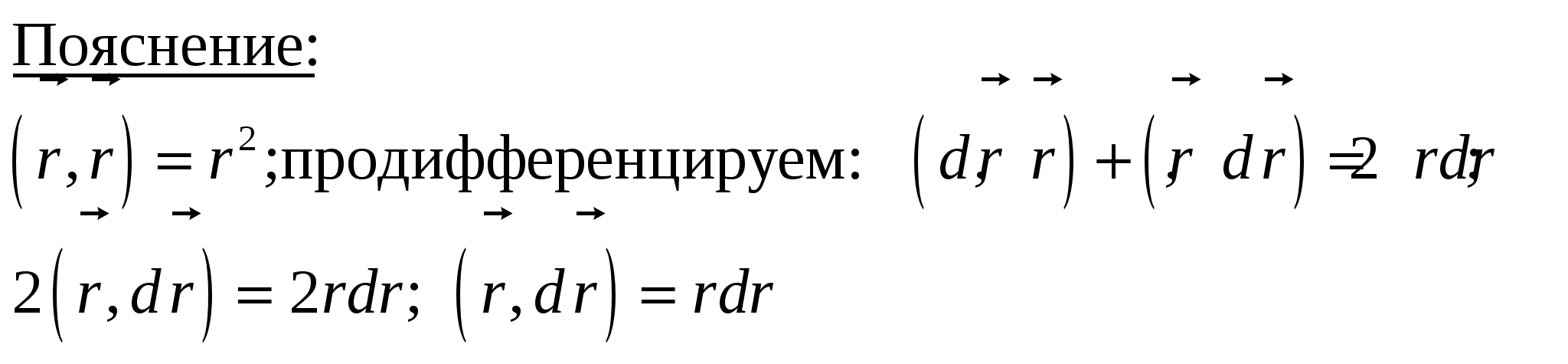 Итак, работа сил электростатического поля по перемещению точечного заряда из положения 1 в положение 2 по контуру Г может быть вычислена по формуле:
Итак, работа сил электростатического поля по перемещению точечного заряда из положения 1 в положение 2 по контуру Г может быть вычислена по формуле:
![]()
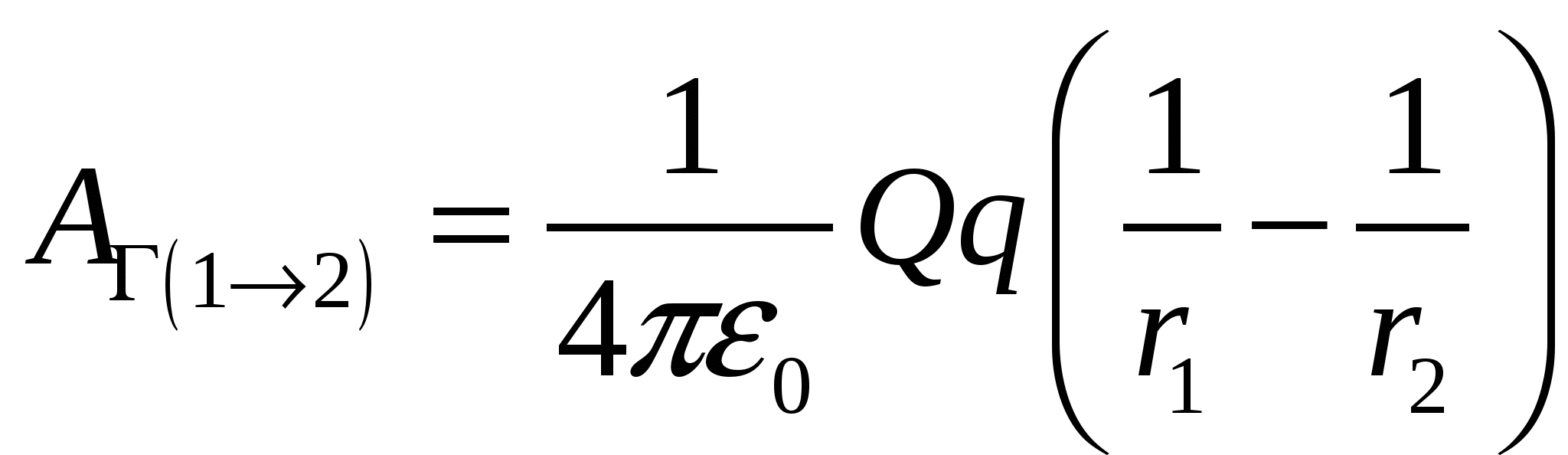 (1)
(1)
2.2. Интегральный признак потенциальности электростатического поля.
Анализируя полученную формулу для работы сил электростатического поля по перемещению заряда q по некоторому контуру Г, можно сделать следующие выводы:
- работа
 не зависит от формы контура Г, а зависит только от начального и конечного положений;
не зависит от формы контура Г, а зависит только от начального и конечного положений; - если точки 1 и 2 совпадают (контур Г – замкнутый), то
 =0, т.е.
=0, т.е.
![]()
![]()
![]()
Линейный интеграл, взятый по замкнутому контуру (замкнутой кривой) Г, называется циркуляцией вектора ![]() . Т.е. утверждается, что циркуляция электростатического поля равна нулю.(Теорема о циркуляции).
. Т.е. утверждается, что циркуляция электростатического поля равна нулю.(Теорема о циркуляции).
Последний результат справедлив и для электростатического поля, созданного любой системой покоящихся точечных зарядов, т.к. по принципу суперпозиции электростатических полей
![]()
![]()
Векторное поле называется потенциальным, если циркуляция этого вектора по
любому замкнутому контуру ![]()
![]() равна нулю.
равна нулю.
Однако этот критерий потенциальности является неудобным на практике, т.к. нужно будет исследовать
всевозможные контуры (что само по себе невозможно), и установить, является ли интеграл по ним равным нулю.
2.3. Локальный (дифференциальный) признак потенциальности электростатического поля.
Н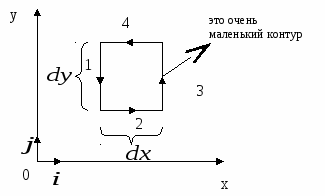 айдем циркуляцию вектора
айдем циркуляцию вектора ![]() по бесконечно малому плоскому прямоугольному контуру
по бесконечно малому плоскому прямоугольному контуру ![]() , расположенному в районе некоторой точки, в декартовой системе координат. Нас будет интересовать конфигурация (линейные размеры) этого контура, поэтому изобразим его достаточно большим. Выберем направление обхода по контуру – против часовой стрелки.
, расположенному в районе некоторой точки, в декартовой системе координат. Нас будет интересовать конфигурация (линейные размеры) этого контура, поэтому изобразим его достаточно большим. Выберем направление обхода по контуру – против часовой стрелки.
Т.к. величины dx и dyявляются очень маленькими, можно считать, что и поле на протяжении этих отрезков также одинаково; будем обозначать поле в каждой точке стороны 1 как ![]() , поле в каждой точке стороны 2 как
, поле в каждой точке стороны 2 как![]() , и так далее. Интеграл по замкнутому контуру в данном случае мы можем заменить на сумму четырех слагаемых:
, и так далее. Интеграл по замкнутому контуру в данном случае мы можем заменить на сумму четырех слагаемых:
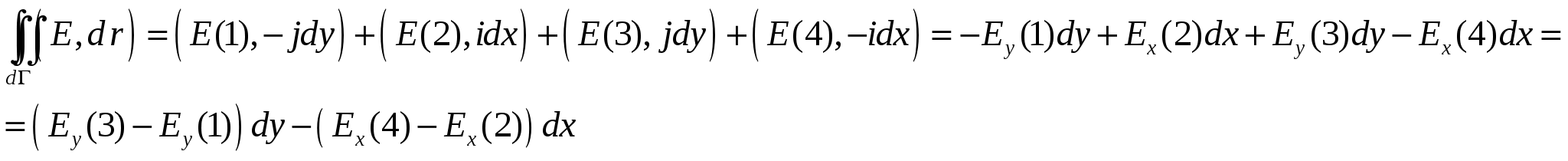
Теперь заметим, что выражение ![]() по сути является приращением y-ковой составляющей поля при переходе из 1 в 3 вдоль оси x. Тогда наше выражение приблизительно равно:
по сути является приращением y-ковой составляющей поля при переходе из 1 в 3 вдоль оси x. Тогда наше выражение приблизительно равно:
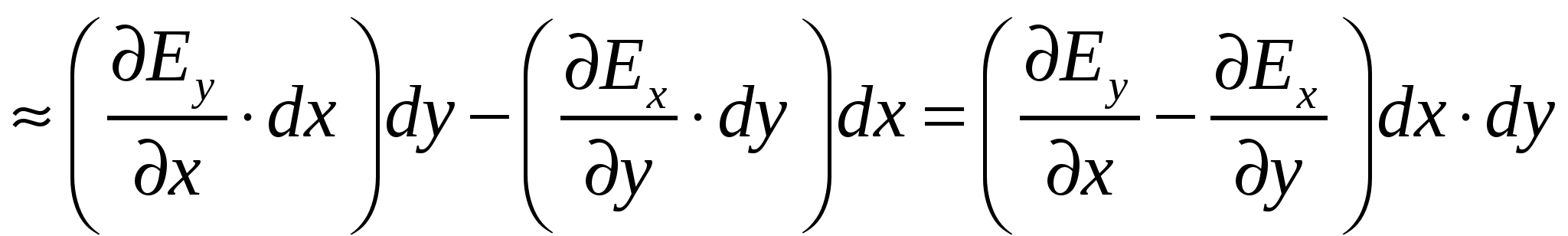
Мы нашли циркуляцию вектора ![]() по элементарному контуру.
по элементарному контуру.
Аналогично для элементарных прямоугольных контуров в плоскостях yzи zx можно получить:
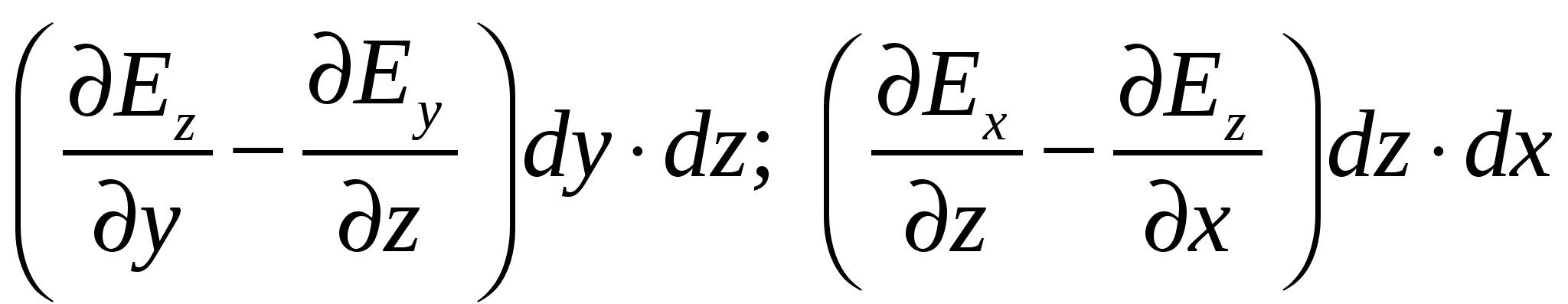
А так как циркуляция вектора ![]() по любому контуру равна нулю, то можно сделать вывод, что в потенциальном поле выполняются одновременно все 3 следующих равенства:
по любому контуру равна нулю, то можно сделать вывод, что в потенциальном поле выполняются одновременно все 3 следующих равенства:
![]() (*)
(*)
То, что выписано – необходимый, а в электростатике – и достаточный признак потенциальности электрического поля в декартовой системе координат.
Выполнение этих равенств проверить на практике гораздо проще, чем проверять интегральный признак потенциальности электростатического поля.
Итак, поле![]() является потенциальным в области, если условия (*) выполняются в каждой точке этой области.
является потенциальным в области, если условия (*) выполняются в каждой точке этой области.
Условия (*) можно компактно записать в векторной форме, если ввести в рассмотрение вектор “ротор” напряженности электрического поля (см. Замечание).
![]() Замечание
Замечание
Ротор вектора![]() определим следующим образом
определим следующим образом
![]()
Векторное произведение вектора оператора градиента и вектора напряженности электрического поля, или ротор![]() можно записать через детерминант
можно записать через детерминант
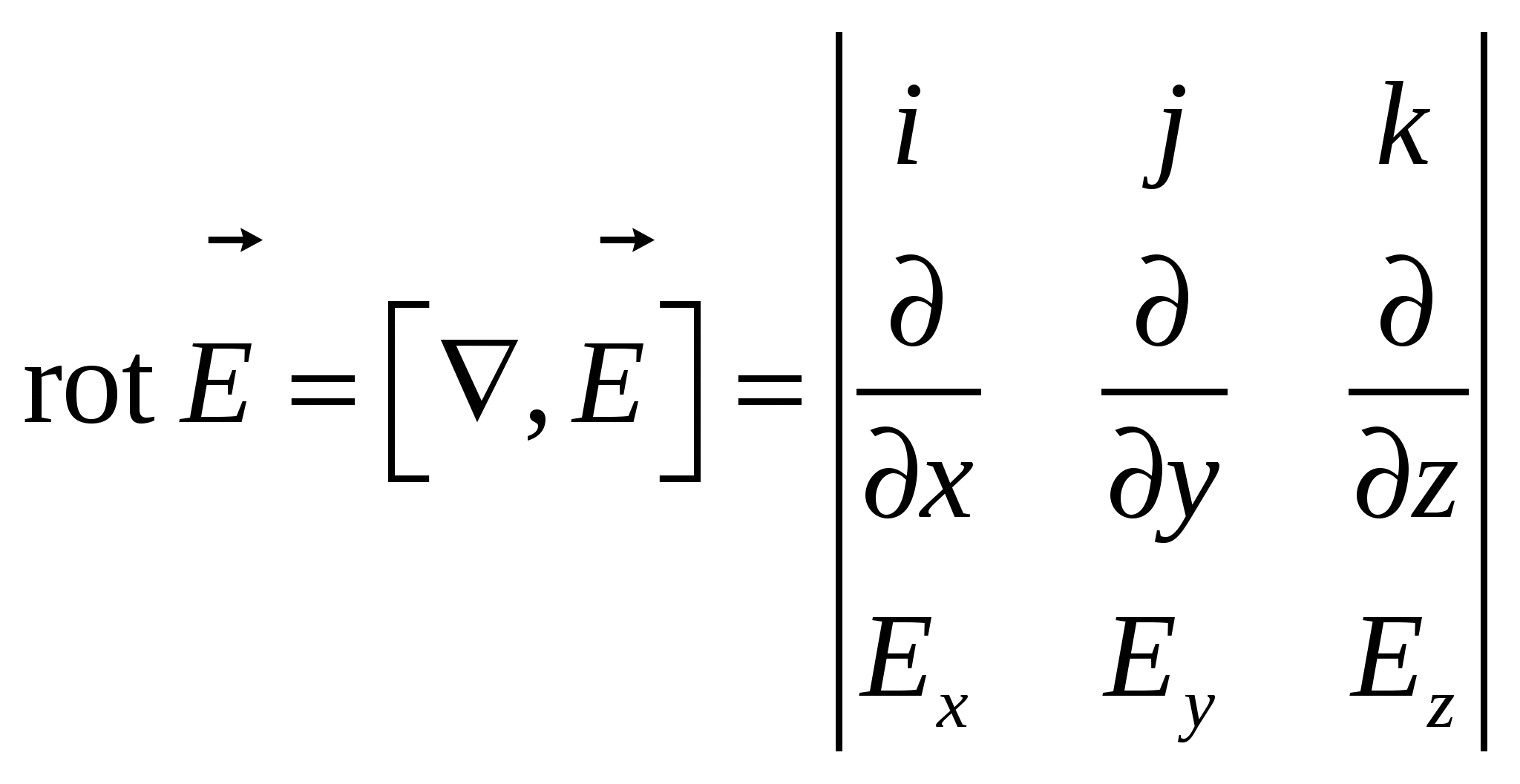
Следовательно, для электростатического поля имеем
![]()
ПОТЕНЦИАЛ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ.
2.4 Определение потенциала. Интегральное соотношение между ![]() .
.
Потенциальное поле векторов ![]() можно описать на скалярном языке с помощью понятия потенциала, он описывает поле более простым способом. Определяется не сам потенциал, а его приращение, по определению это:
можно описать на скалярном языке с помощью понятия потенциала, он описывает поле более простым способом. Определяется не сам потенциал, а его приращение, по определению это:
![]() (2)- приращение потенциала
(2)- приращение потенциала![]() (3) – убыль потенциала.
(3) – убыль потенциала.
Разность потенциалов ![]() между точками 2 и 1 электростатического поля численно равна взятой с обратным знаком работе, совершаемой силами поля, при квазистатическом перемещении единичного положительного заряда по любому пути из точки 1 в точку 2.
между точками 2 и 1 электростатического поля численно равна взятой с обратным знаком работе, совершаемой силами поля, при квазистатическом перемещении единичного положительного заряда по любому пути из точки 1 в точку 2.
2.5. Нормировка потенциала или выбор уровня отсчета.
Перепишем формулу (3) иначе:
![]() – определен с точностью до выбора некой постоянной
– определен с точностью до выбора некой постоянной ![]() , которая нам не известна.
, которая нам не известна.
Существуют два удобных способа выбора значения аддитивной постоянной.
1. Если система зарядов занимает ограниченную область пространства, то потенциал бесконечно удаленной точки обычно полагают равным нулю. Потенциал любой другой точки согласно однозначно определится выражением
![]()
2. В практике электрических измерений часто полагают равным нулю потенциал поверхности Земли. При этом исходят из того, что вследствие очень большой электрической емкости Земли ее потенциал практически неизменен и соединение какого-либо проводника с Землей (заземление) делает его потенциал практически фиксированным. В этом случае
![]()
Когда говорят о потенциале, то имеют ввиду разность потенциалов ![]() между рассматриваемой точкой и точкой, потенциал
между рассматриваемой точкой и точкой, потенциал ![]() которой принят за 0.
которой принят за 0.
Вообще, физический смысл имеет величина, которая может быть измерена. Поэтому говорят, что потенциал ![]() в данной точке физического смысла не имеет, так как нельзя измерить работу в данной точке. Физический же смысл имеет разность потенциалов.
в данной точке физического смысла не имеет, так как нельзя измерить работу в данной точке. Физический же смысл имеет разность потенциалов.
Потенциал характеризуется аддитивностью и он подчиняется принципу суперпозиции, как и вектор напряженности электрического поля.
![]()
Если электрическое поле создано системой точечных зарядов, то потенциал ![]() в данной точке равен алгебраической сумме потенциалов
в данной точке равен алгебраической сумме потенциалов ![]() , созданных в этой точке каждым из зарядов в отдельности.
, созданных в этой точке каждым из зарядов в отдельности.
С использованием разности потенциалов квазистатическая работа сил поля при перемещении заряда q0 по произвольному пути из точки 1 в точку 2 представится на основании (3) как
![]() (4)
(4)
т.е. квазистатическая работа сил поля равна убыли потенциала, умноженной на величину перемещаемого заряда.
Единицей измерения потенциала служит вольт (В). Если между двумя точками пространства для переноса заряда в один кулон требуется совершить работу в один джоуль, то разность потенциалов в этих точках равна одному вольту.
![]()
2.6. Локальное (дифференциальное) соотношение между ![]() и
и ![]() .
.
Рассмотрим 2 близкие точки 1 и 2 на координатной оси OX в электростатическом поле ![]() . В соответствии с определением приращения потенциала, поскольку точки очень близки, а значит и потенциалы близки:
. В соответствии с определением приращения потенциала, поскольку точки очень близки, а значит и потенциалы близки:
![]() .
.
Получается, что ![]() .
.
Если точки 1 и 2 лежат в произвольной точке пространства, то аналогичное соотношение можно получить для проекции напряженности на другие оси декартовой системы координат:
![]()
![]()
Таким образом, вектор ![]() может быть представлен в виде:
может быть представлен в виде:
![]()
![]() – это оператор Гамильтона (1805-1865).
– это оператор Гамильтона (1805-1865).
![]() (5)
(5)
(читается так: «Набла фи»).
2.7. Физический смысл градиента (подробно прочитать- литература 6, стр.80-82)
Рассмотрим приращение потенциала d![]() вдоль произвольно ориентированного элемента перемещения
вдоль произвольно ориентированного элемента перемещения ![]() . Величина d
. Величина d![]() зависит, с одной стороны, от распределения поля
зависит, с одной стороны, от распределения поля ![]() (x, y, z) в пространстве, а с другой стороны, от выбора точек сравнения 2 и 1. Учитывая малость dr, можно записать
(x, y, z) в пространстве, а с другой стороны, от выбора точек сравнения 2 и 1. Учитывая малость dr, можно записать
![]() (6)
(6)
Здесь
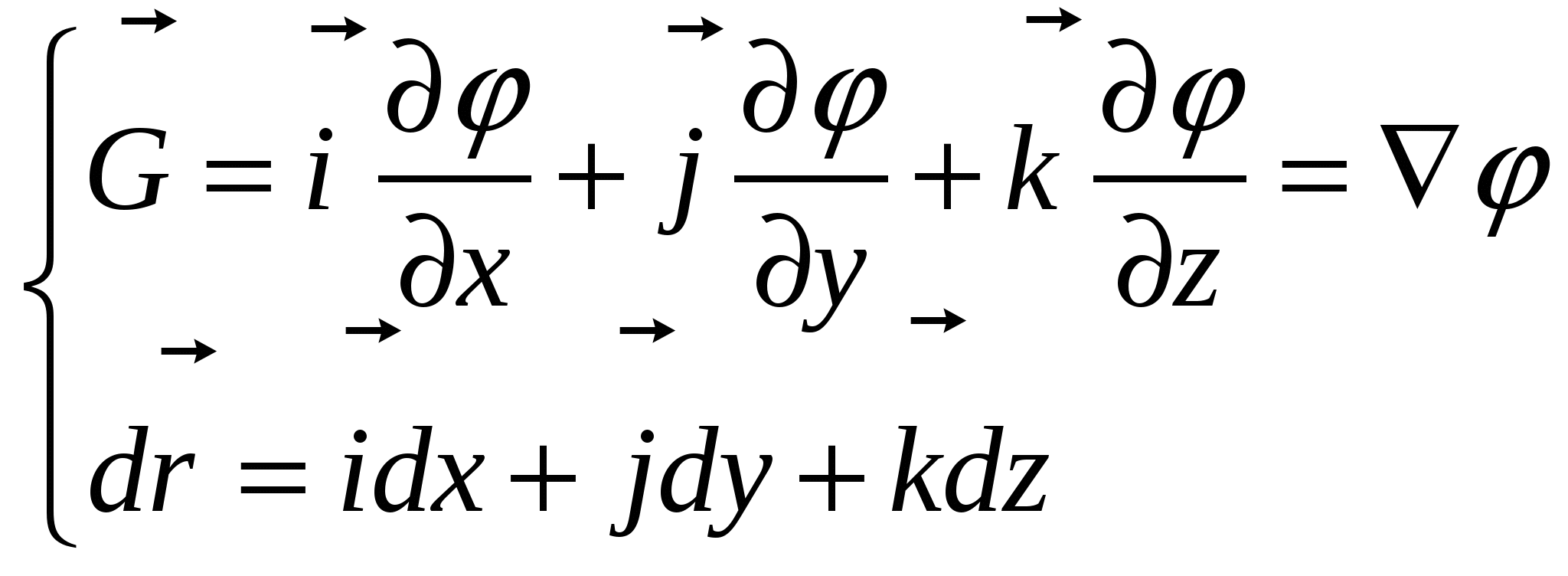
Рассмотрим величину d![]() при перемещении точки 2 по элементарной сфере радиусом dr (вектор
при перемещении точки 2 по элементарной сфере радиусом dr (вектор ![]() меняется только по правлению) (рис.1.). Из формулы (6), записанной в виде
меняется только по правлению) (рис.1.). Из формулы (6), записанной в виде
![]() ,
,
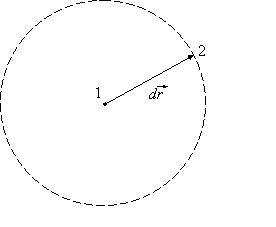
Рис.1. Элементарный вектор ![]() c закрепленным в точке 1 началом. При изменении положения
c закрепленным в точке 1 началом. При изменении положения ![]() в пространстве точка 2 движется по поверхности сферы
в пространстве точка 2 движется по поверхности сферы
видно, что максимальная величина ![]() соответствует такому направлению
соответствует такому направлению ![]() , при котором
, при котором ![]() (так как
(так как ![]() ), другими словами:
), другими словами:
1) направление вектора градиента потенциала указывает направление наиболее быстрого возрастания поля ![]() в пространстве;
в пространстве;
2) величина вектора ![]() определяет “скорость” пространственного изменения поля
определяет “скорость” пространственного изменения поля ![]() в направлении его наиболее быстрого возрастания (Возможно, следовало выразиться как-то осторожней, чтобы не связывать понятие скорости, имеющее смысл производной по времени, с величиной производной по координате, однако такое словоупотребление весьма распространено в литературе);
в направлении его наиболее быстрого возрастания (Возможно, следовало выразиться как-то осторожней, чтобы не связывать понятие скорости, имеющее смысл производной по времени, с величиной производной по координате, однако такое словоупотребление весьма распространено в литературе);
3) “скорость” пространственного изменения потенциала в произвольном направлении (задаваемом вектором ![]() ) равна проекции вектора градиента на это направление.
) равна проекции вектора градиента на это направление.
На основании изложенного выше и выражения (5) приходим к следующему утверждению.
Вектор поля ![]() в данной точке пространства направлен в сторону наиболее резкого уменьшения потенциала, а его величина равна скорости убыли потенциала в этом направлении.
в данной точке пространства направлен в сторону наиболее резкого уменьшения потенциала, а его величина равна скорости убыли потенциала в этом направлении.
Введем понятие эквипотенциальной поверхности – поверхности, во всех точках которой потенциал имеет одно и то же значение.
Выделим поверхность одинакового потенциала ![]() и построим в любой ее точке локальную систему координат ХYZ так, что оси ОХ и ОY будут касательны к эквипотенциальной поверхности, а ось OZ направим по нормали к поверхности в сторону возрастания потенциала (рис. 2).
и построим в любой ее точке локальную систему координат ХYZ так, что оси ОХ и ОY будут касательны к эквипотенциальной поверхности, а ось OZ направим по нормали к поверхности в сторону возрастания потенциала (рис. 2).
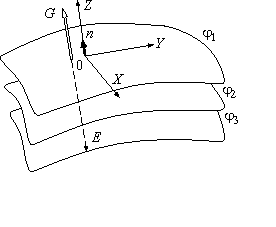
Рис. 2. Взаимное расположение трех эквипотенциальных поверхностей (![]() ), вектора
), вектора![]() градиента потенциала и вектора
градиента потенциала и вектора ![]() напряженности электрического поля. Изображена также локальная декартова прямоугольная система координат XYZ, ось Z которой направлена вдоль нормали
напряженности электрического поля. Изображена также локальная декартова прямоугольная система координат XYZ, ось Z которой направлена вдоль нормали![]() к элементу поверхности
к элементу поверхности ![]()
По построению ![]() в точке 0 и, следовательно,
в точке 0 и, следовательно,
![]() ,
,
т.е. вектор градиента поля, а значит, и вектор![]() , нормален к эквипотенциальной поверхности в любой ее точке. Поскольку направление
, нормален к эквипотенциальной поверхности в любой ее точке. Поскольку направление ![]() определяет направление силовых линий, то очевиден вывод о том, что линии поля нормальны к эквипотенциальным поверхностям.
определяет направление силовых линий, то очевиден вывод о том, что линии поля нормальны к эквипотенциальным поверхностям.
Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью или поверхностью равного потенциала.
Силовые линии электростатического поля всегда перпендикулярны эквипотенциальным поверхностям.
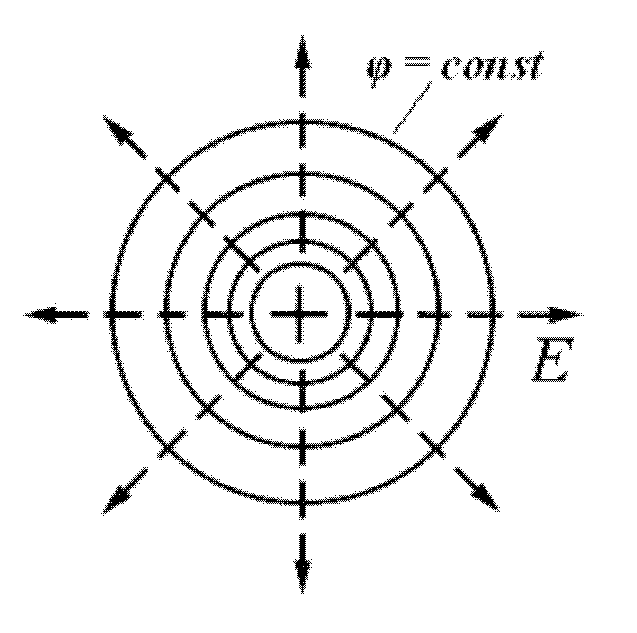
Эквипотенциальные поверхности кулоновского поля точечного заряда – концентрические сферы.
Д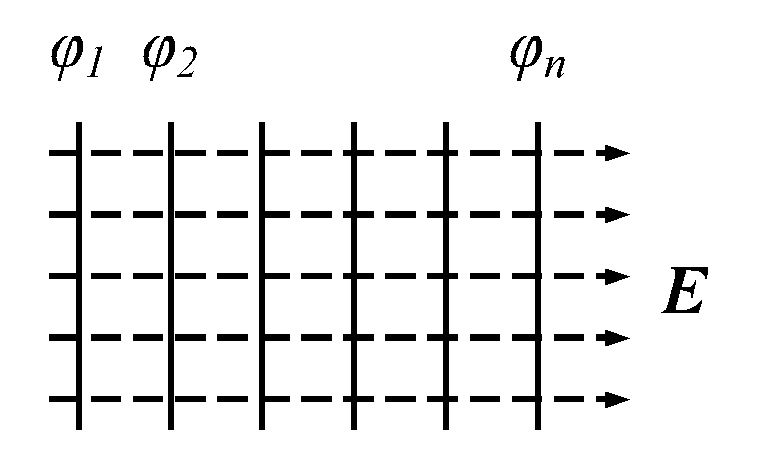
 ля однородного поля эквипотенциальные поверхности параллельные линии.
ля однородного поля эквипотенциальные поверхности параллельные линии.
На рис. представлены картины силовых линий и эквипотенциальных поверхностей некоторых простых электростатических полей.
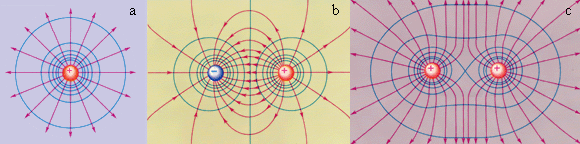 |
| Рисунок
Эквипотенциальные поверхности (синие линии) и силовые линии (красные линии) простых электрических полей: a – точечный заряд; b – электрический диполь; c – два равных положительных заряда |
Вопрос из ОРОКСА
Две линии напряженности электрического поля не могут пересекаться в одной точке. Можно ли утверждать, что две эквипотенциальные поверхности также не могут пересекаться в одной точке?
Ответ: Две эквипотенциальные поверхности могут пересекаться в одной точке при условии, что напряженность поля в этой точке равна нулю. В самом деле, вектор напряженности определяет направление нормали к каждой эквипотенциальной поверхности. Так как поверхности пересекаются, в точке пересечения их нормали не совпадают, а значит, электрическое поле не может иметь определенного направления. Это возможно только при нулевом значении величины поля.
Модель 1.2. Электрическое поле точечных зарядов
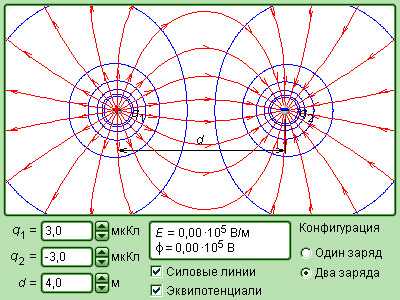 |
Компьютерная модель демонстрирует картину силовых линий и эквипотенциальных поверхностей точечного заряда и системы из двух точечных зарядов. Можно изменять величины зарядов и их знаки, а также расстояние между зарядами. При установке курсора в любой точке и нажатии левой клавиши мыши компьютер высвечивает на дисплее значения модуля вектора напряженности электрического поля ![]() и потенциала φ в данной точке. Следует обратить внимание, что в электрическом поле двух точечных зарядов возможны сферические эквипотенциальные поверхности.
и потенциала φ в данной точке. Следует обратить внимание, что в электрическом поле двух точечных зарядов возможны сферические эквипотенциальные поверхности.
2.7. Примеры вычисления потенциала
Рассмотрим вычисление потенциала поля, созданного некоторыми заряженными телами.
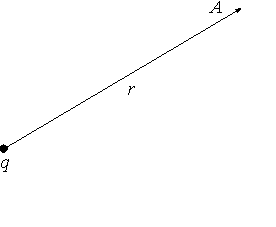
Рис.3. Расположение точки наблюдения А по отношению к точечному источнику поля q
1. Пример Точечный заряд. Используя соотношения (1) и (4) и совмещая точку 1 с точкой наблюдения А (рис.3), а точку 2 удаляя на бесконечность, получим
![]() (7)
(7)
Замечание. До сих пор использовалось понятие векторного поля – поля векторов ![]() (каждой точке пространства ставится в соответствие вектор
(каждой точке пространства ставится в соответствие вектор ![]() ). Представление о потенциале
). Представление о потенциале ![]() как функции точки пространства позволяет ввести понятие скалярного поля – поля чисел
как функции точки пространства позволяет ввести понятие скалярного поля – поля чисел ![]() (каждой точке пространства ставится в соответствие, с точностью до произвольной аддитивной постоянной, число
(каждой точке пространства ставится в соответствие, с точностью до произвольной аддитивной постоянной, число ![]() ). Поэтому в дальнейшем кроме понятий электростатическое поле и поле
). Поэтому в дальнейшем кроме понятий электростатическое поле и поле ![]() , будем использовать понятие поля
, будем использовать понятие поля![]() .
.
2.Пример. Найдем потенциал бесконечной однородно заряженной с линейной плотностью ![]() нити.
нити.
Наша задача найти ![]() как функцию
как функцию ![]() .
.
К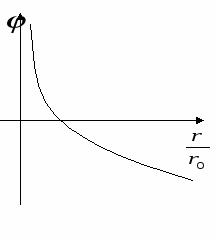
 ак уже было показано для бесконечно длинной нити:
ак уже было показано для бесконечно длинной нити:![]() .
.
Выберем где-нибудь точку из которой мы стартуем, к примеру в точке ![]() , то
, то
![]() .
.
Договоримся, что в точке старта потенциал равен нулю: ![]() , тогда
, тогда
![]() .
.
Это при такой нормировке. Если в такой задаче нормировать ![]() , то получим
, то получим ![]() ,то есть все потенциалы во всех точках бесконечно большие. Кому нужна такая нормировка? Если Вас интересует какой-то конкретный пространственный диапазон, то нормировать надо где-то вблизи этой области, тогда все потенциалами будут конечными приятными числами. От бесконечной нити нельзя уйти на бесконечность, по этой же причине не следует ожидать хорошего результата от
,то есть все потенциалы во всех точках бесконечно большие. Кому нужна такая нормировка? Если Вас интересует какой-то конкретный пространственный диапазон, то нормировать надо где-то вблизи этой области, тогда все потенциалами будут конечными приятными числами. От бесконечной нити нельзя уйти на бесконечность, по этой же причине не следует ожидать хорошего результата от ![]() как суммы потенциалов точечных фрагментов нити, каждый из которых нормирован условием
как суммы потенциалов точечных фрагментов нити, каждый из которых нормирован условием![]() .
.
3.Пример. Потенциал поля точечного диполя (первый способ).
И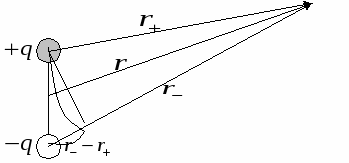 так, мы рассматриваем точечный диполь и точку наблюдения достаточно далеко от этой нашей гантельки.
так, мы рассматриваем точечный диполь и точку наблюдения достаточно далеко от этой нашей гантельки.
Давайте искать потенциал этой точки наблюдения.
Во первых, принцип суперпозиции.
![]()
Во-вторых, как известно
![]()
![]() .
.
Учтя, что ![]() есть проекция вектора
есть проекция вектора ![]() на
на ![]() и то, что расстояние до диполя очень велико, то
и то, что расстояние до диполя очень велико, то

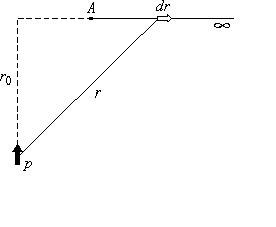
Потенциал поля точечного диполя (второй способ).
Используем готовую формулу для напряженности поля:
![]() . Вот такое выражение мы с вами в свое время вывели. Обопремся на него.
. Вот такое выражение мы с вами в свое время вывели. Обопремся на него.
![]()
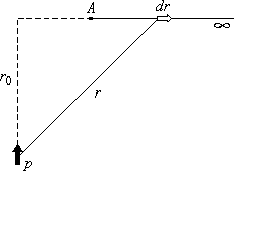
Д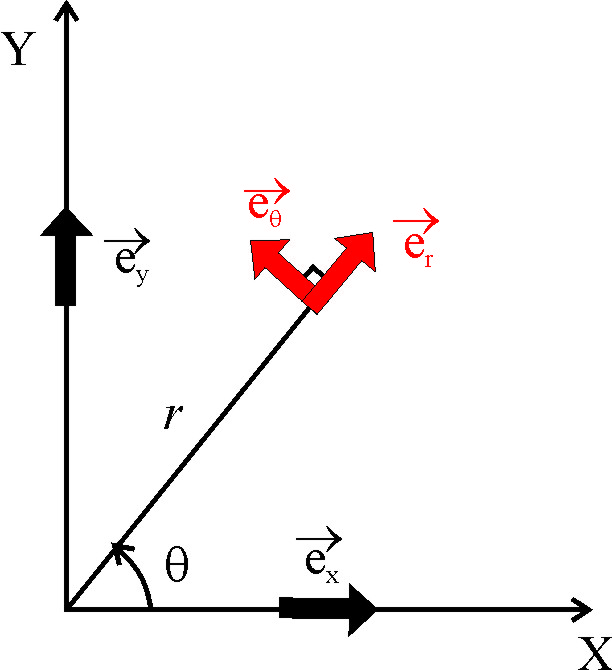 авайте выберем такое направление, чтобы нам было удобно вычислять этот интеграл, так как поле потенциальное, то результат не будет зависеть от вида траектории. Ориентация диполя, направление движения и вектор
авайте выберем такое направление, чтобы нам было удобно вычислять этот интеграл, так как поле потенциальное, то результат не будет зависеть от вида траектории. Ориентация диполя, направление движения и вектор ![]() показаны на рисунке. С учетом некоторых соотношений (5) примет вид:
показаны на рисунке. С учетом некоторых соотношений (5) примет вид:
![]()
Определение вектора ![]() точечного диполя из
точечного диполя из ![]() в полярной системе координат.
в полярной системе координат.
![]() Оператор
Оператор ![]() запишется в полярной системе координат так:
запишется в полярной системе координат так:
![]()
Орты координатных осей декартовой и полярной систем координат (см.рис.)
4.Пример
См. Иродов задача 3.38. (часть2)
Показать, что потенциал диполя с электрическим моментом может быть представлен как![]() , где
, где ![]() –радиус вектор. Найти с помощью этого выражения модуль напряженности электрического поля диполя как функцию
–радиус вектор. Найти с помощью этого выражения модуль напряженности электрического поля диполя как функцию ![]() и
и ![]() .
.![]() – это уже показали выше, отсюда, раскрывая скалярное произведение и продифференцировав формулу для потенциала, мы получим
– это уже показали выше, отсюда, раскрывая скалярное произведение и продифференцировав формулу для потенциала, мы получим ![]() .
.
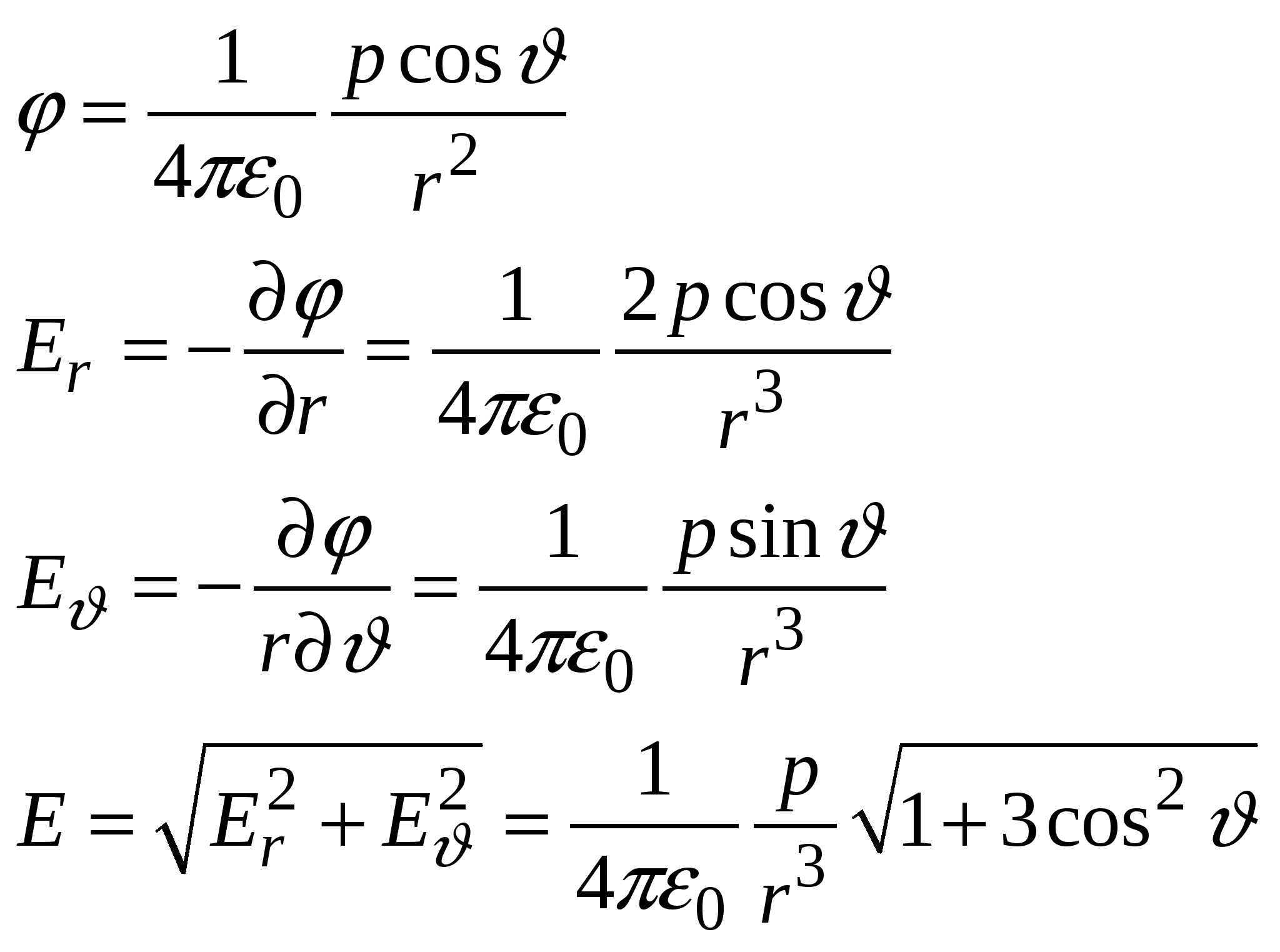
Сводка формул к лекции 2
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
ОПЫТЫ И КОМЬЮТЕРНЫЕ ДЕМОНСТРАЦИИ
Элементарная электростатика
 Электризация трением
Электризация трением
 Электризация через влияние
Электризация через влияние
 Взаимодействие точечных зарядов
Взаимодействие точечных зарядов
 Электростатическая машина
Электростатическая машина
 Генератор Ван-де-Граафа
Генератор Ван-де-Граафа
 Электрический ветер
Электрический ветер
Линейная
плотность заряда
– заряд, приходящийся на единицу длины:

Следовательно,
 .
.
Разность потенциалов
между точками 1
и 2
поля, лежащими на расстоянии r
1
и r
2
от оси цилиндра:

3.
Поле заряженной сферической поверхности
Видно, что выражение
для
 получилось таким же, как и для точечного
получилось таким же, как и для точечного
заряда.
Разность потенциалов

Шар, представляющий
собой диэлектрик, может быть внутри
равномерно заряжен с объемной плотностью
 .
.
Поток вектора через поверхность радиусомr
через поверхность радиусомr
R
(R
– радиус шара) равен
 Заряд
Заряд
внутри сферы радиусомr
равен:
 .
.
По теореме Гаусса
 и
и

За пределами
равномерно заряженного шара выражение
для E
A
будет таким
же, как и полученное нами для полой сферы
 ,
,
только величинаq
будет
равняться
V
:

Разность потенциалов
для точек, лежащих на расстоянии r
R
от центра шара:

и для точек, лежащих
на расстоянии r
R
от центра шара:

2. Проводники в электрическом поле.
Проводниками
называют тела, которые хорошо проводят
электрический ток, в которых есть
свободные электрические заряды, способные
перемещаться по всему объему проводника.
Условия
равновесия зарядов на проводнике:

|
|
Найдем величину
Отсюда:
|
Поскольку внутри
проводника E
=0,
а в непосредственной близости от
поверхности
 ,
,
то это значит, что при переходе из
проводника в пространство за проводником
(в воздух) значение изменяется от 0 до
изменяется от 0 до .
.
Среднее значение
напряженности поля на поверхности
проводника получается равным:

Сила, с которой
поле проводника действует на заряд,
расположенный на его поверхности dS
,
равна:

Давление, испытываемое
поверхностью проводника и обусловленное
избыточными зарядами на его поверхности,
равно:

При помещении
незаряженного проводника в электрическое
поле имеющиеся на нем заряды приходят
в движение – на противоположных
поверхностях возникают избыточные
электрические заряды противоположных
знаков.
Возникающие на
поверхности заряды создают свое поле,
которое в точности равно внешнему, но
противоположно по направлению – внутри
проводника (в полости) поле отсутствует.
Перераспределение
зарядов в проводнике под действием
внешнего поля происходит до тех пор,
пока силовые линии не окажутся
перпендикулярными поверхности проводника.
Равенство нулю
напряженности поля в полости проводника
используют для реализации электрической
защиты, причем оказалось, что электрическая
защита получается достаточно хорошей
не только в случае сплошной металлической
оболочки, но и в случае использования
мелкой металлической сетки.
Соединение
проводником какого-либо тела с землей
называют заземлением. При заземлении
заряженных проводников, в том числе и
тела человека, они теряют заряд и их
потенциал будет равен потенциалу земли.
Заземление корпусов приборов и аппаратов
способствует их безопасной эксплуатации,
т.к. исключает возможность для персонала
оказаться под напряжением корпуса
аппарата и земли.
Рассмотрим
несколько примеров расчёта электростатических
полей с помощью теоремы Гаусса.
1.7.1. Поле бесконечной равномерно заряженной прямолинейной нити
Рассмотрим
равномерно заряженную бесконечно
длинную нить. Линейная плотность заряда
равна .
Заряд,
равномерно распределённый по нити,
обладает симметрией – он симметричен
относительно оси.
Нить
имеет бесконечную длину, поэтому любому
эле-ментарному зарядуdq
1
можно сопоставить другой элементарный
заряд dq
2 ,
расположенный симметрично относительно
некоторой точки в электростатическом
поле.
Поскольку
расстояние от эле-ментарных зарядов до
этой точки одинаково, модули напряжён-ностей
Е
1
и Е
2
одинаковы. Поэтому результирующая
напряжённость
Е
= Е
1 +Е
2
направлена перпен-дикулярно нити (см.
рисунок).
Очевидно,
что и в других точ-ках, расположенных
на таком же расстоянии от нити,
напря-жённость будет иметь такую же
величину и направление.
Элементарные
заряды и точка в поле были выбраны
случайно, поэтому вывод справедлив как
для всех остальных элементарных зарядов,
так и для всех точек поля.
Это
означает, что электрическое поле,
созданное заряженной нитью, симметрично
относительно оси нити. Другими словами
– симметрия поля тождественна симметрии
заряда, создающего поле.
Таким
образом, векторы напряжённости во всех
точках окружающего пространства
перпендикулярны нити и модули напряжённости
на одинаковых расстояниях от нити
одинаковы.
Расчёт
напряжённости поля с помощью теоремы
Гаусса следует начинать с получения
выражения для потока вектора Е
.
В
свою очередь, выражение для потока
следует начинать с выбора формы замкнутой
поверхности и её положения относительно
источника поля.
Расчёт потока
будет максимально прост, если выбрать
такую поверхность, симметрия которой
идентична симметрии создаю-щего поле
заряда.
В данном случае
удобно пользоваться замкнутой поверхностью
с осевой симметрией.
Такой
поверхностью является цилиндр, ось
которого совпадает с нитью. Пусть высота
цилиндра равна l
,
а радиус основания – r
.
Поток
вектора напряжённости поля, созданного
нитью, складывается из потока через
торцевые поверхности цилиндра и потока
через боковую поверхность.
Поток
через торцевые поверхности равен нулю,
так как векторы напряжённости
перпендикулярны нити и, соответ-ственно
угол между векторами Е
и n
равен 90 0,
 .
.
Поток через боковую
поверхность
 .
.
Поскольку
все точки боковой поверхности расположены
на одинаковых расстояниях от нити,
модули напряжённости во всех точках
боковой поверхности цилиндра одинаковы,
т. е.
 .
.
Таков
вид выражения для потока вектора
рассчитываемой напряжённости.
Следующий этап
вычисления напряжённости электро-статического
поля – расчёт суммарного заряда,
охваченного замкнутой поверхностью.
Заряд,
охваченный поверхностью s
,
можно найти так:
 .
.
Тогда, по теореме
Гаусса,

 .
.
 .
.
Таким образом,
напряжённость электрического поля,
создан-ного равномерно заряженной
нитью, прямо пропорциональна линейной
плотности заряда нити и обратно
пропорциональна расстоянию от нити до
интересующей нас точки.
Обратите внимание
– напряжённость обратно пропорцио-нальна
первой степени расстояния от нити
(напряжённость поля точечного заряда
обратно пропорциональна квадрату
расстояния от заряда).
Страница 2 из 4
21. Длинный прямой провод, расположенный в вакууме, несет заряд, равномерно распределенный по всей длине провода с линейной плотностью 2 нКл/м. Определите напряженность Е электростатического поля на расстоянии r = 1 м от провода.
22. Внутренний цилиндрический проводник длинного прямолинейного коаксиального провода радиусом R 1 = 1,5 мм заряжен с линейной плотностью τ 1 = 0,2 нКл/м. Внешний цилиндрический проводник этого провода радиусом R 2 = 3 мм заряжен с линейной плотностью τ 2 = – 0,15 нКл/м. Пространство между проводниками заполнено резиной (ε = 3). Определить напряженность электростатического поля в точках, лежащих от оси провода на расстояниях: 1) r 1 = 1 мм; 2) r 2 = 2 мм; 3) r 3 = 5 мм.

23. Электростатическое поле создается положительно заряженной с постоянной поверхностной плотностью σ = 10 нКл/м 2 бесконечной плотностью. Какую работу надо совершить для того, чтобы перенести электрон вдоль линии напряженности с расстояния r 1 = 2 см до r 2 = 1 см?

24. Электростатическое поле создается положительно заряженной бесконечной нитью с постоянной линейной плотностью τ = 1 нКл/см. Какую скорость приобретет электрон, приблизившись под действием поля к нити вдоль линии напряженности с расстояния r 1 = 2 см до r 2 = 1 см?

25. Одинаковые заряды Q = 100 нКл расположены в вершинах квадрата со стороной a
= 10 см. Определить потенциальную энергию этой системы.

26. В боровской модели атома водорода электрон движется по круговой орбите радиусом r = 52,8 пм, в центре которой находится протон. Определить: 1) скорость электрона на орбите; 2) потенциальную энергию электрона в поле ядра, выразив её в электрон-вольтах.

27. Кольцо радиусом r = 5 см из тонкой проволоки несет равномерно распределенный заряд Q = 10 нКл. Определить потенциал φ электростатического поля: 1) в центре кольца; 2) на оси, проходящей через центр кольца, в точке, удаленной на расстояние a
= 10 см от центра кольца.

28. На кольце с внутренним радиусом 80 см и внешним – 1м равно распределен заряд 10 нКл. Определите потенциал в центре кольца.
29. Металлический шар радиусом 5 см несет заряд Q =
10 нКл. Оп потенциал φ
электростатического поля: 1) на поверхно шара; 2) на расстоянии a
= 2 см от его поверхности. Постройте график зависимости φ(r).
30. Полый шар несет на себе равномерно распределенный заряд. Определить радиус шара, если потенциал в центре шара равен φ 1 = 200 В, а в точке, лежащей от его центра на расстоянии r = 50 см, φ 2 = 40 В.

31. Электростатическое поле создается положительным точечным зарядом. Определить числовое значение и направление градиента потенциала этого поля, если на расстоянии r = 10 см от заряда потенциал равен φ = 100 В.

32. Электростатическое поле создается бесконечной плоскостью, заряженной равномерно с поверхностной плотностью σ =
5 нКл/м 2 Определите числовое значение и направление градиента потенциала этого поля.

33. Электростатическое поле создается бесконечной прямой нитью заряженной равномерно с линейной плотностью τ = 50 пКл/см. Определите числовое значение и направление градиента потенциала в точке на расстоянии r =
0,5 м от нити.
34. Определить линейную плотность бесконечно длинной заряженной нити, если работа сил поля по перемещению заряда Q = 1 нКл с расстояния r 1 = 5 см и r 2 = 2 см в направлении, перпендикулярном нити, равна 50 мкДж.

35. Электростатическое поле создается положительно заряженной бесконечной нитью Протон, двигаясь от нити под действием поля вдоль линии напряженности с расстояния r 1 = 1 см до r 2 = 5 см, изменил свою скорость от 1 до 10 Мм/с Определите линейную плотность заряда нити.
36. Электростатическое поле создается бесконечной плоскостью, равномерно заряженной с поверхностной плотностью сигма = 1 нКл/м 2 . Определить разность потенциалов между двумя точками этого поля, лежащими на расстоянии x 1 = 20 см и x 2 = 50 см от плоскости.

37. Определить поверхностную плотность зарядов на пластинах плоского слюдяного (ε = 7) конденсатора, заряженного до разности потенциалов U = 200 В, если расстояние между его пластинами равно d = 0,5 мм.

38. Электростатическое поле создается равномерно заряженной сфе поверхностью радиусом R = 10 см с общим зарядом Q = 15 нКл. Определите разность потенциалов между двумя точками этого поля, лежащими на расстояниях r 1 = 5 см и r 2 = 15 см от поверхности сферы.
39. Электростатическое поле создается сферой радиусом R = 5 см, равномерно заряженной с поверхностной плотностью сигма = 1 нКл/м 2 . Определить разность потенциалов между двумя точками поля, лежащими на расстояниях r 1 = 10 см и r 2 = 15 см от центра сферы.

40. Электростатическое поле создается равномерно заряженным шаром радиусом R=1 м с общим зарядом Q = 50 нКл. Определите разность потенциалов для точек, лежащих от центра шара на расстояниях 1) r 1 = 1,5 м и r 2 = 2 м; 2) r 1 “= 0,3 м и r 2 ” = 0,8 м.
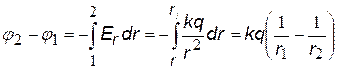
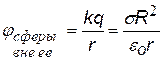 (при j¥ = 0)
(при j¥ = 0) 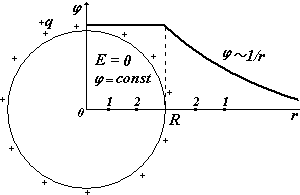
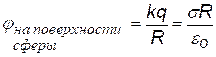
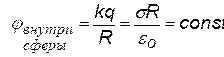
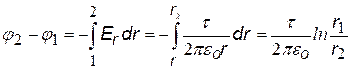
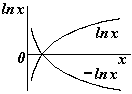 j 1 = 0 при r1 = r0,
j 1 = 0 при r1 = r0,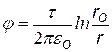
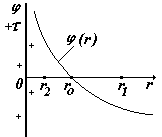
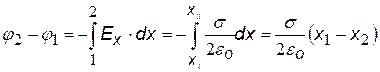
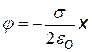 j = 0 при х = 0
j = 0 при х = 0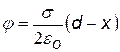 j = 0 при х = d
j = 0 при х = d