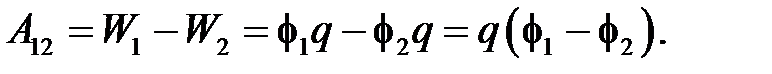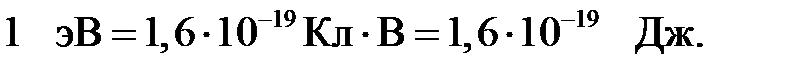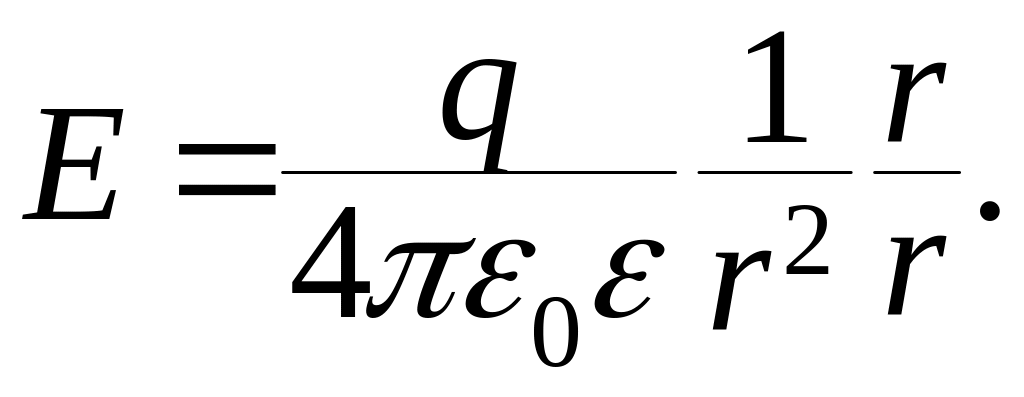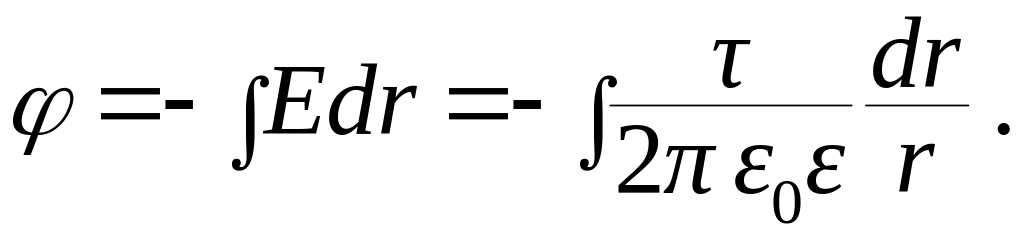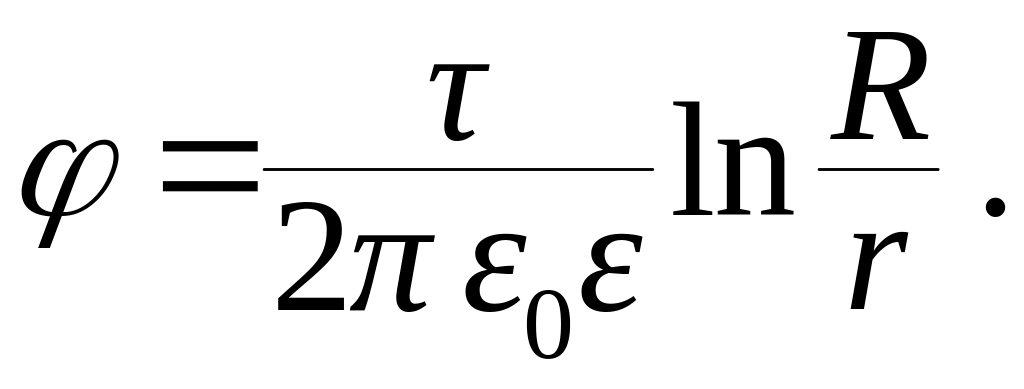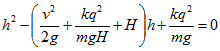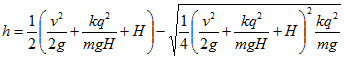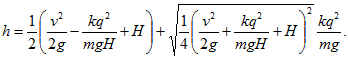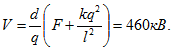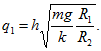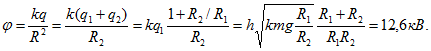Как найти потенциал через радиус - Сайт, где вы сможете решить свои вопросы

Условие задачи:

Определить потенциал шара радиусом 10 см, находящегося в вакууме, если на расстоянии 1 м от его поверхности потенциал равен 20 В.

Задача №6.3.6 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(R=10) см, (l=1) м, (varphi_1=20) В, (varphi_0-?)

Решение задачи:

Потенциал шара (varphi_0) (потенциал в точке A) радиусом (R) и некоторым зарядом (q) определяют по формуле:

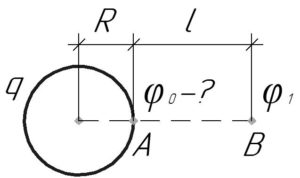
[{varphi _0} = frac{{kq}}{R};;;;(1)]

Таким же образом, потенциал шара (varphi_1) на расстоянии (l) от поверхности шара (потенциал в точке B) можно найти по формуле:

[{varphi _1} = frac{{kq}}{{R + l}};;;;(2)]

Поделим (1) на (2), тогда:

[frac{{{varphi _0}}}{{{varphi _1}}} = frac{{R + l}}{R}]

Решение задачи в общем виде выглядит так:

[{varphi _0} = frac{{{varphi _1}left( {R + l} right)}}{R}]

Посчитаем численный ответ:

[{varphi _0} = frac{{20 cdot left( {0,1 + 1} right)}}{{0,1}} = 220;В = 0,22;кВ]

Ответ: 0,22 кВ.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

6.3.5 На расстоянии 10 м от центра заряженного металлического шара радиусом 3 м
6.3.7 Металлический шар диаметром 30 см заряжен до потенциала 5400 В. Чему равен
6.3.8 На расстоянии 1 м от центра заряженного металлического шара радиусом 3 м

Источник

Потенциал электростатического поля

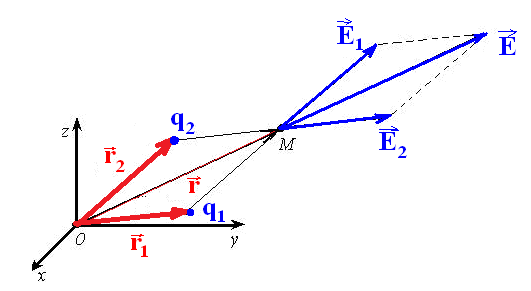
Принцип суперпозиции для вектора напряженности электростатического поля

Рис. 12.2.

Сложение выполняется по правилу треугольника или параллелограмма, “геометрически”, по правилу сложения векторных величин, то есть покоординатно:

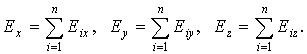(12.2)

Силовая линия. Векторное поле

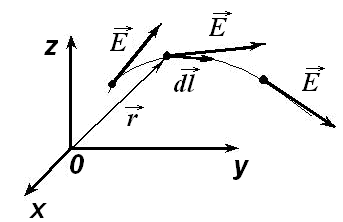Рис. 12.3.1Силовая линия вектора напряженности электростатического поля. Векторное поле

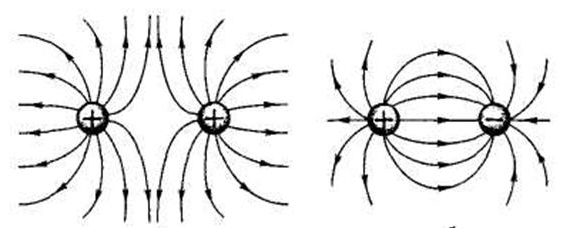
рис. 12.3.2 Примеры линий напряженности зарядовых систем

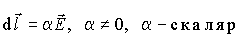(12.3)

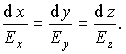(12.4)

Пользуясь понятием “силовая линия векторного поля”, следует иметь в виду два обстоятельства:

Силовых линий существует бесконечное множество.

Силовая линия сама по себе не содержит информации о величине вектора, величину вектора в окрестности элементарной площадки задает густота линий.

Потенциал электростатического поля

Разные пробные заряды q’,q”,… будут обладать в одной и той же точке поля разными потенциальными энергиями. Однако отношение энергии к зарядубудет для всех зарядов одним и тем же. Поэтому можно вести скалярную величину, являющуюся энергетической характеристикой собственно поля – потенциал.

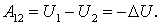
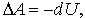
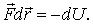При перемещении частицы из одной точки потенциального поля в другую работа, которую производят силы поля, может быть представлена как убыль потенциальной энергии частицы, т. е. Это относится и к элементарному перемещению или

(12.5)

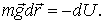
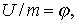
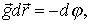: Поделив обе части на т и обозначив получим

(12.6)

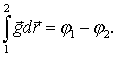(12.7)

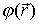
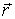
Функцию называют потенциалом поля в точке с радиус-вектором .

Физический смысл имеет не потенциал, а разность потенциалов, поэтому договорились считать, что потенциал точки, удаленной в бесконечность, равен нулю.

Когда говорят «потенциал такой-то точки» – имеют в виду разность потенциалов между этой точкой и точкой, удаленной в бесконечность.

Потенциал численно равен работе, которую совершают силы поля над единичным положительным зарядом при удалении его из данной точки в бесконечность

(или наоборот – такую же работу нужно совершить, чтобы переместить единичный положительный заряд из бесконечности в данную точку поля). При этом потенциал больше нуля, если q > 0.

Электрическое поле, создаваемое системой неподвижных электрических зарядов обладает свойством потенциальности: работа электрического поля по перемещению постоянного точечного заряда вдоль замкнутого контура равна нулю.

Рассмотрим электрическое поле одиночного точечного электрического заряда :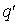

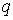
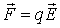Если в точке наблюдения помещен точечный заряд , то по определению:

(12.8)

где – сила, действующая на точечный заряд со стороны электрического поля .

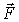
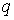
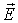
Элементарная работа по перемещению заряда из точки в точку в поле другого заряда:

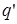
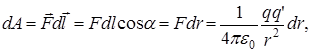
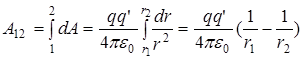
Найдем работу по перемещению пробного заряда из точки 1 в точку 2 в поле, создаваемом точечным зарядом q:

(12.9)

. (12.10)

И в этом случае работа сил не зависит от формы пути. Она является только функцией начального и конечного положения заряда.

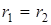
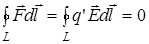
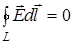
Для замкнутой траектории L она равна нулю, т. к. , т. е.

или (12.11 )

т.е. ЦИРКУЛЯЦИЯ ВЕКТОРА НАПРЯЖЕННОСТИ ПО ЛЮБОМУ ЗАМКНУТОМУ КОНТУРУ РАВНА НУЛЮ.

В механике было приведено следующее определение: «Силы, работа которых не зависит от формы пути, называются консервативными силами, а поля, работа сил которых не зависит от формы пути, называются потенциальными полями». Таким образом, рассмотренное нами электростатическое поле является потенциальным, а кулоновские силы – консервативными.

1)Линии электростатического поля не могут быть замкнутыми.

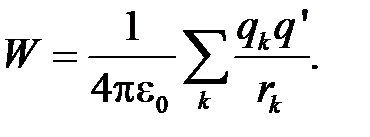
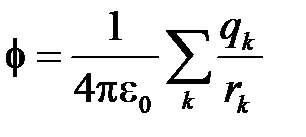
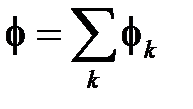
Если поле создается системой зарядов, то, используя принцип суперпозиции, получаем:

Тогда и для потенциала или

т.е. потенциал поля, создаваемый системой зарядов, равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности.

Выразим работу сил электростатического поля через разность потенциалов между начальной и конечной точками:

Или

За единицу φ принимают потенциал в такой точке поля, для перемещения в которую из бесконечности единичного положительного заряда необходимо совершить работу равную единице.

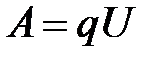
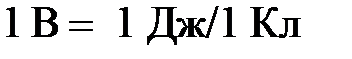
В СИ единица потенциала

Электрон – вольт (эВ) – это работа, совершенная силами поля над зарядом, равным заряду электрона при прохождении им разности потенциалов 1 В, то есть:

Вектор “ротор” напряженности электрического поля :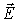

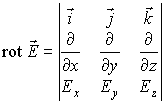
где 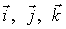– орты декартовой системы координат.

Условие потенциальности поля также имеет вид:

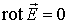(12.12)

Потенциал электростатического поля можно выразить иначе

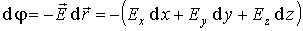(12.13)

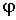
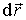
Дифференциал потенциала равен элементарной работе против сил электростатического поля, совершаемой над единичным точечным зарядом на перемещении .

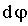
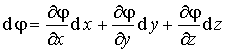Если учесть, что – полный дифференциал, т.е.:

(12.14)

то легко получить:

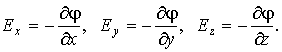(12.15)

В компактной форме записи:

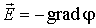(12.16)

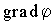
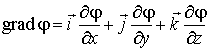где вектор определен соотношениями:

(12.17)

Градиент скалярного поля выделяет направление наискорейшего возрастания скалярной функции, а его модуль численно равен максимальной интенсивности возрастания этой функции.

Скалярное поле часто описывают с помощью “поверхностей уровня”, эквипотенциальных или изоповерхностей, которые определяются уравнением

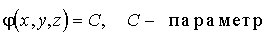(12.18)

На эквипотенциальной поверхности

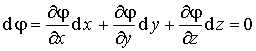(12.19)

что можно переписать в векторном виде:

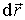
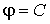
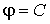
Вектор перпендикулярен любому вектору , принадлежащему поверхности , то есть перпендикулярен элементу площади поверхности .

Следовательно, силовые линии электростатического поля перпендикулярны соответствующим элементам площади эквипотенциальной поверхности.

Иногда встречается обозначение

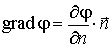(12.21)

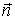
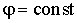
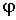
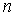
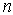
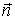
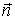
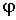
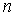
где – вектор единичной нормали (величина безразмерная!) к поверхности в точке, в которой вычисляется вектор , ориентированный в сторону увеличения ; – обозначение координаты ( – величина, имеющая размерность длины) вдоль направления . Таким образом – вектор, направленный вдоль описанного выше направления и численно равный производной от величины по координате вдоль этого направления.

Потенциал произвольной точки пространства определен с точностью до произвольной постоянной:

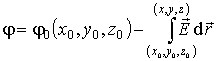(12.22)

При решении большого числа задач (но не всех!) удобно считать, что точка с координатами 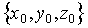расположена “на бесконечности”, а потенциал ее равен нулю.

Потенциал центрально-симметричного поля

Пусть электрическое поле имеет вид Ё(р) = Е(г)—, F — радиус-

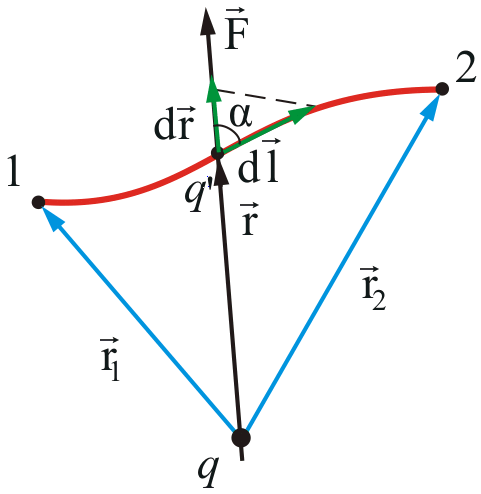
вектор (г = jc/ + у j + zk], г = (х 2 + у 1 + г 2 ) |/2 , Е(г) — некоторая функция. Ищем разность потенциалов между точками F_t = х,/ + yj + z_xk и г₂ = х₂/ +yj + z₂k (рис. 7.10).

Отметим особенность данного поля. Имеем |Ё(г) | = ^ |г| = Е(г) |

(если А = аа, а — число, то й = |а| • |а|), т. е. величина напряженности поля одинакова на сфере радиусом г, а направление вектора Е —

вдоль луча из начала координат (— = п — вектор единичной длины вдоль

такого луча). Поле обладает, как говорят, сферической симметрией.

Пусть / — некоторая кривая, ведущая из точки 1 в точку 2. Имеем:

Вектор d/ ведет из точки г в точку r+dr:F + dr=F + dl, т. е. dr = d/ и dr = dx / + dy j + dz k.

(учтено, что udu = ^d(u 2 )). Этот результат можно было получить еще проще: г dl = г dr = ^d(rr) = ^d(r ! ) = rdr. Таким образом,

Если функция Е(г) предъявлена, интеграл может быть взят.

Существенно, что координаты начальной и конечной точек входят в ответ лишь в комбинации (х 2 + у 2 + г 2 ) |/2 = г, т. е. разность потенциалов между любыми двумя точками, одна из которых взята на сфере г = г,, другая — на сфере г = r_v будет одна и та же.

На сфере х 2 + у 2 + г 2 = г 2 потенциал постоянен. Это следствие сферической симметрии.

1.3. Электрическое поле. Напряженность и потенциал поля

Вокруг всякого электрического заряда всегда существует электрическое поле.

Электрическое поле, созданное неподвижным зарядом (или системой неподвижных зарядов), называется электростатическим.

Посредством электростатического поля осуществляется взаимодействие между зарядами. Само понятие поля оказалось весьма плодотворным и широко используется в современной физике. Появление поля означает, что что-то изменилось в окружающем нас пространстве. Математически поле описывается величиной, меняющейся от точки к точке. Например, можно рассмотреть поле скоростей в текущей жидкости. В каждой точке объема жидкости задан вектор скорости, который может меняться со временем (нестационарное течение), а может и быть постоянным (стационарное течение). Это пример векторного поля. К этому же типу полей относится и поле неподвижных электрических зарядов.

Напишем выражение для силы, действующей на точечный заряд в результате его взаимодействия с системой точечных зарядов (соотношение Дополнения 1)

Здесь — радиус-вектор точки, в которой находится заряд . Заряд , на который, действует сила, в подобных ситуациях иногда называют «пробным» зарядом, выписан отдельным множителем. Выражение, стоящее в круглых скобках, определяется исключительно свойствами той системы зарядов, которая воздействует на заряд . Естественно, что это воздействие (сила) зависит от того, где он находится, соответственно, выражение в круглых скобках зависит от радиус-вектора , определяющего местоположение заряда . Следуя изложенной выше идее об электростатическом поле существующем вокруг каждого заряда и, разумеется, системы зарядов, введем силовую характеристику этого поля, называемую напряженностью электрического поля.

Напряженностью электрического поля называется вектор , равный отношению силы, действующей на точечный заряд к алгебраической величине этого заряда (рис. 1.12)

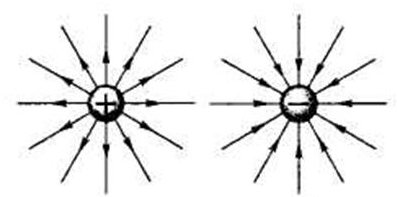
Рис. 1.12. Вектор напряженности электрического поля отрицательного и положительного точечного заряда

Из и определения напряженности вытекает, что напряженность поля произвольной системы покоящихся зарядов можно записать в виде

Действительно, сила, с которой данная система зарядов действует на точечный заряд, равна векторной сумме сил, с которыми действует на него каждый из зарядов системы. Отсюда следует, что напряженность электрического поля системы зарядов определяется векторной суммой напряженностей полей, создаваемых отдельными зарядами системы. Имеет место так называемый принцип суперпозиции (независимого наложения) электрических полей

Напряженность поля, созданного системой неподвижных заряженных тел, равна векторной сумме напряженностей полей, создаваемых каждым телом в отдельности:

Принцип суперпозиции является одним из наиболее общих принципов современной физики. Подчеркнем, что напряженности поля складываются векторно.

На рис. 1.13 иллюстрируется принцип суперпозиции полей на примере поля, создаваемого двумя точечными зарядами.

Рис. 1.13. Принцип суперпозиции электрических полей

Для одного заряда , находящегося в начале координат , для напряженности создаваемого им поля в точке с радиус-вектором получаем (индекс 1 опущен):

Напряженность поля точечного заряда в различных точках пространства, в общем случае различна и по величине и по направлению (рис. 1.14). Поле точечного заряда — центральное поле, центр симметрии поля совпадает с точкой, в которой находится заряд.

Рис. 1.14. Векторы напряженности электрического поля заряда q в разных точках пространства

В СИ единицей измерения напряженности электрического поля является ньютон на кулон (Н/Кл), — то есть за единицу напряженности поля принята напряженность такого поля, в котором на заряд равный 1 Кл действует сила, равная 1 Н:

На практике чаще употребляют другое название этой единицы — «вольт на метр» (В/м) (про единицу «вольт» речь пойдет несколько позже).

Характерные значения напряженностей электрических полей, встречающихся в нашем мире, приведены на рис. 1.15.

Рис. 1.15. Характерные значения напряженностей электрических полей, встречающихся в природе

Обратим внимание на сходство закона Кулона с законом всемирного тяготения

Роль зарядов играют массы, а гравитационная постоянная G аналогична коэффициенту Знак минус соответствует тому, что гравитационное взаимодействие всегда является притяжением. Можно ввести и вектор напряженности гравитационного поля как отношение силы , например, к пробной массе :

Если при этом — масса Земли, а её радиус, то есть ни что иное, как хорошо знакомое ускорение свободного падения м/с 2 (с точностью до весьма малой центробежной силы инерции, входящей в силу тяжести )

Пример 4. Среднее расстояние между электроном и протоном в атоме водорода равно r = 5,3·10 –11 м (рис. 1.16). Найти силы электростатического и гравитационного притяжения между ними и определить отношение этих сил.

Рис. 1.16. Электрон и протон в атоме водорода

Решение. Из закона Кулона имеем

В свою очередь из закона всемирного тяготения следует

Отношение сил не зависит от расстояния между электроном и протоном и равно

Этот расчет показывает, что в масштабах атомов и молекул силы гравитации столь меньше электростатических, что их можно не принимать во внимание.

Почему же в макромире, где мы обитаем, с законом гравитации мы знакомимся после первой же шишки на первых же шагах в детстве, а закон Кулона остается неизвестным многим из наших сограждан даже после окончания средней школы? Дело в том, что в макромире, как мы видели, положительные и отрицательные электрические заряды в телах скомпенсированы, так что в обычной жизни мы имеем дело с относительно небольшими избыточными зарядами. В то же время все тяготеющие массы имеют один и тот же знак, так что никакой компенсации масс не происходит, и силы гравитации проявляют себя в масштабах макромира в большей степени.

Электрическое поле можно задать, указав для каждой точки величину и направление вектора напряженности электрического поля . Для наглядного изображения электрического поля используют силовые линии (или линии векторного поля ).

Линией напряженности электрического поля (силовой линией) называется такая линия, касательная к которой в каждой её точке совпадает по направлению с вектором напряженности электрического поля.

На рис. 1.17 показана силовая линия электрического поля. Векторы напряженности электрического поля направлены по касательной к силовой линии.

Рис. 1.17. Векторы напряженности электрического поля направлены по касательной к силовым линиям

Число линий, пронизывающих перпендикулярную к ним площадку единичной площади, пропорционально величине (модулю) напряженности электрического поля в данном месте. Другими словами силовые линии проводятся гуще там, где модуль напряженности поля больше. Таким образом, конфигурация силовых линий позволяет судить об изменении направления и величины вектора в пространстве. Картина линий векторного поля (не обязательно электрического или магнитного) весьма наглядный графический способ отображения его основных свойств.

Отметим некоторые важные свойства силовых линий электростатического поля:

Рис. 1.18. Силовые линии точечного заряда: 1 — q > 0; 2 — q 3 . Было замечено, что капелька переставала падать при электрическом поле напряженностью 1,95·10 5 В/м. Это означало, что электростатическая сила qE компенсировала силу тяжести mg.

Масса капельки равна

Отсюда находим заряд капельки

то есть капелька несла пять электронных зарядов. Именно в таких экспериментах было обнаружено квантование электрического заряда и определена его минимальная величина e.

Движением заряженных частиц можно управлять, с помощью электрического поля нужной величины и направления. Так происходит, например, в электроннолучевой трубке осциллографа.

На рис. 1.24 показывается движение электронного луча, рисующего на экране электроннолучевой трубки с электрическим отклонением синусоиду. В осциллографе на вертикальные отклоняющие пластины подан усиленный исследуемый сигнал, а на горизонтальные — пилообразное напряжение развёртки. В результате электронный луч «рисует» зависимость исследуемого сигнала от времени на экране осциллографа.

Рис. 1.24. Принцип действия электроннолучевой трубки

Определение напряженности поля очень часто используется в виде

В силу определения (или, очевидным образом, это одно и то же) напряженность электрического поля называют его силовой характеристикой — оно определяет силу, действующую на заряд, помещенный в поле.

Пример 5. В пространство между пластинами плоского конденсатора влетает частица, движущаяся параллельно пластинам вдоль оси конденсатора (рис. 1.25). Начальную кинетическую энергию частица получила, пройдя ускоряющую разность потенциалов Под действием поля конденсатора частица отклоняется к одной из пластин (в зависимости от знака заряда) и в конечном итоге попадает на нее. Это расстояние можно измерить. Известно также расстояние между пластинами и напряжение на конденсаторе. Можно ли по этим данным установить тип частицы (найдя ее удельный заряд, т. е. отношение заряда к массе )?

Решение. Решим задачу сначала методом размерностей. Пройденное расстояние должно быть функцией параметров задачи:

Вспоминая, что произведение потенциала на заряд дает энергию, размерность которой получаем

Рис. 1.25. движение заряженной частицы между пластинами плоского конденсатора

Подставляя эту размерность, получаем уравнение:

Сравнивая размерности в обеих частях равенства, приходим к уравнениям:

Последнее уравнение, следующее из отсутствия в левой части величины размерности времени, сразу дает нам или После этого немедленно находим: Подставляя найденные значения, получаем:

Произвольная степень (показатель степени b определить не удалось) означает, что результат зависит от произвольной функции безразмерного отношения

Вид этой функции мы пока не знаем: если в задачу входят величины одинаковой размерности, то функцию их отношения с помощью анализа размерности найти, естественно, не удастся. Но мы уже можем ответить на вопрос задачи: в ответ не вошли параметры, характеризующие частицу — ни ее масса, ни ее заряд. Все частицы при заданных условиях будут отклоняться одинаково, и использовать такой прибор для их идентификации нельзя.

Приведем теперь точное решение задачи. Начальную скорость частицы находим из соотношения

В конденсаторе частица находится под действием электрического поля и приобретает поперечное ускорение Расстояние до попадания на пластину она пройдет за время t:

откуда находим время полета:

В продольном же направлении за это время частица пролетит расстояние

Мы приходим к тому же выводу о независимости от характеристик частицы. К тому же, теперь найдена функция оставшаяся не определенной в нашем предварительном результате.

В Главе 4 раздела «Механика» было показано, что консервативная сила связана с потенциальной энергией соотношением

Здесь знак — общепринятое обозначение векторного оператора «набла», результат действия которого на скалярную функцию координат есть градиент этой функции. Явный вид оператора набла в декартовых координатах следующий:

Подставив в и разделив на , получаем

Скалярная функция называется потенциалом электрического поля.

Функция , связанная с напряженностью электростатического поля соотношением

,

называется потенциалом электростатического поля.

Как видно из (1.13), потенциальная энергия точечного заряда в поле с потенциалом равна

а действующая на него сила

В Дополнении 3 разобран пример использования этих соотношений.

В СИ единицей измерения потенциала электрического поля является вольт (В):

Напряженность поля определяет силу, действующую в поле на точечный заряд, а потенциал — его потенциальную энергию в этом поле. Поэтому, следуя смыслу соотношений и, напряженность электрического поля называют силовой характеристикой поля, а потенциал — его энергетической характеристикой.

Как и потенциальная энергия, потенциал поля всегда определен с точностью до аддитивной постоянной. Это видно из : поскольку набла есть дифференциальный оператор, потенциалы и физически тождественны, так как им соответствует поле одной и той же напряженности

.

Это позволяет нормировать потенциал, произвольно выбирая некоторую точку и полагая потенциал в этой точке равным нулю

Учитывая, что и напряженность поля, и потенциал поля убывают с ростом расстояния до системы зарядов, создающей поле, во всех тех случаях, когда конечный заряд распределен по конечной области пространства, нормировать потенциал естественно и удобно на «нуль на бесконечности», то есть полагать его равным нулю на бесконечном удалении от системы зарядов

О тех идеализированных случаях, когда нормировка на нуль на бесконечности, именно в силу идеализированности задачи, лишена смысла, будет сказано далее.

Соотношение (1.13) позволяет вычислить напряженность поля по известному потенциалу;

Получим «обратную» связь: выразим потенциал поля через его напряженность. Для этого сравним три выражения: выражение для из (1.18), выражение для вектора бесконечно малого перемещения и выражение для полного дифференциала функции :

Нетрудно видеть, что скалярное произведение двух первых векторов равно полному дифференциалу потенциала

На самом деле это соотношение не новое. Если умножить (1.20) на заряд и учесть связи (1.14) и (1.15), мы получим знакомое по главе 4 раздела «Механика» соотношение, связывающее работу консервативной силы и убыль потенциальной энергии

.

Там же, в разделе «Механика» было показано, что стационарное потенциальное поле консервативно. Из соотношения (1.18) вытекает, что электростатическое поле консервативно во всех тех случаях, когда потенциал поля не зависит от времени.

Интегрируя соотношение (1.20) от точки , потенциал в которой принят равным нулю, до некоторой точки , потенциал в которой нас интересует, вдоль произвольной, удобной для вычислений кривой (поле консервативно и от формы кривой результат не зависти), получаем

Вычислим с помощью (1.21) потенциал поля точечного заряда , находящегося в начале координат, нормировав его на нуль на бесконечном удалении от этого заряда. Воспользуемся для этого законом Кулона в форме (1.9):

При вычислении использовано тождество , справедливое для любого вектора : и являющееся результатом простого дифференцирования определения модуля любого вектора: .

Таким образом, потенциал поля точечного заряда находящегося в начале координат имеет вид

и поле это, как уже отмечалось ранее, центральное: фактически потенциал поля зависит только от .

Учитывая, что стоящей в знаменателе модуль радиус-вектора есть ни что иное как расстояние от заряда, создающего поле до точки наблюдения поля, формулу легко обобщить на случай, когда заряд находится не в начале координат, а в точке с радиус-вектором . В этом случае расстояние от заряда до точки наблюдения поля равно и потенциал поля в точке (при прежней нормировке на нуль на бесконечности) равен

Связь между напряженностью поля и его потенциалом линейная, поэтому принцип суперпозиции для напряженности поля справедлив и для потенциала поля. Другими словами: потенциал поля системы зарядов равен алгебраической сумме потенциалов поля от каждого из зарядов системы. Используя принцип суперпозиции, потенциал поля системы зарядов можно написать сразу :

Здесь — полное число зарядов в системе.

В случае непрерывного распределения заряда по некоторому объему , получим

При непрерывном распределении заряда по некоторой поверхности или кривой , получим соответственно

где и — соответствующие поверхностная и линейная плотности.

В Дополнении 4 разобран пример использования только что полученных соотношений.

Мы не будем рассматривать здесь отдельно вопрос о работе электростатических сил при перемещении в электростатическом поле точечных зарядов и заряженных тел. Электростатическое поле консервативно (рис. 1.26), потенциальная энергия заряда в поле равна , поэтому работа электростатических сил всегда может быть вычислена с помощью соотношений вида

Рис. 1.26. Работа электростатических сил зависит только от положения начальной и конечной точек

Вычислим энергию взаимодействия зарядов, входящих с состав некоторой системы.

Для нумерации этих зарядов удобно использовать два индекса, например, и . Одни и те же заряды системы, один раз это , другой раз это . Подчеркнем, что заряд и заряд это один и тот же 5-ый заряд системы. Такие «сложности» необходимы для компактной записи выражения для их энергии взаимодействия и вот почему. Заряды взаимодействуют попарно, энергия взаимодействия и зарядов согласно равна

Здесь — потенциал заряда в той точке, где находится заряд.

В — взаимодействие заряда самого с собой или его потенциальную энергию в собственном поле мы не рассматриваем.

Поэтому при суммировании энергий попарного взаимодействия зарядов мы обязательно должны учесть, что , во-первых, и, во вторых, каждая пара зарядов должна присутствовать в сумме только один раз. Это можно сделать двумя способами. Первый состоит в том, что при записи двойной суммы, явно оговаривается, например, что :

При втором способе, при соблюдении неравенства , суммирование ведется по всем возможным значениям и , соответственно, слагаемое, отвечающее взаимодействию одной и той же пары зарядов присутствует в сумме дважды, поэтому сумму необходимо разделить на 2. Получается:

В случае непрерывного распределения заряда по некоторому объёму с плотностью , соотношение, к примеру, принимает вид:

В первой из формул в (1.31) — потенциал всех зарядов кроме в той точке , в которой находится , во втором соотношении этот потенциал выписан явно, в третьей выполнена следующая операция: два интеграла, для краткости объединены в один и заряды и выражены через плотность заряда .

Мы не выписываем здесь формулы для случаев распределения заряда по поверхности или вдоль некоторой кривой, они лишь требуют замены в на и .

Для наглядного представления распределения потенциала в пространстве используются эквипотенциальные поверхности.

Эквипотенциальная поверхность (поверхность равного потенциала) — это совокупность точек, имеющих равный потенциал.

Рассмотрим картину эквипотенциальных поверхностей некоторых полей.

Напомним, что как из физических соображений, так и непосредственно из соотношения вытекает взаимная ортогональность силовых линий и эквипотенциальных поверхностей. Действительно, согласно определению, уравнение эквипотенциальной поверхности имеет вид

Дифференцируя это соотношение, получаем

для всех перемещений , касательных к эквипотенциальной поверхности. Значит вектор перпендикулярен эквипотенциальной поверхности. Осталось вспомнить, что вектор направлен по касательной к силовой линии по определению. Утверждение об ортогональности силовых линий и эквипотенциальных поверхностей доказано.

Эквипотенциальные поверхности поля точечного заряда представляют собой концентрические сферы с центром в точке нахождения заряда (см. рис. 1.27). Эквипотенциальные поверхности обозначены сплошными синими линиями, силовые линии — красными пунктирными линиями.

Рис. 1.27. Эквипотенциальные поверхности (сферы) (сплошные линии синего цвета) и силовые линии (пунктирные линии красного цвета) поля точечного заряда

Эквипотенциальные поверхности однородного электрического поля представляют собой плоскости, перпендикулярные силовым линиям и расположенные на одинаковом расстоянии друг от друга (см. рис. 1.28).

Рис. 1.28. Эквипотенциальные поверхности однородного электрического поля

Эквипотенциальные поверхности поля двух одноименных одинаковых точечных зарядов представлены на рис. 1.29.

Рис. 1.29. Эквипотенциальные поверхности двух одноименных одинаковых точечных зарядов

Эквипотенциальные поверхности поля двух разноименных одинаковых по модулю точечных зарядов представлены на рис. 1.30.

Рис. 1.30. Эквипотенциальные поверхности двух разноименных одинаковых по модулю точечных зарядов

Графический вид двумерного (в плоскости z = 0) потенциала электрического поля, создаваемого точечным зарядом, расположенным в начале координат, показан на рис. 1.31.

Рис. 1.31. Вид двумерного (в плоскости z = 0) кулоновского потенциала 1/r вблизи положительного (1) и отрицательного (2) точечного зарядов. В случае (1) положительный пробный заряд натыкается на бесконечно высокий потенциальный барьер, препятствующий проникновению к центру. В случае (2) на пробный заряд действует сила притяжения, и он стремится скатиться в образовавшуюся потенциальную яму

Экспериментальное исследование потенциала поля вокруг заряженного металлического шара с помощью «пламенного» зонда показано на рис. 1.32. Используемый зонд присоединен к электрометру. Для выравнивания потенциала зонда с потенциалом той точки, где он находится, измерительный зонд помещается в пламя небольшой газовой горелки, обеспечивающей ионизацию воздуха и возможность стекания и натекания зарядов на зонд. Демонстрируется уменьшение потенциала при перемещении зонда по радиусу от центра шара и постоянство потенциала при движении зонда по окружности вокруг центра заряженного шара.

Рис. 1.32. Экспериментальное исследование потенциала поля вокруг заряженного металлического шара с помощью «пламенного» зонда

В Дополнении 7 получено полезное соотношение для градиента скалярной функции, зависящей только от модуля радиус-вектора.

[spoiler title=”источники:”]

http://studme.org/226489/matematika_himiya_fizik/potentsial_tsentralno_simmetrichnogo_polya

http://online.mephi.ru/courses/physics/electricity/data/course/1/1.3.html

[/spoiler]

Источник

Найдем
потенциал, создаваемый проводящей
заряженной сферой радиуса R. Как известно,
внутри сферы (при r
< R)
E
= 0;
вне сферы (при r
> R)

С учетом формулы (13.18), связывающей
напряженность и потенциал, находим:

1.

,
отсюда 
= const;

2.

(13.21)

Постоянную
C
выберем из условия, что

при

,
отсюда C
= 0. Потенциал внутри проводящей сферы
имеет одинаковое значение во всех точках
внутри сферы и равен потенциалу на
поверхности:

(13.22)

Потенциал
вне заряженной сферы равен потенциалу
точечного заряда, помещенного в центр
сферы.

На
рис. 13.6 приведен график зависимости
потенциала 
от расстояния до центра сферы r.

Для
проводящего шара получим тот же результат,
что и для сферы.

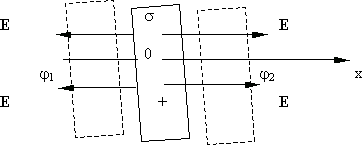
Найдем
теперь потенциал заряженной бесконечной
плоскости с поверхностной плотностью
заряда 
(рис. 13.7).

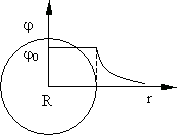
Рис.
13.6.

Напряженность
электрического поля плоскости:

.
Потенциал 
получим в виде

(13.23)

Выберем
начало отсчета потенциала так, чтобы
при x
= 0, потенциал был равен 0, тогда C
= 0.

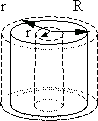
Рис.
13.7. Рис. 13.8.

Потенциал электрического поля заряженной плоскости:

171

(13.24)

Разность
потенциалов между двумя точками поля

(13.25)

Потенциал электрического поля заряженного цилиндра:

Потенциал
заряженного бесконечного цилиндра с
линейной плотностью 
найдем из соотношения:

(13.26)

Потенциал
поля внутри цилиндра (рис. 13.8) является
постоянной величиной при r
< R и равен
потенциалу на поверхности цилиндра,
т.к. E = 0
внутри цилиндра. Потенциал вне заряженного
цилиндра (r
> R):

Если принять, что потенциал j
на поверхности цилиндра (при r
= R)
равен нулю, тогда постоянная

Потенциал
вне цилиндра имеет такую же величину,
как и потенциал заряженной нити,
помещенной на оси цилиндра

(13.27)

Глава 14. Диэлектрики в электростатическом поле

14.1. Проводники и диэлектрики

По
электрическим свойствам твердые тела
можно разделить на проводники и
диэлектрики. Основным отличием
диэлектриков от проводников является
отсутствие в диэлектриках свободных
зарядов, способных перемещаться в
электрическом поле. Проводники содержат
свободные заряды, носителями которых
являются электроны, не связанные с
атомами.

Каждое
вещество может проявлять свойства
диэлектрика и проводника, в зависимости
от внешних условий и времени наблюдения.
Так, заряженный шар из диэлектрика,
например из эбонита, подвешенный на
шелковой нити, может долго сохранять
свой заряд, но через длительное время
заряд все же стечет с поверхности шара.

Если
заряженное тело находится вблизи
другого, первоначально незаряженного
тела, то в проводниках и диэлектриках
происходит электростатическая индукция,
и на соседнем теле появятся заряды
противоположного знака. В проводнике
заряд распределится по поверхности,
внутри проводника заряд будет равен
0, поэтому напряженность электрического
поля E
= 0. В диэлектрике связанные заряды
распределяются по всему объему.

Если
проводник поместить во внешнее
электростатическое поле, то на концах
проводника появятся заряды разного
знака. Если разрезать проводник на две
части, то на каждой останется заряд
одного знака.

В
диэлектрике, помещенном в электростатическое
поле, также появятся на концах разноименные
заряды, но эти заряды нельзя отделить.
В разрезанном диэлектрике суммарный
заряд каждой его части будет равен
нулю.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Теорема Гаусса и постулат Максвелла, представленные в интегральной форме, дают возможность решить ряд задач в тех случаях, когда условия симметрии таковы, что в каждой точке замкнутой поверхности интегрирования (поверхности симметрии), охватывающей заряды, вектор напряженности поля (или электрического смещения )

имеет одно и то же значение и может быть вынесен из-под интеграла.

Пример 1. Точечный заряд q = 10^-9 Кл помещен в начале сферической системы координат. Определить напряжение между точками а (R_a = 4см, q_а = 45^°, j_а = 0^°) и b (R_b = 8см, , q_b = 180^°, j_b = 90^°) и напряженность в тех же точках, если окружающей средой является воздух.

Решение.

Решение будем проводить с помощью теоремы Гаусса (1.9), так как среда однородна.

Поскольку поле точечного заряда характеризуется сферической симметрией, то, если в качестве поверхности интегрирования взять поверхность сферы с центром в точке, где расположен заряд (в нашем случае это начало системы координат), то в любой точке на поверхности этой сферы напряженность поля будет иметь одно и то же значение. Направление же вектора будет совпадать с направлением радиуса, то есть перпендикулярно к поверхности сферы. В связи с этим, интеграл по этой поверхности, составленный по теореме Гаусса, можно преобразовать следующим образом:

Поскольку данный интеграл (согласно теореме Гаусса) равен отношению заряда, помещенного внутри сферы, к диэлектрической проницаемости среды, то напряженность поля будет определяться соотношением

Е_r = q/(4pe₀r²).

Здесь индекс r у напряженности проставлен для того, чтобы показать, что напряженность поля имеет одну составляющую, направленную по радиусу.

Отметим, что данная формула полностью соответствует выражению (1.1), полученному из закона Кулона.

Поскольку напряженность электрического поля в данном случае имеет только радиальную составляющую, величина которой является функцией радиуса и не зависит от угловой координаты, то в указанных в исходном задании точках она будет равна:

E(r_a)=q/(4pe₀r_a²)=10^-9/(4p?8.85·10^-12·0.04²)=5.62кВ/м.

E(r_в)=q/(4pe₀r_в²)=10^-9/(4p8.85·10^-12·0.08²)=1.405кВ/м.

Разность потенциалов между точками а и в определяется при помощи выражения (1.6). Эта разность в потенциальном поле не зависит от пути интегрирования. Поэтому, если разбить путь интегрирования на две части и сначала проводить интегрирование вдоль радиуса от точки а до точки, которая является точкой пересечения продолжения этого радиуса с поверхностью воображаемой сферы с центром в начале координат и радиусом r_в, а затем проводить интегрирование по любой линии, лежащей на поверхности этой серы от данной точки до точки в, то интеграл вдоль этой линии будет равен нулю, поскольку вектор напряженности поля имеет одну составляющую, направленную вдоль радиуса, а подинтегральным выражением в формуле (1.6) является скалярное произведение вектора напряженности поля и вектора dl, который совпадает с касательной к поверхности сферы.

Таким образом, разность потенциалов между точками а и в будет равна

В.

Пример 2. Уединенный проводящий шар радиусом R₀ = 6 см, поверхностная плотность заряда которого s = 0,1*10^-6 Кл/м², помещен в диэлектрик (e_r = 3).

Определить закон изменения напряженности поля и потенциала в функции расстояния r от центра шара, приняв потенциал равным нулю в бесконечности. Рассчитать напряжение между точками, одна из которых лежит на поверхности шара, а другая – на расстоянии 20 см от его поверхности. Вычислить емкость шара.

Решение.

Поле внутри проводящего шара отсутствует. Поле вне шара обладает сферической симметрией, поэтому рассчитывается с помощью теоремы Гаусса точно так же как и для точечного заряда.

Здесь в качестве поверхности интегрирования взята поверхность сферы радиуса r ?

R₀ с центром, совпадающим с центром шара.

Заряд шара определяется через поверхностную плотность

q = s·4p·R₀².

Таким образом, напряженность поля вне шара имеет только одну радиальную составляющую и равна

Е_r = s·R₀²/(e_re₀r²) =

0,1·10^-6·0,06²/(3·8,85·10^-12r²).

Потенциал в любой точке вне шара, находящейся на расстоянии r от его центра, определяется с помощью выражения (1.5), которое с учетом того, что напряженность поля направлена вдоль радиуса, будет иметь следующий вид:

Потенциал шара равен потенциалу любой точки, лежащей на поверхности шара (r = R₀) U =

13,56/0,06 = 173,8 В.

Разность потенциалов между любыми точками А (r = R_A) и В (r = R_В) определяется с помощью следующей формулы:

UA – UВ = 13,56· (1/RA – 1/RВ).

Таким образом, разность потенциалов между точкой, лежащей на поверхности шара, и точкой, отстоящей от поверхности на расстоянии 20 см, равна

UAВ = 13,56· (1/0,06 – 1/0,26) = 173,8 В.

Емкость шара можно определяется выражением (1.19)

С = 4·p·ere0·R0 = 4·p·3·8,85·10-12·0,06 = 2·10-11 Ф.

Пример 3.

Шар из диэлектрика (e_r = 4) заряжен и расположен в воздухе. Объемная плотность заряда является функцией расстояния r от центра шара: r = k*r,

где k = 0,05p [Кл/м⁴].

Радиус шара R = 2см. Рассчитать и построить графики изменения потенциала и напряженности поля вдоль радиуса.

Решение. В

данном случае поле также обладает сферической симметрией, но область не однородна. Поэтому здесь удобнее применять постулат Максвелла (1.10).

Так, при 0 ? r ? R где s – сферическая поверхность радиусом r с

центром, совпадающим с центром шара; v – объем, заключенный внутри этой поверхности.

Перепишем уравнение с учетом симметрии поля

Отсюда находим радиальную составляющую вектора электрического смещения:

D_r = 0,25·k·r².

Напряженность электрического поля, которая также как и вектор электрического смещения направлена по радиусу, внутри шара будет равна

(1.8):

E₁_r = D_r/e_re₀ = 0,25·k·r²/e_re₀.

Вне шара (r ? R) электрическое смещение, исходя из постулата Максвелла, определяется следующим образом:

Следовательно, электрическое смещение и напряженность поля будут равны:

D_r = 0,25·k·R⁴/r²; E_r = D_r/e₀.

Графики изменения напряженности поля и вектора электрического смещения представлены на рис.1.4. Значения напряженности поля и вектора электрического смещения даны в относительных единицах. За базисные значения приняты значения этих величин на поверхности шара, которые для заданных исходных данных соответственно равны E_rb = 4,435·10⁵В/м; D_rb = 1,571·10^-5Кл/м².

Потенциал поля внутри шара можно определить по формуле

где С₁ – постоянная интегрирования.

Принимая потенциал бесконечно удаленной точки равным нулю, определим потенциал любой произвольной точки в области вне шара.

Постоянную интегрирования С₁ можно определить из условия равенства потенциалов U₁ и U₂ на поверхности шара (при r = R)

Отсюда

График изменения потенциала вдоль радиуса также в относительных единицах показан на рис.1.4. За базисное значение потенциала принято значение потенциала на поверхности шара U_b = 35.5кВ.

Отметим, что если бы объемная плотность заряда r оставалась постоянной, то напряженность поля и потенциалы поля в соответствующих подобластях определялись бы следующими выражениями:

E₁ = r·r/(3·e_re₀); U₁ = – r·r²/(6·e_re₀) + C₁;

E₂ = r·R³/(3·e₀·r²);

U₂ = r·R³/(3·e₀·r).

Постоянная С₁ в этом случае определяется также из условия равенства потенциалов U₁ и U₂ на поверхности шара

С₁ = r·R³· (1+2·e_r)/(6·e₀·e_r).

Пример 4. Сферический конденсатор с двухслойным диэлектриком имеет радиус внутренней сферы r₁=12 мм, внутренний радиус наружной сферы – r₃=22 мм и радиус поверхности раздела диэлектриков – r₂=16 мм.

Относительное значение диэлектрической проницаемости внутреннего слоя диэлектрика e_r₁=5, наружного слоя – e_r₂=3. Разрез конденсатора показан на рис.1.5. Заряд конденсатора q = 10^-8Кл.

Определить и построить график изменения напряженности поля вдоль радиуса. Найти разность потенциалов между электродами. Вычислить емкость конденсатора. Изменяя радиус поверхности раздела диэлектриков r₂ и значение диэлектрической проницаемости наружного слоя e_r₂ получить конденсатор с наилучшим использованием двухслойного диэлектрика. Рассчитать емкость данного конденсатора и сопоставить ее с емкостью исходного конденсатора.

Решение. Используя постулат Максвелла для любой сферической поверхности радиусом r, построенной внутри k-го слоя (k=1,2) диэлектрика с диэлектрической проницаемостью e_rk, получим выражение для вектора электрического смещения и напряженности электрического поля

D_k= q/(4pr²); E_k= D_k/(e_rk·e₀) = q/(4pr²·e_rk·e₀).

Максимальное значение напряженности поля в первом слое, очевидно, будет на поверхности внутреннего электрода

E₁_max= q/(4p·r₁²·e_r₁e₀)=10^-8/(4p·12²·10^-6·5·8,85·10^-12) = 1,249·10⁵ В/м.

Максимальное значение напряженности поля во втором слое на сферической поверхности раздела диэлектриков

E₂_max= q/(4pr₂²·e_r₂·e₀)=10^-8/(4p16²·10^-6·3·8,85·10^-12) =1,171*10⁵ В/м.

Графики изменения напряженности поля в диэлектрике вдоль радиуса представлены на рис.1.6. Значения напряженности на графиках приведены в относительных единицах. За базисное значение принято максимальное значение напряженности в первом слое E_b= E₂_max.

Разность потенциалов между электродами определяется при помощи следующего выражения:

Емкость конденсатора равна (1.15)

C=q/U₁₂ = 10^-8/885,6 = 1,129·10^-11Ф.

Отметим, что емкость сферического конденсатора с двухслойным диэлектриком можно определить и по такой формуле

С=С₁С₂/(С₁+С₂),

где С₁ – емкость сферического конденсатора с однослойным диэлектриком с радиусами обкладок r₁ и r₂ и диэлектрической проницаемостью диэлектрика, равной диэлектрической проницаемости первого слоя; С₂ – емкость сферического конденсатора с однослойным диэлектриком с радиусами обкладок r₂ и r₃ и диэлектрической проницаемостью диэлектрика, равной диэлектрической проницаемости второго слоя.

Поскольку емкость сферического конденсатора с однослойным диэлектриком определяется с помощью выражения (1.18), то емкости С₁, С₂ и С будут равны:

С1 = 4·p·8,85·10-12·5·0,012·0,016/(0,016-0,012) = 2,669·10-11Ф;

С2=4·p·8,85·10-12·3·0,016·0,022/(0,022-0,016) = 1,957·10-11Ф;

С=2,669·1,957·10-11(2,669+1,957) = 1,129·10-11Ф.

Для наилучшего использования диэлектриков в конденсаторе необходимо так подобрать толщину слоев, чтобы максимальное значение напряженности поля было одинаковым. Поскольку напряженность поля имеет максимальное значение у внутренней поверхности слоя, то для выполнения этого условия, необходимо, чтобы произведение квадрата внутреннего радиуса слоя на его диэлектрическую проницаемость было постоянным, то есть r₁²e₁= r₂²e₂=const.

Если значение диэлектрической проницаемости оставлять неизменным, а изменять толщину слоев, то с помощью данного выражения можно определить радиус поверхности раздела диэлектриков.

м.

Разность потенциалов U₁₂ и емкость такого конденсатора будут равны: U₁₂=910,13В; C=1,099*10^-11Ф.

Пример 5.

Бесконечно длинная тонкая заряженная нить расположена в воздухе вдоль оси z цилиндрической системы координат (рис. 1.7). Линейная плотность заряда t=10^-9Кл/м. Рассчитать и построить график изменения напряженности поля вдоль радиуса. Определить разность потенциалов между точками

m (r_m=10cм; q_m=270^°) и n (r_n=40cм; q_n=180^°).

Решение. В этом случае поле характеризуется цилиндрической симметрией, то есть во всех точках цилиндрической поверхности, охватывающей заряженную нить, произвольного радиуса r напряженность поля имеет одно и то же значение и направлена перпендикулярно к поверхности. Поэтому, если окружить нить цилиндрической поверхностью длиной l и радиусом r и использовать теорему Гаусса, то можно получить выражение для напряженности поля Е.

График изменения напряженности поля вдоль радиуса представлен на рис. 1.8.

Значение напряженности поля на графике даны в относительных единицах. За базисное значение принято значение напряженности на расстоянии одного миллиметра от начала координат (Е_b=1,798·10⁴ В/м).

Потенциал поля в любой точке m, расположенной на расстоянии r_m от оси провода, равен:

Здесь r_p – расстояние от оси провода до некоторой фиксированной точки пространства р, в которой потенциал принимается равным нулю.

Если за такую точку принять точку, расположенную на расстоянии одного метра от оси провода, то потенциал точки m будет равен:

Изменение потенциала вдоль радиуса представлено на рис. 1.8. Значения потенциала даны также в относительных единицах. За базисное значение потенциала принято значение потенциала в той же точке, что и базисное значение напряженности поля (U_b=124,226 В).

Разность потенциалов между точками, указанными в условии задачи, равна 24,931 В.

Пример 6.

Бесконечно длинный цилиндрический конденсатор с двухслойным диэлектриком имеет радиус внутреннего электрода r₁=1 мм, внутренний радиус внешнего электрода – r₃=4 мм и радиус поверхности раздела диэлектриков – r₂=2 мм.

Относительное значение диэлектрической проницаемости внутреннего слоя диэлектрика e_r₁=5, наружного слоя – e_r₂=2,5. Поперечное сечение конденсатора показано на рис.1.9. Линейная плотность заряда конденсатора t = 10^-8 Кл/м.

Определить и построить график изменения напряженности поля вдоль радиуса. Найти разность потенциалов между электродами.

Вычислить емкость конденсатора на единицу длины.

Решение. Для решения задачи используем обобщенную теорему Гаусса. В качестве поверхности интегрирования возьмем замкнутую цилиндрическую поверхность длиной l и радиусом r (r₁?r?r₃).

Ввиду цилиндрической симметрии (вектор электрического смещения на этой поверхности не изменяется по величине и направлен по радиусу) последнее уравнение можно переписать следующим образом:

D·2·p·r·l = t·l,

откуда

D = D_r = t/(2·p·r).

Напряженность поля в первом слое диэлектрика (r₁ ?r ? r₂) будет при этом равна:

E₁ = D/(e_r₁e₀) = t/(2·p·e_r₁e₀·r).

Во втором слое (r₂ ?r ? r₃) –

E₂ = D/(e_r₂e₀) = t/(2·p·e_r₂e₀·r).

График изменения напряженности поля представлен на рис.1.10. На графике значения напряженности поля представлены в относительных единицах. За базисное значение принято значение напряженности в первом слое при r = r₁, ( E_b = 35,970 кВ/м).

Как видно из рис. 1.10, напряженность поля на границе раздела диэлектриков испытывает скачек. Для лучшего использования изоляции стараются подобрать толщину слоев диэлектрика и их диэлектрическую проницаемость таким образом, чтобы максимальное значение напряженности поля в обоих слоях было одинаково. Это будет соблюдаться при условии r₁e₁ = r₂e₂, как в данном примере.

Разность потенциалов между электродами определяется при помощи выражения (1.6), которое для цилиндрического конденсатора можно переписать в следующем виде:

74,792В.

Емкость конденсатора на единицу его длины будет равна:

С = t/U = 10^-8/74,792 = 0,1337 нФ/м.

Отметим, что емкость цилиндрического конденсатора с двухслойным диэлектриком можно определить и по такой формуле

С=С1С2/(С1+С2),

где С₁ – емкость цилиндрического конденсатора с однослойным диэлектриком с радиусами обкладок r₁ и r₂ и диэлектрической проницаемостью диэлектрика, равной диэлектрической проницаемости первого слоя; С₂ – емкость цилиндрического конденсатора с однослойным диэлектриком с радиусами обкладок r₂ и r₃ и диэлектрической проницаемостью диэлектрика, равной диэлектрическойпроницаемости второго слоя.

Поскольку емкость цилиндрического конденсатора с однослойным диэлектриком определяется с помощью выражения (1.23), то емкости С₁, С₂ и С будут равны:

С = С₁·С₂/(С₁ + С₂) = 0,1337 нФ/м.

Пример 7.

Бесконечно длинный цилиндр, выполненный из диэлектрика, относительное значение диэлектрической проницаемости которого e_r₁ = 4, заряжен и находится в минеральном масле (e_r₂ = 2,5).

Радиус цилиндра r₀ = 5мм (рис. 1.11). Объемная плотность заряда является функцией расстояния от оси цилиндра r = r/10.

Найти законы изменения потенциала и напряженности поля внутри и вне цилиндра в функции расстояния r от оси, приняв потенциал равным нулю на оси цилиндра (r = 0). Построить графики этих функций.

Решение. В

качестве поверхности интегрирования выбирается боковая поверхность цилиндра длиной один метр, радиусом r и с осью, совпадающей с осью исходного цилиндра. При 0 ? r ? r₀ внутри этой поверхности будет находиться заряд, величина которого может быть определена с помощью следующего выражения:

Таким образом, с учетом цилиндрической симметрии поля,

получим

Отсюда

где А₁=9.416·10⁸ В/м³.

В области вне цилиндра (r₀?r??)

Из этого выражения легко определяется напряженность поля вне цилиндра

где А₂=183.432 В.

Потенциал электрического поля внутри цилиндра (при условии, что точка, в которой потенциал поля принимается равным нулю, лежит на оси цилиндра) можно определить следующим образом:

Потенциал поля в области вне цилиндра равен

Здесь В₂ – постоянная интегрирования, которую можно найти из условия равенства потенциалов на поверхности цилиндра.

В.

Распределение напряженности электрического поля и потенциала представлено в относительных единицах на рис. 1.12. За базисные значения напряженности поля и потенциала приняты максимальное значение напряженности на границе раздела сред (Е_max=3.669·10⁴ В/м) и значение потенциала при r=0.019 м (j_в=-284 В).

В частном случае, когда объемная плотность заряда r является постоянной величиной, решение упрощается, и выражения для функции напряженности поля и потенциала будут иметь вид:

где

Пример 8.

Рассчитать электростатическое поле, создаваемое зарядом, который равномерно распределен между двумя цилиндрическими бесконечно длинными поверхностями.

Объемная плотность заряда r=10^-6 Кл/м³.

Радиус внешнего цилиндра R₁=20 см, внутреннего – R₂ =4 см, расстояние между осями цилиндров – а=10 см. Относительное значение диэлектрической проницаемости окружающей среды и обоих цилиндров равно e_r₁=1.

Определить распределение составляющих напряженности электрического поля и потенциала вдоль осей Х и Y (рис. 1.13).

Решение.

Данная задача решается методом наложения. Сначала рассчитывается поле в любой точке М от заряда с объемной плотностью +r, равномерно распределенного по объему всего большого цилиндра. Затем в этой же точке рассчитывается поле от заряда, объемная плотность которого равна -r, равномерно распределенного по объему малого цилиндра. Результирующая напряженность поля Е в любой точке М определяется как векторная сумма напряженности Е₁ и Е₂. Потенциал любой точки определяется также как сумма потенциалов U₁ и U₂.

Так, в точке М, которая находится на расстоянии r₁ от оси большого цилиндра и r₂ от оси малого цилиндра и имеет координаты r₁ и a (рис. 1.14) модули напряженности поля от соответствующих зарядов определяются согласно теореме Гаусса по следующим формулам:

Вектор напряженности Е₁ направлен по радиусу r₁ от оси О большого цилиндра, а вектор Е₂ – по радиусу r₂ к оси О₁ малого цилиндра (рис. 1.14).

Потенциалы поля при этом будут равны:

Здесь С₁ и С₂ – постоянные интегрирования.

Потенциал поля в области между цилиндрами определяется следующим выражением:

Принимая потенциал равным нулю на оси большого цилиндра (r₁=0; r₂=a), найдем постоянную интегрирования С.

С учетом этого, выражение для потенциала в области между цилиндрами окончательно можно записать в следующем виде:

Если поле определяется в области, лежащей внутри малого цилиндра, то напряженность поля в произвольной точке этой области будет определяться при помощи следующего выражения:

Здесь i – единичный орт, направленный вдоль оси Х.

Таким образом, внутри малого цилиндра напряженность поля будет иметь только одну составляющую, направленную вдоль оси Х и являющуюся постоянной величиной.

Потенциал поля при этом будет равен

где В – постоянная интегрирования.

Эта постоянная определяется исходя из равенства потенциалов для точки, лежащей на поверхности малого цилиндра, один из которых рассчитывается по последнему уравнению, а второй – по выражению, справедливому для точек, находящихся в области между цилиндрами.

Определяя с помощью теоремы косинусов r₂ через r₁, выражения для потенциала и напряженности поля можно преобразовать.

Если точка, в которой определяется поле, лежит в области вне цилиндров (r₁?R₁), то модули напряженности поля будут определяться при помощи следующих выражений:

где t₁ и t₂ – линейная плотность зарядов большого и малого цилиндров.

Направление векторов напряженности поля определяется так же, как и для области, лежащей между цилиндрами.

Потенциал поля для области вне цилиндров будет равен

Постоянная интегрирования В₁ определяется из условия равенства потенциалов на поверхности большого цилиндра (r₁=R₁, r₂=R₁-a), один из которых рассчитывается по последнему уравнению, а второй – по выражению, справедливому для точек, находящихся в области между цилиндрами.

Следовательно, окончательно можно записать следующее выражение для определения потенциала в данной области:

Построим графики изменения модуля напряженности поля и потенциала вдоль оси Y при х=0, для чего положим r₁=y; r₂=(y²+a²)^0,5.

При этом выражения для напряженности поля и потенциала можно несколько преобразовать. Так, при 0?y?R₁ они будут иметь следующий вид:

В области вне цилиндров (у?R₁) эти выражения можно записать следующим образом:

Графики изменения данных функций представлены на рис. 1.15.

На графиках все величины даны в относительных величинах. За базисные значения потенциала и напряженности поля приняты значения соответствующих функций на поверхности цилиндра радиусом R₁ (x=0; y=R₁), которые оказались равными U_б=-1057 В,

Е_б=10,94 кВ/м.

На рис. 1.16 представлены графики распределения потенциала и напряженности поля (в относительных единицах) вдоль оси Х (при Y=0).

Пример 9.

Рассчитать электростатическое поле от двух бесконечно длинных, равномерно заряженных, параллельных, тонких проводников, расположенных в воздухе на расстоянии 2d=6 м друг от друга. Проводники имеют одинаковые по величине, но противоположные по знаку заряды, линейная плотность которых равна t=4*10^-9 Кл/м.

Построить график изменения напряженности поля вдоль оси Y (при х=0) и вывести уравнения для построения эквипотенциальных линий и линий поля.

Решение.

Поскольку среда линейна, то данную задачу можно решить методом наложения.

Вначале рассчитываем напряженность поля в любой точке М от правого провода (рис. 1.17), а затем в этой же точке от левого провода. Задача по расчету поля от бесконечно длинного заряженного провода решена в примере 5. Поэтому сразу запишем выражения для определения напряженности поля от правого и левого провода

Направление векторов напряженности поля показано на рис. 1.17. Результирующая напряженность поля определяется как векторная сумма этих векторов

Модуль данной результирующей напряженности поля рассчитывается по формуле

где

E₁_x, E₂_x,

E₁_y, E₂_y—

проекции векторов напряженности поля на соответствующие декартовы оси координат.

Здесь y_м и x_м – координаты произвольной точки М.

В частности, если точка М лежит на оси Y, то (r₁=r₂) результирующая напряженность поля будет направлена вдоль оси Х (Е=Е_х). График распределения данной величины вдоль оси Y представлен на рис. 1.18. Значения напряженности поля на графике даны в относительных единицах, при этом за базисное значение принято значение напряженности в начале координат (x=0, y=0), которое оказалось равным 47,956 В/м.

Потенциал поля в любой точке М определяется также, как сумма потенциалов поля от одного и другого провода

Здесь С – постоянная интегрирования. Эта постоянная будет равна нулю, если принять потенциал точки, которая находится в начале координат, равным нулю.

В этом случае ось OY будет являться эквипотенциальной линией нулевого потенциала.

Все остальные линии равного потенциала являются окружностями с центрами, лежащими на оси ОХ. Координаты этих центров и радиусы окружностей определяются с помощью следующих формул:

Таким образом, если необходимо провести линию равного потенциала через точку, потенциал которой задан (например, 100 В), то надо определить k, используя формулу для потенциала

При построении картины поля, для того чтобы приращение потенциала при переходе от любой линии равного потенциала к соседней оставалось постоянным, должно соблюдаться условие

Здесь В – постоянная; n – порядковый номер линии равного потенциала.

Таким образом, число k при возрастании порядкового номера линии равного потенциала n должно изменяться в геометрической прогрессии.

Линиями поля данной системы заряженных проводников являются дуги окружностей, пересекающихся с проводниками. При этом, центры этих дуг лежат на оси OY и имеют координаты, которые определяются при помощи следующей формулы:

Чтобы при построении картины поля подразделить поле на трубки равного потенциала, необходимо при переходе от любой линии напряженности поля к соседней изменять угол J на постоянную величину.

Пример 10.

Два одинаковых бесконечно длинных проводящих цилиндра расположены в воздухе. Радиус цилиндров R=0.04 м, расстояние между геометрическими осями 2h=0.12 м (рис.1.19).

Напряжение, приложенное к цилиндрам U₁₂=100 В.

Рассчитать электростатическое поле, построить графики изменения напряженности поля и потенциала вдоль оси х.

Найти емкость системы проводов на единицу длины.

Решение.

Поле внутри проводящих проводов отсутствует. Поле же в воздухе будет точно таким, как и поле от двух бесконечно тонких линейных проводников, проходящих через электрические оси данных проводов.

Таким образом, задача по расчету поля двух проводов круглого сечения сводится к нахождению электрических осей проводов, поскольку в дальнейшем расчет поля в воздухе будет аналогичным расчету поля, проведенному в предыдущем примере.

Поскольку поверхность проводящих проводов является поверхностью равного потенциала, то, используя выражения для координаты центра и радиуса линий равного потенциала, которые приведены в примере 9, можно получить формулу для определения координат центра электрических осей проводов b.

В условии задачи задана не линейная плотность зарядов, а разность потенциалов между проводами (разность потенциалов между точками m и n).

Поэтому, прежде всего, следует определить линейную плотность зарядов t. Для этого используем выражение для потенциалов, которое также приведено в предыдущем примере

Здесь r₁ и r₂ – расстояние от электрической оси первого (левого) и второго провода, соответственно, до точки m, которая находится на поверхности первого провода, а r₁^/ и r₂^/ – расстояние от электрической оси первого и второго провода, соответственно, до точки n, которая находится на поверхности второго провода.

С учетом последних соотношений, можно записать выражение для определения линейной плотности зарядов

После определения линейной плотности зарядов и расположения электрических осей проводов, выражения для расчета напряженности поля и потенциала в области вне проводов полностью аналогичны тем, которые приведены в примере 9.

Графики распределения напряженности поля и потенциала вдоль оси ОХ (при y=0) приведены на рис. 1.20. Все значения на графике даны в относительных единицах, причем, за базисные значения приняты значения напряженности поля и потенциала на поверхности правого провода, которые оказались равными Е_б=2904 В/м, j_б=-50 В.

С учетом того, что ось OY является осью симметрии для напряженности поля и осью антисимметрии для потенциала, графики построены только для положительных значений х.

Емкость между двумя проводниками на единицу их длины определяется при помощи следующего выражения:

Пример 11. Рассчитать

электростатическое поле от двух параллельных бесконечно длинных заряженных несоосных проводящих цилиндров, расположенных в воздухе. Радиусы цилиндров R₁=0.02 м и R₂=0.04 м. Расстояние между геометрическими осями D=0.08 м (рис. 1.21). Цилиндры имеют одинаковый по величине, но противоположный по знаку заряд, линейная плотность которого t₁=-t₂=t=10^-8 Кл/м.

Определить разность потенциалов между цилиндрами, емкость системы на единицу длины.

Построить график изменения потенциала поля вдоль оси ОХ (при y=0).

Решение.

Расположим оси цилиндров (О₁ и О₂) так, чтобы их поверхности совпали с поверхностями равного потенциала. Обозначим через h₁ и h₂ расстояние от геометрических осей первого и второго цилиндра до плоскости постоянного (нулевого) потенциала, а через b – расстояние от электрических осей-до этой плоскости. После определения данных величин задача по расчету поля в области вне цилиндров сводится к расчету электростатического поля от двух заряженных бесконечно длинных линейных проводов, проходящих через центры зарядов, и оказывается, таким образом, полностью аналогичной задачам, рассмотренным в предыдущих примерах.

Используя выражение для определения координат центров зарядов, справедливое как для одного, так и для второго провода, составим следующее уравнение:

или

При заданном расположении цилиндров (рис. 1.21) имеем

h₁+h₂=D

и, следовательно,

В этом случае

Разность потенциалов между двумя цилиндрами можно определить по следующей формуле (как и в примере 10):

Здесь r₁^/ и r₂^/ – расстояние от центра электрических осей первого и второго цилиндра, соответственно, до точки n, лежащей на поверхности первого цилиндра; r₁^// и r₂^// – расстояние от центра электрических осей первого и второго цилиндра, соответственно, до точки m, лежащей на поверхности второго цилиндра

r₁^/ = (R₁ + b – h₁) = 0.0131м; r₂^/ = 2b – r₁^/ = 0.0381м;

r₂^// = (R₂ + b – h₂) = 0.0181м; r₁^// = 2b – r₂^// = 0.0331м.

Потенциал любой произвольной точки d будет равен

где r₁ и r₂ – расстояние от электрических осей первого и второго провода до точки d.

Если точка d лежит на оси ОХ между цилиндрами, то

r₂ = b – x; r₁ = b + x;

График изменения потенциала вдоль оси ОХ (при (R₁ – h₁) < x < (h₂ – – R₂)) показан на рис. 1.22.

Емкость системы цилиндров на единицу длины определяется по следующей формуле:

Построение линий равного потенциала и линий поля в области вне цилиндров проводится таким же образом, как и для линейных проводов, которые совпадают с электрическими осями (см. пример 9).

Пример 12. Бесконечно длинный проводящий цилиндр радиусом R₁=2см расположен внутри другого бесконечно длинного проводящего цилиндра радиусом R₂=6см.

Расстояние между геометрическими осями цилиндров D=3см (рис. 1.23). Область между цилиндрами заполнена диэлектриком с относительным значением диэлектрической проницаемости e_r=2.

Цилиндры имеют одинаковый по величине, но противоположный по знаку заряд, линейная плотность которого t₁=-t₂=t=10^-8Кл/м.

Определить разность потенциалов между цилиндрами, емкость системы на единицу длины. Построить график изменения напряженности поля вдоль оси Х (при Y=0) между цилиндрами.

Решение.

Решение данной задачи, как и в предыдущих примерах, сводится к отысканию положения электрических осей.

Полагая, что оси проводов расположены так, что их поверхности совпадают с эквипотенциальными поверхностями электростатического поля, будем иметь:

где h₁ и h₂ – расстояние от геометрических осей цилиндров до плоскости постоянного (нулевого) потенциала; b – расстояние от электрических осей до этой же плоскости.

Последнее выражение можно переписать следующим образом:

Но, поскольку при расположении цилиндров один внутри другого, выполняется равенство

то

Таким образом, выражения для определения h₁, h₂, и b будут иметь следующий вид:

После нахождения положения электрических осей задача по расчету поля в диэлектрике между цилиндрами становится полностью аналогичной задаче по расчету поля от линейных проводов, совпадающих с электрическими осями цилиндров.

Так, потенциал любой точки М, находящейся в области между цилиндрами, будет равен

где r₁ и r₂ – расстояние от электрических осей первого и второго цилиндров соответственно до точки М.

Разность потенциалов между цилиндрами (между точками m и n) при этом будет равна

Здесь r₁^/ и r₂^/ – расстояние от электрических осей первого и второго цилиндров соответственно до точки m, а r₁^// и r₂^// – расстояние от электрических осей этих цилиндров до точки n.

При заданном расположении цилиндров указанные расстояния будут равны

Таким образом, разность потенциалов между цилиндрами U_mn будет составлять величину, равную 67.1В.

Напряженность электрического поля в любой точке, лежащей на оси ОХ между цилиндрами (между точками m и n), находится методом наложения

График изменения данной величины вдоль оси ОХ представлен на рис. 1.24.

Для удобства изображения все величины на рисунке представлены в относительных единицах. За базисное значение напряженности поля принято значение напряженности поля на поверхности малого цилиндра в точке m (E_b =Е_m=8020 В/м), а за базисное значение переменной х – абсолютное значение координаты этой же точки (х_b=|х_m|= 0.0183 м).

Емкость системы проводов на единицу их длины определяется с помощью следующей формулы:

Зная разность потенциалов между цилиндрами и линейную плотность зарядов t емкость С, согласно определению, можно найти и как отношение линейной плотности зарядов к разности потенциалов

Для построения силовых линий и линий равного потенциала можно воспользоваться рекомендациями, данными в предыдущих примерах.

Источник

Решение:

15 Два параллельных тонких кольца радиуса R расположены на расстоянии d друг от друга на одной оси. Найти работу электрических сил при перемещении заряда q_o из центра первого кольца в центр второго, если на первом кольце равномерно распределен заряд q₁, а на втором — заряд q₂.

Решение:

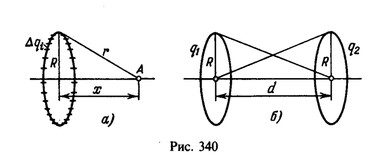
Найдем потенциал, создаваемый зарядом q, находящимся на кольце, в точке А на оси кольца, расположенной на расстоянии
х от его центра (рис. 340, а) и, следовательно, на расстояниях от точек, лежащих на кольце. Разобьем кольцо на отрезки, малые по сравнению с расстоянием r. Тогда заряд , находящийся на каждом отрезке (i — номер отрезка), можно рассматривать как точечный. Он создает в точке А потенциал . Потенциал, создаваемый в точке А всеми отрезками кольца (отстоящими от этой точки на одно и то же расстояние r), будет

В скобках стоит сумма зарядов всех отрезков, т. е. заряд всего кольца q; поэтому

Потенциал Ф₁ поля в центре первого кольца складывается из потенциала, создаваемого зарядом q₁, находящимся на первом кольце, для которого х=0, и потенциала, создаваемого зарядом q₂, находящимся на втором кольце, для которого x=d (рис. 340, б). Аналогично находится потенциал в центре второго кольца:

Окончательно для работы имеем

16 На тонком кольце радиуса R равномерно распределен заряд q. Какова наименьшая скорость υ, которую необходимо сообщить находящемуся в центре кольца шарику массы т с зарядом q_o, чтобы он мог удалиться от кольца в бесконечность?

Решение:
Если заряды q_o и q одного знака, то удалить шарик от кольца в бесконечность можно, сообщив ему бесконечно малую скорость. Если же знаки зарядов разные, то сумма кинетической и потенциальной энергий шарика в центре кольца должна быть равна нулю, так как она равна нулю в бесконечности: , где φ=kq/R — потенциал в центре кольца (см. задачу 17); отсюда

17 На шарик радиуса R=2 см помещен заряд q=4 пКл. С какой скоростью подлетает к шарику электрон, начавший движение из бесконечно удаленной от него точки?

Решение:

18 Между горизонтально расположенными пластинами плоского конденсатора с высоты Н свободно падает незаряженный металлический шарик массы т. На какую высоту h после абсолютно упругого удара о нижнюю пластину поднимется шарик, если в момент удара на него переходит заряд q? Разность потенциалов между пластинами конденсатора равна V, расстояние между пластинами равно d.

Решение:
Внутри конденсатора имеется однородное электрическое поле с напряженностью Е= V/d, направленной вертикально. После удара шарик приобретает заряд того же знака, что и нижняя пластина конденсатора. Поэтому на него будет действовать со стороны электрического поля сила F=qE=qV/d, направленная вверх. Согласно закону сохранения энергии изменение энергии равно работе внешних сил (в данном случае — электрических). Учитывая, что удар абсолютно упругий и что в начальный и конечный моменты шарик имеет лишь потенциальную энергию в поле силы тяжести, получим
откуда

19 Два шарика с одинаковыми зарядами q расположены на одной вертикали на расстоянии Н друг от друга. Нижний шарик закреплен неподвижно, а верхний, имеющий массу m, получает начальную скорость v, направленную вниз. На какое минимальное расстояние h приблизится верхний шарик к нижнему?

Решение:
Согласно закону сохранения энергии

где qV—работа электрических сил, V=kq/H—kq/h — разность потенциалов точек начального и конечного положения верхнего шарика. Для определения h получаем квадратное уравнение:

Решая его, найдем

(знак плюс перед корнем соответствовал бы максимальной высоте, достигнутой шариком, если бы он получил ту же начальную скорость, направленную вверх).

20 Найти максимальное расстояние h между шариками в условиях предыдущей задачи, если неподвижный шарик имеет отрицательный заряд q, а начальная скорость v верхнего шарика направлена вверх.

Решение:

21 Электрон, пролетая в электрическом поле путь от точки а к точке b, увеличил свою скорость с ν_a=1000 км/с до ν_ab = 3000 км/с. Найти разность потенциалов между точками а и b электрического поля.

Решение:
Работа, совершенная над электроном электрическим полем, идет на увеличение кинетической энергии электрона:

откуда

где γ— удельный заряд электрона. Разность потенциалов отрицательна. Так как электрон имеет отрицательный заряд, то скорость электрона увеличивается при его движении в сторону возрастания потенциала.

22 В плоский конденсатор влетает электрон со скоростью ν = 20 000 000 м/с, направленной параллельно пластинам конденсатора. На какое расстояние h от своего первоначального направления сместится электрон за время пролета конденсатора? Расстояние между пластинами d=2 см, длина конденсатора l=5 см, разность потенциалов между пластинами v=200 В.

Решение:
За время пролета t = l/v электрон смещается в направлении действия силы на расстояние

где γ — удельный заряд электрона.

23 Положительно заряженная пылинка массы г находится в равновесии внутри плоского конденсатора, пластины которого расположены горизонтально. Между пластинами создана разность потенциалов V₁=6000 В. Расстояние между пластинами d=5см. На какую величину необходимо изменить разность потенциалов, чтобы пылинка осталась в равновесии, если ее заряд уменьшился на q_o=1000 e?

Решение:
На пылинку действуют сила тяжести mg и сила со стороны электрического поля, где —начальный заряд пылинки и E₁ = V₁/d—напряженность электрического поля в конденсаторе.
Чтобы пылинка могла находиться в равновесии, верхняя пластина конденсатора должна быть заряжена отрицательно. При равновесии
mg = F, или ; отсюда .
Так как уменьшение заряда пылинки на q_o=1000e равносильно увеличению положительного заряда на q_o, то новый заряд пылинки q₂ = q₁+q_o. При равновесии , где V2—новая разность потенциалов между пластинами. Учитывая выражения для q2, q1 и q0, найдем

Таким образом, разность потенциалов нужно изменить на V₂— V₁ = — 980 В (знак минус показывает, что ее нужно уменьшить, так как заряд пылинки увеличился).

24 Решить предыдущую задачу, считая пылинку заряженной отрицательно.

Решение:
Верхняя пластина конденсатора должна быть заряжена положительно. Новый заряд пылинки q₂ = q_1-q_o, где q_o=1000e.
Поэтому (см. задачу 23)

Напряжение между пластинами нужно увеличить на V₂— V₁ = 1460 В.

25 В электрическое поле плоского конденсатора, пластины которого расположены горизонтально, помещена капелька масла, имеющая заряд q=1 е. Напряженность электрического поля подобрана так, что капелька покоится. Разность потенциалов между пластинами конденсатора V =500 В, расстояние между пластинами d=0,5 см. Плотность масла . Найти радиус капельки масла.

Решение:
При равновесии
откуда

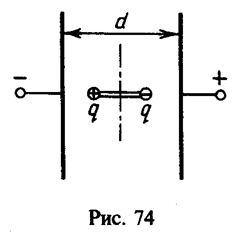
26 Внутри плоского конденсатора, пластины которого расположены вертикально, помещена диэлектрическая палочка длины l=1 см с металлическими шариками на концах, несущими заряды +q и — q(|q|=1 нКл). Палочка может вращаться без трения вокруг вертикальной оси, проходящей через ее середину. Разность потенциалов между пластинами конденсатора V=3 В, расстояние между пластинами d=10см. Какую работу необходимо совершить, чтобы повернуть палочку вокруг оси на 180° по отношению к тому положению, которое она занимает на рис. 74?

Решение:
Напряженность электрического поля в конденсаторе E=V/d.
Разность потенциалов между точками, где расположены заряды,

где —потенциал в точке расположения заряда + q, а —потенциал в точке расположения заряда — q; при этом . При повороте палочки электрические силы совершают работу по переносу заряда — q из точки а в точку b и заряда + q из точки b в точку а, равную

Знак минус означает, что работу должны совершить внешние силы.

27 Внутри плоского конденсатора помещен диэлектрический стержень длины l=3 см, на концах которого имеются два точечных заряда + q и —q (|q|=8нКл). Разность потенциалов между пластинами конденсатора V=3 В, расстояние между пластинами d=8 см. Стержень ориентирован параллельно пластинам. Найти момент сил, действующий на стержень с зарядами.

Решение:

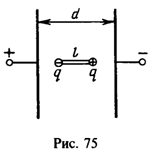
28 На концах диэлектрической палочки длины l=0,5 см прикреплены два маленьких шарика, несущих заряды — q и +q (|q|=10 нКл). Палочка находится между пластинами конденсатора, расстояние между которыми d=10cм (рис.75). При какой минимальной разности потенциалов между пластинами конденсатора V палочка разорвется, если она выдерживает максимальную силу растяжения F=0,01 Н? Силой тяжести пренебречь.

Решение:

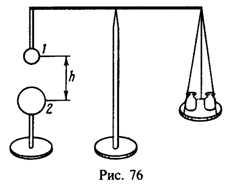
29 Металлический шарик 1 радиуса R₁=1 см прикреплен с помощью диэлектрической палочки к коромыслу весов, после чего весы уравновешены гирями (рис. 76). Под шариком 1 помещают заряженный шарик 2 радиуса R₂=2 см. Расстояние между шариками h = 20 см. Шарики 1 и 2 замыкают между собой проволочкой, а потом проволочку убирают. После этого оказывается, что для восстановления равновесия надо снять с чашки весов гирю массы m = 4мг. До какого потенциала j был заряжен шарик 2 до замыкания его проволочкой с шариком 1?

Решение:
Если до замыкания шарик 2 имел заряд 0, то сумма зарядов шариков 1 и 2 после замыкания q₁+q₂ = q. Потенциалы же их после замыкания одинаковы: . Следовательно, После замыкания шарик 2 действует на шарик 1 с силой
откуда
Начальный потенциал шарика 2