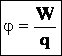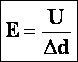Как найти потенциал через скорость

Уравнение
линии тока. Вектор
скорости частицы w
направлен по касательной к линии тока
S;
для
плоского течения это показано на рис.
53. Пусть w_x,
w_y
— проекции
вектора скорости на координатные
оси. Из рис. 53 следует, что

,

,

где
ds
– элемент дуги линии тока. Составим
производные пропорции:

,

,

откуда

.
(6.5)

Мы
получили уравнение линии тока для
плоского течения. В слу­чае трехмерного
(пространственного) потока уравнения
линии тока выводятся аналогично и имеют
вид:

.
(6.5а)

Функция
тока для двухмер­ного течения.
Дифференциальное
уравнение линии тока плоского течения
(6.5) может быть пред­ставлено в виде:

.
(6.5б)

Введем
такую «функцию тока»

ψ(x,
y),
полный дифференциал которой равен левой
части выражения (6.5б):

.
(6.6)

Поскольку
на линии тока согласно формуле (6.5б)
dψ
= 0,
оче­видно, что функция
тока сохраняет вдоль линии тока постоянное
значение.

Полный
дифференциал функции двух переменных
ψ имеет вид:

Рис. 53

.

Сравнивая
это выражение с формулой (6.6), получаем,
что про­изводные функции тока
определяются зависимостями:

,

.
(6.7)

Сама
функция тока может быть определена
интегрированием вы­ражения (6.7).

Рис. 54

К

онтур
поверхности тела, обтекаемого потоком
идеальной жид­кости, сам является
линией тока: в некоторой «критической»
точке набегающий поток раздваивается
и огибает тело. Следовательно, на
обтекаемой поверхности функция тока
постоянна. Но можно, наоборот, рас­сматривать
любую линию тока как контур сечения
твердого тела. Действи­тельно, если
заменить об­ласть, ограниченную
ли­нией тока твердым телом, то остальные
линии тока не изменятся (так как жидкость
мы считаем иде­альной, трение
отсут­ствует). Они дают картину
обтекания такого тела. В этом состоит
принцип отвердения
линий тока, широко применяемый в
гидродинамике идеальной жидкости. Если,
напри­мер, считать отвердевшими линии
тока, проходящие на рис. 54 по координатным
осям х,
у,
то получится
картина течения внутри прямого угла.

Потенциал
скорости.
Функцией скоростного потенциала
или – сокращенно — потенциалом скорости
φ (х,
у,
z)
называется та­кая функция, частные
производные которой равны составляющим
вектора скорости по соответствующим
координатным осям:

,

,

.
(6.8)

Полный дифференциал
функции φ равен

.
(6.9)

Сама
функция скоростного потенциала
определяется интегрирова­нием
выражения (6. 9).

Рис. 55

В

ведение
потенциала скорости позволяет заменить
вектор­ное
поле скорости течения, для изучения
которого нужно знать три
компоненты
по координатным осям, распределением
в про­странстве одной
скалярной
функции φ, что значительно упрощает
исследование. В механике твердого тела
вводится ана­логичное понятие
«потенциала силы»; это скалярная функция,
про­изводные от которой равны
составляющим силы по координатным осям.
Такую же природу имеет в электротехнике
понятие потен­циала электрического
поля: вместо задания в пространстве
вектор­ной величины напряженности
поля вводится скалярная функция
потенциала V,
производные
от которой по координатным осям равны
соответствующим компонентам вектора
напряженности.

Придавая
функции φ определенные значения, получаем
уравне­ния поверхностей равного
потенциала, или эквипотенци­альных
поверхностей
(в случае двухмерного течения — линий
равного потенциала, или эквипотенциалей).

Рассмотрим
связь потенциала скорости и функции
тока. В слу­чае плоского (двухмерного)
течения w_z
= 0;
дифференциал функ­ции тока выражается
формулой (6. 6), дифференциал функции
ско­ростного потенциала, из равенства
(6. 9), формулой

.

Пусть
линия тока ψ = const
такого течения представлена на рис. 55
сплошной линией, эквипотенциаль φ =
const
— пунктир­ной линией.

Проведем
к этим линиям касательные в точке их
пересечения А.
Угол
наклона прямой АВ
к
оси абсцисс определится согласно
урав­нению (6. 5б) выражением

;

угол
наклона прямой AD
выражением

.

Очевидно,
что

и угол β между касательными равен 90º.

Таким
образом, функция тока ψ и потенциал
скорости φ взаимно
ортогональны;
линии тока и эквипотенциали пе­ресекаются
всегда под прямым углом. Это позволяет
по известным эквипотенциалям строить
линии тока и наоборот. Семейства линий
ψ (х,
у)
= const
и φ (х,
у)
= const,
нанесенные на один чертеж, на­зываются
гидродинамической
сеткой течения.
Пример такой сетки был приведен на рис.
54.

Сравнивая
выражения для составляющих скорости
плоского течения w_x
и
w_y
через
функцию тока ψ (6.7) и функцию скорост­ного
потенциала φ (6.8), видим, что функции ψ и
φ связаны усло­виями:

,

.
(6.10)

В
математике эти условия называются
условиями Коши—Римана. При их соблюдении
оказывается возможным использовать
для ис­следования функций ψ и φ
математический аппарат теории функций
комплексной переменной, который широко
применяется в теории потенциального
обтекания геометрически правильных
тел.

В
§ 18 указывалось, что угловая скорость
вращения жидкой частицы в плоском потоке
определяется формулой (6.6). Если те­чение
потенциально, т. е. существует некоторая
функция скорост­ного потенциала φ,
производные которой равны соответствующим
компонентам вектора скорости, то согласно
выражению (6.8) имеем

.

Равенство
нулю угловой скорости вращения
свидетельствует о том, что потенциальное
течение — безвихре­вое,
т. е. вращение частиц в нем отсутствует.
Как будет показано в дальнейшем, у
твердых поверхностей, ограничивающих
поток, вследствие вязкости всегда
формируются зоны вращательных дви­жений,
поэтому вблизи стенок теория потенциального
обтекания неприменима. Однако для
изучения внешнего потока теория
по­тенциала используется с большим
успехом.

Применим
к потенциальному течению несжимаемой
жидкости уравнение неразрывности (2.7):

.

Подставляя
в него выражения для компонентов
скорости через функцию скоростного
потенциала (6.8), получаем

.
(6.11)

Это
уравнение известно в математической
физике под названием уравнения
Лапласа.
Таким образом, для нахождения функции
φ, полностью определяющей кинематику
потенциального потока, необходимо
решить уравнение Лапласа.

Дифференциальное
уравнение в частных производных (6. 11)
имеет бесчисленное множество решений,
поэтому должны быть за­даны дополнительные
(граничные) условия для данной конкретной
задачи. Как уже говорилось в § 2.2, к таким
условиям относятся за­дание скорости
в удалении от обтекаемого тела w_∞
и
условие ра­венства нулю на поверхности
тела нормальной составляющей ско­рости.
При этом предполагается, что жидкость
обтекает тело без отрывов. У поверхности
тела скорость направлена по касательной
(имеет место «скольжение» жидкости).

В
силу того, что сумма любого числа частных
решений уравне­ния Лапласа является
также его решением, оказывается возмож­ным
суммировать потенциалы скорости
простейших течений для получения картины
сложного течения. В этом состоит идея
метода наложения
потенциальных потоков.

Моделирование
потенциальных течений.
Исследование
обтека­ния реальных тел аналитическими
методами представляет в общем случае
большую математическую сложность.
Отыскание функции скоростного потенциала
или функции тока, например, для лопа­точных
профилей наперед заданной формы
оказывается весьма трудным. Эта задача
существенно упрощается с использованием
метода аналогий. Наибольшее развитие
к настоящему времени по­лучило
исследование потенциальных потоков
методом электрогид­родинамической
аналогии (ЭГДА). Он базируется на следующих
положениях.

Согласно
выводам теоретической электротехники
распределение электрического потенциала
в проводнике, как и распределение
по­тенциала в безвихревом потоке
идеальной жидкости, подчиняется уравнению
Лапласа. Действительно, закон Ома,
связывающий силу тока с распределением
потенциала электрического поля,
записы­вается в дифференциальной
форме следующим образом:

;

;

.
(6.
12)

Здесь
i
—
плотность тока, т. е. количество
электричества, проте­кающее в 1 сек,
через
единицу площади проводника; V
– электри­ческий
потенциал; С
— коэффициент электропроводности
(вели­чина, обратная удельному
сопротивлению).

По закону Кирхгофа,
уравнение сплошности электрического
тока имеет вид:

,

т.
е. оно аналогично уравнению неразрывности
(2.7). Подставим в него значение i
из
системы (6.12). При постоянной
электропро­водности среды C

уравнение
сплош­ности принимает вид:

,

(6.11а)

т
.
е. мы опять получили уравнение Лапласа.

Рис. 56

Таким
образом, электрический потенциал V
аналогичен
потен­циалу скорости φ, удельная
плот­ность электрического тока

– ана­логична скорости течения w.
По­этому,
если область распростране­ния
электрического тока геомет­рически
подобна области течения жидкости, а
граничные условия для V
и φ аналогичны,
интегралы уравнения Лапласа (6. 11) и
(6.11a)
будут отличаться лишь про­извольными
постоянными. Эквипотенциальные
поверхности в элек­трическом поле
V
(х,
у,
z)
= const
в этом случае соответствуют
эк­випотенциальным поверхностям в
потоке жидкости φ (х,
у,
z)
= const,
а силовые линии в электрическом поле
соответствуют ли­ниям тока в жидкости.
Практическое использование этой аналогии
состоит в том, что уравнение Лапласа
решается на установке ЭГДА, а результаты
решения переносятся на поток жидкости.

Для
решения задач плоского потенциального
обтекания сейчас преимущественно
используются модели, в которых в качестве
элек­тропроводного материала
применяется бумага с графитовым
по­крытием. Для измерения потенциалов
в различных точках модели измерительная
цепь собирается по мостовой схеме (рис.
56). По­стоянный или переменный ток от
источника тока подводится к ши­нам
Ш1
и
Ш2.
Параллельно
шинам подключен потенциометр R,
на
скользящем контакте К
которого
можно задавать любые проме­жуточные
значения электрического потенциала
между потенциа­лами шин Ш1
и
Ш2.
Указателем
равновесия моста является гальва­нометр
Г,
включенный
в цепь щупа Щ.
Прикасаясь
щупом Щ
к
какой-либо
точке графитированной бумаги, мы подаем
на щуп элек­трический потенциал данной
точки.

Граничные условия
в моделируемом потоке жидкости таковы:

1. Вдали
   от обтекаемого тела на линиях,
   перпендикулярных

   вектору скорости
   (им соответствуют линии установки шин
   на модели, рис. 56), потенциал скорости
   φ
   сохраняет постоянное значение: φ
   = const.

2. На
   поверхности обтекаемого тела (ей
   соответствует вырезанный участок на
   электропроводной бумаге)
   
   .

Задавая
на потенциометре различные значения
электрического потенциала V,
с помощью
щупа находят на модели точки, принад­лежащие
линиям равного потенциала. В этих точках
ток в цепи щупа равен нулю, стрелка
гальванометра не отклоняется. В этом
состоит «аналогия А», позволяющая
построить эквипотенциали пло­ского
потока.

В
силу взаимной ортогональности функций
скоростного потен­циала φ
и тока ψ на установке ЭГДА можно также
смоделировать течение таким образом,
чтобы линии равного потенциала
электри­ческого поля соответствовали
линиям тока в жидкости, силовые линии
— эквипотенциалям в потоке жидкости.
В этом случае на участок модели,
соответствующий обтекаемому телу,
наклеивается электропроводным клеем
модель сечения тела, вырезанная из
ма­териала, электропроводность
которого во много раз превосходит
электропроводность бумаги. Шины
размещаются по сторонам модели вдоль
потока. Построив с помощью щупа
эквипотенциали элек­трического поля,
мы получим картину линий тока в потоке
жидко­сти. Этот способ получил название
«аналогии B».

Построение
гидродинамической сетки течения методом
ЭГДА осуществляется быстро, не требует
высокой квалификации испол­нителей
или сложного оборудования и в то же
время обеспечивает высокую точность
решения. Этим объясняется его широкое
приме­нение.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Макеты страниц

Потенциал. Разность потенциалов. Напряжение.
Потенциал электростатического поля — скалярная величина, равная отношению потен­циальной энергии заряда в поле к этому заряду:   – энергетическая характеристика поля в данной точке. Потенциал не зависит от величины заряда, помещенного в это поле.
Т.к. потенциальная энергия зависит от выбора системы координат, то и потенциал определяется с точностью до постоянной. За точку отсчета потенциала выбирают в зависимости от задачи: а) потенциал Земли, б) потенциал бесконечно удаленной точки поля, в) потенциал отрицательной пластины конденсатора.
– следствие принци­па суперпозиции полей (потенциалы складываютсяалгебраически).
Потенциал численно равен работе поля по перемещению единичного положительного заряда из данной точки электрического поля в бесконечность. В СИ потенциал измеряется в вольтах:
Разность потенциалов
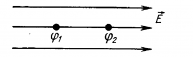
Напряжение — разность значений потенциала в начальной и конечнойточках траектории. Напряжение численно равно работе электростатического поля при перемещении единичного положительного заряда вдоль силовых линий этого поля.          Разность потенциалов (напряжение) не зависит от выбора системы координат!
Единица разности потенциалов    Напряжение равно 1 В, если при перемещении положительного заряда в 1 Кл вдоль силовых линий поле совершает работу в 1 Дж.
Связь между напряженностью и напряжением.
Из доказанного выше:   →      напряженность равна градиенту потенциала (скорости изменения потенциала вдоль направления d).
Из этого соотношения видно: Вектор напряженности направлен в сторону уменьшения потенциала. Электрическое поле существует, если существует разность потенциалов. Единица напряженности:     –   Напряженность поля равна 1 В/м, если между двумя точками поля, находящимися на расстоянии 1 м друг от друга существует разность потенциалов 1 В.
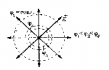
Эквипотенциальные поверхности. ЭПП – поверхности равного потенциала. Свойства ЭПП: – работа при перемещении заряда вдоль эквипотенциальной поверхности не совершается; – вектор напряженности перпендикулярен к ЭПП в каждой ее точке.
Измерение электрического напряжения (разности потенциалов) Между стержнем и корпусом — электрическое поле. Измерение потенциала кондуктора Измерение напряжения на гальваническом элементе Электрометр дает большую точность, чем вольтметр.
Потенциальная энергия взаимодействия зарядов.
Потенциал поля точечного заряда
Потенциал заряженного шара а) Внутри шара Е=0, следовательно, потенциалы во всех точках внутри заряженного металлического шара одинаковы (!!!) и равны потенциалу на поверхности шара. б) Снаружи поле шара убывает обратно пропорционально расстоянию от центра шара, как и в случае точечного заряда.
Перераспределение зарядов при контакте заряженных проводников. Переход зарядов происходит до тех пор, пока потенциалы контактирующих тел не станут равными.

Применим теперь потенциалы Льенара-Вихерта к случаю заряда, движущегося по прямой с постоянной скоростью, и вычислим поле этого заряда. Позже мы повторим этот вывод, используя уже принцип относительности. Мы знаем величину потенциалов в той системе, в которой заряд покоится. Когда заряд движется, то все получается простым релятивистским преобразованием от одной системы к другой. Но теория относительности ведет свое начало от теории электричества и магнетизма. Формулы преобразований Лоренца [см. гл. 15 (вып. 2)]— это открытия, сделанные Лоренцем при исследовании уравнений электричества и магнетизма. И для того чтобы вы понимали, откуда все пошло, я хочу показать вам, что уравнения Максвелла действительно приводят к преобразованиям Лоренца. Я начну с вычисления потенциала равномерно движущегося заряда прямо из электродинамики, из уравнений Максвелла. Мы уже показали, что уравнения Максвелла приводят к потенциалу, полученному в предыдущем параграфе. Стало быть, пользуясь этими потенциалами, мы используем тем самым теорию Максвелла.

Пусть имеется заряд, движущийся вдоль оси х со скоростью v (фиг. 21.8).

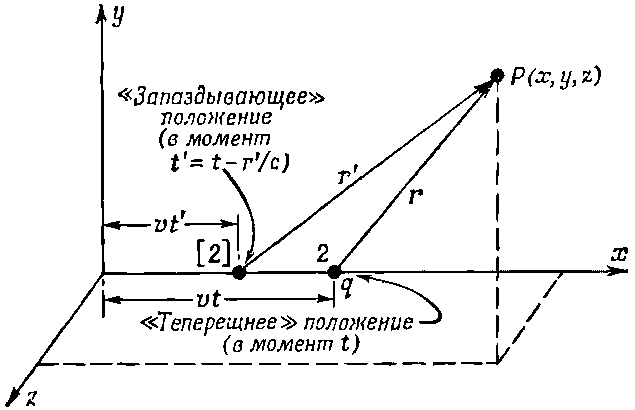
Фиг. 21.8. Определение потенциала в точке Р заряда, движущегося равномерно вдоль оси х.

Нас интересуют потенциалы в точке Р(х, у, z). Если t=0 — момент, в который заряд проходит через начало координат, то в момент t заряд окажется в точке x=vt, y=z=0. А нам нужно знать его положение с учетом запаздывания, т. е. положение в момент

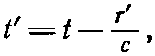(21.35)

где r’ — расстояние от заряда до точки Р в этот запаздывающий момент. В это более раннее время t‘ заряд был в x=vt‘, так что

(21.36)

Чтобы найти r’ или t‘, это уравнение надо сопоставить с (21.35). Исключим сперва r’, решив (21.35) относительно r’ и подставив в (21.36). Возвысив затем обе части в квадрат, получим

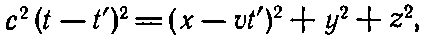
т. е. квадратное уравнение относительно t’. Раскрыв скобки и расположив члены по степеням t‘, получим

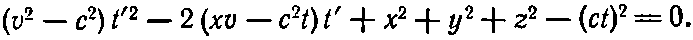
Отсюда найдем

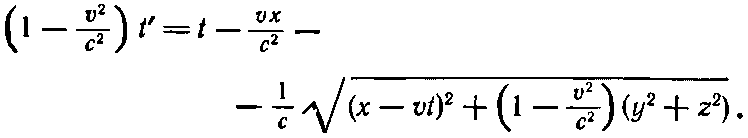(21.37)

Чтобы получить r’, надо это t’ подставить в

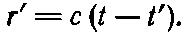
Теперь мы уже можем найти ? из выражения (21.33), имеющего вид

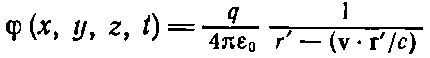(21.38)

(ввиду того, что v постоянно).

Составляющая v в направлении r‘ равна v(x–vt‘)/r‘, так что v·r‘ просто равно v(x–vt‘), а весь знаменатель равен

Подставляя (1-v²/c²)t‘ из (21.37), получаем

Это уравнение становится более понятным, если переписать его в виде

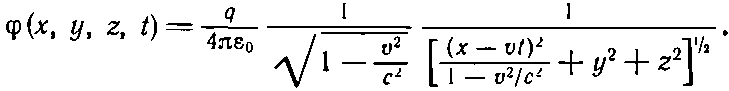(21.39)

Векторный потенциал А — это такое же выражение, но с добавочным множителем v/c²:

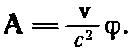
В выражении (21.39) со всей ясностью предстает перед вами начало преобразований Лоренца. Если бы заряд находился в начале координат в своей собственной системе покоя, то его потенциал имел бы вид

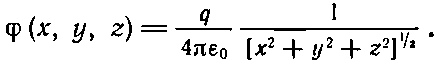
А мы смотрим на него из движущейся системы координат, и нам кажется, что координаты следует преобразовать с помощью формул

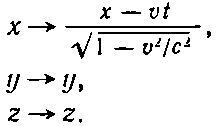
Это обычное преобразование Лоренца. Лоренц вывел его тем же самым способом, каким пользовались и мы.

Но что можно сказать о добавочном множителе 1/?(1-v²/с²), который появился перед дробью в (21.39)? И кроме того, как появляется векторный потенциал А, если он в системе покоя частицы повсюду равен нулю? Мы вскоре покажем, что А и ? вместе составляют четырехвектор, подобно импульсу р и полной энергии U частицы. Добавка 1/?(1—v²/c²) в (21.39)—это тот самый множитель, который появляется всегда, когда преобразуют компоненты четырехвектора, так же как плотность заряда ? преобразуется в ?/?(1-v²/c²). Собственно из формул (21.4) и (21.5) почти очевидно, что А и ? суть компоненты одного четырехвектора, потому что в гл. 13 (вып. 5) уже было показано, что j и ? — компоненты четырехвектора.

Позднее мы более подробно разберем относительность в электродинамике; здесь мы хотели только показать, как естественно уравнения Максвелла приводят к преобразованиям Лоренца. Поэтому не надо удивляться, узнав, что законы электричества и магнетизма уже вполне пригодны и для теории относительности Эйнштейна. Их не нужно даже как-то особо подгонять, как это приходилось делать с ньютоновой механикой.