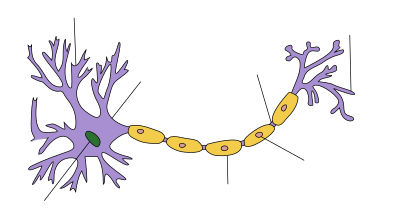
Распространение потенциала действия по аксону
Схематичная иллюстрация передачи нервного импульса вдоль аксона нейрона
Потенциа́л де́йствия («спайк») — волна возбуждения, перемещающаяся по мембране живой клетки в виде кратковременного изменения мембранного потенциала на небольшом участке возбудимой клетки (нейрона или кардиомиоцита), в результате которого наружная поверхность этого участка становится отрицательно заряженной по отношению к внутренней поверхности мембраны, в то время, как в покое она заряжена положительно. Потенциал действия является физиологической основой нервного импульса.
Благодаря работе «натрий-калиевого насоса» концентрация ионов натрия в цитоплазме клетки очень мала по сравнению с окружающей средой. При проведении потенциала действия открываются потенциал-зависимые натриевые каналы и положительно заряженные ионы натрия поступают в цитоплазму по градиенту концентрации, пока он не будет уравновешен положительным электрическим зарядом. Вслед за этим потенциал-зависимые каналы инактивируются и отрицательный потенциал покоя восстанавливается за счёт диффузии из клетки положительно заряженных ионов калия, концентрация которых в окружающей среде также значительно ниже внутриклеточной.
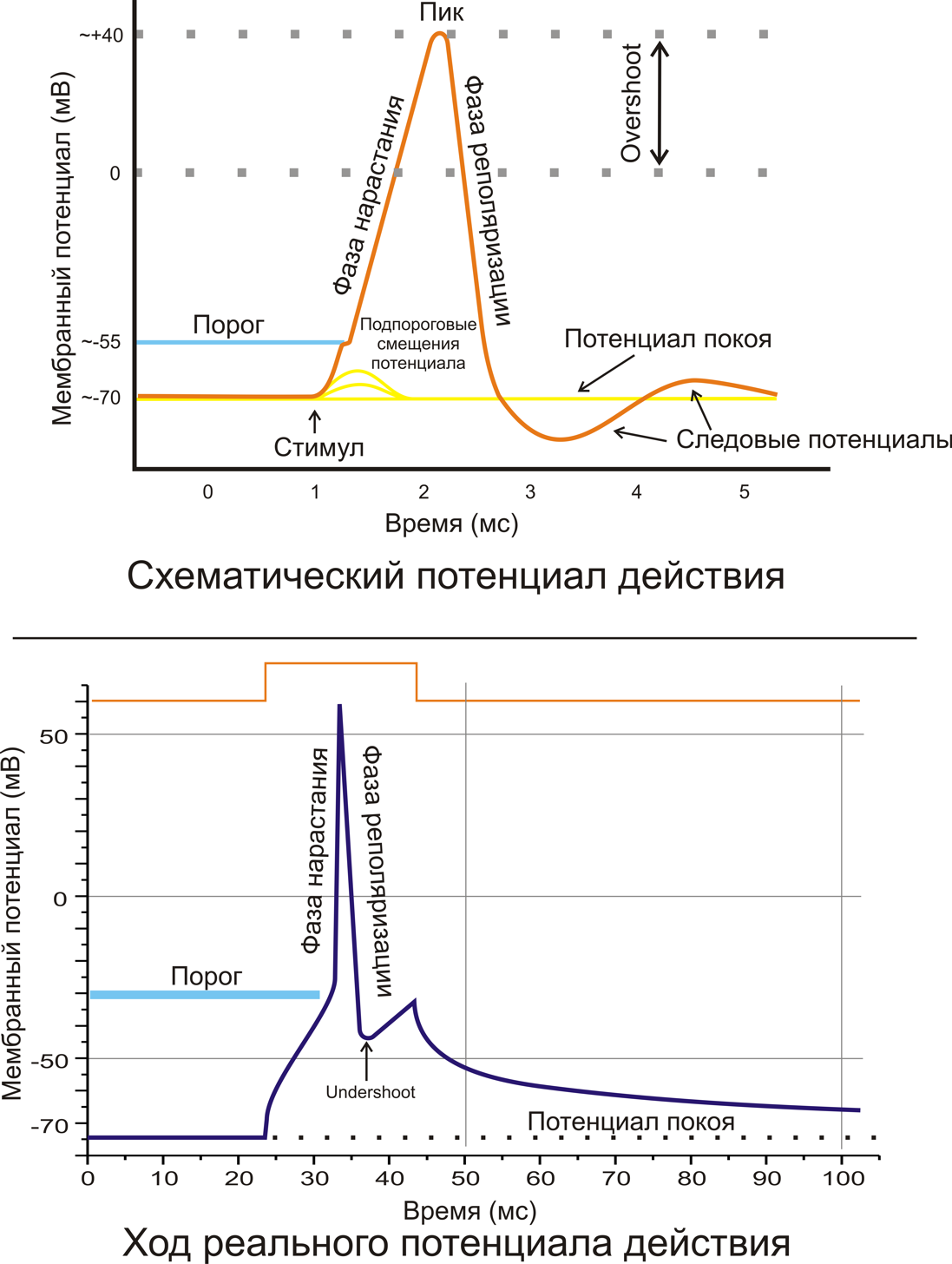
Фазы потенциала действия[править | править код]
- Предспайк — процесс медленной деполяризации мембраны до критического уровня деполяризации (местное возбуждение, локальный ответ).
- Пиковый потенциал, или спайк, состоящий из восходящей части (деполяризация мембраны) и нисходящей части (реполяризация мембраны).
- Отрицательный следовой потенциал — от критического уровня деполяризации до исходного уровня поляризации мембраны (следовая деполяризация).
- Положительный следовой потенциал — увеличение мембранного потенциала и постепенное возвращение его к исходной величине (следовая гиперполяризация).
Общие положения[править | править код]
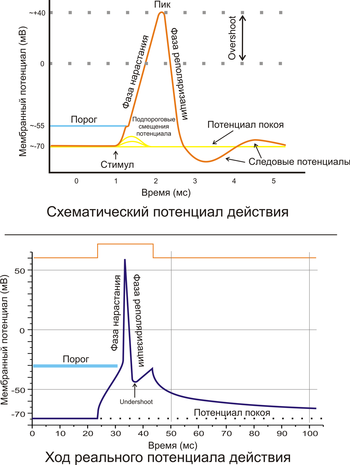
Рис. 2. A. Схематичное изображение идеализированного потенциала действия. B. Реальный потенциал действия пирамидного нейрона гиппокампа крысы. Форма реального потенциала действия обычно отличается от идеализированной.
Поляризация мембраны живой клетки обусловлена отличием ионного состава с её внутренней и наружной стороны. Когда клетка находится в спокойном (невозбуждённом) состоянии, ионы по разные стороны мембраны создают относительно стабильную разность потенциалов, называемую потенциалом покоя. Если ввести внутрь живой клетки электрод и измерить мембранный потенциал покоя, он будет иметь отрицательное значение (около −70 — −90 мВ). Это объясняется тем, что суммарный заряд на внутренней стороне мембраны существенно меньше, чем на внешней, хотя с обеих сторон содержатся и катионы, и анионы. Снаружи — на порядок больше ионов натрия, кальция и хлора, внутри — ионов калия и отрицательно заряженных белковых молекул, аминокислот, органических кислот, фосфатов, сульфатов. Надо понимать, что речь идёт именно о заряде поверхности мембраны — в целом среда и внутри, и снаружи клетки заряжена нейтрально.
Потенциал мембраны может изменяться под действием различных стимулов. Искусственным стимулом может служить электрический ток, подаваемый на внешнюю или внутреннюю сторону мембраны через электрод. В естественных условиях стимулом часто служит химический сигнал от соседних клеток, поступающий через синапс или путём диффузной передачи через межклеточную среду. Смещение мембранного потенциала может происходить в отрицательную (гиперполяризация) или положительную (деполяризация) сторону.
В нервной ткани потенциал действия, как правило, возникает при деполяризации — если деполяризация мембраны нейрона достигает некоторого порогового уровня или превышает его, клетка возбуждается, и от её тела к аксонам и дендритам распространяется волна электрического сигнала. (В реальных условиях на теле нейрона обычно возникают постсинаптические потенциалы, которые сильно отличаются от потенциала действия по своей природе — например, они не подчиняются принципу «всё или ничего». Эти потенциалы преобразуются в потенциал действия на особом немиелинезированном участке аксона — его начальном сегменте, и затем обратно распространяется на сому нейрона и дендриты.

Рис. 3. Простейшая схема, демонстрирующая мембрану с двумя натриевыми каналами в открытом и закрытом состоянии
Это обусловлено тем, что на мембране клетки находятся ионные каналы — белковые молекулы, образующие в мембране поры, через которые ионы могут проходить с внутренней стороны мембраны на наружную и наоборот. Большинство каналов ионо-специфичны — натриевый канал пропускает практически только ионы натрия и не пропускает другие (это явление называют селективностью). Мембрана клеток возбудимых тканей (нервной и мышечной) содержит большое количество потенциал-зависимых ионных каналов, способных быстро реагировать на смещение мембранного потенциала. Деполяризация мембраны в первую очередь вызывает открытие потенциал-зависимых натриевых каналов. Когда одновременно открывается достаточно много натриевых каналов, положительно заряженные ионы натрия устремляются через них на внутреннюю сторону мембраны. Движущая сила в данном случае обеспечивается градиентом концентрации (с внешней стороны мембраны находится намного больше положительно заряженных ионов натрия, чем внутри клетки) и отрицательным зарядом внутренней стороны мембраны (см. Рис. 2).
Поток ионов натрия вызывает ещё бо́льшее и очень быстрое изменение мембранного потенциала, которое и называют потенциалом действия (в специальной литературе обозначается ПД).
Согласно закону «всё-или-ничего» мембрана клетки возбудимой ткани либо не отвечает на стимул совсем, либо отвечает с максимально возможной для неё на данный момент силой. То есть, если стимул слишком слаб и порог не достигнут, потенциал действия не возникает совсем; в то же время, пороговый стимул вызовет потенциал действия такой же амплитуды, как и стимул, превышающий пороговый. Это отнюдь не означает, что амплитуда потенциала действия всегда одинакова — один и тот же участок мембраны, находясь в разных состояниях, может генерировать потенциалы действия разной амплитуды.
После возбуждения нейрон на некоторое время оказывается в состоянии абсолютной рефрактерности, когда никакие сигналы не могут его возбудить снова, затем входит в фазу относительной рефрактерности, когда его могут возбудить исключительно сильные сигналы (при этом амплитуда ПД будет ниже, чем обычно). Рефрактерный период возникает из-за инактивации быстрого натриевого тока, то есть инактивации натриевых каналов (см. ниже).
Распространение потенциала действия[править | править код]
По немиелинизированным волокнам[править | править код]
По немиелинизированному волокну потенциал действия распространяется непрерывно. Проведение нервного импульса начинается с распространением электрического поля. Возникший потенциал действия за счет электрического поля способен деполяризовать мембрану соседнего участка до критического уровня, в результате чего на соседнем участке генерируются новые потенциалы. Сам потенциал действия не перемещается, он исчезает там же, где возник. Главную роль в возникновении нового потенциал действия играет предыдущий.
Если внутриклеточным электродом раздражать аксон посередине, то потенциал действия будет распространяться в обоих направлениях. Обычно же потенциал действия распространяется по аксону в одном направлении (от тела нейрона к нервным окончаниям), хотя деполяризация мембраны происходит по обе стороны от участка, где в данный момент возник потенциал. Одностороннее проведение потенциала действия обеспечивается свойствами натриевых каналов — после открытия они на некоторое время инактивируются и не могут открыться ни при каких значениях мембранного потенциала (свойство рефрактерности). Поэтому на ближнем к телу клетки участке, где до этого уже «прошел» потенциал действия, он не возникает.
При прочих равных условиях распространение потенциала действия по аксону происходит тем быстрее, чем больше диаметр волокна. По гигантским аксонам кальмара потенциал действия может распространяться почти с такой же скоростью, как и по миелинизированным волокнам позвоночных (около 100 м/c).
По миелинизированным волокнам[править | править код]
По миелинизированному волокну потенциал действия распространяется скачкообразно (сальтаторное проведение). Для миелинизированных волокон характерна концентрация потенциалзависимых ионных каналов только в областях перехватов Ранвье; здесь их плотность в 100 раз больше, чем в мембранах безмиелиновых волокон. В области миелиновых муфт потенциалзависимых каналов почти нет. Потенциал действия, возникший в одном перехвате Ранвье, за счет электрического поля деполяризует мембрану соседних перехватов до критического уровня, что приводит к возникновению в них новых потенциалов действия, то есть возбуждение переходит скачкообразно, от одного перехвата к другому. В случае повреждения одного перехвата Ранвье потенциал действия возбуждает 2-й, 3-й, 4-й и даже 5-й, поскольку электроизоляция, создаваемая миелиновыми муфтами, уменьшает рассеивание электрического поля.
«Скачкообразное распространение» увеличивает скорость распространения потенциала действия по миелинизированным волокнам по сравнению с немиелинизированными. Кроме того, миелинизированные волокна толще, а электрическое сопротивление более толстых волокон меньше, что тоже увеличивает скорость проведения импульса по миелинизированным волокнам. Другим преимуществом сальтаторного проведения является его экономичность в энергетическом плане, так как возбуждаются только перехваты Ранвье, площадь которых меньше 1 % мембраны, и, следовательно, необходимо значительно меньше энергии для восстановления трансмембранных градиентов Na+ и K+, расходующихся в результате возникновения потенциал действия, что может иметь значение при высокой частоте разрядов, идущих по нервному волокну.
Чтобы представить, насколько эффективно может быть увеличена скорость проведения за счёт миелиновой оболочки, достаточно сравнить скорость распространения импульса по немиелинизированным и миелинизированным участкам нервной системы человека. При диаметре волокна около 2 µм и отсутствии миелиновой оболочки скорость проведения будет составлять ~1 м/с, а при наличии даже слабой миелинизации при том же диаметре волокна — 15—20 м/с. В волокнах большего диаметра, обладающих толстой миелинововой оболочкой, скорость проведения может достигать 120 м/с.
Скорость распространения потенциала действия по мембране отдельно взятого нервного волокна непостоянна — в зависимости от различных условий эта скорость может очень значительно уменьшаться и, соответственно, увеличиваться, возвращаясь к некоему исходному уровню.
В сердце[править | править код]
Активные свойства мембраны[править | править код]
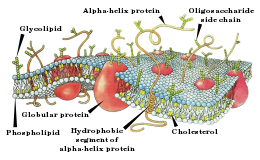
Схема строения мембраны клетки.
Активные свойства мембраны, обеспечивающие возникновение потенциала действия, основываются главным образом на поведении потенциалзависимых натриевых (Na+-) и калиевых (K+-) каналов. Начальная фаза ПД формируется входящим натриевым током, позже открываются калиевые каналы и выходящий K+-ток возвращает потенциал мембраны к исходному уровню. Исходную концентрацию ионов затем восстанавливает натрий-калиевый насос.
По ходу ПД каналы переходят из состояния в состояние: у Na+-каналов основных состояний три — закрытое, открытое и инактивированное (в реальности дело сложнее, но этих трёх достаточно для описания), у K+-каналов два — закрытое и открытое.
Поведение каналов, участвующих в формировании ПД, описывается через проводимость и вычисляется через коэффициенты переноса (трансфера).
Коэффициенты переноса были выведены Ходжкином и Хаксли.[1][2]
- Проводимость для калия GK на единицу площади [S/cm²]
 , ,
|
| где: |
 — коэффициент трансфера из закрытого в открытое состояние для K+-каналов [1/s]; — коэффициент трансфера из закрытого в открытое состояние для K+-каналов [1/s];
|
 — коэффициент трансфера из открытого в закрытое состояние для K+-каналов [1/s]; — коэффициент трансфера из открытого в закрытое состояние для K+-каналов [1/s];
|
 — доля K+-каналов в открытом состоянии; — доля K+-каналов в открытом состоянии;
|
 — доля K+-каналов в закрытом состоянии — доля K+-каналов в закрытом состоянии
|
- Проводимость для натрия GNa на единицу площади [S/cm²]
рассчитывается сложнее, поскольку, как уже было сказано, у потенциал-зависимых Na+-каналов, помимо закрытого/открытого состояний, переход между которыми описывается параметром 

 , ,
|
 , ,
|
| где: | где: |
 — коэффициент трансфера из закрытого в открытое состояние для Na+-каналов [1/s]; — коэффициент трансфера из закрытого в открытое состояние для Na+-каналов [1/s];
|
 — коэффициент трансфера из инактивированного в не-инактивированное состояние для Na+-каналов [1/s]; — коэффициент трансфера из инактивированного в не-инактивированное состояние для Na+-каналов [1/s];
|
 — коэффициент трансфера из открытого в закрытое состояние для Na+-каналов [1/s]; — коэффициент трансфера из открытого в закрытое состояние для Na+-каналов [1/s];
|
 — коэффициент трансфера из не-инактивированного в инактивированное состояние для Na+-каналов [1/s]; — коэффициент трансфера из не-инактивированного в инактивированное состояние для Na+-каналов [1/s];
|
 — доля Na+-каналов в открытом состоянии; — доля Na+-каналов в открытом состоянии;
|
 — доля Na+-каналов в не-инактивированном состоянии; — доля Na+-каналов в не-инактивированном состоянии;
|
 — доля Na+-каналов в закрытом состоянии — доля Na+-каналов в закрытом состоянии
|
 — доля Na+-каналов в инактивированном состоянии. — доля Na+-каналов в инактивированном состоянии.
|
См. также[править | править код]
- Дендритный потенциал действия
- Потенциал покоя
- Электрический потенциал мозга
- Шванновские клетки
Литература[править | править код]
- ↑ Hodgkin A.L., Huxley A.F. (1952). A quantitative description of membrane current and its application to conduction and excitation in nerve Архивная копия от 28 апреля 2019 на Wayback Machine. J. Physiol. (Lond.) 117: 500—544. PMID 12991237 (англ.)
- ↑ J.Malmivuo, R.Plonsey. Bioelectromagnetism Архивная копия от 30 июля 2017 на Wayback Machine. Oxford University Press. New York, Oxford. 1995. (англ.)
Потенциал
действия (ПД) –
это электрофизиологический процесс,
выражающийся в быстром колебании
мембранного потенциала вследствие
перемещения ионов в клетку и из клетки
и способный распространяться
без декремента (без
затухания). ПД
обеспечивает передачу сигналов между
нервными
клетками, нервными центрами и рабочими
органами; в мышцах ПД
обеспечивает процесс электромеханического
сопряжения.
А.
Характеристика
потенциала действия (ПД). Схематично
ПД представлен на рис. 1.3. Величина ПД
колеблется в пределах 80-130 мВ,
длительность пика ПД нервного волокна
0,5-1 мс, волокна скелетной мышцы – до 10
мс с учетом замедле-
14
15

ния
деполяризации в конце ее. Длительность
ПД сердечной мышцы,, 300-400
мс. Амплитуда ПД не зависит от силы
раздражения – она всегда
максимальна для данной клетки в конкретных
условиях: ПД подчиняется
закону «все или ничего», но не подчиняется
закону силовых отношений – закону силы.
ПД либо совсем не возникает при раздражении
клетки, если оно мало, либо возникает и
достигает максимальной величины,
если раздражение является пороговым
или сверхпороговым. Следует отметить,
что слабое (подпороговое) раздражение
может вызвать локальный
потенциал. Он
подчиняется закону силы – с увеличением
силы стимула величина его возрастает.
В составе ПД различают четыре фазы: 1 —
деполяризация,
т. е. исчезновение заряда клетки –
уменьшение мембранного потенциала до
нуля; 2 — инверсия, т. е. изменение заряда
клетки на противоположный, когда
внутренняя сторона мембраны клетки
заряжается положительно, а внешняя –
отрицательно (лат. шуегзю – переворачивание);
3 — реполяризация, т. е. восстановление
исходного заряда клетки, когда внутренняя
поверхность клеточной мембраны снова
заряжается отрицательно, а наружная
-положительно; 4 – следовая гиперполяризация.
Б.
Механизм
возникновения ПД. Если
действие раздражителя на клеточную
мембрану приводит к началу развития
ПД, далее сам процесс развития ПД
вызывает фазовые изменения проницаемости
клеточной мембраны, что обеспечивает
быстрое
16
движение
№+
в клетку, а К+
– из клетки. Это наиболее часто встречаемый
вариант возникновения ПД. Величина
мембранного потенциала
при этом сначала уменьшается, а затем
снова восстанавливается до исходного
уровня. На экране осциллографа отмеченные
изменения
мембранного потенциала предстают в
виде пикового потенциала
– ПД. Он возникает вследствие накопленных
и поддерживаемых
ионными насосами градиентов концентраций
ионов внутри
и вне клетки, т.е. за счет потенциальной
энергии в виде электрохимических
градиентов ионов. Если заблокировать
процесс выработки
энергии, потенциалы действия некоторый
период времени будут возникать. Но
после исчезновения градиентов
концентраций ионов (устранения
потенциальной энергии) клетка генерировать
ПД не будет. Рассмотрим фазы ПД.
1.
Фаза
деполяризации (см.
рис. 1.3 – 1). При действии деполяризующего
раздражителя на клетку (медиатор,
электрический ток)
начальная частичная деполяризация
клеточной мембраны происходит без
изменения ее проницаемости для ионов.
Когда деполяризация
достигает примерно 50% пороговой величины
(50% порогового потенциала), начинает
повышаться проницаемость мембраны
клетки для Ыа+,
причем в первый момент сравнительно
медленно. Естественно, что скорость
входа Ыа+
в клетку при этом невелика. В этот период,
как и во время всей первой фазы
(деполяризации), движущей
силой, обеспечивающей
вход Гч!а+
в клетку, являются
концентрационный и электрический
градиенты. Напомним, что клетка внутри
заряжена отрицательно (разноименные
заряды притягиваются друг к другу),
а концентрация №+
вне клетки в 10-12 раз больше, чем внутри
клетки. Условием,
обеспечивающим
вход №+
в клетку, является увеличение проницаемости
клеточной
мембраны, которая определяется состоянием
воротного механизма
Ыа-каналов (в некоторых клетках, например,
в кардиомиоцитах, в волокнах гладкой
мышцы, важную роль в возникновении
ПД играют и управляемые каналы для
Са2+).
Когда
деполяризация клетки достигает
критической величины (Е , критический
уровень деполяризации – КУД), которая
обычно составляет 50 мВ (возможны и другие
величины), проницаемость мембраны для
Ыа* резко возрастает – открывается
большое число потенциалзависимых
ворот Ыа-каналов – и Ыа+
лавиной устремляется
в клетку. В результате интенсивного
тока Ыа+
внутрь клетки процесс деполяризации
проходит очень быстро. Развивающаяся
деполяризация клеточной мембраны
вызывает дополнительное
увеличение
ее проницаемости и, естественно,
проводимости Ыа+
-открываются
все новые и новые ворота №-каналов, что
придает току Ыа+
в клетку характер регенеративного
процесса. В
итоге ПП
17
исчезает,
становится равным нулю. Фаза деполяризации
на этом заканчивается.
2.
Фаза
инверсии. После
исчезновения ПП вход Ыа+
в клетку продолжается, поэтому число
положительных ионов в клетке превосходит
число отрицательных ионов, заряд внутри
клетки становится положительным,
снаружи – отрицательным. Процесс
перезарядки мембраны представляет
собой вторую фазу потенциала действия
– фазу инверсии (рис. 1.3 – 2). Теперь
электрический градиент препятствует
входу Ыа+
внутрь клетки (положительные заряды
отталкиваются друг от друга),
Ыа-проводимость снижается.
Тем не менее, некоторый период времени
(доли миллисекунды) №+
продолжает входить в клетку — об этом
свидетельствует продолжающееся
нарастание ПД. Это означает, что
концентрационный градиент,
обеспечивающий движение №+
в клетку, сильнее электрического,
препятствующего входу Ыа+
в клетку. Во время деполяризации мембраны
увеличивается проницаемость ее и для
Са2+,
он также идет в клетку, но в нервных
волокнах, нейронах и в клетках
скелетной мускулатуры роль Са2+
в развитии ПД мал.а. В клетках гладкой
мышцы и миокарда его роль существенна.
Таким
образом, вся восходящая часть пика ПД
в большинстве случаев
обеспечивается в основном входом №+
в клетку.
Примерно
через 0,5-1 мс и более после начала
деполяризации (это время зависит от
вида клетки) рост ПД прекращается
вследствие
закрытия ворот натриевых каналов и
открытия ворот К-кана-лов, т. е. увеличения
проницаемости для К+
и резкого возрастания выхода
его из клетки (см. рис. 1.3 – 2). Препятствуют
также росту пика
ПД электрический градиент Ыа+
(клетка внутри в этот момент заряжена
положительно), а также выход К+
из клетки по каналам утечки.
Поскольку К+
находится преимущественно внутри
клетки, он,
согласно концентрационному градиенту,
быстро выходит из клетки после открытия
ворот К+-каналов,
вследствие чего уменьшается число
положительно заряженных ионов в клетке.
Заряд клетки снова начинает уменьшаться.
В фазу инверсии выходу К+
из
клетки способствует также и электрический
градиент. К+
выталкивается положительным зарядом
из клетки и притягивается отрицательным
зарядом снаружи клетки. Так продолжается
до полного
исчезновения положительного заряда
внутри клетки (до конца фазы инверсии
– рис. 1.3-2,
пунктирная линия), когда начинается
следующая фаза ПД – фаза реполяризации.
Калий выходит из клетки не только по
управляемым каналам, ворота которых
открыты, но и по неуправляемым –
каналам утечки, что несколько замедляет
ход восходящей части ПД и ускоряет ход
нисходящей составляющей ПД.
Таким
образом, изменение мембранного потенциала
покоя ведет к последовательному
открытию и закрытию электроуправляе-мых
ворот ионных каналов и движению ионов
согласно электрохимическому
градиенту – возникновению ПД. Все фазы
являются регенеративными
– необходимо только достичь критического
уровня
деполяризации, далее ПД развивается
за счет потенциальной энергии
клетки в виде электрохимических
градиентов, т. е. вторично
активно.
Амплитуда
ПД складывается из величины ПП
(мембранного потенциала покоящейся
клетки) и величины фазы инверсии,
составляющей у разных клеток 10-50 мВ.
Если
мембранный потенциал покоящейся клетки
мал, амплитуда ПД этой клетки небольшая.
3.
Фаза
реполяризации (рис.
1.3-3)
связана с тем, что проницаемость
клеточной мембраны для К+
все еще высока (ворота
калиевых каналов открыты), К+
продолжает быстро выходить из
клетки, согласно концентрационному
градиенту. Поскольку клетка теперь уже
снова внутри имеет отрицательный заряд,
а снаружи – положительный (см. рис.
1.3 – 3), электрический градиент
препятствует выходу К+
из клетки, что снижает его проводимость,
хотя он продолжает выходить. Это
объясняется тем, что действие
концентрационного градиента выражено
значительно сильнее электрического
градиента. Вся нисходящая часть пика
ПД обусловлена выходом К+
из клетки. Нередко в конце ПД наблюдается
замедление реполяризации, что объясняется
уменьшением проницаемости клеточной
мембраны для К+
и замедлением выхода его из клетки
из-за частичного закрытия ворот
К-каналов. Вторая причина замедления
тока К+
из клетки связана с возрастанием
положительного потенциала наружной
поверхности клетки и формированием
противоположно направленного
электрического градиента.
Таким
образом, главную
роль в возникновении ПД играет Ыа+,
входящий
в клетку при повышении проницаемости
клеточной мембраны и обеспечивающий
всю восходящую часть пика ПД.
При замене Ма+
в среде на другой ион, например холин,
ПД в нервной
и мышечной клетках скелетной мускулатуры
не возникает. Однако проницаемость
мембраны для К+
тоже играет важную роль. Если повышение
проницаемости для К+
предотвратить тетраэтиламмонием,
мембрана после ее деполяризации
реполя-ризуется гораздо медленнее,
только за счет медленных неуправляемых
каналов (каналов утечки ионов), через
которые К+
будет выходить из клетки.
18
19

Роль
Са2+
в
возникновении ПД в нервных и мышечных
клетках скелетной мускулатуры
незначительна. Однако Са2+
играет важную роль в возникновении ПД
сердечной и гладкой мышц, в передаче
импульсов от одного нейрона к другому,
от нервного волокна
к мышечному, в обеспечении мышечного
сокращения.
4.
Следовая
гиперполяризация клеточной
мембраны (рис. 1.3 -4) обычно является
следствием еще сохраняющейся повышенной
проницаемости клеточной мембраны для
К+,
она характерна для нейронов. Ворота
К-каналов еще не полностью закрыты,
поэтому К+
продолжает выходить из клетки согласно
концентрационному градиенту, что и
ведет к гиперполяризации клеточной
мембраны. Постепенно проницаемость
клеточной мембраны возвращается к
исходной
(натриевые и калиевые ворота возвращаются
в исходное состояние),
а мембранный потенциал становится таким
же, каким он был до возбуждения клетки.
Ыа/
К-помпа непосредственно за фазы потенциала
действия не отвечает, хотя
она и продолжает работать во время
развития ПД.
Следовая
деполяризация также
характерна для нейронов, она может быть
зарегистрирована и в клетках скелетной
мышцы. Механизм ее изучен недостаточно.
Возможно, это связано с кратковременным
повышением проницаемости клеточной
мембраны для Ыа+
и входом его в клетку согласно
концентрационному и электрическому
градиентам.
В.
Запас
ионов в клетке, обеспечивающих
возникновение возбуждения (ПД), огромен.
Концентрационные градиенты ионов в
результате одного цикла возбуждения
практически не изменяются. Клетка
может возбуждаться до 5105
раз без подзарядки, то
есть без работы Ыа/К-насоса. Число
импульсов, которое генерирует
и проводит нервное волокно, зависит от
его толщины, что определяет
запас ионов. Чем толще нервное волокно,
тем больше запас ионов и больше импульсов
оно может генерировать (от нескольких
сот до нескольких сотен тысяч) без
участия №/К-насо-са. Однако в тонких
С-волокнах на возникновение одного ПД
расходуется
около 1 % концентрационных градиентов
№+и
К+.
Таким образом,
если заблокировать выработку энергии,
то клетка будет еще многократно
возбуждаться и в этом случае. В реальной
же действительности Ыа/К-насос постоянно
переносит Ыа+
из клетки, а К+
возвращает в клетку, в результате
постоянно поддерживается концентрационный
градиент №+
и К+,
что осуществляется
за счет непосредственного расхода
энергии, источником которой является
АТФ.
20
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Потенциал действия — волна возбуждения, перемещающаяся по мембране живой клетки в процессе передачи нервного сигнала. По сути своей представляет электрический разряд — быстрое кратковременное изменение потенциала на небольшом участке мембраны возбудимой клетки (нейрона, мышечного волокна или железистой клетки), в результате которого наружная поверхность этого участка становится отрицательно заряженной по отношению к соседним участкам мембраны, тогда как его внутренняя поверхность становится положительно заряженной по отношению к соседним участкам мембраны. Потенциал действия является физической основой нервного или мышечногоимпульса, играющего сигнальную (регуляторную) роль.
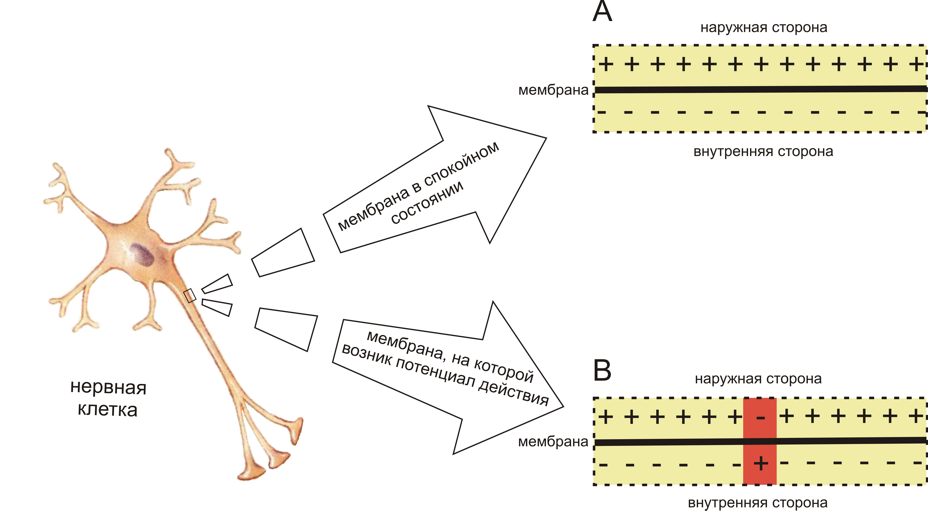
Рис. 1. Схема распределения зарядов по разные стороны мембраны возбудимой клетки в спокойном состоянии (A) и при возникновении потенциала действия (B) (см. объяснения в тексте)
Потенциалы действия могут различаться по своим параметрам в зависимости от типа клетки и даже на различных участках мембраны одной и той же клетки. Наиболее характерный пример различий: потенциал действия сердечной мышцыи потенциал действия большинства нейронов. Тем не менее, в основе любого потенциала действия лежат следующие явления:
- Мембрана живой клетки поляризована — её внутренняя поверхность заряжена отрицательно по отношению к внешней благодаря тому, что в растворе возле её внешней поверхности находится бо́льшее количество положительно заряженных частиц (катионов), а возле внутренней поверхности — бо́льшее количество отрицательно заряженных частиц (анионов).
- Мембрана обладает избирательной проницаемостью — её проницаемость для различных частиц (атомов или молекул) зависит от их размеров, электрического заряда и химических свойств.
- Мембрана возбудимой клетки способна быстро менять свою проницаемостъ для определённого вида катионов, вызывая переход положительного заряда с внешней стороны на внутреннюю (Рис.1).
Первые два свойства характерны для всех живых клеток. Третье же является особенностью клеток возбудимых тканей и причиной, по которой их мембраны способны генерировать и проводить потенциалы действия.
- Фазы потенциала действия
- Предспайк — процесс медленной деполяризации мембраны до критического уровня деполяризации (местное возбуждение, локальный ответ).
- Пиковый потенциал, или спайк, состоящий из восходящей части (деполяризация мембраны) и нисходящей части (реполяризация мембраны).
- Отрицательный следовой потенциал — от критического уровня деполяризации до исходного уровня поляризации мембраны (следовая деполяризация).
- Положительный следовой потенциал — увеличение мембранного потенциала и постепенное возвращение его к исходной величине (следовая гиперполяризация).
Общие положения
Поляризация мембраны живой клетки обусловлена отличием ионного состава с её внутренней и наружной стороны. Когда клетка находится в спокойном (невозбуждённом) состоянии, ионы по разные стороны мембраны создают относительно стабильную разность потенциалов, называемую потенциалом покоя. Если ввести внутрь живой клетки электрод и измерить мембранный потенциал покоя, он будет иметь отрицательное значение (порядка −70 — −90 мВ). Это объясняется тем, что суммарный заряд на внутренней стороне мембраны существенно меньше, чем на внешней, хотя с обеих сторон содержатся и катионы, и анионы. Снаружи — на порядок больше ионов натрия, кальция и хлора, внутри — ионов калия и отрицательно заряженных белковыхмолекул, аминокислот, органических кислот, фосфатов, сульфатов. Надо понимать, что речь идёт именно о заряде поверхности мембраны — в целом среда и внутри, и снаружи клетки заряжена нейтрально.
Потенциал мембраны может изменяться под действием различных стимулов. Искусственным стимулом может служить электрический ток, подаваемый на внешнюю или внутреннюю сторону мембраны через электрод. В естественных условиях стимулом часто служит химический сигнал от соседних клеток, поступающий черезсинапс или путём диффузной передачи через межклеточную среду. Смещение мембранного потенциала может происходить в отрицательную (гиперполяризация) или положительную (деполяризация) сторону.
В нервной ткани потенциал действия, как правило, возникает при деполяризации — если деполяризация мембраны нейрона достигает некоторого порогового уровня или превышает его, клетка возбуждается, и от её тела к аксонам и дендритам распространяется волна электрического сигнала. (В реальных условиях на теле нейрона обычно возникают постсинаптические потенциалы, которые сильно отличаются от потенциала действия по своей природе — например, они не подчиняются принципу «всё или ничего». Эти потенциалы преобразуются в потенциал действия на особом участке мембраны — аксонном холмике, так что потенциал действия не распространяется на дендриты).
Это обусловлено тем, что на мембране клетки находятся ионные каналы — белковые молекулы, образующие в мембране поры, через которые ионы могут проходить с внутренней стороны мембраны на наружную и наоборот. Большинство каналов ионоспецифичны — натриевый канал пропускает практически только ионы натрия и не пропускает другие (это явление называют селективностью). Мембрана клеток возбудимых тканей (нервной и мышечной) содержит большое количество потенциал-зависимых ионных каналов, способных быстро реагировать на смещение мембранного потенциала. Деполяризация мембраны в первую очередь вызывает открытие потенциал-зависимых натриевых каналов. Когда одновременно открывается достаточно много натриевых каналов, положительно заряженные ионы натрия устремляются через них на внутреннюю сторону мембраны. Движущая сила в данном случае обеспечивается градиентом концентрации (с внешней стороны мембраны находится намного больше положительно заряженных ионов натрия, чем внутри клетки) и отрицательным зарядом внутренней стороны мембраны (см. Рис. 2). Поток ионов натрия вызывает ещё бо́льшее и очень быстрое изменение мембранного потенциала, которое и называют потенциалом действия (в специальной литературе обозначается ПД).
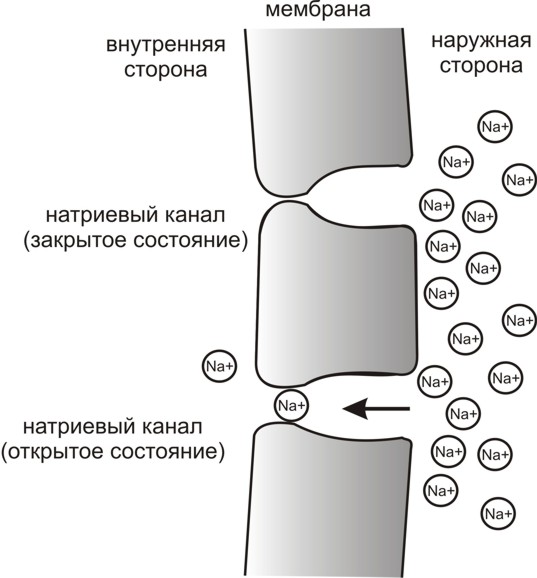
Рис. 3. Простейшая схема, демонстрирующая мембрану с двумя натриевыми каналами в открытом и закрытом состоянии, соответственно
Согласно закону «всё-или-ничего» мембрана клетки возбудимой ткани либо не отвечает на стимул совсем, либо отвечает с максимально возможной для неё на данный момент силой. То есть, если стимул слишком слаб и порог не достигнут, потенциал действия не возникает совсем; в то же время, пороговый стимул вызовет потенциал действия такой же амплитуды, как и стимул, превышающий пороговый. Это отнюдь не означает, что амплитуда потенциала действия всегда одинакова — один и тот же участок мембраны, находясь в разных состояниях, может генерировать потенциалы действия разной амплитуды.
После возбуждения нейрон на некоторое время оказывается в состоянии абсолютной рефрактерности, когда никакие сигналы не могут его возбудить снова, затем входит в фазу относительной рефрактерности, когда его могут возбудить исключительно сильные сигналы (при этом амплитуда ПД будет ниже, чем обычно). Рефрактерный период возникает из-за инактивации быстрого натриевого тока, то есть инактивации натриевых каналов (см. ниже).
Распространение потенциала действия
Распространение потенциала действия по немиелинизированным волокнам
По немиелинизированному волокну ПД распространяется непрерывно. Проведение нервного импульса начинается с распространением электрического поля. Возникший ПД за счет электрического поля способен деполяризовать мембрану соседнего участка до критического уровня, в результате чего на соседнем участке генерируются новые ПД. Сами ПД не перемещаются, они исчезают там же, где возникают. Главную роль в возникновении нового ПД играет предыдущий.
Если внутриклеточным электродом раздражать аксон посередине, то ПД будет распространяться в обоих направлениях. Обычно же ПД распространяется по аксону в одном направлении (от тела нейрона к нервным окончаниям), хотя деполяризация мембраны происходит по обе стороны от участка, где в данный момент возник ПД. Одностороннее проведение ПД обеспечивается свойствами натриевых каналов — после открывания они на некоторое время инактивируются и не могут открыться ни при каких значениях мембранного потенциала (свойство рефрактерности). Поэтому на ближнем к телу клетки участке, где до этого уже «прошел» ПД, он не возникает.
При прочих равных условиях распространение ПД по аксону происходит тем быстрее, чем больше диаметр волокна. По гигантским аксонам кальмара ПД может распространяться почти с такой же скоростью, как и по миелинизированным волокнам позвоночных (около 100 м/c).
Распространение потенциала действия по миелинизированным волокнам
По миелинизированному волокну ПД распространяется скачкообразно (сальтаторное проведение). Для миелинизированных волокон характерна концентрация потенциалзависимых ионных каналов только в областях перехватов Ранвье; здесь их плотность в 100 раз больше, чем в мембранах безмиелиновых волокон. В области миелиновых муфт потенциалзависимых каналов почти нет. ПД, возникший в одном перехвате Ранвье, за счет электрического поля деполяризует мембрану соседних перехватов до критического уровня, что приводит к возникновению в них новых ПД, то есть возбуждение переходит скачкообразно, от одного перехвата к другому. В случае повреждения одного перехвата Ранвье ПД возбуждает 2-ой, 3-ий, 4-ый и даже 5-ый, поскольку электроизоляция, создаваемая миелиновыми муфтами, уменьшает рассеивание электрического поля. Это увеличивает скорость распространения ПД по миелинизированным волокнам по сравнению с немиелинизированными. Кроме того, миелинизированные волокна толще, а электрическое сопротивление более толстых волокон меньше, что тоже увеличивает скорость проведения импульса по миелинизированным волокнам. Другим преимуществом сальтаторного проведения является его экономичность в энергетическом плане, так как возбуждаются только перехваты Ранвье, площадь которых меньше 1 % мембраны, и, следовательно, необходимо значительно меньше энергии для восстановления трансмембранных градиентов Na+ и K+, расходующихся в результате возникновения ПД, что может иметь значение при высокой частоте разрядов, идущих по нервному волокну.
Чтобы представить, насколько эффективно может быть увеличена скорость проведения за счёт миелиновой оболочки, достаточно сравнить скорость распространения импульса по немиелинизированным и миелинизированным участкам нервной системы человека. При диаметре волокна около 2 µм и отсутствии миелиновой оболочки скорость проведения будет составлять ~1 м/с, а при наличии даже слабой миелинизации при том же диаметре волокна — 15-20 м/с. В волокнах большего диаметра, обладающих толстой миелинововой оболочкой, скорость проведения может достигать 120 м/с.
Скорость распространения потенциала действия по мембране отдельно взятого нервного волокна отнюдь не является постоянной величиной — в зависимости от различных условий, эта скорость может очень значительно уменьшаться и, соответственно, увеличиваться, возвращаясь к некоему исходному уровню.
Активные свойства мембраны
Активные свойства мембраны, обеспечивающие возникновение потенциала действия, основываются главным образом на поведении потенциалзависимых натриевых (Na+) и калиевых (K+) каналов. Начальная фаза ПД формируется входящим натриевым током, позже открываются калиевые каналы и выходящий K+-ток возвращает потенциал мембраны к исходному уровню. Исходную концентрацию ионов затем восстанавливает натрий-калиевый насос.
Схема строения мембраны клетки
По ходу ПД каналы переходят из состояния в состояние: у Na+ каналов основных состояний три — закрытое, открытое и инактивированное (в реальности дело сложнее, но этих трёх достаточно для описания), у K+ каналов два — закрытое и открытое.
Поведение каналов, участвующих в формировании ПД, описывается через проводимость и высчиляется черезкоэффициенты переноса (трансфера).
Коэффициенты переноса были выведены Ходжкиным и Хаксли.
Проводимость для калия GK на единицу площади [S/cm²]

Проводимость для натрия GNa на единицу площади [S/cm²]
рассчитывается сложнее, поскольку, как уже было сказано, у потенциал-зависимых Na+ каналов, помимо закрытого/открытого состояний, переход между которыми описывается параметром  , есть ещё инактивированное/не-инактивированное состояния, переход между которыми описывается через параметр
, есть ещё инактивированное/не-инактивированное состояния, переход между которыми описывается через параметр 

 , , |
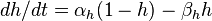 , , |
| где: | где: |
 – коэффициент трансфера из закрытого в открытое состояние для Na+ каналов [1/s]; – коэффициент трансфера из закрытого в открытое состояние для Na+ каналов [1/s]; |
 – коэффициент трансфера из инактивированного в не-инактивированное состояние для Na+ каналов [1/s]; – коэффициент трансфера из инактивированного в не-инактивированное состояние для Na+ каналов [1/s]; |
 – коэффициент трансфера из открытого в закрытое состояние для Na+ каналов [1/s]; – коэффициент трансфера из открытого в закрытое состояние для Na+ каналов [1/s]; |
 – коэффициент трансфера из не-инактивированного в инактивированное состояние для Na+ каналов [1/s]; – коэффициент трансфера из не-инактивированного в инактивированное состояние для Na+ каналов [1/s]; |
 – фракция Na+ каналов в открытом состоянии; – фракция Na+ каналов в открытом состоянии; |
 – фракция Na+ каналов в не-инактивированном состоянии; – фракция Na+ каналов в не-инактивированном состоянии; |
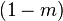 – фракция Na+ каналов в закрытом состоянии – фракция Na+ каналов в закрытом состоянии |
 – фракция Na+ каналов в инактивированном состоянии. – фракция Na+ каналов в инактивированном состоянии. |
Материал из Википедии — свободной энциклопедии

Химический состав живых клеток отличается от внешней среды, причем различия есть не только в сложных молекулах, таких как белки и нуклеиновые кислоты, но и в ионах. Например, во внеклеточной среде преобладают ионы натрия, а в клетке — ионы калия, причем последних на порядок больше. Сама по себе плазматическая мембрана клеток практически непроницаема для ионов, и поэтому для их переноса через мембрану существуют специальные транспортные механизмы — встроенные в мембрану белки. В геноме человека более 800 генов ионных каналов и транспортеров, а общую долю генов, вовлеченных в трансмембранный транспорт, оценивают в 10 % от всех генов, кодирующих белки[1]. В этой серии статей мы рассмотрим механизмы трансмембранного переноса ионов и разнообразие реализуемых ими клеточных функций. Мы также уделим внимание патологиям, вызванным мутациями в генах, кодирующих соответствующие каналы и транспортеры.
Представим себе электрохимическую ячейку — сосуд, разделенный пополам полупроницаемой мембраной, в левой части которого находится 1,0 М раствор KCl, а в правой — 0,1 М KCl. Через мембрану могут проходить катионы K+, но не анионы Cl−. Ионы K+ в результате процесса диффузии будут переходить из левого отсека в правый по градиенту концентрации*, тогда как ионы Cl−, неспособные последовать за катионами, останутся в исходном отсеке. Благодаря такому разделению зарядов на мембране будет накапливаться электрохимический потенциал: избыток анионов с левой стороны мембраны и избыток катионов с правой. Этот потенциал можно измерить, опустив в отсеки электроды, подсоединенные к вольтметру.
Асимметричный поток катионов не будет продолжаться бесконечно: накопленный электрический потенциал (с избытком положительного заряда с левой стороны мембраны) будет противодействовать диффузии ионов калия в левый отсек. Через некоторое время поток ионов K+ из правого отсека в левый сравняется по скорости с потоком из левого отсека в правый, и система достигнет равновесия. Для математического описания подобного равновесия применяют уравнение Нернста (рис. 1).
Рисунок 1 | Электрохимическая ячейка. V — вольтметр. Справа приведено уравнение Нернста, где Eeq — равновесный потенциал; E1 – E2 — разность потенциалов по обе стороны мембраны; R = 8,314 Дж/(моль·K) — универсальная газовая постоянная; T — абсолютная температура (в кельвинах); F = 96485,55 Кл·моль–1 — константа Фарадея; z — степень окисления иона (его заряд); [C]1, 2 — равновесные концентрации ионов по обе стороны мембраны.
Если принять, что равновесные концентрации ионов K+ в нашем примере равны начальным, разность потенциала на мембране при 25 °C приблизительно равна –58 мВ.
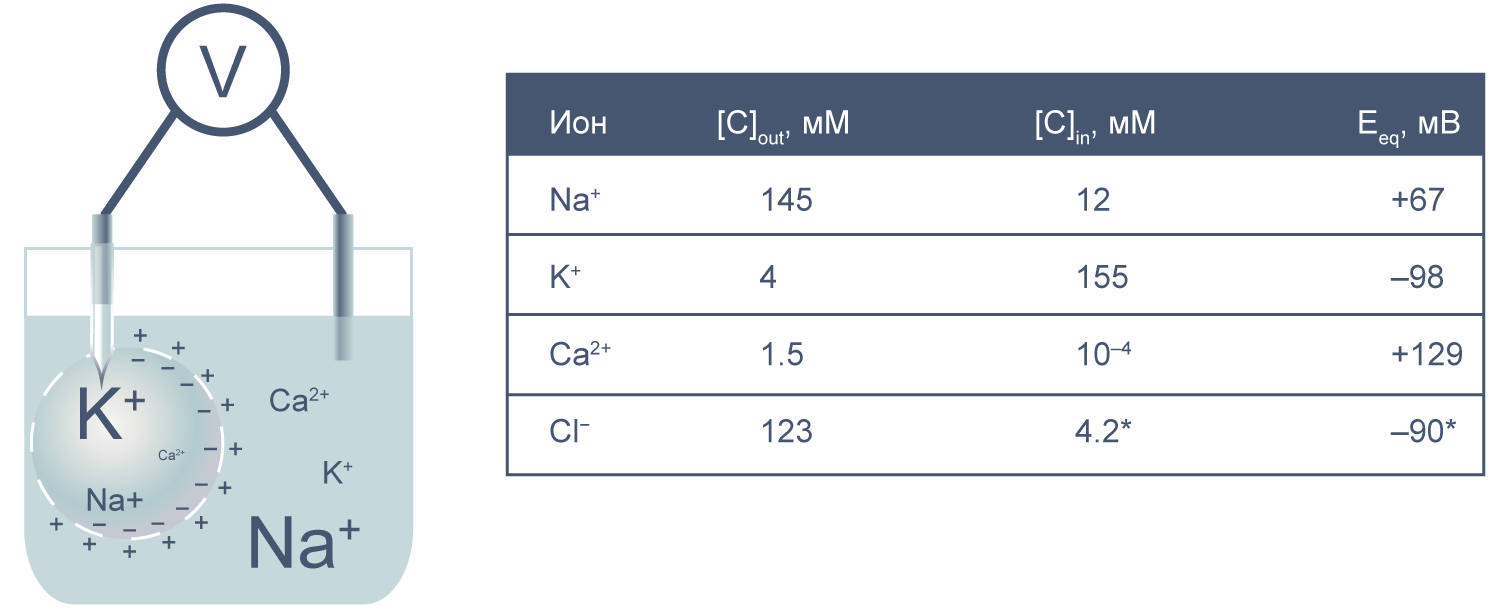
Рисунок 2 | Клетка как электрохимическая ячейка. Справа приведены концентрации основных ионов внутри и вне клетки[2].
Теперь представим, что левая часть нашей электрохимической ячейки — это живая клетка, а правая — внешняя среда. Добавим к этой картине концентрации других физиологически значимых ионов. На мембране клетки также будет накапливаться электрохимический потенциал. Величину электрической составляющей мембранного потенциала измеряют относительно потенциала вне клетки, принимая его за ноль.
В первом приближении можно сказать, что мембрана клетки проницаема для калия и непроницаема для других катионов (Na+, Ca2+) и анионов (в первую очередь для Cl– и отрицательно заряженных участков макромолекул). Ионы калия, выходя из клетки, создают потенциал покоя. Его величина достаточно близка к значению равновесного потенциала для K+, однако строго не равна ему, поскольку в реальности другие катионы и Cl– могут участвовать в формировании потенциала покоя в различных типах клеток. Вычислив равновесные потенциалы для основных ионов, мы получим динамический диапазон величины потенциала на мембране клетки: он не может быть более отрицательным, чем EK, и не может достигать более положительных значений на пике потенциала действия, чем ECa. Причина такого поведения кроется в том, что система стремится к равновесию, и при малейших отклонениях мембранного потенциала в сторону более отрицательных значений, чем EK, K+ будет двигаться по электрохимическому градиенту внутрь клетки, возвращая мембранный потенциал к равновесному потенциалу для калия.
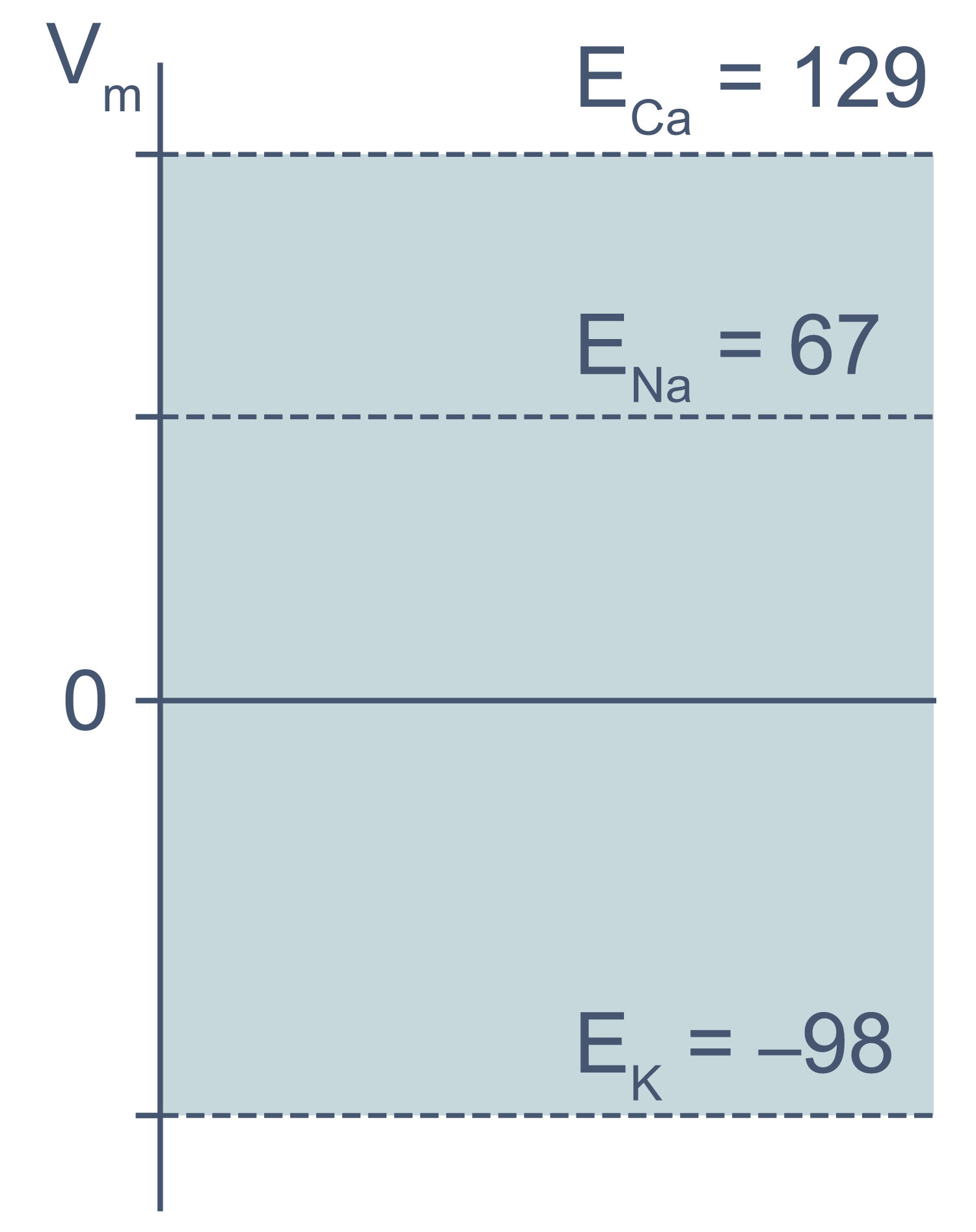
Рисунок 3 | Диапазон возможных значений мембранного потенциала от ЕK до ECa (показан голубым цветом).
Величина потенциала покоя зависит от типа клеток и равна около –30 мВ в невозбудимых клетках и около –80 мВ в возбудимых клетках (нейроны, мышечные и эндокринные клетки). Когда мембранный потенциал более отрицателен, чем потенциал покоя, говорят, что мембрана гиперполяризована, а когда он приближается к нулю или даже принимает положительные значения, говорят о деполяризации мембраны.
В общем случае мембранный потенциал можно вычислить согласно уравнению Гольдмана-Ходжкина-Катца, которое принимает в расчет все основные катионы и анионы:
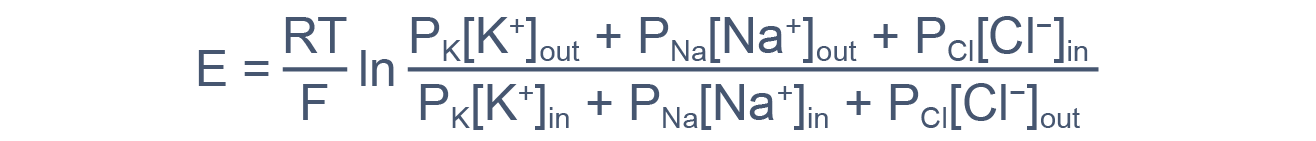
где E — мембранный потенциал; R = 8,314 Дж/(моль·K) — универсальная газовая постоянная; T — абсолютная температура; F = 96485,55 Кл·моль–1 — константа Фарадея; PX — проницаемость мембраны для иона X; [C]in, out — равновесные концентрации ионов внутри и вне клетки. N.B.: для анионов внеклеточная концентрация стоит в знаменателе, а внутриклеточная — в числителе.
Что же обеспечивает проницаемость мембраны для ионов? Заряженные частицы не могут самостоятельно пересекать гидрофобный внутренний слой плазматической мембраны, и поэтому требуются специальные белки, образующие гидрофильную пору, через которую ионы могут двигаться через мембрану. Такие белки называются ионными каналами. Основной вклад в поддержание потенциала покоя вносят калиевые каналы семейств Kir (inward rectifying K+ channels — калиевые каналы внутреннего выпрямления) и K2P (two–pore domain K+ channels — калиевые каналы с двумя поровыми доменами, которые часто называют каналами утечки), а каналы других семейств могут обеспечивать быстрое изменение мембранного потенциала в возбудимых клетках. Каналы могут селективно пропускать определенный тип ионов, например, K+ (как каналы семейства Kir), или более широкий спектр веществ, как, например, коннексины — белки щелевых контактов.
Каналы бывают потенциал-зависимые (потенциал-управляемые), лиганд-зависимые, термо- и механочувствительные — в зависимости от стимула, который управляет открытием и закрытием канала. В роли стимула, таким образом, могут выступать изменения мембранного потенциала, химические агенты, температура, свет, механические и другие стимулы. Один и тот же канал может открываться под действием различных эндо- и экзогенных стимулов. Так, канал TRPV1 активируется повышением температуры более 43 °C[3], кислым pH[4] и разнообразными химическими веществами: капсаицином (алкалоид из перцев рода Capsicum)[3], эндоканнабиноидом анандамидом[5], окситоцином[6] и др.
Физиологическая роль каналов крайне важна. К примеру, мутации в генах, кодирующих белки ионных каналов, лежат в основе патогенеза многих заболеваний человека: некоторых видов эпилепсии[7], муковисцидоза[8], некоторых аритмий[9, 10] и др. Ионные каналы служат мишенями действия многих лекарств, ядов и токсинов.
Однако для формирования потенциала покоя недостаточно одних лишь каналов, ведь нужно создавать и поддерживать концентрационные градиенты на мембране. Основной механизм поддержания градиентов концентрации калия и натрия — это Na/K-АТФаза, фермент, за счет гидролиза одной молекулы АТФ переносящий три Na+ наружу и два K+ внутрь клетки. Она осуществляет электрогенный транспорт: в каждом транспортном цикле при переносе одного дополнительного положительного заряда наружу генерируется некоторая разность потенциалов на мембране. Чтобы оценить этот вклад Na/K-АТФазы в поддержание потенциала покоя, можно заблокировать работу фермента алкалоидом оубаином. Тогда мембрана деполяризуется примерно на 10 мВ[11].
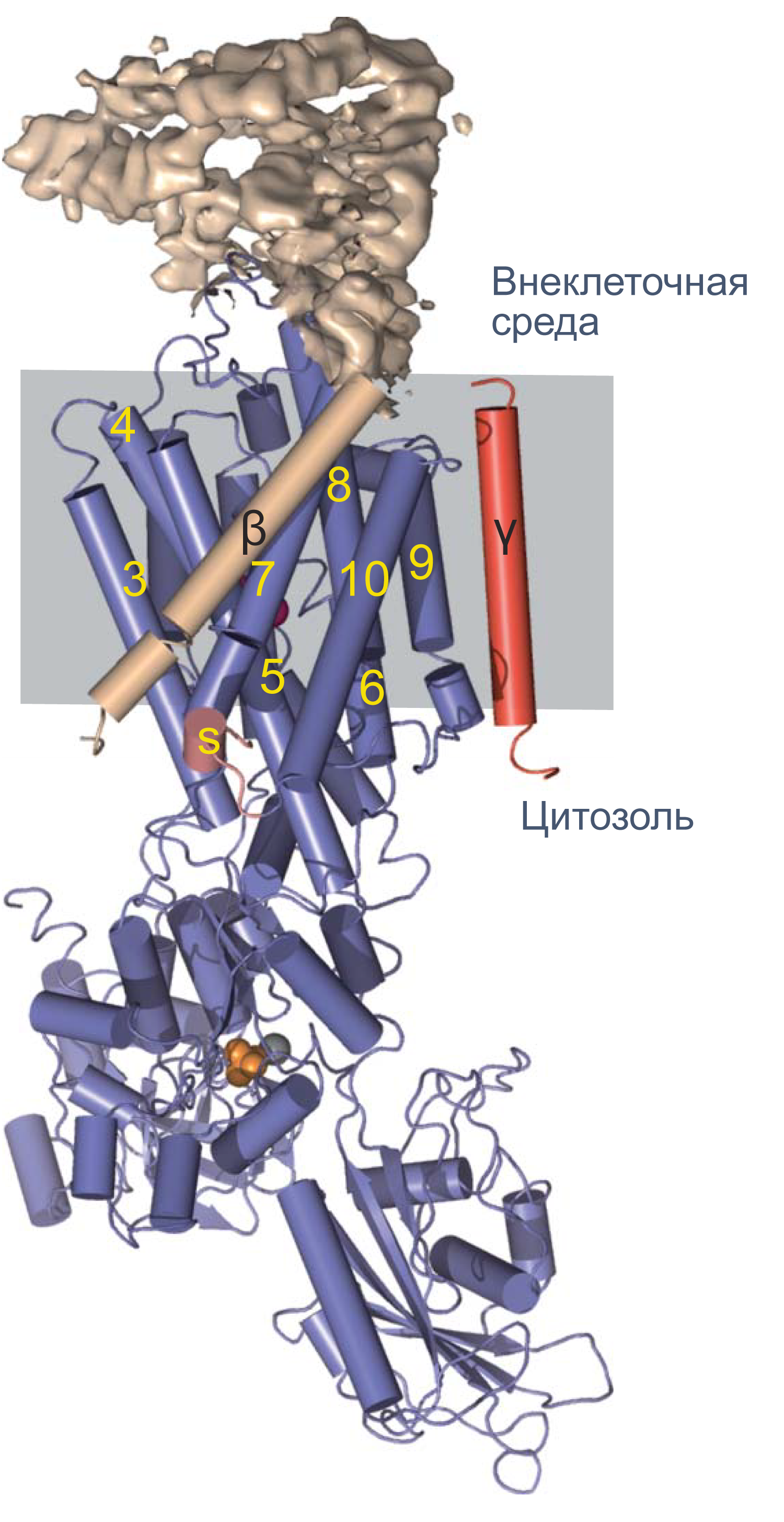
Рисунок 4 | Структура Na/K-АТФазы, полученная методом рентгеновской кристаллографии. Синим цветом показана α-субъединица, красным — γ-субъединица; β-субъединица показана бежевым цветом. Внеклеточная часть β-субъединицы показана в виде электронной плотности. Альфа-спирали изображены цилиндрами, бета-слои — плоскими стрелками[12].
Активный и пассивный транспорт веществ через мембрану
Процессы транспорта веществ через мембрану можно классифицировать по источнику энергии для транспорта. Пассивный транспорт — это движение вещества через канал или транспортер по градиенту концентрации*, то есть за счет энергии электрохимического градиента. Таким способом через калиевые каналы пассивно движутся ионы калия, или осуществляется перенос глюкозы через транспортер GLUT4 (такой тип транспорта еще называют облегченной диффузией, а транспортеры, переносящие только один субстрат — унипортерами). Кроме пассивного транспорта, существует активный транспорт, при котором субстраты переносятся против градиента концентрации с затратой энергии, запасенной клеткой в виде АТФ (например, Na/K-АТФаза).
Некоторые транспортеры сопрягают перенос ионов или молекул против градиента концентрации с движением ионов по градиенту концентрации. Симпортеры переносят различные частицы в одном направлении (например, KCC2 — K–Cl cotransporter 2 — K/Cl котранспортер 2), а антипортеры, или обменники, — в противоположных (например, NHE-1 — Na/H exchanger 1 — Na/H обменник, участвующий в поддержании клеточного pH). Такой транспорт называется вторично-активным.
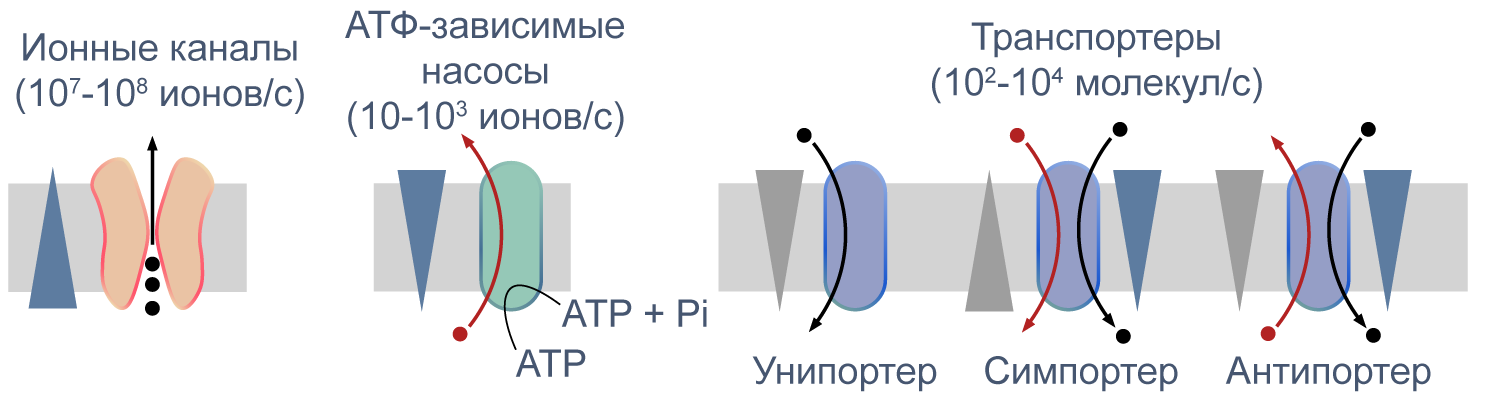
Рисунок 5 | Пассивный и активный транспорт веществ через мембрану. Треугольниками показаны концентрационные градиенты. Черными стрелками показано движение по градиенту концентрации, красными — против градиента концентрации. По [13], с изменениями.
В старой литературе можно встретить концепцию «белков-переносчиков»: до открытия молекулярной идентичности многих каналов и транспортеров (т. е. какая молекула опосредует данный ионный ток и какой ген ее кодирует) существовало представление о переносчиках как о челноках, связывающих субстраты с одной стороны мембраны, диффундирующих через мембрану и высвобождающих субстраты с другой стороны. Однако, когда стали известны аминокислотные последовательности транспортных белков, стало понятно, что все они часто содержат многочисленные трансмембранные домены и образуют сквозной путь через мембрану.
Различия между каналами, транспортерами и насосами заключаются в механизме их работы и регуляции. Каналы представляют собой более или менее селективную пору, через которую ионы могут свободно диффундировать, не вызывая конформационных изменений в белке канала. При токе через отдельный канал в 1 пА по нему проходят 6×106 одновалентных ионов в секунду. Транспортер, связываясь с субстратом, изменяет свою конформацию для переноса субстрата. При ко-транспорте повышается аффинность транспортера в новой конформации к второму субстрату, и субстраты переносятся через мембрану сопряженно. Насосы, также называемые АТФазами, (ауто)фосфорилируются АТФ, и это фосфорилирование значительно изменяет их конформацию и приводит к транслокации субстратов через мембрану. Электрическая проводимость насосов очень мала: Na/K-АТФаза переносит всего около 300 Na+ и 200 K+ в секунду.
Граница между молекулами каналов и транспортеров не всегда строга. Например, семейство хлоридных каналов и транспортеров ClC (англ. Chloride Channel) включает в себя гомологичные друг другу каналы (ClC-1, 2, Ka и Kb) и Cl/H-обменники (ClC-3–7), которые можно превратить в каналы, внеся мутацию в единственный остаток глутамата (т. н. gating glutamate — воротный глутамат) [14]. Na/K-АТФазу также можно превратить в простую пору, например, с помощью палитоксина[15]. Хлоридный канал CFTR относится к группе ABC-транспортеров, однако он использует энергию АТФ не для транспорта ионов, а для регуляции открытия и закрытия канала[16]. Кроме того, существуют данные о том, что везикулярный транспортер глутамата VGLUT1 кроме обмена глутамата на протоны также опосредует не сопряженный с обменом ток Cl− [17].
Клеточная мембрана как электрическая цепь
Липидный бислой мембраны можно представить как резистор (сопротивление) и конденсатор (емкость), соединенные параллельно. Величина сопротивления зависит от плотности каналов в мембране и их функционального состояния. Электроемкость возникает из-за разделения зарядов по обе стороны мембраны тонким слоем диэлектрика (гидрофобными хвостами фосфолипидов).
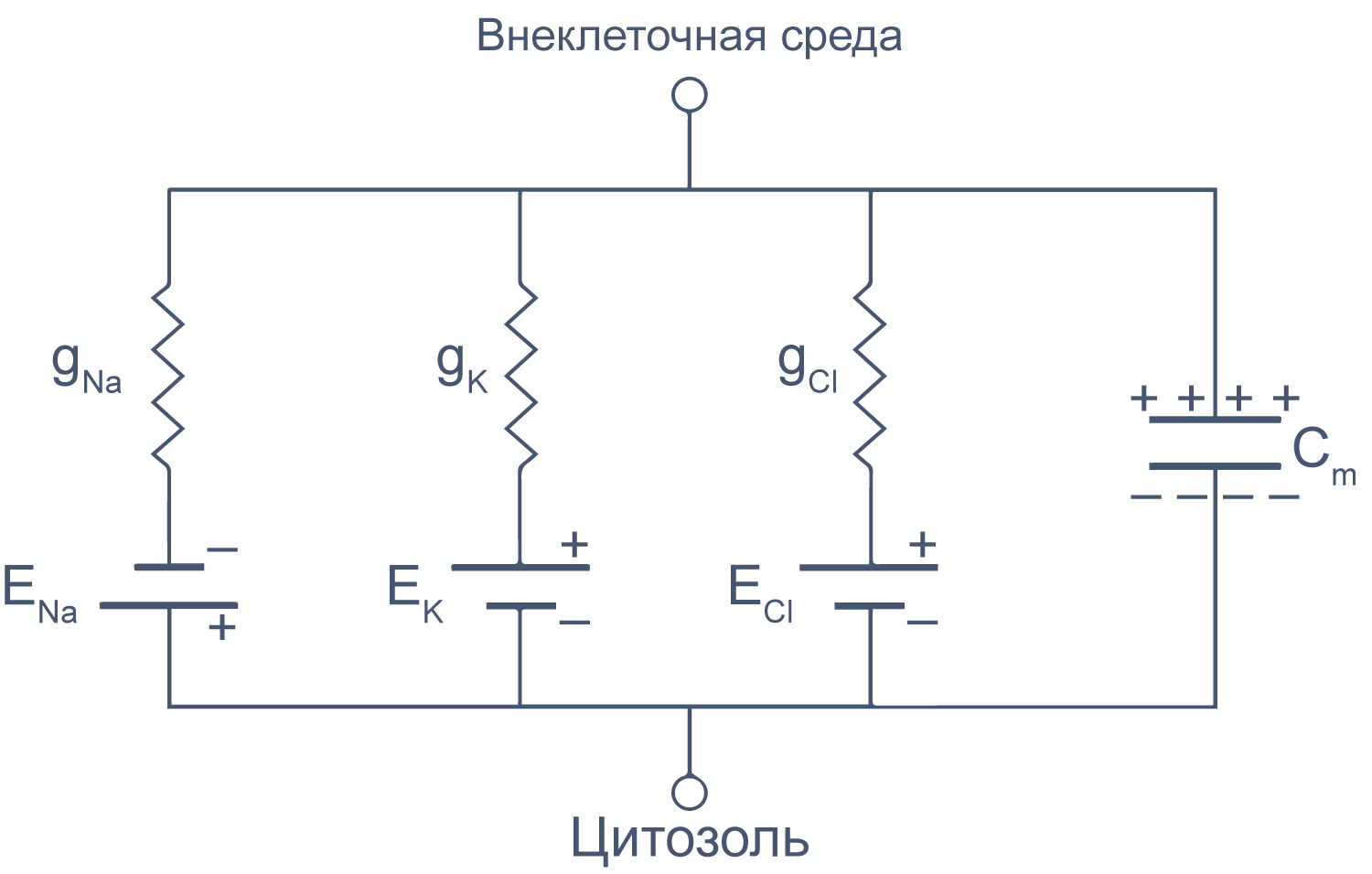
Рисунок 6 | Плазматическая мембрана, представленная в виде RC схемы. gNa, gK, gCl — проводимость** мембраны для ионов Na+, K+ и Cl–, соответственно; ENa, EK, ECl — электродвижущая сила, или равновесные потенциалы для соответствующих ионов, Сm — электроемкость мембраны.
Можно считать, что проводимость (величина, обратная сопротивлению, измеряемая в сименсах) характеризует проницаемые для ионов компоненты структуры мембраны, а емкость — не проницаемые для ионов структуры. Удельная емкость мембраны составляет приблизительно 1 мкФ/см2 или 0,01 пФ/мкм2*** и мало зависит от типа клеток[2]. Это позволяет оценить размер клетки по ее электрическим характеристикам. Высокая электроемкость клеточных мембран задерживает изменения потенциала в ответ на ток. Эту задержку можно выразить через постоянную времени τ, которая равна произведению емкости и параллельно соединенного с ней сопротивления (RC). Если конденсатор зарядить на некоторую величину, а затем дать ему разрядиться через резистор, то потенциал будет убывать экспоненциально согласно формуле V = V0e–t/RC, то есть за каждые τ = RC секунд потенциал будет падать в 1/e раз (на 37 % от исходной величины). Этот расчет применим и к клеточной мембране: падение напряжения при разрядке мембраны будет подчиняться экспоненциальному закону. То есть, если приложить гипер- или деполяризующий стимул, то мембранный потенциал через время τ достигнет 63 % конечного сдвига.
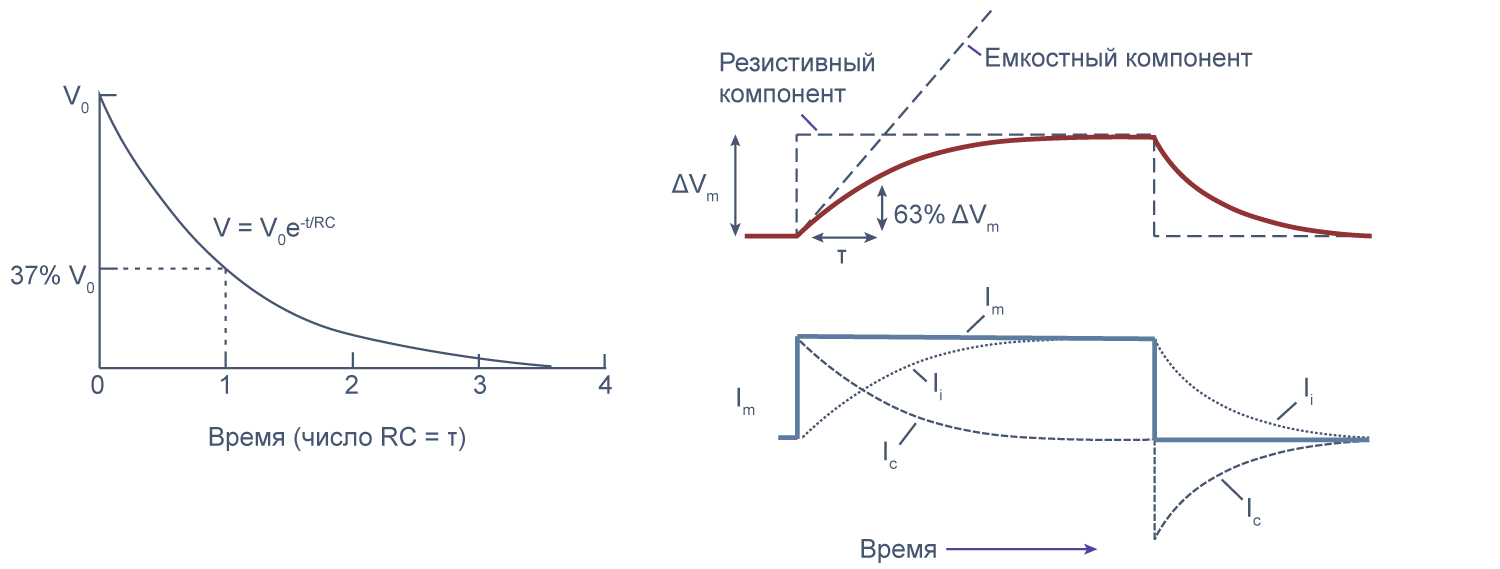
Рисунок 7 | Падение напряжения при разрядке мембраны. Изменение мембранного потенциала при деполяризации мембраны на ΔVm [22], Ic — емкостный ток, Ii — ионный ток, Im — суммарный ток через мембрану. Пояснения в тексте.
Потенциал действия
Возбудимые клетки могут быстро изменять потенциал на мембране и этим запускать внутриклеточные процессы, например, мышечное сокращение или экзоцитоз везикул. Кратковременный локальный скачок мембранного потенциала от приблизительно –80 мВ (значения потенциала покоя) до 0…+20 мВ за счет изменения проницаемости мембраны для ионов называется потенциалом действия.
Для начала рассмотрим потенциал действия в аксонах нейрона на примере гигантского аксона кальмара. Выбор столь экзотического объекта обусловлен историческими причинами. Современная микроэлектродная техника — использование тонких стеклянных микропипеток, заполненных раствором электролита, — была предложена лишь в 1949 году Дж. Лингом и Р. Джерардом[18]. До этого поместить электрод, представлявший собой тонкую проволоку, внутрь клетки, не разрушив ее, можно было только в случае ее крупных размеров. Гигантский аксон кальмара стал идеальным модельным объектом для изучения потенциала действия: его диаметр может достигать 0,5–1 мм. Этот отросток служит для быстрой передачи нервных импульсов у беспозвоночных, у которых отсутствует миелинизация. Внутренним содержимым аксона легко манипулировать, заменяя ионный состав внутриклеточного раствора, а внутрь такого аксона можно поместить электрод для регистрации мембранного потенциала.
Так, в 1939 году А. Ходжкин и Э. Хаксли опубликовали в журнале Nature короткую заметку «Потенциалы действия, зарегистрированные внутри нервного волокна»[19], в которой они описали первый эксперимент по внутриклеточному измерению мембранного потенциала на гигантском аксоне кальмара. Посмотрим на потенциалы действия, которые зарегистрировали исследователи.
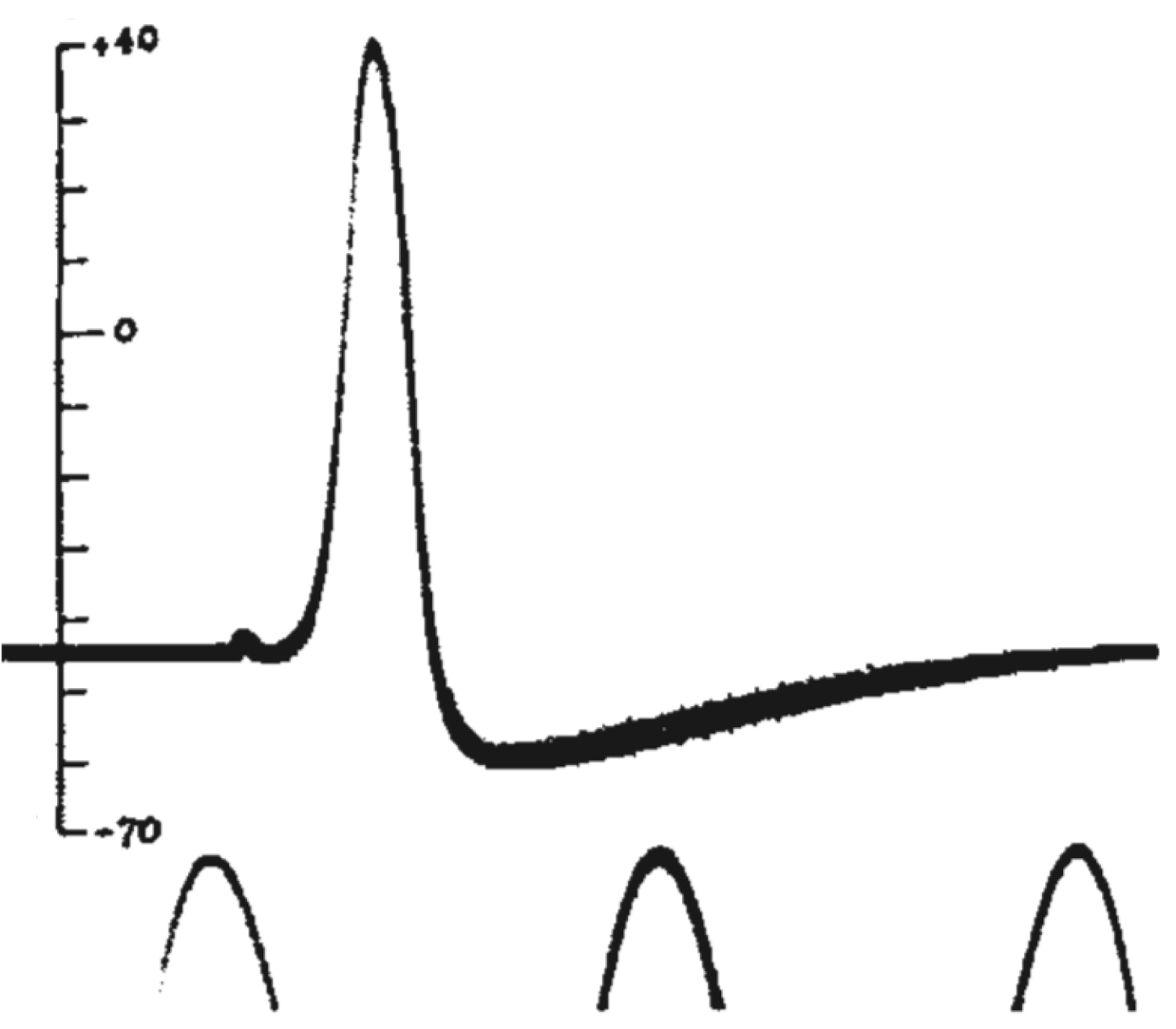
Рисунок 8 | Потенциал действия из статьи А. Ходжкина и Э. Хаксли 1939 года[19]. Потенциал действия был зарегистрирован как разность потенциала между внутренней средой аксона и внешней средой. Пики внизу рисунка — это фрагменты синусоидального сигнала с частотой 500 Гц. Вертикальной чертой отмечен потенциал внутреннего электрода в милливольтах, потенциал морской воды снаружи аксона был принят за ноль.
Мы видим резкую деполяризацию мембраны до положительных значений, а затем более плавное возвращение потенциала к отрицательным значениям, зачастую более отрицательным, чем величина потенциала покоя. Из этих наблюдений следовало два важных вывода: 1) потенциал действия генерируется мембраной клетки, что не было очевидно в 1930-е годы; 2) поскольку измеренная амплитуда потенциала действия была больше величины мембранного потенциала, генерация потенциала действия — это активный процесс, который нельзя объяснить временным «пробоем» в мембране (каким бы наивным такое представление нам не казалось сегодня, в 1930-е так думали многие физиологи). В том же году К. С. Коул и Х. Дж. Кертис[20] зарегистрировали кратковременное изменение проводимости мембраны с 1 мСм/см2 до 40 мСм/см2 при генерации потенциала действия. Эти данные также свидетельствовали о тонкой регуляции этого процесса.
После Второй мировой войны Ходжкин и Хаксли вернулись к своим исследованиям. В 1945 году они опубликовали статью с несколькими дополнительными экспериментами, подтверждающими сформулированные ранее выводы. Но и тогда ионные механизмы потенциала действия оставались неясными.
В 1952 году вышла серия статей, посвященных разгадке механизма генерации потенциала действия. Ведущую роль в этом открытии сыграл новый метод фиксации потенциала с помощью двух электродов (в англоязычной литературе TEVC — two-electrode voltage clamp), разработанный в конце 1940-х годов К. С. Коулом и Дж. Мармонтом[21]. Этот метод позволяет измерять не только потенциал, но и токи при заданном значении мембранного потенциала. Как же осуществляется фиксация потенциала с помощью двух электродов на заданном уровне (Vcmd — «командный потенциал»)? В клетку помещают два электрода, один из которых измеряет потенциал (относительно внеклеточного электрода сравнения) и передает его значение на специальный усилитель, который сравнивает измеренный потенциал со значением командного потенциала. Это устройство вычисляет ток, необходимый для компенсации этой разницы, и подает через второй внутриклеточный электрод ток такой величины, чтобы потенциал на мембране клетки стал равен Vcmd (Vm = Vcmd). Из амплитуды тока, необходимого для компенсации сдвига потенциала до Vcmd, можно сделать вывод о токе через мембрану при данном значении мембранного потенциала. Ток при данном значении потенциала равен току, подаваемому на второй электрод, взятому с обратным знаком.
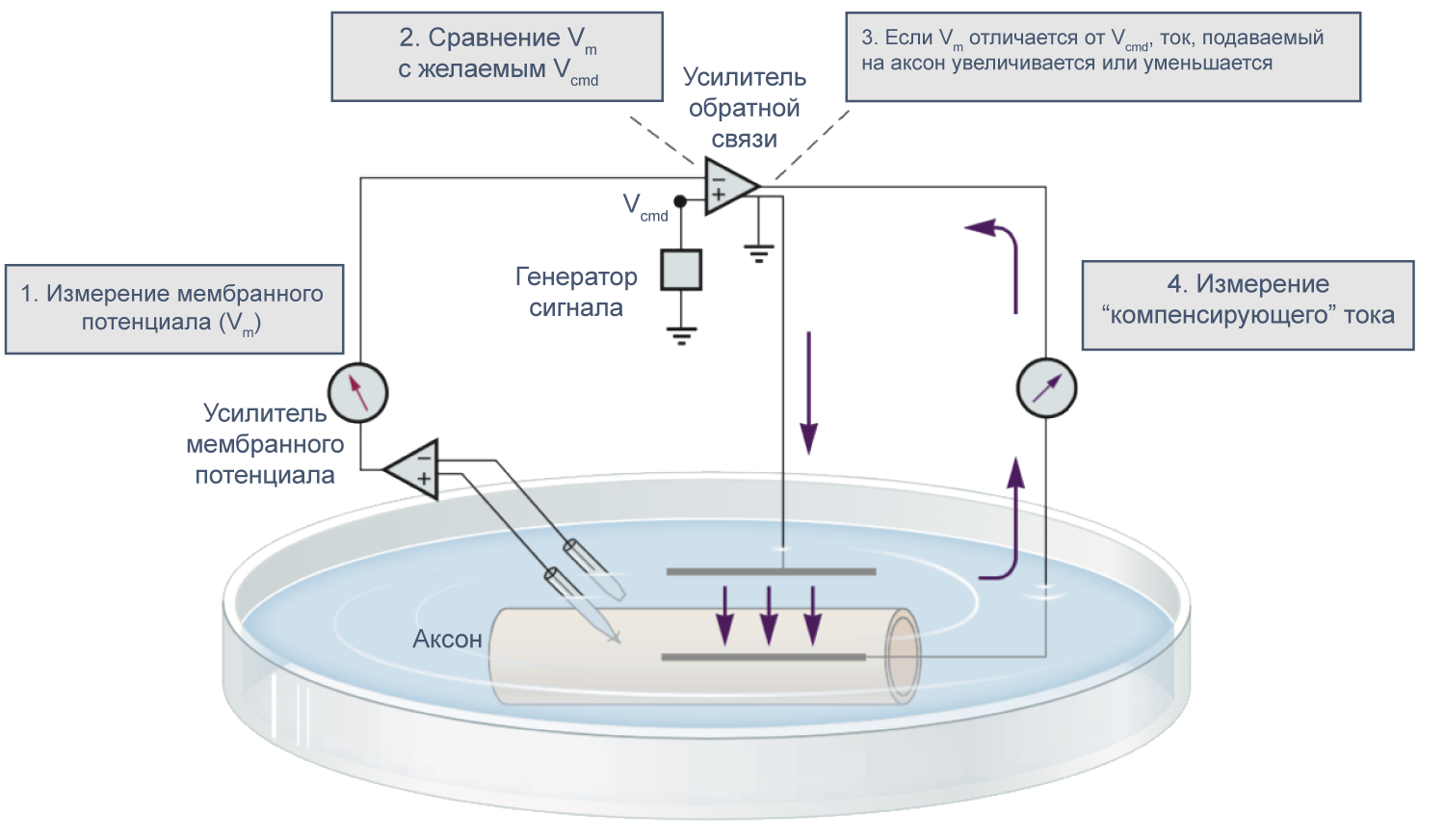
Рисунок 9 | Схема фиксации потенциала с помощью двух электродов[21].
В 1970–80-х годах Эрвин Неер и Берт Сакман (Erwin Neher, Bert Sakmann) предложили метод локальной фиксации потенциала (англ. patch clamp), позволяющий работать с мелкими клетками и токами малой амплитуды и даже регистрировать активность отдельных каналов. Тем не менее, метод фиксации потенциала двумя электродами в микроэлектродной конфигурации используется и сегодня при работе с такими крупными клетками, как ооциты лягушки Xenopus laevis.
Временной ход потенциала действия
Потенциал действия в аксоне можно разделить на 1) фазу быстрой деполяризации до 2) положительных значений (овершута, от англ. overshoot), 3) фазу реполяризации, в которой потенциал возвращается к потенциалу покоя или даже до несколько более отрицательных значений — 4) следовая гиперполяризация.
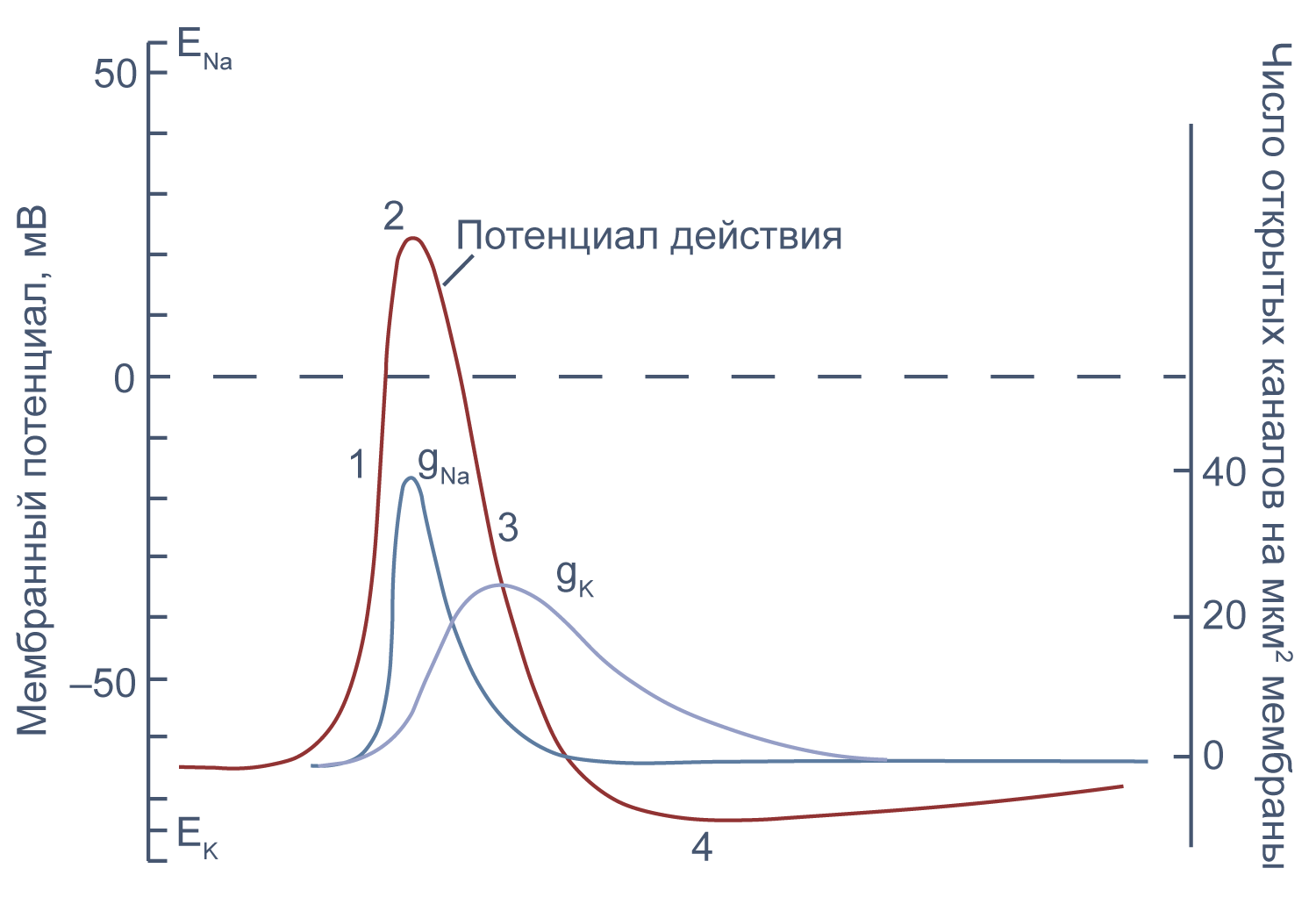
Рисунок 10 | Потенциал действия и изменения проводимости мембраны для Na+ и K+ в гигантском аксоне кальмара. Из [22], с изменениями.
Изменяя ионный состав внутри- и внеклеточного раствора, можно изолировать ионные токи, которые опосредуют изменение мембранного потенциала при потенциале действия. Так, помещая аксон в раствор, в котором натрий заменен на холин, можно изолировать натриевый и калиевый компонент потенциала действия, то есть отдельно измерить калиевый ток[20]. Этого же можно достичь применением блокаторов потенциал-зависимых натриевых и калиевых каналов — тетродотоксина и тетраэтиламмония (TEA).
Чтобы понять взаимосвязь ионных токов и вызванных ими изменений потенциала, рассмотрим всю цепь событий при генерации потенциала действия. Сначала мембрана деполяризуется под действием внешнего стимула: поступления в клетку катионов через лиганд-управляемые каналы, закрытия калиевых каналов или электрической стимуляции в эксперименте. Если деполяризация достигает порогового значения для потенциалзависимых натриевых каналов (Nav), они открываются, натрий по градиенту своей концентрации входит в клетку, и мембрана деполяризуется еще сильнее. Дальнейшая деполяризация влечет за собой лавинообразное открытие все новых натриевых каналов, ток через которые приводит к еще большей деполяризации. Однако эта петля положительной обратной связи не работает бесконечно: открывшись на некоторое время, натриевые каналы инактивируются и не могут открыться вновь, пока мембранный потенциал не вернется к отрицательным значениям.
Механизм инактивации был предложен еще в математической модели Ходжкина и Хаксли[23] на основании кинетических характеристик тока. Они предположили, что в натриевом канале есть три активационные частицы m и одна инактивационная частица h. Когда стала известна аминокислотная последовательность канала, выяснилось, что канал на самом деле имеет четыре гомологичных активационных домена и один инактивационный, однако один из активационных доменов срабатывает значительно медленнее остальных трех, и его влияние на кинетические характеристики тока маскируется происходящей в то же время инактивацией канала (например, [24]).
В то же время деполяризация мембраны приводит к активации потенциал-зависимых калиевых каналов (Kv), которые открываются медленнее, чем натриевые, калий выходит из клетки, и потенциал возвращается к потенциалу покоя и может даже временно стать более отрицательным: пока натриевые каналы инактивированы, потенциал становится ближе к калиевому равновесному потенциалу, и это явление называется следовой гиперполяризацией.
Генерация потенциала действия происходит по принципу «все или ничего». Если деполяризующий стимул не достиг порогового значения, потенциал действия не генерируется. Если же порог был достигнут, положительная обратная связь обеспечивает открытие всех доступных натриевых каналов, и потенциал действия достигает своей максимальной амплитуды.
Если новый стимул приходит во время или сразу после генерации потенциала действия, второй потенциал действия не возникает или обладает меньшей амплитудой, чем первый. Это явление называется рефрактерностью. Стимул, возникший в период абсолютной рефрактерности, не вызывает генерации потенциала действия, а пришедшийся на период относительной рефрактерности вызывает потенциал действия уменьшенной амплитуды, так как часть натриевых каналов все еще инактивирована.
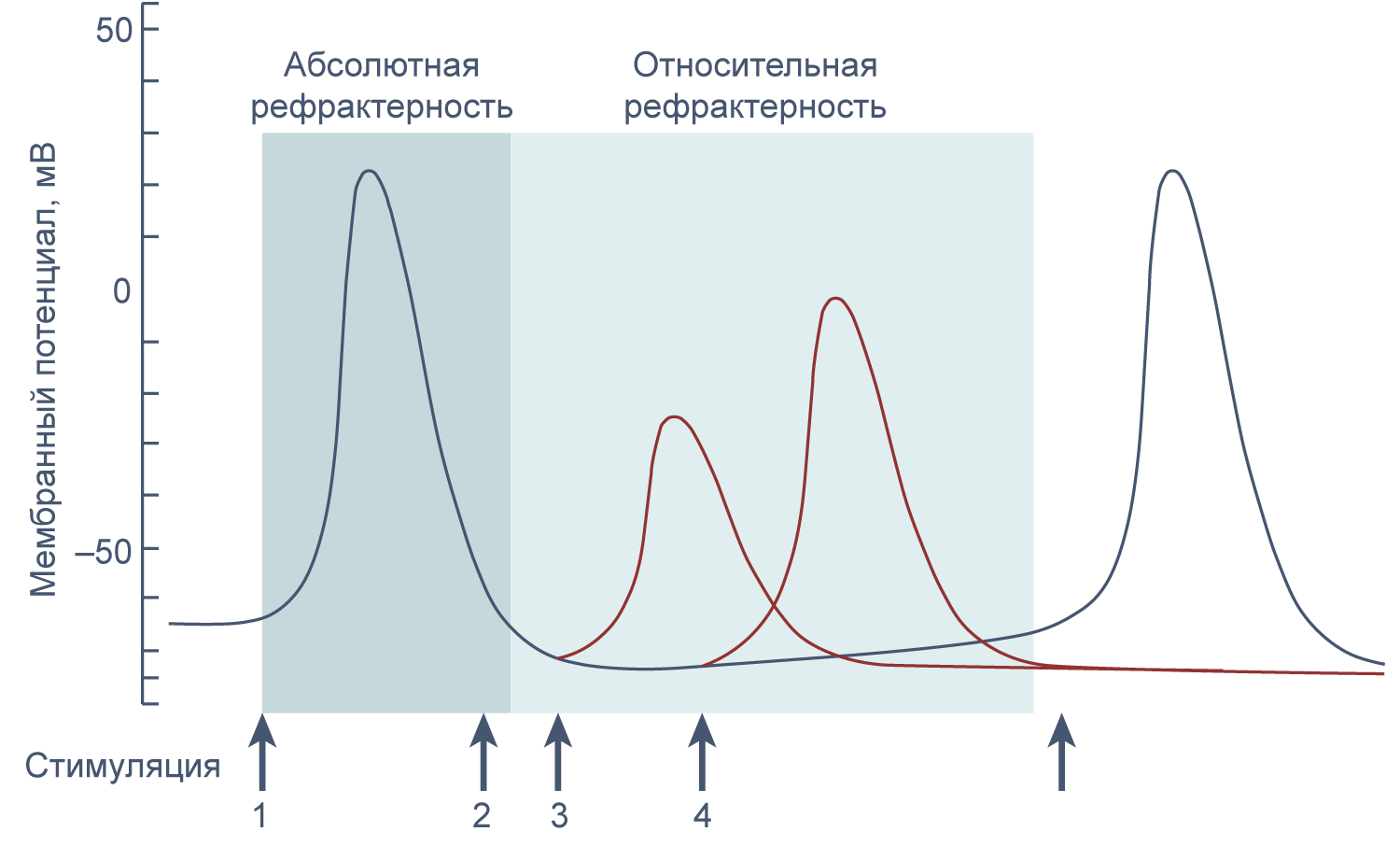
Рисунок 11 | Абсолютная и относительная рефрактерность. Стимуляция в период абсолютной рефрактерности (2) не ведет к генерации потенциала действия, а стимуляция в период относительной рефрактерности (3 и 4) приводит к генерации потенциала действия сниженной амплитуды.
Стоит отметить, что внутриклеточная концентрация физиологически значимых ионов при генерации потенциала действия не меняется, и ионные токи задействуют пренебрежимо малую долю от общего числа Na+ и K+. Это можно проиллюстрировать следующим примером. Рассчитаем число ионов, которое должно пересечь мембрану для деполяризации на 100 мВ. Заряд на мембране равен произведению емкости мембраны и потенциала: Q = CmVm. Удельная емкость мембраны близка к 1 мкФ/см2, а сдвиг потенциала в нашем случае равен 0,1 В. Тогда количество разделенных зарядов равно Q = 10−6 Ф/см2 × 0,1 В = 10−7 Кл/см2. Величина заряда одного иона Na+ или K+ (элементарного заряда) равна 1,6 × 10−19 Кл, тогда количество переносимых через мембрану ионов равно 10−7 Кл/см2 / 1,6 × 10−19 Кл = 6,25 × 1011 ионов/см2, или 6250 ионов/мкм2. Для клетки диаметром 10 мкм площадь поверхности мембраны будет приблизительно равна 4πr2 = 314 мкм2 (в этом расчете для простоты мы считаем клетку гладкой сферой), а объем — 4πr3/3 = 524 мкм3. При внутриклеточной концентрации Na+ 10 мМ, а K+ 150 мМ содержание этих ионов в цитозоле будет равно 3,2 × 109 и 4,7 × 1010 соответственно. В течение одного потенциала действия приблизительно 314 мкм2 × 6,250 ионов/мкм2 ≈ 2 000 000 ионов Na+ входит в клетку в фазе деполяризации и примерно столько же ионов K+ выходит из клетки в фазе реполяризации, что составляет всего 0,06 % от общего числа ионов натрия в клетке. Токи такой величины обычно не изменяют макроскопические концентрации ионов в клетке, поскольку работа Na/K-АТФазы компенсирует эти незначительные изменения. Однако при определенных условиях концентрации Na+ и K+ все же могут измениться, например, при продолжительной стимуляции аксонов с малым диаметром[25].
Распространение возбуждения по аксону
Электрические свойства мембраны помогают понять изменения мембранного потенциала не только во времени, но и в пространстве. Пассивное, или электротоническое распространение возбуждения по мембране происходит без изменения проводимости потенциал-зависимых каналов. Для распространения потенциала действия важен как активный (изменение проводимости натриевых и калиевых каналов), так и пассивный механизмы, поскольку деполяризация, вызывающая открытие новых потенциал-зависимых натриевых каналов, должна достигнуть нового невозбужденного участка аксона, и происходит это благодаря электротоническому распространению возбуждения.
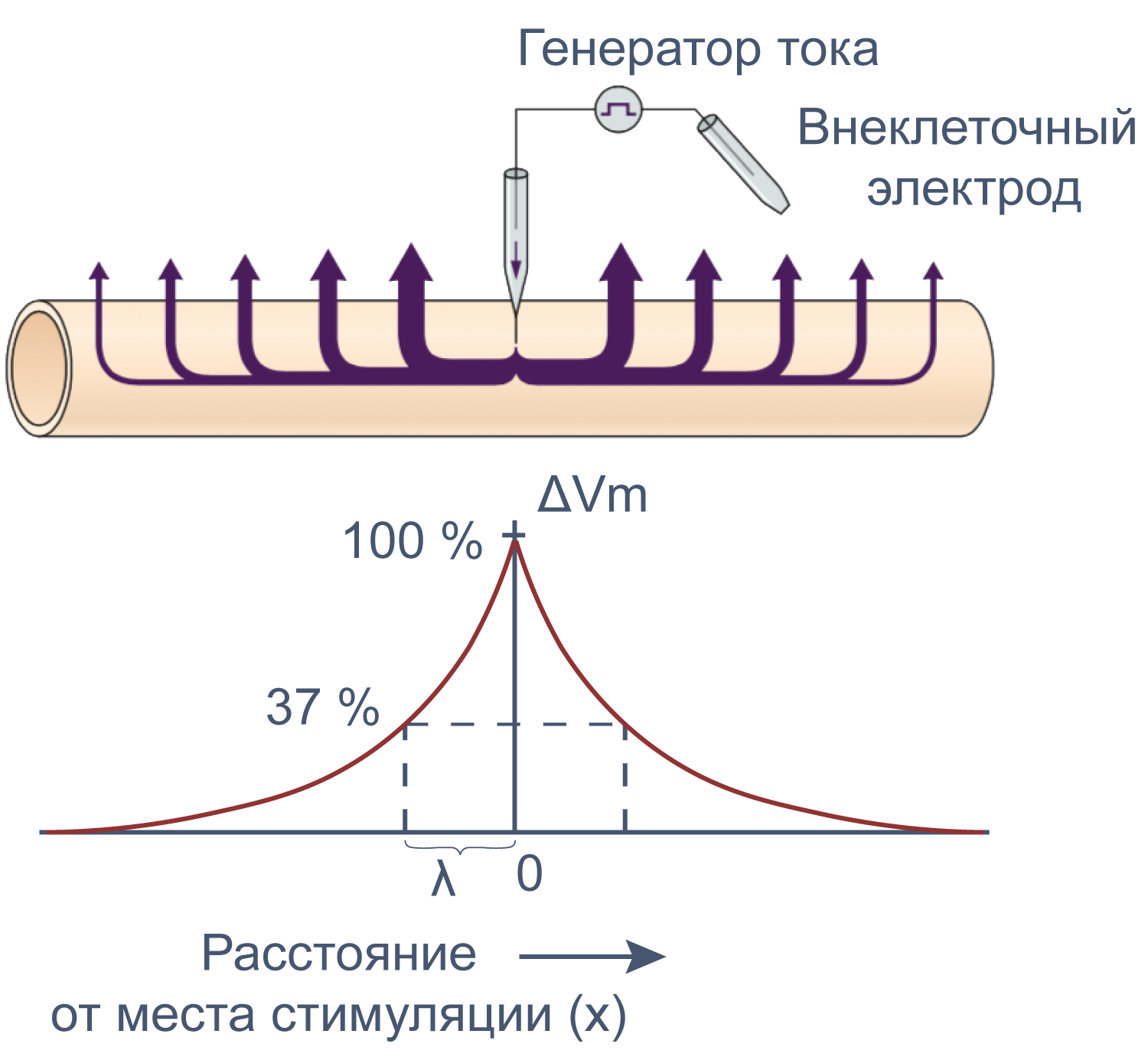
Рисунок 12 | Электротоническое распространение возбуждения. Пояснения в тексте [22].
Сдвиг потенциала в точке, отстоящий на x от места стимуляции, можно вычислить как Ex = E0e–x/λ, где E0 — это сдвиг потенциала в точке стимуляции, а λ — постоянная длины.
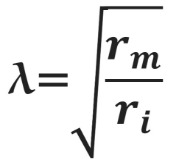
Постоянная длины возрастает с увеличением сопротивления мембраны (rm) и уменьшается с возрастанием сопротивления аксоплазмы (ri), которое в свою очередь зависит от концентрации подвижных зарядов в объеме аксона. Знание этих закономерностей позволяет понять зависимость скорости распространения возбуждения от радиуса (R) аксона. Сопротивление мембраны rm пропорционально 1/2πR, сопротивление аксоплазмы ri — 1/πR2, а емкость мембраны Cm пропорциональна R. По мере увеличения радиуса аксона и rm, и ri уменьшаются, но ri уменьшается сильнее. Постоянная длины увеличивается, следовательно, сдвиг потенциала может распространяться по более крупному аксону дальше. Кроме того, увеличение радиуса аксона ведет к увеличению емкости мембраны, однако этот эффект нивелируется тем, что емкость с увеличением радиуса растет линейно, а уменьшение ri пропорционально квадрату радиуса. Таким образом, проводимость аксоплазмы увеличивается быстрее (при снижении ri), чем растет емкость мембраны, и это позволяет току быстрее достигать невозбужденных участков мембраны более крупного аксона.
Зависимость скорости распространения потенциала действия по аксону от его диаметра объясняет необходимость в гигантских аксонах у кальмара. Однако у позвоночных гигантских аксонов нет, и достаточная скорость проведения нервных импульсов достигается с помощью миелинизации аксонов. Миелиновые оболочки образованы специальными глиальными клетками: олигодендроцитами в центральной нервной системе и клетками Шванна в периферической. Эти клетки оборачивают аксон, образуя вокруг него плотный чехол из десятков слоев плазматической мембраны, который работает как изолятор. Под миелиновой оболочкой очень мало или почти нет натриевых каналов. Они оказываются расположены на небольших участках мембраны аксона между двумя соседними шванновскими клетками или олигодендроцитами — в перехватах Ранвье. Миелиновая оболочка увеличивает скорость проведения потенциала действия благодаря повышению сопротивления мембраны rm. При этом снижаются потери тока через мембрану, и деполяризация может пассивно распространяться на бо́льшие расстояния. Кроме того, из-за снижения емкости мембраны Cm, меньшая доля тока тратится на перезарядку мембраны. Миелинизация делает передачу потенциала действия не только быстрее, но и эффективнее, поскольку натриевые каналы располагаются только в перехватах Ранвье, благодаря чему меньшее количество ионов натрия входит в клетку и меньше энергии требуется на работу Na/K АТФ-азы для поддержания концентрационного градиента.
Потенциалы действия в других возбудимых клетках
Минималистичный натриево-калиевый потенциал действия характерен только для аксонов нейронов. В других частях нейрона и в иных типах возбудимых клеток в генерации потенциала действия принимают участие разнообразные ионные каналы, в том числе калиевые каналы других семейств и кальциевые каналы плазматической мембраны и эндоплазматического ретикулума (ЭПР является внутриклеточным депо кальция; общая концентрация Ca2+ в нем достигает миллимолярных значений, а концентрация свободного кальция находится в микромолярном диапазоне[26]; эти значения на несколько порядков выше, чем 100 нМ свободного Ca2+ в цитозоле в состоянии покоя). Различия в экспрессии генов ионных каналов в различных типах возбудимых клеток порождают разнообразие потенциалов действия, различающихся ионными механизмами, длительностью (от 1,5 мс в аксонах до 500 мс в кардиомиоцитах желудочков), необходимостью внешнего стимула для генерации или наличием собственного ритма. Многие ионные каналы, не участвуя напрямую в генерации потенциала действия, влияют на возбудимость клеток и таким образом вносят вклад в разнообразие электрической активности клеток.
* Принятое в физиологической литературе употребление фраз «по» или «против градиента концентрации» расходится с физическим понятием градиента. В математике и физике градиент направлен в сторону наибольшей скорости возрастания функции или величины; так, если вещество движется в направлении этого вектора, то физиологи говорят о движении «против градиента концентрации», а если в противоположном направлении — то «по градиенту концентрации». Такое словоупотребление прочно закрепилось в литературе, но пусть оно не сбивает вас с толку, когда вы размышляете, откуда взялся минус перед градиентом концентрации в уравнении диффузионного потока (уравнении Фика): J = – D dC/dx, где J — диффузионный поток [моль∙см-2∙с-1], D — коэффициент диффузии [см2∙с-1], а dC/dx— градиент концентрации.
** Проводимость (g = 1/R) — это характеристика скорости движения любых зарядов через мембрану, а проницаемость (P) отражает, насколько легко частицы могут двигаться через мембрану независимо от того, движутся они или нет. Для ионов эти величины связаны. Например, в фазе быстрой деполяризации при потенциале действия возрастает как проводимость, так и проницаемость мембраны для ионов натрия. Однако зачастую, если проницаемость канала для какого-то иона высока из-за высокого сродства участков поры канала для этого иона, такие ионы будут двигаться через канал медленнее, и проводимость будет ниже, чем для других ионов, для которых канал менее проницаем.
*** Удельная емкость чистого липидного бислоя составляет около 0,8 мкФ/см2, разница между электроемкостью мембраны и липидного бислоя возникает из-за обилия встроенных в мембрану белков.
Библиография
- Hediger M.A. et al. The ABCs of membrane transporters in health and disease (SLC series): Introduction // Mol. Aspects Med. 2013. Vol. 34. P. 95–107.
- Hille B. Ion Channels of Excitable Membranes. Third edit. Sinauer Associates, Inc., 2001.
- Caterina M.J. et al. The capsaicin receptor: A heat-activated ion channel in the pain pathway // Nature. 1997. Vol. 389, № 6653. P. 816–824.
- Jordt S.-E., Tominaga M., Julius D. Acid potentiation of the capsaicin receptor determined by a key extracellular site // Proc. Natl. Acad. Sci. 2000. Vol. 97, № 14. P. 8134–8139.
- Smart D. et al. The endogenous lipid anandamide is a full agonist at the human vanilloid receptor (hVR1) // Br. J. Pharmacol. 2000. Vol. 129, № 2. P. 227–230.
- Nersesyan Y. et al. Oxytocin Modulates Nociception as an Agonist of Pain-Sensing TRPV1 // Cell Rep. 2017. Vol. 21, № 6. P. 1681–1691.
- Berkovic S.F. et al. Human epilepsies: interaction of genetic and acquired factors // Trends Neurosci. 2006. Vol. 29, № 7. P. 391–397.
- Welsh M.J., Smith A.E. Molecular mechanisms of CFTR chloride channel dysfunction in cystic fibrosis // Cell. 1993. Vol. 73, № 7. P. 1251–1254.
- Ruan Y., Liu N., Priori S.G. Sodium channel mutations and arrhythmias // Nat. Rev. Cardiol. 2009. Vol. 6, № 5. P. 337–348.
- Giudicessi J.R., Ackerman M.J. Potassium-channel mutations and cardiac arrhythmias – Diagnosis and therapy // Nat. Rev. Cardiol. Nature Publishing Group, 2012. Vol. 9, № 6. P. 319–332.
- Thomas R.C. Electrogenic sodium pump in nerve and muscle cells // Am. J. Physiol. 1972. Vol. 52, № 3. P. 563–594.
- Morth J.P. et al. Crystal structure of the sodium-potassium pump // Nature. 2007. Vol. 450, № 7172. P. 1043–1049.
- Lodish H. et al. Molecular Cell Biology (5th edition) // Biochemistry and Molecular Biology Education. 2003.
- Scheel O. et al. Voltage-dependent electrogenic chloride/proton exchange by endosomal CLC proteins // Nature. 2005. Vol. 436, № 7049. P. 424–427.
- Artigas P., Gadsby D.C. Ouabain affinity determining residues lie close to the Na/K pump ion pathway. // Proc. Natl. Acad. Sci. U. S. A. 2006. Vol. 103, № 33. P. 12613–12618.
- Li, C., Ramjeesingh, M., Wang, W., Garami, E., Hewryk, M., Lee, D., Rommens, J. M., Galley, K., Bear, C. E. ATPase Activity of the Cystic Fibrosis Transmembrane Conductance Regulator // Journal of Biological Chemistry. 1996. № 45 (271). P. 28463–28468.
- Martineau M. et al. VGLUT1 functions as a glutamate/proton exchanger with chloride channel activity in hippocampal glutamatergic synapses // Nat. Commun. Springer US, 2017. Vol. 8, № 1.
- Ling G., Gerard R.W. The normal membrane potential of frog sartorius fibers // J. Cell. Comp. Physiol. Wiley-Blackwell, 1949. Vol. 34, № 3. P. 383–396.
- Hodgkin A.L., Huxley A.F. Action potentials recorded from inside a nerve fibre // Nature. 1939. Vol. 144. P. 710–711.
- Cole K.S., Curtis H.J. Electric Impedance of the Squid Giant Axon During Activity // J. Gen. Physiol. 1939. Vol. 22, № 5. P. 649–670.
- Cole K.S. Mostly membranes // Annu. Rev. Physiol. 1979. Vol. 41, № 1. P. 1–24.
- Kandel E.R. et al. Principles of Neural Science. Fifth Edit. The McGraw-Hill Companies, Inc., 2013. 1709 p.
- Hodgkin A.L., Huxley A.F. A quantitative description of membrane current and its application to conduction and excitation in nerve // J. Physiol. 1952. Vol. 117. P. 500–544.
- Capes D.L. et al. Domain IV voltage-sensor movement is both sufficient and rate limiting for fast inactivation in sodium channels // J. Gen. Physiol. 2013. Vol. 142, № 2. P. 101–112.
- http://www.physiologyweb.com/lecture_notes/neuronal_action_potential/neuronal_action_potential_na_and_k_concentrations_do_not_change_during_an_action_potential.html
- Bygrave F.L., Benedetti A. What is the concentration of calcium ions in the endoplasmic reticulum? // Cell Calcium. Churchill Livingstone, 1996. Vol. 19, № 6. P. 547–551.
Нашли опечатку? Выделите фрагмент и нажмите Ctrl+Enter.

As an action potential (nerve impulse) travels down an axon there is a change in electric polarity across the membrane of the axon. In response to a signal from another neuron, sodium- (Na+) and potassium- (K+)–gated ion channels open and close as the membrane reaches its threshold potential. Na+ channels open at the beginning of the action potential, and Na+ moves into the axon, causing depolarization. Repolarization occurs when K+ channels open and K+ moves out of the axon, creating a change in electric polarity between the outside of the cell and the inside. The impulse travels down the axon in one direction only, to the axon terminal where it signals other neurons.
An action potential occurs when the membrane potential of a specific cell location rapidly rises and falls.[1] This depolarization then causes adjacent locations to similarly depolarize. Action potentials occur in several types of animal cells, called excitable cells, which include neurons, muscle cells, and in some plant cells. Certain endocrine cells such as pancreatic beta cells, and certain cells of the anterior pituitary gland are also excitable cells.[2]
In neurons, action potentials play a central role in cell–cell communication by providing for—or with regard to saltatory conduction, assisting—the propagation of signals along the neuron’s axon toward synaptic boutons situated at the ends of an axon; these signals can then connect with other neurons at synapses, or to motor cells or glands. In other types of cells, their main function is to activate intracellular processes. In muscle cells, for example, an action potential is the first step in the chain of events leading to contraction. In beta cells of the pancreas, they provoke release of insulin.[a] Action potentials in neurons are also known as “nerve impulses” or “spikes“, and the temporal sequence of action potentials generated by a neuron is called its “spike train“. A neuron that emits an action potential, or nerve impulse, is often said to “fire”.
Action potentials are generated by special types of voltage-gated ion channels embedded in a cell’s plasma membrane.[b] These channels are shut when the membrane potential is near the (negative) resting potential of the cell, but they rapidly begin to open if the membrane potential increases to a precisely defined threshold voltage, depolarising the transmembrane potential.[b] When the channels open, they allow an inward flow of sodium ions, which changes the electrochemical gradient, which in turn produces a further rise in the membrane potential towards zero. This then causes more channels to open, producing a greater electric current across the cell membrane and so on. The process proceeds explosively until all of the available ion channels are open, resulting in a large upswing in the membrane potential. The rapid influx of sodium ions causes the polarity of the plasma membrane to reverse, and the ion channels then rapidly inactivate. As the sodium channels close, sodium ions can no longer enter the neuron, and they are then actively transported back out of the plasma membrane. Potassium channels are then activated, and there is an outward current of potassium ions, returning the electrochemical gradient to the resting state. After an action potential has occurred, there is a transient negative shift, called the afterhyperpolarization.
In animal cells, there are two primary types of action potentials. One type is generated by voltage-gated sodium channels, the other by voltage-gated calcium channels. Sodium-based action potentials usually last for under one millisecond, but calcium-based action potentials may last for 100 milliseconds or longer.[citation needed] In some types of neurons, slow calcium spikes provide the driving force for a long burst of rapidly emitted sodium spikes. In cardiac muscle cells, on the other hand, an initial fast sodium spike provides a “primer” to provoke the rapid onset of a calcium spike, which then produces muscle contraction.[3]
Overview[edit]

Shape of a typical action potential. The membrane potential remains near a baseline level until at some point in time, it abruptly spikes upward and then rapidly falls.
Nearly all cell membranes in animals, plants and fungi maintain a voltage difference between the exterior and interior of the cell, called the membrane potential. A typical voltage across an animal cell membrane is −70 mV. This means that the interior of the cell has a negative voltage relative to the exterior. In most types of cells, the membrane potential usually stays fairly constant. Some types of cells, however, are electrically active in the sense that their voltages fluctuate over time. In some types of electrically active cells, including neurons and muscle cells, the voltage fluctuations frequently take the form of a rapid upward (positive) spike followed by a rapid fall. These up-and-down cycles are known as action potentials. In some types of neurons, the entire up-and-down cycle takes place in a few thousandths of a second. In muscle cells, a typical action potential lasts about a fifth of a second. In plant cells, an action potential may last three seconds or more.[4]
The electrical properties of a cell are determined by the structure of its membrane. A cell membrane consists of a lipid bilayer of molecules in which larger protein molecules are embedded. The lipid bilayer is highly resistant to movement of electrically charged ions, so it functions as an insulator. The large membrane-embedded proteins, in contrast, provide channels through which ions can pass across the membrane. Action potentials are driven by channel proteins whose configuration switches between closed and open states as a function of the voltage difference between the interior and exterior of the cell. These voltage-sensitive proteins are known as voltage-gated ion channels.
Process in a typical neuron[edit]
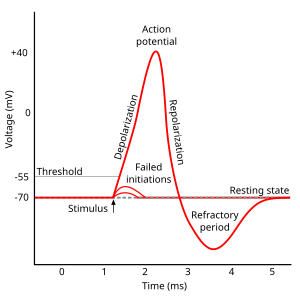
Approximate plot of a typical action potential shows its various phases as the action potential passes a point on a cell membrane. The membrane potential starts out at approximately −70 mV at time zero. A stimulus is applied at time = 1 ms, which raises the membrane potential above −55 mV (the threshold potential). After the stimulus is applied, the membrane potential rapidly rises to a peak potential of +40 mV at time = 2 ms. Just as quickly, the potential then drops and overshoots to −90 mV at time = 3 ms, and finally the resting potential of −70 mV is reestablished at time = 5 ms.
All cells in animal body tissues are electrically polarized – in other words, they maintain a voltage difference across the cell’s plasma membrane, known as the membrane potential. This electrical polarization results from a complex interplay between protein structures embedded in the membrane called ion pumps and ion channels. In neurons, the types of ion channels in the membrane usually vary across different parts of the cell, giving the dendrites, axon, and cell body different electrical properties. As a result, some parts of the membrane of a neuron may be excitable (capable of generating action potentials), whereas others are not. Recent studies have shown that the most excitable part of a neuron is the part after the axon hillock (the point where the axon leaves the cell body), which is called the axonal initial segment, but the axon and cell body are also excitable in most cases.[5]
Each excitable patch of membrane has two important levels of membrane potential: the resting potential, which is the value the membrane potential maintains as long as nothing perturbs the cell, and a higher value called the threshold potential. At the axon hillock of a typical neuron, the resting potential is around –70 millivolts (mV) and the threshold potential is around –55 mV. Synaptic inputs to a neuron cause the membrane to depolarize or hyperpolarize; that is, they cause the membrane potential to rise or fall. Action potentials are triggered when enough depolarization accumulates to bring the membrane potential up to threshold. When an action potential is triggered, the membrane potential abruptly shoots upward and then equally abruptly shoots back downward, often ending below the resting level, where it remains for some period of time. The shape of the action potential is stereotyped; this means that the rise and fall usually have approximately the same amplitude and time course for all action potentials in a given cell. (Exceptions are discussed later in the article). In most neurons, the entire process takes place in about a thousandth of a second. Many types of neurons emit action potentials constantly at rates of up to 10–100 per second. However, some types are much quieter, and may go for minutes or longer without emitting any action potentials.
Biophysical basis[edit]
Action potentials result from the presence in a cell’s membrane of special types of voltage-gated ion channels.[6] A voltage-gated ion channel is a transmembrane protein that has three key properties:
- It is capable of assuming more than one conformation.
- At least one of the conformations creates a channel through the membrane that is permeable to specific types of ions.
- The transition between conformations is influenced by the membrane potential.
Thus, a voltage-gated ion channel tends to be open for some values of the membrane potential, and closed for others. In most cases, however, the relationship between membrane potential and channel state is probabilistic and involves a time delay. Ion channels switch between conformations at unpredictable times: The membrane potential determines the rate of transitions and the probability per unit time of each type of transition.

Action potential propagation along an axon
Voltage-gated ion channels are capable of producing action potentials because they can give rise to positive feedback loops: The membrane potential controls the state of the ion channels, but the state of the ion channels controls the membrane potential. Thus, in some situations, a rise in the membrane potential can cause ion channels to open, thereby causing a further rise in the membrane potential. An action potential occurs when this positive feedback cycle (Hodgkin cycle) proceeds explosively. The time and amplitude trajectory of the action potential are determined by the biophysical properties of the voltage-gated ion channels that produce it. Several types of channels capable of producing the positive feedback necessary to generate an action potential do exist. Voltage-gated sodium channels are responsible for the fast action potentials involved in nerve conduction. Slower action potentials in muscle cells and some types of neurons are generated by voltage-gated calcium channels. Each of these types comes in multiple variants, with different voltage sensitivity and different temporal dynamics.
The most intensively studied type of voltage-dependent ion channels comprises the sodium channels involved in fast nerve conduction. These are sometimes known as Hodgkin-Huxley sodium channels because they were first characterized by Alan Hodgkin and Andrew Huxley in their Nobel Prize-winning studies of the biophysics of the action potential, but can more conveniently be referred to as NaV channels. (The “V” stands for “voltage”.) An NaV channel has three possible states, known as deactivated, activated, and inactivated. The channel is permeable only to sodium ions when it is in the activated state. When the membrane potential is low, the channel spends most of its time in the deactivated (closed) state. If the membrane potential is raised above a certain level, the channel shows increased probability of transitioning to the activated (open) state. The higher the membrane potential the greater the probability of activation. Once a channel has activated, it will eventually transition to the inactivated (closed) state. It tends then to stay inactivated for some time, but, if the membrane potential becomes low again, the channel will eventually transition back to the deactivated state. During an action potential, most channels of this type go through a cycle deactivated→activated→inactivated→deactivated. This is only the population average behavior, however – an individual channel can in principle make any transition at any time. However, the likelihood of a channel’s transitioning from the inactivated state directly to the activated state is very low: A channel in the inactivated state is refractory until it has transitioned back to the deactivated state.
The outcome of all this is that the kinetics of the NaV channels are governed by a transition matrix whose rates are voltage-dependent in a complicated way. Since these channels themselves play a major role in determining the voltage, the global dynamics of the system can be quite difficult to work out. Hodgkin and Huxley approached the problem by developing a set of differential equations for the parameters that govern the ion channel states, known as the Hodgkin-Huxley equations. These equations have been extensively modified by later research, but form the starting point for most theoretical studies of action potential biophysics.
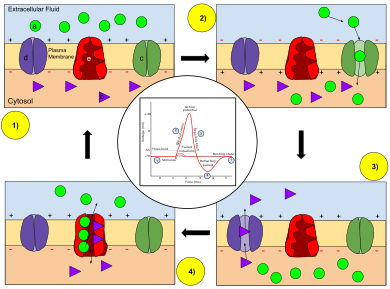
Ion movement during an action potential.
Key: a) Sodium (Na+) ion. b) Potassium (K+) ion. c) Sodium channel. d) Potassium channel. e) Sodium-potassium pump.
In the stages of an action potential, the permeability of the membrane of the neuron changes. At the resting state (1), sodium and potassium ions have limited ability to pass through the membrane, and the neuron has a net negative charge inside. Once the action potential is triggered, the depolarization (2) of the neuron activates sodium channels, allowing sodium ions to pass through the cell membrane into the cell, resulting in a net positive charge in the neuron relative to the extracellular fluid. After the action potential peak is reached, the neuron begins repolarization (3), where the sodium channels close and potassium channels open, allowing potassium ions to cross the membrane into the extracellular fluid, returning the membrane potential to a negative value. Finally, there is a refractory period (4), during which the voltage-dependent ion channels are inactivated while the Na+ and K+ ions return to their resting state distributions across the membrane (1), and the neuron is ready to repeat the process for the next action potential.
As the membrane potential is increased, sodium ion channels open, allowing the entry of sodium ions into the cell. This is followed by the opening of potassium ion channels that permit the exit of potassium ions from the cell. The inward flow of sodium ions increases the concentration of positively charged cations in the cell and causes depolarization, where the potential of the cell is higher than the cell’s resting potential. The sodium channels close at the peak of the action potential, while potassium continues to leave the cell. The efflux of potassium ions decreases the membrane potential or hyperpolarizes the cell. For small voltage increases from rest, the potassium current exceeds the sodium current and the voltage returns to its normal resting value, typically −70 mV.[7][8][9] However, if the voltage increases past a critical threshold, typically 15 mV higher than the resting value, the sodium current dominates. This results in a runaway condition whereby the positive feedback from the sodium current activates even more sodium channels. Thus, the cell fires, producing an action potential.[7][10][11][note 1] The frequency at which a neuron elicits action potentials is often referred to as a firing rate or neural firing rate.
Currents produced by the opening of voltage-gated channels in the course of an action potential are typically significantly larger than the initial stimulating current. Thus, the amplitude, duration, and shape of the action potential are determined largely by the properties of the excitable membrane and not the amplitude or duration of the stimulus. This all-or-nothing property of the action potential sets it apart from graded potentials such as receptor potentials, electrotonic potentials, subthreshold membrane potential oscillations, and synaptic potentials, which scale with the magnitude of the stimulus. A variety of action potential types exist in many cell types and cell compartments as determined by the types of voltage-gated channels, leak channels, channel distributions, ionic concentrations, membrane capacitance, temperature, and other factors.
The principal ions involved in an action potential are sodium and potassium cations; sodium ions enter the cell, and potassium ions leave, restoring equilibrium. Relatively few ions need to cross the membrane for the membrane voltage to change drastically. The ions exchanged during an action potential, therefore, make a negligible change in the interior and exterior ionic concentrations. The few ions that do cross are pumped out again by the continuous action of the sodium–potassium pump, which, with other ion transporters, maintains the normal ratio of ion concentrations across the membrane. Calcium cations and chloride anions are involved in a few types of action potentials, such as the cardiac action potential and the action potential in the single-cell alga Acetabularia, respectively.
Although action potentials are generated locally on patches of excitable membrane, the resulting currents can trigger action potentials on neighboring stretches of membrane, precipitating a domino-like propagation. In contrast to passive spread of electric potentials (electrotonic potential), action potentials are generated anew along excitable stretches of membrane and propagate without decay.[12] Myelinated sections of axons are not excitable and do not produce action potentials and the signal is propagated passively as electrotonic potential. Regularly spaced unmyelinated patches, called the nodes of Ranvier, generate action potentials to boost the signal. Known as saltatory conduction, this type of signal propagation provides a favorable tradeoff of signal velocity and axon diameter. Depolarization of axon terminals, in general, triggers the release of neurotransmitter into the synaptic cleft. In addition, backpropagating action potentials have been recorded in the dendrites of pyramidal neurons, which are ubiquitous in the neocortex.[c] These are thought to have a role in spike-timing-dependent plasticity.
In the Hodgkin–Huxley membrane capacitance model, the speed of transmission of an action potential was undefined and it was assumed that adjacent areas became depolarized due to released ion interference with neighbouring channels. Measurements of ion diffusion and radii have since shown this not to be possible.[citation needed] Moreover, contradictory measurements of entropy changes and timing disputed the capacitance model as acting alone.[citation needed] Alternatively, Gilbert Ling’s adsorption hypothesis, posits that the membrane potential and action potential of a living cell is due to the adsorption of mobile ions onto adsorption sites of cells.[13]
Maturation of the electrical properties of the action potential[edit]
A neuron’s ability to generate and propagate an action potential changes during development. How much the membrane potential of a neuron changes as the result of a current impulse is a function of the membrane input resistance. As a cell grows, more channels are added to the membrane, causing a decrease in input resistance. A mature neuron also undergoes shorter changes in membrane potential in response to synaptic currents. Neurons from a ferret lateral geniculate nucleus have a longer time constant and larger voltage deflection at P0 than they do at P30.[14] One consequence of the decreasing action potential duration is that the fidelity of the signal can be preserved in response to high frequency stimulation. Immature neurons are more prone to synaptic depression than potentiation after high frequency stimulation.[14]
In the early development of many organisms, the action potential is actually initially carried by calcium current rather than sodium current. The opening and closing kinetics of calcium channels during development are slower than those of the voltage-gated sodium channels that will carry the action potential in the mature neurons. The longer opening times for the calcium channels can lead to action potentials that are considerably slower than those of mature neurons.[14] Xenopus neurons initially have action potentials that take 60–90 ms. During development, this time decreases to 1 ms. There are two reasons for this drastic decrease. First, the inward current becomes primarily carried by sodium channels.[15] Second, the delayed rectifier, a potassium channel current, increases to 3.5 times its initial strength.[14]
In order for the transition from a calcium-dependent action potential to a sodium-dependent action potential to proceed new channels must be added to the membrane. If Xenopus neurons are grown in an environment with RNA synthesis or protein synthesis inhibitors that transition is prevented.[16] Even the electrical activity of the cell itself may play a role in channel expression. If action potentials in Xenopus myocytes are blocked, the typical increase in sodium and potassium current density is prevented or delayed.[17]
This maturation of electrical properties is seen across species. Xenopus sodium and potassium currents increase drastically after a neuron goes through its final phase of mitosis. The sodium current density of rat cortical neurons increases by 600% within the first two postnatal weeks.[14]
Neurotransmission[edit]
Anatomy of a neuron[edit]
| Neuron |
|---|
|
Dendrite Soma Axon Nucleus Node of Axon terminal Schwann cell Myelin sheath |
Several types of cells support an action potential, such as plant cells, muscle cells, and the specialized cells of the heart (in which occurs the cardiac action potential). However, the main excitable cell is the neuron, which also has the simplest mechanism for the action potential.
Neurons are electrically excitable cells composed, in general, of one or more dendrites, a single soma, a single axon and one or more axon terminals. Dendrites are cellular projections whose primary function is to receive synaptic signals. Their protrusions, known as dendritic spines, are designed to capture the neurotransmitters released by the presynaptic neuron. They have a high concentration of ligand-gated ion channels. These spines have a thin neck connecting a bulbous protrusion to the dendrite. This ensures that changes occurring inside the spine are less likely to affect the neighboring spines. The dendritic spine can, with rare exception (see LTP), act as an independent unit. The dendrites extend from the soma, which houses the nucleus, and many of the “normal” eukaryotic organelles. Unlike the spines, the surface of the soma is populated by voltage activated ion channels. These channels help transmit the signals generated by the dendrites. Emerging out from the soma is the axon hillock. This region is characterized by having a very high concentration of voltage-activated sodium channels. In general, it is considered to be the spike initiation zone for action potentials,[18] i.e. the trigger zone. Multiple signals generated at the spines, and transmitted by the soma all converge here. Immediately after the axon hillock is the axon. This is a thin tubular protrusion traveling away from the soma. The axon is insulated by a myelin sheath. Myelin is composed of either Schwann cells (in the peripheral nervous system) or oligodendrocytes (in the central nervous system), both of which are types of glial cells. Although glial cells are not involved with the transmission of electrical signals, they communicate and provide important biochemical support to neurons.[19] To be specific, myelin wraps multiple times around the axonal segment, forming a thick fatty layer that prevents ions from entering or escaping the axon. This insulation prevents significant signal decay as well as ensuring faster signal speed. This insulation, however, has the restriction that no channels can be present on the surface of the axon. There are, therefore, regularly spaced patches of membrane, which have no insulation. These nodes of Ranvier can be considered to be “mini axon hillocks”, as their purpose is to boost the signal in order to prevent significant signal decay. At the furthest end, the axon loses its insulation and begins to branch into several axon terminals. These presynaptic terminals, or synaptic boutons, are a specialized area within the axon of the presynaptic cell that contains neurotransmitters enclosed in small membrane-bound spheres called synaptic vesicles.
Initiation[edit]
Before considering the propagation of action potentials along axons and their termination at the synaptic knobs, it is helpful to consider the methods by which action potentials can be initiated at the axon hillock. The basic requirement is that the membrane voltage at the hillock be raised above the threshold for firing.[7][8][20][21] There are several ways in which this depolarization can occur.

When an action potential arrives at the end of the pre-synaptic axon (top), it causes the release of neurotransmitter molecules that open ion channels in the post-synaptic neuron (bottom). The combined excitatory and inhibitory postsynaptic potentials of such inputs can begin a new action potential in the post-synaptic neuron.
Dynamics[edit]
Action potentials are most commonly initiated by excitatory postsynaptic potentials from a presynaptic neuron.[22] Typically, neurotransmitter molecules are released by the presynaptic neuron. These neurotransmitters then bind to receptors on the postsynaptic cell. This binding opens various types of ion channels. This opening has the further effect of changing the local permeability of the cell membrane and, thus, the membrane potential. If the binding increases the voltage (depolarizes the membrane), the synapse is excitatory. If, however, the binding decreases the voltage (hyperpolarizes the membrane), it is inhibitory. Whether the voltage is increased or decreased, the change propagates passively to nearby regions of the membrane (as described by the cable equation and its refinements). Typically, the voltage stimulus decays exponentially with the distance from the synapse and with time from the binding of the neurotransmitter. Some fraction of an excitatory voltage may reach the axon hillock and may (in rare cases) depolarize the membrane enough to provoke a new action potential. More typically, the excitatory potentials from several synapses must work together at nearly the same time to provoke a new action potential. Their joint efforts can be thwarted, however, by the counteracting inhibitory postsynaptic potentials.
Neurotransmission can also occur through electrical synapses.[23] Due to the direct connection between excitable cells in the form of gap junctions, an action potential can be transmitted directly from one cell to the next in either direction. The free flow of ions between cells enables rapid non-chemical-mediated transmission. Rectifying channels ensure that action potentials move only in one direction through an electrical synapse.[citation needed] Electrical synapses are found in all nervous systems, including the human brain, although they are a distinct minority.[24]
“All-or-none” principle[edit]
The amplitude of an action potential is often thought to be independent of the amount of current that produced it. In other words, larger currents do not create larger action potentials. Therefore, action potentials are said to be all-or-none signals, since either they occur fully or they do not occur at all.[d][e][f] This is in contrast to receptor potentials, whose amplitudes are dependent on the intensity of a stimulus.[25] In both cases, the frequency of action potentials is correlated with the intensity of a stimulus.
Despite the classical view of the action potential as a stereotyped, uniform signal having dominated the field of neuroscience for many decades, newer evidence does suggest that action potentials are more complex events indeed capable of transmitting information through not just their amplitude, but their duration and phase as well, sometimes even up to distances originally not thought to be possible.[26][27][28][29]
Sensory neurons[edit]
In sensory neurons, an external signal such as pressure, temperature, light, or sound is coupled with the opening and closing of ion channels, which in turn alter the ionic permeabilities of the membrane and its voltage.[30] These voltage changes can again be excitatory (depolarizing) or inhibitory (hyperpolarizing) and, in some sensory neurons, their combined effects can depolarize the axon hillock enough to provoke action potentials. Some examples in humans include the olfactory receptor neuron and Meissner’s corpuscle, which are critical for the sense of smell and touch, respectively. However, not all sensory neurons convert their external signals into action potentials; some do not even have an axon.[31] Instead, they may convert the signal into the release of a neurotransmitter, or into continuous graded potentials, either of which may stimulate subsequent neuron(s) into firing an action potential. For illustration, in the human ear, hair cells convert the incoming sound into the opening and closing of mechanically gated ion channels, which may cause neurotransmitter molecules to be released. In similar manner, in the human retina, the initial photoreceptor cells and the next layer of cells (comprising bipolar cells and horizontal cells) do not produce action potentials; only some amacrine cells and the third layer, the ganglion cells, produce action potentials, which then travel up the optic nerve.
Pacemaker potentials[edit]
In pacemaker potentials, the cell spontaneously depolarizes (straight line with upward slope) until it fires an action potential.
In sensory neurons, action potentials result from an external stimulus. However, some excitable cells require no such stimulus to fire: They spontaneously depolarize their axon hillock and fire action potentials at a regular rate, like an internal clock.[32] The voltage traces of such cells are known as pacemaker potentials.[33] The cardiac pacemaker cells of the sinoatrial node in the heart provide a good example.[g] Although such pacemaker potentials have a natural rhythm, it can be adjusted by external stimuli; for instance, heart rate can be altered by pharmaceuticals as well as signals from the sympathetic and parasympathetic nerves.[34] The external stimuli do not cause the cell’s repetitive firing, but merely alter its timing.[33] In some cases, the regulation of frequency can be more complex, leading to patterns of action potentials, such as bursting.
Phases[edit]
The course of the action potential can be divided into five parts: the rising phase, the peak phase, the falling phase, the undershoot phase, and the refractory period. During the rising phase the membrane potential depolarizes (becomes more positive). The point at which depolarization stops is called the peak phase. At this stage, the membrane potential reaches a maximum. Subsequent to this, there is a falling phase. During this stage the membrane potential becomes more negative, returning towards resting potential. The undershoot, or afterhyperpolarization, phase is the period during which the membrane potential temporarily becomes more negatively charged than when at rest (hyperpolarized). Finally, the time during which a subsequent action potential is impossible or difficult to fire is called the refractory period, which may overlap with the other phases.[35]
The course of the action potential is determined by two coupled effects.[36] First, voltage-sensitive ion channels open and close in response to changes in the membrane voltage Vm. This changes the membrane’s permeability to those ions.[37] Second, according to the Goldman equation, this change in permeability changes the equilibrium potential Em, and, thus, the membrane voltage Vm.[h] Thus, the membrane potential affects the permeability, which then further affects the membrane potential. This sets up the possibility for positive feedback, which is a key part of the rising phase of the action potential.[7][10] A complicating factor is that a single ion channel may have multiple internal “gates” that respond to changes in Vm in opposite ways, or at different rates.[38][i] For example, although raising Vm opens most gates in the voltage-sensitive sodium channel, it also closes the channel’s “inactivation gate”, albeit more slowly.[39] Hence, when Vm is raised suddenly, the sodium channels open initially, but then close due to the slower inactivation.
The voltages and currents of the action potential in all of its phases were modeled accurately by Alan Lloyd Hodgkin and Andrew Huxley in 1952,[i] for which they were awarded the Nobel Prize in Physiology or Medicine in 1963.[lower-Greek 2] However, their model considers only two types of voltage-sensitive ion channels, and makes several assumptions about them, e.g., that their internal gates open and close independently of one another. In reality, there are many types of ion channels,[40] and they do not always open and close independently.[j]
Stimulation and rising phase[edit]
A typical action potential begins at the axon hillock[41] with a sufficiently strong depolarization, e.g., a stimulus that increases Vm. This depolarization is often caused by the injection of extra sodium cations into the cell; these cations can come from a wide variety of sources, such as chemical synapses, sensory neurons or pacemaker potentials.
For a neuron at rest, there is a high concentration of sodium and chloride ions in the extracellular fluid compared to the intracellular fluid, while there is a high concentration of potassium ions in the intracellular fluid compared to the extracellular fluid. The difference in concentrations, which causes ions to move from a high to a low concentration, and electrostatic effects (attraction of opposite charges) are responsible for the movement of ions in and out of the neuron. The inside of a neuron has a negative charge, relative to the cell exterior, from the movement of K+ out of the cell. The neuron membrane is more permeable to K+ than to other ions, allowing this ion to selectively move out of the cell, down its concentration gradient. This concentration gradient along with potassium leak channels present on the membrane of the neuron causes an efflux of potassium ions making the resting potential close to EK ≈ –75 mV.[42] Since Na+ ions are in higher concentrations outside of the cell, the concentration and voltage differences both drive them into the cell when Na+ channels open. Depolarization opens both the sodium and potassium channels in the membrane, allowing the ions to flow into and out of the axon, respectively. If the depolarization is small (say, increasing Vm from −70 mV to −60 mV), the outward potassium current overwhelms the inward sodium current and the membrane repolarizes back to its normal resting potential around −70 mV.[7][8][9] However, if the depolarization is large enough, the inward sodium current increases more than the outward potassium current and a runaway condition (positive feedback) results: the more inward current there is, the more Vm increases, which in turn further increases the inward current.[7][10] A sufficiently strong depolarization (increase in Vm) causes the voltage-sensitive sodium channels to open; the increasing permeability to sodium drives Vm closer to the sodium equilibrium voltage ENa≈ +55 mV. The increasing voltage in turn causes even more sodium channels to open, which pushes Vm still further towards ENa. This positive feedback continues until the sodium channels are fully open and Vm is close to ENa.[7][8][20][21] The sharp rise in Vm and sodium permeability correspond to the rising phase of the action potential.[7][8][20][21]
The critical threshold voltage for this runaway condition is usually around −45 mV, but it depends on the recent activity of the axon. A cell that has just fired an action potential cannot fire another one immediately, since the Na+ channels have not recovered from the inactivated state. The period during which no new action potential can be fired is called the absolute refractory period.[43][44][45] At longer times, after some but not all of the ion channels have recovered, the axon can be stimulated to produce another action potential, but with a higher threshold, requiring a much stronger depolarization, e.g., to −30 mV. The period during which action potentials are unusually difficult to evoke is called the relative refractory period.[43][44][45]
Peak phase[edit]
The positive feedback of the rising phase slows and comes to a halt as the sodium ion channels become maximally open. At the peak of the action potential, the sodium permeability is maximized and the membrane voltage Vm is nearly equal to the sodium equilibrium voltage ENa. However, the same raised voltage that opened the sodium channels initially also slowly shuts them off, by closing their pores; the sodium channels become inactivated.[39] This lowers the membrane’s permeability to sodium relative to potassium, driving the membrane voltage back towards the resting value. At the same time, the raised voltage opens voltage-sensitive potassium channels; the increase in the membrane’s potassium permeability drives Vm towards EK.[39] Combined, these changes in sodium and potassium permeability cause Vm to drop quickly, repolarizing the membrane and producing the “falling phase” of the action potential.[43][46][21][47]
Afterhyperpolarization[edit]
The depolarized voltage opens additional voltage-dependent potassium channels, and some of these do not close right away when the membrane returns to its normal resting voltage. In addition, further potassium channels open in response to the influx of calcium ions during the action potential. The intracellular concentration of potassium ions is transiently unusually low, making the membrane voltage Vm even closer to the potassium equilibrium voltage EK. The membrane potential goes below the resting membrane potential. Hence, there is an undershoot or hyperpolarization, termed an afterhyperpolarization, that persists until the membrane potassium permeability returns to its usual value, restoring the membrane potential to the resting state.[48][46]
Refractory period[edit]
Each action potential is followed by a refractory period, which can be divided into an absolute refractory period, during which it is impossible to evoke another action potential, and then a relative refractory period, during which a stronger-than-usual stimulus is required.[43][44][45] These two refractory periods are caused by changes in the state of sodium and potassium channel molecules. When closing after an action potential, sodium channels enter an “inactivated” state, in which they cannot be made to open regardless of the membrane potential—this gives rise to the absolute refractory period. Even after a sufficient number of sodium channels have transitioned back to their resting state, it frequently happens that a fraction of potassium channels remains open, making it difficult for the membrane potential to depolarize, and thereby giving rise to the relative refractory period. Because the density and subtypes of potassium channels may differ greatly between different types of neurons, the duration of the relative refractory period is highly variable.
The absolute refractory period is largely responsible for the unidirectional propagation of action potentials along axons.[49] At any given moment, the patch of axon behind the actively spiking part is refractory, but the patch in front, not having been activated recently, is capable of being stimulated by the depolarization from the action potential.
Propagation[edit]
The action potential generated at the axon hillock propagates as a wave along the axon.[50] The currents flowing inwards at a point on the axon during an action potential spread out along the axon, and depolarize the adjacent sections of its membrane. If sufficiently strong, this depolarization provokes a similar action potential at the neighboring membrane patches. This basic mechanism was demonstrated by Alan Lloyd Hodgkin in 1937. After crushing or cooling nerve segments and thus blocking the action potentials, he showed that an action potential arriving on one side of the block could provoke another action potential on the other, provided that the blocked segment was sufficiently short.[k]
Once an action potential has occurred at a patch of membrane, the membrane patch needs time to recover before it can fire again. At the molecular level, this absolute refractory period corresponds to the time required for the voltage-activated sodium channels to recover from inactivation, i.e., to return to their closed state.[44] There are many types of voltage-activated potassium channels in neurons. Some of them inactivate fast (A-type currents) and some of them inactivate slowly or not inactivate at all; this variability guarantees that there will be always an available source of current for repolarization, even if some of the potassium channels are inactivated because of preceding depolarization. On the other hand, all neuronal voltage-activated sodium channels inactivate within several milliseconds during strong depolarization, thus making following depolarization impossible until a substantial fraction of sodium channels have returned to their closed state. Although it limits the frequency of firing,[51] the absolute refractory period ensures that the action potential moves in only one direction along an axon.[49] The currents flowing in due to an action potential spread out in both directions along the axon.[52] However, only the unfired part of the axon can respond with an action potential; the part that has just fired is unresponsive until the action potential is safely out of range and cannot restimulate that part. In the usual orthodromic conduction, the action potential propagates from the axon hillock towards the synaptic knobs (the axonal termini); propagation in the opposite direction—known as antidromic conduction—is very rare.[53] However, if a laboratory axon is stimulated in its middle, both halves of the axon are “fresh”, i.e., unfired; then two action potentials will be generated, one traveling towards the axon hillock and the other traveling towards the synaptic knobs.
Myelin and saltatory conduction[edit]

In saltatory conduction, an action potential at one node of Ranvier causes inwards currents that depolarize the membrane at the next node, provoking a new action potential there; the action potential appears to “hop” from node to node.
In order to enable fast and efficient transduction of electrical signals in the nervous system, certain neuronal axons are covered with myelin sheaths. Myelin is a multilamellar membrane that enwraps the axon in segments separated by intervals known as nodes of Ranvier. It is produced by specialized cells: Schwann cells exclusively in the peripheral nervous system, and oligodendrocytes exclusively in the central nervous system. Myelin sheath reduces membrane capacitance and increases membrane resistance in the inter-node intervals, thus allowing a fast, saltatory movement of action potentials from node to node.[l][m][n] Myelination is found mainly in vertebrates, but an analogous system has been discovered in a few invertebrates, such as some species of shrimp.[o] Not all neurons in vertebrates are myelinated; for example, axons of the neurons comprising the autonomous nervous system are not, in general, myelinated.
Myelin prevents ions from entering or leaving the axon along myelinated segments. As a general rule, myelination increases the conduction velocity of action potentials and makes them more energy-efficient. Whether saltatory or not, the mean conduction velocity of an action potential ranges from 1 meter per second (m/s) to over 100 m/s, and, in general, increases with axonal diameter.[p]
Action potentials cannot propagate through the membrane in myelinated segments of the axon. However, the current is carried by the cytoplasm, which is sufficient to depolarize the first or second subsequent node of Ranvier. Instead, the ionic current from an action potential at one node of Ranvier provokes another action potential at the next node; this apparent “hopping” of the action potential from node to node is known as saltatory conduction. Although the mechanism of saltatory conduction was suggested in 1925 by Ralph Lillie,[q] the first experimental evidence for saltatory conduction came from Ichiji Tasaki[r] and Taiji Takeuchi[s][54] and from Andrew Huxley and Robert Stämpfli.[t] By contrast, in unmyelinated axons, the action potential provokes another in the membrane immediately adjacent, and moves continuously down the axon like a wave.

Comparison of the conduction velocities of myelinated and unmyelinated axons in the cat.[55] The conduction velocity v of myelinated neurons varies roughly linearly with axon diameter d (that is, v ∝ d),[p] whereas the speed of unmyelinated neurons varies roughly as the square root (v ∝√d).[u] The red and blue curves are fits of experimental data, whereas the dotted lines are their theoretical extrapolations.
Myelin has two important advantages: fast conduction speed and energy efficiency. For axons larger than a minimum diameter (roughly 1 micrometre), myelination increases the conduction velocity of an action potential, typically tenfold.[v] Conversely, for a given conduction velocity, myelinated fibers are smaller than their unmyelinated counterparts. For example, action potentials move at roughly the same speed (25 m/s) in a myelinated frog axon and an unmyelinated squid giant axon, but the frog axon has a roughly 30-fold smaller diameter and 1000-fold smaller cross-sectional area. Also, since the ionic currents are confined to the nodes of Ranvier, far fewer ions “leak” across the membrane, saving metabolic energy. This saving is a significant selective advantage, since the human nervous system uses approximately 20% of the body’s metabolic energy.[v]
The length of axons’ myelinated segments is important to the success of saltatory conduction. They should be as long as possible to maximize the speed of conduction, but not so long that the arriving signal is too weak to provoke an action potential at the next node of Ranvier. In nature, myelinated segments are generally long enough for the passively propagated signal to travel for at least two nodes while retaining enough amplitude to fire an action potential at the second or third node. Thus, the safety factor of saltatory conduction is high, allowing transmission to bypass nodes in case of injury. However, action potentials may end prematurely in certain places where the safety factor is low, even in unmyelinated neurons; a common example is the branch point of an axon, where it divides into two axons.[56]
Some diseases degrade myelin and impair saltatory conduction, reducing the conduction velocity of action potentials.[w] The most well-known of these is multiple sclerosis, in which the breakdown of myelin impairs coordinated movement.[57]
Cable theory[edit]

Cable theory’s simplified view of a neuronal fiber. The connected RC circuits correspond to adjacent segments of a passive neurite. The extracellular resistances re (the counterparts of the intracellular resistances ri) are not shown, since they are usually negligibly small; the extracellular medium may be assumed to have the same voltage everywhere.
The flow of currents within an axon can be described quantitatively by cable theory[58] and its elaborations, such as the compartmental model.[59] Cable theory was developed in 1855 by Lord Kelvin to model the transatlantic telegraph cable[x] and was shown to be relevant to neurons by Hodgkin and Rushton in 1946.[y] In simple cable theory, the neuron is treated as an electrically passive, perfectly cylindrical transmission cable, which can be described by a partial differential equation[58]
where V(x, t) is the voltage across the membrane at a time t and a position x along the length of the neuron, and where λ and τ are the characteristic length and time scales on which those voltages decay in response to a stimulus. Referring to the circuit diagram on the right, these scales can be determined from the resistances and capacitances per unit length.[60]
These time and length-scales can be used to understand the dependence of the conduction velocity on the diameter of the neuron in unmyelinated fibers. For example, the time-scale τ increases with both the membrane resistance rm and capacitance cm. As the capacitance increases, more charge must be transferred to produce a given transmembrane voltage (by the equation Q = CV); as the resistance increases, less charge is transferred per unit time, making the equilibration slower. In a similar manner, if the internal resistance per unit length ri is lower in one axon than in another (e.g., because the radius of the former is larger), the spatial decay length λ becomes longer and the conduction velocity of an action potential should increase. If the transmembrane resistance rm is increased, that lowers the average “leakage” current across the membrane, likewise causing λ to become longer, increasing the conduction velocity.
Termination[edit]
Chemical synapses[edit]
In general, action potentials that reach the synaptic knobs cause a neurotransmitter to be released into the synaptic cleft.[z] Neurotransmitters are small molecules that may open ion channels in the postsynaptic cell; most axons have the same neurotransmitter at all of their termini. The arrival of the action potential opens voltage-sensitive calcium channels in the presynaptic membrane; the influx of calcium causes vesicles filled with neurotransmitter to migrate to the cell’s surface and release their contents into the synaptic cleft.[aa] This complex process is inhibited by the neurotoxins tetanospasmin and botulinum toxin, which are responsible for tetanus and botulism, respectively.[ab]
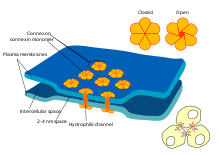
Electrical synapses[edit]
Some synapses dispense with the “middleman” of the neurotransmitter, and connect the presynaptic and postsynaptic cells together.[ac] When an action potential reaches such a synapse, the ionic currents flowing into the presynaptic cell can cross the barrier of the two cell membranes and enter the postsynaptic cell through pores known as connexons.[ad] Thus, the ionic currents of the presynaptic action potential can directly stimulate the postsynaptic cell. Electrical synapses allow for faster transmission because they do not require the slow diffusion of neurotransmitters across the synaptic cleft. Hence, electrical synapses are used whenever fast response and coordination of timing are crucial, as in escape reflexes, the retina of vertebrates, and the heart.
Neuromuscular junctions[edit]
A special case of a chemical synapse is the neuromuscular junction, in which the axon of a motor neuron terminates on a muscle fiber.[ae] In such cases, the released neurotransmitter is acetylcholine, which binds to the acetylcholine receptor, an integral membrane protein in the membrane (the sarcolemma) of the muscle fiber.[af] However, the acetylcholine does not remain bound; rather, it dissociates and is hydrolyzed by the enzyme, acetylcholinesterase, located in the synapse. This enzyme quickly reduces the stimulus to the muscle, which allows the degree and timing of muscular contraction to be regulated delicately. Some poisons inactivate acetylcholinesterase to prevent this control, such as the nerve agents sarin and tabun,[ag] and the insecticides diazinon and malathion.[ah]
Other cell types[edit]
Cardiac action potentials[edit]
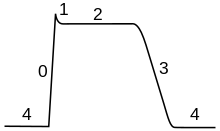
Phases of a cardiac action potential. The sharp rise in voltage (“0”) corresponds to the influx of sodium ions, whereas the two decays (“1” and “3”, respectively) correspond to the sodium-channel inactivation and the repolarizing eflux of potassium ions. The characteristic plateau (“2”) results from the opening of voltage-sensitive calcium channels.
The cardiac action potential differs from the neuronal action potential by having an extended plateau, in which the membrane is held at a high voltage for a few hundred milliseconds prior to being repolarized by the potassium current as usual.[ai] This plateau is due to the action of slower calcium channels opening and holding the membrane voltage near their equilibrium potential even after the sodium channels have inactivated.
The cardiac action potential plays an important role in coordinating the contraction of the heart.[ai] The cardiac cells of the sinoatrial node provide the pacemaker potential that synchronizes the heart. The action potentials of those cells propagate to and through the atrioventricular node (AV node), which is normally the only conduction pathway between the atria and the ventricles. Action potentials from the AV node travel through the bundle of His and thence to the Purkinje fibers.[note 2] Conversely, anomalies in the cardiac action potential—whether due to a congenital mutation or injury—can lead to human pathologies, especially arrhythmias.[ai] Several anti-arrhythmia drugs act on the cardiac action potential, such as quinidine, lidocaine, beta blockers, and verapamil.[aj]
Muscular action potentials[edit]
The action potential in a normal skeletal muscle cell is similar to the action potential in neurons.[61] Action potentials result from the depolarization of the cell membrane (the sarcolemma), which opens voltage-sensitive sodium channels; these become inactivated and the membrane is repolarized through the outward current of potassium ions. The resting potential prior to the action potential is typically −90mV, somewhat more negative than typical neurons. The muscle action potential lasts roughly 2–4 ms, the absolute refractory period is roughly 1–3 ms, and the conduction velocity along the muscle is roughly 5 m/s. The action potential releases calcium ions that free up the tropomyosin and allow the muscle to contract. Muscle action potentials are provoked by the arrival of a pre-synaptic neuronal action potential at the neuromuscular junction, which is a common target for neurotoxins.[ag]
Plant action potentials[edit]
Plant and fungal cells[ak] are also electrically excitable. The fundamental difference from animal action potentials is that the depolarization in plant cells is not accomplished by an uptake of positive sodium ions, but by release of negative chloride ions.[al][am][an] In 1906, J. C. Bose published the first measurements of action potentials in plants, which had previously been discovered by Burdon-Sanderson and Darwin.[62] An increase in cytoplasmic calcium ions may be the cause of anion release into the cell. This makes calcium a precursor to ion movements, such as the influx of negative chloride ions and efflux of positive potassium ions, as seen in barley leaves.[63]
The initial influx of calcium ions also poses a small cellular depolarization, causing the voltage-gated ion channels to open and allowing full depolarization to be propagated by chloride ions.
Some plants (e.g. Dionaea muscipula) use sodium-gated channels to operate movements and essentially “count”. Dionaea muscipula, also known as the Venus flytrap, is found in subtropical wetlands in North and South Carolina.[64] When there are poor soil nutrients, the flytrap relies on a diet of insects and animals.[65] Despite research on the plant, there lacks an understanding behind the molecular basis to the Venus flytraps, and carnivore plants in general.[66]
However, plenty of research has been done on action potentials and how they affect movement and clockwork within the Venus flytrap. To start, the resting membrane potential of the Venus flytrap (-120mV) is lower than animal cells (usually -90mV to -40mV).[66][67] The lower resting potential makes it easier to activate an action potential. Thus, when an insect lands on the trap of the plant, it triggers a hair-like mechanoreceptor.[66] This receptor then activates an action potential which lasts around 1.5 ms.[68] Ultimately, this causes an increase of positive Calcium ions into the cell, slightly depolarizing it.
However, the flytrap doesn’t close after one trigger. Instead, it requires the activation of 2 or more hairs.[65][66] If only one hair is triggered, it throws the activation as a false positive. Further, the second hair must be activated within a certain time interval (0.75 s – 40 s) for it to register with the first activation.[66] Thus, a buildup of calcium starts and slowly falls from the first trigger. When the second action potential is fired within the time interval, it reaches the Calcium threshold to depolarize the cell, closing the trap on the prey within a fraction of a second.[66]
Together with the subsequent release of positive potassium ions the action potential in plants involves an osmotic loss of salt (KCl). Whereas, the animal action potential is osmotically neutral because equal amounts of entering sodium and leaving potassium cancel each other osmotically. The interaction of electrical and osmotic relations in plant cells[ao] appears to have arisen from an osmotic function of electrical excitability in a common unicellular ancestors of plants and animals under changing salinity conditions. Further, the present function of rapid signal transmission is seen as a newer accomplishment of metazoan cells in a more stable osmotic environment.[69] It is likely that the familiar signaling function of action potentials in some vascular plants (e.g. Mimosa pudica) arose independently from that in metazoan excitable cells.
Unlike the rising phase and peak, the falling phase and after-hyperpolarization seem to depend primarily on cations that are not calcium. To initiate repolarization, the cell requires movement of potassium out of the cell through passive transportation on the membrane. This differs from neurons because the movement of potassium does not dominate the decrease in membrane potential; In fact, to fully repolarize, a plant cell requires energy in the form of ATP to assist in the release of hydrogen from the cell – utilizing a transporter commonly known as H+-ATPase.[70][66]
Taxonomic distribution and evolutionary advantages[edit]
Action potentials are found throughout multicellular organisms, including plants, invertebrates such as insects, and vertebrates such as reptiles and mammals.[ap] Sponges seem to be the main phylum of multicellular eukaryotes that does not transmit action potentials, although some studies have suggested that these organisms have a form of electrical signaling, too.[aq] The resting potential, as well as the size and duration of the action potential, have not varied much with evolution, although the conduction velocity does vary dramatically with axonal diameter and myelination.
| Animal | Cell type | Resting potential (mV) | AP increase (mV) | AP duration (ms) | Conduction speed (m/s) |
|---|---|---|---|---|---|
| Squid (Loligo) | Giant axon | −60 | 120 | 0.75 | 35 |
| Earthworm (Lumbricus) | Median giant fiber | −70 | 100 | 1.0 | 30 |
| Cockroach (Periplaneta) | Giant fiber | −70 | 80–104 | 0.4 | 10 |
| Frog (Rana) | Sciatic nerve axon | −60 to −80 | 110–130 | 1.0 | 7–30 |
| Cat (Felis) | Spinal motor neuron | −55 to −80 | 80–110 | 1–1.5 | 30–120 |
Given its conservation throughout evolution, the action potential seems to confer evolutionary advantages. One function of action potentials is rapid, long-range signaling within the organism; the conduction velocity can exceed 110 m/s, which is one-third the speed of sound. For comparison, a hormone molecule carried in the bloodstream moves at roughly 8 m/s in large arteries. Part of this function is the tight coordination of mechanical events, such as the contraction of the heart. A second function is the computation associated with its generation. Being an all-or-none signal that does not decay with transmission distance, the action potential has similar advantages to digital electronics. The integration of various dendritic signals at the axon hillock and its thresholding to form a complex train of action potentials is another form of computation, one that has been exploited biologically to form central pattern generators and mimicked in artificial neural networks.
The common prokaryotic/eukaryotic ancestor, which lived perhaps four billion years ago, is believed to have had voltage-gated channels. This functionality was likely, at some later point, cross-purposed to provide a communication mechanism. Even modern single-celled bacteria can utilize action potentials to communicate with other bacteria in the same biofilm.[72]
Experimental methods[edit]

The study of action potentials has required the development of new experimental methods. The initial work, prior to 1955, was carried out primarily by Alan Lloyd Hodgkin and Andrew Fielding Huxley, who were, along John Carew Eccles, awarded the 1963 Nobel Prize in Physiology or Medicine for their contribution to the description of the ionic basis of nerve conduction. It focused on three goals: isolating signals from single neurons or axons, developing fast, sensitive electronics, and shrinking electrodes enough that the voltage inside a single cell could be recorded.
The first problem was solved by studying the giant axons found in the neurons of the squid (Loligo forbesii and Doryteuthis pealeii, at the time classified as Loligo pealeii).[ar] These axons are so large in diameter (roughly 1 mm, or 100-fold larger than a typical neuron) that they can be seen with the naked eye, making them easy to extract and manipulate.[i][as] However, they are not representative of all excitable cells, and numerous other systems with action potentials have been studied.
The second problem was addressed with the crucial development of the voltage clamp,[at] which permitted experimenters to study the ionic currents underlying an action potential in isolation, and eliminated a key source of electronic noise, the current IC associated with the capacitance C of the membrane.[74] Since the current equals C times the rate of change of the transmembrane voltage Vm, the solution was to design a circuit that kept Vm fixed (zero rate of change) regardless of the currents flowing across the membrane. Thus, the current required to keep Vm at a fixed value is a direct reflection of the current flowing through the membrane. Other electronic advances included the use of Faraday cages and electronics with high input impedance, so that the measurement itself did not affect the voltage being measured.[75]
The third problem, that of obtaining electrodes small enough to record voltages within a single axon without perturbing it, was solved in 1949 with the invention of the glass micropipette electrode,[au] which was quickly adopted by other researchers.[av][aw] Refinements of this method are able to produce electrode tips that are as fine as 100 Å (10 nm), which also confers high input impedance.[76] Action potentials may also be recorded with small metal electrodes placed just next to a neuron, with neurochips containing EOSFETs, or optically with dyes that are sensitive to Ca2+ or to voltage.[ax]

As revealed by a patch clamp electrode, an ion channel has two states: open (high conductance) and closed (low conductance).
While glass micropipette electrodes measure the sum of the currents passing through many ion channels, studying the electrical properties of a single ion channel became possible in the 1970s with the development of the patch clamp by Erwin Neher and Bert Sakmann. For this discovery, they were awarded the Nobel Prize in Physiology or Medicine in 1991.[lower-Greek 3] Patch-clamping verified that ionic channels have discrete states of conductance, such as open, closed and inactivated.
Optical imaging technologies have been developed in recent years to measure action potentials, either via simultaneous multisite recordings or with ultra-spatial resolution. Using voltage-sensitive dyes, action potentials have been optically recorded from a tiny patch of cardiomyocyte membrane.[ay]
Neurotoxins[edit]
Several neurotoxins, both natural and synthetic, are designed to block the action potential. Tetrodotoxin from the pufferfish and saxitoxin from the Gonyaulax (the dinoflagellate genus responsible for “red tides”) block action potentials by inhibiting the voltage-sensitive sodium channel;[az] similarly, dendrotoxin from the black mamba snake inhibits the voltage-sensitive potassium channel. Such inhibitors of ion channels serve an important research purpose, by allowing scientists to “turn off” specific channels at will, thus isolating the other channels’ contributions; they can also be useful in purifying ion channels by affinity chromatography or in assaying their concentration. However, such inhibitors also make effective neurotoxins, and have been considered for use as chemical weapons. Neurotoxins aimed at the ion channels of insects have been effective insecticides; one example is the synthetic permethrin, which prolongs the activation of the sodium channels involved in action potentials. The ion channels of insects are sufficiently different from their human counterparts that there are few side effects in humans.
History[edit]
The role of electricity in the nervous systems of animals was first observed in dissected frogs by Luigi Galvani, who studied it from 1791 to 1797.[ba] Galvani’s results stimulated Alessandro Volta to develop the Voltaic pile—the earliest-known electric battery—with which he studied animal electricity (such as electric eels) and the physiological responses to applied direct-current voltages.[bb]
Scientists of the 19th century studied the propagation of electrical signals in whole nerves (i.e., bundles of neurons) and demonstrated that nervous tissue was made up of cells, instead of an interconnected network of tubes (a reticulum).[77] Carlo Matteucci followed up Galvani’s studies and demonstrated that cell membranes had a voltage across them and could produce direct current. Matteucci’s work inspired the German physiologist, Emil du Bois-Reymond, who discovered the action potential in 1843.[78] The conduction velocity of action potentials was first measured in 1850 by du Bois-Reymond’s friend, Hermann von Helmholtz.[79] To establish that nervous tissue is made up of discrete cells, the Spanish physician Santiago Ramón y Cajal and his students used a stain developed by Camillo Golgi to reveal the myriad shapes of neurons, which they rendered painstakingly. For their discoveries, Golgi and Ramón y Cajal were awarded the 1906 Nobel Prize in Physiology.[lower-Greek 4] Their work resolved a long-standing controversy in the neuroanatomy of the 19th century; Golgi himself had argued for the network model of the nervous system.
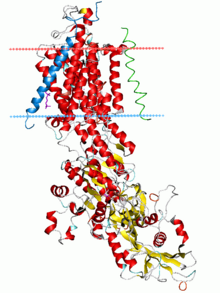
Ribbon diagram of the sodium–potassium pump in its E2-Pi state. The estimated boundaries of the lipid bilayer are shown as blue (intracellular) and red (extracellular) planes.
The 20th century was a significant era for electrophysiology. In 1902 and again in 1912, Julius Bernstein advanced the hypothesis that the action potential resulted from a change in the permeability of the axonal membrane to ions.[bc][80] Bernstein’s hypothesis was confirmed by Ken Cole and Howard Curtis, who showed that membrane conductance increases during an action potential.[bd] In 1907, Louis Lapicque suggested that the action potential was generated as a threshold was crossed,[be] what would be later shown as a product of the dynamical systems of ionic conductances. In 1949, Alan Hodgkin and Bernard Katz refined Bernstein’s hypothesis by considering that the axonal membrane might have different permeabilities to different ions; in particular, they demonstrated the crucial role of the sodium permeability for the action potential.[bf] They made the first actual recording of the electrical changes across the neuronal membrane that mediate the action potential.[lower-Greek 5] This line of research culminated in the five 1952 papers of Hodgkin, Katz and Andrew Huxley, in which they applied the voltage clamp technique to determine the dependence of the axonal membrane’s permeabilities to sodium and potassium ions on voltage and time, from which they were able to reconstruct the action potential quantitatively.[i] Hodgkin and Huxley correlated the properties of their mathematical model with discrete ion channels that could exist in several different states, including “open”, “closed”, and “inactivated”. Their hypotheses were confirmed in the mid-1970s and 1980s by Erwin Neher and Bert Sakmann, who developed the technique of patch clamping to examine the conductance states of individual ion channels.[bg] In the 21st century, researchers are beginning to understand the structural basis for these conductance states and for the selectivity of channels for their species of ion,[bh] through the atomic-resolution crystal structures,[bi] fluorescence distance measurements[bj] and cryo-electron microscopy studies.[bk]
Julius Bernstein was also the first to introduce the Nernst equation for resting potential across the membrane; this was generalized by David E. Goldman to the eponymous Goldman equation in 1943.[h] The sodium–potassium pump was identified in 1957[bl][lower-Greek 6] and its properties gradually elucidated,[bm][bn][bo] culminating in the determination of its atomic-resolution structure by X-ray crystallography.[bp] The crystal structures of related ionic pumps have also been solved, giving a broader view of how these molecular machines work.[bq]
Quantitative models[edit]

Equivalent electrical circuit for the Hodgkin–Huxley model of the action potential. Im and Vm represent the current through, and the voltage across, a small patch of membrane, respectively. The Cm represents the capacitance of the membrane patch, whereas the four g‘s represent the conductances of four types of ions. The two conductances on the left, for potassium (K) and sodium (Na), are shown with arrows to indicate that they can vary with the applied voltage, corresponding to the voltage-sensitive ion channels. The two conductances on the right help determine the resting membrane potential.
Mathematical and computational models are essential for understanding the action potential, and offer predictions that may be tested against experimental data, providing a stringent test of a theory. The most important and accurate of the early neural models is the Hodgkin–Huxley model, which describes the action potential by a coupled set of four ordinary differential equations (ODEs).[i] Although the Hodgkin–Huxley model may be a simplification with few limitations[81] compared to the realistic nervous membrane as it exists in nature, its complexity has inspired several even-more-simplified models,[82][br] such as the Morris–Lecar model[bs] and the FitzHugh–Nagumo model,[bt] both of which have only two coupled ODEs. The properties of the Hodgkin–Huxley and FitzHugh–Nagumo models and their relatives, such as the Bonhoeffer–Van der Pol model,[bu] have been well-studied within mathematics,[83][bv] computation[84] and electronics.[bw] However the simple models of generator potential and action potential fail to accurately reproduce the near threshold neural spike rate and spike shape, specifically for the mechanoreceptors like the Pacinian corpuscle.[85] More modern research has focused on larger and more integrated systems; by joining action-potential models with models of other parts of the nervous system (such as dendrites and synapses), researchers can study neural computation[86] and simple reflexes, such as escape reflexes and others controlled by central pattern generators.[87][bx]
See also[edit]
- Anode break excitation
- Bioelectricity
- Biological neuron model
- Bursting
- Central pattern generator
- Chronaxie
- Frog battery
- Law of specific nerve energies
- Neural accommodation
- Single-unit recording
- Soliton model in neuroscience
Notes[edit]
- ^ In general, while this simple description of action potential initiation is accurate, it does not explain phenomena such as excitation block (the ability to prevent neurons from eliciting action potentials by stimulating them with large current steps) and the ability to elicit action potentials by briefly hyperpolarizing the membrane. By analyzing the dynamics of a system of sodium and potassium channels in a membrane patch using computational models, however, these phenomena are readily explained.[lower-Greek 1]
- ^ These Purkinje fibers are muscle fibers and not related to the Purkinje cells, which are neurons found in the cerebellum.
References[edit]
Footnotes[edit]
- ^ Hodgkin AL, Huxley AF (August 1952). “A quantitative description of membrane current and its application to conduction and excitation in nerve”. The Journal of Physiology. 117 (4): 500–44. doi:10.1113/jphysiol.1952.sp004764. PMC 1392413. PMID 12991237.
- ^ Williams JA (February 1981). “Electrical correlates of secretion in endocrine and exocrine cells”. Fed Proc. 40 (2): 128–34. PMID 6257554.
- ^ “Cardiac Muscle Contraction”. Retrieved 28 May 2021.
- ^ Pickard B (June 1973). “Action Potentials in Higher Plants” (PDF). The Botanical Review. 39 (2): 188. doi:10.1007/BF02859299. S2CID 5026557.
- ^ Leterrier C (February 2018). “The Axon Initial Segment: An Updated Viewpoint”. The Journal of Neuroscience. 38 (9): 2135–2145. doi:10.1523/JNEUROSCI.1922-17.2018. PMC 6596274. PMID 29378864.
- ^ Purves D, Augustine GJ, Fitzpatrick D, et al., eds. (2001). “Voltage-Gated Ion Channels”. Neuroscience (2nd ed.). Sunderland, MA: Sinauer Associates. Archived from the original on 5 June 2018. Retrieved 29 August 2017.
- ^ a b c d e f g h Bullock, Orkand & Grinnell 1977, pp. 150–151.
- ^ a b c d e Junge 1981, pp. 89–90.
- ^ a b Schmidt-Nielsen 1997, p. 484.
- ^ a b c Purves et al. 2008, pp. 48–49; Bullock, Orkand & Grinnell 1977, p. 141; Schmidt-Nielsen 1997, p. 483; Junge 1981, p. 89.
- ^ Stevens 1966, p. 127.
- ^ Schmidt-Nielsen, p. 484.
- ^ Tamagawa H, Funatani M, Ikeda K (January 2016). “Ling’s Adsorption Theory as a Mechanism of Membrane Potential Generation Observed in Both Living and Nonliving Systems”. Membranes. 6 (1): 11. doi:10.3390/membranes6010011. PMC 4812417. PMID 26821050.
- ^ a b c d e Sanes DH, Reh TA (1 January 2012). Development of the nervous system (Third ed.). Elsevier Academic Press. pp. 211–214. ISBN 9780080923208. OCLC 762720374.
- ^ Partridge D (1991). Calcium Channels: Their Properties, Functions, Regulation, and Clinical relevance. CRC Press. pp. 138–142. ISBN 9780849388071.
- ^ Black I (1984). Cellular and Molecular Biology of Neuronal Development | Ira Black | Springer. Springer. p. 103. ISBN 978-1-4613-2717-2. Archived from the original on 17 July 2017.
- ^ Pedersen R (1998). Current Topics in Developmental Biology, Volume 39. Elsevier Academic Press. ISBN 9780080584621.
- ^ Bullock, Orkand & Grinnell 1977, p. 11.
- ^ Silverthorn 2010, p. 253.
- ^ a b c Purves et al. 2008, pp. 49–50; Bullock, Orkand & Grinnell 1977, pp. 140–141; Schmidt-Nielsen 1997, pp. 480–481.
- ^ a b c d Schmidt-Nielsen 1997, pp. 483–484.
- ^ Bullock, Orkand & Grinnell 1977, pp. 177–240; Schmidt-Nielsen 1997, pp. 490–499; Stevens 1966, p. 47–68.
- ^ Bullock, Orkand & Grinnell 1977, pp. 178–180; Schmidt-Nielsen 1997, pp. 490–491.
- ^ Purves et al. 2001.
- ^ Purves et al. 2008, pp. 26–28.
- ^ “Myelination Increases the Spatial Extent of Analog Modulation of Synaptic Transmission: A Modeling Study”.
- ^ Zbili, M.; Debanne, D. (2019). “Past and Future of Analog-Digital Modulation of Synaptic Transmission”. Frontiers in Cellular Neuroscience. 13: 160. doi:10.3389/fncel.2019.00160. PMC 6492051. PMID 31105529.
- ^ Clark, Beverley; Häusser, Michael (8 August 2006). “Neural Coding: Analog Signalling in Axons”. Current Biology. 16 (15): R585–R588. doi:10.1016/j.cub.2006.07.007. PMID 16890514. S2CID 8295969.
- ^ Liu, Wenke; Liu, Qing; Crozier, Robert A.; Davis, Robin L. (2021). “Analog transmission of action potential fine structure in spiral ganglion axons”. Journal of Neurophysiology. 126 (3): 888–905. doi:10.1152/jn.00237.2021. PMC 8461829. PMID 34346782.
- ^ Schmidt-Nielsen 1997, pp. 535–580; Bullock, Orkand & Grinnell 1977, pp. 49–56, 76–93, 247–255; Stevens 1966, pp. 69–79.
- ^ Bullock, Orkand & Grinnell 1977, pp. 53; Bullock, Orkand & Grinnell 1977, pp. 122–124.
- ^ Junge 1981, pp. 115–132.
- ^ a b Bullock, Orkand & Grinnell 1977, pp. 152–153.
- ^ Bullock, Orkand & Grinnell 1977, pp. 444–445.
- ^ Purves et al. 2008, p. 38.
- ^ Stevens 1966, pp. 127–128.
- ^ Purves et al. 2008, pp. 61–65.
- ^ Purves et al. 2008, pp. 64–74; Bullock, Orkand & Grinnell 1977, pp. 149–150; Junge 1981, pp. 84–85; Stevens 1966, pp. 152–158.
- ^ a b c Purves et al. 2008, p. 47; Purves et al. 2008, p. 65; Bullock, Orkand & Grinnell 1977, pp. 147–148; Stevens 1966, p. 128.
- ^ Goldin, AL in Waxman 2007, Neuronal Channels and Receptors, pp. 43–58.
- ^ Stevens 1966, p. 49.
- ^ Purves et al. 2008, p. 34; Bullock, Orkand & Grinnell 1977, p. 134; Schmidt-Nielsen 1997, pp. 478–480.
- ^ a b c d Purves et al. 2008, p. 49.
- ^ a b c d Stevens 1966, pp. 19–20.
- ^ a b c Bullock, Orkand & Grinnell 1977, p. 151; Junge 1981, pp. 4–5.
- ^ a b Bullock, Orkand & Grinnell 1977, p. 152.
- ^ Bullock, Orkand & Grinnell 1977, pp. 147–149; Stevens 1966, pp. 126–127.
- ^ Purves et al. 2008, p. 37.
- ^ a b Purves et al. 2008, p. 56.
- ^ Bullock, Orkand & Grinnell 1977, pp. 160–164.
- ^ Stevens 1966, pp. 21–23.
- ^ Bullock, Orkand & Grinnell 1977, pp. 161–164.
- ^ Bullock, Orkand & Grinnell 1977, p. 509.
- ^ Tasaki, I in Field 1959, pp. 75–121
- ^ Schmidt-Nielsen 1997, Figure 12.13.
- ^ Bullock, Orkand & Grinnell 1977, p. 163.
- ^ Waxman, SG in Waxman 2007, Multiple Sclerosis as a Neurodegenerative Disease, pp. 333–346.
- ^ a b Rall, W in Koch & Segev 1989, Cable Theory for Dendritic Neurons, pp. 9–62.
- ^ Segev I, Fleshman JW, Burke RE (1989). “Compartmental Models of Complex Neurons”. In Koch C, Segev I (eds.). Methods in Neuronal Modeling: From Synapses to Networks. Cambridge, Massachusetts: The MIT Press. pp. 63–96. ISBN 978-0-262-11133-1. LCCN 88008279. OCLC 18384545.
- ^ Purves et al. 2008, pp. 52–53.
- ^ Ganong 1991, pp. 59–60.
- ^ Tandon, Prakash N (1 July 2019). “Jagdish Chandra Bose and Plant Neurobiology: Part I” (PDF). Indian Journal of History of Science. 54 (2). doi:10.16943/ijhs/2019/v54i2/49660. ISSN 0019-5235.
- ^ Felle HH, Zimmermann MR (June 2007). “Systemic signalling in barley through action potentials”. Planta. 226 (1): 203–14. doi:10.1007/s00425-006-0458-y. PMID 17226028. S2CID 5059716.
- ^ Luken JO (December 2005). “Habitats of Dionaea muscipula (Venus’ Fly Trap), Droseraceae, Associated with Carolina Bays”. Southeastern Naturalist. 4 (4): 573–584. doi:10.1656/1528-7092(2005)004[0573:HODMVF]2.0.CO;2. ISSN 1528-7092. S2CID 9246114.
- ^ a b Böhm J, Scherzer S, Krol E, Kreuzer I, von Meyer K, Lorey C, et al. (February 2016). “The Venus Flytrap Dionaea muscipula Counts Prey-Induced Action Potentials to Induce Sodium Uptake”. Current Biology. 26 (3): 286–95. doi:10.1016/j.cub.2015.11.057. PMC 4751343. PMID 26804557.
- ^ a b c d e f g Hedrich R, Neher E (March 2018). “Venus Flytrap: How an Excitable, Carnivorous Plant Works”. Trends in Plant Science. 23 (3): 220–234. doi:10.1016/j.tplants.2017.12.004. PMID 29336976.
- ^ Purves D, Augustine GJ, Fitzpatrick D, et al., editors. Neuroscience. 2nd edition. Sunderland (MA): Sinauer Associates; 2001. Electrical Potentials Across Nerve Cell Membranes.Available from: [1]
- ^ Volkov AG, Adesina T, Jovanov E (May 2007). “Closing of venus flytrap by electrical stimulation of motor cells”. Plant Signaling & Behavior. 2 (3): 139–45. doi:10.4161/psb.2.3.4217. PMC 2634039. PMID 19516982.
- ^
Gradmann, D; Mummert, H in Spanswick, Lucas & Dainty 1980, Plant action potentials, pp. 333–344. - ^ Opritov, V A, et al. “Direct Coupling of Action Potential Generation in Cells of a Higher Plant (Cucurbita Pepo) with the Operation of an Electrogenic Pump.” Russian Journal of Plant Physiology, vol. 49, no. 1, 2002, pp. 142–147.
- ^ Bullock & Horridge 1965.
- ^ Kristan WB (October 2016). “Early evolution of neurons”. Current Biology. 26 (20): R949–R954. doi:10.1016/j.cub.2016.05.030. PMID 27780067.
- ^ Hellier JL (2014). The Brain, the Nervous System, and Their Diseases. ABC-Clio. p. 532. ISBN 9781610693387.
- ^ Junge 1981, pp. 63–82.
- ^ Kettenmann & Grantyn 1992.
- ^ Snell, FM in Lavallée, Schanne & Hébert 1969, Some Electrical Properties of Fine-Tipped Pipette Microelectrodes.
- ^ Brazier 1961; McHenry & Garrison 1969; Worden, Swazey & Adelman 1975.
- ^ Finkelstein GW (2013). Emil du Bois-Reymond : neuroscience, self, and society in nineteenth-century Germany. Cambridge, Massachusetts. ISBN 9781461950325. OCLC 864592470.
- ^ Olesko, Kathryn M., and Frederic L. Holmes. “Experiment, Quantification and Discovery: Helmholtz’s Early Physiological Researches, 1843-50”. In Hermann von Helmholtz and the Foundations of Nineteenth Century Science, ed. David Cahan, 50-108. Berkeley; Los Angeles; London: University of California, 1994.
- ^ Bernstein 1912.
- ^ Baranauskas G, Martina M (January 2006). “Sodium currents activate without a Hodgkin-and-Huxley-type delay in central mammalian neurons”. The Journal of Neuroscience. 26 (2): 671–84. doi:10.1523/jneurosci.2283-05.2006. PMC 6674426. PMID 16407565.
- ^ Hoppensteadt 1986.
- ^ Sato, S; Fukai, H; Nomura, T; Doi, S in Reeke et al. 2005, Bifurcation Analysis of the Hodgkin-Huxley Equations, pp. 459–478.
* FitzHugh, R in Schwann 1969, Mathematical models of axcitation and propagation in nerve, pp. 12–16.
* Guckenheimer & Holmes 1986, pp. 12–16 - ^ Nelson, ME; Rinzel, J in Bower & Beeman 1995, The Hodgkin-Huxley Model, pp. 29–49.
* Rinzel, J & Ermentrout, GB; in Koch & Segev 1989, Analysis of Neural Excitability and Oscillations, pp. 135–169. - ^ Biswas A, Manivannan M, Srinivasan MA (2015). “Vibrotactile sensitivity threshold: nonlinear stochastic mechanotransduction model of the Pacinian Corpuscle”. IEEE Transactions on Haptics. 8 (1): 102–13. doi:10.1109/TOH.2014.2369422. PMID 25398183. S2CID 15326972.
- ^ McCulloch 1988, pp. 19–39, 46–66, 72–141; Anderson & Rosenfeld 1988, pp. 15–41.
- ^ Getting, PA in Koch & Segev 1989, Reconstruction of Small Neural Networks, pp. 171–194.
Journal articles[edit]
- ^ MacDonald PE, Rorsman P (February 2006). “Oscillations, intercellular coupling, and insulin secretion in pancreatic beta cells”. PLOS Biology. 4 (2): e49. doi:10.1371/journal.pbio.0040049. PMC 1363709. PMID 16464129.

- ^ a b Barnett MW, Larkman PM (June 2007). “The action potential”. Practical Neurology. 7 (3): 192–7. PMID 17515599. Archived from the original on 8 July 2011.
- ^ Golding NL, Kath WL, Spruston N (December 2001). “Dichotomy of action-potential backpropagation in CA1 pyramidal neuron dendrites”. Journal of Neurophysiology. 86 (6): 2998–3010. doi:10.1152/jn.2001.86.6.2998. PMID 11731556. S2CID 2915815.
- ^ Sasaki, T., Matsuki, N., Ikegaya, Y. 2011 Action-potential modulation during axonal conduction Science 331 (6017), pp. 599–601
- ^ Aur D, Connolly CI, Jog MS (November 2005). “Computing spike directivity with tetrodes”. Journal of Neuroscience Methods. 149 (1): 57–63. doi:10.1016/j.jneumeth.2005.05.006. PMID 15978667. S2CID 34131910.
- ^ Aur D., Jog, MS., 2010 Neuroelectrodynamics: Understanding the brain language, IOS Press, 2010. doi:10.3233/978-1-60750-473-3-i
- ^ Noble D (November 1960). “Cardiac action and pacemaker potentials based on the Hodgkin-Huxley equations”. Nature. 188 (4749): 495–7. Bibcode:1960Natur.188..495N. doi:10.1038/188495b0. PMID 13729365. S2CID 4147174.
- ^ a b Goldman DE (September 1943). “Potential, Impedance, and Rectification in Membranes”. The Journal of General Physiology. 27 (1): 37–60. doi:10.1085/jgp.27.1.37. PMC 2142582. PMID 19873371.
- ^ a b c d e Hodgkin AL, Huxley AF, Katz B (April 1952). “Measurement of current-voltage relations in the membrane of the giant axon of Loligo”. The Journal of Physiology. 116 (4): 424–48. doi:10.1113/jphysiol.1952.sp004716. PMC 1392219. PMID 14946712.
* Hodgkin AL, Huxley AF (April 1952). “Currents carried by sodium and potassium ions through the membrane of the giant axon of Loligo”. The Journal of Physiology. 116 (4): 449–72. doi:10.1113/jphysiol.1952.sp004717. PMC 1392213. PMID 14946713.
* Hodgkin AL, Huxley AF (April 1952). “The components of membrane conductance in the giant axon of Loligo”. The Journal of Physiology. 116 (4): 473–96. doi:10.1113/jphysiol.1952.sp004718. PMC 1392209. PMID 14946714.
* Hodgkin AL, Huxley AF (April 1952). “The dual effect of membrane potential on sodium conductance in the giant axon of Loligo”. The Journal of Physiology. 116 (4): 497–506. doi:10.1113/jphysiol.1952.sp004719. PMC 1392212. PMID 14946715.
* Hodgkin AL, Huxley AF (August 1952). “A quantitative description of membrane current and its application to conduction and excitation in nerve”. The Journal of Physiology. 117 (4): 500–44. doi:10.1113/jphysiol.1952.sp004764. PMC 1392413. PMID 12991237. - ^ Naundorf B, Wolf F, Volgushev M (April 2006). “Unique features of action potential initiation in cortical neurons” (PDF). Nature. 440 (7087): 1060–3. Bibcode:2006Natur.440.1060N. doi:10.1038/nature04610. PMID 16625198. S2CID 1328840. Archived from the original (PDF) on 20 December 2018. Retrieved 24 September 2019.
- ^ Hodgkin AL (July 1937). “Evidence for electrical transmission in nerve: Part I”. The Journal of Physiology. 90 (2): 183–210. doi:10.1113/jphysiol.1937.sp003507. PMC 1395060. PMID 16994885.
* Hodgkin AL (July 1937). “Evidence for electrical transmission in nerve: Part II”. The Journal of Physiology. 90 (2): 211–32. doi:10.1113/jphysiol.1937.sp003508. PMC 1395062. PMID 16994886. - ^ Zalc B (2006). “The acquisition of myelin: a success story”. Novartis Foundation Symposium. Novartis Foundation Symposia. 276: 15–21, discussion 21–5, 54–7, 275–81. doi:10.1002/9780470032244.ch3. ISBN 978-0-470-03224-4. PMID 16805421.
- ^ Poliak S, Peles E (December 2003). “The local differentiation of myelinated axons at nodes of Ranvier”. Nature Reviews. Neuroscience. 4 (12): 968–80. doi:10.1038/nrn1253. PMID 14682359. S2CID 14720760.
- ^ Simons M, Trotter J (October 2007). “Wrapping it up: the cell biology of myelination”. Current Opinion in Neurobiology. 17 (5): 533–40. doi:10.1016/j.conb.2007.08.003. PMID 17923405. S2CID 45470194.
- ^ Xu K, Terakawa S (August 1999). “Fenestration nodes and the wide submyelinic space form the basis for the unusually fast impulse conduction of shrimp myelinated axons”. The Journal of Experimental Biology. 202 (Pt 15): 1979–89. doi:10.1242/jeb.202.15.1979. PMID 10395528.
- ^ a b Hursh JB (1939). “Conduction velocity and diameter of nerve fibers”. American Journal of Physiology. 127: 131–39. doi:10.1152/ajplegacy.1939.127.1.131.
- ^ Lillie RS (March 1925). “Factors Affecting Transmission and Recovery in the Passive Iron Nerve Model”. The Journal of General Physiology. 7 (4): 473–507. doi:10.1085/jgp.7.4.473. PMC 2140733. PMID 19872151. See also Keynes & Aidley 1991, p. 78
- ^ Tasaki I (1939). “Electro-saltatory transmission of nerve impulse and effect of narcosis upon nerve fiber”. Am. J. Physiol. 127: 211–27. doi:10.1152/ajplegacy.1939.127.2.211.
- ^ Tasaki I, Takeuchi T (1941). “Der am Ranvierschen Knoten entstehende Aktionsstrom und seine Bedeutung für die Erregungsleitung”. Pflügers Archiv für die gesamte Physiologie. 244 (6): 696–711. doi:10.1007/BF01755414. S2CID 8628858.
* Tasaki I, Takeuchi T (1942). “Weitere Studien über den Aktionsstrom der markhaltigen Nervenfaser und über die elektrosaltatorische Übertragung des nervenimpulses”. Pflügers Archiv für die gesamte Physiologie. 245 (5): 764–82. doi:10.1007/BF01755237. S2CID 44315437. - ^ Huxley AF, Stämpfli R (May 1949). “Evidence for saltatory conduction in peripheral myelinated nerve fibres”. The Journal of Physiology. 108 (3): 315–39. doi:10.1113/jphysiol.1949.sp004335. PMC 1392492. PMID 16991863.
* Huxley AF, Stampfli R (February 1951). “Direct determination of membrane resting potential and action potential in single myelinated nerve fibers”. The Journal of Physiology. 112 (3–4): 476–95. doi:10.1113/jphysiol.1951.sp004545. PMC 1393015. PMID 14825228. - ^ Rushton WA (September 1951). “A theory of the effects of fibre size in medullated nerve”. The Journal of Physiology. 115 (1): 101–22. doi:10.1113/jphysiol.1951.sp004655. PMC 1392008. PMID 14889433.
- ^ a b Hartline DK, Colman DR (January 2007). “Rapid conduction and the evolution of giant axons and myelinated fibers”. Current Biology. 17 (1): R29-35. doi:10.1016/j.cub.2006.11.042. PMID 17208176. S2CID 10033356.
- ^ Miller RH, Mi S (November 2007). “Dissecting demyelination”. Nature Neuroscience. 10 (11): 1351–4. doi:10.1038/nn1995. PMID 17965654. S2CID 12441377.
- ^ Kelvin WT (1855). “On the theory of the electric telegraph”. Proceedings of the Royal Society. 7: 382–99. doi:10.1098/rspl.1854.0093. S2CID 178547827.
- ^ Hodgkin AL, Rushton WA (December 1946). “The electrical constants of a crustacean nerve fibre”. Proceedings of the Royal Society of Medicine. 134 (873): 444–79. Bibcode:1946RSPSB.133..444H. doi:10.1098/rspb.1946.0024. PMID 20281590.
- ^ Süudhof TC (2008). “Neurotransmitter release”. Pharmacology of Neurotransmitter Release. Handbook of Experimental Pharmacology. Vol. 184. pp. 1–21. doi:10.1007/978-3-540-74805-2_1. ISBN 978-3-540-74804-5. PMID 18064409.
- ^ Rusakov DA (August 2006). “Ca2+-dependent mechanisms of presynaptic control at central synapses”. The Neuroscientist. 12 (4): 317–26. doi:10.1177/1073858405284672. PMC 2684670. PMID 16840708.
- ^ Humeau Y, Doussau F, Grant NJ, Poulain B (May 2000). “How botulinum and tetanus neurotoxins block neurotransmitter release”. Biochimie. 82 (5): 427–46. doi:10.1016/S0300-9084(00)00216-9. PMID 10865130.
- ^ Zoidl G, Dermietzel R (November 2002). “On the search for the electrical synapse: a glimpse at the future”. Cell and Tissue Research. 310 (2): 137–42. doi:10.1007/s00441-002-0632-x. PMID 12397368. S2CID 22414506.
- ^ Brink PR, Cronin K, Ramanan SV (August 1996). “Gap junctions in excitable cells”. Journal of Bioenergetics and Biomembranes. 28 (4): 351–8. doi:10.1007/BF02110111. PMID 8844332. S2CID 46371790.
- ^ Hirsch NP (July 2007). “Neuromuscular junction in health and disease”. British Journal of Anaesthesia. 99 (1): 132–8. doi:10.1093/bja/aem144. PMID 17573397.
- ^ Hughes BW, Kusner LL, Kaminski HJ (April 2006). “Molecular architecture of the neuromuscular junction”. Muscle & Nerve. 33 (4): 445–61. doi:10.1002/mus.20440. PMID 16228970. S2CID 1888352.
- ^ a b Newmark J (January 2007). “Nerve agents”. The Neurologist. 13 (1): 20–32. doi:10.1097/01.nrl.0000252923.04894.53. PMID 17215724. S2CID 211234081.
- ^ Costa LG (April 2006). “Current issues in organophosphate toxicology”. Clinica Chimica Acta; International Journal of Clinical Chemistry. 366 (1–2): 1–13. doi:10.1016/j.cca.2005.10.008. PMID 16337171.
- ^ a b c Kléber AG, Rudy Y (April 2004). “Basic mechanisms of cardiac impulse propagation and associated arrhythmias”. Physiological Reviews. 84 (2): 431–88. doi:10.1152/physrev.00025.2003. PMID 15044680. S2CID 21823003.
- ^ Tamargo J, Caballero R, Delpón E (January 2004). “Pharmacological approaches in the treatment of atrial fibrillation”. Current Medicinal Chemistry. 11 (1): 13–28. doi:10.2174/0929867043456241. PMID 14754423.
- ^ Slayman CL, Long WS, Gradmann D (April 1976). ““Action potentials” in Neurospora crassa, a mycelial fungus”. Biochimica et Biophysica Acta (BBA) – Biomembranes. 426 (4): 732–44. doi:10.1016/0005-2736(76)90138-3. PMID 130926.
- ^ Mummert H, Gradmann D (December 1991). “Action potentials in Acetabularia: measurement and simulation of voltage-gated fluxes”. The Journal of Membrane Biology. 124 (3): 265–73. doi:10.1007/BF01994359. PMID 1664861. S2CID 22063907.
- ^ Gradmann D (2001). “Models for oscillations in plants”. Aust. J. Plant Physiol. 28 (7): 577–590. doi:10.1071/pp01017.
- ^ Beilby MJ (2007). Action potential in charophytes. International Review of Cytology. Vol. 257. pp. 43–82. doi:10.1016/S0074-7696(07)57002-6. ISBN 978-0-12-373701-4. PMID 17280895.
- ^ Gradmann D, Hoffstadt J (November 1998). “Electrocoupling of ion transporters in plants: interaction with internal ion concentrations”. The Journal of Membrane Biology. 166 (1): 51–9. doi:10.1007/s002329900446. PMID 9784585. S2CID 24190001.
- ^ Fromm J, Lautner S (March 2007). “Electrical signals and their physiological significance in plants”. Plant, Cell & Environment. 30 (3): 249–257. doi:10.1111/j.1365-3040.2006.01614.x. PMID 17263772.
- ^ Leys SP, Mackie GO, Meech RW (May 1999). “Impulse conduction in a sponge”. The Journal of Experimental Biology. 202 (Pt 9) (9): 1139–50. doi:10.1242/jeb.202.9.1139. PMID 10101111.
- ^ Keynes RD (1989). “The role of giant axons in studies of the nerve impulse”. BioEssays. 10 (2–3): 90–3. doi:10.1002/bies.950100213. PMID 2541698.
- ^ Meunier C, Segev I (November 2002). “Playing the devil’s advocate: is the Hodgkin-Huxley model useful?”. Trends in Neurosciences. 25 (11): 558–63. doi:10.1016/S0166-2236(02)02278-6. PMID 12392930. S2CID 1355280.
- ^ Cole KS (1949). “Dynamic electrical characteristics of the squid axon membrane”. Arch. Sci. Physiol. 3: 253–8.
- ^ Ling G, Gerard RW (December 1949). “The normal membrane potential of frog sartorius fibers”. Journal of Cellular and Comparative Physiology. 34 (3): 383–96. doi:10.1002/jcp.1030340304. PMID 15410483.
- ^ Nastuk WL, Hodgkin A (1950). “The electrical activity of single muscle fibers”. Journal of Cellular and Comparative Physiology. 35: 39–73. doi:10.1002/jcp.1030350105.
- ^ Brock LG, Coombs JS, Eccles JC (August 1952). “The recording of potentials from motoneurones with an intracellular electrode”. The Journal of Physiology. 117 (4): 431–60. doi:10.1113/jphysiol.1952.sp004759. PMC 1392415. PMID 12991232.
- ^ Ross WN, Salzberg BM, Cohen LB, Davila HV (December 1974). “A large change in dye absorption during the action potential”. Biophysical Journal. 14 (12): 983–6. Bibcode:1974BpJ….14..983R. doi:10.1016/S0006-3495(74)85963-1. PMC 1334592. PMID 4429774.
* Grynkiewicz G, Poenie M, Tsien RY (March 1985). “A new generation of Ca2+ indicators with greatly improved fluorescence properties”. The Journal of Biological Chemistry. 260 (6): 3440–50. doi:10.1016/S0021-9258(19)83641-4. PMID 3838314. - ^ Bu G, Adams H, Berbari EJ, Rubart M (March 2009). “Uniform action potential repolarization within the sarcolemma of in situ ventricular cardiomyocytes”. Biophysical Journal. 96 (6): 2532–46. Bibcode:2009BpJ….96.2532B. doi:10.1016/j.bpj.2008.12.3896. PMC 2907679. PMID 19289075.
- ^ Milligan JV, Edwards C (July 1965). “Some factors affecting the time course of the recovery of contracture ability following a potassium contracture in frog striated muscle”. The Journal of General Physiology. 48 (6): 975–83. doi:10.1085/jgp.48.6.975. PMC 2195447. PMID 5855511.
* Ritchie JM, Rogart RB (1977). “The binding of saxitoxin and tetrodotoxin to excitable tissue”. Reviews of Physiology, Biochemistry and Pharmacology, Volume 79. Reviews of Physiology, Biochemistry and Pharmacology. Vol. 79. pp. 1–50. doi:10.1007/BFb0037088. ISBN 0-387-08326-X. PMID 335473.
* Keynes RD, Ritchie JM (August 1984). “On the binding of labelled saxitoxin to the squid giant axon”. Proceedings of the Royal Society of London. Series B, Biological Sciences. 222 (1227): 147–53. Bibcode:1984RSPSB.222..147K. doi:10.1098/rspb.1984.0055. PMID 6148754. S2CID 11465181. - ^ Piccolino M (October 1997). “Luigi Galvani and animal electricity: two centuries after the foundation of electrophysiology”. Trends in Neurosciences. 20 (10): 443–8. doi:10.1016/S0166-2236(97)01101-6. PMID 9347609. S2CID 23394494.
- ^ Piccolino M (April 2000). “The bicentennial of the Voltaic battery (1800-2000): the artificial electric organ”. Trends in Neurosciences. 23 (4): 147–51. doi:10.1016/S0166-2236(99)01544-1. PMID 10717671. S2CID 393323.
- ^ Bernstein J (1902). “Untersuchungen zur Thermodynamik der bioelektrischen Ströme”. Pflügers Archiv für die gesamte Physiologie. 92 (10–12): 521–562. doi:10.1007/BF01790181. S2CID 33229139.
- ^ Cole KS, Curtis HJ (May 1939). “Electric Impedance of the Squid Giant Axon During Activity”. The Journal of General Physiology. 22 (5): 649–70. doi:10.1085/jgp.22.5.649. PMC 2142006. PMID 19873125.
- ^ Lapicque L (1907). “Recherches quantitatives sur l’excitationelectrique des nerfs traitee comme une polarisation”. J. Physiol. Pathol. Gen. 9: 620–635.
- ^ Hodgkin AL, Katz B (March 1949). “The effect of sodium ions on the electrical activity of giant axon of the squid”. The Journal of Physiology. 108 (1): 37–77. doi:10.1113/jphysiol.1949.sp004310. PMC 1392331. PMID 18128147.
- ^ Neher E, Sakmann B (April 1976). “Single-channel currents recorded from membrane of denervated frog muscle fibres”. Nature. 260 (5554): 799–802. Bibcode:1976Natur.260..799N. doi:10.1038/260799a0. PMID 1083489. S2CID 4204985.
* Hamill OP, Marty A, Neher E, Sakmann B, Sigworth FJ (August 1981). “Improved patch-clamp techniques for high-resolution current recording from cells and cell-free membrane patches”. Pflügers Archiv. 391 (2): 85–100. doi:10.1007/BF00656997. PMID 6270629. S2CID 12014433.
* Neher E, Sakmann B (March 1992). “The patch clamp technique”. Scientific American. 266 (3): 44–51. Bibcode:1992SciAm.266c..44N. doi:10.1038/scientificamerican0392-44. PMID 1374932. - ^ Yellen G (September 2002). “The voltage-gated potassium channels and their relatives”. Nature. 419 (6902): 35–42. Bibcode:2002Natur.419…35Y. doi:10.1038/nature00978. PMID 12214225. S2CID 4420877.
- ^ Doyle DA, Morais Cabral J, Pfuetzner RA, Kuo A, Gulbis JM, Cohen SL, et al. (April 1998). “The structure of the potassium channel: molecular basis of K+ conduction and selectivity”. Science. 280 (5360): 69–77. Bibcode:1998Sci…280…69D. doi:10.1126/science.280.5360.69. PMID 9525859.
* Zhou Y, Morais-Cabral JH, Kaufman A, MacKinnon R (November 2001). “Chemistry of ion coordination and hydration revealed by a K+ channel-Fab complex at 2.0 A resolution”. Nature. 414 (6859): 43–8. Bibcode:2001Natur.414…43Z. doi:10.1038/35102009. PMID 11689936. S2CID 205022645.
* Jiang Y, Lee A, Chen J, Ruta V, Cadene M, Chait BT, MacKinnon R (May 2003). “X-ray structure of a voltage-dependent K+ channel”. Nature. 423 (6935): 33–41. Bibcode:2003Natur.423…33J. doi:10.1038/nature01580. PMID 12721618. S2CID 4347957. - ^ Cha A, Snyder GE, Selvin PR, Bezanilla F (December 1999). “Atomic scale movement of the voltage-sensing region in a potassium channel measured via spectroscopy”. Nature. 402 (6763): 809–13. Bibcode:1999Natur.402..809C. doi:10.1038/45552. PMID 10617201. S2CID 4353978.
* Glauner KS, Mannuzzu LM, Gandhi CS, Isacoff EY (December 1999). “Spectroscopic mapping of voltage sensor movement in the Shaker potassium channel”. Nature. 402 (6763): 813–7. Bibcode:1999Natur.402..813G. doi:10.1038/45561. PMID 10617202. S2CID 4417476.
* Bezanilla F (April 2000). “The voltage sensor in voltage-dependent ion channels”. Physiological Reviews. 80 (2): 555–92. doi:10.1152/physrev.2000.80.2.555. PMID 10747201. S2CID 18629998. - ^ Catterall WA (February 2001). “A 3D view of sodium channels”. Nature. 409 (6823): 988–9, 991. Bibcode:2001Natur.409..988C. doi:10.1038/35059188. PMID 11234048. S2CID 4371677.
* Sato C, Ueno Y, Asai K, Takahashi K, Sato M, Engel A, Fujiyoshi Y (February 2001). “The voltage-sensitive sodium channel is a bell-shaped molecule with several cavities”. Nature. 409 (6823): 1047–51. Bibcode:2001Natur.409.1047S. doi:10.1038/35059098. PMID 11234014. S2CID 4430165. - ^ Skou JC (February 1957). “The influence of some cations on an adenosine triphosphatase from peripheral nerves”. Biochimica et Biophysica Acta. 23 (2): 394–401. doi:10.1016/0006-3002(57)90343-8. PMID 13412736. S2CID 32516710.
- ^ Hodgkin AL, Keynes RD (April 1955). “Active transport of cations in giant axons from Sepia and Loligo”. The Journal of Physiology. 128 (1): 28–60. doi:10.1113/jphysiol.1955.sp005290. PMC 1365754. PMID 14368574.
- ^ Caldwell PC, Hodgkin AL, Keynes RD, Shaw TL (July 1960). “The effects of injecting ‘energy-rich’ phosphate compounds on the active transport of ions in the giant axons of Loligo”. The Journal of Physiology. 152 (3): 561–90. doi:10.1113/jphysiol.1960.sp006509. PMC 1363339. PMID 13806926.
- ^ Caldwell PC, Keynes RD (June 1957). “The utilization of phosphate bond energy for sodium extrusion from giant axons”. The Journal of Physiology. 137 (1): 12–3P. doi:10.1113/jphysiol.1957.sp005830. PMID 13439598. S2CID 222188054.
- ^ Morth JP, Pedersen BP, Toustrup-Jensen MS, Sørensen TL, Petersen J, Andersen JP, et al. (December 2007). “Crystal structure of the sodium-potassium pump”. Nature. 450 (7172): 1043–9. Bibcode:2007Natur.450.1043M. doi:10.1038/nature06419. PMID 18075585. S2CID 4344526.
- ^ Lee AG, East JM (June 2001). “What the structure of a calcium pump tells us about its mechanism”. The Biochemical Journal. 356 (Pt 3): 665–83. doi:10.1042/0264-6021:3560665. PMC 1221895. PMID 11389676.
- ^ * Fitzhugh R (May 1960). “Thresholds and plateaus in the Hodgkin-Huxley nerve equations”. The Journal of General Physiology. 43 (5): 867–96. doi:10.1085/jgp.43.5.867. PMC 2195039. PMID 13823315.
* Kepler TB, Abbott LF, Marder E (1992). “Reduction of conductance-based neuron models”. Biological Cybernetics. 66 (5): 381–7. doi:10.1007/BF00197717. PMID 1562643. S2CID 6789007. - ^ Morris C, Lecar H (July 1981). “Voltage oscillations in the barnacle giant muscle fiber”. Biophysical Journal. 35 (1): 193–213. Bibcode:1981BpJ….35..193M. doi:10.1016/S0006-3495(81)84782-0. PMC 1327511. PMID 7260316.
- ^ Fitzhugh R (July 1961). “Impulses and Physiological States in Theoretical Models of Nerve Membrane”. Biophysical Journal. 1 (6): 445–66. Bibcode:1961BpJ…..1..445F. doi:10.1016/S0006-3495(61)86902-6. PMC 1366333. PMID 19431309.
* Nagumo J, Arimoto S, Yoshizawa S (1962). “An active pulse transmission line simulating nerve axon”. Proceedings of the IRE. 50 (10): 2061–2070. doi:10.1109/JRPROC.1962.288235. S2CID 51648050. - ^ Bonhoeffer KF (September 1948). “Activation of passive iron as a model for the excitation of nerve”. The Journal of General Physiology. 32 (1): 69–91. doi:10.1085/jgp.32.1.69. PMC 2213747. PMID 18885679.
* Bonhoeffer KF (1953). “Modelle der Nervenerregung”. Naturwissenschaften. 40 (11): 301–311. Bibcode:1953NW…..40..301B. doi:10.1007/BF00632438. S2CID 19149460.
* Van der Pol B (1926). “On relaxation-oscillations”. Philosophical Magazine. 2: 977–992.
* Van der Pol B, Van der Mark J (1928). “The heartbeat considered as a relaxation oscillation, and an electrical model of the heart”. Philosophical Magazine. 6: 763–775. doi:10.1080/14786441108564652.
* Van der Pol B, van der Mark J (1929). “The heartbeat considered as a relaxation oscillation, and an electrical model of the heart”. Arch. Neerl. Physiol. 14: 418–443. - ^ Evans JW (1972). “Nerve axon equations. I. Linear approximations”. Indiana Univ. Math. J. 21 (9): 877–885. doi:10.1512/iumj.1972.21.21071.
* Evans JW, Feroe J (1977). “Local stability theory of the nerve impulse”. Math. Biosci. 37: 23–50. doi:10.1016/0025-5564(77)90076-1. - ^ Keener JP (1983). “Analogue circuitry for the Van der Pol and FitzHugh-Nagumo equations”. IEEE Transactions on Systems, Man and Cybernetics. 13 (5): 1010–1014. doi:10.1109/TSMC.1983.6313098. S2CID 20077648.
- ^ Hooper SL (March 2000). “Central pattern generators”. Current Biology. 10 (5): R176–R179. CiteSeerX 10.1.1.133.3378. doi:10.1016/S0960-9822(00)00367-5. PMID 10713861. S2CID 11388348.
Books[edit]
- Anderson JA, Rosenfeld E, eds. (1988). Neurocomputing: Foundations of Research. Cambridge, Massachusetts: The MIT Press. ISBN 978-0-262-01097-9. LCCN 87003022. OCLC 15860311.
- Bernstein J (1912). Elektrobiologie, die Lehre von den elektrischen Vorgängen im Organismus auf moderner Grundlage dargestellt [Electric Biology, the study of the electrical processes in the organism represented on a modern basis]. Braunschweig: Vieweg und Sohn. LCCN 12027986. OCLC 11358569.
- Bower JM, Beeman D (1995). The Book of GENESIS: Exploring Realistic Neural Models with the GEneral NEural SImulation System. Santa Clara, Calif.: TELOS. ISBN 978-0-387-94019-9. LCCN 94017624. OCLC 30518469.
- Brazier MA (1961). A History of the Electrical Activity of the Brain. London: Pitman. LCCN 62001407. OCLC 556863.
- Bullock TH, Horridge GA (1965). Structure and Function in the Nervous Systems of Invertebrates. A series of books in biology. San Francisco: W. H. Freeman. LCCN 65007965. OCLC 558128.
- Bullock TH, Orkand R, Grinnell A (1977). Introduction to Nervous Systems. A series of books in biology. San Francisco: W. H. Freeman. ISBN 978-0-7167-0030-2. LCCN 76003735. OCLC 2048177.
- Field J, ed. (1959). Handbook of Physiology: a Critical, Comprehensive Presentation of Physiological Knowledge and Concepts: Section 1: Neurophysiology. Vol. 1. Washington, DC: American Physiological Society. LCCN 60004587. OCLC 830755894.
- Ganong, WF (1991). Review of Medical Physiology. Ganong’s Review of Medical Physiology (15th ed.). Norwalk, Conn.: Appleton and Lange. ISBN 978-0-8385-8418-7. ISSN 0892-1253. LCCN 87642343. OCLC 23761261.
- Guckenheimer J, Holmes P, eds. (1986). Nonlinear Oscillations, Dynamical Systems and Bifurcations of Vector Fields. Applied Mathematical Sciences. Vol. 42 (2nd ed.). New York: Springer Verlag. ISBN 978-0-387-90819-9. OCLC 751129941.
- Hoppensteadt FC (1986). An Introduction to the Mathematics of Neurons. Cambridge studies in mathematical biology. Vol. 6. Cambridge: Cambridge University Press. ISBN 978-0-521-31574-6. LCCN 85011013. OCLC 12052275.
- Junge D (1981). Nerve and Muscle Excitation (2nd ed.). Sunderland, Mass.: Sinauer Associates. ISBN 978-0-87893-410-2. LCCN 80018158. OCLC 6486925.
- Kettenmann H, Grantyn R, eds. (1992). Practical Electrophysiological Methods: A Guide for in Vitro Studies in Vertebrate Neurobiology. New York: Wiley. ISBN 978-0-471-56200-9. LCCN 92000179. OCLC 25204689.
- Keynes RD, Aidley DJ (1991). Nerve and Muscle (2nd ed.). Cambridge: Cambridge University Press. ISBN 978-0-521-41042-7. LCCN 90015167. OCLC 25204483.
- Koch C, Segev I, eds. (1989). Methods in Neuronal Modeling: From Synapses to Networks. Cambridge, Massachusetts: The MIT Press. ISBN 978-0-262-11133-1. LCCN 88008279. OCLC 18384545.
- Lavallée M, Schanne OF, Hébert NC, eds. (1969). Glass Microelectrodes. New York: Wiley. ISBN 978-0-471-51885-3. LCCN 68009252. OCLC 686.
- McCulloch WS (1988). Embodiments of Mind. Cambridge, Massachusetts: The MIT Press. ISBN 978-0-262-63114-3. LCCN 88002987. OCLC 237280.
- McHenry LC, Garrison FH (1969). Garrison’s History of Neurology. Springfield, Ill.: Charles C. Thomas. OCLC 429733931.
- Silverthorn DU (2010). Human Physiology: An Integrated Approach (5th ed.). San Francisco: Pearson. ISBN 978-0-321-55980-7. LCCN 2008050369. OCLC 268788623.
- Spanswick RM, Lucas WJ, Dainty J, eds. (1980). Plant Membrane Transport: Current Conceptual Issues. Developments in Plant Biology. Vol. 4. Amsterdam: Elsevier Biomedical Press. ISBN 978-0-444-80192-0. LCCN 79025719. OCLC 5799924.
- Purves D, Augustine GJ, Fitzpatrick D, Hall WC, Lamantia AS, McNamara JO, Williams SM (2001). “Release of Transmitters from Synaptic Vesicles”. Neuroscience (2nd ed.). Sunderland, MA: Sinauer Associates. ISBN 978-0-87893-742-4. LCCN 00059496. OCLC 806472664.
- Purves D, Augustine GJ, Fitzpatrick D, Hall WC, Lamantia AS, McNamara JO, White LE (2008). Neuroscience (4th ed.). Sunderland, MA: Sinauer Associates. ISBN 978-0-87893-697-7. LCCN 2007024950. OCLC 144771764.
- Reeke GN, Poznanski RR, Sporns O, Rosenberg JR, Lindsay KA, eds. (2005). Modeling in the Neurosciences: from Biological Systems to Neuromimetic Robotics. Boca Raton, Fla.: Taylor & Francis. ISBN 978-0-415-32868-5. LCCN 2005298022. OCLC 489024131.
- Schmidt-Nielsen K (1997). Animal Physiology: Adaptation and Environment (5th ed.). Cambridge: Cambridge University Press. ISBN 978-0-521-57098-5. LCCN 96039295. OCLC 35744403.
- Schwann HP, ed. (1969). Biological Engineering. Inter-University Electronics Series. Vol. 9. New York: McGraw-Hill. ISBN 978-0-07-055734-5. LCCN 68027513. OCLC 51993.
- Stevens CF (1966). Neurophysiology: A Primer. New York: John Wiley and Sons. ISBN 9780471824367. LCCN 66015872. OCLC 1175605.
- Waxman SG, ed. (2007). Molecular Neurology. Burlington, Mass.: Elsevier Academic Press. ISBN 978-0-12-369509-3. LCCN 2008357317. OCLC 154760295.
- Worden FG, Swazey JP, Adelman G, eds. (1975). The Neurosciences, Paths of Discovery. Cambridge, Massachusetts: The MIT Press. ISBN 978-0-262-23072-8. LCCN 75016379. OCLC 1500233.
Web pages[edit]
- ^ Fitzhugh R, Izhikevich E (2006). “FitzHugh-Nagumo model”. Scholarpedia. 1 (9): 1349. Bibcode:2006SchpJ…1.1349I. doi:10.4249/scholarpedia.1349.
- ^ “The Nobel Prize in Physiology or Medicine 1963” (Press release). The Royal Swedish Academy of Science. 1963. Archived from the original on 16 July 2007. Retrieved 21 February 2010.
- ^ “The Nobel Prize in Physiology or Medicine 1991” (Press release). The Royal Swedish Academy of Science. 1991. Archived from the original on 24 March 2010. Retrieved 21 February 2010.
- ^ “The Nobel Prize in Physiology or Medicine 1906” (Press release). The Royal Swedish Academy of Science. 1906. Archived from the original on 4 December 2008. Retrieved 21 February 2010.
- ^ Warlow C (June 2007). “The Recent Evolution of a Symbiotic Ion Channel in the Legume Family Altered Ion Conductance and Improved Functionality in Calcium Signaling”. Practical Neurology. BMJ Publishing Group. 7 (3): 192–197. Archived from the original on 14 March 2012. Retrieved 23 March 2013.
- ^ “The Nobel Prize in Chemistry 1997” (Press release). The Royal Swedish Academy of Science. 1997. Archived from the original on 23 October 2009. Retrieved 21 February 2010.
Further reading[edit]
- Aidley DJ, Stanfield PR (1996). Ion Channels: Molecules in Action. Cambridge: Cambridge University Press. ISBN 978-0-521-49882-1.
- Bear MF, Connors BW, Paradiso MA (2001). Neuroscience: Exploring the Brain. Baltimore: Lippincott. ISBN 0-7817-3944-6.
- Clay JR (May 2005). “Axonal excitability revisited”. Progress in Biophysics and Molecular Biology. 88 (1): 59–90. doi:10.1016/j.pbiomolbio.2003.12.004. PMID 15561301.
- Deutsch S, Micheli-Tzanakou E (1987). Neuroelectric Systems. New York: New York University Press. ISBN 0-8147-1782-9.
- Hille B (2001). Ion Channels of Excitable Membranes (3rd ed.). Sunderland, MA: Sinauer Associates. ISBN 978-0-87893-321-1.
- Johnston D, Wu SM (1995). Foundations of Cellular Neurophysiology. Cambridge, Massachusetts: Bradford Book, The MIT Press. ISBN 0-262-10053-3.
- Kandel ER, Schwartz JH, Jessell TM (2000). Principles of Neural Science (4th ed.). New York: McGraw-Hill. ISBN 0-8385-7701-6.
- Miller C (1987). “How ion channel proteins work”. In Kaczmarek LK, Levitan IB (eds.). Neuromodulation: The Biochemical Control of Neuronal Excitability. New York: Oxford University Press. pp. 39–63. ISBN 978-0-19-504097-5.
- Nelson DL, Cox MM (2008). Lehninger Principles of Biochemistry (5th ed.). New York: W. H. Freeman. ISBN 978-0-7167-7108-1.
External links[edit]
![]()
This audio file was created from a revision of this article dated 22 June 2005, and does not reflect subsequent edits.
- Ionic flow in action potentials at Blackwell Publishing
- Action potential propagation in myelinated and unmyelinated axons at Blackwell Publishing
- Generation of AP in cardiac cells and generation of AP in neuron cells
- Resting membrane potential from Life: The Science of Biology, by WK Purves, D Sadava, GH Orians, and HC Heller, 8th edition, New York: WH Freeman, ISBN 978-0-7167-7671-0.
- Ionic motion and the Goldman voltage for arbitrary ionic concentrations at The University of Arizona
- A cartoon illustrating the action potential
- Action potential propagation
- Production of the action potential: voltage and current clamping simulations[permanent dead link]
- Open-source software to simulate neuronal and cardiac action potentials at SourceForge.net
- Introduction to the Action Potential, Neuroscience Online (electronic neuroscience textbook by UT Houston Medical School)
- Khan Academy: Electrotonic and action potential Archived 2 July 2014 at the Wayback Machine