Преподаватель который помогает студентам и школьникам в учёбе.
Потенциал поля точечного заряда в физике – формулы и определение с примерами
Потенциал поля точечного заряда:
Чтобы определить силу электрического поля, мы ввели в него пробный заряд и определили силу воздействия поля на этот заряд.
Напряженность электрического поля является характеристикой силы поля.
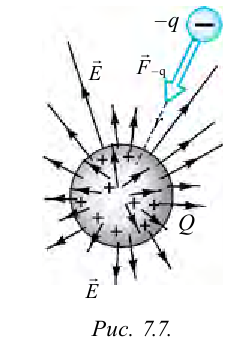
При введении пробного заряда в поле, оно оказывает сопротивление (рис. 7.7). Для преодоления сопротивления необходимо проделать определенную работу.
Как определяется эта выполненная работа?
Эта работа превращается в потенциальную энергию взаимодействия основного заряда и введенного пробного заряда:
Знак минус в формуле показывает, что между зарядами действует сила притяжения.
Потенциальная энергия 
заряда, расположенного на расстоянии 
от положительного неподвижного заряда 
, определяется следующим выражением
Положительный знак в формуле показывает, что между зарядами действует сила отталкивания.
Согласно формуле потенциальная энергия равняется нулю, когда расчет производится для бесконечного расстояния. На таких расстояниях заряды не взаимодействуют.
Таким образом, электрическое поле с приобретением характеристики силы будет иметь и энергетическую характеристику. Энергетическая характеристика поля определяется величиной, которая называется потенциалом поля.
Потенциалом электрического поля точечного заряда называется величина, измеряемая отношением потенциальной энергии взаимодействия основного и введенного в поле пробного заряда к величине пробного заряда:
Потенциал точечного заряда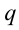 
определяется следующим образом:
Пользуясь понятием потенциала найдем работу, совершаемую при перемещении заряда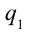 
с расстояния 
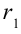на расстояние 
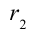от заряда 
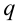, создающего электрическое поле:
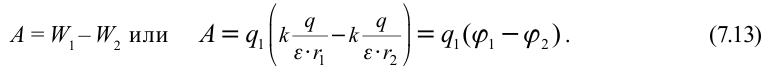
В этом выражении разница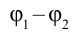 
является разницей потенциалов между точками, называется электрическим напряжением и записывается следующим образом:
Единица измерения потенциала и разность потенциалов называется Вольт (В) в честь итальянского ученого Вольта. Из формулы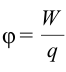 
следует, что 
.
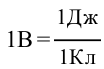Это значит, что разность потенциалов точек равняется 1 вольту, когда заряд, равный 1 кулону, при перемещении из одной точки электрического поля в другую выполняет работу, равную 1 Дж.
Потенциалы точек, расположенных на одинаковых расстояниях от точечного заряда, равны. Если эти точки соединить между собой, образуется поверхность, которая называется эквипотенциальной поверхностью.
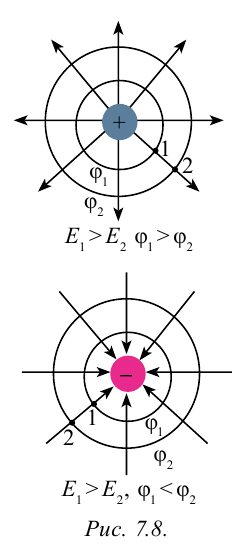
Эквипотенциальная поверхность точечного заряда располагается вокруг заряда в виде сконцентрированных кругов (рис. 7.8). Силовые линии поля проходят перпендикулярно к эквипотенциальной поверхности.
Межу напряженностью электрического поля и разностью потенциалов существует следующее соотношение:
где 
–расстояние между точками, потенциал которых равен 
и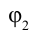 
.
Отсюда получаем единицу измерения напряженности поля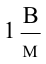 
.
Образец решения задачи:
В металлическую сферу радиусом 5 см, висящую в воздухе, подали заряд 30 нКл. Нужно найти потенциалы поля в точках, находящихся в 2 см от центра заряженной сферы, на поверхности сферы и удаленной от поверхности на расстояние 5 см.
Дано:
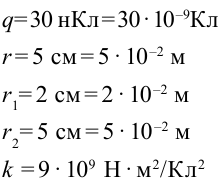
Найти:
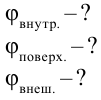
Формула:
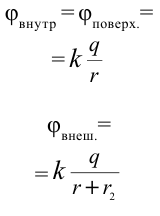
Решение:
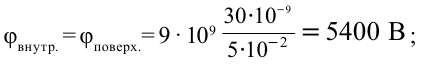
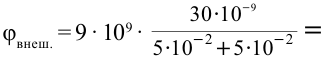
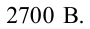
Единица измерения: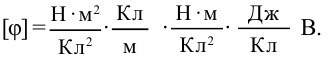 
Ответ: 5400 В; 2700 В.
- Работа электрического поля при перемещении заряда в физике
- Энергия электрического поля
- Электрическое поле заряженных неподвижных тел
- Напряженность электрического поля
- Электростатика
- Закон сохранения заряда в физике
- Электрическое поле заряженного шара
- Электрические явления в физике
Потенциал поля точечного заряда.
Подставим в соотношение для определения
потенциала выражение для напряженности
электрического поля точечного заряда:
.
При интегрировании учтем, что
.
После интегрирования получаем:
.
Потенциал точечного заряда пропорционален
величине заряда и убывает обратно
пропорционально расстоянию, стремясь
на бесконечности к нулю.
Потенциал поля системы зарядов.
Пусть система состоит из
неподвижных точечных зарядов
.
Согласно принципу суперпозиции в любой
точке поля напряженность равна
,
где
–
напряженность поля
-го
точечного заряда в исследуемой точке,
находящейся на расстоянии
от заряда
.
Подставив в соотношение для определения
потенциала значение
,
получим:
,
где
–
потенциал поля
-го
точечного заряда в исследуемой точке.
Таким образом, потенциал системы
точечных зарядов в любой точке пространства
равен алгебраической сумме потенциалов,
создаваемых всеми точечными зарядами
в этой точке.
Если заряды непрерывно распределены
по объему, то сумму следует заменить
объемным интегралом:
,
где интегрирование проводится по объему,
где
.
Аналогичные выражения получаются при
поверхностном и линейном распределении
зарядов:
,
.
Таким образом, зная распределение
зарядов, в принципе можно найти потенциал
и разность потенциалов поля любой
системы зарядов.
Рассмотрим ряд примеров расчета
потенциала и разности потенциалов,
которые понадобятся нам в дальнейшем
изложении.
-
Потенциал поля точечного
диполя.
С
огласно
принципу суперпозиции, учитывая, что
:
Потенциал
поля диполя зависит от его электрического
моментаpи убывает с
расстоянием быстрее, чем потенциал поля
точечного заряда
.
-
Потенциал поля в точках
на оси заряженного кольца.
Для расчета
воспользуемся
линейным интегралом:
,
где
–
заряд кольца. Для всех
– потенциал кольца убывает как потенциал
поля точечного заряда.
В центре кольца (x= 0)
потенциал равен:
.
-
Потенциал в точках на оси
равномерно заряженного круга
.
Д
ля
расчёта
следует
воспользоваться поверхностным интегралом:
.
Представим круг как систему колец с
радиусами
,
тогда
,
,
.
Для
получим:
.
Для точек достаточно удаленных от круга
:
.
Получите самостоятельно этот результат.
-
Потенциал поля объемно
заряженного шара
.
Для простоты расчетов примем
.
Зависимость
для этого случая представлена на рисунке.
Потенциал точек внутри шара
равен заштрихованной площади, согласно
геометрическому смыслу интеграла:
,
т
ак
как потенциал равен работе по перемещению
единичного положительного из данной
точки в бесконечность, где потенциал
принят равным нулю.
Учитывая зависимость:
где
,
получаем для точек внутри шара:
.
Д
ля
точек вне шара
потенциал убывает с расстоянием как
поле точечного заряда:
.
Зависимость
представлена на рисунке, где
,
.
-
Разность потенциалов
двух точек поля заряженной сферы
.
Для точек вне сферы
в однородном диэлектрике
.
Найдем разность потенциалов:
.
П
ри
интегрировании учтено, что
,
где
– приращение модуля радиус-вектора
.
-
Разность потенциалов
двух точек поля заряженного цилиндра
.
Для точек вне цилиндра
в однородном диэлектрике:
,
где
.
.
Лекция 5.
Соседние файлы в папке Физика2
- #
- #
- #
- #
- #
- #
Потенциал электростатического поля точечного заряда
4.9
Средняя оценка: 4.9
Всего получено оценок: 168.
4.9
Средняя оценка: 4.9
Всего получено оценок: 168.
Проявление электрического поля заключается в силовом взаимодействии между зарядами. Электрическое поле имеет ряд характеристик, одной из которых является потенциал. Рассмотрим это понятие, выведем формулу потенциала электростатического поля точечного заряда.
Понятие потенциала
Из курса электродинамики в 10 классе известно, что для определения взаимного влияния электрических зарядов используется понятие напряженности.
Однако для электротехники такая характеристика поля неудобна. В самом деле, напряженность — это векторная величина, предполагающая движение зарядов в пространстве. Но в электротехнических схемах заряды могут двигаться только по проводникам, направление которых однозначно определено. И имеет значение только движение вдоль проводников. Здесь было бы удобнее рассматривать не векторную, а скалярную характеристику поля.
Для введения такой скалярной характеристики вспомним, что основной задачей электротехники является получение и преобразование энергии. А электрическое поле — потенциально, и работа в нем не зависит от пути, по которому двигался заряд. Важна лишь разница потенциальных энергий в конечных точках траектории.
Все это позволяет ввести специальную энергетическую характеристику электростатического поля — потенциал.
Потенциальная энергия взаимодействия двух зарядов равна:
$$W_{потенц}=k{q_1q_2over r}$$
Из этой формулы следует, что потенциальная энергия электрического поля пропорциональна заряду, и отношение потенциальной энергии к этому заряду постоянно. Это отношение и есть потенциал $varphi$:
$$varphi={W_{потенц}over q}$$
Как и в случае с потенциальной энергией, конкретная величина потенциала не несет большой информации. Практически всегда используется разность потенциалов между двумя точками. Зная ее, можно рассчитать работу, которую совершает заряд при движении от одной точки к другой.
Потенциал поля точечного заряда
Из двух приведенных выше формул легко получить формулу потенциала точечного заряда. Подставив первую во вторую, получим:
$$varphi=k{qover r}$$
Коэффициент $k$ здесь, как и в законе Кулона, зависит от выбранной системы единиц. Для системы СИ ($varepsilon_0$ — электрическая постоянная):
$$k={1over 4pivarepsilon_0}$$
Таким образом, потенциал электростатического поля точечного заряда пропорционален величине заряда и обратно пропорционален расстоянию от него. Если $r=∞$, то $varphi=0$. По сути, потенциал поля точечного заряда равен энергии, которая необходима для удаления единичного пробного заряда в бесконечность.
Потенциал системы точечных зарядов
Поскольку электрическое поле потенциально, и в нём действует принцип суперпозиции, это позволяет легко находить потенциал системы зарядов. Он равен алгебраической сумме элементарных зарядов:
$$varphi_{общ} =varphi_1+varphi_2+…+varphi_n$$
Эта же формула используется в том случае, если заряд распределен по телу неравномерно. Тело разбивается на множество элементарных областей, в каждой из которых заряд можно считать точечным. После этого потенциал всех областей суммируется.
Что мы узнали
Электростатический потенциал — это скалярная энергетическая характеристика электростатического поля. Она равна работе, которую надо совершить для того, чтобы удалить пробный единичный заряд из поля в бесконечность. Поскольку электрическое поле потенциально, и в нём работает принцип суперпозиции, потенциал системы точечных зарядов равен сумме потенциалов каждого заряда.
Тест по теме
Доска почёта
Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.9
Средняя оценка: 4.9
Всего получено оценок: 168.
А какая ваша оценка?
Физические задачи по электростатике мало кто любит. Но что поделать, решать их надо. Разберемся, как это делать по-быстрому и с использованием подробных примеров решений задач на разность потенциалов, задач на работу электрического поля и напряженность.
Наш телеграм – полезная информация для абитуриентов и студентов всех специальностей, присоединяйтесь!
Решение задач на разность потенциалов и работу поля: примеры
Задача №1 на потенциальную энергию системы зарядов
Условие
Два точечных заряда величиной 100 нКл и 10 нКл находятся на расстоянии r=10 см друг от друга. Вычислить потенциальную энергию системы этих зарядов.
Решение
Потенциал поля точечного заряда равен:
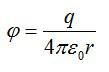
Так что, потенциальная энергия зарядов будет равна:
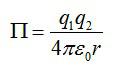
Подставим значения из условия и найдем:
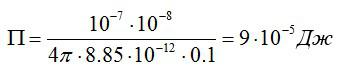
Ответ: П=9*10^-5 Дж.
Задача №2 на определение потенциала заряженных шаров
Условие
Шар радиусом R1=6 см заряжен до потенциала 300 В , а шар радиусом R2=4 см – до потенциала 500 В. Найдите потенциал шаров после того, как их соединили металлическим проводом, емкостью которого можно пренебречь.
Решение
Потенциал шара равен:
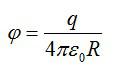
Суммарный заряд двух шаров будет равен:
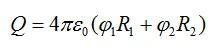
После соединения шаров заряд каждого будет равен:
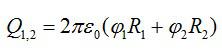
Тогда суммарный потенциал шаров вычислится по формуле:
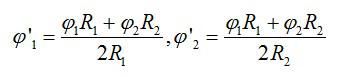
Подставим значения и найдем:
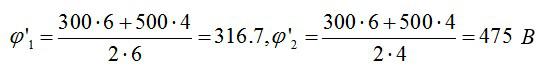
Ответ: 317 В; 475 В.
Задача №3 на разность потенциалов и работу по перемещению заряда
Условие
Заряд переместился между двумя точками с разностью потенциалов 1 кВ, при этом поле совершило работу, равную 40 мкДж. Найдите величину заряда.
Решение
По определению, разность потенциалов равна работе по перемещению заряда, деленной на величину этого заряда:
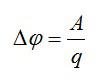
Отсюда можно выразить заряд и вычислить ответ:
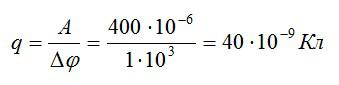
Ответ: 40 нКл.
Задача №4 на работу электрического поля по перемещению заряда
Условие
Два точечных заряда q1=6 мкКл и q2=2 мкКл, находятся на расстоянии а=60 см друг от друга. Какую работу необходимо свершить внешним силам, чтобы уменьшить расстояние между зарядами вдвое?
Решение
Находясь на расстоянии a, точечные заряды обладали потенциальной энергией:
На вдвое меньшем расстоянии энергия зарядов равна:
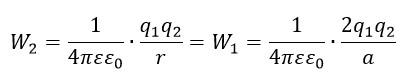
Работа, затраченная на сближение зарядов:
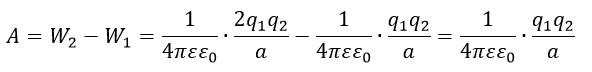
Подставляем числовые данные и вычисляем:
Ответ: A=0,18 Дж.
Задача №5 на движение заряженной частицы в поле
Условие
Электрон влетает в плоский воздушный конденсатор параллельно его пластинам со скоростью V=5·107 м/с. Расстояние между пластинами d=2 см, разность потенциалов U=500 В. Найти отклонение электрона, вызванное полем конденсатора, если длина его пластины l=5 см.
Решение
При движении в электрическом поле конденсатора на электрон действует сила:
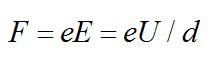
Ускорение электрона, по 2 закону Ньютона, определяется формулой:
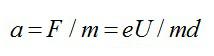
Время движения электрона в конденсаторе вычислим, зная длину пластины и скорость частицы:
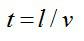
Отклонение электрона будет равно:
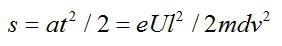
Найдем:
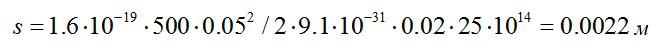
Ответ: 2.2 мм
Вопросы на тему «Работа электрического поля и разность потенциалов»
Вопрос 1. Что такое потенциал электрического поля?
Ответ. Потенциал – скалярная физическая величина, являющаяся энергетической характеристикой электростатического поля.
Потенциал поля равен отношению потенциальной энергии поля (или работы по перемещению заряда из данной точки на нулевой уровень потенциальной энергии) к величине заряда.
Для потенциала применим принцип суперпозиции.
Вопрос 2. Что такое разность потенциалов?
Ответ. Разность потенциалов – это работа по перемещению заряда из одной точки в другую. Разность потенциалов еще называют напряжением, обозначая его как разность потенциалов в начальной и конечной точках траектории заряда.
Вопрос 3. Что происходит с зарядом, когда он попадает в электрическое поле?
Ответ. На заряд со стороны поля действует сила, способная перемещать заряд в поле и совершать работу.
Вопрос 4. Какую природу имеет сила, действующая на заряд? Зависит ли величина работы от траектории заряда в поле?
Ответ. Сила, действующая со стороны поля на заряд, является проявлением электромагнитного взаимодействия. Величина работы поля не зависит от траектории заряда, так как это работа потенциальных (консервативных) сил.
Для наилучшего понимания сути задач на потенциал и работу поля, можно провести параллель между работой по перемещению заряда, потенциальной энергией в механике и работой силы тяжести.
Вопрос 5. Что такое эквипотенциальная поверхность?
Ответ. Это поверхность, во всех точках которой потенциал электрического поля имеет одинаковое значения.
Какие бы задачи вы не решали и где ни учились, профессиональный образовательный сервис для студентов готов оказать помощь с проблемами по учебе любой сложности.
Потенциал. Разность потенциалов. ЗАДАЧИ с решениями
Формулы, используемые на уроках «Решение задач на тему: Работа перемещения заряда в электрическом поле. Потенциал. Разность потенциалов» для подготовки к ЕГЭ.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Металлический шар диаметром d заряжен с поверхностной плотностью зарядов σ. Найти потенциал φ этого шара, если он окружен заземленной проводящей сферой, имеющей общий с шаром центр. Диаметр сферы D. Среда — воздух.
Задача № 2.
Потенциал заряженного шара φ1 = 300 В. Чему равен потенциал φ2 электрического поля этого шара в точке, отстоящей на расстоянии l = 50 см от его поверхности, если радиус шара R = 25 см?
Смотреть решение и ответ
Задача № 3.
Определить потенциал φ точки поля, находящейся на расстоянии а = 9 см от поверхности заряженного шара радиусом R = 1 см, если поверхностная плотность зарядов на шаре σ = 1 • 10–11 Кл/см2. Среда — воздух.
Задача № 4.
В точке 1 поля точечного заряда-источника потенциал φ1 = 40 В, а в точке 2 φ2 = 10 В. Найти потенциал φ в точке М, лежащей посередине между точками 1 и 2 (рис. 3-6). 
Задача № 5.
В трех вершинах квадрата со стороной а = 20 см находятся заряды q1 = 1 • 10–8 Кл, q2 = 2 • 10–8 Кл и q3 = 2 • 10–8 Кл (рис. 3-7). Определить потенциал φ электрического поля, созданного этими зарядами в четвертой вершине. 
Задача № 6.
Четыре одинаковых точечных заряда q расположены на одной прямой на расстоянии r друг от друга. Какую работу А надо совершить, чтобы переместить эти заряды в вершины тетраэдра со стороной r? Среда — вакуум.
Задача № 7.
Два одинаково заряженных шарика диаметрами d = 0,5 см каждый расположены на расстоянии l = 2 см между их поверхностями (рис. 3-14). До какого потенциала φ они заряжены, если сила их отталкивания друг от друга F = 2 мкН? Среда — воздух. 
Задача № 8.
В однородном электрическом поле напряженностью Е = 2 кВ/см переместили заряд q = –20 нКл в направлении силовой линии поля на расстояние d = 10 см. Найти работу поля А, изменение потенциальной энергии поля ΔWп и напряжение (разность потенциалов) U между начальной и конечной точками перемещения.
Смотреть решение и ответ
Задача № 9.
Между двумя горизонтальными плоскостями, заряженными разноименно и расположенными на расстоянии d = 5 мм друг от друга, находится в равновесии капелька масла массой 20 нг (нанограмм) (рис. 3-10). Найти число избыточных электронов N на этой капельке. Среда — воздух. Разность потенциалов между плоскостями U = 2 кВ. 
Задача № 10.
На пластине М поддерживается потенциал φ1 = +80 В, а на пластине N – φ2 = –80 В (рис. 3-11, а). Расстояние между пластинами d = 10 см. На расстоянии d1 = 4 см от пластины М помещают заземленную пластину Р (рис. 3-11, б). Найти изменение напряженности ΔЕ1 поля на участке МР и изменение напряженности поля ΔЕ2 на участке PN при этом. Построить графики зависимостей напряженностей Е = Е(х) и потенциала φ = φ(х) от расстояния между точками поля и пластинами. 
Это конспект по теме «Потенциал. Разность потенциалов. ЗАДАЧИ с решениями». Выберите дальнейшие действия:
- Вернуться к списку конспектов по Физике.
- Проверить свои знания по Физике.
