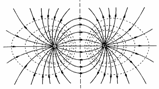
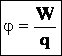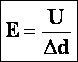Как найти потенциал электростатического поля точечного заряда

Потенциал электростатического поля точечного заряда

4.9

Средняя оценка: 4.9

Всего получено оценок: 168.

4.9

Средняя оценка: 4.9

Всего получено оценок: 168.

Проявление электрического поля заключается в силовом взаимодействии между зарядами. Электрическое поле имеет ряд характеристик, одной из которых является потенциал. Рассмотрим это понятие, выведем формулу потенциала электростатического поля точечного заряда.

Понятие потенциала

Из курса электродинамики в 10 классе известно, что для определения взаимного влияния электрических зарядов используется понятие напряженности.

Рис. 1. Напряженность электрического поля.

Однако для электротехники такая характеристика поля неудобна. В самом деле, напряженность — это векторная величина, предполагающая движение зарядов в пространстве. Но в электротехнических схемах заряды могут двигаться только по проводникам, направление которых однозначно определено. И имеет значение только движение вдоль проводников. Здесь было бы удобнее рассматривать не векторную, а скалярную характеристику поля.

Для введения такой скалярной характеристики вспомним, что основной задачей электротехники является получение и преобразование энергии. А электрическое поле — потенциально, и работа в нем не зависит от пути, по которому двигался заряд. Важна лишь разница потенциальных энергий в конечных точках траектории.

Все это позволяет ввести специальную энергетическую характеристику электростатического поля — потенциал.

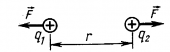
Потенциальная энергия взаимодействия двух зарядов равна:

$$W_{потенц}=k{q_1q_2over r}$$

Из этой формулы следует, что потенциальная энергия электрического поля пропорциональна заряду, и отношение потенциальной энергии к этому заряду постоянно. Это отношение и есть потенциал $varphi$:

$$varphi={W_{потенц}over q}$$

Как и в случае с потенциальной энергией, конкретная величина потенциала не несет большой информации. Практически всегда используется разность потенциалов между двумя точками. Зная ее, можно рассчитать работу, которую совершает заряд при движении от одной точки к другой.

Потенциал поля точечного заряда

Из двух приведенных выше формул легко получить формулу потенциала точечного заряда. Подставив первую во вторую, получим:

$$varphi=k{qover r}$$

Коэффициент $k$ здесь, как и в законе Кулона, зависит от выбранной системы единиц. Для системы СИ ($varepsilon_0$ — электрическая постоянная):

$$k={1over 4pivarepsilon_0}$$

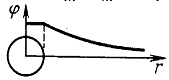
Таким образом, потенциал электростатического поля точечного заряда пропорционален величине заряда и обратно пропорционален расстоянию от него. Если $r=∞$, то $varphi=0$. По сути, потенциал поля точечного заряда равен энергии, которая необходима для удаления единичного пробного заряда в бесконечность.

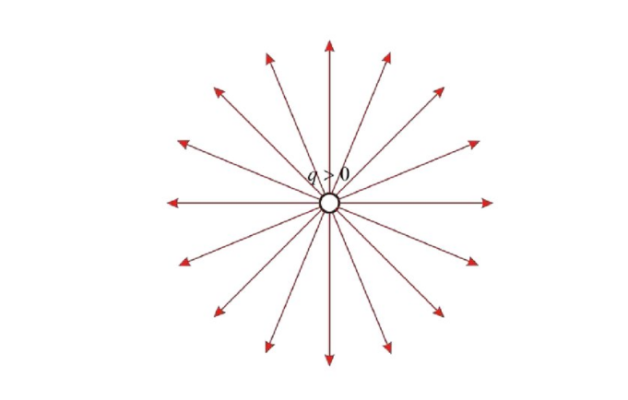
Рис. 2. Силовые линии точечного заряда.

Потенциал системы точечных зарядов

Поскольку электрическое поле потенциально, и в нём действует принцип суперпозиции, это позволяет легко находить потенциал системы зарядов. Он равен алгебраической сумме элементарных зарядов:

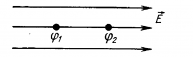
$$varphi_{общ} =varphi_1+varphi_2+…+varphi_n$$

Эта же формула используется в том случае, если заряд распределен по телу неравномерно. Тело разбивается на множество элементарных областей, в каждой из которых заряд можно считать точечным. После этого потенциал всех областей суммируется.

Рис. 3. Потенциал системы зарядов.

Что мы узнали

Электростатический потенциал — это скалярная энергетическая характеристика электростатического поля. Она равна работе, которую надо совершить для того, чтобы удалить пробный единичный заряд из поля в бесконечность. Поскольку электрическое поле потенциально, и в нём работает принцип суперпозиции, потенциал системы точечных зарядов равен сумме потенциалов каждого заряда.

Тест по теме

Доска почёта

Чтобы попасть сюда – пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.9

Средняя оценка: 4.9

Всего получено оценок: 168.

А какая ваша оценка?

Источник

Преподаватель который помогает студентам и школьникам в учёбе.

Потенциал поля точечного заряда в физике – формулы и определение с примерами

Потенциал поля точечного заряда:

Чтобы определить силу электрического поля, мы ввели в него пробный заряд и определили силу воздействия поля на этот заряд.

Напряженность электрического поля является характеристикой силы поля.

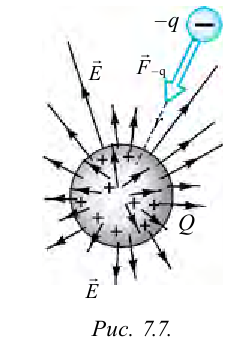
При введении пробного заряда в поле, оно оказывает сопротивление (рис. 7.7). Для преодоления сопротивления необходимо проделать определенную работу.
Как определяется эта выполненная работа?

Эта работа превращается в потенциальную энергию взаимодействия основного заряда и введенного пробного заряда:

Знак минус в формуле показывает, что между зарядами действует сила притяжения.

Потенциальная энергия 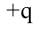заряда, расположенного на расстоянии 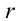от положительного неподвижного заряда 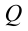, определяется следующим выражением

Положительный знак в формуле показывает, что между зарядами действует сила отталкивания.

Согласно формуле потенциальная энергия равняется нулю, когда расчет производится для бесконечного расстояния. На таких расстояниях заряды не взаимодействуют.

Таким образом, электрическое поле с приобретением характеристики силы будет иметь и энергетическую характеристику. Энергетическая характеристика поля определяется величиной, которая называется потенциалом поля.

Потенциалом электрического поля точечного заряда называется величина, измеряемая отношением потенциальной энергии взаимодействия основного и введенного в поле пробного заряда к величине пробного заряда:

Потенциал точечного заряда 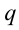определяется следующим образом:

Пользуясь понятием потенциала найдем работу, совершаемую при перемещении заряда 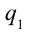с расстояния 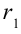на расстояние 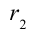от заряда 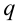, создающего электрическое поле:

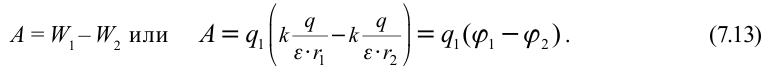
В этом выражении разница 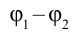является разницей потенциалов между точками, называется электрическим напряжением и записывается следующим образом:

Единица измерения потенциала и разность потенциалов называется Вольт (В) в честь итальянского ученого Вольта. Из формулы 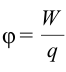следует, что .

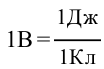Это значит, что разность потенциалов точек равняется 1 вольту, когда заряд, равный 1 кулону, при перемещении из одной точки электрического поля в другую выполняет работу, равную 1 Дж.

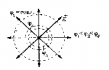
Потенциалы точек, расположенных на одинаковых расстояниях от точечного заряда, равны. Если эти точки соединить между собой, образуется поверхность, которая называется эквипотенциальной поверхностью.

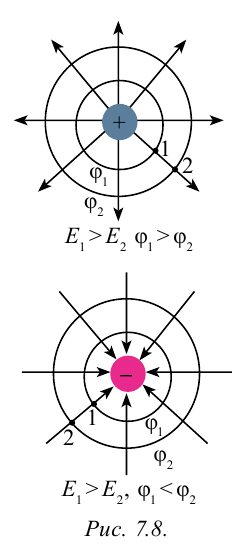
Эквипотенциальная поверхность точечного заряда располагается вокруг заряда в виде сконцентрированных кругов (рис. 7.8). Силовые линии поля проходят перпендикулярно к эквипотенциальной поверхности.

Межу напряженностью электрического поля и разностью потенциалов существует следующее соотношение:

где 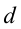–расстояние между точками, потенциал которых равен 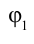и .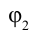
Отсюда получаем единицу измерения напряженности поля .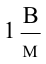

Образец решения задачи:

В металлическую сферу радиусом 5 см, висящую в воздухе, подали заряд 30 нКл. Нужно найти потенциалы поля в точках, находящихся в 2 см от центра заряженной сферы, на поверхности сферы и удаленной от поверхности на расстояние 5 см.

Дано:

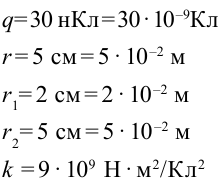
Найти:

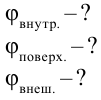
Формула:

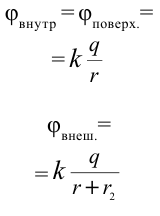
Решение:

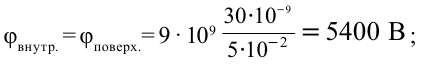
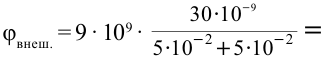
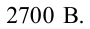
Единица измерения: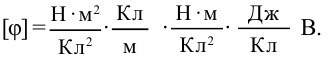

Ответ: 5400 В; 2700 В.

Работа электрического поля при перемещении заряда в физике
Энергия электрического поля
Электрическое поле заряженных неподвижных тел
Напряженность электрического поля
Электростатика
Закон сохранения заряда в физике
Электрическое поле заряженного шара
Электрические явления в физике

Источник

Потенциал поля точечного заряда.

Подставим в соотношение для определения
потенциала выражение для напряженности
электрического поля точечного заряда:

При интегрировании учтем, что
.

После интегрирования получаем:

Потенциал точечного заряда пропорционален
величине заряда и убывает обратно
пропорционально расстоянию, стремясь
на бесконечности к нулю.

Потенциал поля системы зарядов.

Пусть система состоит из
неподвижных точечных зарядов.
Согласно принципу суперпозиции в любой
точке поля напряженность равна,
где–
напряженность поля-го
точечного заряда в исследуемой точке,
находящейся на расстоянииот заряда.

Подставив в соотношение для определения
потенциала значение
,
получим:

где
–
потенциал поля-го
точечного заряда в исследуемой точке.

Таким образом, потенциал системы
точечных зарядов в любой точке пространства
равен алгебраической сумме потенциалов,
создаваемых всеми точечными зарядами
в этой точке.

Если заряды непрерывно распределены
по объему, то сумму следует заменить
объемным интегралом:

где интегрирование проводится по объему,
где
.

Аналогичные выражения получаются при
поверхностном и линейном распределении
зарядов:

Таким образом, зная распределение
зарядов, в принципе можно найти потенциал
и разность потенциалов поля любой
системы зарядов.

Рассмотрим ряд примеров расчета
потенциала и разности потенциалов,
которые понадобятся нам в дальнейшем
изложении.

Потенциал поля точечного
диполя.

Согласно
принципу суперпозиции, учитывая, что:

Потенциал
поля диполя зависит от его электрического
моментаpи убывает с
расстоянием быстрее, чем потенциал поля
точечного заряда.

Потенциал поля в точках
на оси заряженного кольца.

Для расчета
воспользуемся
линейным интегралом:

где
–
заряд кольца. Для всех

– потенциал кольца убывает как потенциал
поля точечного заряда.

В центре кольца (x= 0)
потенциал равен:

Потенциал в точках на оси
равномерно заряженного круга
.

Для
расчётаследует
воспользоваться поверхностным интегралом:

Представим круг как систему колец с
радиусами
,
тогда,,.

Для
получим:

Для точек достаточно удаленных от круга
:

Получите самостоятельно этот результат.

Потенциал поля объемно
заряженного шара
.

Для простоты расчетов примем
.

Зависимость
для этого случая представлена на рисунке.
Потенциал точек внутри шараравен заштрихованной площади, согласно
геометрическому смыслу интеграла:

так
как потенциал равен работе по перемещению
единичного положительного из данной
точки в бесконечность, где потенциал
принят равным нулю.

Учитывая зависимость:

где
,
получаем для точек внутри шара:

Для
точек вне шарапотенциал убывает с расстоянием как
поле точечного заряда:

Зависимость
представлена на рисунке, где

Разность потенциалов
двух точек поля заряженной сферы
.

Для точек вне сферы
в однородном диэлектрике

Найдем разность потенциалов:

П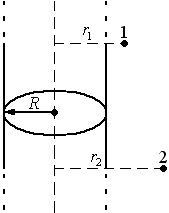ри
интегрировании учтено, что,
где– приращение модуля радиус-вектора.

Разность потенциалов
двух точек поля заряженного цилиндра
.

Для точек вне цилиндра
в однородном диэлектрике:

где
.

Лекция 5.

Соседние файлы в папке Физика2

Источник

У этого термина существуют и другие значения, см. Потенциал.

Классическая электродинамика

Электричество · Магнетизм
Электростатика Закон Кулона Теорема Гаусса Электрический дипольный момент Электрический заряд Электрическая индукция Электрическое поле Электростатический потенциал
Магнитостатика Закон Био — Савара — Лапласа Закон Ампера Магнитный момент Магнитное поле Магнитный поток Магнитная индукция
Электродинамика Векторный потенциал Диполь Потенциалы Лиенара — Вихерта Сила Лоренца Ток смещения Униполярная индукция Уравнения Максвелла Электрический ток Электродвижущая сила Электромагнитная индукция Электромагнитное излучение Электромагнитное поле
Электрическая цепь Закон Ома Законы Кирхгофа Индуктивность Радиоволновод Резонатор Электрическая ёмкость Электрическая проводимость Электрическое сопротивление Электрический импеданс
Ковариантная формулировка Тензор электромагнитного поля Тензор энергии-импульса 4-потенциал 4-ток
См. также: Портал:Физика

Электростатический потенциа́л — скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию, которой обладает единичный положительный пробный заряд, помещённый в данную точку поля. Единицей измерения потенциала в Международной системе единиц (СИ) является вольт (русское обозначение: В; международное: V), 1 В = 1 Дж/Кл (подробнее о единицах измерения — см. ниже).

Электростатический потенциал — специальный термин для возможной замены общего термина электродинамики скалярный потенциал в частном случае электростатики (исторически электростатический потенциал появился первым, а скалярный потенциал электродинамики — его обобщение). Употребление термина электростатический потенциал определяет собой наличие именно электростатического контекста. Если такой контекст уже очевиден, часто говорят просто о потенциале без уточняющих прилагательных.

Электростатический потенциал равен отношению потенциальной энергии взаимодействия заряда с полем к величине этого заряда:

${displaystyle varphi ={frac {W_{p}}{q_{p}}}.}$

Напряжённость электростатического поля и потенциал varphi связаны соотношением^[1]

${displaystyle int limits _{A}^{B}mathbf {E} cdot mathbf {dl} =varphi (A)-varphi (B),}$

или обратно^[2]:

Здесь nabla — оператор набла, то есть в правой части равенства стоит минус градиент потенциала — вектор с компонентами, равными частным производным от потенциала по соответствующим (прямоугольным) декартовым координатам, взятый с противоположным знаком.

Воспользовавшись этим соотношением и теоремой Гаусса для напряжённости поля ${mathbf nabla }cdot {mathbf E}={rho over varepsilon _{0}}$ , легко увидеть, что электростатический потенциал удовлетворяет уравнению Пуассона в вакууме. В единицах системы СИ:

${displaystyle {nabla }^{2}varphi =-{rho over varepsilon _{0}},}$

где varphi — электростатический потенциал (в вольтах), rho — объёмная плотность заряда (в кулонах на кубический метр), а ${displaystyle varepsilon _{0}}$ — электрическая постоянная (в фарадах на метр).

Неоднозначность определения потенциала[править | править код]

Поскольку потенциал (как и потенциальная энергия) может быть определён с точностью до произвольной постоянной (и все величины, которые можно измерить, а именно напряженности поля, силы, работы — не изменятся, если мы выберем эту постоянную так или по-другому), непосредственный физический смысл (по крайней мере, пока речь не идет о квантовых эффектах) имеет не сам потенциал, а разность потенциалов, которая определяется как:

${displaystyle varphi _{1}-varphi _{2}={frac {A_{f}^{q^{*}1to 2}}{q^{*}}},}$

где:

$varphi _{1}$

— потенциал в точке 1,

$varphi _{2}$

— потенциал в точке 2,

$A_{{f}}^{{q^{{*}}1to 2}}$

— работа, совершаемая полем при переносе пробного заряда $q^{{*}}$

из точки 1 в точку 2.

При этом считается, что все остальные заряды при такой операции «заморожены» — то есть неподвижны во время этого перемещения (имеется в виду вообще говоря скорее воображаемое, а не реальное перемещение, хотя в случае, если остальные заряды действительно закреплены — или пробный заряд исчезающе мал по величине — чтобы не вносить заметного возмущения в положения других — и переносится достаточно быстро, чтобы остальные заряды не успели заметно переместиться за это время, формула оказывается верной и для вполне реальной работы при реальном перемещении).

Впрочем, иногда для снятия неоднозначности используют какие-нибудь «естественные» условия. Например, часто потенциал определяют таким образом, чтобы он был равен нулю на бесконечности для любого точечного заряда — и тогда для любой конечной системы зарядов выполнится на бесконечности это же условие, а над произвольностью выбора константы можно не задумываться (конечно, можно было бы выбрать вместо нуля любое другое число, но ноль — «проще»).

Единицы измерения[править | править код]

В СИ за единицу разности потенциалов принимают вольт (В).

Разность потенциалов между двумя точками поля равна одному вольту, если для перемещения между ними заряда в один кулон нужно совершить работу в один джоуль: 1 В = 1 Дж/Кл (L²MT⁻³I⁻¹).

В СГС единица измерения потенциала не получила специального названия. Разность потенциалов между двумя точками равна одной единице потенциала СГСЭ, если для перемещения между ними заряда величиной одна единица заряда СГСЭ нужно совершить работу в один эрг.

Приближенное соответствие между величинами: 1 В = 1/300 ед. потенциала СГСЭ.

Использование термина[править | править код]

Широко используемые термины напряжение и электрический потенциал имеют несколько иной смысл, хотя нередко используются неточно как синонимы электростатического потенциала. В отсутствие меняющихся магнитных полей напряжение равно разности потенциалов.

Кулоновский потенциал[править | править код]

Иногда термин кулоновский потенциал используется просто для обозначения электростатического потенциала как полный синоним. Однако можно сказать, что в целом эти термины несколько различаются по оттенку и преимущественной области применения.

Также под кулоновским могут понимать потенциал любой природы (то есть не обязательно электрический), который при точечном или сферически симметричном источнике имеет зависимость от расстояния ${frac 1r}$ (например, гравитационный потенциал в теории тяготения Ньютона, хотя последний чаще всё же называют ньютоновским, так как он был изучен в целом раньше), особенно если надо как-то обозначить весь этот класс потенциалов в отличие от потенциалов с другими зависимостями от расстояния.

Формула электростатического потенциала (кулоновского потенциала) точечного заряда в вакууме:

${displaystyle varphi =k{frac {q}{r}},}$

где обозначен коэффициент, зависящий от системы единиц измерения — например, в СИ:

$k={frac 1{4pi varepsilon _{0}}}$

= 9·10⁹ В·м/Кл,

— величина заряда, — расстояние от заряда-источника до точки, для которой рассчитывается потенциал.

Можно показать, что эта формула верна не только для точечных зарядов, но и для любого сферически симметричного заряда конечного размера, например, равномерно заряженного шара, правда, только в свободном от заряда пространстве — то есть, например, над поверхностью шара, а не внутри его.
Кулоновский потенциал в приведенном выше виде используется в формуле кулоновской потенциальной энергии (потенциальной энергии взаимодействия системы электростатически взаимодействующих зарядов):

${displaystyle W=sum _{i<j}k{frac {q_{i}q_{j}}{r_{ij}}}={frac {1}{2}}sum _{ineq j}k{frac {q_{i}q_{j}}{r_{ij}}}.}$

В электродинамике[править | править код]

Когда присутствуют изменяющиеся во времени магнитные поля (что справедливо, при изменяющихся во времени электрических полей и наоборот), то невозможно описать электрическое поле в терминах скалярного потенциала V, поскольку электрическое поле больше не является консервативным: циркуляция ${displaystyle textstyle int _{C}mathbf {E} cdot mathrm {d} {boldsymbol {ell }}}$ зависит от пути, потому что (см. Закон индукции Фарадея).

Вместо этого всё ещё можно определить скалярный потенциал, дополнив его магнитным векторным потенциалом A. В частности, А определен так чтобы

{displaystyle mathbf {B} =mathbf {nabla } times mathbf {A} ,,}

где B — магнитное поле. Поскольку дивергенция магнитного поля всегда равно нулю из-за отсутствия магнитных монополей, то A всегда существует. Учитывая это, величина

${displaystyle mathbf {F} =mathbf {E} +{frac {partial mathbf {A} }{partial t}}}$

является консервативным полем по закону Фарадея, и поэтому можно написать

${displaystyle mathbf {E} =-mathbf {nabla } V-{frac {partial mathbf {A} }{partial t}},,}$

где V — скалярный потенциал, определённый консервативным полем F.

Электростатический потенциал — это частный случай этого определения, где A не зависит от времени. С другой стороны, для изменяющихся во времени полей,

${displaystyle -int _{a}^{b}mathbf {E} cdot mathrm {d} {boldsymbol {ell }}neq V_{(b)}-V_{(a)},,}$

в отличие от электростатики.

См. также[править | править код]

Гальвани-потенциал
Вольта-потенциал
Векторный потенциал электромагнитного поля
4-потенциал
Стандартный электродный потенциал
Степень окисления
Гравитационный потенциал
Ядерный потенциал

Примечания[править | править код]

Литература[править | править код]

Алешкевич В. А. Электромагнетизм. — М.: Физматлит, 2014. — 404 с. — 700 экз. — ISBN 978-5-9221-1555-1.

Источник

Потенциал. Разность потенциалов. Напряжение.
Потенциал электростатического поля — скалярная величина, равная отношению потенциальной энергии заряда в поле к этому заряду: – энергетическая характеристика поля в данной точке. Потенциал не зависит от величины заряда, помещенного в это поле.
Т.к. потенциальная энергия зависит от выбора системы координат, то и потенциал определяется с точностью до постоянной. За точку отсчета потенциала выбирают в зависимости от задачи: а) потенциал Земли, б) потенциал бесконечно удаленной точки поля, в) потенциал отрицательной пластины конденсатора.
– следствие принципа суперпозиции полей (потенциалы складываютсяалгебраически).
Потенциал численно равен работе поля по перемещению единичного положительного заряда из данной точки электрического поля в бесконечность. В СИ потенциал измеряется в вольтах:
*Разность потенциалов*

*Напряжение — разность значений потенциала в начальной и конечнойточках траектории.* Напряжение численно равно работе электростатического поля при перемещении единичного положительного заряда вдоль силовых линий этого поля. Разность потенциалов (напряжение) не зависит от выбора системы координат!
Единица разности потенциалов Напряжение равно 1 В, если при перемещении положительного заряда в 1 Кл вдоль силовых линий поле совершает работу в 1 Дж.
Связь между напряженностью и напряжением.
Из доказанного выше: → напряженность равна градиенту потенциала (скорости изменения потенциала вдоль направления d).
Из этого соотношения видно: Вектор напряженности направлен в сторону уменьшения потенциала. Электрическое поле существует, если существует разность потенциалов. Единица напряженности: – Напряженность поля равна 1 В/м, если между двумя точками поля, находящимися на расстоянии 1 м друг от друга существует разность потенциалов 1 В.
Эквипотенциальные поверхности. ЭПП – поверхности равного потенциала. Свойства ЭПП: – работа при перемещении заряда вдоль эквипотенциальной поверхности не совершается; – вектор напряженности перпендикулярен к ЭПП в каждой ее точке.

*Измерение электрического напряжения (разности потенциалов)* Между стержнем и корпусом — электрическое поле. Измерение потенциала кондуктора Измерение напряжения на гальваническом элементе Электрометр дает большую точность, чем вольтметр.
*Потенциальная энергия взаимодействия зарядов.*

*Потенциал поля точечного заряда*

*Потенциал заряженного шара* а) Внутри шара Е=0, следовательно, потенциалы во всех точках внутри заряженного металлического шара одинаковы (!!!) и равны потенциалу на поверхности шара. б) Снаружи поле шара убывает обратно пропорционально расстоянию от центра шара, как и в случае точечного заряда.
*Перераспределение зарядов при контакте заряженных проводников.* Переход зарядов происходит до тех пор, пока потенциалы контактирующих тел не станут равными.