Как найти потенциал который равен нулю

Потенциал

Электростатическое поле является потенциальным. Что такое потенциальное поле? Пусть электростатическое поле перемещает заряд между двумя точками. Работа сил поля по перемещению заряда между этими точками не зависит от формы пути, а зависит только от положения самих точек. Такое поле и называется потенциальным.

Так как электростатическое поле потенциально, то для него возможно ввести понятие потенциала.

А почему нужно перемещать заряд в бесконечность? Считается, что в бесконечности поле равно нулю и потенциал равен нулю. Если ещё раз прочесть определение потенциала, то можно понять, что перемещая заряд в бесконечность, мы перемещаем его в точку, в которой потенциал равен нулю. В качестве точки с нулевым потенциалом можно было бы выбрать любую точку, но обычно выбирается бесконечность.

Ещё вопрос: почему важно для определения потенциала то, что электростатическое поле потенциально? В потенциальном поле работа не зависит от формы пути, значит потенциал может характеризовать поле в точке. Ведь если бы работа поля по перемещению заряда в бесконечность зависила от формы пути, то премещая заряд разными путями, мы получили бы различные значения потенциала для одной точки. Но работа в случае электростатического поля не зависит от формы пути, значит значение потенциала в точке будет только одно, а это означает, что потенциал может характеризовать поле в данной точке.

Для различных точек электростатического поля мы можем однозначно указать значение потенциала. Правда здесь есть одна тонкость: перед тем как указывать значение потенциала для любой точки нужно значение потенциала в определённой точке принять равным нулю (или какой-то определённой величине). Таковой точкой мы выбрали бесконечность. Здесь важно понять, что когда мы говорим о потенциале поля в данной точке, то другая точка, куда (или откуда) будем перемещать заряд, заранее известна.

Потенциал является скалярной величиной.

Формула потенциала φ точки электростатического поля заряда q на расстоянии r от него:

Разность потенциалов (напряжение) между 2-мя точками поля равняется отношению работы поля по перемещению заряда из начальной точки в конечную к этому заряду:

,

Так как работа по перемещению заряда в потенциальном поле не зависит от формы траектории, то, зная напряжение между двумя точками, мы определим работу, которая совершается полем по перемещению единичного заряда.

Если есть несколько точечных зарядов, значит, потенциал поля в некоторой точке пространс­тва определяется как алгебраическая сумма потенциалов электрических полей каждого заряда в данной точке:

.

Эквипотенциальной поверхностью, или поверхностью равного потенциала, является поверхность, для любых точек которой разность потенциалов равна нулю. Это означяет, что работа по перемещению заряда по такой поверхности равна нулю, следовательно, линии напряженности электрического поля перпендикулярны эквипотенциальным поверхностям. Эквипотенциальные поверхности однородного поля представляют собой плоскости, а точечного заряда — концентрические сферы.

Вектор напряженности (как и сила ) перпендикулярен эквипотенциальным поверхнос­тям. Эквипотенциальной является поверхность любого проводника в электростатическом поле, так как силовые линии перпендикулярны поверхности проводника. Внутри проводника разность потенциалов между любыми его точками равна нулю.

Напряжение и напряженность однородного поля .

В однородном электрическом поле напряженность E в каждой точке одинакова, и работа A по перемещению заряда q параллельно на расстояние d между двумя точками с потенциалами φ₁, и φ₂ равна:

,

.

Т.о., напряженность поля пропорциональна разности потенциалов и направлена в сторону уменьшения потенциала. Поэтому положительный заряд будет двигаться в сторону уменьшения потенциала, а отрицательный — в сторону его увеличения.

Единицей напряжения (разности потенциалов) является вольт. Исходя из формулы , , разность потенциалов между двумя точками равна одному вольту, если при перемещении заряда в 1 Кл между этими точками поле совершает работу в 1 Дж.

Автор Влад Шестаков задал вопрос в разделе ВУЗы, Колледжи

Если напряженность электростатического поля в некоторой точке равна нулю.обязательно ли что потенциал в этой точке = 0? и получил лучший ответ

Ответ от Vladimir Shchookin[гуру]
Копирую первую часть ответа АНДРЕЯ (Так, как напряженность электрического поля равна градиенту потенциала, то если потенциал в этой точке будет равен постоянной величине (константе) , т. е. не зависеть от координат, то электростатическое поле в точке будет равно 0, т. к. в этом случае производные от потенциала по координатам будут равны 0.) и говорю, что вовсе нет. Пример: поле двух параллельных плоскостей, заряженных разноимённо с равными по абсолютному значению поверхностными плотностями зарядов.
JELAYU USPEXOV .
Vladimir Shchookin.

Потенциал. Разность потенциалов.

Разность потенциалов (напряжение) между 2-мя точками поля равняется отношению работы поля по перемещению заряда из начальной точки в конечную к этому заряду:

,

Так как работа по перемещению заряда в потенциальном поле не зависит от формы траектории, то, зная напряжение между двумя точками, мы определим работу, которая совершается полем по перемещению единичного заряда.

Если есть несколько точечных зарядов, значит, потенциал поля в некоторой точке пространс­тва определяется как алгебраическая сумма потенциалов электрических полей каждого заряда в данной точке:

.

Эквипотенциальной поверхностью, или поверхностью равного потенциала, является поверхность, для любых точек которой разность потенциалов равна нулю. Это означяет, что работа по перемещению заряда по такой поверхности равна нулю, следовательно, линии напряженности электрического поля перпендикулярны эквипотенциальным поверхностям. Эквипотенциальные поверхности однородного поля представляют собой плоскости, а точечного заряда — концентрические сферы.

Вектор напряженности (как и сила ) перпендикулярен эквипотенциальным поверхнос­тям. Эквипотенциальной является поверхность любого проводника в электростатическом поле, так как силовые линии перпендикулярны поверхности проводника. Внутри проводника разность потенциалов между любыми его точками равна нулю.

Напряжение и напряженность однородного поля .

В однородном электрическом поле напряженность E в каждой точке одинакова, и работа A по перемещению заряда q параллельно на расстояние d между двумя точками с потенциалами φ₁, и φ₂ равна:

,

.

Т.о., напряженность поля пропорциональна разности потенциалов и направлена в сторону уменьшения потенциала. Поэтому положительный заряд будет двигаться в сторону уменьшения потенциала, а отрицательный — в сторону его увеличения.

Единицей напряжения (разности потенциалов) является вольт. Исходя из формулы , , разность потенциалов между двумя точками равна одному вольту, если при перемещении заряда в 1 Кл между этими точками поле совершает работу в 1 Дж.

Электрический потенциал простыми словами: формулы, единица измерения

Электрический потенциал – это скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию, которой обладает единичный положительный пробный заряд, помещённый в данную точку поля.

Если вы хотите расширить свои знания об электрическом потенциале или сначала узнать, что такое электрический потенциал, то вы пришли по адресу.

Простое объяснение

В классической механике рассмотрение проблемы с точки зрения энергии может значительно упростить ситуацию по сравнению с рассмотрением ее с точки зрения сил, действующих на систему. В частности, в этом контексте существенную роль играет тот факт, что энергия является сохраняющейся переменной.

Также в классической электродинамике рассмотрение на энергетическом уровне оказывается очень полезным. Поэтому электрический потенциал φ (также называемый электростатическим потенциалом) определяется как отношение потенциальной энергии E_пот пробного электрического заряда и его величины электрического заряда q: φ = E_пот / q .

Возможность определения такого электрического потенциала обусловлена тем, что электрическое поле E распределения заряда и результирующая электростатическая сила F_c на пробном электрическом заряде является консервативной силой, подобной гравитационной силе.

Электрический потенциал имеет единицу измерения вольт В или также джоуль на кулон Дж / Кл .

Формулы

В этом разделе мы познакомим вас с двумя важными формулами для электрического потенциала определенных распределений электрических зарядов. Мы также кратко обсудим аналогию между электрическим потенциалом и гравитацией.

Пластинчатый конденсатор

Мы рассматриваем ситуацию, когда две плоские пластины расположены параллельно на расстоянии d друг от друга. Кроме того, пусть одна из двух пластин заряжена положительно, а другая – отрицательно. Такая комбинация также называется пластинчатым конденсатором. Обозначим точку на положительной пластине через A, а точку на отрицательной пластине через B. Тогда для разности потенциалов между этими двумя точками получим:

Здесь E – величина электрического поля между двумя пластинами, которое предполагается однородным. Такая разность потенциалов также называется электрическим напряжением, которое существует между этими двумя точками.

Из этого уравнения видно, что электрический потенциал на положительно заряженной пластине (пластина A) выше, чем потенциал на отрицательно заряженной пластине (пластина B). Поэтому положительный заряд в пластинчатом конденсаторе перемещается к отрицательной пластине. В общем случае электрическое поле – а значит, и направление движения положительного заряда – направлено в ту сторону, в которой электрический потенциал убывает быстрее всего.

Рис. 1. Пластинчатый конденсатор

Аналогия с гравитационным полем

Если умножить уравнение (приведенное выше в статье) на величину электрического заряда q пробного электрического заряда и предположить, что отрицательно заряженная пластина имеет электрический потенциал, равный нулю, то электрическая потенциальная энергия на расстоянии h от пластины равна:

E_{пот. эл} = q * φ = q * E * h

Здесь φ обозначает электрический потенциал в точке пробного электрического заряда.

Сравним это уравнение с потенциальной энергией в однородном гравитационном поле:

E_{пот. гр} = m * g * h .

Мы определяем, что количество заряда электрического q играет роль массы m, а величина электрического поля E играет роль гравитационного ускорения g. Масса, находящаяся на высоте h над землей, ускоряется по направлению к земле под действием земного притяжения.

Таким образом, масса движется в том направлении, в котором уменьшается ее потенциальная энергия. Аналогично, положительный электрический заряд движется в направлении, в котором его электрическая потенциальная энергия будет уменьшаться. Поскольку электрическая потенциальная энергия и электрический потенциал линейно связаны, это наблюдение аналогично тому, что положительно заряженная частица движется в направлении уменьшения электрического потенциала.

Рис. 2. Аналогия с гравитационным полем

Подобно потенциальной энергии, только разность потенциалов имеет физический смысл, поскольку при определении электрического потенциала необходимо произвольно определить точку отсчета, от которой затем можно обозначить другие точки в пространстве. В этом смысле электрический потенциал сам по себе не имеет реального физического смысла, поскольку для данной точки в пространстве его значение можно изменить, выбрав другую точку отсчета. Таким образом, электрический потенциал ведет себя подобно высоте, потому что вы не можете говорить о высоте, пока у вас нет точки отсчета.

На топографической карте – пути, вдоль которых высота не меняется, называются изолиниями. Аналогично, пути, вдоль которых электрический потенциал постоянен, называются эквипотенциальными линиями.

Заряженные частицы

Предположим, что частица с зарядом q находится в начале выбранной нами системы координат. Пусть положение другой точки равно r и пусть r – расстояние между двумя точками. Для электрического потенциала в точке r действует следующее соотношение:

φ (r) = q / 4 * π * ε₀ * r ,

здесь ε₀ – электрическая постоянная.

В этом уравнении предполагается, что под действием электрического поля положительный пробный электрический заряд переносится из бесконечности в положение r.

Примеры задач

Наконец, давайте вместе рассчитаем небольшой пример. Предположим, что электрон ускоряется от отрицательно заряженной пластины к положительно заряженной через разность потенциалов 2000 В. Как изменяется потенциальная энергия электрона?

Для разности электрических потенциалов между двумя пластинами: φ_B – φ_A = ΔE_пот / q , преобразованной в искомое изменение потенциальной энергии, получаем:

Величина электрического заряда электрона равна q_e = e = – 1,6 * 10 -19 Кл и поэтому получаем:

ΔE_пот = e * ( φ_B – φ_A ) = – 1,6 * 10 -19 Кл * 2000 В = -3,2 * 10 -19 Дж.

Обратите внимание, что [ В ] = Дж / Кл. Кроме того, мы предположили, что пластина с точкой B заряжена положительно, поэтому перед 2000 В нет знака минус. Расчет показывает, что потенциальная энергия электрона уменьшается.

Найти потенциал электрического поля в точке, лежащей посредине между двумя

Найти потенциал электрического поля в точке, лежащей посредине между двумя зарядами по 50 нКл, расположенными на расстоянии 1 м в вакууме.

Задача №6.3.9 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Решение задачи:

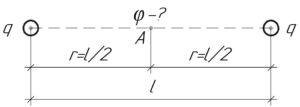
Так как заряды одинаковы, и они находятся на одинаковом расстоянии (r) от точки A, в которой нужно определить потенциал, значит потенциалы электрических полей в точке A, создаваемых каждым зарядом, также одинаковы. Это видно из формулы:

Здесь (k) – коэффициент пропорциональности, равный 9·10 9 Н·м 2 /Кл 2 .

Учитывая, что точка A находится посредине между двумя зарядами ((r=frac)), то:

Искомый потенциал (varphi) равен сумме потенциалов электрических полей в точке A, создаваемых каждым зарядом, поскольку потенциал – величина скалярная. Учитывая вышесказанное, имеем:

В итоге решение задачи в общем виде выглядит так:

Ответ: 1,8 кВ.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

2018-05-14   

Определить потенциал в точке 1 схемы (рис.), полагая потенциал точки О равным нулю. Написать по аналогии (используя симметрию полученной формулы) выражения для потенциалов в точках 2 и 3.

Решение:

В цепи ABDEA, используя $- Delta phi = 0$

$- mathcal{E}_{3} + frac{q_{1} }{C_{3} } + frac{q_{1} + q_{2} }{C_{1} } + mathcal{E}_{1} = 0$ (1)

Аналогично в цепи ODEF, О

$frac{q_{1} + q_{2} }{C_{1} } + mathcal{E}_{1} – mathcal{E}_{2} + frac{q_{2} }{C_{2} } = 0$ (2)

Решая уравнения (1) и (2), получаем,

$q_{1} + q_{2} = frac{ mathcal{E}_{2}C_{2} – mathcal{E}_{1}C_{2} – mathcal{E}_{1}C_{3} + mathcal{E}_{3}C_{3} }{ frac{C_{3} }{C_{1} } + frac{C_{2} }{C_{1} } + 1 }$

Тогда, $phi_{1} – phi_{0} = phi_{1} = – frac{(q_{1} + q_{2} )}{C_{1} }$, так как ($phi_{0} = 0$)

$= frac{ mathcal{E}_{1} (C_{2} + C_{3} ) – mathcal{E}_{2}C_{2} – mathcal{E}_{3}C_{3} }{C_{1} + C_{2} + C_{3} }$

И используя симметрию, $phi_{2} = frac{ mathcal{E}_{2} (C_{1} + C_{3} ) – mathcal{E}_{1}C_{1} – mathcal{E}_{3}C_{3} }{C_{1} + C_{2} + C_{3} }$

а также $phi_{3} = frac{ mathcal{E}_{3} (C_{1} + C_{2} ) – mathcal{E}_{1}C_{1} – mathcal{E}_{2}C_{2} }{C_{1} + C_{2} + C_{3} }$

§
15. ПОТЕНЦИАЛ. ЭНЕРГИЯ СИСТЕМЫ ЭЛЕКТРИЧЕСКИХ
ЗАРЯДОВ. РАБОТА ПО ПЕРЕМЕЩЕНИЮ ЗАРЯДА
В ПОЛЕ

Основные
формулы

 Потенциал
электрического поля есть величина,
равная отношению потенциальной энергии
точечного положительного заряда,
помещенную в данную точку поля, к этому
заряду;

=П/Q,

или
потенциал электрического поля есть
величина, равная отношению работы сил
поля по перемещению точечного
положительного заряда из данной точки
поля в бесконечность к этому заряду:

=A/Q.

Потенциал
электрического поля в бесконечности
условно принят равным нулю.

Отметим, что при
перемещении заряда в электрическом
поле работа A_в.с
внешних сил равна по модулю работе A_с.п
сил поля и противоположна ей по знаку:

A_в.с=
– A_с.п.

 Потенциал
электрического поля, создаваемый
точечным зарядом Q на
расстоянии r от заряда,

.

 Потенциал
электрического поля, создаваемого
металлической, несущей заряд Q сферой
радиусом R, на расстоянии
гот центра сферы:

внутри сферы
(r<R) ;

на поверхности
сферы (r=R)

;

вне сферы (r>R) .

Во всех приведенных
для потенциала заряженной сферы формулах
 есть диэлектрическая
проницаемость однородного безграничного
диэлектрика, окружающего сферу.

 Потенциал
электрического поля, созданного системой
п точечных зарядов, в данной точке
в соответствии с принципом суперпозиции
электрических полей равен алгебраической
сумме потенциалов ₁,
₂, … , _n,
создаваемых отдельными точечными
зарядами Q₁,
Q₂, …, Q_n:

 Энергия W
взаимодействия системы точечных зарядов
Q₁, Q₂,
…, Q_n
определяется работой, которую эта
система зарядов может совершить при
удалении их относительно друг друга
в бесконечность, и выражается формулой

,

где _i
— потенциал поля, создаваемого всеми
п–1 зарядами (за исключением 1-го) в
точке, где расположен заряд Q_i.

 Потенциал связан
с напряженностью электрического поля
соотношением

Е= –grad.

В случае электрического
поля, обладающего сферической симметрией,
эта связь выражается формулой

,

или в скалярной
форме

,

а
в случае однородного поля, т. е. поля,
напряженность которого в каждой точке
его одинакова как по модулю, так и по
направлению,

E=(₁–₂,)/d,

где ₁
и ₂
— потенциалы точек двух эквипотенциальных
поверхностей; d —
расстояние между этими поверхностями
вдоль электрической силовой линии.

 Работа, совершаемая
электрическим полем при перемещении
точечного заряда Q из
одной точки поля, имеющей потенциал ₁,
в другую, имеющую потенциал ₂,

A=Q(₁—₂),
или
,

где E_l
— проекция вектора напряженности Е
на направление перемещения; dl
— перемещение.

В случае однородного
поля последняя формула принимает вид

A=QElcos,

где l
— перемещение;  —
угол между направлениями вектора Е
и перемещения l.

Примеры
решения задач

Пример 1.
Положительные заряды Q₁=3
мкКл и Q₂=20
нКл находятся в вакууме на расстоянии
r₁=l,5
м друг от друга. Определить работу A,
которую надо совершить, чтобы сблизить
заряды до расстояния r₂=1
м.

Решение.
Положим, что первый заряд Q₁
остается неподвижным, а второй Q₂
под действием внешних сил перемещается
в поле, созданном зарядом Q₁,
приближаясь к нему с расстояния r₁=t,5
м до r₂=1 м.

Работа А’
внешней силы по перемещению заряда Q
из одной точки поля с потенциалом
₁
в другую, потенциал которой ₂,
равна по модулю и противоположна по
знаку работе А сил поля по перемещению
заряда между теми же точками:

А’= —А.

Работа А сил
поля по перемещению заряда A=Q(₁—₂).
Тогда работа А’ внешних сил может
быть записана в виде

A‘=
–Q(₁—₂)=Q(₂—₁). (1)

Потенциалы точек
начала и конца пути выразятся формулами

;

.

Подставляя выражения
₁
и ₂ в
формулу (1) и учитывая, что для данного
случая переносимый заряд Q=Q₂,
получим

. (2)

Если
учесть, что 1/(4₀)=910⁹
м/Ф, то после подстановки значений
величин в формулу (2) и вычисления найдем

A‘=180 мкДж.

Пример 2. Найти
работу А поля по перемещению заряда
Q=10 нКл из точки 1
в точку 2 (рис. 15.1), находящиеся между
двумя разноименно заряженными с
поверхностной плотностью =0,4
мкКл/м² бесконечными параллельными
плоскостями, расстояние l
между которыми равно 3 см.

Решение.
Возможны два способа решения задачи.

1-й способ.
Работу сил поля по перемещению заряда
Q из точки 1 поля с потенциалом ₁
в точку 2 поля с потенциалом ₂
найдем по формуле

A=Q(₁—₂). (1)

Для определения
потенциалов в точках 1 и 2 проведем
через эти точки эквипотенциальные
поверхности I и II.
Эти поверхности будут плоскостями, так
как поле между двумя равномерно
заряженными бесконечными параллельными
плоскостями однородно. Для такого поля
справедливо соотношение

₁—₂=El, (2)

где Е —
напряженность поля; l
— расстояние между эквипотенциальными
поверхностями.

Напряженность
поля между параллельными бесконечными
разноименно заряженными плоскостями
E=/₀.
Подставив это выражение Е в формулу
(2) и затем выражение ₁—₂
в формулу (1), получим

A=Q(/₀)l.

2-й способ. Так
как поле однородно, то сила, действующая
на заряд Q, при его перемещении
постоянна. Поэтому работу перемещения
заряда из точки 1 в точку 2 можно
подсчитать по формуле

A=Fr
cos, (3)

где F
— сила, действующая на заряд; r
— модуль перемещения заряда Q
из точки 1 в точку 2; 
— угол между направлениями перемещения
и силы. Но F=QE=Q(/₀).
Подставив это выражение F в равенство
(3), а также заметив, что rcos=l,
получим

A=Q(/₀)l. (4)

Таким образом, оба
решения приводят к одному и тому же
результату.

Подставив в
выражение (4) значение величин Q,
, ₀
и l, найдем

A=13,6
мкДж.

Пример 3. По
тонкой нити, изогнутой по дуге окружности
радиусом R,
равномерно распределен заряд с линейной
плотностью =10 нКл/м.
Определить напряженность Е и
потенциал 
электрического поля, создаваемого таким
распределенным
зарядом в точке О, совпадающей с
центром кривизны дуги. Длина l
нити составляет 1/3 длины окружности и
равна 15 см.

Решение. Выберем
оси координат так, чтобы начало координат
совпадало с центром кривизны дуги, а
ось у была симметрично расположена
относительно концов дуги (рис. 15.2). На
нити выделим элемент длины dl.
Заряд dQ=dl,
находящийся на выделенном участке,
можно считать точечным.

Определим
напряженность электрического поля в
точке О. Для этого найдем сначала
напряженность dE
поля, создаваемого зарядом dQ:

,

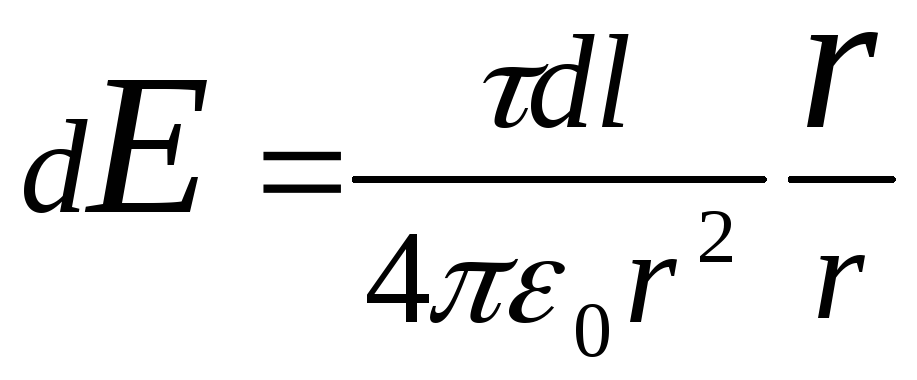
где r
—радиус-вектор, направленный от элемента
dl к
точке, напряженность в которой вычисляется.
Выразим вектор dE через проекции dE_x
c и dE_y
на оси координат:

,

где i
и j — единичные векторы
направлений (орты).

Напряженность Е
найдем интегрированием:

.

Интегрирование
ведется вдоль дуги длины l.
В силу симметрии интеграл

равен нулю. Тогда

, (1)

где
.
Так как r=R=const
и dl=Rd.
то

Подставим найденное
выражение dE_y
в (1) и, приняв во внимание симметричное
расположение дуги относительно оси Оу,
пределы интегрирования возьмем от 0 до
/3, а результат
удвоим;

.

Подставив указанные
пределы и выразив R
через длину дуги (3l=2r),
получим

.

Из этой формулы
видно, что вектор Е совпадает с
положительным направлением оси Оу
Подставив значение 
и l в последнюю формулу и сделав
вычисления, найдем

E=2,18
кВ/м.

Определим потенциал
электрического поля в точке О. Найдем
сначала потенциал d,
создаваемый точечным зарядом dQ
в точке О:

Заменим r
на R и произведем
интегрирование:

.Так
как l=2R/3,
то

=/(6₀).

Произведя вычисления
по этой формуле, получим

=188 В.

Пример 4.
Электрическое поле создана длинным
цилиндром радиусом R=1
см, равномерно заряженным с
линейной плотностью =20
нКл/м. Определить разность потенциалов
двух точек этого поля, находящихся на
расстояниях a₁=0,5
см и а₂=2 см от поверхности
цилиндра, в средней его части.

Решение. Для
определения разности потенциалов
воспользуемся соотношением между
напряженностью поля и изменением
потенциала Е= —grad.
Для поля с осевой симметрией, каким
является поле цилиндра, это соотношение
можно записать в виде

Е= –(d/dr),
или d=
—Еdr.

Интегрируя последнее
выражение, найдем разность потенциалов
двух точек, отстоящих на r₁
и r₂ от оси
цилиндра;

. (1)

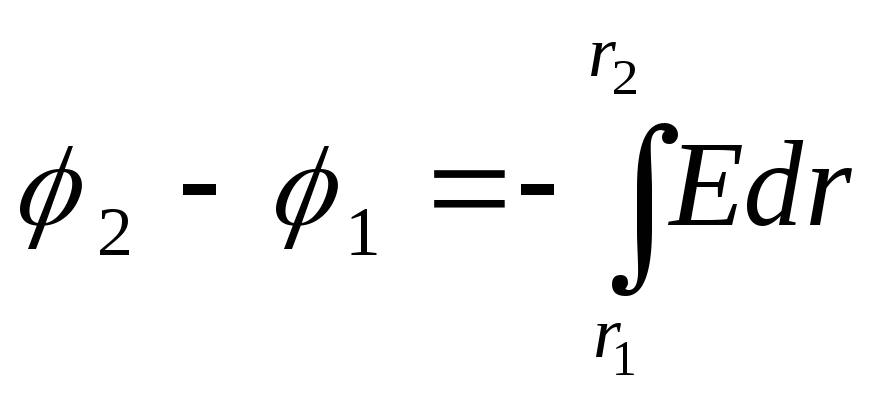
Так как цилиндр
длинный и точки взяты вблизи его средней
части, то для выражения напряженности
поля можно воспользоваться формулой
.
Подставив это выражение Е в равенство
(1), получим

(2)

Так как величины
r₂ и r₁
входят в формулу в виде отношения, то
их можно выразить в любых, но только
одинаковых единицах:

r₁=R+a₁=1,5
см; r₂=R+a₂=3
см.

Подставив значения
величия , ₀,
r₁ и r₂
в формулу (2) и вычислив, найдем

₁—₂=250
В.

Пример 5.
Электрическое поле создано тонким
стержнем, несущим равномерно распределенный
по длине заряд =0,1
мкКл/м. Определить потенциал 
поля в точке, удаленной от концов стержня
на расстояние, равное длине стержня.

Решение. Заряд,
находящийся на стержне, нельзя считать
точечным, поэтому непосредственно
применить для вычисления потенциала
формулу

, (1)

справедливую
только для точечных зарядов, нельзя. Но
если разбить стержень на элементарные
отрезки dl,
то заряд dl,
находящийся на каждом из них, можно
рассматривать как точечный и тогда
формула (1) будет справедлива. Применив
эту формулу, получим

, (2)

где r
— расстояние точки, в которой
определяется потенциал, до элемента
стержня.

Из рис. 15.3 следует,
что dl=(rd/cos).
Подставив это выражение dl
в формулу (2), найдем.

Интегрируя
полученное выражение в пределах от ₁
да ₂,
получим потенциал, создаваемый всем
зарядом, распределенным на стержне:.

В
силу симметрии расположения точки А
относительно концов стержня имеем ₂=₁
и поэтому.

Следовательно,

.Так
как

Рис 15.3

(см. табл. 2), то.

Подставляя пределы
интегрирования, получим

Сделав вычисления
по этой формуле, найдем

=990 В.

Пример 6.
Электрон со скоростью v=1,8310⁶
м/с влетел в однородное электрическое
поле в направлении, противоположном
вектору напряженности поля. Какую
разность потенциалов U
должен пройти электрон, чтобы обладать
энергией E_i=13,6
эВ*? (Обладая такой энергией, электрон
при столкновении с атомом водорода
может ионизировать его. Энергия 13,6 эВ
называется энергией ионизации водорода.)

Решение.
Электрон должен пройти такую разность
потенциалов U, чтобы приобретенная
при этом энергия W в
сумме с кинетической энергией T,
которой обладал электрон перед вхождением
в поле, составила энергию, равную энергии
ионизации E_i,
т. е. W+T=E_i.
Выразив в этой формуле W=eU
и Т =(mv²/2),
получим eU+(mv²/2)=E_i.
Отсюда.

___________________

* Электрон-вольт
(эВ) — энергия, которую приобретает
частица, имеющая заряд, равный заряду
электрона, прошедшая разность потенциалов
1 В. Эта внесистемная единица энергии в
настоящее время допущена к применению
в физике.

Произведем
вычисления в единицах СИ:

U=4,15 В.

Пример 7. Определить
начальную скорость υ₀
сближения про­тонов, нахо­дя­щихся
на достаточно большом расстоянии друг
от друга, если минимальное расстояние
r_min, на которое
они могут сблизиться, равно 10^-11
см.

Р е ш е н и е. Между
двумя протонами действуют силы
оттал­кивания, вслед­ствие чего
движение протонов будет замедленным.
Поэтому задачу можно ре­шить как в
инерциальной системе коор­динат
(связанной с центром масс двух протонов),
так и в неинер­циальной (связанной с
одним из ускоренно движу­щихся
протонов). Во втором случае законы
Ньютона не имеют места. Примене­ние
же принципа Даламбера затруднительно
из-за того, что ускорение системы будет
переменным. Поэтому удобно рассмотреть
задачу в инерциальной сис­теме отсчета.

Поместим начало
координат в центр масс двух протонов.
По­скольку мы имеем дело с одинаковыми
частицами, то центр масс будет находиться
в точке, делящей пополам отрезок,
соединяющий частицы. Относительно
центра масс частицы будут иметь в любой
момент времени одинаковые по модулю
скоро­сти. Когда частицы находятся
на достаточно большом расстоянии друг
от друга, скорость υ₁ каждой
частицы равна половине υ₀,
т. е. υ₁ =υ₀/2.

Для решения задачи
применим закон сохранения энергии,
со­гласно кото­рому полная механическая
энергия Е изолированной системы
постоянна, т. е.

Е=Т+П,

где Т – сумма
кинетических энергий обоих протонов
относительно центра масс; П – потенциальная
энергия системы зарядов.

Выразим потенциальную
энергию в начальный П₁ и конечный
П₂ моменты движения.

В начальный момент,
согласно условию задачи, протоны
нахо­дились на большом расстоянии,
поэтому потенциальной энергией можно
пренебречь (П₁=0). Следовательно,
для начального момента полная энергия
будет равна кинетической энергии T₁
протонов, т. е.

E=T_l.
(1)

В конечный момент,
когда протоны максимально сблизятся,
скорость и кинети­ческая энергия
равны нулю, а полная энергия будет равна
потенциальной энер­гии П₂, т. е.

Е=П₂.
(2)

Прирав­няв правые
части равенств (1) и (2), получим

T₁=П₂.
(3)

Кинети­ческая
энергия равна сумме кинетических энергий
про­тонов:

(4)

Потенциальная
энергия системы двух зарядов Q₁
и Q₂, находя­щихся
в вакууме, определяется по формуле
,
где r – расстоя­ние
между зарядами. Воспользовавшись этой
формулой, полу­чим

(5)

С учетом равенств
(4) и (5) формула (3) примет вид

откуда

Выполнив вычисления
по полученной формуле, найдем υ₀=2,35
Мм/с.

Пример
8. Электрон без на­чальной скорости
прошел разность потен­циалов U₀=10
кВ и влетел в пространство между
пластинами плоского конденсатора,
заряжен­ного до разности потенциалов
U_l=100 В, по ли­нии АВ,
парал­лельной пластинам (рис. 15.4).
Рас­стояние d между пла­стинами
равно 2 см. Длина l₁
­пластин конденсатора в нап­равлении
по­лета элек­трона, равна 20 cм.
Определить рас­стояние ВС на
экране Р, от­стоящем от конденсатора
на l₂=1 м.

Р е ш е н и е. Движение
электрона внутри конденсато­ра
складыва­ется из двух дви­жений: 1)
по инерции вдоль линии АВ с постоянной
скоро­стью υ₀, приобретенной
под действием разности потенциалов U₀,
кото­рую электрон прошел до
конденсатора; 2) равномерно ускоренного
дви­жения в вертикальном направлении
к положительно заряженной пла­стине
под действием постоянной силы поля
конденсатора. По вы­ходе из конденсатора
электрон будет двигаться равномерно
со скоро­стью υ, которую он имел
в точке М в момент вылета из
кон­денсатора.

Из рис. 15.4 видно,
что искомое расстояние |BC|=h₁+h₂,
где с h₁ – рас­стояние, на
которое сместится электрон в вертикальном
направлении во время движения в
конденсаторе; h₂ – расстояние
между точкой D на эк­ране, в которую
электрон попал бы, двигаясь по выходе
из конденса­тора по направлению
начальной скорости υ₀, и точкой
С, в которую электрон попадет в
действительности.

Выразим отдельно
h₁ и h₂. Пользуясь
формулой длины пути равно­мерно
ускоренного движе­ния, найдем

.
(1)

где а – ускорение,
полученное электроном под действием
поля конден­сатора; t- время полета
электрона внутри конденсатора.

По второму закону
Ньютона a=F/m, где F – сила, с которой
поле дей­ствует на электрон; т- его
масса. В свою очередь, F
=eE=eU₁/d, где е – заряд
электрона; U₁ – разность
потенциалов между пластинами конден­сатора;
d – расстояние между ними. Время
полета электрона внутри конденсатора
найдем из фор­мулы пути равномерного
движения
,
откуда

где l₁
– длина конденсатора в направлении
полета электрона. Выраже­ние скорости
найдем из условия равенства работы,
совер­шенной полем при перемещении
электрона, и приобретенной им кинетической
энер­гии:.
Отсюда

(2)

Подставляя в
формулу (1) последовательно значения а,
F, t и υ₀²
из со­ответствующих выражений,
получим

Длину отрезка h₂
найдем из подобия треугольников MDC
и век­тор­ного:

(3)

где υ₁
– скорость электрона в вертикальном
направлении в точке М; l₂–
расстояние от конденсатора до экрана.

Скорость υ₁
найдем по формуле υ₁=at, которая
с учетом выра­жений для а, F и t
примет вид

Подставив выражение
υ₁ в формулу (3), получим
,
или, заменив υ₀² по
формуле (3), найдем

Окончательно для
искомого расстояния |BC|
будем иметь

|BC|=­

­Подставив
значения величин U₁, U₀,
d, l₁ и l₂
в последнее выражение и произведя
вычисления, получим |BC|=5,5cм.

Задачи

Потенциальная
энергия и потенциал поля точечных
зарядов

15.1. Точечный
заряд Q = 10 нКл, находясь в некоторой
точке поля, обладает потенциальной
энергией П = 10 мкДж. Найти потенциал φ
этой точки поля.

5.2. При перемещении
заряда Q=20 нКл между двумя точками
поля внеш­ними силами была совершена
работа А=4 мкДж. Определить работу
A₁ сил поля и разность Δφ
потенциалов этих точек поля.

15.3. Электрическое
поле создано точечным положительным
заря­дом Q₁=6 нКл. Положительный
заряд Q₂ переносится из точки
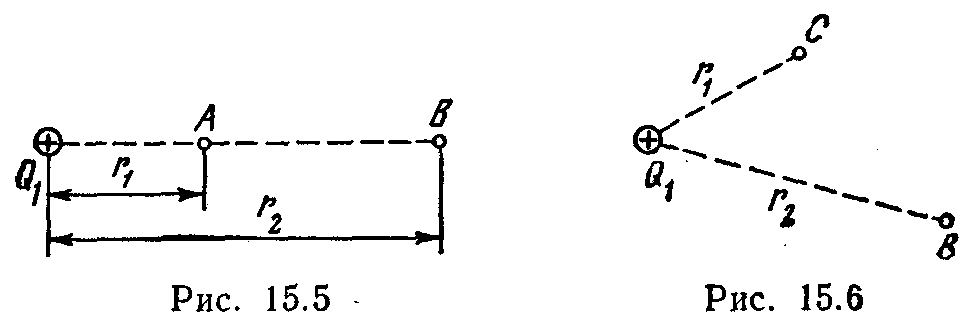
А этого поля в точку В (рис. 15.5).
Каково изменение потенциаль­ной
энергии ΔП, приходящееся на единицу
переносимого заряда, если r₁=20
см и r₂=50 см?

15.4. Электриче­ское
поле создано точечным зарядом Q_l=50
нКл. Не пользуясь понятием потенциала,
вычислить работу А в
нешних
сил по пе­ремещению точечного заряда
Q₂= -2 нКл из точки С в точку
В

(рис. 15.6), если r₁=10
см, r₂=20 см.
Определить также измене­ние ΔП
потенциальной энергии сис­темы
зарядов.

15.5. Поле создано
точечным зарядом Q=1 нКл. Определить
потен­циал φ поля в точке, удаленной
от заряда на расстояние r=20
см.

15.6. Определить
потенциал φ электрического поля в точке,
,удаленной от зарядов Q₁= -0,2
мкКл и Q₂=0,5 мкКл соответственно
на r₁=15 см и r₂=25
см. Определить также минимальное и
мак­симальное расстояния между
зарядами, при которых возможно решение.

15.7. Заряды Q₁=1
мкКл и Q₂= -1 мкКл находятся
на рас­стоянии d=10 см. Определить
напряженность Е и потенциал φ поля
в точке, уда­ленной на рас­стояние
r= 10 см от первого
заряда и лежащей на линии, проходящей
через первый заряд перпенди­кулярно
направлению от Q₁ к Q₂.

15.8. Вычислить
потенциальную энергию П системы двух
точеч­ных зарядов Q₁=100 нКл
и Q₂=10 нКл, находящихся на
рас­стоянии d=10 см друг от друга.

15.9. Найти
потенциальную энергию П системы трех
точечных за­рядов Q₁=10 нКл,
Q₂=20 нКл и Q₃= -30
нКл, расположенных в вершинах
равностороннего треугольника со стороной
длиной a=10 см.

15.10. Какова
потенциальная энергия П системы четырех
одинако­вых то­чечных зарядов Q=10
нКл, расположенных в верши­нах квадрата
со стороной дли­ной а=10 см? .

15.11. Определить
потенциальную энергию П системы четырех
то­чечных зарядов, расположенных в
вершинах квадрата со стороной дли­ной
a=10 см. За­ряды одинаковы по модулю
Q=10 нКл,но два из них отрицательны.
Рассмотреть два возможных случая
расположения зарядов.

15.12.
Поле создано двумя точечными зарядами
+2Q и -Q, находящимися на
расстоянии d=12 см друг от друга.
Определить геометрическое место точек
на плоскости, для которых потенциал
равен нулю (написать уравнение линии
нулевого потенциала).

5.13. Система
состоит из трех зарядов – двух одинаковых
по величине Q₁=|Q₂|=1
мкКл и противоположных по знаку и заряда
Q=20 нКл, расположенного точке 1
посередине между двумя другими зарядами
системы (рис. 15.7). Определить изменение
потенциальной энергии ΔП системы при
переносе заряда Q из точ­ки 1 в
точку 2. Эти точки удалены от отрицательного
заряда Q₁ на расстояние а=0,2
м.

У этого термина существуют и другие значения, см. Потенциал.

Классическая электродинамика
Электричество · Магнетизм
Электростатика Закон Кулона Теорема Гаусса Электрический дипольный момент Электрический заряд Электрическая индукция Электрическое поле Электростатический потенциал
Магнитостатика Закон Био — Савара — Лапласа Закон Ампера Магнитный момент Магнитное поле Магнитный поток Магнитная индукция
Электродинамика Векторный потенциал Диполь Потенциалы Лиенара — Вихерта Сила Лоренца Ток смещения Униполярная индукция Уравнения Максвелла Электрический ток Электродвижущая сила Электромагнитная индукция Электромагнитное излучение Электромагнитное поле
Электрическая цепь Закон Ома Законы Кирхгофа Индуктивность Радиоволновод Резонатор Электрическая ёмкость Электрическая проводимость Электрическое сопротивление Электрический импеданс
Ковариантная формулировка Тензор электромагнитного поля Тензор энергии-импульса 4-потенциал 4-ток
См. также: Портал:Физика

Электростатический потенциа́л — скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию, которой обладает единичный положительный пробный заряд, помещённый в данную точку поля. Единицей измерения потенциала в Международной системе единиц (СИ) является вольт (русское обозначение: В; международное: V), 1 В = 1 Дж/Кл (подробнее о единицах измерения — см. ниже).

Электростатический потенциал — специальный термин для возможной замены общего термина электродинамики скалярный потенциал в частном случае электростатики (исторически электростатический потенциал появился первым, а скалярный потенциал электродинамики — его обобщение). Употребление термина электростатический потенциал определяет собой наличие именно электростатического контекста. Если такой контекст уже очевиден, часто говорят просто о потенциале без уточняющих прилагательных.

Электростатический потенциал равен отношению потенциальной энергии взаимодействия заряда с полем к величине этого заряда:

Напряжённость электростатического поля и потенциал связаны соотношением^[1]

или обратно^[2]:

Здесь  — оператор набла, то есть в правой части равенства стоит минус градиент потенциала — вектор с компонентами, равными частным производным от потенциала по соответствующим (прямоугольным) декартовым координатам, взятый с противоположным знаком.

Воспользовавшись этим соотношением и теоремой Гаусса для напряжённости поля , легко увидеть, что электростатический потенциал удовлетворяет уравнению Пуассона в вакууме. В единицах системы СИ:

где  — электростатический потенциал (в вольтах),  — объёмная плотность заряда (в кулонах на кубический метр), а  — электрическая постоянная (в фарадах на метр).

Неоднозначность определения потенциала[править | править код]

Поскольку потенциал (как и потенциальная энергия) может быть определён с точностью до произвольной постоянной (и все величины, которые можно измерить, а именно напряженности поля, силы, работы — не изменятся, если мы выберем эту постоянную так или по-другому), непосредственный физический смысл (по крайней мере, пока речь не идет о квантовых эффектах) имеет не сам потенциал, а разность потенциалов, которая определяется как:

где:

 — потенциал в точке 1,

 — потенциал в точке 2,

 — работа, совершаемая полем при переносе пробного заряда из точки 1 в точку 2.

При этом считается, что все остальные заряды при такой операции «заморожены» — то есть неподвижны во время этого перемещения (имеется в виду вообще говоря скорее воображаемое, а не реальное перемещение, хотя в случае, если остальные заряды действительно закреплены — или пробный заряд исчезающе мал по величине — чтобы не вносить заметного возмущения в положения других — и переносится достаточно быстро, чтобы остальные заряды не успели заметно переместиться за это время, формула оказывается верной и для вполне реальной работы при реальном перемещении).

Впрочем, иногда для снятия неоднозначности используют какие-нибудь «естественные» условия. Например, часто потенциал определяют таким образом, чтобы он был равен нулю на бесконечности для любого точечного заряда — и тогда для любой конечной системы зарядов выполнится на бесконечности это же условие, а над произвольностью выбора константы можно не задумываться (конечно, можно было бы выбрать вместо нуля любое другое число, но ноль — «проще»).

Единицы измерения[править | править код]

В СИ за единицу разности потенциалов принимают вольт (В).

Разность потенциалов между двумя точками поля равна одному вольту, если для перемещения между ними заряда в один кулон нужно совершить работу в один джоуль: 1 В = 1 Дж/Кл (L²MT⁻³I⁻¹).

В СГС единица измерения потенциала не получила специального названия. Разность потенциалов между двумя точками равна одной единице потенциала СГСЭ, если для перемещения между ними заряда величиной одна единица заряда СГСЭ нужно совершить работу в один эрг.

Приближенное соответствие между величинами: 1 В = 1/300 ед. потенциала СГСЭ.

Использование термина[править | править код]

Широко используемые термины напряжение и электрический потенциал имеют несколько иной смысл, хотя нередко используются неточно как синонимы электростатического потенциала. В отсутствие меняющихся магнитных полей напряжение равно разности потенциалов.

Кулоновский потенциал[править | править код]

Иногда термин кулоновский потенциал используется просто для обозначения электростатического потенциала как полный синоним. Однако можно сказать, что в целом эти термины несколько различаются по оттенку и преимущественной области применения.

Также под кулоновским могут понимать потенциал любой природы (то есть не обязательно электрический), который при точечном или сферически симметричном источнике имеет зависимость от расстояния (например, гравитационный потенциал в теории тяготения Ньютона, хотя последний чаще всё же называют ньютоновским, так как он был изучен в целом раньше), особенно если надо как-то обозначить весь этот класс потенциалов в отличие от потенциалов с другими зависимостями от расстояния.

Формула электростатического потенциала (кулоновского потенциала) точечного заряда в вакууме:

где обозначен коэффициент, зависящий от системы единиц измерения — например, в СИ:

= 9·10⁹ В·м/Кл,

 — величина заряда,  — расстояние от заряда-источника до точки, для которой рассчитывается потенциал.

• Можно показать, что эта формула верна не только для точечных зарядов, но и для любого сферически симметричного заряда конечного размера, например, равномерно заряженного шара, правда, только в свободном от заряда пространстве — то есть, например, над поверхностью шара, а не внутри его.
• Кулоновский потенциал в приведенном выше виде используется в формуле кулоновской потенциальной энергии (потенциальной энергии взаимодействия системы электростатически взаимодействующих зарядов):

  

В электродинамике[править | править код]

Когда присутствуют изменяющиеся во времени магнитные поля (что справедливо, при изменяющихся во времени электрических полей и наоборот), то невозможно описать электрическое поле в терминах скалярного потенциала V, поскольку электрическое поле больше не является консервативным: циркуляция зависит от пути, потому что (см. Закон индукции Фарадея).

Вместо этого всё ещё можно определить скалярный потенциал, дополнив его магнитным векторным потенциалом A. В частности, А определен так чтобы

где B — магнитное поле. Поскольку дивергенция магнитного поля всегда равно нулю из-за отсутствия магнитных монополей, то A всегда существует. Учитывая это, величина

является консервативным полем по закону Фарадея, и поэтому можно написать

где V — скалярный потенциал, определённый консервативным полем F.

Электростатический потенциал — это частный случай этого определения, где A не зависит от времени. С другой стороны, для изменяющихся во времени полей,

в отличие от электростатики.

См. также[править | править код]

• Гальвани-потенциал
• Вольта-потенциал
• Векторный потенциал электромагнитного поля
• 4-потенциал
• Стандартный электродный потенциал
• Степень окисления
• Гравитационный потенциал
• Ядерный потенциал

Примечания[править | править код]

Литература[править | править код]

• Алешкевич В. А. Электромагнетизм. — М.: Физматлит, 2014. — 404 с. — 700 экз. — ISBN 978-5-9221-1555-1.