Задача 2.2:
Вычислить электродный потенциал
металлического электрода при заданной
активной концентрации (активности)
катионов металла (см. табл. 3).
Таблица 3 – Варианты
заданий
|
Металл |
Активность |
|
|
a |
Железо |
0.001 |
|
b |
Марганец |
0.001 |
|
c |
Цинк |
0.01 |
|
d |
Никель |
0.0001 |
|
e |
Хром |
0.001 |
|
f |
Медь |
0.001 |
|
g |
Серебро |
0.1 |
|
h |
Свинец |
0.01 |
|
i |
Олово |
0.0001 |
|
j |
Цинк |
0.0001 |
|
k |
Железо |
0.001 |
|
l |
Цинк |
0.01 |
|
m |
Хром |
0.001 |
|
n |
Олово |
0.01 |
|
o |
Медь |
0.001 |
Пример решения
задачи:
Электродный
потенциал окислительно-восстановительной
системы рассчитывается по уравнению
Нернста.

где
![]() стандартный электродный потенциал
стандартный электродный потенциал
металла, В; n – заряд иона металла; [Ox]
и [Red] – концентрация окисленной и
восстановленной формы ионов металла в
растворе его соли, моль/л; R- универсальная
газовая постоянная, R=8.31 Дж/моль.К;
Т – температура, Т=298 К; F-
постоянная Фарадея, F=96500 Кл/моль.
Для металлических
электродов при стандартных условиях
(Р=101.3 кПа, Т=298 К) уравнение принимает
вид:

2.3. Электроды и электродные процессы в гальваническом элементе
Задача 2.3:
Гальванический элемент состоит из двух
стандартных металлических электродов
(см. табл. 4). Укажите анод и катод и знаки
их зарядов; запишите уравнения электродных
процессов и схему гальванического
элемента. Составьте уравнение
токообразующей реакции в ионной и
молекулярной форме.
Таблица 4 – Варианты
заданий
|
Электроды |
||
|
a |
Cr/CrCl3 |
Zn/ZnCl2 |
|
b |
Ni/NiSO4 |
Cu/CuSO4 |
|
c |
Cu/CuSO4 |
Ag/AgNO3 |
|
d |
Cr/CrCl3 |
Cu/Cu(NO3)2 |
|
e |
Al/Al2(SO4)3 |
Mg/MgCl2 |
|
f |
Cu/CuSO4 |
Sn/SnCl2 |
|
g |
Mg/MgSO4 |
Sn/SnSO4 |
|
h |
Pb/Pb(NO3)2 |
Fe/FeSO4 |
|
i |
Sn/SnCl2 |
Ni/NiSO4 |
|
j |
Ni/NiSO4 |
Sn/SnCl2 |
|
k |
Au/Au(NO3)3 |
Cu/CuCl2 |
|
l |
Zn/ZnSO4 |
Ag/AgNO3 |
|
m |
(Pt)H2/H2SO4 |
Zn/ZnSO4 |
|
n |
Mg/MgSO4 |
Zn/Zn(NO3)2 |
|
o |
Ni/NiSO4 |
Sn/SnCl2 |
|
p |
Cr/Cr2(SO4)3 |
Ag/AgNO3 |
Для решения данной
задачи воспользуйтесь рядом СЭП.
Помните, что анод
– это электрод с меньшим потенциалом,
а катод – с большим.
Пример решения
задачи:
Гальванический
элемент состоит из двух стандартных
электродов – алюминиевого Al/AlCl3
и цинкового Zn/ZnCl2.
Учитывая значение
СЭП: алюминиевый электрод (φ0
= -1.66 В), имеющий меньшее значение φ0,
является восстановителем, на нем
происходит процесс окисления, т.е.
анодный процесс:
Al0
– 3e = Al3+,
электрод
Al/Al3+
–
анод.
Цинковый электрод
с большим значением СЭП (φ0
= -0.76 В) является окислителем, на нем
протекает процесс восстановления, т.е.
катодный процесс:
Zn2+
+2e
= Zn0,
электрод Zn/Zn2+
– катод.
Всегда соблюдается
соотношение φкатода
> φанода.
При работе
гальванического элемента электроны по
внешней цепи передаются от анода к
катоду, следовательно, анод заряжается
отрицательно, а катод – положительно.
Схему гальванического
элемента принято записывать в строку,
слева – анод, справа – катод с указанием
знака заряда:
A(-):
Al/AlCl3
|| ZnCl2/Zn
:(+)K
Двойная черта
означает внутреннюю цепь (контакт между
электролитами), она представляет
проницаемую для анионов диафрагму или
электролитический мост, по которому
диффундируют анионы из катодного
пространства в анодное.
Уравнение
токообразующей реакции составляется
с учетом электронного баланса.
Ионное уравнение:
2Al
+ 3Zn2+
= 2 Al3+
+ 3Zn
Молекулярное
уравнение: 2Al
+ 3ZnCl2
= 2AlCl3
+ 3Zn
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
23.11.2019279.04 Кб0n1.doc
- #
- #
Потенциал электрода E в химии и электрохимии, согласно определению, представляет собой электродвижущую силу ячейки, построенной из двух электродов.
На границе раздела между электродом и электролитом из-за процесса переноса заряженных частиц возникает электродный потенциал, связанный с удельной адсорбцией ионов и ориентацией полярных молекул, в том числе растворителя.
Электродный потенциал представляет собой электрический потенциал на электродном компоненте. В ячейке имеется электродный потенциал для катода и электродный потенциал для анода. Разность между электродными потенциалами катода и анода будет равна потенциалу ячейки:
E ячейки = E катода – E анода
Таким образом потенциал электрода зависит от характера и состава контактных фаз и от кинетики электродных реакций на границе раздела.
Разность потенциалов зависит от конкретных веществ, составляющих электроды. Для любой электрической ячейки общий потенциал представляет собой сумму сумм, вырабатываемых реакциями на двух электродах.
Электрохимический ряд напряжений металлов
На практике были измерены напряжения большого числа электродов, подключая их в ячейку со стандартным водородным электродом, который представляет собой газообразный водород при 1 атмосфере, барботирующий поверх платиновой проволоки, погруженной в 1 М раствор (вод.). Этот стандартный электрод произвольно был назначен в качестве обладателя потенциала в 0 вольт (он был взят за отправную точку шкалы), а измерение ЭДС всей ячейки позволяет определить потенциал другого, изучаемого электрода. В таблице 1 приведены некоторые стандартные потенциалы для электродов, при которых происходит измерение.
Значения данных стандартных электродных потенциалов измерены для следующих условий:
Температура 298,15 К (25,00°С, 77,00°F).
Эффективная концентрация 1 моль/л.
Парциальное давление 101,325 кПа (абсолютное) (1 атм, 1,01325 бар) для каждого газообразного реагента. Данное давление считается традиционным для подобного рода.
Таблица электродных потенциалов
| Е, В | Полуреакция |
|---|---|
| 2.87 | F2(г) + 2 e- → 2F(ж) |
| 1.36 | Cl2(г) + 2 e→2Cl (ж) |
| 1.20 | Pt2+(ж) + 2 e→ Pt(тв) |
| 0.92 | Hg2+(ж) + 2 e→Hg(I) |
| 0.53 | I2(тв) + 2 е→ 2I(ж) |
| 0.34 | Cu2+(ж) + 2 e→Cu(тв) |
| 0 | 2H+(ж) + 2 e → H2(г) |
| -0.13 | Pb2+(ж) + 2e → Pb(тв) |
| -0.26 | Ni2+(ж) + 2 e → Ni(тв)2 |
| -0.44 | Fe2+(ж) + 2 e→Fe(тв) |
| -0.76 | Zn2+(ж) + 2 e→Zn(тв) |
| -1.66 | Al3+(ж) + 3 e→Al(тв) |
| -2.71 | Na+(ж) + e→Na(тв) |
| -2.87 | Ca2+(ж) + 2 e→Ca(тв) |
| -2.91 | K+(ж) + e→K(тв) |
| -3.04 | Li+(ж) + e→Li(тв) |
В середине списка вы увидите 0 вольт – произвольно назначенный за стандартный водородный электрод; все остальные потенциалы относительны к полуреакции водорода.
Уравнение Нернста
В электрохимии уравнение Нернста представляет собой уравнение, которое связывает восстановительный потенциал электрохимической реакции (полуреакции) со стандартным электродным потенциалом, температурой и активностью (часто аппроксимируемыми концентрациями) химических веществ, подвергающихся восстановлению и окислению. Это самое важное уравнение в области электрохимии. Оно было названо в честь Вальтера Нернста, немецкого физика и химика, который сформулировал уравнение:
Е=Е0+RTnFln(a)Е=Е^0 + frac{RT}{nF} ln(a),
где EE – электродный потенциал (В);
E0E^0 – нормальный (стандартный) электродный потенциал (В);
RR – универсальная газовая постоянная равная 8,313 Дж/К · моль;
ТТ – температура (по шкале Кельвина);
nn – заряд иона;
FF – постоянная Фарадея 96500 Кл/моль;
aa – активность ионов.
Чтобы упростить расчет вместо активности ионов можно использовать концентрацию:
Е=Е0+RTnFln(C)Е=Е^0+frac{RT}{nF} ln(C).
Тест по теме «Электродные потенциалы»
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 13 мая 2020 года; проверки требуют 7 правок.
В электрохимии стандартный электродный потенциал, обозначаемый Eo, E0, или 
Вычисление стандартных электродных потенциалов[править | править код]
Электродный потенциал не может быть получен эмпирически. Потенциал гальванической ячейки вытекает из «пары» электродов. Таким образом, невозможно определить величину для каждого электрода в паре, используя эмпирически полученный потенциал гальванической ячейки. Для этого установлен водородный электрод, для которого этот потенциал принят равным 0,00 В, и любой электрод, для которого электродный потенциал ещё неизвестен, может быть соотнесён со стандартным водородным электродом с образованием гальванической ячейки — и в этом случае потенциал гальванической ячейки даёт потенциал неизвестного электрода.
Так как электродные потенциалы традиционно определяют как восстановительные потенциалы, знак окисляющегося металлического электрода должен быть изменён на противоположный при подсчёте общего потенциала ячейки. Также нужно иметь в виду, что потенциалы не зависят от количества передаваемых электронов в полуреакциях (даже если оно различно), так как они рассчитаны на 1 моль переданных электронов. Отсюда при расчёте какого-либо электродного потенциала на основании двух других следует проявлять внимательность.
Например:
Fe3+ + 3e− → Fe(тв) −0,036 В
Fe2+ + 2e− → Fe(тв) −0,44 В
Для получения третьего уравнения:
Fe3+ + e− → Fe2+ (+0,77 В)
следует умножить потенциал первого уравнения на 3, перевернуть второе уравнение(поменять знак) и умножить его потенциал на 2. Сложение этих двух потенциалов даст стандартный потенциал третьего уравнения.[источник не указан 1613 дней]
Таблица стандартных электродных потенциалов[править | править код]
Чем больше Eo, тем легче их можно восстановить (тем более сильными окислителями они являются). И наоборот: низкий отрицательный потенциал означает, что данная форма является сильным восстановителем.
Например, F2 (Eo= 2,87 В) — окислитель, Li+ (Eo= −3,05 В) — восстановитель. Таким образом, Zn2+(Eo= −0,76 В), может быть окислен любым другим электродом, стандартный потенциал которого больше −0,76 В. (напр., H+(0 В), Cu2+(0,16 В), F2(2,87 В)) и может быть восстановлен любым электродом, стандартный потенциал которого меньше −0,76 В (напр., H−(−2,23 В), Na+(−2,71 В), Li+(−3,05 В)).
Связь Eo с энергией Гиббса[править | править код]
В гальванической ячейке, где протекает самопроизвольная (энергия Гиббса носит “-” отрицательных характер) окислительно-восстановительная реакция заставляющая ячейку производить электрический потенциал и совершать работу во внешней цепи. Тогда Энергия Гиббса ΔGo должна быть отрицательной и в соответствии со следующим уравнением, описывающем связь свободной энергии с работой электрического тока по переносу электричества, выражаться:
- ΔGoяч = -nFEoяч
где n это количество молей электронов на моль продуктов, а F является постоянной Фарадея, ~96485 Кл/моль. Таким образом применимы следующие правила:
- если Eoяч> 0, тогда процесс самопроизвольный (гальваническая ячейка)
- если Eoяч< 0, тогда процесс несамопроизвольный (электролитическая ячейка)
Нестандартные условия[править | править код]
Стандартные электродные потенциалы даны при стандартных условиях. Однако реальные ячейки действуют и при нестандартных условиях. При данном стандартном потенциале потенциал при нестандартных эффективных концентрациях может быть вычислен с использованием уравнения Нернста:

Величины E0 зависят от температуры (кроме стандартного водородного электрода), концентрации и обычно относятся к стандартному водородному электроду при этой температуре. Для конденсированных фаз величины потенциалов также зависят от давления.
См. также[править | править код]
- Таблица стандартных электродных потенциалов
- Восстановительный потенциал
- Абсолютный электродный потенциал
- Электрохимический потенциал
- Равновесный электродный потенциал
- Уравнение Нернста
- Электрохимическая ячейка
- Гальваническая ячейка
Литература[править | править код]
- Zumdahl, Steven S., Zumdahl, Susan A (2000) Chemistry (5th ed.), Houghton Mifflin Company. ISBN 0-395-98583-8
- Atkins, Peter, Jones, Loretta (2005) Chemical Principles (3rd ed.), W.H. Freeman and Company. ISBN 0-7167-5701-X
- Zu, Y, Couture, MM, Kolling, DR, Crofts, AR, Eltis, LD, Fee, JA, Hirst, J (2003) Biochemistry, 42, 12400-12408
- Shuttleworth, SJ (1820) Electrochemistry (50th ed.), Harper Collins.
Ссылки[править | править код]
- [www.xumuk.ru/encyklopedia/2/5296.html Электродный потенциал]
- Онлайн-справочник стандартных электродных потенциалов
|
|
Некоторые внешние ссылки в этой статье ведут на сайты, занесённые в спам-лист. Эти сайты могут нарушать авторские права, быть признаны неавторитетными источниками или по другим причинам быть запрещены в Википедии. Редакторам следует заменить такие ссылки ссылками на соответствующие правилам сайты или библиографическими ссылками на печатные источники либо удалить их (возможно, вместе с подтверждаемым ими содержимым). Список проблемных ссылок
|
Стандартные электродные потенциалы металлов
Указывают на меру окислительно-восстановительной способности металла и его ионов. Металлы в виде простых веществ – восстановители, ионы металлов – окислители.
Чем наиболее отрицателен электродный потенциал, тем выше способность металла посылать ионы в раствор и тем сильнее проявляет себя металл как восстановитель (например, Li, Na, K). И наоборот, чем наиболее положителен потенциал металлического электрода, тем большей окислительной способностью обладают его ионы.
Активные металлы начала ряда, а также щелочные и щелочноземельные вытесняют водород из воды, Например,
2K + 2H2O ⟶ 2KOH + H2.
Металлы, расположенные между магнием и кадмием, обычно не вытесняют водород из воды. На поверхности этих металлов образуются оксидные пленки, обладающие защитным действием.
Все металлы, стоящие в ряду стандартных электродных потенциалов до водорода, вытесняют его из растворов кислот с концентрацией (активностью) ионов водорода 1 моль/л. Например,
Zn + HCl ⟶ ZnCl2 + H2.
Чем дальше расположены друг от друга в ряду напряжений два данных металла, тем наибольшую ЭДС будет иметь составленный из них гальванический элемент.
Уравнение Нернста
Потенциал металлического электрода зависит от природы металла, концентрации (активности) ионов металла в растворе, температуры. Если условия отличаются от стандартных, например, если концентрация ионов металла в растворе не равна 1 моль/л, то электродный потенциал металла не является стандартным и его либо определяют экспериментально, либо вычисляют.
При экспериментальном определении составляется гальванический элемент, одним из электродов которого является измеряемый, а вторым – стандартный водородный электрод:
(катод) Pt, H2/2H+ || /(анод),
и определяется его электродвижущая сила как разность равновесных потенциалов катода и анода (ЭДС=│Ек−Еа│). Так как потенциал стандартного водородного электрода равен нулю (( = 0,00 В), то ЭДС элемента будет равна потенциалу измеряемого электрода.
Для вычисления электродного потенциала в нестандартных условиях применяют уравнение Нернста
Так как металл – твердое вещество и вступает в реакцию только с поверхности, его концентрация постоянна и не должна входит в уравнение. Поэтому для вычисления электродных потенциалов металла уравнение Нернста приобретает более простой вид
где – стандартный электродный потенциал, В,
R – газовая постоянная, равная 8,314 Втс/моль∙К,
Т − температура, К,
n − число электронов, участвующих в окислительно-восстановительном процессе.
F – число Фарадея, равное 96500 Кл/моль;
активность ионов металла, моль/л.
При подстановке числовых значений R, F и стандартной температуры Т = 298 К и при переходе к десятичным логарифмам, уравнение Нернста принимает еще более простой вид:
Ну, удивил, тоже мне! – сказал бы кто-то, ведь ясное-то дело: где электрический потенциал – там и заряд, а где заряд – там и потенциал рядом околачивается! Чего проще?!
 Наличие, известных нам из курса физики, непосредственных, по большей части, прямых соотношений между потенциалом и зарядом, ни у кого сомнения не вызывает (у меня, спешу вас успокоить, – тоже). Если заряд тела отрицательный, то и потенциал – отрицательный, если заряд тела положительный, то и потенциал поля вокруг этого тела – понятное дело – такой же! А если заряда вообще нет, то и о потенциале вспоминать не стоит – нет его и точка! И всё бы было хорошо, но (гром и молния!), на свете ЕСТЬ такое себе «зазеркалье», в котором при положительном заряде будет отрицательный потенциал, при нулевом заряде будет ненулевой потенциал (и откуда ему взяться!?), а при нулевом потенциале (безобразию нет предела!) – совсем ненулевой заряд! И имя этому зазеркалью – контакт металла и раствора! И если кому-то, после этого, вдруг стало казаться, что Земля – плоская, то скажу, что наши верные законы физики остались стоять на своём месте! Но обо всём по порядку.
Наличие, известных нам из курса физики, непосредственных, по большей части, прямых соотношений между потенциалом и зарядом, ни у кого сомнения не вызывает (у меня, спешу вас успокоить, – тоже). Если заряд тела отрицательный, то и потенциал – отрицательный, если заряд тела положительный, то и потенциал поля вокруг этого тела – понятное дело – такой же! А если заряда вообще нет, то и о потенциале вспоминать не стоит – нет его и точка! И всё бы было хорошо, но (гром и молния!), на свете ЕСТЬ такое себе «зазеркалье», в котором при положительном заряде будет отрицательный потенциал, при нулевом заряде будет ненулевой потенциал (и откуда ему взяться!?), а при нулевом потенциале (безобразию нет предела!) – совсем ненулевой заряд! И имя этому зазеркалью – контакт металла и раствора! И если кому-то, после этого, вдруг стало казаться, что Земля – плоская, то скажу, что наши верные законы физики остались стоять на своём месте! Но обо всём по порядку.
Если мы возьмём пластину из любого металла и опустим её в раствор его соли, содержащей ионы этого металла (рис. 2), 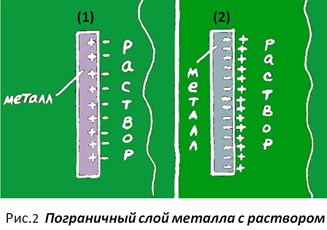 то при этом может произойти одна из двух ситуаций: поверхность металла зарядится, либо (1) положительно, либо (2) отрицательно и на нём возникнет двойной электрический слой (ДЭС) (Определение ДЭС – см. п. 1 второй части этой статьи).
то при этом может произойти одна из двух ситуаций: поверхность металла зарядится, либо (1) положительно, либо (2) отрицательно и на нём возникнет двойной электрический слой (ДЭС) (Определение ДЭС – см. п. 1 второй части этой статьи).
Но как, же тогда может быть, чтобы заряд поверхности металла в растворе был равен нулю, если во всех случаях на металле ЕСТЬ определённый заряд? Чтобы понять это, мы должны ближе подступиться к нашему «зазеркалью». И первым его кирпичиком является понятие остандартном электродном потенциале металла в растворе.
Стандартным электродным потенциалом металла называется такой потенциал металла, находящегося в равновесии со своими ионами в растворе при стандартных условиях, который измерен относительно стандартного водородного электрода. (Определение стандартного водородного электрода и стандартных условий – см. п. 2 второй части статьи). Сама же шкала потенциалов, отсчитанных от стандартного водородного электрода, называется водородной шкалой. Стандартный электродный потенциал является равновесным, то есть таким потенциалом, при котором между металлом и раствором не протекает электрический ток.
Стандартные электродные потенциалы меди и железа будут равны +0,337 В и -0,44 В соответственно (см. п. 3 второй части статьи), а электродные полуреакции будут выглядеть так:
Cu2+ + 2ē = Сu0 и Fe2+ + 2ē = Fe0
Составим из этих электродов гальванический элемент (рис.3) и рассчитаем ЭДС получившегося гальванического элемента, используя правило:
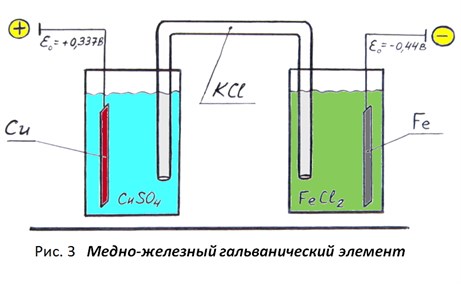
ЭДС гальванического элемента равна разности между потенциалами его положительного и отрицательного электродов.
Тогда мы получим:
E = ε₀ (Cu0/Cu2+) – ε₀ (Fe0/Fe2+) = +0,337 – (-0,44) = 0,777 В
Но, правду говоря, на практике очень нечасто используются электроды гальванических элементов, находящиеся в стандартных условиях! А в нестандартных условиях потенциалы электродов рассчитывают при помощи уравнения Нернста, которое в упрощённом виде будет выглядеть так:
ε = ε₀ + (0,059/n) · Lg(Ox/Red),
где n – количество электронов, принимающих участие в полуреакции;
Ox – концентрация окисленной формы в степени, равной коэффициенту, стоящему при окисленной форме в полуреакции;
Red – концентрация восстановленной формы в степени, равной коэффициенту, стоящему возле восстановленной формы в полуреакции (для твёрдого металла Red = 1);
ε₀ – стандартный электродный потенциал, В.
Рассчитаем ЭДС медно-железного гальванического элемента, если концентрация CuSO4 на медном электроде составляет 1,8 моль/л, а концентрация FeCl2 на железном электроде – 0,7 моль/л. Для этого рассчитаем сначала потенциалы медного и железного электродов:
ε (Cu0/Cu2+) = 0,337 + (0,059/2) · Lg (1,81/1) = 0,3445 В
ε (Fe0/Fe2+) = -0,44 + (0,059/2) · Lg (0,71/1) = -0,4446 В
Тогда ЭДС будет равна:
E = ε(Cu0/Cu2+) – ε(Fe0/ Fe2+) = 0,3445 – (-0,4446) = 0,7891 В
«Э-дэ-э-эсы, по-тен-ци-а-а-лы» – скажете вы, а заряд поверхности всё равно у меди будет положительным, а у железа отрицательным! И здесь вы совершенно правы! Однако, в этот раз, вам просто повезло! Если вы думаете, что знак заряда поверхности металла всегда такой же, как знак его потенциала в водородной шкале, то вас ждёт горькое разочарование! Прямо сейчас мы прыгнем в наше обещанное зазеркалье! А дверью в него является понятие о потенциале нулевого заряда металлов.
Потенциалом нулевого заряда металла в растворе является такой его потенциал, отсчитанный в водородной шкале, при котором заряд на его поверхности равен нулю. Потенциал нулевого заряда является неравновесным потенциалом. Кстати, если замкнуть электроды нашего медно-железного гальванического элемента, то потенциалы его электродов тоже станут неравновесными (но не нулевыми!).
Потенциал нулевого заряда металлов, определённый в стандартных условиях, при отсутствии в растворе поверхностно-активных веществ, называется стандартным потенциалом нулевого заряда (СПНЗ) или нулевой точкой металла. Обозначим его как (ψ₀).
Каждый металл имеет свою собственную нулевую точку, принимаемую за ноль потенциала, а соответствующая ему шкала потенциалов называется приведенной шкалой или ψ-шкалой потенциалов (читается «фи-шкала») (см. п.4 второй части статьи).
Нулевая точка (ψ₀) для медного электрода равна -0,2 В, а для железного -0 В. Рассчитаем теперь ψ-потенциалы для меди и железа при стандартных условиях, используяформулу для расчёта ψ-потенциала в общем виде:
ψ = ε – ψ₀
Тогда для меди: ψ(Cu) = +0,337 – (-0,2) = +0,537 В,
а для железа: ψ(Fe) = -0,44 – 0 = -0,44 В.
Знак ψ-потенциала показывает знак заряда на поверхности электрода. И пока всё хорошо – знаки потенциалов и зарядов совпадают! А теперь заменим железный электрод на кадмиевый (стандартный потенциал которого не очень отличается), на котором происходит процесс:
Cd2+ + 2ē = Cd0 ε₀ (Cd0/Cd2+) = -0,403 В, ψ₀ = -0,7 В
Тогда ψ-потенциал равновесного кадмиевого электрода будет равен:
Ψ(Cd) = ε₀ – ψ₀ = -0,403 – (-0,7) = +0,297 В
Вот тут и начались наши чудеса! Знак ψ-потенциала кадмия – положительный, значит, и заряд на его поверхности – тоже положительный. Однако при всём этом потенциал кадмиевого электрода в водородной шкале – отрицательный!
Если мы, используя внешний источник тока, принудительно установим потенциал кадмиевого электрода в водородной шкале на уровне ноль вольт, то заряд поверхности металла никак не будет нулевым. ψ-потенциал его тогда будет равен 0 – (-0,7) = +0,7 В – и заряд поверхности будет положительным! Если же принудительно установить потенциал кадмиевого электрода на уровне -0,7 В, (такие манипуляции вряд ли возможны без особых последствий), тогда ψ = -0,7 – (-0,7) = 0 В. В этом случае при ненулевом потенциале электрода его заряд будет равен нулю (так как ψ-потенциал равен нулю).
Таким образом, ψ-потенциал используется на практике исключительно для определения знака и относительной величины заряда поверхности металла в растворе и с его помощьюнельзя рассчитывать ЭДС! Для расчёта ЭДС служит водородная шкала потенциалов, с помощью которой, в свою очередь, нельзя определять знак заряда поверхности металла.
Но если с ЭДС всё понятно, то – спросите вы – зачем нам вообще знать о знаке заряда поверхности металла? Нам что, без этого не обойтись что ли?! Вот именно так и есть! Не обойтись! Если мы вспомним о том, что все поверхностно-активные вещества – это соединения катионные, анионные или нейтральные, в которых поверхностную активность проявляет соответственно катион, анион, либо нейтральная молекула, то нам станет совершенно ясно, что от заряда поверхности металла зависит то, будет ли адсорбироваться конкретное ПАВ на данном металле или нет, то есть, будет ли оно влиять на электродный процесс.
Поэтому знание знака заряда металла – это один из важнейших ключей к управлению гальваническими процессами, без которого современной гальванотехники просто не может быть!
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
