Как найти потенциал металлического шара

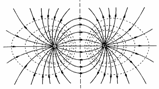
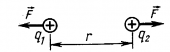
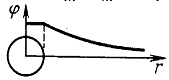
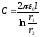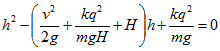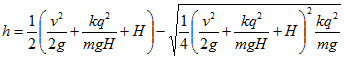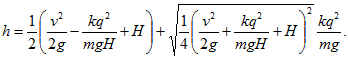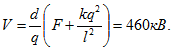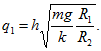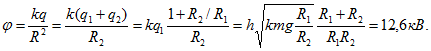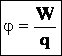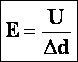Потенциалы простейших электрических полей.

Из соотношения
,
определяющего связь между напряженностью
и потенциалом электрического поля,
следует формула для вычисления потенциала
поля:

где интегрирование
производится вдоль силовой линии поля;
С – произвольная постоянная, с точностью
до которой определяется потенциал
электрического поля.

Если направление
поля
совпадает с направлением радиус–вектора(),
то вычисления можно производить по
формуле:

.

Рассмотрим ряд
примеров на применение этой формулы.

Пример1.
Потенциал поля точечного заряда
(рисунок).

При
полагают, что,
тогда.
Таким образом, потенциал поляточечного
заряда
определяется по формуле:

Пример
2. Потенциал
поля металлического заряженного шара.

а)
Изолированный шар
(рисунок).

при
,
т.е. внутри шара=const.

Вне
шара
.

При
φ = 0, следовательно, С = 0.

– вне шара.

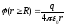
Для определения
используем свойство непрерывности
потенциала: при переходе через границу
поверхности шара, потенциал не претерпевает
скачка. Полагая в последней формулеr
=R,
находим:

– внутри шара.

б)
Заземленный
шар (рисунок).

.

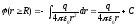
При
,
то есть– вне шара.

Внутри
шара φ(r
≤ 0) = φ₀
= 0. Разность потенциалов U
двух точек на силовой линии электрического
поля заряженного шара определяется по
формуле:

.

Пример
3. Потенциал
поля заряженной нити (рисунок).

При
:

В итоге получаем:

Разность
потенциалов U
(рис.2.17) двух точек на силовой линии поля
заряженной нити:

Пример
4. Потенциал
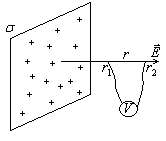
поля заряженной плоскости (рисунок).

Разность потенциалов
U
(см. рисунок) двух точек на силовой линии
поля заряженной плоскости:

.

Проводники в электростатическом поле

Опыт показывает,
что при равновесии электрические заряды
распределяются на внешней
поверхности
проводников (см. рисунок). Поэтому,
согласно теореме Гаусса, электрическое
поле внутри проводника
,
а потенциал φ
= const.

Рисунок. Опыт,
иллюстрирующий равновесное распределение
зарядов на проводнике.

Из сказанного
следует, что при равновесии зарядов
поверхность проводника является
эквипотенциальной.
Вблизи поверхности заряженного проводника
силовые линии перпендикулярны его
поверхности, и поэтому работа по
перемещению заряда вдоль любой линии
на поверхности проводника
.

При внесении
незаряженного проводника в электрическое
поле на его внешней поверхности появляются
индукционные заряды противоположного
знака, электрическое поле которых
компенсирует внутри проводника внешнее
поле. На этом свойстве проводников
основано действие электростатической
защиты.

Электроемкость проводников. Конденсаторы.

Заряд q,
сообщенный уединенному проводнику
создает вокруг него электрическое поле,
напряженность которого пропорциональна
величине заряда. Потенциал поля φ, в
свою очередь, связан с напряженностью
поля также пропорциональной зависимостью.
Следовательно, заряд и потенциал
уединенного проводника связаны между
собой линейной зависимостью:

q
= Cφ

Коэффициент
пропорциональности С называется
электроемкостью
(или просто емкостью)
проводника. Емкость проводника зависит
от его формы и размеров, а также свойств
окружающей проводник среды. Если
проводник находится в непроводящей
среде с диэлектрической проницаемостью
ε, то его емкость увеличивается в ε раз.

Единицы измерения
электроемкости в СИ:

Пара проводников,
между которыми имеется разность
потенциалов, называется простейшим
конденсатором.
Индуцированные на проводниках заряды
равны по величине и противоположны по
знаку. Заряд каждой пластины по абсолютной
величине

Если пространство
между проводниками заполнено средой с
диэлектрической проницаемостью ε, то

где
С₀
– емкость конденсатора в вакууме.

Вычислим емкость
простых конденсаторов.

Согласно определению,
емкость конденсатора:

,
где

(интеграл берется
вдоль силовой линии поля между обкладками
конденсатора).

Следовательно,
общая формула для вычисления емкости
любого конденсатора есть:

Рассмотрим ряд
примеров на применение этой формулы.

Пример 1.
Емкость плоского конденсатора (рисунок
ниже).

Рис.4.3. Плоский
конденсатор.

,

Здесь S
– площадь одной пластины. В итоге
получаем

Пример 2.
Емкость цилиндрического конденсатора
(рисунок ниже).

Рисунок. Цилиндрический
конденсатор.

Мы имеем

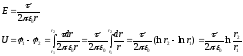
l

Заряд
равен:
,
l
– длина конденсатора; r₁,
r₂-радиусы
электродов

.

+

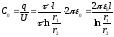
Пример 3.
Емкость сферического конденсатора и
уединенного шара (рисунок

ниже).

Рисунок. Сферический
конденсатор.

Уединенный
шар может рассматриваться как сферический
конденсатор при
и:

Рисунок. Уединенный
шар.

В итоге имеем:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Потенциал. Разность потенциалов. ЗАДАЧИ с решениями

Формулы, используемые на уроках «Решение задач на тему: Работа перемещения заряда в электрическом поле. Потенциал. Разность потенциалов» для подготовки к ЕГЭ.

---

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

---

Задача № 1.
 Металлический шар диаметром d заряжен с поверхностной плотностью зарядов σ. Найти потенциал φ этого шара, если он окружен заземленной проводящей сферой, имеющей общий с шаром центр. Диаметр сферы D. Среда — воздух.

---

Задача № 2.
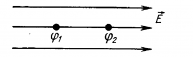
 Потенциал заряженного шара φ₁ = 300 В. Чему равен потенциал φ₂ электрического поля этого шара в точке, отстоящей на расстоянии l = 50 см от его поверхности, если радиус шара R = 25 см?

---

Задача № 3.
 Определить потенциал φ точки поля, находящейся на расстоянии а =  9 см от поверхности заряженного шара радиусом R = 1 см, если поверхностная плотность зарядов на шаре σ = 1 • 10^–11 Кл/см². Среда — воздух.

---

Задача № 4.
 В точке 1 поля точечного заряда-источника потенциал φ₁ = 40 В, а в точке 2 φ₂ = 10 В. Найти потенциал φ в точке М, лежащей посередине между точками 1 и 2 (рис. 3-6). 

---

Задача № 5.
 В трех вершинах квадрата со стороной а = 20 см находятся заряды q₁ = 1 • 10^–8 Кл, q₂ = 2 • 10^–8 Кл и q₃ = 2 • 10^–8 Кл (рис. 3-7). Определить потенциал φ электрического поля, созданного этими зарядами в четвертой вершине. 

---

Задача № 6.
 Четыре одинаковых точечных заряда q расположены на одной прямой на расстоянии r друг от друга. Какую работу А надо совершить, чтобы переместить эти заряды в вершины тетраэдра со стороной r? Среда — вакуум.

---

Задача № 7.
Два одинаково заряженных шарика диаметрами d = 0,5 см каждый расположены на расстоянии l = 2 см между их поверхностями (рис. 3-14). До какого потенциала φ они заряжены, если сила их отталкивания друг от друга F = 2 мкН? Среда — воздух. 

---

Задача № 8.
 В однородном электрическом поле напряженностью Е = 2 кВ/см переместили заряд q = –20 нКл в направлении силовой линии поля на расстояние d = 10 см. Найти работу поля А, изменение потенциальной энергии поля ΔW_п и напряжение (разность потенциалов) U между начальной и конечной точками перемещения.

---

Задача № 9.
 Между двумя горизонтальными плоскостями, заряженными разноименно и расположенными на расстоянии d = 5 мм друг от друга, находится в равновесии капелька масла массой 20 нг (нанограмм) (рис. 3-10). Найти число избыточных электронов N на этой капельке. Среда — воздух. Разность потенциалов между плоскостями U = 2 кВ. 

---

Задача № 10.
 На пластине М поддерживается потенциал φ₁ = +80 В, а на пластине N – φ₂ = –80 В (рис. 3-11, а). Расстояние между пластинами d = 10 см. На расстоянии d₁ = 4 см от пластины М помещают заземленную пластину Р (рис. 3-11, б). Найти изменение напряженности ΔЕ₁ поля на участке МР и изменение напряженности поля ΔЕ₂ на участке PN при этом. Построить графики зависимостей напряженностей Е = Е(х) и потенциала φ = φ(х) от расстояния между точками поля и пластинами. 

---

Это конспект по теме «Потенциал. Разность потенциалов. ЗАДАЧИ с решениями». Выберите дальнейшие действия:

• Вернуться к списку конспектов по Физике.
• Проверить свои знания по Физике.

Решение:


15 Два параллельных тонких кольца радиуса R расположены на расстоянии d друг от друга на одной оси. Найти работу электрических сил при перемещении заряда q_o из центра первого кольца в центр второго, если на первом кольце равномерно распределен заряд q₁, а на втором — заряд q₂.

Решение:

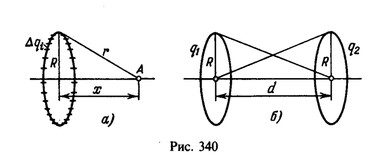
Найдем потенциал, создаваемый зарядом q, находящимся на кольце, в точке А на оси кольца, расположенной на расстоянии
х от его центра (рис. 340, а) и, следовательно, на расстояниях от точек, лежащих на кольце. Разобьем кольцо на отрезки, малые по сравнению с расстоянием r. Тогда заряд , находящийся на каждом отрезке (i — номер отрезка), можно рассматривать как точечный. Он создает в точке А потенциал . Потенциал, создаваемый в точке А всеми отрезками кольца (отстоящими от этой точки на одно и то же расстояние r), будет

В скобках стоит сумма зарядов всех отрезков, т. е. заряд всего кольца q; поэтому

Потенциал Ф₁ поля в центре первого кольца складывается из потенциала, создаваемого зарядом q₁, находящимся на первом кольце, для которого х=0, и потенциала, создаваемого зарядом q₂, находящимся на втором кольце, для которого x=d (рис. 340, б). Аналогично находится потенциал в центре второго кольца:

Окончательно для работы имеем

16 На тонком кольце радиуса R равномерно распределен заряд q. Какова наименьшая скорость υ, которую необходимо сообщить находящемуся в центре кольца шарику массы т с зарядом q_o, чтобы он мог удалиться от кольца в бесконечность?

Решение:
Если заряды q_o и q одного знака, то удалить шарик от кольца в бесконечность можно, сообщив ему бесконечно малую скорость. Если же знаки зарядов разные, то сумма кинетической и потенциальной энергий шарика в центре кольца должна быть равна нулю, так как она равна нулю в бесконечности: , где φ=kq/R — потенциал в центре кольца (см. задачу 17); отсюда

17 На шарик радиуса R=2 см помещен заряд q=4 пКл. С какой скоростью подлетает к шарику электрон, начавший движение из бесконечно удаленной от него точки?

Решение:


18 Между горизонтально расположенными пластинами плоского конденсатора с высоты Н свободно падает незаряженный металлический шарик массы т. На какую высоту h после абсолютно упругого удара о нижнюю пластину поднимется шарик, если в момент удара на него переходит заряд q? Разность потенциалов между пластинами конденсатора равна V, расстояние между пластинами равно d.

Решение:
Внутри конденсатора имеется однородное электрическое поле с напряженностью Е= V/d, направленной вертикально. После удара шарик приобретает заряд того же знака, что и нижняя пластина конденсатора. Поэтому на него будет действовать со стороны электрического поля сила F=qE=qV/d, направленная вверх. Согласно закону сохранения энергии изменение энергии равно работе внешних сил (в данном случае — электрических). Учитывая, что удар абсолютно упругий и что в начальный и конечный моменты шарик имеет лишь потенциальную энергию в поле силы тяжести, получим
откуда

19 Два шарика с одинаковыми зарядами q расположены на одной вертикали на расстоянии Н друг от друга. Нижний шарик закреплен неподвижно, а верхний, имеющий массу m, получает начальную скорость v, направленную вниз. На какое минимальное расстояние h приблизится верхний шарик к нижнему?

Решение:
Согласно закону сохранения энергии

где qV—работа электрических сил, V=kq/H—kq/h — разность потенциалов точек начального и конечного положения верхнего шарика. Для определения h получаем квадратное уравнение:

Решая его, найдем

(знак плюс перед корнем соответствовал бы максимальной высоте, достигнутой шариком, если бы он получил ту же начальную скорость, направленную вверх).

20 Найти максимальное расстояние h между шариками в условиях предыдущей задачи, если неподвижный шарик имеет отрицательный заряд q, а начальная скорость v верхнего шарика направлена вверх.

Решение:


21 Электрон, пролетая в электрическом поле путь от точки а к точке b, увеличил свою скорость с ν_a=1000 км/с до ν_ab = 3000 км/с. Найти разность потенциалов между точками а и b электрического поля.

Решение:
Работа, совершенная над электроном электрическим полем, идет на увеличение кинетической энергии электрона:

откуда

где γ— удельный заряд электрона. Разность потенциалов отрицательна. Так как электрон имеет отрицательный заряд, то скорость электрона увеличивается при его движении в сторону возрастания потенциала.

22 В плоский конденсатор влетает электрон со скоростью ν = 20 000 000 м/с, направленной параллельно пластинам конденсатора. На какое расстояние h от своего первоначального направления сместится электрон за время пролета конденсатора? Расстояние между пластинами d=2 см, длина конденсатора l=5 см, разность потенциалов между пластинами v=200 В.

Решение:
За время пролета t = l/v электрон смещается в направлении действия силы на расстояние

где γ — удельный заряд электрона.

23 Положительно заряженная пылинка массы г находится в равновесии внутри плоского конденсатора, пластины которого расположены горизонтально. Между пластинами создана разность потенциалов V₁=6000 В. Расстояние между пластинами d=5см. На какую величину необходимо изменить разность потенциалов, чтобы пылинка осталась в равновесии, если ее заряд уменьшился на q_o=1000 e?

Решение:
На пылинку действуют сила тяжести mg и сила со стороны электрического поля, где —начальный заряд пылинки и E₁ = V₁/d—напряженность электрического поля в конденсаторе.
Чтобы пылинка могла находиться в равновесии, верхняя пластина конденсатора должна быть заряжена отрицательно. При равновесии
mg = F, или ; отсюда .
Так как уменьшение заряда пылинки на q_o=1000e равносильно увеличению положительного заряда на q_o, то новый заряд пылинки q₂ = q₁+q_o. При равновесии , где V2—новая разность потенциалов между пластинами. Учитывая выражения для q2, q1 и q0, найдем

Таким образом, разность потенциалов нужно изменить на V₂— V₁ = — 980 В (знак минус показывает, что ее нужно уменьшить, так как заряд пылинки увеличился).

24 Решить предыдущую задачу, считая пылинку заряженной отрицательно.

Решение:
Верхняя пластина конденсатора должна быть заряжена положительно. Новый заряд пылинки q₂ = q_1-q_o, где q_o=1000e.
Поэтому (см. задачу 23)

Напряжение между пластинами нужно увеличить на V₂— V₁ = 1460 В.

25 В электрическое поле плоского конденсатора, пластины которого расположены горизонтально, помещена капелька масла, имеющая заряд q=1 е. Напряженность электрического поля подобрана так, что капелька покоится. Разность потенциалов между пластинами конденсатора V =500 В, расстояние между пластинами d=0,5 см. Плотность масла . Найти радиус капельки масла.

Решение:
При равновесии
откуда

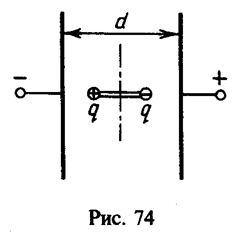
26 Внутри плоского конденсатора, пластины которого расположены вертикально, помещена диэлектрическая палочка длины l=1 см с металлическими шариками на концах, несущими заряды +q и — q(|q|=1 нКл). Палочка может вращаться без трения вокруг вертикальной оси, проходящей через ее середину. Разность потенциалов между пластинами конденсатора V=3 В, расстояние между пластинами d=10см. Какую работу необходимо совершить, чтобы повернуть палочку вокруг оси на 180° по отношению к тому положению, которое она занимает на рис. 74?

Решение:
Напряженность электрического поля в конденсаторе E=V/d.
Разность потенциалов между точками, где расположены заряды,

где —потенциал в точке расположения заряда + q, а —потенциал в точке расположения заряда — q; при этом . При повороте палочки электрические силы совершают работу по переносу заряда — q из точки а в точку b и заряда + q из точки b в точку а, равную

Знак минус означает, что работу должны совершить внешние силы.

27 Внутри плоского конденсатора помещен диэлектрический стержень длины l=3 см, на концах которого имеются два точечных заряда + q и —q (|q|=8нКл). Разность потенциалов между пластинами конденсатора V=3 В, расстояние между пластинами d=8 см. Стержень ориентирован параллельно пластинам. Найти момент сил, действующий на стержень с зарядами.

Решение:


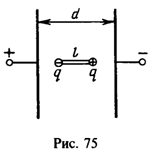
28 На концах диэлектрической палочки длины l=0,5 см прикреплены два маленьких шарика, несущих заряды — q и +q (|q|=10 нКл). Палочка находится между пластинами конденсатора, расстояние между которыми d=10cм (рис.75). При какой минимальной разности потенциалов между пластинами конденсатора V палочка разорвется, если она выдерживает максимальную силу растяжения F=0,01 Н? Силой тяжести пренебречь.

Решение:


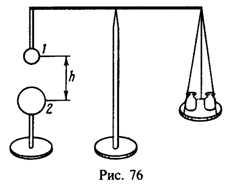
29 Металлический шарик 1 радиуса R₁=1 см прикреплен с помощью диэлектрической палочки к коромыслу весов, после чего весы уравновешены гирями (рис. 76). Под шариком 1 помещают заряженный шарик 2 радиуса R₂=2 см. Расстояние между шариками h = 20 см. Шарики 1 и 2 замыкают между собой проволочкой, а потом проволочку убирают. После этого оказывается, что для восстановления равновесия надо снять с чашки весов гирю массы m = 4мг. До какого потенциала j был заряжен шарик 2 до замыкания его проволочкой с шариком 1?

Решение:
Если до замыкания шарик 2 имел заряд 0, то сумма зарядов шариков 1 и 2 после замыкания q₁+q₂ = q. Потенциалы же их после замыкания одинаковы: . Следовательно, После замыкания шарик 2 действует на шарик 1 с силой
откуда
Начальный потенциал шарика 2

Потенциал. Разность потенциалов. Напряжение.
Потенциал электростатического поля — скалярная величина, равная отношению потен­циальной энергии заряда в поле к этому заряду:   – энергетическая характеристика поля в данной точке. Потенциал не зависит от величины заряда, помещенного в это поле.
Т.к. потенциальная энергия зависит от выбора системы координат, то и потенциал определяется с точностью до постоянной. За точку отсчета потенциала выбирают в зависимости от задачи: а) потенциал Земли, б) потенциал бесконечно удаленной точки поля, в) потенциал отрицательной пластины конденсатора.
– следствие принци­па суперпозиции полей (потенциалы складываютсяалгебраически).
Потенциал численно равен работе поля по перемещению единичного положительного заряда из данной точки электрического поля в бесконечность. В СИ потенциал измеряется в вольтах:
Разность потенциалов
Напряжение — разность значений потенциала в начальной и конечнойточках траектории. Напряжение численно равно работе электростатического поля при перемещении единичного положительного заряда вдоль силовых линий этого поля.          Разность потенциалов (напряжение) не зависит от выбора системы координат!
Единица разности потенциалов    Напряжение равно 1 В, если при перемещении положительного заряда в 1 Кл вдоль силовых линий поле совершает работу в 1 Дж.
Связь между напряженностью и напряжением.
Из доказанного выше:   →      напряженность равна градиенту потенциала (скорости изменения потенциала вдоль направления d).
Из этого соотношения видно: Вектор напряженности направлен в сторону уменьшения потенциала. Электрическое поле существует, если существует разность потенциалов. Единица напряженности:     –   Напряженность поля равна 1 В/м, если между двумя точками поля, находящимися на расстоянии 1 м друг от друга существует разность потенциалов 1 В.
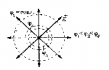
Эквипотенциальные поверхности. ЭПП – поверхности равного потенциала. Свойства ЭПП: – работа при перемещении заряда вдоль эквипотенциальной поверхности не совершается; – вектор напряженности перпендикулярен к ЭПП в каждой ее точке.
Измерение электрического напряжения (разности потенциалов) Между стержнем и корпусом — электрическое поле. Измерение потенциала кондуктора Измерение напряжения на гальваническом элементе Электрометр дает большую точность, чем вольтметр.
Потенциальная энергия взаимодействия зарядов.
Потенциал поля точечного заряда
Потенциал заряженного шара а) Внутри шара Е=0, следовательно, потенциалы во всех точках внутри заряженного металлического шара одинаковы (!!!) и равны потенциалу на поверхности шара. б) Снаружи поле шара убывает обратно пропорционально расстоянию от центра шара, как и в случае точечного заряда.
Перераспределение зарядов при контакте заряженных проводников. Переход зарядов происходит до тех пор, пока потенциалы контактирующих тел не станут равными.