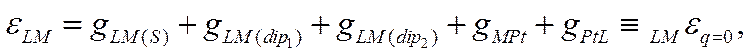Гальвани-потенциал на границе двух металлов
Электродный
потенциал представляет собой сложную
величину, определяемую тремя отдельными
скачками потенциала: скачком потенциала
на границе металл электрода – платина
и скачками потенциала на границах металл
– раствор и платина – раствор. Теория
возникновения электродного потенциала
должна основываться поэтому на
определённых представлениях о природе
как скачка потенциала между двумя
металлами, так и скачка потенциала на
границе металл – раствор.
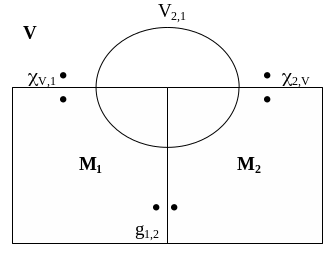
Рассмотрим
вначале гальвани-потенциал g1,2
между двумя металлами. Соотношение,
существующее между вольта- и
гальвани-потенциалами, можно найти,
используя правило, по которому сумма
всех работ переноса элементарного
заряда по замкнутому контуру равна нулю
(см. рис. 18):
V,1
+ g1,2
+
2,V
+ V2,1
= 0 ,
g1,2
= V1,2
+ 1,V
– 2,V
. (3)
|
|
Рис. |
Работа
переноса частицы i с
зарядом zF
из одной фазы в другую определяется,
как известно, разностью электрохимических
потенциалов этой заряженной частицы в
двух фазах:
–
=
–
+ zi
F (
–
)
=
–
+ zi
Fg1,2 . (4)
В условиях равновесия
–
= 0 и
g1,2
= (
–
)/
zi
F .
(5)
Если обе фазы – металлы, то в
обмене между ними участвуют электроны,
заряд которых zi
F = – F.
Для этого случая можно написать
g1,2 =
. (6)
Уравнение (6)
могло бы служить основой для расчёта
гальвани-потенциала, если бы были
известны химические потенциалы электронов
в двух фазах. Однако, как уже отмечалось,
определить для заряженных частиц
изменение только химических потенциалов
невозможно, поскольку при их переносе
из одной фазы в другую одновременно с
химической работой совершается также
и электрическая.
Получим выражение
для вольта-потенциала между фазами 1 и
2: подставим значение g1,2
из уравнения (3) в уравнение (4):
–
=
–
+ zi
F1,V
– zi
F2,V
+ zi
F V1,2
=
(
+ zi
F1,V
) – (
+ zi
F2,V)
+ zi
F V1,2
= –
+
+ zi
F V1,2
.
V1,2 =
. (7)
Для частного случая контакта
двух металлов
V1,2 =
(8)
(е
– работа выхода электрона из металла).
Работа выхода
электрона доступна непосредственному
экспериментальному определению, и
поэтому при помощи уравнения (8) можно
рассчитать величину вольта-потенциала.
Чем меньше работа выхода электрона из
данного металла, тем при данной температуре
большее число электронов может покинуть
металл и перейти в вакуум и тем
положительнее будет заряд обкладки
дипольного слоя в металле. Если сблизить
два металла с различными работами
выхода, то электроны будут переходить
от металла с меньшей работой выхода к
металлу с большей. В результате этого
первый металл зарядится положительно,
а второй – отрицательно. Например, для
пары CuZn
VCu,
Zn = 0,3 В,
тогда как ЭДС системы ZnZnSO4CuSO4Cu
равна 1,11 В. Таким образом, потенциал
V1, 2 составляет
заметную долю обратимой ЭДС электрохимической
системы.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Двойной электрический слой на границе электрод – электролит. Электрокапиллярные явления. Нулевые точки металлов, страница 9
Наряду с
терминами: «нулевая точка» и «потенциал максимума электрокапиллярной кривой»
широко употребляются, как их синонимы, также «потенциал нулевого заряда» и
«потенциал незаряженной поверхности», что вносит большую путаницу в электрохимическую
литературу. Для того чтобы избежать возможных недоразумений, автор предложил
разграничить понятия «нулевая точка» (или «потенциал нулевого заряда») и
«потенциал незаряженной поверхности» (или «потенциал максимума
электрокапиллярной кривой»), каждому из них присвоить свой символ и употреблять
эти термины в соответствии с их содержанием. Основанием для такого
разграничения послужили следующие соображения. Потенциал максимума
электрокапиллярной кривой ртути (или другого металла) всегда отвечает ее
назаряженной поверхности; это значение потенциала целесообразно называть
«потенциалом незаряженной поверхности» и обозначать как еq=0. Положение максимума электрокапиллярной кривой и величина
отвечающего ему потенциала для данных металла и растворителя меняются в
широких пределах в зависимости от природы и концентрации веществ, присутствующих
в растворе. В то же время частное значение потенциала незаряженной поверхности,
полученное в растворе, не содержащем никаких поверхностно-активных частиц
(кроме молекул растворителя) является константой, характерной для данного
металла и данного растворителя; это частное значение потенциала незаряженной
поверхности целесообразно называть «нулевой точкой» и обозначать как εn. Нулевая точка и потенциал незаряженной
поверхности находятся между собой примерно в таком же соотношении, как равновесный
и стандартный потенциалы электрода. Последний, как известно, представляет собой
частный случай равновесного электродного потенциала εr , который реализуется в растворе с активностями всех участников
электродной реакции, равными единице. В обоих случаях необходимо
соответствующим образом задать состав раствора, чтобы получить величину,
являющуюся характерной константой для данной электродной системы. Допустим, что
имеется цепь, составленная из металла, опущенного в раствор его ионов, и
стандартного водородного электрода. Э.д.с. этой цепи, равную электродному
потенциалу εLM металла Μ в условной водородной шкале, можно записать, в соответствии с
уравнением (IX-13), в следующем виде:
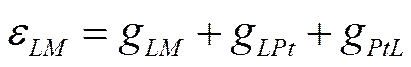
В свою очередь,
гальвани-потенциал на границе раствор—металл, можно представить, согласно
уравнению (IX-23), как сумму четырех слагаемых
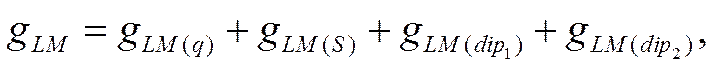
где индексы q, S, dip1 и dip2 относятся
соответственно к потенциал-определяющим ионам, к специфически адсорбирующимся
ионам, диполям растворителя и к диполям любого неионизированного органического
вещества. Если gLM(q) =
0, то поверхность металла
лишена заряда и потенциал электрода должен отвечать потенциалу незаряженной
поверхности
В согласии со
сказанным ранее, потенциал незаряженной поверхности металла зависит от природы
этого металла, от примененного электрода сравнения, от природы растворителя и
от состава раствора. Для выбранных металла и растворителя величина LMεq=0 может
быть различной в зависимости от величины дия(8) (т· е· от
природы и концентрации поверхностно-активных ионов) и qLM (dip2) (т.е. от природы и концентрации поверхностно-активных
дипольных молекул). Если же, однако, не толькоqLM(q)=0,
но и qLM(S) =
0 и qLM (dip)2 = 0. т.е. если в растворе нет никаких
поверхностно-активных частиц, кроме молекул растворителя L, то вместо (Х-55) получим
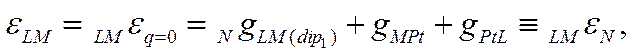
Как следует из
(Х-56), это частное значение потенциала незаряженной поверхности (т. е. нулевая
точка LMεN
) должно быть константой,
так как оно равно сумме трех постоянных величин.
Нулевую точку
можно выразить и через соответствующие вольта-потенциалы
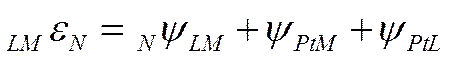
Вольта-потенциал
между металлом и раствором должен быть при этом вполне определенной величиной (NψLM), отвечающей
разности внешних потенциалов межу металлом Μ и раствором, в котором потенциал металла равен его нулевой точке.
Определенная
таким образом нулевая точка была выбрана за нуль в «приведенной» или «φ-шкале» потенциалов, предложенной автором в 1946—1951 гг.
Потенциал φ в приведенной шкале определяется как
разность между потенциалом электрода в данных условиях и его нулевой точкой
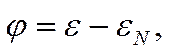
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание – внизу страницы.
Теорема Гаусса и постулат Максвелла, представленные в интегральной форме, дают возможность решить ряд задач в тех случаях, когда условия симметрии таковы, что в каждой точке замкнутой поверхности интегрирования (поверхности симметрии), охватывающей заряды, вектор напряженности поля (или электрического смещения
)
имеет одно и то же значение и может быть вынесен из-под интеграла.
Пример 1. Точечный заряд q = 10-9 Кл помещен в начале сферической системы координат. Определить напряжение между точками а (Ra = 4см, qа = 45°, jа = 0°) и b (Rb = 8см, , qb = 180°, jb = 90°) и напряженность в тех же точках, если окружающей средой является воздух.
Решение.
Решение будем проводить с помощью теоремы Гаусса (1.9), так как среда однородна.
Поскольку поле точечного заряда характеризуется сферической симметрией, то, если в качестве поверхности интегрирования взять поверхность сферы с центром в точке, где расположен заряд (в нашем случае это начало системы координат), то в любой точке на поверхности этой сферы напряженность поля будет иметь одно и то же значение. Направление же вектора будет совпадать с направлением радиуса, то есть перпендикулярно к поверхности сферы. В связи с этим, интеграл по этой поверхности, составленный по теореме Гаусса, можно преобразовать следующим образом:
.
Поскольку данный интеграл (согласно теореме Гаусса) равен отношению заряда, помещенного внутри сферы, к диэлектрической проницаемости среды, то напряженность поля будет определяться соотношением
Еr = q/(4pe0r2).
Здесь индекс r у напряженности проставлен для того, чтобы показать, что напряженность поля имеет одну составляющую, направленную по радиусу.
Отметим, что данная формула полностью соответствует выражению (1.1), полученному из закона Кулона.
Поскольку напряженность электрического поля в данном случае имеет только радиальную составляющую, величина которой является функцией радиуса и не зависит от угловой координаты, то в указанных в исходном задании точках она будет равна:
E(ra)=q/(4pe0ra2)=10-9/(4p?8.85·10-12·0.042)=5.62кВ/м.
E(rв)=q/(4pe0rв2)=10-9/(4p8.85·10-12·0.082)=1.405кВ/м.
Разность потенциалов между точками а и в определяется при помощи выражения (1.6). Эта разность в потенциальном поле не зависит от пути интегрирования. Поэтому, если разбить путь интегрирования на две части и сначала проводить интегрирование вдоль радиуса от точки а до точки, которая является точкой пересечения продолжения этого радиуса с поверхностью воображаемой сферы с центром в начале координат и радиусом rв, а затем проводить интегрирование по любой линии, лежащей на поверхности этой серы от данной точки до точки в, то интеграл вдоль этой линии будет равен нулю, поскольку вектор напряженности поля имеет одну составляющую, направленную вдоль радиуса, а подинтегральным выражением в формуле (1.6) является скалярное произведение вектора напряженности поля и вектора dl, который совпадает с касательной к поверхности сферы.
Таким образом, разность потенциалов между точками а и в будет равна

Пример 2. Уединенный проводящий шар радиусом R0 = 6 см, поверхностная плотность заряда которого s = 0,1*10-6 Кл/м2, помещен в диэлектрик (er = 3).
Определить закон изменения напряженности поля и потенциала в функции расстояния r от центра шара, приняв потенциал равным нулю в бесконечности. Рассчитать напряжение между точками, одна из которых лежит на поверхности шара, а другая – на расстоянии 20 см от его поверхности. Вычислить емкость шара.
Решение.
Поле внутри проводящего шара отсутствует. Поле вне шара обладает сферической симметрией, поэтому рассчитывается с помощью теоремы Гаусса точно так же как и для точечного заряда.
Здесь в качестве поверхности интегрирования взята поверхность сферы радиуса r ?
R0 с центром, совпадающим с центром шара.
Заряд шара определяется через поверхностную плотность
q = s·4p·R02.
Таким образом, напряженность поля вне шара имеет только одну радиальную составляющую и равна
Еr = s·R02/(ere0r2) =
0,1·10-6·0,062/(3·8,85·10-12r2).
Потенциал в любой точке вне шара, находящейся на расстоянии r от его центра, определяется с помощью выражения (1.5), которое с учетом того, что напряженность поля направлена вдоль радиуса, будет иметь следующий вид:
Потенциал шара равен потенциалу любой точки, лежащей на поверхности шара (r = R0) U =
13,56/0,06 = 173,8 В.
Разность потенциалов между любыми точками А (r = RA) и В (r = RВ) определяется с помощью следующей формулы:
UA – UВ = 13,56· (1/RA – 1/RВ).
Таким образом, разность потенциалов между точкой, лежащей на поверхности шара, и точкой, отстоящей от поверхности на расстоянии 20 см, равна
UAВ = 13,56· (1/0,06 – 1/0,26) = 173,8 В.
Емкость шара можно определяется выражением (1.19)
С = 4·p·ere0·R0 = 4·p·3·8,85·10-12·0,06 = 2·10-11 Ф.
Пример 3.
Шар из диэлектрика (er = 4) заряжен и расположен в воздухе. Объемная плотность заряда является функцией расстояния r от центра шара: r = k*r,
где k = 0,05p [Кл/м4].
Радиус шара R = 2см. Рассчитать и построить графики изменения потенциала и напряженности поля вдоль радиуса.
Решение. В
данном случае поле также обладает сферической симметрией, но область не однородна. Поэтому здесь удобнее применять постулат Максвелла (1.10).
Так, при 0 ? r ? R где s – сферическая поверхность радиусом r с
центром, совпадающим с центром шара; v – объем, заключенный внутри этой поверхности.
Перепишем уравнение с учетом симметрии поля
Отсюда находим радиальную составляющую вектора электрического смещения:
Dr = 0,25·k·r2.
Напряженность электрического поля, которая также как и вектор электрического смещения направлена по радиусу, внутри шара будет равна
(1.8):
E1r = Dr/ere0 = 0,25·k·r2/ere0.
Вне шара (r ? R) электрическое смещение, исходя из постулата Максвелла, определяется следующим образом:
Следовательно, электрическое смещение и напряженность поля будут равны:
Dr = 0,25·k·R4/r2; Er = Dr/e0.
Графики изменения напряженности поля и вектора электрического смещения представлены на рис.1.4. Значения напряженности поля и вектора электрического смещения даны в относительных единицах. За базисные значения приняты значения этих величин на поверхности шара, которые для заданных исходных данных соответственно равны Erb = 4,435·105В/м; Drb = 1,571·10-5Кл/м2.
Потенциал поля внутри шара можно определить по формуле
,
где С1 – постоянная интегрирования.
Принимая потенциал бесконечно удаленной точки равным нулю, определим потенциал любой произвольной точки в области вне шара.

Постоянную интегрирования С1 можно определить из условия равенства потенциалов U1 и U2 на поверхности шара (при r = R)

Отсюда

График изменения потенциала вдоль радиуса также в относительных единицах показан на рис.1.4. За базисное значение потенциала принято значение потенциала на поверхности шара Ub = 35.5кВ.
Отметим, что если бы объемная плотность заряда r оставалась постоянной, то напряженность поля и потенциалы поля в соответствующих подобластях определялись бы следующими выражениями:
E1 = r·r/(3·ere0); U1 = – r·r2/(6·ere0) + C1;
E2 = r·R3/(3·e0·r2);
U2 = r·R3/(3·e0·r).
Постоянная С1 в этом случае определяется также из условия равенства потенциалов U1 и U2 на поверхности шара
С1 = r·R3· (1+2·er)/(6·e0·er).
Пример 4. Сферический конденсатор с двухслойным диэлектриком имеет радиус внутренней сферы r1=12 мм, внутренний радиус наружной сферы – r3=22 мм и радиус поверхности раздела диэлектриков – r2=16 мм.
Относительное значение диэлектрической проницаемости внутреннего слоя диэлектрика er1=5, наружного слоя – er2=3. Разрез конденсатора показан на рис.1.5. Заряд конденсатора q = 10-8Кл.
Определить и построить график изменения напряженности поля вдоль радиуса. Найти разность потенциалов между электродами. Вычислить емкость конденсатора. Изменяя радиус поверхности раздела диэлектриков r2 и значение диэлектрической проницаемости наружного слоя er2 получить конденсатор с наилучшим использованием двухслойного диэлектрика. Рассчитать емкость данного конденсатора и сопоставить ее с емкостью исходного конденсатора.
Решение. Используя постулат Максвелла для любой сферической поверхности радиусом r, построенной внутри k-го слоя (k=1,2) диэлектрика с диэлектрической проницаемостью erk, получим выражение для вектора электрического смещения и напряженности электрического поля
Dk = q/(4pr2); Ek = Dk/(erk·e0) = q/(4pr2·erk·e0).
Максимальное значение напряженности поля в первом слое, очевидно, будет на поверхности внутреннего электрода
E1max = q/(4p·r12·er1e0)=10-8/(4p·122·10-6·5·8,85·10-12) = 1,249·105 В/м.
Максимальное значение напряженности поля во втором слое на сферической поверхности раздела диэлектриков
E2max = q/(4pr22·er2·e0)=10-8/(4p162·10-6·3·8,85·10-12) =1,171*105 В/м.
Графики изменения напряженности поля в диэлектрике вдоль радиуса представлены на рис.1.6. Значения напряженности на графиках приведены в относительных единицах. За базисное значение принято максимальное значение напряженности в первом слое Eb= E2max.
Разность потенциалов между электродами определяется при помощи следующего выражения:
Емкость конденсатора равна (1.15)
C=q/U12 = 10-8/885,6 = 1,129·10-11Ф.
Отметим, что емкость сферического конденсатора с двухслойным диэлектриком можно определить и по такой формуле
С=С1С2/(С1+С2),
где С1 – емкость сферического конденсатора с однослойным диэлектриком с радиусами обкладок r1 и r2 и диэлектрической проницаемостью диэлектрика, равной диэлектрической проницаемости первого слоя; С2 – емкость сферического конденсатора с однослойным диэлектриком с радиусами обкладок r2 и r3 и диэлектрической проницаемостью диэлектрика, равной диэлектрической проницаемости второго слоя.
Поскольку емкость сферического конденсатора с однослойным диэлектриком определяется с помощью выражения (1.18), то емкости С1, С2 и С будут равны:
С1 = 4·p·8,85·10-12·5·0,012·0,016/(0,016-0,012) = 2,669·10-11Ф;
С2=4·p·8,85·10-12·3·0,016·0,022/(0,022-0,016) = 1,957·10-11Ф;
С=2,669·1,957·10-11(2,669+1,957) = 1,129·10-11Ф.
Для наилучшего использования диэлектриков в конденсаторе необходимо так подобрать толщину слоев, чтобы максимальное значение напряженности поля было одинаковым. Поскольку напряженность поля имеет максимальное значение у внутренней поверхности слоя, то для выполнения этого условия, необходимо, чтобы произведение квадрата внутреннего радиуса слоя на его диэлектрическую проницаемость было постоянным, то есть r12e1= r22e2=const.
Если значение диэлектрической проницаемости оставлять неизменным, а изменять толщину слоев, то с помощью данного выражения можно определить радиус поверхности раздела диэлектриков.
м.
Разность потенциалов U12 и емкость такого конденсатора будут равны: U12=910,13В; C=1,099*10-11Ф.
Пример 5.
Бесконечно длинная тонкая заряженная нить расположена в воздухе вдоль оси z цилиндрической системы координат (рис. 1.7). Линейная плотность заряда t=10-9Кл/м. Рассчитать и построить график изменения напряженности поля вдоль радиуса. Определить разность потенциалов между точками
m (rm=10cм; qm=270°) и n (rn=40cм; qn=180°).
Решение. В этом случае поле характеризуется цилиндрической симметрией, то есть во всех точках цилиндрической поверхности, охватывающей заряженную нить, произвольного радиуса r напряженность поля имеет одно и то же значение и направлена перпендикулярно к поверхности. Поэтому, если окружить нить цилиндрической поверхностью длиной l и радиусом r и использовать теорему Гаусса, то можно получить выражение для напряженности поля Е.
График изменения напряженности поля вдоль радиуса представлен на рис. 1.8.
Значение напряженности поля на графике даны в относительных единицах. За базисное значение принято значение напряженности на расстоянии одного миллиметра от начала координат (Еb=1,798·104 В/м).
Потенциал поля в любой точке m, расположенной на расстоянии rm от оси провода, равен:

Здесь rp – расстояние от оси провода до некоторой фиксированной точки пространства р, в которой потенциал принимается равным нулю.
Если за такую точку принять точку, расположенную на расстоянии одного метра от оси провода, то потенциал точки m будет равен:
.
Изменение потенциала вдоль радиуса представлено на рис. 1.8. Значения потенциала даны также в относительных единицах. За базисное значение потенциала принято значение потенциала в той же точке, что и базисное значение напряженности поля (Ub=124,226 В).
Разность потенциалов между точками, указанными в условии задачи, равна 24,931 В.
Пример 6.
Бесконечно длинный цилиндрический конденсатор с двухслойным диэлектриком имеет радиус внутреннего электрода r1=1 мм , внутренний радиус внешнего электрода – r3=4 мм и радиус поверхности раздела диэлектриков – r2=2 мм.
Относительное значение диэлектрической проницаемости внутреннего слоя диэлектрика er1=5, наружного слоя – er2=2,5. Поперечное сечение конденсатора показано на рис.1.9. Линейная плотность заряда конденсатора t = 10-8 Кл/м.
Определить и построить график изменения напряженности поля вдоль радиуса. Найти разность потенциалов между электродами.
Вычислить емкость конденсатора на единицу длины.
Решение. Для решения задачи используем обобщенную теорему Гаусса. В качестве поверхности интегрирования возьмем замкнутую цилиндрическую поверхность длиной l и радиусом r (r1?r?r3).
.
Ввиду цилиндрической симметрии (вектор электрического смещения на этой поверхности не изменяется по величине и направлен по радиусу) последнее уравнение можно переписать следующим образом:
D·2·p·r·l = t·l,
откуда
D = Dr = t/(2·p·r).
Напряженность поля в первом слое диэлектрика (r1 ?r ? r2) будет при этом равна:
E1 = D/(er1e0) = t/(2·p·er1e0·r).
Во втором слое (r2 ?r ? r3) –
E2 = D/(er2e0) = t/(2·p·er2e0·r).
График изменения напряженности поля представлен на рис.1.10. На графике значения напряженности поля представлены в относительных единицах. За базисное значение принято значение напряженности в первом слое при r = r1, ( Eb = 35,970 кВ/м).
Как видно из рис. 1.10, напряженность поля на границе раздела диэлектриков испытывает скачек. Для лучшего использования изоляции стараются подобрать толщину слоев диэлектрика и их диэлектрическую проницаемость таким образом, чтобы максимальное значение напряженности поля в обоих слоях было одинаково. Это будет соблюдаться при условии r1e1 = r2e2, как в данном примере.
Разность потенциалов между электродами определяется при помощи выражения (1.6), которое для цилиндрического конденсатора можно переписать в следующем виде:
74,792В.
Емкость конденсатора на единицу его длины будет равна:
С = t/U = 10-8/74,792 = 0,1337 нФ/м.
Отметим, что емкость цилиндрического конденсатора с двухслойным диэлектриком можно определить и по такой формуле
С=С1С2/(С1+С2),
где С1 – емкость цилиндрического конденсатора с однослойным диэлектриком с радиусами обкладок r1 и r2 и диэлектрической проницаемостью диэлектрика, равной диэлектрической проницаемости первого слоя; С2 – емкость цилиндрического конденсатора с однослойным диэлектриком с радиусами обкладок r2 и r3 и диэлектрической проницаемостью диэлектрика, равной диэлектрическойпроницаемости второго слоя.
Поскольку емкость цилиндрического конденсатора с однослойным диэлектриком определяется с помощью выражения (1.23), то емкости С1, С2 и С будут равны:
С = С1·С2/(С1 + С2) = 0,1337 нФ/м.
Пример 7.
Бесконечно длинный цилиндр, выполненный из диэлектрика, относительное значение диэлектрической проницаемости которого er1 = 4, заряжен и находится в минеральном масле (er2 = 2,5).
Радиус цилиндра r0 = 5мм (рис. 1.11). Объемная плотность заряда является функцией расстояния от оси цилиндра r = r/10.

Решение. В
качестве поверхности интегрирования выбирается боковая поверхность цилиндра длиной один метр, радиусом r и с осью, совпадающей с осью исходного цилиндра. При 0 ? r ? r0 внутри этой поверхности будет находиться заряд, величина которого может быть определена с помощью следующего выражения:
Таким образом, с учетом цилиндрической симметрии поля,
получим
Отсюда
где А1=9.416·108 В/м3.
В области вне цилиндра (r0?r??)
Из этого выражения легко определяется напряженность поля вне цилиндра
где А2=183.432 В.
Потенциал электрического поля внутри цилиндра (при условии, что точка, в которой потенциал поля принимается равным нулю, лежит на оси цилиндра) можно определить следующим образом:
Потенциал поля в области вне цилиндра равен
Здесь В2 – постоянная интегрирования, которую можно найти из условия равенства потенциалов на поверхности цилиндра.
В.
Распределение напряженности электрического поля и потенциала представлено в относительных единицах на рис. 1.12. За базисные значения напряженности поля и потенциала приняты максимальное значение напряженности на границе раздела сред (Еmax=3.669·104 В/м) и значение потенциала при r=0.019 м (jв=-284 В).
В частном случае, когда объемная плотность заряда r является постоянной величиной, решение упрощается, и выражения для функции напряженности поля и потенциала будут иметь вид:
где

Рассчитать электростатическое поле, создаваемое зарядом, который равномерно распределен между двумя цилиндрическими бесконечно длинными поверхностями.
Объемная плотность заряда r=10-6 Кл/м3.
Радиус внешнего цилиндра R1=20 см, внутреннего – R2 =4 см, расстояние между осями цилиндров – а=10 см. Относительное значение диэлектрической проницаемости окружающей среды и обоих цилиндров равно er1=1.
Определить распределение составляющих напряженности электрического поля и потенциала вдоль осей Х и Y (рис. 1.13).
Решение.
Данная задача решается методом наложения. Сначала рассчитывается поле в любой точке М от заряда с объемной плотностью +r, равномерно распределенного по объему всего большого цилиндра. Затем в этой же точке рассчитывается поле от заряда, объемная плотность которого равна -r, равномерно распределенного по объему малого цилиндра. Результирующая напряженность поля Е в любой точке М определяется как векторная сумма напряженности Е1 и Е2. Потенциал любой точки определяется также как сумма потенциалов U1 и U2.
Так, в точке М, которая находится на расстоянии r1 от оси большого цилиндра и r2 от оси малого цилиндра и имеет координаты r1 и a (рис. 1.14) модули напряженности поля от соответствующих зарядов определяются согласно теореме Гаусса по следующим формулам:
Вектор напряженности Е1 направлен по радиусу r1 от оси О большого цилиндра, а вектор Е2 – по радиусу r2 к оси О1 малого цилиндра (рис. 1.14).
Потенциалы поля при этом будут равны:
Здесь С1 и С2 – постоянные интегрирования.
Потенциал поля в области между цилиндрами определяется следующим выражением:
Принимая потенциал равным нулю на оси большого цилиндра (r1=0; r2=a), найдем постоянную интегрирования С.
С учетом этого, выражение для потенциала в области между цилиндрами окончательно можно записать в следующем виде:
Если поле определяется в области, лежащей внутри малого цилиндра, то напряженность поля в произвольной точке этой области будет определяться при помощи следующего выражения:
Здесь i – единичный орт, направленный вдоль оси Х.
Таким образом, внутри малого цилиндра напряженность поля будет иметь только одну составляющую, направленную вдоль оси Х и являющуюся постоянной величиной.
Потенциал поля при этом будет равен
где В – постоянная интегрирования.
Эта постоянная определяется исходя из равенства потенциалов для точки, лежащей на поверхности малого цилиндра, один из которых рассчитывается по последнему уравнению, а второй – по выражению, справедливому для точек, находящихся в области между цилиндрами.
Определяя с помощью теоремы косинусов r2 через r1, выражения для потенциала и напряженности поля можно преобразовать.
.
Если точка, в которой определяется поле, лежит в области вне цилиндров (r1?R1), то модули напряженности поля будут определяться при помощи следующих выражений:
где t1 и t2 – линейная плотность зарядов большого и малого цилиндров.
Направление векторов напряженности поля определяется так же, как и для области, лежащей между цилиндрами.
Потенциал поля для области вне цилиндров будет равен
Постоянная интегрирования В1 определяется из условия равенства потенциалов на поверхности большого цилиндра (r1=R1, r2=R1-a), один из которых рассчитывается по последнему уравнению, а второй – по выражению, справедливому для точек, находящихся в области между цилиндрами.
Следовательно, окончательно можно записать следующее выражение для определения потенциала в данной области:
Построим графики изменения модуля напряженности поля и потенциала вдоль оси Y при х=0, для чего положим r1=y; r2=(y2+a2)0,5.
При этом выражения для напряженности поля и потенциала можно несколько преобразовать. Так, при 0?y?R1 они будут иметь следующий вид:
В области вне цилиндров (у?R1) эти выражения можно записать следующим образом:
Графики изменения данных функций представлены на рис. 1.15.
На графиках все величины даны в относительных величинах. За базисные значения потенциала и напряженности поля приняты значения соответствующих функций на поверхности цилиндра радиусом R1 (x=0; y=R1), которые оказались равными Uб=-1057 В,
Еб=10,94 кВ/м.
На рис. 1.16 представлены графики распределения потенциала и напряженности поля (в относительных единицах) вдоль оси Х (при Y=0).
Пример 9.
Рассчитать электростатическое поле от двух бесконечно длинных, равномерно заряженных, параллельных, тонких проводников, расположенных в воздухе на расстоянии 2d=6 м друг от друга. Проводники имеют одинаковые по величине, но противоположные по знаку заряды, линейная плотность которых равна t=4*10-9 Кл/м.
Построить график изменения напряженности поля вдоль оси Y (при х=0) и вывести уравнения для построения эквипотенциальных линий и линий поля.
Решение.
Поскольку среда линейна, то данную задачу можно решить методом наложения.
Вначале рассчитываем напряженность поля в любой точке М от правого провода (рис. 1.17), а затем в этой же точке от левого провода. Задача по расчету поля от бесконечно длинного заряженного провода решена в примере 5. Поэтому сразу запишем выражения для определения напряженности поля от правого и левого провода
Направление векторов напряженности поля показано на рис. 1.17. Результирующая напряженность поля определяется как векторная сумма этих векторов
Модуль данной результирующей напряженности поля рассчитывается по формуле
где
E1x, E2x,
E1y, E2y—
проекции векторов напряженности поля на соответствующие декартовы оси координат.
Здесь yм и xм – координаты произвольной точки М.
В частности, если точка М лежит на оси Y, то (r1=r2) результирующая напряженность поля будет направлена вдоль оси Х (Е=Ех). График распределения данной величины вдоль оси Y представлен на рис. 1.18. Значения напряженности поля на графике даны в относительных единицах, при этом за базисное значение принято значение напряженности в начале координат (x=0, y=0), которое оказалось равным 47,956 В/м.
Потенциал поля в любой точке М определяется также, как сумма потенциалов поля от одного и другого провода
Здесь С – постоянная интегрирования. Эта постоянная будет равна нулю, если принять потенциал точки, которая находится в начале координат, равным нулю.
В этом случае ось OY будет являться эквипотенциальной линией нулевого потенциала.
Все остальные линии равного потенциала являются окружностями с центрами, лежащими на оси ОХ. Координаты этих центров и радиусы окружностей определяются с помощью следующих формул:
Таким образом, если необходимо провести линию равного потенциала через точку, потенциал которой задан (например, 100 В), то надо определить k, используя формулу для потенциала
При построении картины поля, для того чтобы приращение потенциала при переходе от любой линии равного потенциала к соседней оставалось постоянным, должно соблюдаться условие
Здесь В – постоянная; n – порядковый номер линии равного потенциала.
Таким образом, число k при возрастании порядкового номера линии равного потенциала n должно изменяться в геометрической прогрессии.
Линиями поля данной системы заряженных проводников являются дуги окружностей, пересекающихся с проводниками. При этом, центры этих дуг лежат на оси OY и имеют координаты, которые определяются при помощи следующей формулы:
Чтобы при построении картины поля подразделить поле на трубки равного потенциала, необходимо при переходе от любой линии напряженности поля к соседней изменять угол J на постоянную величину.
Пример 10.
Два одинаковых бесконечно длинных проводящих цилиндра расположены в воздухе. Радиус цилиндров R=0.04 м, расстояние между геометрическими осями 2h=0.12 м (рис.1.19).
Напряжение, приложенное к цилиндрам U12=100 В.
Рассчитать электростатическое поле, построить графики изменения напряженности поля и потенциала вдоль оси х.
Найти емкость системы проводов на единицу длины.
Решение.
Поле внутри проводящих проводов отсутствует. Поле же в воздухе будет точно таким, как и поле от двух бесконечно тонких линейных проводников, проходящих через электрические оси данных проводов.
Таким образом, задача по расчету поля двух проводов круглого сечения сводится к нахождению электрических осей проводов, поскольку в дальнейшем расчет поля в воздухе будет аналогичным расчету поля, проведенному в предыдущем примере.
Поскольку поверхность проводящих проводов является поверхностью равного потенциала, то, используя выражения для координаты центра и радиуса линий равного потенциала, которые приведены в примере 9, можно получить формулу для определения координат центра электрических осей проводов b.
В условии задачи задана не линейная плотность зарядов, а разность потенциалов между проводами (разность потенциалов между точками m и n).
Поэтому, прежде всего, следует определить линейную плотность зарядов t. Для этого используем выражение для потенциалов, которое также приведено в предыдущем примере
Здесь r1 и r2 – расстояние от электрической оси первого (левого) и второго провода, соответственно, до точки m, которая находится на поверхности первого провода, а r1/ и r2/ – расстояние от электрической оси первого и второго провода, соответственно, до точки n, которая находится на поверхности второго провода.
С учетом последних соотношений, можно записать выражение для определения линейной плотности зарядов
После определения линейной плотности зарядов и расположения электрических осей проводов, выражения для расчета напряженности поля и потенциала в области вне проводов полностью аналогичны тем, которые приведены в примере 9.
Графики распределения напряженности поля и потенциала вдоль оси ОХ (при y=0) приведены на рис. 1.20. Все значения на графике даны в относительных единицах, причем, за базисные значения приняты значения напряженности поля и потенциала на поверхности правого провода, которые оказались равными Еб=2904 В/м, jб=-50 В.
С учетом того, что ось OY является осью симметрии для напряженности поля и осью антисимметрии для потенциала, графики построены только для положительных значений х.
Емкость между двумя проводниками на единицу их длины определяется при помощи следующего выражения:
Пример 11. Рассчитать
электростатическое поле от двух параллельных бесконечно длинных заряженных несоосных проводящих цилиндров, расположенных в воздухе. Радиусы цилиндров R1=0.02 м и R2=0.04 м. Расстояние между геометрическими осями D=0.08 м (рис. 1.21). Цилиндры имеют одинаковый по величине, но противоположный по знаку заряд, линейная плотность которого t1=-t2=t=10-8 Кл/м.
Определить разность потенциалов между цилиндрами, емкость системы на единицу длины.
Построить график изменения потенциала поля вдоль оси ОХ (при y=0).
Решение.
Расположим оси цилиндров (О1 и О2) так, чтобы их поверхности совпали с поверхностями равного потенциала. Обозначим через h1 и h2 расстояние от геометрических осей первого и второго цилиндра до плоскости постоянного (нулевого) потенциала, а через b – расстояние от электрических осей-до этой плоскости. После определения данных величин задача по расчету поля в области вне цилиндров сводится к расчету электростатического поля от двух заряженных бесконечно длинных линейных проводов, проходящих через центры зарядов, и оказывается, таким образом, полностью аналогичной задачам, рассмотренным в предыдущих примерах.
Используя выражение для определения координат центров зарядов, справедливое как для одного, так и для второго провода, составим следующее уравнение:
или
При заданном расположении цилиндров (рис. 1.21) имеем
h1+h2=D
и, следовательно,
.
В этом случае
Разность потенциалов между двумя цилиндрами можно определить по следующей формуле (как и в примере 10):
Здесь r1/ и r2/ – расстояние от центра электрических осей первого и второго цилиндра, соответственно, до точки n, лежащей на поверхности первого цилиндра; r1// и r2// – расстояние от центра электрических осей первого и второго цилиндра, соответственно, до точки m, лежащей на поверхности второго цилиндра
r1/ = (R1 + b – h1) = 0.0131м; r2/ = 2b – r1/ = 0.0381м;
r2// = (R2 + b – h2) = 0.0181м; r1// = 2b – r2// = 0.0331м.
Потенциал любой произвольной точки d будет равен
где r1 и r2 – расстояние от электрических осей первого и второго провода до точки d.
Если точка d лежит на оси ОХ между цилиндрами, то
r2 = b – x; r1 = b + x;
График изменения потенциала вдоль оси ОХ (при (R1 – h1) < x < (h2 – – R2)) показан на рис. 1.22.
Емкость системы цилиндров на единицу длины определяется по следующей формуле:
Построение линий равного потенциала и линий поля в области вне цилиндров проводится таким же образом, как и для линейных проводов, которые совпадают с электрическими осями (см. пример 9).
Пример 12. Бесконечно длинный проводящий цилиндр радиусом R1=2см расположен внутри другого бесконечно длинного проводящего цилиндра радиусом R2=6см.
Расстояние между геометрическими осями цилиндров D=3см (рис. 1.23). Область между цилиндрами заполнена диэлектриком с относительным значением диэлектрической проницаемости er=2.
Цилиндры имеют одинаковый по величине, но противоположный по знаку заряд, линейная плотность которого t1=-t2=t=10-8Кл/м.
Определить разность потенциалов между цилиндрами, емкость системы на единицу длины. Построить график изменения напряженности поля вдоль оси Х (при Y=0) между цилиндрами.
Решение.
Решение данной задачи, как и в предыдущих примерах, сводится к отысканию положения электрических осей.
Полагая, что оси проводов расположены так, что их поверхности совпадают с эквипотенциальными поверхностями электростатического поля, будем иметь:
где h1 и h2 – расстояние от геометрических осей цилиндров до плоскости постоянного (нулевого) потенциала; b – расстояние от электрических осей до этой же плоскости.
Последнее выражение можно переписать следующим образом:
Но, поскольку при расположении цилиндров один внутри другого, выполняется равенство
то
Таким образом, выражения для определения h1, h2, и b будут иметь следующий вид:
После нахождения положения электрических осей задача по расчету поля в диэлектрике между цилиндрами становится полностью аналогичной задаче по расчету поля от линейных проводов, совпадающих с электрическими осями цилиндров.
Так, потенциал любой точки М, находящейся в области между цилиндрами, будет равен
где r1 и r2 – расстояние от электрических осей первого и второго цилиндров соответственно до точки М.
Разность потенциалов между цилиндрами (между точками m и n) при этом будет равна
Здесь r1/ и r2/ – расстояние от электрических осей первого и второго цилиндров соответственно до точки m, а r1// и r2// – расстояние от электрических осей этих цилиндров до точки n.
При заданном расположении цилиндров указанные расстояния будут равны
Таким образом, разность потенциалов между цилиндрами Umn будет составлять величину, равную 67.1В.
Напряженность электрического поля в любой точке, лежащей на оси ОХ между цилиндрами (между точками m и n), находится методом наложения
График изменения данной величины вдоль оси ОХ представлен на рис. 1.24.
Для удобства изображения все величины на рисунке представлены в относительных единицах. За базисное значение напряженности поля принято значение напряженности поля на поверхности малого цилиндра в точке m (Eb =Еm=8020 В/м), а за базисное значение переменной х – абсолютное значение координаты этой же точки (хb=|хm|= 0.0183 м).
Емкость системы проводов на единицу их длины определяется с помощью следующей формулы:
Зная разность потенциалов между цилиндрами и линейную плотность зарядов t емкость С, согласно определению, можно найти и как отношение линейной плотности зарядов к разности потенциалов
Для построения силовых линий и линий равного потенциала можно воспользоваться рекомендациями, данными в предыдущих примерах.
Содержание
- Механизм возникновения скачка потенциала на границе раздела фаз. Электродный потенциал. Уравнение Нернста.
- Возникновение скачка потенциала на границе фаз
- 43 Возникновение скачка потенциала на границе раздела металл-раствор.
- Скачок потенциала на границе «металл – электролит»
Механизм возникновения скачка потенциала на границе раздела фаз. Электродный потенциал. Уравнение Нернста.



Электро́дный потенциа́л — разность электрических потенциалов между электродом и находящимся с ним в контакте электролитом (чаще всего между металлом и раствором электролита).
Возникновение электродного потенциала обусловлено переносом заряженных частиц через границу раздела фаз, специфической адсорбцией ионов, а при наличии полярных молекул (в том числе молекул растворителя) — ориентационной адсорбцией их. Величина электродного потенциала в неравновесном состоянии зависит как от природы и состава контактирующих фаз, так и от кинетических закономерностей электродных реакций на границе раздела фаз.
Равновесное значение скачка потенциалов на границе раздела электрод/раствор определяется исключительно особенностями электродной реакции и не зависит от природы электрода и адсорбции на нём поверхностно-активных веществ. Эту абсолютную разность потенциалов между точками, находящимися в двух разных фазах, нельзя измерить экспериментально или рассчитать теоретически.
В электрохимии стандартный электродный потенциал, обозначаемый E O , является мерой индивидуального потенциала обратимого электрода (в равновесии) в стандартном состоянии, которое осуществляется в растворах при эффективной концентрации в 1 моль/кг и в газах при давлении в 1 атмосферу или 100 кПа (килопаскалей). Объёмы чаще всего взяты при 25 °C. Основой для электрохимической ячейки, такой как гальваническая ячейка всегда является окислительно-восстановительная реакция, которая может быть разбита на две полуреакции: окисление на аноде (потеря электрона) и восстановление на катоде (приобретение электрона). Электричество вырабатывается вследствие различия электростатического потенциала двух электродов. Эта разность потенциалов создаётся в результате различий индивидуальных потенциалов двух металлов электродов по отношению к электролиту.
Уравнение Нернста — уравнение, связывающее окислительно-восстановительный потенциал системы с активностями веществ, входящих в электрохимическое уравнение, и стандартными электродными потенциалами окислительно-восстановительных пар.
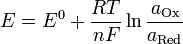
Если в формулу Нернста подставить числовые значения констант 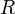
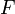
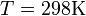
Источник
Возникновение скачка потенциала на границе фаз



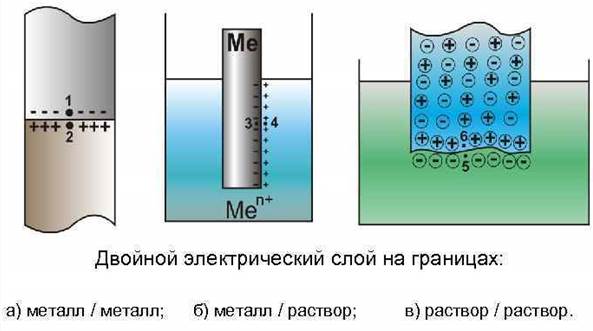
Скачки потенциала возникают на границах: 1) Ме1 – Ме2 — контактный потенциал; 2) Ме – раствор – электрохимический потенциал; 3) раствор 1 – раствор 2 – диффузионный потенциал.
Между электродом и контактирующим с ним раствором электролита возникает разность электрических потенциалов (скачок потенциала), называемая электродным потенциалом. Возникновение его связано с протеканием на границе Ме – раствор равновесных электрохимических реакций.
Причины возникновения электрохимического потенциала:
Энергию, необходимую для отрыва иона от металла, обозначим UМе, выделяющуюся при сольватации (гидратации) иона в растворе через Uсольв. Энергия UМе зависит только от природы Ме, энергия Uсольв зависит от природы ионов, их активности в растворе и от природы растворителя.
Если металлическую пластинку (электрод) опустить в раствор своей соли, то в зависимости от соотношения UМе / Uсольв возможны различные начальные электродные процессы.
а) ТД условие образования отрицательного заряда на поверхности Ме:
энергия Uсольв > UМе; хим .потенциал μ Ме > μ раствора
ион переходит из Ме в раствор, Ме заряжается отрицательно
б) ТД условие образования положительного заряда на поверхности Ме:
При условной записи электродов границу проводников I и II рода обозначают вертикальной чертой. Например, для медного электрода (медная пластина, опущенная в раствор соли меди) условная запись имеет вид:
Вертикальная линия характеризует поверхность раздела между 2-мя фазами; слева указываются ионы, находящиеся в растворе – окисленная форма; справа – электродный материал – восстановленная форма.
Измерить абсолютное значение электродного потенциала, возникающего на границе металл – раствор, невозможно, так как для подключения измерительного прибора необходим второй металлический электрод, на котором при погружении в раствор сразу же образуется свой собственный двойной электрический слой, т. е. скачок потенциала. В этом случае измеряют только относительную величину потенциала по отношению к электроду, принятому за стандарт (электрод сравнения), при этом будет измерена разность потенциалов двух электродов, называемая электродвижущей силой (ЭДС) цепи.
Таким образом, электродным потенциалом называют ЭДС электрохимической цепи, составленной из стандартного и исследуемого электрода.
Обычно в качестве электрода сравнения используют стандартный водородный электрод, потенциал которого условно принят за нуль при всех температурах. Водородный электрод представляет платиновую пластину, покрытую тончайшим порошком платины (платиновой чернью), которая опущена в раствор с активностью ионов водорода ан+ = 1 (обычно 1 М раствор H2SO4) и омывается током чистого Н2 при нормальном давлении (101325 Па).

Электрохимическая схема стандартного электрода:
На водородном электроде протекает следующая реакция:
Н + + е → ½ Н2
Условным потенциалом электрода называют ЭДС гальванического элемента, составленного из исследуемого электрода и стандартного водородного электрода при соблюдении условий:
-диффузионный потенциал отсутствует;
-водородный электрод размещается слева, исследуемый – справа;
-полурекция на исследуемом электроде записывается как реакция восстановления (такая реакция называемая потенциалопределяющей).
Условный потенциал электрода называют стандартным условным потенциалом, если активности всех участников электродной полурекции равны единице.
Значения стандартных электродных потенциалов (Е о ) являются константой, свойственной каждому электроду, и приведено в справочных таблицах физико-химических величин при 25°С.
Относительно потенциала стандартного водородного электрода, принятого за нуль, все стандартные потенциалы металлических электродов будут или положительнее, или отрицательнее его.
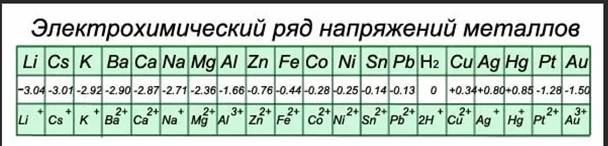
Если расположить Ме в порядке возрастания значений их стандартных потенциалов, то получится ряд стандартных электродных потенциалов, или электрохимический ряд напряжений:
На практике водородный электрод используется редко, вместо него используют другие электроды сравнения,потенциалы которых предварительно точно определяют относительно водородного электрода.
Источник
43 Возникновение скачка потенциала на границе раздела металл-раствор.
Если пластину любого металла погрузить в воду или раствор электролита, содержащий ионы этого металла, то небольшая часть металла перейдет в раствор, в форме положительно заряженных ионов, а сама пластина , концентрируя на себе избыток свободных электронов , приобретает отрицательный заряд. Такому переходу содействует связывание ионов металла с молекулами воды (растворителя).В итоге устанавливается равновесие
Me 2+ + m H2O ↔ Me 2+ · m H2O
Me + m H2O ↔ Me 2+ · m H2O +2e
Положительно заряженные ионы Me +2 , перешедшие в раствор, концентрируются у поверхности пластины, приобретающей отрицательный заряд, в результате возникает двойной электрический слой (ДЭС) , обусловливающий резкий скачок электрического потенциала на границе металл — раствор электролита.
Эту разность электрических потенциалов или скачок потенциала на границе металл-раствор электролита называют электродным потенциалом.
Величина электродного потенциала зависит от природы металла, концентрации, точнее активности ионов металла в растворе и температуры.
Математически эта зависимость выражается уравнением В.Г.Нернста (1888).
а в случае разбавленных растворов полностью диссоциирующих солей данного металла
где E 0 Me— стандартный электродный потенциал
R- универсальная газовая постоянная
F- постоянная Фарадея
n — заряд иона металла
аMe, n + , [ Me n + ] – активность или концентрация ионов металла (мольл)
После перехода от натурального логарифма к десятичному и подстановки значений
44 Возникновение скачка потенциала на границе раздела фаз вызывается различными причинами, зависящими от природы граничащих фаз. Металлы, имеющие отрицательные значения электродных потенциалов , стоящие левее водорода, способны его вытеснять из разбавленных растворов кислот. Чем меньше электродный потенциал металла Е 0 ,тем легче он окисляется и труднее восстанавливается из своих ионов. Чем меньше алгебраическая величина потенциала, тем выше восстановительная способность этого металла и тем ниже окислительная способность его ионов (в ряду стандартных электродных потенциалов).
Электрохимический ряд активности (ряд напряжений, ряд стандартных электродных потенциалов) металлов — последовательность, в которой металлы расположены в порядке увеличения их стандартных электрохимических потенциалов, отвечающих полуреакции восстановления катиона металла Me n+ : Me n+ + nē → Me.
Металлы, потенциал к-рых менее положительный, чем у кислородного электрода, термодинамически неустойчивы в контакте с О2 (или воздухом) и водой. Поэтому электрохимический ряд напряжений служит для ориентировочных оценок скорости электрохим. коррозии в водных р-рах при обычных температурах, а также для выбора безопасных контактных пар (гальванич. пар) разнородных металлов. Если металл электроотрицательнее, чем Н2, то может идти активный коррозионный процесс.
Ряд напряжений характеризует сравнительную активность металлов в окислительно-восстановительных реакцияхв водных растворах.
Источник
Рассмотрим систему, состоящую из металлического электрода, погруженного в раствор, содержащий катионы того же металла (раствор соли). Если металл находится в контакте, например, с водным раствором электролита небольшой концентрации, то на границе раздела фаз «металл – электролит» протекают следующие процессы (рис.8.2).
1. В результате физико-химического взаимодействия между диполями воды и поверхностными ионами металла происходит его растворение. Особенности химической связи в металлах приводят к тому, что в раствор переходят только ионы металла, а электроны остаются в кристалле. В результате электрод приобретает избыточный отрицательный, а раствор – избыточный положительный заряды.
Рис. 8‑2 Схема возникновения обменного двойного электрического слоя на границе «металл – раствор электролита»
Самопроизвольное протекание этого процесса обусловлено как энтальпийным, так и энтропийным факторами. Переход ионов металла из кристалла в раствор приводит к уменьшению энтальпии системы(DH 0) вследствие разупорядочивания системы. Этот процесс можно записать как реакцию окисления металла:
2. Наличие катионов металла в растворе и отрицательный заряд электрода за счет избыточных электронов обусловливает протекание обратного процесса: катионы металла переходят из раствора на поверхность электрода. При этом они теряют свою гидратную оболочку и встраиваются в кристаллическую решетку, что приводит к уменьшению величин отрицательного заряда электрода и положительного заряда раствора. Этот процесс можно записать как реакцию восстановления металла:
В результате протекания этих процессов система придет в состояние равновесия. Скорости первого и второго процессов будут равны:
При этом потенциал электрода и концентрация катионов в растворе сохранят постоянное равновесное значение.
Необходимо отметить, что концентрация катионов металла в растворе будет различной в зависимости от расстояния до поверхности электрода (рис.7.3). Максимальным ее значение будет непосредственно у поверхности электрода (C 0 ). За счет процесса диффузии ионы металла будут двигаться от поверхности электрода в объем раствора, при этом их концентрация уменьшится до величины C в глубине раствора. Таким образом, в состоянии равновесия установится постоянный градиент концентрации катионов.
Примечание. С точки зрения термодинамики, в состоянии равновесия энергия (химический потенциал) поверхностных атомов металла равна энергии (химическому потенциалу) гидратированных ионов металла в растворе.
На границе «электрод – электролит» возникает обменный двойной электрический слой, образованный с одной стороны избыточными электронами в электроде, а с другой – избыточными положительными ионами металла в растворе (противоионами). Он рассматривается как единая электронейтральная система: заряд электрода равен сумме зарядов противоионов.
Поскольку существует разделение зарядов в пространстве, то между металлом и раствором возникает разность потенциалов j. Говорят, что при контакте металла с электролитом на границе раздела возникает скачок электрического потенциала – электродный потенциал.
Ионы металла, образующие двойной электрический слой, распределены в растворе следующим образом (рис.8.3).
1. Часть ионов располагается на расстоянии порядка радиуса гидратированного иона от поверхности металла, образуя плотный слой, толщина которого составляет величину dп
10 –10 м. Концентрация ионов металла в нем равна C 0 , падение потенциала (jп) происходит линейно.
Рис. 8‑3 Распределение концентрации ионов Ме n + (а) и потенциала (б) в ионной части двойного электрического слоя: а) – изменение концентрации ионов Ме n + в электролите в зависимости от расстояния до электрода; C 0 – концентрация в плотном слое; C – концентрация в объеме электролита; б) –изменение электродного потенциала в зависимости от расстояния до электрода; jп – падение потенциала в плотном слое, jд – падение потенциала в диффузном слое; dп – толщина плотного слоя; dд – толщина диффузного слоя
2. Другая часть ионов за счет диффузии перемещается в глубь раствора, образуя диффузный слой. Концентрация ионов уменьшается от C 0 до величины концентрации ионов металла в электролите C. Толщина диффузного слоя зависит от концентрации ионов металла в электролите и составляет величину порядка dд
10 –9 ÷10 –5 м. Падение потенциала в диффузном слое (jд) происходит нелинейно. С увеличением концентрации катионов в электролите диффузия уменьшается, соответственно уменьшается и толщина диффузного слоя. В растворах с концентрацией 0,1 ÷ 1,0 моль/л он практически отсутствует.
Очевидно, что величина скачка потенциала на границе раздела «металл – электролит» (j) равна сумме величин падения потенциала в плотном (jп) и диффузном (jд) слоях двойного электрического слоя.
Примечание. При большой концентрации ионов металла в растворе, малой энергии их гидратации, большой работе выхода ионов из металла, а также адсорбции на электродах поверхностно-активных ионов и молекул, которые могут содержаться в электролите, система придет в равновесие при преобладании перехода ионов металла из раствора на электрод. В этом случае двойной электрический слой и скачок потенциала соответственно образуют катионы, адсорбированные на металле и избыточные анионы в растворе.
Электродный потенциал возникает и в случае, если металл находится в контакте с неводным раствором электролита. Поскольку равновесие зависит от энергии сольватации иона металла, то величина потенциала будет зависеть от природы растворителя.
Уравнение Нернста
При определении величины электродного потенциала и его зависимости от внешних условий могут быть использованы как термодинамические, так и кинетические модели.
Определить величину электродного потенциала можно, рассмотрев термодинамические условия равновесия системы «металл – раствор электролита», содержащего катионы того же металла. В этом случае в системе протекает обратимая реакция:
При ее записи обычно молекулы воды не указывают, не забывая, что они играют здесь основную роль:
На границе раздела «металл – электролит» образуется двойной электрический слой и возникает скачок потенциала.
Изменение свободной энергии Гиббса в состоянии равновесия (DG=0) будет равно изменению энергии Гиббса химической реакции (DrG) плюс работа электрических сил по переносу ионов (Me n+ ) через двойной электрический слой:
Работа, осуществляемая по переносу одного моля положительно заряженных ионов через двойной электрический слой, равна:
где j – электродный потенциал [В]; NA = 6,02×10 23 [моль -1 ] – число Авогадро; ē = 1,6×10 -19 [Кл] – заряд электрона; n – заряд иона (в единичных электрических зарядах); F = ē×NA » 96500 Кл/моль – число Фарадея.
Следовательно, изменение энергии Гиббса при образовании двойного электрического слоя равно:
При изобарно-изотермическом процессе Me n+ + nē ↔Me 0 изменение энергии Гиббса, согласно уравнению изотермы реакции, равно:
DrG = 

здесь R = 8,314 Дж/моль×К – универсальная газовая постоянная; Т – температура, К; Кр – константа равновесия реакции, 
— n×F×j = 

В стандартных условиях при Т = 298 К и 

Зависимость электродного потенциала от температуры и концентрации катионов металла в растворе имеет вид
j = j 0 + 
Это уравнение получило название уравнение Нернста (Nernst) для электродного потенциала.
1. В общем случае для электродной реакции Ox + nē ↔Red уравнение Нернста записывается как

2. Для точных расчетов электродных потенциалов в уравнении Нернста вместо концентрации ионов (Ci) в растворах электролитов необходимо использовать их активность (ai). В общем случае 

Определить величину электродного потенциала можно также из кинетической модели образования двойного электрического слоя.
При контакте металла с электролитом двойной электрический слой и соответственно электродный потенциал возникают в результате протекания двух процессов: перехода ионов металла из кристалла в раствор –Me 0 +xH2O®Me n + (H2O)x+nē – реакция окисления и перехода катионов из раствора на поверхность электрода – Me n + (H2O)x+nē®Me 0 +xH2O — реакция восстановления. В состояние равновесия система придет при выравнивании скоростей этих процессов (см. кинетическое условие равновесия). В результате установившегося равновесия реакции
на границе «электрод – электролит» возникнет электродный потенциал j.
Скорости реакций восстановления и окисления, согласно закону действующих масс, будут зависеть от концентрации реагирующих веществ. Для прямой реакции (восстановление ионов металла) скорость пропорциональна их концентрации в растворе: 




Величины энергий активации можно оценить, рассмотрев энергетическую диаграмму процесса Me n + (H2O)x + nē ↔ Me 0 + xH2O (рис.8-4).
Представим реакцию восстановления как процесс дегидратации иона металла (образование свободного иона) и последующее встраивание его в кристаллическую решетку металла. Реакцию окисления представим как два последовательных процесса: выход иона металла (Me n + ) из кристаллической решетки электрода в вакуум и его гидратация с образованием в растворе иона Me n + (H2O)x.
Рис. 8‑4 Энергетическая диаграмма процесса Me n+ (H2O)x + nē ↔ Me 0 + xH2O
Пусть E – энергия свободного иона металла в вакууме; EM – энергия поверхностного атома металла; Eaq – энергия гидратированного иона металла в растворе. В состоянии равновесия, в результате возникновения скачка потенциала на границе «электрод – электролит», энергия поверхностного иона металла изменяется на величину DE = n·F·j. На рис.7-4 показано изменение энергии поверхностных ионов при концентрации катионов в электролите меньше равновесной.
Из энергетической диаграммы видно, что для перехода в раствор ион металла должен обладать энергией, равной 

В состоянии равновесия скорости прямой и обратной реакций будут равны: 

Если предположить, что предэкспоненциальные множители для прямой и обратной реакций имеют величину одного порядка 


где 
Из кинетической модели следует, что стандартный электродный потенциал главным образом определяется соотношением энергии гидратированного иона металла в растворе и энергии поверхностного атома металла электрода.
Электроды
Из уравнения Нернста следует, что потенциал электрода при данной температуре определяется стандартным электродным потенциалом (j 0 ) и концентрацией (активностью) ионов, участвующих в реакции. В зависимости от особенностей электродных реакций различают несколько типов электродов.
Электроды первого рода. К электродам первого рода относятся металлические электроды, находящиеся в контакте с раствором, содержащим катионы этого же металла. Схематически электрод первого рода можно представить как Me n + |Me 0 . Электродная реакция, протекающая на нем:
Потенциал электрода первого рода зависит от концентрации ионов металла, которые являются потенциалопределяющими:

Пример. 1. Медный электрод погружен в раствор сульфата меди Cu 2+ |Cu 0 :
электродная реакция Cu 2+ + 2ē Û Cu 0 ;
электродный потенциал 
2. Серебряный электрод погружен в раствор нитрата серебра Ag + |Ag 0 : электродная реакция Ag + + ē ↔ Ag 0 ,
электродный потенциал
Электроды первого рода являются обратимыми: изменение направления тока в цепи изменяет лишь направление реакцииMe n + + nē ↔ Me 0 , не изменяя саму реакцию:
(Me n + + nē ® Me 0 – процесс восстановления;
Me 0 ® Me n + + nē – процесс окисления).
Примечание. Существуют электроды первого рода, обратимые относительно аниона, например,Se 2- |Se 0 :
электродная реакция Se 0 +2ē ↔ Se 2-
электродный потенциал 
Электроды второго рода. К электродам второго рода относятся металлические электроды, покрытые слоем труднорастворимого соединения этого же металла (MeAn), находящиеся в контакте с электролитом, содержащим такие же анионы (An n- ).
Схематически электрод можно представить как
Электродная реакция, протекающая на нем:
MeAn+ nē ↔ Me 0 + An n —
Потенциал электрода второго рода определяется равновесием двух процессов:
1. Равновесие «труднорастворимое соединение – раствор электролита», которое определяет концентрацию иона металла:
MeAn↔ Me n + + An n — ; 
где ПР – произведение растворимости труднорастворимого соединения MeAn.
2. Равновесие «металл — катион металла» Me n + + nē ↔ Me 0 , которое определяет возникновение электродного потенциала:

Потенциал электрода будет определяться суммарным уравнением MeAn+ nē ↔ Me 0 + An n — :



Таким образом, потенциал электрода второго рода зависит от концентрации аниона (потенциалопределяющий ионAn n — ):

где 

Пример. Хлорсеребряный электрод AgCl,Ag 0 | Cl — .
Металлический серебряный электрод, на поверхность которого нанесен тонкий слой труднорастворимой соли хлорида серебра (ПРAgCl=1,8×10 -10 ), контактирует с раствором сильного электролита хлорида калия (КCl ® К + + Cl — ) (рис. 8.5).
Рис. 8‑5 Схема хлорсеребряного электрода
AgCl + ē ↔ Ag 0 + Cl —

Газовые электроды. Газовый электрод представляет собой металлический проводник, на поверхности которого адсорбированы молекулы газа, который находится в контакте с электролитом, содержащим ионы этого же газа. В системе устанавливается равновесие между молекулами газа, находящимися на поверхности металлического электрода, и ионами этого газа в электролите. Металлический проводник служит только для передачи электронов между внешней цепью и раствором (создает электропроводящий контакт между газом и раствором). При этом материал электрода не должен участвовать в электрохимическом равновесии. Как правило, такими материалами являются металлы платиновой группы, в частности сама платина. Они не принимают непосредственного участия в реакциях с раствором и в то же время, являясь гетерогенными катализаторами, ускоряют установление электродного равновесия.
Наиболее важными с практической точки зрения являются водородный и кислородный электроды.
1. Водородный электрод (2H + |H2 0 ,Pt) представляет собой платиновый электрод, помещенный в раствор, содержащий ионы водорода (раствор серной кислоты), через который пропускают газообразный водород (рис. 8.6).
На границе раздела «платина – раствор серной кислоты» устанавливается равновесие 2H + + 2ē ↔ H2, и возникает электродный потенциал, величина которого зависит от относительного парциального давления газа и концентрации ионов водорода:
Рис. 8‑6 Схема водородного электрода
При стандартном давлении газообразного водорода (р 0 =1,013×10 5 Па) электродный потенциал водородного электрода зависит только от концентрации ионов водорода: 


где 
Потенциал водородного электрода в стандартных условиях (стандартный водородный электрод) условно принимается равным нулю: 
В случае нейтрального и щелочного электролита (pH ³7) уравнение реакции электродного процесса водородного электрода записывается как
2. Кислородный электрод (OH — |O2,Pt). Если в устройстве, схема которого приведена на рис.7.6, вместо водорода пропускать газообразный кислород (О2), а в качестве электролита использовать не кислоту, а раствор щелочи, то на границе раздела «платина – электролит» устанавливается равновесие: О2 + 2H2O + 4ē ↔ 4OH — . Величина электродного потенциала в данном случае зависит от относительного парциального давления кислорода и концентрации гидроксо-ионов:

При стандартных условиях потенциал кислородного электрода зависит только от концентрации ионов OH — . Эту зависимость представляют обычно как зависимость потенциала от pH раствора ( 

В случае электролита с pH + + 4ē ↔ 2H2O
Примечание. Необходимо отметить, что при электролизе и электрохимической коррозии металлов могут образовываться воородный и кислородный газовые электроды.
Окислительно-восстановительные электроды (редокс-электроды). В рассмотренных до сих пор типах электродов одной из форм веществ, между которыми за счет реакции Ox + nē ↔ Red возникает потенциал, является материал электрода или вещество, адсорбированное поверхностью электрода. Металлический электрод, контактирующий с электролитом, содержащим одновременно как окисленную (Ox), так и восстановленную (Red) форму вещества, называется окислительно-восстановительным или редокс-электродом.
Материалы, используемые в редокс-электродах, должны удовлетворять требованиям, рассмотренным для газовых электродов. Таким материалом является, например, платина.
Схематически такой электрод можно представить как Ox,Red|Pt. Электродная реакция, протекающая на поверхности платины, Ox + nē ↔ Red.
В состоянии равновесия потенциал электрода определяется соотношением концентраций окисленной и восстановленной формы вещества в электролите:

Этот потенциал называется равновесным редокс-потенциалом окислительно-восстановительной системы.
Пример1. Простые окислительно-восстановительные системы.
В растворе, контактирующем с платиновым электродом, одновременно находятся катионы олова Sn 2+ и Sn 4+ (например, раствор хлоридов олова SnCl2 и SnCl4) − Sn 4+ ,Sn 2+ |Pt. В результате реакции Sn 4+ + 2ē ↔ Sn 2+ устанавливается равновесие. Редокс-потенциал будет равен:

Пример 2. Сложные окислительно-восстановительные системы. В электродной реакции принимают участие молекулы воды, ионы H + или OH — . Например, для системы Cr2O7 2- ,Cr 3+ ,H + |Pt реакция, за счет которой возникает электродный потенциал, может быть представлена в виде
где Cr2O7 2- – окисленная, а Cr 3+ – восстановленная формы вещества.
Редокс-потенциал будет равен:

Из уравнения видно, что редокс-потенциал сложной окислительно-восстановительной системы зависит не только от соотношения концентраций окисленной и восстановленной форм вещества, но и от концентрации ионов водорода (рН раствора).

Рис. 8‑7 Схема стеклянного электрода
Материал мембраны обменивается своими ионами с ионами внутреннего и внешнего растворов электролитов. В результате этого процесса поверхность мембраны и раствор приобретают электрические заряды противоположного знака – возникает скачок потенциала. Как правило, преимущественно происходит обмен ионами одного вида, поэтому эти электроды называют ионоселективными.
В состоянии равновесия величина электродного потенциала линейно зависит от концентрации ионов во внешнем растворе. Это позволяет использовать данные электроды для определения концентрации ионов в анализируемом растворе. В настоящее время созданы ионселективные электроды для нескольких десятков катионов и анионов. Важнейшим из них является стеклянный электрод (рис. 8.7). Его потенциал зависит от концентрации ионов водорода: j =j 0 + А×рН, где А – const, поэтому он используется для определения рН растворов.
Определение концентрации ионов водорода (рН анализируемого раствора) сводится к измерению разности потенциалов между стеклянным электродом и электродом сравнения, погруженными в анализируемый раствор. В качестве электрода сравнения используют электроды, потенциал которых не зависит от концентрации ионов водорода, например хлорсеребряный электрод. В этом случае величина измеряемой разности потенциалов пропорциональна рН анализируемого раствора.
Способов экспериментального определения и расчета абсолютных величин электродных потенциалов не существует. С достаточной степенью точности можно измерить разность потенциалов Dj между двумя электродами в электрохимической системе. Если равновесие в такой системе достигнуто в стандартных условиях: активность (концентрация) потенциалопределяющих ионов 1 моль/л; температура Т 0 =298 К; давление газов р 0 =1,013×10 5 Па; ток во внешней цепи I=0 А, то измеряемая Dj равна разности между стандартными электродными потенциалами: Dj= j 0 1-j 0 2.
Если один из электродов принять в качестве электрода сравнения, стандартный потенциал которого условно считать равным нулю, то измеренная разность потенциалов будет являться потенциалом второго электрода относительно первого. В качестве электрода сравнения часто используют стандартный водородный электрод.
В рассматриваемой паре электродов потенциал стандартного водородного электрода может быть как больше, так и меньше стандартного потенциала измеряемого. Например, для электродов первого рода электрохимические могут быть записаны как
Таким образом, потенциал измеряемого электрода относительно водородного может быть отрицательным: 

Измеренные относительно водородного электрода величины стандартных электродных потенциалов сведены в таблицу в порядке их возрастания (см. пример). Такую последовательность называют рядом стандартных электродных потенциалов окислительно-восстановительных систем. Из общего ряда выделяют последовательность для электродов первого рода – металлы, находящиеся в контакте с раствором, содержащим катион этого же металла (Me n + |Me 0 ). Она называется электрохимическим рядом напряжений металлов.
Пример. Стандартные электродные потенциалы (j 0 , В) и их электродные реакции. Жирным шрифтом выделены электроды первого рода.
| Электрод | Электродная реакция | j 0 , В | |
| Li + |Li 0 | Li + + ē ↔ Li 0 | -3,02 | |
| K + |K 0 | K + + ē ↔ K 0 | -2,92 | |
| Ca 2+ |Ca 0 | Ca 2+ + 2ē ↔ Ca 0 | -2,87 | |
| Na + |Na 0 | Na + + ē ↔ Na 0 | -2,71 | |
| Mg 2+ |Mg 0 | Mg 2+ + 2ē ↔ Mg 0 | -2,34 | |
| Al 3+ |Al 0 | Al 3+ + 3ē ↔ Al 0 | -1,67 | |
| Zn 2+ |Zn 0 | Zn 2+ + 2ē ↔ Zn 0 | -0,76 | |
| Cr 3+ |Cr 0 | Cr 3+ + 3ē ↔ Cr 0 | -0,74 | |
| Cr 3+ ,Cr 2+ |Pt | Cr 3+ + ē ↔ Cr 2+ pH £ 7 | -0,41 | |
| Fe 2+ |Fe 0 | Fe 2+ + 2ē ↔ Fe 0 | -0,44 | |
| Cd 2+ |Cd 0 | Cd 2+ + 2ē ↔ Cd 0 | -0,40 | |
| Ni 2+ |Ni 0 | Ni 2+ + 2ē ↔ Ni 0 | -0,25 | |
| Sn 2+ |Sn 0 | Sn 2+ + 2ē ↔ Sn 0 | -0,14 | |
| Pb 2+ |Pb 0 | Pb 2+ + 2ē ↔ Pb 0 | -0,13 | |
| Fe 3+ |Fe 0 | Fe 3+ + 3ē ↔ Fe 0 | -0,04 | |
| 2H + |H2 0 ,Pt | 2H + + 2ē↔H2 | 0,00 | |
| Sn 4+ ,Sn 2+ |Pt | Sn 4+ + 2ē ↔ Sn 2+ pH £ 7 | +0,15 | |
| Cl — |AgCl,Ag 0 | AgCl + ē ↔ Ag 0 + Cl — pH
7 |
+0,22 | |
| Cu 2+ |Cu 0 | Cu 2+ + 2ē ↔ Cu 0 | +0,34 | |
| OH — |O2,Pt | О2 + 2H2O + 4ē ↔ 4OH — pH ³ 7 | +0,40 | |
| Fe 3+ ,Fe 2+ |Pt | Fe 3+ + ē ↔ Fe 2+ pH £ 7 | +0,77 | |
| NO3 — ,NO2,H + |Pt | NO3 — + 2H + + ē ↔ NO2 + H2O | +0,80 | |
| Ag + |Ag 0 | Ag + + ē ↔ Ag 0 | +0,80 | |
| Hg 2+ |Hg 0 (ж) | Hg 2+ + 2ē ↔ Hg 0 | +0,85 | |
| NO3 — ,NH4 + ,H + |Pt | NO3 — + 10H + + 8ē ↔ NH4 + + 3H2O | +0,87 | |
| Cr2O7 2- ,Cr 3+ ,H + |Pt | Cr2O7 2+ + 14H + + 6ē ↔ 2Cr 3+ + 7H2O pH — | Cl2 0 ,Pt | 2 Cl — + 2ē ↔ Cl 2 | +1,36 |
| Au 3+ |Au 0 | Au 3+ + 3ē ↔ Au 0 | +1,50 | |
| Au + |Au 0 | Au + + ē ↔ Au 0 | +1,69 | |
| PbO2,H + ,SO4 2- ,PbSO4|Pt | PbO2+4H + +SO4 2- +2ē↔PbSO4 + 2H2O pH 3+ ,Co 2+ |Pt | Co 3+ + ē ↔ Co 2+ pH £ 7 | +1,81 |
| S2O8 2- ,SO4 2- |Pt | S2O8 2- + 2ē ↔ 2SO4 2- pH
7 |
+2,01 | |
| 2F — |F2 0 ,Pt | 2 F — + 2ē ↔ F2 pH ³ 7 | +2,87 |
Величина стандартного электродного потенциала j 0 электрода первого рода является мерой восстановительной способности атома металла и окислительной способности его иона. Чем она меньше, тем легче атом отдает электроны, соответственно металл обладает более высокой восстановительной способностью. Чем она больше, тем легче ион принимает электроны, являясь более сильным окислителем.
Эти же закономерности относятся к редокс-электродам. Чем отрицательнее потенциал, тем более сильным восстановителем является восстановленная (Red) форма вещества. И, наоборот, с увеличением потенциала возрастает окислительная способность окисленной формы (Ox).
Источник
…
Электродные потенциалы. ЭДС реакции
Окислительно — восстановительный потенциал является частным, узким случаем понятия электродного потенциала. Рассмотрим подробнее эти понятия.
В ОВР передача электронов восстановителями окислителям происходит при непосредственном контакте частиц, и энергия химической реакции переходит в теплоту.
Энергия любой ОВР, протекающей в растворе электролита, может быть превращена в электрическую энергию, если, например, окислительно-восстановительные процессы разделить пространственно, т.е. передача электронов восстановителем будет происходить через проводник электричества.
Это реализовано в гальванических элементах, где электрическая энергия получается из химической энергии окислительно-восстановительной реакции.
Элемент Даниэля-Якоби
Рассмотрим гальванический элемент Даниэля-Якоби, в котором левый сосуд наполнен раствором сульфата цинка ZnSO4, с опущенной в него цинковой пластинкой, а правый сосуд – раствором сульфата меди CuSO4, с опущенным в него медной пластинкой.
Взаимодействие между раствором и пластиной, которая выступает в качестве электрода, способствует тому, чтобы электрод приобрел электрический заряд.
Возникающая на границе металл-раствор электролита разность потенциалов, называется электродным потенциалом. Значение и знак (+ или -) электродного потенциала определяются природой раствора и находящегося в нем металла.
При погружении металлов в растворы их солей более активные из них (Zn, Fe и др.) заряжаются отрицательно, а менее активные (Cu, Ag, Au и др.) положительно.
Результатом соединения цинковой и медной пластинки проводником электричества, является возникновение в цепи электрического тока за счет перетекания электронов с цинковой к медной пластинке по проводнику.
При этом происходит уменьшение количества электронов в цинке, что компенсируется переходом Zn2+ в раствор т.е. происходит растворение цинкового электрода — анода (процесс окисления).
Zn — 2e— = Zn2+
В свою очередь, рост количества электронов в меди компенсируется разряжением ионов меди, содержащихся в растворе, что приводит к накоплению меди на медном электроде – катоде (процесс восстановления):
Cu2+ + 2e— = Cu
Таким образом, в элементе Даниэля-Якоби происходит такая реакция:
Zn + Cu2+ = Zn2+ + Cu
Zn + CuSO4 = ZnSO4 + Cu
Количественно охарактеризовать окислительно-восстановительные процессы позволяют электродные потенциалы, измеренные относительно нормального водородного электрода (его потенциал принят равным нулю).
Чтобы определить стандартные электродные потенциалы используют элемент, одним из электродов которого является испытуемый металл (или неметалл), а другим является водородный электрод. По найденной разности потенциалов на полюсах элемента определяют нормальный потенциал исследуемого металла.
Окислительно-восстановительный потенциал
Значениями окислительно-восстановительного потенциала пользуются в случае необходимости определения направления протекания реакции в водных или других растворах.
Проведем реакцию
2Fe3+ + 2I— = 2Fe2+ + I2
таким образом, чтобы йодид-ионы и ионы железа обменивались своими электронами через проводник.
В сосуды, содержащие растворы Fe3+ и I—, поместим инертные (платиновые или угольные) электроды и замкнем внутреннюю и внешнюю цепь. В цепи возникает электрический ток.
Йодид-ионы отдают свои электроны, которые будут перетекать по проводнику к инертному электроду, погруженному в раствор соли Fe3+:
2I— — 2e— = I2
2Fe3+ + 2e— = 2Fe2+
Процессы окисления-восстановления происходят у поверхности инертных электродов. Потенциал, который возникает на границе инертный электрод – раствор и содержит как окисленную, так восстановленную форму вещества, называется равновесным окислительно-восстановительным потенциалом.
Факторы, влияющие на значение окислительно-восстановительного потенциала
Значение окислительно-восстановительного потенциала зависит от многих факторов, в том числе и таких как:
1) Природа вещества (окислителя и восстановителя)
2) Концентрация окисленной и восстановленной форм.
При температуре 25°С и давлении 1 атм. величину окислительно-восстановительного потенциала рассчитывают с помощью уравнения Нернста:
E = E° + (RT/nF)ln(Cок/Cвос), где
E – окислительно-восстановительный потенциал данной пары;
E°- стандартный потенциал (измеренный при Cок = Cвос);
R – газовая постоянная (R = 8,314 Дж);
T – абсолютная температура, К
n – количество отдаваемых или получаемых электронов в окислительно-восстановительном процессе;
F – постоянная Фарадея (F = 96484,56 Кл/моль);
Cок – концентрация (активность) окисленной формы;
Cвос– концентрация (активность) восстановленной формы.
Подставляя в уравнение известные данные и перейдя к десятичному логарифму, получим следующий вид уравнения:
E = E° + (0,059/n)lg(Cок/Cвос)
При Cок > Cвос, E > E° и наоборот, если Cок < Cвос, то E < E°
3) Кислотность раствора
Для пар, окисленная форма которых содержит кислород (например, Cr2O72-, CrO42-, MnO4—) при уменьшении pH раствора окислительно-восстановительный потенциал возрастает, т.е. потенциал растет с ростом H+. И наоборот, окислительно-восстановительный потенциал падает с уменьшением H+.
4) Температура
При увеличении температуры окислительно-восстановительный потенциал данной пары также растет.
Стандартные окислительно-восстановительные потенциалы представлены в таблицах специальных справочников. Следует иметь ввиду, что рассматриваются только реакции в водных растворах при температуре ≈ 25°С.
Такие таблицы дают возможность сделать некоторые выводы:
Что можно определить по значению окислительно-восстановительного потенциала
- Величина и знак стандартных окислительно-восстановительных потенциалов, позволяют предсказать какие свойства (окислительные или восстановительные) будут проявлять атомы, ионы или молекулы в химических реакциях, например
E°(F2/2F—) = +2,87 В – сильнейший окислитель
E°(K+/K) = — 2,924 В – сильнейший восстановитель
Окислительно-восстановительная пара будет обладать тем большей восстановительной способностью, чем больше числовое значение ее отрицательного потенциала, а окислительная способность тем выше, чем больше положительный потенциал.
- Возможно определить какое из соединений одного элемента будет обладать наиболее сильным окислительными или восстановительными свойствами.
- Возможно предсказать направление ОВР. Известно, что работа гальванического элемента имеет место при условии, что разность потенциалов имеет положительное значение. Протекание ОВР в выбранном направлении также возможно, если разность потенциалов имеет положительное значение. ОВР протекает в сторону более слабых окислителей и восстановителей из более сильных, например, реакция
Sn2+ + 2Fe3+ = Sn4+ + 2Fe2+
практически протекает в прямом направлении, т.к.
E° (Sn4+/Sn2+) = +0,15 В,
E° (Fe3+/Fe2+) = +0,77 В,
т.е. E° (Sn4+/Sn2+) < E° (Fe3+/Fe2+).
Реакция
Cu + Fe2+ = Cu2+ + Fe
невозможна в прямом направлении и протекает только справа налево, т.к.
E° (Сu2+/Cu) = +0,34 В,
E° (Fe2+/Fe) = — 0,44 В,
E° (Fe2+/Fe) < E° (Сu2+/Cu).
В процессе ОВР количество начальных веществ уменьшается, вследствие чего Е окислителя падает, а E восстановителя возрастает. При окончании реакции, т.е. при наступлении химического равновесия потенциалы обоих процессов выравниваются.
- Если при данных условиях возможно протекание нескольких ОВР, то в первую очередь будет протекать та реакция, у которой разность окислительно-восстановительных потенциалов наибольшая.
- Пользуясь справочными данными, можно определить ЭДС реакции.
Как определить электродвижущую силу (ЭДС) реакции?
Рассмотрим несколько примеров реакций и определим их ЭДС:
- Mg + Fe2+ = Mg2+ + Fe
- Mg + 2H+ = Mg2+ + H2
- Mg + Cu2+ = Mg2+ + Cu
E° (Mg2+/Mg) = — 2,36 В
E° (2H+/H2) = 0,00 В
E° (Cu2+/Cu) = +0,34 В
E° (Fe2+/Fe) = — 0,44 В
Чтобы определить ЭДС реакции, нужно найти разность потенциала окислителя и потенциала восстановителя
ЭДС = Е0ок — Е0восст
- ЭДС = — 0,44 — (- 2,36) = 1,92 В
- ЭДС = 0,00 — (- 2,36) = 2,36 В
- ЭДС = + 0,34 — (- 2,36) = 2,70 В
Все вышеуказанные реакции могут протекать в прямом направлении, т.к. их ЭДС > 0.
Связь константы равновесия и окислительно — восстановительного потенциала
Если возникает необходимость определения степени протекания реакции, то можно воспользоваться константой равновесия.
Например, для реакции
Zn + Cu2+ = Zn2+ + Cu
Применяя закон действующих масс, можно записать
K = CZn2+/CCu2+
Здесь константа равновесия К показывает равновесное соотношение концентраций ионов цинка и меди.
Значение константы равновесия можно вычислить, применив уравнение Нернста
E = E° + (0,059/n)lg(Cок/Cвос)
Подставим в уравнение значения стандартных потенциалов пар Zn/Zn2+ и Cu/Cu2+, находим
E0Zn/Zn2+ = -0,76 + (0,59/2)lgCZn/Zn2+
E0Cu/Cu2+ = +0,34 + (0,59/2)lgCCu/Cu2+
В состоянии равновесия E0Zn/Zn2+ = E0Cu/Cu2+, т.е.
-0,76 + (0,59/2)lgCZn2+ = +0,34 + (0,59/2)lgCCu2+, откуда получаем
(0,59/2)( lgCZn2 — lgCCu2+) = 0,34 – (-0,76)
lgK = lg (CZn2+/CCu2+) = 2(0,34 – (-0,76))/0,059 = 37,7
K = 1037,7
Значение константы равновесия показывает, что реакция идет практически до конца, т.е. до того момента, пока концентрация ионов меди не станет в 1037,7 раз меньше, чем концентрация ионов цинка.
Константа равновесия и окислительно-восстановительный потенциал связаны общей формулой:
lgK = (E10 -E20 )n/0,059, где
K — константа равновесия
E10 и E20 – стандартные потенциалы окислителя и восстановителя соответственно
n – число электронов, отдаваемых восстановителем или принимаемых окислителем.
Если E10 > E20, то lgK > 0 и K > 1.
Следовательно, реакция протекает в прямом направлении (слева направо) и если разность (E10 — E20) достаточно велика, то она идет практически до конца.
Напротив, если E10 < E20, то K будет очень мала.
Реакция протекает в обратном направлении, т.к. равновесие сильно смещено влево. Если разность (E10 — E20) незначительна, то и K ≈ 1 и данная реакция не идет до конца, если не создать необходимых для этого условий.
Зная значение константы равновесия, не прибегая к опытным данным, можно судить о глубине протекания химической реакции. Следует иметь ввиду, что данные значений стандартных потенциалов не позволяют определить скорость установления равновесия реакции.
По данным таблиц окислительно-восстановительных потенциалов возможно найти значения констант равновесия примерно для 85000 реакций.
Как составить схему гальванического элемента?
Приведем рекомендации ИЮПАК, которыми следует руководствоваться, чтобы правильно записать схемы гальванических элементов и протекающие в них реакции:
- ЭДС элемента — величина положительная, т.к. в гальваническом элементе работа производится.
- Значение ЭДС гальванической цепи – это сумма скачков потенциалов на границах раздела всех фаз, но, учитывая, что на аноде происходит окисление, то из значения потенциала катода вычитают значение потенциала анода.
Таким образом, при составлении схемы гальванического элемента слева записывают электрод, на котором происходит процесс окисления (анод), а справа – электрод, на котором происходит процесс восстановления (катод).
- Граница раздела фаз обозначается одной чертой — |
- Электролитный мостик на границе двух проводников обозначается двумя чертами — ||
- Растворы, в которые погружен электролитный мостик записываются слева и справа от него (если необходимо, здесь же указывается концентрация растворов). Компоненты одной фазы, при этом записываются через запятую.
Например, составим схему гальванического элемента, в котором осуществляется следующая реакция:
Fe0 + Cd2+ = Fe2+ + Cd0
В гальваническом элементе анодом является железный электрод, а катодом – кадмиевый.
Анод Fe0|Fe2+ || Cd2+|Cd0Катод
Типичные задачи на составление схем гальванического элемента и вычисление ЭДС реакции с решениями вы найдете здесь.