Потенциалы нулевого заряда и нулевые точки металлов
Из уравнения
Липпмана следует, что в точке максимума
э.к.к. заряд поверхности металла равен
нулю. Оствальд предположил, что в точке
максимума э.к.к. нулю равен также и
потенциал электрода, поэтому именно
его следует взять за основу шкалы
потенциалов. Такая шкала была названа
абсолютной или оствальдовской
шкалой потенциалов. Так как потенциал
максимума э.к.к. в растворах ПИАВ
составляет » – 0,2 В
(по н.в.э.), то, по Оствальду, для получения
абсолютного потенциала какого-либо
электрода надо из значения его электродного
потенциала по водородной шкале вычесть
– 0,2 В. Однако полученные таким образом
потенциалы в свете современных
представлений нельзя считать абсолютными.
Скачок потенциала на границе электрод
– раствор не эквивалентен электродному
потенциалу, а составляет лишь некоторую
его часть; необходимо учесть еще и
контактную разность потенциалов между
металлом (в данном случае ртутью) и
платиной. Кроме того, скачок потенциала
металл – раствор включает в себя, помимо
слагаемого, возникающего за счет ионного
обмена (который в точке максимума э.к.к.
равен нулю), также слагаемое, обязанное
ориентации диполей растворителя, и нет
оснований считать, что в точке максимума
э.к.к. этот скачок потенциала равен нулю.
Если бы Оствальд
был прав, то максимум э.к.к. находился
бы всегда при одном и том же значении
электродного потенциала независимо от
состава раствора и от природы металла.
Такое предположение не оправдывается
на опыте. Было найдено, что положение
максимума э.к.к. оказывается иным, если
вместо ртути использовать легкоплавкие
сплавы или амальгамы. Таким образом,
потенциалы максимумов э.к.к. не могут
служить основанием для создания
абсолютной шкалы потенциалов. В то же
время эти потенциалы, названные Фрумкиным
потенциалами нулевого заряда
или нулевыми точками металлов,
имеют принципиальное значение в
электрохимии. На их основе Фрумкину
удалось дать одно из наиболее удачных
решений проблемы Вольта.
Термины «потенциал
нулевого заряда» и «нулевая точка»
употреблялись как синонимы. Антропов
предложил разграничить эти понятия,
присвоить каждому из них свой символ и
употреблять в соответствии с их
содержанием. Потенциал нулевого заряда
(п.н.з.; Еq=0 ),
подобно равновесному потенциалу, может
для данного металла и растворителя
приобретать любые значения в зависимости
от состава раствора, то есть он не
является специфической константой.
Только одно значение потенциала нулевого
заряда, полученное в растворе, не
содержащем ПАВ (или непосредственно в
чистом растворителе), может рассматриваться
как константа (при данных р и Т),
характеризующая систему металл –
растворитель. Это частное значение
потенциала нулевого заряда целесообразно
назвать нулевой точкой (н.т.; ЕN
). Нулевая точка, подобно стандартному
потенциалу, отвечает вполне определенному
составу раствора. Нулевую точку можно
попытаться рассчитать теоретически,
используя определенные физические
свойства металла и растворителя.
Определенная
таким образом нулевая точка была выбрана
за нуль в приведенной шкале, или
j–шкале,
потенциалов, предложенной
Антроповым. Потенциал j
в приведенной шкале определяется как
разность между потенциалом электрода
в данных условиях и его нулевой точкой:
j =
Е – ЕN .
Обе величины в правой части
уравнения должны быть выражены в одной
и той же условной (например, в водородной)
шкале; j-потенциал
при этом не зависит от выбранной условной
шкалы. Поскольку для разных металлов
величины ЕN не
совпадают, то для каждого металла должна
быть своя собственная приведенная
шкала, основанная на его нулевой точке.
Приведенная
шкала, следовательно, отличается и от
любой условной, и от абсолютной шкалы
потенциалов. В приведенной шкале для
каждого электрода потенциал отсчитывается
от своего собственного нуля; неверно
поэтому применять j-шкалу
для решения проблем, связанных с
термодинамикой электрохимических
систем или с электродным равновесием
(нельзя определить направление реакции
и ЭДС системы). Однако j-потенциал
служит приближенной мерой заряда
электрода по отношению к раствору.
Равенство j-потенциалов
двух металлов указывает на то, что ионные
скачки потенциалов и заряды поверхности
этих металлов примерно одинаковы. Знание
j-потенциалов позволяет
сравнивать различные металлы в отношении
условий адсорбции на них ПАВ.
В некоторых
случаях наряду с приведенной j-шкалой
может оказаться полезной приведенная
j¢-шкала, в которой
отсчет ведется от п.н.з. :
j¢
= Е – Еq=o
.
Подобная j¢-шкала
относится к отдельной э.к.к., в то время
как j-шкала – к данному
электроду и растворителю.
Лекция
12
Строение
двойного электрического слоя на границе
электрод – раствор
При изучении электрокинетических и
электрокапиллярных явлений были
установлены определённые опытные
закономерности. Корректная теория
строения двойного электрического слоя
металл – электролит должна давать их
истолкование. Эти же факты служат
критерием справедливости тех или иных
вариантов теории двойного электрического
слоя.
Наиболее важные
результаты, полученные при изучении
электрокинетических и электрокапиллярных
явлений, сводятся к следующему.
1.
Наряду с общим скачком потенциала на
границе металл – электролит gM,L
, входящим
как зависящее от концентрации слагаемое
в величину электродного потенциала Е,
существует также электрокинетический,
или z-потенциал,
не совпадающий с общим скачком потенциала.
Обычно
z-потенциал
по абсолютной величине меньше gM,L–
и Е-потенциала, и его зависимость от
состава раствора более сложная. С
увеличением концентрации электролита
z-потенциал
в большинстве случаев (если только в
растворе нет поверхностно-активных
ионов) уменьшается и стремится к нулю.
При изменении концентрации раствора
знак z-потенциала
может меняться на обратный, хотя знак
Е-потенциала остаётся тем же самым.
Такое изменение знака z-потенциала
и соответствующая ему перезарядка
поверхности металла наблюдается в
присутствии поверхностно-активных и
поливалентных ионов.
2.
Дифференциальная ёмкость, рассчитанная
из электрокапиллярных кривых или
измеренная непосредственно, зависит
от потенциала электрода. Она имеет
минимальное значение в области
потенциалов, примыкающих к потенциалу
незаряженной поверхности в данном
растворе. Для растворов, не содержащих
поверхностно-активных веществ, значение
ёмкости в точке максимума электрокапиллярной
кривой закономерно уменьшается по мере
разбавления раствора. На отрицательной
(нисходящей) ветви электрокапиллярной
кривой ёмкость обычно меньше, чем на
положительной (восходящей) ветви, и в
растворах многих электролитов она мало
изменяется с потенциалом.
Было
предпринято несколько попыток создания
отвечающих действительности представлений
о строении двойного электрического
слоя на границе между металлом и
раствором; основные из них рассматриваются
ниже.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Потенциал земли равен 0 — что это значит
Потенциал земли в электротехнике — это общая точка отсчета, если система не изолирована. Всем известно, что потенциал на поверхности Земли равен нулю. Но что это за ноль — условный или нет? Вопросов на самом деле много, а информации не хватает. Даже специалисты в этой области толком не разобрались и постоянно выдвигают новые гипотезы. Постараемся и мы разобраться с землей в электротехнике.
Электрическое поле Земли
Принято считать, что земля обладает отрицательным зарядом, среднее значение которого оценивается в полмиллиона кулонов. Положительный заряд, соответствующий отрицательному заряду Земли, находится на высоте нескольких десятков километров в слое положительно заряженных (ионизованных) молекул. Линии земного электрического поля идут от этого слоя к поверхности Земли. Напряженность вблизи земной поверхности имеет значение около 130 В/м. По мере подъема электрическое поле Земли ослабевает.
Судя по первой теории, поверхность Земли никак не может обладать нулевым потенциалом. Соответственно отрицательный потенциал земли в электротехнике берется как условная точка отсчета.
Есть также и теория, по которой потенциал на поверхности земли должен быть равен нулю, а все кулоновские силы, в любом удалении от нее, должны быть скомпенсированы. Тогда часть мантии планеты (верхний слой земли) должна содержать отрицательные заряды, а часть — положительные.
Ломать голову над вопросом, какая из этих теорий верная, мы не будем. Это не принципиально, и неважно какой именно потенциал у поверхности земли. Важно лишь то, что все на поверхности земли находится в его поле. И если даже потенциал не равен нулю, то в вопросах электротехники Землю можно брать как условную точку отсчета с нулевым потенциалом.
Потенциал земли равен 0 — примеры из электротехники
Рассмотрим примеры использования нулевого потенциала земли в электротехнике. А для наглядности воспользуемся интерактивным эмулятором Multisim, позволяющим моделировать и тестировать электрические схемы.
Схема будет состоять из источника переменного напряжения (однофазного генератора), заземления и нагрузки. В качестве нагрузки используем 10 резисторов по 1 Ом, соединенных последовательно. А так как провод — это тоже нагрузка, то представим, что каждый резистор — это отдельный участок провода.
Особенностью программы Multisim является то, что моделирование без заземления не работает. А так как нас интересуют потенциалы в цепи до и после подключения заземления, то выходом из ситуации является внесение в схему гальванической развязки (трансформатора).
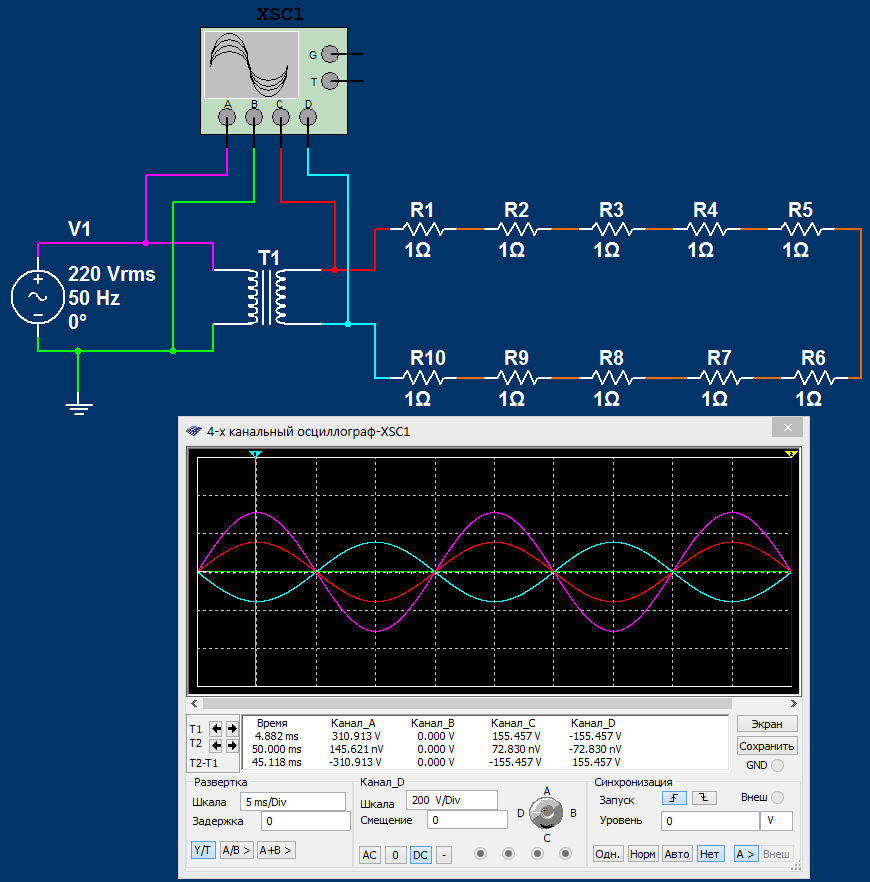
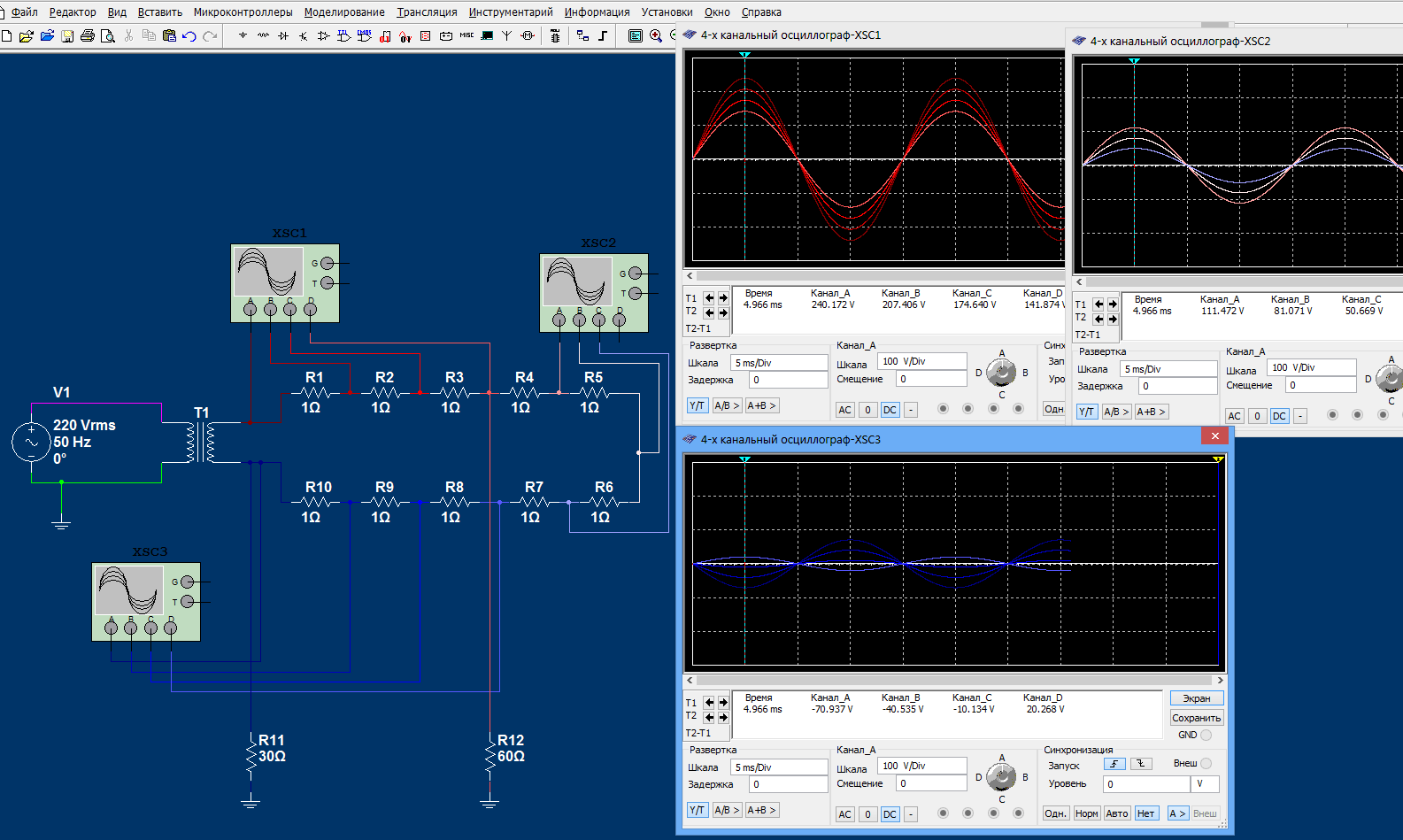
Упрощенно напряжение — это разность потенциалов. Однофазный генератор при вращении ротора индуцирует на фазной обмотке синусоидальную ЭДС. То есть на выводах генератора (начале и конце фазной обмотки) появляется напряженность, изменяющаяся со временем. Так как действующее значение напряжение генератора из примера 220 Вольт, то амплитудное значение должно быть 220×√2 ≈ 310 Вольт. При этом амплитуда напряженности каждого вывода генератора должна быть 310/2 = 155 Вольт. Все это мы можем увидеть, подключив к рассматриваемой цепи осциллограф.
Мы уже отмечали, что программа не будет работать, если в цепи не будет хотя бы одной заземленной точки. Поэтому для анализа потенциалов выводов генератора без заземления рассмотрим точки после гальванической развязки — выводы вторичной обмотки трансформатора. К этим выводам подключены каналы C и D осциллографа. Рассмотрим момент времени, когда напряженность на выводах будет максимальной (амплитудное значение). Потенциал на одном выводе трансформатора будет +155 Вольт (канал C, красный график), а на другом -155 Вольт (канал D, бирюзовый график). Заземлив один из выводов генератора, мы создаем в этой точке нулевой потенциал (канал B, зеленый график). С учетом этого нулевого потенциала, потенциал на оставшемся выводе меняется с +155 до +310 Вольт (канал A, фиолетовый график). У такой трансформации есть интересные особенности, которые многие просто не знают или не понимают. Далее постараемся разобраться в этом интересном вопросе.
Первое, что нужно знать и понимать, — каким образом образуется электрическое поле при замыкании цепи. Для этого удобнее перейти с переменного на постоянный ток. К сожалению заменить генератор переменного тока на генератор постоянного тока у нас не получится, так как трансформатор в цепи с постоянным током не работает. Поэтому мы будем работать с амплитудным значением переменного напряжения, рассматривать конкретный момент времени — точку на пике графике и анализировать этот момент как постоянный ток.
Распространение электрического поля после замыкания цепи происходит со скоростью близкой к скорости света. Но не это важно. Важная особенность заключается в том, что электрическое поле в проводнике с током создают поверхностные заряды. Плотность поверхностного заряда постепенно уменьшается по мере удаления от источника тока. Именно этот заряд создает электрическое поле, существующее внутри и вне проводника, на всем его протяжении. Вдоль проводника, по которому течет постоянный электрический ток, потенциал уменьшается от максимального значения на одном конце проводника до минимального — на другом.
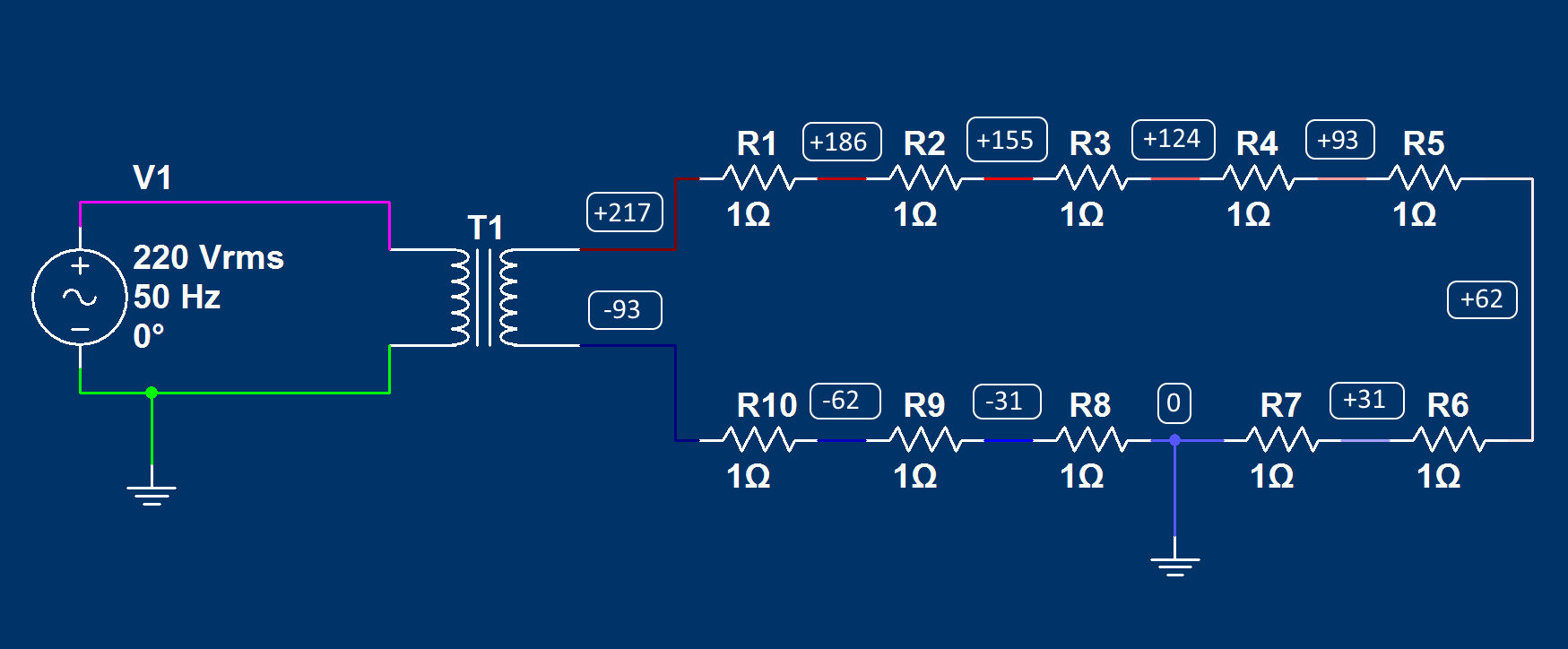
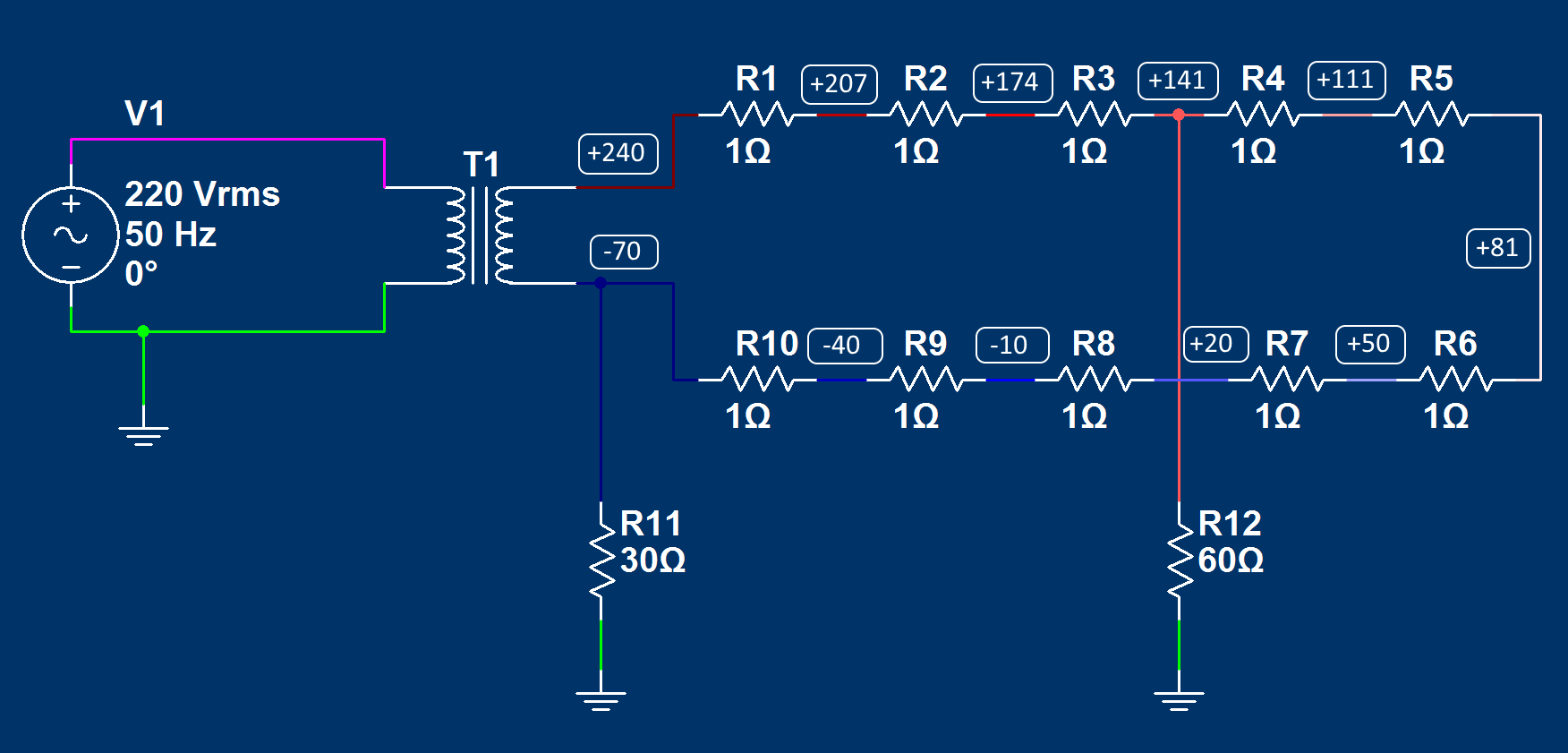
Теперь понятно, для чего нам нужны были резисторы — мы условно разделили проводник на 10 частей. Сопротивление каждого участка 1 Ом. Посмотрим, как изменяются потенциалы на границах этих участков:
Для удобства восприятия перенесем значения потенциалов в точках из осциллографов на схему:
Как видно, после образования стационарного электрического поля потенциал вдоль провода от плюса к минусу плавно изменился. Изменяется он за счет разной плотности поверхностных зарядов. При этом количество положительных и отрицательных зарядов в каждом сечении не меняется. Меняется только баланс их размещения, что в совокупности с изначальным полем на выводах генератора создает такую разность потенциалов на поверхности проводника. Важно отметить, что несмотря на кажущуюся компактность нашей схемы, нужно учитывать реальный масштаб измерений. Ведь в реальности участок с сопротивлением 1 Ом — это провод длинной в сотни метров (зависит от материала и сечения). Также стоит отметить, что с учетом сопротивления цепи 10 Ом потенциалы в точках, разделенных участками в 1 Ом, будут отличаться от соседних точек на величину равную ± 31 Вольт.
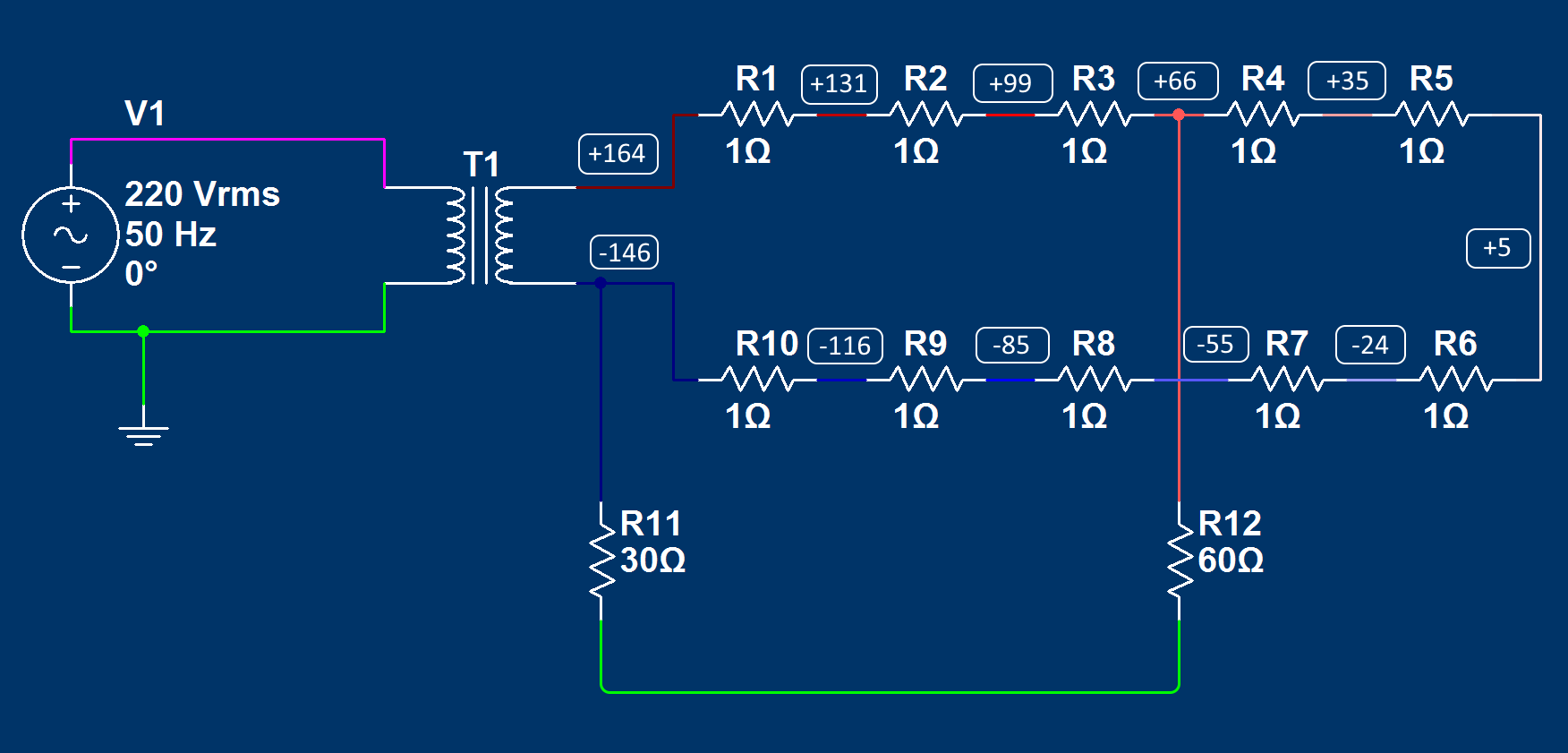
Заземлим произвольную точку цепи и посмотрим, что получится:
Для удобства восприятия также перенесем значения потенциалов в точках из осциллографов на схему:
Напряжение между какой-нибудь точкой электрической цепи и землей называют потенциалом этой точки. Очевидно, что потенциал заземленной точки равен нулю, и это мы видим из показаний осциллографа. То есть точка с нулевым потенциалом на проводе сместилась в место соединения с землей, и с учетом этого потенциалы остальных точек изменились. Но важно понимать, что ничего кардинального не произошло. В цепи как протекал ток, так и протекает. Пропорция поверхностного заряд в цепи также не изменилась. Изменилась только напряженность различных участков за счет внесения в цепь напряженности земли в 0 Вольт. Также при соединении с землей одной точки цепи ток в землю не ответвляется, если вся остальная часть цепи имеет достаточно хорошую изоляцию.
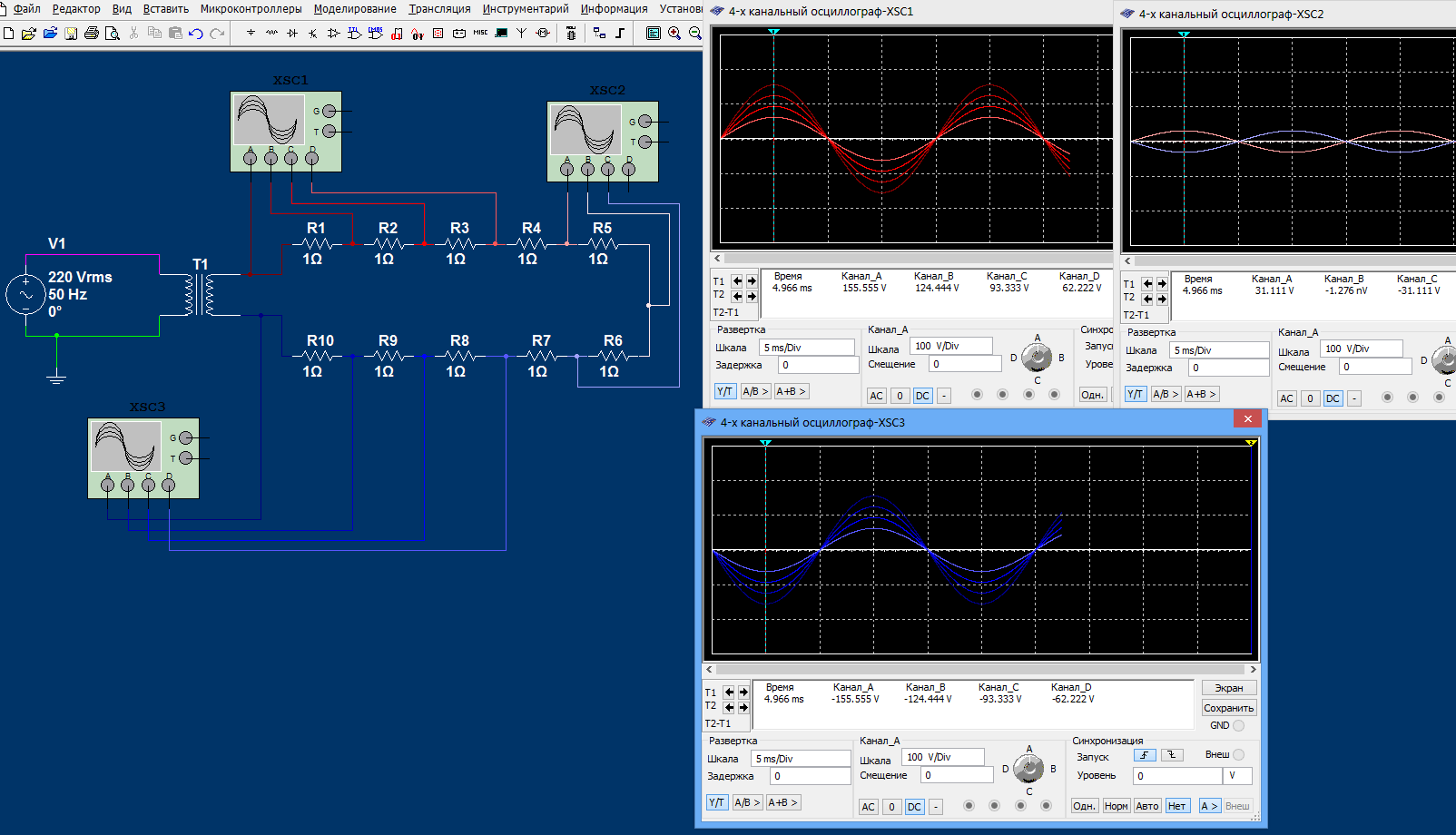
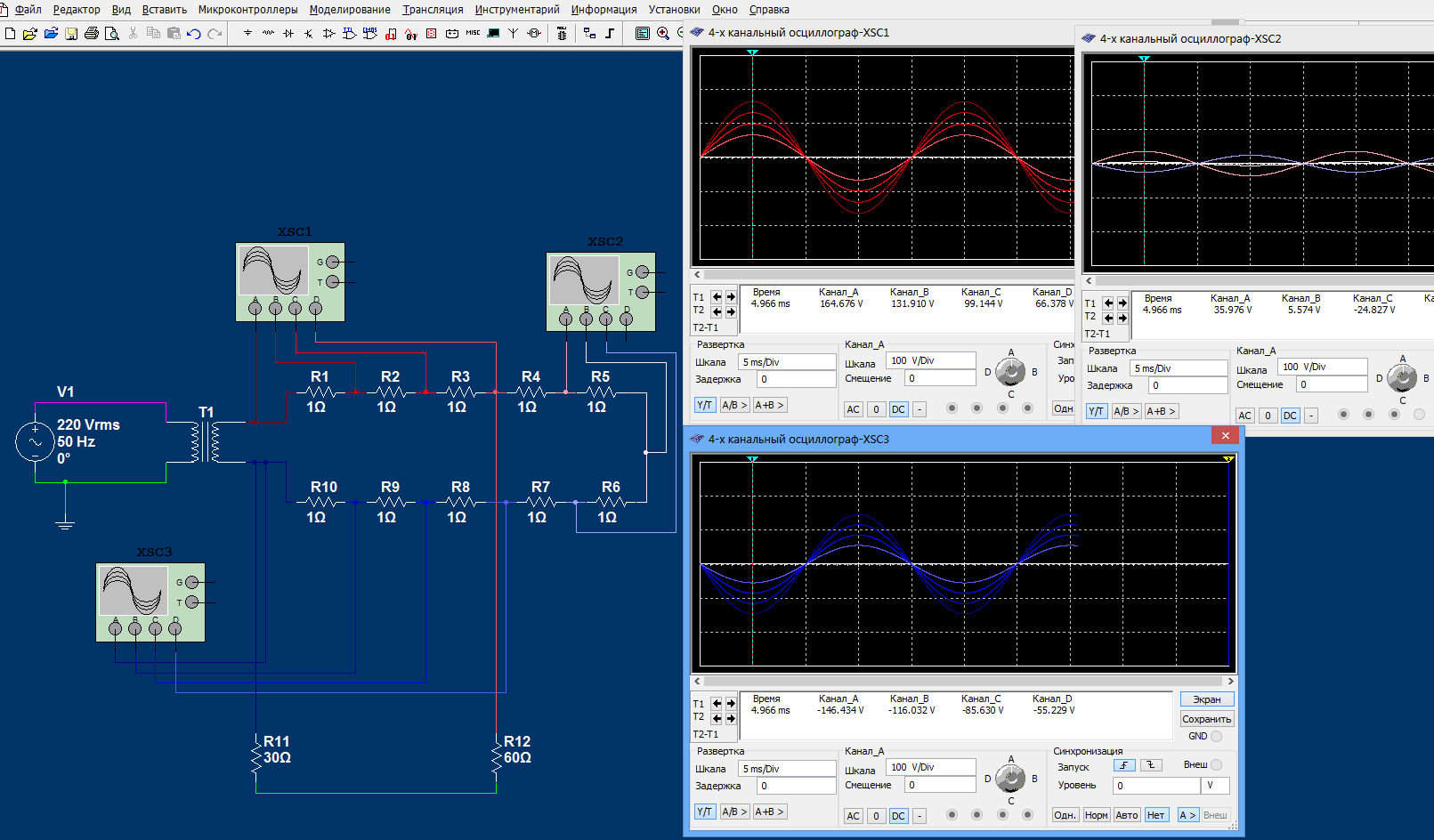
Другое дело, если заземляются одновременно две точки электрической цепи. В этом случае создается параллельная цепь и распределение токов может измениться. Смоделируем такую ситуации. Для лучшего восприятия и понимания примем, что резисторы (R4+R5+R6+R7) — это условная нагрузка (электрочайник), (R1+R2+R3) и (R10+R9+R8) — это провода, соединяющие выводы генератора с нагрузкой. Один вывод заземлен (сопротивление заземлителя 30 Ом), а провод от незаземленного вывода повредился (произошло замыкание на землю, сопротивление растеканию 60 Ом).
Перенесем значения потенциалов в точках из осциллографов на схему:
Как видно, заземлив одновременно две точки электрической цепи, мы создали параллельную цепь. В связи с этим потенциалы в точках опять изменились. Здесь хочется отметить, что так как через землю по параллельной замкнутой цепи также протекает ток, то поверхностный заряд (его плотность) во всей цепи также изменился.
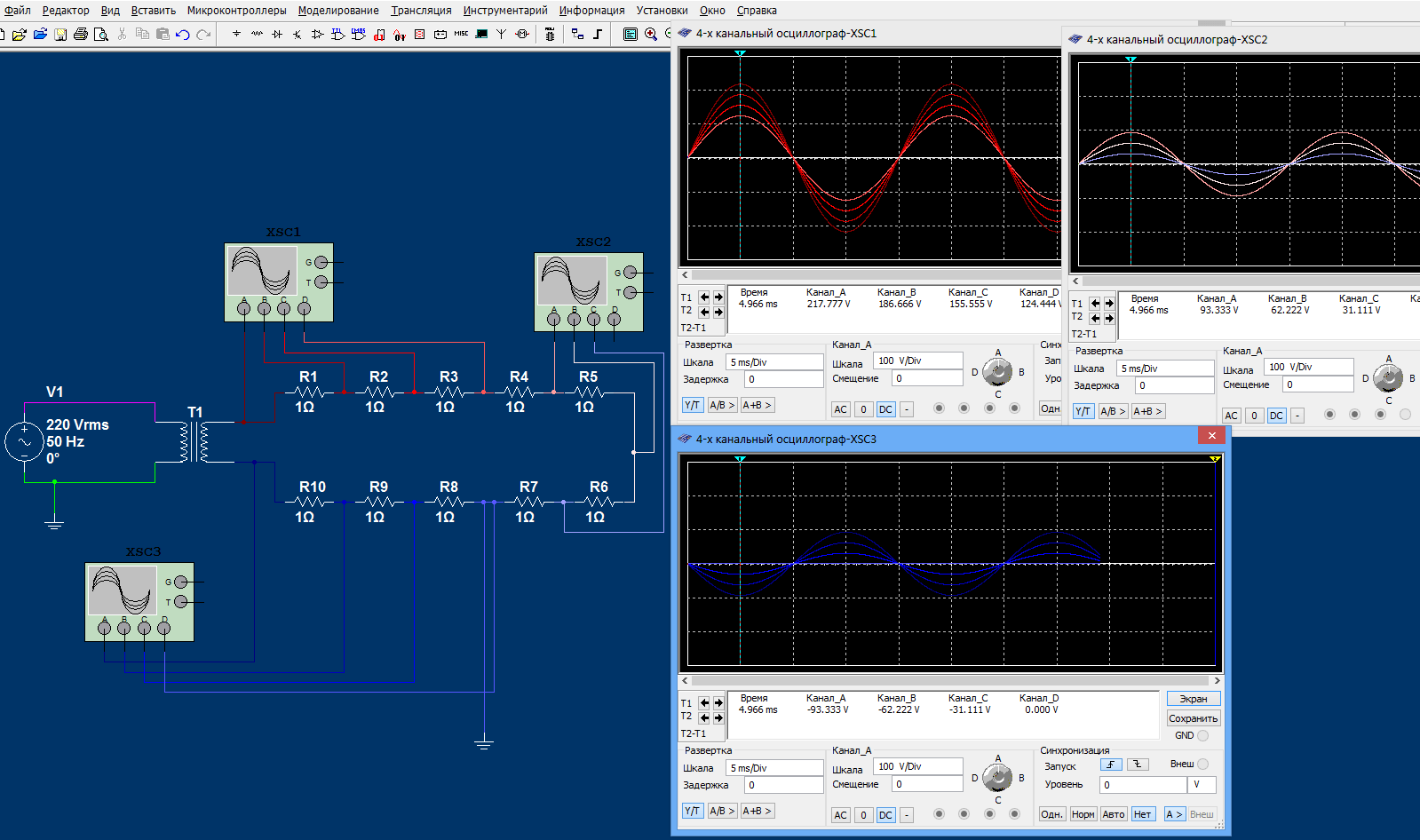
Так как параллельная цепь через землю — это все равно электрическая цепь, то возникает логичный вопрос, можно ли убрать в схеме заземление, а резисторы R11 и R12 просто соединить между собой? Можно. Сила тока и напряжения в участках цепи не изменятся. Изменится только распределение потенциалов в точках цепи. А это в электротехнических расчетах особой роли не играет.
Покажем, как распределяться потенциалы при добавлении параллельной незаземленной цепи:
Перенесем значения потенциалов в точках из осциллографов на схему:
Подводя итог, можно отметить, что нулевой потенциал земли особого влияния на электрическую цепь не оказывает. Да, меняются потенциалы в точках. Но при этом сама разность между ними остается неизменной. И в электротехнике именно разность потенциалов является основой при анализе цепи.
Понятие электрического потенциала является одним из важных основ теории электростатики и электродинамики. Понимание его сущности является необходимым условием для дальнейшего изучения этих разделов физики.
Содержание
- 1 Что такое электрический потенциал
- 2 Свойства потенциала
- 3 Разность потенциалов
- 4 Эквипотенциальные поверхности
Что такое электрический потенциал
Пусть в поле, создаваемым неподвижным зарядом Q, помещён единичный заряд q, на который действует сила Кулона F=k*Qq/r.
Здесь и далее k=((1/4)*π* ε0* ε), где ε0 — электрическая постоянная (8,85*10-12 Ф/м), а ε – диэлектрическая постоянная среды.
Внесённый заряд под действием этой силы может перемещаться, а сила при этом совершит определенную работу. Это означает, что система из двух зарядов обладает потенциальной энергией, зависящей от величины обоих зарядов и расстояния между ними, причём величина этой потенциальной энергии не зависит от величины заряда q. Здесь и вводится определение электрического потенциала – он равен отношению потенциальной энергии поля к величине заряда:
φ=W/q,
где W – потенциальная энергия поля, создаваемого системой зарядов, а потенциал является энергетической характеристикой поля. Чтобы переместить заряд q в электрическом поле на какое-то расстояние, надо затратить определённую работу на преодоление кулоновских сил. Потенциал точки равен работе, которую надо затратить для перемещения единичного заряда из этой точки в бесконечность. При этом надо отметить, что:
- эта работа будет равна убыли потенциальной энергии заряда (A=W2-W1);
- работа не зависит от траектории перемещения заряда.
В системе СИ единицей измерения потенциала является один Вольт (в русскоязычной литературе обозначается буквой В, в зарубежной – V). 1 В=1Дж/1 Кл, то есть, можно говорить о потенциале точки в 1 вольт, если для перемещения заряда в 1 Кл в бесконечность потребуется совершить работу в 1 Джоуль. Название выбрано в честь итальянского физика Алессандро Вольта, внесшего значительный вклад в развитие электротехники.
Чтобы наглядно представить, что такое потенциал, его можно сравнить с температурой двух тел или температурой, замеренной в разных точках пространства. Температура служит мерой нагрева объектов, а потенциал – мерой электрической заряженности. Говорят, что одно тело нагрето более другого, также можно сказать, что одно тело заряжено более, а другое – менее. Эти тела обладают разным потенциалом.
Значение потенциала зависит от выбора системы координат, поэтому требуется какой-то уровень, который надо принять за ноль. При измерении температуры за базовую границу можно принять, например, температуру тающего льда. Для потенциала за нулевой уровень обычно принимают потенциал бесконечно удаленной точки, но для решения некоторых задач за нулем можно считать, например, потенциал земли или потенциал одной из обкладок конденсатора.
Свойства потенциала
Среди важных свойств потенциала надо отметить следующие:
- если поле создается несколькими зарядами, то потенциал в конкретной точке будет равен алгебраической (с учетом знака заряда) сумме потенциалов, создаваемых каждым из зарядов φ=φ1+φ2+φ3+φ4+φ5+…+φn;
- если расстояния от зарядов таковы, что сами заряды можно считать точечными, то суммарный потенциал считается по формуле φ=k*(q1/r1+q2/r2+q3/r3+…+qn/rn), где r – расстояние от соответствующего заряда то рассматриваемой точки.
Если поле образовано электрическим диполем (двумя связанными зарядами противоположного знака), то потенциал в любой точке, находящейся на расстоянии r от диполя будет равен φ=k*p*cosά/r2, где:
- p – электрическое плечо диполя, равное q*l, где l – расстояние между зарядами;
- r – расстояние до диполя;
- ά – угол между плечом диполя и радиус-вектором r.
Если точка лежит на оси диполя, то cosά=1 и φ=k*p/r2.
Разность потенциалов
Если две точки обладают определённым потенциалом, и если они не равны, то говорят о том, что между двумя точками существует разность потенциалов. Разность потенциалов возникает между точками:
- потенциал которых определяется зарядами разных знаков;
- точкой с потенциалом от заряда любого знака и точкой с нулевым потенциалом;
- точками, имеющими потенциал равного знака, но отличающимися по модулю.
То есть, разность потенциалов не зависит от выбора системы координат. Можно провести аналогию с бассейнами с водой, расположенными на разной высоте относительно нулевой отметки (например, уровня моря).
Вода каждого бассейна имеет определенную потенциальную энергию, но если соединить два любых бассейна трубкой, то в каждой из них возникнет поток воды, расход которой определяется не только размерами трубки, но и разностью потенциальных энергий в гравитационном поле Земли (то есть, разностью высот). Абсолютное значение потенциальных энергий значения в данном случае не имеет.
Точно так же, если соединить проводником две точки с разным потенциалом, по нему потечёт электрический ток, определяемый не только сопротивлением проводника, но и разностью потенциалов (но не их абсолютным значением). Продолжая аналогию с водой, можно сказать, что вода в верхнем бассейне скоро закончится, и если не найдется той силы, которая переместит воду обратно наверх (например, насоса), то и поток очень быстро прекратится.
Так и в электрической цепи – чтобы поддерживать разность потенциалов на определенном уровне, потребуется сила, переносящая заряды (точнее, носители зарядов) к точке с наибольшим потенциалом. Такая сила называется электродвижущей силой и сокращенно обозначается ЭДС. ЭДС может носить различную природу – электрохимическую, электромагнитную и т.п.
На практике имеет значение в основном разность потенциалов между начальной и конечной точками траектории движения носителей зарядов. В этом случае эту разность называют напряжением, и оно в СИ также измеряется в вольтах. О напряжении в 1 Вольт можно говорить, если поле совершает работу в 1 Джоуль при перемещении заряда в 1 Кулон из одной точки в другую, то есть 1В=1Дж/1Кл, и Дж/Кл также может являться единицей измерения разности потенциалов.
Эквипотенциальные поверхности
Если потенциал нескольких точек одинаков, и эти точки образуют поверхность, то такая поверхность называется эквипотенциальной. Таким свойством обладает, например, сфера, описанная вокруг электрического заряда, ведь электрическое поле убывает с расстоянием одинаково во все стороны.
Все точки этой поверхности имеют одинаковую потенциальную энергию, поэтому при перемещении заряда по такой сфере работа затрачиваться не будет. Эквипотенциальные поверхности систем из нескольких зарядов имеют более сложную форму, но у них есть одно интересное свойство – они никогда не пересекаются. Силовые линии электрического поля всегда перпендикулярны поверхностям с одинаковым потенциалом в каждой их точке. Если эквипотенциальную поверхность рассечь плоскостью, получится линия равных потенциалов. Она имеет те же свойства, что и эквипотенциальная поверхность. На практике равный потенциал имеют, например, точки на поверхности проводника, помещенного в электростатическое поле.
Разобравшись с понятием потенциала и разности потенциалов, можно приступать к дальнейшему изучению электрических явлений. Но не ранее, потому что без понимания базовых принципов и понятий углубить знания не получится.
From Wikipedia, the free encyclopedia
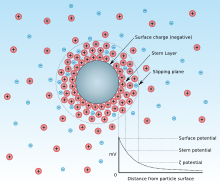
Electrical double layer (EDL) around a negatively charged particle in suspension in water.
The point of zero charge (pzc) is generally described as the pH at which the net charge of total particle surface (i.e. absorbent’s surface) is equal to zero, which concept has been introduced in the studies dealt with colloidal flocculation to explain pH affecting the phenomenon.[1]
A related concept in electrochemistry is the electrode potential at the point of zero charge. Generally, the pzc in electrochemistry is the value of the negative decimal logarithm of the activity of the potential-determining ion in the bulk fluid.[2] The pzc is of fundamental importance in surface science. For example, in the field of environmental science, it determines how easily a substrate is able to adsorb potentially harmful ions. It also has countless applications in technology of colloids, e.g., flotation of minerals. Therefore, the pzc value has been examined in many application of adsorption to the environmental science.[3][4] The pzc value is typically obtained by titrations and several titration method has been developed.[5][6] Related values associated with the soil characteristics exist along with the pzc value, including zero point of charge (zpc), point of zero net charge (pznc), etc.[7]
Term definition of point of zero charge[edit]
The point of zero charge is the pH for which the net surface charge of adsorbent is equal to zero. This concept has been introduced by an increase of interest in the pH of the solution during adsorption.[1] The reason why pH has attracted much attention is that the adsorption of some substances is very dependent on pH. The pzc value is determined by the characteristics of an adsorbent. For example, the surface charge of adsorbent is described by the ion that lies on the surface of the particle (adsorbent) structure like image. At the lower pH, hydrogen ions (protons, H+) would be adsorbed more than other cations (adsorbate) so that the other cations would be less adsorbed in the case of the negatively charged particle. On the other hand, if the surface is positively charged and pH is increased, anions will be less adsorbed as hydroxide ions are increased. From the view of the adsorbent, if the pH is below the pzc value, the surface charge of adsorbent would be positive so that the anions can be adsorbed. Conversely, if the pH is above the pzc value, the surface charge would be negative so that the cations can be adsorbed.
For example, the charge on the surface of silver iodide crystals may be determined by the concentration of iodide ions in the solution above the crystals. Then, the pzc value of the AgI surface will be described by the concentration of I− in the solution (or negative decimal logarithm of this concentration, pI−).
Relation of pzc to isoelectric point[edit]
The pzc is the same as the isoelectric point (iep) if there is no adsorption of other ions than the potential determining H+/OH− at the surface.[8] This is often the case for pure (“pristine surface”) oxides in water. In the presence of specific adsorption, pzc and isoelectric point generally have different values.
Method of experimental determination[edit]
The pzc is typically obtained by acid-base titrations of colloidal dispersions while monitoring the electrophoretic mobility of the particles and the pH of the suspension. Several titrations are required to distinguish pzc from iep, using different electrolytes (including varying the electrolyte ionic strength). Once satisfactory graphs are obtained (acid/base amount—pH, and pH—zeta potential), the pzc is established as the common intersection point (cip) of the lines. Therefore, pzc is also sometimes referred to as cip.
[edit]
Besides pzc, iep, and cip, there are also numerous other terms used in the literature, usually expressed as initialisms, with identical or (confusingly) near-identical meaning: zero point of charge (zpc), point of zero net charge (pznc), point of zero net proton charge (pznpc), pristine point of zero charge (ppzc), point of zero salt effect (pzse), zero point of titration (zpt) of colloidal dispersion, and isoelectric point of the solid (ieps)[9] and point of zero surface tension (pzst[10] or pzs[11]).
Application in electrochemistry[edit]
In electrochemistry, the electrode-electrolyte interface is generally charged. If the electrode is polarizable, then its surface charge depends on the electrode potential.
IUPAC defines[2] the potential at the point of zero charge as the potential of an electrode (against a defined reference electrode) at which one of the charges defined is zero.
The potential of zero charge is used for determination of the absolute electrode potential in a given electrolyte.
IUPAC also defines the potential difference with respect to the potential of zero charge as:
- Epzc = E − Eσ=0
where:
- Epzc is the electrode potential difference with respect to the point of zero charge, Eσ=0
- E is the potential of the same electrode against a defined reference electrode in volts
- Eσ=0 is the potential of the same electrode when the surface charge is zero, in the absence of specific adsorption other than that of the solvent, against the reference electrode as used above, in volts
The structure of electrolyte at the electrode surface can also depend on the surface charge, with a change around the pzc potential. For example, on a platinum electrode, water molecules have been reported to be weakly hydrogen-bonded with “oxygen-up” orientation on negatively charged surfaces, and strongly hydrogen-bonded with nearly flat orientation at positively charged surfaces.[12]
At pzc, the colloidal system exhibits zero zeta potential (that is, the particles remain stationary in an electric field), minimum stability (exhibits maximum coagulation or flocculation rate), maximum solubility of the solid phase, maximum viscosity of the dispersion, and other peculiarities.
Application in environmental geochemistry[edit]
In the field of environmental science, adsorption is involved in many parts of technologies that can eliminate pollutants and governs the concentration of chemicals in soils and/or atmosphere. When studying pollutant degradation or the geochemical process, the pzc value related to adsorption has been examined. For example, natural and organic substrates including wood ash, sawdust, etc. are to be used as an adsorbent by eliminating harmful heavy metals like arsenic, cobalt, mercury ion and so forth in contaminated neutral drainage (CND), which is a passive reactor that could possible metal adsorption with low-cost materials. Therefore, the pzc values of the organic substrates were evaluated to optimize the selection of materials in CND.[3] Another example is that the emission of nitrous acid, which controls the atmosphere’s oxidative capacity. Different soil pH leads to the different surface charges of minerals so the emission of nitrous acid would be varied, further impacting on the biological cycle involved in the nitrous acid species.[4]
Further reading[edit]
- Kosmulski M. (2009). Surface Charging and Points of Zero Charge. CRC Press; 1st edition (Hardcover). ISBN 978-1-4200-5188-9
References[edit]
- ^ a b Sposito, Garrison (1998). “On Points of Zero Charge”. Environmental Science & Technology. 32 (19): 2815–2819. Bibcode:1998EnST…32.2815S. doi:10.1021/es9802347. ISSN 0013-936X.
- ^ a b IUPAC Gold Book
- ^ a b Bakatula, Elisee Nsimba; Richard, Dominique; Neculita, Carmen Mihaela; Zagury, Gerald J. (2018). “Determination of point of zero charge of natural organic materials”. Environmental Science and Pollution Research. 25 (8): 7823–7833. doi:10.1007/s11356-017-1115-7. ISSN 1614-7499. PMID 29294236. S2CID 3946219.
- ^ a b Donaldson, Melissa A.; Bish, David L.; Raff, Jonathan D. (2014). “Soil surface acidity plays a determining role in the atmospheric-terrestrial exchange of nitrous acid”. Proceedings of the National Academy of Sciences. 111 (52): 18472–18477. Bibcode:2014PNAS..11118472D. doi:10.1073/pnas.1418545112. ISSN 0027-8424. PMC 4284574. PMID 25512517.
- ^ Nasiruddin Khan, M.; Sarwar, Anila (2007). “Determination of points of zero charge of natural and treated adsorbents”. Surface Review and Letters. 14 (3): 461–469. Bibcode:2007SRL….14..461N. doi:10.1142/S0218625X07009517. ISSN 0218-625X.
- ^ Bakatula, Elisee Nsimba; Richard, Dominique; Neculita, Carmen Mihaela; Zagury, Gerald J. (2018). “Determination of point of zero charge of natural organic materials”. Environmental Science and Pollution Research. 25 (8): 7823–7833. doi:10.1007/s11356-017-1115-7. ISSN 0944-1344. PMID 29294236. S2CID 3946219.
- ^ Kosmulski, Marek (2001). “Chemical Properties of Material Surfaces”. Surfactant Science. 20011074. doi:10.1201/9780585418049. ISBN 978-0-8247-0560-2. ISSN 2155-6512.
- ^ Sposito, Garrison (1998). “On Points of Zero Charge”. Environmental Science & Technology. 32 (19): 2815–2819. Bibcode:1998EnST…32.2815S. doi:10.1021/es9802347. ISSN 0013-936X.
- ^ Marek Kosmulski, “Chemical Properties of Material Surfaces”, Marcel Dekker Inc., 2001.
- ^ Jean-Pierre Jolivet, “Metal Oxide Chemistry and Synthesis”, John Wiley & Sons, 2000.
- ^ R. J. Stol & P. L. de Bruyn; “Thermodynamic stabilization of colloids”; Journal of Colloid and Interface Science; 1980; 75 (1): pp. 185–198.
- ^ Osawa, Masatoshi; Tsushima, Minoru; Mogami, Hirokazu; Samjeské, Gabor; Yamakata, Akira (2008). “Structure of Water at the Electrified Platinum−Water Interface: A Study by Surface-Enhanced Infrared Absorption Spectroscopy”. J. Phys. Chem. C. 112 (11): 4248–4256. doi:10.1021/jp710386g.
Потенциал. Эквипотенциальные поверхности.
В механике взаимодействие тел характеризует силой или потенциальной энергией. Электрическое поле, которое обеспечивает взаимодействие между электрически заряженными телами, также характеризуют двумя величинами. Напряженность электрического поля — это силовая характеристика. Теперь введем энергетическую характеристику — потенциал. С помощью этой величины можно будет сравнивать между собой любые точки электрического поля. Таким образом, потенциал как характеристика поля должен зависеть от значения заряда, содержащегося в этих точках. Поделим обе части формулы A = W1 — W2 на заряд q, получим
Отношение W/q не зависит от значения заряда и принимается за энергетическую характеристику, которую называют потенциалом поля в данной точке. Обозначают потенциал буквой φ.
Потенциал электрического поля φ — скалярная энергетическая характеристика поля, которая определяется отношением потенциальной энергии W положительного заряда q в данной точке поля к величине этого заряда:
Единица потенциала — вольт:
Подобно потенциальной энергии значения потенциала в данной точке зависит от выбора нулевого уровня для отсчета потенциала. Чаще всего в электродинамике за нулевой уровень берут потенциал точки, лежащей в бесконечности, а в электротехнике — на поверхности Земли.
С введением потенциала формулу для определения работы по перемещению заряда между точками 1 и 2 можно записать в виде
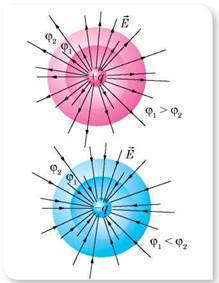
Поскольку при перемещении положительного заряда в направлении вектора напряженности электрическое поле выполняет положительную работу A = q (φ1 — φ2 )> 0, то потенциал φ1 больше чем потенциал φ2 . Таким образом, напряженность электрического поля направлена в сторону уменьшения потенциала.
Если заряд перемещать с определенной точки поля в бесконечность, то работа A = q (φ — φ∞ ). Поскольку φ∞ = 0, то A = qφ. Таким образом, величина потенциала φ определенной точки поля определяется работой, которую выполняет электрическое поле, перемещая единичный положительный заряд из этой точки в бесконечность,
Если электрическое поле создается точечным зарядом q, то в точке, лежащей на расстоянии r от него, потенциал вычисляют по формуле
По этой формуле рассчитывают и потенциал поля заряженного шара. В таком случае r — это расстояние от центра шара до выбранной точки поля. С этой формулы видно, что на одинаковых расстояниях от точечного заряда, который создает поле, потенциал одинаков. Все эти точки лежат на поверхности сферы, описанной радиусом r вокруг точечного заряда. Такую сферу называют эквипотенциальной поверхностью.
Эквипотенциальные поверхности — геометрическое место точек в электрическом поле, которые имеют одинаковый потенциал, — один из методов наглядного изображения электрических полей.
Силовые линии всегда перпендикулярны эквипотенциальных поверхностей. Это означает, что работа сил поля по перемещению заряда по эквипотенциальной поверхности равна нулю.
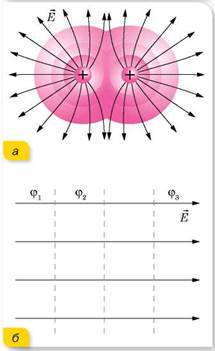
В случае наложения электрических полей, созданных несколькими зарядами, потенциал электрического поля равен алгебраической сумме потенциалов полей, созданных отдельными зарядами, φ = φ1 + φ2 + φ3 . Эквипотенциальные поверхности таких систем имеют сложную форму. Например, для системы из двух одинаковых по значению одноименных зарядов эквипотенциальные поверхности имеют вид, изображенный на рисунке. Эквипотенциальные поверхности однородного поля явлются плоскостями.
Разность потенциалов
Практическое значение имеет не сам потенциал в точке, а изменение (разница) потенциала φ1 — φ2 , которое не зависит от выбора нулевого уровня отсчета потенциала. Разность потенциалов φ1 — φ2 еще называют напряжением и обозначают латинской буквой U. Тогда формула для работы по перемещению заряда приобретает вид
Напряжение U — это физическая величина, определяемая работой электрического поля по перемещению единичного положительного заряда между двумя точками поля,
Единица разности потенциалов (напряжения), как и потенциала, — вольт,
Поскольку работа сил поля по перемещению заряда зависит только от разности потенциалов, то в случае перемещения заряда с первой эквипотенциальной поверхности на другую (потенциалы которых соответственно φ1 и φ2 ) выполненная полем работа не зависит от траектории этого движения.
Связь напряженности электрического поля с напряжением
Из формул A = Eqd и A = qU можно установить связь между напряженностью и напряжением электрического поля: Ed = U. С этой формулы следует:
- чем меньше меняется потенциал на расстоянии d, тем меньше есть напряженность электрического поля;
- если потенциал не меняется, то напряженность равна нулю;
- напряженность электрического поля направлена в сторону уменьшения потенциала.
Поскольку
то именно из этой формулы и выводится еще одна единица напряженности — вольт на метр,