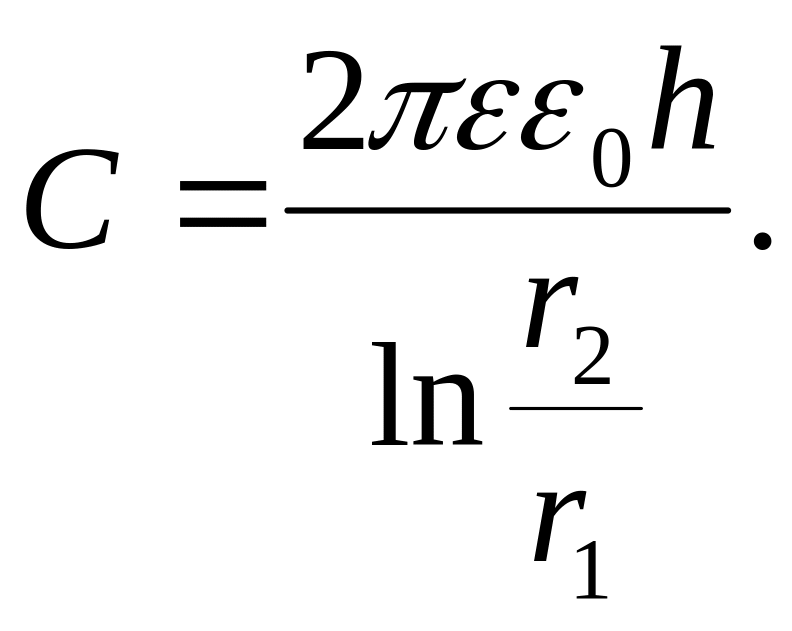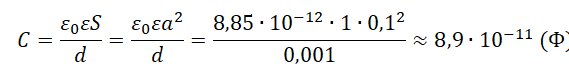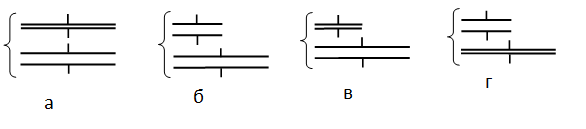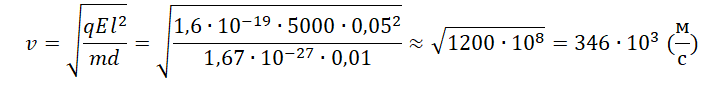Для школьников и студентов.
Первое правило.
Если в цепи есть точки (узлы), в которых сходятся обкладки конденсаторов, не соединённые с источниками напряжения, то алгебраическая сумма зарядов на этих обкладках равна нулю.
Это утверждение находится в согласии с законом сохранения заряда. Появляющиеся заряды на этих обкладках являются наведёнными или индуцированными (см. Занятие 52. Явление электростатической индукции).
Второе правило.
Кроме узлов, о которых говорится в первом правиле, следует найти в цепи другие точки равного потенциала и тоже соединить их в узлы. Потенциал одного из узлов принимают за нуль. Надо расставить знаки на обкладках конденсаторов. Заряд каждого конденсатора выразить через его ёмкость и разность потенциалов того участка, в который включен конденсатор. Эти уравнения плюс уравнения, записанные по первому правилу, позволят найти заряд каждого конденсатора, ёмкость батареи конденсаторов.
В качестве примера приведём решение следующей задачи.
Итак, применение первого и второго правил позволило в данной задаче найти потенциал точки О и заряды обкладок конденсаторов, соединённых в точке О. Оказалось, что заряды обкладок первого и второго конденсаторов, обведённые пунктирной линией, положительны, а обкладка третьего конденсатора заряжена отрицательно. Алгебраическая сумма зарядов этих обкладок равна нулю (проявление закона сохранения заряда).
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.
Предыдущая запись: Как найти ёмкость батареи конденсаторов, состоящей из одинаковых конденсаторов, включенных по одному в каждое ребро проволочного куба?
Следующая запись: Как найти ёмкость батареи конденсаторов, соединённых так, как показано на рисунке?
Ссылки на занятия до электростатики даны в Занятии 1.
Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45.
-
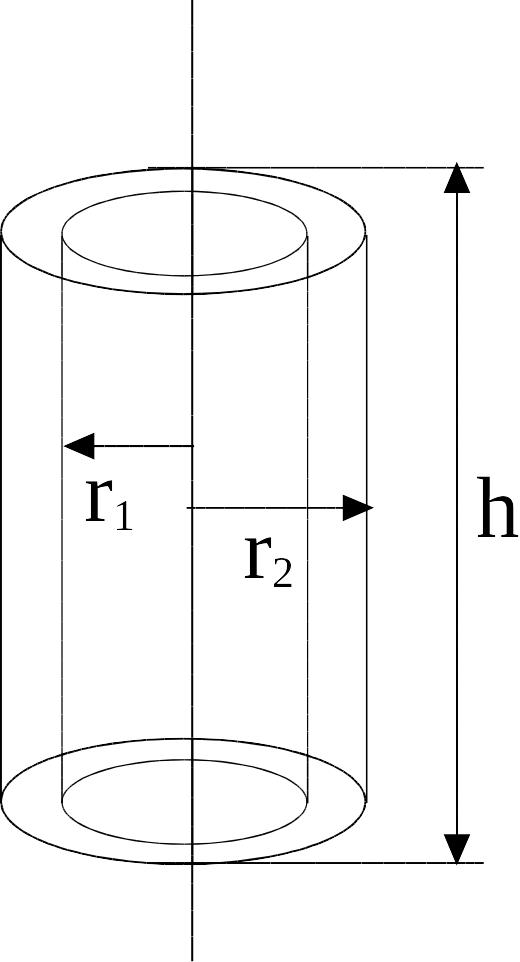
Цилиндрический конденсатор
-
состоит
из двух полых коаксиальных металлических
цилиндров с радиусамии
,
вставленных один в другой. -
Заряды
на обкладкахи
,
-
высота
цилиндра
;
. -
В
этом случае можно вычислять разность
потенциалов
между обкладками по формуле для поля,
создаваемого бесконечно длинным прямым
цилиндром
радиуса,
равномерно заряженным с постоянной
линейной плотностью
:
, -
Тогда
Пример
цилиндрического
конденсатора – лейденская банка.
Если
зазор между обкладками конденсатора
мал
,
то
и
,
где
– боковая площадь обкладки.
Таким
образом, электроемкость
любого конденсатора пропорциональна
диэлектрической проницаемости вещества,
заполняющего зазор между обкладками.
Кроме электроемкости
конденсатор характеризуется пробивным
напряжением. Это разность потенциалов
между обкладками, при которой может
произойти пробой.
1.3.5. Соединения конденсаторов
-
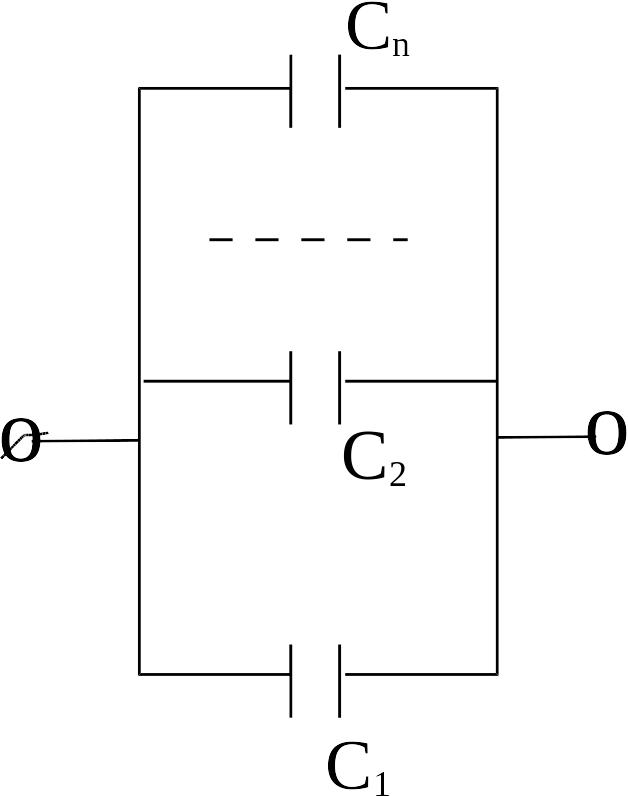
П
араллельное
соединение.
-
Емкости
конденсаторов соответственно равны
. -
Разности потенциалов
для всех конденсаторов одинаковы, -
поэтому заряды
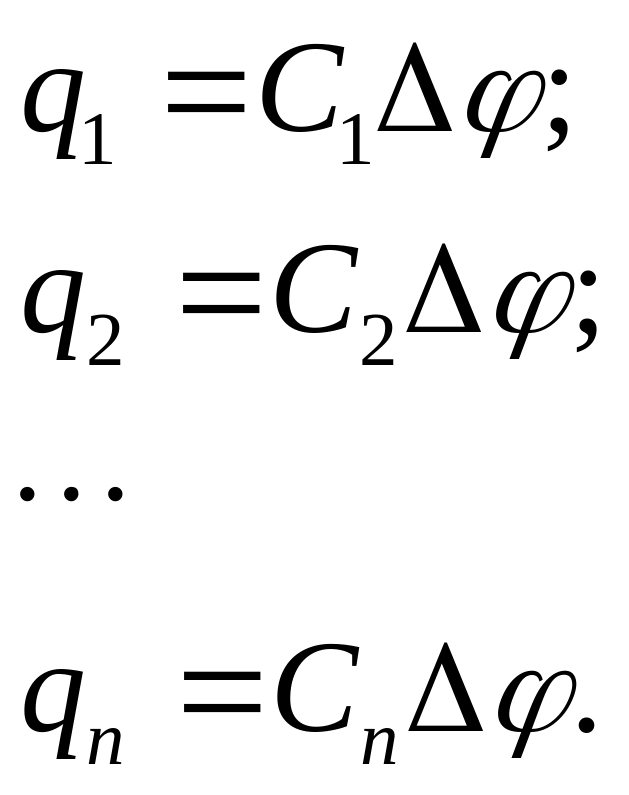
-
Заряд всей батареи
.
Но, с
другой стороны
,
тогда
-
Последовательное
соединение.
-
В
этом случае
-
(заряды всех пластин одинаковы)
-
-
отсюда
– при последовательном соединении
конденсаторов величина, обратная общей
электроемкости, равна сумме величин,
обратных электроемкостям отдельных
конденсаторов. -
То
есть результирующая электроемкостьвсегда меньше минимальной электроемкости,
входящей в батарею.
Лекция14/
7
1.4.Энергия электрического поля
1.4.1.Энергия заряженного проводника
Будем считать
среду, в которой находятся электрические
заряды и заряженные тела, однородной и
изотропной, не обладающей сегнетоэлектрическими
свойствами.
Заряжая некоторый
проводник, необходимо совершить
определенную работу против кулоновских
сил отталкивания между одноименными
электрическими зарядами.
Эта работа идет
на увеличение электрической энергии
заряженного проводника, которая в данном
случае аналогична потенциальной энергии
в механике.
Рассмотрим
проводник, имеющий
-
электроемкость
,
-
заряд
-
и
потенциал.
Работа,
совершаемая против сил электростатического
поля при перенесении заряда
из бесконечности на проводник равна
.
Для
того, чтобы зарядить тело от нулевого
потенциала до потенциала
,
необходимо совершить работу
.
Ясно,
что энергия
заряженного тела равна той работе,
которую нужно совершить, чтобы зарядить
это тело:
.
Энергию
называют
собственной энергией заряженного тела.
Ясно, что собственная
энергия есть не что иное, как энергия
электростатического поля этого тела
1.4.2.Энергия заряженного конденсатора
Пусть
-
потенциал
обкладки конденсатора, на которой
находится заряд,
равен
-
а
потенциал обкладки, на которой находится
заряд,
.
Энергия
такой системы зарядов
равна:
,
то
есть равна собственной энергии системы
зарядов,
где
– напряжение между обкладками конденсатора,
.
Найдем энергию
-
плоского
конденсатора.
Энергия,
заключенная в единице объема
электростатического поля называется
объемной
плоскостью энергии.
Эта объемная
плоскость должна быть одинаковой во
всех точках однородного поля, а полная
энергия поля пропорциональна его объему.
Известно,
что
,
,
тогда
для энергии имеем:
,
но
– объем электростатического поля между
обкладками конденсатора,
то
есть
.
Тогда
объемная
плотность энергии
однородного электростатического поля
конденсатора равна
,
то есть определяется
его напряженностью или смещением.
В
случае неоднородных электрических
полей
.
-
сферического
конденсатора.
На
расстоянии
от центра заряженного шара напряженность
его электростатического
поля равна
.
Рассмотрим
бесконечно тонкий шаровой слой,
заключенный между сферами радиусов
и
.
Объем
такого слоя:
.
Энергия
слоя
,
следовательно
.
Тогда
полная энергия заряженного шара равна:
,
где
– радиус
шара.
Но
емкость шара
,
следовательно,
– энергия
электростатического поля сферического
конденсатора
равна
его собственной энергии,
так как заряженное тело потому и обладает
электрической энергией, что при его
зарядке была совершена работа против
сил создаваемого им электростатического
поля.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Конденсатор служит для накопления электрического заряда. Он представляет собой два проводника, разделенных слоем диэлектрика.
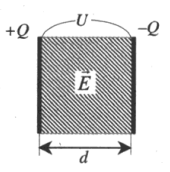
Плоский конденсатор — система двух разноименно заряженных пластин.
Разность потенциалов U (В) между обкладками конденсатора (напряжение между пластинами), определяется произведением напряженности создаваемого ими электрического поля на расстояние между ними:
U=Ed
Электроемкость конденсатора
Определение
Электрическая емкость — характеристика проводника, мера его способности накапливать электрический заряд.
Электроемкость обозначается как C. Единица измерения электрической емкости — Фарад (Ф).
Электроемкость конденсатора определяется формулой:
C=ε0εSd
- ε0 — диэлектрическая постоянная, равная 8,85∙10–12 Кл2/(Н∙м2);
- ε — диэлектрическая проницаемость среды;
- S (м2) — площадь каждой пластины.
Внимание! У воздушного конденсатора диэлектрическая проницаемость среды равна 1.
Связь между электроемкостью конденсатора, зарядом и напряжением определяется формулами:
C=QU=qU
Важно! Электроемкость конденсатора зависит только от площади его пластин, расстояния между ними и диэлектрической проницаемости среды. От заряда и напряжения эта величина не зависит.
Энергия конденсатора
Формула энергии конденсатора
Энергия конденсатора связана с его электроемкостью и вычисляется по следующим формулам:
Wэ=q22C=CU22
Подсказки к задачам
| Конденсатор отключен от источника | q = q′ |
| Конденсатор подключен к источнику | U = U′ |
| Количество теплоты и энергия конденсатора | Q = ∆Wэ |
Пример №1. Вычислить электроемкость плоского воздушного конденсатора с квадратными пластинами со стороной 10 см, расположенными на расстоянии 1 мм друг от друга. Ответ округлить до десятых.
10 см = 0,1 м
1 мм = 0,001 м
Так как между обкладками конденсатора находится воздух, примем диэлектрическую проницаемость среды за единицу.
Площадь квадратной пластины равна квадрату ее стороны:
S = a2
Соединения конденсаторов
| Последовательное соединение | Параллельное соединение | |
| Схема | 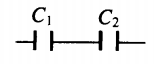 |
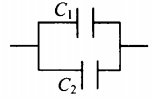 |
| Напряжение |
U=U1+U2 |
U=U1=U2 |
| Заряд |
q=q1=q2 |
q=q1+q2 |
| Электроемкость |
1C=1C1+1C2 |
C=C1+C2 |
Подсказки к задачам
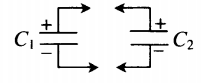
| Два конденсатора, электроемкости которых C1 и C2, заряжены до напряжения U1 и U2. Найдите разность потенциалов после соединения конденсаторов одноименными полюсами. | Схема соединения конденсаторов одноименными полюсами:
Заряд системы после соединения: q′ Электрическая емкость системы: C′ Напряжение: U′ |
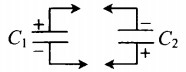
| Два конденсатора, электроемкости которых C1 и C2, заряжены до напряжения U1 и U2. Найдите разность потенциалов после соединения конденсаторов разноименными полюсами. |
Схема соединения конденсаторов разноименными полюсами: Заряд системы после соединения: q′ Электрическая емкость системы: C′ Напряжение: U′ |
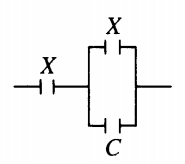
Пример №2. К конденсатору, электрическая емкость которого C = 16 пФ, подключают два одинаковых конденсатора емкостью X: один параллельно, а второй — последовательно (см. рисунок). Емкость образовавшейся батареи конденсаторов равна емкости C. Какова емкость X? Ответ округлите до десятых.
Электрическая емкость параллельного соединения равна:
Cпарал=X+C
Электроемкость последовательного соединения:
1Cпослед=1Cпарал+1X=1X+C+1X
Учтем, что суммарная электроемкость равна C:
1C=1X+C+1X
Преобразуем, умножим выражение на CX(X+C):
X(X+C)=CX+C(X+C)
Раскроем скобки:
X2+XC=CX+CX+C2
X2−CX−C2=0
Решив уравнение, получим: X = 25,9 пФ.
Разбор задач на тему «Заряженная частица в поле конденсатора»
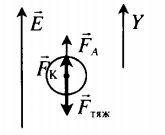
| Шарик, находящийся в масле плотностью ρ, «висит» в поле плоского конденсатора. Плотность вещества шарика ρш > ρ, его радиус r, расстояние между обкладками конденсатора d. Каков заряд шарика, если электрическое поле направлено вверх, а разность потенциалов между обкладками U? | Условие равновесия исходит из второго закона Ньютона:
−Fтяж+−FK+−FA=0 ρш > ρ, поэтому −Fтяж> −FA. В этом случае сила Кулона направлена вверх, а заряд шарика положительный. Схематически это можно отобразить так: Проекция второго закона Ньютона на ось ОУ: FK+FA=Fтяж Сила тяжести равна произведению объема на плотность шарика и на ускорение свободного падения: Fтяж=ρш43πr3g Архимедова сила равна произведению объема шарика на плотность масла и на ускорение свободного падения: FА=ρ43πr3g Сила Кулона: FK=qUd qUd+ρ43πr3g=ρш43πr3g q=(ρш43πr3g−ρ43πr3g)dU=4πr3gd(ρш−ρ)3U |
| Маленький шарик с зарядом q и массой m, подвешенный на невесомой нити с коэффициентом упругости k, находится между вертикальными пластинами воздушного конденсатора. Расстояние между обкладками конденсатора d. Какова разность потенциалов между обкладками конденсатора U, если удлинение нити ∆l? | 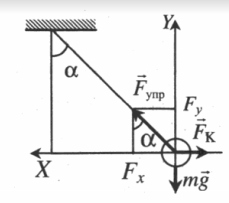
Условие равновесия исходит из второго закона Ньютона: −Fтяж+−FK+−Fупр=0 Проекции на оси ОХ и ОУ соответственно: Fупрsinα−FK=0 Fупрcosα−mg=0 Отсюда: kΔlsinα=qUd kΔlcosα=mg Чтобы избавиться от угла α, возведем уравнения в квадрат и сложим их: (kΔl)2sin2α+(kΔl)2cos2α=(qUd)2+(mg)2 (kΔl)2(sin2α+cos2α)=(qUd)2+(mg)2 sin2α+cos2α=1 (kΔl)2=(qUd)2+(mg)2 U=dq√(kΔl)2−(mg)2 |
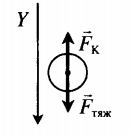
| Пластины плоского конденсатора расположены горизонтально на расстоянии d друг от друга. Напряжение на пластинах конденсатора U. В пространстве между пластинами падает капля жидкости. Масса капли m, ее заряд q. Определите расстояние между пластинами. Влиянием воздуха на движение капли пренебречь. | Второй закон Ньютона в векторной форме:
−Fтяж+−FK=0 Проекция на вертикальную ось: Fтяж−FK=0 Fтяж=mg FK=qUd mg=qUd d=qUmg |
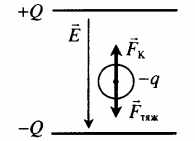
| Между двумя параллельными горизонтально расположенными диэлектрическими пластинами создано однородное электрическое поле с напряженностью −E, направленное вертикально вниз. Между пластинами помещен шарик на расстоянии d от верхней пластины и b от нижней. Заряд шарика –q, масса m. Шарик освобождают, и он начинает двигаться. Через какой промежуток времени t шарик ударится об одну из пластин, если система находится в поле силы тяжести Земли? | Второй закон Ньютона в векторной форме:
−Fтяж+−FK=m−a Согласно условию данной задачи, сила тяжести противоположно направлена силе Кулона. Построим рисунок: Если Fтяж > FK, то шарик движется с ускорением вниз. Ускорение и перемещение в этом случае равны: a=mg−qEm s=b Если Fтяж < FK, то шарик движется с ускорением верх. Ускорение и перемещение в этом случае равны: a=qE−mgm s=d Начальная скорость шарика равна нулю. Поэтому перемещение также равно: s=at22 Сделаем вычисления для случая Fтяж > FK: at22=b mg−qEmt22=b t=√2bmmg−qE Выполняя вычисления для случая Сделаем вычисления для случая Fтяж < FK, получим: t=√2bmqE−mg |
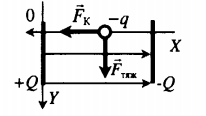
| Между двумя параллельными, вертикально расположенными диэлектрическими пластинами создано однородное электрическое поле, напряженность которого −E и направлена слева направо. Между пластинами помещен шарик на расстоянии b от левой пластины и d от правой. Заряд шарика –q, масса m. Шарик освобождают, и он начинает двигаться. Найдите смещение шарика по вертикали ∆h до удара об одну из пластин. Пластины имеют достаточно большой размер. | Второй закон Ньютона в векторной форме:
−Fтяж+−FK=m−a Если сила Кулона направлена вправо, то sx = d. Если сила Кулона направлена вправо, то sx = b. Учитывая, что заряд меньше нуля, а вектор напряженности направлен вправо, делаем вывод, что кулоновская сила направлена влево. Из проекций второго закона Ньютона выразим проекции ускорения на оси ОХ и ОУ соответственно: ax=qEm ay=g Проекции перемещений на эти же оси: sx=axt22 sx=Δh=gt22 axt22=b Или: qEmt22=b Так как время движения шарика по вертикали и горизонтали одинаково: t2=2Δhg=2mbqE Δh=mbgqE |
Задание EF17979
Введите ответ в поле ввода
Плоский конденсатор подключён к гальваническому элементу. Как изменятся при уменьшении зазора между обкладками конденсатора три величины: ёмкость конденсатора, величина заряда на его обкладках, разность потенциалов между ними?
Для каждой величины определите соответствующий характер изменения:
- увеличится
- уменьшится
- не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
1.Определить, от чего зависит емкость конденсатора, и как она изменится при уменьшении зазора между его обкладками.
2.Определить, от чего зависит величина заряда конденсатора, и как она изменится после уменьшения зазора между его обкладками.
3.Определить, от чего зависит разность потенциалов между обкладками конденсатора, и как она изменится при уменьшении зазора.
Решение
Емкость конденсатора определяется формулой:
C=ε0εSd
Следовательно, емкость имеет обратно пропорциональную зависимость от расстояния между обкладками. Если расстояние уменьшить, то емкость увеличится.
Вот как взаимосвязана электроемкость и заряд конденсатора:
C=qU
Мы выяснили, что электроемкость увеличивается. Следовательно, увеличится и заряд, так как они имеют прямо пропорциональную зависимость.
С учетом того, что плоский конденсатор подключен к гальваническому элементу, разность потенциалов никак не зависит от расстояния между обкладками. Поэтому величина U остается неизменной.
Ответ: 113
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18574
Воспользовавшись оборудованием, представленным на рис. 1, учитель собрал модель плоского конденсатора (рис. 2), зарядил нижнюю пластину положительным зарядом, а корпус электрометра заземлил. Соединённая с корпусом электрометра верхняя пластина конденсатора приобрела отрицательный заряд, равный по модулю заряду нижней пластины. После этого учитель сместил одну пластину относительно другой не изменяя расстояния между ними (рис. 3). Как изменились при этом показания электрометра (увеличились, уменьшились, остались прежними)? Ответ поясните, указав, какие явления и закономерности Вы использовали для объяснения. Показания электрометра в данном опыте прямо пропорциональны разности потенциалов между пластинами конденсатора.
Алгоритм решения
1.Проанализировать каждый этап эксперимента.
2.Установить, от чего зависит угол отклонения стрелки электрометра.
3.Выяснить, что поменяется при смещении одной пластины конденсатора относительно другой, и что при этом произойдет со стрелкой электрометра.
Решение
На первом рисунке стрелка и стержень электрометра, соединённые с нижней пластиной, но изолированные от корпуса, заряжаются положительно. Поэтому стрелка отклоняется на некоторый угол. В верхней пластине и металлическом корпусе электрометра происходит перераспределение свободных электронов таким образом, что верхняя пластина заряжается отрицательно.
На втором рисунке заряды пластин одинаковы по модулю и противоположны по знаку, пластины образуют конденсатор с ёмкостью:
C=ε0εSd
S — площадь перекрытия пластин, d — расстояние между ними, ε — диэлектрическая проницаемость диэлектрика между пластинами.
Характер изменения угла отклонения стрелки совпадает с изменением разности потенциалов между пластинами: при увеличении разности потенциалов увеличивается угол отклонения, при уменьшении разности потенциалов угол уменьшается.
На рисунке 3 площадь перекрытия пластин уменьшилась. Следовательно, уменьшилась электроемкость, которая имеет обратно пропорциональную зависимость от разности потенциалов:
C=qU
Заряд остается постоянным, поскольку система изолированная — заряду просто некуда деться. Поэтому с уменьшением электроемкость растет разность потенциалов. Поэтому показания электрометра увеличатся.
Ответ: Увеличатся
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18695
Ученик изучает свойства плоского конденсатора. Какую пару конденсаторов (см. рисунок) он должен выбрать, чтобы на опыте обнаружить зависимость ёмкости конденсатора от расстояния между его обкладками?
Алгоритм решения
- Установить, какие величины в данном эксперименте должны быть переменными, а какие — постоянными.
- Найти рисунок с парой конденсаторов, удовлетворяющий требованиям, выявленным в шаге 1.
Решение
Чтобы на опыте обнаружить зависимость ёмкости конденсатора от расстояния между его обкладками, нужно сохранить все величины постоянными, кроме самого расстояния. Поэтому площади обкладок должны быть одинаковыми, но расстояние между ними разными, как на рисунке 1.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18703
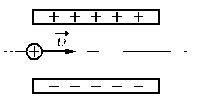
Ответ записать в км/с, округлив до десятков.
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Выполнить рисунок. Указать направление движения протона и силы, действующие на него.
3.Выяснить, при каком условии протон успеет вылететь из конденсатора.
4.Выполнить решение в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса протона: m = 1,67∙10–27 кг.
• Заряд протона: q = 1,6∙10–19 Кл.
• Расстояние между обкладками конденсатора: d = 1 см.
• Длина пластин конденсатора: l = 5 см.
• Напряженность однородного поля внутри конденсатора: E = 5000 В/м.
1 см = 0,01 м
5 см = 0,05 м
Сделаем рисунок:
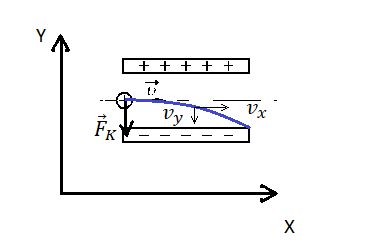
Изначально протон обладает только горизонтальной скоростью v, равной vx. Влетев в однородное электростатическое поле внутри конденсатора, протон обретает вертикальную компоненту скорости, которая растет за счет ускорения, придаваемого кулоновскими силами. Положительно заряженный протон притягивается нижней отрицательно зараженной пластиной конденсатора.
Чтобы протон вылетел из конденсатора, его горизонтальная компонента скорости должна быть достаточной для того, чтобы частица не притянулась к нижней пластине раньше. Время, которое понадобится протону для преодоления длины пластин конденсатора со скоростью vx:
t=lvx=lv
Протон влетел в пространство между обкладками конденсатора на одинаковом расстоянии от них. Следовательно, прежде чем он упадет на нижнюю пластину, по оси OY он переместится на расстояние, равное 0,5d. Так как начальная компонента скорости равна нулю (мы пренебрегаем силой тяжести):
0,5d=at22
Протон вылетит из конденсатора, а не упадет на его пластину, если время горизонтального перемещения до конца пластин будет как минимум равно времени падения. Выразим время падения:
t=√da
Приравняем правые части уравнений времени и получим:
lv=√da
Отсюда скорость равна:
v=√al2d
Ускорение выразим из второго закона Ньютона:
FK=ma=qUd
a=qUmd
Но известно, что:
U=Ed
Поэтому:
a=qEdmd=qEm
Отсюда:
Минимальная скорость, с которой протон должен влететь в конденсатор, составляет 346∙103 м/с. Округлим до десятков и переведем в км/с. Получим 350 км/с.
Ответ: 350
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 6k
Конденсатором называется система, состоящая из двух проводников, расположенных достаточно близко друг от друга. Проводники называют обкладками конденсатора. Если на обкладки конденсатора поместить равные по модулю и противоположные по знаку заряды, то разность потенциалов (напряжение) между обкладками будет пропорциональна заряду обкладок, т. е. отношение заряда к напряжению не будет зависеть от заряда. На основании этого утверждения, которое приводим без доказательства, вводится понятие электроёмкости (ёмкости конденсатора).
Ёмкостью конденсатора называется отношение заряда $$ Q$$ одной из обкладок к разности потенциалов $$ U$$ между этой обкладкой и соседней:
| $$ C={displaystyle frac{Q}{U}}$$. | (10.1) |
Если взят заряд на положительно заряженной обкладке, то $$ Q>0, U>0$$ и получится $$ C>0$$. Если заряд взят на отрицательной обкладке, то Q<0, U<0Q<0,;U<0 и опять будет $$ C>0$$. Итак, из определения ёмкости следует, что ёмкость величина положительная. В системе СИ ёмкость измеряется в фарадах: `1″Ф”=1` Кл/В.
Требование близости обкладок друг к другу связано с тем, что для независимости $$ C$$ от $$ Q$$ в (10.1) нужно, чтобы поле от зарядов на обкладках было сосредоточено практически полностью между обкладками, т. е. все силовые линии, начинающиеся на одной обкладке, заканчивались только на другой и не уходили на окружающие тела. В этом случае окружающие тела не будут влиять на ёмкость конденсатора.
Можно вывести, что ёмкость плоского конденсатора
| $$ C={displaystyle frac{varepsilon {varepsilon }_{0}S}{d}}$$. | (10.2) |
Здесь $$ S$$ – площадь обкладок, $$ d$$ – расстояние между ними, $$ varepsilon $$ – диэлектрическая проницаемость диэлектрика между обкладками.
При последовательном соединении изначально не заряженных конденсаторов с ёмкостями $$ {C}_{1}, {C}_{2}, …$$, общий заряд равен заряду каждого конденсатора, общее напряжение равно сумме напряжений на отдельных конденсаторах, общая ёмкость определяется из формулы: $$ {displaystyle frac{1}{C}}={displaystyle frac{1}{{C}_{1}}}+{displaystyle frac{1}{{C}_{2}}}+…$$
Полезно помнить формулу для частного случая последовательного соединения двух конденсаторов: $$ C={displaystyle frac{{C}_{1}{C}_{2}}{{C}_{1}+{C}_{2}}}$$.
Для последовательно соединённых n одинаковых конденсаторов ёмкостью $$ {C}_{1}$$ каждый $$ C={C}_{1}/n.$$
Если последовательно соединены предварительно заряженные конденсаторы, то применение перечисленных выше свойств и формул может привести к неправильному результату!
При параллельном соединении конденсаторов с емкостями $$ {C}_{1,} {C}_{2}, …$$ общий заряд равен сумме зарядов отдельных конденсаторов, общее напряжение равно напряжению на каждом, общая ёмкость равна сумме ёмкостей:
$$ C={C}_{1}+{C}_{2}+…$$
 |
| Рис. 10.1 |
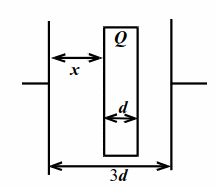
В плоский конденсатор параллельно его обкладкам вставлена пластина из диэлектрика с диэлектрической проницаемостью $$ varepsilon $$ (рис. 10.1). Площадь обкладок конденсатора и пластины $$ S$$, толщина пластины $$ d$$, расстояние между обкладками $$ 3d$$. Найти ёмкость такого конденсатора.
Пусть расстояние от пластины до левой обкладки конденсатора $$ x$$. Наклеим мысленно на обе стороны пластины тонкую проводящую и незаряженную фольгу. От этого ничего не изменится. Обе фольги можно рассматривать как своеобразные провода, соединяющие три последовательно соединённых конденсатора с расстояниями $$ x$$, $$ d$$ и $$ 2d-x$$. Для общей ёмкости $$ C$$:
$$ {displaystyle frac{1}{C}}={displaystyle frac{x}{{varepsilon }_{0}S}}+{displaystyle frac{d}{varepsilon {varepsilon }_{0}S}}+{displaystyle frac{2d-x}{{varepsilon }_{0}S}}$$.
Окончательно $$ C={displaystyle frac{varepsilon {varepsilon }_{0}S}{d(2varepsilon +1)}}.$$ Заметим, что не заданная в условии величина $$ x$$ «исчезла» в процессе решения.
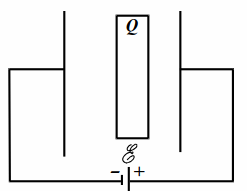 |
| Рис. 10.2 |
В плоский конденсатор ёмкостью $$ C$$ вставлена параллельно обкладкам плоская проводящая пластина с зарядом $$ Q$$ (рис. 10.2). Конденсатор подсоединён к источнику с ЭДС $$ mathcal{E}$$. Площади пластины и обкладок конденсатора равны. Толщина пластины равна расстоянию от неё до правой обкладки и составляет четверть от расстояния между обкладками. Найти заряд конденсатора.
Пусть $$ d$$ – расстояние между обкладками, $$ S$$ – их площадь. Пусть $$ q$$ заряд правой обкладки. Тогда заряд левой будет $$ -q$$, т. к. заряд в значительных количествах не может накапливаться на соединительных проводах и в источнике. Направим ось $$ x$$ влево (рис. 10.3).
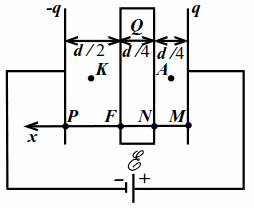 |
| Рис. 10.3 |
Заметим, что поле внутри пластины отсутствует и разность потенциалов $$ {varphi }_{N}-{varphi }_{F}$$ между точками $$ N$$ и $$ F$$ равна нулю. Кроме того, заряды на поверхностях пластины создают вне пластины такое же поле, как и заряд $$ Q$$, если бы его расположить на любой из двух поверхностей пластины. Это легко показать отдельно.
Разность потенциалов $$ {varphi }_{M}-{varphi }_{P}$$ между точками $$ M$$ и $$ P$$ равна $$ mathcal{E}$$. Поэтому
$$ ({varphi }_{M}-{varphi }_{N})+({varphi }_{N}-{varphi }_{F})+({varphi }_{F}-{varphi }_{P})=mathcal{E}$$.
У нас $$ {varphi }_{M}-{varphi }_{N}={E}_{A}{displaystyle frac{d}{4}}, {varphi }_{N}-{varphi }_{F}=0, {varphi }_{F}-{varphi }_{P}={E}_{K}{displaystyle frac{d}{2}}$$.
Здесь – $$ {E}_{A}$$ и $$ {E}_{K}$$ – проекции напряжённости результирующего поля на ось `x`. По принципу суперпозиции полей
$$ {E}_{A}={displaystyle frac{q}{2{varepsilon }_{0}S}}-{displaystyle frac{Q}{2{varepsilon }_{0}S}}-{displaystyle frac{-q}{2{varepsilon }_{0}S}}={displaystyle frac{1}{2{varepsilon }_{0}S}}left(2q-Qright)$$,
$$ {E}_{K}={displaystyle frac{q}{2{varepsilon }_{0}S}}+{displaystyle frac{Q}{2{varepsilon }_{0}S}}-{displaystyle frac{-q}{2{varepsilon }_{0}S}}={displaystyle frac{1}{2{varepsilon }_{0}S}}left(2q+Qright)$$.
Подставляя выражения для $$ {E}_{A}$$, $$ {E}_{K}$$ и разностей потенциалов в первое
уравнение, получим после упрощений $$ 6q+Q=8mathcal{E}{displaystyle frac{{varepsilon }_{0}S}{d}}$$.
Так как $$ {displaystyle frac{{varepsilon }_{0}S}{d}}=C$$, то $$ q=(8Cmathcal{E}-Q)/6$$.
Следует заметить, что знак найденного заряда правой обкладки зависит от соотношения заданных в условии задачи величин.
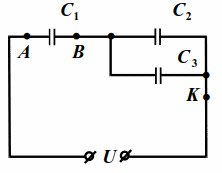 |
| Рис. 10.4 |
На схему (рис. 10.4) подано напряжение `U=24` В. Ёмкости конденсаторов `C_1=1` мкФ, $$ {C}_{2}=2$$ мкФ, $$ {C}_{3}=3$$ мкФ. Найти напряжения на конденсаторах.
В задачах, где есть схемы с конденсаторами, обычно предполагается, что схемы собраны из первоначально незаряженных конденсаторов.
Ёмкость между точками $$ B$$ и $$ K$$:
$$ {C}_{BK}={C}_{2}+{C}_{3}=5$$ мкФ.
Общая емкость: $$ {C}_{AK}={displaystyle frac{{C}_{1}{C}_{BK}}{{C}_{1}+{C}_{BK}}}={displaystyle frac{5}{6}}$$ мкФ.
Общий заряд всей батареи конденсаторов $$ {q}_{AK}={C}_{AK}U=20·{10}^{-6 }mathrm{Кл}.$$
Так как заряд $$ {q}_{1}$$ конденсатора $$ {C}_{1}$$ равен заряду батареи, то напряжение на этом конденсаторе $$ {U}_{1}={q}_{1}/{C}_{1}={q}_{AK}/{C}_{1}=20$$ В. Напряжения на конденсаторах $$ {C}_{2}$$ и $$ {C}_{3}$$ равны напряжению между точками $$ B$$ и $$ K$$ и в сумме с $$ {U}_{1}$$ дают $$ U$$.
Поэтому $$ {U}_{2}={U}_{3}={U}_{BK}=U-{U}_{1}=4$$ В.
Приведённая в задаче схема негромоздкая, и ответ легко получить в общем виде:
$$ {U}_{1}={displaystyle frac{{C}_{2}+{C}_{3}}{{C}_{1}+{C}_{2}+{C}_{3}}}U=20$$ B,
$$ U2=U3={displaystyle frac{{C}_{1}}{{C}_{1}+{C}_{2}+{C}_{3}}}U=4$$ B.
Проводники электричества — это вещества и материалы, которые хорошо проводят электричество. Схема из двух проводящих пластин, расположенных параллельно друг другу, называется плоским конденсатором.
Однако конденсаторы — это не только искусственные устройства. Часто в природе мы встречаем системы, которые можно рассматривать как плоские конденсаторы. Примером такого «конденсатора» являются клеточные мембраны внутри вашего тела (рис. 1). Знаете ли вы, какова напряженность электрического поля внутри такой мембраны?
Клеточная мембрана: биологическая мембрана, функция которой заключается в отделении внутренней части клетки от внешней среды. Эта мембрана состоит из двух липидных слоев. Между его стенками существует разность потенциалов. Это позволяет ему реагировать на внешние раздражители.
Что такое плоский конденсатор?
Плоский конденсатор — это расположение двух параллельных друг другу металлических пластин, называемых обкладками конденсатора. Пусть площадь каждой из этих пластин равна S, а расстояние между крышками равно d. На рисунке 2 показана схема заряженного плоского конденсатора.
Линии электрического поля обозначены на рис. 2. В каждой точке вектор напряженности электрического поля одинаков, т.е. поле однородно.
Согласно закону Гаусса, значение напряженности поля от каждой обкладки составляет: E+/- = σ / 2ε0 .
Закон Гаусса (для электричества):
Закон Гаусса (для электричества): уравнение, связывающее электрическое поле и его источник. Оно гласит, что поток ФE напряженности электрического поля Е, проникающий через любую замкнутую поверхность S, равен суммарному заряду q внутри этой поверхности, деленному на диэлектрическую проницаемость вакуума.
Напротив, результирующая напряженность поля от обоих покрытий составляет:
E = E+ + E— = 2 * σ / 2ε0 = σ / ε0 , где
σ — плотность поверхностного заряда, определяемая как отношение заряда q, накопленного на поверхности, к величине площади поверхности S: σ = q / S ,
ε0 — диэлектрическая проницаемость вакуума, ε0 = 8,85 · 10-12 Ф · м−1 .
Таким образом:
E = q / S * ε0
Из приведенной выше формулы мы можем определить единицу напряженности поля — [ В / м ].
Таким образом, единицей напряженности электрического поля, помимо ньютона на кулон, является вольт на метр.
Расчет разности потенциалов между обкладками плоского конденсатора
Итак, мы уже знаем, как выглядит поле между обкладками плоского конденсатора. Теперь рассмотрим, существует ли связь между разностью потенциалов и напряженностью электростатического поля в конденсаторе. В конце концов, и напряженность, и потенциал являются величинами, характеризующими электростатическое поле.
По определению, разность потенциалов ΔV между точками A и B электрического поля равна отношению работы, необходимой для переноса пробного заряда между этими точками (WAB), к величине этого заряда.
ΔV = WAB / q
Единицей измерения потенциала является вольт, который мы обозначаем символом В.
В случае плоского конденсатора, когда мы перемещаем заряд в однородном электрическом поле, работа WAB равна скалярному произведению вектора силы, действующей на образец заряда, и вектора смещения с длиной, равной расстоянию между обкладками d, и возвратом, соответствующим возврату вектора напряженности электрического поля (рис. 3).
WAB = F * d
Из определения напряженности электрического поля следует, что: F = E * q
То есть:
WAB = F * d = E * q * d = q * E * d * cos α
Где α (угол между вектором напряженности электрического поля и вектором смещения) равен 0, т.е. cosα = 1. Поэтому:
WAB = E * d * q
Подставляя приведенную выше формулу для: ΔV = WAB / q = q * E * d / q = E * d
Эта формула определяет связь между разностью потенциалов и напряженностью электрического поля в плоском конденсаторе.
Теперь преобразуем эту формулу, чтобы получить зависимость напряженности поля от разности потенциалов:
E = ΔV / d
Эта формула говорит нам, что величина напряженности поля в плоском конденсаторе равна отношению разности потенциалов между обкладками этого конденсатора к расстоянию между этими обкладками. Таким образом, мы видим, что напряженность поля в плоском конденсаторе E прямо пропорциональна разности потенциалов между его обкладками ∆V. Это означает, что если разность потенциалов между обкладками конденсатора увеличится (например, в два раза), то значение напряженности поля между обкладками также увеличится (также в два раза).
Формула для напряженности поля:
E = q / S * ε0
справедлива для вакуумного конденсатора. Если у нас есть диэлектрик между обкладками конденсатора, мы все равно должны учитывать его относительную электрическую проницаемость εr, которая является безразмерной величиной.
Тогда формула принимает вид:
E = q / S * ε0 * εr