III. Основы электродинамики
Тестирование онлайн
Работа электростатического поля
Рассмотрим ситуацию: заряд q0 попадает в электростатическое поле. Это электростатическое поле тоже создается каким-то заряженным телом или системой тел, но нас это не интересует. На заряд q0 со стороны поля действует сила, которая может совершать работу и перемещать этот заряд в поле.



Работа электростатического поля не зависит от траектории. Работа поля при перемещении заряда по замкнутой траектории равна нулю. По этой причине силы электростатического поля называются консервативными, а само поле называется потенциальным.
Потенциал
Система “заряд – электростатическое поле” или “заряд – заряд” обладает потенциальной энергией, подобно тому, как система “гравитационное поле – тело” обладает потенциальной энергией.
Физическая скалярная величина, характеризующая энергетическое состояние поля называется потенциалом данной точки поля. В поле помещается заряд q, он обладает потенциальной энергией W. Потенциал – это характеристика электростатического поля.


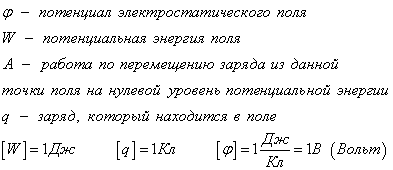
Вспомним потенциальную энергию в механике. Потенциальная энергия равна нулю, когда тело находится на земле. А когда тело поднимают на некоторую высоту, то говорят, что тело обладает потенциальной энергией.
Касательно потенциальной энергии в электричестве, то здесь нет нулевого уровня потенциальной энергии. Его выбирают произвольно. Поэтому потенциал является относительной физической величиной.
В механике тела стремятся занять положение с наименьшей потенциальной энергией. В электричестве же под действием сил поля положительно заряженное тело стремится переместится из точки с более высоким потенциалом в точку с более низким потенциалом, а отрицательно заряженное тело – наоборот.
Потенциальная энергия поля – это работа, которую выполняет электростатическая сила при перемещении заряда из данной точки поля в точку с нулевым потенциалом.
Рассмотрим частный случай, когда электростатическое поле создается электрическим зарядом Q. Для исследования потенциала такого поля нет необходимости в него вносить заряд q. Можно высчитать потенциал любой точки такого поля, находящейся на расстоянии r от заряда Q.


Диэлектрическая проницаемость среды имеет известное значение (табличное), характеризует среду, в которой существует поле. Для воздуха она равна единице.
Разность потенциалов
Работа поля по перемещению заряда из одной точки в другую, называется разностью потенциалов
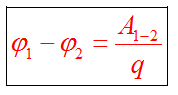
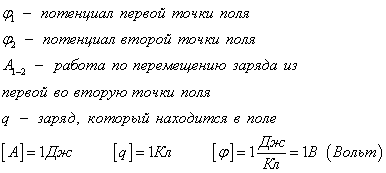
Эту формулу можно представить в ином виде


Эквипотенциальная поверхность (линия) – поверхность равного потенциала. Работа по перемещению заряда вдоль эквипотенциальной поверхности равна нулю.
Напряжение
Разность потенциалов называют еще электрическим напряжением при условии, что сторонние силы не действуют или их действием можно пренебречь.
Напряжение между двумя точками в однородном электрическом поле, расположенными по одной линии напряженности, равно произведению модуля вектора напряженности поля на расстояние между этими точками.
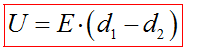

От величины напряжения зависит ток в цепи и энергия заряженной частицы.
Принцип суперпозиции
Потенциал поля, созданного несколькими зарядами, равен алгебраической (с учетом знака потенциала) сумме потенциалов полей каждого поля в отдельности
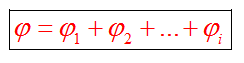
Как определить знак потенциала
Зависимость напряженности и потенциала от расстояния
Напряжение в природе
Энергия взаимодействия зарядов*
Работа электростатического поля
Рассмотрим ситуацию: заряд q0 попадает в электростатическое поле. Это электростатическое поле тоже создается каким-то заряженным телом или системой тел, но нас это не интересует. На заряд q0 со стороны поля действует сила, которая может совершать работу и перемещать этот заряд в поле.

Работа электростатического поля не зависит от траектории. Работа поля при перемещении заряда по замкнутой траектории равна нулю. По этой причине силы электростатического поля называются консервативными
, а само поле называется
потенциальным
.
Движение заряда в электрическом поле
Когда носитель электрического заряда оказывается в электростатическом поле, на него неизбежно начинает действовать кулоновская сила. Это приводит к тому, что носитель заряда начинает перемещаться в пространстве, если, конечно, кулоновские силы не скомпенсированы другими, противодействующими силами. Рассмотрим случай, когда в электрическом поле оказался пробный заряд
q
совершенно свободный от действия других сил. Как только этот заряд окажется в зоне действия силовых линий электрического поля, то на него будет действовать сила в соответствии с Законом Кулона.
Как известно, механическая сила является векторной величиной, а значит имеет и величину, и направление. Носитель заряда в электрическом поле начнет менять свое энергетическое состояние. Как это проявляется? Одноименные заряды отталкиваются, а разноименные притягиваются. Наш заряд в зависимости от знака начнет сближаться с противоположным ему знаком заряда, которое и образует электрическое поле. Легче всего это увидеть, посмотрев на силовые линии напряженности поля. Согласно правилам они имеют направление от заряда +Q
к заряду
-Q
, иначе говоря выходят из
положительных
зарядов (источника) и заходят в
отрицательные
заряды (источника).
Советуем изучить Аккумулятор для шуруповерта: новые возможности для эффективной работы
Направление силы действия на пробный заряд q
определить очень легко, если он положительный, то сила будет направлена по силовым линиям поля, а если отрицательный, то против силовых линий. Траектория движения будет зависеть от начальной скорости заряда, ее величины и направления. Действующая сила будет ускорять заряд, то есть его скорость по величине и направлению будет меняться в сторону действия кулоновской силы.
Движение заряда q
в электрическом поле
На рисунке изображена примерная траектория движения заряда +q
, имеющего некоторую начальную скорость
V
. Если бы заряд имел противоположный знак, то траектория движения была бы зеркально отражена от оси X, и заряд бы двигался в сторону пластины (+). По оси Y можно изобразить шкалу потенциала, которая так же будет иметь полярность.
Спрашивается. Что это за шкала и как определить где больший, а где меньший потенциал? Учитывая, что по определению и по действующим правилам силовые линии выходят из зарядов (+) и уходят в бесконечность, где потенциал равен нулю, то максимальный положительный потенциал будет в начале силовых линий от источника, а максимальный отрицательный потенциал там, где линии заходят в источник поля. Наш заряд +q
, изображенный на рисунке выше будет двигаться от большего потенциала к меньшему, тем самым уменьшая потенциальную энергию поля, а точнее, преобразуя ее в кинетическую энергию. Если же в нашем случае был заряд
-q
, то для него потенциалы поменяли бы знак, арифметически, за счет умножения на -1, он всё также бы двигался в сторону уменьшения энергии поля.
Потенциал
Система «заряд — электростатическое поле» или «заряд — заряд» обладает потенциальной энергией, подобно тому, как система «гравитационное поле — тело» обладает потенциальной энергией.
Физическая скалярная величина, характеризующая энергетическое состояние поля называется потенциалом
данной точки поля. В поле помещается заряд q, он обладает потенциальной энергией W. Потенциал — это характеристика электростатического поля.

Вспомним потенциальную энергию в механике. Потенциальная энергия равна нулю, когда тело находится на земле. А когда тело поднимают на некоторую высоту, то говорят, что тело обладает потенциальной энергией.
Касательно потенциальной энергии в электричестве, то здесь нет нулевого уровня потенциальной энергии. Его выбирают произвольно. Поэтому потенциал является относительной физической величиной.
В механике тела стремятся занять положение с наименьшей потенциальной энергией. В электричестве же под действием сил поля положительно заряженное тело стремится переместится из точки с более высоким потенциалом в точку с более низким потенциалом, а отрицательно заряженное тело — наоборот.
Потенциальная энергия поля — это работа, которую выполняет электростатическая сила при перемещении заряда из данной точки поля в точку с нулевым потенциалом.
Рассмотрим частный случай, когда электростатическое поле создается электрическим зарядом Q. Для исследования потенциала такого поля нет необходимости в него вносить заряд q. Можно высчитать потенциал любой точки такого поля, находящейся на расстоянии r от заряда Q.

Диэлектрическая проницаемость среды имеет известное значение (табличное), характеризует среду, в которой существует поле. Для воздуха она равна единице.
Падение потенциала вдоль проводника
На концах проводника, помещенного в электрическое поле, начинает наблюдаться разность потенциалов. Вследствие этого электроны начинают перемещаться в сторону увеличения разности. В проводнике возникает электрический ток. Свободные электроны продвигаются вдоль проводника до тех пор, пока разница ни будет равна нулю. На практике для поддержания заданной величины тока цепи запитываются от источников напряжения или тока. Разница заключается в следующем:
Советуем изучить Мощные магниты
- Источник тока поддерживает в цепи постоянный ток вне зависимости от сопротивления нагрузки;
- Источник напряжения поддерживает на своих зажимах строго постоянную ЭДС, независимо от величины потребляемого тока.
Разница потенциалов (падение напряжения) пропорциональна расстоянию от концов проводника, то есть обладает линейной зависимостью.
Как определить знак потенциала
При решении задач возникает много путаницы при определении знака потенциала, разности потенциалов, работы.
На рисунке изображены линии напряженности. В какой точке поля потенциал больше?
Верный ответ — точка 1. Вспомним, что линии напряженности начинаются на положительном заряде, а значит положительный заряд находится слева, следовательно максимальным потенциалом обладает крайняя левая точка.
Если происходит исследование поля, которое создается отрицательным зарядом, то потенциал поля вблизи заряда имеет отрицательное значение, в этом легко убедиться, если в формулу подставить заряд со знаком «минус». Чем дальше от отрицательного заряда, тем потенциал поля больше.
Если происходит перемещение положительного заряда вдоль линий напряженности, то разность потенциалов и работа являются положительными. Если вдоль линий напряженности происходит перемещение отрицательного заряда, то разность потенциалов имеет знак «+», работа имеет знак «-«.
Порассуждайте самостоятельно отрицательные или положительные значения будут принимать работа и разность потенциалов, если заряд перемещать в обратном направлении относительно линий напряженности.
Основные формулы электричества
Изучение основ электродинамики, электрики невозможно без определения электрического поля, точных зарядов, сопротивления и прочих явлений.

Поэтому важно рассмотреть все основные формулы электричества и примеры решения задач с их использованием.
Закон Кулона
Согласно короткому описанию, это физический закон, который говорит о взаимодействии между прямо стоящими точечными электрозарядами в зависимости от того, на каком расстоянии они находятся. Согласно полному определению, формулировка обозначает, что между двумя точками в виде электрических зарядов формируется вакуум. Там появляется конкретная сила, которая пропорциональна умножению их модульных частиц, поделенных на квадратный показатель расстояния.
Расстояние — длина, которая соединяет заряды. Сила взаимодействия направлена по отрезку. Кулоновская сила — сила, отталкивающая при зарядах минус-минус и плюс-плюс и притягательная при минус-плюс и плюс-минус.
Обратите внимание! Электрическая сила формула выглядит так: F=k⋅|q1|⋅|q2|/r2, где F — сила заряда, q — величина заряда, r — вектор или расстояние между зарядами, а k — коэффициент пропорциональности. Последний равен c2·10−7 Гн/м.

Решение задачи с законом Кулона. При наличии заряженных шариков, которые находятся на расстоянии 15 см и отталкиваются с силой 1 Н в поиске начального заряда, выявить неизвестное можно, переведя основные единицы в систему СИ и подставив величины в указанную формулу. Выйдет значение 2 * 5 * 10 (-8) = 10 (-7).
Напряженность поля уединенного точечного заряда
Электрическое поле будучи материей, создаваемой электрическими точечными зарядами, характеризуется разными величинами, в том числе напряженностью. Напряженность выступает векторной величиной или силовой характеристикой поля, которая направлена в сторону электростатического взаимодействия зарядов. Чтобы получить ее, нужно использовать формулу E = k (q / r (2)), где Е — векторное поле.

Согласно данной формулировке, напряженность поля заряда имеет обратную пропорциональность квадратному значению расстояния от заряда. То есть если промежуток увеличивается в несколько раз, показатель напряжения снижается в четыре.
Применить закон можно для решения задач. Например, неизвестен радиус. Тогда нужно преобразовать константу. Нужно решить уравнение E / r (2) = kq, подставив известные числа.
Потенциал точки в поле точечного заряда
Потенциалом в электростатическом поле называется скалярная величина, которая равна делению потенциального показателя энергии заряда на него. Он не зависит от величины q, которая помещена в область. Так как потенциальный показатель энергии зависит от того, какая выбрана система координат, то потенциал определяется с точностью до постоянной. Он равен работе поле, которое смещает единичный положительный заряд в бесконечность. Выражается через ф = W / q =const.
Вам это будет интересно Особенности люменов и люксов

Обратите внимание! В задачах можно преобразовывать константу. Если неизвестно W, то можно поделить q на ф, а если q — то, W на ф.
Потенциальная энергия заряда в электростатическом поле

Потенциальная энергия заряда q1 в поле точечного заряда
Во время перемещения заряженных частиц по полю из одной точки в другую они совершают некую работу за определенный временной промежуток. Потенциальная энергия в этих точках не зависит от того, какой путь держат заряженные частицы. Энергия первого заряда пропорциональна его модулю. Выражается это все в формуле, представленной на картинке ниже. Задачи решать можно, используя представленную константу и вставляя известные значения.

Теорема Гаусса
Основной закон в электродинамике, входящий в уравнения Максвелла. Это следствие из кулоновского умозаключения и принципа суперпозиции. По ней вектор напряжения поля движется сквозь произвольное значение замкнутой поверхности, окруженной зарядами. Он имеет пропорциональность сумме заряженных частиц, которые находятся внутри этого замкнутого пространства. Указанный вектор поделен на е0. Все это выражается формулой, указанной ниже.

Напряженность электрического поля вблизи от поверхности проводника
Напряженность суммарного пространства заряженных частиц имеет прямую пропорциональность поверхностному показателю их плотности. Если в задаче требуется найти напряженность, а поверхностная заряженная плотность это сигма, то нужно нарисовать цилиндр и обозначить, что поток сквозь его боковую поверхность равен 0. В таком случае линии напряженности будут параллельны боковой поверхности. Получится, что ф = 2ф, осн =2еs, а 2es =q / 2ε0.

Емкость плоского конденсатора
Емкостью называется проводниковая характеристика, по которой электрический заряд может накапливать энергию. Плоским конденсатором называются несколько противоположно заряженных пластин, разделенных диэлектрическим тонким слоем. Емкостью плоского конденсатора считается его характеристика, способность к накоплению электрической энергии.
Обратите внимание! Это физическая величина, которая равна делению заряда на разность потенциалов его обкладки. Зарядом при этом служит заряженная одна пластина.
Если в задаче требуется узнать емкость конденсатора из двух пластин с площадью в 10(-2) квадратных метров и в них находится 2*10(-3) метровый лист, ε0 электрическая постоянная с 8,85×10-12 фарад на метр и ε=6 — диэлектрическая проницаемость слюды. В таком случае нужно вставить значения в формулу C= ε* ε* S/d.

Энергия плоского конденсатора
Поскольку любая частица конденсатора имеет способность запаса энергии, который сохранен на конденсаторной обкладке, вычислить эту самую Е просто, поскольку чтобы элемент зарядился, ему нужно совершить работу. Работа совершается полем. В результате была выведена следующая формула: Еp = А = qEd, где А является работой, d — расстоянием.

Формулы для постоянного электрического тока
Постоянный электрический ток не изменяется в величине и направлении. Он используется для расчета замкнутой, однородной цепи, мощности и прочих параметров. Поэтому важно знать формулы для него и основные законы, связанные с ним.
Вам это будет интересно Описание распределительной коробки

Закон Ома для участка однородной цепи
Чтобы электрический ток существовал, нужно поле. Для его образования, нужны потенциалы или разность их, выраженная напряжением. Ток будет направлен на снижение потенциалов, а электроны начнут свое передвижение в обратном направлении. В 1826 г. Г. Ом провел исследование и сделал заключение: чем больше показатель напряжения, тем больше ток, который проходит через участок.
К сведению! Смежные проводники при этом проводят электричество по-разному. То есть каждый элемент имеет свою проводимость, электрическое сопротивление.
В результате, согласно теореме Ома, сила тока для участка однородной цепи будет иметь прямую пропорциональность показателю напряжения на нем и обратную пропорциональность проводниковому сопротивлению.

По формуле I = U / R, где I считается силой тока, U — напряжением, а R — электрическим сопротивлением, последнее значение можно найти, если p * l / S, где p является удельным проводниковым сопротивлением, l — длиной проводника, а S — площадью поперечного проводникового сечения.
Закон Ома для замкнутой цепи с источником тока
Ом сделал формулу и для замкнутой цепи. По ней ток на этом участке из токового источника, имеющего внутреннее и внешнее нагрузочное сопротивление, равен делению электродвижущей силы источника на сумму внутреннего и внешнего сопротивления. Она выглядит так: I = e / R + r, где I является токовой силой, е — ЭДС, R — сопротивлением, а r — внутренней сопротивляемостью источника напряжения.
Обратите внимание! В физическом смысле по этому закону, чем выше показатель ЭДС, тем выше источник энергии, больше скорость движения зарядов. Чем выше сопротивляемость, тем ниже величина тока.

Работа постоянного тока
Энергия, когда проходит через проводник, упорядоченно двигается в носитель. Во время движения она совершает работу. В результате работой постоянного тока называется деятельность поля, направленная на перенос электрических зарядов по проводнику. Она равна умножению I на совершаемое работой напряжение и время.
Закон Джоуля-Ленца
Когда электричество проходит через какой-то проводник с сопротивляемостью, всегда высвобождается теплота. Количество тепла, которое высвободилось за определенный промежуток времени, определяет закон Джоуля-Ленца. По формуле мощность тепла равняется умножению плотности электричества на напряжение — w =j * E = oE(2).
Обратите внимание! В практическом понимании закон имеет значение для снижения потери электроэнергии, выбора проводника для электроцепи, подбора электронагревательного прибора и использования плавкого предохранителя для защиты сети.

Полная мощность, развиваемая источником тока
Мощность — работа, которая совершается за одну секунду времени. Электрическая мощность является физической величиной, которая характеризует скорость передачи с преобразованием электроэнергии.
Работа, которая развивается источником электроэнергии по всей цепи, это полная мощность. Ее можно определить по формуле Р = El, где E считается ЭДС, а I — величиной токовой характеристики.
К сведению! Если есть линейная нагрузка, то полный мощностный показатель равен квадратному корню из квадратов активной и реактивной работы источника. Если есть нелинейная нагрузка, то она равна квадратному корню из квадратов активной и неактивной работы источника.

В практических измерениях такая работа выражается в киловаттах в час. Используется, чтобы измерять потребление электричества в бытовых и производственных условиях, определять выработанную электрическую энергию в электрическом оборудовании.
Полезная мощность
Максимальная или полезная мощность — та, что выделяется во внешнем промежутке цепи, то есть во время нагрузки резистора. Она может быть применена для выполнения каких-либо задач. Подобное понятие можно применить, чтобы рассчитать, как работает электрический двигатель или трансформатор, который способен на потребление активной и реактивной составляющей.
Вам это будет интересно Особенности дифференциального тока

Полезный мощностный показатель можно рассчитать по трем формулам: P = I 2R, P = U2 / r, P = IU, где I является силой тока на определенном участке цепи; U — напряжением на части клемм (зажимов) токового источника, а R — сопротивлением нагрузки или внешней цепью.
Коэффициент полезного действия источника тока
Коэффициентом полезного действия токового источника называется деление полезного мощностного показателя на полный. Если внутреннее сопротивление источника равно внешнему, то половина результатов всей работы будет утеряна в источнике, а другая половина будет выделена на нагрузке. В такой ситуации КПД будет равен 50 %.
Если рассматривать это понятие наиболее полно, то когда электрические заряды перемещаются по замкнутой электрической цепи, источник тока выполняет определенную полезную и полную работу. Совершая первую, он перемещает заряды во внешнюю цепь. Делая вторую работу, заряженные частицы перемещаются по всему участку.

Обратите внимание! Полезное действие достигается, когда сопротивление внешней электроцепи будет иметь определенное значение, зависящее от источника и нагрузки. Соотношения полезной работы на полную выражают формулой: η = Аполез / Аполн = Рполез / Рполн = U/ε = R / (R + r).
Первое правило Кирхгофа
Согласно первому закону Кирхгофу, токовая сумма в любом участке электрической цепи равняется нулевому значению. Направленный заряд к узлу положительный, а от него — отрицательный. Алгебраическая токовая сумма зарядов, которые направлены к узлу, равна сумме тех, которые направлены от него. Если перевести это правило, то можно получить следующее определение: сколько тока попадает в узел, столько и выходит из него. Это правило вытекает из закона о сохранности заряженных частиц.
Благодаря решению линейных уравнений на основе кирхгофских правил можно отыскать все токовые значения и напряжения на участках постоянного, переменного и квазистационарного электротоков.
Обратите внимание! В электотехнике правило Кирхгофа имеет особое значение, поскольку оно универсально для решения многих поставленных задач в теории электроцепи. С помощью него можно рассчитать сложные электрические цепи. Применяя его, можно получить систему линейных уравнений относительно токам или напряжениям на всех межузловых ветвях цепей.

Второе правило Кирхгофа
Второе кирхгофское правило вытекает из первого и третьего максвеллского уравнения. По нему алгебраическая сумма напряжений на резистивных элементах замкнутого участка равна сумме ЭДС, которая входит в него. Если на участке нет ЭДС, то суммарный показатель падения напряжения равен нулевому значению. Если еще проще, то во время полного обхода контура потенциал изменяется. Он возвращается на исходное значение.
Частый случай для участка одного контура — это закон Ома. Составляя уравнения напряжений для контура, требуется подобрать его положительный обход. Чтобы это сделать, нужно знать, что при подборе обхода показатель падения напряжения ветви будет положительным, если обходное направление в ветви совпадает с тем, которое было ранее выбрано. Если оно не совпадает, то показатель напряжения ветви будет отрицательным.
Важно! Второе правило Кирхгофа можно использовать в линейной или нелинейной линеаризованной цепи при любом изменении токов и напряжения.

В результате, чтобы понять основы физики явлений, электрики, электродинамики и с успехом использовать знания в процессе жизнедеятельности, необходимо знать выведенные теоремы, законы, формулы и правила в области электричества, которые представлены выше. Например, представляя, как выглядит та или иная формула, можно решить любую задачу в учебнике по физике или жизни.
Глава 18. Напряженность и потенциал электрического поля.Силовые линии электрического поля
Для характеристики создаваемого зарядами электрического поля вводятся две величины — напряженность электрического поля и его потенциал. Напряженность характеризует силу, действующую со стороны поля на внесенный в него пробный заряд. Если в какой-то точке поля на заряд 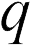 действует сила
действует сила 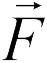 , то напряженность электрического поля в этой точке равна
, то напряженность электрического поля в этой точке равна
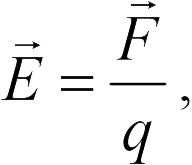
где 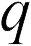 — заряд, который мы взяли, чтобы «попробовать» поле в данной точке. Такой заряд называется «пробным». Пробный заряд не должен искажать распределение зарядов, создающих поле, и потому должен быть достаточно мал. В формулу (18.1) пробный заряд входит со своим знаком (не модуль), поэтому, как следует из (18.1), вектор напряженности поля в некоторой точке направлен так же, как и вектор силы, действующей в этой точке на положительный пробный заряд.
— заряд, который мы взяли, чтобы «попробовать» поле в данной точке. Такой заряд называется «пробным». Пробный заряд не должен искажать распределение зарядов, создающих поле, и потому должен быть достаточно мал. В формулу (18.1) пробный заряд входит со своим знаком (не модуль), поэтому, как следует из (18.1), вектор напряженности поля в некоторой точке направлен так же, как и вектор силы, действующей в этой точке на положительный пробный заряд.
Найдем напряженность электрического поля, создаваемого точечным зарядом  . Для этого возьмем произвольный пробный заряд
. Для этого возьмем произвольный пробный заряд  и поместим его в точку, находящуюся на расстоянии
и поместим его в точку, находящуюся на расстоянии 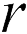 от заряда
от заряда  . Сила, действующую на пробный заряд со стороны заряда
. Сила, действующую на пробный заряд со стороны заряда  , определяется законом Кулона (17.1), (17.2). Поэтому согласно (18.1) имеем
, определяется законом Кулона (17.1), (17.2). Поэтому согласно (18.1) имеем

где  . Направлен вектор напряженности от заряда
. Направлен вектор напряженности от заряда  , если
, если 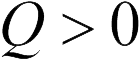 , и к нему, если
, и к нему, если 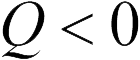 .
.
Пусть поле создается несколькими зарядами  … В этом случае его напряженность равна векторной сумме напряженностей тех полей, которые создаются каждым зарядом в отдельности. Действительно, из принципа суперпозиции следует, что на пробный заряд в этом случае действует сила
… В этом случае его напряженность равна векторной сумме напряженностей тех полей, которые создаются каждым зарядом в отдельности. Действительно, из принципа суперпозиции следует, что на пробный заряд в этом случае действует сила 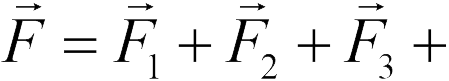 . где
. где 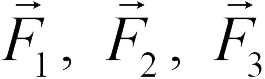 . — силы, действующие на пробный заряд со стороны каждого заряда
. — силы, действующие на пробный заряд со стороны каждого заряда 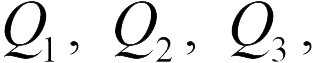 . Поэтому из (18.1) получаем
. Поэтому из (18.1) получаем
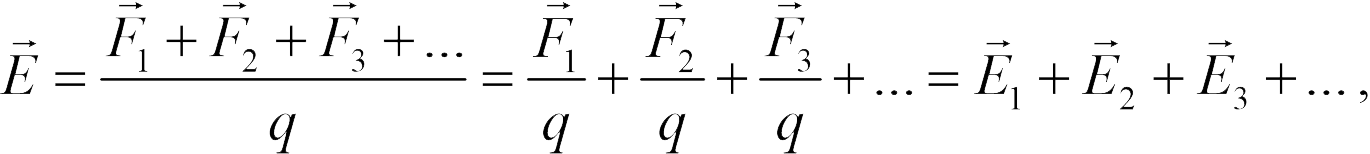
где 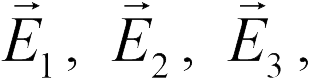 . — напряженности тех полей, которые создавались бы каждым зарядом в отдельности в отсутствие других зарядов. Утверждение (18.3) называется принципом суперпозиции для полей. Формула (18.2) и принцип суперпозиции позволяют вычислить поле, создаваемое любым заряженным телом — с помощью мысленного разбиения его на точечные части и суммирования напряженностей, создаваемых всеми таким частями. Однако из-за математической сложности такой процедуры, она не входит в программу школьного курса физики. Школьник должен знать без вывода результат ее применения к заряженным сферам и плоскостям. Из формул (17.4), (17.5) получаем для напряженности поля сферы радиуса
. — напряженности тех полей, которые создавались бы каждым зарядом в отдельности в отсутствие других зарядов. Утверждение (18.3) называется принципом суперпозиции для полей. Формула (18.2) и принцип суперпозиции позволяют вычислить поле, создаваемое любым заряженным телом — с помощью мысленного разбиения его на точечные части и суммирования напряженностей, создаваемых всеми таким частями. Однако из-за математической сложности такой процедуры, она не входит в программу школьного курса физики. Школьник должен знать без вывода результат ее применения к заряженным сферам и плоскостям. Из формул (17.4), (17.5) получаем для напряженности поля сферы радиуса 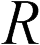 , равномерно заряженной зарядом
, равномерно заряженной зарядом  , в точке на расстоянии
, в точке на расстоянии 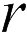 от центра сферы:
от центра сферы:

где 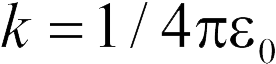 , а из формулы (17.6) для напряженности поля равномерно заряженной плоскости
, а из формулы (17.6) для напряженности поля равномерно заряженной плоскости

где  — заряд плоскости,
— заряд плоскости, 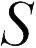 — площадь,
— площадь,  — поверхностная плотность зарядов плоскости.
— поверхностная плотность зарядов плоскости.
Электрическое поле можно изобразить графически (на современном русском языке — визуализировать) с помощью силовых линий. Силовые линии — это такие воображаемые линии, касательные к которым в каждой точке совпадают по направлению с вектором напряженности в этой точке. Вообще говоря, силовые линии проходят через каждую точку поля (кроме тех точек, где  ), но поскольку так их нарисовать нельзя, условились проводить их с определенной густотой в зависимости от величины поля: чем гуще расположены силовые линии, тем больше величина напряженности поля.
), но поскольку так их нарисовать нельзя, условились проводить их с определенной густотой в зависимости от величины поля: чем гуще расположены силовые линии, тем больше величина напряженности поля.
Второй характеристикой электрического поля является его потенциал. Основная идея введения этой величины заключается в следующем. Если электрический заряд перемещается в электрическом поле (созданном другими зарядами), то со стороны поля на него действуют силы, и, следовательно, поле совершает работу. Потенциал поля — это такая функция точки поля  , что работа
, что работа 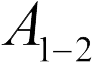 , совершаемая полем над точечным пробным зарядом
, совершаемая полем над точечным пробным зарядом 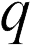 при его перемещении из точки с радиусом-вектором
при его перемещении из точки с радиусом-вектором  в точку с радиусом-вектором
в точку с радиусом-вектором 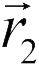 , равна
, равна

(именно в такой последовательности). Из формулы (18.6) следует, что работа, которую совершает поле при перемещении заряда, не зависит от формы траектории, а определяется только начальной и конечной ее точками. В частности, при перемещении тела по замкнутой траектории поле совершает нулевую работу.
Поскольку в формулу (18.6), входит разность потенциалов двух точек поля, потенциал определен с точностью до постоянной. Эту постоянную всегда можно выбрать так, что потенциал любой заданной точки поля можно сделать равным нулю. Как правило, в качестве такой точки выбирают бесконечно удаленную от зарядов точку поля, считая ее потенциал равным нулю. Из формулы (18.6) следует, что потенциал любой точки поля равен отношению работы, которую совершает электрическое поле при перемещении пробного заряда из этой точки в ту точку, потенциал которой выбран равным нулю, к пробному заряду.
Можно доказать, что если поле создается точечным зарядом  , то потенциал на расстоянии
, то потенциал на расстоянии 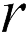 от заряда при условии, что потенциал бесконечно удаленной точки принят за нуль, равен
от заряда при условии, что потенциал бесконечно удаленной точки принят за нуль, равен
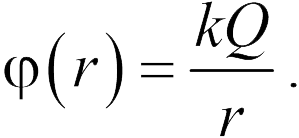
Важно отметить, что в формулу (18.7) входит заряд  со знаком (не модуль!), т.е. потенциал поля, создаваемого положительным зарядом, — положительный, отрицательным — отрицательный.
со знаком (не модуль!), т.е. потенциал поля, создаваемого положительным зарядом, — положительный, отрицательным — отрицательный.
Для потенциалов справедлив принцип суперпозиции: если поле создается несколькими точечными зарядами, то потенциал любой его точке равен алгебраической сумме потенциалов (18.7), создаваемых в этой точке каждым точечным зарядом. Это правило позволяет найти потенциал поля, создаваемого протяженным заряженным телом: нужно мысленно разделить тело на малые («точечные») части, по формуле (18.7) найти потенциал поля, создаваемого каждой такой частью, а затем сложить полученные результаты.
Для решения задач ЕГЭ нужно знать (без вывода) формулу потенциала поля равномерно заряженной сферы. Пусть имеется сфера радиуса  , равномерно заряженная зарядом
, равномерно заряженная зарядом  . Тогда потенциал точки поля, расположенной на расстоянии
. Тогда потенциал точки поля, расположенной на расстоянии 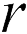 центра сферы, равен
центра сферы, равен

(точка нулевого потенциала выбрана на бесконечности).
Часто в задачах ЕГЭ по физике используется связь напряженности однородного электрического поля и разности потенциалов двух точек поля, лежащих на одной силовой линии. Для нахождения этой связи возьмем положительный пробный заряд 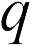 , перенесем его из первой точки во вторую вдоль силовой линии и найдем работу, которую совершает при этом электрическое поле. Поскольку поле действует на заряд с постоянной силой
, перенесем его из первой точки во вторую вдоль силовой линии и найдем работу, которую совершает при этом электрическое поле. Поскольку поле действует на заряд с постоянной силой  , угол между перемещением и этой силой равен нулю (заряд движется вдоль силовой линии), поэтому работа сил поля равна
, угол между перемещением и этой силой равен нулю (заряд движется вдоль силовой линии), поэтому работа сил поля равна  , где
, где 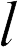 — расстояние между исследуемыми точками. С другой стороны, по определению потенциала работа поля равна
— расстояние между исследуемыми точками. С другой стороны, по определению потенциала работа поля равна  . Приравнивая эти работы, находим
. Приравнивая эти работы, находим
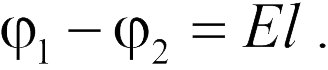
Подчеркнем, что формула (18.9) справедлива только для однородного поля, а точки 1 и 2 должны лежать на одной силовой линии.
Рассмотрим теперь задачи.
Величина напряженности электрического поля, создаваемого точечным зарядом (задача 18.1.1), определяется формулой (18.2)
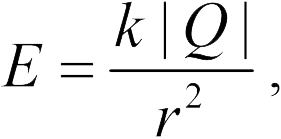
где 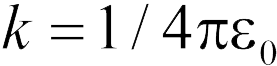 (ответ 1).
(ответ 1).
Размерность напряженности электрического поля (задача 18.1.2) можно найти из связи напряженности поля и потенциала (см. формулу (18.9)). А поскольку размерность потенциала в международной системе единиц СИ – вольт, из формулы (18.9) имеем:

где квадратные скобки обозначают размерность (ответ 3).
Для определения напряженности поля используют пробный заряд (см. формулу (18.1)). Однако напряженность (18.1) ни от знака, ни от величины пробного заряда не зависят (задача 18.1.3). Это связано с тем, что сила  в (18.1) линейно зависит от пробного заряда
в (18.1) линейно зависит от пробного заряда  , и он сокращается в (18.1). Если взять пробный заряд отрицательным, то направление вектора
, и он сокращается в (18.1). Если взять пробный заряд отрицательным, то направление вектора  числителе (18.1) изменится по сравнению со случаем положительного пробного заряда, но отношение
числителе (18.1) изменится по сравнению со случаем положительного пробного заряда, но отношение 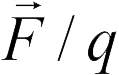 будет направлено противоположно вектору
будет направлено противоположно вектору 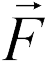 , т.е. направление вектора
, т.е. направление вектора 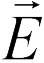 не изменится (ответ 4).
не изменится (ответ 4).
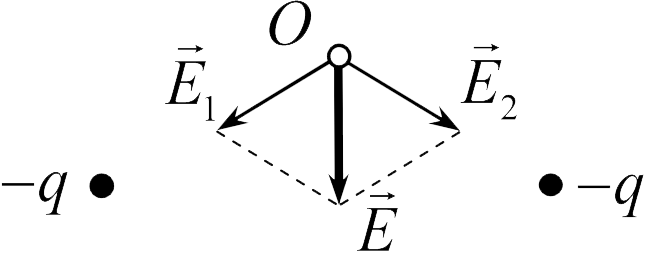
Для нахождения поля, созданного двумя точечными зарядами (задача 18.1.4), используем принцип суперпозиции. Напряженности полей, создаваемых в точке  каждым зарядом в отдельности, показаны тонкими векторами и отмечены как
каждым зарядом в отдельности, показаны тонкими векторами и отмечены как 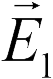 и
и 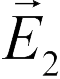 . Поскольку модули этих векторов равны, вектор их суммы направлен вертикально вниз (ответ 4).
. Поскольку модули этих векторов равны, вектор их суммы направлен вертикально вниз (ответ 4).
По определению силовые линии — это такие воображаемые линии, касательные к которым в каждой точке совпадают по направлению с вектором напряженности в этой точке (задача 18.1.5 — ответ 4).
Поскольку силовые линии поля в задаче 18.1.6 направлены направо, то направо направлен и вектор напряженности в каждой точке. Поэтому направо будет направлен и вектор силы, действующий со стороны этого поля на положительные точечный заряд (ответ 2).
Поскольку все траектории движения заряда I, II и III в задаче 18.1.7 начинаются и заканчиваются в тех же точках, то работа поля над зарядом при его движении по всем трем траекториям одинакова (ответ 4).
Разность потенциалов двух точек однородного электрического поля (задача 18.1.8) найдем по формуле (18.9):


Поскольку вектор напряженности электрического поля в любой точке направлен от заряда, то силовые линии поля расходятся радиально, являясь везде прямыми (см.рисунок). Таким образом, правильный ответ в задаче 18.1.9 — 1.
По определению потенциала имеем для работы поля в задаче 18.1.10


Силовые линии электрического поля строятся так, что их густота пропорциональна величине поля: чем гуще силовые линии, тем больше величина напряженности. Поэтому в задаче 18.2.1  (ответ 2).
(ответ 2).
Рисунок в задаче 18.2.2 — тот же самый, что и в предыдущей задаче, однако логика получения ответа совсем другая. Чтобы сравнить потенциалы в точках 1 и 2 перенесем из первой точке во вторую положительный пробный заряд и найдем работу поля. Так как  , и если работа положительна, то
, и если работа положительна, то 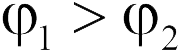 , если отрицательна — наоборот. Очевидно, работа поля при перемещении положительного заряда из точки 1 в точку 2 положительна. Действительно, стрелки на силовых линиях направлены вправо, следовательно, и сила, действующая на положительный заряд, направлена вправо, туда же направлен и вектор перемещения заряда, поэтому косинус угла между силой и перемещением положителен на всех элементарных участках траектории, поэтому положительна работа. Таким образом
, если отрицательна — наоборот. Очевидно, работа поля при перемещении положительного заряда из точки 1 в точку 2 положительна. Действительно, стрелки на силовых линиях направлены вправо, следовательно, и сила, действующая на положительный заряд, направлена вправо, туда же направлен и вектор перемещения заряда, поэтому косинус угла между силой и перемещением положителен на всех элементарных участках траектории, поэтому положительна работа. Таким образом 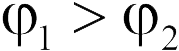 (ответ 1), причем этот результат является следствием направления стрелок на силовых линиях, а не переменной густоты силовых линий.
(ответ 1), причем этот результат является следствием направления стрелок на силовых линиях, а не переменной густоты силовых линий.
В задаче 18.2.3 используем формулу для потенциала поля точечного заряда. Поскольку потенциал поля обратно пропорционален расстоянию до заряда, создающего поле (см. формулу (18.7)),

(ответ 2). Другими словами, на втрое большем расстоянии от точечного заряда потенциал его поля втрое меньше.

Очевидно, искомая в задаче 18.2.4 точка, находится между зарядами. В этой точке величины напряженностей полей 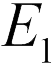 и
и 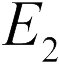 , создаваемых каждым зарядом, должны быть равны (см. рисунок). Используя формулу (18.2), получаем
, создаваемых каждым зарядом, должны быть равны (см. рисунок). Используя формулу (18.2), получаем
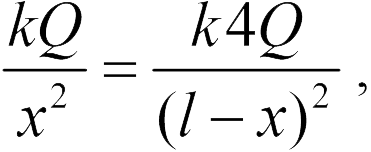
где 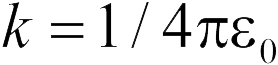 . Отсюда находим
. Отсюда находим 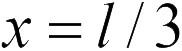 (ответ 3).
(ответ 3).
Используя принцип суперпозиции для потенциалов и формулу для потенциала поля точечного заряда (18.7), получим для искомой точки (задача 18.2.5)

где 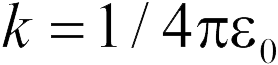 . Отсюда находим
. Отсюда находим  (ответ 2).
(ответ 2).
Поскольку все заряды в задаче 18.2.6 одинаковы, то напряженность поля, созданного в центре квадрата каждой парой зарядов, лежащих на одной диагонали, равна нулю. Поэтому равна нулю и напряженность электрического поля, созданного всеми четырьмя зарядами (ответ 2).
В задачах 18.2.7 и 18.2.8 используем принцип суперпозиции. Векторы напряженности полей, создаваемых верхней и нижней пластинами 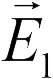 и
и 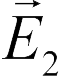 соответственно показаны на рисунках (левый рисунок относится к задаче 18.2.7, правый — к 18.2.8). Из этих рисунков следует, что в области II для задачи 18.2.7 и в областях I и III для задачи 18.2.8 векторы
соответственно показаны на рисунках (левый рисунок относится к задаче 18.2.7, правый — к 18.2.8). Из этих рисунков следует, что в области II для задачи 18.2.7 и в областях I и III для задачи 18.2.8 векторы  и
и  направлены противоположно. А поскольку величина напряженности поля плоскости не зависит от расстояния до нее (формула (18.5)), а заряды плоскостей одинаковы по величине, напряженность суммарного поля в этих областях равна нулю.
направлены противоположно. А поскольку величина напряженности поля плоскости не зависит от расстояния до нее (формула (18.5)), а заряды плоскостей одинаковы по величине, напряженность суммарного поля в этих областях равна нулю.
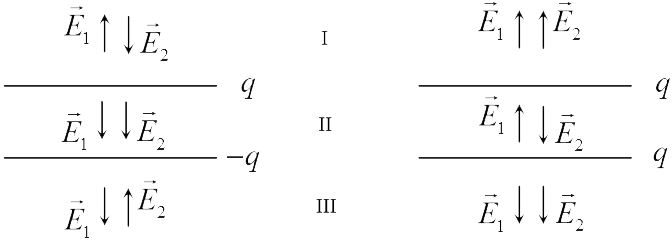
Таким образом, правильный ответ в задаче 18.2.7 — 2, в задаче 18.2.8 — 3. Отметим, что полученный результат является приближенным и справедлив в пределе бесконечно больших пластин. Для конечных пластин поле в указанных областях будет малым, но отличным от нуля, причем величина поля будет наибольшей около краев пластин.
По принципу суперпозиции для потенциалов имеем (задача 18.2.9)  . Если убрать либо первый, либо второй заряды, то потенциал в исследуемой точке станет равным соответственно
. Если убрать либо первый, либо второй заряды, то потенциал в исследуемой точке станет равным соответственно  или
или 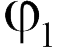 . Отсюда находим
. Отсюда находим 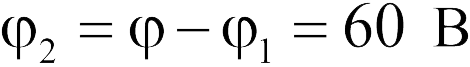 (ответ 2).
(ответ 2).
Согласно формуле (18.8) потенциал поля в любой точке внутри сферы равен потенциалу на ее поверхности

где 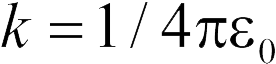 . Поэтому правильный ответ в задаче 18.2.10 — 4.
. Поэтому правильный ответ в задаче 18.2.10 — 4.
Определение напряженности электрического поля с помощью потенциала
Формулу можно использовать для определения разности потенциалов между двумя точками электрического поля, если напряженность поля в области между этими точками известна. Обращая эту формулу мы можем выразить напряженность электрического поля через его потенциал, т. е., зная V, мы сможем определить Е.
Посмотрим, как это делается.
Уравнение можно переписать в дифференциальной форме:
где dV — бесконечно малая разность потенциалов между точками на расстоянии dl друг от друга, а El — составляющая напряженности электрического поля в направлении этого бесконечно малого перемещения dl.
Тогда:
Таким образом, составляющая напряженности электрического поля по любому направлению равна градиенту потенциала в этом направлении, взятому с обратным знаком. Градиентом величины V называется ее производная по определенному направлению dV/dl. Если направление не указывается, то градиент соответствует направлению наиболее быстрого изменения V; это соответствует направлению вектора Е в данной точке, поскольку именно в таком направлении составляющая вектора Е совпадает с полной величиной напряженности поля:
Если расписать составляющие вектора Е по координатам х, у, z и в качестве l взять направления вдоль осей х у, z, то уравнение (24.8) можно записать в виде:
Здесь dV/dx — частная производная V по направлению х при условии, что у и z фиксированы.
В последнем примере мы вычислили напряженность электрического поля Е диполя в произвольной точке пространства. Складывая векторы напряженностей, создаваемых каждым зарядом в отдельности, получить этот результат было бы гораздо сложнее. Вообще говоря, для многих распределений зарядов гораздо проще рассчитать потенциал, а затем по формуле (24.9) — напряженность электрического поля Е, чем вычислять по закону Кулона по отдельности Е для каждого заряда: скалярные величины складывать намного проще, чем векторы.
Электростатическая потенциальная энергия
Предположим, что точечный заряд q перемещают в пространстве из точки а в точку b, электрические потенциалы в которых, обусловленные другими зарядами, равны соответственно Va и Vb. Изменение электростатической потенциальной энергии заряда q в поле других зарядов составляет:
Пусть теперь имеется система нескольких точечных зарядов. Чему равна электростатическая потенциальная энергия системы?
Удобнее всего выбрать за нуль потенциальную энергию зарядов на очень больших (в идеале бесконечно больших) расстояниях друг от друга. Потенциальная энергия уединенного точечного заряда Q1 равна нулю, поскольку в отсутствие других зарядов на него не действует никакая сила. Если к нему поднести второй точечный заряд, Q2, потенциал в точке, где находится второй заряд, будет равен:
Здесь r1 2 — расстояние между зарядами. Потенциальная энергия двух зарядов равна:
Она характеризует работу, необходимую для перемещения заряда Q2 из бесконечности (V = 0) на расстояние r1 2 до заряда Qi (или со знаком минус работу, необходимую для разнесения зарядов на бесконечно большое расстояние).
Если система состоит из трех зарядов, то ее полная потенциальная энергия будет равна работе по перемещению всех трех зарядов из бесконечности в место их расположения. Работа по сближению зарядов Q2 и Q1 определяется выражением (24.10);
чтобы перенести заряд Q3 из бесконечности в точку на расстоянии r1 3 от Q1 и на расстоянии r2 3 от Q2, требуется совершить работу:
В этом случае потенциальная энергия системы трех точечных зарядов будет равна:
Для системы четырех зарядов выражение для потенциальной энергии будет содержать шесть таких членов и т.п. (При составлении подобных сумм необходимо следить за тем, чтобы не учитывать одну и ту же пару дважды). Часто нас интересует не полная электростатическая потенциальная энергия, а лишь часть ее. Например, может возникнуть необходимость найти потенциальную энергию одного диполя в присутствии другого диполя. Во взаимодействии участвуют четыре заряда: Q1 и -Q1 первого диполя и Q2 и -Q2 второго диполя.
Потенциальная энергия одного диполя и в присутствии другого (иногда ее называют энергией взаимодействия) представляет собой работу по сближению диполей с бесконечно большого расстояния. В этом случае нас не интересует взаимная потенциальная энергия зарядов Q1 и -Q1 или Q2 и -Q2; выражение для потенциальной энергии двух диполей будет содержать лишь четыре члена, соответствующие энергиям взаимодействия между зарядами: Q1 и Q2 ; Q1 и -Q2 ; -Q1 и Q2 ; -Q1 и -Q2.
Заключение
Электрический потенциал в любой точке пространства определяется как электростатическая потенциальная энергия единицы заряда. Разность потенциалов между двумя точками определяется взятой с обратным знаком работой, которая совершается полем при перемещении единичного электрического заряда между этими точками. Разность потенциалов измеряется в вольтах (1 В = 1 Дж/Кл) и иногда называется напряжением. Изменение потенциальной энергии заряда q при прохождении им разности потенциалов Vbа равно ?U = qVba.
Разность потенциалов Vbа между точками b и a в однородном электрическом поле напряженностью Е определяется формулой V = — Ed, где d — расстояние вдоль силовой линии поля между этими точками.
В неоднородном электрическом поле Е соответствующее выражение имеет вид .
Таким образом, зная Е, всегда можно определить Vbа. Если значение V известно, то составляющие напряженности поля Е можно найти, обращая приведенное соотношение:
Эквипотенциальные линии или поверхности представляют собой геометрическое место точек одного потенциала; они всюду перпендикулярны силовым линиям поля. Электрический потенциал уединенного точечного заряда Q относительно нулевого потенциала (на бесконечности) равен:
Потенциал произвольного распределения зарядов можно определить, суммируя (интегрируя) потенциалы отдельных зарядов.
где r — расстояние от элемента заряда dq до точки, в которой определяется V.
Продолжение следует. Коротко о следующей публикации:
Электрическая емкость, диэлектрики, накопление электрической энергии.
Конденсатор — устройство для накопления электрического заряда, который состоит из двух проводников (обкладок), расположенных близко друг к другу, но не соприкасающихся.
III. Основы электродинамики
Рассмотрим ситуацию: заряд q0 попадает в электростатическое поле. Это электростатическое поле тоже создается каким-то заряженным телом или системой тел, но нас это не интересует. На заряд q0 со стороны поля действует сила, которая может совершать работу и перемещать этот заряд в поле.

Работа электростатического поля не зависит от траектории. Работа поля при перемещении заряда по замкнутой траектории равна нулю. По этой причине силы электростатического поля называются консервативными, а само поле называется потенциальным.
Потенциал
Система «заряд — электростатическое поле» или «заряд — заряд» обладает потенциальной энергией, подобно тому, как система «гравитационное поле — тело» обладает потенциальной энергией.
Физическая скалярная величина, характеризующая энергетическое состояние поля называется потенциалом данной точки поля. В поле помещается заряд q, он обладает потенциальной энергией W. Потенциал — это характеристика электростатического поля.


Вспомним потенциальную энергию в механике. Потенциальная энергия равна нулю, когда тело находится на земле. А когда тело поднимают на некоторую высоту, то говорят, что тело обладает потенциальной энергией.
Касательно потенциальной энергии в электричестве, то здесь нет нулевого уровня потенциальной энергии. Его выбирают произвольно. Поэтому потенциал является относительной физической величиной.
В механике тела стремятся занять положение с наименьшей потенциальной энергией. В электричестве же под действием сил поля положительно заряженное тело стремится переместится из точки с более высоким потенциалом в точку с более низким потенциалом, а отрицательно заряженное тело — наоборот.
Потенциальная энергия поля — это работа, которую выполняет электростатическая сила при перемещении заряда из данной точки поля в точку с нулевым потенциалом.
Рассмотрим частный случай, когда электростатическое поле создается электрическим зарядом Q. Для исследования потенциала такого поля нет необходимости в него вносить заряд q. Можно высчитать потенциал любой точки такого поля, находящейся на расстоянии r от заряда Q.

Диэлектрическая проницаемость среды имеет известное значение (табличное), характеризует среду, в которой существует поле. Для воздуха она равна единице.
Разность потенциалов
Работа поля по перемещению заряда из одной точки в другую, называется разностью потенциалов
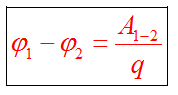
Эту формулу можно представить в ином виде

Эквипотенциальная поверхность (линия) — поверхность равного потенциала. Работа по перемещению заряда вдоль эквипотенциальной поверхности равна нулю.
Напряжение
Разность потенциалов называют еще электрическим напряжением при условии, что сторонние силы не действуют или их действием можно пренебречь.
Напряжение между двумя точками в однородном электрическом поле, расположенными по одной линии напряженности, равно произведению модуля вектора напряженности поля на расстояние между этими точками.
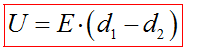
От величины напряжения зависит ток в цепи и энергия заряженной частицы.
Принцип суперпозиции
Потенциал поля, созданного несколькими зарядами, равен алгебраической (с учетом знака потенциала) сумме потенциалов полей каждого поля в отдельности
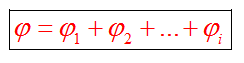
Как определить знак потенциала
При решении задач возникает много путаницы при определении знака потенциала, разности потенциалов, работы.
На рисунке изображены линии напряженности. В какой точке поля потенциал больше?

Верный ответ — точка 1. Вспомним, что линии напряженности начинаются на положительном заряде, а значит положительный заряд находится слева, следовательно максимальным потенциалом обладает крайняя левая точка.
Если происходит исследование поля, которое создается отрицательным зарядом, то потенциал поля вблизи заряда имеет отрицательное значение, в этом легко убедиться, если в формулу подставить заряд со знаком «минус». Чем дальше от отрицательного заряда, тем потенциал поля больше.
Если происходит перемещение положительного заряда вдоль линий напряженности, то разность потенциалов и работа являются положительными. Если вдоль линий напряженности происходит перемещение отрицательного заряда, то разность потенциалов имеет знак «+», работа имеет знак «-«.
Порассуждайте самостоятельно отрицательные или положительные значения будут принимать работа и разность потенциалов, если заряд перемещать в обратном направлении относительно линий напряженности.
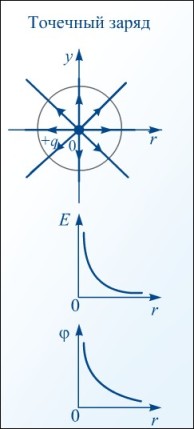
Зависимость напряженности и потенциала от расстояния
Потенциал поля, созданного равномерно заряженной сферой радиусом R и зарядом q на расстоянии r от центра сферы, равен


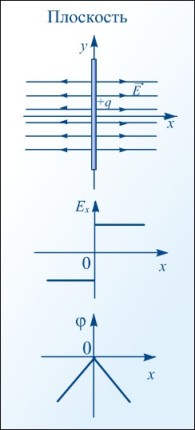

Напряжение в природе
Напряжение в клетках сетчатки глаза при попадания в них света около 0,01 В.
Напряжение в телефонных сетях может достигать 60 В.
Электрический угорь способен создавать напряжение до 650 В.

Энергия взаимодействия зарядов*
Из определения потенциала следует, что потенциальная энергия электростатического взаимодействия двух зарядов q1 и q2, находящихся на расстоянии r друг от друга, численно равна работе, которая совершается при перемещении точечного заряда q2 из бесконечности в данную точку поля, созданного зарядом q1
Электрический потенциал — это скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию, которой обладает единичный положительный пробный заряд, помещённый в данную точку поля.
Если вы хотите расширить свои знания об электрическом потенциале или сначала узнать, что такое электрический потенциал, то вы пришли по адресу.
Простое объяснение
В классической механике рассмотрение проблемы с точки зрения энергии может значительно упростить ситуацию по сравнению с рассмотрением ее с точки зрения сил, действующих на систему. В частности, в этом контексте существенную роль играет тот факт, что энергия является сохраняющейся переменной.
Также в классической электродинамике рассмотрение на энергетическом уровне оказывается очень полезным. Поэтому электрический потенциал φ (также называемый электростатическим потенциалом) определяется как отношение потенциальной энергии Eпот пробного электрического заряда и его величины электрического заряда q: φ = Eпот / q .
Возможность определения такого электрического потенциала обусловлена тем, что электрическое поле E распределения заряда и результирующая электростатическая сила Fc на пробном электрическом заряде является консервативной силой, подобной гравитационной силе.
Электрический потенциал имеет единицу измерения вольт В или также джоуль на кулон Дж / Кл .
Формулы
В этом разделе мы познакомим вас с двумя важными формулами для электрического потенциала определенных распределений электрических зарядов. Мы также кратко обсудим аналогию между электрическим потенциалом и гравитацией.
Пластинчатый конденсатор
Мы рассматриваем ситуацию, когда две плоские пластины расположены параллельно на расстоянии d друг от друга. Кроме того, пусть одна из двух пластин заряжена положительно, а другая — отрицательно. Такая комбинация также называется пластинчатым конденсатором. Обозначим точку на положительной пластине через A, а точку на отрицательной пластине через B. Тогда для разности потенциалов между этими двумя точками получим:
φВ — φA = — E * d .
Здесь E — величина электрического поля между двумя пластинами, которое предполагается однородным. Такая разность потенциалов также называется электрическим напряжением, которое существует между этими двумя точками.
Из этого уравнения видно, что электрический потенциал на положительно заряженной пластине (пластина A) выше, чем потенциал на отрицательно заряженной пластине (пластина B). Поэтому положительный заряд в пластинчатом конденсаторе перемещается к отрицательной пластине. В общем случае электрическое поле — а значит, и направление движения положительного заряда — направлено в ту сторону, в которой электрический потенциал убывает быстрее всего.

Аналогия с гравитационным полем
Если умножить уравнение (приведенное выше в статье) на величину электрического заряда q пробного электрического заряда и предположить, что отрицательно заряженная пластина имеет электрический потенциал, равный нулю, то электрическая потенциальная энергия на расстоянии h от пластины равна:
Eпот. эл = q * φ = q * E * h
Здесь φ обозначает электрический потенциал в точке пробного электрического заряда.
Сравним это уравнение с потенциальной энергией в однородном гравитационном поле:
Eпот. гр = m * g * h .
Мы определяем, что количество заряда электрического q играет роль массы m, а величина электрического поля E играет роль гравитационного ускорения g. Масса, находящаяся на высоте h над землей, ускоряется по направлению к земле под действием земного притяжения.
Таким образом, масса движется в том направлении, в котором уменьшается ее потенциальная энергия. Аналогично, положительный электрический заряд движется в направлении, в котором его электрическая потенциальная энергия будет уменьшаться. Поскольку электрическая потенциальная энергия и электрический потенциал линейно связаны, это наблюдение аналогично тому, что положительно заряженная частица движется в направлении уменьшения электрического потенциала.

Подобно потенциальной энергии, только разность потенциалов имеет физический смысл, поскольку при определении электрического потенциала необходимо произвольно определить точку отсчета, от которой затем можно обозначить другие точки в пространстве. В этом смысле электрический потенциал сам по себе не имеет реального физического смысла, поскольку для данной точки в пространстве его значение можно изменить, выбрав другую точку отсчета. Таким образом, электрический потенциал ведет себя подобно высоте, потому что вы не можете говорить о высоте, пока у вас нет точки отсчета.
На топографической карте — пути, вдоль которых высота не меняется, называются изолиниями. Аналогично, пути, вдоль которых электрический потенциал постоянен, называются эквипотенциальными линиями.
Заряженные частицы
Предположим, что частица с зарядом q находится в начале выбранной нами системы координат. Пусть положение другой точки равно r и пусть r — расстояние между двумя точками. Для электрического потенциала в точке r действует следующее соотношение:
φ (r) = q / 4 * π * ε0 * r ,
здесь ε0 — электрическая постоянная.
В этом уравнении предполагается, что под действием электрического поля положительный пробный электрический заряд переносится из бесконечности в положение r.
Примеры задач
Наконец, давайте вместе рассчитаем небольшой пример. Предположим, что электрон ускоряется от отрицательно заряженной пластины к положительно заряженной через разность потенциалов 2000 В. Как изменяется потенциальная энергия электрона?
Для разности электрических потенциалов между двумя пластинами: φB — φA = ΔEпот / q , преобразованной в искомое изменение потенциальной энергии, получаем:
ΔEпот = q * ( φB — φA ) .
Величина электрического заряда электрона равна qe = e = — 1,6 * 10-19 Кл и поэтому получаем:
ΔEпот = e * ( φB — φA ) = — 1,6 * 10-19 Кл * 2000 В = -3,2 * 10-19 Дж.
Обратите внимание, что [ В ] = Дж / Кл. Кроме того, мы предположили, что пластина с точкой B заряжена положительно, поэтому перед 2000 В нет знака минус. Расчет показывает, что потенциальная энергия электрона уменьшается.
Список использованной литературы
- Соколович Ю. А., Богданова Г. С. Физика: Справочник с примерами решения задач. – 2-е издание передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.
- Мякишев Г. Я., Буховцев Б. Б., Сотский Н. Н. Физика: Учеб. для общеобразоват. учреждений. Базовый и профильный уровни. 19-е издание – М.: Просвещение, 2010.
Работа электростатического поля
Рассмотрим ситуацию: заряд q0 попадает в электростатическое поле. Это электростатическое поле тоже создается каким-то заряженным телом или системой тел, но нас это не интересует. На заряд q0 со стороны поля действует сила, которая может совершать работу и перемещать этот заряд в поле.

Работа электростатического поля не зависит от траектории. Работа поля при перемещении заряда по замкнутой траектории равна нулю. По этой причине силы электростатического поля называются консервативными
, а само поле называется
потенциальным
.
Характеристики электрического поля
Человек быстро понял, что электрическое поле есть, уже в XVIII веке – либо раньше – нарисована опилками его картина. Люди увидели линии, выходившие из полюсов. По аналогии стали пытаться изобразить электрическое поле. К примеру, Шарль Кулон на исходе восемнадцатого столетия открыл закон притяжения и отталкивания зарядов. Записав формулу, понял, что эквипотенциальные линии силы взаимодействия концентрически расходятся вокруг точечного скопления электричества, а траектории движения – прямолинейны.
Так оказалась изображена первая картина электрического поля. Напоминает картину, как исследователи представляли магнитное, но с гигантской разницей: в природе нашлись заряды обоих знаков. Линии напряжённости уходят в бесконечность (в теории, безусловно, закончатся). А магнитные заряды поодиночке не найдены, линии их всегда замыкаются в видимой области пространства.

Первая картина электрического поля
В остальном нашлось много общего, к примеру, заряды одинакового знака отталкиваются, а разных – притягиваются. Это справедливо для магнитов и электричества. Гильберт заметил, что магнетизм – сильная субстанция, которую сложно экранировать или уничтожить, а электричество легко разрушается влагой и прочими веществами. Дёгтя в бочку добавил Кулон, который, следуя Бенджамину Франклину, присвоил электронам отрицательный заряд. Хотя речь шла о количестве флюида. И избыток электронов следовало назвать положительным.
Как результат, линии напряжённости поля располагаются в направлении обратном правильному. Потенциал растёт не туда… Главными характеристиками электрического поля считаются:
- Напряжённость – показывает, какая сила действует на положительный единичный заряд в данной точке со стороны поля.
- Потенциал – показывает, какую работу способно затратить поле, чтобы переместить единичный пробный положительный заряд в бесконечно удалённую точку.
- Напряжение – разность потенциалов между двумя точками. Напряжение определяется исключительно относительно некоторого уровня.
Наиболее вероятно происхождение терминов из латинского языка. Напряжённость ввёл в обиход, предположительно, Алессандро Вольта, а потенциал называется по наименованию типа поля, которое указанной величиной характеризуется: работа по перемещению заряда не зависит от траектории, равна разнице потенциалов начальной и конечной точки. Следовательно, на замкнутой траектории равна нулю.
Потенциал
Система «заряд — электростатическое поле» или «заряд — заряд» обладает потенциальной энергией, подобно тому, как система «гравитационное поле — тело» обладает потенциальной энергией.
Физическая скалярная величина, характеризующая энергетическое состояние поля называется потенциалом
данной точки поля. В поле помещается заряд q, он обладает потенциальной энергией W. Потенциал — это характеристика электростатического поля.

Вспомним потенциальную энергию в механике. Потенциальная энергия равна нулю, когда тело находится на земле. А когда тело поднимают на некоторую высоту, то говорят, что тело обладает потенциальной энергией.
Касательно потенциальной энергии в электричестве, то здесь нет нулевого уровня потенциальной энергии. Его выбирают произвольно. Поэтому потенциал является относительной физической величиной.
В механике тела стремятся занять положение с наименьшей потенциальной энергией. В электричестве же под действием сил поля положительно заряженное тело стремится переместится из точки с более высоким потенциалом в точку с более низким потенциалом, а отрицательно заряженное тело — наоборот.
Потенциальная энергия поля — это работа, которую выполняет электростатическая сила при перемещении заряда из данной точки поля в точку с нулевым потенциалом.
Рассмотрим частный случай, когда электростатическое поле создается электрическим зарядом Q. Для исследования потенциала такого поля нет необходимости в него вносить заряд q. Можно высчитать потенциал любой точки такого поля, находящейся на расстоянии r от заряда Q.

Диэлектрическая проницаемость среды имеет известное значение (табличное), характеризует среду, в которой существует поле. Для воздуха она равна единице.
Понятие потенциала в физике
Что такое потенциал в физике? Это понятие очень часто применяется для описания качеств сил и полей самой разной природы. Скалярная функция, характеризующая некоторую величину, представляющуюся вектором, – вот что это потенциал. Гравитационный потенциал описывает соответствующее поле. В термодинамике это понятие применяется для системной внутренней энергии, в механике – для той или иной приложенной к предмету силы.
Электрика, прежде всего, интересует, что такое потенциал в электричестве. Из общего определения нетрудно вывести, что характеристика электрополя – это электрический потенциал. В своей статической форме электрический потенциал показывает потенциальную энергию одиночного «плюсового» заряда, помещаемого в данное место электрополя, и является одной из разновидностей электромагнитного потенциала. Вторая его форма – векторная (в отличие от скалярной), описывает магнитное поле.
Важно! Характеристика поля, описывающая зависимость работы при передвижении исключительно от исходной точки и места назначения, – это потенциальность поля. Траектория перемещения в этом случае на работу не влияет.
Как определить знак потенциала
При решении задач возникает много путаницы при определении знака потенциала, разности потенциалов, работы.
На рисунке изображены линии напряженности. В какой точке поля потенциал больше?
Верный ответ — точка 1. Вспомним, что линии напряженности начинаются на положительном заряде, а значит положительный заряд находится слева, следовательно максимальным потенциалом обладает крайняя левая точка.
Если происходит исследование поля, которое создается отрицательным зарядом, то потенциал поля вблизи заряда имеет отрицательное значение, в этом легко убедиться, если в формулу подставить заряд со знаком «минус». Чем дальше от отрицательного заряда, тем потенциал поля больше.
Если происходит перемещение положительного заряда вдоль линий напряженности, то разность потенциалов и работа являются положительными. Если вдоль линий напряженности происходит перемещение отрицательного заряда, то разность потенциалов имеет знак «+», работа имеет знак «-«.
Порассуждайте самостоятельно отрицательные или положительные значения будут принимать работа и разность потенциалов, если заряд перемещать в обратном направлении относительно линий напряженности.
Что такое электрический потенциал и разница потенциалов
Для наглядности можно рассмотреть доходчиво на простом примере две металлических монеты, которые нагреть до разных температур:
- Т1 = 100 ̊С;
- Т2 =70 ̊С.
ΔТ = 100 – 70 = 30 ̊С – разница температур будет в 30 градусов.
Если соединить монеты, тепло начнет перемещаться: более нагретая – будет отдавать тепло и остывать, менее нагретая – принимает тепло, разогревается больше. Таким образом, происходит теплообмен до выравнивания температуры на двух монетах.
В нашем случае рассматривается электрический потенциал, монеты или другие предметы можно зарядить электрическим зарядом, в этом случае будет перемещаться не тепло, а заряженные частицы от большего заряда к меньшему заряду, произойдет выравнивание потенциалов до сбалансированного состояния зарядов. Таким образом, временно возникает электрический ток.

В международной системе измерения СИ электрический потенциал измеряют как работу электрического поля по перемещению положительного заряда из определенной точки магнитного поля на бесконечно удаленное расстояние.
Величина потенциала измеряется вольтами:
1В = 1Дж/1Кл, где:
- Дж – энергия магнитного поля, измеряется в Джоулях;
- Кл – величина заряда, измеряется в Кулонах;
Разница между потенциалами двух зарядов, как в случае с нагревом монет, будет:
ΔВ = 100В – 70В = 30В.

Разницу потенциалов в электрических цепях между двумя токопроводящими поверхностями, чаще всего это бывают провода, корпуса электроустановок, водопроводные тубы, шины заземления, называют напряжением и обозначают буквой «U».
Не вдаваясь в подробности физических процессов, принимается за аксиому, что в промышленных электрических цепях за объект с абсолютно нулевым потенциалом принимается земля. Поэтому напряжение в цепи измеряется относительно заземляющего контура.
Разность потенциалов (напряжение)
Напряжение является одним из важнейших терминов в электрике, оно описывается как работа, совершаемая электрополем с целью перемещения некоторого заряда из одной точки в другую. По аналогии с гравитацией, заряд при помещении в зону действия поля обладает потенциалом, который можно сравнить с соответствующим видом энергии у тела. Величина электрического потенциала прямо пропорциональна степени полевой напряженности и величине самого заряда.
Что такое фаза в электричестве
Встает вопрос: потенциал в чем измеряется? Правильнее будет сказать, в чем обычно измеряется разность потенциалов, так как работники электротехники имеют дело именно с этой величиной в форме напряжения. Для самого потенциала специальной измерительной единицы не существует. В СИ принято измерять разность в вольтах (В). Она равна одному вольту в том случае, если для транспортировки заряда в один кулон из одной точки электрополя в другую потребуется совершить работу в один джоуль.
Важно! Измерить напряжение можно с помощью специального устройства – вольтметра. Стрелочная разновидность прибора, использующаяся на школьных уроках физики, оснащена градуированной шкалой, базирующейся на угле отклонения проволочной рамки, по которой проходит электроток. Помимо него, существуют и приборы с цифровым дисплеем, а также мультиметры, способные работать в нескольких режимах и измеряющие разные величины, описывающие электроцепь. Для измерения важно правильно подключить щупы.

Проводники в электростатическом поле
Размещение проводника в электростатическом поле приводит к тому, что поле начнет действовать на носители заряда внутри проводящего предмета. Носители начинают перемещаться до тех пор, пока электростатическое поле вне поверхности ни обратится в нуль.
Поскольку поле внутри вещества отсутствует, то во всех точках проводящего материала энергия будет постоянной, а поверхность эквипотенциальной. Векторы напряженности поля направлены под прямым углом в любой точке поверхности проводника.

Под действием поля заряды внутри проводника отсутствуют, поскольку они сосредоточены исключительно на поверхности. Этот факт используется при экранировке – защите тел от влияния внешних электромагнитных и электростатических полей. Для экранирования может использоваться не только сплошной проводящий материал, но и сетка, так называемая «клетка Фарадея».

Также свойство перемещения заряженных частиц (электронов) используется в электростатических генераторах для получения напряжения в несколько миллионов вольт.
