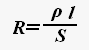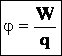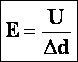Как найти потенциал полого шара

Сообщения без ответов | Активные темы | Избранное

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей

Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения

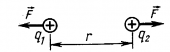
1.

Формулировка
закона Кулона: «Сила
электростатического взаимодействия
между двумя точечными электрическими
зарядами прямо пропорциональна
произведению величин зарядов, обратно
пропорциональна квадрату расстояния
между ними и направлена вдоль соединяющей
их прямой так, что одноименные заряды
отталкиваются, а разноименные
притягиваются».

Следует
отметить, что закон Кулона применим для
расчета взаимодействия точечных зарядов
и тел шарообразной формы при равномерном
распределении заряда по их поверхности
или объёму.

Точечным
зарядом называется
заряженное тело, размерами которого
можно пренебречь по сравнению с
расстояниями до других тел, несущих
электрический заряд.

Напряженность
электрического поля. Количественной
характеристикой силового действия
электрического поля на заряженные тела
служит векторная величина E,
называемая напряжённостью
электрического поля.

E = F / q _пр.

Она определяется
отношением силы F,
действующей со стороны поля на точечный
пробный заряд q_пр,
помещенный в рассматриваемую точку
поля, к величине этого заряда

Принцип
суперпозиции. Напряжённость
поля, создаваемого системой неподвижных
точечных зарядов q₁, q₂, q₃, , q_n,
равна векторной сумме напряжённостей
электрических полей, создаваемых каждым
из этих зарядов в
отдельности:
                                          

где r_i –
расстояние между зарядом q_i и
рассматриваемой точкой поля.

Принцип
суперпозиции,
позволяет рассчитывать не только
напряжённость поля системы точечных
зарядов, но и напряженность поля в
системах, где имеет место непрерывное
распределение заряда. Заряд тела можно
представить как сумму элементарных
точечных зарядов dq

 Поток
вектора напряжённости
электрического поля через
любую произвольно выбранную замкнутую
поверхность пропорционален заключённому
внутри этой поверхности электрическому
заряду

 —
поток
вектора напряжённости электрического
поля через замкнутую поверхность .

 

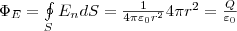
Напряженность
поля, создаваемого, бесконечной равномерно
заряженной плоскостью.

Пусть
плоскость имеет бесконечную протяженность
и заряд на единицу площади равен σ. Из
законов симметрии следует, что поле
направлено всюду перпендикулярно
плоскости, и если не существует никаких
других внешних зарядов, то поля по обе
стороны плоскости должны быть одинаковы.
Ограничим часть заряженной плоскости
воображаемым цилиндрическим ящиком,
таким образом, чтобы ящик рассекался
пополам и его образующие были
перпендикулярны, а два основания, имеющие
площадь S каждое, параллельны заряженной
плоскости (рис 1.10).

Суммарный
поток вектора; напряженности равен
вектору  ,
умноженному на площадь S первого
основания, плюс поток вектора  через
противоположное основание. Поток
напряженности через боковую поверхность
цилиндра равен нулю, т.к. линии напряженности
их не пересекают. Таким образом,  С
другой стороны по теореме Гаусса

Следовательно

но  тогда
напряженность поля бесконечной равномерно
заряженной плоскости будет равна

Напряженность
поля равномерно заряженной бесконечной
прямолинейной нити (или цилиндра).

Предположим,
что полая цилиндрическая поверхность
радиуса R заряжена с постоянной линейной
плотностью  .

Проведем
коаксиальную цилиндрическую поверхность
радиуса  Поток
вектора напряженности через эту
поверхность

По
теореме Гаусса

Из
последних двух выражений определяем
напряженность поля, создаваемого
равномерно заряженной нитью:

Электростатическое
поле шара.

Пусть
имеем шар радиуса R, равномерно заряженный
с объемной плотностью . 

В
любой точке А, лежащей вне шара на
расстоянии r от его центра (r>R), его поле
аналогично полю точечного заряда  ,
расположенного в центре шара. Тогда вне
шара

(13.10)

а
на его поверхности (r=R)

(13.11)

В
точке В, лежащей внутри шара на расстояний
r от его центра (r>R), поле определяется
лишь зарядом ,
заключенным внутри сферы радиусом r.
Поток вектора напряженности через эту
сферу равен

с
другой стороны, в соответствии с теоремой
Гаусса

Из
сопоставления последних выражений
следует

2.

Электростатический
потенциа́л (см.
также кулоновский
потенциал) — скалярная энергетическая характеристика электростатического
поля,
характеризующая потенциальную
энергию поля,
которой обладает единичный заряд,
помещённый в данную точку поля. Единицей
измерения потенциала
является, таким образом, единица
измерения работы,
деленная на единицу измерения заряда

Напряжённость
электростатического поля  и
потенциал  связаны
соотношением

или
обратно:

Физический
смысл потенциала –
работа по переносу заряда из точки в
бесконечность.

 потенциал
точечного заряда.

Потенциал
поля в данной точке пространства равен
работе, которую совершают электрические
силы при удалении единичного положительного
заряда из данной точки в бесконечность.

Потенциал
φ∞ поля точечного заряда Q на расстоянии
r от него относительно бесконечно
удаленной точки вычисляется следующим
образом:
 

Потенциал
от заряженного шара вычислим через
электрическое поле, при этом удобно
ноль потенциала установить на
бесконечности.  Общая формула для
потенциала всевозможных шаров (полых,
сплошных):

Подставляя
вместо E найденные
значения, получим:

любой шар, потенциал вне шара (такой же, как от точечного заряда):
внутри полого шара потенциал не меняется (R – радиус шара):
внутри заряженного равномерно по объёму сплошного шара:

3.

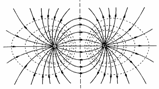
Электри́ческий
ди́польный моме́нт — векторная физическая
величина,
характеризующая, наряду с суммарным
зарядом (и реже используемыми высшими
мультипольными моментами), электрические
свойства системы заряженных
частиц (распределения зарядов)
в смысле создаваемого ею поля и действия
на нее внешних полей. Главная после
суммарного заряда и положения системы
в целом (ее радиус-вектора) характеристика
конфигурации зарядов системы при
наблюдении ее издали.

Вектор
поляризации —
векторная физическая величина,
равная дипольному
моменту единицы
объёма вещества, возникающему при его
поляризации, количественная
характеристика диэлектрической
поляризации

Диэлектрическая
поляризация обусловлена смещением
связанных зарядов вещества
во внешнем электрическом поле относительно
их расположения при отсутвии внешнего
электрического поля. Если выделить
какой либо объём в диэлектрике,
то в результате приложения поля на его
поверхности могут возникнуть поверхностные
электрические заряды .
Такие заряды могут возникнуть или
благодаря смещению электронной
оболочки относительно ядра
атома, или же в результате переориентации
молекул, которые имеют собственный дипольный
момент.

Нормальную
к поверхности составляющую вектора
поляризации определяют как

где  — орт нормали
к поверхности.

Из-за
поляризации диэлектрика на поверхность
пластины, об-ращенную в сторону
положительно заряженной плоскости,
выступают отрицательно за-ряженные
части молекул, а с противоположной
стороны пластины – соответственно
вы-ступают части молекул, заряженные
положительно. Эти заряды называют
связанными. Они возникают на поверхности
диэлектрика лишь при наличии  внешнего
электри-ческого поля. Плотность связанных
зарядов пропорциональна величине
Е_n(нормальной
к поверхности диэлектрика составляющей
напряженности внешнего элек-трического
поля Е).

Для
количественного описания эффекта
ослабления внешнего электрического
поля в диэлектрике вводится безразмерная
величина ε ,
называемая диэлектрической
проницаемостью среды.
Она показывает, во сколько раз в
диэлектрике ослабляется нормальная
составляющая Е_n внешнего
элек-трического поля. В рассмотренном
примере поле Е_д в
диэлектрике равно

Е_д =
Е/ε  (1.62)Напряженность поля точечного
заряда q, помещенного в однородный
диэлектрик с диэлектрической
проницае-мостью ε, будет равна

Для
описания электрического поля в
диэлектриках поми-мо напряженности
электрического поля часто используют
еще одну векторную величину,
называемую электрическим
смещением (индукцией) D.

D =
ε₀εE(1.64)

Удобство
применения этой величины обусловлено
тем, что нормальная составляющая вектора
электрического смещения D не
изменяется при переходе через границу
диэлектрика. Единицей электрического
смещения служит кулон на квадратный
метр (Кл/м²).

Электрическое
смещение  —
векторная величина, равная сумме вектора
напряжённости электрического поля и
вектора поляризации (Кл/м²).

Поток
вектора D  сквозь
поверхность:

Уравнения
для вектора индукции в СГС имеют вид
(2ая пара уравнений
Максвелла)

Здесь  — плотность свободных зарядов,
а  — плотность
тока свободных зарядов.
Введение вектора ,
таким образом, позволяет исключить из
уравнений Максвелла неизвестные
молекулярные токи и поляризационные
заряды.

6.

Если
уединенный проводник имеет заряд q, то
вокруг него существует электрическое
поле, потенциал которого на поверхности
проводника равен  ,
а емкость – С. Увеличим заряд на величину
dq. При переносе заряда dq из бесконечности
должна быть совершена работа равная  .
Но потенциал электростатического поля
данного проводника в бесконечности
равен нулю  .
Тогда

При
переносе заряда dq с проводника в
бесконечность такую же работу совершают
силы электростатического поля.
Следовательно, при увеличении заряда
проводника на величину dq возрастает
потенциальная энергия поля, т.е.

Проинтегрировав
данное выражение, найдем потенциальную
энергию электростатического поля
заряженного проводника при увеличении
его заряда от нуля до q:

Применяя
соотношение  ,
можно получить следующие выражения для
потенциальной энергии W:

(16.2)

Для
заряженного конденсатора разность
потенциалов (напряжение) равна  поэтому
соотношение для полной энергии его
электростатического поля имеют вид

Будем
рассматривать уединенный
проводник,
т. е. проводник, значительно удаленный
от других проводников, тел и зарядов.
Его потенциал, как известно, прямо
пропорционален заряду проводника. Из
опыта известно, что разные проводники,
будучи при этом одинаково заряженными,
имеют различные потенциалы. Поэтому
для уединенного проводника можно
записать 

 

Величину 

 (1) 

называют электроемкостью (или
просто емкостью)
уединенного проводника. Емкость
уединенного проводника задается зарядом,
сообщение которого проводнику изменяет
его потенциал на единицу. 

Емкость
уединенного проводника зависит от его
размеров и формы, но не зависит от
материала, формы и размеров полостей
внутри проводника, а также его агрегатного
состояния. Причиной этому есть то, что
избыточные заряды распределяются на
внешней поверхности проводника. Емкость
также не зависит ни от заряда проводника,
ни от его потенциала. 

Единица
электроемкости — фарад (Ф):
1 Ф — емкость такого уединенного
проводника, у которого потенциал
изменяется на 1 В при сообщении ему
заряда 1 Кл. 

Согласно
формуле потенциала точечного заряда,
потенциал уединенного шара радиуса R,
который находится в однородной среде
с диэлектрической проницаемостью ε,
равен 

 

Применяя
формулу (1), получим, что емкость
шара 

 (2) 

Из
этого следует, что емкостью 1 Ф обладал
бы уединенный шар, находящийся в вакууме
и имеющий радиус R=C/(4πε₀)≈9•10⁶ км,
что примерно в 1400 раз больше радиуса
Земли (электроемкость Земли С≈0,7 мФ)

Конденса́тор (от лат. condensare —
«уплотнять», «сгущать») — двухполюсник с
определённым значением ёмкости и
малой омической проводимостью;
устройство для накопления заряда и
энергии электрического поля. Конденсатор
является пассивным электронным
компонентом. В простейшем варианте
конструкции состоит из двух электродов
в форме пластин (называемых обкладками),
разделённых диэлектриком,
толщина которого мала по сравнению с
размерами обкладок

Примерами
конденсаторов с другой конфигурацией
обкладок могут служить сферический и
цилиндрический конденсаторы. Сферический
конденсатор –
это система из двух концентрических
проводящих сфер радиусов R₁ и R₂. Цилиндрический
конденсатор –
система из двух соосных проводящих
цилиндров радиусов R₁ и R₂ и
длины L.
Емкости этих конденсаторов, заполненных
диэлектриком с диэлектрической
проницаемостью ε, выражаются формулами: 

(сферический конденсатор),  (цилиндрический конденсатор).

Основной
характеристикой конденсатора является
его ёмкость,
характеризующая способность конденсатора
накапливать электрический
заряд.
В обозначении конденсатора фигурирует
значение номинальной ёмкости, в то время
как реальная ёмкость может значительно
меняться в зависимости от многих
факторов. Реальная ёмкость конденсатора
определяет его электрические свойства.
Так, по определению ёмкости, заряд на
обкладке пропорционален напряжению между
обкладками (q
= CU).
Типичные значения ёмкости конденсаторов
составляют от единиц пикофарад до тысяч
микрофарад. Однако существуют конденсаторы
(ионисторы)
с ёмкостью до десятков фарад.

Ёмкость
плоского конденсатора, состоящего из
двух параллельных металлических пластин
площадью S каждая,
расположенных на расстоянии d друг
от друга, в системе СИ
выражается формулой: ,
где  — относительная
диэлектрическая проницаемость среды,
заполняющей пространство между пластинами
(в вакууме равна единице),  —электрическая
постоянная,
численно равная 8,854187817·10⁻¹² Ф/м. Эта
формула справедлива, лишь когда d много
меньше линейных размеров пластин.

Для
получения больших ёмкостей конденсаторы
соединяют параллельно. При этом напряжение
между обкладками всех конденсаторов
одинаково. Общая ёмкость батареи
параллельно соединённых
конденсаторов равна сумме ёмкостей
всех конденсаторов, входящих в батарею.

7.

Электрический
ток – упорядоченное
движение заряженных частиц под действием
сил электрического поля или сторонних
сил.

За
направление тока выбрано направление
движения положительно заряженных
частиц.

Электрический
ток называют постоянным,
если сила тока и его направление не
меняются с течением времени.

Сила
тока –
скалярная физическая величина, равная
отношению заряда, прошедшего через
проводник, ко времени, за которое этот
заряд прошел.

где I –
сила тока, q – величина
заряда (количество электричества), t –
время прохождения заряда.

Как
правило, большая часть работы электрического
тока выделяется в виде тепла. Мощностью тепловых
потерь называется величина, равная количеству
выделившегося тепла в единицу
времени. Согласно закону Джоуля —
Ленца мощность тепловых потерь в
проводнике пропорциональна силе
протекающего тока и приложенному
напряжению:

Мощность
измеряется в ваттах.

Плотность
тока –
векторная физическая величина, равная
отношению силы тока к площади поперечного
сечения проводника.

где j –плотность
тока,  S – площадь
сечения проводника.

Направление
вектора плотности тока совпадает с
направлением движения положительно
заряженных частиц.

Напряжение – скалярная
физическая величина, равная отношению
полной работе кулоновских и сторонних
сил при перемещении положительного
заряда на участке к значению этого
заряда.

где A – полная
работа сторонних и кулоновских сил,  q –
электрический заряд.

Электрическое
сопротивление –
физическая величина, характеризующая 
электрические свойства участка цепи.

где ρ –
удельное сопротивление проводника, l – длина
участка проводника,  S – площадь
поперечного сечения проводника.

Проводимостью называется
величина, обратная сопротивлению

где  G – проводимость.

Для
существования постоянного электрического
тока необходимо наличие свободных
заряженных частиц и наличие источника
тока. в котором осуществляется
преобразование какого-либо вида энергии
в энергию электрического поля.

Источник
тока –
устройство, в котором осуществляется
преобразование какого-либо вида энергии
в энергию электрического поля. В источнике
тока на заряженные частицы в замкнутой
цепи действуют сторонние силы. Причины
возникновения сторонних сил в различных
источниках тока различны. Например в
аккумуляторах и гальванических элементах
сторонние силы возникают благодаря
протеканию химических реакций, в
генераторах электростанций они возникают 
при движении проводника в магнитном
поле, в фотоэлементах – при действия
света на электроны в металлах и
полупроводниках.

Электродвижущей
силой источника тока называют
отношение работы сторонних сил к величине
положительного заряда, переносимого
от отрицательного полюса источника
тока к положительному.

Закон
Ома для однородного участка цепи.

Сила
тока в однородном участке цепи прямо
пропорциональна напряжению при постоянном
сопротивлении участка  и обратно
пропорциональна сопротивлению участка
при постоянном напряжении.

где U – напряжение
на участке,  R –
сопротивление участка.

Закон
Ома для произвольного участка цепи,
содержащего источник постоянного тока.

где   φ₁ – φ₂ + ε = U напряжение
на заданном участке цепи, R –
электрическое сопротивление  заданного
участка цепи.

Закон
Ома для полной цепи.

Сила
тока в полной цепи равна отношению
электродвижущей силы источника к сумме
сопротивлений внешнего и внутреннего
участка цепи.

где R – электрическое
сопротивление внешнего участка цепи,  r –
электрическое сопротивление внутреннего
участка цепи.

  Исходя
из закона Ома имеем:

      А
мы знаем, что  или .
Отсюда можно записать

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

В этой заметке разберем одну из задачек по электродинамике. Постараюсь привести максимально подробное решение, которое будет полезно учащимся 1-2 курсов физико-математических факультетов. Кто скучал по электродинамике и интегралам – ставим жирный лайк, чтоб я чаще писал про это 🙂 Доброго времени суток, друзья, мы начинаем…

Задача

Шар из однородного изотропного диэлектрика с диэлектрической проницаемостью ε и радиуса R заряжен сторонним зарядом q с объемной плотностью, линейно меняющейся от значения 0 в центре до максимального значения на поверхности шара. Считая, что шар находится в воздухе, определить потенциал во всей области изменения радиуса.

Решение:

Для начала нам нужно сделать рисунок к задаче. К любой задаче надо пытаться делать рисунок. Не потому что это нужно для кого-то или для красоты. Это нужно для того, чтобы наш мозг лучше визуализировал происходящее, строил абстрактные модели и логические цепочки.

1. По условию сказано, что плотность заряда диэлектрического шара меняется линейно, значит функционально мы можем выразить это так ( с проверкой граничных условий):

2. Нам задан именно общий заряд q, а не максимальная плотность. Поэтому эту неизвестную константу попробуем найти из условия нормировки.

3. Для начала найдем напряженность внешнего электрического поля (вне шара), а также потенциал вне шара. Для этого применим теорему Гаусса:

4. Теперь найдем напряженность электрического поля внутри шара. Для этого замкнутой поверхностью выберем сфера с радиусом r < R, центр которой будет совпадать с центром нашего шара. Симметрия подсказывает, что напряженность направленно радиально и одинакова по величине на всей поверхности. Применяем также теорему Гаусса. Учитываем, что внутри шара диэлектрик с заданной диэлектрической проницаемостью.

5. Теперь, зная внешнее и внутреннее поля, найдем потенциал внутри шара.

Первый интеграл в начале нашей формулы имеет смысл работы по переносу единичного положительного заряда из бесконечно удаленной точки в точку на поверхности шара r = R. Второй интеграл имеет смысл работы по переносу единичного положительного заряда с поверхности шара внутрь на радиус r < R. Обратим внимание, что внешний и внутренний потенциал сшиваются на границе при r = R.

Задача решена.

Понравилась заметка? Поставьте лайк, подпишитесь на канал! Вам не сложно, а мне очень приятно 🙂

Если Вам нужен репетитор по физике, математике или информатике/программированию, Вы можете написать мне или в мою группу Репетитор IT mentor в VK
Библиотека с книгами для физиков, математиков и программистов
Репетитор IT mentor в Instagram
Репетитор IT mentor в telegram

Потенциал. Разность потенциалов. Напряжение.
Потенциал электростатического поля — скалярная величина, равная отношению потен­циальной энергии заряда в поле к этому заряду:   – энергетическая характеристика поля в данной точке. Потенциал не зависит от величины заряда, помещенного в это поле.
Т.к. потенциальная энергия зависит от выбора системы координат, то и потенциал определяется с точностью до постоянной. За точку отсчета потенциала выбирают в зависимости от задачи: а) потенциал Земли, б) потенциал бесконечно удаленной точки поля, в) потенциал отрицательной пластины конденсатора.
– следствие принци­па суперпозиции полей (потенциалы складываютсяалгебраически).
Потенциал численно равен работе поля по перемещению единичного положительного заряда из данной точки электрического поля в бесконечность. В СИ потенциал измеряется в вольтах:
Разность потенциалов
Напряжение — разность значений потенциала в начальной и конечнойточках траектории. Напряжение численно равно работе электростатического поля при перемещении единичного положительного заряда вдоль силовых линий этого поля.          Разность потенциалов (напряжение) не зависит от выбора системы координат!
Единица разности потенциалов    Напряжение равно 1 В, если при перемещении положительного заряда в 1 Кл вдоль силовых линий поле совершает работу в 1 Дж.
Связь между напряженностью и напряжением.
Из доказанного выше:   →      напряженность равна градиенту потенциала (скорости изменения потенциала вдоль направления d).
Из этого соотношения видно: Вектор напряженности направлен в сторону уменьшения потенциала. Электрическое поле существует, если существует разность потенциалов. Единица напряженности:     –   Напряженность поля равна 1 В/м, если между двумя точками поля, находящимися на расстоянии 1 м друг от друга существует разность потенциалов 1 В.
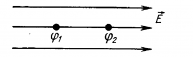
Эквипотенциальные поверхности. ЭПП – поверхности равного потенциала. Свойства ЭПП: – работа при перемещении заряда вдоль эквипотенциальной поверхности не совершается; – вектор напряженности перпендикулярен к ЭПП в каждой ее точке.
Измерение электрического напряжения (разности потенциалов) Между стержнем и корпусом — электрическое поле. Измерение потенциала кондуктора Измерение напряжения на гальваническом элементе Электрометр дает большую точность, чем вольтметр.
Потенциальная энергия взаимодействия зарядов.
Потенциал поля точечного заряда
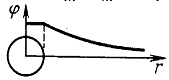
Потенциал заряженного шара а) Внутри шара Е=0, следовательно, потенциалы во всех точках внутри заряженного металлического шара одинаковы (!!!) и равны потенциалу на поверхности шара. б) Снаружи поле шара убывает обратно пропорционально расстоянию от центра шара, как и в случае точечного заряда.
Перераспределение зарядов при контакте заряженных проводников. Переход зарядов происходит до тех пор, пока потенциалы контактирующих тел не станут равными.