Определение напряженности электрического поля с помощью потенциала
Публикации по материалам Д. Джанколи. “Физика в двух томах” 1984 г. Том 2.
Формулу  можно использовать для определения разности потенциалов между двумя точками электрического поля, если напряженность поля в области между этими точками известна. Обращая эту формулу мы можем выразить напряженность электрического поля через его потенциал, т. е., зная V, мы сможем определить Е.
можно использовать для определения разности потенциалов между двумя точками электрического поля, если напряженность поля в области между этими точками известна. Обращая эту формулу мы можем выразить напряженность электрического поля через его потенциал, т. е., зная V, мы сможем определить Е.
Посмотрим, как это делается.
Уравнение можно переписать в дифференциальной форме:
dV = -E·dl = -Eldl,
где dV – бесконечно малая разность потенциалов между точками на расстоянии dl друг от друга, а El – составляющая напряженности электрического поля в направлении этого бесконечно малого перемещения dl.
Тогда:

Таким образом, составляющая напряженности электрического поля по любому направлению равна градиенту потенциала в этом направлении, взятому с обратным знаком. Градиентом величины V называется ее производная по определенному направлению dV/dl. Если направление не указывается, то градиент соответствует направлению наиболее быстрого изменения V; это соответствует направлению вектора Е в данной точке, поскольку именно в таком направлении составляющая вектора Е совпадает с полной величиной напряженности поля:

Если расписать составляющие вектора Е по координатам х, у, z и в качестве l взять направления вдоль осей х у, z,
то уравнение (24.8) можно записать в виде:

Здесь dV/dx – частная производная V по направлению х при условии, что у и z фиксированы.
В последнем примере мы вычислили напряженность электрического поля Е диполя в произвольной точке пространства. Складывая векторы напряженностей, создаваемых каждым зарядом в отдельности, получить этот результат было бы гораздо сложнее. Вообще
говоря, для многих распределений зарядов гораздо проще рассчитать потенциал, а затем по формуле (24.9) – напряженность электрического поля Е, чем вычислять по закону Кулона по отдельности Е для каждого заряда: скалярные величины складывать намного проще, чем
векторы.
Электростатическая потенциальная энергия
Предположим, что точечный заряд q перемещают в пространстве из точки а в точку b, электрические потенциалы
в которых, обусловленные другими зарядами, равны соответственно Va и Vb. Изменение электростатической
потенциальной энергии заряда q в поле других зарядов составляет:
ΔU = Ub – Ua = q(Vb – Va) = qVba
Пусть теперь имеется система нескольких точечных зарядов. Чему равна электростатическая потенциальная энергия системы?
Удобнее всего выбрать за нуль потенциальную энергию зарядов на очень больших (в идеале бесконечно больших) расстояниях друг от друга.
Потенциальная энергия уединенного точечного заряда Q1 равна нулю, поскольку в отсутствие других зарядов на него не действует никакая сила. Если к нему поднести второй точечный заряд, Q2, потенциал в точке, где находится второй заряд, будет равен:

Здесь r1 2 – расстояние между зарядами. Потенциальная энергия двух зарядов равна:

Она характеризует работу, необходимую для перемещения заряда Q2 из бесконечности (V = 0) на расстояние r1 2 до
заряда Qi (или со знаком минус работу, необходимую для разнесения зарядов на бесконечно большое расстояние).
Если система состоит из трех зарядов, то ее полная потенциальная энергия будет равна работе по перемещению всех трех зарядов из бесконечности в место их расположения. Работа по сближению зарядов Q2 и Q1 определяется выражением (24.10);
чтобы перенести заряд Q3 из бесконечности в точку на расстоянии r1 3 от Q1 и на расстоянии r2 3 от Q2, требуется совершить работу:

В этом случае потенциальная энергия системы трех точечных зарядов будет равна:

Для системы четырех зарядов выражение для потенциальной энергии будет содержать шесть таких членов и т.п. (При составлении подобных сумм необходимо следить за тем, чтобы не учитывать одну и ту же пару дважды).
Часто нас интересует не полная электростатическая потенциальная энергия, а лишь часть ее. Например, может возникнуть необходимость найти потенциальную энергию одного диполя в присутствии другого диполя. Во взаимодействии участвуют четыре заряда: Q1 и -Q1 первого диполя и Q2 и -Q2 второго диполя.
Потенциальная энергия одного диполя и в присутствии другого (иногда ее называют энергией взаимодействия) представляет собой работу по сближению диполей с бесконечно большого расстояния. В этом случае нас не интересует взаимная потенциальная энергия зарядов Q1 и -Q1 или Q2 и -Q2; выражение для потенциальной энергии двух диполей будет содержать лишь четыре члена, соответствующие энергиям взаимодействия между зарядами: Q1 и Q2 ; Q1 и -Q2 ; -Q1 и Q2 ; -Q1 и -Q2.
Заключение
Электрический потенциал в любой точке пространства определяется как электростатическая потенциальная энергия единицы заряда. Разность потенциалов между двумя точками определяется взятой с обратным знаком работой, которая совершается полем при перемещении единичного электрического заряда между этими точками. Разность потенциалов измеряется в вольтах (1 В = 1 Дж/Кл) и иногда называется напряжением. Изменение
потенциальной энергии заряда q при прохождении им разности потенциалов Vbа равно ΔU = qVba.
Разность потенциалов Vbа между точками b и a в однородном электрическом поле напряженностью Е определяется формулой V = — Ed, где d – расстояние вдоль силовой линии поля между этими точками.
В неоднородном электрическом поле Е соответствующее выражение имеет вид  .
.
Таким образом, зная Е, всегда можно определить Vbа. Если значение V известно, то составляющие
напряженности поля Е можно найти, обращая приведенное соотношение:
Еx = -dV/dх , Еy = -dV/dу , Ez = -dV/dz .
Эквипотенциальные линии или поверхности представляют собой геометрическое место точек одного потенциала; они всюду перпендикулярны силовым линиям поля. Электрический потенциал уединенного точечного заряда Q относительно нулевого потенциала (на бесконечности) равен:

Потенциал произвольного распределения зарядов можно определить, суммируя (интегрируя) потенциалы отдельных зарядов.
где r – расстояние от элемента заряда dq до точки, в которой определяется V.
Продолжение следует. Коротко о следующей публикации:
Электрическая емкость, диэлектрики, накопление электрической энергии.
Конденсатор – устройство для накопления электрического заряда, который состоит из двух проводников (обкладок), расположенных близко друг к другу, но не соприкасающихся.
Альтернативные статьи:
Постоянный ток, Переменный ток.
Замечания и предложения принимаются и приветствуются!
Рассмотрим
вычисление потенциала поля, созданного
некоторыми заряженными телами.
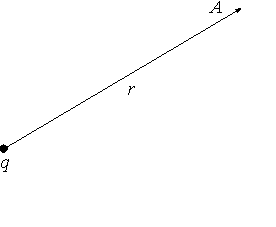
Рис.3.
Расположение точки наблюдения А по
отношению к точечному источнику поля
q
1.
Пример
Точечный
заряд.
Используя соотношения (1) и (4) и совмещая
точку 1 с точкой наблюдения А
(рис.3), а точку 2 удаляя на бесконечность,
получим
![]() (7)
(7)
Замечание.
До сих пор использовалось понятие
векторного поля – поля векторов
![]() (каждой точке пространства ставится в
(каждой точке пространства ставится в
соответствие вектор![]() ).
).
Представление о потенциале
![]() как
как
функции точки пространства позволяет
ввести понятие скалярного поля – поля
чисел
![]()
(каждой точке пространства ставится в
соответствие, с точностью до произвольной
аддитивной постоянной, число
![]() ).
).
Поэтому в дальнейшем кроме понятий
электростатическое поле и поле
![]() ,
,
будем использовать понятие поля![]() .
.
2.Пример. Найдем потенциал бесконечной однородно заряженной с линейной плотностью нити.
Наша задача найти
![]()
как функцию
![]() .
.
К
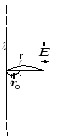 ак
ак
уже было показано для бесконечно длинной
нити:![]() .
.
Выберем где-нибудь
точку из которой мы стартуем, к примеру
в точке
![]() ,
,
то
![]() .
.
Договоримся, что
в точке старта потенциал равен нулю:
![]() ,
,
тогда
![]() .
.
Это при такой
нормировке. Если в такой задаче нормировать
![]() ,
,
то получим![]() ,то
,то
есть все потенциалы во всех точках
бесконечно большие. Кому нужна такая
нормировка? Если Вас интересует какой-то
конкретный пространственный диапазон,
то нормировать надо где-то вблизи этой
области, тогда все потенциалами будут
конечными приятными числами. От
бесконечной нити нельзя уйти на
бесконечность, по этой же причине не
следует ожидать хорошего результата
от![]() как суммы потенциалов точечных фрагментов
как суммы потенциалов точечных фрагментов
нити, каждый из которых нормирован
условием![]() .
.
3.Пример. Потенциал поля точечного диполя (первый способ).
И так,
так,
мы рассматриваем точечный диполь и
точку наблюдения достаточно далеко от
этой нашей гантельки.
Давайте искать
потенциал этой точки наблюдения.
Во первых, принцип
суперпозиции.
![]()
Во-вторых, как
известно
![]()
![]() .
.
Учтя, что
![]() есть проекция вектора
есть проекция вектора![]() на
на![]() и то, что расстояние до диполя очень
и то, что расстояние до диполя очень
велико, то
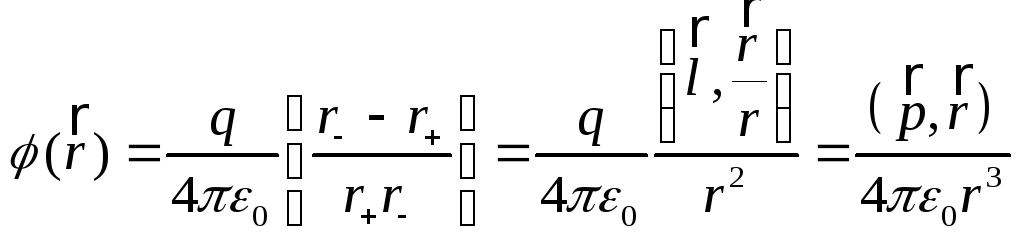
Потенциал поля точечного диполя (второй способ).
Используем готовую
формулу для напряженности поля:
![]() .
.
Вот такое выражение мы с вами в свое
время вывели. Обопремся на него.
![]()
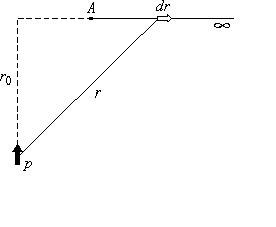
Д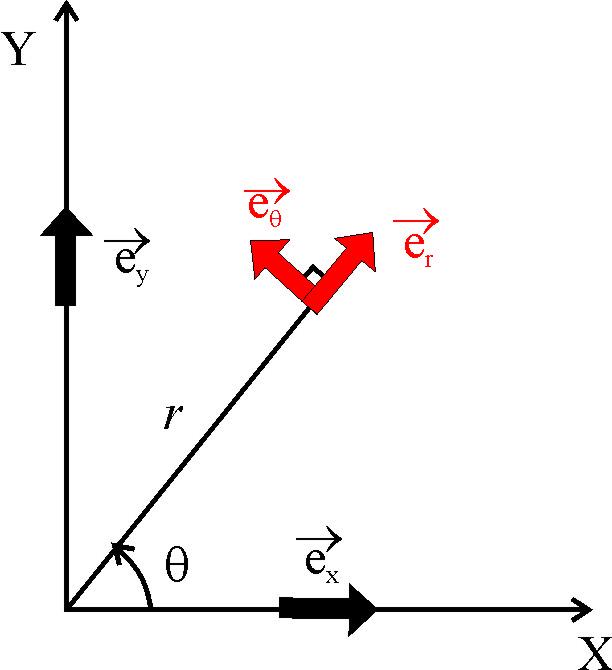 авайте
авайте
выберем такое направление, чтобы нам
было удобно вычислять этот интеграл,
так как поле потенциальное, то результат
не будет зависеть от вида траектории.
Ориентация диполя, направление движения
и вектор![]() показаны
показаны
на рисунке. С учетом некоторых соотношений
(5) примет вид:
![]()
Определение
вектора
![]() точечного
точечного
диполя из
![]() в
в
полярной системе координат.
![]() Оператор
Оператор
![]() запишется в полярной системе координат
запишется в полярной системе координат
так:
![]()
Ортыкоординатных
осей декартовой и полярной систем
координат (см.рис.)
4.Пример
См. Иродов задача
3.38. (часть2)
Показать, что
потенциал диполя с электрическим
моментом может быть представлен как![]() ,
,
где![]() –радиус
–радиус
вектор. Найти с помощью этого выражения
модуль напряженности электрического
поля диполя как функцию![]() и
и![]() .
.
![]() –
–
это уже показали выше, отсюда, раскрывая
скалярное произведение и продифференцировав
формулу для потенциала, мы получим
![]() .
.
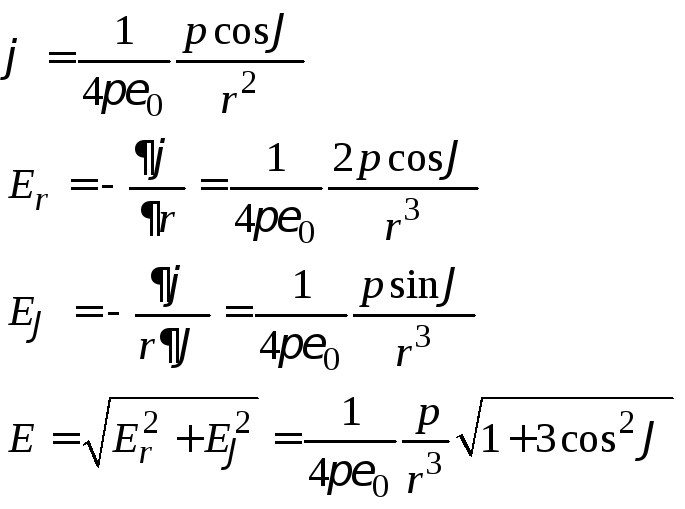
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Глава 18. Напряженность и потенциал электрического поля.Силовые линии электрического поля
Для характеристики создаваемого зарядами электрического поля вводятся две величины — напряженность электрического поля и его потенциал. Напряженность характеризует силу, действующую со стороны поля на внесенный в него пробный заряд. Если в какой-то точке поля на заряд 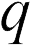 действует сила
действует сила 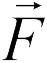 , то напряженность электрического поля в этой точке равна
, то напряженность электрического поля в этой точке равна
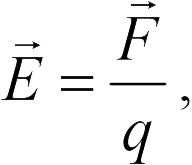
где 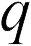 — заряд, который мы взяли, чтобы «попробовать» поле в данной точке. Такой заряд называется «пробным». Пробный заряд не должен искажать распределение зарядов, создающих поле, и потому должен быть достаточно мал. В формулу (18.1) пробный заряд входит со своим знаком (не модуль), поэтому, как следует из (18.1), вектор напряженности поля в некоторой точке направлен так же, как и вектор силы, действующей в этой точке на положительный пробный заряд.
— заряд, который мы взяли, чтобы «попробовать» поле в данной точке. Такой заряд называется «пробным». Пробный заряд не должен искажать распределение зарядов, создающих поле, и потому должен быть достаточно мал. В формулу (18.1) пробный заряд входит со своим знаком (не модуль), поэтому, как следует из (18.1), вектор напряженности поля в некоторой точке направлен так же, как и вектор силы, действующей в этой точке на положительный пробный заряд.
Найдем напряженность электрического поля, создаваемого точечным зарядом  . Для этого возьмем произвольный пробный заряд
. Для этого возьмем произвольный пробный заряд  и поместим его в точку, находящуюся на расстоянии
и поместим его в точку, находящуюся на расстоянии 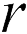 от заряда
от заряда  . Сила, действующую на пробный заряд со стороны заряда
. Сила, действующую на пробный заряд со стороны заряда  , определяется законом Кулона (17.1), (17.2). Поэтому согласно (18.1) имеем
, определяется законом Кулона (17.1), (17.2). Поэтому согласно (18.1) имеем

где  . Направлен вектор напряженности от заряда
. Направлен вектор напряженности от заряда  , если
, если 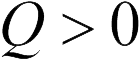 , и к нему, если
, и к нему, если 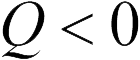 .
.
Пусть поле создается несколькими зарядами  … В этом случае его напряженность равна векторной сумме напряженностей тех полей, которые создаются каждым зарядом в отдельности. Действительно, из принципа суперпозиции следует, что на пробный заряд в этом случае действует сила
… В этом случае его напряженность равна векторной сумме напряженностей тех полей, которые создаются каждым зарядом в отдельности. Действительно, из принципа суперпозиции следует, что на пробный заряд в этом случае действует сила 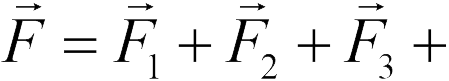 . где
. где 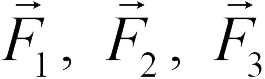 . — силы, действующие на пробный заряд со стороны каждого заряда
. — силы, действующие на пробный заряд со стороны каждого заряда 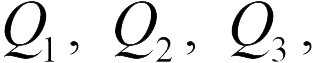 . Поэтому из (18.1) получаем
. Поэтому из (18.1) получаем
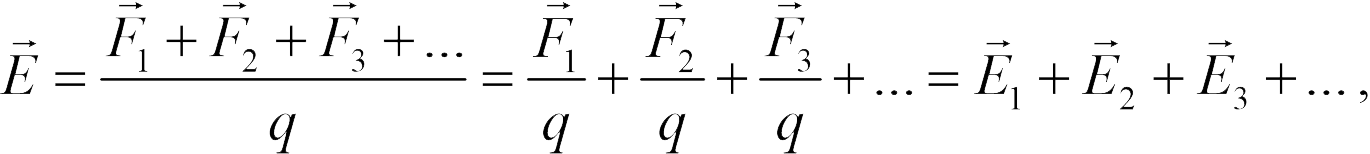
где 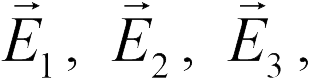 . — напряженности тех полей, которые создавались бы каждым зарядом в отдельности в отсутствие других зарядов. Утверждение (18.3) называется принципом суперпозиции для полей. Формула (18.2) и принцип суперпозиции позволяют вычислить поле, создаваемое любым заряженным телом — с помощью мысленного разбиения его на точечные части и суммирования напряженностей, создаваемых всеми таким частями. Однако из-за математической сложности такой процедуры, она не входит в программу школьного курса физики. Школьник должен знать без вывода результат ее применения к заряженным сферам и плоскостям. Из формул (17.4), (17.5) получаем для напряженности поля сферы радиуса
. — напряженности тех полей, которые создавались бы каждым зарядом в отдельности в отсутствие других зарядов. Утверждение (18.3) называется принципом суперпозиции для полей. Формула (18.2) и принцип суперпозиции позволяют вычислить поле, создаваемое любым заряженным телом — с помощью мысленного разбиения его на точечные части и суммирования напряженностей, создаваемых всеми таким частями. Однако из-за математической сложности такой процедуры, она не входит в программу школьного курса физики. Школьник должен знать без вывода результат ее применения к заряженным сферам и плоскостям. Из формул (17.4), (17.5) получаем для напряженности поля сферы радиуса 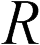 , равномерно заряженной зарядом
, равномерно заряженной зарядом  , в точке на расстоянии
, в точке на расстоянии 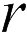 от центра сферы:
от центра сферы:

где 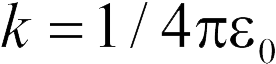 , а из формулы (17.6) для напряженности поля равномерно заряженной плоскости
, а из формулы (17.6) для напряженности поля равномерно заряженной плоскости

где  — заряд плоскости,
— заряд плоскости, 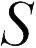 — площадь,
— площадь,  — поверхностная плотность зарядов плоскости.
— поверхностная плотность зарядов плоскости.
Электрическое поле можно изобразить графически (на современном русском языке — визуализировать) с помощью силовых линий. Силовые линии — это такие воображаемые линии, касательные к которым в каждой точке совпадают по направлению с вектором напряженности в этой точке. Вообще говоря, силовые линии проходят через каждую точку поля (кроме тех точек, где  ), но поскольку так их нарисовать нельзя, условились проводить их с определенной густотой в зависимости от величины поля: чем гуще расположены силовые линии, тем больше величина напряженности поля.
), но поскольку так их нарисовать нельзя, условились проводить их с определенной густотой в зависимости от величины поля: чем гуще расположены силовые линии, тем больше величина напряженности поля.
Второй характеристикой электрического поля является его потенциал. Основная идея введения этой величины заключается в следующем. Если электрический заряд перемещается в электрическом поле (созданном другими зарядами), то со стороны поля на него действуют силы, и, следовательно, поле совершает работу. Потенциал поля — это такая функция точки поля  , что работа
, что работа 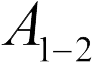 , совершаемая полем над точечным пробным зарядом
, совершаемая полем над точечным пробным зарядом 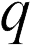 при его перемещении из точки с радиусом-вектором
при его перемещении из точки с радиусом-вектором  в точку с радиусом-вектором
в точку с радиусом-вектором 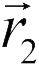 , равна
, равна

(именно в такой последовательности). Из формулы (18.6) следует, что работа, которую совершает поле при перемещении заряда, не зависит от формы траектории, а определяется только начальной и конечной ее точками. В частности, при перемещении тела по замкнутой траектории поле совершает нулевую работу.
Поскольку в формулу (18.6), входит разность потенциалов двух точек поля, потенциал определен с точностью до постоянной. Эту постоянную всегда можно выбрать так, что потенциал любой заданной точки поля можно сделать равным нулю. Как правило, в качестве такой точки выбирают бесконечно удаленную от зарядов точку поля, считая ее потенциал равным нулю. Из формулы (18.6) следует, что потенциал любой точки поля равен отношению работы, которую совершает электрическое поле при перемещении пробного заряда из этой точки в ту точку, потенциал которой выбран равным нулю, к пробному заряду.
Можно доказать, что если поле создается точечным зарядом  , то потенциал на расстоянии
, то потенциал на расстоянии 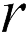 от заряда при условии, что потенциал бесконечно удаленной точки принят за нуль, равен
от заряда при условии, что потенциал бесконечно удаленной точки принят за нуль, равен
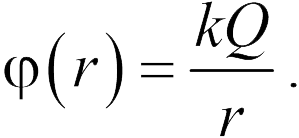
Важно отметить, что в формулу (18.7) входит заряд  со знаком (не модуль!), т.е. потенциал поля, создаваемого положительным зарядом, — положительный, отрицательным — отрицательный.
со знаком (не модуль!), т.е. потенциал поля, создаваемого положительным зарядом, — положительный, отрицательным — отрицательный.
Для потенциалов справедлив принцип суперпозиции: если поле создается несколькими точечными зарядами, то потенциал любой его точке равен алгебраической сумме потенциалов (18.7), создаваемых в этой точке каждым точечным зарядом. Это правило позволяет найти потенциал поля, создаваемого протяженным заряженным телом: нужно мысленно разделить тело на малые («точечные») части, по формуле (18.7) найти потенциал поля, создаваемого каждой такой частью, а затем сложить полученные результаты.
Для решения задач ЕГЭ нужно знать (без вывода) формулу потенциала поля равномерно заряженной сферы. Пусть имеется сфера радиуса  , равномерно заряженная зарядом
, равномерно заряженная зарядом  . Тогда потенциал точки поля, расположенной на расстоянии
. Тогда потенциал точки поля, расположенной на расстоянии 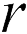 центра сферы, равен
центра сферы, равен

(точка нулевого потенциала выбрана на бесконечности).
Часто в задачах ЕГЭ по физике используется связь напряженности однородного электрического поля и разности потенциалов двух точек поля, лежащих на одной силовой линии. Для нахождения этой связи возьмем положительный пробный заряд 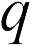 , перенесем его из первой точки во вторую вдоль силовой линии и найдем работу, которую совершает при этом электрическое поле. Поскольку поле действует на заряд с постоянной силой
, перенесем его из первой точки во вторую вдоль силовой линии и найдем работу, которую совершает при этом электрическое поле. Поскольку поле действует на заряд с постоянной силой  , угол между перемещением и этой силой равен нулю (заряд движется вдоль силовой линии), поэтому работа сил поля равна
, угол между перемещением и этой силой равен нулю (заряд движется вдоль силовой линии), поэтому работа сил поля равна  , где
, где 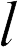 — расстояние между исследуемыми точками. С другой стороны, по определению потенциала работа поля равна
— расстояние между исследуемыми точками. С другой стороны, по определению потенциала работа поля равна  . Приравнивая эти работы, находим
. Приравнивая эти работы, находим
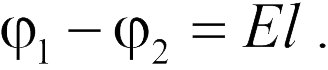
Подчеркнем, что формула (18.9) справедлива только для однородного поля, а точки 1 и 2 должны лежать на одной силовой линии.
Рассмотрим теперь задачи.
Величина напряженности электрического поля, создаваемого точечным зарядом (задача 18.1.1), определяется формулой (18.2)
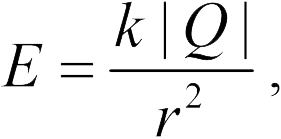
где 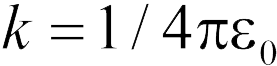 (ответ 1).
(ответ 1).
Размерность напряженности электрического поля (задача 18.1.2) можно найти из связи напряженности поля и потенциала (см. формулу (18.9)). А поскольку размерность потенциала в международной системе единиц СИ – вольт, из формулы (18.9) имеем:

где квадратные скобки обозначают размерность (ответ 3).
Для определения напряженности поля используют пробный заряд (см. формулу (18.1)). Однако напряженность (18.1) ни от знака, ни от величины пробного заряда не зависят (задача 18.1.3). Это связано с тем, что сила  в (18.1) линейно зависит от пробного заряда
в (18.1) линейно зависит от пробного заряда  , и он сокращается в (18.1). Если взять пробный заряд отрицательным, то направление вектора
, и он сокращается в (18.1). Если взять пробный заряд отрицательным, то направление вектора  числителе (18.1) изменится по сравнению со случаем положительного пробного заряда, но отношение
числителе (18.1) изменится по сравнению со случаем положительного пробного заряда, но отношение 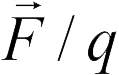 будет направлено противоположно вектору
будет направлено противоположно вектору 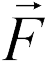 , т.е. направление вектора
, т.е. направление вектора 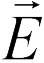 не изменится (ответ 4).
не изменится (ответ 4).
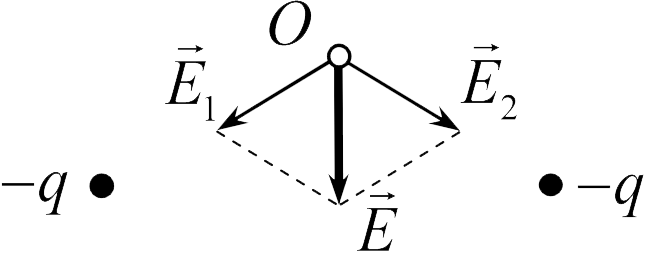
Для нахождения поля, созданного двумя точечными зарядами (задача 18.1.4), используем принцип суперпозиции. Напряженности полей, создаваемых в точке  каждым зарядом в отдельности, показаны тонкими векторами и отмечены как
каждым зарядом в отдельности, показаны тонкими векторами и отмечены как 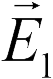 и
и 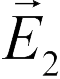 . Поскольку модули этих векторов равны, вектор их суммы направлен вертикально вниз (ответ 4).
. Поскольку модули этих векторов равны, вектор их суммы направлен вертикально вниз (ответ 4).
По определению силовые линии — это такие воображаемые линии, касательные к которым в каждой точке совпадают по направлению с вектором напряженности в этой точке (задача 18.1.5 — ответ 4).
Поскольку силовые линии поля в задаче 18.1.6 направлены направо, то направо направлен и вектор напряженности в каждой точке. Поэтому направо будет направлен и вектор силы, действующий со стороны этого поля на положительные точечный заряд (ответ 2).
Поскольку все траектории движения заряда I, II и III в задаче 18.1.7 начинаются и заканчиваются в тех же точках, то работа поля над зарядом при его движении по всем трем траекториям одинакова (ответ 4).
Разность потенциалов двух точек однородного электрического поля (задача 18.1.8) найдем по формуле (18.9):


Поскольку вектор напряженности электрического поля в любой точке направлен от заряда, то силовые линии поля расходятся радиально, являясь везде прямыми (см.рисунок). Таким образом, правильный ответ в задаче 18.1.9 — 1.
По определению потенциала имеем для работы поля в задаче 18.1.10


Силовые линии электрического поля строятся так, что их густота пропорциональна величине поля: чем гуще силовые линии, тем больше величина напряженности. Поэтому в задаче 18.2.1  (ответ 2).
(ответ 2).
Рисунок в задаче 18.2.2 — тот же самый, что и в предыдущей задаче, однако логика получения ответа совсем другая. Чтобы сравнить потенциалы в точках 1 и 2 перенесем из первой точке во вторую положительный пробный заряд и найдем работу поля. Так как  , и если работа положительна, то
, и если работа положительна, то 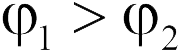 , если отрицательна — наоборот. Очевидно, работа поля при перемещении положительного заряда из точки 1 в точку 2 положительна. Действительно, стрелки на силовых линиях направлены вправо, следовательно, и сила, действующая на положительный заряд, направлена вправо, туда же направлен и вектор перемещения заряда, поэтому косинус угла между силой и перемещением положителен на всех элементарных участках траектории, поэтому положительна работа. Таким образом
, если отрицательна — наоборот. Очевидно, работа поля при перемещении положительного заряда из точки 1 в точку 2 положительна. Действительно, стрелки на силовых линиях направлены вправо, следовательно, и сила, действующая на положительный заряд, направлена вправо, туда же направлен и вектор перемещения заряда, поэтому косинус угла между силой и перемещением положителен на всех элементарных участках траектории, поэтому положительна работа. Таким образом 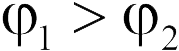 (ответ 1), причем этот результат является следствием направления стрелок на силовых линиях, а не переменной густоты силовых линий.
(ответ 1), причем этот результат является следствием направления стрелок на силовых линиях, а не переменной густоты силовых линий.
В задаче 18.2.3 используем формулу для потенциала поля точечного заряда. Поскольку потенциал поля обратно пропорционален расстоянию до заряда, создающего поле (см. формулу (18.7)),

(ответ 2). Другими словами, на втрое большем расстоянии от точечного заряда потенциал его поля втрое меньше.

Очевидно, искомая в задаче 18.2.4 точка, находится между зарядами. В этой точке величины напряженностей полей 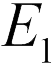 и
и 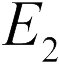 , создаваемых каждым зарядом, должны быть равны (см. рисунок). Используя формулу (18.2), получаем
, создаваемых каждым зарядом, должны быть равны (см. рисунок). Используя формулу (18.2), получаем
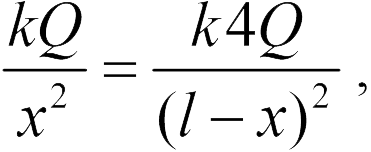
где 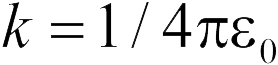 . Отсюда находим
. Отсюда находим 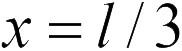 (ответ 3).
(ответ 3).
Используя принцип суперпозиции для потенциалов и формулу для потенциала поля точечного заряда (18.7), получим для искомой точки (задача 18.2.5)

где 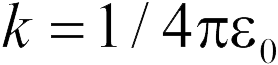 . Отсюда находим
. Отсюда находим  (ответ 2).
(ответ 2).
Поскольку все заряды в задаче 18.2.6 одинаковы, то напряженность поля, созданного в центре квадрата каждой парой зарядов, лежащих на одной диагонали, равна нулю. Поэтому равна нулю и напряженность электрического поля, созданного всеми четырьмя зарядами (ответ 2).
В задачах 18.2.7 и 18.2.8 используем принцип суперпозиции. Векторы напряженности полей, создаваемых верхней и нижней пластинами 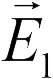 и
и 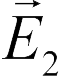 соответственно показаны на рисунках (левый рисунок относится к задаче 18.2.7, правый — к 18.2.8). Из этих рисунков следует, что в области II для задачи 18.2.7 и в областях I и III для задачи 18.2.8 векторы
соответственно показаны на рисунках (левый рисунок относится к задаче 18.2.7, правый — к 18.2.8). Из этих рисунков следует, что в области II для задачи 18.2.7 и в областях I и III для задачи 18.2.8 векторы  и
и  направлены противоположно. А поскольку величина напряженности поля плоскости не зависит от расстояния до нее (формула (18.5)), а заряды плоскостей одинаковы по величине, напряженность суммарного поля в этих областях равна нулю.
направлены противоположно. А поскольку величина напряженности поля плоскости не зависит от расстояния до нее (формула (18.5)), а заряды плоскостей одинаковы по величине, напряженность суммарного поля в этих областях равна нулю.
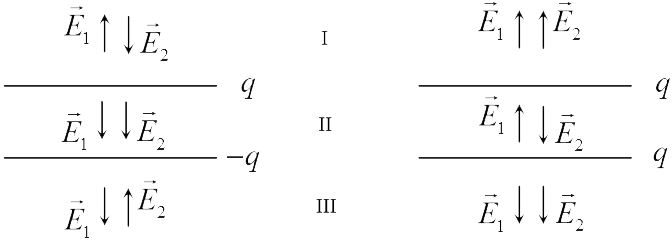
Таким образом, правильный ответ в задаче 18.2.7 — 2, в задаче 18.2.8 — 3. Отметим, что полученный результат является приближенным и справедлив в пределе бесконечно больших пластин. Для конечных пластин поле в указанных областях будет малым, но отличным от нуля, причем величина поля будет наибольшей около краев пластин.
По принципу суперпозиции для потенциалов имеем (задача 18.2.9)  . Если убрать либо первый, либо второй заряды, то потенциал в исследуемой точке станет равным соответственно
. Если убрать либо первый, либо второй заряды, то потенциал в исследуемой точке станет равным соответственно  или
или 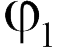 . Отсюда находим
. Отсюда находим 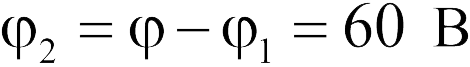 (ответ 2).
(ответ 2).
Согласно формуле (18.8) потенциал поля в любой точке внутри сферы равен потенциалу на ее поверхности

где 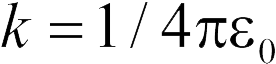 . Поэтому правильный ответ в задаче 18.2.10 — 4.
. Поэтому правильный ответ в задаче 18.2.10 — 4.
Определение напряженности электрического поля с помощью потенциала
Формулу можно использовать для определения разности потенциалов между двумя точками электрического поля, если напряженность поля в области между этими точками известна. Обращая эту формулу мы можем выразить напряженность электрического поля через его потенциал, т. е., зная V, мы сможем определить Е.
Посмотрим, как это делается.
Уравнение можно переписать в дифференциальной форме:
где dV — бесконечно малая разность потенциалов между точками на расстоянии dl друг от друга, а El — составляющая напряженности электрического поля в направлении этого бесконечно малого перемещения dl.
Тогда:
Таким образом, составляющая напряженности электрического поля по любому направлению равна градиенту потенциала в этом направлении, взятому с обратным знаком. Градиентом величины V называется ее производная по определенному направлению dV/dl. Если направление не указывается, то градиент соответствует направлению наиболее быстрого изменения V; это соответствует направлению вектора Е в данной точке, поскольку именно в таком направлении составляющая вектора Е совпадает с полной величиной напряженности поля:
Если расписать составляющие вектора Е по координатам х, у, z и в качестве l взять направления вдоль осей х у, z, то уравнение (24.8) можно записать в виде:
Здесь dV/dx — частная производная V по направлению х при условии, что у и z фиксированы.
В последнем примере мы вычислили напряженность электрического поля Е диполя в произвольной точке пространства. Складывая векторы напряженностей, создаваемых каждым зарядом в отдельности, получить этот результат было бы гораздо сложнее. Вообще говоря, для многих распределений зарядов гораздо проще рассчитать потенциал, а затем по формуле (24.9) — напряженность электрического поля Е, чем вычислять по закону Кулона по отдельности Е для каждого заряда: скалярные величины складывать намного проще, чем векторы.
Электростатическая потенциальная энергия
Предположим, что точечный заряд q перемещают в пространстве из точки а в точку b, электрические потенциалы в которых, обусловленные другими зарядами, равны соответственно Va и Vb. Изменение электростатической потенциальной энергии заряда q в поле других зарядов составляет:
Пусть теперь имеется система нескольких точечных зарядов. Чему равна электростатическая потенциальная энергия системы?
Удобнее всего выбрать за нуль потенциальную энергию зарядов на очень больших (в идеале бесконечно больших) расстояниях друг от друга. Потенциальная энергия уединенного точечного заряда Q1 равна нулю, поскольку в отсутствие других зарядов на него не действует никакая сила. Если к нему поднести второй точечный заряд, Q2, потенциал в точке, где находится второй заряд, будет равен:
Здесь r1 2 — расстояние между зарядами. Потенциальная энергия двух зарядов равна:
Она характеризует работу, необходимую для перемещения заряда Q2 из бесконечности (V = 0) на расстояние r1 2 до заряда Qi (или со знаком минус работу, необходимую для разнесения зарядов на бесконечно большое расстояние).
Если система состоит из трех зарядов, то ее полная потенциальная энергия будет равна работе по перемещению всех трех зарядов из бесконечности в место их расположения. Работа по сближению зарядов Q2 и Q1 определяется выражением (24.10);
чтобы перенести заряд Q3 из бесконечности в точку на расстоянии r1 3 от Q1 и на расстоянии r2 3 от Q2, требуется совершить работу:
В этом случае потенциальная энергия системы трех точечных зарядов будет равна:
Для системы четырех зарядов выражение для потенциальной энергии будет содержать шесть таких членов и т.п. (При составлении подобных сумм необходимо следить за тем, чтобы не учитывать одну и ту же пару дважды). Часто нас интересует не полная электростатическая потенциальная энергия, а лишь часть ее. Например, может возникнуть необходимость найти потенциальную энергию одного диполя в присутствии другого диполя. Во взаимодействии участвуют четыре заряда: Q1 и -Q1 первого диполя и Q2 и -Q2 второго диполя.
Потенциальная энергия одного диполя и в присутствии другого (иногда ее называют энергией взаимодействия) представляет собой работу по сближению диполей с бесконечно большого расстояния. В этом случае нас не интересует взаимная потенциальная энергия зарядов Q1 и -Q1 или Q2 и -Q2; выражение для потенциальной энергии двух диполей будет содержать лишь четыре члена, соответствующие энергиям взаимодействия между зарядами: Q1 и Q2 ; Q1 и -Q2 ; -Q1 и Q2 ; -Q1 и -Q2.
Заключение
Электрический потенциал в любой точке пространства определяется как электростатическая потенциальная энергия единицы заряда. Разность потенциалов между двумя точками определяется взятой с обратным знаком работой, которая совершается полем при перемещении единичного электрического заряда между этими точками. Разность потенциалов измеряется в вольтах (1 В = 1 Дж/Кл) и иногда называется напряжением. Изменение потенциальной энергии заряда q при прохождении им разности потенциалов Vbа равно ?U = qVba.
Разность потенциалов Vbа между точками b и a в однородном электрическом поле напряженностью Е определяется формулой V = — Ed, где d — расстояние вдоль силовой линии поля между этими точками.
В неоднородном электрическом поле Е соответствующее выражение имеет вид .
Таким образом, зная Е, всегда можно определить Vbа. Если значение V известно, то составляющие напряженности поля Е можно найти, обращая приведенное соотношение:
Эквипотенциальные линии или поверхности представляют собой геометрическое место точек одного потенциала; они всюду перпендикулярны силовым линиям поля. Электрический потенциал уединенного точечного заряда Q относительно нулевого потенциала (на бесконечности) равен:
Потенциал произвольного распределения зарядов можно определить, суммируя (интегрируя) потенциалы отдельных зарядов.
где r — расстояние от элемента заряда dq до точки, в которой определяется V.
Продолжение следует. Коротко о следующей публикации:
Электрическая емкость, диэлектрики, накопление электрической энергии.
Конденсатор — устройство для накопления электрического заряда, который состоит из двух проводников (обкладок), расположенных близко друг к другу, но не соприкасающихся.
III. Основы электродинамики
Рассмотрим ситуацию: заряд q0 попадает в электростатическое поле. Это электростатическое поле тоже создается каким-то заряженным телом или системой тел, но нас это не интересует. На заряд q0 со стороны поля действует сила, которая может совершать работу и перемещать этот заряд в поле.

Работа электростатического поля не зависит от траектории. Работа поля при перемещении заряда по замкнутой траектории равна нулю. По этой причине силы электростатического поля называются консервативными, а само поле называется потенциальным.
Потенциал
Система «заряд — электростатическое поле» или «заряд — заряд» обладает потенциальной энергией, подобно тому, как система «гравитационное поле — тело» обладает потенциальной энергией.
Физическая скалярная величина, характеризующая энергетическое состояние поля называется потенциалом данной точки поля. В поле помещается заряд q, он обладает потенциальной энергией W. Потенциал — это характеристика электростатического поля.


Вспомним потенциальную энергию в механике. Потенциальная энергия равна нулю, когда тело находится на земле. А когда тело поднимают на некоторую высоту, то говорят, что тело обладает потенциальной энергией.
Касательно потенциальной энергии в электричестве, то здесь нет нулевого уровня потенциальной энергии. Его выбирают произвольно. Поэтому потенциал является относительной физической величиной.
В механике тела стремятся занять положение с наименьшей потенциальной энергией. В электричестве же под действием сил поля положительно заряженное тело стремится переместится из точки с более высоким потенциалом в точку с более низким потенциалом, а отрицательно заряженное тело — наоборот.
Потенциальная энергия поля — это работа, которую выполняет электростатическая сила при перемещении заряда из данной точки поля в точку с нулевым потенциалом.
Рассмотрим частный случай, когда электростатическое поле создается электрическим зарядом Q. Для исследования потенциала такого поля нет необходимости в него вносить заряд q. Можно высчитать потенциал любой точки такого поля, находящейся на расстоянии r от заряда Q.

Диэлектрическая проницаемость среды имеет известное значение (табличное), характеризует среду, в которой существует поле. Для воздуха она равна единице.
Разность потенциалов
Работа поля по перемещению заряда из одной точки в другую, называется разностью потенциалов
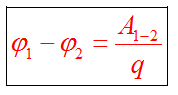
Эту формулу можно представить в ином виде

Эквипотенциальная поверхность (линия) — поверхность равного потенциала. Работа по перемещению заряда вдоль эквипотенциальной поверхности равна нулю.
Напряжение
Разность потенциалов называют еще электрическим напряжением при условии, что сторонние силы не действуют или их действием можно пренебречь.
Напряжение между двумя точками в однородном электрическом поле, расположенными по одной линии напряженности, равно произведению модуля вектора напряженности поля на расстояние между этими точками.
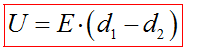
От величины напряжения зависит ток в цепи и энергия заряженной частицы.
Принцип суперпозиции
Потенциал поля, созданного несколькими зарядами, равен алгебраической (с учетом знака потенциала) сумме потенциалов полей каждого поля в отдельности
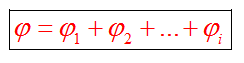
Как определить знак потенциала
При решении задач возникает много путаницы при определении знака потенциала, разности потенциалов, работы.
На рисунке изображены линии напряженности. В какой точке поля потенциал больше?

Верный ответ — точка 1. Вспомним, что линии напряженности начинаются на положительном заряде, а значит положительный заряд находится слева, следовательно максимальным потенциалом обладает крайняя левая точка.
Если происходит исследование поля, которое создается отрицательным зарядом, то потенциал поля вблизи заряда имеет отрицательное значение, в этом легко убедиться, если в формулу подставить заряд со знаком «минус». Чем дальше от отрицательного заряда, тем потенциал поля больше.
Если происходит перемещение положительного заряда вдоль линий напряженности, то разность потенциалов и работа являются положительными. Если вдоль линий напряженности происходит перемещение отрицательного заряда, то разность потенциалов имеет знак «+», работа имеет знак «-«.
Порассуждайте самостоятельно отрицательные или положительные значения будут принимать работа и разность потенциалов, если заряд перемещать в обратном направлении относительно линий напряженности.
Зависимость напряженности и потенциала от расстояния
Потенциал поля, созданного равномерно заряженной сферой радиусом R и зарядом q на расстоянии r от центра сферы, равен


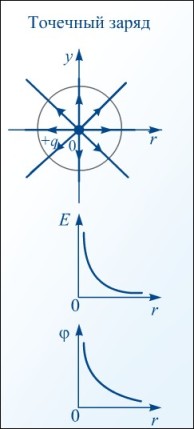
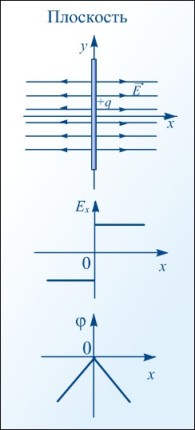

Напряжение в природе
Напряжение в клетках сетчатки глаза при попадания в них света около 0,01 В.
Напряжение в телефонных сетях может достигать 60 В.
Электрический угорь способен создавать напряжение до 650 В.

Энергия взаимодействия зарядов*
Из определения потенциала следует, что потенциальная энергия электростатического взаимодействия двух зарядов q1 и q2, находящихся на расстоянии r друг от друга, численно равна работе, которая совершается при перемещении точечного заряда q2 из бесконечности в данную точку поля, созданного зарядом q1
Как определить потенциал
Потенциал является энергетической характеристикой электрического поля. Для того чтобы найти его значение, нужно потенциальную энергию заряда в данной точке электрического поля поделить на сам заряд. Для различных типов полей используются разные формулы расчета потенциала.
Вам понадобится
- – линейка.
Инструкция
Если известна потенциальная энергия заряда тела в данной точке электрического поля (условно, это работа по перемещению заряда в бесконечность), то найдите потенциал, поделив эту потенциальную энергию в Джоулях на величину заряда в Кулонах: φ=Wp/q,где: φ – величина искомого потенциала,Wp – потенциальная энергия заряда тела,q – величина заряда.Потенциал измеряется в вольтах.
Если электрическое поле образовано точечным зарядом, то для определения потенциала его поля в любой точке, найдите расстояние от этой точки до заряда. Тогда потенциал поля в данной точке будет равен произведению коэффициента 9•10^9 на значение заряда поделенному на расстояние до заряда в метрах: φ=9•10^9•q/r,где:r – расстояние до заряда.
В том случае, когда поле образуется сферой, то рассматривайте два случая. Потенциал поля в точке, которая находится внутри сферы или на ее поверхности равен произведению коэффициента 9•10^9 на заряд сферы, поделенный на ее радиус:φ=9•10^9•Q/R, где:Q – заряд сферы,R – радиус сферы. Данная формула применяется независимо от того, в каком месте сферы находится точка пространства.
Если точка пространства находится вне сферы, то рассчитайте потенциал поля как произведение коэффициента 9•10^9 на значение заряда сферы поделенного на расстояние от точки пространства до центра сферы:φ=9•10^9•Q/R,в данном случае, R – расстояние от точки до центра сферы.
Для того чтобы определить потенциал поля, образованного другими заряженными поверхностями, с помощью теоремы Гаусса определите напряженность поля, образованного этими поверхностями. После этого найдите расстояние от поверхности до точки пространства, в которой определяется потенциал. Для этого из точки опустите перпендикуляр к поверхности. Чтобы найти потенциал, умножьте значение напряженности электрического поля в данной точке на измеренное расстояние:φ=Е•d, где:Е – значение напряженности электрического поля,d – расстояние от поверхности до точки.
Если между источником электрического поля находится некоторое вещество, то все результаты, которые получаются при расчете, нужно поделить на значение диэлектрической проницаемости среды, которая находится между точкой поля и его источником.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Преподаватель который помогает студентам и школьникам в учёбе.
Потенциал поля точечного заряда в физике – формулы и определение с примерами
Потенциал поля точечного заряда:
Чтобы определить силу электрического поля, мы ввели в него пробный заряд и определили силу воздействия поля на этот заряд.
Напряженность электрического поля является характеристикой силы поля.
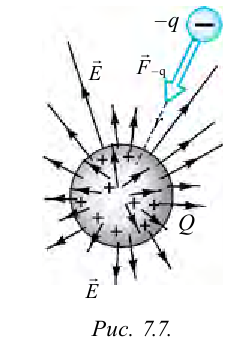
При введении пробного заряда в поле, оно оказывает сопротивление (рис. 7.7). Для преодоления сопротивления необходимо проделать определенную работу.
Как определяется эта выполненная работа?
Эта работа превращается в потенциальную энергию взаимодействия основного заряда и введенного пробного заряда:

Знак минус в формуле показывает, что между зарядами действует сила притяжения.
Потенциальная энергия 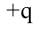 заряда, расположенного на расстоянии
заряда, расположенного на расстоянии 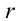 от положительного неподвижного заряда
от положительного неподвижного заряда 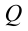 , определяется следующим выражением
, определяется следующим выражением

Положительный знак в формуле показывает, что между зарядами действует сила отталкивания.
Согласно формуле потенциальная энергия равняется нулю, когда расчет производится для бесконечного расстояния. На таких расстояниях заряды не взаимодействуют.
Таким образом, электрическое поле с приобретением характеристики силы будет иметь и энергетическую характеристику. Энергетическая характеристика поля определяется величиной, которая называется потенциалом поля.
Потенциалом электрического поля точечного заряда называется величина, измеряемая отношением потенциальной энергии взаимодействия основного и введенного в поле пробного заряда к величине пробного заряда:

Потенциал точечного заряда 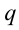 определяется следующим образом:
определяется следующим образом:

Пользуясь понятием потенциала найдем работу, совершаемую при перемещении заряда 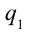 с расстояния
с расстояния 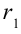 на расстояние
на расстояние 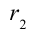 от заряда
от заряда 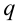 , создающего электрическое поле:
, создающего электрическое поле:
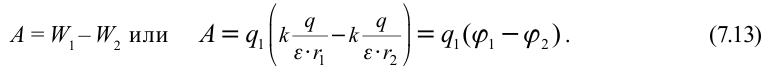
В этом выражении разница 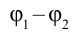 является разницей потенциалов между точками, называется электрическим напряжением и записывается следующим образом:
является разницей потенциалов между точками, называется электрическим напряжением и записывается следующим образом:

Единица измерения потенциала и разность потенциалов называется Вольт (В) в честь итальянского ученого Вольта. Из формулы 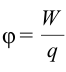 следует, что
следует, что 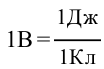 .
.
Это значит, что разность потенциалов точек равняется 1 вольту, когда заряд, равный 1 кулону, при перемещении из одной точки электрического поля в другую выполняет работу, равную 1 Дж.
Потенциалы точек, расположенных на одинаковых расстояниях от точечного заряда, равны. Если эти точки соединить между собой, образуется поверхность, которая называется эквипотенциальной поверхностью.
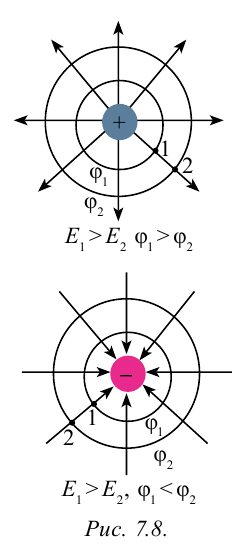
Эквипотенциальная поверхность точечного заряда располагается вокруг заряда в виде сконцентрированных кругов (рис. 7.8). Силовые линии поля проходят перпендикулярно к эквипотенциальной поверхности.
Межу напряженностью электрического поля и разностью потенциалов существует следующее соотношение:

где 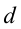 –расстояние между точками, потенциал которых равен
–расстояние между точками, потенциал которых равен 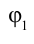 и
и 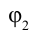 .
.
Отсюда получаем единицу измерения напряженности поля 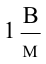 .
.
Образец решения задачи:
В металлическую сферу радиусом 5 см, висящую в воздухе, подали заряд 30 нКл. Нужно найти потенциалы поля в точках, находящихся в 2 см от центра заряженной сферы, на поверхности сферы и удаленной от поверхности на расстояние 5 см.
Дано:
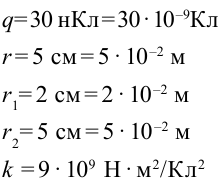
Найти:
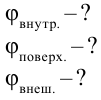
Формула:
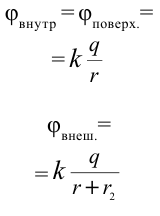
Решение:
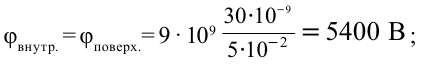
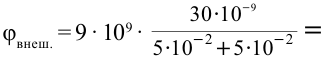
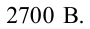
Единица измерения: 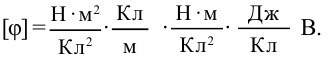
Ответ: 5400 В; 2700 В.
- Работа электрического поля при перемещении заряда в физике
- Энергия электрического поля
- Электрическое поле заряженных неподвижных тел
- Напряженность электрического поля
- Электростатика
- Закон сохранения заряда в физике
- Электрическое поле заряженного шара
- Электрические явления в физике

