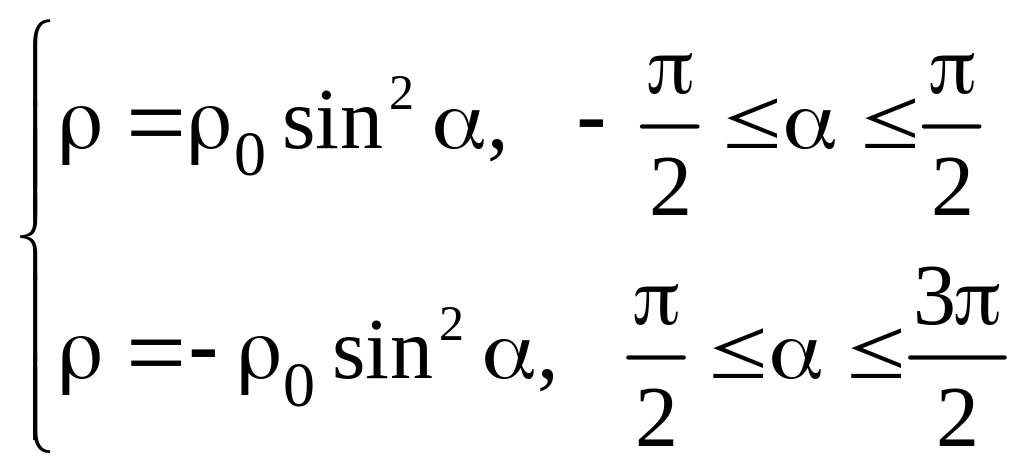Условие задачи:
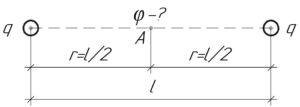
Найти потенциал электрического поля в точке, лежащей посредине между двумя зарядами по 50 нКл, расположенными на расстоянии 1 м в вакууме.
Задача №6.3.9 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(q=50) нКл, (r=frac{l}{2}), (l=1) м, (varphi-?)
Решение задачи:
[{varphi _0} = frac{{kq}}{r}]
Здесь (k) – коэффициент пропорциональности, равный 9·109 Н·м2/Кл2.
Учитывая, что точка A находится посредине между двумя зарядами ((r=frac{l}{2})), то:
[{varphi _0} = frac{{2kq}}{l}]
Искомый потенциал (varphi) равен сумме потенциалов электрических полей в точке A, создаваемых каждым зарядом, поскольку потенциал – величина скалярная. Учитывая вышесказанное, имеем:
[varphi = {varphi _0} + {varphi _0}]
[varphi = 2{varphi _0}]
В итоге решение задачи в общем виде выглядит так:
[varphi = frac{{4kq}}{l}]
Произведём вычисления:
[varphi = frac{{4 cdot 9 cdot {{10}^9} cdot 50 cdot {{10}^{ – 9}}}}{1} = 1800;В = 1,8;кВ]
Ответ: 1,8 кВ.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.3.8 На расстоянии 1 м от центра заряженного металлического шара радиусом 3 м
6.3.10 Сколько электронов следует передать металлическому шарику радиусом 7,2 см
6.3.11 Определить разность потенциалов (по модулю) между точками, отстоящими
Потенциал. Разность потенциалов. ЗАДАЧИ с решениями
Формулы, используемые на уроках «Решение задач на тему: Работа перемещения заряда в электрическом поле. Потенциал. Разность потенциалов» для подготовки к ЕГЭ.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Металлический шар диаметром d заряжен с поверхностной плотностью зарядов σ. Найти потенциал φ этого шара, если он окружен заземленной проводящей сферой, имеющей общий с шаром центр. Диаметр сферы D. Среда — воздух.
Задача № 2.
Потенциал заряженного шара φ1 = 300 В. Чему равен потенциал φ2 электрического поля этого шара в точке, отстоящей на расстоянии l = 50 см от его поверхности, если радиус шара R = 25 см?
Смотреть решение и ответ

Задача № 3.
Определить потенциал φ точки поля, находящейся на расстоянии а = 9 см от поверхности заряженного шара радиусом R = 1 см, если поверхностная плотность зарядов на шаре σ = 1 • 10–11 Кл/см2. Среда — воздух.
Задача № 4.
В точке 1 поля точечного заряда-источника потенциал φ1 = 40 В, а в точке 2 φ2 = 10 В. Найти потенциал φ в точке М, лежащей посередине между точками 1 и 2 (рис. 3-6).
Задача № 5.
В трех вершинах квадрата со стороной а = 20 см находятся заряды q1 = 1 • 10–8 Кл, q2 = 2 • 10–8 Кл и q3 = 2 • 10–8 Кл (рис. 3-7). Определить потенциал φ электрического поля, созданного этими зарядами в четвертой вершине.
Задача № 6.
Четыре одинаковых точечных заряда q расположены на одной прямой на расстоянии r друг от друга. Какую работу А надо совершить, чтобы переместить эти заряды в вершины тетраэдра со стороной r? Среда — вакуум.
Задача № 7.
Два одинаково заряженных шарика диаметрами d = 0,5 см каждый расположены на расстоянии l = 2 см между их поверхностями (рис. 3-14). До какого потенциала φ они заряжены, если сила их отталкивания друг от друга F = 2 мкН? Среда — воздух.
Задача № 8.
В однородном электрическом поле напряженностью Е = 2 кВ/см переместили заряд q = –20 нКл в направлении силовой линии поля на расстояние d = 10 см. Найти работу поля А, изменение потенциальной энергии поля ΔWп и напряжение (разность потенциалов) U между начальной и конечной точками перемещения.
Смотреть решение и ответ
Задача № 9.
Между двумя горизонтальными плоскостями, заряженными разноименно и расположенными на расстоянии d = 5 мм друг от друга, находится в равновесии капелька масла массой 20 нг (нанограмм) (рис. 3-10). Найти число избыточных электронов N на этой капельке. Среда — воздух. Разность потенциалов между плоскостями U = 2 кВ.
Задача № 10.
На пластине М поддерживается потенциал φ1 = +80 В, а на пластине N – φ2 = –80 В (рис. 3-11, а). Расстояние между пластинами d = 10 см. На расстоянии d1 = 4 см от пластины М помещают заземленную пластину Р (рис. 3-11, б). Найти изменение напряженности ΔЕ1 поля на участке МР и изменение напряженности поля ΔЕ2 на участке PN при этом. Построить графики зависимостей напряженностей Е = Е(х) и потенциала φ = φ(х) от расстояния между точками поля и пластинами.
Это конспект по теме «Потенциал. Разность потенциалов. ЗАДАЧИ с решениями». Выберите дальнейшие действия:
- Вернуться к списку конспектов по Физике.
- Проверить свои знания по Физике.
Нахождение потенциала
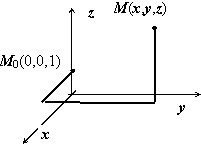
В предыдущем разделе мы доказали, что если выполняются условия потенциальности поля $bar { a } (mathbf { textit { M } } )$, то $varphi (M)=intlimits_ { mathop { M_0 M } limits^cup } { bar { a } dbar { r } } $, где $M_0 in V$ – фиксированная точка. Обычно, если в точке $mathbf { textit { O } } (0,0,0)$ поле не имеет особенностей, то в качестве точки $M_0 (x_0 ,y_0 ,z_0 )$ берётся именно эта точка, если в этой точке поле не определено, берётся другая точка.
Интегрирование ведут по пути, состоящим из отрезков, параллельных координатным осям. В результате получим $varphi (M)=intlimits_ { x_0 } ^x { P(x,y_0 ,z_0 )dx } +intlimits_ { y_0 } ^y { Q(x,y,z_0 )dy } +intlimits_ { z_0 } ^z { R(x,y,z)dz } $.
Пример 1
Доказать, что поле $bar { a } (x,y,z)=frac { ycos (xy) } { z } bar { i } +frac { xcos (xy) } { z } bar { j } -frac { sin (xy) } { z^2 } bar { k } $ потенциально и найти потенциал этого поля.
Решение
Мы будем доказывать, что это поле потенциально в любой односвязной области $mathbf { textit { V } } $, не содержащей точку $mathbf { textit { O } } (0,0,0)$. Условие безвихревости поля $bar { a } $:
$rotbar { a } (M)=left| { begin{array} { l } ,bar { i } ,,,,bar { j } ,,,bar { k } \ frac { partial } { partial x } ,,frac { partial } { partial y } ,,frac { partial } { partial z } \ ,P,,Q,,,R \ end{array} }right|=left( { frac { partial R } { partial y } -frac { partial Q } { partial z } }right)bar { i } +left( { frac { partial P } { partial z } -frac { partial R } { partial x } }right)bar { j } +left( { frac { partial Q } { partial x } -frac { partial P } { partial y } }right)bar { k } =0$ в координатной форме сводится к равенствам $frac { partial R } { partial y } =frac { partial Q } { partial z } , frac { partial P } { partial z } =frac { partial R } { partial x } , frac { partial Q } { partial x } =frac { partial P } { partial y } $.
В нашем поле $P(x,y,z)=frac { ycos (xy) } { z } , Q(x,y,z)=frac { xcos (xy) } { z } ,R(x,y,z)=-frac { sin (xy) } { z^2 } $. Находим производные:
$frac { partial R } { partial y } =-frac { xcos (xy) } { z^2 } $,
$frac { partial Q } { partial z } =-frac { xcos (xy) } { z^2 } =frac { partial R } { partial y } $,
$frac { partial P } { partial z } =-frac { ycos (xy) } { z^2 } $,
$frac { partial R } { partial x } =-frac { ycos (xy) } { z^2 } =frac { partial P } { partial z } $,
$frac { partial Q } { partial x } =frac { cos (xy)-xysin (xy) } { z } $,
$frac { partial P } { partial y } =frac { cos (xy)-xysin (xy) } { z } =frac { partial Q } { partial x } $ Потенциальность поля доказана.
Ищем потенциал. Интеграл $varphi (M)=intlimits_ { mathop { M_0 M } limits^cup } { bar { a } dbar { r } } $ вычисляем по изображённому на рисунке пути, отправляясь от точки $mathbf { textit { M } } _ { 0 } $(0,0,1). $varphi (x,y,z)=intlimits_0^x { frac { 0cdot cos (xcdot 0) } { 1 } dx } +intlimits_0^y { frac { xcdot cos (xy) } { 1 } dy } -intlimits_1^z { frac { sin (xy) } { z^2 } dz } = =left. { sin (xy) }right|_0^y +left. { frac { sin (xy) } { z } }right|_1^z =sin (xy)+left[ { frac { sin (xy) } { z } -sin (xy) }right]=frac { sin (xy) } { z } $.
Если бы мы взяли в качестве точки $mathbf { textit { M } } _ { 0 } $ другую точку $mathbf { textit { M } } _ { 1 } $, то получили бы выражение, отличающееся на некоторую постоянную { более точно, на $C=intlimits_ { mathop { M_0 M_1 } limits^cup } { bar { a } dbar { r } } )$, поэтому $varphi (x,y,z)= frac { sin (xy) } { z } +C$.
Электростатическое
поле точечного заряда характеризуется
не только вектором напряженности
(см. (3.1)), но и потенциалом :
. (4.1)
Из (4.1) видно,
что потенциал – это скалярная величина,
которая может быть как положительная,
так и отрицательная в зависимости от
знака заряда.
Используя
принцип суперпозиции полей, можно
найти потенциал результирующего
электрического поля в заданной точке
О как алгебраическую сумму
потенциалов полей, созданных каждым
зарядом независимо друг от друга (см.
рис. 1):
(4.2)
Задача 5.
Используя
условие задачи 4, найти потенциал
электрического поля в точке Р.
Решение:
Подставим данные из задачи 4 в формулу
(4.2):
кВ
Ответ: рез
= 34,1 кВ
4.1
Заряд
находится в вершине квадрата со стороной
,
а заряд
– в центре. Найти потенциал электрического
поля в точке Р, находящейся в другой
вершине этого квадрата (см. рис.).
мкКл,
мкКл,
м.
Ответ: 34,5 кВ
4.2 З
аряды
и
находятся в соседних вершинах квадрата
со стороной
.
Найти потенциал электрического поля в
точке Р, делящей сторону квадрата на
два равных отрезка (см. рис.).
мкКл,
мкКл,
м.
Ответ: 44 кВ
4.3 З
аряды
и
находятся в соседних вершинах квадрата
со стороной
.
Найти потенциал электрического поля в
точке Р, находящейся на середине
противоположной стороны квадрата (см.
рис.).
мкКл,
мкКл,
м.
Ответ: 24 кВ
4.4
Заряд
находится в вершине квадрата со стороной
,
а заряд
– на середине стороны. Найти потенциал
электрического поля в точке Р, находящейся
на середине противоположной стороны
квадрата (см. рис.).
мкКл,
мкКл,
м.
Ответ: 26 кВ
4.5 З
аряд
находится в вершине квадрата со стороной
,
а заряд
– на середине стороны. Найти потенциал
электрического поля в точке Р, находящейся
на середине стороны квадрата (см. рис.).
мкКл,
мкКл,
м.
Ответ: 34 кВ
4.6 З
аряд
находится в вершине квадрата со стороной
,
а заряд
– на середине стороны. Найти потенциал
электрического поля в точке Р, находящейся
в противоположной вершине квадрата
(см. рис.).
мкКл,
мкКл,
м.
Ответ: 22 кВ
5. Расчет потенциала электрического поля, с озданного распределенным зарядом.
Электрическое
поле часто создается не дискретными
зарядами, а распределенными в пространстве
с плотностью
.
Тогда необходимо разбить заряженную
область на малые элементы с объемом
и зарядом
(см. рис.3). При расчете потенциала в
некоторой точке пространства О принцип
суперпозиции (4.2) для бесконечного числа
таких элементов будет выглядеть следующим
образом:
(5.1)
– где
– расстояние от малого элемента с
зарядом
до точки О.
Часто заряд
распределяется вдоль тонкой линии,
тогда заряд малого элемента длины
лучше выражать через линейную плотность
заряда
,
и уравнение (5.1) преобразуется в
(5.2)
Задача 6.
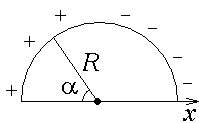
Положительный
заряд распределен по тонкому полукольцу
радиуса R = 1 м с линейной
плотностью
,
где 0< < ,
0 = 1
мкКл/м. Определить потенциал, создаваемый
этим зарядом в центре полукольца.
Решение:
Выделим элемент
dl = Rd
на полуокружности и, учитывая, что
расстояние от элемента до точки О
равно
,
по формуле (5.2) рассчитаем потенциал в
точке О:
= 9,42 кВ
Ответ:
9,42 кВ
Задача 7
Тонкий
стержень заряжен неравномерно.
Электрический заряд распределен по
нему с линейной плотностью
,
где х – координата точки на стержне,
b = 1 м – длина стержня, 0
= 1 мкКл/м. Чему равна величина потенциала,
создаваемого этим зарядом в начале
координат О, совпадающем с концом
стержня?
Решение:
Выделим
элементарный заряд dq
на стержне длиной dx
на расстоянии х от начала координат
О (см. рис.5). Учитывая, что r
= x, а
dq
= dx,
найдем по формуле (5.2) потенциал в точке
О:
= 4,5 кВ
Ответ: 4,5 кВ
5.1
Вдоль стержня длины
равномерно распределен заряд
.
Найти потенциал в точке
на продолжении стержня на расстоянии
от его конца (см. рис.).
м,
м,
мкКл.
Ответ: 6,2 кВ
5.2
Вдоль стержня длины
равномерно распределен заряд с линейной
плотностью
.
Найти потенциал в точке
на продолжении стержня на расстоянии
от его конца (см. рис.).
м,
м,
мкКл/м.
Ответ: 6,2 кВ
5.3 П
оложительный
заряд распределен по тонкому кольцу
радиуса
с линейной плотностью
.
Определить потенциал, создаваемый этим
зарядом в центре кольца.
R
= 1 м,
мкКл/м.
Ответ: 28 кВ
5.4. П
оложительный
заряд распределен по тонкому кольцу
радиуса
с линейной плотностью
.
Определить потенциал, создаваемый этим
зарядом в центре кольца.
R
= 1 м,
мкКл/м.
Ответ: 57 кВ
5.5
Положительный заряд распределен по
тонкому кольцу радиуса
с линейной плотностью
.
Определить потенциал, создаваемый этим
зарядом в центре кольца.
R
= 1 м,
мкКл/м.
Ответ: 75 кВ
5.6
Тонкий стержень заряжен неравномерно.
Электрический заряд распределен по
нему с линейной плотностью
,
где х – координата точки на стержне,
b – длина стержня. Чему равна величина
потенциала, создаваемого этим зарядом
в начале координат О, совпадающем с
концом стержня?
м,
мкКл/м.
Ответ: 9 кВ
5.7 П
оложительный
заряд распределен по тонкому полукольцу
радиуса
с линейной плотностью
.
Определить потенциал, создаваемый этим
зарядом в центре полукольца.
м,
мкКл/м.
Ответ: 14 кВ
5.8
Положительный заряд распределен по
тонкому полукольцу радиуса
с линейной плотностью
.
Определить потенциал, создаваемый этим
зарядом в центре полукольца.
R
= 1 м,
мкКл/м.
Ответ: 14 кВ
5
.9э.
Электрон перемещается в кулоновском
поле заряженной частицы из точки А в
точку В в одном случае по траектории 1,
в другом случае по траектории 2. Как
соотносятся величины работ, совершаемых
электрическим полем над электроном, в
этих двух случаях?
а)
;
б)
;
в)
;
г)
6. Расчет напряженности электрического
поля,
созданного распределенным зарядом.
Применение
принципа суперпозиции (3.2) для нахождения
напряженности электрического поля
в векторной форме вызывает большие
трудности из-за бесконечного числа
элементарных зарядов dq,
распределенных в пространстве. В этом
случае необходимо воспользоваться не
векторным сложением вкладов полей
,
а сложением их проекций:
,
(6.1)
Задача 8
З
аряд
распределен по тонкому полукольцу
радиуса
= 1 м с линейной плотностью
.
Определить
проекцию на ось
напряженности электрического поля,
создаваемого этим зарядом в центре
полукольца, если
мкКл/м.
Решение:
Как видно из
рис.6, проекция на ось х напряженности
электрического поля, созданного
элементарным зарядом
в точке О равна:
(6.3)
Учитывая, что
,
а
,
получим

Ответ: 4,5
кВ/м
6.1
Вдоль стержня длины
равномерно распределен заряд
.
Найти величину напряженности электрического
поля в точке
на продолжении стержня на расстоянии
от его конца (см. рис.).
м,
м,
мкКл.
Ответ: 4,5 кВ/м
6.2
Вдоль стержня длины
равномерно распределен заряд с линейной
плотностью
.
Найти величину напряженности электрического
поля в точке
на продолжении стержня на расстоянии
от его конца (см. рис.).
м,
м,
мкКл/м.
Ответ: 4,5 кВ/м
6.3
Заряд распределен по тонкому кольцу
радиуса
с линейной плотностью
.
Определить
величину проекции на ось
напряженности электрического поля,
создаваемого этим зарядом в центре
кольца, если
R
= 1 м,
мкКл/м.
Ответ: 12 кВ/м
6.4
Тонкий стержень заряжен неравномерно.
Электрический заряд распределен по
нему с линейной плотностью
,
где х – координата точки на стержне,
b – длина стержня. Чему равна величина
напряженности электрического поля,
создаваемого этим зарядом в начале
координат О, совпадающем с концом
стержня?
м,
мкКл/м.
Ответ: 9,0 кВ/м
6.5
Тонкий стержень заряжен неравномерно.
Электрический заряд распределен по
нему с линейной плотностью
,
где х – координата точки на стержне,
b – длина стержня. Чему равна величина
напряженности электрического поля,
создаваемого этим зарядом в начале
координат О, совпадающем с концом
стержня?
м,
мкКл/м.
Ответ: 4,5 кВ/м
6.6
Заряд распределен по тонкому
полукольцу радиуса
с линейной плотностью
.
Определить
проекцию на ось
напряженности электрического поля,
создаваемого этим зарядом в центре
полукольца, если R =
1 м,
мкКл/м.
Ответ: 12 кВ/м
6.7
Заряд распределен по тонкому кольцу
радиуса
с линейной плотностью
.
Определить
величину проекции на ось
напряженности электрического поля,
создаваемого этим зарядом в центре
кольца, если
R
= 1 м,
мкКл/м.
Ответ: 7,2 кВ/м
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
§ 6. Потенциал поля точечного заряда и заряда, равномерно распределённого по сферической поверхности
Примем потенциал бесконечности равным нулю. Тогда, используя (5.2), можно вывести, что на расстоянии $$ r$$ от точечного заряда $$ Q$$ потенциал электростатического поля:
| $$ varphi =k{displaystyle frac{Q}{r}}$$. | (6.1) |
 |
| Рис. 6.1 |
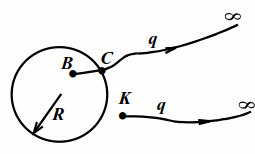
Возьмём теперь заряд $$ Q$$, равномерно распределённый по сфере радиуса $$ R$$ (рис. 6.1).
Для нахождения потенциала на расстоянии $$ r$$ от центра сферы перенесём мысленно пробный заряд $$ q$$ из исследуемой точки в бесконечность и применим формулу (5.2). Для произвольной точки $$ K$$ вне сферы $$ {varphi }_{K}={A}_{Kinfty }/q$$, где $$ {A}_{Kinfty }$$ – работа сил поля над $$ q$$ при его перемещении из т. $$ K$$ в бесконечность. Эта работа не изменится, если весь заряд $$ Q$$ сферы поместить в центр сферы, т. к. поля обоих зарядов $$ Q$$ при $$ r>R$$ совпадают (см. §3). Для точечного заряда $$ Q$$ отношение $$ {A}_{Kinfty }/q$$ есть потенциал его поля в т. $$ K$$, который находится по формуле (6.1). Итак, для сферы $$ {varphi }_{K}=kQ/r$$. В предельном случае при $$ r=R$$ получим потенциал сферы, равный `kQ//R`.
Для произвольной точки $$ B$$ внутри сферы $$ {varphi }_{B}={A}_{BCinfty }/q={A}_{BC}+{A}_{Cinfty }/q$$.
Здесь $$ {A}_{Binfty }$$, $$ {A}_{BC}$$ и $$ {A}_{Cinfty }$$ – работа сил поля над зарядом $$ q$$ на участках $$ BCinfty $$, `BC` и $$ Cinfty .$$ Внутри сферы поля нет, сила на $$ q$$ со стороны поля не действует и $$ {A}_{BC}=0$$. Тогда $$ {varphi }_{B}={A}_{Cinfty }/q$$. Но правая часть последнего равенства есть потенциал т. $$ C$$, т. е. потенциал сферы, равный `kQ//R`. Значит, потенциал любой точки внутри сферы равен потенциалу сферы: $$ {varphi }_{B}=kQ/R$$.
Итак, для заряда $$ Q$$, равномерно распределённого по сфере радиуса $$ R$$ потенциал поля вне сферы равен потенциалу точечного заряда, равного заряду сферы и помещённого в центре сферы (как и для напряжённости), а потенциал внутри сферы один и тот же и равен потенциалу сферы:
$$ varphi =k{displaystyle frac{Q}{r}}$$ при $$ r>R, varphi =k{displaystyle frac{Q}{R}}$$ при $$ rle R$$.
В двух вершинах прямоугольника со сторонами $$ a$$ и $$ 2a$$ (рис. 6.2) закреплены точечные заряды $$ Q$$ и $$ 3Q$$. Какую минимальную работу надо совершить, чтобы переместить точечный заряд $$ 4Q$$ из состояния покоя из вершины $$ B$$ в вершину $$ C$$?
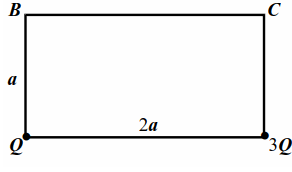 |
| Рис. 6.2 |
Здесь идёт речь о работе $$ A$$, которую необходимо совершить нам против электрических сил при переносе заряда $$ 4Q$$. Работа $$ A$$ в сумме с работой $$ {A}_{1}$$ сил электростатического поля над зарядом $$ 4Q$$ равна изменению кинетической энергии перемещаемого заряда:
$$ A+{A}_{1}=∆K$$
Отсюда $$ A=-{A}_{1}+∆K$$.
Работа $$ A$$ будет минимальной, если величина $$ ∆K$$ минимальна, т. е. заряд $$ 4Q$$ придёт в вершину $$ C$$ с нулевой скоростью, т. е. $$ ∆K=0.$$ Итак, $$ A=-{A}_{1}.$$ Работа сил поля над зарядом $$ {A}_{1}=4Q({varphi }_{B}-{varphi }_{C}), $$ где
$$ {varphi }_{B}=k{displaystyle frac{Q}{a}}+k{displaystyle frac{3Q}{asqrt{5}}}, {varphi }_{C}=k{displaystyle frac{Q}{asqrt{5}}}+k{displaystyle frac{3Q}{a}}$$
– потенциалы результирующего поля, созданного зарядами $$ Q$$ и $$ 3Q$$ в вершинах $$ B$$ и $$ C$$.
Окончательно
$$ A={displaystyle frac{8(sqrt{5}-1)}{sqrt{5}}}{displaystyle frac{k{Q}^{2}}{a}}>0$$.
В центре сферы радиусом $$ R$$ находится точечный заряд $$ Q>0$$. По сфере равномерно распределён заряд $$-4Q<0$$. Найти потенциалы $$ {varphi }_{A}, {varphi }_{C}$$ на расстояниях $$ R/2$$ и $$ 2R$$ от центра сферы (рис. 6.3).
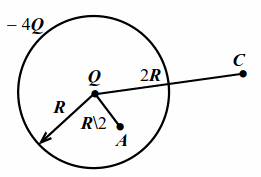 |
| Рис. 6.3 |
Потенциал в любой точке равен сумме потенциалов полей, созданных в этой точке зарядами $$ Q$$ и $$ -4Q$$. Для точек $$ A$$ и $$ C$$ :
$$ {varphi }_{A}=k{displaystyle frac{Q}{R/2}}+k{displaystyle frac{-4Q}{R}}=-2k{displaystyle frac{Q}{R}}$$,
$$ {varphi }_{C}=k{displaystyle frac{Q}{2R}}+k{displaystyle frac{-4Q}{2R}}=-{displaystyle frac{3}{2}}k{displaystyle frac{Q}{R}}$$.