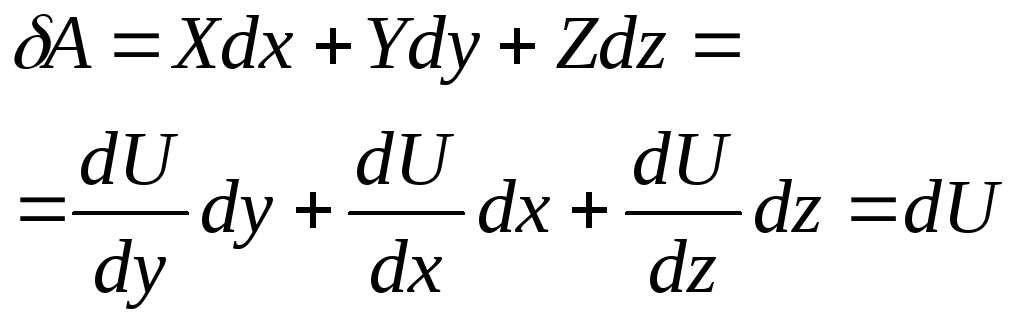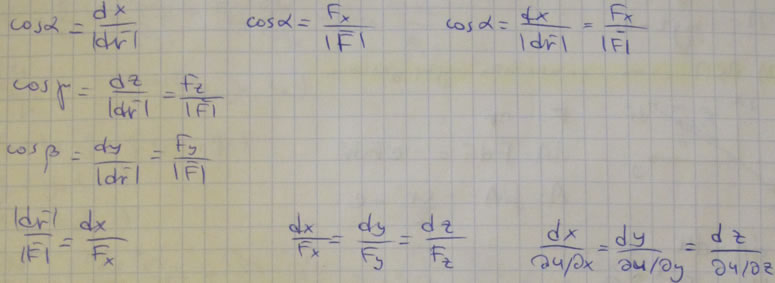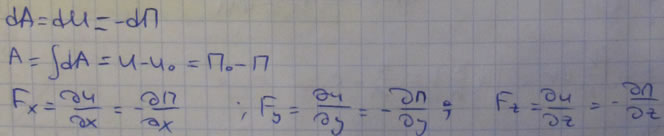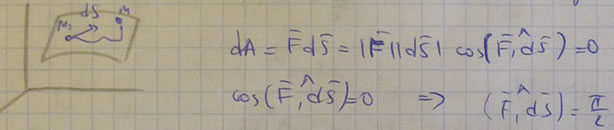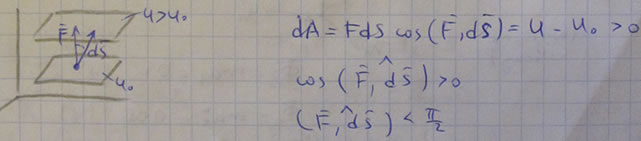Содержание:
Потенциальное силовое поле:
Для вычисления работы силы на каком-либо перемещении в общем случае необходимо знать закон движения точки на этом перемещении. Есть класс сил, для которых работа не зависит от характера движения точки на рассматриваемом перемещении. Эти силы называют потенциальными, и они имеют важное значение в различных областях механики и физики.
Потенциальное силовое поле и силовая функция
Силовым полем называют часть пространства, в каждой точке которого на материальную точку действует определенная сила, зависящая от координат точки и времени. Силовое поле считают стационарным, если действующие силы не зависят от времени. Если же силы зависят от времени, то силовое поле является нестационарным.
Силовое поле называют потенциальным, если имеется силовая функция
Функцию 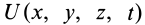
Рис. 72
Рассмотрим основные свойства силовой функции стационарного силового поля. Из (77) следует, что силовая функция определяется с точностью до постоянной, так как для проекций силы на координатные оси требуются только частные производные по координатам от этой функции и добавление постоянной к функции 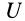
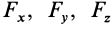
т. e.
Таким образом, элементарная работа силы в потенциальном силовом поле равна полному дифференциалу от силовой функции. Иногда это свойство силовой функции принимают за ее определение; тогда (77) получают из (78).
Полная работа силы 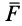
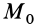
т.е.
где
Следовательно, полная работа силы на каком-либо перемещении точки равна разности значений силовой функции в конечной и начальной точках перемещения и не зависит от формы траектории, по которой оно совершается, если силовая функция является однозначной.
Из (79) следует, что работа силы в потенциальном силовом поле по любому замкнутому пути равна нулю, так как значение силовой функции в начальной и конечной точках перемещения одинаково, если силовая функция не принимает других значений после возвращения в первоначальную точку.
Силовая функция может принимать другие значения после возвращения в первоначальную точку в зависимости от количества обходов, если область, ограниченная замкнутым путем обхода, содержит в себе специальные особые точки силовой функции.
Если применить понятие вектор-градиента от скалярной функции
где 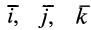
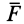
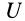
Определим условия, которые позволяют по силам силового поля устанавливать, будет ли силовое поле потенциальным.
Если силовая функция 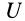
Так как
то
Аналогично,
Таким образом, полученные условия имеют вид
В векторном исчислении доказывается, что условия (80) не только необходимы, но и достаточны для существования силовой функции. Если использовать вектор вихря 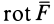
то условия (80) можно выразить более кратко:
Таким образом, для того чтобы силовое поле было потенциальным, необходимо и достаточно, чтобы оно было безвихревым.
Непотенциальными силами являются силы сопротивления, зависящие от скорости, и силы трения. Силы сухого трения не будут потенциальными, так как хотя сила трения постоянна и не зависит от скорости, но направление силы трения от скорости зависит.
- Заказать решение задач по теоретической механике
Поверхности уровня и силовые линии
Если рассматривать точки потенциального силового поля, в которых силовая функция имеет одно и то же значение, например 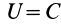
Уравнение поверхности уровня имеет вид
Отметим некоторые свойства поверхностей уровня.
1. Работа силы равна нулю, если начальная и конечная точки перемещения лежат на одной поверхности уровня. Действительно,
Если начальная и конечная точки лежат на одной поверхности уровня, то 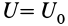
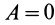
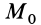
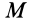
2. Сила в потенциальном силовом поле всегда перпендикулярна поверхности уровня или, точнее, касательной плоскости поверхности уровня. Действительно, пусть имеем поверхность уровня 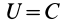
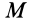
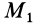
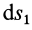
С другой стороны,
Так как 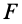
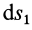
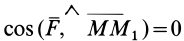
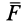
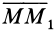
3. Сила в потенциальном силовом поле всегда направлена в сторону возрастающих значений силовой функции. Для
доказательства этого свойства силы возьмем точку 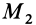
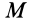
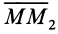
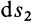
так как 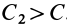
Рис. 73
Следовательно,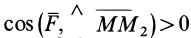
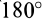
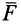
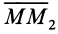
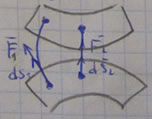
4. Если все силовое поле разбить поверхностями уровня на 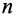
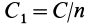
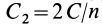
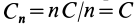
Рис. 74
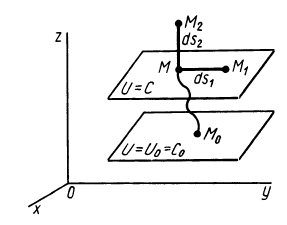
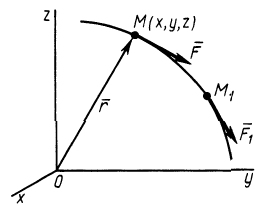
Наряду с поверхностями уровня в силовом поле вводят понятие силовой линии, т. е. такой линии, в каждой точке которой сила направлена по касательной к этой линии (рис. 74). Так как вектор 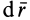
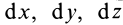
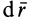
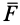
Эти дифференциальные уравнения относительно координат 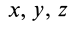
Потенциальная энергия
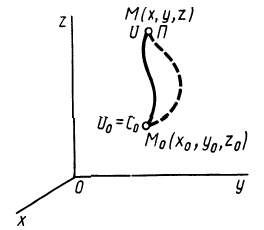
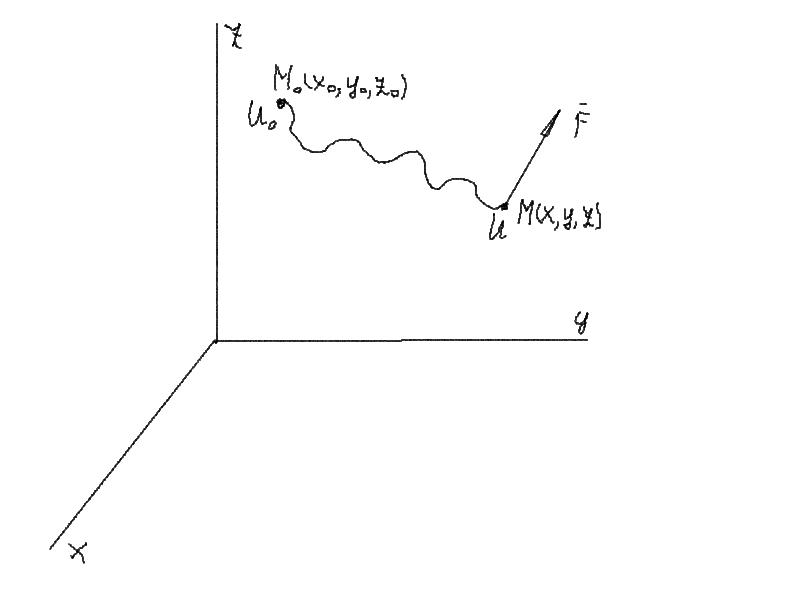
В случае потенциального силового поля наряду с силовой функцией можно ввести другую функцию, характеризующую запас энергии в данной точке поля,— потенциальную энергию в этой точке (рис. 75), или потенциальную энергию материальной точки в рассматриваемой точке силового поля.
Потенциальной энергией 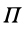
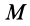
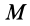
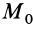
или
Рис. 75
Постоянная 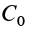
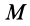
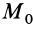
На основании (77) и (82) имеем:
Из (78), (79) и (82) соответственно получаем
Из приведенных формул следует, что 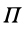
или
Потенциальную энергию в какой-либо точке поля с точностью до произвольной постоянной можно определить как значение силовой функции в этой же точке, взятое со знаком минус. По существу, достаточно одной из функций 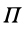
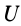
Понятие потенциальной энергии было введено раньше, чем силовая функция. Силовая функция более удобна, так как некоторые формулы, содеражащие эту функцию, не имеют знака минус.
Примеры вычисления силовых функций
Если вычислить силовую функцию, то на основании (82′) будет известна и потенциальная энергия. Вычислим силовые функции однородного поля силы тяжести, силового поля линейной силы упругости и силового поля силы притяжения, действующей по закону Ньютона.
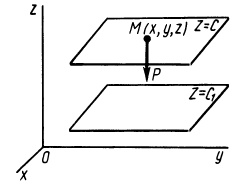
Силовая функция однородного поля силы тяжести. Если ось 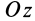
Вычисляя элементарную работу силы 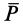
Так как элементарная работа является полным дифференциалом, то силовое поле силы тяжести является потенциальным и силовая функция этого поля определяется по формуле
По формуле (83) определяют силовую функцию однородного поля силы тяжести, т. е. поля, в котором сила тяжести постоянна по модулю и направлению. Уравнение поверхности уровня 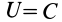
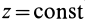
Рис. 76
Силовая функция линейной силы упругости
Для линейной силы упругости (см. рис. 62) имеем:
Следовательно
так как 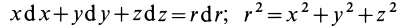
Силовую функцию линейной силы упругости определяют по формуле
Поверхностями уровня 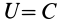
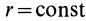
Силовая функция силы притяжения по закону Ньютона
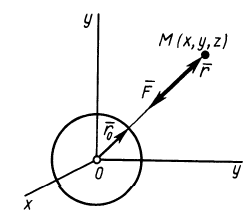
Вычислим силовую функцию поля земного притяжения. Если выбрать начало координат в центре Земли (рис. 77), то сила притяжения точки земным шаром 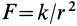
Сила F направлена к центру Земли; следовательно, вводя единичный вектор 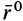
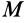
Проецируя силу 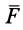
Тогда
так как 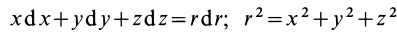
Рис. 77
Таким образом, силовая функция силы притяжения, по закону Ньютона,
Постоянную 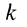
где 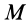
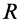
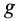
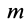
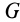
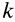
Силовая функция и потенциальная энергия системы
Для механической системы в потенциальном силовом поле можно ввести силовую функцию как функцию, зависящую от координат всех точек системы, т. е. от положения системы в силовом поле. Если система состоит из 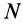
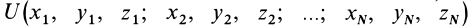
Сумма элементарных работ всех сил, действующих на точки системы, определяется по формуле
или
Таким образом, сумма элементарных работ сил поля, действующих на механическую систему, равна полному дифференциалу от силовой функции. Если вычислить сумму работ, которую совершат силы поля, действующие на механическую систему при перемещении системы из положения 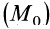
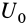
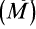
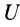
или
Следовательно, сумма работ сил поля, действующих на систему при перемещении системы из одного начального положения в другое, равна разности значений силовой функции в конечном и начальном положениях системы.
Потенциальной энергией системы 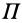
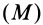
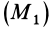
где 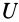
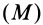
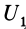
Из (86) — (89) следует:
- Закон сохранения механической энергии
- Принцип Даламбера
- Динамические реакции при вращении твердого тела вокруг неподвижной оси
- Векторное исчисление
- Дифференциальное уравнение движения системы
- Теоремы об изменении количества движения и о движении центра масс
- Теорема об изменении кинетического момента
- Теорема об изменении кинетической энергии
Тема:
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
Лекция
8Д
Потенциальное
силовое поле
-
Потенциальное
силовое поле и силовая функция. -
Потенциальная
энергия. -
Примеры потенциальных
силовых полей. -
Закон сохранения
механической энергии.
-
Потенциальное
силовое поле и силовая функция.
Силовым полем
называют часть пространства, в каждой
точке которого на материальную точку
действует определённая сила, зависящая
от координат точки.
Силовое поле
считают стационарным, если действующие
силы не изменяются с изменением времени.
Если же силы зависят от времени, то
силовое поле является нестационарным.
|
|
Стационарное
Г
`F
Функцию U(x,y,z)
силовой |
|
Основные |
|
|
1) Элементарная |
|
|
2) Полная |
|
|
3) Если
то силу `F |
|
|
Определим |
|
|
Если силовая так как то Аналогично |
|
|
Или rot`F |
|
|
Таким образом, |
2. Потенциальная
энергия
Потенциальной
энергией П
силового поля в точке М
называется работа, которую совершают
силы поля при перемещении материальной
точки М
в начальную точку Мо.
|
|
|
|
То есть потенциальную |
|
|
Потенциальная
|
|
|
Геометрическое
Это уравнение |
3. Примеры
потенциальных силовых полей
Поле
силы тяжести
|
|
Тогда уравнение |
|
Для механической
То |
Поле
линейной силы упругости
|
|
Так как
|
|
Следовательно, |
4. Закон сохранения
механической энергии
Для
материальной точки
Теорема об изменении
кинетической энергии запишется:
Если материальная
точка движется в потенциальном силовом
поле, то
Следовательно
или
где h
– постоянная величина
Обозначая Е
– полную
механическую энергию точки
При движении точки
в потенциальном силовом поле её полная
механическая энергия остаётся постоянной
величиной.
Для
механической системы
Теорему об изменении
кинетической энергии для системы можно
записать
Если система
движется в потенциальном силовом поле,
то
где П – потенциальная
энергия внутренних и внешних сил,
действующих на систему. Следовательно,
Полная механическая
энергия при движении системы в
потенциальном силовом поле внешних
и внутренних сил
является постоянной величиной.
Соседние файлы в папке ЛЕКЦИИ ТЕОРМЕХ
- #
- #
- #
- #
- #
- #
- #
Содержание:
- Теория потенциального силового поля
- Две основные задачи в теории потенциального силового поля
- Эквипотенциальные поверхности. Потенциальная энергия. Теорема об изменении полной механической энергии
- Закон сохранения механической энергии. Методологическое значение законов сохранения в механике
Потенциальное силовое поле – это часть пространства, в каждой точке которого на материальную точку действует сила, зависящая от координат точки и времени
Силовое поле называют стационарным, если силы не зависят явно от времени. Если силы зависят от времени явно то поле – нестационарное.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Теория потенциального силового поля
В общем случае сила, действующая на материальную
точку, может быть функцией координат, скорости и времени. Широкое распространение имеют силы, зависящие только от координат материальной точки, которая движется. Эти силы называют позиционными.
К таким силам относятся силы упругости, гравитации, электрического и магнитного полей и
некоторые другие
Силовым полем называют часть пространства, в котором на материальную точку, которая движется в нем действуют силы, которые зависят от координат и времени, но не зависят от скорости:

Если сила явно не зависит от времени, то силовое поле называют стационарным, если
зависит – нестационарным. Понятие силового поля распространяется также на систему материальных точек. В этом случае силовым полем называют часть пространства, в котором на материальные точки системы действуют силы, зависящие от координат точек системы, которые движутся и от времени:

Силовыми полями являются электрические, магнитные, электромагнитные поля, поле гравитации Земли, упругие среды.
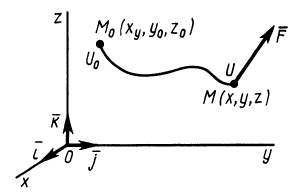
Стационарное силовое поле называют потенциальным, если работа сил поля, которые действуют на материальную точку, не зависит от формы ее траектории, а является однозначной функцией координат начального и конечного положений точки, которая движется. В этом случае каждой точке такого поля соответствует определенное значение работы, которую выполняют силы поля при переходе материальной точки от начала координат в эту точку поля (рис. 18.1). Итак, можно считать 


Физический смысл силовой функции 
заданное.
Для удобства рассуждений исходное положение точки совместим с началом осей
координат
Теорема. Работа силы. действующей на материальную точку во время ее движения в потенциальном поле, равна разности силовых функций в ее конечном и начальном положениях.
Доказательство. Пусть под действием силы материальная точка движется по траектории из исходного положения 

этим положением, через 




(см. рис. 18.1), для вычисления работы 





или

где 
Из соотношения (18.3) имеем:

что и требовалось доказать.
Если рассматривать элементарное перемещение материальной точки по траектории, учитывая, что бесконечно малый прирост функции с точностью до бесконечно малых величин второго порядка малости, совпадает с дифференциалом этой функции, то очевидно, что элементарная работа силы в потенциальном силовом поле равна полному дифференциалу силовой функции, то есть

Итак, приходим к выводу, что только в потенциальном силовом поле элементарная работа является полным дифференциалом некоторой силовой функции, то есть
С доказанной теоремы следует, что во время движения материальной точки по замкнутой траектории в потенциальном силовом поле работа сил на этих траекториях равна нулю.
Две основные задачи в теории потенциального силового поля
Две основные задачи, возникающие в теории потенциального силового поля, состоят в том, чтобы:
1) по заданной силой, которая действует на материальную точку, определить силовую функцию;
2) по известной силовой функцией определить силу.
Первая из этих задач решается просто. Интегрируя (18.5), определяем силовую функцию

с точностью до аддитивной постоянной С.
Чтобы решить вторую задачу, снова воспользуемся соотношением (18.5). при этом элементарную работу выразим по формуле (17.49), а полный дифференциал силовой функции трех переменных 

Поскольку 

Последнее равенство перепишем так:

Поскольку дифференциалы 

Итак, проекции силы равны частным производным от силовой функции по соответствующими координатами.
модуль силы

а ее направление определим по направляющими косинусами:

где 
Очевидно, что

Как известно из векторного вычисления, вектор, проекции которого на оси координат выражаются частных производных от скалярной функции координат по координатами,
называется градиентом этой функции, поэтому:

Если в потенциальном силовом поле движется система 

или в векторной форме

С помощью формул (18.10) легко установить аналогичный критерий существования силовой функции.
Пользуясь свойством вторых смешанных частных производных от силовой функции



или, учитывая выражения (18.10), получим:

В векторной форме условия (18.18) примут вид:

Равенства (18.18) являются необходимыми и достаточными аналитическими условиями существования силовой функции
Пример 1. Проекции силы.
Является ли силовое поле, в котором действует сила, потенциальным?
Решение. Пользуясь аналитическим критерием (18.18), определим частные производные
от проекций силы по соответствующим координата. Имеем 
Итак, рассматриваемое силовое поле не является потенциальным.
Пример 2. Найти такие значения 
Решение. Согласно критерию потенциальности силового поля (18.18), найдем
По анализу частных производных видим, что равенства
возможные только при 

Итак, силовое поле, силы которого удовлетворяют условиям задачи, будет потенциальным только при 
Эквипотенциальные поверхности. Потенциальная энергия. Теорема об изменении полной механической энергии
Эквипотенциальными, или изоповерхностями, или поверхностями уровня называют геометрическое место точек, на котором силовая функция остается постоянной:


Поскольку силовая функция, согласно (18.6), определяется с точностью до произвольного постоянного слагаемого, то за нулевой уровень можно взять любую эквипотенциальную поверхность.
Докажем, что сила, действующая в потенциальном поле, направлена нормально к эквипотенциальным поверхностям в сторону увеличения силовой функции. Это облегчает определение вида эквипотенциальной поверхности.
Поскольку 


тогда 



Введение понятия эквипотенциальной поверхности углубляет физический смысл силовой
функции, которую можно рассматривать как роботу, выполняемую силами потенциального силового поля для перемещения материальной точные, (и системы) с любого положения на нулевой эквипотенциальные поверхности в любое положение на заданной эквипотенциальной поверхности.
Для характеристики свойств .механичного движения в потенциальном силовом поле вводят еще одну функцию. П, которая называется потенциальной энергией материальной точки или системы материальных точек. Потенциальная энергия равна силовой функции со знаком минус:

Итак, потенциальная энергия – это работа, выполняемая силами потенциального поля во время движения материальной точки из заданного положение в ее исходное положение.
Согласно формуле (18.6),

Ha основе равенства (18.5)

Отсюда следует, что

то есть полная работа силы в потенциальном поле равна разности потенциальной энергии в начальном и конечном положениях точки. Воспользовавшись соотношением (18.10) и учитывая (18.21), выразим проекции силы через потенциальную энергию:

В механике рассматривают сумму кинетической Т и потенциальной П энергий, которую называют полной механической энергией

и разницу кинетической и потенциальной энергий, которую называют кинетическим потенциалом или функцией Лагранжа.

Эта функция играет важную роль в аналитической механике. Докажем теорему об изменении полной механической энергии.
Теорема. Прирост полной механической энергии системы материальных точек на
произвольном перемещении равен работе не потенциальных сил на этом перемещении.
Доказательство. Пусть на материальные точки системы действуют потенциальные и не потенциальные силы. Воспользуемся теоремой о изменение кинетической энергии в дифференциальной форме. Эту теорему, с учетом (18.23), можно представить в виде

где 


Интегрируя это равенство, получим

Теорема доказана.
Закон сохранения механической энергии. Методологическое значение законов сохранения в механике
Теорема. Во время движения материальной точки или системы точек в потенциальном
силовом поле полная механическая энергия остается постоянной.
Доказательство. Согласно теореме о изменение кинетической энергии (17.43), имеем




где 
Формула (18.31) выражает закон сохранения механической энергии. Этот закон является частным случаем общего закона сохранения и превращения энергии, установленный в середине XIX в. исследованиями Ю. Майера (1814-1878), Д. Джоуля (1818- 1889), Г. Гельмгольца (1821-1894), У. Ренкина (1820-1872).
На основе закона сохранения механической энергии силы, имеющие потенциал, называются консервативными. Силы, которые не имеют потенциала, то есть силы, которые зависят от скорости движения материальной точки (силы сопротивления среды), называются рассеивающими или диссипативными. Для этих сил условия закона сохранения механической энергии не выполняются, поскольку часть ее переходит в другую форму энергии, например в тепловую, электрическую и др.
Невозможность построения вечного двигателя следует из теоремы об изменении механической энергии, а также из закона сохранения механической энергии.
Энергия является общей мерой различных форм движения материи. Закон сохранения и превращения энергии касается всех процессов, происходят в природе – физических, химических, биологических и других, и заключается в том, что энергия, как общая мера движения материи при преобразовании одной ее формы в другую, не исчезает и не появляется, а переходит в эквивалентных количественных соотношениях.
В законе сохранения механической энергии говорится о превращении кинетической энергии в потенциальную и наоборот. В общем законе сохранения энергии этот результат распространяется на любые формы движения материи – электрическую, тепловую, химическую и др.
Однако не только закон сохранения, но и теорема об изменении полной механической энергии – это отдельные случаи общего закона сохранения и превращения энергии. Действительно, если в соотношении (18.30) работа потенциальных сил положительная 

Еще в конце первой половины XVIII в. М. В. Ломоносов установил один из общих законов природы – закон сохранения материи и движения. «Все встречающиеся в при роде изменения происходят так, что если к чему-либо нечто прибавилось, то это отнимается у чего-то другого. Так, сколько материи прибавляется к какому-нибудь телу, столько же теряется у другого”. Поскольку это общий закон природы, то он распространяется и на правила движения: тело, которое своим толчком побуждает другое тело к движению, столько же теряет от своего движения, сколько сообщает другому, которое оно толкнуло”.
Очевидно, что все закономерности, характеризующие процессы преобразования и сохранения материи и движения в различных формах, с конкретными проявлениями общего закона сохранения материи и движения. В частности, в теоретической механике рассматриваются законы сохранения различных мер механического движения – количества движения, кинетического момента и механической энергии.
Закон сохранения материи и движения имеет огромное научное и методическое значения, поскольку является естественно-научной основой материализма. Утверждая, что материя и движение не создаются и не уничтожаются, что материя, которая движется, способна к различным преобразований, и рассматривая материю в органической связи с движением, общий закон сохранения материи и движения является доказательством единства мира и всеобщности движения. Закон сохранения материи и движения во всех своих конкретных проявлениях является теоретической основой различных расчетов в естествознании и технике; эти расчеты связанные с преобразованием материи и движения из одной в другую.
“Мы не только можем показать преобразования энергии из одной формы в другую, которые
постоянно происходят в природе, – писал Ф. Энгельс, – а даже можем осуществлять их
в лаборатории и промышленности и притом так, что данному количеству энергии в одной форме всегда соответствует определенное количество энергии в какой-то другой форме.
Да, мы можем выразить единицу теплоты в килограмм -метрах, а единицы или любые количества электрической или химической энергии – снова в единицах теплоты, и
наоборот; мы можем так же измерить количество энергии, полученной и потребленной каким ни будь живым организм, и выразить ее в любой единице, например в единицах теплоты”.
Следует отметить, что общий характер закона сохранения массы и энергии четко понимал М. В. Ломоносов еще в 1748 p., что видно из его письма к Л. Эйлеру.
Пример 3. Телу, находящийся на наклонной плоскости, задана начальная скорость 


Решение. Рассмотрим сначала движение тела вверх с исходного положения 1 в конечное
положение 2, которое соответствует остановке тела.
Применяя теорему об изменении кинетической энергии, имеем

где
Работа 


Эта работа равна

где 
Согласно закону Амонтона0Кулона сила трения равна:

где 
В результате уравнение (1) примет вид:

Теперь рассмотрим движение тела вниз из положения 2 в исходное 1.В уравнение (1) в этом случае нужно подставить
Касаемо работы на этом отрезке, то сила тяжести будет выполнять положительную работу, а сила трения- отрицательную, по этому:

С выражений (4) и (5) найдем:

При отсутствии трения 

то есть тело вернулось бы в исходное положение с той же скоростью. Наличие трения приводит к тому, что 


Этот результат естественно согласуется с теоремой об изменении полной энергии системы (18.30).
Действительно, при возвращении тела в исходное положение прирост потенциальной энергии
Остается только прирост кинетической энергии, который определяется работой 
Услуги по теоретической механике:
- Заказать теоретическую механику
- Помощь по теоретической механике
- Заказать контрольную работу по теоретической механике
Учебные лекции:
- Статика
- Система сходящихся сил
- Момент силы
- Пара сил
- Произвольная система сил
- Плоская произвольная система сил
- Трение
- Расчет ферм
- Расчет усилий в стержнях фермы
- Пространственная система сил
- Произвольная пространственная система сил
- Плоская система сходящихся сил
- Пространственная система сходящихся сил
- Равновесие тела под действием пространственной системы сил
- Естественный способ задания движения точки
- Центр параллельных сил
- Параллельные силы
- Система произвольно расположенных сил
- Сосредоточенные силы и распределенные нагрузки
- Кинематика
- Кинематика твердого тела
- Движения твердого тела
- Динамика материальной точки
- Динамика механической системы
- Динамика плоского движения твердого тела
- Динамика относительного движения материальной точки
- Динамика твердого тела
- Кинематика простейших движений твердого тела
- Общее уравнение динамики
- Работа и мощность силы
- Обратная задача динамики
- Поступательное и вращательное движение твердого тела
- Плоскопараллельное (плоское) движение твёрдого тела
- Сферическое движение твёрдого тела
- Движение свободного твердого тела
- Сложное движение твердого тела
- Сложное движение точки
- Плоское движение тела
- Статика твердого тела
- Равновесие составной конструкции
- Равновесие с учетом сил трения
- Центр масс
- Колебания материальной точки
- Относительное движение материальной точки
- Статические инварианты
- Дифференциальные уравнения движения точки под действием центральной силы и их анализ
- Динамика системы материальных точек
- Общие теоремы динамики
- Теорема об изменении кинетической энергии
- Теорема о конечном перемещении плоской фигуры
- Метод кинетостатики
- Вращения твердого тела вокруг неподвижной точки
Потенциальное силовое поле. Силовая функция и потенциальная энергия поля. Поверхности уровня и их свойства.
Свойства поверхностей уровня.
Из лекций:
Силовым полем называют часть пространства в каждой точке которого на материальную точку действует сила зависящая от координат.
Если сила не зависит от времени, то силовое поле называется стационарным, если не зависит – нестационарным.
Силовое поле – потенциальное, если имеется силовая функция U, зависящая от координат.
Например, в декартовой системе координат: U(x,y,z,t)
– потенциальное силовое поле
Вектор-градиент скалярной величины:
Основные свойства U стационарного потенциального силового поля.
Полная работа силы не зависит от пути перемещения.
Полная работа силы поля на каком-либо перемещении равна разности значений силовой функции в конечной и начальной точках перемещения и не зависит от формы траектории (если силовая функция является однозначной) (при нестационарном поле это определение полной работы не действует).
Частный случай: Работа силы потенциального силового поля равна нулю, при перемещении точки по замкнутой траектории.
Силовые линии потенциального силового поля (ПСП) – линии, в каждой точке которых сила направлена по касательной к этой линии.
Потенциальной энергией (П) потенциального силового поля (ПСП) в заданной точке называется работа, которую совершают силы поля при перемещении материальной точки из данной точки в начальную.
П = AMMo = U0 – U = C0 – U = -U
AMMo = U0 – U
Для всех точек U0=const одинаковое.
П = -U + const
Потенциальную энргию какой либо точки ПСП с точностью до константы можно определить как значение U в этой точке со знаком “минус” (-U).
Поверхности уровня – поверхности, все точки которых имеют одинаковые значения силовой функции.
U(x,y,z)=C
Свойства поверхностей уровня:
1) Работа силы равна нулю, если начальные и конечные точки перемещения лежат на одном уровне.
A=U – U0=U – U=0
2) Сила потенциального силового поля (ПСП) всегда перпендикулярна плоскости касательной к поверхности уровня.
3) Сила всегда направлена в сторону возрастания силовой функции.
4) Если поверхности уровня сближаются, то сила возрастает.
A=F1S1=F2S2
Используются технологии uCoz
Центральная сила — сила, линия действия которой при любом положении тела, к которому она приложена, проходит через точку, называемую центром силы (точка 
Примерами центральных сил являются силы тяготения и Кулона, направленные вдоль линии, соединяющей точечные массы или точечные заряды.
Проще всего центральные силы вводятся для физических систем, состоящих из конечного числа объектов, размерами которых можно пренебречь (материальных точек), или, иногда, некоторых эквивалентных им, состоящих из протяжённых объектов с фиксированной внутренней структурой[2]. Распределенные системы, в которых действуют центральные силы, в общем случае[3] не могут быть представлены конечным количеством материальных точек. В случае распределённых систем общим подходом является разбиение их на очень большое (в пределе бесконечное) количество элементов малого (в пределе стремящегося к нулю) размера каждый (которые и рассматриваются как материальные точки), между которыми действуют центральные силы в соответствии с определением, данным выше. Таким образом, в этом случае центральной, собственно, является каждая элементарная сила, а реальная сила является суммой (суперпозицией) таких элементарных сил.
Классическая физика вводит также понятие поля центральной силы для области трёхмерного пространства, в котором действуют центральные силы.
[4]
Рис.1 К определению центральной силы: 
(где M – момент сил, 
свидетельствующее о равенстве нулю момента силы относительно центра силы:
Силовые поля[править | править код]
Этим полям соответствуют кулоновские силы (силы электростатического взаимодействия) и силы гравитационные (силы Всемирного тяготения). Сходство между ними заключается в том, что они могут быть обнаружены во время взаимодействия материальных объектов, причем в случае гравитации свойством, обуславливающим это взаимодействие, является масса, а в случае кулоновского взаимодействия — заряд, этой массой переносимый. Заряды, не связанные с массой, классической физике неизвестны.
Величина, характеризующая интенсивность центрального силового поля, представляет собой вектор, направленный по линии, соединяющей точечный источник и заданную точку поля.
Потенциальные центральные поля[править | править код]
Работа центральной силы[править | править код]
Элементарная работа 
(в общем случае изменяющей свою величину и направление), при перемещении на столь малый отрезок своей траектории, что на нём вектор силы может считаться неизменным, то есть на расстояние 

где 

При перемещении на расстояние от 





Рассматривая движение в декартовой системе координат, центральную силу можно представить в виде геометрической суммы её проекций на координатные оси:

где 


Потенциал поля[править | править код]
Не для всякого поля силы совершаемая ею работа зависит лишь от положения начальной и конечной точек движения. Иными словами, не зависит от формы пути.
Упомянутый интеграл не будет зависеть от формы пути лишь в том случае, если будет существовать некая первообразная функция 
её частные производные будут соответствовать проекциями силы (по существующему обычному соглашению — с точностью до знака):
В этом случае функция 
Но это станет возможным лишь при одновременном выполнении равенств:

Для центральных сил это условие выполняется. Поле, в котором выполнены эти условия, называется безвихревым полем. Поэтому потенциальные поля суть поля безвихревые.[5]
Знак минус в формуле, связывающей потенциальную функцию и силу, определяется желанием отождествить потенциальную функцию с потенциальной энергией[6] (в противном случае можно было бы обойтись без знака минус, что иногда и делается при введении потенциальной функции чисто формально, особенно для векторного поля, не имеющего характера силы).
Связь с потенциальной энергией естественно осуществляется через работу.
Представляется естественным считать, что вектор напряжённости поля направлен ОТ источника поля, (что привычно принимается при описании электростатического поля при взаимодействии одноимённых зарядов[7]) Тогда, зафиксировав точку, находящуюся на расстоянии 

То же можно сказать и в случае, если поле продвинуло тело дальше 
И эти работы может быть названа с точностью до постоянной потенциалом точки: 

Тогда совершённая полем работа будет равна разности потенциалов, взятой со знаком «минус»

Таким образом работа силы на пути из начальной точки в конечную равна изменению потенциальной функции, являющейся скалярной функцией расстояния. В таком случае для каждой точки пути можно с точностью до постоянной величины приписать свой потенциал:
Поле как градиент потенциала[править | править код]
В поле центральной силы её составляющая по данной оси представляет собой скорость изменения потенциальной функции по этой же оси или же градиент функции по заданному направлению.
Для описания изменения потенциальной функции по произвольному направлению в теории поля введён векторный дифференциальный оператор, имеющий вид:
Применяя этот оператор к потенциальной функции получаем, что в данной точке поля сила является (с точностью до знака) градиентом потенциала:
Знак минус, по обычному соглашению присутствующий в этой формуле, связан с тем, чтобы функция U могла быть отождествлена с потенциальной энергией (хотя чисто формально потенциальная функция могла бы быть выбрана и с другим знаком, если такого отождествления не предполагается).
Кулоновское поле[править | править код]
Напряженность кулоновского поля определяется вектором 

или, переходя, к скалярной форме записи:

Здесь 








Кулоновские силы[править | править код]
Объектом действия кулоновского поля является материальное тело, несущее заряд 
В таком случае на него действует механическая (ньютонова) сила электрического происхождения, равная произведению величины заряда на напряжённость поля:
или, с учётом ():


Специфической особенностью кулоновского поля является то, что вектор его напряжённости направлен либо ОТ источника поля в случае совпадение знака заряда источника и объекта взаимодействия, либо направлен К источнику в случае разноимённости зарядов. Это значит, что заряженные материальные тела в первом случае будут испытывать отталкивающую силу, а в противоположном — силу сближающую их.
Ещё одним свойством кулоновского поля является техническая возможность выделить область пространства, в котором оно будет в требуемой степени отсутствовать (клетка Фарадея)
Поле гравитации[править | править код]
В русскоязычной литературе интенсивность поля тяготения называют «ускорением свободного падения» 

Или, переходя к скалярной форме записи:

Здесь 




[9]
Силы гравитации[править | править код]
Объектом действия поля гравитации является материальное тело, имеющее массу 
В таком случае на него действует механическая сила, равная произведению массы 
Тогда, с учётом ():

или, в скалярном представлении:

Специфической особенностью сил гравитации является то, что они всегда являются силами притяжения. Кроме того, силы гравитации всепроникающи, и от них невозможно защититься никаким экраном. Это свойство объединяет силы гравитации с фиктивными силами инерции, существующими в любой неинерциальной системе отсчёта. Подобная аналогия имеет своей основой фундаментальные свойства пространства, изучения которых выходит за рамки классической физики.[10]
Потенциал поля гравитации[править | править код]
Подставляя в (6) значение силы Всемирного тяготения из (20), получаем с учётом того, что работа была совершена против поля:

Таким образом каждой точке гравитационного поля можно с точностью до постоянной присвоить свой потенциал, как:

Движение под действием центральной силы[править | править код]
В общем случае любую траекторию тела, рассматриваемого как материальная точка, можно представить в виде пространственной кривой, состоящей из сопряжённых поворотов в различных плоскостях вокруг мгновенных центров поворота с различными значениями радиуса поворота 
Но кривизна траектории отнюдь не значит, что на тело действует некая сила, для каждого момента являющейся силой центростремительной.
Замечание
Последняя оговорка весьма существенна. Так, например, для земного наблюдателя бомба, сброшенная с летящего равномерно и прямолинейно летательного аппарата движется по параболе. Но для пилота она падает вертикально под действием единственной в данном случае силы тяжести (если не принимать во внимание снос из-за сопротивления воздуха). Никаких сил, вызывающих искривление траектории, здесь нет. Центростремительные силы возникают не потому, что траектория крива, но потому, что они являются выражением реально имеющего место силового взаимодействия движущегося объекта со своим окружением.
Считается, что в центре силы находится источник силы, которым может быть тяготеющая масса, либо электрический заряд в случае, если рассматриваемая сила есть характеристика соответствующего силового поля. Центр силы в общем случае не совпадает с мгновенным центром поворота — точка 
[4]
Как видно на Рис.1 единственная действующая между телами 



При этом


Непосредственно из определения понятий о моментах силы и момента количества движения (момента импульса) следует экспериментально подтверждаемый факт, что скорость изменения момента импульса вращающегося тела 


Однако в поле центральной силы её момент всегда равен нулю (Формула (1)). Из этого непосредственно следует, что при любом движении тела в поле центральной силы момент количества движения движущегося под её действием тела остаётся постоянным:

Но, поскольку постоянство вектора есть одновременно и сохранение его направления в пространстве, то заметаемая при движении тела площадка всегда лежит в одной и той же плоскости. Из этого следует, что любая траектория движения тела под действием центральной силы есть плоская кривая.
Наиболее часто движение тел в гравитационном поле изучают в области небесной механики, где преобладают гравитационные воздействия, и потому изучаемая система взаимодействующих сил может рассматриваться как консервативная система, то есть такая, в которой сохраняется полная энергия тела в виде суммы потенциальной и кинетической энергии.[4]

причём 

Рис.2 К вопросу о зависимости параметров орбиты от полной энергии планеты
Воспользовавшись определением кинетического момента:

А для движения по нормали к траектории:


Тогда выражение для полной энергии тела будет иметь вид:

Введя в рассмотрение эффективный потенциал 

Получаем возможность связать диапазон изменения длины радиус-вектора траектории тела с запасённой им энергией, что представлено на рис.2[13]
Так при минимальной энергии движущегося тела 

Если энергия движения тела больше, скажем 


Наконец, при энергии 

Примечания[править | править код]
- ↑ Центральная сила // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1998. — Т. 5. — С. 425—426. — 760 с. — ISBN 5-85270-101-7.
- ↑ Имеются в виду сферически симметричные объекты (или объекты, достаточно мало отличающиеся от сферически симметричных, так чтобы можно было считать их сферически симметричными в рамках рабочего приближения).
- ↑ По сути — почти в любом случае, кроме описанных выше; даже в таком простом случае, как кулоновское взаимодействие абсолютно твёрдых тел несферической формы с фиксированными на них распределёнными зарядами, обычно невозможно свести вычисление сил к силам между небольшим количеством материальных точек.
- ↑ 1 2 3 Физический энциклопедический словарь/ Гл. ред. А. М. Прохоров. Ред.кол. Д. М. Алексеев, А. М. Бонч-Бруевич,А. С. Боровик-Романов и др. -М.: Сов.энциклопедия, 1983.-323 с.,ил, 2 л.цв.ил.
- ↑ 1 2 Бронштейн И. Н. Семендяев К. А. Справочник по математике. М.: Издательство «Наука» Редакция справочной физико-математической литературы.1964.
- ↑ Поскольку сохраняться должна сумма потенциальной и кинетической энергий, в направлении действия силы (которая может разгонять в этом направлении частицу, увеличивая тем самым её кинетическую энергию) потенциальная энергия убывает.
- ↑ Тамм И. Е. Основы теории электричества
- ↑ ГОСТ 8.417-2002. Единицы величин
- ↑ Ulrich Leute. Physik und ihre Anwendungen in Technik und Umwelt: Carl Hanser Verlag; München, Wien- 2004 ISBN 3-446-22884-5
- ↑ Хайкин, Семён Эммануилович|С. Э. Хайкин. Силы инерции и невесомость. М.,1967 г. Издательство «Наука». Главная редакция физико-математической литературы.
- ↑ Ulrich Leute. Physik und ihre Anwendungen in Technik und Umwelt: Carl Hanser Verlag; München, Wien- 2004 ISBN 3-446-22884-5
- ↑ Klaus Dransfeld, Paul Kleine, Georg Michael Kalvius. Physik I. Oldenbourg Wissenschaftsverlag GmbH 2001 ISBN 3-486-25416-2
- ↑ ‘
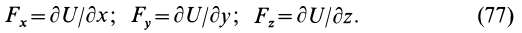
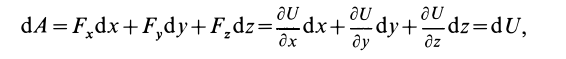

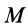

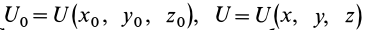
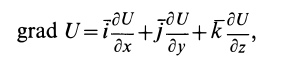
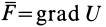
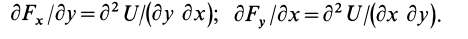
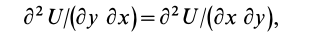
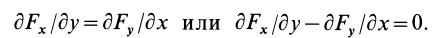
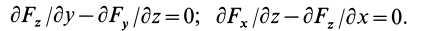
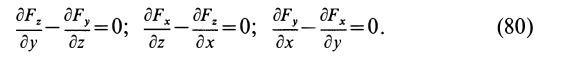
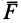
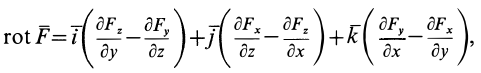

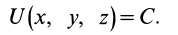
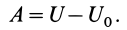
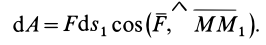
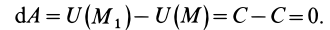
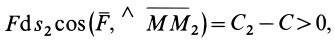
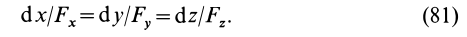
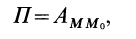
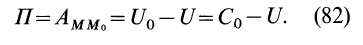
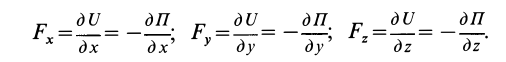
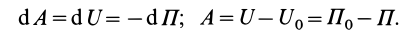

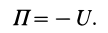
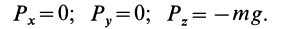
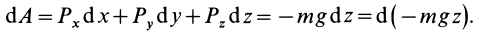
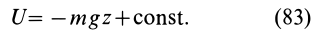
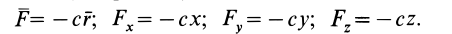
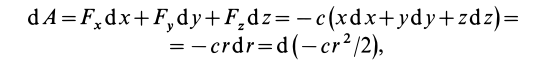
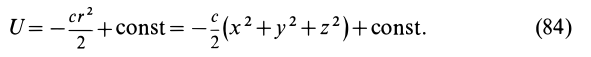
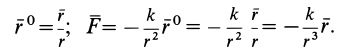
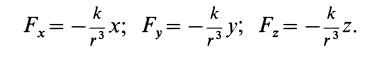
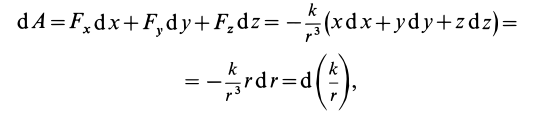
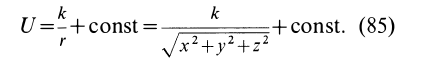
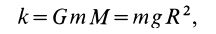
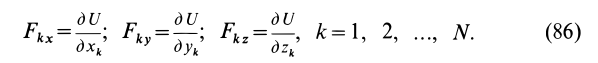
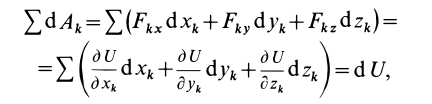

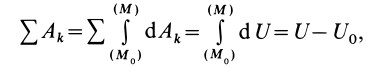

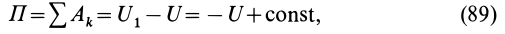

 де
де